偏角法圆曲线放样-
圆曲线的详细测设-偏角法

∆������
������������ ������������
工程测量
道路桥梁工程技术专业教学资源库
工程测量
2 测设数据的计算
道路桥梁工程技术专业教学资源库
测设数据的计算
测设数据的计算
根据几何原理,偏角值∆������等于相应
弧长������������所对的圆心角������������ 的一半,
09
道路中线逐桩坐标计算
道路桥梁工程技术专业教学资源库
C目 录 ONTENTS 1 偏角法的原理 2 测设数据的计算 3 测设方法 4 优缺点及适用性
道路桥梁工程技术专业教学资源库
工程测量
工程测量
1 偏角法的原理
道路桥梁工程技术专业教学资源库
偏角法的原理
偏角法的原理:
以ZY(YZ)点至曲线上任一桩 点������������ 的弦线与切线之间的弦切 角(称为偏角)∆������和弦长������������来确 定������������ 点的位置。
配置水平度盘读数为00°00′ 00″ ,顺时针 转动照准部,拨出各桩点的偏角值,并
������������ ������������
沿视线方向量取对应的弦长,即可得各
桩点。
工程测量
道路桥梁工程技术专业教学资源库
工程测量
4 优缺点及适用性
道路桥梁工程技术专业教学资源库
优点 缺点 适用性
优缺点及适用性
工程测量
• 测设精度较高,实用性较强,灵活性 较好。
• 须保证通视并便于量距。
• 适用于地形较复杂的地区。
道路桥梁工程技术专业教学资源库
总结
工程测量
偏角法是以ZY点或YZ点起,根据加 密桩点的偏角和弦长进行测设。 适用于地形较复杂的地区。
圆曲线的施工放样

偏角法在圆曲线施工放样中的应用随着人们审美观念的改变,人们建造房屋,不局限于四四方方的建筑,把外观设计成各种曲线、流线形,其中最常见的是圆曲线。
圆曲线的施工放样比较复杂,实地放样前需进行一定的内业计算,根据图纸的尺寸及设计要求,确定圆曲线主点的元素,然后,根据工程的特点,从便于施工放样出发,建立不同的坐标方式和计算公式。
现介绍保定高开区某建筑的圆曲线部分的施工放样。
由设计图纸可知,圆曲线的半径R=560m,圆曲线夹角a=28030’,曲线的主点A、B已经在轴线测量时定出,主要是对曲线上加密点的测设,在这里,我主要是采用偏角法测设加密点位。
1、计算测设数据由已知可计算也圆曲线的切线长T和曲线长L,T=Rtga/2=304.06mL=Raл/180=278.546m△3 c△2△1 cφφφA根据平面几何原理,偏角(弦切角)等于所夹弧的圆心角的一半,则偏角△与弦长C的计算公式分别为:△=φ/2C=2Rsinφ/2每隔一定的弧长l测设一点,即把圆弧分成n等份,则l=L/n,那么曲线上各点的偏角为第一点偏角的整数倍,即△1=a/2n=180*l/2ЛR△2=2△1△3=3△1……△n=n△1=a/2加密时,把圆曲线分成20等份,即把半圆分成10等份,则分偏角依次为:a/4=7007’30”△1=0042’45” △2=1025’30”△3=2008’15” △4=2051’00”△5=3033’45” △6=4016’30”△7=4059’15” △8=5042’00”△9=6024’45” △10=7007’30”C=2Rsin△1=13.927m。
2、实测1)在起点A上安置经纬仪,瞄准转折点定出切线方向,并使水平度盘读数为0000’00”。
2)顺时针方向转动照准部,使度盘的读数为0042’45”,并沿视线方向测设13.927m的水平距离,定出圆曲线上的第一点。
3)继续转动照准部,使水平度盘的读数为1025’30”,从第一点测设13.927m的水平距离与视线方向相交,定出第二点。
曲线放样

3. 缓和曲线终点纵坐标
4.内移距p
6.缓和曲线偏角
β0
Y
R
y0 1 0 arctg 0 x0 3
δ0
ZH
P
m y0 x0
b0
7.缓和曲线反偏角
X
5.切垂距 m = x0 Rsinβ0
b0 = β
0
δ
0
21
曲线综合要素计算及主点测设
1、ZH(直缓点) 2、HY (缓圆点)
m
x0
JD
一、曲线主点
T
y0
E0
β
0
HY
p
QZ
YH
L
b0
δ
0
3、QZ (曲中点)
ZH
l0
HZ
4、YH (圆缓点)
R
β
β
0
0
5、HZ (缓直点)
O
22
图 5 加缓和曲线后曲线综合示意图
二、曲线综合要素计算
切线长 : 曲线长 :
α T = (R + p )tg +m 2 L = R (α 2β 0 ) π +2l 0 180°
19
缓和曲线常数
将lp=l0代入缓和曲线方程(2)得:
1.缓和曲线切线角 2. 缓和曲线终点横坐标
l0 180 0 2R 3 l0 x0 l 0 2 40 R 2 4 l0 l0 y0 6 R 336R 3
p =(y0 + Rcosβ0)- R
JD 2
三、圆曲线主点测设
测设步骤如下:
1、仪器设臵在JD上,分别以ZD和JD2定向,自交 点起分别沿视线方向量切线长T,即得ZY和YZ点; 2、后视YZ,拨角(180-α)/2,放样 外矢距E,得QZ.
曲线放样方法

实验:曲线放样实验仪器与工具:全站仪、花杆、测钎、红蓝铅笔、钉子、斧头等实验目的与要求:1、掌握偏角法放样单圆曲线测设过程2、掌握偏角法放样单圆曲线的测设数据的计算方法实验内容与步骤:1、根据给定的曲线半径R=80m和转角α=68°42′,计算其余曲线要素。
2、计算主点里程(其中JD里程为DK3+284.56)直圆(ZY)点里程 = JD里程– T曲中(QZ)点里程 = 直圆(ZY)点里程+ L/2圆直(YZ)点里程 = 曲中(QZ)点里程 + L/23、准备偏角法放样数据里程弧长偏角水平度盘读数备注ZY:QZ:QZ:YZ:4、主点的测设1)将全站仪安置在交点JD对中整平。
2)定ZY点和YZ点。
分别以线路的两个切线方向定向,自交点起分别沿线路的切向方向量取切线长T,定出ZY和YZ点3)定QZ点。
以线路的一个切线方向定向,度盘配置为0º0′0″,顺转望远镜,当水平度盘读数为1(180)2α-时,定出角分线方向,量外矢距E定出曲线中点QZ。
5、偏角法测设曲线细部点2180(sec1)22T R tgRLE Rq T Lααπα=⨯⨯⨯=︒=-=-1)将仪器置于ZY点,盘左位置用望远镜瞄准JD,置水平度盘读数为0º0′0″。
2)检查:瞄准QZ点,其水平度盘读数应为α/4,瞄准YZ点,其水平度盘读数应为α/2,误差应在±1ˊ之内。
若超限,仪器应重新移至JD处,重新测设圆曲线主点。
3)旋转仪器,使度盘读数为第1细部点的偏角,将钢尺零点对准ZY点,将花杆放在钢尺的刻度为弦长C1处,左右移动花杆使其对准望远镜的视线,所得点位即为细部点1。
4)旋转仪器,使度盘读数为第2细部点的偏角,将钢尺零点对准细部点1点,将花杆放在钢尺的刻度为弦长C处,左右移动花杆使其对准望远镜的视线,所得点位即为细部点2。
以后各点,可依此类推。
5)检查:继续进行以后各桩点的测设工作,按上法测至QZ点,检查分弦长度是否与计算值相符,其误差应小于1/1000,即(分弦之差/ 曲线半长)<(1/1000),若误差超限,则应分析原因,重新测设。
偏角法测设平面曲线

偏角法测设铁路平面曲线实习报告实习步骤一、在交点处拨角放样方法 1、放样主点 ① 放样ZH 点在交点处安置全站仪,以任一方向为起始方向,定出一个距离为50.296 m 的点,以该点作为ZH 点 ② 放样QZ 点因为曲中点在曲线中点,偏角为曲线偏角的一半,故偏角为80°,距离为外矢距E=3.276 ③ 放样HZ 点将全站仪相对ZH 点方向反拨160°,距离仍为50.296 m ④ 放样HY 、YH 点首先计算出HY 、YH 点坐标550022220303029.983404020030hy l x l R l =-=-=⨯⨯ 3000.756hy l y Rl ==69.127,7.652yh yh x y ==计算出偏角和距离,放样出这两个主点arctanii jd iy x x δ=-,221()()jd i jd i d x x y y =-+-2、放样加桩点1) 缓和曲线部分坐标计算① 根据桩点里程计算桩点坐标500022300406l x l R l l y Rl ⎧=-⎪⎪⎨⎪=⎪⎩曲线资料 R=200 L0=30 α右=20 ZHDK =335.79T=50.296 L=99.813 E=3.276 q=0.778 x0=29.983 y0=0.75 直缓点里程 ZH0+335.79 第一个十米桩里程为0+345.79010l =,5022101010.0004020030x =-=⨯⨯,30100.028620030y ==⨯⨯ ② 根据坐标计算偏角偏角0000.028arctanarctan 022350.29610.000jd y x x δ︒'''===--由于交点到直缓方向置盘为180度,反拨0223︒''' 度盘读数为18002231795736︒︒︒''''''-=,故将全站仪实现定在该方向③ 计算出距离确定点根据两点之间的距离公式计算出交点到桩点的距离221()()jd i jd i d x x y y =-+-22(50.2969.999)(00.028)40.297=-+-=④ 放样让跑尺员将棱镜立在全站仪视线方向,测出距离,并前后调整,直至距离等于40.297为止,将木桩定在该点。
用偏角法放样圆弧曲线

其 外 轮廓 立 面 做 成 圆弧 形 。 在这 种 情 况 下 ,有 时 受施 工 条 件 的 限 制 而 无 法 采 用 由 圆心 直 接 画弧 的 放 样 方 法 ,可 以使 用 偏 角法 放 样 圆 弧 曲线 。例 如某 建 筑 物平 面 呈半 圆形 ,各项 尺寸 如 图 1 示 ,圆心 处 的建筑 物 已 所
先期 施 工 ,进 行外 围圆弧放 线 。
一
径 ,可以计算其他各个元素。圆曲线的测设分两步进
行 ,先 测设 曲线 上起 控 制 作用 的主 点 ;依 据 主 点再 测
设 曲线上每隔一定距离 的里程桩 ,详细地标顶曲线位
置 。 为 了在 实 地 测 设 圆 曲 线 的 主 点 ,需 要 知 道 切 线
一
一 一| ~、、 一
、
\
长 、. 曲线长及外距 ,这些元素称为主点测设元素 。一
…
√
般情况 下 ,当地形 变 化不 大 ,曲线长 度小 于4m I,测 0E ] , " 设 曲线 的 三个 主 点 已经 能 够满 足设 计 和施 工 的需 要 。
董≮ … - 分 : 4
霉稚 免
碣 嘲 弧《 鞭 ’ 驻 蠢 缱
用偏 角冼放样 围弧 曲 线
河南 许 昌职业技术学院建工 系 张红字
【 摘.要】 实际的 工程 应用 当 中,如 果曲 线较 长 ,地 形 变化 大 ,放 样 曲线 的三 个主 点 已不 能满足 设计 和施 工 的需 在
要 ,还 需要 按 照 一定 的桩 距 ,在 曲 线上 测设 整桩 和 加桩 :这个 过程 称 为 圆 曲线 的详 细测 设 。偏 角 法是进 行 圆弧 曲线
一
2放样数据计算 : . 弦长= R i / ),式 中 R —半 径 , — — 弦 2s n( 2 —
极坐标-偏角法放样及其精度分析111

极坐标--偏角法放样及其精度分析陈兆林[摘要]施工单位在曲线放样时,常用极坐标法和偏角法,本文根据工程实践提出一种改良的放样方法,极坐标—偏角法,并从理论上证明其精度能满足曲线放样的要求。
[关键词]施工测量精度1前言用极坐标法放样时,无须预先放出曲线主点,而直接在控制点上一次性完成,无误差积累,放样精度高,受地形限制小,但放样元素的计算较为繁锁,且对放样工具要求高。
用偏角法放样时,放样元素计算简捷,放样工具要求低,但具有误差累积性,且逐渐增大。
为取二者精华,特提出以下方法:极坐标—偏角法,该法具有放样速度快、精度高的特点。
2放样方法2.1极坐标法首先将曲线上各细部点的坐标计算出来,然后由各点坐标值和已知点坐标进行放样,无需叙述详细过程。
2.2偏角法2.2.1放样元素的计算只需计算出细部点和ZH(HZ)连线与切线方向的偏角及弦长即可.2.2.2放样将仪器架于各主点,除第一点外,采用方向和距离交会的方法放出各细部点位.2.3极坐标—偏角法以圆曲线为例进行讨论2.3.1 放样元素的计算(1)计算各主点(ZY ,QZ ,YZ)的坐标X ZY=X JDn+T*cosα(JD n-JD n-1)Y ZY=Y JDn+T*sinα(JD n-JD n-1)X QZ= X JDn+E*cosα(JD n-Q Z)Y QZ= Y JDn+E*sinα(JD n-Q Z)其中:当路线右偏时α(JD n-Q Z)= α(JD n-JD n-1)-[(180-α)/2]当左偏时:α(JD n-Q Z)= α(JD n-JD n-1)+ [(180-α)/2]X YZ=X JDn+T*cosα(JD n-JD n+1)Y ZY=Y JDn+T*sinα(JD n-JD n+1)(2)按极坐标法计算各主点放样元素(3)按偏角法计算曲线各细部点放样元素(偏角、弦长).2.3.2 放样(1)按极坐标法放样,放出各主点;(2)放样曲线细部点;将仪器架于主点(ZY)采用偏角法放样各细部点(注:百米桩采用极坐标法防止或减小误差累积).3 精度分析3.1 极坐标法点位误差主要以下误差影响M²=m D²+(mβ/ρ*s)2+m e2+s/b(s/b-2cosβ)*m ey2+ζ2其中:M:放样点位误差m D:测距误差 m D=A+B*D 全站仪m D=±(3±2ppm*D) ㎜测距仪m D=±(3㎜+2ppm*D)mβ:放样角度误差: 全站仪:(2″) ±8″测距仪: (2″) ±8″m e :对中误差me=±3㎜m ey:垂直于定向边方向的对中误差 m ey=±3㎜s : 放样边长 s=300mb : 定向边长 b=400mβ: 放样角度,最不利角度: β=180°ζ:标定误差: ζ=±3㎜所以:M=±14.6㎜3.2偏角法细部点相对于曲线主点误差为:(令弦长=弧长)m12=(m s/s*l)2+( mβ/ρ*l)2令 (m s/s*l)2=m t2 ( mβ/ρ*l)2=mμ2则: m12= m t2+ mμ2m22=(m s/s*L)2+( mβ/ρ*2L)2+ m12= m12+m t2+4mμ2m32= m22+m t2+9mμ2即: m n2= m t2* mμ2*m2n-1 (n=1,2……)注: m s/s:钢尺丈量精度(相对). L:桩距所以,采用偏角法时,误差累积严重,故当曲线较长时,应采用分散放样的方法以控制点位误差.3.3极坐标—偏角法应用此法时,百米桩采用极坐标法放样,而非百米桩为偏角法放样,当不考虑对中及标点误差时,则百米桩相对于曲线主点的点位误差m pr为:m pr2=m02+ ( mβ/ρ*s)2非百米桩相对于曲线主点的点位误差:m pr+L2=(m s/s*L)2+[ mβ/ρ*(S+L)]2+ m pr2m2pr+2L=(m s/s*L)2+[ mβ/ρ*(S+L)]2+ m2pr+L………………M2pr+nL=(m s/s*L)2+[ mβ/ρ*(S+L)]2+ m pr+(n-1)L2所以,点位误差和累积限制在100m内.若取曲线长分别为1000m和2000m,则可计算出900m至1000m及1900m和2000m桩相对于曲线主点的点位误差.若:一般钢尺丈量距离取: m s/s=1/1000 L=20mm D=3㎜+2ppm*Dmβ=±8″按交通部颁发的公路路线勘测规范要求,各细部点相对于邻近主点的点位误差:横向:(半径方向)<±10㎝.纵向:(切线方向)≤±(S/1000+0.1).注:S:细部点至主点距离.比较两表可看出,放样精度满足要求.4 结论(1)用极坐标法放样时,能满足要求,但速度较慢;(2)偏角法放样点位误差累积严重,对于长曲线不宜采用;(3)极坐标—偏角法能满足精度要求;(4)对于非全站型仪器的充分利用,并结合山区、半山区的实际测量放样条件比较实用。
圆曲线放样

24
3、将AP1延长一倍到 ,即使AP1=P1P2=C值,与由 量偏距d交会得P2点,且
精选ppt
25
弦线偏距法特点:
方便快捷,但精度较低,放样误差累计快, 因此不宜连续放样多点。在地下工程掘进时, 可以用它指示曲线段的开挖方向。等到巷道 掘进并砌好一定长度后,用导线的方法建立 控制点,然后从控制点出发,按坐标放样放 出曲线上的点。也就是说,本方法仅用来粗 略的指示巷道掘进方向。
E R se 1 c 3 0 s0 e 2 4 c 8 5 1 7 .7(m 7 ) 2 2
D 2 T L 2 6 . 7 8 1 1 . 0 3 2 . 9 3 5 ( m ) 3
精选ppt
10
②计算主点桩里程
JD -)T
ZY +)L
YZ -)L/2
QZ +)D/2 JD
测设分两步进行,先测设圆曲线的三个主点(直圆点 ZY、曲中点QZ和圆直点YZ),再详细测设圆曲线 上按规定桩距各副点(中桩点)。
精选ppt
6
(一)、圆曲线上各点的名称
JD—线路转角点,称为交点 ZY—直线与圆曲线的接点, 称为直圆点 QZ—圆曲线的中点, 称为曲中。 YZ—圆曲线与直线的接点, 称为圆直点。 圆曲线主点—JD、ZY、QZ、YZ 称为圆曲线主点 圆曲线主点测设: 在实地上标定出圆曲线主点的工作。
5.95
1°08′11″
+140 +160
25.95 45.95
4°57′22″ 8°46′33″
QZ K3+181.60
+200
49.14
9°23′06″
+220 +240
YZ K3+249.14
5 圆曲线偏角法放样及中桩坐标计算 - 副本

该线元半径就等于交点至圆心的边长;
3 、依据圆心至交点方位角为计算圆曲线细部点 坐标的基准线,计算线元细部点至基准线的 圆心角,使用半径作为圆心至细部点的边长。 4 、运用坐标正算原理,计算线路曲线范围 待求点P的坐标。
2018/10/24
ZY切线方位角走向148 °01 ′ 37 ″ ,试计算K6+000处中桩坐标?
根据上述学到的知识分别使用偏角弦长计算法和圆心角半径计算法进行计算!
2018/10/24
计算案例
已知线路某圆曲线线元交点桩号K3+984.56 ,圆曲线半径R=180m,该线元转角38°56 ′ 24 ″,试计
算该圆曲线T 、L 、E 曲线要素及主点桩号?
1 、將曲线中桩坐标计算,转换为直线
坐标计算; 2 、通过ZY点切线方位角走向和ZY点
至待求点P的弦切角,进行旋转,
求出ZY点至待求点P的弦长走向方位角; 3 、通过曲线要素计算ZY点至曲线 待求点P的弦长; 4 、运用坐标正算原理,计算线路曲线范围 待求点P的坐标。
2018/10/24
圆曲线中桩坐标计算原理
201749中桩坐标计算04计算原理06案例计算圆曲线圆曲线偏角法放样原理偏角法是以曲线起点或终点至曲线上任一点p的弦长与切线之间的偏角弦切角和弦长来确定曲线范围内放样点p的平面位置
圆曲线偏角法放样 及中桩坐标计算
01
放样原理 放样过程 案例计算 计算原理 计算过程 案例计算
讲解人:刘芳超 讲解时间:2017.4.9
圆心坐标计算:
圆曲线范围 任意一点P计算公式:
2018/10/24
计算案例
圆曲线放样
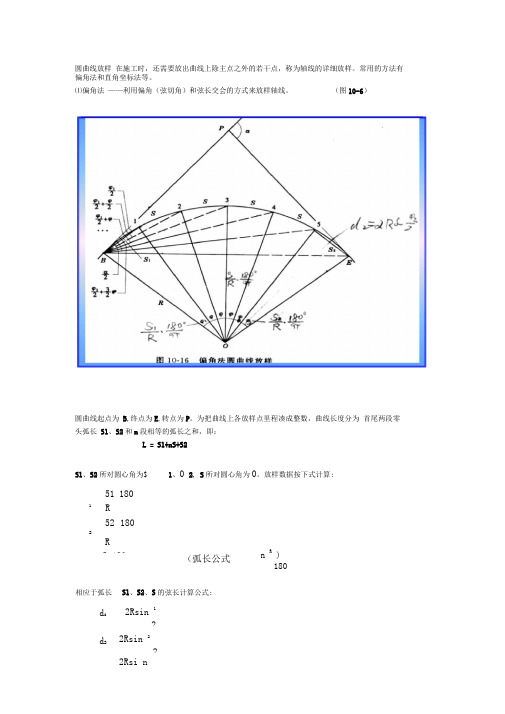
圆曲线放样在施工时,还需要放出曲线上除主点之外的若干点,称为轴线的详细放样。
常用的方法有偏角法和直角坐标法等。
⑴偏角法——利用偏角(弦切角)和弦长交会的方式来放样轴线。
(图10-6)圆曲线起点为B,终点为E,转点为P。
为把曲线上各放样点里程凑成整数,曲线长度分为首尾两段零头弧长S1、S2和n段相等的弧长之和,即:L = S1+nS+S2S1、S2所对圆心角为$ 1、0 2, S所对圆心角为0。
放样数据按下式计算:511801R521802RS 180 (弧长公式n R )180相应于弧长S1、S2、S的弦长计算公式:d i 2Rsin 12d2 2Rsin 222Rsi n圆曲线上各点的偏角(弦切角等于弦长所对圆心角的一半)为:PB1 12PB2 1 22PB3 1 22 21 2PB412 2 21 32 2 2PBE 12 2 +1 2 2放样过程:将仪器安置于圆曲线起点ZY(即B点)上,后视JD(P)点,并将水平度盘置于零,拨角/ PB1,在此方向上量取di,得1点;然后,再拨角/ PB2,钢尺零点对准1 点,以d为半径,摆动钢尺到经纬仪方向线上,得2点;再拨角/ PB3,钢尺零点对准2点,以d为半径,摆动钢尺到经纬仪方向线上,得3点;依此类推…当拨角/ PBE时,视线应当通过圆曲线的终点YZ点。
YZ点至圆曲线上最后一个细部点的距离应为d2。
以此检查放样质量。
⑵直角坐标法一一切线支距法,以曲线起点ZY或终点YZ为坐标原点,以切线为x轴,切线的垂线为y轴,如图10-17所示。
根据坐标xi、yi放样曲线上各细部点。
ZY R图1 0- 1 7 貢角坐标法圆曲线放样设各细部点之间的弧长为S,所对应的圆心角为0,则X Rsin(i )y R[1 cos()]S 180R已知R,又给定S值后,即可求出待放样的细部点坐标。
S值一般为10m、20m、30m等整数值。
放样前可按上述公式计算,将计算得结果列表备用。
交点偏角法测设圆曲线

交点偏角法测设圆曲线在公路、铁路的路线圆曲线测设中,一般是在测设出曲线各主点后,随之在直圆点或圆直点进行圆曲线详细测设。
其测设的方法很多,诸如偏角法、切线支距法、弦线支距法、延弦法等。
这些方法有一个共同点:均是在定测阶段放样出的线路交点处设站,以路线后视方向定向,在实地定出曲线主点,然后将仪器置于曲线主点(一般是在曲线起点)处,以路线交点为后视方向定向,进行圆曲线详细测设。
这些方法在实际施测过程中,由于各种地形条件的限制以及施测方法的特点,可能会出现以下三种情况:(1)在曲线主点处无法设站。
(2)后视方向太近,定向不准。
(3)误差积累较大。
为此,在交点可以设站的情况下,可以采用一种新的测设方法—交点偏角法。
1 线路的转向一般由圆曲线和缓和曲线完成,下面分两种情况介绍图11.1 在圆曲线与两直线段间加设了两段缓和曲线,线路的转向由三段曲线完成如图1所示:ZH(A)为直缓点、HY(B)为缓圆点、YH(C)为圆缓点、HZ(E)为缓直点、QZ(F)为曲中点,它们称为曲线主点;E为外矢距;JD(D)为线路交点;α为线路转角;R为圆曲线半径;O为圆曲线圆心;L为圆曲线上某待测设点i至QZ(F)点间的弧长。
计算公式推导如下:由图1所表示的几何关系,可得出iF所对的圆心角Φ及iF弦长:Φ=180°L/(πR)(1)iF=2Rsin(Φ/2)(2)=2Rsin[90°L/(πR)](3)∵在ΔiOF中,iO=FO (4)∴κ=λ (5)∴λ=180°-Φ/2=90°-90°L/(πR)(6)∴Ψ=180°-λ=90°+90°L/(πR)(7)又根据余弦定理得:Di=(E2+iF2-2E×iF×cosΨ)1/2(8)将(3)、(7)式带入(8)式并化简得:Di=E2+4Rsin2[90°L/(πR)(R+E)](9)又根据正弦定理得:γ=arcsin[iF×sinΨ/(iD)] (10)将(3)、(7)、(9)式带入(10)并化简得:γ=arcsin{R×sin[180°L/(πR)]/Di}(11)∴β=(90°-α2)-γ=(90°-α/2)- arcsin{R×sin[180°L/(πR)]/Di}(12)其中:E=(R+p)sec(α/2)-R(p=L02/(24R),为因加设缓和曲线圆曲线相对于切线的内移量;L0为缓和曲线长度)。
圆曲线(偏角法,切线支距法,极坐标法

圆曲线(偏角法,切线支距法,极坐标法一、圆曲线测量方法(一)偏角法1. 原理- 偏角法是以曲线起点(或终点)至曲线上任一点的弦线与切线之间的弦切角(偏角)和弦长来确定待放点的位置。
- 设圆曲线半径为R,弧长为l,对应的圆心角为φ(弧度制),则φ=(l)/(R)。
偏角δ=(φ)/(2)(因为弦切角等于圆心角的一半)。
2. 计算步骤- 首先计算圆曲线的要素,如切线长T = Rtan(α)/(2)(α为圆曲线的转角),曲线长L = Rα(α为弧度制),外矢距E = R(sec(α)/(2)-1)。
- 然后将曲线按一定的弧长l进行分段(一般为等分段),计算每段弧长对应的偏角δ_i。
- 对于第i段弧长l_i,偏角δ_i=(l_i)/(2R)(弧度制),换算为度分秒形式方便测量。
- 根据起点(或终点)的切线方向,依次拨出偏角δ_i,并量取相应的弦长c_i = 2Rsinδ_i,从而确定曲线上各点的位置。
(二)切线支距法1. 原理- 切线支距法是以曲线起点(或终点)为坐标原点,以切线为x轴,过原点的半径为y轴,建立直角坐标系。
曲线上任一点P的位置用坐标(x,y)表示,根据圆曲线的方程来计算坐标值。
- 圆曲线的方程为y = R(1 - cosφ),x = Rsinφ,其中φ为圆心角(从起点到该点所对应的圆心角)。
2. 计算步骤- 同样先计算圆曲线的要素。
- 将曲线按一定的圆心角Δφ进行分段(一般为等分段)。
- 对于第i段圆心角φ_i = iΔφ,计算该点的坐标x_i = Rsinφ_i,y_i = R(1 - cosφ_i)。
- 根据计算出的坐标值,从原点沿切线方向量取x值,再垂直于切线方向量取y 值,从而确定曲线上各点的位置。
(三)极坐标法1. 原理- 极坐标法是在已知控制点的基础上,以控制点为极点,以某一方向为极轴,通过测量待定点相对于极点的极径ρ和极角θ来确定待定点的位置。
- 在圆曲线测量中,一般以曲线起点(或终点)附近的控制点为极点,以切线方向为极轴方向。
偏角法在曲线坐标计算中的应用

偏角法在曲线坐标计算中的应用摘要:曲线计算是线路坐标计算中的一个重点和难点,目前我们常使用的坐标计算方法是切线支距法。
偏角法是利用偏向角和距离放样的一种方法,结合坐标计算的一些特性推导出坐标计算公式,这样能够更快、更准的计算出施工放样坐标来,同时也是一种检测坐标计算的方法。
关键词:偏角法曲线计算圆曲线缓和曲线随着科技的飞速发展,测量仪器也发生了很大的变化。
随着经纬仪慢慢淘汰,全站仪、gps等测量仪器逐渐走进了我们的施工中,原来角度和距离的计算也就慢慢变成了坐标的计算。
偏角法是角度和距离放样的一种手段,但是将偏角法与坐标计算的一些特性进行结合我们就能推导出一种直接计算坐标的方法。
下面我们将具体公式的进行推导:(1)缓和曲线如图所示:曲线为缓和曲线(中国目前采用的缓和曲线的线性为回旋曲线,回旋曲线的曲率半径与曲线长度乘积为固定常熟ρl=C,其特点是起点与直线相连(ZH点或HZ点),曲率半径ρ→∞,缓和曲线终点与园曲线相连(HY点或YH点),曲率半径最小ρ=R(R为圆曲线半径)),缓和曲线长度为ls,圆曲线半径为R,JD坐标为(XJD,YJD),切线长为T,ZH(HZ)点切线方位角为A1(弧度单位),P点为缓和曲线上的任意一点,该点至曲线起点的弧长为,P点切线与起点的切线夹角为β,求P点的坐标(该坐标即为在施工坐标系中的坐标)当ρ=R时,有= s,则C=R s ,这样就有…………………………①(以下所有角度均为弧度表示)在P点取微分弧段d ,所对应的偏角为dβ,d 产生坐标增量dx,dy。
则有(将①式代入求的)两边积分得(所求β为弧度值,若要化成角度还需乘上)…②若令,则(此时β为YH(HY)点偏角)因为已知条件有A1,即可求出P点的切线方位角(ζ为转向符号,当为左偏时为-1,右偏时为+1)d 产生了坐标增量(dx,dy),在直角三角形中有…………………………………………………………………………③将③式中的cosβ,sinβ按照泰勒级数展开可得………………………………………………④将④代入③中并积分得(因为是多项式,一般计算取前两项即可)…………………………………………………………………⑤求出x,y后即可求出P点到ZH(HZ)点的直线距离,及P点的弦长,……⑥,若令P点的弦线与ZH点的夹角为η,当η很小时,根据极限的定义,可知sinη= ……⑦则可求出缓和曲线上任意点的弦线方位角(ζ为转向符号,当为左偏时为-1,右偏时为+1)将⑤⑥⑦三式合并即可求出缓和曲线的弦长公式………………⑧已知JD的坐标和A1、T即可求出ZH(HZ)点的坐标公计算出了ZH(HZ)点的坐标之后即可求出缓和曲线上任意点的坐标:第一缓和曲线:…………………………⑨第二缓和曲线:………………………⑩(A1是由ZH点指向JD,A2是由JD点指向HZ点)(2)圆曲线当我们在缓和曲线阶段计算至HY(YH)点的时候,我们可以计算出HY(YH)的坐标同时也能计算出HY(YH)点的切线方位角,根据圆曲线的特性和在缓和曲线中我们推算坐标的思路,我们就可以直接写出公式。
偏角法圆曲线放样-

铁路隧道施工测量——偏角法圆曲线放样摘要测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
两者各有长短,只有结合使用,才能发挥出最大的工作效率。
关键词铁路隧道测量圆曲线偏角法测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
1偏角法原理已知圆曲线上A、B两点位置及AB弧长,也知道BC弧长,放样C点位置。
如图1所示:切线切线图1AB6 1=ZBOD=arcsin通过图1不难得出:科技论文一铁路隧道施工测量在圆曲线半径足够大的情况下,我们用弧长代替弦长,即用弧长AB代替线段AB。
皿一,°.弧长AB贝|3 1=ZBOD=arcsin ------2 R同样地,我们可以推出弧长BC6 2=arcsln -------2 R在实际施工放样中,A、B两点是我们事先埋设的导线控制点(在线路中线上),C点是我们需要样的里程的中点,弧长AB变成了A、B两点的里程差,弧长BC变成了8、C两点的里程差。
经纬仪架设于B点,后视A点,如果曲线是右曲线,照准部顺时针拨6= 6 1+ 6 2+180°,如果曲线是左曲线,照准部逆时针拨6= 6 1+ 6 2+180°,仪器望远镜十字划丝即对准C点方向,C点的里程用钢尺拉即可。
2偏角法误差分析在以上原理论述中提到的用弧长代替弦长、用钢尺拉放样位置里程以及要求A、B两点都在曲线中线上都有可能产生误差,误差有多大呢,我们分析一下。
2.1里程代替距离误差分析在上述中,弧长代替弦长前提是半径足够大的情况下,就一般情况来说,产生的误差有多大呢?福厦铁路客运专线一般的曲线半径为4500米,假设后视距离100米,前视距离50米,用46表示偏角误差。
简述偏角法放样细部点操作流程

简述偏角法放样细部点操作流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!偏角法放样细部点操作流程如下:1. 准备工作- 收集相关资料:包括设计图纸、施工说明、现场实际情况等。
曲线放样PPT课件

x0
5.切垂距 m = x0 Rsinβ0
δ0 b0
y0
7.缓和曲线反偏角
X
b0
=
β 0
δ0
20
第20页/共57页
曲线综合要素计算及主点测设
一、曲线主点
1、ZH(直缓点) 2、HY (缓圆点) 3、QZ (曲中点)
T x0
m
p
ZH
l0
JD
y0
E0
QZ
HY L
β0
YH b0
δ0
HZ
4、YH (圆缓点) 5、HZ (缓直点)
1、仪器设置在JD上,分别以ZD和JD2定向,自交 点起分别沿视线方向量切线长T,即得ZY和YZ点; 2、后视YZ,拨角(180-α)/2,放样
外矢距E,得QZ.
E
JD 1
(180-α)/2
QZ
ZY 1
YZ
1
ZD
ZY
2
YZ 2
JD
注意:主点放样后,要用木桩标定点位,2并注明里程。
图 5 2 主第点10里页/共程5推7页算
设整米加桩。
第29页/共57页
29
正拨与反拨 若切线方向的水平度盘读数为0°00′00″
正拨: 平盘读数 = 偏角值 反拨: 平盘读数=360°- 偏角值。
3
c3
2
正拨
P
P
反拨
c2
δp,3
c1
1 δp,2
δp,1
30
第30页/共57页
二、偏角计算
j
1.圆曲线偏角
i δi,j
R
δi , j
= li , j 2R
5.在始切线上的垂
第五章 曲线放样

第四章 曲线放样第一节 概 述各种线路中采用的曲线有:圆曲线、缓和曲线、回头曲线和复曲线。
圆曲线:是一种以R 半径为定数的曲线;缓和曲线:是一种曲率半径按一定规律变化(由大到小或由小到大)的曲线;综合曲线:由缓和曲线和圆曲线组成的曲线通常称为综合曲线。
回头曲线: 线路的转向角接近0180<α<0360时,称为回头曲线。
复曲线:在一条曲线上采用不同半径的圆曲线组成的曲线。
竖曲线:按定点的位置可分为凸形竖曲线和凹形竖曲线,按性质可分为圆曲线型竖曲线和抛物线型竖曲线。
由于受地面自然坡度的影响,线路在立面内的坡度也要发生变化,当相邻两个地段的坡度代数差超过规定的限度时,在变坡点处必须采用曲线连接这种设置在竖直面内的曲线称为竖曲线。
第二节 圆曲线的放样测设曲线时,要根据线路的转向角和曲线半径计算曲线的元素,先测出曲线的起点和终点,然后进行曲线的详细测设。
一、圆曲线元素计算圆曲线的起点以ZY 表示;圆曲线的中点以QZ 表示;圆曲线的终点用YZ 表示;交点以JD 表示(以上均为汉语拼音的头一个字母),称为圆曲线主点。
圆曲线元素包括交点偏角α,曲线半径R ,切线长T ,曲线长L ,曲线外矢距0E 及切曲差q 。
其函数关系为: 2αtgR T ⋅=ρα1⋅⋅=R L)12(sec0-=αR E ; L T q -=2实际工作中转向角α是用经纬仪实测得到的,半径R 是根据线路等级和地形条件由设计给定的。
例一: 某线路交点5JD 的转向角4002520'''=α,半径400=R 米,试求:圆曲线元素。
解: 根据公式: 2αtgR T ⋅==196.54米)12(sec0-=αR E =45.68米ρα1⋅⋅=R L =365.36米L T q -=2=27.72米二、圆曲线主点的里程计算依据交点的里程,根据切线长T 和曲线长L 计算曲线主点的里程。
上例中交点的里程桩号为37.8131+Dh ,求曲线主点的里程,步骤如下:为了对整个计算进行检核,曲线终点的里程可用下列方法求得,结果应该相同。
工程测量课件平面曲线的放样方法

H
21
7.4 平面曲线的放样方法
小结: 1、曲线主要点的测设方法;
2、曲线的详细测设方法(极坐标法、坐标法、偏角法、 切线支距法)。
本章目录
H
22
退出
下一节
感谢下 载
H
23
感谢下 载
H
24
(二)有缓和曲线的圆曲线主要点的测设 其他平面曲线的主要点测设与上述测设方法基本一致,在此 不在赘述。 若在测设平面曲线时采用极坐标法或坐标法,也可按本章第 三节中介绍的曲线坐标计算的方法,计算出主要点和细部点在测 量坐标系中的坐标,把主要点和细部点一并测设,不再细分之。
H
7
7.4 平面曲线的放样方法
(三)偏角法 闭合差及其处理
闭合差的允许值是分纵向(沿线路方向)闭合差fx与横向 (沿曲线半径方向)闭合差fy来考虑的。
若纵向闭合差fx小于1/2000、横向闭合差fy小于10cm时,可根 据曲线上各点到ZH点(或HZ点)的距离,按长度比例进行分配。
用偏角法测设曲线的计算和操作方H法都比较简单、灵活,19 且 可以自行闭合,自行检核,故应用比较广泛。
的半径R、线路转向角α及缓和 曲线的长度l0,确定曲线的要素 T、E、L、q。
缓和曲线的切线角: 0
l0 2R
切垂距:m
l0 2
l
3 0
240 R
2
圆曲线内移值:p
l
2 0
24 R
切线长:T 曲线长: L
m R p tan R a 2 0
180
2
2
l
0
外矢距: H
7.4 平面曲线的放样方法
二、曲线的详细测设方法
(四)切线支距法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铁 路 隧 道 施 工 测 量——偏角法圆曲线放样摘 要 测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
两者各有长短,只有结合使用,才能发挥出最大的工作效率。
关键词 铁路隧道 测量 圆曲线 偏角法测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
1偏角法原理已知圆曲线上A 、B 两点位置及AB 弧长,也知道BC 弧长,放样C 点位置。
如图1所示:切线切线δ2δ1C圆心(O )BDA图1通过图1不难得出:δ1=∠BOD=arcsinRAB2在圆曲线半径足够大的情况下,我们用弧长代替弦长,即用弧长AB 代替线段AB 。
则δ1=∠BOD=arcsinRAB2弧长 同样地,我们可以推出δ2=arcsinRBC2弧长 在实际施工放样中,A 、B 两点是我们事先埋设的导线控制点(在线路中线上),C 点是我们需要样的里程的中点,弧长AB 变成了A 、B 两点的里程差,弧长BC 变成了B 、C 两点的里程差。
经纬仪架设于B 点,后视A 点,如果曲线是右曲线,照准部顺时针拨δ=δ1+δ2+180°,如果曲线是左曲线,照准部逆时针拨δ=δ1+δ2+180°,仪器望远镜十字划丝即对准C 点方向,C 点的里程用钢尺拉即可。
2偏角法误差分析在以上原理论述中提到的用弧长代替弦长、用钢尺拉放样位置里程以及要求A 、B 两点都在曲线中线上都有可能产生误差,误差有多大呢,我们分析一下。
2.1里程代替距离误差分析在上述中,弧长代替弦长前提是半径足够大的情况下,就一般情况来说,产生的误差有多大呢?福厦铁路客运专线一般的曲线半径为4500米,假设后视距离100米,前视距离50米,用△δ表示偏角误差。
则 △δ1= arcsinR AB 2弧长- arcsin R AB2弦长, △δ2= arcsinR BC 2弧长- arcsin RBC2弦长 弦长AB=100m ,则弧长AB=100.0020577m 则△δ1=1.31×10-5。
弦长BC=50m ,则弧长AB=50.00025721m则△δ2=1.47×10-6°,△δ=△δ1+△δ2=1.47×10-5。
引起的中线偏移sin △δ×50m=1.28×10-5m 。
2.2用钢尺拉里程误差分析用钢尺拉C 点里程,在实际操作中,很难做到没有误差,如果前视距离50m ,C 点的里程从B 点用钢尺拉误差应该不会超过50cm ,我们放宽一点,里程误差按照1m 进行计算。
同样假设后视距离100米,实际前视距离50米,测量前视距离为51m ,曲线半径为4500米,用△δ表示偏角误差,E 表示引起的中线偏移。
C C'E△δ2δ2'Bδ2切线图2如图2所示,引起的偏角误差 △δ=△δ2=δ2’-δ2= arcsinRBC 2'- arcsin R BC 2= arcsin 2450051⨯-arcsin 2450050⨯=6.37×10-3。
引起的中线偏移E=sin △δ×50m=5.56×10-3m 2.3 A 、B 点偏离中线误差分析要求A 、B 两点完全在线路中线上,我们实际操作过程中也是很难做到丝毫不差的,同样假设后视距离100米,前视距离50米曲线半径为4500米,用△δ表示偏角误差,E 表示引起的中线偏移。
2.3.1假设A 点不在线路中线上偏移1cm ,如图3所示△δ2δ2δ2'切线BA'A1cm图3△δ=δ1’-δ1=AB 01.0×π︒180=0°0’20.7” E= E=sin △δ×50m=5.02×10-3m(2)假设B 点不在线路中线上,偏移1cm ,如图4所示θE1cmC'CB'BA图4图中∠ABC=∠AB ’C ’可认为ABC 组合体以A 点为旋转轴顺时针旋转θ角,就到了AB ’C ’位置。
θ=AB 01.0×π︒180=10001.0×π︒180 E=︒360θ×AC ×2π=︒360θ×150×2π=1.5×10-2m以上可以看出,多中可能性引起的误差中,B 点中线位置偏移引起的误差最大,所以我们在埋设B 点的时候要用全站仪精测,在B 点假设仪器对中也要非常精确,把B 点的误差控制在2mm 范围内,埋设的点位要注意保护,避免机械在上面碾压造成点偏位,同时埋设的点要经常复测,如有过大偏移时则不能继续使用。
话说回来,即便中线有1~2公分误差,在隧道早期施工中也是允许的,例如隧道的开挖或初期支护测量。
在后期施工中(仰拱施工后)A 点、B 点的埋设做到精确也相对容易。
其它因素引起的误差都是可以忽略的。
3偏角法实际应用3.1福厦铁路客运专线站前工程Ⅲ标段坑山隧道,整个隧道位于R=4500m 的圆曲线上,线路为左曲线。
实际施工是从隧道出口(既大里程往小里程)施工,分别在里程DIK178+210和DIK178+142埋设线路中点,放样DIK178+098处线路中线,可按如下步骤进行:仪器:电子经纬仪3.1.1在142点架设仪器(点号用里程暂替); 3.1.2后视210点; 3.1.3水平度盘归零;3.1.4照准部顺时针旋转180°42’46.9”;(如图5)δ1=arcsin45002142210⨯-=0°25’58.5”δ2=arcsin 4500298142⨯-=0°16’48.4”δ=δ1+δ2+180°=180°42’46.9”3.1.5打开激光,通过调整竖直角,激光所指位置在098处打点。
δ1δ2DIK178+210DIK178+142DIK178+098图53.2 A点不在线路中线上也是可以的,如图六所示,A点不在线路中线上,那么δ1就不能按照偏角法的公式进行计算,但是,我们仍然可以按照偏角法来放样。
(如图6所示)δ1实际上是后视方位角(BA的方位角)和B点处切线方位角的夹角。
计算BA的方位角可以先用全站仪把A、B两点实际坐标测出来,再进行计算。
计算B点处切线方位角,可将B点里程前推100mDEδ1δ2BC切线A图6(D点),后推100m(E点),ED的方位角便等于B点处的切线方位角。
E、D的坐标可由曲线要素求出。
两者相减便等于δ1,要注意δ1的正负,图六所示δ1便为负值。
看起来计算比较繁,实际上也是一劳永逸,在接下来的一段时期中,δ1是固定不变的,而且A点不在中线埋设更容易保护。
3.3后视点转移我们在测量的时候也许有这样的经历,后视点位置选的不好,后视经常被东西挡住或者因为施工A 点要被破坏掉。
也许刚做好的A点就面临夭折的危险,重新埋设A点再计算δ1又比较麻烦。
我也遇到了这样的事情,因为隧道下台阶开挖,埋设于上台阶的A点眼看就要被破坏了,我是这样做的(如图7所示)。
选择一个好的地方做A’点,建议做在初期支护后的拱墙上,可以砸个钉子,选择这个位置有几个好处:3.3.1位置比较高,不容易被挡住;3.3.2比较安全,免遭被机械碾压的危险;3.3.3拱墙有喷射混凝土,机构本身比较稳定。
在B点架仪器,分别读出BA’、BA水平角,计算出BA’、BA水平角度差(θ),如图中所示情况δ=δ1+δ2+180°-θ, θ前的正、负号看情况决定。
AA'Bδ1δ1'θ切线图74偏角法优缺点4.1仪器要求不高选择使用偏角法放样也是迫不得已,如果当时有一台全站仪的话,我可能也不会去研究使用偏角法放样,因为手头上只有一台电子经纬仪。
全站仪最便宜的也要两、三万块钱,而一台经纬仪只要花几千块就可以买到,相比之下确实节省了一部分开支。
4.2放样速度快隧道施工每个循环都要测量放样,如果放样时间过长就会影响整个循环。
偏角法放样方便快捷,仪器架好以后拨一个角就可以了,加上用水平仪测高程的时间,每个循环放样20分钟到半个小时就可以搞定。
4.3不易出错在使用偏角法放样中,偏角的大小仅和放样里程有关,而且里程即便有点误差也没有关系,不像坐标法那样,放样需要输入坐标,那么多数字摁来摁去最容易出错。
用坐标法放样,里程稍微取大一点,计算出来的坐标可能就跑到掌子面里面去了,还要再调整里程,重新计算,来来回回浪费了不少时间。
4.4偏角法适用范围比较狭窄偏角法只能放养线路中线,边线需要用尺从中线往两侧拉,不能放养具体点位,决定了它不能完全取代其它方法,它最适用于隧道开挖等这种不需要放样具体点位的施工。
偏角法需要坐标法配合放样导线控制点,决定了它对坐标法以及全站仪有很强的依赖性。
5结束语综合上述,偏角法是一种放样速度非常快捷,不容易出错,仅需一台经纬仪就可以使用的放样方法。
它要求曲线半径足够大,适用于铁路隧道施工。
它使用范围的局限性决定了它不能完全取代其它方法。
它同我们经常使用的坐标法相较,两者各有长短,结合使用,才能发挥出最大的工作效率,这种方法在福厦铁路客运专线的隧道施工中被广泛应用。
