东南大学电磁场与电磁波6.4-6.8
东南大学电磁场与电磁波3.4—3.5
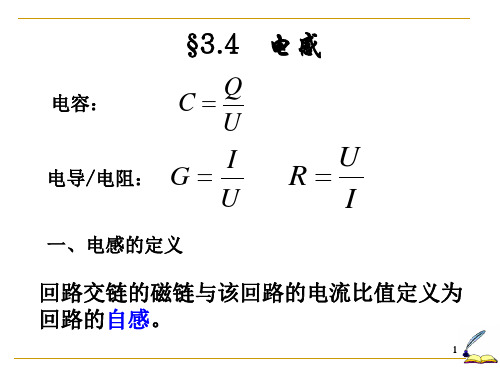
0 I d 0 d 0 dzdR 2 R
R2 I 1 1 0 R2 0 Le0 dz dR ln 0 R 1 2 R I I 2 R1
15 15
e0
总电感为 L Li1 Li 2 Le0
后面讨论时变电磁场时,同轴线的内外导体可以当作理想导电体, 因而内外导电体中不可能存在时变电磁场。因此,当同轴线工作于时 变电磁场时,内外导体中的磁通皆可忽略,只须考虑内外导体之间的 磁通,同轴线单位长度内的电感等于外电感,即
' e " e
21 0 RAD RBC M ln I1 2 RAC RBD
1)若回路方向相反,互感会改变吗? 它反映了什么物理意义?
18 18
2)铁板放在两线圈的下方,互感是增加了,还是减少 了?为什么?如何计算?
)置于两对线圈的下方 3) 铁板插入两线圈之间后,互感是增加还是减少? 为什么?自感是否增加?
Li 2
i 2
I
d I
i2
2 2 R3 I 1 1 R R 2 2 dz ( 3 ) dR 2 2 R2 2 R I 0 R3 R2
14 14
2 2 2 2 2 R3 R R ( R R 2 3 2 3 2 3 2) ) ln 故 ( 2 2 2 2 2 2 2 R3 R2 R2 2 ( R3 R2 ) 8 ( R3 R2 )
0 I DR ln R
Le 0
0 DR 0 I D ln ln( ) I R R
e 0
用矢量磁位计算互感和自感 如图所示两个线形回路,设 导线和周围媒质的磁导率都 是 0 。回路通有电流,其对 外作用中心可看成是在导线 的几何中心上。
东南大学《电磁场与电磁波》课件10

a
2k z l 2 p p kz l
12/24/2012
m kx , a
n ky b
Lab of Photonics & Optical Communications SEU, China
分布式谐振腔等效电路
k k k
2 2 x 2 y 2
2 z 2 2
Q
G0
谐振腔研究的思路框图
Lab of Photonics & Optical Communications SEU, China 12/24/2012
一、谐振频率0
谐振腔中谐振频率 0 ( 或 f0) 和谐振 波长 0 是最基本参数,但是要注意 0 是 不变量,而0则与媒质r0有关。 在一个封闭系统中,电能与磁能相 等称之为谐振。谐振腔的规律同样服从 Maxwell 方程组,可导出 Helmholtz 方程。
- 差别:电磁辐射,空间电磁振荡源
Lab of Photonics & Optical Communications SEU, China
12/24/2012
Lab of Photonics & Optical Communications SEU, China
12/24/2012
Lab of Photonics & Optical Communications SEU, China
1 1 2al 2 , 101 2 a l a2 l 2
12/24/2012
Lab of Photonics & Optical Communications SEU, China
已知,金属波导TE10模中
电磁场与电磁波(第三版)课后答案第6章

第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
电磁场与电磁波基础教程(第2版)习题解答

《电磁场与电磁波基础教程》(第2版)习题解答第1章1.1 解:(1)==A B=C(2))))23452A x y zB y zC x z ==+-=+=-,,;A a a a a a -a a a a a A(3)()()+2431223x y z x y z =+-+-+=--=+;A B a a a a a a A B (4)()()23411x y z y z ⋅=+-⋅-+=-;A B a a a a a (5)()()234104x y z y z x y z ⨯=+-⋅-+=---;A B a a a a a a a a (6)()()()1045242x y z x z ⨯⋅=-++⋅-=-;A B C a a a a a(7)()()()x 2104522405x y z x z y ⨯⨯=-++⨯-=-+A B C a a a a a a a a 。
1.2解:cos 68.56θθ⋅===︒;A B A BA 在B 上的投影cos 1.37B A θ===A ;B 在A 上的投影cos 3.21A B θ===B 。
1.3 解:()()()()()()()4264280⋅=-++-=正交A B 。
1.4 解:1110x x y y z z x y y z z y ⋅=⋅=⋅=⋅=⋅=⋅=,,;;a a a a a a a a a a a a 0x x y y z z ⨯=⨯=⨯=;a a a a a a x y z y z x z x y ⨯=⨯=⨯=;,a a a a a a a a a 。
1.5 解:(1)111000z z z z ρρϕϕρϕϕρ⋅=⋅=⋅=⋅=⋅=⋅=,,;,,a a a a a a a a a a a a ;000z z z z z ρρϕϕρϕϕρρϕ⨯=⨯=⨯=⨯=⨯=⨯=,,;,,a a a a a a a a a a a a a a a 。
电磁场与电磁波(第4版)第6章部分习题参考解答

G
G E(z)
G
=
eGx100e− j(β z+90D )
+
G ey
200e− jβ z
由 ∇ × E = − jωμ0H 得
G H
(z)
=
−
1 jωμ0
∇×
G E(z)
=
−
1 jωμ0
⎡ ⎢
G ex
⎢∂
⎢ ⎢
∂x
G ey ∂ ∂y
G ez ∂ ∂zຫໍສະໝຸດ ⎤ ⎥ ⎥ ⎥ ⎥=
−
1 jωμ0
G (−ex
∂Ey ∂z
G (1) 电场 E = 0 的位置;(2) 聚苯乙烯中 Emax 和 Hmax 的比值。
解:(1)
令
z
'
=
z
−
0.82
,设电场振动方向为
G ex
,则在聚苯乙烯中的电场为
G E1 ( z
')
=
G Ei
(z
')
+
G Er
(z
')
=
G −ex
j2Eim
sin
β
z
'
G 故 E1(z ') = 0 的位置为 β z ' = −nπ, (n = 0,1, 2,")
G ex
G × Ei (x)
G = ez
1
− j2 πx
e3
12π
A/m
G
G
(2) 反射波电场 Er 和磁场 Hr 的复矢量分别为
G Er (x) =
G
j2 πx
−ey10e 3
G V/m , Hr (x)
电磁场与电磁波理论(第二版)(徐立勤,曹伟)第6章习题解答

第6章习题解答6.1 已知空气中存在电磁波的电场强度为 ()80cos 6π102πy E e E t z =⨯+V /m试问:此波是否为均匀平面波?传播方向是什么?求此波的频率、波长、相速以及对应的磁场强度H 。
解:均匀平面波是指在与电磁波传播方向相垂直的无限大平面上场强幅度、相位和方向均相同的电磁波。
电场强度瞬时式可以写成复矢量j 0ekzy E e E -=。
该式的电场幅度为0E ,相位和方向均不变,且0z E e ⋅=⇒z E e ⊥,此波为均匀平面波。
传播方向为沿着z -方向。
由时间相位86π10t t ω=⨯ ⇒ 86π10ω=⨯ 波的频率Hz 1038⨯=f 波数2πk =波长2π 1 m k λ== 相速p 310 m/s v kω==⨯ 由于是均匀平面波,因此磁场为j 0w w1() e kz z x E H e E e Z Z -=-⨯= 6.2 有一频率为600MHz 的均匀平面波在无界理想介质(r r 4,1εμ==)中沿x +方向传播。
已知电场只有y 分量,初相位为零,且010t t ==s 时,1x =m 处的电场强度值为800kV/m 。
试写出E 和H 的瞬时表达式。
解:根据题意,角频率812π10ω=⨯,r r 0028πk cωωεμεμεμ====,因此 80cos(12π108π)y E e E t x =⨯-由s 10=t ,m 1=x 处的电场强度值为kV /m 800,可以得到kV/m 8000=E8800cos(12π108π) kV/m y E e t x =⨯-根据电场的瞬时表达式可以写出电场的复矢量为j8π800e kV/m x y E e -=波阻抗为()0r w r 060π ΩZ μμμεεε===。
因此磁场强度复矢量为 j8πw 140() e kA/m 3πxx z H e E e Z -=⨯= 因此,磁场的瞬时表达式为840cos(12π108π)3πzH e t x =⨯- 6.3 在无界理想介质中,均匀平面波的电场强度为 ()80sin 2π102πx E e E t z =⨯-V /m已知介质的r 1μ=,试求其r ε,并写出H 的表达式。
谢处方《电磁场与电磁波》(第4版)课后习题-第6章 均匀平面波的反射与透射【圣才出品】

第6章 均匀平面波的反射与透射(一)思考题6.1 试述反射系数和透射系数的定义,它们之间存在什么关系?答:(1)反射波电场振幅E rm与入射波电场振幅E im的比值为分界上的反射系数;透射波电场振幅E tm与入射波电场振幅E im的比值为分界面上的透射系数。
(2)反射系数Γ和透射系数τ之间的关系为:6.2 什么是驻波?它与行波有何区别?答:频率和振幅均相同,振动方向一致,传播方向相反的两列波叠加后形成的波叫驻波。
行波在介质中传播时,其波等相面随时间前移,而驻波的波形不向前推进。
6.3 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,反射系数大于0?在什么情况下,反射系数小于0?答:均匀平面波垂直入射到两种理想媒质分界时,当时,反射系数Γ>0;当时,反射系数Γ<0。
6.4 均匀平面波向理想导体表面垂直入射时,理想导体外面的合成波具有什么特点?答:均匀平面波向理想导体表面入射时,理想导体外面的合成波具有特点如下:合成波电场和磁场的驻波在时间上有的相移,在空间上也错开了且在导体边界上,电场为零。
驻波的坡印廷矢量的平均值为零,不发生电磁能量的传输过程,仅在两个波节之间进行电场能量和磁场能量的交换。
6.5 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,分界面上的合成波电场为最大值?在什么情况下,分界面上的合成波电场为最小值?答:当均匀平面波垂直入射到两种理想媒质分界面时,的位置时,分界面上的合成波电场为最大值。
的位置时,分界面上的合成波电场为最小值。
6.6 一个右旋圆极化波垂直入射到两种媒质分界面上,其反射波是什么极化波?答:右旋圆极化。
6.7 试述驻波比的定义,它与反射系数之间有什么关系?答:驻波比的定义是合成波的电场强度的最大值与最小值之比,即6.8 什么是波阻抗?在什么情况下波阻抗等于媒质的本征阻抗?答:在空间任意点,均匀平面波的电场与磁场强度的模值之比称为自由空间的波阻抗,在均匀无耗各向同性的无界媒质中,均匀平面波的电场与磁场的模值之比称为媒质中的阻波抗。
电磁场与电磁波课后答案_郭辉萍版1-6章

第一章 习题解答1.2给定三个矢量A ,B ,C : A =x a +2y a -3z a B = -4y a +z aC =5x a -2za求:错误!未找到引用源。
矢量A 的单位矢量A a ; 错误!未找到引用源。
矢量A 和B 的夹角AB θ; 错误!未找到引用源。
A ·B 和A ⨯B错误!未找到引用源。
A ·(B ⨯C )和(A ⨯B )·C ;错误!未找到引用源。
A ⨯(B ⨯C )和(A ⨯B )⨯C解:错误!未找到引用源。
A a =A A=(x a +2y a -3z a ) 错误!未找到引用源。
cos AB θ=A ·B /A BAB θ=135.5o错误!未找到引用源。
A ·B =-11, A ⨯B =-10x a -y a -4z a 错误!未找到引用源。
A ·(B ⨯C )=-42(A ⨯B )·C =-42错误!未找到引用源。
A ⨯(B ⨯C )=55x a -44y a -11z a(A ⨯B )⨯C =2x a -40y a +5z a1.3有一个二维矢量场F(r)=x a (-y )+y a (x),求其矢量线方程,并定性画出该矢量场图形。
解:由dx/(-y)=dy/x,得2x +2y =c1.6求数量场ψ=ln (2x +2y +2z )通过点P (1,2,3)的等值面方程。
解:等值面方程为ln (2x +2y +2z )=c 则c=ln(1+4+9)=ln14 那么2x +2y +2z =141.9求标量场ψ(x,y,z )=62x 3y +ze 在点P (2,-1,0)的梯度。
解:由ψ∇=x a x ψ∂∂+y a y ψ∂∂+z a zψ∂∂=12x 3y x a +182x 2y y a +ze z a 得ψ∇=-24x a +72y a +z a1.10 在圆柱体2x +2y =9和平面x=0,y=0,z=0及z=2所包围的区域,设此区域的表面为S: 错误!未找到引用源。
电磁场与电磁波习题讲解

电磁场与电磁波习题讲解静电场的基本内容2.7 半径分别为a和b(a>b),球心距离为c(c<a-b)的两球面间均匀分布有体密度为ρV的电荷,如图所示。
求空间各区域的电通量密度。
解:由于两球面间的电荷不是球对称分布,不能直接用高斯定律求解。
但可把半径为b的小球面内看作同时具有体密度分别为±ρV的两种电荷分布,这样在半径为a的大球体内具有体密度为ρV的均匀电荷分布,而在半径为b的小球体内则具有体密度为-ρV的均匀电荷分布。
空间任一点的电场是这两种电荷所产生的电场的叠加。
以球体a的球心为原点建立球坐标系,设场点为P(r),场点到球体b球心的距离矢量为r’。
分三种情形讨论。
如果场点位于大球体外的区域,则大小球体产生的电场强度分别为如果场点位于大球体内的实心区域,则大小球体产生的电场强度分别为如果场点位于小球体内的空腔区域,则大小球体产生的电场强度分别为恒定电场的基本内容2.17一个有两层介质(ε1, ε2)的平行板电容器,两种介质的电导率分别为σ1和σ2,电容器极板的面积为S,如图所示。
在外加电压为U时,求:(1)电容器的电场强度;(2)两种介质分界面上表面的自由电荷密度;(3)电容器的漏电导;(4)当满足参数σ1ε2=σ2ε1时,问G/C=?(C为电容器电容)。
恒定磁场的基本内容4.4如果在半径为a,电流为I的无限长圆柱导体内有一个不同轴的半径为b的圆柱空腔,两轴线间距离为c,且c+b<a。
求空腔内的磁通密度。
解:将空腔中视为同时存在J和-J的两种电流密度,这样可将原来的电流分布分解为两个均匀的电流分布:一个电流密度为J、均匀分布在半径为a 的圆柱内,另一个电流密度为-J、均匀分布在半径为b的圆柱内。
由安培环路定律,分别求出两个均匀分布电流的磁场,然后进行叠加即可得到圆柱内外的磁场。
首先,面电流密度为其次,设场点为P(r),场点到圆柱a轴心的距离矢量为ρ,到圆柱b轴心的距离矢量为ρ’。
东南大学电磁场与电磁波东南大学电磁场与电磁波3.1-3.3

线电流I位于两铁板之间的磁场
18:14:15
线电荷
位于两平行导体间的电场 18 18
二、恒流磁场的矢量磁位
•标量磁位只适用于无自由电流区域。要找 到一位函数,能应用于有电流和无电流区 域,且可通过此位函数的微分得到磁感应 强度。
18:14:15
19 19
◇ 为了简化磁场的求解,通常采用间接方法。 ◇ 由磁场的散度为零,引入矢量磁位。 ◇ 利用磁场的旋度方程导出矢量磁位满足的微分方程。 由 B 0
第三章 恒定电流的磁场
§3.1 恒流磁场的基本方程
18:14:15
1 1
•
实验表明,导体中有恒定电流通过时,在导
体内部和它周围的媒质中 ,不仅有恒定电场 , 同时还有不随时间变化的磁场 ,简称 恒定磁场 (Static Magnetic Field)。 •
恒定磁场和静电场是性质完全不同的两种场,
但在分析方法上却有许多共同之处。学习本章时,
AnB
H dl
磁位m 与积分路径的关系
14 14
18:14:15
AmB
H dl mA mB
( B)
mA
( A)
H dl
m L H dl
18:14:15
磁位m 与积分路径的关系
15 15
磁场中求积分
AlBmA
H dl I H dl I
18:14:15
z I
0
x
1
x
I
dl
8 8
C
H dl I
H 2 r I H
I 2 r
a
0 I a 2 r B H 1 I a 2 r
东南大学电磁场与电磁波 5jie

负号表示感应电流产生的磁场总是 阻碍原磁场的变化 引起磁通变化的原因分为三类: • 回路不变,磁场随时间变化 d B dS S t dt 称为感生电动势,这是变压器工 作的原理,又称为变压器电势。
18:15:29
d dt
感生电动势的参考方向
感生电动势
•
回路切割磁力线,磁场不变
否则这种时变的传导电流在理想导电体内部会产生时变磁场。由此 可见,在理想导电体内部不可能存在时变电磁场及时变的传导电流, 它们只可能分布在理想导电体的表面。 已知在任何边界上,电场强度的切向分量及磁感应强度的法向分 量是连续的,因此理想导体表面上不可能存在电场切向分量及磁场法 向分量,只可能存在法向电场及切向磁场。也就是说,时变电场必须 垂直于理想导电体的表面,而时变磁场必须与其表面相切,如下图示。
18:15:29
4.三种电流
(1)传导电流:自由电荷在导电媒质中定向移动而形成的,它只能 存在于导电媒质中,产生的焦耳-楞次热。 (2)运流电流:电荷在无阻力空间的运动而形成的,不产生的热量, 其数学表达式为 J v ,其中 为电荷运动速度, 为电荷密 v V 度。
(3)位移电流:变化的电场和介质极化的结果,它可以存在空间的 任何地方,产生的热量不符合焦耳-楞次定律。
• 全电流定律——麦克斯韦第一方程, 表明传导电流 和变化的电场都能产生磁场;
• 电磁感应定律——麦克斯韦第二方程,表明电荷和变化 的磁场都能产生电场;
• 磁通连续性原理——表明磁场是无源场,磁力线总是 闭合曲线; • 高斯定律——表明电荷以发散的方式产生电场(变化 的磁场以涡旋的形式产生电场)。 • 麦克斯韦第一、二方程是独立方程,后面两个方程 可以从中推得。 • 静态场和恒定场是时变场的两种特殊形式。
东南大学电磁场与电磁波6.4-6.8

媒质1
得
jk1 z jk1 z a E e a E x m x me Em Em
0
均匀平面波垂
jk1 z m
E ax E e
E E E ax E e
jk1 z m
ax E e
jk1 z m
E H + a y m e jk1z Z1
电磁波不能穿入理想导体,到达 18:15:21 分界面时将被反射回来。
E E H H H a y m e jk1z a y m e jk1z Z1 Z1
17 17
1区的合成波电磁场的复数表示(教科书改变了z坐标的方向, 这里不变)
◇一般情况 R 和 T 是复数。表明分界面上反射波和透射波将引入一附加相移。 ◇若媒质1、2为理想介质则Z1、Z2为实数,在z=0的分界面上
Z1 Z 2 R 0 反射波电场与入射波电场同相相加,合成波电场为最大,磁场为最小。 Z1 Z 2 R 0 合成波电场为最小,磁场为最大。
其夹角
Eom sin(t x ) arctan arctan (t x ) Ex Eom cos(t x ) 18:15:21 Ey
因此合成矢量 E 的幅度不变,但其指向则以角频率在与传播
方向垂直的平面里旋转。这就是圆极化波。
圆极化波有不同的旋转方向。我们规定如电场强度矢量 E
13 13
jk1 z jk1 z E E1 E1 a x Em e a E 1 x m1e
1区合成波
Em Em 1 jk1z H H H ay e a y 1 e jk1z Z1 Z1 1 1
电磁场与电磁波课后答案郭辉萍版16章

电磁场与电磁波课后答案-郭辉萍版1-6章第一章 习题解答1.2给定三个矢量A ,B ,C : A =xa +2y a -3zaB= -4ya +zaC=5xa -2za求:⑴矢量A 的单位矢量Aa ; ⑵矢量A 和B 的夹角ABθ;⑶A ·B 和A ⨯B⑷A ·(B ⨯C )和(A ⨯B )·C ; ⑸A ⨯(B ⨯C )和(A ⨯B )⨯C 解:⑴Aa =A A=149++=(xa +2y a -3za )14⑵cos ABθ=A ·B /ABAB θ=135.5o⑶A ·B =-11, A ⨯B=-10xa-y a -4za⑷A ·(B ⨯C )=-42 (A ⨯B )·C =-42⑸A ⨯(B ⨯C )=55xa -44y a -11za(A ⨯B )⨯C =2xa -40y a +5za1.3有一个二维矢量场F(r)=xa (-y )+ya (x),求其矢量线方程,并定性画出该矢量场图形。
解:由dx/(-y)=dy/x,得2x +2y =c1.6求数量场ψ=ln (2x +2y +2z )通过点P (1,2,3)的等值面方程。
解:等值面方程为ln (2x +2y +2z )=c则c=ln(1+4+9)=ln14 那么2x +2y +2z =141.9求标量场ψ(x,y,z )=62x 3y +ze 在点P (2,-1,0)的梯度。
解:由ψ∇=xaxψ∂∂+yayψ∂∂+zazψ∂∂=12x 3yxa +182x2y ya +zeza 得ψ∇=-24xa +72y a +za1.10 在圆柱体2x +2y =9和平面x=0,y=0,z=0及z=2所包围的区域,设此区域的表面为S: ⑴求矢量场A 沿闭合曲面S 的通量,其中矢量场的表达式为A=x a 32x +y a (3y+z )+za (3z -x)⑵验证散度定理。
东南大学电磁场与电磁波6.1-6.3

E y H x z t H x E y 消去Hx t 消去E z y
Ex Ex 2 0 2 z t
2 2
Ey
2
z
2
2
Ey
2
t
2
2
0
Hy
2
z
2
Hy
2
t
2
0
Hx Hx 0 2 2 z t
·电磁波:变化的电磁场脱离场源后在空间的传播。 ·平面电磁波:等相位面为平面构成的电磁波。 ·均匀平面电磁波:等相位面上E、H 处处相等 的电磁波。若电磁波沿x轴方向传播,则 H=H(x,t),E=E(x,t)。 ·平面电磁波知识结构框图。
x方向传播的一组均匀平面波
◇ 麦氏方程及由它导出的波动方程对任意方式随时间变的 电磁场都适用。 ◇ 随时间作正弦变化的电磁场,称为时谐场。 ◇ 在一定条件下任意方式随时间变化的电磁场可展为时 谐正弦分量的傅里叶级数。
因此在真空中的均匀平面波,其电场方向、磁场方向 及电磁波传播方向三者之间相互正交,满足右手螺旋 关系;电场与磁场相位相等;电场与磁场的幅度之比 等于波阻抗。
以其中一组沿+z方向的平面波为例:
E ax Ex ax f1 ( z vt )
1 H a y H y a y f1 ( z vt ) Z
波动方程成为齐次方程:
2 E E 2 E 2 0 t t
2 H H 2 H 2 0 t t
如果是时谐电磁场,用场量用复矢量表示, 并采用复介电常数, 2 j 2 (1 j
Z
f1 ( z vt )的物理意义
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2
长轴与短轴、轴比: Exom , Eyom 分别为椭圆的两个轴长,其中长着称为长轴,
短者称为短轴,长短轴之比称为轴比。 椭圆极化波也有左旋、右旋之分,其旋 向的规定和判断方法与圆极化波一样。
y
x
椭圆极化波的分解和合成
椭圆极化的平面波 18:15:21 9 9
◇ 当
其夹角
Eom sin(t x ) arctan arctan (t x ) Ex Eom cos(t x ) 18:15:21 Ey
因此合成矢量 E 的幅度不变,但其指向则以角频率在与传播
方向垂直的平面里旋转。这就是圆极化波。
圆极化波有不同的旋转方向。我们规定如电场强度矢量 E
13 13
jk1 z jk1 z E E1 E1 a x Em e a E 1 x m1e
1区合成波
Em Em 1 jk1z H H H ay e a y 1 e jk1z Z1 Z1 1 1
在z=0处,由于没有感应面电流,故分界面两侧其电场和磁场的切向分量 连续。
均匀平面波垂直入射到 两种媒质分界面上
H a y H e
1
jk1z m1
Em a y 1 e jk1z Z1
透射波
18:15:21
jk2 z E2 a x Em e 2
jk2 z H2 ay Hm 2e Em 2 jk2 z a y e Z2
圆极化波的分解和合成 空间某一点圆极化波电场沿时间轴的分布
18:15:21 7 7
三、椭圆极化波
若 E x和 E y 振幅、相位都不相同。则合成波为椭圆极化波。
E a x Ex a y E y
Ex Exom cos( t kz x ) E y E yom cos( t kz y )
z 0
媒质1
得
jk1 z jk1 z a E e a E x m x me Em Em
0
均匀平面波垂直入射到 理想导体平面上
入射波
1区的合成波
jk1 z m
E ax E e
E E E ax E e
jk1 z m
ax E e
E E 0 或
E E 0
18:15:21
理想导体表面的垂直入射
16 16
E+
入
x
+
反射波
jk1 e jk1z Z1
H
E
反
y
z
H
由边界条件 Et Ex 媒质2 2
z 0
0(2区电场为零)
12 12
jk1 z E1 a x Em 1e
E
1
x E
2
jk z 入射波 H1 a y H m 1e
1
H1
E1
反
入
H
2
透
y
z
Em a y 1 e jk1z Z1
1 a z E1 Z1
H1
媒质1
媒质2
反射波
jk1 z E1 a x Em 1e
Z=0时
E ax Ex ay Ey ax Exom cos(t x ) ay Eyom cos(t y )
记
x y ,消去t
可得
8 8
18:15:21
Ey Ex E y Ex 2 2 cos sin E Exom E yom Exom yom
S2 (0, t ) E2 (0, t ) H 2 (0, t )
( E1 (0, t ) E1 (0, t ))( H1 (0, t ) H1 (0, t )) ( E1 (0, t )) 2 ( E1 (0, t )) 2 Z1 Z1 入射波带到界面处的功率减去反射波带回到媒质1 中的功率等于透射波带入媒质2中的功率。
E ax E e
m
jk1 z
e
jk1z
a 2jE
x
m
sin k1 z
E jk1z jk1z 2E H ay e e ay cos k1 z Z1 Z1
jk1 z m
E H + a y m e jk1z Z1
电磁波不能穿入理想导体,到达 18:15:21 分界面时将被反射回来。
E E H H H a y m e jk1z a y m e jk1z Z1 Z1
17 17
1区的合成波电磁场的复数表示(教科书改变了z坐标的方向, 这里不变)
E E E
得
Em E 1 m1
m1
m1
m2
Em1 Em1 Em 2 Z1 Z1 Z2
Em 2 Em1
Z 2 Z1 Z 2 Z1
定义反射系数和透射系数
Em Z Z R 1 2 1 Em1 Z2 Z1
2Z 2 Z 2 Z1
Em 2Z 2 T 2 Em1 Z2 Z1
x x
椭圆、圆与直线极化的 关系
在一般情况下:
arctan
Ey Ex
arctan
Eyom cos(t y ) Exom cos(t x )
2 2 a2 b2 Exom Eyom
b 令椭圆的长轴与x轴的夹角为 : arctan a
tan2
18:15:21
18:15:21 3 3
2 2 2 2 E Ex Ey ( Exom cos t )2 ( E yom cos t ) 2 Exom E yom cos t
其夹角
arctan
Ey Ex
arctan
Eyom Exom
arctan
Eyom Exom
const
不随时间变,合成场强的大小随时间变化,但方向始终 在与x轴成 角的直线上。即电场向量的矢端轨迹是直线。
电场强度 E 的方向就是极化方向,
极化方向与传播方向一起构成极化面。
这种情况称为直线极化波。
y
线极化波的分解和合成
18:15:21
x
4 4 直线极化的平面波
二、圆极化波
,则合成波为圆极化波。 E x 与 E y 等幅,相位相差 2 E ax Ex ay Ey ax Eom cos(t kz x ) ay Eom sin(t kz x )
90 , Eyom Exom Eom 时,椭圆极化
0
→ 圆极化。
y y
◇ 当 0时, 椭圆极化 → 直线极化。 若 E 的变化轨迹在 x 轴上( 0 ) ,称为 x 轴取 向的线极化波。 若 E 的变化轨迹在 y 轴上 ( 90 ) ,称为 y 轴取 向的线极化波。
§ 6.4电磁波的极化
• 电磁波极化的概念非常重要: 1)使用边界条件需要; 2)应用中需要。 • 电磁波极化的定义:空间任意一个固定点上电磁波电场强 度矢量的空间指向随时间变化的方式。 • 极化的由来:均匀平面波由于没有纵向场分量,只有两个 横向场分量。这两个横向场分量有各自的相位,合成后总 的场量的方向就取决于它们之间的相位差。
理想介质表面的垂直入射演示 18:15:21 15 15 垂直入射到理想介质表面的电磁磁场的时空关系
二、正弦平面电磁波对理想导电媒质表面垂 直入射
理想导体:= 透入深度:=0
Z ( j )
内部 E=0 , H=0 。 无折射,全反射 R 1, T 0 Z2=0 场量参考方向可以任意设:
E x 与 E y同相或反相
E ax Exom cos(t kz x ) a y Eyom cos(t kz x )
在空间任取一点,比如 kz x 0 观察合成矢量
E ax Ex ay Ey ax Exom cos(t ) ay Eyom cos(t )
与电磁波传播方向符合右手螺旋关系(以右手的四指随E 的矢端运动,则姆指就指出了波的传播方向),则其称为 右旋圆极化波,反之称为左旋圆极化波。
左旋与右旋、判断方法:
右旋圆极化波方程:
E ax Eom cos(t kz x ) a y Eom sin(t kz x ) ax Eom cos(t kz x ) a y Eom cos(t kz x ) 2
极化的应用:
1)目标的极化信息 2)极化隔离 3)极化复用 4)极化分集
18:15:21
11 11
§ 6.5 正弦平面电磁波向不同媒质 界面的垂直入射
均匀平面波在无限大均匀介质中传播按直线进行。若在 传播路径上媒质不均匀,会发生波的反射和透射(折射)。
一、正弦平面电磁波向不同媒质分界面垂直 入射
18:15:21
jx
a y Eyome )e
j y
jkz
Ex Exom cos( t kz x ) E y E yom cos( t kz y )
根据极化方式的不同可大致分为三类
18:15:21 2 2
一、线极化波
前面所述的沿z方向传播的平面波的电场方向不随时 间变化。我们可设定电场方向沿x方向或y方向。一般情 况下,沿z方向传播的均匀平面波电场同时存在x方向分 量和y方向分量:Ex(z,t)和Ey(z,t)。 如果电场两分量的振幅不同,但相位相同,或差180°
◇一般情况 R 和 T 是复数。表明分界面上反射波和透射波将引入一附加相移。 ◇若媒质1、2为理想介质则Z1、Z2为实数,在z=0的分界面上
