几何证明举例4
八年级数学理科班讲义教学-几何证明

B CD AOB CE DA A CB ’ CA B C B ’ C 8、八年级数学理科班:直角三角形全等判定、性质姓名一、【直角三角形全等的特殊判定方法】知识要点:一条直角边和斜边对应相等的两个直角三角形全等。
简记为HL 。
1、【定理证明】已知:如图,在Rt △ABC 和Rt △A’B’C’中,∠C=∠C’=90°,AC=A’C’,AB=A’B’ 求证: Rt △ABC ≌Rt △A’B’C’2、【直角三角形全等判定方法梳理】如图,具有下列条件的Rt △ABC 和Rt △A’B’C’(其中∠C=∠C’=90°)是否全等?如果全等在( )里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在( )里打“×”. (1)AC=A’C’,∠A=∠A’ ( ) _______ (2)AC=A’C’,BC=B’C’ ( ) _______ (3)AB=A’B’,BC=B’C’ ( ) _______ (4)∠A=∠A’,∠B=∠B’ ( ) ________3、【应用练习】 选择题1.下列说法正确的有( )① 斜边和一条直角边对应相等的两个直角三角形全等② 两条边分别相等的两个直角三角形全等 ③ 两条直角边对应相等的两个直角三角形全等 ④ 斜边相等的两个等腰直角三角形全等A .1个B .2个C .3个D .4个2.已知,如图,BD ⊥AC 于D,CE ⊥AB 于E,BD 与CE 相交于O , 且BD=CE ,则图中全等的三角形共有( )A .1对B .2对C .3对D .4对3.如果两个三角形的两条边和其中一边上的高对应相等,那么这两个三角形的第三边 所对的角( )A .相等B .不相等C .互余或相等D .相等或互补4.如图,已知:∠A=∠D=90°,AB=CD,求证:AC=DBBC F E DABC FE D AB C F E D A5.如图,已知:AB=CD,AE ⊥BC,DF ⊥BC,BF=CE.求证:AB ∥CD6.如图,已知:AB=AE, ∠B=∠E=90°,AF 垂直平分CD,求证:BC=DE7.如图,已知:AD 平分∠BAC,DB ⊥AB,DF ⊥AC 于点F ,ED=CD,求证:AC=AE+2BE.8.已知:AC ⊥BC ,AD ⊥BD ,AD=BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F , 求证:CE=DF二、直角三角形的性质 1、【定理】①直角三角形的两个锐角互余(显然) ②直角三角形斜边上的中线等于斜边的一半 2、【定理证明】已知:在Rt △ABC 中,∠ACB=90°,CD 是斜边AB 的中线.求证:AB CD 21例1.如图,△ABC中,BD⊥AC于D,CE⊥AB与E,连接DE,取BC的中点M,DE的中点N,问:MN与DE有什么样的位置关系,并说明理由。
(完整版)初中几何证明题五大经典(含答案)
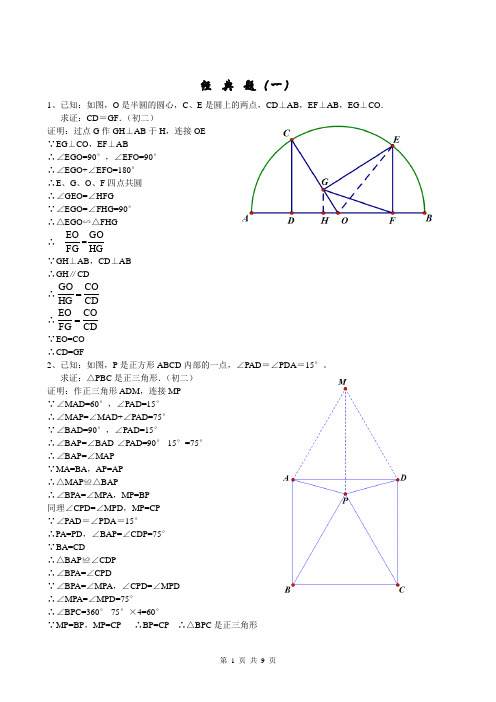
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
2017年秋八年级数学上册 19.2 证明举例(4)教案 沪教版五四制

重点
运用定义、定理、公理,证明命题,掌握数学语言的转化.
难点
正确分析问题,把握解题的关键,会构造有效的图形解决问题.
教学
准备
全等三角形的性质和判定,等腰三角形、直角三角形的性质,等腰三角形的判定,其他几何性质等.
学生活动形式
讨论,交流,总结,练习
教学过程
设计意图
课题引入:
课前练习
1、已知:如图,AB=AC,D、E分别是AB、AC上的点,且AD=AE。
知识呈现:
新课探索一
例题1已知:如图,DB⊥AB,DC⊥AC,且∠1=∠2。
求证:AD⊥BC。
新课探索二
探索如图△ABC是等腰直角三角形,且∠ACB=90°,E是AC上一点,延长BC到D,使CD=CE,联结BE,AD。则BE与AD在数量上有什么关系?在位置上又有什么特殊关系?
课内练习
1、已知:如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,点M在CD上,∠AOM=∠BOM。
证明举例
课题
19.2(4)证明举例
设计
依据
(注:只在开始新章节教学课必填)
教材章节分析:
学生学情分析:
Hale Waihona Puke 课型新授课教学
目
标
能利用定义、定理、公理等证明命题,掌握数学语言的转化.
经历命题证明的分析过程,感受解决几何证明问题的一般方法,体会数学语言的转化功能.
数学的几何推理是非常严谨的,每一步必须有理有据,因果关系严密
求证:OM⊥CD。
课堂小结:
利用等腰三角形的判定、性质及三线合一,使证题过程简单化。(注重证明线与线垂直)。
课外
作业
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理)勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果三角形的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴ ∴.【证法2】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
几何证明(4个概念2个性质3个判定2个定理2个应用2种思想方法1个轨迹)八年级数学上册沪教版

2 个性质3个判定
考点05 线段的垂直平分线
7.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
(D )
8.已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
(2)区别:定义、公理、定理都是真命题,都可以作为进一步判断其
他命题真假的依据,只不过公理是最原始的依据;而命题不一定是真
命题,因而不能作为进一步判断其他命题真假的依据.
考点04 互逆定理
6. [2022·江苏无锡宜兴市二模]下列命题的逆命题成立的是
①同旁内角互补,两直线平行
①④ .
②等边三角形是锐角三角形
证明:过点Q作MN⊥AB,垂足为点C,
故∠QCA=∠QCB=90°.
在Rt△QCA 和Rt△QCB中,
∵QA=QB,QC=QC,
∴Rt△QCA≌Rt△QCB(H.L.).
∴AC=BC.
∴点Q在线段AB的垂直平分线上.
你能根据分析
中后一种添加辅
助线的方法,写
出它的证明过程
吗?
考点06 角 平 分 线
AB=CB,
∴Rt△ABE≌Rt△CBF(HL).
15.如图,点B,E,F,C在同一条直线上,AE⊥BC,DF⊥BC,
AB=DC,BE=CF.试判断AB与CD的位置关系,并证明.
A
解:AB//CD,理由如下:
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°
B
F
∵在Rt△ABE和Rt△DCF中, AB=DC,
解析几何中证明四点共圆的四种方法

解析几何中证明四点共圆的四种方法作者:徐加生来源:《新高考·高三语数外》2010年第04期圆具有丰富的几何性质,它与三种圆锥曲线之间有着千丝万缕的内在联系.圆的性质的应用是近几年高考命题中体现“在知识交汇点设计问题”这一思路的良好素材,应引起我们足够的重视.本文介绍证明四点共圆问题的四种方法,供同学们参考.一、直接求出圆的方程例1设0=1和双曲线x2cosθ-y2sinθ=1有四个不同的交点.(1) 求θ的取值范围;(2) 证明这四个交点共圆,并求该圆半径的取值范围.解析(1) 将方程x2sinθ+y2cosθ=1和x2cosθ-y2sinθ=1联立,解得x2=sinθ+cosθ,y2=cosθ-sinθ.由两曲线有四个交点,知x2>0,y2>0. 又0(2) 由(1)得x2+y2=2cos θ0二、利用圆系方程来判断例2由抛物线y2=2px(p>0)外一点P引抛物线的两条割线PAB,PCD,其倾斜角分别为α,β,且α+β=π,问A,B,C,D四点能否共圆?解析设点P 坐标为(a,b),又直线PAB的斜率为tan α,直线PCD的斜率为tan β(显然α,β均不等于0与),故而直线PAB的方程为y-b-tanα(x-a)=0,直线PCD的方程为y-b-tanβ(x-a)=0.又α+β=π,于是将两方程相乘(合并),可得直线PAB, PCD合并起来的轨迹方程为(y-b)2-tan2α(x-a)2=0.又抛物线的方程为y2-2px=0,故A,B,C,D四点坐标都满足方程(y-b)2-tan2α(x-a)2+λ(y2-2px)=0,即tan2αx2-(λ+1)y2-2(atan2α-pλ)x+2by+a2tan2α-b2=0.令λ+1=-tan2α且4(atan2α-pλ)2+4b2-4(a2tan2α-b2)>0,则上述方程表示圆,故而当点P 坐标适当时,A,B,C,D四点可以共圆.三、证明同弦所对的圆周角相等或互补例3设A,B是双曲线x2-=1上的两点,N(1,2)是线段AB的中点.如果线段AB的垂直平分线与双曲线相交于C,D两点,那么A,B,C,D四点是否共圆?为什么?解析设A(x1,y1),B(x2,y2),则-=1,-=1,x1+x2=2,y1+y2=4.将前两式相减,得(x1-x2)(x1+x2)=(y1-y2)(y1+y2);将后两式代入,得=1,即直线AB的斜率为1,故易得直线AB的方程为x-y+1=0.因为CD是线段AB的垂直平分线,故易得直线CD的方程为x+y-3=0.将直线AB的方程x-y+1=0与双曲线方程x2-=1联立,可解得交点A(-1,0)和B(3,4)(不妨设);将直线CD的方程x+y-3=0与双曲线方程x2-=1联立,可解得交点C(-3-2,6+2)和D(-3+2,6-2)(不妨设).则=(-2-2,6+2),=(-2+2,6-2),=(-6-2,2+2),=(-6+2,2-2).容易计算得cos∠CAD==0,cos∠CBD==0,故∠CAD=∠CBD=90°.于是无论点A,B在直线CD的同侧还是异侧(实际上,这里显然A,B在CD的异侧),都有A,B,C,D四点共圆.例4设A,B是椭圆3x2+y2=λ上的两点,N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C,D两点.(1) 确定λ的取值范围,并求直线AB的方程;(2) 试判断是否存在这样的λ,使得A,B,C,D四点在同一个圆上?并说明理由.解析(1) 设A(x1,y1),B(x2,y2),则3+=λ,3+=λ,x1+x2=2,y1+y2=6.将前两式相减,得3(x1-x2)(x1+x2)+(y1-y2)(y1+y2)=0;将后两式代入,得=-1,即直线AB的斜率为-1,故易得直线AB的方程为x+y-4=0.将直线AB的方程代入椭圆的方程,整理得4x2-8x+16-λ=0 ①,故Δ=64+16(λ-16)>0,得λ>12,即λ的取值范围为[12,+∞).(2) 因为 CD垂直平分线段AB,所以直线CD的方程为y-3=x-1.将其代入椭圆的方程,整理得4x2+4x+4-λ=0 ②.解方程①、②,可得A1+,3-,B1-,3+,C-+,+,D--,-,则AC2 =2+2,AD2 =2+2,所以AC2+AD2=2(λ-3).又CD2=(λ-3)+(λ-3)=2(λ-3),故AC2+AD2=CD2,所以AC⊥AD.同理,BC⊥BD.于是无论A,B在CD的同侧还是异侧(实际上,这里显然A,B在CD的异侧),都有A,B,C,D四点共圆.所以只要λ>12,总有A,B,C,D四点共圆.点评在解例3和例4时,都是先求出A,B,C,D四个点的坐标,然后以CD为弦,求出角CAD和CBD,并发现它们既相等又互补,于是得出A,B,C,D四点共圆.只是在求角时,例3利用向量数量积的定义,例4利用余弦定理(勾股定理是余弦定理的特例). 注意,如果两个角相等而不互补,则两点须在弦的同侧;如果两个角互补而不相等,则两点须在弦的异侧.四、找圆心证半径相等例5设p>0是一常数,若直线x-2y-2p=0与抛物线y2=2px交于A,B两点,又O为抛物线的顶点,C(0,4p)为定点,判断A,B,O,C四点是否可以共圆?解析若A,B,O,C四点共圆,则此圆的圆心应该是弦AB的垂直平分线与弦OC的垂直平分线的交点.设A(x,y),B(x,y),则它们的坐标同时满足方程x-2y-2p=0和y2=2px,将二式联立,消去x,得y2-4py-4p2=0.而弦AB的中点H的坐标为,,即H(6p,2p),则弦AB的垂直平分线方程为2x+y-14p=0.又弦OC的垂直平分线方程是y=2p,故圆心即为点H.又可得AB====4p,而易得OH=2p,CH=2p,即有OH=CH=AH=BH.所以A,B,O,C四点可以共圆.1. 已知椭圆+=1的两个焦点分别为F,F,问椭圆上是否存在点P,使△PFF的面积为1?若存在,这样的点P有几个?这些点P是否可能在同一个圆上?1. 由椭圆+=1,得FF=2c=2 .又由△PFF的面积S=|FF||y|=1,得|y|=1,即△PFF边FF上的高为1.而椭圆短半轴长为,故由椭圆的对称性,知满足条件的点有四个,P,P,P,P .且这四点到原点距离相等,故这四点共圆.。
“四点共圆”在几何证明中的作用

“四点共圆”在几何证明中的作用
几何证明讲究严密的逻辑推理,有时仅一步之遥而将你拒之门外。
要迈出这一步,需要有充分的理由。
下面谈谈笔者的体验。
一、介绍“四点共圆”
在初中几何《圆》一章中,用反证法可证明:在一条线段同一旁有两个点,如果它们对这条线段两端所形成的视角相等,则这两点和线段两端点四点共圆。
二、证明“四点共圆”
如图⑴所示:M、N为线段AB同旁两点且∠M=∠N,则A、B、M、N四点共圆。
证明:设过A、B、N三点的圆为⊙O,假若点M在圆内,则有∠AM″B>∠AMB=∠N;假若点M在圆外则有∠AM′B<∠AMB=∠N。
因此,只有当M点在圆上时∠M=∠N。
所以A、B、M、N四点共圆。
三、应用“四点共圆”
用这个结论对下面这道题的证明起了十分重要的作用。
例题:如图⑵,B、C、D、E在同一直线L上,且BC=DE,∠1=∠2。
求证:AC=AD
分析:要证AC=AD,首先想到需要证△ABC≌△ADE或△ABD≌△AEC,但难度太大(你不妨试试)。
下面我们用“四点共圆”
证明:过A作AFL 且AF=BC(或DE),连结CF,EF。
由平行四边形判定定理可知,四边形ABCF和ADEF都是平形四边形。
∴∠1=∠3,∠2=∠4
又∠1=∠2
∴∠3=∠4
由四点共圆法可知:A、C、E、F 四点共圆,且AF、CE为圆内两条平行弦平行弦所夹弧相等,同圆中相等弧所对弦相等。
∴AC=EF
又∵AD=EF(四边形ADEF是平行四边形)
∴AC=AD。
几何法证明不等式(精选多篇)

几何法证明不等式(精选多篇)^2(a,b∈r,且a≠b)设一个正方形的边为c,有4个直角三角形拼成这个正方形,设三角形的一条直角边为a,另一条直角边为b,(b>a)a=b,刚好构成,若a不等于b时,侧中间会出现一个小正方形,所以小正方形的面积为(b-a)^2,经化简有(b+a)^2=4ab,所以有((a+b)/2)^2=ab,又因为(a^2+b^2)/2>=ab,所以有((a+b)/2)^2<=(a^2+b^2)/2,又因为a不等与b,所以不取等号可以在直角三角形内解决该问题=^2-(a^2+b^2)/2=/4=-(a-b)^2/4<0能不能用几何方法证明不等式,举例一下。
比如证明sinx不大于x(x范围是0到兀/2,闭区间)做出一个单位圆,以o为顶点,x轴为角的一条边任取第一象限一个角x,它所对应的弧长就是1*x=x那个角另一条边与圆有一个交点交点到x轴的距离就是sinx因为点到直线,垂线段长度最小,所以sinx小于等于x,当且尽当x=0时,取等已经有的方法:第一数学归纳法2种;反向归纳法(特殊到一般从2^k过渡到n);重复递归利用结论法;凸函数性质法;能给出其他方法的就给分(a1+a2+...+an)/n≥(a1a2...an)^(1/n)一个是算术,一个是几何。
人类认认识算术才有几何,人类吃饱了就去研究细微的东西,所以明显有后者小于前者的结论,这么简单都不懂,叼佬就是叼佬^_^搞笑归搞笑,我觉得可以这样做,题目结论相当于证(a1+a2+...+an)/n-(a1a2...an)^(1/n)≥0我们记f(a1,a2,……,an)=(a1+a2+...+an)/n-(a1a2...an)^(1/n)这时n看做固定的。
我们讨论f的极值,它是一个n元函数,它是没有最大值的(这个显然)我们考虑各元偏导都等于0,得到方程组,然后解出a1=a2=……=an再代入f中得0,从而f≥0,里面的具体步骤私下聊,写太麻烦了。
