电磁场 第3章作业题解答
教科版高中物理必修第三册课后习题 第3章 电磁场与电磁波初步 分层作业27 电磁波的发现及其应用

分层作业27电磁波的发现及其应用A组必备知识基础练题组一对麦克斯韦电磁场理论的理解1.关于麦克斯韦电磁场理论,下列说法正确的是()A.在赫兹发现电磁波的实验基础上,麦克斯韦提出了完整的电磁场理论B.麦克斯韦第一个预言了电磁波的存在,赫兹第一个用实验证实了电磁波的存在C.变化的电场可以在周围的空间产生电磁波D.变化的磁场在周围的空间一定产生变化的电场题组二各种电磁波的共性及个性的比较2.(多选)关于生活中遇到的各种波,下列说法正确的是()A.电磁波可以传递信息B.声波不能传递信息C.手机在通话时涉及的波既有电磁波又有声波D.太阳光中的可见光是电磁波3.(多选)为了体现高考的公平、公正,高考时在考场使用了手机信号屏蔽器,该屏蔽器在工作过程中以一定的速度由低端频率向高端频率扫描,该扫描速度可以在手机接收报文信号时形成乱码干扰,手机不能检测从基站发出的正常数据,使手机不能与基站建立连接,达到屏蔽手机信号的目的,手机表现为搜索网络、无信号、无服务系统等现象。
由以上信息可知()A.由于手机信号屏蔽器的作用,考场内没有电磁波B.即使有手机信号屏蔽器作用,考场内仍有电磁波C.手机信号屏蔽器工作时基站发出的电磁波不能传播到考场内D.手机信号屏蔽器是通过发射电磁波干扰手机工作来达到目的的4.关于电磁波传播速度表达式v=λf,下列说法正确的是()A.波长越长,传播速度越快B.频率越高,传播速度越快C.发射能量越大,传播速度越快D.电磁波的传播速度与传播介质有关B组关键能力提升练5.某处产生了一电磁波,该电磁波()A.一定是横波B.不能在真空中传播C.只能沿着某一方向传播D.在空气中的传播速度约为3×107 m/s6.验钞机发出的光能使钞票上的荧光物质发光,电视机、空调的遥控器发出的光能控制电视机、空调的工作状态。
对于它们发出的光,下列判断正确的是() A.它们发出的都是红外线B.它们发出的都是紫外线C.验钞机发出的是红外线,遥控器发出的是紫外线D.验钞机发出的是紫外线,遥控器发出的是红外线7.目前雷达发出的电磁波频率多在200~1 000 MHz的范围内,下列关于电磁波的说法正确的是()A.真空中,上述频率范围的电磁波的波长在30~150 mB.电磁波是由恒定不变的电场或磁场产生的C.波长越短的电磁波,越容易绕过障碍物,便于远距离传播D.测出从发射无线电波到接收反射回来的无线电波的时间,就可以确定障碍物的距离8.某广播电台发射“中波”段某套节目的信号、家用微波炉中的微波、VCD机中的激光(可见光)、人体透视用的X光,都是电磁波,它们的频率分别为f1,f2,f3,f4,则()A.f1>f2>f3>f4B.f1<f2<f3<f4C.f1<f3<f2<f4D.f1>f2<f3<f49.太阳表面温度约为6 000 K,主要发出可见光;人体温度约为310 K,主要发出红外线;宇宙空间的温度约为3 K,所发出的辐射称为“3 K背景辐射”,它是宇宙“大爆炸”之初在空间上保留下的余热。
教科高二版物理选修3—1第3章 磁场练习含答案

(高二)教科版物理选修3—1第3章磁场练习含答案教科版选修3--1第三章磁场1、把一根长直导线平行地放在磁针的正上方附近,当导线中有电流通过时,磁针会发生偏转.首先观察到这个实验现象的物理学家是()A.奥斯特B.爱因斯坦C.牛顿D.伽利略2、螺线管正中间的上方悬挂一个通有顺时针方向电流的小线圈,线圈的平面与螺线管的轴线在同一竖直面内,如图所示.当开关S合上时(一小段时间内),从上方俯视,线圈应该()A.顺时针方向转动,同时向左移动B.逆时针方向转动,同时向右移动C.顺时针方向转动,同时悬线的拉力减小D.逆时针方向转动,同时悬线的拉力增大3、在实验精度要求不高的情况下,可利用罗盘来测量电流产生磁场的磁感应强度.具体做法是:在一根南北方向放置的直导线的正下方10 cm处放一个罗盘.导线没有通电时罗盘的指针(小磁针的N极)指向北方;当给导线通入电流时,发现罗盘的指针偏转一定角度,根据偏转角度即可测定电流磁场的磁感应强度.现已测出此地的地磁场水平分量B e=5.0×10-5 T,通电后罗盘指针停在北偏东60°的位置(如图所示).由此测出该通电直导线在其正下方10 cm处产生磁场的磁感应强度大小为()A.5.0×10-5 T B.1.0×10-4 TC.8.66×10-5 T D.7.07×10-5 T4、(多选)一束混合粒子流从一发射源射出后,进入如图所示的磁场中,分离为1、2、3三束,则下列判断正确的是()A.1带正电B.1带负电C.2不带电D.3带负电5、薄铝板将同一匀强磁场分成Ⅰ、Ⅱ两个区域,高速带电粒子可穿过铝板一次,在两个区域内运动的轨迹如图所示,半径R1>R2.假定穿过铝板前后粒子电荷量保持不变,则该粒子()A.带正电B.在Ⅰ、Ⅱ区域的运动速度大小相同C.在Ⅰ、Ⅱ区域的运动时间相同D.从Ⅱ区域穿过铝板运动到Ⅰ区域6、如图所示,在等边三角形的三个顶点a、b、c处各有一条长直导线垂直穿过纸面,导线中通有大小相等的恒定电流,方向垂直纸面向里.过c点的导线所受安培力的方向()A.与ab边垂直,指向左边B.与ab边垂直,指向右边C.与ab边平行,竖直向上D.与ab边平行,竖直向下7、三根完全相同的长直导线互相平行,通以大小和方向都相同的电流.它们的截面处于一个正方形abcd的三个顶点a、b、c处,如图所示.已知每根通电长直导线在其周围产生的磁感应强度与距该导线的距离成反比,通电导线b在d 处产生的磁场其磁感应强度大小为B,则三根通电导线产生的磁场在d处的总磁感应强度大小为()A.2B B.3BC.322 B D.32B8、一个带电粒子沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示,径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电荷量不变).从图中情况可以确定()A.粒子从a到b,带正电B.粒子从a到b,带负电C.粒子从b到a,带正电D.粒子从b到a,带负电9、截面为矩形的载流金属导线置于磁场中,如图所示,将出现下列哪种情况()A.在b表面聚集正电荷,而a表面聚集负电荷B.在a表面聚集正电荷,而b表面聚集负电荷C.在a、b表面都聚集正电荷D.无法判断a、b表面聚集何种电荷10、如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是()A.棒中的电流变大,θ角变大B.两悬线等长变短,θ角变小C.金属棒质量变大,θ角变大D.磁感应强度变大,θ角变小11、长10 cm的通电直导线,通过1 A的电流,在磁场强弱、方向都一样的空间(匀强磁场)中某处受到的磁场力为0.4 N,则该磁场的磁感应强度() A.等于4 T B.大于或等于4 TC.小于或等于4 T D.上述说法都错误12、如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).13、如图所示,有一对平行金属板,两板相距为0.05 m,电压为10 V;两板之间有匀强磁场,磁感应强度大小为B0=0.1 T,方向与金属板平行并垂直于纸面向里.图中右边有一半径R为0.1 m、圆心为O的圆形区域内也存在匀强磁场,磁感应强度大小为B=33T,方向垂直于纸面向里.一正离子沿平行于金属板面,从A点垂直于磁场的方向射入平行金属板之间,沿直线射出平行金属板之间的区域,并沿直径CD方向射入圆形磁场区域,最后从圆形区域边界上的F点射出.已知速度的偏向角θ=π3,不计离子重力.求:(1)离子速度v的大小;(2)离子的比荷q m;(3)离子在圆形磁场区域中运动时间t.(高二)教科版物理选修3—1第3章磁场练习含答案教科版选修3--1第三章磁场1、把一根长直导线平行地放在磁针的正上方附近,当导线中有电流通过时,磁针会发生偏转.首先观察到这个实验现象的物理学家是()A.奥斯特B.爱因斯坦C.牛顿D.伽利略A[奥斯特发现了电流的磁效应,即把一根长直导线平行地放在磁针的正上方附近,当导线中有电流通过时,磁针会发生偏转,故A正确.]2、螺线管正中间的上方悬挂一个通有顺时针方向电流的小线圈,线圈的平面与螺线管的轴线在同一竖直面内,如图所示.当开关S合上时(一小段时间内),从上方俯视,线圈应该()A.顺时针方向转动,同时向左移动B.逆时针方向转动,同时向右移动C.顺时针方向转动,同时悬线的拉力减小D.逆时针方向转动,同时悬线的拉力增大D[闭合S后,螺线管左端为S极,右端为N极,由左手定则知圆环右边受垂直于纸面向里的安培力,左边受垂直于纸面向外的安培力,所以从上向下看线圈逆时针方向转动,当转动到线圈与纸面垂直时,线圈等效为左端为N极、右端为S极的磁针,由磁极间的作用力可知悬线拉力增大.]3、在实验精度要求不高的情况下,可利用罗盘来测量电流产生磁场的磁感应强度.具体做法是:在一根南北方向放置的直导线的正下方10 cm处放一个罗盘.导线没有通电时罗盘的指针(小磁针的N极)指向北方;当给导线通入电流时,发现罗盘的指针偏转一定角度,根据偏转角度即可测定电流磁场的磁感应强度.现已测出此地的地磁场水平分量B e=5.0×10-5 T,通电后罗盘指针停在北偏东60°的位置(如图所示).由此测出该通电直导线在其正下方10 cm处产生磁场的磁感应强度大小为()A.5.0×10-5 T B.1.0×10-4 TC.8.66×10-5 T D.7.07×10-5 TC[将罗盘放在通电直导线下方,罗盘静止时罗盘指针所指方向为该处的合磁场方向,如图,所以电流在该处产生的磁场的磁感应强度为B1=Btan θ,代入数据得:B1=8.66×10-5 T.C正确.]4、(多选)一束混合粒子流从一发射源射出后,进入如图所示的磁场中,分离为1、2、3三束,则下列判断正确的是()A.1带正电B.1带负电C.2不带电D.3带负电ACD[ 根据左手定则,带正电的粒子左偏,不偏转说明不带电,带负电的粒子向右偏,因此选A、C、D.]5、薄铝板将同一匀强磁场分成Ⅰ、Ⅱ两个区域,高速带电粒子可穿过铝板一次,在两个区域内运动的轨迹如图所示,半径R1>R2.假定穿过铝板前后粒子电荷量保持不变,则该粒子()A.带正电B.在Ⅰ、Ⅱ区域的运动速度大小相同C.在Ⅰ、Ⅱ区域的运动时间相同D.从Ⅱ区域穿过铝板运动到Ⅰ区域C[粒子穿过铝板受到铝板的阻力,速度将减小. 由r=m vBq可得粒子在磁场中做匀速圆周运动的轨道半径将减小,故可得粒子由Ⅰ区域运动到Ⅱ区域,结合左手定则可知粒子带负电,选项A、B、D错误;由T=2πmBq可知粒子运动的周期不变,粒子在Ⅰ区域和Ⅱ区域中运动的时间均为t=12T=πmBq,选项C正确.]6、如图所示,在等边三角形的三个顶点a、b、c处各有一条长直导线垂直穿过纸面,导线中通有大小相等的恒定电流,方向垂直纸面向里.过c点的导线所受安培力的方向()A.与ab边垂直,指向左边B.与ab边垂直,指向右边C.与ab边平行,竖直向上D.与ab边平行,竖直向下A[等边三角形的三个顶点a、b、c处均有一通电导线,且导线中通有大小相等的恒定电流.由安培定则可得:导线a、b的电流在c处的合磁场方向竖直向下.再由左手定则可得:安培力的方向是与ab边垂直,指向左边.]7、三根完全相同的长直导线互相平行,通以大小和方向都相同的电流.它们的截面处于一个正方形abcd的三个顶点a、b、c处,如图所示.已知每根通电长直导线在其周围产生的磁感应强度与距该导线的距离成反比,通电导线b在d 处产生的磁场其磁感应强度大小为B,则三根通电导线产生的磁场在d处的总磁感应强度大小为()A.2B B.3BC.322 B D.32BB[设正方形边长为l,则导线b在d处形成的磁场磁感应强度大小B=k2l ;ac两根导线在d处形成的磁场磁感应强度大小均为:B a=B c=kl=2B;则三根通电导线产生的磁场在d处的总磁感应强度大小为B总=2B a+B=3B.]8、一个带电粒子沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示,径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电荷量不变).从图中情况可以确定()A .粒子从a 到b ,带正电B .粒子从a 到b ,带负电C .粒子从b 到a ,带正电D .粒子从b 到a ,带负电D [垂直于磁场方向射入匀强磁场的带电粒子受洛伦兹力作用,使粒子做匀速圆周运动,半径R =m v qB .由于带电粒子使沿途的空气电离,粒子的能量减小,又据E k =12m v 2知,v 在减小,故R 减小,可判定粒子从b 向a 运动;另据左手定则,可判定粒子带负电.]9、截面为矩形的载流金属导线置于磁场中,如图所示,将出现下列哪种情况( )A .在b 表面聚集正电荷,而a 表面聚集负电荷B .在a 表面聚集正电荷,而b 表面聚集负电荷C .在a 、b 表面都聚集正电荷D .无法判断a 、b 表面聚集何种电荷A [金属导体靠自由电子导电,金属中正离子并没有移动,而电流由金属导体中的自由电子的定向移动(向左移动)形成.根据左手定则,四指应指向电流的方向,让磁感线垂直穿过手心,拇指的指向即为自由电子的受力方向.也就是说,自由电子受洛伦兹力方向指向a 表面一侧,实际上自由电子在向左移动的同时,受到指向a 表面的作用力,并在a 表面进行聚集,由于整个导体是呈电中性的(正、负电荷总量相等),所以在b 的表面“裸露”出正电荷层,并使b 表面电势高于a 表面电势,A 正确.]10、如图所示,金属棒MN 两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M 向N 的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是()A.棒中的电流变大,θ角变大B.两悬线等长变短,θ角变小C.金属棒质量变大,θ角变大D.磁感应强度变大,θ角变小A [导体棒受力如图所示.tan θ=Fmg=BILmg;棒中电流I变大,θ角变大,故A正确;两悬线等长变短,θ角不变,故B错误;金属棒质量变大,θ角变小,故C错误;磁感应强度变大,θ角变大,故D错误.]11、长10 cm的通电直导线,通过1 A的电流,在磁场强弱、方向都一样的空间(匀强磁场)中某处受到的磁场力为0.4 N,则该磁场的磁感应强度() A.等于4 T B.大于或等于4 TC.小于或等于4 T D.上述说法都错误B[题目中没有给出导线如何放置,若导线与磁场垂直,则由磁感应强度定义式得出B=FIL=0.41×0.1T=4 T.若导线放置时没与磁场垂直,此时受磁场力为0.4 N,根据磁感应强度定义式B=FIL可知此处磁感应强度将大于4 T,故B正确.]12、如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).解析:如图所示,由于质子在O 点的速度垂直于板NP ,所以粒子在磁场中做圆周运动的圆心O ′一定位于NP 所在的直线上.如果直径小于ON ,则轨迹将是圆心位于ON 之间的一段半圆弧.(1)如果质子恰好从N 点射出,R 1=d 4,q v 0B 1=m v 20R 1. 所以B 1=4m v 0dq .(2)如果质子恰好从M 点射出R 22-d 2=⎝ ⎛⎭⎪⎫R 2-d 22,q v 0B 2=m v 20R 2,得B 2=4m v 05dq . 所以B 应满足4m v 05dq ≤B ≤4m v 0dq .答案:4m v 05dq ≤B ≤4m v 0dq13、如图所示,有一对平行金属板,两板相距为0.05 m ,电压为10 V ;两板之间有匀强磁场,磁感应强度大小为B 0=0.1 T ,方向与金属板平行并垂直于纸面向里.图中右边有一半径R 为0.1 m 、圆心为O 的圆形区域内也存在匀强磁场,磁感应强度大小为B =33 T ,方向垂直于纸面向里.一正离子沿平行于金属板面,从A 点垂直于磁场的方向射入平行金属板之间,沿直线射出平行金属板之间的区域,并沿直径CD 方向射入圆形磁场区域,最后从圆形区域边界上的F点射出.已知速度的偏向角θ=π3,不计离子重力.求:(1)离子速度v 的大小;(2)离子的比荷q m ;(3)离子在圆形磁场区域中运动时间t.解析:(1)离子在平行金属板之间做匀速直线运动,洛伦兹力与电场力大小相等,即:B 0q v =qE 0E 0=U d解得v =2 000 m/s.(2)在圆形磁场区域,离子做匀速圆周运动,由洛伦兹力公式和牛顿第二定律有:Bq v =m v 2r由几何关系有:tan θ2=R r解得离子的比荷为:q m =2×104 C/kg.(3)弧CF 对应圆心角为θ,离子在圆形磁场区域中运动时间t ,t =θ2π·TT =2πm qB解得t =3π6×10-4 s ≈9×10-5 s.答案:(1)2 000 m/s (2)2×104 C/kg (3)9×10-5 s。
电磁场与电磁波:第三章作业答案
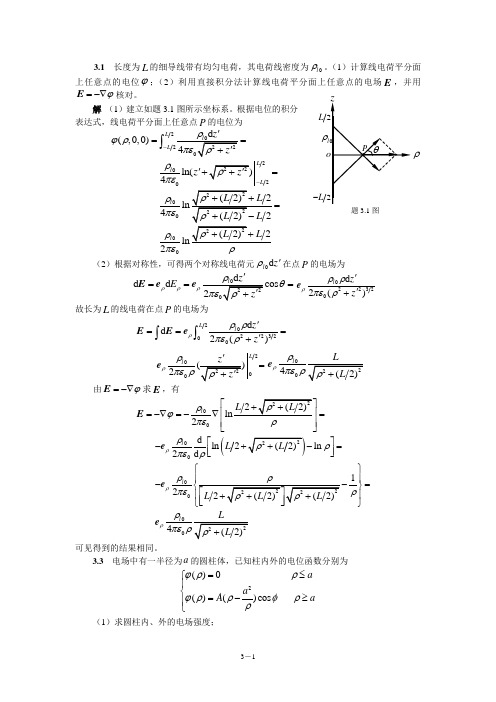
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。
电磁场与电磁波课后习题答案第3章(杨儒贵编着)

第三章 静电场3-1 已知在直角坐标系中四个点电荷分布如习题图3-1所示,试求电位为零的平面。
解 已知点电荷q 的电位为rq 4πεϕ=,令)0,1,0(1q q -=,)0,1,3(2q q +=,)0,0,1(3q q -=,)0,0,0(4q q +=,那么,图中4个点电荷共同产生的电位应为∑=414ii r q πεϕ令0=ϕ,得 0 4 4 4 44321=+-+-r qr q r q r q πεπεπεπε 由4个点电荷的分布位置可见,对于x =1.5cm 的平面上任一点,4321 ,r r r r ==,因此合成电位为零。
同理,对于x =0.5cm 的平面上任一点,3241 ,r r r r ==,因此合成电位也为零。
所以,x =1.5cm 及x =0.5cm 两个平面的电位为零。
3-2 试证当点电荷q 位于无限大的导体平面附近时,导体表面上总感应电荷等于)(q -。
证明 建立圆柱坐标,令导体表面位于xy 平面,点电荷距离导体表面的高度为h ,如图3-2所示。
那么,根据镜像法,上半空间的电场强度为32023101 4 4r q r q πεπεr r E -=X 习题图3-1(r , z )习题图3-2电通密度为)(43223110r r q r r E D -==πε 式中 232231])([h z r r -+=; 232232])([h z r r ++=那么,⎥⎥⎥⎦⎤⎪⎪⎪⎭⎫ ⎝⎛+++-++-+⎢⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛++--+=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++++--+-+=z z zh z r hz h z r h z h z r r h z r r q h z r h z r h z r h z r q e e e e e e D r r r 232223222322232223222322])([])([ ])([])([4 ])([)(])([)(4ππ 已知导体表面上电荷的面密度n s D =ρ,所以导体表面的感应电荷为2322232223220)(2][][4h r qh h r h h r h q D z zs +-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++-+-===ππρ 则总的感应电荷为q h r r r qh r r S q s ss -=+-===⎰⎰⎰∞∞2322)(d d 2d 'πρρ3-3 根据镜像法,说明为什么只有当劈形导体的夹角为π的整数分之一时,镜像法才是有效的?当点电荷位于两块无限大平行导体板之间时,是否也可采用镜像法求解。
教科版高中物理必修第三册课后习题 第3章 电磁场与电磁波初步 分层作业24 磁场 磁感线

分层作业24 磁场磁感线A组必备知识基础练题组一对磁场的理解1.如图所示,某磁场的一条磁感线。
其上有A、B两点,则( )A.A点的磁场一定强B.B点的磁场一定强C.因为磁感线是直线,A、B两点的磁场一样强D.条件不足,无法判断2.小磁针放置在匀强磁场中,小磁针静止时的指向正确的是( )题组二对磁感线的进一步认识3.(多选)磁场中某区域的磁感线如图所示,a、b、c、d、e是磁场中的5个点,b、e两点所在的磁感线为一直线,其中c、d两点关于该直线对称,下列说法正确的是( )A.这5个位置中,e点的磁场最强B.a点没有磁感线穿过,所以a点磁场一定为零C.c、d两点关于直线对称,所以c、d两点磁场方向相同D.b、e两点在同一直线上,所以b、e两点磁场方向相同4.冰箱门软磁条的外部磁感线正面图如图所示,下列说法正确的是( )A.磁感线越密的地方磁场越弱B.软磁条内部a位置应为N极C.磁感线与电场线一样真实存在于空间之中D.软磁条内部ab之间的磁感线方向应为a指向b题组三安培定则5.为了判断一个未知正负极的蓄电池极性,某同学将该蓄电池通过电阻跟螺线管连接起来,发现小磁针的N极立即向螺线管偏转,如图所示。
用M、N和P、Q分别表示蓄电池和螺线管两极,下列判断正确的是( )A.电源M端为正极B.电源N端为正极C.螺线管P端为S极D.螺线管内部磁场方向由P指向Q6.如图所示,环形导线周围有三只小磁针a、b、c,闭合开关S后,三只小磁针N极的偏转方向是( )A.全向里B.全向外C.a向里,b、c向外D.a、c向外,b向里7.(多选)如图所示为电流产生磁场的分布图。
正确的分布图是( )B组关键能力提升练8.铁棒A能吸引小磁针,铁棒B能排斥小磁针,若将铁棒A靠近铁棒B,则( )A.A、B一定相互吸引B.A、B一定相互排斥C.A、B之间有可能无磁场力作用D.A、B可能相互吸引,也可能相互排斥9.中国宋代科学家沈括在《梦溪笔谈》中最早记载了地磁偏角:“以磁石磨针锋,则能指南,然常微偏东,不全南也。
教科版高中物理必修第三册课后习题 第3章 电磁场与电磁波初步 分层作业26 电磁感应现象及其应用

分层作业26 电磁感应现象及其应用A组必备知识基础练题组一电磁感应现象与电流的磁效应1.关于电磁感应现象,下列说法正确的是( )A.闭合线圈放在变化的磁场中,必然有感应电流产生B.闭合正方形线圈在匀强磁场中垂直磁感线运动,必然产生感应电流C.穿过闭合线圈的磁通量变化时,线圈中有感应电流D.只要穿过电路的磁通量发生变化,电路中就一定有感应电流产生2.假设航天员登月后,想探测一下月球表面是否有磁场,他手边有一个灵敏电流表和一个小线圈,则下列推断正确的是( )A.直接将电流表放于月球表面,根据电流表有无示数来判断磁场的有无B.将电流表与线圈连成闭合回路,使线圈沿某一方向运动,若电流表无示数,则可以判断月球表面无磁场C.将电流表与线圈连成闭合回路,使线圈沿某一方向运动,若电流表有示数,则可以判断月球表面有磁场D.将电流表与线圈连成闭合回路,使线圈在某一平面内沿各个方向运动,若电流表无示数,则可以判断月球表面无磁场3.如图所示实验装置中用于研究电磁感应现象的是( )题组二产生感应电流的条件4.如图所示,线圈两端接在电流表上组成闭合电路。
在下列情况中,电流表指针不发生偏转的是( )A.线圈不动,磁铁插入线圈B.线圈不动,磁铁从线圈中拔出C.磁铁不动,线圈上、下移动D.磁铁插在线圈内不动5.某学生做探究感应电流的产生条件的实验,将电流表、线圈A和B、蓄电池、开关用导线连接成如图所示的实验电路,当他闭合、断开开关时,电流表的指针都没有偏转,其原因是( )A.开关位置接错B.电流表的正、负极接反C.线圈B的接头3、4接反D.蓄电池的正、负极接反6.(多选)下列情况能产生感应电流的是( )A.如图甲所示,导体AB顺着磁感线运动B.如图乙所示,条形磁铁插入或拔出线圈时C.如图丙所示,小螺线管A插入大螺线管B中不动,开关S一直接通时D.如图丙所示,小螺线管A插入大螺线管B中不动,开关S一直接通,当改变滑动变阻器的阻值时B组关键能力提升练7.(多选)如图所示,线圈abcd在磁场区域ABCD中,下列哪种情况下线圈中有感应电流产生( )A.把线圈变成圆形(周长不变)B.使线圈在磁场中加速平移C.使磁场增强或减弱D.使线圈以过ab的直线为轴旋转8.(多选)如图所示的实验中,在一个足够大的磁体形成的竖直向下的磁场中,如果导体棒AB沿水平方向前后运动的速度大小为v1,两磁极沿水平方向前后运动的速度大小为v2,则( )A.当v1=v2,且方向相同时,可以产生感应电流B.当v1=v2,且方向相反时,可以产生感应电流C.当v1≠v2时,方向相同或相反都可以产生感应电流D.当v2=0时,v1的方向改为与磁感线的夹角为θ,且0°<θ<90°,可以产生感应电流9.(多选)如图所示,线框ABCD从有界的匀强磁场区域穿过,下列说法正确的是( )A.进入匀强磁场区域的过程中,ABCD中有感应电流B.在匀强磁场中加速运动时,ABCD中有感应电流C.在匀强磁场中匀速运动时,ABCD中没有感应电流D.离开匀强磁场区域的过程中,ABCD中没有感应电流10.如图所示,在条形磁铁的外面套着一个闭合金属弹簧线圈P,现用力从四周拉弹簧线圈,使线圈包围的面积变大,则下列关于穿过弹簧线圈磁通量的变化以及线圈中是否有感应电流产生的说法正确的是( )A.磁通量增大,有感应电流产生B.磁通量增大,无感应电流产生C.磁通量减小,有感应电流产生D.磁通量减小,无感应电流产生C组核心素养拔高练11.探究感应电流产生的条件的实验电路如图所示。
高等电磁场理论习题解答(作业)

第一章基本电磁理论1-1 利用Fourier 变换, 由时域形式的Maxwell方程导出其频域形式。
(作1-2—1-3)解:付氏变换和付氏逆变换分别为:麦氏方程:对第一个方程进行付氏变换:(时谐电磁场)同理可得:上面四式即为麦式方程的频域形式。
1-2 设各向异性介质的介电常数为当外加电场强度为(1) ;(2) ;(3) ;(4) ;(5)求出产生的电通密度。
(作1-6)解:将E分别代入,得:1-3 设各向异性介质的介电常数为试求:(1) 当外加电场强度时,产生的电通密度D;(2) 若要求产生的电通密度,需要的外加电场强度E。
(作1-7—1-8)解:即:.附:又所以1-6 已知理想导电体表面上某点的电磁场为试求该点表面电荷及电流密度。
解:由已知条件,理想导体表面某点:(1-6-1)(1-6-2)知该点处的法向单位矢量为: (1-6-3)理想导体表面上的电磁场满足边界条件:(1-6-4)(1-6-5)将(1-6-2)、(1-6-3)式代入(1-6-4)式,得该点处的表面电流密度为:(1-6-6)将(1-6-1)、(1-6-3)式代入(1-6-5)式,得该点处的表面电荷密度为:(1-6-7)1-9 若非均匀的各向同性介质的介电常数为, 试证无源区中的时谐电场强度满足下列方程:(作1-9)证明:非均匀各向同性介质中(无源区)的时谐电磁场满足(1-9-1)(1-9-2)对(1-9-2)式两边取旋度,并利用(1-9-1)得又所以 (1-9-3)又在非均匀各向同性介质中即 (1-9-4)将(1-9-4)代入(1-9-3),得即第2章平面电磁波2-1 导出非均匀的各向同性线性媒质中,正弦电磁场应该满足的波动方程及亥姆霍兹方程。
解:非均匀各向同性线性媒质中,正弦电磁场满足的Maxwell方程组为(2-1-1)(2-1-2)(2-1-3)(2-1-4)对(2-1-2)式两边取旋度,并应用(2-1-1)得即对(2-1-1)式两边取旋度,并应用(2-1-2)得所以非均匀各向同性媒质中,正弦电磁场满足的波动方程为 (2-1-5)(2-1-6)由(2-1-4)式得即 (2-1-7)由(2-1-3)式得即 (2-1-8)利用矢量关系式,并将(2-1-7)(2-1-8)式代入,得电磁场满足的亥姆霍兹方程为(2-1-9)(2-1-10)均匀介质中,无源区中2-4 推导式(2-2-8)。
电磁场与电磁波第三章习题及参考答案

第3章习题3-1 半径为的薄圆盘上电荷面密度为s ρ,绕其圆弧轴线以角频率旋转形成电流,求电流面密度。
解:圆盘以角频率旋转,圆盘上半径为r 处的速度为r ω,因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中,每立方米体积中大约有28105.8⨯个自由电子。
如果铜线的横截面为210cm ,电流为A 1500。
计算 1) 电流密度;2) 电子的平均漂移速度; 解:1)电流密度m A S I J /105.11010150064⨯=⨯==- 2) 电子的平均漂移速度 v J ρ=,3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m J v /101.11036.1105.14106-⨯=⨯⨯==ρ 3-3 一宽度为cm 30传输带上电荷均匀分布,以速度s m /20匀速运动,形成的电流,对应的电流强度为A μ50,计算传输带上的电荷面密度。
解:电流面密度为m A L I J S /7.1663.050μ===因为 v J S S ρ= 所以 2/33.8207.166m C v J S S μρ=== 3-4 如果ρ是运动电荷密度,U是运动电荷的平均运动速度,证明:0=∂∂+∇⋅+⋅∇tU U ρρρ证:如果ρ是运动电荷密度,U是运动电荷的平均运动速度,则电流密度为U J ρ=代入电荷守恒定律tJ ∂∂-=⋅∇ρ得0=∂∂+∇⋅+⋅∇t U U ρρρ3-5 由m S /1012.17⨯=σ的铁制作的圆锥台,高为m 2,两端面的半径分别为cm 10和cm 12。
求两端面之间的电阻。
解:用两种方法(1)如题图3.5所示⎰⎰==2122)(tan zz lz dzS dl R ασπσ)11()(tan 1212z z -=ασπ 01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α,m r z 1201.0/12.0tan /22===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R (2)设流过的电流为I ,电流密度为2rI S I J π==电场强度为 2r IJ E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上,媒质1的参数为2,/10011==r m S εσ,电流密度的大小为2/50m A ,方向和界面法向的夹角为030;媒质2的参数为4,/1022==r m S εσ。
电磁场与电磁波(第四版)课后答案 第三章习题

3.23一电荷量为 q 质量为 m 的小带电体,放置在无限长导体 平面下方,与平面距离 h 。求 q 的值以使带电体上受到的 −3 静电力恰好与重力相平衡(设 m = 2 ×10 kg , h = 0.02m)。 解:小带电体可视为一点电荷 q ,它所受静电力,来自导体
' 平板的感应电荷,也就是镜像电荷 q(平面上方 h 处, q' =−q)对它的作用力。
a2 ϕ = A(r − ) cos ϕ r
r≥a
(1)求圆柱内、外的电场强度; (2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。 解: (1)电场
在
处 ur r ur a 2 uu a2 E = − er A cos ϕ (1 + 2 ) − eϕ A(1 − 2 sin ϕ ) r r 即 ur ur uu r a2 A a2 A E = er (− A − 2 ) cos ϕ + eϕ ( A − 2 sin ϕ ) ( r ≥ a ) r r
由安培环路定律有315无限长直线电流垂直于磁导率分别为的两种磁介质的交界面试求1两种媒质中的磁感应以z轴为中心为半径做一个圆形回路c由安培环路定律有16319同轴线内导体是半径为a的圆柱外导体是半径为b的薄圆柱面其厚度可忽略不计
第三章 习题
3.3 有一半径为 a 的圆柱体,已知柱内外的电位函数分别为 ϕ =0 r≤a
E1t = E2t = E
En = 0
所以此题仍可用高斯定理
∫
S
ur u r D dS = q
求解,即
D1S1 + D2 S2 = q
4π r 2 4π r 2 ε1 E + ε2E =q 2 2
所以
E=
大学电磁场课后答案第三章

ε1 ε 2 − ) σ1 σ 2 ε1 ε 2 ≠ σ1 σ 2
因此,分界面上存在自由电荷的条件是
3-8
在导体中有恒定电流而其周围媒质的电导率为零时,试证明导体表面电通量密度的法 向分量 Dn = σ , 但矢量关系 D = e n σ 不成 立( 式中 e n 是导体表面向 外的法 线单位矢 量)。
W = ∑ σϕi ∫
i =1 n
n
Si
n ∂ϕ ∂ϕ − dS dS = ∑ σϕi ∫ S i ∂n ∂n ' i =1 n n Jn ' dS = ∑ ϕi J ' dS ϕi I i = ∑ ∫ Si n ∂n i =1 i =1
= ∑ σϕi ∫
i =1
Si
故命题得证。 3-10 有一非均匀导电媒质板,厚度为 d ,其两侧面为良导体电极,下板表面与坐标 z = 0 重 ρ − ρ R2 1 合, 介质的电阻率为 ρ R = = ρ R1 + R1 z, 介电常数为 ε 0 , 而其中有 J = e z J 0 的 γ d 均匀电流。试求:1) 介质中的自由电荷密度。2) 两极板间的电位差。3) 面积为 A 的 一块介质板中的功率损耗。
u v
R铁=
单位长度的水柱电阻为
ρ铁 S铁
=
8.7 × 10 −8 π (0.025 2 − 0.02 2 ) ρ水 S水
R水=
=
0.01 π 0.02 2
当水管中的电流为 20A 时,水柱和铁管中的电流之比为
I水 I铁
又根据题意
=
R铁 R水
=1.5 × 10 −5
(1)
I 水+I 铁=20 A
所以将(1)、(2)联立求解,可得管壁和水中的电流强度
电磁场与电磁波(第三版)课后答案第3章

第三章习题解答3.1 真空中半径为a 的一个球面,球的两极点处分别设置点电荷q 和q -,试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。
解 由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e22322232()[]2d 4()()aq a arr r a r a ππ--=++⎰ 221201)0.293()aqa q q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型,其球体内均匀分布有总电荷量为Ze -的电子云,在球心有一正电荷Ze (Z 是原子序数,e 是质子电荷量),通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ,试证明之。
解 位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为 333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为32234344r r ar Ze rr r ρπππ==-D e e 故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中,体密度为30C m ρ, 两圆柱面半径分别为a 和b ,轴线相距为c )(a b c -<,如题3.3图()a 所示。
求空间各部分的电场。
解 由于两圆柱面间的电荷不是轴对称分布,不能直接用高斯定律求解。
但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布,这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布,而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布,如题3.3图()b 所示。
电磁场与电磁兼容习题答案与详解_第3章

电磁场与电磁兼容习题答案与详解第三章3.2 已知自由空间传播的均匀平面电磁波,电场强度为: 22042041010πππj z j zj e e +----+=y x a a E )/(m V试求:①该电磁波向何方向传播;②该电磁波的频率f ;③该电磁波的极化方式;④该电磁波的磁场强度H ;⑤与该波传播方向垂直的单位面积流过的的平均功率。
解: ①z k a a=即是+z 方向②π20=k rad/m m k 1.02==∴πλ 9103v ⨯==∴λf Hz③zj y x e a j a E π2044)1010(---+=()z 20t cos 10E 4x πϖ-=- ⎪⎭⎫⎝⎛+-=-2z 20t cos 10E 4y ππϖ1E E 2y 2x =+∴ ()z 20-t tg E E xyπϖ-=由上可知,该波为左旋圆极化波。
④zj x y z j y x z z e a j a e a j a a E a H ππππη2052040)(1210)(120101-----=+⨯=⨯= A/m ⑤[]ππ1210)()(121010Re 21Re 21954---*=⎥⎦⎤⎢⎣⎡+⨯+⨯=⨯=z x y y x a a j a a j a H E S 平均 W/m23.5 已知真空中传播的平面电磁波的电场强度为: )]23(30.05-t 10)cos[635(),(7z y x t +-⨯+=ππy x a a r E V/m 试求:①电场强度的振幅、波矢量及波长;②磁场强度矢量),(t r H ;③平均坡印亭矢量平均S 。
解:①m v E m /10315=+=m rad a a a k z y x /)233(05.0 +-=πππ2.043905.0=++=km k102==πλ ②)233(41z y x k a a a k k a +-== ⋅+⨯+-=⨯=)3(5)233(4801),(1),(0y x z y x k a a a a a t r E a t H πηγ [])233(05.0106cos 7z y x t +--⨯ππ =[])233(05.0106cos )323(4817z y x t a a a z y x +--⨯++-πππ③m V e a a E z y x j y x /)3(5)233(05.0+--+=π m A e a a a H z y x j z y x /)323(481)233(05.0+--++-=ππ[]ππηπ48524010021/)233(485Re 21202*===+-=⨯=E m W a a a H E S z y x 平均3.6 在1=r μ,4=r ε,0=σ的媒质中有一均匀平面波,其电场强度为: )3sin(),z (0πω+-=kz t t E E 。
电磁场与电磁波第三版答案第三章

《电磁场与电磁波》——习题详解第三章 恒定电流的电场和磁场3-1 一个半径为 a 的球内均匀分布着总量为 q 的电荷,若其以角速度 ω 绕一直径匀 速旋转,求球内的电流密度. 解:传导电流:导体中的自由电子或半导体中的自由电荷在电场作用下作定向 运动所形成的电流. 运流电流: 带电粒子在真空或气体中运动时形成的电流. 本题求的是运流电流. 选 取 球 坐 标系 . 设 转 轴和 直 角 坐 标系 的 z 轴 重 合 , 球 内 某 一点 的 坐标为 ( r , θ , φ ),则电流密度为v v J =ρv =q v 3qω r sin θ v eφ ω r sin θ eφ = 2 4π a 3 4π a 3注意到球面坐标的有向面积元为v v v v d S = er r 2 sin θ d θ d φ + eθ r sin θ d r d φ + eφ r d r d θ可以得到总电流为I=∫∫Sv v J dS =∫ ∫0πJr d r d θ =0aqω 2π2π总电流也可以通过电流强度的定义计算. 因为球体转动一周的时间为 T = 所以ω,I=3-2球形电容器内,外极板的半径分别为 a , b ,其间媒质的电导率为 σ ,当外加 电压为 U 0 时,计算功率损耗并求电阻. 解:设内,外极板之间的总电流为 I .由对称性,可以得到极板间的电流密q qω = T 2π度为v J= v E=I24π r I v e 2 r 4πσ rv er ,U0 = E d r =a∫bI 1 1 4πσ a b 25习题三从而I=v 4πσU 0 σU 0 v ,J = er 1 1 1 1 2 r a b a b2单位体积内功率损耗为 U0 J 1 1 p= =σ r 2 σ a b 2总功率损耗为P=∫b ap 4π r d r =24πσ U 02 1 1 a b2∫d r 4πσ U 02 = 2 1 1 a r a bb由P =U 02 ,得 R R= 1 1 1 4πσ a b 3-3土壤的电导率为 σ . 略去地面的影 一个半径为 a 的导体球作为电极深埋地下, 响,求电极的接地电阻. 解: 当不考虑地面影响时, 这个问题就相当于计算位于无限大均匀导电媒质中的导体球的恒定电流问题.设导体球的电流为 I ,则任意点的电流密度为v J=I 4π rI2v v er , E =I 4πσ rI2v er导体球面的电位为(选取无穷远处为电位零点)U =接地电阻为∫∞a4πσ r2dr =4πσ aR=3-4U 1 = I 4πσ a在无界非均匀导电媒质(电导率和介电常数均是坐标的函数)中,若恒定电流存 在,证明媒质中的自由电荷密度为 ρ = E (ε 证明:由方程 J = 0 得vε σ ) . σv26《电磁场与电磁波》——习题详解v v v v J = (σ E ) = E σ + σ E = 0即E = 故有vσ v Eσρ = D = (ε E ) = E ε + ε Ev ε σ v v = E ε ε E = E ε σ σ σ vvvv3-5如图 3-1,平板电容器间由两种媒质完全填充,厚度分别为 d1 和 d 2 ,介电常数 分别为 ε 1 和 ε 2 ,电导率分别为 σ 1 和 σ 2 ,当外加电压 U 0 时,求分界面上的自 由电荷面密度. 解:设电容器极板之间的电流密度为 J ,则J = σ 1 E1 = σ 2 E2E1 =于是Jσ1, E2 =Jσ2U0d1 d2ε1,σ1 ε2,σ2U0 =即Jd1σ1+Jd 2σ2图 3-1J=U0σ1 σ 2分界面上的自由面电荷密度为d1+d2ρ S = D2 n D1n = ε 2 E2 ε 1 E1 = ε ε U0 = 2 1 σ σ d1 d 2 1 2 +3-6 ε2σ2ε1 J σ1 σ1 σ 2内,外导体半径分别为 a , c 的同轴线,其间填充两种漏电媒质,电导率分别27习题三为 σ 1 ( a < r < b )和 σ 2 ( b < r < c ),求单位长度的漏电电阻. 解:设每单位长度从内导体向外导体的电流为 I ,则电流密度为v J=各区域的电场为I2π rv erv E1 = v E2 =内,外导体间的电压为I2πσ 1rv er ( a < r < b ) v er ( b < r < c )I2πσ 2 rU0 =∫c av v E dr =∫I dr + 2πσ 1 r ab∫ 2πσ r = 2πσb 2cI drIln1b I c + ln a 2πσ 2 b因而,单位长度的漏电电阻为R=3-71 1 U b c = ln + ln I 2πσ 1 a 2πσ 2 b一个半径为 10cm 的半球形接地电极,电极平面与地面重合,如图 3-2,若土 壤的电导率为 0.01S/m,求当电极通过的电流为 100A 时,土壤损耗的功率. 解:半球形接地器的电导为G = 2πσ a接地电阻为I σ a图 3-21 1 R= = G 2πσ a土壤损耗的功率为100 2 = ≈ 1.59 ×106 W P=I R= 2πσ a 2π × 0.01× 0.12I23-8一个正 n 边形(边长为 a )线圈中通过的电流为 I ,试证此线圈中心的磁感应强 度为B= 0 nI π tan 2π a n解:先计算有限长度的直导线在线圈中心产生的磁场.使用公式B=0 I (sin α1 sin α 2 ) 4π r28《电磁场与电磁波》——习题详解并注意到α1 = α 2 =2π π = 2n n设正多边形的外接圆半径是 a .由于r π = cos a n所以,中心点的磁感应强度为B=3-9 0 nI π tan 2π a n求载流为 I ,半径为 a 的圆形导线中心的磁感应强度. 解:电流元 I d l 在中心处产生的磁场为vv v v 0 I d l × er dB = 4π r2各电流元在中心处产生的磁场在同一方向,并注意 的磁场为 3-100 I2a∫rdl2=2π ,所以,圆心处 a.一个载流 I1 的长直导线和一个载流 I 2 的圆环(半径为 a )在同一平面内,圆心 与导线的距离是 d .证明两电流之间的相互作用力为 0 I1 I 2 1 d a d22BdF解:选取图 3-3 所示的坐标.直线电流产生的 I1 磁感应强度为I2 d图 3-3v I v 0 I1 v B1 = 0 1 eφ = eφ 2π r 2π (d + a cos θ )v v v F = I 2 d l 2 × B1θ a∫由对称性可以知道,圆电流环受到的总作用力仅仅有水平分量, d l2 × eφ 的 水平分量为 a cos θ d θ ,再考虑到圆环上,下对称,得vvF=使用公式 0 I1 I 2 2π∫π20 0 I1 I 2 a cos θ dθ = π d + a cos θ∫π0d 1 d θ d + a cos θ 29习题三∫π0dθ = d + a cos θπd a22最后得出二回路之间的作用力为 0 I1 I 2 力). 3-11 d 1 (负号表示吸引 2 2 d a 内,外半径分别为 a , b 的无限长空心圆柱中均匀分布着轴向电流 I ,求柱 内,外的磁感应强度. 解:法一:取积分回路为半径为 r ,圆心在轴上的圆,由安培定律 r≤a 时∫lv v v v H dl = 0 H = 0 B = 0a<r≤b 时 v v H dl =∫lI π (r 2 a 2 ) π (b a 2 )2(r 2 a 2 ) I H 2π r = 2 b a2 H = (r 2 a 2 ) I 2π r (b 2 a 2 )v v (r 2 a 2 ) I 0 v er B = 0 H = 2π r (b 2 a 2 )r >b时∫lv v H dl = I v H= I v er2π r v v I v B = 0 H = 0 er 2π r法二:使用圆柱坐标系.电流密度沿轴线方向为30《电磁场与电磁波》——习题详解 r<a 0, I J = , a<r <b 2 2 π (b a ) 0, b<r 由电流的对称性,可以知道磁场只有圆周分量.用安培定律计算不同区域的磁 场.当 r < a 时,磁场为零.当 a < r < b 时,选取安培回路为半径等于 r 且与导电 圆柱的轴线同心的圆.该回路包围的电流为I ′ = Jπ (r 2 a 2 ) =由 B dl = 2π rB =I (r 2 a 2 ) b2 a2∫vv 0 I ′ ,得 0 I (r 2 a 2 ) B= 2π r (b 2 a 2 )当 r > b 时,回路内包围的总电流为 I ,于是 B = 3-120 I . 2π r两个半径都为 a 的圆柱体,轴间距为 d , d < 2a (如图 3-4).除两柱重叠部 分 ( R 区域) 外,柱间有大小相等,方向相反的电流,密度为 J ,求 R 区域 的B.v解:在重叠区域分别加上量值相等(密度为 J ),方向相反的电流分布,可以 将原问题电流分布化为一个圆柱体内均匀分布正向电流,另一个圆柱体内均匀分布 反向电流.由其产生的磁场可以通过叠加原理计算. 由沿正方向的电流(左边圆柱)在重叠y区域产生的磁感应强度为 B1 :∫B1 d l = 2π r1 B1 = 0π r12 JJ r1r2JB1 = 0 r1 J2o1 vdo2x其方向为左边圆周方向 eφ 1 .图 3-4由沿负方向的电流(右边圆柱)在重叠区域产生的磁感应强度为 B2 :B2 = 0 r2 J231习题三其方向为右边圆柱的圆周方向 eφ 2 . 注意:vv v v v v v eφ1 = ez × eρ1 , eφ 2 = ez × eρ 2 v v v Jv v v B = B1 + B2 = 0 ez × (r1eρ 1 r2 eρ 2 ) 2 Jv J v v = 0 ez × (d ex ) = 0 d e y 2 2 v v v v v 3-13 证明矢位 A1 = ex cos y + e y sin x 和 A2 = e y (sin x + x sin y ) 给出相同的磁场 v B ,并证明它们得自相同的电流分布.它们是否均满足矢量泊松方程?为什么? 证明:与给定矢位相应的磁场为v v ex ey v v B1 = × A1 = x y cos y sin x v ex v v B2 = × A2 = x 0v ez v = ez (cos x + sin y ) z 0 v ez v = ez (cos x + sin y ) z 0v ey y sin x + x sin y所以,两者的磁场相同.与其相应的电流分布为v v 1 1 v v J1 = × B1 = (ex cos y + e y sin x)00v 1 v v J2 = (ex cos y + e y sin x)0可以验证,矢位 A1 满足矢量泊松方程,即vv v v v v 2 A1 = 2 (e x cos y + e y sin x) = (e x cos y + e y sin x) = 0 J 1但是,矢位 A2 不满足矢量泊松方程,即v32《电磁场与电磁波》——习题详解v v v v 2 A2 = 2 [e y (sin x + x sin y )] = e y (sin x + x sin y ) ≠ 0 J 2这是由于 A2 的散度不为零.当矢位不满足库仑规范时,矢位与电流的关系为vv v v v × × A2 = 2 A2 + ( A2 ) = 0 J 2可以验证,对于矢位 A2 ,上式成立,即vv v v 2 A2 + ( A2 ) = e y (sin x + x sin y ) + ( x cos y )v v v = e y (sin x + x sin y ) + ex cos y e y x sin y v v = e y sin x + ex cos y v = 0 J 23-14 半径为 a 的长圆柱面上有密度为 J S 的面电流, 电流方向分别为沿圆周方向和 沿轴线方向,分别求两种情况下柱内,外的 B . 解:(1)当面电流沿圆周方向时,由问题的对称性可以知道,磁感应强度仅仅 是半径 r 的函数,而且只有轴向方向的分量,即vvv v B = ez Bz (r )由于电流仅仅分布在圆柱面上,所以,在柱内或柱外, × B = 0 .将 B = ez Bz (r ) 代入 × B = 0 ,得vvvvv v B × B = eφ z = 0 r即磁场是与 r 无关的常量.在离柱面无穷远处的观察 点,由于电流可以看成是一系列流向相反而强度相同的电流 元之和,所以磁场为零.由于 B 与 r 无关,所以在柱外的任 一点处,磁场恒为零 . 为了计算柱内的磁场, 选取安培回路为图 3-5 所示的矩 形回路vh图 3-533习题三∫lv v B d l = hB = h 0 J S因而柱内任一点处, B = e z 0 J S (2) 当面电流沿轴线方向时,由对称性可知,空间的磁场仅仅有圆周分量,且 只是半径的函数.在柱内,选取安培回路为圆心在轴线并且位于圆周方向的圆.可 以得出,柱内任一点的磁场为零.在柱外,选取圆形回路, B d l =lvv∫vv 0 I ,与该回路交链的电流为 2π aJ S , B d l = 2π rB ,所以l∫vvv v a B = eφ 0 J S r 3-15 一对无限长平行导线,相距 2a ,线上载有大小相等,方向相反的电流 I (如 v v 图 3-6),求磁矢位 A ,并求 B .解:将两根导线产生的磁矢位看作是单个导线产生的磁矢位的叠加,对单个 导线,先计算有限长度产生的磁矢位.设导线长度为 l ,导线 1 的磁矢位为(场点选 在 xoy 平面)A1 =0 I 4π∫ I l / 2 + [(l / 2) 2 + r12 ]l / 2 dz = 0 ln 2 2 12 2π r1 l / 2 (r + z ) 1l/2当 l → ∞ 时,有y A1 =0 I l ln r1 2π-ar2 I图 3-6r1 a I x同理,导线 2 产生的磁矢位为A2 = 由两个导线产生的磁矢位为0 I l ln r2 2πv v l v I l A = ez ( A1 + A2 ) = ez 0 ln ln r 2π 1 r2 v 0 I r2 v 0 I ( x + a) 2 + y 2 = ez ln = ez ln 2π r1 4π ( x a) 2 + y 2相应的磁场为34《电磁场与电磁波》——习题详解v v A v A v B = × A = ex z e y z y x v I = ex 0 2π y y ( x + a) 2 + y 2 ( x a) 2 + y 2 x+a xa v I ey 0 2 2 2 2 2π ( x + a) + y ( x a) + y v v v v v v 3-16 由无限长载流直导线的 B 求矢位 A (用 B d S = A d l , 并且 r = r0 处为∫S∫C磁矢位的参考零点),并验证 × A = B . 解:设导线和 z 轴重合.由于电流只有 z 分量,磁矢位也只有 z 分量.用安培 环路定律,可以得到直导线的磁场为vvv I v B = 0 eφ 2π r 选取矩形回路 C ,如图 3-7 所求.在此回路上,注意到磁矢位的参考点.磁矢位的线积分为∫ ∫SCv v A d l = Az hv v BdS =∫∫0 I Ih r d r d z = 0 ln r0 2π r 2πIBh r0 r图 3-7由此得到I r Az (r ) = 0 ln r0 2π可以验证rv v I v A v B = × A = z eφ = 0 eφ 2π r r3-17 证明 xoy 平面上半径为 a , 圆心在原点的圆电流环(电流为 I )在 z 轴上的磁标 位为 m = 1 2 2 1 2 2 (a + z ) 证明:法一:由毕奥萨伐尔定律可求得,z 轴上某一点的磁感应强度为:Iz35习题三v B=Ia 22( a + z )2 2 3/ 2v ezv v B H = =Ia 2 v e 2 2 3/ 2 z 2(a + z )由 H = m = (v m v m v m v e + e + e ) x x y y z z可得 m Ia 2 = z 2( a 2 + z 2 ) 3 / 2 m = ∫ Ia 2 Iz dz = +C 2 2 3/ 2 2 2( a + z ) 2(a + z 2 )1 / 2当 z → ∞ 时, m = 0 ,求得C=所以I 2 z ) ( a + z 2 )1 / 22 m = (1 I 2法二:整个圆形回路在轴线上产生的磁场,由于对称,仅仅有轴向分量.使用 叠加原理,可以计算出轴线上任一点的磁场强度为Ia 2 H= 2( a 2 + z 2 ) 3 2由磁标位与磁场强度的关系式 H = m ,可以得到m =3-18∫∞zHdz =∫∞z Ia 2 I z d z = 1 2 2 12 2 2 32 2 (a + z ) 2(a + z )一个长为 L ,半径为 a 的圆柱状磁介质沿轴向方向均匀磁化(磁化强度为M 0 ),求它的磁矩.若 L = 10cm , a = 2cm , M 0 = 2 A / m ,求出磁矩的值. 解:均匀磁化介质内的磁化电流为零.在圆柱体的顶面与底面,有v v v Jms = M × n = 036《电磁场与电磁波》——习题详解在侧面v v v v v v J m s = M × n = M 0 ez × er = M 0 eφ侧面的总电流为I = JmsL = M 0L磁矩为m = IS = Iπ a 2 = M 0 Lπ a 2代入相关数值后得m = M 0 Lπ a 2 = 2 × 0.1× π × 0.02 2 = 2.512 × 10 4 A m 23-19 球心在原点,半径为 a 的磁化介质球中, M = M 0 磁化电流的体密度和面密度. 解:磁化电流的体密度为vz2 v ez ( M 0 为常数) ,求 a2v v Jm = × M = 0在球面上v v v z2 v v v J m s = M × n = M 0 ez × er = M 0 2 sin θ eφ a注意,在球面上v v z = a cos θ , J m s = M 0 cos 2 θ sin θ eφ3-20 证明磁介质内部的磁化电流是传导电流的( r 1 )倍. 证明:由于 J = × H , J m = × Mvvvv因而 3-21v v v v v v v B = H = 0 ( H + M ) , M = 1 H = ( r 1) H 0 v v J m = ( r 1) J已知内,外半径分别为 a , b 的无限长铁质圆柱壳(磁导率为 )沿轴向有恒 定的传导电流 I ,求磁感应强度和磁化电流.37习题三解: 考虑到问题的对称性, 用安培环路定律可以得出各个区域的磁感应强度. 当 r < a 时, B = 0vv I (r 2 a 2 ) v 当 a < r < b 时, B = eφ 2π r (b 2 a 2 )当 r > b 时, B = 当 a < r < b 时,v0 I v eφ 2π rv v I (r 2 a 2 ) v 1 v M = ( r 1) H = ( r 1) B = ( r 1) eφ 2π r (b 2 a 2 ) v v v 1 (rM ρ ) v ( r 1) I J m = × M = ez = ez r r π (b 2 a 2 )当 r > b 时, J m = 0 在 r = a 处,磁化强度 M = 0 ,所以vvv v v v v J m s = M × n = M × (er ) = 0在 r = b 处,磁化强度 M =v Jms3-22( r 1) I v eφ ,所以 2π b v v v v ( 1) I v = M × n = M × er = r ez 2π b v设 x < 0 的半空间充满磁导率为 的均匀磁介质, x > 0 的空间为真空,线电流 I 沿 z 轴方向,如图 3-8,求磁感应强度和磁场强度. 解:由恒定磁场的边界条件,可以判断出,在磁介质和真空中,磁感应强度相 同,而磁场强度不同.由问题的对称性,选取以 z 轴为轴线,半径为 r 的圆环为安 培回路,有∫注意到lv v H d l = π rH 1 + π rH 2 = Iy0H1 =1B1, H2 =2B2, B1 = B2 = BIx图 3-838《电磁场与电磁波》——习题详解1 = 0 , 2 = 因而得B= 0 I π ( 0 + )r其方向沿圆周方向. 3-23 已知在半径为 a 的无限长圆柱导体内有恒定电流 I 沿轴向方向.设导体的磁 导率为 1 ,其外充满磁导率为 2 的均匀磁介质,求导体内,外的磁场强度, 磁感应强度,磁化电流分布. 解:考虑到问题的对称性,在导体内,外分别选取与导体圆柱同轴的圆环作 为安培回路,并注意电流在导体内是均匀分布的.可以求出磁场强度如下:Ir v eφ 2π a 2 v I v r > a 时, H = eφ 2π r磁感应强度如下:v r ≤ a 时, H =v Ir v r ≤ a 时, B = 1 2 eφ 2π a v 2 I v r > a 时, B = eφ 2π r为了计算磁化电流,要求出磁化强度:v v v v Ir I v , J m = × M = e z 1 1 r ≤ a 时, M = eφ 1 1 2 2π a 2 0 0 π av v v v I r > a 时, M = eφ 2 1 , Jm = × M = 0 0 2π r在 r = a 的界面上计算面电流时,可以理解为在两个磁介质之间有一个很薄的 真空层.这样,其磁化面电流就是两个磁介质的磁化面电流之和,即v v v v v J m s = M 1 × n1 + M 2 × n2这里的 n1 , n2 分别是从磁介质到真空的单位法向.如果取从介质 1 到介质 2 的单位法向是 n ,则有vvvv v v v v J m s = M1 × n M 2 × n39习题三代入界面两侧的磁化强度,并注意到 n = er ,得vvv I v v 2 I J m s = e z 1 1 2π a + ez 1 2π a 0 0 I v = ez 2 1 0 0 2π a3-24 试证长直导线和其共面的正三角形之间的互感为M=0 a (a + b) ln1 + b a π 3 其中 a 是三角形的高,b 是三角形平行于长直导线的边至直导线的距离(且该 边距离直导线最近). 证明:取如图 3-9 所示的坐标.直线电流 I 产生的磁场为B=0 I 2π x由图 3-9 知道,三角形三个顶点的坐标分别为 A(b, a3 ) , B (b, a3) ,C (a + b,0) ,直线 AC 的方程为 z=互感磁通为z A I1 b B图 3-91 (a + b x) 3C b+axΨ = BdS = 2∫∫a +b b0 I 1 (a + b x) d x 2π x 3=0 I a (a + b) ln1 + b a π 3 0 a (a + b) ln1 + b a π 3 直线与矩形回路的互感为M=3-25无限长的直导线附近有一矩形回路(二者不共面,如图 3-10),试证它们之间 的互感为40《电磁场与电磁波》——习题详解M =0 a R ln 2 2 12 2π [2b( R c ) + b 2 + R 2 ]1 2b a R R1图 3-10IIc证明:直线电流 I 产生的磁场为 B =0 I ,作积分,得出磁通量 2π rΨ = BdS =注意:∫∫R1 R 0 Ia Ia R d r = 0 ln 1 R 2π r 2π1 2 1 2 1 2R1 = [c + (b + R c ) ] = [2b( R c ) + b + R ]2 2 2 2 2 2 2 2将其代入,即可得到互感. 3-26 外导体的内半径为 b , 通过的电流为 I . 空气绝缘的同轴线, 内导体半径为 a , 设外导体壳的厚度很薄,因而其储存的能量可以忽略不计.计算同轴线单位 长度的储能,并由此求单位长度的自感. 解:设内导体的电流均匀分布,用安培环路定律可求出磁场.r < a 时, H =Ir 2π a 2 I a < r < b 时, H = 2π rWm =单位长度的磁场能量为∫a01 H 2 2π r d r + 2 0∫b a1 H 2 2π r d r 2 0=0 I 2 0 I 2 b ln + 16π 4π aL=故得单位长度的自感为0 0 b + ln 8π 2π a41习题三其中第一项是内导体的内自感. 3-27 一个长直导线和一个圆环(半径为 a )在同一平面,圆心与导线的距离是 d , 证明它们之间互感为M = 0 (d d 2 a 2 )证明:设直导线位于 z 轴上,由其产生的磁场I r d θB=0 I 0 I = 2π x 2π (d + r cos θ ) 0 I其中各量的含义如图 3-11 所示,磁通量为图 3-11Φ = BdS =∫∫∫0 2π 0a2π 02π (d + r cos θ )2πr dθ d r上式先对 θ 积分,并用公式∫得dθ = d + a cos θd 2 a2Φ = 0 I所以互感为 3-28∫ardr d r2 20= 0 I (d d 2 a 2 )M = 0 (d d 2 a 2 )如图 3-12 所示的长密绕螺线管(单位长度 n 匝),通过的电流为 I ,铁心的磁 导率为 ,面积为 S ,求作用在它上面的力. 解:在忽略边缘影响时,密绕螺线管内部的磁场是一个均匀磁场,其值为H = NI , 管外磁场为零. 设螺线管的长度为 L , 铁心位于螺线管内的部分长度为 x , 总的磁场能量为Wm =1 1 Sx( NI ) 2 + 0 S ( L x)( NI ) 2 2 2Wm xL● ● ● ● ● ● ●用电流不变情形下的虚位移公式,得到铁心受力 x0SF==I1 ( 0 ) SN 2 I 2 2× × × × × × × 图 3-12力的方向沿 x 增加的方向.42。
《电磁场与电磁波》课后习题解答(第三章)

【习题 3.1】
解:设导线沿 ez 方向,电流密度均匀分布 则
J ez
4
I d
2
ez
4
2 (10 )
3
2
cos(2 50t ) ez
8
106 cos(2 50t( ) A
m2
)
导线内的电场
E
J
ez
8 106 cos 2 50t ez 4.39 102 cos 2 50t (V / m) 7 5.8 10
J s n H er H ez 395.1cos(4 108 t ) A / m
(3) r 20mm, z 25mm 处的表面电荷密度
7 2 s n D 0 r er E 0. 7 8 1 0 sin ( 48 t1 0 C ) m /
B 1.328 6 107 0 sin 6 107 t cos zex t
1.328 6 107 4 107 sin 6 107 t cos zex 100sin 6 107 t cos zex
所以有
E
B t
ex
又因为
ey y 0
ex 1 1 E ( D) [ ( z 6 107 t )ex ] 2.5 0 2.5 0 x Ex (e y Ex E 1 ez x ) ey 4.52 1010 ey z y 2.5 0
ey y 0
ez z 0
12
= 4 81 8.854 10
i 6.28 109 E = i 4.5 i 4 E
6
电磁学第三章习题答案

第三章3.1 解:因螺绕环内的磁感应强度I n B 0μ=,所以副线圈中的感应电动势为VdtdI S dtd Sdtd 30103.1nN B N N --⨯===Φ=με副副副感应电流为A103.6RI 4-⨯==ε3.2 解:(1)设线圈发现→n 与→B 的夹角为零度时作为计时的起点,则t 时刻线圈中的感应电动势为tNBS dt t B d dt d ωωωεsin )cos S (-N-N==Φ=由此可以看出,当2t πω=或23t πω=时,即线圈法线与地磁场→B 的夹角为2π或23π时,感应电动势的值最大,此时ωεNBS m=(2)97N==ωεBS m 匝3.3 解:因距直导线为r 处的ri πμ2B 0=,所以(1)穿过回路ABCD 的磁通量t I a b l ldr riS d B basωπμπμsin ln 22000⎪⎭⎫⎝⎛==⋅=Φ⎰⎰⎰→→(2)回路ABCD 中的感应电动势 tI ab l dtωπωμεcos )(ln2d 00-=Φ-=3-5解:设t=0时,线圈与直导线处于同一平面内。
t 时刻俯视线圈与导线的相对位置如图3-19所示。
此时,线圈的有效面积是宽为AB 长为2a 的与长直导线共面的矩形面积。
穿过此有效面积的磁通量t t ab b a t ab b a b Ia tt ωωωπωμsin cos 21cos 21d )(d ε222220⎪⎭⎫⎝⎛-++++=Φ-=3-10解:设l 正方向如图3-23所示,则ac 段产生的感应电动势Vbc vB l d B l d B cbba30109.160cos 0)()(-→→→→→→⨯=+=⋅⨯+⋅⨯=⎰⎰ννε故感应电动势的方向为c a →,即c 点的电位高。
所以 V3oc 109.1U -⨯-=3-13解:(1)a,b 间的感应电动势22222121)(NBRR N B R B ldl B l d B d RLbaππωωυεε=⋅⋅===⋅⨯==⎰⎰⎰→→→(2)因ε的方向从轮心指向边缘,故在外电路上,I 的方向为b 指向a 。
电磁场叶齐政第三章答案

荷 q' (平面上方 h 处, q' q )对它的作用力
q2
fe
4 0 (2h)2
令 f e 与重力 mg 大小相等,有
q2
mg
4 0 (2h)2
即������ = 4ℎ√������������0������������
3.12
解:设q1受电场力为������1, ������1是q2和分界面上产生感应电荷共同产生的电场对q1产生的电场 力。同理 q2 受电场力为������2 ,是q1和分界面上产生的感应电荷共同产生的电场对q2 的电场 力。
2
3.9 解: 1)嵌入金属壳后,球形电容器的电场有变化,原因如下: 当嵌入金属壳 S 后将球形电容器内电介质分成两部分,S 成为这两部分电介质的分界面。 在该分界面上电位处的相等,即 S 面是等势面。类似地,我们也可把(a)图中的介质分成 如(b)图一样的两部分,显然在(a)图中,S 对应的分界面不再是等势面,因此(a)(b) 两图中的边缘问题的边界条件不相同,其解必不同。 2)若金属球壳与球形电容器同心,则 S 的嵌入不改变边缘问题的边界条件,因此不改变电 场的分布,因为球形电容器中的等势面正好是与球心同心一簇同心球面。
=
������0⁄ln
������2 ������1
∗
1 ������
当������ = ������1时
������������������������
=
������0 ln������2⁄������1
∗
1 ������1
对������1 ∗ ln ������2⁄������1求导得到 ������1 = ������2⁄ⅇ时������������������������最小为ⅇ������0 ∕ ������2
教科版高中物理必修第三册课后习题 第3章 电磁场与电磁波初步 分层作业25 磁感应强度 磁通量

分层作业25 磁感应强度磁通量A组必备知识基础练题组一对磁感应强度的理解1.下列关于磁感应强度的方向说法正确的是( )A.某处磁感应强度的方向就是一小段通电导线放在该处时所受磁场力的方向B.小磁针受磁场力的方向就是该处磁感应强度的方向C.垂直于磁场放置的通电导线的受力方向就是磁感应强度的方向D.磁场中某点的磁感应强度的方向就是该点的磁场方向2.先后在磁场中A、B两点引入长度相等的短直导线,导线与磁场方向垂直。
如图所示,图中a、b两图线分别表示在磁场中A、B两点导线所受的力F与通过导线的电流I的关系。
下列说法正确的是( )A.A、B两点磁感应强度相等B.A点的磁感应强度大于B点的磁感应强度C.A点的磁感应强度小于B点的磁感应强度D.无法比较磁感应强度的大小题组二磁感应强度与电场强度的比较3.关于静电场中的电场强度和磁场中的磁感应强度,下列说法正确的是( )A.电场强度是矢量,真空中点电荷的电场强度定义式为E=k Qr2B.电场强度的公式E=U,适用于任何静电场dC.磁感应强度B是矢量,其定义式为B=FILD.由磁感应强度公式B=F知,磁感应强度的大小与直线电流的大小和受力IL大小有关题组三磁通量4.如图所示,正方形线圈abcd的一半处于匀强磁场中,线圈平面与磁场方向垂直。
在线圈以ab为轴旋转90°的过程中,穿过线圈的磁通量大小( )A.一直减小B.先增大后减小C.先减小后增大D.先不变后减小5.如图所示,面积是0.5 m2的矩形导线圈处于磁感应强度为20 T的匀强磁场中,线圈平面与磁场垂直,如图中Ⅰ位置,则穿过该线圈的磁通量是多少?若线圈平面与磁场方向夹角为60°,如图中Ⅱ位置,则穿过该线圈的磁通量又是多少?题组四磁场的叠加问题6.用长导线以如图甲所示方式缠绕螺线管,当电流为I时,测得螺线管内轴线中点A的磁感应强度大小为B。
若将导线对折缠绕螺线管,两种绕法螺线管上的线圈匝数相同,如图乙所示,通过相同电流I时,则在螺线管内A点的磁感应强度大小为( )A.0B.0.5BC.BD.2B7.如图所示,两根互相平行的长直导线分别过纸面上的M、N点,且与纸面垂直,导线中通有大小相等、方向相反的电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和
1
1 x
2
xd
2 x
可以解得
xd
1
2U 0 x 1 2 d
(0 x d )
和
2
1U 0 x 2d U 0 ( d x 2d ) 1 2 d
根据 E ,可以得到平板电容器中两种介质中的电场分布为
E1 1 ex d1 2 U0 ex dx 1 2 d
解:已知空间的电位分布,由 E 和 2 / 0 可以分别计算出电场强度和体电荷 密度。 (1) E ex 2 Ax B (2) E A ex yz ey xz ez xy
02 2 A 0
利用公式: sh( x y) sh x ch y ch x sh y ,得
C1 D1 nπ(x a) nπy sh sin nπa b b ch b nπ a x nπy CD 令常数 En 1 1 ,则通解可写成: x, y En sh sin nπa b b ch b
(V/m) (C/m2 )
3.11 如题 3.11 图所示的平板电容器中, 分别以两种不同的方式填充两种不同的介质 1 和 2 。 当两极板之间外加电压 U 0 时,试求电容器中电位和电场的分布以及电容器的电容。 解:对于图 a:忽略边缘效应,可以认为电位分布也只与 x 有关,均满足一维拉普拉斯方程:
,则由题意可知
et E1t ex 20 ey 10 E1 et E1t en E1n ex 20 ey 10 ez 50 en E1n ez 50 en D1n 2 0en E1n ez 100 0
E1t E2t et E1t et E2t 两种电介质的交界面上无自由电荷,则边界条件为 或 ,则 D1n D2 n en D1n en D2 n
x, y
将上式对 n 求和,得该边值问题的解:
( x, y) En sh
n 1
nπ a x nπy sin b b
02 0
(3) E e (2 A sin Bz ) e A cos ez B
02 0 4 A sin
Bz
Bz A sin 0 3 A sin
无限长导体圆柱上电位为 0,即 (a) 0 ,可得 D C ln a ,则通解可写为:
C ln
a
( a)
C a C 0 a
导体圆柱表面的面电荷密度为: S n
S
介质中 空气中
a
《电磁场与天线 A》作业题解答
第 3 章 静电场及其边值问题的解法
3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度: (1) x, y, z Ax 2 Bx C ; (3) , , z A 2 sin B z ; (2) x, y, z Axyz ; (4) r , , Ar 2 sin cos 。
nπx nπx nπy 则通解亦为: x, y C2 ch C1 sh D1 sin b b b nπa nπa nπy 代入边界条件: 3 a, y C2 ch 0 C1 sh D1 sin b b b (0 y b)
U0 x 2d
(0 x d )
U d ex 0 dx 2d
根据 E ,可以得到平板电容器中的电场强度: E ex 对 x 0 平板上 en ex ,面电荷密度分别为
U0 1 2d S en D ex E U 0 2 2d
1 sin 0 2 r sin
z
即
d d sin d d
0
绝缘缝隙
0 无限大导体平面 y o
将上述方程分别直接积分,得出通解为
C ln tan D 2
4/ 10
x
(题第 3.16 图)
et E2t = et E1t ex 20 ey 10 en D2 n en D2 n ez 100 0 en E2 n 5 ez 20 0
1/ 10
《电磁场与天线 A》作业题解答
E2 = et E2t + en E2 n ex 20 ey 10 ez 20 所以,zx100 0 ey 50 0 ez 100 0
3.6 有 2 0 和 5 0 的两种电介质分别分布在 z 0 和 z 0 的半无限大空间。 已知 z 0 时
E ex 20 ey 10 ez 50 V / m 。试求 z 0 时的 D 。
E1 , D1 解:设 E2 , D2 ( z 0) ( z 0)
和
E2 2 ex
d 2 1 U 0 ex dx 1 2 d
对 x 0 平板上 en ex ,面电荷密度为: S en D1 ex 1 E1 总电量为:
1 2 U 0 1 2 d
Q S 2S
(4) E er 2 Ar sin cos e Ar cos cos e Ar sin
02 0 6 A sin cos
A cos 2 cos A cos sin sin
nπa sh nπa nπa b C ,代入通解得 由于 D1 0 ,则 C1 sh C2 ch 0 C2 nπa 1 b b ch b
5/ 10
《电磁场与天线 A》作业题解答
x, y
C1 nπx nπa nπx nπa nπy sh ch ch sh D1 sin nπa b b b b b ch b
单位长度导体圆柱上的电量为: s1 a 1 s 2 a 1 l 1 或:
l C C a 1 0 a 1 l 1 C π( 0 ) a a
于是得到导体圆柱外的电位和电场强度分别为
π( 0 )
U0
和
E e
1 e r
1 r sin ln tan 0 2
U0
3.18 题图所示矩形空间区域内的电位分布,已知边界条件为: (1) 1 U 0 , 2 3 4 0 ; (2) 2 U 0 ,
1 0 , 3 4 0 ; n
) 1 ( ) ( 0 ( a) ( ) ( ) ( ) 2 ( a) 0
1、2 均满足一维拉普拉斯方程,即
2 1 2 2 1 d d1 0 d d 1 d d 2 0 dr d
C1 sh(k y x) C2 ch(k y x) D1 sin(k y y ) D2 cos(k y y )
由边界条件 2 4 0 ,即由 ( x, b) ( x,0) 0 可得:
D2 0 和
ky
nπ b
(n 1, 2, 3, )
d 2 ( x) 2 0 dx
2
y
y
且由介质分界面的边界条件 1 2 可知, 两种介质中的电位分布是相
o x x
同的,其通解为:
o
( x) Cx D
根据已知条件
x 0
0 U0
,解得 D 0 和 C
x2d
U0 ,即平板电容器中的电位分布为: 2d
介质中 空气中
3/ 10
《电磁场与天线 A》作业题解答
将上述两方程分别直接积分两次,得通解:
1 C1 ln D1
和
2 C 2ln D
2
在介质分界面上任一点电位皆连续 1 2 ,则 C1 C2 C 和 D1 D2 D ,即
1 ( ) 2 ( ) ( ) C ln D
l
ln
a
和
E e
π( 0 )
l
1
3.16 顶端夹角为 2 0 的带电导体圆锥垂直于无限大的接地导体平面,但两者之间有一缝隙。 当圆锥所加电压为 U 0 时,试求圆锥体与导体平面之间的电位分布及电场强度。 解:由于圆锥体与导体平面之间的电位分布均仅为坐标 的函数,满足一维的拉普拉斯程
d 2 0 ,两种介质中的电位分布的通解可以分别设为 dx 2
2/ 10
《电磁场与天线 A》作业题解答
1 C1 x D1 (0 x d )
根据已知条件 1 x 0 0 和 2
x2 d
和
2 C 2 x D2 d ( x 2 d )
x d
U 0 ,以及分界面处的边界条件 1 x d 2
y S上 y S下
总电量为:
Q 1
U0 U S S 2 0 S 1 2 U 0 2d 2d 2d
电容器的电容为: C
Q S 1 2 U0 2d
对于图 b:忽略边缘效应,同样可认为电位分布也只与 x 有关,均满足一维拉普拉斯方 程 2 ( x)
解:(1) 本题属于二维边值问题: ( x, y) ,其电位 满足的 Laplace 方程 2 0 可用分离变量法求解。
2 2 由题意可知:y 方向具有齐次边界条件,则 k y 0 , k x2 k y 0 ,其通解形式为:
