三年级奥数专题:长方形与正方形的面积
小学奥数长方形正方形面积求解(一)课件

正方形面积>长方形面积
11
(每个正方形小格边长1厘米,所以每个正方形小格的面积是1平方厘米。)
B A
长方形A的周长: (4+6)×2=20(厘米) 长方形A的面积: 4×6=24(平方厘米)
长方形B的周长: (3+7)×2=20(厘米) 长方形B的面积: 3×7=21(平方厘米)
12
(每个正方形小格边长1厘米,所以每个正方形小格的面积是1平方厘米。)
23
二、面积求解 1.求下面图形的面积(单位:厘米)
12 3
10
3
24
不是规则的长方形或正方形,要把原图进行割补, 使其变成规则图形再求解面积。 1.割,分割成两个规则的图形,分别求解每个图 形的面积,然后相加就是总面积。 2.补,补成一个规则的大图形,分别求解大图形 的面积和补充的面积,用大图形面积减去补充的 面积就是要求的面积。
完整的大正方形边长是6厘米,面积是 6×6=36(平方厘米)
残缺正方形的面积=36-9=27(平方厘米)
34
图形的面积: =1个完整正方形的面积+1个残缺正方形的面积
图形的面积: =36+27=63(平方厘米)
35
三、长、宽发生变化
1.一个正方形,如果宽不变,长增加6米,那么它的面积 增加54平方米,如果长不变,宽减少3米,那么它的面积 减少36平方米,这个长方形原来的面积是多少平方米?
小长方形的长=面积÷宽 75 ÷5=15
5
28
75 15
大长方形宽为15
42
大长方形的长原来是28, 大长方形宽为15
这道乘法题,一个因数是 28,一个因数是15
正确的积是28×15=420
三年级下册数学试题-奥数培优讲义:面积计算(无答案)全国通用

面积计算【专题简析】我们已学会了计算长方形、正方形的面积,知道长方形的面积=长×宽,正方形的面积=边长×边长。
利用这些知识我们能解决许多有关面积的问题。
在解答比较复杂的关于长方形、正方形面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧。
因此,敏锐的观察力和灵活的思维在解题中十分重要。
【典型例题】【例1】一个长方形花坛,长5米,宽4米,这个花坛的面积是多少?【试一试】1.制作一张小卡片,长9厘米,宽5厘米,至少需要多少面积的材料?2.一块正方形的布,边长为5米,这块布的面积是多少?【例2】一个长为6厘米,宽为4厘米的长方形纸片,沿长方形的长剪去2厘米后,剩下部分是什么图形?剩下部分的面积是多少?1.把一个长为10米,宽为6米的长方形铁片,沿长剪去4米后,剩下部分的面积是多少?2.把一个长为9分米,宽为8分米的长方形,沿长剪去1分米后,剩下部分的面积是多少?【例3】把一张长为4米,宽为3米的长方形木板,剪成一个面积最大的正方形,这个正方形木板的面积是多少平方米?【试一试】1.把一张长6厘米,宽4厘米的长方形纸,剪成一个面积最大的正方形,这张正方形纸的面积是多少?2.把一块长2分米,宽6分米的长方形铁板,切割成一个面积最大的正方形,这个正方形铁板的面积是多少?【例4】学校里有一个正方形花坛,四周种了一圈绿篱,绿篱总长20米,求花坛的面积是多少平方米?【试一试】1.一个正方形的周长为36厘米,那么这个正方形的面积是多少平方厘米?2.运动场有一个正方形的游泳池,在游泳池的四周贴上瓷砖,瓷砖总长400米,求游泳池的面积是多少平方米?【例5】求下面图形的面积(单位:厘米)。
【试一试】求下面图形的面积。
(单位:厘米)1.【※例6】有两个相同的长方形,长是8厘米,宽是3厘米。
如果把他们按下图叠放,这个图形的面积是多少?【※试一试】1.两张边长为8厘米的正方形纸片,一部分叠在一起放在桌上(如下图),问桌子被盖住的面积是多少?2.求阴影部分的面积。
(三年级)长方形和正方形的面积奥数题训练

(三年级)长方形和正方形的面积奥数题训
练
题一:
一个长方形的长为10cm,宽为5cm。
计算它的面积。
解答:
长方形的面积可以通过将长乘以宽来计算。
根据题目给出的数据,我们可以使用以下公式来计算面积:
面积 = 长 ×宽
将给定的数值代入公式,即可得到答案:
面积 = 10cm × 5cm = 50cm²
所以,该长方形的面积为50平方厘米。
题二:
一个正方形的边长为20cm。
计算它的面积。
解答:
正方形的面积可以通过将边长的平方来计算。
根据题目给出的数据,我们可以使用以下公式来计算面积:
面积 = 边长²
将给定的数值代入公式,即可得到答案:
面积 = 20cm × 20cm = 400cm²
所以,该正方形的面积为400平方厘米。
题三:
一个长方形的面积是36平方米,宽为6米,求它的长。
解答:
根据题目给出的数据,我们可以使用以下公式来计算长方形的长:
面积 = 长 ×宽
将给定的数值代入公式,即可得到答案:
36平方米 = 长 × 6米
解方程,可以得出:
36 = 长 × 6
长 = 36 / 6 = 6米
所以,该长方形的长为6米。
总结:
通过这些奥数题训练,我们研究了如何计算长方形和正方形的面积。
对于长方形,可以使用长乘以宽的方式计算面积;对于正方形,可以使用边长的平方来计算面积。
【奥数小神童】三年级数学竞赛试题- 巧求面积(二) 北师大版(含答案)

巧求面积(二)【名师解析】我们已经学会了计算长方形、正方形的面积,知道长方形的面积=长×宽,正方形的面积=边长×边长。
利用这些知识我们能解决许多有关面积的问题。
在解答比较复杂的关于长方形、正方形的面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧。
因此,敏锐的观察力和灵活的思维在解题中十分重要。
例1:把6个边长为4厘米的小正方形如下图拼成一个长方形,这个长方形的面积为多少平方厘米?练习:把6个长为3厘米、宽为2厘米的小长方形如下图拼成一个大长方形,这个大长方形的面积是多少?例2:下图是由5个边长为3厘米的正方形组成的图形,求此图形的面积。
练习:下图是由6个边长为2厘米的正方形组成的,求此图形的面积。
例3: 4个相同的宽为2厘米的长方形拼成一个大长方形.大长形的面积多少平方厘米?练习:四个同样大小的长方形正好拼成一个正方形,正方形的周长为64厘米,长方形面积是多少?例4 六个同样大小的长方形正好拼成一个如下图的正方形,正方形周长为48厘米,每个长方形面积是多少?练习:一个长方形的面积是正方形的4倍,正方形边长与长方形的宽为6厘米。
长方形长多少厘米?例5 四个完全相同的小长方形拼车下图,大正方形的面积是81平方厘米,小长方形的宽为2厘米,小正方形的面积是多少平方厘米?练习:如图所示,十个相同的小长方形拼成一个大长方形。
已知小长方形的宽是15厘米,求大长方形的面积是多少平方厘米?例6:求下图中阴影部分的面积。
(单位:分米)227练:两张边长8厘米的正方形纸,一部分叠在一起放在桌上(如下图),桌面被盖住的面积是多少?888448例7:如图,阴影部分是一个长方形,它的四周是四个正方形,如果这四个正方形的周长的和是240厘米,面积的和是1000平方厘米,那么阴影部分的面积是多少平方厘米。
练习:一个长为10厘米、宽为6厘米的长方形将一个边长为5厘米的正方形遮住了一部分,如图14所示。
学而思三年级奥数第九讲长方形与正方形

学而思三年级奥数第九讲长方形与正方形知识点:长方形的面积=长×宽正方形的面积=边长×边长不规则图形面积的计算方法与技巧合理平移、分析、转化等,即转化为标准的图形来进行面积计算。
例1 有一长方形草坪,长31米,宽26米,草坪中间留了1米的路,路把草坪分成4块(如图),求草坪的实有面积是多少?例2如下图,求出阴影部分的面积。
(四角是边长为10厘米的正方形)例3 如图,在一个正方形的水池周围,围绕着宽5米的小花园,小花园的面积为300平方米,水池的面积是多少平方米?例4 如图,求出阴影部分的面积。
(单位:厘米)例5 如图,图中大正方形比小正方形的边长多4厘米,大正方形的面积比小正方形的面积多96平方厘米,大正方形和小正方形的面积各是多少?例6如图,大正方形的面积比小正方形的面积大32平方厘米,求这两个正方形的面积。
(单位:厘米)例7 如图,正方形中套着一个长方形,正方形的边长是12分米,长方形的四个角的顶点恰好把正方形的四条边都分成两段,其中长的一段是短的一段的3倍,这个长方形的面积是多少?例8 用同样大小的长方形小纸片,摆成了如下图的形状,已知小纸片的宽度是12厘米,求阴影部分面积的和。
同步练习1、用长36厘米的一根铁丝围成一个正方形,它的面积是多少?用这根铁丝围成一个长12厘米的长方形,它的面积是多少?2、如图,有一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是一个正方形,周围是花圃,花圃的面积是多少平方米?(单位:米)3、下图是由6个相等的三角形拼成的图形,求这个图形的面积?4、有两个相同的长方形,长13厘米,宽5厘米,如果把它们按如下图叠放在一起,这个图形的面积是多少?5、有一块菜地长16米,宽8米,如下图菜地中间留了2条宽2米的路,把菜地平均分成四块,每一块地的面积是多少?6、一个正方形,如果边长增加2厘米,它的面积增加16平方厘米,求原正方形面积?7、个周长为60分米的长方形,把它的长缩短6分米后,再把它的宽增加6分米,得到的新长方形面积比原来多24平方分米。
三年级奥数第20讲长方形和正方形的面积
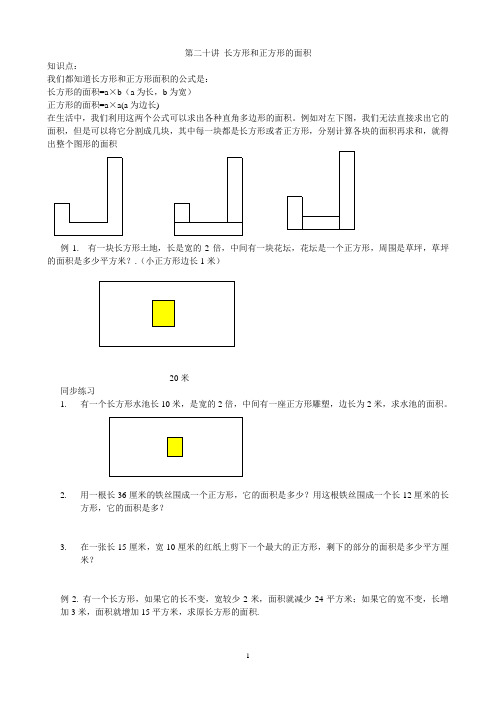
第二十讲长方形和正方形的面积知识点:我们都知道长方形和正方形面积的公式是:长方形的面积=a×b(a为长,b为宽)正方形的面积=a×a(a为边长)在生活中,我们利用这两个公式可以求出各种直角多边形的面积。
例如对左下图,我们无法直接求出它的面积,但是可以将它分割成几块,其中每一块都是长方形或者正方形,分别计算各块的面积再求和,就得出整个图形的面积例1. 有一块长方形土地,长是宽的2倍,中间有一块花坛,花坛是一个正方形,周围是草坪,草坪的面积是多少平方米?.(小正方形边长1米)20米同步练习1.有一个长方形水池长10米,是宽的2倍,中间有一座正方形雕塑,边长为2米,求水池的面积。
2.用一根长36厘米的铁丝围成一个正方形,它的面积是多少?用这根铁丝围成一个长12厘米的长方形,它的面积是多?3.在一张长15厘米,宽10厘米的红纸上剪下一个最大的正方形,剩下的部分的面积是多少平方厘米?例2. 有一个长方形,如果它的长不变,宽较少2米,面积就减少24平方米;如果它的宽不变,长增加3米,面积就增加15平方米,求原长方形的面积.同步练习1.有一个长方形,如果宽不变,长增加4米,面积就增加24平方米;如果长不变,宽增加3米,面积就增加36平方米,求原长方形的面积。
2.有一个长方形,如果它的宽减少2米,或者长减少3米那么它的面积都减少24平方米,求原来的这个长方形的面积。
3.一个长方形,长16厘米,如果长减少6厘米,就变成了一个正方形,它的面积减少了多少平方厘米?例3. 有一个正方形水池,如下图的阴影部分,在他的周围修一个宽8米的花坛,花坛的面积是480平方米,求水池的边长。
同步精练1.街心花园中一个正方形花坛四周有一米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?2.下图是一个长50米,宽25米的标准游泳池。
它的周围铺设了宽2米的白瓷地砖(阴影部分)。
求游泳池面积和地砖的面积。
三年级奥数(40讲)《举一反三》第37讲 面积计算

第37讲面积计算一、知识要点:我们已经学会了计算长方形、正方形的面积,知道长方形的面积=长×宽,正方形的面积=边长×边长。
利用这些知识我们能解决许多有关面积的问题。
在解答比较复杂的关于长方形、正方形的面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧。
因此,敏锐的观察力和灵活的思维在解题中十分重要。
二、精讲精练例1把一张长为4米,宽为3米的长方形木板,剪成一个面积最大的正方形。
这个正方形木板的面积是多少平方米?练习一1、把一张长6厘米,宽4厘米的长方形纸剪成一个面积最大的正方形,这张正方形纸的面积是多少平方厘米?2、把一块长2米、宽6分米的长方形铁板切割成一个面积最大的正方形,这个正方形铁板的面积是多少?例2学校里有一个正方形花坛,四周种了一圈绿篱,绿篱总长20米。
花坛的面积是多少平方米?练习二1、一个正方形的周长为36厘米,那么这个正方形的面积是多少平方厘米?2、运动场有一个正方形的游泳池,在游泳池四周粘上瓷砖,瓷砖总长400米,求游泳池的面积是多少平方米。
例3求下面图形的面积。
(单位:厘米)14321、计算下面图形的面积。
(单位:厘米)(1)15203040(2)31122例4有两个相同的长方形,长是8厘米,宽是3厘米。
如果把它们按下图叠放,这个图形的面积是多少?1、两张边长8厘米的正方形纸,一部分叠在一起放在桌上(如下图),桌面被盖住的面积是多少?8884482、求下图中阴影部分的面积。
(单位:分米)例5一个长方形若长增加2厘米,面积就增加10平方厘米,若宽减少3厘米,面积就减少18平方厘米。
求原来长方形的面积。
1、一个长方形,若长减少5厘米,面积就减少50平方厘米,若宽增加7厘米,面积就增加28平方厘米。
原来长方形的面积是多少平方厘米?2、一个正方形若边长都增加4厘米,面积就增加56平方厘米。
原来正方形的面积是多少平方厘米?三、课后作业1、将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形,那么剪下的另一个小长方形的面积是多少?2、在公园里有两个花圃,它们的周长相等。
奥数班三年级下册第13讲---正方形和长方形的面积(

5
【典型例题】
例3:有一个边长为8厘米的小正方形,把它的边长分别增加6厘米,做 成一个大正方形.大正方形的面积比小正方形的面积多多少?
方法一: 大正方形边长:8+6=14cm
大正方形面积:14×14=196cm2
小正方形面积:8×8=64cm2
现在的长: 15 - 5=10m 现在的宽: 8 - 5=3m 现在的面积: 10×3=30m2 原来的面积: 15×8=120m2 减少的面积: 120 - 30=90m2 答:得到的小长方形的面积比原来长方形的面积少90平方厘米。
13
【课堂精练】 5. 教室南面的墙壁,长8米,宽3米。墙上有3个3平方米的窗户。现在要 粉刷这面墙壁,要粉刷的面积是多少平方米?
面积: 6×6=36dm2 答:这个正方形铁板的面积是36平方分米。
11
【课堂精练】 3. 在一块长20米,宽16米的田地上种棉花,平均每平方米种棉花8株, 这块地共可以种多少株棉花?
面积: 20×16=320m2 产量: 320×8=2560千克 答:这块地共可以种2560株棉花。
12
【课堂精练】 4. 把一个长是15米,宽是8米的长方形的长和宽都分别减少5米。得到 的小长方形的面积比原来长方形的面积少多少?
长:(14-4)÷2=5m 面积: 5 × 4 = 20m2 答:养鸡场的占地面积是20平方米。
7
【典型例题】
例5:一个大长方形被两条平行于它的两条边的线段分成四个较小的长 方形,其中三个长方形的面积如下图所求,求第四2×6=12cm2
1
6
41
方法二:
2
82
三年级奥数第27次课:巧用矩形面积公式(教师版)

三年级奥数第27次课:巧用矩形面积公式(教师版)【我生命中最最最重要的朋友们,请你们认真听老师讲并且跟着老师的思维走。
学业的成功重在于考点的不断过滤,相信我赠予你们的是你们学业成功的过滤器。
谢谢使用!!!】巧用矩形面积公式一、考点、热点回顾求正方形和长方形面积的公式:正方形的面积=a×a(a为边长),长方形的面积=a×b(a为长,b为宽)。
利用这两个公式可以计算出各种各样的直角多边形的面积。
例如,对左下图,我们无法直接求出它的面积,但是通过将它分割成几块,其中每一块都是正方形或长方形(见右下图),分别计算出各块面积再求和,就得出整个图形的面积。
二、典型例题例1 、右图中的每个数字分别表示所对应的线段的长度(单位:米)。
这个图形的面积等于多少平方米?分析与解:将此图形分割成长方形有下面两种较简单的方法,图形都被分割成三个长方形。
根据这两种不同的分割方法,都可以计算出图形的的面积。
5×2+(5+3)×3+(5+3+4)×2=58(米2);或5×(2+3+2)+3×(2+3)+4×2=58(米2)。
上面的方法是通过将图形分割成若干个长方形,然后求图形面积的。
实际上,我们也可以将图形“添补”成一个大长方形(见下图),然后利用大长方形与两个小长方形的面积之差,求出图形的面积。
(5+3+4)×(2+3+2)-2×3-(2+3)×4=58(米2);或(5+3+4)×(2+3+2)-2×(3+4)-3×4=58(米2)。
由例1看出,计算直角多边形面积,主要是利用“分割”和“添补”的方法,将图形演变为多个长方形的和或差,然后计算出图形的面积。
其中“分割”是最基本、最常用的方法。
例2 、右图为一个长50米、宽25米的标准游泳池。
它的四周铺设了宽2米的白瓷地砖(阴影部分)。
求游泳池面积和地砖面积。
小学奥数专题: 巧求面积(1)

第二讲巧求面积(1)知识导航一、长方形与正方形的面积1、已知长方形的长与宽,长方形的面积等于长乘宽的积。
2、已知正方形的边长,正方形的面积等于正方形边长的平方。
二、面积计算中的割补法1、如果一个复杂图形经过分割可以变成几个简单图形,可以通过算出简单图形的面积再相加来计算复杂图形的面积。
2、如果一个复杂图形可以看成一个简单图形去掉一个或几个简单图形,再通过算出整体与去掉部分的差来计算复杂图形的面积。
3、有时我们需要先割后补,分割后将分割成的几部分面积重新拼接,将复杂图形的面积转化成一个容易计算的图形面积,然后再进行计算。
典型例题一(基本图形的面积)例1 如图所示,两个正方形的边长分别为a=10厘米和b=20厘米,求阴影部分的面积。
典型例题二(通过分割将复杂图形转化为基本图形)例2 下图中各角度均为直角,求这个图形的面积。
(单位:厘米)练习如图所示,多边形ABEFGD是由一个长方形ABCD及一个正方形CEFG拼成的,线段的长度如图所示,求多边形ABEFGD的面积。
(单位:厘米)典型例题三(割补法求复杂图形的面积)例3 如图所示,小区里的草地长16米,宽8米,草地中间留了宽2米的路,把草地平均分成四块,每一块地的面积是多少?练习一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积。
典型例题四(其他方法求复杂图形的面积)例4 如图所示,一个长方形广场的正中央有一个长方形的水池,水池长8米,宽3米。
水池周围用边长为1米的方砖一圈一圈地向外铺,恰好铺了若干圈,共用了152块砖,那么共铺了多少圈?练习如图所示,从一个正方形的木板上锯下宽1米的一个长方形木条后,剩下的长方形面积为6平方米,问锯下的长方形木条的面积是多少?课后巩固1.一个长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?2.如图所示,街心花园里有一个正方形花坛,四周有一条宽1米的小路,如果小路的面积是12平方米,那么中间花坛的面积是多少平方米?3.如图所示,四边形ABCD为正方形,已知对角线AC长为12厘米,求正方形ABCD的面积。
三年级奥数知识复习与提高

第一部分三年级课本知识复习与提高第1讲长方形和正方形的周长与面积知识方法我们已经学会了长方形和正方形的周长与面积计算,掌握了“长方形周长=(长+宽)2”,“正方形周长=边长4”;“长方形面积=长宽”,“正方形面积=边长边长”。
在运用这些基本知识解决相关问题时,一定要仔细观察,认真思考,找出条件和问题之间有什么联系,应先求什么,再求什么,最后灵活运用公式进行计算。
重点点拨例1 :把两个边长是6厘米的正方形拼成一个长方形,这个长方形的周长是多少厘米?分析在解决这类关于图形剪拼问题时,可以借助画示意图的方法帮助理解题意,找到问题解决的方法。
如题目两个边长是6厘米的正方形拼成一个长方形,可以这样拼,要求这个长方形的周长可以先求出这个长方形的长和周长看成由6个6厘米长的线段围成的,这样也可以求出这个长方形的周长。
解答(1)62=12(厘米)(2)66=36(厘米)(12+6) 2=18+2=36(厘米)答:这个长方形的周长是36厘米。
例2:一根铁丝正好可以围成一个边长是18厘米的正方形,如果用它重新围一个长是24厘米的长方形,这个长方形的宽是多少厘米?分析用一根铁丝正好围成一个正方形,那么这个正方形的周长就是这根铁丝的长度,又用这根铁丝围成一个长方形,那么这根铁丝的长度就是围成的这根长方形的周长,然后根据长方形周长公式,求出长方形的宽。
解答 184=72(厘米)722-24=12(厘米)答:这个长方形的宽是12厘米。
例3:把一个边长是16分米的正方形纸裁成4个完全一样的小正方形,这4个小正方形的周长和比原来的大正方形周长增加了多少?分析将边长是16分米的正方形沿水平方向裁一刀,周长和比原来大正方形周长增加2个边长;再沿竖直方向裁一刀,又增加2个边长,一共增加了4个边长。
座椅这4个小正方形的周长和比原来的大正方形周长增加了4个边长。
解答 16 4=64(分米)答:这4个小正方形的周长和比原来的大正方形周长增加了64分米。
三年级面积奥数题思维训练题

三年级面积奥数题思维训练题一、基础题型。
1. 一个长方形的长是8厘米,宽是5厘米,这个长方形的面积是多少平方厘米?- 解析:长方形的面积 = 长×宽,所以这个长方形的面积是8×5 = 40平方厘米。
2. 正方形的边长是6分米,它的面积是多少平方分米?- 解析:正方形的面积 = 边长×边长,所以这个正方形的面积是6×6=36平方分米。
3. 一个长方形花坛长12米,宽8米,这个花坛的面积是多少平方米?如果每平方米能种3株花,这个花坛一共能种多少株花?- 解析:- 长方形花坛面积 = 长×宽=12×8 = 96平方米。
- 每平方米种3株花,一共能种96×3 = 288株花。
4. 有一块正方形手帕,边长为15厘米,它的面积是多少平方厘米?- 解析:正方形面积 = 边长×边长,所以手帕面积为15×15 = 225平方厘米。
5. 一个长方形的长增加3厘米,宽不变,面积增加18平方厘米,原来长方形的宽是多少厘米?- 解析:长增加3厘米,宽不变,增加的面积就是增加的长乘以原来的宽。
所以原来的宽=18÷3 = 6厘米。
二、组合图形面积。
6. 如图,一个大长方形由两个小长方形组成,左边小长方形长8厘米,宽3厘米,右边小长方形长5厘米,宽3厘米,求大长方形的面积。
- 解析:- 大长方形的长是8 + 5=13厘米,宽是3厘米。
- 面积 = 长×宽=13×3 = 39平方厘米。
7. 有一个组合图形,由一个正方形和一个长方形组成。
正方形边长为4分米,长方形长6分米,宽4分米,求组合图形的面积。
- 解析:- 正方形面积=4×4 = 16平方分米。
- 长方形面积=6×4 = 24平方分米。
- 组合图形面积=16+24 = 40平方分米。
8. 如下图,一个长方形被分成了一个正方形和一个小长方形。
三年级长方形面积奥数题

三年级长方形面积奥数题
一、奥数例题
1. 一个长方形,如果它的长不变,宽增加4米,面积就增加36平方米;如果它的宽不变,长增加5米,面积就增加25平方米。
原长方形的面积是多少平方米?
解析:
当长不变,宽增加4米时,增加的面积就是长乘以增加的宽,即长公式平方米,所以长为公式米。
当宽不变,长增加5米时,增加的面积就是宽乘以增加的长,即宽公式平方米,所以宽为公式米。
那么原长方形的面积 = 长公式宽=公式平方米。
2. 有一个长方形花坛,长为10米,宽为8米。
现在要在花坛四周铺一条宽为1米的石子路,求石子路的面积。
解析:
我们可以把铺了石子路后的大长方形的长和宽求出来。
长为公式
米(因为两边都增加了1米),宽为公式米。
大长方形的面积为公式平方米。
原来长方形花坛的面积为公式平方米。
所以石子路的面积 = 大长方形面积原来长方形花坛面积,即公式
平方米。
3. 一个长方形的长是18厘米,宽是12厘米,把它剪成两个相同的小长方形,这两个小长方形的面积之和与原来长方形的面积相比有什么变化?每个小长方形的面积是多少?
解析:
把一个长方形剪成两个相同的小长方形,这两个小长方形的面积之和与原来长方形的面积是相等的,因为总面积没有增加也没有减少。
原来长方形的面积 = 长公式宽=公式平方厘米。
每个小长方形的面积 = 原来长方形面积公式,即公式
平方厘米。
三年级下册数学奥数试题-长方形和正方形的面积

奥数长方形和正方形的周长和面积【专题精析】一个平面图形的大小叫做它的面积。
长方形面积=长×宽,正方形面积=边长×边长。
面积单位之间的进率为1平方米=100平方分米=10000平方厘米。
例1、已知图中大正方形ABCD 的面积比小正方形AFGE 的面积多216平方厘米。
问:大、小正方形的面积各是多少平方厘米?巩固练习1、如图,是一个长为8厘米,宽5厘米的长方形,从中间剪去一个边长为5厘米的正方形。
问:剩下部分的面积是多少平方厘米?2、求下图的周长和面积(用多种方法)6cm J5cm8cm【拓展提高】 1、求阴影部分的面积。
2、如图正方形鱼池,四周是3米宽的路,路的面积共60平方米。
问:这个鱼池占地面积是多少平方米?3、计算下面阴影部分的面积。
(o 是小正方形的中心点)24cm16cm8cm16cm12cm9cmo6cm4、(1)已知长方形的长为18厘米,如果长方形的宽增加6厘米,等到的长方形面积为原来的3倍,那么原长方形的面积是多少平方厘米?(2)一个长方形由一根长120厘米的铁丝围成,已知长方形的长比宽多12厘米,那么围成的长方形面积是多少平方厘米?5、一个长方形被2条直线分成4部分,其中三个长方形的面积分别是80平方厘米,20平方厘米和50平方厘米。
问:图中阴影部分面积是多少平方厘小学数学文化知识阿基里斯追不上乌龟历曾经有一个非常的逻辑学悖论,叫阿基里斯追不上乌龟。
内容很有趣,说的是一名长跑运动员叫阿基里斯。
一次,他和一只乌龟赛跑。
假设运动员的速度是乌龟的12倍,这场比赛的结果是显而易见的,乌龟一定会输。
现在我们把乌龟的起跑线放在运动员前面12千米处。
那么结果会是如何呢?有人认为,这名运动员永远也追不上乌龟!理由是:当运动员跑了12千米时,那只乌龟也跑了1千米,在运动员的前面。
当运动员又跑了1千米的时候,那只乌龟又跑了1/12千米,还是在运动员前面。
就这样一直跑下去,虽然每次距离都在拉近,但是运动员每次都必须先到达乌龟的起始地点,那么这时又相当于他们两个相距一段路程跑步了。
三年级奥数专题:长方形与正方形的面积

三年级奥数专题:长方形与正方形的面积(A)(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--六、长方形与正方形的面积(A 卷)年级 班 姓名 得分一、填空1.右图是一幢楼房的平面图形,它的面积是 平方米.(单位:米)2.北京某四合院子正好是个边长10米的正方形,在院子中央修了一条宽2米的“十字形”甬路,如图.这条“十字形”甬路的面积是 平方米?3.右图中有四个正方形,图①的边长是32厘米,图②的边长是图①边长的一半;图③的边长是图②边长的一半;图④的边长是图③边长的一半.(1)图中图①(最大的正方形)的面积是图④(最小的正方形)面积的 倍?并说出图④的面积是图①面积的)()(. (2)图中图①的周长是图④的周长的 倍?并说出图④的周长是图①周长的)()(. 4.右图中有3个长方形,图①长32厘米,宽16厘米;图②的长、宽分别是图①长、宽的一半;图③的长、宽分别是图②长、宽的一半.(1)图①的面积是图③面积的 倍?并说出图③的面积是图①面积的)()(. (2)图①的周长是图③周长的 倍?并说出图③的周长是图①周长的)()(.5.有大、小两个长方形,对应边的距离均为1厘米,如果两个长方形之间(阴影部分)部分的面积是16平方厘米,且小长方形的长是宽的2倍.求大长方形的面积是小正方形的 倍.1 2 4 5①③ ②6.将边长为24厘米的正方形纸剪成四块同样大小的长方形纸,每块长方形纸的边长是 ,宽是 ;周长是 ;面积是 .7.一个长方形原来的长是12厘米,宽是7厘米.现在把长和宽都减少2厘米,那么面积共减少了平方厘米?8.长方形花坛四周有一条2米宽的路,这条路的面积是156平方米.该花坛的周长是米.9.有一个长方形,长与宽各增加8分米,面积增加208平方分米,求原长方形的周长是分米.10.大正方形中有一个小正方形,两正方形的周长差是8厘米,面积差是20平方厘米.大正方形的边长是厘米?二、解答题11.把20分米长的线段分成两段,并在每一段上作一正方形(如下图).已知两个正方形的面积差为40平方分米,求每个正方形的面积.12.有一块长方形的玻璃,从长边截去20厘米宽的一块后,剩下的玻璃正好是块正方形,它的周长是160厘米.原来长方形玻璃的周长和面积各是多少?13.有一个机器零件,如图.中间是一个大正方形,边长是6厘米;每边正中向外凸出一个小正方形,边长都是2厘米.(1)这个机器零件的周长是多少?(2)这个机器零件的面积是多少?20分米14.右图中有六个正方形,较小的正方形都由较大的正方形的四边中点连接而成.已知最大的正方形的边长为10cm ,那么最小的正方形的面积等于 2cm .———————————————答 案——————————————————————1. 11平方米. 1×5+(4-1)×2=11(平方米).2. 36平方米. 2×10+(10-2)÷2×2×2=36(平方米).3. (1)64倍;641. (2)8倍;81. 4. (1)16倍;161. (2)4倍;41. 5. 3倍.6. 24厘米;6厘米;60厘米;144平方厘米.7. 34平方厘米. 12×2+(7-2)×2=34(平方厘米).8. 140米.9. 36分米.10. 24厘米.二、解答题 1.解:阴影部分的长20分米相当于两个正方形边长的和,宽相当于两个正方形边长的差.40÷20=2(分米)(20+2)÷2=11(分米) 11×11=121(平方分米) 20-11=9(分米) 9×9=81(平方分米)答:大正方形面积是121平方分米,小正方形面积是81平方分米.2.周长:200厘米.160÷4=40(厘米)(40+20)×2+40×2=200(厘米).面积:2400平方厘米.(40+20)×40=2400(平方厘米).3.周长40厘米. 2×5×4=40(厘米)20 dm面积52平方厘米. 2×2×4+6×6=52(平方厘米). 4.2813cm . ()281321212121211010cm =⨯⨯⨯⨯⨯⨯。
小学三年级奥数面积计算

小学三年级奥数面积计算在小学三年级的数学学习中,面积计算是一个重要的内容。
通过学习面积计算,孩子们可以在日常生活中更好地应用数学知识,进一步提高他们的数学能力。
本文将介绍小学三年级奥数面积计算的相关知识和方法。
一、正方形的面积计算正方形是指四边相等且四个角都是直角的四边形。
正方形的面积计算可以通过边长的平方得到,公式为:面积 = 边长 ×边长。
例如,一个正方形的边长为3厘米,那么它的面积就是3厘米 × 3厘米 = 9平方厘米。
二、长方形的面积计算长方形是指具有两对相等且平行的边的四边形。
长方形的面积计算可以通过长和宽的乘积得到,公式为:面积 = 长 ×宽。
例如,一个长方形的长为5厘米,宽为4厘米,那么它的面积就是5厘米 × 4厘米 = 20平方厘米。
三、三角形的面积计算三角形是指具有三个边和三个角的多边形。
计算三角形面积的方法有很多种,这里介绍一种简单的方法——底乘高除以2。
具体公式为:面积 = 底 ×高 ÷ 2。
例如,一个三角形的底长为6厘米,高为3厘米,那么它的面积就是6厘米 × 3厘米 ÷ 2 = 9平方厘米。
四、圆的面积计算圆是指由一个平面围绕着它的中心点画出的封闭曲线,圆的面积计算可以通过半径的平方乘以π(π的近似值为 3.14159)得到,公式为:面积 = 半径 ×半径× π。
例如,一个圆的半径为2厘米,那么它的面积就是2厘米 × 2厘米 × 3.14159 = 12.56636平方厘米。
五、综合题目下面我们通过一个综合题目来练习面积计算:某田径场为长方形,长为60米,宽为40米,场地四周沿着跑道边缘修建了一个2米宽的跑道,求整个田径场的面积。
解题方法:首先计算跑道的面积,根据长方形面积计算公式,跑道的面积 = (60 + 2 × 2) ×(40 + 2 × 2)平方米 = 64 × 44平方米 = 2816平方米。
小学奥数长方形正方形面积求解(二)

× 花圃的面积
需要知道
花圃里可以种的鲜花数:
已知 长 × 宽
200×6=1200(株)
花圃的面积:
上一张 下一张
每平方米种6株花
25×8=200(平方米)
4.数学课本长26厘米,宽18厘米,用下面这张纸包书皮合 适吗?
40厘米
30厘米
上一张
下一张
解析
包书皮的时候需要将书的封面封底都要包好
40厘米
上一张 下一张
思路二这种方法在实际生活中是不
可取的,面积相同的图形可以是各种形 状,这张纸的面积虽然大于课本封面封 底的面积和,可能实际是这张纸又细又 长无法包数学书。
60厘米
18厘米
26 厘 米
20 厘 米
上一张
பைடு நூலகம்下一张
5. 教室北面的墙壁长 7米,宽 3 米,其中有 2 扇窗户,每扇 窗户的面积是 4 平方米。现在要粉刷这面墙壁,要粉刷的
答:收割机半小时可以给4500平方米的麦田收割
上一张
下一张
3. 在一个长是 25 米、宽是 8 米的长方形花圃里种鲜花,如
果每平方米的地方正好适合种 6 株花,那么这个花圃里一
共可以种多少株鲜花?
25米
8米
上一张
下一张
解析
要求这个花圃里一共可以种多少株鲜花
需要知道
花圃里可种1200株的鲜花数
每平方米种6株花
1200米
压路机压路的宽度是2米
2米 上一张 下一张
有一辆收割机,每分钟行驶 75米,收割的宽度是 2米。收 割机半小时可以给多少平方米的麦田收割?
上一张 下一张
解析
方法一:
三年级奥数长方形和正方形的周长与面积

三年级奥数长方形和正方形的周长与面积------------------------------------------作者xxxx------------------------------------------日期xxxx第一讲正方形和长方形的周长与面积例1、把两个边长是6厘米的正方形拼成一个长方形,这个长方形的周长和面积分别是多少?例2、把一个边长是16分米的正方形纸裁成4个完全一样的小正方形,这4个小正方形的周长和比原来的大正方形的周长增加的多少?例3、你能求出以下图形的周长和面积吗?例4、如图,王阿姨家长7米,宽5米的菜地中间有一条1米宽的小路,求菜地中种植蔬菜的面积是多少?例5、一个长方形,如果长增加3厘米,面积就增加15平方厘米。
如果宽减少3厘米,面积就减少24平方厘米。
求原来长方形的面积?例6、为了更好的开展体育活动,学校准备将长60米、宽40米的长方形操场进行矿建,长增加40米,宽增加20米,操场的面积增加了多少平方米?例7、从一张边长7厘米的正方形纸片中,最多能裁出多少个长4厘米,宽1厘米的长方形纸条?例8、如图是两块大小不同的草坪,重叠部分是一个花坛,求草坪的面积是多少?‘例9、一个正方形的边长是20厘米,中间套着一个长方形,长方形的四个角的这个长方形的面积的多少?例10、有图中大正方形比小正方形的边长长2厘米,大正方形的面积不小正方形的面积多1平方分米。
大正方形的面积是多少平方厘米?练习与思考1、一个长方形是由两个边长是8分米的正方形拼成的,这个长方形的周长和面积分别是多少?2、一根铁丝围成一个长18厘米、宽12厘米的长方形,如果用它重新围成一个正方形,这个正方形的边长是多少厘米?3、把一张边长是9厘米的正方形纸裁成4个完全一样的小正方形,这4个小正方形的周长比原来的大正方形的周长增加了多少?4、把一个长50厘米,宽38厘米的长方形,剪成一个最大的正方形,面积减少了多少平方厘米?5、在一张边长是25厘米的正方形中,剪去一个宽为5厘米的长方形,剩下部分的面积是多少?6、一个长方形,如果长增加4米,面积就增加4000方分米,如果宽减少3米,面积就减少9000平方分米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六、长方形与正方形的面积(A 卷)
年级 班 姓名 得分 一、填空
1.右图是一幢楼房的平面图形,它的面积是 平方米. (单位:米)
2.北京某四合院子正好是个边长10米的正方形,在院子中央修了一条宽2米的“十字形”甬路,如图.这条“十字形”甬路的面积是 平方米?
3.右图中有四个正方形,图①的边长是32厘米,图②的边长是图①边长的一半;图③的边长是图②边长的一半;图④的边长是图③边长的一半.
(1)图中图①(最大的正方形)的面积是图④(最小的正方形)面积的 倍?并说出图④的面积是图①面积的
)
(
)(. (2)图中图①的周长是图④的周长的 倍?并说出图④的周长是图①周长的)
(
)(.
4.右图中有3个长方形,图①长32厘米,宽16厘米;图②的长、宽分别是图①长、宽的一半;图③的长、宽分别是图②长、宽的一半.
(1)图①的面积是图③面积的 倍?并说出图③的面积是图①面积的
)
(
)(. (2)图①的周长是图③周长的 倍?并说出图③的周长是图①周长的)
(
)(.
5.有大、小两个长方形,对应边的距离均为1厘米,如果两个长方形之间(阴影部分)部分的面积是16平方厘米,且小长方形的长是宽的2倍.求大长方形的面积是小正方形的 倍.
6.将边长为24厘米的正方形纸剪成四块同样大小的长方形纸,每块长方形纸的边长是 ,宽是 ;周长是 ;面积
1
2
4
5
①
③
②
是 .
7.一个长方形原来的长是12厘米,宽是7厘米.现在把长和宽都减少2厘米,那么面积共减少了 平方厘米?
8.长方形花坛四周有一条2米宽的路,这条路的面积是156平方米.该花坛的周长是 米.
9.有一个长方形,长与宽各增加8分米,面积增加208平方分米,求原长方形的周长是 分米.
10.大正方形中有一个小正方形,两正方形的周长差是8厘米,面积差是20平方厘米.大正方形的边长是 厘米?
二、解答题
11.把20分米长的线段分成两段,并在每一段上作一正方形(如下图).已知两个正方形的面积差为40平方分米,求每个正方形的面积.
12.有一块长方形的玻璃,从长边截去20厘米宽的一块后,剩下的玻璃正好是块正方形,它的周长是160厘米.原来长方形玻璃的周长和面积各是多少?
13.有一个机器零件,如图.中间是一个大正方形,边长是6厘米;每边正中向外凸出一个小正方形,边长都是2厘米.
(1)这个机器零件的周长是多少? (2)这个机器零件的面积是多少?
14.右图中有六个正方形,较小的正方形都由较大的正方形的四边中点连接而成.已知最大的正方形的边长为10cm ,那么最小的正方形的面积等于 2cm .
20分米
———————————————答 案——————————————————————
1. 11平方米. 1×5+(4-1)×2=11(平方米).
2. 36平方米. 2×10+(10-2)÷2×2×2=36(平方米).
3. (1)64倍;641. (2)8倍;81
.
4. (1)16倍;16
1. (2)4倍;41
.
5. 3倍.
6. 24厘米;6厘米;60厘米;144平方厘米.
7. 34平方厘米. 12×2+(7-2)×2=34(平方厘米). 8. 140米. 9. 36分米. 10. 24厘米.
二、解答题
1.解:阴影部分的长20分米相当于两个正方形边长的和,宽相当于两个正方形边长的差. 40÷20=2(分米)
(20+2)÷2=11(分米) 11×11=121(平方分米)
20-11=9(分米) 9×9=81(平方分米)
答:大正方形面积是121平方分米,小正方形面积是81平方分米.
2.周长:200厘米.
160÷4=40(厘米)
(40+20)×2+40×2=200(厘米). 面积:2400平方厘米.
(40+20)×40=2400(平方厘米).
3.周长40厘米. 2×5×4=40(厘米)
面积52平方厘米. 2×2×4+6×6=52(平方厘米).
4.2813cm . ()
281
321212*********cm =⨯⨯⨯⨯⨯⨯
20 dm。
