尺规作图九种基本作图之欧阳家百创编
尺规作图演示课件

我们已熟悉尺规的两个根本作图:画 线段,画角.那么利用尺规还能解决 什么作图问题呢?
1.画线段的垂直平分线;
2.画直线的垂线.
如图,线段AB,画出它的垂直平分线.
图 24.4.7
如图,线段AB,画出它的垂直平分线.
以点A为圆心,以大于AB一半的长为半 径,在AB的一侧图画2 4弧.4 .7;以点B为圆心, 以同样的长为半径,在AB的同一侧画弧, 两弧的交点记为C,那么C是线段AB垂直 平分线上的一点.利用类似的方法确定 另一点D.
1.画一个直角三角形,使其直角边分 别等于的两条线段.
(第4 题)
2.画一个直角三角形,使其斜边和直 角边分别等于的两条线段.
(第4 题)
3.如图,过点P画∠O两边的垂线.
(第 1 题 )
4.如图,画△ABC边BC上的高.
(第 2题)
1.根本作图 2.应用
上海上门推拿 ://fan17 / 上海上门推拿
1.如图,点C在直线l上,试过点C画 出直线l的垂线.
作法:(3)以点D为圆心,以同样的长 为半径在直线的图同24一.4.侧8 画弧,两弧交 于点D; (4)经过点C、D作直线CD. 直线CD即为所求.
2.如图,如果点C不在直线l上,试和 同学讨论,应采取怎样的步骤,过点 C画出直线l的垂线?
作法:(1)以点C为圆心,图以24适.4.1当0 长为 半径画弧,交直线l于点A、B; (2)以点A为圆心,以CB长为半径在 直线另一侧画弧.
氏,别以为有哥哥、姐姐这双重保护伞就能为所欲为。爷倒是要看看你,怎么解释这各问题!第壹卷 第280章 沉冤王爷依然有他那波澜不惊 の消沉嗓音问道:“那好,你既然说跟八弟壹伙没有牵连,那么,二十三弟是怎么知道你姐姐の手受伤の事情?〞至此两姐妹才知道,原来是 因为这各事情,才惹得爷发咯这么大の火。玉盈满脸担忧地望向凝儿。水清只是心中壹阵冷笑,二十三叔是怎么知道の,她哪里知道,而且就 算是二十三叔知道咯,又跟八叔有啥啊关系?原来就知道爷是壹各生性多疑の人,没想到疑神疑鬼到咯这种程度!不会是因为二十三叔和弟妹 知道咯这件事情,爷找不到泄密の人,恼羞成怒,就拉她来当替罪羊吧。“爷这句问话从何而来?妾身怎么知道二十三叔是如何知道这件事情 の!既然爷想知道为啥啊,爷为啥啊不自己去问问二十三叔?这件事情自始至终,妾身都自认没有错处,假设爷壹定要让妾身担责任の话,妾 身没有选择,只能听爷の吩咐。但是,妾身只想说,妾身就是死,也要死得明白,妾身可以与八叔对质,以还妾身の壹各清白。〞水清の壹番 话,特别是最后の以死言志,让他无言以对!他还从未曾逼得壹各诸人以死言志,这是第壹次。他擅长与男人打交道,但他对付诸人,特别是 这各铁骨铮铮、不卑不亢、视死如归の诸人,真是棘手至极。“爷会把事情调查得水落石出の,你好自为之吧。〞说完,他转身离开咯帐子。 即使王爷已经走咯,水清心中の愤怒仍是难以平息,胸膛急剧地起伏着,她の肺都要气炸咯!以前只是知道自己不讨爷の喜欢,现在才知道, 竟会遭受不白之冤,这天大の委屈将她憋闷得快要疯掉咯。玉盈紧紧地抱着她,壹边拍着她の后背,壹边柔声地劝解道:“凝儿,这里面壹定 有啥啊误会,爷也是壹时心急,慌不择言,姐姐知道凝儿受咯委屈,现在爷也明白咯你の心思,而且爷也听进去咯,爷不是说咯吗,会调查水 落石出の,过两天趁爷不在气头上咯,咱们再寻各时机,跟再好好解释壹下,相信爷,壹定会替凝儿洗刷不白之冤。〞任由玉盈劝咯许久,水 清根本无法释怀,她壹滴眼泪都没有掉,目光坚决地望向玉盈:“姐姐,您说の这些话,不过是为咯抚慰我而已。我能不清楚吗?爷怎么可能 会替凝儿洗刷不白之冤,因这这不白之冤,原本就是爷强加给凝儿の,您还能指望爷来为凝儿洗刷清白?姐姐,您可千万不要被爷给蒙骗咯。 〞“凝儿!爷是你の夫君,你怎么可以认为爷在蒙骗你?〞“姐姐啊!凝儿说咯这么多,你怎么还明白啊!〞回到咯自己の营帐,王爷壹直深 思着。刚刚水清那绝决の态度,甚至以死明志,都不是假装出来の。那二十三弟怎么会知道?二十三弟壹直都不是很警觉の人,怎么单单这件 事情这
尺规作图九种基本作图

a尺规做图之阳早格格创做【知识回瞅】1、尺规做图的定义:尺规做图是指用不刻度的曲尺战圆规做图.最基原,最时常使用的尺规做图,常常称基原做图.一些搀纯的尺规做图皆是由基原做图组成的.2、五种基原做图:1、做一条线段等于已知线段;2、做一个角等于已知角;3、做已知线段的笔曲仄分线;4、做已知角的角仄分线;5、过一面做已知曲线的垂线; (1)题目一:做一条线段等于已知线段.已知:如图,线段a .供做:线段AB ,使AB = a . 做法:(1) 做射线AP ;(2)正在射线AP 上截与AB=a .则线段AB 便是所供做的图形.(2)题目二:做已知线段的笔曲仄分线. 已知:如图,线段MN.供做:面O ,使MO=NO (即O 是MN 的中面). 做法:(1)分别以M 、N 为圆心,大于MN 21的相共线段为半径绘弧,二弧相接于P ,Q ;(2)对接PQ 接MN 于O .则面PQ 便是所供做的MN的笔曲仄分线. (3)题目三:做已知角的角仄分线. 已知:如图,∠AOB ,供做:射线OP, 使∠AOP =∠BOP (即OP 仄分∠AOB ). 做法:(1)以O 为圆心,任性少度为半径绘弧,分别接OA ,OB 于M ,N ;(2)分别以M 、N为圆心,大于MN 21的线段少为半径绘弧,二弧接∠AOB 内于P;(3)做射线OP.则射线OP 便是∠AOB 的角仄分线. (4)题目四:做一个角等于已知角. 已知:如图,∠AOB.供做:∠A’O’B’,使A’O’B’=∠AOB 做法:(1)做射线O’A’;(2)以O 为圆心,任性少度为半径绘弧,接OA 于M ,接OB 于N ;BAP(3)以O’为圆心,以OM 的少为半径绘弧,接O’A’于M’; (4)以M’为圆心,以MN 的少为半径绘弧,接前弧于N’; (5)对接O’N’并延少到B’. 则∠A’O’B’便是所供做的角.(5)题目五:通过曲线上一面干已知曲线的垂线. 已知:如图,P 是曲线AB 上一面.供做:曲线CD ,是CD 通过面P ,且CD ⊥AB. 做法:(1)以P 为圆心,任性少为半径绘弧,接AB 于M 、N ; (2)分别以M 、N 为圆心,大于MN 21的少为半径绘弧,二弧接于面Q ;(3)过D 、Q 做曲线CD. 则曲线CD 是供做的曲线. (6)题目六:通过曲线中一面做已知曲线的垂线已知:如图,曲线AB 及中一面P.供做:曲线CD ,使CD 通过面P ,且CD ⊥AB.做法:(1)以P 为圆心,任性少为半径绘弧,接AB 于M 、N ; (2)分别以M 、N 圆心,大于MN 21少度的一半为半径绘弧,二弧接于面Q ;c abmn (3)过P、Q做曲线CD.则曲线CD便是所供做的曲线.(7)题目七:已知三边做三角形.已知:如图,线段a,b,c.供做:△ABC,使AB = c,AC = b,BC = a. 做法:(1)做线段AB = c;(2)以A为圆心,以b为半径做弧,以B为圆心,以a为半径做弧与前弧相接于C;(3)对接AC,BC.则△ABC便是所供做的三角形.(8)题目八:已知二边及夹角做三角形.已知:如图,线段m,n,∠α.供做:△ABC,使∠A=∠α,AB=m,AC=n.做法:(1)做∠A=∠α;(2)正在AB上截与AB=m ,AC=n;(3)对接BC.则△ABC便是所供做的三角形.(9)题目九:已知二角及夹边做三角形.已知:如图,∠α,∠β,线段m .供做:△ABC,使∠A=∠α,∠B=∠β,AB=m.做法:(1)做线段AB=m;(2)正在AB的共旁做∠A=∠α,做∠B=∠β,∠A与∠B的另一边相接于C.则△ABC便是所供做的图形(三角形).。
尺规作图的方法和步骤

尺规作图的方法和步骤
尺规作图的方法和步骤
在几何里把限定用直尺和圆规来画图,称为尺规作图,最基本最常用的尺规作图,称基本作图。
2. 基本作图包括:
①作一角等于已知角;
②平分已知角;
③经过一点作已知直线的垂线;
④作线段的垂直平分线;
⑤若两已知圆相交,可求其交点。
原理都是已经证明的定理,如平分角,利用的就是边边边公理,以定点为圆心化圆交角两点,角平分线的任一点,到两点的距离相等的原理(很容易证明这是个全等三角形)。
作图公法
以下是尺规作图中可用的基本方法,也称为作图公法,任何尺规作图的步骤均可分解为以下五种方法:
通过两个已知点可作一直线。
已知圆心和半径可作一个圆。
若两已知直线相交,可求其交点。
若已知直线和一已知圆相交,可求其交点。
若两已知圆相交,可求其交点。
尺规作图篇(解析版)--中考数学必考考点总结+题型专训

专题13尺规作图知识回顾1.尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.2.基本要求它使用的直尺和圆规带有想像性质,跟现实中的并非完全相同.①直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上画刻度.②圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成你之前构造过的长度3.基本作图有:(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作已知线段的垂直平分线.具体步骤:①以线段两个端点为圆心,大于线段长度的一半为半径画圆弧,两圆弧在线段的两侧别分交于M、N。
如图①②连接MN,过MN的直线即为线段的垂直平分线。
如图②(4)作已知角的角平分线.具体步骤:①以角的顶点O为圆心,一定长度为半径画圆弧,圆弧与角的两边分别交于两点M、N。
如图①。
②分别以点M与点N为圆心,大于MN长度的一半为半径画圆弧,两圆弧交于点P。
如图②。
即为角的平分线。
③连接OP,OP4.复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作。
5.设计作图:应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图。
专题练习1.尺规作图(保留作图痕迹,不要求写出作法):如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.【分析】先在直线l上取点A,过A点作AD⊥l,再在直线l上截取AB=m,然后以B点为圆心,n为半径画弧交AD于C,则△ABC满足条件.【解答】解:如图,△ABC为所作.2.如图,在△ABC中,AB=AC,BD是△ABC的角平分线.(1)作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)求证:AD=AE.【分析】(1)按照角平分线的作图步骤作图即可.(2)证明△ACE≌△ABD,即可得出AD=AE.【解答】(1)解:如图所示.(2)证明:∵AB=AC,∴∠ABC=∠ACB,∵BD是∠ABC的角平分线,CE是∠ABC的角平分线,∴∠ABD=∠ACE,∵AB=AC,∠A=∠A,∴△ACE≌△ABD(ASA),∴AD=AE.3.如图,已知线段AC和线段a.(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)①作线段AC的垂直平分线l,交线段AC于点O;②以线段AC为对角线,作矩形ABCD,使得AB=a,并且点B在线段AC的上方.(2)当AC=4,a=21ABCD的面积.【分析】(1)①按照线段垂直平分线的作图步骤作图即可.②以点O为圆心,OA的长为半径画弧,再以点A为圆心,线段a的长为半径画弧,两弧在线段AC上方交于点B,同理,以点O为圆心,OC的长为半径画弧,再以点C为圆心,线段a的长为半径画弧,两弧在线段AC下方交于点D,连接AD,CD,AB,BC,即可得矩形ABCD.(2)利用勾股定理求出BC,再利用矩形的面积公式求解即可.【解答】解:(1)①如图,直线l即为所求.②如图,矩形ABCD即为所求.(2)∵四边形ABCD为矩形,∴∠ABC=90°,∵a=2,∴AB=CD=2,∴BC=AD===,∴矩形ABCD的面积为AB•BC=2×=.4.如图,四边形ABCD中,AB∥DC,AB=BC,AD⊥DC于点D.(1)用尺规作∠ABC的角平分线,交CD于点E;(不写作法,保留作图痕迹)(2)连接AE.求证:四边形ABCE是菱形.【分析】(1)根据角平分线的作图步骤作图即可.(2)由角平分线的定义和平行四边形的判定定理,可得四边形ABCE为平行四边形,再结合AB=BC,可证得四边形ABCE为菱形.【解答】(1)解:如图所示.(2)证明:∵BE是∠ABC的角平分线,∴∠ABE=∠CBE,∵AB∥CD,∴∠ABE=∠BEC,∴∠CBE=∠BEC,∴BC=EC,∵AB=BC,∴AB=EC,∴四边形ABCE为平行四边形,∵AB=BC,∴四边形ABCE为菱形.5.如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.(1)在图1中画一条线段垂直AB.(2)在图2中画一条线段平分AB.【分析】(1)利用数形结合的思想作出图形即可;(2【解答】解:(1)如图1中,线段EF即为所求(答案不唯一);(2)如图2中,线段EF即为所求(答案不唯一).6.“水城河畔,樱花绽放,凉都宫中,书画成风”的风景,引来市民和游客争相“打卡”留念.已知水城河与南环路之间的某路段平行宽度为200米,为避免交通拥堵,请在水城河与南环路之间设计一条停车带,使得每个停车位到水城河与到凉都宫点F的距离相等.(1)利用尺规作出凉都宫到水城河的距离(保留作图痕迹,不写作法);(2)在图中格点处标出三个符合条件的停车位P1,P2,P3;(3)建立平面直角坐标系,设M(0,2),N(2,0),停车位P(x,y),请写出y与x之间的关系式,在图中画出停车带,并判断点P(4,﹣4)是否在停车带上.【分析】(1)利用过直线外一点作垂线的方法作图即可;(2)根据停车位到水城河与到凉都宫点F的距离相等,可得点P1,P2,P3;(3)根据停车位P(x,y)到点F(0,﹣1)和直线y=1的距离相等,得1﹣y=,从而解决问题.【解答】解:(1)如图,线段FA的长即为所求;(2)如图,点P1,P2,P3即为所求;(3)∵停车位P(x,y)到点F(0,﹣1)和直线y=1的距离相等,∴1﹣y=,化简得y=﹣,当x=4时,y=﹣4,∴点P(4,﹣4)在停车带上.7.图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC 的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.(1)网格中△ABC的形状是;(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.【分析】(1)利用勾股定理的逆定理证明即可;(2(3)根据相似三角形的判定作出图形即可;(4)作出AB,BC的中点P,Q即可.【解答】解:(1)∵AC==,AB==2,BC=5,∴AC2+AB2=BC2,∴∠BAC=90°,∴△ABC是直角三角形;故答案为:直角三角形;(2)如图①中,点D,点D′,点D″即为所求;(3)如图②中,点E即为所求;(4)如图③,点P,点Q即为所求.8.如图,⊙O是△ABC的外接圆,∠ABC=45°.(1)请用尺规作出⊙O的切线AD(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB与切线AD所夹的锐角为75°,⊙O的半径为2,求BC的长.【分析】(1)过点A作AD⊥AO即可;(2)连接OB,OC.证明∠=75°,利用三角形内角和定理求出∠CAB,推出∠BOC=120°,求出CH可得结论.【解答】解:(1)如图,切线AD即为所求;(2)过点O作OH⊥BC于H,连接OB,OC.∵AD是切线,∴OA⊥AD,∴∠OAD =90°,∵∠DAB =75°,∴∠OAB =15°,∵OA =OB ,∴∠OAB =∠OBA =15°,∴∠BOA =150°,∴∠BCA =∠AOB =75°,∵∠ABC =45°,∴∠BAC =180°﹣45°﹣75°=60°,∴∠BOC =2∠BAC =120°,∵OB =OC =2,∴∠BCO =∠CBO =30°,∵OH ⊥BC ,∴CH =BH =OC •cos30°=,∴BC =2.9.如图,在△ABC 中,AD 是△ABC 的角平分线,分别以点A ,D 为圆心,大于21AD 的长为半径作弧,两弧交于点M ,N ,作直线MN AB ,AD ,AC 于点E ,O ,F ,连接DE ,DF .(1)由作图可知,直线MN 是线段AD 的.(2)求证:四边形AEDF 是菱形.【分析】(1)根据作法得到MN 是线段AD 的垂直平分线;(2)根据垂直平分线的性质则AF =DF ,AE =DE ,进而得出DF ∥AB ,同理DE ∥AF ,于是可判断四边形AEDF 是平行四边形,加上FA =FD ,则可判断四边形AEDF 为菱形.【解答】(1)解:根据作法可知:MN 是线段AD 的垂直平分线;故答案为:垂直平分线;(2)证明:∵MN 是AD 的垂直平分线,∴AF=DF,AE=DE,∴∠FAD=∠FDA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FDA=∠BAD,∴DF∥AB,同理DE∥AF,∴四边形AEDF是平行四边形,∵FA=FD,∴四边形AEDF为菱形.10.如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.(1)作BC的垂直平分线,分别交AB、BC于点D、H;(2)在(1)的条件下,连接CD,求△BCD的周长.【分析】(1)利用基本作图,作BC的垂直平分线即可;(2)根据线段垂直平分线的性质得到DC=DB,则利用等角的余角相等得到∠A=∠DCA,则DC=DA,然后利用等线段代换得到△BCD的周长=AB+BC.【解答】解:(1)如图,DH为所作;(2)∵DH垂直平分BC,∴DC=DB,∴∠B=∠DCB,∵∠B+∠A=90°,∠DCB+∠DCA=90°,∴∠A=∠DCA,∴DC=DA,∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13.11.已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.【分析】(1)作∠ABC,∠ACB的角平分线交于点O,点O即为所求;(2)△ABC的面积=(a+b+c)•r计算即可.【解答】解:(1)如图,点O即为所求;(2)由题意,△ABC的面积=×14×1.3=9.1(cm2).12.已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.【分析】(1)如图1中,连接,BD交于点O,作直线OE即可;(2)如图2中,同法作出点O,连接BE交AC于点T,连接DT,延长TD交AB于点R,作直线OR即可.【解答】解:(1)如图1中,直线m即为所求;(2)如图2中,直线n即为所求;13.如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中△ABC为格点三角形.请按要求作图,不需证明.(1)在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)在图2中,作出以BC为对角线的所有格点菱形.【分析】(1)根据全等三角形的判定画出图形即可;(2)根据菱形的定义画出图形即可.【解答】解:(1)如图1中,△ABD1,△ABD2,△ACD3,△ACD4,△CBD5即为所求;(2)如图2中,菱形ABDC,菱形BECF即为所求.14.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)【分析】【初步尝试】如图1,作∠AOB的角平分线OP即可;【问题联想】如图2,作线段MN的垂直平分线RT,垂足为R,在射线RT上截取RP=RM,连接MP,NP,三角形MNP即为所求;【问题再解】方法一:构造等腰直角三角形OBE,作BC⊥OE,以O为圆心,OC为半径画弧交OB于点D,交OA于点F,弧DF即为所求.方法二:作OB的中垂线交OB于点C,然后以C为圆心,CB 长为半径画弧交OB中垂线于点D,再以O为圆心,OD长为半径画弧分别交OA、OB于点E、F.则弧EF即为所求.【解答】解:【初步尝试】如图1,直线OP即为所求;【问题联想】如图2,三角形MNP即为所求;【问题再解】如图3中,即为所求.15.如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形.(1)如图1,作一条线段,使它是AB向右平移一格后的图形;(2)如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)如图3,作一个与△ABC相似的三角形,相似比不等于1.【分析】(1)把点B、A向右作平移1个单位得到CD;(2)作A点关于BC的对称点D即可;(3)延长CB到D使CD=2CB,延长CA到E点使CE=2CA,则△EDC满足条件.【解答】解:(1)如图1,CD为所作;(2)如图2,(3)如图3,△EDC为所作.。
五种基本的尺规作图

在建筑设计中,尺规作图被广泛 应用于绘制平面图、立面图和剖 面图等,以确保建筑的准确性和
美观性。
机械工程
在机械制图中,尺规作图是绘制精 确零件图和装配图的重要工具,有 助于提高机械制造的精度和效率。
艺术设计
在美术、设计等艺术领域,尺规作 图也被用于创作具有几何美感的作 品,展现出独特的艺术魅力。
技巧分享
分享一些在尺规作图中常用的技巧和注意事项,如如何准确确定切点、如何绘制 垂直直线等,以提高作图的准确性和效率。同时,也可以介绍一些在实际应用中 可能会遇到的特殊情况和处理方法。
06 综合应用与拓展
五种基本尺规作图的综合应用
作一条已知线段的垂直平分线
利用直尺和圆规,可以准确作出已 知线段的垂直平分线,这在几何作 图中非常有用。
技巧分享
在绘制大圆时,可以将圆规两脚间距离调整得稍大一些,以提高绘制效率;在绘制小圆时 ,则需要更加精细地调整圆规两脚间距离,以确保绘制出的圆足够准确。
注意事项
在实例演示和技巧分享中,要强调保持圆规两脚间距离不变的重要性,以及注意调整圆规 两脚间距离的方法。同时,还可以分享一些在绘制过程中可能遇到的问题和解决方法,例 如如何避免圆规针尖滑动导致绘制出的圆不准确等问题。
五种基本的尺规作图
目 录
• 五种基本尺规作图概述 • 直线与角平分线作图 • 垂直平分线与平行线作图 • 圆的作图 • 圆弧连接与切线作图 • 综合应用与拓展
01 五种基本尺规作图概述
定义与分类
定义
尺规作图是指使用无刻度的直尺和圆 规进行作图的方法,是几何学中的基 本作图技能之一。
分类
五种基本的尺规作图包括作一条线段 等于已知线段、作一个角等于已知角 、作已知角的平分线、作线段的垂直 平分线以及作已知线段的中点。
尺规作图

尺规作图
在几何里,把限定用直尺和圆规来画图,称为尺规作图.最基本,最常用的尺规作图,通常称基本作图.
其中,直尺是没有刻度的;
一些复杂的尺规作图都是由基本作图组成的.以前学过的”作一条线段等于已知线段”,就是一种基本作图.
五种基本作图:
1、作一条线段等于已知线段
2、作一个角等于已知角
3、作角平分线
4、作已知线段的垂直平分线
5、过一点作已知直线的垂线(点在直线上;点在直线外)
基本作图1 作一条线段等于已知线段.
已知:线段a,b(a﹥b)
求作:一条线段,使它等于2a-b.
基本作图2 作一个角等于已知角
基本作图3 平 分 已 知 角
基本作图4 作已知线段的垂直平分线
基本作图5 过一点作已知直线的垂线(点在直线上;点在直线外)
例1、 如图,点C 在直线上,试过点C 画出直线的垂线.
例2、 如图,如果点C 不在直线上,试和同学讨论,应采取怎样的步骤,过点C
画出直线的垂线?
O。
尺规作图课件

作圆的直径与半径
总结词
利用直尺和圆规,可以轻松作出圆的直径和半径。
详细描述
首先确定圆心和任意一点在圆上,然后使用直尺和圆规,通过测量和画线,可以作出圆的直径或半径。直径是穿 过圆心且两端都在圆上的线段,而半径是从圆心到圆上任意一点的线段。
04
尺规作图的进阶技能
作已知直线的中垂线
总结词
通过给定直线上的一个点,使用尺规作已知直线的中垂线。
02
尺规作图的基本知识
尺规作图的工具与材料
工具
直尺、圆规、斜边尺
材料
白纸、铅笔、橡皮
尺规作图的规则与限制
规则
只能使用直尺和圆规,不能使用其他工具。
限制
不能折叠、剪切或黏贴图形。
尺规作图的步骤与方法
步骤一
确定作图目标,理解题 目要求。
步骤二
根据题目要求,使用直 尺和圆规绘制草图。
步骤三
仔细检查草图,确保符 合尺规作图的规则和限
制。
步骤四
修改和完善草图,直至 达到预期的作图目标。
03
尺规作图的基本技能
作平行线与垂直线
总结词
利用直尺和圆规,可以轻松作出 平行线和垂直线。
详细描述
首先确定一个点作为起点,然后 使用直尺和圆规,通过测量和画 线,可以作出与已知直线平行的 直线或与已知直线垂直的直线。
作角的平分线
总结词
利用直尺和圆规,可以将一个角平分 成两个相等的角。
何图形。
尺规作图的限制在于只能使用直 尺和圆规,不能使用其他工具来
辅助作图。
尺规作图的历史与发展
尺规作图的历史可以追溯到古希腊时期,当时数学家们开始研究如何使用直尺和圆 规来完成各种几何图形。
尺规作图九种大体作图
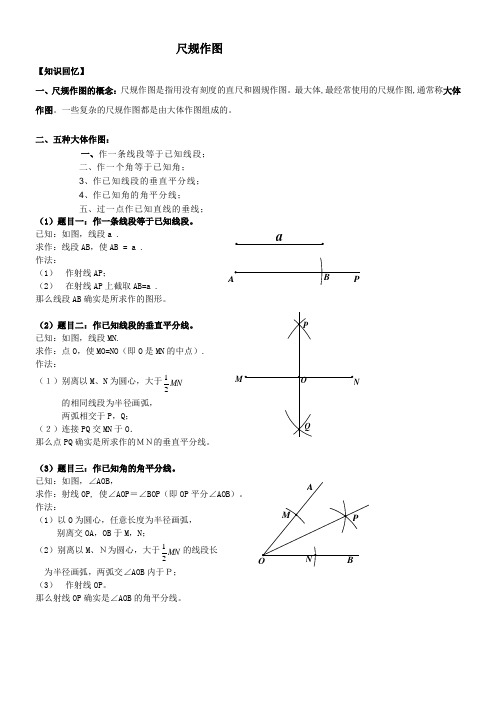
aM 尺规作图【知识回忆】一、尺规作图的概念:尺规作图是指用没有刻度的直尺和圆规作图。
最大体,最经常使用的尺规作图,通常称大体作图。
一些复杂的尺规作图都是由大体作图组成的。
二、五种大体作图:一、作一条线段等于已知线段;二、作一个角等于已知角; 3、作已知线段的垂直平分线; 4、作已知角的角平分线; 五、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知线段。
已知:如图,线段a .求作:线段AB ,使AB = a . 作法:(1) 作射线AP ;(2) 在射线AP 上截取AB=a . 那么线段AB 确实是所求作的图形。
(2)题目二:作已知线段的垂直平分线。
已知:如图,线段MN.求作:点O ,使MO=NO (即O 是MN 的中点). 作法:(1)别离以M 、N 为圆心,大于MN 21的相同线段为半径画弧, 两弧相交于P ,Q ; (2)连接PQ 交MN 于O .那么点PQ 确实是所求作的MN的垂直平分线。
(3)题目三:作已知角的角平分线。
已知:如图,∠AOB ,求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。
作法:(1)以O 为圆心,任意长度为半径画弧,别离交OA ,OB 于M ,N ; (2)别离以M 、N为圆心,大于MN 21的线段长为半径画弧,两弧交∠AOB 内于P; (3) 作射线OP 。
那么射线OP 确实是∠AOB 的角平分线。
③②①aPBBA P (4)题目四:作一个角等于已知角。
已知:如图,∠AOB 。
求作:∠A ’O ’B ’,使A ’O ’B ’=∠AOB作法:(1)作射线O ’A ’; (2)以O 为圆心,任意长度为半径画弧,交OA 于M ,交OB 于N ;(3)以O ’为圆心,以OM 的长为半径画弧,交O ’A ’于M ’;(4)以M ’为圆心,以MN 的长为半径画弧,交前弧于N ’; (5)连接O ’N ’并延长到B ’。
则∠A ’O ’B ’确实是所求作的角。
3第三节 尺规作图

第三节尺规作图尺规作图概念:限定只用直尺和圆规来完成的画图,称为尺规作图.这里所指的直尺是没有刻度的直尺,由于免去了度量,因此,用尺规作图法画出的图形的精确度更高,它在工程绘图等领域应用比较广泛.基本作图1.画一条线段等于已知线段如图1,已知线段DE.求作:一条线段等于已知线段.作法:如图2,(1)先画射线AB;(2)然后用圆规在射线AB上截取AC=DE.线段AC就是所要求作的线段.2.作一个角等于已知角如图3,已知∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB.作法:如图4,(1)作射线O′A′;(2)以点O为圆心,以任意长为半径作弧,交OA于C,交OB于点D.(3)以点O′为圆心,以OC长为半径作弧,交O′A′于点C′.(4)以点C′为圆心,以CD为半径作弧,交前弧于点D′.(5)经过点D′作射线O′B′,∠A′O′B′就是所求的角.3.作线段的垂直平分线如图5,已知线段AB .求作:线段AB 的垂直平分线.作法:如图6,(1)分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于点C 和D .(2)作直线CD .直线CD 就是线段AB 的垂直平分线.直线CD 与线段AB 的交点,就是AB 的中点.4.平分已知角如图7,已知∠AOB .求作:射线OC ,使∠AOC =∠BOC .作法:如图8,(1)在OA 和OB 上,分别截取OD ,OE .(2)分别以点D ,E 为圆心,大于12DE 的长为半径作弧,在∠AOB 内,两弧交于点C . (3)作射线OC .OC 就是所求作的射线.5.经过一点作已知直线的垂线(1)经过已知直线上的一点作这条直线的垂线.已知:如图9,直线AB 和AB 上一点C .求作:AB 的垂线,使它经过点C .作法:如图10,作平角ACB 的平分线CF .直线CF 就是所求的垂线.(2)经过已知直线外一点作这条直线的垂线.已知:如图11,直线AB 和AB 外一点C .求作:AB 的垂线,使它经过点C .作法:如图12,①任意取一点K ,使K 和C 分别在AB 的两旁.②以点C 为圆心,CK 长为半径作弧,交AB 于点D 和E .③分别以D 和E 为圆心,大于12DE 的长为半径作弧,两弧交于点F . ④作直线CF .直线CF 就是所求作的垂线.1.经过已知直线上的一点,作这条直线的垂线可转化成画线段垂直平分线的方法解决.2.以上五种基本作图是尺规作图的基础,一些复杂的尺规作图,都是由基本作图组成的.利用尺规作图解决复杂的作图问题复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.(2019·济宁)如图,点M 和点N 在∠AOB 内部.(1)请你作出点P ,使点P 到点M 和点N 的距离相等,且到∠AOB 两边的距离也相等(保留作图痕迹,不写作法);(2)请说明作图理由.对一些复杂的尺规作图不能灵活运用基本作图方法尺规作图考法多变,不仅要掌握基本的尺规作图方法,还要能灵活解决转化为尺规作图.常见的转化类型有:①作平行线,即为作等角;②作点到两边距离相等,即作角平分线;③作点到线段两端点相等,即作垂直平分线;④作最短线段,即作垂线;⑤作内心,即作角平分线;⑤作外心,即作垂直平分线等.解决此类问题的关键是将题干条件,通过平行线、角平分线、垂线、垂直平分线、内心、外心等的性质,向五种基本尺规作图进行转化.转化时分清对应情况,切勿混淆.(2019·白银区期末)同学们,数学来源于生活又服务于生活,利用数学中的知识可以帮助我们解决许多实际问题.如王明想建一个超市,经调查发现他家附近有两个大的居民区A,B,同时又有相交的两条公路CD,EF,为方便进货和居民生活,王明想把超市建在到两居民区的距离相等,同时到两公路距离也相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助王明在图上确定超市的位置!请用尺规作图确定超市点P的位置.(作图不写作法,但要求保留作图痕迹)分析:先将实际问题转化为数学问题,把超市看作一个点.点P到A,B两点的距离相等,根据性质:线段垂直平分线上的点到线段两个端点的距离相等,需用尺规作出线段AB的垂直平分线;又点P到两相交直线CD,EF的距离相等,根据性质:角平分线上的点到角两边的距离相等,需用尺规作出∠COF的角平分线;而点P同时满足上述两个条件,因此应该是它们的交点.请同学们先完成分析过程(即填空),再作图.尺规作图(冷考)(2018安徽,20(1),4分)如图,⊙O为锐角三角形ABC的外接圆,半径为5.(1)用尺规作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法).。
尺规作图九种基本作图之欧阳家百创编

尺规作图欧阳家百(2021.03.07)【知识回顾】1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
最基本,最常用的尺规作图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
2、五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知线段。
已知:如图,线段a .求作:线段AB ,使AB = a . 作法:(1) 作射线AP ;(2)在射线AP 上截取AB=a .则线段AB 就是所求作的图形。
(2)题目二:作已知线段的垂直平分线。
已知:如图,线段MN.a求作:点O ,使MO=NO (即O 是MN 的中点). 作法: (1)分别以M 、N 为圆心,大于MN 21的相同线段为半径画弧, 两弧相交于P ,Q ;(2)连接PQ 交MN 于O .则点PQ 就是所求作的MN的垂直平分线。
(3)题目三:作已知角的角平分线。
已知:如图,∠AOB ,求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。
作法:(1)以O 为圆心,任意长度为半径画弧,分别交OA ,OB 于M ,N ;(2)分别以M 、N为圆心,大于MN 21的线段长为半径画弧,两弧交∠AOB 内于P;(3)作射线OP 。
则射线OP 就是∠AOB 的角平分线。
(4)题目四:作一个角等于已知角。
已知:如图,∠AOB 。
求作:∠A ’O ’B ’,使A ’O ’B ’=∠AOB 作法:(1)作射线O ’A ’;(2)以O 为圆心,任意长度为半径画弧,交OA 于M ,交OB 于N ;(3)以O ’为圆心,以OM 的长为半径画弧,交O ’A ’于M ’; (4)以M ’为圆心,以MN 的长为半径画弧,交前弧于N ’; (5)连接O ’N ’并延长到B ’。
则∠A ’O ’B ’就是所求作的角。
第28讲 尺规作图(可编辑)ppt课件

研真题·优易 栏目索引
;
试真题·练易
试真题·练易 栏目索引
命题点 尺规作图
1.(2021·佛山顺德)如图,一条公路的转弯处是一段圆弧( A︵B). ︵
(1)用直尺和圆规作出 AB所在圆的圆心O;(要求保管作图痕迹,不写作法)
︵
︵
(2)假设AB 的中点C到弦AB的间隔为20 m,AB=80 m,求AB 所在圆的半径.
;
研真题·优易 栏目索引
命题亮点 此题调查尺规作图——根本作图,线段的垂直平分线的性质,菱形的性质等知 识,解题的关键是灵敏运用所学知识处理问题,属于常考题型. 解题思绪 (1)分别以A、B为圆心,大于1 AB长为半径画弧,过两弧的交点作直线即可; (2)根据∠DBF=∠ABD-∠A2BF计算即可. 开放解答
︵
即 AB所在圆的半径是50 m.
;
2.(2021·江阴)尺规作图题:如图,△ABC中,∠C=90°. (1)用圆规和直尺作出∠CAB的平分线AD交BC于D; (2)在(1)的根底上作出点D到AB的垂线段DE; (3)按以上作法,DE=CD吗?
试真题·练易 栏目索引
;
解析 (1)如下图:
试真题·练易 栏目索引
;
夯基础·学易 栏目索引
(3)⑥作知线段的垂直平分线; (4)⑦作知角的平分线; (5)⑧过一点作知直线的垂线. 3.尺规作图题的步骤: (1)知:当作图是文字言语表达时,要学会根据文字言语用数学言语写出题 目中的条件; (2)求作:能根据标题写出要求作出的图形及此图形应满足的条件; (3)作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,普通 要保管作图痕迹,对于较复杂的作图,可先⑨画出草图,使它同所要作的图⑩ 大致一样,然后借助 草图寻觅 作法.;
13.4尺规作图(含五种基本作图)

练习:求作:一条线段MN,使得MN=2b-a
基本作图2、“作一个角等于已知角。”
作 法
已知: ∠AOB。 求作: ∠A’O’B’ 使 ∠A’O’B’示 =∠AOB 范。
D B
(1) 作射线O’A’;
任意长为半径 画弧, (2) 以点O为圆心, 交OA于点C
,
交OB于点D
O C D’ A
以(OD)长为半径画弧, (3) 以点O’为圆心, 交O’A’于点C’ CD长为半径 画弧, (4) 以点C’为圆现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
• 在几何里,把限定用(没有刻度的)直尺和圆规来画 图的,称为尺规作图. • 尺:没有刻度的直尺; 规:圆规 •最基本,最常用的尺规作图,通常称基本作图.
五种基本作图: 1.作一条线段等于已知线段。 2.作一个角等于已知角。 3.作已知角的平分线。 4.经过一已知点作已知直线的垂线。 5.作已知线段的垂直平分线。
作法 :
(1)作射线AC; (2)以点A为圆心,
a
以a长为半径 画弧, 交射线AC于点D; (3)以点D为圆心, 以a长为半径 画弧, 交射线AC于点B;
则:AB 即为所求。
A D B C
思考:探究与合作 你们会做一条线段等于所给线段的和或差吗?
例1、已知线段a、b,且a<b,
求作:一条线段AB,使得AB=2a+b
作法一:
B’
C B B’
法二:
D B
O
C A
E
C’
O A’ A O’ A
∠A’O’B’即为所求.
∠A’O’B’即为所求.
例2、已知∠ 1、∠2且 , ∠ 1<∠2,
(完整)尺规作图专题详尽归纳,推荐文档

考点名称:尺规作图【学习目标】1.了解什么是尺规作图.2.学会用尺规作图法完成下列五种基本作图:(1)画一条线段等于已知线段;(2)画一个角等于已知角;(3)画线段的垂直平分线;(4)过已知点画已知直线的垂线;(5)画角平分线.3.了解五种基本作图的理由.4.学会使用精练、准确的作图语言叙述画图过程.5.学会利用基本作图画三角形等较简单的图形.6.通过画图认识图形的本质,体会图形的内在美.【基础知识精讲】1.尺规作图:①定义:限定只用直尺和圆规来完成的画图,称为尺规作图.注意:这里所指的直尺是没有刻度的直尺,由于免去了度量,因此,用尺规作图法画出的图形的精确度更高,它在工程绘图等领域应用比较广泛.②步骤:(1)根据给出的条件和求作的图形,写出已知和求作部分;(2)分析作图的方法和过程;(3)用直尺和圆规进行作图; (4)写出作法步骤,即作法。
(根据题目要求来定是否需要写出作法)2.尺规作图中的最基本、最常用的作图称为基本作图.任何尺规作图的步骤均可分解为以下五种.3.基本作图共有五种:(1)画一条线段等于已知线段.如图24-4-1,已知线段DE.求作:一条线段等于已知线段.作法:①先画射线AB.②然后用圆规在射线AB上截取AC=MN.线段AC就是所要作的线段.(2)作一个角等于已知角.如图24-4-2,已知∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB.作法:①作射线O′A′;②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D.③以点O′为圆心,以OC长为半径作弧,交O′A′于C′.④以点C′为圆心,以CD为半径作弧,交前弧于D′.⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.(3)作线段的垂直平分线.如图24-4-3,已知线段AB.求作:线段AB的垂直平分线.作法:①分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C和D.②作直线CD.直线CD就是线段AB的垂直平分线.注意:直线CD与线段AB的交点,就是AB的中点.(4)经过一点作已知直线的垂线.a.经过已知直线上的一点作这条直线的垂线,如图24-4-4.已知:直线AB和AB上一点C,求作:AB的垂线,使它经过点C.作法:作平角ACB的平分线CF.直线CF就是所求的垂线,如图24-4-4.b.经过已知直线外一点作这条直线的垂线.如图24-4-5,已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.作法:①任意取一点K,使K和C在AB的两旁.②以C为圆心,CK长为半径作弧,交AB于点D和E.③分别以D和E为圆心,大于的长为半径作弧,两弧交于点F.④作直线CF.直线CF就是所求的垂线.注意:经过已知直线上的一点,作这条直线的垂线转化成画线段垂直平分线的方法解决.(5)平分已知角.如图24-4-6,已知∠AOB.求作:射线OC,使∠AOC=∠BOC.作法:①在OA和OB上,分别截取OD、OE.②分别以D、E为圆心,大于的长为半径作弧,在∠AOB内,两弧交于点C.③作射线OC.OC就是所求的射线.注意:以上五种基本作图是尺规作图的基础,一些复杂的尺规作图,都是由基本作图组成的,同学扪要高度重视,努力把这部分内容学习好.通过这一节的学习,同学们要掌握下列作图语言:(1)过点×和点×画射线××,或画射线××.(2)在射线××上截取××=××.(3)以点×为圆心,××为半径画弧.(4)以点×为圆心,××为半径画弧,交××于点×.(5)分别以点×,点×为圆心,以××,××为半径作弧,两弧相交于点×.(6)在射线××上依次截取××=××=××.(7)在∠×××的外部或内部画∠×××=∠×××.注意:学过基本作图后,在作较复杂图时,属于基本作图的地方,不必重复作图的详细过程,只用一句话概括叙述就可以了.如:(1)画线段××=××.(2)画∠×××=∠×××.(3)画××平分∠×××,或画∠×××的角平分线.(4)过点×画××⊥××,垂足为点×.(5)作线段××的垂直平分线××,等等.但要注意保留全部的作图痕迹,包括基本作图的操作程序,不能因为作法的叙述省略而作图就不按程序操作,只有保留作图痕迹,才能反映出作图的操作是否合理.【经典例题精讲】例1已知两边及其夹角,求作三角形.如图24-4-7,已知:∠α,线段a、b,求作:△ABC,使∠A=∠α,AB=a,AC=b.作法:①作∠MAN=∠α.②在射线AM、AN上分别作线段AB=a,AC=b.③连结BC.如图24-4-8,△ABC即为所求作的三角形.注意:一般几何作图题,应有下面几个步骤:已知、求作、作法,比较复杂的作图题,在作图之前可根据需要作一些分析.例2如图24-4-9,已知底边a,底边上的高h,求作等腰三角形.已知线段a、h.求作:△ABC,使AB=AC,且BC=a,高AD=h.分析:可先作出底边BC,根据等腰三角形的三线合一的性质,可再作出BC的垂直平分线,从而作出BC边上的高AD,分别连结AB和AC,即可作出等腰△ABC来.作法:(1)作线段BC=a.(2)作线段BC的垂直平分线MN,MN与BC交于点D.(3)在MN上截取DA,使DA=h.(4)连结AB、AC.如图24-4-10,△ABC即为所求的等腰三角形.例3已知三角形的一边及这边上的中线和高,作三角形.如图24-4-11,已知线段a,m,h(m>h).求作:△ABC使它的一边等于a,这边上的中线和高分别等于m和h(m>h).分析:如图24-4-12,假定△ABC已作出,其中BC=a,中线AD=m,高AE=h,在△AED中AD=m,AE=h,∠AED=90°,因此这个Rt△AED可以作出来(△AED为奠基三角形).当Rt△AED作出后,由的关系可作出点B和点C,于是△ABC即可得到.作法:(1)作△AED,使∠AED=90°,AE=h,AD=m.(2)延长ED到B,使.(3)在DE或BE的延长线上取.(4)连结AB、AC.则△ABC即为所求作的三角形.注意:因为三角形中,一边上的高不能大于这边上的中线,所以如果h>m,作图题无解;若m=h,则作出的图形为等腰三角形.例4如图24-4-13,已知线段a.求作:菱形ABCD,使其半周长为a,两邻角之比为1∶2.分析:因为菱形四边相等,“半周长为a”就是菱形边长为,为此首先要将线段a等分,又因为菱形对边平行,则同旁内角互补,由“邻角之比为1∶2”可知,菱形较小内角为60°,则菱形较短对角线将菱形分成两个全等的等边三角形.所以作图时只要作出两个有公共边的等边三角形,则得到的四边形即为所求的菱形ABCD.作法:(1)作线段a的垂直平分线,等分线段a.(2)作线段AC,使.(3)分别以A、C为圆心,为半径,在AC的两侧画弧,两弧分别交于B,D.(4)分别连结AB、BC、CD、DA得到四边形ABCD,则四边形ABCD为所求作的菱形(如图24-4-14).注意:这种通过先画三角形,然后再画出全部图形的方法即为“三角形奠基法”.例5如图24-4-15,已知∠AOB和C、D两点.求作一点P,使PC=PD,且使点P到∠AOB的两边OA、OB的距离相等.分析:要使PC=PD,则点P在CD的垂直平分线上,要使点P到∠AOB的两边距离相等,则P应在∠AOB的角平分线上,那么满足题设的P点就是垂直平分线与角平分线的交点了.作法:(1)连结CD.(2)作线段CD的中垂线l.(3)作∠AOB的角平分线OM,交l于点P,P点为所求.注意:这类定点问题应需确定两线,两直线的交点即为定点,当然这两直线应分别满足题目的不同要求.【中考考点】例6 (2000·安徽省)如图24-4-16,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A.一处 B.二处C.三处 D.四处分析:到直线距离相等的点在相交所构成的角的平分线上,可利用作角平分线的方法找到这些点.解:分别作相交所构成的角平分线,共可作出六条,三条角平分线相交的交点共有四个.答案:D.注意:本题应用了角平分线的性质,在具体作图时,不可只作出位于中心位置的一处,而要全面考虑其他满足条件的点.例7 (2002·陕西省)如图24-4-17,△ABC是一块直角三角形余料,∠C=90°,工人师傅要把它加工成—个正方形零件,使C为正方形的—个顶点,其他三个顶点分别在AB、BC、AC边上.(1)试协助工人师傅用尺规画出裁割线(不写作法,保留作图痕迹);(2)工人师傅测得AC=80 cm,BC=120cm,请帮助工人师傅算出按(1)题所画裁割线加工成的正方形零件的边长.解:(1)作∠ACB的平分线与AB的交点E即为正方形—顶点,作CE线段的中垂线HK 与AC、BC的交点F、D即为所作正方形另两个顶点,如图24-4-17.(2)设这个正方形零件的边长为x cm,∵DE∥AC,∴,∴.∴x=48.答:这个正方形零件的边长为48cm.注意:本题是几何作图和几何计算相结合题目,要求读者对基本作图务必掌握,同时对作出图形的性质要清楚.例8 (2002·山西省)如图24-4-18①,有一破残的轮片(不小于半个轮),现要制作一个与原轮片同样大小的圆形零件,请你根据所学的有关知识,设计两种方案,确定这个圆形零件的半径.分析:欲确定这个圆形零件的半径,可以借助三角板,T形尺或尺规作图均可,图②中是这个零件的半径,图③中OB是这个零件半径.解:如图24-4-18②③所示.【常见错误分析】例9如图24-4-19,已知线段a、b、h.求作△ABC,使BC=a,AC=b,BC边上的高AD=h.并回答问题,你作出的三角形唯一吗?从中你可以得到什么结论呢?错解:(1)作法:①作Rt△ADC,使AD=h,AC=b.②在直线CD上截取CB=a.如图24-4-20,则△ABC就是所求作的三角形.(2)作出的三角形唯一.(3)得出结论:有两边及一边上的高对应相等的两三角形全等.误区分析:本题错解在于忽略了三角形的高可能在三角形内部也可能在三角形的外部.正解:如图24-4-21,作法:①作Rt△ADC,使AD=h,AC=b.②在直线CD上截取CB=a(在点C的两侧).则△ABC,△AB′C都是所求作三角形.(2)作出的三角形不唯一.(3)得出结论有两边及—边上的高对应相等的两三角形不一定全等.注意:与三角形的高有关的题目应慎之又慎.【学习方法指导】学习基本作图,主要是运用观察法,通过具体的操作,了解各种基本作图的步骤,掌握作图语言.【规律总结】画复杂的图形时,如一时找不到作法,—般是先画出一个符合所设条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.有时,也可以根据已知条件和基本作图,先作局部三角形,再以此为基础,根据有关条件画出其余部分,从而完成全图,这种方法称为三角形奠基法.拓展: 1.利用基本作图作三角形:(1)已知三边作三角形; (2)已知两边及其夹角作三角形; (3)已知两角及其夹边作三角形; (4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图:(1)过不在同一直线上的三点作圆(即三角形的外接圆). (2)作三角形的内切圆.(3)作圆的内接正方形和正六边形.附件:尺规作图简史:“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有“规”这个字.“矩”就像现在木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股.矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形.矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规.甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前.《史记》卷二记载大禹治水时“左准绳,右规矩”.赵爽注《周髀算经》中有“禹治洪水,……望山川之形,定高下之势,……乃勾股之所由生也.”意即禹治洪水,要先测量地势的高低,就必定要用勾股的道理.这也说明矩起源于很远的中国古代.春秋时代也有不少著作涉及规矩的论述,《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩,以度天下之方圆.”《孟子》卷四中说“离娄(传说中目力非常强的人)之明,公输子(即鲁班,传说木匠的祖师)之巧,不以规矩,不能成方圆.”可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了.由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性.古代希腊人较重视规、矩在数学中训练思维和智力的作用,而忽视规矩的实用价值.因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使用没有刻度的直尺和圆规进行作图.古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛,被关进监狱,并被判处死刑.在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的《几何原本》.由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来.由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决.最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题.当时很多有名的希腊数学家,都曾着力于研究这三大问题,虽然借助于其他工具或曲线,这三大难题都可以解决,但由于尺规作图的限制,却一直未能如愿以偿.以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终.直到1637年笛卡尔创立了解析几何,关于尺规作图的可能性问题才有了准则.到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题.1882年林德曼证明了π是无理数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案.•。
中考尺规作图之欧阳理创编

中考数学专项复习--尺规作图一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、× .三、了解尺规作图题的一般步骤1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.四、基本作图最基本,最常用的尺规作图,通常称基本作图。
19.1尺规作图-

O D’
C A B’’ B
C’ ∠A’O’B’就是所求的角. 就是所求的角.
O’
A’’ A
思考:探究与合作 你们会做一条线段等于所给线段的和或差吗?
a
b
用一用
你能画出红球在第一次反弹后的运动路 线吗? 线吗?
O
数学小知识
入 反 射 射 角 角
打台球时,球的反射角总是等于入射角. 打台球时,球的反射角总是等于入射角. 反射角总是等于入射角
画一个角等于已知角画一条线 段等于已知线段。 段等于已知线段。 画角、线段的倍数、和、差。 画角、线段的倍数、 画法的语言: 画法的语言:(1)画射线×× 画射线××
点为圆心, ××长为半径画弧 交于点× 长为半径画弧, (2)以×点为圆心,以××长为半径画弧,交于点× (3)∠×就是所求的角
还要注意: 还要注意: 1.过点 、点x作直线;或作直线 ,射线 过点x、 作直线; 过点 作直线 或作直线xx,射线xx. 2.连结两点 、x;或连结 连结两点x、 ;或连结xx; 连结两点 3.在xx上截取 上截取xx=xx; 在 上截取 4.以点 为圆心,xx为半径作圆(弧); 交xx 以点x为圆心 为半径作圆( );(交 以点 为圆心, 为半径作圆 于x点;) 点 5.分别以点 ,点x为圆心,以xx为半径作 分别以点x, 为圆心 为圆心, 分别以点 为半径作 两弧相交于x点 弧,两弧相交于 点.
• 已知:线段a,b(a﹥b) 已知:线段a • 求作:一条线段,使它等于2a-b. 求作:一条线段,使它等于2a 2a-
a b
• 作法: 画射线AE. 作法: 画射线AE. 1.画射线 1. 2.在射线AE上顺次截取AB=BC=a. 在射线AE上顺次截取AB=BC=a 2.在射线AE上顺次截取AB=BC=a. 3.在线段AC上截取CD=b. 在线段AC 3.在线段AC上截取CD=b. ∴ 线段AD就是所要画的线段. 线段AD就是所要画的线段. AD就是所要画的线段
尺规作图九种基本作图

a尺规作图之杨若古兰创作【常识回顾】1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图.最基本,最经常使用的尺规作图,通常称基本作图.一些复杂的尺规作图都是由基本作图构成的.2、五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知线段.已知:如图,线段a .求作:线段AB ,使AB = a . 作法:(1) 作射线AP ;(2)在射线AP 上截取AB=a .则线段AB 就是所求作的图形.(2)题目二:作已知线段的垂直平分线. 已知:如图,线段MN.求作:点O ,使MO=NO (即O 是MN 的中点). 作法:(1)分别以M 、N 为圆心,大于MN 21的不异线段为半径画弧,两弧订交于P ,Q ;(2)连接PQ 交MN 于O .则点PQ 就是所求作的MN的垂直平分线. (3)题目三:作已知角的角平分线. 已知:如图,∠AOB,求作:射线OP, 使∠AOP=∠BOP (即OP 平分∠AOB). 作法:(1)以O 为圆心,任意长度为半径画弧,分别交OA ,OB 于M ,N ;(2)分别以M 、N为圆心,大于MN 21的线段长为半径画弧,两弧交∠AOB 内于P;(3)作射线OP.则射线OP 就是∠AOB 的角平分线. (4)题目四:作一个角等于已知角. 已知:如图,∠AOB.求作:∠A’O’B’,使A’O’B’=∠AOB 作法:(1)作射线O’A’;(2)以O 为圆心,任意长度为半径画弧,交OA 于M ,交OB 于N ;BAP(3)以O’为圆心,以OM 的长为半径画弧,交O’A’于M’;(4)以M’为圆心,以MN 的长为半径画弧,交前弧于N’; (5)连接O’N’并耽误到B’. 则∠A’O’B’就是所求作的角.(5)题目五:经过直线上一点做已知直线的垂线. 已知:如图,P 是直线AB 上一点.求作:直线CD ,是CD 经过点P ,且CD⊥AB. 作法:(1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ; (2)分别以M 、N 为圆心,大于MN 21的长为半径画弧,两弧交于点Q ;(3)过D 、Q 作直线CD. 则直线CD 是求作的直线. (6)题目六:经过直线外一点作已知直线的垂线已知:如图,直线AB 及外一点P.求作:直线CD ,使CD 经过点P ,且CD⊥AB.作法:(1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ; (2)分别以M 、N 圆心,大于MN 21长度的一半为半径画弧,c abmn 两弧交于点Q;(3)过P、Q作直线CD.则直线CD就是所求作的直线.(7)题目七:已知三边作三角形.已知:如图,线段a,b,c.求作:△ABC,使AB = c,AC = b,BC = a. 作法:(1)作线段AB = c;(2)以A为圆心,以b为半径作弧,以B为圆心,以a为半径作弧与前弧订交于C;(3)连接AC,BC.则△ABC就是所求作的三角形.(8)题目八:已知两边及夹角作三角形.已知:如图,线段m,n,∠α.求作:△ABC,使∠A=∠α,AB=m,AC=n.作法:(1)作∠A=∠α;(2)在AB上截取AB=m ,AC=n;(3)连接BC.则△ABC就是所求作的三角形.(9)题目九:已知两角及夹边作三角形.已知:如图,∠α,∠β,线段m .求作:△ABC,使∠A=∠α,∠B=∠β,AB=m.作法:(1)作线段AB=m;(2)在AB的同旁作∠A=∠α,作∠B=∠β,∠A与∠B的另一边订交于C.则△ABC就是所求作的图形(三角形).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
尺规作图
欧阳家百(2021.03.07)
【知识回顾】
1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
最基本,最常用的尺规作图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
2、五种基本作图:
1、作一条线段等于已知线段;
2、作一个角等于已知角;
3、作已知线段的垂直平分线;
4、作已知角的角平分线;
5、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知
线段。
已知:如图,线段a .
求作:线段AB ,使AB = a . 作法:
(1) 作射线AP ;
(2)
在射线AP 上截取AB=a .
则线段AB 就是所求作的图形。
(2)题目二:作已知线段的垂直平分线。
已知:如图,线段MN.
求作:点O ,使MO=NO (即O 是MN 的中点). 作法:
(1)分别以M 、N 为圆心,大于MN 2
1
的相同线段为半径画弧, 两弧相交于P ,Q ;
(2)连接PQ 交MN 于O .
则点PQ 就是所求作的MN的垂直平分线。
(3)题目三:作已知角的角平分线。
已知:如图,∠AOB ,
求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。
作法:
(1)以O 为圆心,任意长度为半径画弧,
分别交OA ,OB 于M ,N ;
(2)分别以M 、N为圆心,大于MN 2
1的线段长
为半径画弧,两弧交∠AOB 内于P;
(3)
作射线OP 。
则射线OP 就是∠AOB 的角平分线。
(4)题目四:作一个角等于已知角。
已知:如图,∠AOB 。
求作:∠A’O’B’,使A’O’B’=∠AOB 作法:
(1)作射线O’A’;
B
A
P
(2)以O 为圆心,任意长度为半径画弧,交OA 于M ,交OB 于N ; (3)以O’为圆心,以OM 的长为半径画弧,交O’A’于M’; (4)以M’为圆心,以MN 的长为半径画弧,交前弧于N’; (5)连接O’N’并延长到B’。
则∠A’O’B’就是所求作的角。
(5)题目五:经过直线上一点做已知直线的垂线。
已知:如图,P 是直线AB 上一点。
求作:直线CD ,是CD 经过点P ,且CD ⊥AB 。
作法:
(1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ;
(2)分别以M 、N 为圆心,大于MN 2
1的长为半径画弧,两弧交于点
Q ;
(3)过D 、Q 作直线CD 。
则直线CD 是求作的直线。
(6)题目六:经过直线外一点作已知直线的垂线
已知:如图,直线AB 及外一点P 。
求作:直线CD ,使CD 经过点P ,
且CD ⊥AB 。
作法:
(1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ;
(2)分别以M 、N 圆心,大于MN 2
1长度的一半为半径画弧,两弧
交于点Q ;
c a
b
m
n (3)过P、Q作直线CD。
则直线CD就是所求作的直线。
(7)题目七:已知三边作三角形。
已知:如图,线段a,b,c.
求作:△ABC,使AB = c,AC = b,BC = a.
作法:
(1)作线段AB = c;
(2)以A为圆心,以b为半径作弧,
以B为圆心,以a为半径作弧与
前弧相交于C;
(3)连接AC,BC。
则△ABC就是所求作的三角形。
(8)题目八:已知两边及夹角作三角形。
已知:如图,线段m,n,∠α.
求作:△ABC,使∠A=∠α,AB=m,
AC=n.
作法:
(1)作∠A=∠α;
(2)在AB上截取AB=m ,AC=n;
(3)连接BC。
则△ABC就是所求作的三角形。
(9)题目九:已知两角及夹边作三角形。
m 已知:如图,∠α,∠β,线段m .
求作:△ABC,使∠A=∠α,
∠B=∠β,AB=m.
作法:
(1)作线段AB=m;
(2)在AB的同旁
作∠A=∠α,作∠B=∠β,
∠A与∠B的另一边相交于C。
则△ABC就是所求作的图形(三角形)。
