美国数学竞赛AMCAB试题及答案
2018年美国数学竞赛 AMC 试题

2018 AIME I ProblemsProblem 1Let be the number of ordered pairs ofintegers with and such that thepolynomial can be factored into the product of two (not necessarily distinct) linear factors with integer coefficients. Find the remainder when is divided by .Problem 2The number can be written in base as , can be written inbase as , and can be written in base as , where . Find the base- representation of .Problem 3Kathy has red cards and green cards. She shuffles the cards and laysout of the cards in a row in a random order. She will be happy if and only if all the red cards laid out are adjacent and all the green cards laid out are adjacent. For example, card orders RRGGG, GGGGR, or RRRRR will make Kathy happy,but RRRGR will not. The probability that Kathy will be happy is ,where and are relatively prime positive integers. Find . Problem 4In and . Point lies strictlybetween and on and point lies strictly between and on sothat . Then can be expressed in the form ,where and are relatively prime positive integers. Find .Problem 5For each ordered pair of real numbers satisfyingthere is a real number such thatFind the product of all possible values of .Problem 6Let be the number of complex numbers with the propertiesthat and is a real number. Find the remainder when is divided by .Problem 7A right hexagonal prism has height . The bases are regular hexagons with side length . Any of the vertices determine a triangle. Find the number of these triangles that are isosceles (including equilateral triangles).Problem 8Let be an equiangular hexagon suchthat , and . Denote the diameter of the largest circle that fits inside the hexagon. Find .Problem 9Find the number of four-element subsets of with the propertythat two distinct elements of a subset have a sum of , and two distinct elements of a subset have a sum of . Forexample, and are two such subsets.Problem 10The wheel shown below consists of two circles and five spokes, with a label at each point where a spoke meets a circle. A bug walks along the wheel, starting at point . At every step of the process, the bug walks from one labeled point to an adjacent labeled point. Along the inner circle the bug only walks in a counterclockwise direction, and along the outer circle the bug only walks in a clockwise direction. For example, the bug could travel along thepath , which has steps. Let be the number of paths with steps that begin and end at point . Find the remainder when is divided by .Problem 11Find the least positive integer such that when is written in base , its two right-most digits in base are .Problem 12For every subset of , let be the sum of the elements of , with defined to be . If is chosen at random among allsubsets of , the probability that is divisible by is , where and are relatively prime positive integers. Find .Problem 13Let have side lengths , , and .Point lies in the interior of , and points and are the incentersof and , respectively. Find the minimum possible areaof as varies along .Problem 14Let be a heptagon. A frog starts jumping at vertex . From any vertex of the heptagon except , the frog may jump to either of the two adjacentvertices. When it reaches vertex , the frog stops and stays there. Find the number of distinct sequences of jumps of no more than jumps that end at .Problem 15David found four sticks of different lengths that can be used to form three non-congruent convex cyclic quadrilaterals, , which can each be inscribed in a circle with radius . Let denote the measure of the acute angle made by the diagonals of quadrilateral , and define and similarly. Supposethat , , and . All three quadrilaterals have thesame area , which can be written in the form , where and are relatively prime positive integers. Find .2018 AMC 8 ProblemsProblem 1An amusement park has a collection of scale models, with ratio , of buildings and other sights from around the country. The height of the United States Capitol is 289 feet. What is the height in feet of its replica to the nearest whole number?Problem 2What is the value of the productProblem 3Students Arn, Bob, Cyd, Dan, Eve, and Fon are arranged in that order in a circle. They start counting: Arn first, then Bob, and so forth. When the number contains a 7 as a digit (such as 47) or is a multiple of 7 that person leaves the circle and the counting continues. Who is the last one present in the circle?Problem 4The twelve-sided figure shown has been drawn on graph paper. What is the area of the figure in ?Problem 5What is the valueof ?Problem 6On a trip to the beach, Anh traveled 50 miles on the highway and 10 miles on a coastal access road. He drove three times as fast on the highway as on the coastal road. If Anh spent 30 minutes driving on the coastal road, how many minutes did his entire trip take?Problem 7The -digit number is divisible by . What is the remainder when this number is divided by ?Problem 8Mr. Garcia asked the members of his health class how many days last week they exercised for at least 30 minutes. The results are summarized in the following bar graph, where the heights of the bars represent the number of students.What was the mean number of days of exercise last week, rounded to the nearest hundredth, reported by the students in Mr. Garcia's class?Problem 9Tyler is tiling the floor of his 12 foot by 16 foot living room. He plans to place one-foot by one-foot square tiles to form a border along the edges of the room and to fill in the rest of the floor with two-foot by two-foot square tiles. How many tiles will he use?Problem 10The of a set of non-zero numbers is the reciprocal of the average of the reciprocals of the numbers. What is the harmonic mean of 1, 2, and 4?Problem 11Abby, Bridget, and four of their classmates will be seated in two rows of three for a group picture, as shown.If the seating positions are assigned randomly, what is the probability that Abby and Bridget are adjacent to each other in the same row or the same column?Problem 12The clock in Sri's car, which is not accurate, gains time at a constant rate. One day as he begins shopping he notes that his car clock and his watch (which is accurate) both say 12:00 noon. When he is done shopping, his watch says 12:30 and his car clock says 12:35. Later that day, Sri loses his watch. He looks at his car clock and it says 7:00. What is the actual time?Problem 13Laila took five math tests, each worth a maximum of 100 points. Laila's score on each test was an integer between 0 and 100, inclusive. Laila received the same score on the first four tests, and she received a higher score on the last test. Her average score on the five tests was 82. How many values are possible for Laila's score on the last test?Problem 14Let be the greatest five-digit number whose digits have a product of . What is the sum of the digits of ?Problem 15In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?Problem 16Professor Chang has nine different language books lined up on a bookshelf: two Arabic, three German, and four Spanish. How many ways are there to arrange the nine books on the shelf keeping the Arabic books together and keeping the Spanish books together?Problem 17Bella begins to walk from her house toward her friend Ella's house. At the same time, Ella begins to ride her bicycle toward Bella's house. They each maintain a constant speed, and Ella rides 5 times as fast as Bella walks. The distancebetween their houses is miles, which is feet, and Bella covers feet with each step. How many steps will Bella take by the time she meets Ella?Problem 18How many positive factors does have?Problem 19In a sign pyramid a cell gets a "+" if the two cells below it have the same sign, and it gets a "-" if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a "+" at the top of the pyramid?Problem 20In a point is on with and Point ison so that and point is on so that What is the ratio of the area of to the area ofProblem 21How many positive three-digit integers have a remainder of 2 when divided by 6, a remainder of 5 when divided by 9, and a remainder of 7 when divided by 11?Problem 22Point is the midpoint of side in square and meets diagonal at The area of quadrilateral is What is the areaofProblem 23From a regular octagon, a triangle is formed by connecting three randomly chosen vertices of the octagon. What is the probability that at least one of the sides of the triangle is also a side of the octagon?Problem 24In the cube with opposite vertices and and are the midpoints of edges and respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What isProblem 25How many perfect cubes lie between and , inclusive?2018 AMC 10A ProblemsProblem 1What is the value ofProblem 2Liliane has more soda than Jacqueline, and Alice has more soda than Jacqueline. What is the relationship between the amounts of soda that Liliane and Alice have?Liliane has more soda than Alice.Liliane has more soda than Alice.Liliane has more soda than Alice.Liliane has more soda than Alice.Liliane has more soda than Alice.Problem 3A unit of blood expires after seconds. Yasin donates a unit of blood at noon of January 1. On what day does his unit of blood expire?Problem 4How many ways can a student schedule 3 mathematics courses -- algebra, geometry, and number theory -- in a 6-period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other 3 periods is of no concern here.)Problem 5Alice, Bob, and Charlie were on a hike and were wondering how far away the nearest town was. When Alice said, "We are at least 6 miles away," Bob replied, "We are at most 5 miles away." Charlie then remarked, "Actually the nearest town is at most 4 miles away." It turned out that none of the three statements were true. Let be the distance in miles to the nearest town. Which of the following intervals is the set of all possible values of ?Problem 6Sangho uploaded a video to a website where viewers can vote that they like or dislike a video. Each video begins with a score of 0, and the score increases by 1 for each like vote and decreases by 1 for each dislike vote. At one point Sangho saw that his video had a score of 90, and that of the votes cast on his video were like votes. How many votes had been cast on Sangho's video at that point?Problem 7For how many (not necessarily positive) integer values of is the value of an integer?Problem 8Joe has a collection of 23 coins, consisting of 5-cent coins, 10-cent coins, and 25-cent coins. He has 3 more 10-cent coins than 5-cent coins, and the total value of his collection is 320 cents. How many more 25-cent coins does Joe have than 5-cent coins?Problem 9All of the triangles in the diagram below are similar to iscoceles triangle , inwhich . Each of the 7 smallest triangles has area 1, and has area 40. What is the area of trapezoid ?Problem 10Suppose that real number satisfies. What is the valueof ?Problem 11When fair standard -sided die are thrown, the probability that the sum of the numbers on the top faces is can be written as, where is a positive integer. What is ?Problem 12How many ordered pairs of real numbers satisfy the following system ofequations?Problem 13A paper triangle with sides of lengths 3, 4, and 5 inches, as shown, is folded so that point falls on point . What is the length in inches of the crease?Problem 14What is the greatest integer less than or equal toProblem 15Two circles of radius 5 are externally tangent to each other and are internally tangent to a circle of radius 13 at points and , as shown in the diagram. The distance can be written in the form , where and are relatively prime positive integers. What is ?Problem 16Right triangle has leg lengths and . Including and , how many line segments with integer length can be drawn from vertex to a point on hypotenuse ?Problem 17Let be a set of 6 integers taken from with the property that if and are elements of with , then is not a multiple of . What is the least possible values of an element inProblem 18How many nonnegative integers can be written in theformwhere for ?Problem 19A number is randomly selected from the set , and a number is randomly selected from . What is the probabilitythat has a units digit of ?Problem 20A scanning code consists of a grid of squares, with some of its squares colored black and the rest colored white. There must be at least one square of each color in this grid of squares. A scanning code is called if its look does not change when the entire square is rotated by a multiple of counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?Problem 21Which of the following describes the set of values of for which thecurves and in the real -plane intersect at exactly points?Problem 22Let and be positive integers suchthat , , ,and . Which of the following must be a divisor of ?Problem 23Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths 3 and 4 units. In the corner where those sides meet at a right angle, he leaves a small unplantedsquare so that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from to the hypotenuse is 2 units. What fraction of the field is planted?Problem 24Triangle with and has area . Let be the midpointof , and let be the midpoint of . The angle bisectorof intersects and at and , respectively. What is the area of quadrilateral ?Problem 25For a positive integer and nonzero digits , , and , let be the -digit integer each of whose digits is equal to ; let be the -digit integer each of whose digits is equal to , and let be the -digit (not -digit) integer each of whose digits is equal to . What is the greatest possiblevalue of for which there are at least two values of such that ?2018 AMC 10B ProblemsProblem 1Kate bakes a 20-inch by 18-inch pan of cornbread. The cornbread is cut into pieces that measure 2 inches by 2 inches. How many pieces of cornbread does the pan contain?Problem 2Sam drove 96 miles in 90 minutes. His average speed during the first 30 minutes was 60 mph (miles per hour), and his average speed during the second 30 minutes was 65 mph. What was his average speed, in mph, during the last 30 minutes?Problem 3In the expression each blank is to be filled in with one of the digits or with each digit being used once. How many different values can be obtained?Problem 4A three-dimensional rectangular box with dimensions , , and has faces whose surface areas are 24, 24, 48, 48, 72, and 72 square units. What is ?Problem 5How many subsets of contain at least one prime number?Problem 6A box contains 5 chips, numbered 1, 2, 3, 4, and 5. Chips are drawn randomly one at a time without replacement until the sum of the values drawn exceeds 4. What is the probability that 3 draws are required?Problem 7In the figure below, congruent semicircles are drawn along a diameter of a large semicircle, with their diameters covering the diameter of the large semicircle with no overlap. Let be the combined area of the small semicircles and be the area of the region inside the large semicircle but outside the small semicircles. The ratio is 1:18. What is ?Problem 8Sara makes a staircase out of toothpicks as shown:This is a 3-step staircase and uses 18 toothpicks. How many steps would be in a staircase that used 180 toothpicks?Problem 9The faces of each of 7 standard dice are labeled with the integers from 1 to 6. Let be the probability that when all 7 dice are rolled, the sum of the numbers on the top faces is 10. What other sum occurs with the same probability ?Problem 10In the rectangular parallelepiped shown, , , and . Point is the midpoint of . What is the volume of the rectangular pyramid with base and apex ?Problem 11Which of the following expressions is never a prime number when is a prime number?Problem 12Line segment is a diameter of a circle with . Point , not equal to or , lies on the circle. As point moves around the circle, the centroid (center of mass) of traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?Problem 13How many of the first numbers in the sequence are divisible by ?Problem 14A list of positive integers has a unique mode, which occurs exactly times. What is the least number of distinct values that can occur in the list?Problem 15A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper, as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box, point in the figure on the right. The box has base length and height . What is the area of the sheet of wrapping paper?Problem 16Let be a strictly increasing sequence of positive integers suchthat What is the remainderwhen is divided by ?Problem 17In rectangle , and . Points and lie on ,points and lie on , points and lie on , and points and lie on so that and the convex octagon is equilateral. The length of a side of this octagon can be expressed in the form , where , , and are integers and is not divisible by the square of any prime. What is ?Problem 18Three young brother-sister pairs from different families need to take a trip in a van. These six children will occupy the second and third rows in the van, each of which has three seats. To avoid disruptions, siblings may not sit right next to each other in the same row, and no child may sit directly in front of his or her sibling. How many seating arrangements are possible for this trip?Problem 19Joey and Chloe and their daughter Zoe all have the same birthday. Joey is 1 year older than Chloe, and Zoe is exactly 1 year old today. Today is the first of the 9 birthdays on which Chloe's age will be an integral multiple of Zoe's age. What will be the sum of the two digits of Joey's age the next time his age is a multiple of Zoe's age?Problem 20A function is defined recursivelyby and for allintegers . What is ?Problem 21Mary chose an even -digit number . She wrote down all the divisors of in increasing order fromleft to right: . At some moment Mary wrote as a divisor of . What is the smallest possible value of the next divisor written to the right of ?Problem 22Real numbers and are chosen independently and uniformly at random from the interval . Which of the following numbers is closest to the probability that and are the side lengths of an obtuse triangle?Problem 23How many ordered pairs of positive integers satisfy theequation where denotes the greatest common divisor of and , and denotes their least common multiple?Problem 24Let be a regular hexagon with side length . Denote by , , and the midpoints of sides , , and , respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of and ?Problem 25Let denote the greatest integer less than or equal to . How many real numbers satisfy the equation ?2018 AMC 12A ProblemsProblem 1A large urn contains balls, of which are red and the rest are blue. How many of the blue balls must be removed so that the percentage of red balls in the urn will be ? (No red balls are to be removed.)Problem 2While exploring a cave, Carl comes across a collection of -pound rocks worth each, -poundrocks worth each, and -pound rocks worth each. There are at least of each size. He can carry at most pounds. What is the maximum value, in dollars, of the rocks he can carry out of the cave?Problem 3How many ways can a student schedule 3 mathematics courses -- algebra, geometry, and number theory -- in a 6-period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other 3 periods is of no concern here.)Problem 4Alice, Bob, and Charlie were on a hike and were wondering how far away the nearest town was. When Alice said, "We are at least 6 miles away," Bob replied, "We are at most 5 miles away." Charlie then remarked, "Actually the nearest town is at most 4 miles away." It turned out that none of the three statements were true. Let be the distance in miles to the nearest town. Which of the following intervals is the set of all possible values of ?Problem 5What is the sum of all possible values of for which the polynomials andhave a root in common?Problem 6For positive integers and such that , both the mean and the median ofthe set are equal to . What is ?Problem 7For how many (not necessarily positive) integer values of is the value of an integer?Problem 8All of the triangles in the diagram below are similar to iscoceles triangle , in which. Each of the 7 smallest triangles has area 1, and has area 40. What is the area of trapezoid ?Problem 9Which of the following describes the largest subset of values of within the closed interval forwhich for every between and , inclusive?How many ordered pairs of real numbers satisfy the following system of equations?Problem 11A paper triangle with sides of lengths 3,4, and 5 inches, as shown, is folded so that point falls on point . What is the length in inches of the crease?Problem 12Let be a set of 6 integers taken from with the property that if and are elements of with , then is not a multiple of . What is the least possible value of an element inProblem 13How many nonnegative integers can be written in the formwherefor ?Problem 14The solutions to the equation , where is a positive real number other thanor , can be written as where and are relatively prime positive integers. What is ?A scanning code consists of a grid of squares, with some of its squares colored black and therest colored white. There must be at least one square of each color in this grid of squares. A scanning code is called if its look does not change when the entire square is rotated by a multiple of counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?Problem 16Which of the following describes the set of values of for which the curves andin the real -plane intersect at exactly points?Problem 17Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths 3 and 4 units. In the corner where those sides meet at a right angle, he leaves a small unplanted squareso that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from to the hypotenuse is 2 units. What fraction of the field is planted?Triangle with and has area . Let be the midpoint of, and let be the midpoint of . The angle bisector of intersects and atand , respectively. What is the area of quadrilateral ?Problem 19Let be the set of positive integers that have no prime factors other than , , or . The infinite sumof the reciprocals of the elements of can be expressed as , where and are relatively primepositive integers. What is ?Problem 20Triangle is an isosceles right triangle with . Let be the midpoint ofhypotenuse . Points and lie on sides and , respectively, so thatand is a cyclic quadrilateral. Given that triangle has area , the length canbe written as , where , , and are positive integers and is not divisible by the square of any prime. What is the value of ?Problem 21Which of the following polynomials has the greatest real root?Problem 22The solutions to the equations and whereform the vertices of a parallelogram in the complex plane. The area of thisparallelogram can be written in the form where and are positive integersand neither nor is divisible by the square of any prime number. What isProblem 23In and Points and lie on sidesand respectively, so that Let and be the midpoints of segmentsand respectively. What is the degree measure of the acute angle formed by linesandProblem 24Alice, Bob, and Carol play a game in which each of them chooses a real number between 0 and 1. The winner of the game is the one whose number is between the numbers chosen by the other two players. Alice announces that she will choose her number uniformly at random from all the numbers between 0 and 1, and Bob announces that he will choose his number uniformly at random from all thenumbers between and Armed with this information, what number should Carol choose to maximize her chance of winning?Problem 25For a positive integer and nonzero digits , , and , let be the -digit integer each of whosedigits is equal to ; let be the -digit integer each of whose digits is equal to , and let bethe -digit (not -digit) integer each of whose digits is equal to . What is the greatest possible value of for which there are at least two values of such that ?2018 AMC 12B ProblemsProblem 1Kate bakes 20-inch by 18-inch pan of cornbread. The cornbread is cut into pieces that measure 2 inches by 2 inches. How many pieces of cornbread does the pan contain?Problem 2Sam drove 96 miles in 90 minutes. His average speed during the first 30 minutes was 60 mph (miles per hour), and his average speed during the second 30 minutes was 65 mph. What was his average speed, in mph, during the last 30 minutes?Problem 3A line with slope 2 intersects a line with slope 6 at the point . What is the distance between the -intercepts of these two lines?Problem 4A circle has a chord of length , and the distance from the center of the circle to the chord is . What is the area of the circle?Problem 5How many subsets of contain at least one prime number?Suppose cans of soda can be purchased from a vending machine for quarters. Which of the following expressions describes the number of cans of soda that can be purchased for dollars, where 1 dollar is worth 4 quarters?Problem 7What is the value ofProblem 8Line segment is a diameter of a circle with . Point , not equal to or , lies on the circle. As point moves around the circle, the centroid (center of mass) of traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?Problem 9What isProblem 10A list of positive integers has a unique mode, which occurs exactly times. What is the least number of distinct values that can occur in the list?Problem 11。
2000-2012美国AMC10中文版试题及答案

2000到2012年AMC10美国数学竞赛0 0P 0 A 0 B 0 C 0D 0 全美中学数学分级能力测验(AMC 10)2000年 第01届 美国AMC10 (2000年2月 日 时间75分钟)1. 国际数学奥林匹亚将于2001年在美国举办,假设I 、M 、O 分别表示不同的正整数,且满足I ⨯M ⨯O =2001,则试问I +M +O 之最大值为 。
(A) 23 (B) 55 (C) 99 (D) 111 (E) 6712. 2000(20002000)为 。
(A) 20002001 (B) 40002000 (C) 20004000 (D) 40000002000 (E) 200040000003. Jenny 每天早上都会吃掉她所剩下的聪明豆的20%,今知在第二天结束时,有32颗剩下,试问一开始聪明豆有 颗。
(A) 40 (B) 50 (C) 55 (D) 60 (E) 754. Candra 每月要付给网络公司固定的月租费及上网的拨接费,已知她12月的账单为12.48元,而她1月的账单为17.54元,若她1月的上网时间是12月的两倍,试问月租费是 元。
(A) 2.53 (B) 5.06 (C) 6.24 (D) 7.42 (E) 8.775. 如图M ,N 分别为PA 与PB 之中点,试问当P 在一条平行AB 的直 在线移动时,下列各数值有 项会变动。
(a) MN 长 (b) △P AB 之周长 (c) △P AB 之面积 (d) ABNM 之面积(A) 0项 (B) 1项 (C) 2项 (D) 3项 (E) 4项 6. 费氏数列是以两个1开始,接下来各项均为前两项之和,试问在费氏数列各项的个位数字中, 最后出现的阿拉伯数字为 。
(A) 0 (B) 4 (C) 6 (D) 7 (E) 97. 如图,矩形ABCD 中,AD =1,P 在AB 上,且DP 与DB 三等分∠ADC ,试问△BDP 之周长为 。
美国数学竞赛AMC8 -- 2010年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 -- 2010年真题解析(英文解析+中文解析)Problem 1Answer: CSolution:Given that these are the only math teachers at Euclid Middle School and we are told how many from each class are taking the AMC 8, we simply add the three numbers to find the total.11+8+9=28.中文解析:参加竞赛的学生总人数是:11+8+9=28. 答案是C。
Problem 2Answer: DSolution:Substitute a=5, b=10 into the expression for a@b to get: 5@10=(5*10)/(5+10)=50/15=10/3.中文解析:(5*10)/(5+10)=50/15=10/3. 答案是D。
Problem 3Answer: CSolution:The highest price was in Month 1, which was $17. The lowest price was in Month 3, which was $10. 17 is 17/10 =170% of 10, and is 170-100=70% more than 10. Therefore, the answer is 70. 中文解析:最高价是1月,17美元。
最低价格是3月10美元。
最高价比最低价多:(17-10)/10=70%。
答案是C。
Problem 4Answer: CSolution:Putting the numbers in numerical order we get the list 0,0,1,2,3,3,3,4 The mode is 3, The median is (2+3)/2=2.5. The average is 2. is The sum of all three is 3+2.5+2=7.5.中文解析:这组数按照从小到大的顺序排列是:0,0,1,2,3,3,3,4. 中位数Median是2.5;mode 是3,mean是16/8=2. 因此mean,median,mode的和是: 2.5+3+2=7.5. 答案是C。
美国数学竞赛AMC8 -- 2005年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2005年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:If x is the number, then 2x=60 and x=30. Dividing the number by 2 yields 15.中文解析:按照Connie的计算,这个数乘以2是60,可知这个数是30. 应该做的计算是30除以2,因而正确答案应该是15. 答案是B。
Problem 2Answer: CSolution:Karl paid 5*2.5=$12.5. 20% of this cost that he saved is 12.5*0.2=$2.5.中文解析:Karl按原价买了5个文件夹,支付的费用是:2.5*5=12.5. 折扣价是:1.25*0.8=10。
如果Karl 等一天,可以省2.5元。
答案是C.Problem 3Answer: DSolution:Rotating square ABCD counterclockwise 45° so that the line of symmetry BD is a vertical line makes it easier to see that 4 squares need to be colored to match its corresponding square.中文解析:如上图所示,以BD为对称轴,标蓝色的方块需要涂黑。
共4块,答案是D。
Problem 4Answer: CSolution:The perimeter of the triangle is 6.1+8.2+9.7=24cm. A square's perimeter is four times its side length, since all its side lengths are equal. If the square's perimeter is 24, the side length is24/4=6, and the area is 6*6=36.中文解析:三角形的周长是:6.1+8.2+9.7=24. 正方形的周长和三角形相等,也是24,则其边长是24/4=6. 其面积是:6*6=36. 答案是C。
历届美国数学建模竞赛赛题(汉语版)

历届美国数学建模竞赛赛题, 1985-2006AMCM1985问题-A 动物群体的管理AMCM1985问题-B 战购物资储备的管理AMCM1986问题-A 水道测量数据AMCM1986问题-B 应急设施的位置AMCM1987问题-A 盐的存贮AMCM1987问题-B 停车场AMCM1988问题-A 确定毒品走私船的位置AMCM1988问题-B 两辆铁路平板车的装货问题AMCM1989问题-A 蠓的分类AMCM1989问题-B 飞机排队AMCM1990问题-A 药物在脑内的分布AMCM1990问题-B 扫雪问题AMCM1991问题-A 估计水塔的水流量AMCM1992问题-A 空中交通控制雷达的功率问题AMCM1992问题-B 应急电力修复系统的修复计划AMCM1993问题-A 加速餐厅剩菜堆肥的生成AMCM1993问题-B 倒煤台的操作方案AMCM1994问题-A 住宅的保温AMCM1994问题-B 计算机网络的最短传输时间AMCM1995问题-A 单一螺旋线AMCM1995问题-B A1uacha Balaclava学院AMCM1996问题-A 噪音场中潜艇的探测AMCM1996问题-B 竞赛评判问题AMCM1997问题-A Velociraptor(疾走龙属)问题AMCM1997问题-B为取得富有成果的讨论怎样搭配与会成员AMCM1998问题-A 磁共振成像扫描仪AMCM1998问题-B 成绩给分的通胀AMCM1999问题-A 大碰撞AMCM1999问题-B “非法”聚会AMCM1999问题- C 大地污染AMCM2000问题-A空间交通管制AMCM2000问题-B: 无线电信道分配AMCM2000问题-C:大象群落的兴衰AMCM2001问题- A: 选择自行车车轮AMCM2001问题-B:逃避飓风怒吼(一场恶风…)AMCM2001问题-C我们的水系-不确定的前景AMCM2002问题-A风和喷水池AMCM2002问题-B航空公司超员订票AMCM2002问题-C蜥蜴问题AMCM2003问题-A: 特技演员AMCM2003问题-C航空行李的扫描对策AMCM2004问题-A:指纹是独一无二的吗?AMCM2004问题-B:更快的快通系统AMCM2004问题-C:安全与否?AMCM2005问题-A:.水灾计划AMCM2005问题-B:TollboothsAMCM2005问题-C:.Nonrenewable ResourcesAMCM2006问题-A:用于灌溉的自动洒水器的安置和移动调度AMCM2006问题-B:通过机场的轮椅AMCM2006问题-C:在与HIV/爱滋病的战斗中的交易AMCM85问题-A 动物群体的管理在一个资源有限,即有限的食物、空间、水等等的环境里发现天然存在的动物群体。
美国数学竞赛AMC8 -- 2008年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2008年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:50-12-24=14中文解析:总共花的钱是:12+12*2=36元。
剩余50-36=14元。
答案是BProblem 2Answer: ASolution:We can derive that c=8,L=6, U=7,and E=1. Therefore, the answer is 8671.中文解析:这10个字母的对应关系是: B -0;E-1; S-2; ......K -9. 按照这个对应关系:C-8,L-6,U-7,E-1. 即8671. 答案是A。
Problem 3Answer: ASolution:We can go backwards by days, but we can also backwards by weeks. If we go backwards by weeks, we see that February 6 is a Friday. If we now go backwards by days, February 1 is a Sunday.中文解析:13日是周五,则13-7=6,即6日也是周五,则倒推2月1日是周日。
答案是A。
Problem 4Answer: CSolution:The area outside the small triangle but inside the large triangle is 16-1=15. This is equally distributed between the three trapezoids. Each trapezoid has an area of 15/3=5.中文解析:大三角形的面积等于小的等边三角形的面积加上3个梯形的面积。
据此,三个梯形的面积是16-1=15. 每个梯形的面积是15/3=5. 答案是C。
精选美国amc中文版试题及答案

2000到2012年A M C10美国数学竞赛P 0 A 0B 0 C0 D 0 全美中学数学分级能力测验(AMC 10)2000年 第01届 美国AMC10 (2000年2月 日 时间75分钟)1. 国际数学奥林匹亚将于2001年在美国举办,假设I 、M 、O 分别表示不同的正整数,且满足I ?M ?O =2001,则试问I ?M ?O 之最大值为 。
(A) 23 (B) 55 (C) 99 (D) 111 (E) 6712. 2000(20002000)为 。
(A) 20002001 (B) 40002000 (C) 20004000 (D) 40000002000 (E) 200040000003. Jenny 每天早上都会吃掉她所剩下的聪明豆的20%,今知在第二天结束时,有32颗剩下,试问一开始聪明豆有 颗。
(A) 40 (B) 50 (C) 55 (D) 60 (E) 754. Candra 每月要付给网络公司固定的月租费及上网的拨接费,已知她12月的账单为12.48元,而她1月的账单为17.54元,若她1月的上网时间是12月的两倍,试问月租费是 元。
(A) 2.53 (B) 5.06 (C) 6.24 (D) 7.42 (E) 8.775. 如图M ,N 分别为PA 与PB 之中点,试问当P 在一条平行AB 的直在线移动时,下列各数值有 项会变动。
(a) MN 长 (b) △PAB 之周长 (c) △PAB 之面积 (d) ABNM 之面积 (A) 0项 (B) 1项 (C) 2项 (D) 3项 (E) 4项6. 费氏数列是以两个1开始,接下来各项均为前两项之和,试问在费氏数列各项的个位数字中, 最后出现的阿拉伯数字为 。
(A) 0 (B) 4 (C) 6 (D) 7 (E) 97. 如图,矩形ABCD 中,AD =1,P 在AB 上,且DP 与DB 三等分 ?ADC ,试问△BDP 之周长为 。
AMC 美国数学竞赛试题+详解 英文版

2013 AMC8 Problems1.Danica wants to arrange her model cars in rows with exactly 6 cars in each row. She now has 23 model cars. What is the smallest number of additional cars she must buy in order to be able to arrange all her cars this way?2.A sign at the fish market says, "50% off, today only: half-pound packages for just $3 perpackage." What is the regular price for a full pound of fish, in dollars?What is the value of?3.4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill? 5.Hammie is in thegrade and weighs 106 pounds. His quadruplet sisters are tiny babiesand weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11.Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12.At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13.When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14.Abe holds 1 green and 1 red jelly bean in his hand. Bea holds 1 green, 1 yellow, and 2 red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?15.If , , and , what is the product of , , and ?16.A number of students from Fibonacci Middle School are taking part in a community serviceproject. The ratio of -graders to -graders is , and the the ratio of -graders to-graders is . What is the smallest number of students that could be participating in the project?17.The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18.Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?19.Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20.A rectangle is inscribed in a semicircle with longer side on the diameter. What is thearea of the semicircle?21.Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23.Angle of is a right angle. The sides of are the diameters of semicirclesas shown. The area of the semicircle on equals , and the arc of the semicircle onhas length . What is the radius of the semicircle on ?24.Squares , , and are equal in area. Points and are the midpointsof sides and , respectively. What is the ratio of the area of the shaded pentagonto the sum of the areas of the three squares?25.A ball with diameter 4 inches starts at point A to roll along the track shown. The track iscomprised of 3 semicircular arcs whose radii are inches, inches, andinches, respectively. The ball always remains in contact with the track and does notslip. What is the distance the center of the ball travels over the course from A to B?2013 AMC8 Problems/Solutions1. ProblemDanica wants to arrange her model cars in rows with exactly 6 cars in each row. She now has 23 model cars. What is the smallest number of additional cars she must buy in order to be able to arrange all her cars this way?Solution:In order to have her model cars in perfect, complete rows of 6, Danica must have a number ofcars that is a multiple of 6. The smallest multiple of 6 which is larger than 23 is 24, so she'll need to buy more model car.2.A sign at the fish market says, "50% off, today only: half-pound packages for just $3 per package." What is the regular price for a full pound of fish, in dollars?ProblemSolution: The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.What is the value of?3. ProblemNotice that we can pair up every two numbers to make a sum of 1:SolutionTherefore, the answer is .4. ProblemEight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill.What was the total bill?Each of her seven friends paidto cover Judi's portion. Therefore, Judi's portion mustbe. Since Judi was supposed to payof the total bill, the total bill must be.Solution5.Hammie is in thegrade and weighs 106 pounds. His quadruplet sisters are tiny babiesand weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these fivechildren or the median weight, and by how many pounds?ProblemLining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds. SolutionThe average weight of the five kids is .Therefore, the average weight is bigger, bypounds, making the answer.6. The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example,. What is the missing number in the top row?ProblemSolutionLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.Solution 1: Working BackwardsWe see that, making.It follows that, so.Another way to do this problem is to realize what makes up the bottommost number. Thismethod doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Solution 2: Jumping Back to the StartAgain, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7. Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass,Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clearthe crossing at a constant speed. Which of the following was the most likely number of cars inthe train?ProblemIf Trey saw, then he saw.Solution 12 minutes and 45 seconds can also be expressed asseconds.Trey's rate of seeing cars,, can be multiplied byon the top andbottom (and preserve the same rate):. It follows that the most likely number of cars is.2 minutes and 45 seconds is equal to.Solution 2Since Trey probably counts around 6 cars every 10 seconds, there are groups of 6cars that Trey most likely counts. Since, the closest answer choice is.8. A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?ProblemFirst, there areways to flip the coins, in order.Solution The ways to get two consecutive heads are HHT and THH. The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9. The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then onwhich jump will he first be able to jump more than 1 kilometer?ProblemThis is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that. SolutionHowever, because the first term isand not, the solution to the problem is10. What is the ratio of the least common multiple of 180 and 594 to the greatest common factorof 180 and 594?ProblemTo find either the LCM or the GCF of two numbers, always prime factorize first. Solution 1The prime factorization of . The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in bothfactorizations and multiply. = 18. Thus the answer = =.We start off with a similar approach as the original solution. From the prime factorizations, the GCF is 18.Similar SolutionIt is a well known fact that. So we have,.Dividing by 18 yields .Therefore, .11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?ProblemWe use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, letrepresent the time.SolutionOn Monday, he was at a rate of . So,.For Wednesday, he walked at a rate of . Therefore,.On Friday, he walked at a rate of. So,. Adding up the hours yields++=.We now find the amount of time Grandfather would have taken if he walked atperday. Set up the equation,.To find the amount of time saved, subtract the two amounts: -=.To convert this to minutes, we multiply by 60.Thus, the solution to this problem is12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?ProblemFirst, find the amount of money one will pay for three sandals without the discount. We have.SolutionThen, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. ProblemWhen Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?Let the two digits be and. SolutionThe correct score was . Clara misinterpreted it as. The difference between thetwo iswhich factors into. Therefore, since the difference is a multiple of 9,the only answer choice that is a multiple of 9 is.14.Abe holds 1 green and 1 red jelly bean in his hand. Bea holds 1 green, 1 yellow, and 2 red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?ProblemThe probability that both show a green bean is. The probability that both show ared bean is . Therefore the probability isSolution15. If ,, and , what is the product of, , and ?ProblemSolutionTherefore,.Therefore,.To most people, it would not be immediately evident that , so we can multiply 6'suntil we get the desired number:, so.Therefore the answer is16. A number of students from Fibonacci Middle School are taking part in a community serviceproject. The ratio of-graders to-graders is, and the the ratio of-graders to-graders is . What is the smallest number of students that could be participating inthe project?ProblemSolutionWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Solution 1: AlgebraTherefore, the ratio of 8th graders to 7th graders to 6th graders is. Since the ratiois in lowest terms, the smallest number of students participating in the project is.The number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and7th graders. The numbers ofstudents isSolution 2: Fakesolving17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?ProblemThe mean of these numbers is. Therefore the numbers are, so the answer isSolution 1Let thenumber be . Then our desired number is.Solution 2Our integers are , so we have that.Let the first term be. Our integers are. We have,Solution 318.Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?ProblemThere arecubes on the base of the box. Then, for each of the 4 layers abovethe bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are4 feet left), there arecubes. Hence, the answer is.Solution 1 We can just calculate the volume of the prism that was cut out of the originalbox. Each interior side of the fort will be 2 feet shorter than each side of the outside. Since thefloor is 1 foot, the height will be 4 feet. So the volume of the interior box is.Solution 2The volume of the original box is . Therefore, the number of blockscontained in the fort is19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?ProblemIf Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, ifHannah did worse than Bridget, there is no way Bridget could have known that she didn't getthe highest in the class. Therefore, Hannah did better than Bridget, so our order isSolution20. Arectangle is inscribed in a semicircle with longer side on the diameter. What is thearea of the semicircle?ProblemSolutionA semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem,. The area is21. ProblemSamantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?SolutionThe number of ways to get from Samantha's house to City Park is, and the number ofways to get from City Park to school is. Since there's one way to go through CityPark (just walking straight through), the number of different ways to go from Samantha's house to City Park to school22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?ProblemThere are 61 vertical columns with a length of 32 toothpicks, and there are 33 horizontal rowswith a length of 60 toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks. Thus, our answer isSolution23.Angleof is a right angle. The sides ofare the diameters of semicircles as shown. The area of the semicircle on equals, and the arc of the semicircle onhas length . What is the radius of the semicircle on?ProblemIf the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagorean theorem says that the other side has length 15, so the radius is.Solution 1We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of the largest is , and the middle one is , so the radius is .Solution 224. Squares, , andare equal in area. Pointsandare the midpointsof sidesand, respectively. What is the ratio of the area of the shaded pentagonto the sum of the areas of the three squares?ProblemSolution 1First let(whereis the side length of the squares) for simplicity. We can extenduntil it hits the extension of. Call this point. The area of trianglethen isThe area of rectangleis. Thus, our desired area is. Now, the ratio of the shaded area to the combined area of the three squares is.Solution 2Let the side length of each square be 1.Let the intersection ofandbe .Since, . Sinceand are vertical angles, theyare congruent. We also haveby definition.So we haveby congruence. Therefore,.Since andare midpoints of sides,. This combined withyields.The area of trapezoidis.The area of triangleis.So the area of the pentagon is .The area of the 3 squares is . Therefore, .Solution 3Let the intersection of andbe .Now we haveand .Because both triangles has a side on congruent squares therefore.Becauseand are vertical angles. Also bothand are right angles so .Therefore by AAS (Angle, Angle, Side) . Then translating/rotating the shadedinto the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25.A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, andinches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of the ball travels over the course from A to B?ProblemThe radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departurefrom the length of the track means that the answer is .Solution 1The total length of all of the arcs is . Since we want the path fromthe center, the actual distance will be shorter. Therefore, the only answer choice less thanis . This solution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump. Solution 2。
2023年AMC10美国数学竞赛A卷附中文翻译和答案

2023AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) (B)(C)(D) (E)4. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) (C) (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A∪B, the union of A and B?(A) 5 (B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) (B) (C)(D) (E)8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7 (B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A) (B)(C)(D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13 (B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) (B)(C)(D) (E)15. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A) (B) (C) (D) (E)17. In the eight-term sequence A, B, C, D, E, F, G, H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17 (B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B?(B) (C) (D) (E)(A)19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2023, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) (B) (C) (D) (E)21. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) (B) (C) (D) (E)22. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A) (B) (C) (D) (E)an integer. A point X in the interior of R is25. Let R be a square region andcalled n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500 (B) 1560 (C) 2320 (D) 2480 (E) 25002023AMC10美国数学竞赛A卷1. 某通讯公司手机每月基本费为20美元, 每传送一则简讯收 5美分(一美元=100 美分)。
2011AMC10美国数学竞赛A卷附中文翻译和答案

2011AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) 29(B)518(C)13(D) 718(E) 234. Let X and Y be the following sums of arithmetic sequences: X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of Y X?(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) 373 (C) 887 (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A ∪B, the union of A and B?(A) 5(B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A)2(7)0x +=(B) -350x += (C) 20= (D)80= (E) -340x -=8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20(B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7(B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A)4964 (B) 2532 (C) 78 (D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13(B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12(B) 20 (C) 72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference? (A)136 (B) 112 (C) 16 (D) 14 (E) 51815. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged 55 miles per gallon. How long was the trip in miles?(A) 140(B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A)(B) (C) 2 (D) (E) 617. In the eight-term sequence A, B, C, D, E, F, G , H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17(B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point oftangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B? (A) 32π- (B) 2π (C) 2 (D) 34π (E) 12π+19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2011, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42(B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect? (A)16 (B) 15 (C) 14 (D) 13 (E) 1221. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8 coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) 711(B) 913(C) 1115(D) 1519(E) 151622. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of thesame unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A)112 (B) (C) (D) 16 (E)25. Let R be a square region and 4n an integer. A point X in the interior of R is called n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500(B) 1560 (C) 2320 (D) 2480 (E) 25002011AMC10美国数学竞赛A 卷1. 某通讯公司手机每个月基本费为20美元, 每传送一则简讯收 5美分(一美元=100 美分)。
2014-2015年度美国”数学大联盟杯赛“(中国赛区)初赛-(十、十一、十二年级).doc

2014-2015年度美国”数学大联盟杯赛“(中国赛区)初赛(十、十一、十二年级)一、选择题(每小题10分,答对加10分,答错不扣分,共100分,请将正确答案A 、B 、C 或者D 写在每题后面的圆括号内。
)正确答案填写示例如下:=-⨯⨯20522 ? (A )A)5 B)15 C)25 D)301. Meg loves her megaphone! The large circular end has a circumference that is the reciprocal of its diameter. What is the area of the circle? ( )A)π14 B) π12 C) 14 D) 122. How many solutions does the equation x x +=233 have? ( )A)0 B)1 C)2 D)43. If y x =-1, which of the following is always true for any value of x ? ( )A) ()()x y -=-2211B) ()()x x y y -=-222211 C) ()()x x y y --=-222211 D) ()()()()x x y y -+=-+22221111 4. Lee the crow ate a grams of feed that was 1% seed, b grams of feed that was 2% seed, and c grams of feed that was 3% seed. If combined, all the feed he ate was 1.5% seed. What is a in terms of b and c ?( )A)b c +3B)b c +3 C)b c +23 D)b c +32 5. If <x 0 and <.x 2001, then x -1 must be ( )A)less than -10B)between-0.1 and 0 C)between 0and 0.1 D) greater than 106. At 9:00 A.M., the ratio of red to black cars in a parking lot was 1 to 5. An hour later the number of red cars had increased by 2, the number of black cars had decreased by 5, and the ratio of red to black cars was 1 to 4. How many black cars were in the lot at 10:00 A.M.? ( )A)13 B)15 C)60 D)657. If x ≠1and x ≠-1, then ()()()x x x x x --++-32241111=( ) A)x -21 B) x +21 C) x -241 D) x -341 8. The Camps are driving at a constant rate. At noon they had driven 300 km.At 3:30 P.M. they had driven 50% further than they had driven by 1:30 P.M.What is their constant rate in km/hr? ( )A)150 B)120 C)100 D)909. The letters in DIGITS can be arranged in how many orders without adjacent I ’s? ( )A)240 B)355 C)600 D)71510. Al, Bea, and Cal each paint at constant rates, and together they are painting a house. Al and Bea togethercould do the job in 12 hours; Al and Cal could to it in 15, and Bea and Cal could do it in 20. How many hours will it take all three working together to paint the house?( )A)8.5 B)9 C)10 D)10.5二、填空题(每小题10分,答对加10分,答错不扣分,共200分)11. What is the sum of the degree-measures of the angles at the outer points ,,,A B C D and E of a five-pointed star, as shown? Answer: . 12. What is the ordered pair of positive integers (,k b ), with the least value of k , which satisfiesk b ⋅⋅=34234?Answer: .13. A face-down stack of 8 playing cards consisted of 4 Aces (A ’s) and 4 Kings (K ’s).After I revealed and then removed the top card, I moved the new top card to thebottom of the stack without revealing the card. I repeated this procedure until thestack without revealing the card. I repeated this procedure until the stack was leftwith only 1 card, which I then revealed. The cards revealed were AKAKAKAK ,in that order. If my original stack of 8 cards had simply been revealed one card at atime, from top to bottom (without ever moving cards to the bottom of the stack),in what order would they have been revealed?Answer: .14. For what value of a is one root of ()x a x a -+++=222120 twice the other root?Answer: .15. Each time I withdrew $32 from my magical bank account, the account ’sremaining balance doubled. No other account activity was permitted. My fifth$32 withdrawal caused my account ’s balance to become $0. With how manydollars did I open that account?Answer: .16. In how many ways can I select six of the first 20 positive integers, disregarding the order in which these sixintegers are selected, so that no two of the selected integers are consecutive integers?Answer: .17. If, for all real ,()()xx f x f x =-21, what is the numerical value of f (3)?Answer: .18. How many pairs of positive integers (without regard to order) have a least common multiple of 540?Answer: .19. If the square of the smaller of consecutive positive integers is x , what is the square of the larger of thesetwo integers, in terms of x ?Answer: .20. A pair of salt and pepper shakers comes in two types: identical and fraternal.Identical pairs are always the same color. Fraternal pairs are the same colorhalf the time. The probability that a pair of shakers is fraternal is p andthat a pair is identical is .q p =-1 If a pair of shakers is of the same color, AE DCBword 格式-可编辑-感谢下载支持 determine, in terms of the variable q alone, the probability that the pair is identical. Answer: .21. As shown, one angle of a triangle is divided into four smaller congruentangles. If the lengths of the sides of this triangle are 84, 98, and 112, as shown,how long is the segment marked x ?Answer: .22. How long is the longer diagonal of a rhombus whose perimeter is 60, if threeof its vertices lie on a circle whose diameter is 25, as shown?Answer: .23. The 14 cabins of the Titanic Mail Boat are numbered consecutively from1 through 14, as are the 14 room keys. In how many different ways canthe 14 room keys be placed in the 14 rooms, 1 per room, so that, for everyroom, the sum of that room ’s number and the number of the key placed inthat room is a multiple of 3?Answer: .24. For some constant b , if the minimum value of ()x x b f x x x b -+=++2222is 12, what is the maximum value of ()f x ? Answer: .25. If the lengths of two sides of a triangle are 60cos A and 25sin A , what is the greatest possible integer-length of the third side?Answer: .26. {}n a is a geometric sequence in which each term is a positive number. If a a =5627, what is the value oflog log log ?a a a +++3132310Answer: . 27. What is the greatest possible value of ()=sin cos ?f x x x ++3412Answer: .28. Let C be a cube. Triangle T is formed by connecting the midpoints of three edges of cube C . What is the greatest possible measure of an angle of triangle T ?Answer: .29. Let a and b be two real numbers. ()sin f x a x b x =++34 and (lg log )f =3105. What is the value of (lg lg )f 3?Answer: .30. Mike likes to gamble. He always bets all his chips whenever the number of chips he has is <=5. He always bets n (10-)chips whenever the number of chips he has is greater than 5 and less than 10. He continues betting until either he has no chips or he has more than 9 chips. For every round, if he bets n chips. The probability that he wins or loses in each round is 50%. If Mike begins with 4 chips, what is the probability that he loses all his chips?Answer: .1129884xword格式-可编辑-感谢下载支持。
2021年美国数学竞赛AMC-12A 真题加答案解析(英文版)

(A) 15 (B) 30 (C) 45 (D) 60 (E) 75
⇣
⌘
⇣
⌘
Solution. The student computed 66
1
+
ab 100
; the correct answer is 66
1
+
ab 99
. Thus,
✓
◆
66 · (a b) ·
1 99
1 100
= 0.5 =) a b = (E) 75
⌅
p Problem 2. Under what conditions is a2 + b2 = a + b true, where a and b are real numbers?
(A) It is never true
(B) It is true if and only if ab = 0
(C) It is true if and only if a + b 0
• all of his happy snakes can add, • none of his purple snakes can subtract
• all of his snakes that can’t subtract also can’tonclusions can be drawn about Tom’s snakes?
(A) 10, 272 (B) 11, 700 (C) 13, 362 (D) 14, 238 (E) 15, 426
Solution. Let the first number mentioned be 10n; the second is n. Then 10n + n = 17, 402, from
AMC美国数学竞赛AMC.B 试题及答案解析
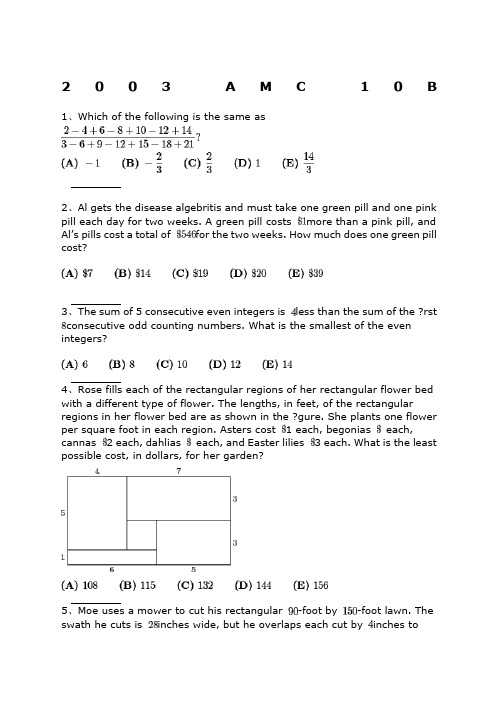
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。
