清华大学附中高考数学复习讲义平面几何(无答案)

合集下载

高考数学一轮复习第十三章立体几何 13.1 平面的基本性质讲义

§13.1 平面的基本性质命题探究考纲解读考点内容解读要求五年高考统计常考题型预测热度 2013 2014 2015 2016 2017 平面的基本性质空间点、线、面关系判断 A填空题 ★☆☆分析解读平面的基本性质是立体几何的基础,高考很少单独考查,但只有充分认识平面的基本性质,才能为学好后面的平行与垂直打下坚实的基础.五年高考考点平面的基本性质1.(2015福建改编,7,5分)若l,m 是两条不同的直线,m 垂直于平面α,则“l⊥m”是“l∥α”的条件.答案必要而不充分2.(2013安徽理改编,3,5分)在下列命题中,不是．．公理的是 (填序号). ①平行于同一个平面的两个平面相互平行②过不在同一条直线上的三点,有且只有一个平面③如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 ④如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线答案 ①三年模拟A 组 2016—2018年模拟·基础题组考点平面的基本性质 1.(2017江苏宿迁中学月考)在正方体ABCD-A 1B 1C 1D 1中,O 是BD 1的中点,直线A 1C 交平面AB 1D 1于点M,给出下列四个结论:①A 1、M 、O 三点共线;②M、O 、A 1、A 四点共面;③A、O 、C 、M 四点共面; ④B 、B 1、O 、M 四点共面.其中正确结论的序号是 .答案①②③2.(苏教必2,一,2,变式)下列命题中,正确的个数为.①梯形可以确定一个平面;②若两条直线和第三条直线所成的角相等,则这两条直线平行;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.答案 23.(苏教必2,一,2,变式)如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.求证:(1)E、C、D1、F四点共面;(2)CE、D1F、DA三线共点.证明(1)如图,连结EF、CD1、A1B.∵E、F分别是AB、AA1的中点,∴EF∥BA1,EF=BA1.又A1B∥D1C,∴EF∥CD1,∴E、C、D1、F四点共面.(2)易知EF=C D.∵EF∥CD1,∴CE与D1F必相交,设交点为P,如图所示.则由P∈CE,CE⊂平面ABCD,得P∈平面AB CD.同理P∈平面ADD1A1.又平面ABCD∩平面ADD1A1=DA,∴P∈直线DA.∴CE、D1F、DA三线共点.B组2016—2018年模拟·提升题组(满分:20分时间:10分钟)解答题(共15分)如图,在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,H为直线B1D与平面ACD1的交点.求证:D1、H、O三点共线.证明连结BD、B1D1,OD1,如图.则BD∩AC=O,∵BB1 DD1,∴四边形BB1D1D为平行四边形,又H∈B1D,B1D⊂平面BB1D1D,∴H∈平面BB1D1D,∵平面ACD1∩平面BB1D1D=OD1,H∈平面ACD1,∴H∈OD1.即D1、H、O三点共线.C组2016—2018年模拟·方法题组方法证明点共线、线共点等的方法如图,在空间四边形ABCD中,E,G分别为BC,AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.求证:(1)E,F,H,G四点共面;(2)EF,GH,BD交于一点.证明(1)连结GE,FH,因为E,G分别为BC,AB的中点,所以GE∥AC,GE=AC.又因为DF∶FC=DH∶HA=2∶3,所以FH∥AC,FH=AC.从而FH∥GE,FH≠GE.所以四边形EFHG是一个梯形,故E,F,H,G四点共面.(2)因为四边形EFHG是一个梯形,且FH∥GE,所以直线EF与GH相交.设交点为O,则O∈GH,O∈EF.因为GH⊂平面ABD,EF⊂平面BCD,所以O∈平面ABD,O∈平面BCD.又因为平面ABD∩平面BCD=BD,所以O∈BD.所以EF,GH,BD交于一点.。

2025年新人教版高考数学一轮复习讲义第七章 §7.10 立体几何中的动态、轨迹问题

设 AB＝a，BC＝b，则 a2＋b2＋22＝ 5，可得 a2＋b2＝1，
所以 V＝2ab≤a2＋b2＝1，当且仅当 a＝b＝ 22时，等号成立.
如图，设AC，BD相交于点O，
因为BO⊥AC，BO⊥AA1，AC∩AA1＝A，AC，AA1⊂平面A1ACC1，所以 BO⊥平面 A1ACC1，因为直线 BP 与平面 A1ACC1
2π 则在此过程中动点M形成的轨迹长度为___8___.
如图，设 AC 的中点为 M0 ， △ADE 沿 DE 翻折 90°，此时平面A′DE⊥平面ABCD，取CD中点P，CE中点Q，PQ中点N，连接PQ，MP，MQ，MN，M0P，M0Q，M0N. MP＝M0P＝12AD＝12，MQ＝M0Q＝12AE＝12，PQ＝12DE＝ 22，△MPQ 和△M0PQ 是等腰直角三角形，
1 2 3 4 5 6 7 8 9 10
知BP⊥平面ACN，CN⊂平面ACN，所以BP⊥CN，所以动点Q的轨迹为线段CN，在Rt△ABN，Rt△RAB中，∠BAN＝∠ARB，所以Rt△ABN∽Rt△RAB，
则BANB＝ARBA，得 BN＝12，易得 CN＝ BN2＋BC2＝
212＋12＝
5 2.
题型一平行、垂直中的动态轨迹问题
例1 如图，在棱长为a的正方体ABCD－A1B1C1D1 中，E，F，G，H，N分别是CC1，C1D1，DD1，CD， BC的中点，M在四边形EFGH边上及其内部运动，
若MN∥平面A1BD，则点M轨迹的长度是
A. 3a
B. 2a
3a C. 2
√D.
2a 2
连接HN，GN(图略)， ∵在棱长为a的正方体ABCD－A1B1C1D1中，E，F，G，H，N分别是 CC1，C1D1，DD1，CD，BC的中点，则GH∥BA1，HN∥BD，又GH⊄平面A1BD，BA1⊂平面A1BD， ∴GH∥平面A1BD，同理可证得NH∥平面A1BD，又GH∩HN＝H，GH，HN⊂平面GHN，

21直线与圆圆与圆的位置关系专题复习讲义-高考数学一轮复习专题讲义(学生版)

目录直线与圆、圆与圆的位置关系 (2)【课前诊断】 (2)【知识点一：直线与圆位置关系】 (3)【典型例题】 (5)考点一：直线与圆位置关系的判定 (5)考点二：圆的切线方程 (6)考点三：直线与圆相交弦 (7)【知识点二：圆与圆的位置关系】 (8)【典型例题】 (9)考点一：圆与圆的位置关系 (9)考点二：圆与圆的公共弦 (9)考点三：圆与圆的公切线问题 (10)【小试牛刀】 (10)【巩固练习——基础篇】 (11)【巩固练习——提高篇】 (12)直线与圆、圆与圆的位置关系【课前诊断】成绩（满分10）：完成情况：优/中/差1．已知点A (－4，－5)，B (6，－1)，则以线段AB 为直径的圆的方程为( ) A ．(x ＋1)2＋(y －3)2＝29 B ．(x －1)2＋(y ＋3)2＝29 C ．(x ＋1)2＋(y －3)2＝116 D ．(x －1)2＋(y ＋3)2＝1162．圆心在y 轴上，且过点(3,1)的圆与x 轴相切，则该圆的方程是( ) A ．x 2＋y 2＋10y ＝0 B ．x 2＋y 2－10y ＝0 C ．x 2＋y 2＋10x ＝0 D ．x 2＋y 2－10x ＝03．若圆C 经过坐标原点与点(4,0)，且与直线y ＝1相切，则圆C 的方程是__________________．4．已知圆C ：x 2＋y 2＋kx ＋2y ＝－k 2，当圆C 的面积取最大值时，圆心C 的坐标为__________．5. 圆的方程是，则圆心的坐标是（）A. B. C.D.6. 圆上的点到原点的最大距离是( ) A. B.D.107. 过点与且圆心在直线上的圆的方程为（）A.B.C.D.8. 两圆和的连心线方程为（）A. B. C. D.1)(2)(2)(4)0x x y y -++-+=（11)-（，11)2-（，1,2)-（1,1)2--（223)(1)25x y ++-=（5-11)A -（，1,1)B -（20x y +-=223)(1)4x y -++=（221)(1)4x y -+-=（22+3)(1)4x y +-=（22+1)(1)4x y ++=（22460x y x y +-+=2260x y x +-=30x y ++=250x y --=390x y --=4370x y -+=【知识点一：直线与圆位置关系】1：直线与圆的位置关系由平面几何知，直线与圆有三种位置关系：（1）直线与圆相交，有两个公共点；（2）直线与圆相切，只有一个公共点；（3）直线与圆相离，没有公共点.直线Ax ＋By ＋C ＝0与圆(x －a )2＋(y －b )2＝r 2的位置关系及判断一览表位置关系相交相切相离公共点个数 2个1个0个判定方法几何法：设圆心到直线的距离22||++=+Aa Bb C d A Bd r < d r = d r >代数法：由()()2220++=⎧⎪⎨-+-=⎪⎩Ax By C x a y b r消元得到一元二次方程的判别式∆0∆> 0∆= 0∆<图形2.圆的切线方程的问题（1）过圆上一点的切线方程：与圆相切于点的切线方程是；与圆相切于点的切线方程是：；与圆相切于点的切线方程是；222x y r +=()11x y ，211x x y y r +=222x y r +=()cos sin r r θθ，cos sin 0x y r θθ+-=()()222x a y b r -+-=()11x y ，()()()()211x a x a y b y b r --+--=（2）过圆外一点的切线方程：设是圆外一点，求过点的圆的切线方程. 当两条切线斜率都存在时，设切线方程是，即，求出待定系数k ，就可写出切线方程.当有一条切线斜率不存在时，斜率不存在的切线方程为，切线斜率存在的切线方程的求法同上.3. 直线与圆相交的弦长的求法（1）几何法如图所示，直线l 与圆C 相交于A ，B 两点，线段AB 的长即为l 与圆相交的弦长. 设弦心距为d ，半径为r ，弦为AB ，则有（2）代数法直线l 与圆交于，直线l 的斜率存在，设为k ，则联立直线方程和圆的方程得方程组.方法一：解方程组得点A 、B 的坐标，再由两点间的距离公式求弦长. 方法二：消去一个未知数得到一个一元二次方程，利用根与系数的关系可得弦长，其中k 为直线的斜率且k≠0.特别地，当k=0时，可直接利用计算；当k 不存在时，可直接利用计算. 温馨提示①几何法构造了直角三角形，计算量小，非常适合求直线与圓相交的弦长.②代数法是方程思想在解析几何中的重要体现，也是解析几何的实质，即用代数法研究几何问题.()000P x y ，()()222x a y b r -+-=0P ()00y y k x x -=-000kx y kx y --+=r =0x x =AB =()()1122A x y B x y ，，，AB 1212AB x y =-=-12AB x x =-12AB y y =-【典型例题】考点一：直线与圆位置关系的判定例1.直线与圆的位置关系为A.相切B.相交但直线不过圆心C.直线过圆心D.相离例2. 已知直线方程，圆的方程当为何值时，圆与直线(1)有两个公共点； (2)只有一个公共点； (3)没有公共点．例3.已知(,)M a b 在圆外，则直线1ax by +=与圆O 的位置关系是A.相切B.相交C.相离D.不确定练习1. 当为何值时，直线与圆相交、相切、相离？1y x =+221x y +=10mx y m ---=224210.x y x y -+=+-m 22:1O x y +=k 2y kx =-222x y +=考点二：圆的切线方程例1. 求经过点（1，7）且与圆相切的直线方程.例2.圆，在点处的切线方程为A. B. C.D.练习1.过点作圆的切线，求此切线的方程．练习2. 已知圆的方程为x 2 + y 2 = 25，则过点(－3，4)的圆的切线方程为.练习3. 已知圆C ：(x －1)2＋(y ＋2)2＝10，求满足下列条件的圆的切线方程．(1)与直线l 1：x ＋y －4＝0平行； (2)与直线l 2：x －2y ＋4＝0垂直； (3)过切点A (4，－1)．2225x y +=2240x y x +-=P 20x +-=40x +-=+40x -=+20x -=3(4)-A ，22()(31)1x y --+=________考点三：直线与圆相交弦例1.直线l 经过点P （5，5）并且与圆相交截得的弦长为l 的方程.例2.求直线被圆截得的弦长．例3.圆截得的劣弧所对的圆心角的大小为.例4.过点的直线中，被圆截得的弦为最短的直线的方程为 A.B. C.D.练习1过原点且倾斜角为的直线被圆所截得的弦长为B.2D.练习2.直线得的劣弧所对的圆心角为. 练习3. 过圆内的点作一条直线l ，使它被该圆截得的线段最短，则直线l 的方程 A. B. C.D.22:25O x y +=l ：3+60x y -=C ：22240x y y --=+224x y +=0y +-=________3π()21，222420x y x y +-+=350x y --=350x y +-=31=0x y --310x y +-=0602240x y y +-=y =224x y +=________222440x y x y +-+-=(3,0)M 30x y +-=30x y --=430x y +-=430x y --=【知识点二：圆与圆的位置关系】由平面几何知，圆与圆有五种位置关系（由远及近）：外离，外切，相交，内切，内含.设两圆222111()()x a y b r -+-=与222222()()x a y b r -+-=的圆心距为d ，我们可以得到：221212()()d a a b b =-+-12r r >）：位置关系关系式图示外离12d r r >+外切12d r r =+相交1212r r d r r -<<+内切12d r r =-内含120d r r ≤<-【典型例题】考点一：圆与圆的位置关系例1 圆与的位置关系是A.相离B.外切C.内切D.相交例2 若圆与圆相交，则的取值范围是A. B. C.D. 或练习1. 圆与圆的位置关系是A.外离B.相交C.内切D.外切练习2. 如果圆C ：x 2＋y 2－2ax －2ay ＋2a 2－4＝0与圆O ：x 2＋y 2＝4总相交，那么实数a 的取值范围是______________________．考点二：圆与圆的公共弦例1 两圆和的公共弦所在直线的方程是____________．例2. 若圆与圆的公共弦长为，.练习1. 求经过两圆22640x y x和226280x y y的交点且圆心在直线40xy 上的圆的方程．222x y +=22430x y y +++=2221:240C x y mx m +-+-=2222:24480C x y x my m ++-+-=m 12255m -<<-1205m -<<1225m -<<12255m -<<-02m <<()222(2)1x y ++-=22(2)(5)16x y -+-=2260x y x +-=224x y +=23x =224x y +=22260(0)x y ay a ++-=>a =________1考点三：圆与圆的公切线问题例1.两相交圆的公切线有且仅有A.1条B.2条C.3条D.4条练习1. 到点A (－1,2)，B (3，－1)的距离分别为3和1的直线有________条．【小试牛刀】1．两圆和的位置关系是( )（A ）内切（B ）相交（C ）外切（D ）外离2．圆截直线所得弦长是( )（A（B（C ）（D3. 圆与直线相切，正实数b 的值为( )（A ）（B ）1（C ）（D ）34.过圆内的点作一条直线l ，使它被该圆截得的线段最短，则直线l 的方程是( ) （A ）（B ）（C ）（D ）5.★★已知圆，直线，则直线与的位置关系是（）（A ）一定相离（B ）一定相切（C ）相交且一定不过圆心（D ）相交且可能过圆心6.★过点的直线l 被圆，则直线l 的斜率为________．7.★上的点到直线的距离的最大值为________．2210x y +-=221:4240C x y x y +-+-=221:4460C x y x y +-++=50x y --=122430x y y +-+=+b=0y +121-222440x y x y +-+-=(3,0)M 30x y +-=30x y --=430x y +-=430x y --=22:21C x y x +-=(1)1y k x =-+l C (1,2)--222210x y x y +--+=2216x y +=3x y -=1.若直线与圆相切，则的值为（A ）（B ）（C ）（D ）2.圆：和：的位置关系是（A ）外切（B ）内切（C ）相交（D ）相离3.直线和圆的关系是（A ）相离（B ）相切或相交（C ）相交（D ）相切 4．过点(2,1)的直线中，被圆截得的弦为最短的直线的方程为（A ）（B ）（C ）（D ）5．两圆和的公切线有且仅有（A ）1条（B ）2条（C ）3条（D ）4条6.过原点且倾斜角为的直线被圆所截得的弦长为.7.设是圆上的点，则M 点到直线的最短距离是.8.过点与圆相切的切线方程为.9.圆与圆的公共弦所在的直线方程为.10．★★当m 为何值时，直线与圆相交、相切、相离？y x b =+222x y +=b 4±2±±1C 224x y +=2C 2268240x y x y +-+-=:1(1)l y k x -=-2220x y y +-=22240x y x y +-+=350x y --=350x y +-=310x y --=310x y --=221:2220C x y x y +++-=222:4210C x y x y +--+=0602240x y x +-=________M 22(5)(3)9x y -+-=3420x y +-=________(3,2)P -22(2)(1)25x y ++-=________2240x y y +-=2268240x y x y +-+-=________10mx y m ---=224210x y x y +--+=1．台风中心从A地以20 km/h的速度向东北方向移动，离台风中心30 km内的地区为危险区，城市B在A地正东40 km处，则城市B处于危险区内的时间为()A．0.5 h B．1 hC．1.5 h D．2 h2．若圆22221x y by b外离，则,a b满足的条件是22x y ax a和222________．3．若圆x2＋y2＝4与圆x2＋y2＋2ay－6＝0(a>0)的公共弦的长为a＝________. 4．已知点(1,)A a，圆O：x 2＋y 2＝4.(1)若过点A的圆O的切线只有一条，求实数a的值及切线方程；(2)若过点A且在两坐标轴上截距相等的直线被圆O截得的弦长为a的值．。

第4节直线与圆、圆与圆的位置关系--2025年高考数学复习讲义及练习解析

第四节直线与圆、圆与圆的位置关系1．直线与圆的位置关系设圆C ：(x －a )2＋(y －b )2＝r 2，直线l ：Ax＋By ＋C ＝0，圆心C (a ，b )到直线l 的距离为d ，由x －a ）2＋（y －b ）2＝r 2，＋By＋C ＝0，消去y (或x )，得到关于x (或y )的一元二次方程，其判别式为Δ.位置关系相离相切相交图形量化方程观点Δ01<0Δ02＝0Δ03>0几何观点d 04>rd 05＝rd 06<r2．圆与圆的位置关系(⊙O 1，⊙O 2的半径分别为r 1，r 2，d ＝|O 1O 2|)位置关系图形几何法公切线条数外离d >r 1＋r 2四条外切d＝r1＋r2三条相交|r1－r2|<d<r1＋r2两条内切d＝|r1－r2|一条内含0≤d<r1－r2无1．圆的切线方程常用的结论(1)过圆x2＋y2＝r2上一点P(x0，y0)的圆的切线方程为x0x＋y0y＝r2.(2)过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2. 2．直线被圆截得的弦长的求法(1)几何法：弦心距d、半径r和弦长|AB|的一半构成直角三角形，弦长|AB|＝2r2－d2.(2)代数法：设直线y＝kx＋m与圆x2＋y2＋Dx＋Ey＋F＝0相交于点M，N，将直线方程代入圆的方程中，消去y，得关于x的一元二次方程，则|MN|＝1＋k2·（x M＋x N）2－4x M x N. 3．圆与圆的位置关系的常用结论(1)两圆相交时，其公共弦所在的直线方程由两圆方程相减得到．(2)两个圆系方程①过直线Ax＋By＋C＝0与圆x2＋y2＋Dx＋Ey＋F＝0交点的圆系方程为x2＋y2＋Dx＋Ey＋F ＋λ(Ax＋By＋C)＝0(λ∈R)；②过圆C1：x2＋y2＋D1x＋E1y＋F1＝0和圆C2：x2＋y2＋D2x＋E2y＋F2＝0交点的圆系方程为x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0(λ≠－1)(其中不含圆C2，所以注意检验C2是否满足题意，以防丢解)．1．概念辨析(正确的打“√”，错误的打“×”)(1)若直线平分圆的周长，则直线一定过圆心．()(2)若两圆相切，则有且只有一条公切线．()(3)若直线的方程与圆的方程组成的方程组有解，则直线与圆相交或相切．()(4)在圆中最长的弦是直径．()答案(1)√(2)×(3)√(4)√2．小题热身(1)(人教A选择性必修第一册习题2.5T1改编)直线y＝x＋1与圆x2＋y2＝1的位置关系为()A．相切B．相交但直线不过圆心C．直线过圆心D．相离答案B解析圆心为(0，0)，到直线y＝x＋1，即x－y＋1＝0的距离d＝12＝22，而0<22<1，所以直线与圆相交，但直线不过圆心．故选B.(2)(人教A选择性必修第一册2.5.2练习T2改编)圆O1：x2＋y2－2x＝0与圆O2：x2＋y2＋4y ＝0的位置关系是()A．外离B．外切C．相交D．内切答案C解析圆O1：x2＋y2－2x＝0的标准方程为(x－1)2＋y2＝1，圆心为O1(1，0)，半径为r1＝1，圆O2：x2＋y2＋4y＝0的标准方程为x2＋(y＋2)2＝4，圆心为O2(0，－2)，半径为r2＝2，所以两圆的圆心距为|O1O2|＝（－1）2＋（－2）2＝5，所以1＝|r1－r2|<|O1O2|<r1＋r2＝3，因此两圆的位置关系为相交．故选C.(3)(人教A选择性必修第一册习题2.5T2改编)以点(3，－1)为圆心且与直线3x＋4y＝0相切的圆的方程是________________．答案(x－3)2＋(y＋1)2＝1解析由题意得，r＝|3×3＋4×（－1）|32＋42＝1，因此圆的方程为(x－3)2＋(y＋1)2＝1.(4)(人教A选择性必修第一册习题2.2T3改编)已知圆C：x2＋y2－6x－4y＋4＝0.若一直线被圆C所截得的弦的中点为M(2，3)，则该直线的方程为________________．答案y＝x＋1解析圆C：x2＋y2－6x－4y＋4＝0化为标准方程为(x－3)2＋(y－2)2＝9，则圆心为C(3，2)，k CM＝3－22－3 1.设所求的直线为m.由圆的几何性质可知，k m·k CM＝－1，所以k m＝1，所以所求的直线方程为y－3＝1·(x－2)，即y＝x＋1.考点探究——提素养考点一直线与圆的位置关系例1(1)(2023·江西九江二模)直线l：mx－y－2＋m＝0(m∈R)与圆C：x2＋(y－1)2＝16的位置关系为________．答案相交解析由mx－y－2＋m＝0(m∈R)，得m(x＋1)－y－2＝0(m∈R)，＋1＝0，y－2＝0，解得＝－1，＝－2，所以直线l过定点(－1，－2)，又因为(－1)2＋(－2－1)2＝10<16，得(－1，－2)在圆内，所以直线l与圆C总相交．(2)(2024·广东湛江廉江中学高三第二次月考)已知直线x＋y＋2＝0与圆x2＋y2＝r2相切，则r 的值为________．答案±2解析由直线x＋y＋2＝0与圆x2＋y2＝r2相切，得|2|12＋12＝|r|，即|r|＝2，故r的值为± 2.【通性通法】判断直线与圆的位置关系的两种方法特别地，对于过定点的直线，也可以通过定点在圆内部或圆上判定直线和圆有公共点．【巩固迁移】1．(2023·陕西榆林模拟)已知点P(x0，y0)为圆C：x2＋y2＝2上的动点，则直线l：x0x－y0y＝2与圆C的位置关系为()A．相交B．相离C．相切D．相切或相交答案C解析由题意可得x20＋y20＝2，于是圆心C到直线l的距离d＝2x20＋y20＝22＝2＝r，所以直线l与圆C相切．故选C.2．已知圆O：x2＋y2＝4上到直线l：x＋y＝a的距离等于1的点至少有2个，则a的取值范围为________．答案(－32，32)解析由圆的方程可知圆心为(0，0)，半径为2.因为圆上到直线l：x＋y＝a的距离等于1的点至少有2个，所以圆心到直线l的距离d＜r＋1＝3，即d＝|－a|2<3，解得－32＜a＜32.考点二圆的弦长、切线问题(多考向探究)考向1弦长问题例2(1)(2024·四川西昌期末)直线l：x－3y cosθ＝0被圆x2＋y2－6x＋5＝0截得的最大弦长为()A．3B．5C．7D．3答案C解析因为圆x2＋y2－6x＋5＝0，所以其圆心为(3，0)，半径r＝2，于是圆心(3，0)到直线l：x－3y cosθ＝0的距离为d＝31＋3cos2θ，因为cosθ∈[－1，1]，所以cos2θ∈[0，1]，所以d＝31＋3cos2θ∈32，3，因为直线l与圆相交，所以d<2，所以d∈32，又因为弦长为2r2－d2＝24－d2，所以当d取得最小值32时，弦长取得最大值，为7.故选C.(2)(2023·海南华侨中学二模)已知直线x－3y＋8＝0和圆x2＋y2＝r2(r>0)相交于A，B两点．若|AB|＝6，则r的值为________．答案5解析因为圆心(0，0)到直线x－3y＋8＝0的距离d＝81＋3＝4，由|AB|＝2r2－d2，可得6＝2r2－42，解得r＝5.【通性通法】求直线被圆截得的弦长的两种方法【巩固迁移】3．设圆x2＋y2－2x－2y－2＝0的圆心为C，直线l过(0，3)与圆C交于A，B两点，若|AB|＝23，则直线l 的方程为()A ．3x ＋4y －12＝0或4x －3y ＋9＝0B ．3x ＋4y －12＝0或x ＝0C ．4x －3y ＋9＝0或x ＝0D ．3x －4y ＋12＝0或4x ＋3y ＋9＝0答案B解析当直线l 的斜率不存在，即直线l 的方程为x ＝0时，弦长为23，符合题意；当直线l 的斜率存在时，可设直线l 的方程为y ＝kx ＋3，由弦长为23，半径为2可知，圆心到该直线的距离为1，从而有|k ＋2|k 2＋1＝1，解得k ＝－34.综上，直线l 的方程为x ＝0或3x ＋4y －12＝0.故选B.4．(2023·新课标Ⅱ卷)已知直线l ：x －my ＋1＝0与⊙C ：(x －1)2＋y 2＝4交于A ，B 两点，写出满足“△ABC 的面积为85”的m 的一个值：________．答案，－2，12，－12中任意一个皆可以解析设点C 到直线AB 的距离为d ，由弦长公式得|AB |＝24－d 2，所以S △ABC ＝12×d ×24－d 2＝85，解得d ＝455或d ＝255，由d ＝|1＋1|1＋m 2＝21＋m 2，所以21＋m 2＝455或21＋m 2＝255，解得m ＝±2或m ＝±12.考向2切线问题例3(1)在平面直角坐标系中，过点A (3，5)作圆O ：x 2＋y 2－2x －4y ＋1＝0的切线，则切线的方程为()A ．5x －12y ＋45＝0B ．y ＋5＝0C ．x －3＝0或5x －12y ＋45＝0D ．y －5＝0或12x －5y ＋45＝0答案C解析因为32＋52－2×3－4×5＋1>0，点(3，5)在圆外，且x 2＋y 2－2x －4y ＋1＝0的圆心为(1，2)，半径为2.若切线的斜率不存在，即x ＝3，圆心(1，2)到直线x ＝3的距离为2，故直线x ＝3是圆的切线；若切线的斜率存在，设切线方程为y －5＝k (x －3)，即kx －y －3k ＋5＝0，则|k －2－3k ＋5|k 2＋1＝2，则|3－2k |k 2＋1＝2，两边平方得12k ＝5，k ＝512，所以y －5＝512(x －3)，即5x－12y ＋45＝0.综上，切线的方程为5x －12y ＋45＝0或x －3＝0.故选C.(2)由直线y ＝x ＋1上的一点向圆(x －3)2＋y 2＝1引切线，则切线长的最小值为________．答案7解析设直线上一点P ，切点为Q ，圆心为M ，M 的坐标为(3，0)，则|PQ |即为切线长，|MQ |为圆M 的半径，长度为1，|PQ |＝|PM |2－|MQ |2＝|PM |2－1，要使|PQ |最小，即求|PM |的最小值，此题转化为求直线y ＝x ＋1上的点到圆心M 的最小距离．设圆心到直线y ＝x ＋1的距离为d ，则d ＝|3－0＋1|12＋（－1）2＝22，所以|PM |的最小值为22，此时|PQ |＝|PM |2－1＝（22）2－1＝7.【通性通法】1．求过圆上一点(x 0，y 0)的圆的切线方程：先求切点与圆心连线的斜率k ，再由垂直关系，求得切线斜率为－1k ，由点斜式方程可求得切线方程，如果k ＝0或k 不存在，则由图形可直接得到切线方程为y ＝y 0或x ＝x 0.2．求过圆外一点(x 0，y 0)的圆的切线方程当切线斜率存在时，圆的切线方程的求法：(1)几何法：设切线方程为y －y 0＝k (x －x 0)，利用点到直线的距离公式表示出圆心到切线的距离d ，然后令d ＝r ，进而求得k .(2)代数法：设切线方程为y －y 0＝k (x －x 0)，与圆的方程组成方程组，消元后得到一个一元二次方程，然后令判别式Δ＝0，进而求得k .注意验证斜率不存在的情况．3．涉及与圆的切线有关的线段长度范围(或最值)问题，可以利用几何图形求解，也可以把所求线段长表示为关于圆心与直线上的点的距离的函数的形式，利用求函数值域的方法求解．【巩固迁移】5．(2023·河南开封模拟)已知圆M 过点A (1，3)，B (1，－1)，C (－3，1)，则圆M 在点A 处的切线方程为()A ．3x ＋4y －15＝0B ．3x －4y ＋9＝0C ．4x ＋3y －13＝0D ．4x －3y ＋5＝0答案A解析设圆M 的一般方程为x 2＋y 2＋Dx ＋Ey ＋F ＝0.＋3E ＋F ＋10＝0，－E ＋F ＋2＝0，3D ＋E ＋F ＋10＝0，＝1，＝－2，＝－5，所以圆M 的方程为x 2＋y 2＋x －2y －5＝0，圆心为－12，所以直线AM的斜率k AM ＝3－11＋12＝43，所以圆M 在点A 处的切线方程为y －3＝－34(x －1)，即3x ＋4y －15＝0.故选A.6．(2023·新课标Ⅰ卷)过点(0，－2)与圆x 2＋y 2－4x －1＝0相切的两条直线的夹角为α，则sin α＝()A ．1B ．154C ．104D ．64答案B解析解法一：因为x 2＋y 2－4x －1＝0，即(x －2)2＋y 2＝5，可得圆心C (2，0)，半径r ＝5，过点P (0，－2)作圆C 的切线，切点为A ，B ，因为|PC |＝22＋（－2）2＝22，则|PA |＝|PC |2－r 2＝3，可得sin ∠APC ＝522＝104，cos ∠APC ＝322＝64，则sin ∠APB ＝sin2∠APC ＝2sin ∠APC cos ∠APC ＝2×104×64＝154，cos ∠APB ＝cos2∠APC ＝cos 2∠APC －sin 2∠APC ＝＝－14<0，即∠APB 为钝角，所以sin α＝sin(π－∠APB )＝sin ∠APB ＝154.故选B.解法二：圆x 2＋y 2－4x －1＝0的圆心C (2，0)，半径r ＝5，过点P (0，－2)作圆C 的切线，切点为A ，B ，连接AB ，可得|PC |＝22＋（－2）2＝22，则|PA |＝|PB |＝|PC |2－r 2＝3，因为|PA |2＋|PB |2－2|PA |·|PB |cos ∠APB ＝|CA |2＋|CB |2－2|CA |·|CB |cos ∠ACB ，且∠ACB ＝π－∠APB ，则3＋3－6cos ∠APB ＝5＋5－10cos(π－∠APB )，即3－3cos ∠APB ＝5＋5cos ∠APB ，解得cos ∠APB ＝－14<0，即∠APB 为钝角，则cos α＝cos(π－∠APB )＝－cos ∠APB ＝14，又α为锐角，所以sinα＝1－cos2α＝154.故选B.解法三：圆x2＋y2－4x－1＝0的圆心C(2，0)，半径r＝5，若切线斜率不存在，则切线方程为x＝0，则圆心到切线的距离d＝2<r，不符合题意；若切线斜率存在，设切线方程为y＝kx－2，即kx－y－2＝0，则|2k－2|k2＋1＝5，整理得k2＋8k＋1＝0，且Δ＝64－4＝60>0.设两切线斜率分别为k1，k2，则k1＋k2＝－8，k1k2＝1，可得|k1－k2|＝（k1＋k2）2－4k1k2＝215，所以tanα＝|k1－k2|1＋k1k2＝15，即sinαcosα＝15，可得cosα＝sinα15，则sin2α＋cos2α＝sin2α＋sin2α15＝1，又α则sinα>0，解得sinα＝154.故选B.7．(2024·陕西西安碑林区校级月考)已知圆M：(x－x0)2＋(y－y0)2＝8，点T(－3，4)，从坐标原点O向圆M作两条切线OP，OQ，切点分别为P，Q，若切线OP，OQ的斜率分别为k1，k2，k1·k2＝－1，则|TM|的取值范围为________．答案[1，9]解析由题意可知，直线OP的方程为y＝k1x，直线OQ的方程为y＝k2x，∵OP，OQ与圆M相切，∴|k1x0－y0|1＋k21＝22，|k2x0－y0|1＋k22＝22，分别对两个式子进行两边平方，整理可得21（8－x20）＋2k1x0y0＋8－y20＝0，22（8－x20）＋2k2x0y0＋8－y20＝0，∴k1，k2是方程k2(8－x20)＋2kx0y0＋8－y20＝0的两个不相等的实数根，易知8－x20≠0，∴k1·k2＝8－y208－x20，又k1·k2＝－1，∴8－y208－x20＝－1，即x20＋y20＝16，则圆心M的轨迹是以(0，0)为圆心，4为半径的圆．又|TO|＝9＋16＝5，∴|TO|－4≤|TM|≤|TO|＋4，∴1≤|TM|≤9.考点三圆与圆的位置关系例4(1)(2024·广东揭阳期末)圆O1：x2＋y2＝1与圆O2：x2＋y2－4x＋1＝0的位置关系为() A．相交B．相离C．外切D．内切答案A解析圆O1：x2＋y2＝1的圆心为O1(0，0)，半径为r1＝1.圆O2：x2＋y2－4x＋1＝0的圆心为O2(2，0)，半径为r2＝3.|O1O2|＝2，r2－r1<|O1O2|<r2＋r1，所以两圆相交．故选A.(2)(多选)(2023·吉林期中)点P在圆C1：x2＋y2＝1上，点Q在圆C2：x2＋y2－6x＋8y＋24＝0上，则()A．|PQ|的最小值为0B．|PQ|的最大值为7C ．两个圆心所在直线的斜率为－43D ．两个圆相交弦所在直线的方程为6x －8y －25＝0答案BC解析根据题意，圆C 1：x 2＋y 2＝1，其圆心C 1(0，0)，半径R ＝1，圆C 2：x 2＋y 2－6x ＋8y ＋24＝0，即(x －3)2＋(y ＋4)2＝1，其圆心C 2(3，－4)，半径r ＝1，圆心距|C 1C 2|＝9＋16＝5，则|PO |的最小值为|C 1C 2|－R －r ＝3，最大值为|C 1C 2|＋R ＋r ＝7，故A 错误，B 正确；对于C ，圆心C 1(0，0)，圆心C 2(3，－4)，则两个圆心所在直线的斜率k ＝－4－03－0＝－43，故C 正确；对于D ，两圆的圆心距|C 1C 2|＝5，则|C 1C 2|>R ＋r ＝2，两圆外离，不存在公共弦，故D 错误．故选BC.(3)(2022·新高考Ⅰ卷)写出与圆x 2＋y 2＝1和(x －3)2＋(y －4)2＝16都相切的一条直线的方程：________．答案x ＝－1或7x －24y －25＝0或3x＋4y －5＝0解析如图，因为圆x 2＋y 2＝1的圆心为O (0，0)，半径r 1＝1，圆(x －3)2＋(y －4)2＝16的圆心为A (3，4)，半径r 2＝4，所以|OA |＝5，r 1＋r 2＝5，所以|OA |＝r 1＋r 2，所以两圆外切，公切线有三种情况：①易知公切线l 1的方程为x ＝－1.②另一条公切线l 2与公切线l 1关于过两圆圆心的直线l 对称．易知过两圆圆心的直线l 的方程为y ＝43x ，＝－1，＝43x ，＝－1，＝－43，由对称性可知公切线l21，设公切线l 2的方程为y ＋43＝k (x ＋1)，则点O (0，0)到l 2的距离为1，所以1＝|k －43|k 2＋1，解得k ＝724，所以公切线l 2的方程为y ＋43＝724(x ＋1)，即7x －24y －25＝0.③还有一条公切线l 3与直线l ：y ＝43x 垂直．设公切线l 3的方程为y ＝－34x ＋t ，易知t ＞0，则点O (0，0)到l 3的距离为1，所以1解得t ＝54，所以公切线l 3的方程为y ＝－34x ＋54，即3x ＋4y －5＝0.综上，所求直线方程为x ＝－1或7x －24y －25＝0或3x ＋4y －5＝0.【通性通法】(1)判断两圆的位置关系时常用几何法，即利用两圆圆心之间的距离与两圆半径之间的关系，一般不采用代数法．(2)若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差消去x 2，y 2项得到．【巩固迁移】8．(2024·安徽芜湖模拟)已知圆M ：x 2＋y 2－2ay ＝0(a >0)截直线x ＋y ＝0所得线段的长度是22，则圆M 与圆N ：(x －1)2＋(y －1)2＝1的位置关系是()A ．内切B ．相交C ．外切D ．相离答案B解析由题意，得圆M 的标准方程为x 2＋(y －a )2＝a 2，圆心(0，a )到直线x ＋y ＝0的距离d＝a2，所以2a 2－a 22＝22，解得a ＝2，圆M 、圆N 的圆心距|MN |＝2，小于两圆半径之和3，大于两圆半径之差1，故两圆相交．故选B.9．(2023·云南丽江期中)圆C 1：x 2＋y 2－6x －10y －2＝0与圆C 2：x 2＋y 2＋4x ＋14y ＋4＝0公切线的条数为()A ．1B ．2C ．3D ．4答案C解析根据题意，圆C 1：x 2＋y 2－6x －10y －2＝0，即(x －3)2＋(y －5)2＝36，其圆心为(3，5)，半径r ＝6；圆C 2：x 2＋y 2＋4x ＋14y ＋4＝0，即(x ＋2)2＋(y ＋7)2＝49，其圆心为(－2，－7)，半径R ＝7，两圆的圆心距|C 1C 2|＝（－2－3）2＋（－7－5）2＝13＝R ＋r ，所以两圆相外切，其公切线有3条．故选C.10．(2024·江苏启东中学阶段考试)已知P 是圆M ：x 2－4x ＋y 2－4y ＋6＝0上一动点，A ，B 是圆C ：x 2＋2x ＋y 2＋2y －2＝0上的两点，若|AB |＝23，则|PA →＋PB →|的取值范围为________．答案[42－2，82＋2]解析由题意知，点P 所在圆M ：(x －2)2＋(y －2)2＝2，且A ，B 所在圆C ：(x ＋1)2＋(y ＋1)2＝4的圆心为C (－1，－1)，半径为2.设D 是AB 的中点，连接CD ，则CD 垂直平分AB ，则|CD |1，所以点D 在以C 为圆心，1为半径的圆上，即点D 所在圆C 1：(x＋1)2＋(y ＋1)2＝1，又由PA →＋PB →＝2PD →，可得|PA →＋PB →|＝2|PD →|，|PD →|即为圆M ：x 2－4x ＋y 2－4y ＋6＝0上的点与圆C 1：(x ＋1)2＋(y ＋1)2＝1上的点的距离，因为|MC 1|＝（2＋1）2＋（2＋1）2＝32，所以32－1－2≤|PD →|≤32＋1＋2，即|PA →＋PB →|的取值范围为[42－2，82＋2]．课时作业一、单项选择题1．(2023·福建泉州模拟)已知圆C ：x 2＋y 2＋2x －4y ＝0，直线l ：2x －y －1＝0，则直线l 与圆C 的位置关系是()A ．相交B ．相切C ．相离D ．相交且直线过圆C 的圆心答案B解析由x 2＋y 2＋2x －4y ＝0，可得(x ＋1)2＋(y －2)2＝5，故圆心C (－1，2)，半径r ＝5，则圆心到直线l ：2x －y －1＝0的距离d ＝|－2－2－1|22＋1＝55＝5＝r ，故直线l 与圆C 相切．故选B.2．(2024·黑龙江大庆质检)若直线kx －y ＋1－2k ＝0与圆C ：(x －1)2＋y 2＝4相交于A ，B 两点，则|AB |的最小值为()A ．23B ．22C ．3D ．2答案B解析直线kx －y ＋1－2k ＝0，即k (x －2)－(y －1)＝0恒过定点M (2，1)，而(2－1)2＋12＝2<4，即点M 在圆C 内，因此当且仅当AB ⊥CM 时，|AB |最小，而圆C 的圆心C (1，0)，半径r ＝2，|CM |＝2，所以|AB |min ＝2r 2－|CM |2＝24－2＝2 2.故选B.3．(2023·河北联考一模)直线l ：ax ＋by －4＝0与圆O ：x 2＋y 2＝4相切，则(a －3)2＋(b －4)2的最大值为()A ．16B ．25C ．49D ．81答案C解析由直线l 与圆O 相切可得，圆心O (0，0)到直线l 的距离等于圆的半径，即|－4|a 2＋b 2＝2，故a 2＋b 2＝4，即点(a ，b )在圆O 上，(a －3)2＋(b －4)2的几何意义为圆上的点(a ，b )与点(3，4)之间距离的平方，由a 2＋b 2＝4，得圆心为(0，0)，因为32＋42>4，所以点(3，4)在圆a 2＋b 2＝4外，所以点(a ，b )到点(3，4)的距离的最大值为圆心到(3，4)的距离与圆半径之和，即d ＋r ＝（3－0）2＋（4－0）2＋2＝7，所以(a －3)2＋(b －4)2的最大值为72＝49.故选C.4．(2023·广东汕头模拟)已知圆C 1：(x －3)2＋(y ＋4)2＝1与C 2：(x －a )2＋(y －a ＋3)2＝9恰好有4条公切线，则实数a 的取值范围是()A ．(－∞，0)∪(4，＋∞)B ．(－∞，1－6)∪(1＋6，＋∞)C ．(0，4)D ．(－∞，－1)∪(3，＋∞)答案D解析因为圆C 1：(x －3)2＋(y ＋4)2＝1与C 2：(x －a )2＋(y －a ＋3)2＝9恰好有4条公切线，所以圆C 1与C 2外离，所以（a －3）2＋（a －3＋4）2>4，解得a >3或a <－1，即实数a 的取值范围是(－∞，－1)∪(3，＋∞)．故选D.5．(2023·山东青岛模拟)已知直线l ：3x ＋my ＋3＝0，曲线C ：x 2＋y 2＋4x ＋2my ＋5＝0，则下列说法正确的是()A ．“m >1”是“曲线C 表示圆”的充要条件B ．当m ＝33时，直线l 与曲线C 表示的圆相交所得的弦长为1C ．“m ＝－3”是“直线l 与曲线C 表示的圆相切”的充分不必要条件D ．当m ＝－2时，曲线C 与圆x 2＋y 2＝1有两个公共点答案C解析对于A ，曲线C ：x 2＋y 2＋4x ＋2my ＋5＝0⇒(x ＋2)2＋(y ＋m )2＝m 2－1，曲线C 表示圆，则m 2－1>0，解得m <－1或m >1，所以“m >1”是“曲线C 表示圆”的充分不必要条件，A 错误；对于B ，当m ＝33时，直线l ：x ＋3y ＋1＝0，曲线C ：(x ＋2)2＋(y ＋33)2＝26，圆心到直线l 的距离d ＝|－2＋3×（－33）＋1|1＋3＝5，所以弦长为2r 2－d 2＝226－25＝2，B 错误；对于C ，若直线l 与圆相切，则圆心到直线l 的距离d ＝|－6－m 2＋3|9＋m 2＝m 2－1，解得m ＝±3，所以“m ＝－3”是“直线l 与曲线C 表示的圆相切”的充分不必要条件，C 正确；对于D ，当m ＝－2时，曲线C ：(x ＋2)2＋(y －2)2＝3，其圆心坐标为(－2，2)，r ＝3，曲线C 与圆x 2＋y 2＝1的圆心距为（－2－0）2＋（2－0）2＝22>3＋1，故两圆相离，没有公共点，D 错误．故选C.6．(2024·山东淄博期末)已知圆C ：(x －1)2＋y 2＝2，直线l ：y ＝kx －2，若直线l 上存在点P ，过点P 引圆的两条切线l 1，l 2，使得l 1⊥l 2，则实数k 的取值范围是()A ∞，－43∪[0，＋∞)B ∞，－43∪[0，1)C ∞，－43∪[1，＋∞)D ．－43，1答案A解析圆心C (1，0)，半径r ＝2，设P (x ，y )，因为两切线l 1⊥l 2，如图，设切点为A ，B ，则PA ⊥PB ，由切线性质定理，知PA ⊥AC ，PB ⊥BC ，|PA |＝|PB |，所以四边形PACB 为正方形，所以|PC |＝2，则点P 的轨迹是以(1，0)为圆心，2为半径的圆，方程为(x －1)2＋y 2＝4，直线l ：y ＝kx －2过定点(0，－2)，直线方程即kx －y －2＝0，只要直线与点P 的轨迹(圆)有交点即可，即大圆的圆心到直线的距离小于等于半径，即d ＝|k －2|k 2＋1≤2，解得k ≥0或k ≤－43，即实数k ∞，－43∪[0，＋∞)．故选A.7．已知实数x ，y 满足x 2＋y 2－4x －2y －4＝0，则x －y 的最大值是()A ．1＋322B ．4C ．1＋32D ．7答案C解析解法一：令x －y ＝k ，则x ＝k ＋y ，代入原式，化简得2y 2＋(2k －6)y ＋k 2－4k －4＝0，因为存在实数y ，则Δ≥0，即(2k －6)2－4×2(k 2－4k －4)≥0，化简得k 2－2k －17≤0，解得1－32≤k ≤1＋32，故x －y 的最大值是32＋1.故选C.解法二：x 2＋y 2－4x －2y －4＝0，整理得(x －2)2＋(y －1)2＝9，令x ＝3cos θ＋2，y ＝3sin θ＋1，其中θ∈[0，2π]，则x －y ＝3cos θ－3sin θ＋1＝32cos 1，因为θ∈[0，2π]，所以θ＋π4∈π4，9π4，则当θ＋π4＝2π，即θ＝7π4时，x －y 取得最大值32＋1.故选C.解法三：由x 2＋y 2－4x －2y －4＝0，可得(x －2)2＋(y －1)2＝9，设x －y ＝k ，则圆心到直线x －y ＝k 的距离d ＝|2－1－k |2≤3，解得1－32≤k ≤1＋3 2.故选C.8．(2023·甘肃酒泉三模)若直线3x －y －3＝0分别与x 轴、y 轴交于点A ，B ，动点P 在圆x 2＋(y －1)2＝1上，则△ABP 面积的取值范围是()A ．[2，32]B ．[3，23]C ．[3，33]D ．[22，32]答案C解析如图所示，因为直线3x －y －3＝0与坐标轴的交点A (3，0)，B (0，－3)，则|AB |＝3＋9＝23，圆x 2＋(y －1)2＝1的圆心为C (0，1)，半径为r ＝1，则圆心C (0，1)到直线3x －y －3＝0的距离为d ＝|－1－3|3＋1＝2，所以圆x 2＋(y －1)2＝1上的点P 到直线3x －y －3＝0的距离的最小值为d －r ＝2－1＝1，最大距离为d ＋r ＝2＋1＝3，所以△ABP 面积的最小值为12×23×1＝3，最大值为12×23×3＝33，即△ABP 面积的取值范围为[3，33]．故选C.二、多项选择题9．(2024·湖北武汉期末)已知圆x2＋y2＝4，直线l：y＝x＋b.若圆上恰有三个点到直线l的距离都等于1，则b的可能值为()A．－1B．－2C．1D．2答案BD解析由圆x2＋y2＝4，可得圆心为(0，0)，半径为2，要使圆上恰有三个点到直线l的距离都等于1，则圆心到直线的距离为1，所以|b|2＝2－1，所以b＝± 2.故选BD.10．已知圆O1：x2＋y2－2x－3＝0和圆O2：x2＋y2－2y－1＝0的交点为A，B，则() A．圆O1和圆O2有两条公切线B．直线AB的方程为x－y＋1＝0C．圆O2上存在两点P和Q使得|PQ|>|AB|D．圆O1上的点到直线AB的最大距离为2＋2答案ABD解析对于A，因为两圆相交，所以有两条公切线，故A正确；对于B，将两圆方程作差可得－2x＋2y－2＝0，即得公共弦AB的方程为x－y＋1＝0，故B正确；对于C，直线AB过圆O2的圆心(0，1)，所以线段AB是圆O2的直径，故圆O2中不存在比AB长的弦，故C错误；对于D，圆O1的圆心坐标为(1，0)，半径为2，圆心到直线AB：x－y＋1＝0的距离为|1＋1| 2＝2，所以圆O1上的点到直线AB的最大距离为2＋2，D正确．故选ABD.三、填空题11．(2023·广东深圳校考二模)过点(1，1)且被圆x2＋y2－4x－4y＋4＝0所截得的弦长为22的直线方程为________．答案x＋y－2＝0解析圆x2＋y2－4x－4y＋4＝0，即(x－2)2＋(y－2)2＝4，圆心为(2，2)，半径r＝2，若弦长l＝22，则圆心到直线的距离d＝2，显然直线的斜率存在，设直线方程为y－1＝k(x－1)，即kx－y－k＋1＝0，所以d＝|2k－2－k＋1|k2＋（－1）2＝2，解得k＝－1，所以直线方程为x＋y－2＝0.12．若A为圆C1：x2＋y2＝1上的动点，B为圆C2：(x－3)2＋(y＋4)2＝4上的动点，则线段AB长度的最大值是________．答案8解析圆C1：x2＋y2＝1的圆心为C1(0，0)，半径r1＝1，圆C2：(x－3)2＋(y＋4)2＝4的圆心为C2(3，－4)，半径r2＝2，所以|C1C2|＝5.因为|C1C2|>r1＋r2，所以圆C1与圆C2外离．又A 为圆C1上的动点，B为圆C2上的动点，所以线段AB长度的最大值是|C1C2|＋r1＋r2＝5＋1＋2＝8.13．(2024·浙江校考模拟预测)已知圆C1：x2＋y2＝4和圆C2：(x－3)2＋(y－2)2＝1，则过点MC1，C2都相切的直线方程为________(写出一个即可)．答案x＝2或5x＋12y－26＝0(写出一个即可)解析若过M的切线斜率不存在，即为x＝2，此时显然与两圆都相切；若过M的切线斜率存在，不妨设为y－43＝k(x－2)，则C1(0，0)，C2(3，2)到y－43＝k(x－2)的距离分别为d1＝|2k－43|k2＋1＝2，d2＝|k－23|k2＋1＝1，解得k＝－512，即y－43＝－512(x－2)，即5x＋12y－26＝0.综上，过M且与两圆都相切的直线方程为x＝2或5x＋12y－26＝0(写出一个即可)．14．(2024·云南大理一模)已知圆C：x2＋y2－2x－4y＋1＝0，过点A(1，1)的相互垂直的两条直线分别交圆C于点M，N和P，Q，则四边形MQNP面积的最大值为________．答案7解析圆C：x2＋y2－2x－4y＋1＝0，即(x－1)2＋(y－2)2＝4，点A(1，1)在圆C内部，设圆心C到直线PQ和MN的距离分别为d1，d2，则有|PQ|＝24－d21，|MN|＝24－d22，且d21＋d22＝|CA|2＝1，所以四边形MQNP的面积S＝12|PQ|·|MN|＝24－d21·4－d22≤7，当且仅当d1＝d2＝22时，等号成立，故四边形MQNP面积的最大值为7.四、解答题15．(2024·辽宁大连月考)已知圆C：(x－2)2＋(y－3)2＝4外有一点P(4，－1)，过点P作直线l.(1)当直线l与圆C相切时，求直线l的方程；(2)当直线l的倾斜角为135°时，求直线l被圆C所截得的弦长．解(1)由题意知，圆C的圆心为(2，3)，半径r＝2.当斜率不存在时，直线l的方程为x＝4，此时圆C与直线l相切；当斜率存在时，设直线l的方程为y＋1＝k(x－4)，即kx－y－4k－1＝0，则圆心到直线的距离为d＝r，即|2k－3－4k－1|1＋k2＝2，解得k＝－34，所以此时直线l的方程为3x＋4y－8＝0.综上，直线l的方程为x＝4或3x＋4y－8＝0.(2)当直线l 的倾斜角为135°时，直线l 的方程为x ＋y －3＝0，圆心到直线l 的距离d ＝|2＋3－3|2＝ 2.故所求弦长为2r 2－d 2＝222－（2）2＝2 2.16．已知点P (2，2)，圆C ：x 2＋y 2－8y ＝0，过点P 的动直线l 与圆C 交于A ，B 两点，线段AB 的中点为M ，O 为坐标原点．(1)求点M 的轨迹方程；(2)当|OP |＝|OM |时，求直线l 的方程及△POM 的面积．解(1)圆C 的方程可化为x 2＋(y －4)2＝16，所以圆心为C (0，4)，半径为4.设M (x ，y )，则CM →＝(x ，y －4)，MP →＝(2－x ，2－y )．由题意，得CM →·MP →＝0，故x (2－x )＋(y －4)(2－y )＝0，即(x －1)2＋(y －3)2＝2.所以点M 的轨迹方程是(x －1)2＋(y －3)2＝2.(2)由(1)可知点M 的轨迹是以点N (1，3)为圆心，2为半径的圆．由于|OP |＝|OM |，故O 在线段PM 的垂直平分线上，又P 在圆N 上，从而ON ⊥PM .因为ON 的斜率为3，所以直线l 的斜率为－13，故直线l 的方程为x ＋3y －8＝0.又|OM |＝|OP |＝22，O 到直线l 的距离为|－8|12＋32＝4105，所以|PM |＝2＝4105，所以S △POM ＝12×4105×4105＝165.17．(多选)(2023·重庆一中模拟)已知⊙E ：(x －2)2＋(y －1)2＝4，过点P (5，5)作圆E 的两条切线，切点分别为M ，N ，则下列命题中正确的是()A ．|PM |＝21B ．直线MN 的方程为3x ＋4y －14＝0C ．圆x 2＋y 2＝1与圆E 共有4条公切线D ．若过点P 的直线与圆E 交于G ，H 两点，则当△EHG 的面积最大时，|GH |＝22答案ABD解析因为圆E 的方程为(x －2)2＋(y －1)2＝4，所以圆心E 的坐标为(2，1)，半径为2，所以|EM |＝|EN |＝2，又P (5，5)，所以|PE |＝（5－2）2＋（5－1）2＝5，由已知得PM ⊥ME ，PN ⊥NE ，所以|PM |＝|PE |2－|EM |2＝21，A 正确；因为PM ⊥ME ，PN ⊥NE ，所以P ，M ，E ，N 四点共圆，且圆心为PE 的中点，线段PE 的中点坐标为所以圆F ＋(y －3)2＝254，即x 2－7x ＋y 2－6y ＋15＝0，因为52－2<|EF |＝52<52＋2，所以圆E 与圆F 相交，又圆E 的方程可化为x 2－4x ＋y 2－2y ＋1＝0，所以圆E 与圆F 的公共弦方程为3x ＋4y －14＝0，故直线MN 的方程为3x ＋4y －14＝0，B 正确；圆x 2＋y 2＝1的圆心O 的坐标为(0，0)，半径为1，因为|OE |＝5，2－1<|OE |<1＋2，所以圆x 2＋y 2＝1与圆E 相交，故两圆只有2条公切线，C 错误；设∠HEG ＝θ，则θ∈(0，π)，△EHG 的面积S ＝12EH ·EG sin θ＝2sin θ，所以当θ＝π2时，△EHG 的面积取最大值2，此时|GH |＝4＋4＝22，D 正确．故选ABD.18．(2023·福建龙岩统考二模)已知M 是圆C ：x 2＋y 2＝2上一个动点，且直线l 1：m (x －3)－n (y －2)＝0与直线l 2：n (x －2)＋m (y －3)＝0(m ，n ∈R ，m 2＋n 2≠0)相交于点P ，则|PM |的最小值是____________．答案2解析由两直线方程可知，l 1，l 2分别过定点A (3，2)，B (2，3)，且两直线互相垂直，设AB的中点为O ，则如图所示，则两直线的交点P 的轨迹为以O 为圆心，AB 为直径的圆O ，|AB |＝2，|OC |＝522，可知两圆相离，设直线OC 交圆C 于点E ，交圆O 于点D ，显然|PM |≥|ED |＝|OC |－|CE |－|OD |＝522－2－22＝ 2.。

第48讲、直线、平面平行的判定与性质(教师版)2025高考数学一轮复习讲义

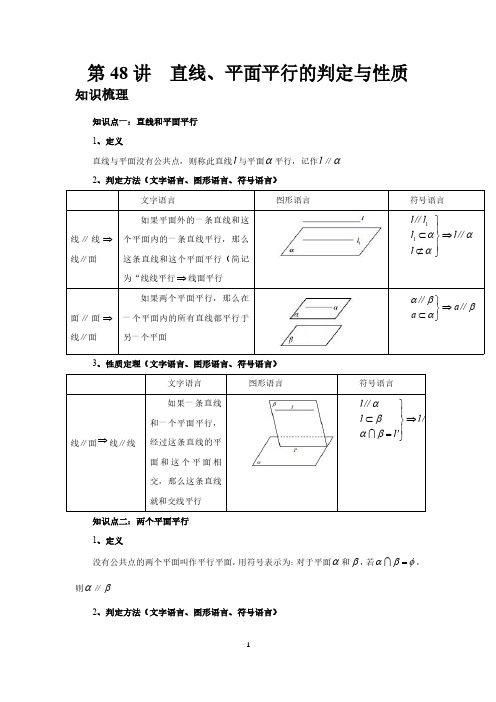
第48讲直线、平面平行的判定与性质知识梳理知识点一：直线和平面平行1、定义直线与平面没有公共点，则称此直线l 与平面α平行，记作l ∥α2、判定方法（文字语言、图形语言、符号语言）文字语言图形语言符号语言线∥线⇒线∥面如果平面外的一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行（简记为“线线平行⇒线面平行11l l ll l ααα⎫⎪⊂⇒⎬⎪⊄⎭∥∥面∥面⇒线∥面如果两个平面平行，那么在一个平面内的所有直线都平行于另一个平面a a αββα⎫⇒⎬⊂⎭∥∥3、性质定理（文字语言、图形语言、符号语言）文字语言图形语言符号语言线∥面⇒线∥线如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行l l l l l αβαβ⎫⎪'⊂⇒⎬⎪'=⎭∥∥知识点二：两个平面平行1、定义没有公共点的两个平面叫作平行平面，用符号表示为：对于平面α和β，若αβφ= ，则α∥β2、判定方法（文字语言、图形语言、符号语言）文字语言图形语言符号语言判定定理线∥面⇒面∥面如果一个平面内有两条相交的直线都平行于另一个平面，那么这两个平面平行（简记为“线面平行⇒面面平行,,a b a b Pαα⊂⊂= a b ββαβ⇒∥，∥∥线⊥面⇒面∥面如果两个平面同垂直于一条直线，那么这两个平面平行l l ααβ⊥⎫⇒⎬⊥⎭∥β3、性质定理（文字语言、图形语言、符号语言）文字语言图形语言符号语言面//面⇒线//面如果两个平面平行，那么在一个平面中的所有直线都平行于另外一个平面////a a αββα⎫⇒⎬⊂⎭性质定理如果两个平行平面同时和第三个平面相交，那么他们的交线平行（简记为“面面平行⇒线面平行”）////.a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭面//面⇒线⊥面如果两个平面中有一个垂直于一条直线，那么另一个平面也垂直于这条直线//l l αββα⎫⇒⊥⎬⊥⎭【解题方法总结】线线平行、线面平行、面面平行的转换如图所示．性质性质性质判定判定判定线∥面线∥线面∥面（1）证明直线与平面平行的常用方法：①利用定义，证明直线a与平面α没有公共点，一般结合反证法证明；②利用线面平行的判定定理，即线线平行⇒线面平行．辅助线的作法为：平面外直线的端点进平面，同向进面，得平行四边形的对边，不同向进面，延长交于一点得平行于第三边的线段；③利用面面平行的性质定理，把面面平行转化成线面平行；（2）证明面面平行的常用方法：①利用面面平行的定义，此法一般与反证法结合；②利用面面平行的判定定理；③利用两个平面垂直于同一条直线；④证明两个平面同时平行于第三个平面．（3）证明线线平行的常用方法：①利用直线和平面平行的判定定理；②利用平行公理；必考题型全归纳题型一：平行的判定例1．（2024·湖南岳阳·高三湖南省岳阳县第一中学校考开学考试）若α、β是两个不重合的平面，①若α内的两条相交直线分别平行于β内的两条直线，则//αβ；②设α、β相交于直线l，若α内有一条直线垂直于l，则α⊥β；③若α外一条直线l与α内的一条直线平行，则//lα；以上说法中成立的有（）个．A．0B．1C．2D．3【答案】C【解析】对于①，设12,l l ⊂平面α，且12l l A ⋂=，由直线与平面平行的判定定理可知1//l β，2//l β，再由平面与平面平行的判定定理可知//αβ，则①正确；对于②，设α、β交于直线l ，若α内有一条直线垂直于l ，则α、β可能垂直也可能不垂直，则②错误；对于③，由直线与平面平行的判定定理可知//l α，则③正确，故选：C ．例2．（2024·全国·高三对口高考）过直线l 外两点作与l 平行的平面，那么这样的平面（）A ．不存在B ．只有一个C ．有无数个D ．不能确定【答案】D【解析】过直线l 外两点作与l 平行的平面，如果两点所在的直线与已知直线相交，则这样的平面不存在；如果两点所在的直线与已知直线平行，则这样的平面有无数个；如果两点所在的直线与已知直线异面，则这样的平面只有一个．因此只有D 正确．故选：D ．例3．（2024·福建泉州·校联考模拟预测）如图，点A ，B ，C ，M ，N 为正方体的顶点或所在棱的中点，则下列各图中，不满足直线//MN 平面ABC 的是（）A ．B ．C．D．【答案】DMN EF AC，MN⊄平面ABC，AC⊂平面ABC，【解析】对于A，由正方体的性质可得////MN平面ABC，能满足；所以直线//MN AD，MN⊄平面ABC，AD⊂对于B，作出完整的截面ADBCEF，由正方体的性质可得//MN平面ABC，能满足；平面ABC，所以直线//MN，MN⊄平面ABC，BD⊂对于C，作出完整的截面ABCD，由正方体的性质可得//BD平面ABC，MN平面ABC，能满足；所以直线//对于D ，作出完整的截面，如下图ABNMHC ，可得MN 在平面ABC 内，不能得出平行，不能满足．故选：D ．变式1．（2024·湖南岳阳·高三湖南省岳阳县第一中学校考开学考试）a ，b ，c 为三条不重合的直线，α，β，γ为三个不重合的平面，现给出下面六个命题：①a c ∥，b c ∥，则a b ∥；②若a γ∥，b γ∥，则a b ∥；③c α∥，c β∥，则αβ∥；④若αγ∥，βγ∥，则αβ∥；⑤若c α∥，a c ∥，则a αP ；⑥若a γ∥，αγ∥，则a αP ．其中真命题的个数是（）A ．4B ．3C ．2D ．1【答案】C【解析】a ，b ，c 为三条不重合的直线，α，β，γ为三个不重合的平面，①a c ∥，b c ∥，则a b ∥，满足直线与直线平行的传递性，所以①正确；②a γ∥，b γ∥，则a ，b 可能平行，可能相交，也可能异面，所以②不正确；③c α∥，c β∥，则α，β可能平行，也可能相交，所以③不正确；④αγ∥，βγ∥，则αβ∥，满足平面与平面平行的性质，所以④正确；⑤c α∥，a c ∥，则a αP 或a α⊂，所以⑤不正确；⑥a γ∥，αγ∥，则a αP 或a α⊂，所以⑥不正确；故选：C ．变式2．（2024·全国·高三专题练习）设α，β为两个不同的平面，则α∥β的一个充分条件是（）A ．α内有无数条直线与β平行B ．α，β垂直于同一个平面C ．α，β平行于同一条直线D ．α，β垂直于同一条直线【答案】D【解析】对于A ：α内有无数条直线与β平行推不出α∥β，只有α内所有直线与β平行才能推出，故A 错误；对于B ：α，β垂直于同一平面，得到α∥β或α与β相交，故B 错误；对于C ：α，β平行于同一条直线，得到α∥β或α与β相交，故C 错误；对于D ：因为垂直与同一条直线的两平面平行，故α，β垂直于同一条直线可得α∥β，故：D 正确．故选：D【解题方法总结】排除法：画一个正方体，在正方体内部或表面找线或面进行排除．题型二：线面平行构造之三角形中位线法例4．（2024·广东河源·高三校联考开学考试）如图，在四棱锥P ABCD -中，,E F 分别为,PD PB 的中点，连接EF ．（1）当G 为PC 上不与点,P C 重合的一点时，证明：//EF 平面BDG ；【解析】（1）因为,E F 分别为,PD PB 的中点，所以EF BD ∥，因为EF ⊄平面BDG ，BD ⊂平面BDG ，所以EF //平面BDG ．例5．（2024·贵州毕节·校考模拟预测）如图，在三棱柱111ABC A B C -中，侧面11ACC A 是矩形，AC AB ⊥，12,(2)AB AA AC t t ===>，1120A AB ∠=︒,E F 分别为棱11,A B BC 的中点，G 为线段CF 的中点．（1）证明：1//A G 平面AEF ．（2）若三棱锥A GEF -的体积为1，求t ．【解析】（1）连接1A B ，交AE 于点O ，连接OF ，由题意，四边形11ABB A 为平行四边形，所以11AB A B =，因为E 为11A B 中点，∴112A E AB =，∴1AOE 与BOA △相似，且相似比为12，∴112A O OB =，又∵F ，G 为BC ，CF 中点，∴12GF BF =，所以1//OF AG ，又OF ⊂平面AEF ，1AG ⊄平面AEF ，所以1//A G 平面AEF ．（2）由A GEF G AEFV V --=由（1）1//A G 平面AEF ，则点1A 与G 到平面AEF 的距离相等．所以11A GEF G AEF A AEF F AA E V V V V ----===，由侧面11ACC A 是矩形，则1AC AA ⊥，又AC AB ⊥，且1AA AB A = ，1AA ⊂平面11ABB A ，AB ⊂平面11ABB A ，所以AC ⊥平面11ABB A ，F 是BC 的中点，所以F 到平面11ABB A 的距离为12AC ，又1120A AB ∠=︒，则1160B A A ∠=︒，所以11111111121sin 601223232F AA E C AA E AA E V V S AC t --==⨯⋅=⨯⨯⨯⨯⨯⋅=oV ，所以t =例6．（2024·黑龙江大庆·统考二模）如图所示，在正四棱锥P ABCD -中，底面ABCD 的中心为O ，PD 边上的垂线BE 交线段PO 于点F ，2PF FO =．（1）证明：EO //平面PBC ；【解析】（1）证明：如图，延长FO 至点M ，使FO OM =，连接MD ，∵底面ABCD 的中心为O ，∴PO ⊥平面ABCD ，∴PO BD ⊥，∵BO OD =，FOB DOM ∠=∠，∴FOB DOM ≌，∴FBO MDO ∠=∠，∴FB DM ∥，∴EF DM ∥，∴PF PEFM ED=而2PF FO FM ==，∴PE ED =，∴EO PB ∥，∵PB ⊂平面PBC ，EO ⊄平面PBC ，∴//EO 平面PBC ；变式3．（2024·全国·高三专题练习）如图，四棱锥P ABCD -中，四边形ABCD 为梯形，//AB CD ，AD AB ⊥，24AB AP DC ===，2PB AD ==PD =M ，N 分别是PD ，PB 的中点．（1）求证：直线//MN 平面ABCD ；【解析】（1）连接BD ， M ，N 分别是PD ，PB 的中点．∴//MN BD ，又 MN ⊄平面ABCD ，BD ⊂平面ABCD∴直线//MN 平面ABCD变式4．（2024·陕西汉中·高三统考期末）如图，在三棱柱111ABC A B C -中，1AA ⊥平面ABC ，且12AA AB BC AC ====，点E 是棱AB 的中点．（1）求证：1//BC 平面1A CE ；（2）求三棱锥11E ACC -的体积．【解析】（1）连接1AC 交1AC 于点F ，连接EF ，E 是AB 的中点，F 是1AC 的中点，∴1EF BC ∥，EF ⊂ 平面1A CE ，1BC ⊄平面1A CE ，∴1//BC 平面1A CE ；（2）过E 作EG AC ⊥于G ，1AA ⊥ 平面ABC ，EG ⊂平面ABC ，1AA EG ∴⊥，又11,AC AA A AC AA ⊂=∩，平面11AAC C ，EG ∴⊥平面11AAC C ，在等边ABC 中，E 是AB 的中点，,2EG AC AB ⊥=，2EG ∴=．所以三棱锥11E ACC -的体积为11111112233223E A CC A CC V S EG -=⋅=⨯⨯⨯⨯△．变式5．（2024·全国·高三专题练习）如图，在四棱锥P ABCD -中，四边形ABCD 是正方形，1PD AD ==，PD ⊥平面ABCD ，点E 是棱PC 的中点，点F 是棱PB 上的一点，且EF PB ⊥．（1）求证：//PA 平面EDB ；（2）求点F 到平面EDB 的距离．【解析】（1）连接AC 交BD 于G ，连接EG ，如图所示．因为四边形ABCD 是正方形，所以G 是AC 的中点，又点E 是棱PC 的中点，所以EG 是PAC △的中位线，所以//PA EG ，又PA ⊄平面EDB ，EG ⊂平面EDB ，所以//PA 平面EDB ．（2）因为PD ⊥平面ABCD ，DC ，BC ⊂平面ABCD ，所以PD DC ⊥，PD BC ⊥，又BC CD ⊥，CD PD D = ，CD ，PD ⊂平面PCD ，所以BC ⊥平面PCD ，又PC ，DE ⊂平面PCD ，所以PC BC ⊥，DE BC ⊥．在PDC △中，PD DC ⊥，1PD CD ==，E 是PC 的中点，所以2PE EC DE ===，DE PC ⊥，又DE BC ⊥，BC PC C ⋂=，BC ，PC ⊂平面PBC ，所以DE ⊥平面PBC ，所以DE 是三棱锥D BEF -的高．在PBC 中，PC BC ⊥，PC =1BC =，所以PB 所以Rt Rt BCP EFP ，所以PC BP BC PF EP EF ==，得3PC EP PF BP ⋅==，6BC EP EF BP ⋅==，BF 111133218D BEF BEF V S DE BF EF DE -=⋅=⨯⨯⋅⋅= ．在BDE △中，BD =，22DE =，2BE =，所以222BD DE BE =+，所以DE BE ⊥，所以124BDE S DE BE =⋅= ．设点F 到平面EDB 的距离为h ，所以11318F BDE BDE D BEF V S h h V --=== ，解得h =即点F 到平面EDB 变式6．（2024·新疆昌吉·高三校考学业考试）如图，在正方体1111ABCD A B C D -中，E 是棱1DD 的中点．（1）证明：1//BD 平面AEC ；（2）若正方体棱长为2，求三棱锥D AEC -的体积．【解析】（1）连接BD 交AC 于O ，连接OE ，如图，因为在正方体1111ABCD A B C D -中，底面ABCD 是正方形，则O 是BD 的中点，又E 是1DD 的中点，则OE 是1BDD 的中位线，故1//OE BD ，又OE ⊂面AEC ，1BD ⊄面AEC ，所以1//BD 平面AEC ．（2）因为正方体1111ABCD A B C D -中，AD ⊥平面11DCC D ，所以111112122332323D AEC A DEC DEC V V S AD DE CD AD --==⋅=⨯⨯⨯⨯=⨯⨯⨯⨯= ．【解题方法总结】（1）初学者可以拿一把直尺放在PB 位置（与PB 平齐），如图一；（2）然后把直尺平行往平面ACE 方向移动，直到直尺第一次落在平面ACE 内停止，如图二；（3）此时刚好经过点E （这里熟练后可以直接凭数感直接找到点E ），此时直尺所在的位置就是我们要找的平行线，直尺与AC 相交于点F ，连接EF ，如图三；（4）此时PB EF 、长度有长有短，连接PB EF 、并延长刚好交于一点D ，刚好构成A 型模型（E 为PD 中点，则F 也为BD 中点，若E 为等分点，则F 也为BD 对应等分点），PB EF ∥，如图四．图一图二图三图四题型三：线面平行构造之平行四边形法例7．（2024·天津滨海新·高三校考期中）如图，四棱锥P ABCD -的底面是菱形，平面PAD ⊥底面ABCD ，E ，F 分别是AB ，PC 的中点，6AB =，5DP AP ==，60BAD ∠=︒．（1）求证：//EF 平面PAD ；【解析】（1）证明：取PD 中点G ，连接,AG FG ，因为,F G 分别是,PC PD 的中点，所以1,2FG CD FG CD =∥，又因为底面ABCD 是菱形，E 是AB 的中点，所以1,2AE CD AE CD =∥，所以,FG AE FG AE =∥，所以四边形AEFG 是平行四边形，所以EF AG ∥，又EF ⊄平面PAD ，AG ⊂平面PAD ，所以//EF 平面PAD ．例8．（2024·全国·高三专题练习）如图，四棱台ABCD EFGH -的底面是菱形，且π3BAD ∠=，DH ⊥平面ABCD ，2EH =，3DH =，4=AD ．（1）求证：//AE 平面BDG ；（2）求三棱锥F BDG -的体积．【解析】（1）连接AC 交BD 于点O ，连接,EG GO ，几何体ABCD EFGH -为四棱台，,,,A C G E ∴四点共面，且EG ⊂平面EFGH ，AC ⊂平面ABCD ，平面//EFGH 平面ABCD ，//EG AC ∴；四边形EFGH 和ABCD 均为菱形，π3BAD ∠=，2EH =，4=AD ，12EG AC AO ∴===∴四边形AOGE 为平行四边形，//AE GO ∴，又GO ⊂平面BDG ，AE ⊄平面BDG ，//AE ∴平面BDG ．（2）连接GE 交FH 于K ，DH ⊥Q 平面ABCD ，平面//ABCD 平面EFGH ，DH ∴⊥平面EFGH ，又GE Ì平面EFGH ，GE DH ∴⊥，GE FH ⊥ ，DH FH H ⋂=，,DH FH ⊂平面BDHF ，GE ∴⊥平面BDHF ；四边形EFGH 为菱形，π3FEH BAD ∠=∠=，2EF =，GK ∴=11143332F BDG G BDF BDF V V S GK --∴==⋅=⨯⨯⨯=例9．（2024·全国·高三专题练习）如图，在正三棱柱111ABC A B C -中，1,,D D F 分别是BC ，11B C ，11A B 的中点，4BC BE =，ABC 的边长为2．（1）求证：：//EF 平面11ADD A ；【解析】（1）证明：取11A D 的中点G ，连接FG ，DG ，根据题意可得11//FG B D ，且1112FG B D =，12DE BD =，由三棱柱得性质知11//BD B D ，所以//FG BD ，则四边形DGEF 是平行四边形，所以//EF DG ，因为EF ⊄面11ADD A ，DG ⊂面11ADD A ，所以//EF 面11ADD A ．变式7．（2024·重庆沙坪坝·高三重庆南开中学校考阶段练习）如图，在三棱柱111ABC A B C -中，1AA ⊥底面ABC ，AB AC ==2BC =，1AA D 、E 分别为棱BC 、11A B 的中点，12A P PB = ，12C Q QE = ．（1）求证：//PQ 平面1C AD ；【解析】（1）证明：取11B C 中点F ，连接1A F 、FB ．因为E 是11A B 的中点，且12C Q QE = ，故Q 为111A B C △的重心，所以1A 、Q 、F 共线，且12AQ QF=，又12A P PB = ，故11AQ A P QF PB =，所以//PQ BF ，因为11//BB CC 且11BB CC =，则四边形11BB C C 为平行四边形，故11//BC B C 且11BC B C =，因为D 、F 分别为BC 、11B C 的中点，所以，1//C F BD 且1C F BD =，则四边形1FC DB 为平行四边形，所以1//BF DC ，所以1//PQ DC ，又PQ ⊄平面1C AD ，1DC ⊂平面1C AD ，所以//PQ 面1C AD ．变式8．（2024·天津红桥·高三天津市复兴中学校考阶段练习）如图所示，在四棱锥P ABCD -中，BC 平面PAD ，12BC AD =，E 是PD 的中点．（1）求证：BC AD ∥；（2）求证：CE 平面PAB ；（3）若M 是线段CE 上一动点，则线段AD 上是否存在点N ，使MN 平面PAB ？说明理由．【解析】（1）在四棱锥P ABCD -中，BC 平面PAD ，BC ⊂平面ABCD ，AD ⊂平面PAD ，平面ABCD ⋂平面PAD AD =，所以BC AD ∥；（2）如下图，取F 为AP 中点，连接,EF BF ，由E 是PD 的中点，所以EF AD ∥且12EF AD =，由（1）知BC AD ∥，又12BC AD =，所以EF BC ∥且EF BC =，所以四边形BCEF 为平行四边形，故CE BF ∥，而CE ⊂平面PAB ，BF ⊄平面PAB ，则CE 平面PAB ．（3）取AD 中点N ，连接CN ，EN ，因为E ，N 分别为PD ，AD 的中点，所以EN PA ∥，因为EN ⊄平面PAB ，PA ⊂平面PAB ，所以EN 平面PAB ，线段AD 存在点N ，使得MN 平面PAB ，理由如下：由（2）知：CE 平面PAB ，又CE EN E = ，CE ⊂平面CEN ，EN ⊂平面CEN ，所以平面CEN 平面PAB ，又M 是CE 上的动点，MN ⊂平面CEN ，所以MN 平面PAB ，所以线段AD 存在点N ，使得MN 平面PAB ．【解题方法总结】（1）初学者可以拿一把直尺放在EF 位置，如图一；（2）然后把直尺平行往平面PAB 方向移动，直到直尺第一次落在平面PAB 内停止，如图二；（3）此时刚好经过点B （这里熟练后可以直接凭数感直接找到点B ），此时直尺所在的位置就是我们要找的平行线，直尺与PA 相交于点O ，连接BO ，如图三；（4）此时PB EF 、长度相等（感官上相等即可，若感觉有长有短则考虑法一A 型的平行），连接OE ，刚好构成平行四边形BFEO 型模型（E 为PD 中点，O 也为PA 中点，OE 为三角形PAD 中位线），OB EF ∥，如图四．图一图二图三图四题型四：线面平行转化为面面平行例10．（2024·全国·高三专题练习）如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，且四边形ABCD 是正方形，E ，F ，G 分别是棱BC ，AD ，PA 的中点．（1）求证：//PE 平面BFG ；（2）若2AB =，求点C 到平面BFG 的距离．【解析】（1）连接DE ，∵ABCD 是正方形，E ，F 分别是棱BC ，AD 的中点，∴DF BE =，//DF BE ，∴四边形BEDF 是平行四边形，∴//DE BF ，∵G 是PA 的中点，∴//FG PD ，∵,PD DE ⊄平面BFG ，,FG BF ⊂平面BFG ，∴//PD 平面BFG ，//DE 平面BFG ，∵PD DE D =I ，直线,PD DE 在平面PDE 内，∴平面//PDE 平面BFG ，∵PE ⊂平面PDE ，∴//PE 平面BFG ．（2）∵PD ⊥平面ABCD ，//FG PD ，∴FG ⊥平面ABCD ，过C 在平面ABCD 内，作CM BF ⊥，垂足为M ，则FG CM ⊥，∵FG BF F =I ，又直线FG ，BF 在平面BFG 内，∴CM ⊥平面BFG ，∴CM 的长是点C 到平面BFG 的距离，∵BCF △中，FB CF =∴由等面积可得CM ==∴点C 到平面BFG例11．（2024·全国·模拟预测）如图，在多面体ABCDMP 中，四边形ABCD 是菱形，且有60DAB ∠=︒，1AB DM ==，2PB =，PB ⊥平面ABCD ，PB DM ∥．（1）求证：//AM 平面PBC ；【解析】（1）因为四边形ABCD 是菱形，所以AD BC ∥，又AD ⊂平面PBC ，BC ⊂平面PBC ，所以//AD 平面PBC ，因为PB DM ∥，PB ⊂平面PBC ，DM ⊄平面PBC ，所以//DM 平面PBC ，又因为AD MD D =I ，,AD MD ⊂平面ADM ，所以平面//ADM 平面PBC ，又AM ⊂平面AMD ，所以//AM 平面PBC ．例12．（2024·江西赣州·统考模拟预测）如图，在三棱柱111ABC A B C -中，侧面11AAC C 是矩形，侧面11BB C C 是菱形，160B BC ∠= ，D 、E 分别为棱AB 、11B C 的中点，F 为线段1C E 的中点．（1）证明：//AF 平面1A DE ；【解析】（1）证明：取11AC 的中点M ，连接AM 、EM 、FM ，因为11//AA BB 且11AA BB =，故四边形11AA B B 为平行四边形，所以，11//AB A B 且11AB A B =，因为D 为AB 的中点，则11//AD A B 且1112AD A B =，因为M 、E 分别为11AC 、11B C 的中点，所以，11//EM A B 且1112EM A B =，所以，//AD EM 且AD EM =，故四边形ADEM 为平行四边形，所以，//AM DE ，因为AM ⊄平面1A DE ，DE ⊂平面1A DE ，所以，//AM 平面1A DE ，因为M 、F 分别为11AC 、1C E 的中点，所以，1//FM A E ，因为FM ⊄平面1A DE ，1A E ⊂平面1A DE ，所以，//FM 平面1A DE ，因为⋂=AM FM M ，AM 、FM ⊂平面AFM ，所以，平面//AFM 平面1A DE ，因为AF ⊂平面AFM ，故//AF 平面1A DE ．变式9．（2024·上海·模拟预测）直四棱柱1111ABCD A B C D -，AB DC ，AB ⊥AD ，AB ＝2，AD ＝3，DC ＝4（1）求证：11//A B DCC D 面；【解析】（1）由题意得11//A A D D ，//AB CD ，1,A A AB ⊄平面1D CD ，1,D D CD ⊂平面1D CD ，∴1//A A 平面1D CD ，//AB 平面1D CD而1A A AB A = ，∴平面1//A AB 平面1D CD ，又1A B ⊂ 平面1,A AB 1//A B ∴平面1DCC D变式10．（2024·广东深圳·高三深圳外国语学校校考开学考试）如图，多面体ABCDEF 中，四边形ABCD 为矩形，二面角A CD F --的大小为45 ，//DE CF ，CD DE ⊥，2AD =，3DC =．（1）求证：//BF 平面ADE ；【解析】（1）证明：因为四边形ABCD 是矩形，所以，//BC AD ，因为BC ⊂平面BCF ，AD ⊄平面BCF ，所以//AD 平面BCF ，因为//DE CF ，CF ⊂平面BCF ，DE ⊄平面BCF ，所以//DE 平面BCF ，因为AD DE D ⋂=，AD 、DE ⊂平面ADE ，则平面//BCF 平面ADE ，因为BF ⊂平面BCF ，所以，//BF 平面ADE ．变式11．（2024·全国·高三对口高考）已知正方形ABCD 和正方形ABEF ，如图所示，N 、M 分别是对角线AE 、BD 上的点，且EN BM AN MD=．求证：//MN 平面EBC ．【解析】证明：过点N 作//NF BE 交AB 于点F ，连接FM ，因为//NF BE ，则EN BF AN AF =，又因为EN BM AN MD =，则BF BM AF DM=，所以，//FM AD ，因为四边形ABCD 为矩形，则//BC AD ，所以，//FM BC ，因为//NF BE ，NF ⊄平面BCE ，BE ⊂平面BCE ，所以，//NF 平面BCE ，因为//FM BC ，FM ⊄平面BCE ，BC ⊂平面BCE ，所以，//FM 平面BCE ，因为NF FM F = ，NF 、FM ⊂平面MNF ，所以，平面//MNF 平面BCE ，因为MN ⊂平面MNF ，所以，//MN 平面MNF ．【解题方法总结】本法原理：已知平面α∥平面β，则平面β里的任意直线均与平面α平行题型五：利用线面平行的性质证明线线平行例13．（2024·河南·高三校联考阶段练习）已知四棱锥P ABCD -，底面为菱形,ABCD PD ⊥平面ABCD ，2,,3PD AD CD BAD E π===∠=为PC 上一点．（1）平面PAD ⋂平面PBC l =，证明：BC l ∥；【解析】（1）证明：因为,BC AD BC ⊄∥平面,PAD AD ⊂平面PAD ，所以BC ∥平面PAD ，又因为平面PAD ⋂平面PBC l =，所以BC l ∥．例14．（2024·河南·高三校联考阶段练习）已知四棱锥P ABCD -，底面ABCD 为菱形，PD ⊥平面ABCD ，2PD AD CD ===，π3BAD ∠=，E 为PC 上一点．（1）平面PAD ⋂平面PBC l =，证明：//BC l ．（2）当直线BE 与平面BCD 的夹角为π6时，求三棱锥P BDE -的体积．【解析】（1）因为//,BC AD BC ⊄平面,PAD AD ⊂平面PAD ，所以BC //平面PAD ，BC ⊂平面PBC ，又因为平面PAD ⋂平面PBC l =，所以//BC l ．（2）过点E 作CD 的垂线，垂足为M ，则//PD EM ，因为PD ⊥平面ABCD ，所以EM ⊥平面BCD ，若点E 为PC 中点，则点M 为CD 的中点，此时11,,2EM PD BM CD BM ==⊥=，所以直线BE 与平面BCD 的夹角为π6EBM ∠=，即点E 为PC 中点时满足题意，因为PD ⊥平面ABCD ，所以BM ⊂平面ABCD ，所以PD BM ⊥，又因为BM CD ⊥，PD CD D ⋂=，,PD CD ⊂平面PCD ，所以BM ⊥平面PCD ，所以点B 到平面PCD 的距离为BM =故11.33P BDE B PDE V V --==⨯例15．（2024·重庆万州·统考模拟预测）如图1所示，在四边形ABCD 中，BC CD ⊥，E 为BC 上一点，22AE BE AD CD ====，CE AECD 沿AE 折起，使得BC =，得到如图2所示的四棱锥．（1）若平面BCD 平面ABE l =，证明：//CD l ；【解析】（1）在图1中，因为BC CD ⊥，CE 1CD =，所以2DE =，sin 2CDE ∠=，又π0,2CDE ⎛⎫∠∈ ⎪⎝⎭，所以π3∠=CDE ，因为2DE =，2AE AD ==，所以π3DEA ∠=，故//CD AE ，在图2中，因为//CD AE ，AE ⊂平面ABE ，CD ⊄平面ABE ，所以//CD 平面ABE ，因为CD ⊂平面BCD ，平面BCD 平面ABE l =，所以//CD l ；变式12．（2024·北京东城·高三北京市第十一中学校考阶段练习）如图所示，在直三棱柱111ABC A B C -中，AC BC ⊥，12AC BC CC ===，点D 、E 分别为棱11AC 、11B C 的中点，点F 是线段1BB 上的点（不包括两个端点）．（1）设平面DEF 与平面ABC 相交于直线m ，求证：11A B m //；【解析】（1）证明：因为点D 、E 分别为棱11AC 、11B C 的中点，则11//DE A B ，在三棱柱111ABC A B C -中，四边形11AA B B 为平行四边形，所以，11//A B AB ，则//DE AB ，因为DE ⊄平面ABC ，BC ⊂平面ABC ，所以，//DE 平面ABC ，因为DE ⊂平面DEF ，平面DEF ⋂平面ABC m =，所以，//m DE ，故11//m A B ．变式13．（2024·全国·高三专题练习）如图，四棱锥P ABCD -的底面边长为8的正方形，四条侧棱长均为点,,,G E F H 分别是棱,,,PB AB CD PC 上共面的四点，平面GEFH ⊥平面ABCD ，//BC 平面GEFH ．证明：//GH EF ．【解析】因为BC ∥平面GEFH ，BC ⊂平面PBC ，且平面PBC ⋂平面GEFH GH =，所以GH ∥BC ，因为BC ∥平面GEFH ，BC ⊂平面ABCD ，且平面ABCD ⋂平面GEFH EF =，所以EF ∥BC ，所以GH ∥EF ．变式14．（2024·江苏扬州·江苏省高邮中学校考模拟预测）如图，三棱台ABC DEF -中，2AB DE =，M 是EF 的中点，点N 在线段AB 上，4AB AN =，平面DMN ⋂平面ADFC l =．（1）证明：MN l ∥；【解析】（1）证明：取FD 的中点G ，连接GM ，AG ，因为M 是EF 的中点，所以GM DE ∥，12GM DE =，因为三棱台ABC DEF -中，DE AB ∥，12DE AB =，4AB AN =，所以GM AN ∥，GM AN =，即四边形ANMG 为平行四边形，所以MN GA ∥，因为MN ⊂平面ADFC ，GA ⊂平面ADFC ，所以//MN 平面ADFC ，因为MN ⊂平面DMN ，平面DMN ⋂平面ADFC l =，所以MN l ∥．【解题方法总结】如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行题型六：面面平行的证明例16．（2024·河南郑州·高三郑州外国语学校校考阶段练习）如图，在四棱锥P ﹣ABCD 中，平面PAD ⊥平面ABCD ，PA ＝PD ，AB ＝AD ，PA ⊥PD ，AD ⊥CD ，∠BAD ＝60°，M ，N 分别为AD ，PA 的中点．（1）证明：平面BMN∥平面PCD；【解析】（1）证明：连接BD，如图∵AB＝AD，∠BAD＝60°，∴△ABD为等边三角形，∵M为AD的中点，∴BM⊥AD，∵AD⊥CD，又CD，BM⊂平面ABCD，∴BM∥CD，又BM⊄平面PCD，CD⊂平面PCD，∴BM∥平面PCD，∵M，N分别为AD，PA的中点，∴MN∥PD，又MN⊄平面PCD，PD⊂平面PCD，∴MN∥平面PCD．又BM，MN⊂平面BMN，BM∩MN＝M，∴平面BMN∥平面PCD．例17．（2024·山东临沂·高三校考阶段练习）如图，在多面体ABCDEF 中，ABCD 是正方形，2AB =，DE BF =，//BF DE ，M 为棱AE 的中点．（1）求证：平面//BMD 平面EFC ；【解析】（1）连AC 交BD 于N ，则N 为AC 的中点，因为M 为AE 的中点，所以//MN CE ，因为MN ⊄平面EFC ，CE ⊂平面EFC ，所以//MN 平面EFC ，因为//BF DE ，BF DE =，所以四边形BDEF 是平行四边形，所以//BD EF ，因为BD ⊄平面EFC ，EF ⊂平面EFC ，所以//BD 平面EFC ，因为BD MN N = ，,BD MN ⊂平面BMD ，所以平面//BMD 平面EFC ．32．（2024·河北·统考模拟预测）在圆柱12O O 中，等腰梯形ABCD 为底面圆1O 的内接四边形，且1AD DC BC ===，矩形ABFE 是该圆柱的轴截面，CG 为圆柱的一条母线，1CG =．（1）求证：平面1O CG ∥平面ADE ；【解析】（1）在圆柱12O O 中，AE CG ∥，AE ⊄平面1O CG ，CG ⊂平面1O CG ，故AE ∥平面1O CG ；连接1DO ，因为等腰梯形ABCD 为底面圆1O 的内接四边形，1AD DC BC ===，故111π3AO D CO D BO C ∠=∠=∠=，则1AO D 为正三角形，故11π3O AD CO B ∠=∠=，则1AD O C ∥，AD ⊄平面1O CG ，1O C ⊂平面1O CG ，故AD ∥平面1O CG ；又,,AE AD A AE AD ⋂=⊂平面ADE ，故平面ADE ∥平面1O CG ．例18．（2024·甘肃定西·统考模拟预测）如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，60BAD ∠= ，AC 与BD 交于点O ，OP ⊥底面ABCD ，OP =E ，F 分别是棱PA ，PB 的中点，连接OE ，OF ，EF ．（1）求证：平面//OEF 平面PCD ；（2）求三棱锥O PEF -的体积．【解析】（1）因为底面ABCD 是菱形，AC 与BD 交于点O所以O 为AC 中点，点E 是棱PA 的中点，F 分别是棱PB 的中点，所以OE 为三角形ACP 的中位线，OF 为三角形BDP 的中位线，所以//OE PC ，//OF DP ，OE ⊄ 平面DCP ，PC ⊂平面DCP ，//OE ∴平面DCP ，OF ⊄Q 平面DCP ，DP ⊂平面DCP ，//OF ∴平面DCP ，而OE OF O ⋂=，OE ⊂平面OEF ，OF ⊂平面OEF ，∴平面//OEF 平面PCD ．（2）因为底面ABCD 是边长为2的菱形，60BAD ∠= ，所以BAD 为等边三角形，所以1,OB OA ==因为OP ⊥底面ABCD ，OA ⊂底面ABCD ，OB ⊂底面ABCD ，所以OP OA ⊥，OP OB ⊥，所以POA 和POB 均为直角三角形，所以PA =，2PB ==，所以22222cosPAB +-∠==所以sin 4PAB ∠=，所以1222PAB S PAB =⨯∠ ，设点O 到平面PEF 的距离为h ，根据体积相等法可知O PAB P OAB V V --=，所以1111332h =⨯⨯，所以5h =．111111334348O PEF PEF PAB V S h S -⎛⎫=⋅⋅=⨯=⨯= ⎪⎝⎭，故三棱锥O PEF -的体积为18．变式15．（2024·四川南充·统考三模）如图所示，已知,AC BD 是圆锥SO 底面的两条直径，M 为劣弧 BC的中点．（1）证明：SM AD ⊥；（2）若2π3BOC ∠=，E 为线段SM 上的一点，且2SE EM =，求证：平面BCE 平面SAD ．【解析】（1）连接MO 并延长交AD 于N ，如图所示，M 为劣弧 BC的中点，MO ∴是BOC ∠的角平分线，MN ∴平分AOD ∠，OA OD = ，MN AD ∴⊥，又在圆锥SO 中，SO ⊥平面ABCD ，AD ⊂平面ABCD ，SO AD ∴⊥，MN ，SO ⊂平面SMN ，且MN SO O ⋂=，AD ∴⊥平面SMN ，又SM ⊂ 平面SMN ，AD SM ∴⊥．（2）设MO 交BC 于F ，显然OF 平分BOC ∠，且OF BC ⊥，又2π3BOC ∠=，π3COF ∠∴=，∴在COF 中，12OF CO =，F ∴为OM 的中点，同理12ON OD =，2NF FM ∴=，又2SE EM = ，12ME MF SE NF ∴==，EF SN ∴∥，SN ⊂ 平面SAD ，且EF ⊄平面SAD ，EF ∴ 平面SAD ，又在平面ABCD 中，,BC MN AD MN ⊥⊥，BC AD ∴∥，又AD ⊂平面SAD ，且BC ⊄平面SAD ，BC ∴ 平面SAD ，又EF ，BC ⊂平面BCE ，且EF BC F ⋂=，∴平面BCE 平面SAD ．【解题方法总结】常用证明面面平行的方法是在一个平面内找到两条相交直线与另一个平面分别平行或找一条直线同时垂直于这两个平面．证明面面平行关键是找到两组相交直线分别平行．题型七：面面平行的性质例19．（2024·全国·高三专题练习）如图，在四棱柱1111ABCD A B C D -中，底面ABCD 为梯形，//AD BC ，平面1A DCE 与1BB 交于点E ．求证：1//EC A D ．【解析】由四棱柱1111ABCD A B C D -可知，1//BE AA ，1AA ⊂平面1AA D ，BE ⊄平面1AA D ，所以//BE 平面1AA D ；又//AD BC ，AD ⊂平面1AA D ，BC ⊄平面1AA D ，所以//BC 平面1AA D ；又BC BE B = ，BE ⊂平面BCE ，BC ⊂平面BCE ；所以平面//BCE 平面1AA D ，又平面1A DCE ⋂平面BCE EC =，平面1A DCE ⋂平面11AA D A D =，所以1//EC A D ．例20．（2024·辽宁·朝阳市第一高级中学校联考三模）如图，直四棱柱1111ABCD A B C D -被平面α所截，截面为CDEF ，且EF DC =，1242DC AD A E ===，π3ADC ∠=，平面EFCD与平面ABCD ．（1）证明：//AD BC ；【解析】（1）在直四棱柱1111ABCD A B C D -中，平面//ABCD 平面1111D C B A ，平面//ABCD CD α= ，平面1111A B C D EF α⋂=，则//EF CD ，而1111//,C D CD C D CD =，又EF CD =，因此1111//,C D EF C D EF =，则四边形11EFC D 是平行四边形，1111//A D B C ，所以//AD BC ．例21．（2024·安徽滁州·安徽省定远中学校考二模）如图，在三棱柱111ABC A B C -中，四边形11AAC C 是边长为4的菱形．AB BC =，点D 为棱AC 上动点（不与A ，C 重合），平面B 1BD 与棱A 1C 1交于点E ．（1）求证：1BB DE //；【解析】（1）11//BB CC ，且1BB ⊄平面11AAC C ，1CC ⊂平面11AAC C ，1//BB ∴平面11AAC C ，又1BB ⊂ 平面1B BD ，且平面1B BD 平面11ACC A DE =，1//BB DE ∴；变式16．（2024·北京·高三专题练习）如图，在多面体ABCDEF 中，面ABCD 是正方形，DE ⊥平面ABCD ，平面//ABF 平面CDE ，A ，D ，E ，F 四点共面，2AB DE ==，1AF =．（1）求证：//AF DE ；【解析】（1）因为平面//ABF 平面CDE ，A ，D ，E ，F 四点共面，且平面ABF 平面ADEF AF =，平面CDE ⋂平面ADEF DE =，所以//AF DE ．变式17．（2024·全国·高三专题练习）在如图所示的圆柱中，AB ，CD 分别是下底面圆O ，上底面圆1O 的直径，AD ，BC 是圆柱的母线，E 为圆O 上一点，P 为DE 上一点，且OP ∥平面BCE ．（1）求证：DP PE =；【解析】（1）如图，连接1O P ，1O O ，因为BC 为母线，所以1OO BC ∥，又BC ⊂平面BCE ，所以1OO ∥平面BCE ．因为OP ∥平面BCE ，所以平面1OPO 平面BCE ．又因为平面DCE 平面11OPO O P =，平面DCE 平面BCE CE =，所以1O P CE ，因为1O 是CD 的中点，所以P 是DE 的中点，即DP PE =．【解题方法总结】如果两个平行平面同时和第三个平面相交，那么他们的交线平行（简记为“面面平行⇒线面平行”）题型八：平行关系的综合应用例22．（2024·全国·高三专题练习）已知正方体1111ABCD A B C D -中，P ､Q 分别为对角线BD ､1CD 上的点，且123CQ BP QD PD ==．（1）求证：//PQ 平面11A D DA ；（2）若R 是AB 上的点，AR AB的值为多少时，能使平面//PQR 平面11A D DA ？请给出证明．【解析】（1）连结CP 并延长与DA 的延长线交于M 点，因为四边形ABCD 为正方形，所以//BC AD ，故~PBC PDM △△，所以23CP BP PM PD ==，又因为123CQ BP QD PD ==，所以123CQ CP QD PM ==，所以1//PQ MD ．又1MD ⊂平面11A D DA ，PQ ⊄平面11A D DA ，故//PQ 平面11A D DA ．（2）当AR AB 的值为35时，能使平面//PQR 平面11A D DA．证明：因为35AR AB =，即有23BR RA =，故BR BP RA PD=．所以//PR DA ．又DA ⊂平面11A D DA ，PR ⊄平面11A D DA ，所以//PR 平面11A D DA ，又PQ PR P ⋂=，//PQ 平面11A D DA ．所以平面//PQR 平面11A D DA ．例23．（2024·全国·高三专题练习）如图、三棱柱111ABC A B C -的侧棱1AA 垂直于底面ABC ，ABC 是边长为2的正三角形，1=3AA ，点D 在线段1A B 上且12A D DB =，点E 是线段11B C 上的动点．当11B E EC 为多少时，直线//DE 平面11ACC A？【解析】当点E 是线段11B C 上靠近点1B 的三等分点，即1112B E EC =时，//DE 平面11ACC A ．过点D 作1//DF A A 交11AB 于点F ，过点F 作11//EF AC 交11B C 于点E ，连接DE，11//,EF AC EF ⊄ 平面11ACC A ，11AC ⊂平面11ACC A，//EF ∴平面11ACC A ，1//FD A A ，FD ⊄面11ACC A ，1A A ⊂平面11ACC A ，。

直线与圆、圆与圆的位置关系课件-2025届高三数学一轮复习

, 到直线： − − = 的距离 =

≤ + ，解得−

≤≤

.

−−
+
=

+
≤ ，即
考点二直线与圆位置关系的应用
角度1 圆的切线问题（链接高考）
例2 (2023·新课标Ⅰ卷)过点 , − 与圆 + − − = 相切的两条直
（2）过圆 + = 外一点 , 作圆的两条切线，则两切点所在
直线方程为 + = .
2.圆与圆的位置关系的常用结论
（1）两圆相交时，其公共弦所在的直线方程由两圆方程相减得到.
（2）两个圆系方程
①过直线 + + = 与圆 + + + + = 交点的圆系方
（其中不含圆，所以注意检验是否满足题意，以防丢解）.
1.若经过点 −, − 的直线与圆 + = 相切，则该直线在轴上的截
距为(

A.

)
√

C.−

B.5
解析：选C.因为 −

+ −

D.−
= ，所以点在圆上，
所以切线方程为− − = ,令 = 得 =
+ − − = 相交.
方法三：圆的方程可化为 −

+ = ,
所以圆的圆心为 , ，半径为3.
圆心到直线 − + − = 的距离为
+−
+
=

+
≤ < ,所以直线与圆相交.故选C.

高考数学一轮总复习第七章立体几何 3空间直线平面的平行课件

//．
②结论：//平面．
证明：如图，取的中点，连接，，则//，//.
因为 ⊄ 平面， ⊂ 平面，所以//平面．
同理可得//平面．
又 ∩ = ，， ⊂ 平面，所以平面//平面．
又 ⊂ 平面，所以//平面．
平面 ∩ 平面 = ．
①判断与的位置关系，并证明你的结论；
②判断与平面的位置关系，并证明你的结论．
解：①结论：//．
证明：因为//， ⊄ 平面， ⊂ 平面，所以//
平面．又因为 ⊂ 平面，平面 ∩ 平面 = ，所以
平面1 ，
所以//平面1 ，//平面1 .
又 ∩ = ，, ⊂ 平面，
所以平面//平面1 .
因为 ⊂ 平面，所以//平面1 ．
图1
（方法二）连接交1 于点，连接交1 于点，连接，如
图2.
在三棱柱 − 1 1 1 中，1 1 //，1 //1 ，
证明：由题意,得 = 6, = 2 3,sin ∠ = sin ∠ =
sin ∠ =
3
,所以∠
3
= ∠.由为的中点,得 ⊥ .
又 ⊥ ,所以//，则为的中点.
由,,,分别为,,,的中点，得////.
【教材梳理】
1.直线与直线平行
（1）基本事实4.
文字语言
平行
平行于同一条直线的两条直线______
图形语言
符号语言
说明
基本事实4表明了平行线的传递性
（2）等角定理.
平行
如果空间中两个角的两条边分别对应______，那么这两个角
文字语言
相等或互补
___________
图形语言
符号语言
2.直线与平面平行
般需要连接特殊点、画辅助线，再证明线线平行，从而得到线面平行.第二种方法常

2024年高考数学复习培优讲义专题15---几何法求二面角,线面角(含解析)

专题3-1几何法求二面角，线面角立体几何空间向量求解过程，丧失了立体几何求解的乐趣，无形中也降低了学生的空间想象能力。

这是空间向量求解的巨大优点，也是缺点，就这么共存着。

其实不建系而直接计算真的很比较锻炼空间想象的能力，方法上也更灵活一些，对于备考的中档学生来说，2种方法都要熟练掌握。

方法介绍一、定义法：交线上取点等腰三角形共底边时作二面角步骤第一步：在交线l上取一点O第二步：在α平面内过O点作l的垂线OA第三步：在β平面内过O点作l的垂线OB∠AOB即为二面角，余弦定理求角αβl OAB二、三垂线法（先作面的垂直）—后续计算小使用情况：已知其中某个平面的垂线段第二步：过垂直B作l的垂线OB∠AOB即为二面角且△AOB为直角三角形，邻比斜三、作2次交线的垂线作二面角步骤第一步：作AO⊥l第二步：作OB⊥l连接AB，∠AOB即为二面角，余弦定理求角四、转换成线面角作二面角步骤第一步：作AO⊥l第二步：作AB⊥β(找不到垂足B的位置用等体积求AB长)连接AB，∠AOB即为二面角△AOB为直角三角形，邻比斜五、转换成线线角—计算小，也是法向量的原理提问：什么时候用？若α平面存在垂线AB，且β平面存在垂线AC则α平面与β平面的夹角等于直线AC与AB的夹角αβlOABαβlOABβαOABCαβlOAB六、投影面积法——面积比（三垂线法进阶）将cos θ＝边之比∣面积之比，从一维到二维，可多角度求出两面积，最后求解如图△ABC 在平面α上的投影为△A 1BC ，则平面α与平面ABC 的夹角余弦值1cos A BCABCθ=△△即cos θ=投影原S S补充：即使交线没有画出来也可以直接用例题：一题多解2023汕头二模T20如图在正方体ABCD －A 1B 1C 1D 1中，PQ 是所在棱上的中点.1C 1CD ABA B 1αBCAA 1D（1）求平面APQ 与平面ABCD 夹角的余弦值（2）补全截面APQ2023全国乙卷数学(理)T9——由二面角求线面角P C 1CDABA B 1P C 1DABA B 1P C 1CDABA B 1P C 1DABA B 1P C 1CDABA B 1PC 1DABA B 11．已知ABC 为等腰直角三角形，AB 为斜边，ABD △为等边三角形，若二面角C AB D −−为150︒，则直线CD 与平面ABC 所成角的正切值为（）A ．15B ．25C ．35D ．252021·新高考1卷·T20——由二面角求线段长2．如图，在三棱锥A BCD −中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D −−的大小为45︒，求三棱锥A BCD −的体积.题型一定义法1．如图，在三棱锥S—ABC 中，SC ⊥平面ABC ，点P 、M 分别是SC 和SB 的中点，设PM=AC =1，∠ACB =90°，直线AM 与直线SC 所成的角为60°.(1)求证：平面MAP ⊥平面SAC . (2)求二面角M—AC—B 的平面角的正切值；2．(湛江期末)如图，在三棱锥P －ABC 中，PA ⊥平面ABC ，点M ，N 分别是PB ，AC 的中点，且MN ⊥A C ．（1）证明：BC ⊥平面PA C ．（2）若PA ＝4，AC ＝BC ＝22，求平面PBC 与平面AMC 夹角的余弦值．(几何法比较简单)3．如图1，在平行四边形ABCD 中，60,2,4A AD AB ∠=︒==，将ABD △沿BD 折起，使得点A 到达点P ，如图2．重点题型·归类精讲(1)证明：平面BCD⊥平面P AD；(2)当二面角D PA B−−的平面角的正切值为6时，求直线BD与平面PBC夹角的正弦值．题型二三垂线法4．(佛山期末)如图，四棱锥P－ABCD中，AB∥CD，∠BAD＝90°，12PA AD AB CD===，侧面PAD⊥底面ABCD，E为PC的中点．（1）求证：BE⊥平面PCD；（2）若PA＝PD，求二面角P－BC－D的余弦值．5．如图，在四棱锥P -ABCD 中，△P AD 是以AD 为斜边的等腰直角三角形，,,224,23BC AD CD AD AD CD BC PB ⊥====∥ （2023广州一模T19）（1）求证：AD PB ⊥；（2）求平面P AB 与平面ABCD 交角的正弦值.6．如图，在三棱锥A BCD −中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点．（1）证明：OA CD ⊥；（2）若OCD 是边长为2的等边三角形，点E 在棱AD 上，2DE EA =且二面角E BC D −−的大小为60，求三棱锥A BCD −的体积．7．（2023·浙江·统考二模）如图，在三棱柱111ABCA B C 中，底面ABC ⊥平面11AA B B ，ABC 是正三角形，D 是棱BC 上一点，且3CD DB =，11A A A B =.(1)求证：111B C A D ⊥；(2)若2AB =且二面角11A BC B −−的余弦值为35，求点A 到侧面11BB C C 的距离.8．如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，ABC 和ACD 均为正三角形，4AC =，3BE =.(1)在线段AC 上是否存在点F ，使得BF ∥平面ADE ?说明理由； (2)求平面CDE 与平面ABC 所成的锐二面角的正切值.题型三作2次交线的垂线9．在三棱锥S ABC −中,底面△ABC 为等腰直角三角形,90SAB SCB ABC ∠=∠=∠=︒. （杭州二模）（1）求证：AC ⊥SB ；（2）若AB ＝2，22SC =，求平面SAC 与平面SBC 夹角的余弦值．题型四找交线10．如图，在四棱锥P －ABCD 中，底面ABCI )是平行四边形，∠ABC ＝120°，AB ＝1，BC ＝2，PD ⊥C D ． (1)证明：AB ⊥PB ；(2)若平面PAB ⊥平面PCD ，且102PA =，求直线AC 与平面PBC 所成角的正弦值．（广东省二模T19）题型五转换成线线角湖北省武汉市江汉区2023届高三上学期7月新起点考试11．在直三棱柱111ABC A B C −中，已知侧面11ABB A 为正方形，2BA BC ==，D ，,E F 分别为AC ，BC ，CC 1的中点，BF ⊥B 1D ．(1)证明：平面B 1DE ⊥平面BCC 1B 1；(2)求平面BC 1D 与平面1B DE 夹角的余弦值六、题型六投影面积法12．(2022·惠州第一次调研)如图，在四棱锥P －ABCD 中，已知//AB CD ，AD ⊥CD ，BC BP =，CD ＝2AB＝4，△ADP 是等边三角形，E 为DP 的中点．(1)证明：AE ⊥平面PCD ；(2)若2,PA =求平面PBC 与平面PAD 夹角的余弦值13．(2022深圳高二期末)如图(1)，在直角梯形ABCD 中，AB //CD ，AB ⊥BC ，且12,2BC CD AB ===取AB 的中点O ，连结OD ，并将△AOD 沿着OD 翻折，翻折后23AC =M ，N 分别是线段AD ，AB 的中点，如图(2)．（1）求证：AC⊥OM.（2）求平面OMN与平面OBCD夹角的余弦值．专题3-1几何法求二面角，线面角立体几何空间向量求解过程，丧失了立体几何求解的乐趣，无形中也降低了学生的空间想象能力。

高考专题讲义 22平面解析几何(一).

二、命题分析从近几年各省份的高考信息可以看出，高考对本单元的命题呈现如下特点：(1)高考题型中选择、填空、解答题均有所涉及，分值约占20分左右，比重较高．3.过P1(x1，y1)，P2(x2，y2)的直线方程(1)若x1＝x2，且y1≠y2时，直线垂直于x轴，方程为；(2)若x1≠x2，且y1＝y2时，直线垂直于y轴，方程为；(3)若x1＝x2＝0，且y1≠y2时，直线即为y轴，方程为；[解析] 由已知，直线的斜率解得tan α＝3或tan α＝－13(舍去)．由点斜式得y －1＝3(x －2)，即3x －y －5＝0.(3)解方程组⎩⎪⎨⎪⎧x －2y －3＝02x －3y －2＝0，得⎩⎪⎨⎪⎧x ＝－5y ＝－4，即两条直线的交点为(－5，－4)．由两点式得y －1－4－1＝x －2－5－2，即5x －7y －3＝0.（四）典型例题1.命题方向：直线的倾斜角与斜率[例1] 已知线段PQ 两端点的坐标分别为P (－1,1)和Q (2,2)，若直线l ：x ＋my ＋m ＝0与线段PQ 有交点，求实数m 的取值范围．[分析] 求m 的范围，关键是能够画出它们的图像，结合图像求解，能够知道直线l 过定点(0，－1)．[解析] 当m ＝0时，直线l 的方程为x ＝0，显然l 与PQ 相交．当m ≠0时，k PA ＝－1－10－－＝－2，k QA ＝－1－20－2＝32，l ：y ＋1＝－1mx .因为l 与线段PQ 相交，－1m ≥32或－1m≤－2， ∴m ∈⎣⎢⎡⎭⎪⎫－23，0或m ∈⎝ ⎛⎦⎥⎤0，12.所以m 的取值范围为⎣⎢⎡⎦⎥⎤－23，12.[点评] 解答已知直线过定点A 且与已知线段PQ 有交点，求其中参数的取值范围问题时，常用数形结合法，求出定点A 与线段PQ 的两个端点连线的斜率，根据图形列出不等式组，解不等式组即可．注意：研究两直线的位置关系时，一定要注意斜率不存在的情况．跟踪练习1：(2)在分析直线的倾斜角和斜率的关系时，要根据正切函数到π2(α≠π2)时，k 由0增大到＋∞，当负无穷大趋近于0.解决此类问题时，也可采用数形结合思想，借助图形直观作出判断．，d<0，a>c，d>0，a<cd>0，从而c<a<0，b<0，c始终平分圆x2＋y2＋2x－4y＋1＝A ．(－∞，1]B ．(0,1]C ．(0,1)D ．(－∞，1)[答案] A[解析] 由题意知直线过圆心(－1，－2)， ∴－2a －2b ＋4＝0，∴a ＋b ＝2， ∴ab ≤a 2＋b 22＝a ＋b2－2ab2，∴ab ≤1.4．已知直线l 1∶y ＝x ，l 2∶ax －y ＝0，其中a 为实数，当这两条直线的夹角在(0，π12)内变动时，a 的取值范围是( ) A ．(33，1)∪(1，3) B ．(33，3) C ．(33，1)D ．(1，3)[答案] A[解析] 因为k 1＝1，k 2＝a ，由数形结合知，直线l 2的倾斜角α∈(π6，π4)∪(π4，π3)，所以直线l 2的斜率a ∈(33，1)∪(1，3)． 5．过点P (－1,2)且方向向量为a ＝(－1,2)的直线方程为( ) A ．2x ＋y ＝0 B ．x －2y ＋5＝0 C ．x －2y ＝0D ．x ＋2y －5＝0[答案] A[解析] 因为方向向量a ＝(－1,2)，所以直线的斜率k ＝－2，又过点P (－1,2)，所以由点斜式求得直线方程为2x ＋y ＝0.6．(2011·山东济宁)已知点A (1,3)，B (－2，－1)，若直线l ∶y ＝k (x －2)＋1与线段AB 相交，则k 的取值范围( )A ．k ≥12B ．k ≤－2C ．k ≥12或k ≤－2D ．－2≤k ≤12[答案] D[解析] 如图，l 过P (2,1)，k PA ≤k ≤k PB ，k PA ＝3－11－2＝－2，而k PB ＝12，∴－2≤k ≤12.7．过抛物线y 2＝43x 的焦点，且与圆x 2＋y 2－2y ＝0相切的直线方程是( ) A.3x ＋y －3＝0，y ＝0B.3x －y －3＝0，y ＝0C.3x ＋y ＋3＝0，3x －y ＋3＝0D.3x ＋3y －3＝0，3x －3y －3＝0 [答案] A[解析] 抛物线焦点F (3，0)，圆的方程x 2＋(y －1)2＝1，由图知过焦点F 且与圆相切的直线有两条，其中一条是y ＝0故排除C 、D.另一条斜率小于0，故选A.8．已知f (x )＝log 2(x ＋1)，且a >b >c >0，则f a a ，f b b ，f cc的大小关系是( ) A.f a a >f b b >f cc B.f c c >f b b >f aa C.f b b >f a a >f ccD.f a a >f c c >f bb[答案] B[解析] 作函数f (x )＝log 2(x ＋1)的图像，易知f x x 表示直线的斜率．∴f c c >f b b >f a a，故选B.二、填空题9．一条直线l 过点P (1,4)，分别交x 轴，y 轴的正半轴于A 、B 两点，O 为原点，则△AOB 的面积最小时直线l 的方程为________．[答案] 4x ＋y －8＝0[解析] 设l ：x a ＋y b＝1(a ，b >0)．因为点P (1,4)在l 上，所以1a ＋4b ＝1.由1＝1a ＋4b ≥24ab⇒ab ≥16，所以S △AOB ＝12ab ≥8.解方程组⎩⎪⎨⎪⎧2x －y －2＝0－x ＋－y ＋3＝0得⎩⎪⎨⎪⎧x ＝113y ＝163，k ＝163－0113－3＝8.∴所求的直线方程为y ＝8(x －3)，即8x －y －24＝0. 方法二设所求的直线方程y ＝k (x －3)，则⎩⎪⎨⎪⎧y ＝k x －2x －y －2＝0，解得⎩⎪⎨⎪⎧ x A ＝3k －2k －2y A＝4kk －2由⎩⎪⎨⎪⎧y ＝k x －x ＋y ＋3＝0，解得⎩⎪⎨⎪⎧x B ＝3k －3k ＋1y B＝－6kk ＋1∵P (3,0)是线段AB 的中点， ∴y A ＋y B ＝0，即4k k －2＋－6k k ＋1＝0， ∴k 2－8k ＝0，解得k ＝0或k ＝8. 又∵当k ＝0时，x A ＝1，x B ＝－3，此时x A ＋x B 2＝1－32≠3，∴k ＝0舍去，∴所求的直线方程为y ＝8(x －3)，即8x －y －24＝0.方法三设点A (x 1，y 1)在l 1上，点B (x 2，y 2)在l 2上，则 ⎩⎪⎨⎪⎧2x 1－y 1－2＝0x 2＋y 2＋3＝0x 1＋x 2＝6y 1＋y 2＝0，解得⎩⎪⎨⎪⎧ x 1＝113y 1＝163或⎩⎪⎨⎪⎧x 2＝73y 2＝－163∴k ＝k AB ＝－163－16373－113＝8，∴所求的直线方程为8x －y －24＝0.13．已知i ＝(1,0)，j ＝(0,1)，经过原点O 以u ＝i ＋m j 为方向向量的直线与经过定点A (0,1)，以v ＝m i －j 为方向向量的直线相交于点P ，其中m ∈R ，当点P 变动时，试问是否存在一个定点Q ，使得|PQ |为定值？若存在，求出的前提下，参数的个数越少越好．．有一个附近有进出水管的容器，每单位时间进出的水量是一定的，设从某时刻开始分钟内既进水又出水，得到时间x(分)本题是一个实际应用问题，综合性较强，通过分析题意可知是一个分段函数问题，即直线的方程．因此，由直线的点斜式方程即可求出．时，直线段过点O(0,0)，A(10＝2010＝＝30－2040－10＝13，＝13(＝13x ＋503.＝13，所以＝－53.＝－53，又过点＝－53(＝－53＋2903.综上所述，y ＝⎩⎪⎨⎪⎧2x x13x ＋503x ，－53x ＋2903x若点P 1、P 2的坐标分别为(x 1，y 1)，(x 2，y 2)，且线段P 1P 2的中点M 的坐标为(x ，y )，则⎩⎪⎨⎪⎧x ＝x 1＋x 22y ＝y 1＋y22，此公式为线段P 1P 2的中点坐标公式． 3．直线l 1A 1x ＋B 1y ＋C 1＝0与l 2A 2x ＋B 2y ＋C 2＝0的交点坐标就是⎩⎪⎨⎪⎧A 1x ＋B 1y ＋C 1＝0A 2x ＋B 2y ＋C 2＝0的．4．点A (x 1，y 1)、B (x 2，y 2)间的距离：|AB |＝x 2－x 12＋y 2－y 125．点P (x 0，y 0)到直线lAx ＋By ＋C ＝0的距离：d ＝|Ax 0＋By 0＋C |A 2＋B 2.6．两平行线间距离：两平行直线l 1Ax ＋By ＋C 1＝0与l 2Ax ＋By ＋C 2＝0间的距离为d ＝|C 2－C 1|A 2＋B 2. （三）基础自测1．(2010·安徽文)过点(1,0)且与直线x －2y －2＝0平行的直线方程是( ) A ．x －2y －1＝0 B ．x －2y ＋1＝0 C ．2x ＋y －2＝0 D ．x ＋2y －1＝0 [答案] A[解析] 该题考查直线方程的求法(点斜式)所求直线斜率为12，过点(1,0)由点斜式y ＝12(x －1)，即x －2y －1＝0.2．(2009·安徽文)直线l 过点(－1,2)且与直线2x －3y ＋4＝0垂直，则l 的方程是( )A ．3x ＋2y －1＝0B ．3x ＋2y ＋7＝0C ．2x －3y ＋5＝0D ．2x －3y ＋8＝0 [答案] A[解析] 本题考查直线方程的点斜式，以及两条的垂直关系．∵直线l 与直线2x －3y ＋4＝0垂直， ∴直线l 的斜率k ＝－32，又∵直线l 过点(－1,2)， ∴其方程为y －2＝－32(x ＋1)，即3x ＋2y －1＝0.3．曲线y ＝k |x |及y ＝x ＋k (k >0)能围成三角形，则k 的取值范围是( ) A ．0<k <1 B ．0<k ≤1 C ．k >1 D ．k ≥1 [答案] C[解析] 数形结合法．在同一坐标系中作出两函数的图像，可见k ≤1时围不成三角形，k >1时能围成三角形．4．(2011·庐江模拟)若直线x a ＋y b＝1通过点M (cos α，sin α)，则( )∴－3a ＋b ＋4＝0，即b ＝3a －4(不合题意) ∴此种情况不存在，即k 2≠0. 若k 2≠0，即k 1，k 2都存在，∵k 1＝a b，k 2＝1－a ，l 1⊥l 2， ∴k 1·k 2＝－1，即a b(1－a )＝－1①又∵l 1过点(－3，－1)，∴－3a ＋b ＋4＝0② 由①②联立，解得a ＝2，b ＝2. (2)∵l 2的斜率存在，l 1∥l 2， ∴直线l 1的斜率存在，∴k 1＝k 2. 即a b＝1－a ③又∵坐标原点到这两条直线的距离相等，l 1∥l 2. ∴l 1，l 2在y 轴上的截距互为相反数．即4b＝b ④由③④联立解得⎩⎪⎨⎪⎧a ＝2b ＝－2或⎩⎪⎨⎪⎧a ＝23b ＝2.∴a ，b 的值为2和－2或23和2.（四）典型例题1.命题方向：两直线的位置关系[例1] 已知两条直线l 1(3＋m )x ＋4y ＝5－3m ，l 22x ＋(5＋m )y ＝8.当m 分别为何值时，l 1与l 2：(1)相交？(2)平行？(3)垂直？[解析] 当m ＝－5时，显然l 1与l 2相交；当m ≠－5时，易得两直线l 1和l 2的斜率分别为k 1＝－3＋m 4，k 2＝－25＋m，它们在y 轴上的截距分别为b 1＝5－3m 4，b 2＝85＋m .(1)由k 1≠k 2，得－3＋m 4≠－25＋m，m ≠－7且m ≠－1.∴当m ≠－7且m ≠－1时，l 1与l 2相交．(2)由⎩⎪⎨⎪⎧k 1＝k 2，b 1≠b 2，得⎩⎪⎨⎪⎧－3＋m 4＝－25＋m ，5－3m 4≠85＋m ，解得m ＝－7.∴当m ＝－7时，l 1与l 2平行．(3)由k 1k 2＝－1，得－3＋m 4·(－25＋m )＝－1，解得m ＝－133.∴当m ＝－133时，l 1与l 2垂直．[点评] 运用有斜率的两直线平行或垂直的条件处理两直线位置关系时，要紧紧抓住k 1，k 2及b 1，b 2之间的关系，需要注意的是“有斜率”这一前提条件，否则会使解题不严谨甚至导致错误．如题：当k 取何值时，两直线x ＋ky ＝0和kx ＋(1－k )y ＝0互相垂直？很可能漏掉解k ＝0.判断两条直线平行、垂直、重合时，不要忘记考虑两条直线中有一条或两条直线的斜率均不存在的情况．在两条直线l 1、l 2斜率都存在且不重合的条件下，才有l 1∥l 2⇔k 1＝k 2与l 1⊥l 2⇔k 1·k 2＝－1.在斜率不存在或斜率为零情况下讨论两直线位置关系宜用数形结合求解．跟踪练习1已知两直线l 1x ＋y sin θ－1＝0和l 22x sin θ＋y ＋1＝0，试求θ的值，使得： (1)l 1∥l 2； (2)l 1⊥l 2.[解析] (1)方法1：当sin θ＝0时，l 1的斜率不存在，l 2的斜率为0，l 1显然不平行于l 2，当sin θ≠0时，k 1＝－1sin θ，k 2＝－2sin θ.欲使l 1∥l 2，只要－1sin θ＝－2sin θ，即sin θ＝±22.∴θ＝k π±π4，k ∈Z ，此时两直线截距不相等．∴当θ＝k π±π4，k ∈Z 时，l 1∥l 2.方法2：要使l 1∥l 2，需2sin 2θ－1＝0，且1＋sin θ≠0，即sin θ＝±22，∴θ＝k π±π4，k ∈Z. ∴当θ＝k π±π4，k ∈z 时，l 1∥l 2.(2)方法1：当sin θ＝0时，l 1的斜率不存在，l 2的斜率为0，故l 1⊥l 2.此时θ＝k π(k ∈Z)．当sin θ≠0时，k 1＝－1sin θ，k 2＝－2sin θ，要使l 1⊥l 2，则k 1·k 2＝－1，即－1sin θ·(－2sin θ)＝－1，显然无解，故当θ＝k π(k ∈Z)时，l 1⊥l 2.[解析] 解法1：若直线l 的斜率不存在，则直线l 的方程为x ＝3，此时与l 1、l 2的交点分别为A ′(3，－4)、B ′(3，－9)，截得的线段A ′B ′的长|A ′B ′|＝|－4＋9|＝5，符合题意. 若直线l 的斜率存在，则设直线l 的方程为y ＝k (x －3)＋1(k ≠－1)．解方程组⎩⎪⎨⎪⎧y ＝k x －＋1，x ＋y ＋1＝0，得A (3k －2k ＋1，－4k －1k ＋1)．解方程组⎩⎪⎨⎪⎧y ＝k x －＋1，x ＋y ＋6＝0，得B (3k －7k ＋1，－9k －1k ＋1)．由|AB |＝5.得(3k －2k ＋1－3k －7k ＋1)2＋(－4k －1k ＋1＋9k －1k ＋1)2＝52.解之得，k ＝0，∴直线l 方程为y ＝1. 综上可知，所求l 的方程为x ＝3或y ＝1. 解法2：因为平行线间的距离d ＝|6－1|2＝522，如图，直线l 被两平行线截得的线段为5，设直线l 与两平行线的夹角为θ，则sin θ＝22，∴θ＝45°. 因为两平行线的斜率是－1，故所求直线的斜率不存在或零．又因为直线l 过点P (3,1)，所以直线l 的方程为x ＝3或y ＝1.3.命题方向：对称问题[例3] 求直线l 1：y ＝2x ＋3关于直线l ：y ＝x ＋1对称的直线l 2的方程． [分析] 转化为点关于直线的对称，利用方程组求解．[解析] 解法1：由⎩⎪⎨⎪⎧y ＝2x ＋3y ＝x ＋1得直线l 1与l 2的交点坐标为(－2，－1)，在l 1上任取一点A (0,3)，则A 关于直线l 的对称点B (x 1，y 1)一定在l 2上，由⎩⎪⎨⎪⎧y 1－3x 1＝－1y 1＋32＝x 12＋1得⎩⎪⎨⎪⎧x 1＝2y 1＝1，即B (2,1)．∴l 2的方程为y －1＝1＋12＋2(x －2)．即x －2y ＝0.解法2：设所求直线上一点P (x ，y )，则在直线l 1上必存在一点P 1(x 0，y 0)与点P 关于直线l 对称．由题设：直线PP 1与直线l 垂直，且线段PP 1的中点P 2⎝⎛⎭⎪⎫x ＋x 02，y ＋y 02在直线l 上．∴⎩⎪⎨⎪⎧y 0－yx 0－x ·1＝－1y ＋y 02＝x ＋x 02＋1，变形得⎩⎪⎨⎪⎧x 0＝y －1y 0＝x ＋1，代入直线l 1：y ＝2x ＋3得x ＋1＝2×(y －1)＋3，整理得x －2y ＝0.所以所求直线方程为x －2y ＝0.解法3：由⎩⎪⎨⎪⎧y ＝2x ＋3y ＝x ＋1知直线l 1与l 的交点坐标为(－2，－1)，∴设直线l 2的方程为y ＋1＝k (x ＋2)，即kx －y ＋2k －1＝0.在直线l 上任取一点(1,2)，由题设知点(1,2)到直线l 1、l 2的距离相等，由点到直线的距离公式得|k －2＋2k －1|12＋k 2＝|2－2＋3|22＋－2，解得k ＝12(k ＝2舍去)，[点评] 对称问题是解析几何中的一个重要题型，是高考热点之一．两条曲线关于一条直线对称常转化为曲线上的点关于直线对称来解决．求点P (x 0，y 0)关于直线l ：Ax ＋By ＋C ＝0的对称点Q (x 1，y 1)的坐标，可利用PQ ⊥l 及线段PQ 被l 平分这两个条件建立方程组求解，本题解法2就是利用这种方法结合“代入法”求轨迹方程的思想方法解题的．这是解这类问题的一个通法．∴直线l 2的方程为x －2y ＝0.跟踪练习3在直线l 3x －y －1＝0上求一点P ，使得： (1)P 到A (4,1)和B (0,4)的距离之差最大； (2)P 到A (4,1)和C (3,4)的距离之和最小．[分析] (1)在直线l 上求一点P ，使P 到两定点的距离之和最小①当两定点A 、B 在直线l 的异侧时，由两点之间线段最短及三角形中任意两边之和都大于第三边可知，点P 为AB 连线与l 的交点；点P 到两定点距离之和的最小值为②当两定点A 、B 在直线l 的同侧时，作点A 、B 的距离之和最小．(2)在直线上求一点P ，使P 到两定点的距离之差的绝对值最大①当两定点A 、B 在直线l 的同侧时l 上任取一点P ′，则有||P ′B②当两定点A 、B 在直线l 的异侧时，作点||PB |－|PA ′||＝|A ′B |时，达到最大．∵||P ′B |－|P ′A ′||≤|A ′B[解析] (1)如图(1)所示，设点则k BB ′·k l ＝－1，即3·b －a∴a ＋3b －12＝0①又由于线段BB ′的中点坐标为即3a －b －6＝0②解①②得a ＝3，b ＝3.∴B ′(3,3)．∴3×a 2－b ＋42－1＝0.即3a －b －6＝0②解①②得a ＝3，b ＝3.∴B ′(3,3)．于是AB ′的方程为y －13－1＝x －43－4，即2x ＋y －9＝0.解⎩⎪⎨⎪⎧3x －y －1＝02x ＋y －9＝0，得⎩⎪⎨⎪⎧x ＝2y ＝5，即l 与AB ′的交点坐标为P (2,5)．(2)如图(2)所示，设C 关于l 的对称点为C ′，求出C ′的坐标为(35，245)，∴AC ′所在直线的方程为19x ＋17y －93＝0，AC ′和l 交点坐标为(117，267)，故P 点坐标为(117，267).（五）思想方法点拨1．求两直线交点坐标就是解方程组．即把几何问题转化为代数问题．2．要理解“点点距”、“点线距”、“线线距”之间的联系及各公式的特点．特别提示：求两平行线间的距离时，一定化成l 1Ax ＋By ＋C 1＝0，l 2Ax ＋By ＋C 2＝0的形式．3．在使用点到直线的距离公式时，应注意以下几点：(1)若给出的方程不是一般式，则应先把方程化为一般式，再利用公式求点到直线的距离； (2)若P 在直线l 上，则点P 到直线l 的距离为0，公式仍成立．4．在使用两平行线间的距离公式时，要先把两直线中x 、y 的系数化为相同，且都化成一般式后再用公式． 5．判断两条直线平行或垂直时，不要忘记考虑两条直线中有一条或两条直线均无斜率的情形，在两条直线l 1、l 2斜率都存在，且不重合的条件下，才有l 1∥l 2⇔k 1＝k 2与l 1⊥l 2⇔k 1k 2＝－1.用直线的一般式方程判断两直线的位置关系时，A 1A 2＋B 1B 2＝0⇔两直线垂直，但A 1B 2－A 2B 1＝0与两直线平行不等价．用比例关系A 1A 2≠B 1B 2判断相交，A 1A 2＝B 1B 2≠C 1C 2判断平行，A 1A 2＝B 1B 2＝C 1C 2判断重合，应用方便，但前提是A 2B 2C 2≠0，它们都不是等价条件．6．直线系方程有些问题中所给的直线方程常常含有一个参数，对于含有一个参数的直线方程，往往不是平行线系，就是过定点的直线系．(1)平行线系．①与直线Ax ＋By ＋C ＝0平行的直线系方程为Ax ＋By ＋m ＝0(m ≠C )，其中m 为参数． ②与直线Ax ＋By ＋C ＝0垂直的直线系方程为Bx －Ay ＋m ＝0，其中m 为参数． ③斜率为k (定值)的平行线系方程为y ＝kx ＋b ，其中k 为常数，b 为参数． (2)过定点的直线系．①过定点P (x 0，y 0)的直线系方程为A (x －x 0)＋B (y －y 0)＝0(A 、B 不全为零)．②过两条直线l 1A 1x ＋B 1y ＋C 1＝0和l 2A 2x ＋B 2y ＋C 2＝0的交点的直线系方程为A 1x ＋B 1y ＋C 1＋λ(A 2x＋B 2y ＋C 2)＝0(λ∈R)(不包括直线l 2)．7．对称问题对称性问题是解析几何应用较为广泛的的一类问题，归纳起来有 (1)点关于点的对称点．①点P (x ，y )关于O (0,0)的对称点P ′(－x ，－y )． ②点P (x ，y )关于点(a ，b )的对称点P ′(2a －x,2b －y )． (2)点关于直线的对称点．①点(x ，y )关于x 轴，y 轴，直线y ＝x 的对称点分别为(x ，－y )，(－x ，y )，(y ，x )． ②点A (a ，b )关于直线x ＋y ＋C ＝0的对称点A ′的坐标为(－b －C ，－a －C )． ③点A (a ，b )关于直线x －y ＋C ＝0的对称点A ′的坐标为(b －C ，a ＋C )．④点A (a ，b )关于直线Ax ＋By ＋C ＝0(B ≠0)的对称点A ′的坐标为(m ，n )，则有⎩⎪⎨⎪⎧n －b m －a －AB＝－1，A a ＋m 2＋B b ＋n2＋C ＝0.(3)曲线Cf (x ，y )＝0与曲线C ′g (x ，y )＝0关于点P (a ，b )对称，则曲线C ′上任一点M ′(x ，y )，关于P 的对称点M (2a －x,2b －y )在曲线C 上，即f (2a －x,2b －y )＝0.(4)曲线Cf (x ，y )＝0关于直线y ＝kx ＋b 对称曲线为C ′g (x ，y )＝0，则C ′上任一点P 关于直线y ＝kx＋b 对称的点，必在曲线C 上，即曲线关于直线的对称问题转化为点．关于直线的对称问题。

高考数学总复习第八章平面解析几何

＝m2＋1≥1，所以 ≤α＜ .故倾斜角
2－1
4
2
[ )π π
α 的取值范围是， . 42
2．经过 P(0，－1)作直线 l，若直线 l 与连接 A(1，－2)，B(2,1)的线段总有公共点，则
直线 l 的斜率 k 和倾斜角 α 的取值范围分别为________，________.
解析：如图所示，结合图形，若 l 与线段 AB 总有公共点，则
∴Error!得 k＜0.
( ) 1
11
∴S△AOB＝2·|OA|·|OB|＝2·
2－ k
·(1－2k)
( ) [ ( ) ] 1 1
1
1
＝ 4－－4k ≥ 4＋2
2k
2
－ ·－4k k
1 ＝4，当且仅当－＝－4k，
k
1
1
即 k＝－时，△AOB 的面积有最小值 4，此时直线 l 的方程为 y－1＝－ (x－2)，即 x
2；令 x＝0，得 y＝－2，即 l1 与 y 轴的交点为(0，－2)，直线 l1 的倾斜角为 135°，∴直线 l2 的倾斜角为 135°－90°＝45°，∴l2 的斜率为 1，故 l2 的方程为 y＝x－2，即 x－y－2＝0.
答案：－2 x－y－2＝0
1．点斜式、斜截式方程适用于不垂直于 x 轴的直线；两点式方程不能表示垂直于 x，
[ ] [ ] π π π 5π
A. ， ∪ ， 62 2 6
[ ] [ ) π 5π
B. 0， ∪ ，π 66
[ ]5π
C. 0， 6
[ ] π 5π
D. ， 66
3 解析：选 B 设直线的倾斜角为 θ，则 tan θ＝－ cos α，

第46讲、空间几何体的结构特征、表面积(教师版)2025高考数学一轮复习讲义

第46讲空间几何体的结构特征、表面积与体积知识梳理知识点一：构成空间几何体的基本元素—点、线、面（1）空间中，点动成线，线动成面，面动成体．（2）空间中，不重合的两点确定一条直线，不共线的三点确定一个平面，不共面的四点确定一个空间图形或几何体（空间四边形、四面体或三棱锥）．知识点二：简单凸多面体—棱柱、棱锥、棱台1、棱柱：两个面互相平面，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱．（1）斜棱柱：侧棱不垂直于底面的棱柱；（2）直棱柱：侧棱垂直于底面的棱柱；（3）正棱柱：底面是正多边形的直棱柱；（4）平行六面体：底面是平行四边形的棱柱；（5）直平行六面体：侧棱垂直于底面的平行六面体；（6）长方体：底面是矩形的直平行六面体；（7）正方体：棱长都相等的长方体．2、棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥．（1）正棱锥：底面是正多边形，且顶点在底面的射影是底面的中心；（2）正四面体：所有棱长都相等的三棱锥．3、棱台：用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫做棱台，由正棱锥截得的棱台叫做正棱台．简单凸多面体的分类及其之间的关系如图所示．知识点三：简单旋转体—圆柱、圆锥、圆台、球1、圆柱：以矩形的一边所在的直线为旋转轴，其余三边旋转形成的面所围成的几何体叫做圆柱．2、圆柱：以直角三角形的一条直角边所在的直线为旋转轴，将其旋转一周形成的面所围成的几何体叫做圆锥．3、圆台：用平行于圆锥底面的平面去截圆锥，底面和截面之间的部分叫做圆台．4、球：以半圆的直径所在的直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称为球（球面距离：经过两点的大圆在这两点间的劣弧长度）．知识点四：组合体由柱体、锥体、台体、球等几何体组成的复杂的几何体叫做组合体．知识点五：表面积与体积计算公式表面积公式表面积柱体2直棱柱底=+S ch S 2(斜棱柱底''=+S c l S c 为直截面周长)2222()圆锥=+=+S r rl r r l πππ锥体12正棱锥底'=+S nah S 2()圆锥=+=+S r rl r r l πππ台体1()2正棱台上下'=+++S n a a h S S 22)圆台（''=+++S r r r l rl π球24=S R π体积公式知识点六：空间几何体的直观图1、斜二测画法斜二测画法的主要步骤如下：（1）建立直角坐标系．在已知水平放置的平面图形中取互相垂直的Ox ，Oy ，建立直角坐标系．（2）画出斜坐标系．在画直观图的纸上（平面上）画出对应图形．在已知图形平行于x 轴的线段，在直观图中画成平行于''O x ，''O y ，使45'''∠= x O y （或135 ），它们确定的平面表示水平平面．（3）画出对应图形．在已知图形平行于x 轴的线段，在直观图中画成平行于'x 轴的线段，且长度保持不变；在已知图形平行于y 轴的线段，在直观图中画成平行于'y 轴，且长度变为原来的一般．可简化为“横不变，纵减半”．（4）擦去辅助线．图画好后，要擦去'x 轴、'y 轴及为画图添加的辅助线（虚线）．被挡住的棱画虚线．注：4．2、平行投影与中心投影平行投影的投影线是互相平行的，中心投影的投影线相交于一点．必考题型全归纳题型一：空间几何体的结构特征例1．（2024·安徽·高三校联考阶段练习）已知几何体，“有两个面平行，其余各面都是平行四边形”是“几何体为棱柱”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【解析】由棱柱定义知棱柱有两个面平行，其余各面都是平行四边形，故满足必要性；但有两个面平行，其余各面都是平行四边形的几何体不一定是棱柱，例如两个底面全等的斜棱柱拼接的几何体不是棱柱，如图所示：，故不满足充分性，故选：B例2．（2024·全国·高三对口高考）设有三个命题；甲：底面是平行四边形的四棱柱是平行六面体；乙：底面是矩形的平行六面体是长方体；丙：直四棱柱是平行六面体．以上命题中真命题的个数为（）A．0个B．1个C．2个D．3个【答案】B【解析】由平行六面体的定义可得底面是平行四边形的四棱柱是平行六面体；命题甲正确；底面是矩形的平行六面体的侧棱不一定垂直于底面，故该几何体不一定为长方体，命题乙错误；直四棱柱的底面不一定为平行四边形，故直四棱柱不一定是平行六面体，命题丙错误；正确的命题只有一个.故选：B例3．（2024·全国·高三专题练习）下列命题：①有两个面平行，其他各面都是平行四边形的几何体叫做棱柱；②有两侧面与底面垂直的棱柱是直棱柱；③过斜棱柱的侧棱作棱柱的截面，所得图形不可能是矩形；④所有侧面都是全等的矩形的四棱柱一定是正四棱柱．其中正确命题的个数为（）A．0B．1C．2D．3【答案】A【解析】①如图1，满足有两个面平行，其他各面都是平行四边形，显然不是棱柱，故①错误；ABB A与底面垂直，但不是直棱柱，②错误；②如图2，满足两侧面11ACC A为矩形，③如图3，四边形11即过斜棱柱的侧棱作棱柱的截面，所得图形可能是矩形，③错误；④所有侧面都是全等的矩形的四棱柱不一定是正四棱柱，因为两底面不一定是正方形，④错误．故选：A变式1．（2024·新疆·统考模拟预测）下列命题中正确的是（）A．有两个平面平行，其余各面都是平行四边形的几何体是棱柱.B．各个面都是三角形的几何体是三棱锥.C．夹在圆柱的两个平行截面间的几何体还是一个旋转体.D．圆锥的顶点与底面圆周上任意一点的连线都是母线.【答案】D【解析】如图所示的几何体满足两个平面平行，其余各面都是平行四边形，但它不是棱柱，A错；正八面体的各面都是三角形，不是三棱锥，B错；如果两个平行截面与圆柱的底面平行，则是旋转体，如果这两个平行截面与圆柱的底面不平行，则不是旋转体．C错；根据圆锥的定义，D正确．故选：D．变式2．（2024·全国·高三专题练习）下列说法正确的是（）A．三角形的直观图是三角形B．直四棱柱是长方体C．平行六面体不是棱柱D．两个平面平行，其余各面是梯形的多面体是棱台【答案】A【解析】对A，根据直观图的定义，三角形的直观图是三角形，故A对；对B，底面是长方形的直四棱柱是长方体，故B错；对C，平行六面体一定是棱柱，故C错；两个平面平行，其余各面是梯形的多面体，当侧棱延长后不交于同一点时，不是棱台，故D 错；故选：A变式3．（2024·全国·高三专题练习）给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥；③棱台的上、下底面可以不相似，但侧棱长一定相等.其中正确命题的个数是（）A．0B．1C．2D．3【答案】A【解析】①不一定，只有当这两点的连线平行于轴时才是母线；②不一定，当以斜边所在直线为旋转轴时，其余两边旋转形成的面所围成的几何体不是圆锥，如图所示，它是由两个同底圆锥组成的几何体；③错误，棱台的上、下底面相似且是对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等.故选：A.变式4．（2024·全国·高三专题练习）如图所示，观察四个几何体，其中判断正确的是（）A．是棱台B．是圆台C．不是棱柱D．是棱锥【答案】D【解析】对A，侧棱延长线不交于一点，不符合棱台的定义，所以A错误；对B，上下两个面不平行，不符合圆台的定义，所以B错误；对C，将几何体竖直起来看，符合棱柱的定义，所以C错误；对D ，符合棱锥的定义，正确．故选：D ．【解题方法总结】空间几何体结构特征的判断技巧（1）紧扣结构特征是判断的关键，依据条件构建几何模型，在条件不变的情况下，变换模型中的线面关系或增加线、面等基本元素，然后再依据题意判定．（2）说明一个命题是错误的，只要举出一个反例即可．题型二：空间几何体的表面积例4．（2024·湖北武汉·统考模拟预测）已知某圆锥的母线长、底面圆的直径都等于球的半径，则球与圆锥的表面积之比为（）A ．8B ．163C ．316D ．18【答案】B【解析】设圆锥的母线长为l ，底面圆的半径为r ，球的半径为R ，则2l r R ==，即2R r =，2l r =，球的表面积2214π16πS R r ==，圆锥的表面积22222ππ2ππ3πS rl r r r r =+=+=，则212216π163π3S r S r ==.故选：B.例5．（2024·河南郑州·统考模拟预测）在一个正六棱柱中挖去一个圆柱后，剩余部分几何体如图所示．已知正六棱柱的底面正六边形边长为3cm ，高为4cm ，内孔半径为1cm ，则此几何体的表面积是（）2cm．A．726πB．728π+C．726π+D．606π+【答案】C【解析】所求几何体的侧面积为()234672cm ⨯⨯=，上下底面面积为()()22136π22πcm 22⎛⎫⨯-⨯= ⎪ ⎪⎝⎭，挖去圆柱的侧面积为()22π48πcm⨯=，则所求几何体的表面积为()()2726πcm +．故选：C ．例6．（2024·安徽安庆·安庆一中校考三模）陀螺起源于我国，最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知，底面圆的直径12cm AB =，圆柱体部分的高6cm BC =，圆锥体部分的高4cm CD =，则这个陀螺的表面积（单位：2cm ）是（）A ．(144π+B ．(144π+C ．(108π+D ．(108π+【答案】C【解析】由题意可得圆锥体的母线长为l ==所以圆锥体的侧面积为112π2⋅⋅=，圆柱体的侧面积为12π672π⨯=，圆柱的底面面积为2π636π⨯=，所以此陀螺的表面积为()()272π36π108cm ++=+，故选：C.变式5．（2024·西藏拉萨·统考一模）位于徐州园博园中心位置的国际馆（一云落雨），使用现代科技雾化“造云”，打造温室客厅，如图，这个国际馆中3个展馆的顶部均采用正四棱锥这种经典几何形式，表达了理性主义与浪漫主义的对立与统一.其中最大的是3号展馆，其顶部所对应的正四棱锥底面边长为19.2m ，高为9m ，则该正四棱锥的侧面面积与底面面积之比约为（）13.16≈）A ．2B ．1.71C ．1.37D ．1【答案】C【解析】如图，设H 为底面正方形ABCD 的中心，G 为BC 的中点，连接PH ，HG ，PG ，则PH HG ⊥，PG BC ⊥，所以13.16PG ===≈，则144226.322 1.3719.2PBCABCDBC PGS PG S AB BC AB ⨯⨯⨯==≈≈⨯正方形△，故选：C.变式6．（2024·湖南长沙·高三校联考阶段练习）为了给热爱朗读的师生提供一个安静独立的环境，某学校修建了若干“朗读亭”.如图所示，该朗读亭的外形是一个正六棱柱和正六棱锥的组合体，正六棱柱两条相对侧棱所在的轴截面为正方形，若正六棱锥的高与底面边长的比为2:3，则正六棱锥与正六棱柱的侧面积的比值为（）A．8B．24C ．19D ．127【答案】B【解析】设正六边形的边长为a，由题意正六棱柱的高为2a，因为正六棱锥的高与底面边长的比为2:3，所以正六棱锥的高为2 3 a，正六棱锥的母线长为，正六棱锥的侧面积21162S=⨯；正六棱柱的侧面积226212S a a a=⋅⋅=，所以12SS=.故选：B.变式7．（2024·河北·统考模拟预测）《九章算术》是我国古代的数学名著.其“商功”中记载：“正四面形棱台（即正四棱台）建筑物为方亭.”现有如图所示的烽火台，其主体部分为一方亭，将它的主体部分抽象成1111ABCD A B C D-的正四棱台（如图所示），其中上底面与下底面的面积之比为1:16，方亭的高为棱台上底面边长的3倍.已知方亭的体积为3567m，则该方亭的表面积约为（）2.2≈1.7≈1.4≈）A．2380m B．2400m C．2450m D．2480m【答案】C【解析】设方亭相应的正四棱台的上底面边长11A B a=，则4AB a=，棱台的高3h a=，所以(2213165673V a a a=⨯+=，解得3a=，所以正四棱台的上底面边长为3m，下底面边长为12m，棱台的高为9m，2=，由于各侧面均为相等的等腰梯形，所以()1142ABB Aa aS+=所以方亭的表面积22222216417450m 4S a a a a =++⨯=+≈.故选：C变式8．（2024·甘肃张掖·高台县第一中学校考模拟预测）仿钧玫瑰紫釉盘是收藏于北京故宫博物院的一件明代宣德年间产的瓷器．该盘盘口微撇，弧腹，圈足．足底切削整齐．通体施玫瑰紫釉，釉面棕眼密集，美不胜收．仿钧玫瑰紫釉盘的形状可近似看成是圆台和圆柱的组合体，其口径为15.5cm ，足径为9.2cm ，顶部到底部的高为4.1cm ，底部圆柱高为0.7cm ，则该仿钧玫瑰紫釉盘圆台部分的侧面积约为（）（参考数据：π的值取3 4.6≈）A ．2143.1cm B ．2151.53cm C ．2155.42cm D ．2170.43cm 【答案】D【解析】方法1：设该圆台的母线长为l ，高为h ，两底面圆的半径分别为R ，r （其中R r >），则215.5cm R =，29.2cm r =，()4.10.7 3.4cm h =-=，所以()46m .c l ==≈，故圆台部分的侧面积为()()21π3(7.75 4.6) 4.6170.43cm S R r l =+≈⨯+⨯=．故选：D方法2（估算法）：若按底面直径为15.5cm ，高为3.4cm 的圆柱估算圆台部分的侧面积得()2315.5 3.4158.1cm S '≈⨯⨯=，易知圆台的侧面积应大于所估算的圆柱的侧面积，故此仿钧玫瑰紫釉盘圆台部分的侧面积大于2158.1cm ，对照各选项可知只有D 符合．故选：D【解题方法总结】（1）多面体的表面积是各个面的面积之和．（2）旋转体的表面积是将其展开后，展开图的面积与底面面积之和．（3）组合体的表面积求解时注意对衔接部分的处理．题型三：空间几何体的体积例7．（2024·广东梅州·统考三模）在马致远的《汉宫秋》楔子中写道：“毡帐秋风迷宿草，穹庐夜月听悲笳.”毡帐是古代北方游牧民族以为居室、毡制帷幔.如图所示，某毡帐可视作一个圆锥与圆柱的组合体，圆锥的高为4，侧面积为15π，圆柱的侧面积为18π，则该毡帐的体积为（）A ．39πB ．18πC ．38πD ．45π【答案】A【解析】设圆柱的底面半径为r ，高为h ，圆锥的母线长为l ，因为圆锥的侧面积为15π，所以15πrl π=，即15rl =.因为2224l r =+，所以联立解得3r =（负舍）.因为圆柱的侧面积为18π，所以218πrh π=，即2318πh π⨯=，解得3h =，所以该毡帐的体积为221π4π39π3r r h ⨯+=.故选：A.例8．（2024·重庆沙坪坝·高三重庆一中校考阶段练习）若某圆锥的侧面展开图是一个半径为2）A B ．8C ．27D ．27【答案】C【解析】设圆锥底面半径为r ，因为母线长为2l =,则半圆弧长π2πl ===底面周长2πr =，所以1r =，圆锥的高为PO =如图，设O B x '=，则EB =，设OO h '=，则PO h '=-，因为PO O BPO OA''=，∴11x =所以)13h x -=，∴23x =，)2429V h ==⨯，故选：C ．例9．（2024·山东青岛·高三统考期中）已知正四棱锥的各顶点都在同一个球面上，球的体积为36π，则该正四棱锥的体积最大值为（）A ．18B ．643C ．814D ．27【答案】B【解析】如图，设正四棱锥的底面边长2AB a =，高PO h =，外接球的球心为M ，则OD =，因为球的体积为34π36π3R =，所以球的半径为3R =，在Rt MOD △中，222MD OD OM =+，即22232(3)a h =+-，所以正四棱锥的体积为2211249(3)333V Sh a h h h ⎡⎤==⨯=--⎣⎦整理得3224(0)3V h h h =-+>，则2282(4)V h h h h '=-+=--，当04h <<时，0V '>，当4h >时，0V '<，所以3224(0)3V h h h =-+>在(0,4)上递增，在(4,)+∞上递减，所以当4h =时，函数取得最大值3226444433-⨯+⨯=，故选：B变式9．（2024·湖北武汉·高三统考开学考试）攒尖是我国古代建筑中屋顶的一种结构形式，宋代称为最尖，清代称攒尖，通常有圆形攒尖､三角攒尖､四角攒尖､八角攒尖，也有单檐和重檐之分，多见于亭阁式建筑､园林建筑.下面以四角攒尖为例，如图，它的屋顶部分的轮廓可近似看作一个正四棱锥.已知正四棱锥的底面边长为5米，则其体积为（）立方米.A ．B ．24C ．D ．72【答案】B【解析】如图所示，在正四棱锥P ABCD -中，连接,AC BD 于O ，则O 为正方形ABCD 的中心，连接OP ，则底面边长AB =6BD ==，132==BO BD .又5BP =，故高4OP ==.故该正四棱锥体积为(214243V =⨯⨯=.故选：B变式10．（2024·广东河源·高三校联考开学考试）最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》（1247年）.该书第二章为“天时类”，收录了有关降水量计算的四个例子，分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和“竹器验雪”.如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量（平地降雪厚度=器皿中积雪体积除以器皿口面积），已知数据如图（注意：单位cm ），则平地降雪厚度的近似值为（）A ．91cm 12B ．31cm 4C ．95cm 12D ．97cm 12【答案】C【解析】如图所示，可求得器皿中雪表面的半径为204015cm 4+=，所以平地降雪厚度的近似值为()2221π2010151015953cmπ2012⨯⨯++⨯=⨯.故选：C变式11．（2024·浙江·校联考模拟预测）如图是我国古代量粮食的器具“升”，其形状是正四棱台，上、下底面边长分别为20cm 和10cm，侧棱长为．“升”装满后用手指或筷子沿升口刮平，这叫“平升”．则该“升”的“平升”约可装()31000cm 1L =（）A ．1.5LB ．1.7LC ．2.3LD ．2.7L【答案】C【解析】根据题意画出正四棱台的直观图，其中底面ABCD 是边长为20的正方形，底面1111D C B A 是边长为10的正方形，侧棱1C C =记底面ABCD 和底面1111D C B A 的中心分别为O 和1O ，则1O O 是正四棱台的高.过1C 作平面ABCD 的垂线，垂足为E ，则E AC ∈且11C E O O ，11C E O O =，所以1111111022OE O C A C ====，112022OC AC ===，故CE OC OE =-=所以棱台的高110h C E ==，由棱台的体积公式得3311((400100200)10 2.310cm 2.3L 33V S S h '=+=++⨯≈⨯=．故选：C .【解题方法总结】求空间几何体的体积的常用方法公式法规则几何体的体积，直接利用公式割补法把不规则的几何体分割成规则的几何体，或者把不规则的几何体补成规则的几何体等体积法通过选择合适的底面来求几何体体积的一种方法，特别是三棱锥的体积题型四：直观图例10．（2024·辽宁锦州·渤海大学附属高级中学校考模拟预测）已知用斜二测画法画梯形OABC 的直观图O A B C ''''如图所示，3O A C B ''''=，C E O A ''''⊥，8OABC S =，//C D y '''轴，C E ''=，D ¢为O A ''的三等分点，则四边形OABC 绕y 轴旋转一周形成的空间几何体的体积为．【答案】48π【解析】在直观图中，1C D E ''''=，所以在还原图中，2CD =，如图，在直观图中，3O A C B ''''=，D ¢为O A ''的三等分点，所以在还原图中，3OA CB =，D 为OA 的三等分点，又在直观图中，//C D y '''轴，所以在还原图中，//CD y 轴，则CD OA ⊥，所以()11244822OABC S CD OA CB CB CB =⨯+=⨯⨯==，则2CB =，故6OA =，123OD OA ==，所以四边形OABC 是等腰梯形，所以四边形OABC 绕y 轴旋转一周所形成的空间几何体的体积等于一个圆台的体积减去一个圆锥的体积，即()22211152π8ππ44662π2248π3333V =⨯+⨯+⨯-⨯⨯=-=．故答案为：48π.例11．（2024·全国·高三对口高考）若正ABC 用斜二测画法画出的水平放置图形的直观图为A B C ''' ，当A B C '''ABC 的面积为．【答案】【解析】A B C ''' 是正ABC 的斜二测画法的水平放置图形的直观图，如图所示，设B C a ''=，则A B C ''' 的面积为1sin 452a O A ⋅⋅⋅'︒='O A a ∴=''，ABC ∴ 的面积为11222S a OA a O A a ''=⋅=⋅⋅==故答案为：例12．（2024·四川成都·高三统考阶段练习）用斜二测画法画出的某平面图形的直观图如图所示，边A B ''与C D ''平行于x '轴.已知四边形A B C D ''''的面积为21cm ，则原平面图形的面积为2cm .【答案】【解析】根据题意得45B A D '''∠= ，原四边形为一个直角梯形，且CD C D ''=，AB A B ''=，2AD A D ''=，())()21sin 45124A B C D S A B C D A D A B C D A D cm ''''=+⋅=''''''''''''+⋅= 梯形，则()A B C D A D ''''''+⋅=所以，()()())211222ABCD S AB CD AD A B C D A D A B C D A D cm '''''''''''=+⋅=+⋅=+⋅='梯形.故答案为：变式12．（2024·全国·高三专题练习）如图，A O B ''' 是用斜二测画法得到的△AOB 的直观图，其中23O A O B ''''==，，则AB 的长度为．【答案】【解析】把直观图A O B '''V 还原为AOB ,如图所示：根据直观图画法规则知,2,2236OA O A OB O B ''''====⨯=,所以AB 的长度为AB ==故答案为：.变式13．（2024·上海浦东新·高三上海市川沙中学校考期末）有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形（如图所示）.45,1,ABC AB AD DC BC ∠===⊥ ，则这块菜地的面积为【答案】22+【解析】过A 作AE BC ⊥于E ，在直观图中， 45ABC ∠= ，1AB AD ==，DC BC ⊥，所以1,2EC BE ==，12BC ∴=+，故原平面图形的上底为1，下底12+，高为2，所以这块菜地的面积为1(11222S =⨯+⨯=故答案为：22+.变式14．（2024·上海宝山·高三上海交大附中校考开学考试）我们知道一条线段在“斜二测”画法中它的长度可能会发生变化的，现直角坐标系平面上一条长为4cm 线段AB 按“斜二测”画法在水平放置的平面上画出为A B ''，则A B ''最短长度为cm （结果用精确值表示）【解析】如图1所示，可以将平面内所有长为4的线段平移至图中O 点为起点，则它们的终点形成以O 为圆心，半径为4的圆周.以两条互相垂直的直径为坐标轴，建立平面直角坐标系.然后在斜二测画法下画出该圆的直观图，如图2，形成一个椭圆，由斜二测的性质可知，在图2，该椭圆长半轴为4，且经过点A '，易知122OA OA '==且45xO y '︒∠=，所以A '，设椭圆的方程为：222116x y b +=，将A '代入得：222116b +=，解得b ==由椭圆的性质可知，椭圆上的点中，短轴端点到原点的距离b 最小，即7即为所求.故答案为：7.变式15．（2024·陕西延安·校考一模）如图，梯形ABCD 是水平放置的一个平面图形的直观图，其中=45∠ ABC ，1AB AD ==，DC BC ⊥，则原图形的面积为．【答案】22+【解析】因为1AB AD ==，=45∠ ABC ，DC BC ⊥，所以12BC =+，12A D A B ''=''=，，12B C =+''所以()112222222S A D B C A B '''⎛⎫=+⋅=⨯+⨯=+ ⎪ ⎪⎝⎭'''．故答案为：22+．变式16．（2024·全国·高三专题练习）如图，用斜二测画法画一个水平放置的平面图形的直观图为一个正方形，则原来图形的面积是．【答案】【解析】由直观图可知，在直观图中,，由斜二测画法的特点，知该平面图形的直观图的原图形如图所示所以原图图形为平行四边形，底面边长为1，位于y 轴的对角线长为，所以原来图形的面积为1S =⨯=.故答案为：【解题方法总结】斜二测法下的直观图与原图面积之间存在固定的比值关系：2S =4S 直原．题型五：展开图例13．（2024·山东青岛·统考三模）已知圆锥的底面半径为1，侧面展开图为半圆，则该圆锥内半径最大的球的表面积为．【答案】43π/43π【解析】设圆锥母线长为l ，由题意2π1πl ⨯=，2l =，圆锥内半径最大的球与圆锥相切，作出圆锥的轴截面PAB ，截球得大圆为圆锥轴截面三角形的内切圆O ，,D E 是切点，如图，易知PD 是圆锥的高，O 在PD 上，由2,1PA BD ==得π6BPD ∠=，因此π3ABP ∠=，所以1π26OBD DBP ∠=∠=，πtan 63OD BD =，所以圆锥内半径最大的球的表面积为24π4π(33S =⨯=，故答案为：4π3．例14．（2024·全国·高三专题练习）如图，在直三棱柱111ABC A B C -的侧面展开图中，B ，C 是线段AD 的三等分点，且AD =．若该三棱柱的外接球O 的表面积为12π，则1AA =．【答案】【解析】由该三棱柱的外接球O 的表面积为12π，设外接球得半径为r ，则24π12πr =，解得r =，由题意，取上下底面三角形得中心，分别为,E F ，EF 得中点即为外接圆圆心O ，作图如下：则OC r ==，EF ⊥平面ABC ，12EF AA OF ==，CF ⊂Q 平面ABC ，OF CF ∴⊥，在等边ABC 中，2sin 6013CF BC =⋅⋅= ，在Rt OFC △中，OF ，12AA OF ==故答案为：例15．（2024·上海普陀·高三统考期中）2022年4月16日，神舟十三号载人飞船返回舱在东风着陆场预定区域成果着陆．如图，在返回过程中使用的主降落伞外表面积达到1200平方米，若主降落伞完全展开后可以近似看着一个半球，则完全展开后伞口的直径约为米（精确到整数）【答案】28【解析】设主降落伞展开后所在球体的半径为R ，由题可得221200R π=，解得14R ≈，故完全展开后伞口的直径约为28米.故答案为：28.变式17．（2024·山东淄博·统考一模）已知圆锥的底面半径为1，其侧面展开图为一个半圆，则该圆锥的体积为．【解析】∵圆锥的底面半径为1，∴侧面展开图的弧长为2π，又∵侧面展开图是半圆，∴侧面展开图的半径为2，即圆锥的母线长为2，故圆锥的高为=2113V π=⋅变式18．（2024·安徽·蚌埠二中校联考模拟预测）如图，在三棱锥P -ABC 的平面展开图中，CD AB ∥，AB AC ⊥，22AB AC ==，CD =，cos BCF ∠65=，则三棱锥-P ABC 外接球表面积为．【答案】14π【解析】由题意可知，DC AC ⊥，CD CF =AD AE ==，BC =在 BCF 中，2222cos 10BF CF BC CF BC BCF =+-⋅∠=，则BE BF ==因为222AB BE AE +=，所以AB BE ⊥，在三棱锥P -ABC 外接球的球心为O ，PC AC ⊥，PB AB ⊥，记PA 中点为O ，OC OB OA OP ===，即三棱锥P -ABC 外接球的球心为点O ，半径222PA AD R ===，所以外接球表面积为14π．故答案为：14π变式19．（2024·全国·高三专题练习）已知三棱锥P －ABC 的底面ABC 为等边三角形．如图，在三棱锥P －ABC 的平面展开图中，P ，F ，E 三点共线，B ，C ，E三点共线，cos 26PCF ∠=，PC =PB ＝．【答案】【解析】由题意可知，△CEF 为等边三角形，所以60CEF EFC ∠=∠= ，则120PFC ∠= ，由cos 26PCF ∠=可知sin 26PCF ∠=，在△PCF中，由正弦定理得：sin 3sin1202PC PCF PF ∠===．在△PCE 中，由余弦定理得：()()221333EF EF EF EF =++-+⋅，解得1EF =或4EF =-（舍去），所以1AB BC CE ===，则4PE =，2BE =，在△PBE 中，由余弦定理得21642412PB =+-⨯=，所以PB =．故答案为：变式20．（2024·安徽黄山·统考一模）如图，在四棱锥P -ABCD 的平面展开图中，正方形ABCD 的边长为4，ADE V 是以AD 为斜边的等腰直角三角形，90HDC FAB ∠=∠=︒，则该四棱锥外接球被平面PBC 所截的圆面的面积为.【答案】365π【解析】该几何体的直观图如下图所示分别取,AD BC 的中点,O M ，连接,OMPM2,4,PO OM PM ==== 222,OP OM PM OP OM∴+=∴⊥又PO AD ⊥ ，所以由线面垂直的判定定理得出PO ⊥平面ABCD 以点O为坐标原点，建立空间直角坐标系(2,0,0),(2,4,0),(2,4,0)A B C -，(2,0,0),(0,0,2)D P -设四棱锥P ABCD -外接球的球心()0,2,N a PN NA = ，()224244a a ∴+-=++，解得0a =设平面PBC 的法向量为(,,)n x y z = (2,4,2),(2,4,2),(0,2,2)PB PC NP =-=--=- 20.020.0x y z PB n x y z PC n ⎧+-=⎧=⇒⎨⎨-+-==⎩⎩ ，取2z =，则(0,1,2)n = 四棱锥P ABCD -外接球的球心到面PBC的距离为cos ,5n NP d NP n NP NP n NP⋅=⋅=⋅==又NP PBC 所截的圆的半径r =所以平面PBC 所截的圆面的面积为2365r ππ=.故答案为：365π变式21．（2024·山西大同·高三统考阶段练习）如图，在三棱锥-P ABC 的平面展开图中，1AC =，AB AD ==AB AC ⊥，AB AD ⊥，30CAE ∠=︒，则三棱锥-P ABC 的外接球的表面积为．【答案】7π【解析】还原出如图所示的三棱锥B PAC -，AB AC ⊥ ，AB AD ⊥，AB ∴⊥平面PAC ，设平面PAC 的截面圆心为O '，半径为r ，球心为O ，球半径为R ，在PAC △中，由余弦定理可得2222cos3013211PC AC AP AC AP =+-⋅⋅=+-⨯⨯ ，则1PC =，这由正弦定理得22sin 30PC r ==，1r =，122OO AB '== ，2R ∴==，∴外接球的表面积2472S ππ⎫==⎪⎪⎝⎭.故答案为：7π.【解题方法总结】多面体表面展开图可以有不同的形状，应多实践，观察并大胆想象立体图形与表面展开图的关系，一定先观察立体图形的每一个面的形状．题型六：最短路径问题例16．（2024·福建福州·高一福建省福州屏东中学校考期末）如图，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P 出发，绕圆锥爬行一周后回到点P 处，若该小虫爬行的最短路程为）.A ．3B ．27C ．81D ．3【答案】C 【解析】作出该圆锥的侧面展开图，如图所示：该小虫爬行的最短路程为1PP ，。

2025届高考数学一轮复习讲义立体几何与空间向量之空间直线、平面的垂直

⋂＝
⑬
ቋ⇒α⊥β
⊥
⇒l⊥α
二、基础题练习
1. 在空间中，α，β是两个不同的平面， m ， n 是两条不同的直线，下列说法错误的
是(
C )
A. 若m⊥α，m∥n，n⊂β，则α⊥β
B. 若α∥β，m⊥α，n⊥β，则m∥n
C. 若α∥β，m⊂α，n⊂β，则m∥n
D. 若α⊥β，m⊂α，α∩β＝n，m⊥n，则m⊥β
三、知识点例题讲解及方法技巧总结
命题点1
线面垂直的判定与性质
例1 [2024惠州市二调节选]如图，已知平行六面体 ABCD － A 1 B 1 C 1 D 1中，底面
ABCD 是正方形，侧面 ADD 1 A 1是矩形，点 P 为 D 1 C 1的中点，且 PD ＝ PC .
求证： DD 1⊥平面 ABCD .
因为 AB 1∥ DC 1，所以直线 AB 1与 AD 1所成的角即直线 DC 1与 AD 1所
成的角.
又 AD 1＝ AB 1＝ B 1 D 1，所以△ AB 1 D 1为正三角形，
所以∠ D 1 AB 1＝60°，所以直线 AD 1与 AB 1所成角的大小为60°，
即直线 AD 1与 DC 1所成角的大小为60°.
D 与正方体的12条棱所成的角都相等.连接 BD 1，与平面 A 1 C 1 D 交于点 O ，连接 A 1
1
3
O ，则 BD 1⊥平面 A 1 C 1 D ，则α＝∠ D 1 A 1 O ，且 D 1 O ＝ BD 1＝
3
1
＝3
1 1
1
＝
3
，故选B.
3
3
，所以
3
sin α＝
4. [教材改编]在正方体 ABCD － A 1 B 1 C 1 D 1中，直线 AB 与 A 1 D 1所成角的大小

2025届高考数学一轮复习讲义立体几何与空间向量之空间直线、平面的平行

∴ A 1 B ∥平面 DCC 1 D 1.
例2 [北京高考节选]如图，在正方形 AMDE 中， B ， C 分别为 AM ， MD 的中点.在五
棱锥 P － ABCDE 中， F 为棱 PE 的中点，平面 ABF 与棱 PD ， PC 分别交于点 G ，
H . 求证： AB ∥ FG .
[解析] 在正方形 AMDE 中，因为 B 是 AM 的中点，所以 AB ∥ DE .
∴ BD 1∥平面 ACE .
易得直线 BA 1， BC 1， BB 1均与平面 ACE 不平行.
2. [多选/教材改编]若直线 a 平行于平面α，则(
A. 平面α内有且只有一条直线与a平行
B. 平面α内有无数条直线与a平行
C. 平面α内存在无数条与a不平行的直线
D. 平面α内任意一条直线都与a平行
又 AB ⊄平面 PDE ， DE ⊂平面 PDE ，
所以 AB ∥平面 PDE .
因为 AB ⊂平面 ABF ，且平面 ABF ∩平面 PDE ＝ FG ，
所以 AB ∥ FG .
方法技巧
1. 证明线线平行常用的方法
(1)利用线面平行的性质定理.
(2)利用面面平行的性质定理.
(3)利用中位线，对应线段成比例，平行四边形的性质等.
4. 两个平面平行，其中一个平面内的任意一条直线平行于另一个平面.
5. 夹在两个平行平面之间的平行线段长度相等.
6. 经过平面外一点有且只有一个平面与已知平面平行.
二、基础题练习
1. [教材改编]在正方体 ABCD － A 1 B 1 C 1 D 1中， E 为 DD 1的中点，则下列直线中与
平面＝2，∴ AB
DE ，
∴四边形 ABED 为平行四边形，

北京市清华大学附中2015届全国高校自主招生考试数学复习讲义：平面几何(无答案)

平面几何一、考试要求：平面几何是自主招生考试中北约、华约、卓越共同考查的内容，主要考查平面图形中三边角关系以及长度、角度、面积的计算；考查学生逻辑思维能力，推理认证能力及计算能力.二、知识准备：定理：梅涅劳斯定理：设△ABC 的三边BC 、CA 、AB 或他们的延长线与一条不经过其顶点的直线交于P 、Q 、R 三点，则1=∙∙RBAR QA CQ PC BP . 梅涅劳斯逆定理：设P 、Q 、R 分别是△ABC 的三边BC 、CA 、AB 或他们的延长线上三点，若有1=∙∙RBAR QA CQ PC BP ，则P 、Q 、R 三点在同一条直线上. 三、题型训练：类型一：凸多边形有关的计算或证明例1：（2012北约）求证：若圆内接五边形的两个角都相等，则它为正五边形.例2：（2008北约）求证：边长为1的正五边形对角线长为215+.例4：（2013北约）如果锐角△ABC 的外接圆圆心为O ，求O 到三角形三边距离比.例5：（2009北大）圆内接四边形ABCD 中，AB=1，BC=2，CD=3，DA=4.求圆的半径.例6：（2011北约）在△ABC 中，若c b a 2≥+，证明60≤∠c .其中∠A,∠B,∠C 的对边分别为c b a ,,. 例7：（2009中国科技大）如图：已知D ，E ，F 分别为BC ，AC ，AB 的三等分点.且EC ＝２AE ，BD ＝２CD ，AF ＝２BF ，若1=∆ABC S ，试求PQR S ∆.例８：（２０１１华约）如图，已知△ABC 的面积为２，D ，E 分别为边AB ，AC 上的点， F 为线段DE 上一点，设z DEDF y AC AE x AB AD ===,,，且1=-+x z y .则△BD 下面积的最大值为（）A.278 B. 2710 C. 2714 D. 2716例9：（2010五校）如图，△ABC 的两条交线AD ，BE 交于H ，其外接圆圆心为O ，过O OF 垂直BC 于F ，OH 与AF 相交于G ，则△OFG 与△GAH 面积之比为（）A. 1:4B. 1:3C. 2:5D. 1:2例10：（2011北大保送）在△ABC 内有一点P ，满足PCA PAC PAB PBC ∠=∠=∠=∠. 求证：△ABC 的三边边长成等比数列.例11：（2009南京大学）P 为△ABC 内一点，它到三边BC ，CA ，AB 的距离分别为321,,d d d ，S 为△ABC 的面积.求证：sc b ad c d b d a 2)(2321++≥++（这里c b a ,,分别表示BC ， CA ，AB 的长）.例14：（2007克罗地亚国家采训队）已知：S 为△ABC 内一点，证明：当S 到△ABC 三边距离的积取最大值时，S 为△ABC 的重心.例15：在锐角△ABC 中，111,,C B A 分别为BC ，CA ，AB 的中点，O 为△ABC 外接圆的圆心，若外接圆半径为1，证明：6111111≥++OC OB OA .。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平面几何
一、考试要求：平面几何是自主招生考试中北约、华约、卓越共同考查的内容，主要考查平面图形中三边角关系以及长度、角度、面积的计算；考查学生逻辑思维能力，推理认证能力及计算能力.
二、知识准备：
定理：梅涅劳斯定理：设△ABC 的三边BC 、CA 、AB 或他们的延长线与一条不经过其顶点的直线交于P 、Q 、R 三点，则1=••RB AR QA CQ PC BP . 梅涅劳斯逆定理：设P 、Q 、R 分别是△ABC 的三边BC 、CA 、AB 或他们的延长线上三点，若有
1=••RB
AR QA CQ PC BP ，则P 、Q 、R 三点在同一条直线上. 三、题型训练：
类型一：凸多边形有关的计算或证明
例1：（2012北约）求证：若圆内接五边形的两个角都相等，则它为正五边形.
例2：（2008北约）求证：边长为1的正五边形对角线长为2
15+.
例4：（2013北约）如果锐角△ABC 的外接圆圆心为O ，求O 到三角形三边距离比.
例5：（2009北大）圆内接四边形ABCD 中，AB=1，BC=2，CD=3，DA=4.求圆的半径.
例6：（2011北约）在△ABC 中，若c b a 2≥+，证明
60≤∠c .其中∠A,∠B,∠C 的对边分别为c b a ,,.
例7：（2009中国科技大）如图：已知D ，E ，F 分别为BC ，AC ，AB 的三等分点.且EC ＝２AE ，BD ＝２CD ，AF ＝２BF ，若1=∆ABC S ，试求PQR S ∆.
例８：（２０１１华约）如图，已知△ABC 的面积为２，D ，E 分别为边AB ，AC 上的点， F 为线段DE 上一点，设z DE
DF y AC AE x AB AD ===,,，且1=-+x z y .则△BD 下面积的最大值为（） A. 278 B. 2710 C. 2714 D.
2716 例9：（2010五校）如图，△ABC 的两条交线AD ，BE 交于H ，其外接圆圆心为O ，过O OF 垂直BC 于F ，OH 与AF 相交于G ，则△OFG 与△GAH 面积之比为（）
A. 1:4
B. 1:3
C. 2:5
D. 1:2
例10：（2011北大保送）在△ABC 内有一点P ，满足PCA PAC PAB PBC ∠=∠=∠=∠. 求证：△ABC 的三边边长成等比数列
.
例11：（2009南京大学）P 为△ABC 内一点，它到三边BC ，CA ，AB 的距离分别为321,,d d d ，
S 为△ABC 的面积.求证：s
c b a
d c d b d a 2)(2
321++≥++（这里c b a ,,分别表示BC ， CA ，AB 的长）.
例14：（2007克罗地亚国家采训队）已知：S 为△ABC 内一点，证明：当S 到△ABC 三边距离的积取最大值时，S 为△ABC 的重心.
例15：在锐角△ABC 中，111,,C B A 分别为BC ，CA ，AB 的中点，O 为△ABC 外接圆的圆心，若外接圆半径为1，证明：61111
11≥++OC OB OA .。

清华大学附中高考数学复习讲义 平面几何(无答案)

高考数学一轮复习 第十三章 立体几何 13.1 平面的基本性质讲义

2025年新人教版高考数学一轮复习讲义 第七章 §7.10 立体几何中的动态、轨迹问题