逻辑推理PPT课件
合集下载
逻辑推理问题-说谎问题PPT课件

谎言者悖论
定义
一个陈述声称自己是假的。
例子
“我正在说的这句话是假的。”
分析
如果这句话是真的,则它是假的;如果它是假的,则它是真的。因此, 这句话既不是真的也不是假的,形成了一个悖论。
其他类型的说谎问题
01
悖论的实例
如“罗素悖论”、“理发师悖论”等。
02
涉及多个陈述的复杂说谎问题
例如,有两个人分别说“我们两个人中至少有一个人在说谎”和“我们
根据已知的前提和推理规则,推导出结论,判断说谎 者。
模态逻辑分析方法
80%
可能性和必然性
分析说谎者话语中的模态词,如 “可能”、“必然”等,推断其 真实意图。
100%
模态悖论
探讨说谎者悖论等模态悖论在说 谎问题中的应用。
80%
模态推理规则
运用模态逻辑的推理规则,分析 说谎者的陈述,揭示真相。
多值逻辑分析方法
说谎的心理学和社会学问题
说谎的心理动机
说谎者可能出于自我保护、谋取私利、逃避责任等心理动机而说谎。
说谎的社会影响
说谎可能对社会造成负面影响,如破坏信任、导致误解、引发冲突等。
说谎与社交技巧
在社交场合中,适当的“白色谎言”有时被视为一种社交技巧,用于避免冲突或保护他人 感情。然而,这并不意味着所有谎言都是可接受的,需要根据具体情况进行道德和伦理的 考量。
意外绞刑悖论
定义
一个法官告诉囚犯,在下周的某天会对囚犯处以绞刑,而具 体哪一天将出人意料。然而到了周末,囚犯仍未被处刑,于 是囚犯根据法官的条件推理出自己不会被处刑,但结果却在 周日被处刑。
分析
囚犯的推理基于法官的条件,但法官可以违反自己的条件来 处刑囚犯。因此,囚犯的推理虽然看似合理,但实际上并不 成立。
小学四年级奥数-数学逻辑推理课件

数教程》等。
在线课程
利用在线课程资源,如“学而 思”、“腾讯课堂”等平台上 的奥数课程,进行系统学习。
练习题集
选择适合的练习题集,如《小 学奥数千题巧解》等,进行有
针对性的练习。
数学逻辑推理游戏
通过数学逻辑推理游戏,如“ 数独”、“逻辑拼图”等,提
高数学逻辑推理能力。
THANKS
感谢观看
03
数学逻辑推理应用
数字推理
总结词
通过数字的变化规律,推导出未知数 。
详细描述
数字推理题通常给出一些数字序列, 要求找出其中的规律,并推导出下一 个数字。常见的数字推理规律包括递 增、递减、循环等。
图形推理
总结词
通过观察图形的变化规律,判断未知图形。
详细描述
图形推理题通常给出一些图形序列,要求找出其中的规律,并判断出下一个图形。常见的图形推理规律包括旋转 、对称、拼接等。
间接推理
总结词
理解间接推理的概念,掌握通过反证法、假设法等间接方法得出结论的技巧。
详细描述
间接推理是通过否定或质疑某些条件,进而推断出与原命题相反的结论的过程 。常用的间接推理方法包括反证法、假设法等。
归纳与演绎推理
总结词
了解归纳和演绎推理的基本概念,初步掌握其应用方法。
详细描述
归纳推理是从个别到一般的推理过程,通过观察和实验得出一般性结论;演绎推 理则是从一般到个别的推理过程,根据一般性原理推导出个别结论。
应用题推理
总结词
通过分析应用题的已知条件,推导出未知量。
详细描述
应用题推理题通常涉及实际问题的解决,如路程、时间、速度等问题。解题时需要仔细分析已知条件 ,并运用数学逻辑推理方法,推导出未知量。
在线课程
利用在线课程资源,如“学而 思”、“腾讯课堂”等平台上 的奥数课程,进行系统学习。
练习题集
选择适合的练习题集,如《小 学奥数千题巧解》等,进行有
针对性的练习。
数学逻辑推理游戏
通过数学逻辑推理游戏,如“ 数独”、“逻辑拼图”等,提
高数学逻辑推理能力。
THANKS
感谢观看
03
数学逻辑推理应用
数字推理
总结词
通过数字的变化规律,推导出未知数 。
详细描述
数字推理题通常给出一些数字序列, 要求找出其中的规律,并推导出下一 个数字。常见的数字推理规律包括递 增、递减、循环等。
图形推理
总结词
通过观察图形的变化规律,判断未知图形。
详细描述
图形推理题通常给出一些图形序列,要求找出其中的规律,并判断出下一个图形。常见的图形推理规律包括旋转 、对称、拼接等。
间接推理
总结词
理解间接推理的概念,掌握通过反证法、假设法等间接方法得出结论的技巧。
详细描述
间接推理是通过否定或质疑某些条件,进而推断出与原命题相反的结论的过程 。常用的间接推理方法包括反证法、假设法等。
归纳与演绎推理
总结词
了解归纳和演绎推理的基本概念,初步掌握其应用方法。
详细描述
归纳推理是从个别到一般的推理过程,通过观察和实验得出一般性结论;演绎推 理则是从一般到个别的推理过程,根据一般性原理推导出个别结论。
应用题推理
总结词
通过分析应用题的已知条件,推导出未知量。
详细描述
应用题推理题通常涉及实际问题的解决,如路程、时间、速度等问题。解题时需要仔细分析已知条件 ,并运用数学逻辑推理方法,推导出未知量。
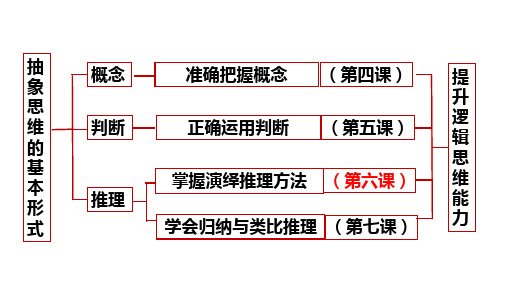
6.1 推理与演绎推理概述 课件(共27张PPT)高中政治统编版选择性必修3 逻辑与思维
甲说乙说谎,乙说丙说谎,丙说甲和乙都说谎。以下正确的说法是( ) A.甲和乙诚实,丙是说谎者 B.甲和丙说谎,乙是诚实者 C.乙和丙说谎,甲是诚实者 D.乙和丙诚实,甲是说谎者
解析: ①根据题干三个条件,假设甲诚实,那么乙就是说谎者;乙是说 谎者,则丙诚实;若丙诚实,则甲和乙都是说谎者,这个推演结果与我 们的初始假设“甲诚实”不一致(矛盾),于是可定论:甲不诚实。②从 定论“甲不诚实”,可推知乙诚实;从乙诚实,推知丙说谎;从丙说谎, 推出甲和乙不都说谎(乙诚实),推演结果成立,结论是:甲和丙说谎, 乙诚实。故选B。
作案的 不是我
甲
乙
丙
丁
经查证,四个人的口供中只有一个是假的。➢ 谁是作案人?你的结论是如何得出的。
推理过程: 乙:丁是案犯
丁:作案的不是我
两判断有矛盾,根据矛盾律,不可能同真,必有一假
四个人的口供中只有一个是假的。
甲:案犯是丙 丙:如果我作案,那么丁是主犯
根据矛盾律,乙、丁必有一假
甲、丙为真
丙、丁为作案人 (丁说了假话)
形式逻辑的研究对象是推理结构,不研究每个推理所反映的认识对象的 具体内容。
①告诉人们正确的思维应该运用怎样的推理结构,以及运用推理结 构时应该遵循哪些规则; ②帮助人们识别什么样的推理结构是正确的,什么样的推理结构是 不正确的。
正确理解:逻辑学不研究每个推理所反映的认识对象的具体内容。 逻辑学本身只能告诉我们前提和结论之间的逻辑规则,而不具体解决前提真实与否 的问题。前提真实与否只有靠各门具体科学,靠实践来解决。
一、推理的含义与种类
1、判断形成的两条途径
一是通过实践,直接对对象进行观察或调查,然后作出判断; 二是借助已有的判断,合乎逻辑地推出一个新的判断。(推理)
冀教版 六年级数学上册 8.2 简单的逻辑推理问题课件(共23张ppt)

作案者是谁呢?[选自教材P95 练一练 第3题]
甲
肯定是乙干的,我发现他最近总大把花钱。
乙
是丁干的,他以前就有贪污盗窃的行为。
丙 那天我在厂里上班,根本没去过银行,不是我干的。
丁
乙和我有仇,他有意诬陷我。
甲
肯定是乙干的,我发现他最近总大把花钱。
×
乙
是丁干的,他以前就有贪污盗窃的行为。
×
丙 那天我在厂里上班,根本没去过银行,不是我干的。 √
简单的逻辑推理问题
冀教版六年级数学上册
有语文、数学和品德与生活三本书,下面三人各拿 一本。小刚拿的是什么书?小莉呢?
我拿的是 语文书。
小莉
我拿的不是数学书。 品德与生活
小刚
数学
小红
一个正方体骰子,六个面上分别刻有 1、2、3、4、5、 6 这六个点数。从三个不同的角度看这个骰子,看到 的点数如下:
从图(1)可以看出 5 点的对面不是 4 点和 6 点; 从图(3)可以看出 5 点的对面不是 1 点和 3 点; 所以 5 点的对面只能是( 2 )点; 那么 6 点的对面只能是( 1 )点。
拿出手中的骰子检验判断的结果是否正确。 说一说骰子对面两个点数有什么特点? 对面两个点数的和都是7。
归纳总结
丫丫 李明第一名( ) 王欣第三名( )
亮亮 张宏第一名( ) 赵亮第四名( )
聪聪 赵亮第二名( ) 王欣第一名( )
丫丫 李明第一名( √ ) 王欣第三名( × ) 亮亮 张宏第一名( × ) 赵亮第四名( √ ) 聪聪 赵亮第二名( × ) 王欣第一名( √ )
假设丫丫猜测的“李明第一名”是正确的, 那么“王欣第三名”就是错误的, 列表推理发现:李明和王欣都是第一名,所以假设错误。
甲
肯定是乙干的,我发现他最近总大把花钱。
乙
是丁干的,他以前就有贪污盗窃的行为。
丙 那天我在厂里上班,根本没去过银行,不是我干的。
丁
乙和我有仇,他有意诬陷我。
甲
肯定是乙干的,我发现他最近总大把花钱。
×
乙
是丁干的,他以前就有贪污盗窃的行为。
×
丙 那天我在厂里上班,根本没去过银行,不是我干的。 √
简单的逻辑推理问题
冀教版六年级数学上册
有语文、数学和品德与生活三本书,下面三人各拿 一本。小刚拿的是什么书?小莉呢?
我拿的是 语文书。
小莉
我拿的不是数学书。 品德与生活
小刚
数学
小红
一个正方体骰子,六个面上分别刻有 1、2、3、4、5、 6 这六个点数。从三个不同的角度看这个骰子,看到 的点数如下:
从图(1)可以看出 5 点的对面不是 4 点和 6 点; 从图(3)可以看出 5 点的对面不是 1 点和 3 点; 所以 5 点的对面只能是( 2 )点; 那么 6 点的对面只能是( 1 )点。
拿出手中的骰子检验判断的结果是否正确。 说一说骰子对面两个点数有什么特点? 对面两个点数的和都是7。
归纳总结
丫丫 李明第一名( ) 王欣第三名( )
亮亮 张宏第一名( ) 赵亮第四名( )
聪聪 赵亮第二名( ) 王欣第一名( )
丫丫 李明第一名( √ ) 王欣第三名( × ) 亮亮 张宏第一名( × ) 赵亮第四名( √ ) 聪聪 赵亮第二名( × ) 王欣第一名( √ )
假设丫丫猜测的“李明第一名”是正确的, 那么“王欣第三名”就是错误的, 列表推理发现:李明和王欣都是第一名,所以假设错误。
《经典逻辑推理》PPT课件

25
• 合一:
• 寻找项对变量的代换以使两表达式一致,就叫合一
• 设有公式集F={F1,F2,…,Fn},若存在一个代换使 得F1 = F2 =…= Fn ,则称为公式集F的一个合 一代换,且称F1,F2,…,Fn是可合一的。
• 例如:对于公式集F={P(x,y,f(y)),P(a,g(x),z)},则 ={a/x,g(a)/y,f(g(a))/z}是公式F的一个合一。(原
2) 小前提,这是关于所研究的具体情况或个别事实的判断;
3) 结论,这是由大前提推出的适合于小前提所示情况的新判 断。
例如:1) 足球运动员的身体都是强壮的;
2) 高波是一名足球运动员;
3) 所以,高波的身体是强壮的。
2021/7/11
郑州大学振动工程研究所
3
• 归纳推理——归纳推理是从足够多的事例中 归纳出一般性纳论的推理过程,是一种从个 别到一般的推理。归纳推理又分为完全归纳 和不完全归纳两种。
2021/7/11
郑州大学振动工程研究所
5
• Ⅱ. 确定性推理,不确定性推理(按推理时所
用知识的确定性来划分)
•
• 确定性推理—— 指推理时所用的知识都是精确的 ,推出的结论也是确定的,其真值或为“真”, 或为“假”,没有第三种情况出现。
• 下面将要讨论的经典逻辑推理就属于这一类。
• 不确定性推理——指推理时所用的知识不都是精 确的,推出的结论也不完全是肯定的,其真值位 于“真”和“假”之间,命题的外延模糊不清。
2021/7/11
郑州大学振动工程研究所
17
• 双向推理
• 双向推理是指正向推理与逆向推理同时进行, 且在推理过程中的某一步骤上“碰头”的一种 推理方式。
逻辑推理(进阶)ppt课件

思路总结
练习5:甲、乙、丙、丁四人同时参加全国小学数学夏令营。 赛前甲、乙、丙分别做了预测。 甲说:“丙 第1名,我第3名。”乙说:“我第1名,丁第4名。”丙说:“丁第2名,我第3名。”成绩揭晓后,发现他们 每人只说对了一半你能说出他们的名次吗?
练习6:三只小猴子聪聪、淘淘、皮皮见到一个水果,他们分别判断这是什么水果聪聪判断:不是苹果, 也不是梨。淘淘判断:不是苹果,而是桃子。 皮皮判断:不是桃子,而是苹果。 老猴子告诉他们:有一只小猴子的判断完全正确,有一只小猴子说对了-半,而另一只小猴子完全说错了。 你知道三只小猴中谁是对的,谁是错的谁是只对一半的吗?
比大小解题思路总结: 第一步:确定题型是比大小 第二步:列出选项,用大于号,小于号链接 第三步:根据题意进行找最大最小
练习1 田田比牛牛跑得慢,牛牛比加加跑得快,加加比减减跑得快,减减比田田跑得快。 谁跑得最快? 谁跑得最慢?
练习2 2号大楼比3号大楼高,4号大楼比3号大楼低,1号大楼比2号大楼高,1号大楼比4号大楼高,几 号大楼是最高的?几号大楼是最低的?
搭配问题解题思路总结: 第一步:确定题型是搭配问题 第二步:画表法(连线法)先画已知条件,注意隐藏条件 第三步:根据题意找到突破点(矛盾点)进行突破
练习3:刘玉、马明、王建三个男孩都有一个妹妹,是小雅、小花、丽丽。6个人在一起打球,举 行男女混合双打。事先规定,兄妹两人不ቤተ መጻሕፍቲ ባይዱ伴。第一盘刘玉和丽丽对王建和小雅; 第二盘王建和小花对刘玉和马明的妹妹。问丽丽、小雅和小花各是谁的妹妹?
红红
丁丁
田田
牛牛题型1:乐乐排老顺师 序
【解析】因为“牛牛在丁丁和田田之前爬到终点”,所以牛牛比丁丁和田田爬得快,他们三人的排队顺序是: 牛牛→丁丁→田田或牛牛→田田→丁丁。 又因为“田田是紧跟着牛牛之后爬到终点的”,这时他们三人的排 队顺序是:牛牛一田田→丁丁。 最后我们来分析“有两个人在乐乐老师之后、丁丁之前爬到终点的”,这样可 以判断出乐乐老师的位置应该是第一。 最后得出结论这五人登山到终点的顺序依次是:乐乐老师一牛牛→田田 →丁丁→红红。
幼儿园的数学思维与逻辑推理,主题班会ppt课件

效果
幼儿能够在家庭和幼儿园的共 同培养下,全面发展数学思维 与逻辑推理能力,增强学习兴
趣和动力。
THANKS
[ 感谢观看 ]
幼儿园的数学思维与逻
辑推理,主题班会ppt
课件
汇报人:可编辑
2023-12-24
CONTENTS 目录
• 数学思维与逻辑推理的重要性 • 幼儿园数学思维的培养 • 幼儿园逻辑推理能力的培养 • 实践案例分享
CHAPTER 01
数学思维与逻辑推理的重要性
日常生活中的数学思维与逻辑推理
01
02
03
亲子互动
家长可以与幼儿一起进行数学游 戏、解谜等活动,增进亲子关系
,同时培养幼儿的数学思维。
日常生活中的实践
家长可以在日常生活中引导幼儿运 用数学思维解决实际问题,如购物 时计算找零、制作手工时运用几何 知识等。
鼓励和肯定
家长应鼓励幼儿在数学思维方面的 表现,并及时给予肯定和赞扬,以 增强幼儿的自信心和学习动力。
在日常生活活动中,引导幼儿运用数学思维解决实际问题,如测 量身高、计算时间等。
音乐和艺术中的应用
在音乐和艺术活动中,引导幼儿运用数学思维探索节奏、对称等概 念,培养幼儿的审美和创造力。
科学实验中的应用
在科学实验中,引导幼儿运用数学思维进行观察、测量和记录,培 养幼儿的探究精神和科学素养。
家庭如何配合幼儿园培养数学思维
购物时计算找零
在超市购物时,结账后需 要计算找零,这需要运用 数学思维和逻辑推理能力 。
安排时间与计划
在日常生活中,我们需要 合理安排时间,制定计划 ,这需要运用数学思维和 逻辑推理能力。
解决实际问题
在生活中遇到实际问题时 ,我们需要运用数学思维 和逻辑推理能力来找到解 决方案。
幼儿能够在家庭和幼儿园的共 同培养下,全面发展数学思维 与逻辑推理能力,增强学习兴
趣和动力。
THANKS
[ 感谢观看 ]
幼儿园的数学思维与逻
辑推理,主题班会ppt
课件
汇报人:可编辑
2023-12-24
CONTENTS 目录
• 数学思维与逻辑推理的重要性 • 幼儿园数学思维的培养 • 幼儿园逻辑推理能力的培养 • 实践案例分享
CHAPTER 01
数学思维与逻辑推理的重要性
日常生活中的数学思维与逻辑推理
01
02
03
亲子互动
家长可以与幼儿一起进行数学游 戏、解谜等活动,增进亲子关系
,同时培养幼儿的数学思维。
日常生活中的实践
家长可以在日常生活中引导幼儿运 用数学思维解决实际问题,如购物 时计算找零、制作手工时运用几何 知识等。
鼓励和肯定
家长应鼓励幼儿在数学思维方面的 表现,并及时给予肯定和赞扬,以 增强幼儿的自信心和学习动力。
在日常生活活动中,引导幼儿运用数学思维解决实际问题,如测 量身高、计算时间等。
音乐和艺术中的应用
在音乐和艺术活动中,引导幼儿运用数学思维探索节奏、对称等概 念,培养幼儿的审美和创造力。
科学实验中的应用
在科学实验中,引导幼儿运用数学思维进行观察、测量和记录,培 养幼儿的探究精神和科学素养。
家庭如何配合幼儿园培养数学思维
购物时计算找零
在超市购物时,结账后需 要计算找零,这需要运用 数学思维和逻辑推理能力 。
安排时间与计划
在日常生活中,我们需要 合理安排时间,制定计划 ,这需要运用数学思维和 逻辑推理能力。
解决实际问题
在生活中遇到实际问题时 ,我们需要运用数学思维 和逻辑推理能力来找到解 决方案。
小学三四年级奥数之逻辑推理ppt课件

表
红 黄蓝
格
芬芬 丽丽
法 齐齐
根据条件,逐步进行排除,分析得到答案.
小试锋芒:
小华、小云和小平是同班同学,他们各参加一个体育兴
趣小组。游泳、篮球、跳高。已知:(1)小云不喜欢游泳; (3)小华才是篮球小组的主力队员。(2)小平从来没有 去过篮球小组;问:他们各自参加哪个体育兴趣小组?
小华 小云 小平
游泳
篮球
跳高
第三关:特征问题
同住一间寝室的甲、乙、丙、丁四个人分别来自上海、南京、北京
和沈阳。已知:
(1) 甲不是来自上海,也不是来自北京; (2)乙的家乡不是南京,也不是上海; (3) 如果甲不是来自南京,那么丙就是来自上海; (4)丁的家乡不是北京和上海。 那么他们四个人分别来自哪儿?
表 格
上海 南京 北京 沈阳
修指甲 做头发 化妆 看书
A
×
√
×
×
B
×
×
×
√
C
√
×
×
×
D
×
×
√
×
第四关:神奇正方体
有一个正方体,每个面上分别写上字母 A、B、C、 D、E、F,你能根据下面三个图,找出正方体上相对的 两个面上的字母各是什么吗?
排除法
小试锋芒:
有一个正方体,每个面上分别写上数字 1、2、3、4、 5、6,你能根据下面三个图,找出正方体上相对的两个 面上的数字各是什么吗?
真名:工藤新一 又名:江户川柯南 性格:自信、勇敢、机智…… 擅长:推理、足球…… 名言:真相永远只有一个!
三年级数学逻辑推理
•
在日常生活中,有些问题常常要求
我们主要通过分析和推理,而不是计算得
逻辑推理 趣味数学 精美课件【免费】(共9张PPT)

已知:甲不在北京
乙不在天津 在北京的人不教化学
在天津的人教数学 乙不教物理 根据以上情况判断,甲、乙、丙三人分别 处在何处教什么课程
THANKS
在一次军事训练中,长官对集合的士兵说:
侦
“现在考考你们跑步的速度,你们在我讲完
探
话后到图书馆把我放在桌子上的一本书中的
测
100元拿来,谁第一个抢到,钱就归他,钱放
试
在书的第163至164页之间。”
热
说完大家争先恐后的跑向图书馆,有
身
一名士兵却站在原地,说说他为什么不去?
题
侦探测试入门题
A、B、C、D四名学生,已知B 不是最高的,但比A、D高,A又比 D高。
张老师再三追问,B他说们:都承2认是说蓝的话色中一,半5是红色。
玻璃,黄先生闻声赶去,问:“一定是你们
可可说:“是毛毛C打说破的:。1是红色,4是白色。
请你按照从高到矮的顺序排列这四名学生。
有红、黄、蓝、D白说、绿:五3种是颜色蓝的色玻璃,珠5各是一粒白,色用纸。包着并编上号码,有五个小朋友来猜
结广果来拆 学开校纸开包田一径看运E,动说每会:个,人其2都中是恰一黄好个只项色猜目对是,了由4一5是名半运,绿动且员色每进包。行只1有00一米个短人跑猜比对赛。,赛后5名观众介绍了比赛结果;
黄在先北 生京的的后人院不有结教四果化个学孩拆子开在纸玩球包,一打碎看了,每个人都恰好只猜对了一半,且每包只有一个人猜对。你知 添添:“我没道做,各欣包欣也分没别做。包着什么颜色的玻璃珠吗?
甲、乙、丙三人分别在北京、天津、上海的中学教数学、物理、化学。
侦探测试高级题
甲、乙、丙三人分别在北京、天津、上海 的中学教数学、物理、化学。
请你按照从高到矮的顺序排列 这四名学生。
乙不在天津 在北京的人不教化学
在天津的人教数学 乙不教物理 根据以上情况判断,甲、乙、丙三人分别 处在何处教什么课程
THANKS
在一次军事训练中,长官对集合的士兵说:
侦
“现在考考你们跑步的速度,你们在我讲完
探
话后到图书馆把我放在桌子上的一本书中的
测
100元拿来,谁第一个抢到,钱就归他,钱放
试
在书的第163至164页之间。”
热
说完大家争先恐后的跑向图书馆,有
身
一名士兵却站在原地,说说他为什么不去?
题
侦探测试入门题
A、B、C、D四名学生,已知B 不是最高的,但比A、D高,A又比 D高。
张老师再三追问,B他说们:都承2认是说蓝的话色中一,半5是红色。
玻璃,黄先生闻声赶去,问:“一定是你们
可可说:“是毛毛C打说破的:。1是红色,4是白色。
请你按照从高到矮的顺序排列这四名学生。
有红、黄、蓝、D白说、绿:五3种是颜色蓝的色玻璃,珠5各是一粒白,色用纸。包着并编上号码,有五个小朋友来猜
结广果来拆 学开校纸开包田一径看运E,动说每会:个,人其2都中是恰一黄好个只项色猜目对是,了由4一5是名半运,绿动且员色每进包。行只1有00一米个短人跑猜比对赛。,赛后5名观众介绍了比赛结果;
黄在先北 生京的的后人院不有结教四果化个学孩拆子开在纸玩球包,一打碎看了,每个人都恰好只猜对了一半,且每包只有一个人猜对。你知 添添:“我没道做,各欣包欣也分没别做。包着什么颜色的玻璃珠吗?
甲、乙、丙三人分别在北京、天津、上海的中学教数学、物理、化学。
侦探测试高级题
甲、乙、丙三人分别在北京、天津、上海 的中学教数学、物理、化学。
请你按照从高到矮的顺序排列 这四名学生。
逻辑判断-逻辑推理ppt课件

方法一、
所有+所有→所有 肯定+肯定→肯定
有些+所有→有些 肯定+否定→否定
方法二、画图
.
22
三段论习题
有些教授留长发,因此,有些留长发的是科学 家。为使上述推理成立,需要补充以下哪项作 为前提? A.有些教授是科学家 B.所有科学家都是教授 C.所有教授都是科学家 D.有些科学家不是教授
.
23
第三章 直言命题
2.2 推理规则
四大错误的推理
一. 所有A是B × 所有B是A 二. 有些A非B × 有些B非A 三. 所有A是B × 有些B非A 四. 有些A是B × 有些A非B
例如:
所例有如广:东人是南方人
推有例不些如出人:不是男人 所推所有不有南出长方沙人人是都广是东星人城人 例有推如些不:男出人不是人 有些同学是优秀学生 有些星城人不是长沙人 推不出
所以,有些恒星是太空中的双子星。
推理II:有些太空中的双子星不是恒星,
所以,有些恒星不是太空中的双子星。
A.都正确
B.都不正确
C.I正确,II不正确 D.II正确,I不正确
.
14
2.2 推理规则
所有南京人都是江苏人;所有南京人都喜欢吃咸
鸭;有些江苏人喜欢旅游。如果以上断定成立,
那么下列哪项能够推出?
.
20
三段论习题
参加培训的学生有些通过了考试。因此,参加 培训的有些女同学通过了考试。为使上述推理 成立,需要补充以下哪项作为前提? A.参加培训的学生都是女同学 B.参加培训的男生有些通过了考试 C.参加培训的有些女同学没有通过考试 D.有些参加培训的学生是女同学
.
21
三段论的做题方法:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
乙:“是丁打碎的。“
乙和丁的结论正好相反,因而说谎的肯定在
“乙和丁两人中间”,从而可知甲、丙说真话, 丙:“我没有打碎玻璃。“ 也就是丙没有打碎玻璃,显然是“丁”打碎玻
丁:“我才不干这种事。“ 璃。
深深了解学生的老师说:“他们中有三位绝不会说谎。”那么到底是 谁打碎了玻璃呢?
.
8
直接推理法 :抽取关键条件 逻辑推理 假设推理法
答案:丙全说对了,甲说对一半, 乙全说错了。
.
14
直接推理法 :抽取关键条件 逻辑推理 假设推理法 :提出假设,推出矛盾
综合推理法
.
15
案例7:
从前有三个和尚,一个讲真话,一个讲假话,另有一个有时讲真话,有时讲假话。
一天,一位智者遇到这三个和尚, 他问第一位和尚:“你后面是哪位和尚?” 和尚回答:”讲真话的。“ 他又问第二位和尚:”你是哪一位?“ 得到的回答是:”有时讲真话,有时讲假话的。“ 他问第三个和尚:”你前面的是哪位和尚?“ 第三人和尚说:”讲假话的。“
.
1
案例1:
一天某银行发生一起重大失窃案。警察拘留了甲、乙、丙、丁 四名嫌疑犯。下面是他们的口供:
甲说:“肯定是乙干的。” 乙说:“是丁干的,他以前就是贪污和盗窃行为。“ 丙说:“那天我在厂里上班,根本没去过银行,不是我干的。“ 丁说:“乙和我有仇,他有意诬陷我。“ 经过调查核实,这四人当中只有一人的口供是真实的。作案者是谁呢?
这样一来,甲说的也是对的,不是假 话。这样,前后就产生了矛盾。所以甲说 的不可能是假话,只能是真话。
同理,剩下的三人中只能是丙说真话。乙和丁说的都 是假话,即丙不是案犯,乙是案犯,再由丙所述为真话, 即丁是案犯。
.
11
案例5:
假设推理法
我国有“三山五岳”之说,其中五岳是指:东岳泰山,南岳衡山,西岳华山, 北岳恒山和中岳嵩山。一位老师 拿出这五座山岳的图片,并在图片上标出数学数字, 他让五位学生来辨别,每人说出两个。学生回答如下:
综合推理法
.
9
案例4:
一位法官在审理一起盗窃案中,对涉及的四名嫌疑犯甲、乙、丙、丁 进行了审问。四人分别供述如下:
甲说:“案犯在乙、丙、丁三人之中。” 乙说:“我没有作案,是丙偷的。” 丙说:“在甲和丁中间有一人是案犯。” 丁说:“乙说的是事实。”
经过充分的调查,证实这四人中有两人说了真话,另外两人说的是假话。 请你做一名公正的法官,对此案进行裁决,确认谁是案犯。
.ቤተ መጻሕፍቲ ባይዱ
2
乙说:“是丁干的,他以前就是贪污和盗窃行为。“ 丁说:“乙和我有仇,他有意诬陷我。“
乙和丁说的话相互矛盾,必然有一人说的是真话,所以就可以 推理出甲和丙说的都是假话。
.
3
甲说:“肯定是乙干的。” 甲说的是假话,推出不是乙干的。”
丙说:“那天我在厂里上班,根本没去过银行,不是我干的。“ 丙说的是假话,推出是丙干的。”
因为每人都说对了半句,说错半句,因此可以推出戊说的前半句是错误, 后半句正确,即2不是华山,5是泰山。
甲:2是泰山,3是华山。
甲说的前半句错误码,后半句正确,即3是华山;
乙:4是恒山,2是嵩山。
由戊所说得知,2不是华山,5是泰山;
丙:1是衡山,5是恒山。
丁:4是恒山,3是嵩山。 戊:2是华山,5是泰山。
根据他们的回答,智者马上分清了他们各是哪一位和尚,请你说出智者的答案。
.
16
一天,一位智者遇到这三个和尚,
他问第一位和尚:“你后面是哪位和尚?” 和尚回答:”讲真话的。“
他又问第二位和尚:”你是哪一位?“ 得到的回答是:”有时讲真话,有时讲假话的。“
由丙所说得知,5不是恒山,1是衡山; 由乙所说得知,4不是恒山,2是嵩山;
由丁所说得知,3不是嵩山,4是恒山;
答案:1是衡山;2是嵩山;3是华山;
4是恒山;5是泰.山。
13
案例6:
假设推理法
某地质学院的学生对一种矿石进行观察和鉴别:
甲判断:不是铁,也不是铜。 乙判断:不是铁,而是锡。 丙判断:不是锡,而是铁。
.
10
甲说:“案犯在乙、丙、丁三人之中。”
乙说:“我没有作案,是丙偷的。” 丙说:“在甲和丁中间有一人是案犯。”
如果甲说的是假话,那么剩下三人 中有一人说的也是假话,另外两人说的 是真话。
丁说:“乙说的是事实。”
可是乙和丁两人的观点一致,所以在 剩下的三人中只能是丙说了假话,乙和丁 说的都是真话。即“丙是盗窃犯”。
甲:2是泰山,3是华山。 乙:4是恒山,2是嵩山。
丙:1是衡山,5是恒山。
丁:4是恒山,3是嵩山。 戊:2是华山,5是泰山。
老师发现五个学生都只说对了一半,那么正确的说法应该是什么呢?
.
12
老师发现五个学生都只说对了一半,那么正确的说法应该是什么呢?
假如甲说的前半句正确,后半句错误,,则2是泰山,3不是华山;
.
5
第一证人说:“我只知道甲是无罪的。”
第二证人说:“我只知道乙是无罪的。”
第三证人的证词是伪证, 也就是说前面两个人中 至少有一个人是真的。
第三证人说:“前面两个证词中至少有一个人是真的。”
第四证人说:“我可肯定第三个证人的证词是假的。”
.
6
案例3:
直接推理法
甲、乙、丙、丁四位同学在广场上踢足球,打碎了玻璃窗,有人问 他们时,他们这样说:
经检验证明:有一个人的判断完全正确,有一个人说对了一半,而另一个人完全说错了。
你知道三人中谁是对的,谁是错的,谁是只对一半的吗?
假设甲全对,即“不是铁,也不是铜”。那么乙说的“不是铁”说对了,则“而是锡”错 可知“不是锡”正确。又甲全对,乙说对一半,则丙全错。 所以丙说:“不是锡”错了,与刚才推理矛盾。同理可推知,乙全对也矛盾。
.
4
案例2:
直接推理法
在一桩谋杀案中,有两个嫌疑犯甲和乙。另有四个证人正在受到讯问。
第一证人说:“我只知道甲是无罪的。” 第二证人说:“我只知道乙是无罪的。” 第三证人说:“前面两个证词中至少有一个人是真的。” 第四证人说:“我可以肯定第三个证人的证词是假的。”
通过调查研究,已证实第四个证人说了实话,请你分析一下,凶手是谁?
甲:“玻璃是丙也可能是丁打碎的。“ 乙:“是丁打碎的。“ 丙:“我没有打碎玻璃。“ 丁:“我才不干这种事。“
深深了解学生的老师说:“他们中有三位绝不会说谎。”那么到底是 谁打碎了玻璃呢?
.
7
案例3:
甲、乙、丙、丁四位同学在广场上踢足球,打碎了玻璃窗,有人问 他们时,他们这样说:
甲:“玻璃是丙也可能是丁打碎的。“
