标准正交向量组和正交矩阵
标准正交基

A1
,
A2
,
An
, An En
(8)
练习:
1.设1 (0,1,1,0,0),2 (1,1,0,1,0),3 (4,5,0,0,1). 求L(1, 2 ,3 )的一个标准正交基.
答案:
标准正交基为:
1
1 2
(0,1,1,0,0), 2
1 10
因为 m n,
所以必有向量 不能被 1,2, ,m 线性表出,
作向量 m1 k11 k22 kmm ( 0)
ki R 待定.
证明续: 从正交向量组的性质知
(i ,m1 ) ( ,i ) ki (i ,i ), i 1, 2, , m.
证明 设有一组数 k1, k2 , , kr使得
k11 k22 krr 0 等号两边的向量分别和1作内积
k11 k22 krr , 1 0, 1 展开得 k1 1,1 k2 2,1 kr r ,1 0
L(1, 2 , , i ) L(1,2, ,i ), i 1, 2, , n
证: 基本方法─逐个构成出满足要求的 1,2 ,
首先,可取
1
1
| 1
|1
.
,n .
证明续:
一般地,假定已求出 1,2 , ,m 是单位正交的 ,且
L(1, 2 , , i ) L(1,2 , ,i ), i 1, 2, , m (4) 当 m n 时,因为有 m1 L(1, 2 , , m ), 由(4)知 m1不能被 1,2 , ,m线性表出.
于是取
ki
( ,i ) , (i ,i )
正交矩阵——精选推荐

第五章 二次型除特别指明外,本章都是在实数域内进行的讨论.§5.1 正交矩阵一、向量的内积1.定义:① 设有n 维行向量α = (a 1, a 2, ……, a n ) ,β = (b 1,b 2, ……, b n ) ,定义α与β的内积为: α βT = a 1 b 1 + a 2 b 2 + …… + a n b n . ② α 与 β 正交: α βT = 0 .注:非零向量正交一定线性无关(反之不成立).③ 对n 维列向量 α = (a 1, a 2, ……, a n )T ,β = (b 1,b 2, ……, b n )T , α与β的内积为: α T β = a 1 b 1 + a 2 b 2 + …… + a n b n , α与β正交,则: α T β = 0 .说明:①.我们采用符号<α,β>统一表示n 维向量α和β的内积.②.在大家熟知的三维普通空间,建立笛卡儿坐标系后,矢量(也称向量)k a j a i a a r r r r321++= 和 kb j b i b b r r r r 321++=可以作为特例.不过用行(或列)矩阵[即行(或列)向量]表示内积(亦称点积、数量积)b a rr ⋅时,必须写成[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⋅321321b b b a a a b a rr . 2.性质:① 对称: α βT = β αT ;( <α,β> = <β,α> ) ② 数乘(齐次):( λ α ) βT = α ( λ βT ) = λ ( α βT ) ; ③ 分配(可加):( α + β) γT = α γT + β γT ;④ 自身相乘非负: α αT ≥ 0 ;仅当 α = 0 时, α αT = 0 . 3.向量的长度(或模): 22221Tn a a a +++==L ααα ,为非负的实数.性质:① 非负:α≥ 0 ;仅当 α = 0 时, α αT = 0 ; ② 数乘(齐次): ααk k = ;③ 单位向量及非零向量单位化:若1=α,则α为n 维单位向量.对非零向量α ,都可单位化:ααβ= . ④ 三角不等式: βαβα+≤+ ; ⑤ 柯西-施瓦茨不等式:222T )(βαβα≤ .二、向量正交化1.正交向量组定义:若向量组α1,α2,……,αs 中的向量两两正交,则称该向量组是一个正交向量组. 重要的n 维正交向量组:)0,,0,1(1L =e ,)0,,1,0(2L =e ,……,),,0,0(n n L =e .2.向量组正交化方法(Schmidt 正交化方法):有一线性无关的向量组α1,α2,……,α r ,但不是正交向量组,用施密特(Schmidt )正交化方法可以将其转化为一组正交且单位化的向量组. ① 正交化:令 11αβ= 1111222,,ββββααβ><><−= 222231111333,,,,ββββαββββααβ><><−><><−= ……111122221111,,,,,,−−−−><><−−><><−><><−=r r r r r r r r r ββββαββββαββββααβL ② 单位化:令111ββγ=,222ββγ=,……,rr r ββγ=.(课后看教材P.156之例6和例7.) 三、正交矩阵1.定义:设A 为n 阶实方阵,若A T A = I ,则称A 为n 阶正交方阵.2.性质:① 若A A T = I ,则A 为正交矩阵; ② 若A T = A -1 ,则A 为正交矩阵; ③ 若A 为正交矩阵,则行列式1±=A ;④ n 阶实方阵A 为正交矩阵的充分必要条件是A 的列向量为一个相互正交的单位向量组;(用定义A T A = I 说明)⑤ n 阶实方阵A 为正交矩阵的充分必要条件是A 的行向量为一个相互正交的向量组;⑥ 若A ,B 为n 阶正交矩阵,则AB ,BA 也是n 阶正交矩阵;因 ( AB )T ( AB ) = B T A T AB = B T B = I . ⑦ 正交矩阵的特征值的模等于1 .(证明略) 四、向量的正交变换:1.定义:设A 为n 阶正交矩阵,X 为任意一个n 维向量,则称Y = A X为正交变换.2.重要性质:向量X 经正交变换后长度(模)不变.因 X X X AX A X AX AX Y Y Y =====T T T T T )()( .3.推论:两个向量做相同正交变换后,内积不变,几何图形的形状不变. 五、实对称矩阵1. n 阶实对称矩阵A 的性质:[ 简单性质:A A A A A A ===T T )(,,]① 特征值都是实数;② 不同特征值对应的特征向量正交;证明: A T = A , AX 1 = λ1X 1 , AX 2 = λ 2 X 2 , λ1 ≠ λ 2 ;( AX 1 ) T = ( λ1X 1 ) T , ( X 1 ) T A T = λ1 ( X 1 ) T ;( X 1 ) T A = λ1 ( X 1 ) T , ( X 1 ) T A X 2 = λ1 ( X 1 ) T X 2 ;λ 2 ( X 1 ) T X 2 = λ1 ( X 1 ) T X 2 , ( λ 2 - λ1)[ ( X 1 ) T X 2 ] = 0 ;( X 1 ) T X 2 = 0 .③ 有n 个线性无关的实特征向量;④ 必有正交矩阵P ,使得P -1AP = P T AP = D = diag( λ1, λ2,…, λn )其中λ1, λ2,…, λn 恰为A 的n 个特征值(重根按重数依次计入);(证明:略)2.把n 阶实对称矩阵A 用正交矩阵对角化的步骤: ① 求出A 的相异特征值λ1, λ2,…, λ 5 ;② 对每个特征值λ i ,求出( λ i I – A ) X = 0 的一个基础解系,然后再正交化、单位化;③ 将求得的n 个相互正交的单位特征向量X 1, X 2, ……, X n 作为列向量排成矩阵P (就是所求的正交矩阵);④ 计算),,,,,diag(11s i i T λλλλ==−L L AP P AP P ,即为所求(n 个对角元素的值可能有重复). 六、例题(P.162例9亦P.132例4)设三阶矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=122212221A ,求正交矩阵P ,使P T AP 为对角矩阵.解:① 由A 的特征方程0=−λA I ,求其特征值λ:1221105551222122210−λ−−−λ−+λ−λ−λ−λ=−λ−−−−λ−−−−λ=−λ=A I 2)1)(5(10211005+λ−λ=+λ−−λ−+λ−λ=解得51=λ,132−=λ=λ;② 求对应51=λ的特征向量,解齐次线性方程组 0X A I =−)5( ;由 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−−→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−−−→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−−−−−=−000110112330330112422242224)5(A I ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→000110101 ,得同解方程组 ⎩⎨⎧=−=−003231x x x x ,令 33~x x = , 则 3132~,~x x x x == ,得特征向量 []T1111=X ;单位化: T1313131⎥⎦⎤⎢⎣⎡=P ; ③ 求对应132−=λ=λ的特征向量,由 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−−−−−−−−=−−000000111222222222)(A I ,得同解方程组 0321=++x x x ,令 3322~,~x x x x == ,得特征向量 []T2011−=X , []T3101−=X ; [与书不同,都对]正交化:[]T22011−==X α ,[][]TTT 22223331212101121101,,⎥⎦⎤⎢⎣⎡−−=−−−=><><−=αααααX X ;单位化: T22202121⎥⎦⎤⎢⎣⎡−==ααP , T333626161⎦⎤⎢⎣⎡−==ααP ; [与书不同] ④ 所求正交矩阵为[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−==62031612131612131221P P P P . [与书不同]本题附:① 可以验证 P T AP = diag ( 5, -1, -1 ).⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−=6203161213161213112221222162616102121313131T AP P ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−=1000100056203561213561213562616102121313131 . ② 用书上的P ,同样也可以验证 P T AP = diag ( 5, -1, -1 ).作业(P.162):1; 6.(1); 8;附录:关于复矩阵的共轭问题① 复矩阵的共轭矩阵 —— 每一矩阵元都取共轭;即复矩阵A = (ai j )的共轭矩阵为)(j ia=A.② 复向量的共轭向量 —— 每一元素都取共轭.。
标准正交基

ki R 待定.
§2 标准正交基
从正交向量组的性质知
( i , m1 ) ( , i ) ki ( i , i ),
于是取
( , i ) ki , ( i , i )
i 1,2, , m .
i 1,2, , m ,
可得 ( i , m 1 ) 0 ,
( i , j ) 1 i j, 0 i j
i , j 1,2,, n
(1)
③ n 维欧氏空间V中的一组基 1 , , n 为标准正交基 当且仅当其度量矩阵 A ( i , j ) En . ④ n 维欧氏空间V中标准正交基的作用: 设 1 , , n为V的一组标准正交基,则
§2 标准正交基
例2. 在 R[ x ]4 中定义内积为
( f , g ) f ( x ) g( x )dx
1 1
求 R[ x ]4 的一组标准正交基. (由基 1, x , x 2 , x 3 出发作正交化)
2 3 1, x , x , x 解: 取 1 2 3 4
§2 标准正交基
3
3 x i y j z k , x i y j z k R 设 1 1 1 2 2 2 ① 从 ( , i ) x1 , ( , j ) y1 , ( , k ) z1 得 ( , i ) i ( , j ) j ( , k ) k
2 再单位化得标准正交向量组 1 ,2 ,,m .
i
1 | i |
i , i 1,2,, m
§2 标准正交基
例1. 把 1 (1,1,0,0), 2 (1,0,1,0),
5.1向量组规范正交化

x2
x2
x4 x4
a4
令x2
c1
2 (0,0,1,1)
2
,
1 0
x4
c2
c1
1 0 0
c2
0 11
则a1, a2 , a3, a4即为所求
解(1)法二a1, a2线性无关,可取3 (1,0,0,0),4 (0,0,1,0)
使a1,
a2
,
3
,
线性无关。
4
将a1
,
a3
[a3, b1] [b1, b1]
b1
[a3 [b2
, ,
b2 b2
] ]
b2
3,5,1,1 8 1,1,1,1 140,2,1,3 1,1,2,0
4
14
再单位化, 得规范正交向量组如下
e1
b1 b1
1 1,1,1,1 1 , 1 , 1 , 1
2
2 2 2 2
e2
b2 b2
(ii) 齐次性 x x ; R
(iii) 三角不等式 x y x y .
证 (i) 与(ii) 是显然的,下面证明 (iii) , (iii) 三角不等式 x y x y .
x y 2 [ x y , x y ] [ x, x ] 2 [x, y] [ y, y ] ,
例2 用施密特正交化方法,将向量组
a1 (1,1,1,1), a2 (1,1,0,4), a3 (3,5,1,1)
正交规范化.
解 先正交化, 取 b1 a1 1,1,1,1
b2
a2
a2 , b1 b1 , b1
b1
1,1,0,4
1
1
1
1 1
4-2标准正交基

α1,α2,…,αm两两正交,则称α1,α2,…,αm是V的 , 两两正交, , 的 , 又都是单位向量, 一个正交基;如果α1,α2,…,αm又都是单位向量, 一个正交基; 正交基 的一个标准正交基 则称α1,α2,…,αm是V的一个标准正交基. , 的一个标准正交基.
定义4.7 定义4.7 设α1,α2,…,αm是欧氏空间 的一个基.如果 , 是欧氏空间V的一个基.
1 1 1 1 1 1 α 3 = ,− ,0, ,0 为R4的一个基 ,α 4 = − , , 的一个基. 2 2 2 2 2 2
T T
说明 1)自然基 1,e2,…,en是Rn标准正交基. 标准正交基. )自然基e ,
T
T
4
3)向量空间V的任意向量α ,在V中的一个标准正交基 )向量空间 的任意向量 中的一个标准正交基 α1,α2,…,αm下的坐标为: = k α + k α + L + k α , 下的坐标为: α
由单位向量组成的正交向量组称为标准正交向量组. 由单位向量组成的正交向量组称为标准正交向量组. 标准正交向量组
2
正交向量组是线性无关的. 定理4.2 正交向量组是线性无关的. 定理 , 是正交向量组, 证 设α1,α2,…,αm是正交向量组,并有一组数使 k1α1 + k2α2 + … + kmαm= 0. , , , )对上式的两边做内积, 用αi(i=1,2,…,m)对上式的两边做内积,得 <k1α1 + k2α2 + … + kmαm ,αi >= <0 ,αi> 0 k1<α1, αi> + k2<α2, αi> + … + km<αm, αi>= 0 因α1, α2, …, αm两两正交, 所以<αi, αj>= 0( i ≠ j, ), 两两正交 所以 , 故 ki<αi,αi>=0,(i=1,2,…,m) , , , , ) 所以< 因αi ≠ 0,所以 αi,αi>≠0,故ki =0(i=1,2,…,m). , ( , , , ) 于是向量组α1,α2,…,αm线性无关 , 线性无关.
线性代数课件-正交矩阵

,b2,b3
且b 1
,b2,b3与a1
,
a2,a3等价.
令 3 3 k11 k22 , 为使
1, 3 2, 3 0 , 则 可推出
k1
3 , 1,
1 1
,
k2
3 , 2 ,
2 2
,
于是
3
3
3 , 1,
1 1
1
3 , 2 ,
2 2
2
,
1, 2 , 3 是与1, 2 , 3 等价的正交向量组 .
1 正交的概念 当 ( x, y) 0 时 , 称向量 x 与 y 正交. (orthogonal)
由定义知,若 x ,则 x 与任何向量都正交.
2 正交向量组的概念 若一非零向量组中的向量两两正交,则称该向
量组为正交向量组.
3 正交向量组的性质
定理1 若 n 维向量 α1,α2 , ,αr 是一组两两正交的 非零向量 , 则 α1,α2 , ,αr 线性无关.
1 1
a2 0 , 1
a3
1 1
2
0 1
2
2 . 1
四、正交矩阵与正交变换
1. 定义 若实矩阵 A 满足 AAT=ATA=I ,则称 A 为正交矩阵 .
2. 性质 1 A1 AT,
2 A 1 ,
3 AT , A1, AB也是正交方阵
4 A 为正交矩阵 A的行列向量组
证明 设有 1,2 , ,r 使 11 22 r 0
以a1T 左乘上式两端,得 11T1 0 由 1 0 1T1 1 2 0,
同理可得2 r 0. 故1,2 , ,r线性无关.
如:a1 1,0,0,a2 0,1,0,a3 0,0,1
b1 1,0,0,b2 1,1,0,b3 1,1,1
5.3 n维向量空间的正交化

返回
1. 定义 若实矩阵 A 满足 AAT=ATA=I ,则称 A 则称 为正交矩阵 . 2. 性质
(1) A = A , (2) A = A = I =1.
T T 2
正交矩阵的乘积也是正 交矩阵. T T T T 设 A A = AA = I B B = BB = I , 则
β1 = (β1 , β1 )
4 4 1 = (α1 , α1 ) + (α2 , α2 ) + (α3 , α3 ) = 1 , 9 9 9 同样 ,β2 = β3 = 1 .
α2 = X1 = (1, 0, − 1) , ( X2 , α2 ) 1 α3 = X2 − α2 = (0, 1, − 1) − (1, 0, − 1) (α2 , α2 ) 2
1 = (− 1, 2, − 1) . 2
返回
将 X1 , X2 正交化:
例4 将 α1 = (1, 1, 1) , α2 = (1, 2, 1) ,α3 = (0, − 1, 1) 标准正交化. 解 设 β1 = α1 = (1, 1, 1), 4 (α2 , β1 ) β2 = α2 − β1 = (1, 2, 1) − (1, 1, 1) 3 (β1 , β1 )
是 Rn 的标准正交基 .
1 1 1 1 0 0, ,3 = (0, 0) 1 α1 = ,, ,2 = − , α α , 2 2 2 2 3 是 R 的标准正交基 .
返回
α1 , α2 ,L,αs 满足: (1) (αi , α j ) = 0 , (i ≠ j, αi ≠ 0, α j ≠ 0) (2) αi = 1, (i = 1, 2,L, s) ( α Lα 则称α1, 2, , s 为标准 规范)正交向量组.
向量组的正交性与正交矩阵

证:
设k11 k22 ... kmm O (i , k11 k22 ... kmm ) (i , O) 0 k1 (i , 1 ) k2 (i , 2 ) ... km (i , m ) 0 Q 1,2 ,..., m为正交向量组, 则(i, j ) 0, (i j) ki (i , i ) 0 由于i O, 即(i , i ) 0 ki 0 ( i =1,2,·,m ) · ·
2.在R4中求由下列向量生成的子空间的维数和一组正 交规范基 α1=(2,0,1,1),α2=(-1,-1,-1,-1), α3=(1,-1,0,0),α4=(0,-2,-1,-1)
1.求由下列向量组生成的向量空间 V L 1,2 ,3 ,4 ,5 的维数和一组正交规范基,并用它表示向量组中剩余的向 量。
即1 ,2 ,.., n为单位正交向量组。
方法一、用定理。 方法二、用定义。
1/ 9 8 / 9 4 / 9 A 8 / 9 1 / 9 4 / 9 , A正交吗? 4 / 9 4 / 9 7 / 9 正交
1 8 4 A 8 1 4 , A正交吗? 4 4 7
2 .. n
1T 1 1T 2 T T 2 1 2 2 .. .. T T n 2 n 1
.. 1T n T .. 2 n .. .. T .. n n
0 0 ( i , i ) 1, ( i , j ) 0 .. (i j ) 1
五、正交矩阵:
T 若 1.定义4: n阶方阵A满足A A E,则称A为n阶正交矩阵。
2.性质:(i)
线性代数第五章

1.内积 2.向量旳范数 3.许瓦兹不等式
x x1 , x2 , , xn T , y y1 , y2 , , yn T
称 xT y x1 y1 x2 y2 xn yn
为向量 x与 y 旳内积,记为 x , y.
2
内积满足下列运算规律:
⑴ x, y y, x
⑵ kx , y kx ,y
15
三.正交矩阵与正交变化
1. 正交矩阵
1.正交矩阵 2.正交变换
定义5.2 假如 n阶方阵 A 满足AT A I
则称 A 为正交矩阵.
定理5.3 假如 A , B均为 n 阶正交矩阵,
那么:⑴ A1 AT
⑵ AT 即 A1 为正交矩阵
⑶
1 2
A A
A A
为
2n
阶正交矩阵
⑷ AB,BA 都是正交矩阵
8
定理5.2 若 1 , 2 , , r为 n 维正交向
量组,且 r n ,则必有非零 n 维向量 x , 使 x 与 1 , 2 , , r 两两正交.
推论:对 rr n个两两正交旳 n 维非零向量,总
能够添上 n r个 n 维非零向量,使 n 个向
量两两正交,从而这 n 个向量就构成了向量空
第五章 特征值 特征向量 二次型
第一讲 正交向量组与正交矩阵 第二讲 方阵旳特征值与特征向量 第三讲 相同矩阵与实对称矩阵旳对角化 第四讲 二次型及其原则形 第五讲 惯性定理和正定二次型 第六讲 习题课
1
第一讲 正交向量组与正交矩阵
一.向量旳内积与许瓦兹
(Schwarz)不等式
1.内积
内积定义:对 n维列向量
19
第二讲 方阵旳特征值和特征向量
1.定义
线性代数-正交矩阵

的一个规范正交基. e1 , e2 ,, en是Rn的规范正交基
e
T i
e
j
0, 1,
i j; i j.
1 1 0 0
2
2
0
0
e1
1 2
,e2
1
2
, e3
1 2
,e4
Y Y TY X T AT AX X T X X
正交变换保持向量的长度不变.
本节小结 内积与正交变换 α,β αTβ
1. 正交向量组 [αi ,α j ] (αTi ,α j ) 0
线性无关(Th5.3)
2. 规范正交化 正交基
必可逆
3. 正交矩阵 三条性质
正交规范基 i eTi a [ei ,a] AT A E AT A1
(1,1,1)
(
1 2
, 1,
1) 2
则 β1,β2,β3为正交向量组. 然后再单位化得
e1
1
1
1 (
1 ,0, 2
1 ), e2 2
1 2
2 (
1, 3
1, 3
1
), 3
e3
1 3
3 (
1 , 6
2, 6
1 ). 6
那末,e1,e2,e3 就是所求的正交单位向量组.
附加定义设n维向量e1,e2, ,er是向量空间V(V Rn)的一个基,
内积的基本性质 [, ] a1b1 a2b2 anbn (1) [, ] [, ]
(2) [k, ] kk[a1,b1 ]k[a2,bk2] kanbn (3) [1 2, ] [1 , ] [ 2 , ]
2.6 标准正交基
则称a1 , a2 , … , an 为 向量 在基 1 , 2 ,, n 下的坐标, 记作 ( a1 , a2 , … , an ) .
二、向量的内积
1.Def .
给定Rn中向量
a1 a2 an
n i1
b1 b2 , bn
i j 0
T
1 0 0 1 2 0 0
0 0 , n 1
是两两正交的.
( i j ; i , j 1, 2 , ..., s )
则称向量组1, 2,…,s 为正交向量组. 正交向量组1,2,…,s 中无零向量.
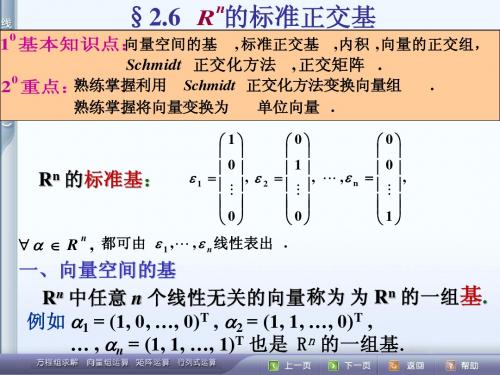
§2.6 R 的标准正交基
n
0
向量空间的基 , 标准正交基 , 内积 , 向量的正交组, 1 基本知识点: Schmidt 正交化方法 , 正交矩阵 . 0 熟练掌握利用 Schmidt 正交化方法变换向量组 . 2 重点:
熟练掌握将向量变换为 单位向量 .
1 0 0 0 1 0 , , , n , 1 2 0 0 1
a1 a2 an
n R ,
都可由 1 , , n 线性表出 .
a1 0 0
0 0 0 a2 a 1 1 a 2 2 a n n an 0
QTQ=
sin
co s sin
1 cos 0
0 1
3.5 标准正交向量组

9
[1 , r ] [ 2 , r ] r r 1 2 [1 , 1 ] [ 2 , 2 ]
2014年4月21日7时27分
(2)单位化,取
1 2 e1 , e2 , 1 2
那么 e1 , e2 ,
r , er r
, er 为V 的一个标准正交基
1 1 4 例2:设 1 2 , 2 3 , 3 1 ,把这组 1 1 0 向量正交单位化
从而 k1 = 0
同理可证,k2 = k3 = … = kr =0 综上所述, α1, α2, …, αr 线性无关
2014年4月21日7时27分 6
三、施密特正交单位化 定义5:若两两正交的单位向量组构成向量空间的基, 则称它们为标准正交基 如:
1 0 0 0 0 1 0 0 1 ,2 ,3 ,4 0 0 1 0 0 0 0 1
称两两正交的不含零向量的向量组为正交向量组
注:零向量与任何向量都正交
2014年4月21日7时27分 5
定理1:正交向量组必线性无关
证明:设α1, α2, …, αr 是正交向量组,存在k1, k2, …, kr
使得 则 即 k1α1 + k2α2 + … + kr αr = 0 [α1, k1 α1 + k2 α2 + … + kr αr]= [α1, 0] =0 k1 [α1, α1] + k2 [α1, α2] + … + kr [α1, αr]=0 k1 [α1, α1] = 0
高等代数第九章 2第二节 标准正交基

返回
上页
下页
因为度量矩阵是正定矩阵的,根据第五章关 于正定二次型的结果,正定矩阵合同于单位矩阵. 这说明在n维欧氏空间中存在一组基,它的度量矩 阵是单位矩阵. 由此断言
结论 在n维欧氏空间中,标准正交基是存在的. 在标准正交基下,向量的坐标可以通过内积 简单地表示出来,即 (1 , )1 ( 2 , ) 2 ( n , ) n (2)
返回
上页
下页
例3 欧氏空间Rn的基
i (0,,0, 1 ,0,,0) i 1, 2 ,, n
(i)
是Rn的一个标准正交基.
返回
上页
下页
(5)
(5)式相当于一个矩阵的等式
ATA=E ,
或者
返回
(6)
A-1=AT .
上页 下页
我们引入
定义7 n级实数矩阵A称为正交矩阵,如果ATA=E . 因此,以上分析表明,由标准正交基到标准正 交基的过渡矩阵是正交矩阵;反过来,如果第一组 基是标准正交基,同时过渡矩阵是正交矩阵,那么
第二组基一定也是标准正交基.
向量η1,η2,…,ηn .
| 1 | 求出η1,η2,…,ηm ,它们是单位正交的,具有性质
返回 上页 下页
首先,可取 1
1
1 . 一般地,假定已经
L(ε1,ε2,…,εi)=L(η1,η2,…,ηi),i=1,2, …,m.
下一步求ηm+1. 因为L(ε1,ε2,…,εm)=L(η1,η2,…,ηm),所以εm+1 不能被线性表出. 按定理1证明的方法,作向量
返回 上页 下页
正交矩阵

正交矩阵
如果:A A T =E,或A T A=E,则n阶实矩阵A称为正交矩阵,若A为单位正交阵,则满足以下条件:
1) A T是正交矩阵
2)(E为单位矩阵)
3) A的各行是单位向量且两两正交
4) A的各列是单位向量且两两正交
5) (Ax,Ay)=(x,y) x,y∈R
6) |A| = 1或-1
7)逆也是正交阵;
任何正交矩阵的行列式是+1 或−1。
反过来不是真的
定理
1. 方阵A正交的充要条件是A的行(列) 向量组是单位正交向量组;
2. 方阵A正交的充要条件是A的n个行(列)向量是n维向量空间的一组标
准正交基;
3. A是正交矩阵的充要条件是:A的行向量组两两正交且都是单位向量;
4. A的列向量组也是正交单位向量组。
5. 正交方阵是欧氏空间中标准正交基到标准正交基的过渡矩阵。
在矩阵论中,实数正交矩阵是方块矩阵Q,它的转置矩阵是它的逆矩阵,如果正交矩阵的行列式为+1,则我们称之为特殊正交矩阵。
第二节标准正交基

(5)
(5) 式相当于一个矩阵的等式
ATA = E ,
(6)
或者
A-1 = AT .
定义 7 n 级实数矩阵 A 称为正交矩阵,如
果 ATA = E . 因此,以上分析表明,由标准正交基到标准正
交基的过渡矩阵是正交矩阵;反过来,如果第一组 基是标准正交基,同时过渡矩阵是正交矩阵,那么
第二组基一定也是标准正交基. 最后我们指出,根据逆矩阵的性质,由
i j.
(1)
显然,(1) 式完全刻画了标准正交基的性质. 换句
话说,一组基为标准正交基的充分必要条件是:
它的度量矩阵为单位矩阵. 因为度量矩阵是正定的.
根据第五章关于正定二次型的结果,正定矩阵合同 于单位矩阵. 这说明在 n 维欧氏空间中存在一组基, 它的度量矩阵是单位矩阵. 由此可以断言,在 n 维 欧氏空间中,标准正交基是存在的.
理 1 证明中的方法,作向量
m
m1 m1 ( m1,i )i . i 1
显然
m +1 0 , 且 (m +1 , i) = 0 ,i = 1 , 2 , … , m .
令
m1
m1 | m1
|
.
则 1 , 2 , … , m , m +1 就是一单位正交向量组.
同时
L(1 , 2 , … , m +1 ) = L(1 , 2 , … , m +1) .
交向量组的方法称为施密特(Schimidt)正交化过程.
三、举例
例1 设
1
1
4
a1 2 , a2 3 , a3 1 ,
1
1
0
试用施密特正交化过程把这组向量变成单位正交
11第4章2正交矩阵

得特征值
1 2 1, 3 10
14
(2)求特征向量 对于 1 2 1,
1 由 I A 2 2 得一个基础解系
解方程组 I A X 0
2 1 2 2 4 4 0 0 0 0 0 0 4 4 T T 1 2,1, 0 , 2 2, 0,1 2
对于
3 8
得到特征向量
3 (2, 1, 2)
1 1,
取 3
1 1 0.5 [2,1 ] 1 2 2 1 2 0 2 [ 1,1 ] 0 2 1 0.5
I A x 0
4 2 4 x1 0 2 1 2 x2 0 4 2 4 x 0 3
,2 (, 1 0, 1 ) (, 1 2, 0) 得到两个线性无关的特征向量 1
2 问A能否对角化?请说明理由。
解
因 是矩阵A的特征向量,故存在数,使得A ,
2 1 2 1 1 即 5 a 3 1 1 , 1 b 2 1 1 1 得 2 a , 1 b
0 0 1 0 0 1
定义4.6 如果一个方阵P满足 则称矩阵P为正交矩阵。
PT P I (或 PPT I ),
2
例1 证明
6 2 3 1 是正交矩阵。 验证矩阵 A 3 6 2 7 2 3 6 因为 6 2 3 6 3 2 1 1 T AA 3 6 2 2 6 3 7 7 2 3 6 3 2 6 49 0 0 1 0 49 0 I 49 0 0 49
正交矩阵是什么意思

正交矩阵是什么意思
正交矩阵是实数特殊化的酉矩阵,是数学运算的一种方法,在数学领域有着较高的地位。
在矩阵论中,实数正交矩阵是方块矩阵,它的转置矩阵是它的逆矩阵,如果正交矩阵的行列式为加一,则称之为特殊正交矩阵。
正交矩阵定理有:
1、方阵正交的充要条件是,行和列向量组是单位正交向量组;
2、方阵正交的充要条件是,n个行和列向量是n维向量空间的一组标准正交基;
3、正交矩阵的充要条件是,行向量组两两正交且都是单位向量;
4、列向量组也是正交单位向量组;
5、正交方阵是欧氏空间中标准正交基到标准正交基的过渡矩阵。
