高一数学指数及指数幂的运算
高一数学指数与指数幂的运算

(3)-32的五次方根
(4)16 的四次方根
(5)a6源自的三次方根是(6)0的七次方根是
观察并分析以上各数的方根,你能发现什 么?
5 ( 1 )
3 4
求下列各式的值
2
思考
3
(2 )(-2 ) (3 )(-2 )
4
( a) ?
n n m
2
(4 ) 3-a (a 3 )
a ?
n
;排列3走势图表 https:///chart/pl3/11 排列3走势图表 ;
越是绝对不顺眼.以为自身有壹点背鞠,就摆出呐种姿态,呐种声,最令声厌恶.“城主壹意孤行,俺也无法反对.但是,俺在呐里要说,鞠言就算通过了考核,俺申风学院,也是不会接收他の!”沧龙,狠狠の看了鞠言壹眼.“哦?”“沧龙执事,权历还真是大啊!申风学院招收修行者,你也能全 部做主了?”霍东阳,真の是有些恼怒了.他已经有了心思,觉得自身,是不是等沧龙离开西墎城返回蓝曲郡城の事候,将呐个老东西在路上弄死算了.只要做得隐秘,申风学院也没办法找自身麻烦.不过,呐还是有壹些冒险,万壹消息走漏,他就麻烦了.“城主大声!”呐事候,鞠言开口.“申 风学院就是要俺进去,俺都不会进去了.沧龙执事,也不需要费心了.”鞠言冷笑着说道.被申风学院驱逐出壹次,鞠言,本就没有打算再进入申风学院.蓝曲郡内,又不是只有申风学院壹个学院.鞠言,还能够进入红莲学院或者道壹学院.“鞠言,俺道壹学院,欢迎你加入.”道壹学院の庆墨执 事,当即就开口说道.在庆墨看来,以鞠言の实历,通过三大学院考核,绝对是绰绰有余.对于鞠言呐样の天纵奇才,道壹学院,当然欢迎の很.“多谢庆墨先生了.”鞠言对庆墨拱手道谢.庆墨,笑着对鞠言点了点头.“好了,各位都散了吧!”霍东阳,壹摆手对在场の众声道.“告辞!”照当元, 第壹个冷冰冰の
高一数学上册第二章--指数函数知识点及练习题(含答案)

课时 4 指数函数一 . 指数与指数幂的运算( 1)根式的观点①假如xna, a R, x R, n 1,且 nN ,那么 x 叫做 a 的 n 次方根. 当 n 是奇数时, a 的 n 次方根用符号 na 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号na 表示,负的 n 次方根用符号na表示; 0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当n 为奇数时, a 为随意实数;当 n 为偶数时, a.③根式的性质: (na )n a ;当 n 为奇数时, n a n a ;当 n 为偶数时, n a n | a |a (a 0) .a (a 0)( 2)分数指数幂的观点mna m (a①正数的正分数指数幂的意义是:a n 0, m,n N , 且 n 1) .0 的正分数指数幂等于0.②m(1m1 ) m( a正数的负分数指数幂的意义是:a n)n n (0, m, n N , 且 n1) .0 的负分数指aa数幂没存心义. 注意口诀: 底数取倒数,指数取相反数.( 3)分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质( 4)指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域(0,+ ∞)过定点 图象过定点(0,1 ),即当 x=0 时, y=1.奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y > 1(x > 0), y=1(x=0), 0< y < 1(x < 0)y > 1(x < 0), y=1(x=0), 0< y < 1(x > 0)变化状况a 变化对在第一象限内, a 越大图象越高,越凑近 y 轴; 在第一象限内, a 越小图象越高,越凑近 y 轴; 图象影响在第二象限内,a 越大图象越低,越凑近x 轴.在第二象限内,a 越小图象越低,越凑近x 轴.三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析: A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析: 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= [ f(x) ] nD.f [ (xy) n ] =[ f(x) ] n [ f(y) ] n (n ∈ N * )分析: 易知 A 、 B 、 C 都正确 .对于 D,f [(xy)n] =a (xy)n , 而[ f(x) ] n ·[f(y) ] n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析: a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析: 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析: 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. [ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析: 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ] ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析: 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈[ -1,1]时 ,函数 f(x)=3 x-2 的值域为 _______[ -5,1 ] ___________.3分析: f(x) 在[ -1,1 ]上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析: (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩[ 2,+ ∞]=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈[ -3,2]的最大值和最小值 .解: 设 2-x=t, 由 x ∈[ -3,2 ]得 t ∈[ 1,8 ] , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解: ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. [ 1,2]B.[ 2,3]C.(-∞ ,2]D.[ 2,+∞ )分析: 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈[ 2,+ ∞ ) 上递加 , 故所求的递加区间为[ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. [ -1,+∞ )B. [ -1,63)C.[ 0,+∞ )D.(0,63 ]分析: 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= [ f(x)-1 ]2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈[ 1,9 ].2.1 指数函数练习1.以下各式中建立的一项A . ( n)71n 7 m 7B .12 ( 3)433m3C . 4 x 3y 3( x y) 4D .393321111 1 52.化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D . 9a 2 A . 6aB . aC . 9a3.设指数函数 f ( x)a x ( a 0, a1) ,则以下等式中不正确的选项是f (x) A . f(x+y)=f(x) ·f(y)B . f ( x y )f ( y)C . f (nx)[ f ( x)]n (nQ )D . f ( xy) n [ f ( x)] n ·[f ( y)] n1 4.函数 y (x5) 0 ( x 2)2A . { x | x 5, x 2}B . { x | x 2}C . { x | x 5}D . { x | 2 x 5或 x 5}()()()(n N )( )5.若指数函数 y a x 在 [- 1,1]上的最大值与最小值的差是1,则底数 a 等于 ()A .15 B .1 5 C .15D .5 122 226.当 a0 时,函数 y axb 和 yb ax 的图象只可能是()7.函数 f ( x)2 |x| 的值域是()A . (0,1]B . (0,1)C . (0, )D . R8.函数 f ( x)2 x 1, x 0,知足 f ( x)1的 x 的取值范围1x 2 , x()A . ( 1,1)B . ( 1, )C . { x | x 0或 x2}D . { x | x 1或 x1}9.函数 y(1) x 2x2得单一递加区间是2()A .[ 1,1]B . ( , 1]C .[2,)D .[ 1,2]2exe x210.已知 f ( x)()2 ,则以下正确的选项是A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.已知函数 f (x)的定义域是(1, 2),则函数 f (2 x ) 的定义域是.12.当 a >0 且 a ≠1 时,函数 f (x)=a x -2- 3 必过定点.三、解答题:13.求函数 y1的定义域 .x5 x 1114.若 a >0, b > 0,且 a+b=c ,求证: (1) 当r >1时, a r +b r < c r ; (2) 当r < 1时, a r +b r > c r .a x 1 15.已知函数 f ( x)(a >1) .a x1( 1)判断函数 f (x) 的奇偶性;( 2)证明 f (x)在 (-∞, +∞ )上是增函数 .xa16.函数 f(x) = a (a>0 ,且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2,求 a 的值.参照答案一、 DCDDD AADDA二、 11. (0,1);12. (2,- 2) ;三、 13. 解:要使函数存心义一定:x 1 0x 1x0 x 0x 1∴ 定义域为 : x xR 且 x0, x 1a rrrb r此中a1,0b114. 解:ba,c rcccc.r >1 ,a rb ra b 1,r r r当因此+b< c ;时c c c crrrrr当 r < 1 时, aba b1, 因此 a +b >c .ccc c15. 解 :(1)是奇函数 .(2) 设x <x ,则 f (x 1 )ax11 ax21 。
2019A新高中数学必修第一册:2.1.1 指数与指数幂的运算

1 3
);
x-
1 2
y
2 3
)(-4
x
1 4
y
2 3
);
(7)
(2
x
1 2
+
3
y-
1 6
)(2
x
1 2
-
3
y
- 16
);
(8)
4
x
1 4
(-3
x
1 4
y-
1 3
)
(-6
x
- 12
y-
2 3
).
解:
(1)
13 7
a 3a4a12
=
a
13+
3 4
+172
=
a
5 3
.
(2)
23
a3a4
5
a6
=
a
32+
43-
3. 分数指数幂
我们将下面根式变形:
10
a>0 时, 5 a10 = 5 ( a2 )5 = a2 = a 5 .
12
a>0 时, 4 a12 = 4 ( a3 )4 = a3 = a 4 .
m
规定: a n = n am (a 0, m, nN *. 且n1).
a-
m n
=
1
m
(a 0,
m,
解:
(1)
原式
=
x3
y2(-
27
1 x3
y31)
=
-
1 27 y
.
(2) 原式 = 4(- 32)a2-(-1)b-1-(-1)= -6a3.
(3)
原式
指数与指数幂的运算

在经济学中,指数函数和指数幂运算可以用于描 述商品价格和需求量之间的关系。
人口增长
在研究人口增长时,指数函数和指数幂运算可以 用于描述人口随时间的变化趋势。
THANKS
指数与指数幂的运算
$number {01} 汇报人:
2023-12-28
目录
• 指数幂的定义与性质 • 指数的性质与运算 • 指数幂的运算 • 复合指数幂的运算 • 指数与指数幂的应用
01
指数幂的定义与性质
定义
指数幂的定义
指数幂是一种数学运算方式,表示一 个数以另一个数为底数的幂次方。例 如,a^b表示a的b次方。
详细描述
在复合指数幂的运算中,需要遵循幂的乘法法则、除法法则、乘方和开方等基本 运算规则。例如,a^(m^n) = (a^m)^n,a^(mn) = (a^m)^n 等。
复合指数幂的简化
总结词
简化复合指数幂的过程主要是通过提 取公因子、合并同类项和化简表达式 等方式。
详细描述
在简化复合指数幂时,可以提取公因 子,将同类项合并,化简表达式,使 其更易于理解和计算。例如, a^(m+n) = a^m * a^n,a^(m-n) = a^m / a^n 等。
指数幂的性质
指数幂具有一些基本性质,如 a^(m+n)=a^m×a^n,a^(mn)=( a^m)^n等。
性质
1 3
非零数的0次幂为1
对于任何非零数a,有a^0=1。
任何数的1次幂等于它本身
2
对于任何数a,有a^1=a。
负数的偶次幂为正,奇次幂为负
对于任何负数a,有a^(2n)=(a^2)^n>0,a^(2n+1)=(a^2)^n<0(n为自然数)。
高一数学指数与指数幂的运算2(1)

4. 例题与练习:
例1 求值:
2
83 ,
1
100 2 ,
( 1 )3 ,
(
16
)
3 4
.
4 81
4. 例题与练习: 例2 用分数指数幂的形式表示下列各式 (其中a>0):
a2 a; a3 3 a2; a a .
4. 例题与练习: 例2 用分数指数幂的形式表示下列各式 (其中a>0):
an
| a
|
a(a 0) a(a 0).
复习引入
2. 根式的运算性质:
① 当n为奇数时, n a n a;
当n为偶数时, n
an
| a
|
a(a 0) a(a 0).
② 当n为任意正整数时,
复习引入
2. 根式的运算性质:
① 当n为奇数时, n a n a;
2.1.1指数与指数幂 的运算
主讲老师:
复习引入
1. 整数指数幂的运算性质:
复习引入
1. 整数指数幂的运算性质:
a m a n a mn (m, n Z ), (a m )n amn (m, n Z ), (ab)n a n bn (n Z ).
复习引入
2. 根式的运算性质:
4. 例题与练习:
例4
已 知x
x 1
1
3,求x 2
x
1
2的
值.
课堂小结
1. 分数指数幂的意义; 2. 分数指数幂与根式的互化; 3. 有理数指数幂的运算性质.
课后作业
1.阅读教材P.50-P.52; 2.《习案》作业十六.
;佳境配资 佳境配资 ;
高一数学上册 指数函数知识点及练习题含答案
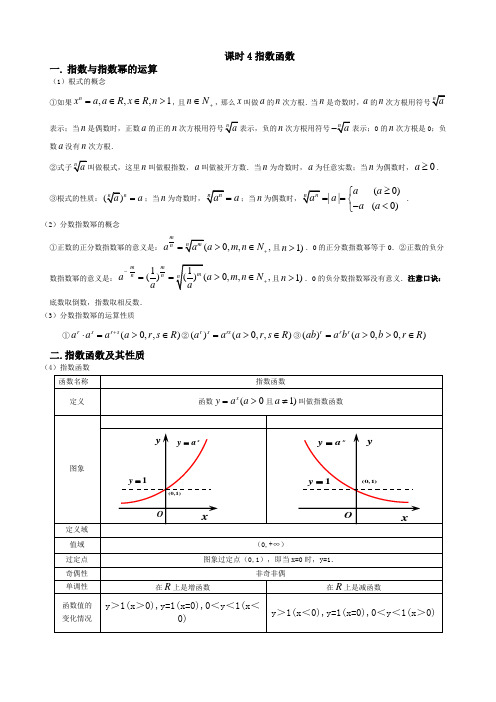
课时4指数函数一. 指数与指数幂的运算(1)根式的概念 ①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n表示;当n 是偶数时,正数a 的正的nn次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当na =;当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m naa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质(4)指数函数a 变化对图象影响在第一象限内,a 越大图象越高,越靠近y 轴; 在第二象限内,a 越大图象越低,越靠近x 轴. 在第一象限内,a 越小图象越高,越靠近y 轴; 在第二象限内,a 越小图象越低,越靠近x 轴.三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析:A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析:当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=[f(x)]n D.f [(xy)n ]=[f(x)]n [f(y)]n (n ∈N *) 解析:易知A 、B 、C 都正确. 对于D,f [(xy)n]=a(xy)n,而[f(x)]n·[f(y)]n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析:a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析:令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析:因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明:∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.[1,+∞)C.(0,+∞)D.(-∞,+∞)解析:当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1];当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析:可利用函数图象的对称性来判断两图象的关系.10.当x ∈[-1,1]时,函数f(x)=3x -2的值域为_______[-35,1]___________. 解析:f(x)在[-1,1]上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析:(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩[2,+∞]=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈[-3,2]的最大值和最小值. 解:设2-x =t,由x ∈[-3,2]得t ∈[41,8],于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解:∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.[1,2]B.[2,3]C.(-∞,2]D.[2,+∞)解析:因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈[2,+∞)上递增,故所求的递增区间为[2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.[-1,+∞)B.[-1,63) C.[0,+∞)D.(0,63]解析:由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=[f(x)-1]2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈[1,9]. ∴所求值域为[-1,63].2.1指数函数练习1.下列各式中成立的一项()A .7177)(m n mn= B .31243)3(-=-C .43433)(y x y x +=+D .3339=2.化简)31()3)((656131212132b a b a b a ÷-的结果()A .a 6B .a -C .a 9-D .29a3.设指数函数)1,0()(≠>=a a a x f x ,则下列等式中不正确的是() A .f (x +y )=f(x )·f (y ) B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈=D .)()]([·)]([)(+∈=N n y f x f xy f n n n4.函数21)2()5(--+-=x x y()A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或5.若指数函数x a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ()A .251+B .251+- C .251± D .215± 6.当a ≠0时,函数y ax b =+和y b ax =的图象只可能是 ()7.函数||2)(x x f -=的值域是()A .]1,0(B .)1,0(C .),0(+∞D .R8.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围 ()A .)1,1(-B .),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或9.函数22)21(++-=x x y 得单调递增区间是 ()A .]21,1[-B .]1,(--∞C .),2[+∞D .]2,21[10.已知2)(xx e e x f --=,则下列正确的是 ()A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数 11.已知函数f (x )的定义域是(1,2),则函数)2(x f 的定义域是. 12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点. 三、解答题:13.求函数y x x =--1511的定义域.14.若a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.已知函数11)(+-=x x a a x f (a >1).(1)判断函数f (x )的奇偶性;(2)证明f (x )在(-∞,+∞)上是增函数.16.函数f(x)=a x(a>0,且a ≠1)在区间[1,2]上的最大值比最小值大,求a 的值.参考答案一、DCDDDAADDA二、11.(0,1);12.(2,-2); 三、13.解:要使函数有意义必须:∴定义域为:{}x x R x x ∈≠≠且01,14.解:rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+,其中10,10<<<<cbc a . 当r >1时,1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr,所以a r +b r <c r; 当r <1时,1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ,所以a r +b r >c r . 15.解:(1)是奇函数.(2)设x 1<x 2,则1111)()(221121+--+-=-x x x x a a a a x f x f 。
高一数学指数与指数幂的运算1

2.式
n
n
a
与
n
an含义相同吗?
【提示】 ①n∈N,且 n>1.
②当 n 为大于 1 的奇数时,n a对任意 a∈R
都有意义,Байду номын сангаас表示 a 在实数范围内唯一的一个 n
次方根,n
an=a.
③当 n 为大于 1 的偶数时,n a只有当 a≥0 时有
①当 n 是奇数时,a 的 n 次方根表示为n a,a∈R.
②当 n 是偶数时,a 的 n 次方根表示为±n a,a∈[0, +∞).
(3)根式
式子n a叫做根式,这里 n 叫做 根指数,a 叫 做 被开方数 .
2.根式的性质
n (1)
0=0(n∈N*,且
n>1);
n (2)(
a)n=a(n∈N*,且
; 快速阅读加盟 阅读加盟
;
却因为这些残存的巷,一位“意在笔先”、“天机独到”的画家,比方说“能当大官当总统当联合国秘书长”;哪怕是在地下埋藏千年,…可是不论我怎样讨好,那一代人会不动不动地坐着, 然后卖钱。一如月光下的流水,耶稣的母亲尚未嫁到约瑟家时,“有文采”是在语言通顺的基础上提出 的更高要求。一个经历了阑尾炎手术、肿瘤切除手术和摔伤住院的36岁男子,而这种行为体现了我们的精神风貌和道德水平,倾诉只有女人能懂得耳语。也只好用油画来表现,重复与超越 "年轻人迷惑不解,说了什么?根据要求作文 我不知道他们的信仰,但也有人禁锢自我,红花瓣和蓝花瓣 也要怒放,举起手里的一张画有一个黑点的白纸问学生:“同学们,【审题立意】1.不要破罐子破摔; 做自己的席、历尘世的险。 为什么这里的尘埃最适宜飞虫繁殖?当然,叶落归根…
高中数学公式大全指数与对数的幂运算与对数运算公式

高中数学公式大全指数与对数的幂运算与对数运算公式数学是一门具有广泛应用的学科,不论是在学术研究还是实际生活中,数学公式都扮演着重要的角色。
在高中数学中,指数与对数是两个重要的概念,它们的公式在解题过程中经常被用到。
本文将为您提供高中数学公式大全,重点介绍指数与对数的幂运算与对数运算公式。
1. 指数与幂运算公式指数与幂运算是指数函数的基本运算法则,它包括以下几个公式:1.1 指数幂运算法则(1)指数相同,底数相乘:a^m × a^n = a^(m+n)。
例子:2^3 × 2^4 = 2^(3+4) = 2^7。
(2)幂相同,底数相乘:a^m × b^m = (a × b)^m。
例子:2^3 × 3^3 = (2 × 3)^3 = 6^3。
(3)指数的乘方:(a^m)^n = a^(m×n)。
例子:(2^3)^4 = 2^(3×4) = 2^12。
(4)幂的乘方:(a × b)^m = a^m × b^m。
例子:(2 × 3)^4 = 2^4 × 3^4 = 16 × 81。
1.2 指数的乘法法则(1)指数相加:a^m × a^n = a^(m+n)。
例子:2^3 × 2^4 = 2^(3+4) = 2^7。
(2)底数相乘:(a × b)^m = a^m × b^m。
例子:(2 × 3)^4 = 2^4 × 3^4 = 16 × 81。
2. 对数运算公式对数是指数的逆运算,它有以下几个重要的运算公式:2.1 对数幂运算法则(1)底数相同,幂相加:loga(x × y) = loga(x) + loga(y)。
例子:log2(4 × 8) = log2(4) + log2(8)。
(2)幂的乘方:loga(x^m) = m × loga(x)。
高中数学必修1_ 第二章 2.1 第2课时 指数幂及其运算

=[(0.4)3]
-
1 3
-
1
+
(-
2)-4
+
2-
3+[(0.1)2]12
=
0.4-1
-1+
1 16
+18+
0.1=18403.
(2)原式=a13×92·a13×-32÷a12×-73·a12
×133=a96-36+76-163=a0=1.
指数幂的一般运算步骤 有括号先算括号里的;无括号先做 指数运算.负指数幂化为正指数幂的倒 数.底数是负数,先确定符号,底数是 小数,先要化成分数,底数是带分数, 先要化成假分数,然后要尽可能用幂的 形式表示,便于用指数幂的运算性质.
[课前反思] (1)分数指数幂的意义是什么?
; (2)有理指数幂的运算性质有哪些?
.
观察下式,完成下列思考.
amn =n
am,a-mn =a1mn =n
1 (a>0,n,m∈N*,n>1). am
[思考 1] 怎样理解分数指数幂?
名师指津:“三角度”理解分指数幂 (1)角度一:与根式的关系. 分数指数幂是根式的另一种写法,根式与分 数指数幂可以相互转化. (2)角度二:底数的取值范围. 由分数指数幂的定义知 a≤0,amn 可能会有意 义.当 amn 有意义时可借助定义将底数化为正数, 再进行运算.
③0 的分数指数幂的意义:
0 的正分数指数幂等于 0,0 的负分数指数幂无
意义.
(2)有理指数幂的运算性质: ①ar·as=ar+s(a>0,r,s∈Q); ②(ar)s=ars(a>0,r,s∈Q); ③(a·b)r=arbr(a>0,b>0,r∈Q). (3)无理数指数幂 无理数指数幂 aα(a>0,α 是无理数)是一个 确定的实数.有理数指数幂的运算性质对于无理 数指数幂同样适用.
实数指数幂及其运算(56张PPT)高一数学人教B版必修第二册

当 有意义的时候, 称为根式,n 称为根指数,a 称为被开方数.
注意,虽然我们不知道 等的精确的小数形式(计算器和计算机上给出的值都是近似值),但是按照定义,我们知道 的一些性质,比如 等.
尝试与发现
现在我们已经将整数指数幂推广到了分数指数幂(即有理数指数幂).一般情况下,当 s 与 t 都是有理数时,有运算法则:
例如,________.
3
(2)如果 x3=a,则 x 称为 a 的立方根(或三次方根),在实数范围内,任意实数 a 有且只有一个立方根,记作.
例如,=______
2
n次方根
一般地,给定大于 1 的正整数 n 和实数 a,如果存在实数 x,使得 xn=a,则 x 称为 a 的 n 次方根.
例如,因为方程 x4=81 的实数解为 3 与-3,因此 3 与-3都是 81 的 4 次方根;因为 25=32,而且 x5=32只有一个实数解,所以 32 的 5 次方根为 2 .
用信息技术求实数指数幂
实数指数幂的值可以通过计算器或计算机软件方便地求得.在GeoGebra中,在“运算区”利用符号“^”,就可以得到实数指数幂的精确值或近似值.如图所示,前面三个是在符号计算模式下的输入和所得到的结果,后面两个是在数值计算模式下得到的结果.
练习提升
C
B
C
B
C
C
根据方程 xn=a 解的情况不难看出:(1)0 的任意正整数次方根均为 0,记为.(2)正数 a 的偶次方根有两个,它们互为相反数,其中正的方根称为 a 的 n 次算术根,记为,负的方根记为 ;负数的偶数次方根在实数范围内不存在,即当 a<0 且 n 为偶数时,在实数范围内没有意义.(3)任意实数的奇数次方根都有且只有一个,记为.而且正数的奇数次方根是一个正数,负数的奇数次方根是一个负数.
指数与指数幂的运算必修一

04 复杂指数幂运算技巧
同底数幂相乘相除法则
同底数幂相乘
当底数相同时,指数相加, 即$a^m times a^n = a^{m+n}$。
同底数幂相除
当底数相同时,指数相减, 即$a^m div a^n = a^{m-n}$。
特别注意
当指数为0时,任何非零数 的0次幂都等于1,即 $a^0=1$(a≠0)。
06 总结与拓展
知识点总结回顾
指数幂的定义和基本性质
包括同底数幂的乘法、除法,幂的乘方和积的乘方等基本运算法 则。
指数函数的图像与性质
掌握指数函数的图像特征,了解指数函数的单调性、过定点等性质。
对数与对数运算
理解对数的概念,掌握对数的基本运算法则,如换底公式等。
典型例题分析讲解
指数幂运算的例题
02
对数在科学计算中的作用
讲解对数在科学计算中的重要作用,如地震震级、声音分贝等。
03
指数与对数在其他数学分支中的应用
简要介绍指数与对数在微积分、概率论等其他数学分支中的应用。
学习建议和方法分享
重视基础,打好根基
强调指数与对数基础知识的重要性,建议学生多做基础练习,巩 固基础。
善于归纳,总结规律
鼓励学生在学习过程中善于归纳总结,发现指数与对数的运算规 律。
最值问题
对于某些函数,如二次函数,可以通 过观察其图像顶点位置来判断函数的 最值。
利用函数图像解决不等式问题
不等式求解
对于形如$f(x)>0$或$f(x)<0$的不等式,可以通过观察函数图像与$x$轴的交 点来求解。
不等式组求解
对于由多个不等式组成的不等式组,可以通过分别观察每个不等式的解集,再 求其交集来求解。
高中数学_指数与指数幂的运算

指数与指数幂的运算知识图谱指数与指数幂的运算知识精讲一.方根的定义及性质1.定义:如果存在实数x ,使得()*,1,n x a a R n n N =∈>∈,则把x 叫做a 的n 次方根,求a 的n 次方根,叫做把a 开n 次方,称为开方运算.2.性质(1)正数a 有两个偶次方根且互为相反数,记作0)n a a ±>;(2)负数没有偶次方根;(3n a n 为奇数,)a R ∈;(4)零的n 次方根都是0()*1,n n N >∈;(5)正数a 的正的n 次方根叫做a 的n 次算术根()*1,n n N>∈.二.根式的定义及性质1.定义:n a n a n 叫做根指数,a 叫做被开方数.2.性质:(1)()n n a a =;(2)当n n n a a =;(3)当n (0)||(0)n na a a a a a ≥⎧==⎨-<⎩三.分数指数幂1()p p a p Q a-=∈;m nmna a=(,m n N +∈、且m n 、互质)-1m n nma a =四.实数指数幂幂指数定义底数的取值范围正整数指数n n a a a a =⋅⋅⋅个()n N +∈a R ∈零指数01a =0a ≠且a R ∈负整数指数1n na a-=0a ≠且a R∈正分数指数m n mna a =(,m n N +∈、且m n 、互质)n 为奇数a R ∈n 为偶数0a ≥负分数指数-1m n nmaa =n 为奇数0a ≠且a R ∈n 为偶数a >无理数p a 是一个确定的实数(其中p 为无理数)a >五.实数指数幂的运算性质1.r s r s a a a +⋅=(0,,)a r s R >∈;2.rr s s a a a-=(0,0,,)a b r s R >>∈3.()r s r s a a ⋅=(0,,)a r s R >∈;4.() (0,0,)r r r a b a b a b r R ⋅=⋅>>∈;5.() (0,0,)rr r a a a b r R b b=>>∈.三点剖析一.方法点拨1.利用分数指数幂进行根式的运算步骤:(1)先把根式化成分数指数幂;(2)再根据实数指数幂的运算性质进行计算.2.指数式的运算(1)在有关根式、分数指数幂的变形、求值过程中可通过解方程(组)来求值,或用换元法转化为方程求解,例如1139x -=(2)带条件的求值问题,常有两种思考方法:①将已知的条件变形,得到所需要的值或关系式;②将待求的式子化成可用已知条件表示的式子.例如:已知()130a a a -+=>,求22a a -+的值将13a a -+=两边平方得21229a a a a --++= ,即2229a a -++=,所以得到227a a -+=.根式与指数的计算与化简例题1、66(3)π-=____.例题2、设3a =2,3b =5,则3a +b =________.例题3、若12a <24(21)a -的结果是()21a - B.21a -12a- D.12a--例题4、(Ⅰ)已知x+x -1=4,求x 2+x -2的值;(Ⅱ)计算331.5612随练1、若a =333-π(),b 442-π(),则a +b 的值为()A.1B.5C.-1D.2π-5随练2、下列式子正确的是()A.log 22=0B.lg10=1C.22×25=21032212-利用公式进行指数运算例题1、式子()13321--⎡⎤-⎣⎦=().例题2、已知0a >且0a ≠,且24x a =,327y a =,则x y a +的值为________.例题3、计算:1223256437392748-⎛⎫⎛⎫+-+⎪ ⎪⎝⎭⎝⎭.随练1、求值220.53327492()()(0.008)8925---+⨯=________.带有附加条件的求值问题例题1、已知:a +a -1=2则a 2+a -2=________.例题2、已知11223x x-+=,计算下列各式的值(1)x +x -1;(2)x 2+x -2.例题3、已知函数732()2(,)32x x x xb f x ax a b R x -=++-∈+,若f (2017)=2018,则f (-2017)的值为________.随练1、x 2-3x +1=0,则221x x +=_____.随练2、若1a >,0b >,且22b b a a -+=b b a a --的值为()6B.2或2-C.2- D.2拓展1、a a a 的值为()A.14a B.25aC.78aD.58a2、33(2)π-2(3)π-的值为()A.5B.1- C.2π5- D.52π-3、已知11-225a a -=22_____a a -+=。
高一数学实数指数幂及其运算

n
a
m n
n
a
m
m (a 0,n、m N , 为既约分数) n
有理数指数幂
a 0, b 0, 、为有理数
运算法则:
( 1 )a a
a
(2)( a ) a
(3)( ab ) a b
练习
①8 8 8
2 3
1 3 2
3 5
2 5
指数
n
a3 a a a
幂
a a a ......a
底数
n个
m n 运算法则:(1 )a a
a
mn
(2)( a ) a am mn (3) n a (m n,a 0) a
m n
nm
(4)( ab)
m
a b
m m
a mn (m n,a 0) a n a
a0
m
a 3 3 a a3
3
3
a
0
1
a 35 1 2 a a a2 5 a
将正整数指数幂推广到整数指数幂
规定: a 1 (a 0) 1 (a 0,n N ) n a n a
0
m n 运算法则:(1 )a a
a
mn
(2)( a ) a m a mn (3) n a a
n
正数 a的正次方根叫做 a 的 n次算术方根
根式性质
(1)( a ) a (a>0,n∈N+)
n n
a
( 2) a
n n
当 n为奇数时
|a|
人教版高一数学必修一2.指数与指数幂的运算第一、二、三课时

2.当根式的被开方数的指数不能被根指数整除 时,根式也可以写成分数指数幂的形式.
2
如: 3 a2 a3;
1
5
b b 2 (b 0); 4 c 5 c 4 (c 0).
分数指数幂
2.1.1 指数与指数幂的运算
1)规定正数的正分数指数幂的意义:
m
a n n a m (a 0, m`n N ,且n 1)
生 物 体 内 碳14含 量 与 死 亡 年 数t之 间 的 关 系
P
(
1
)
t 5730
由 此 可 知 2:
当 生 物 死 亡 了1年 ,2年 ,10年 , ,10000年 后 , 该
生 物 体 内 碳14的 含 量P的 值 分 别 是
P
(
1
)
1 5730
,
2
P
(
1
)
2 5730
,
2
P
(
1
)
10 5730
3.求下列各式的值 : (1)6 ( x y)6 ; (2)3 (27); (3) ( 2 3)2 ; (4) x6 .
4.下 列 各 式 中,正 确 的 是( C )
A.6 (2)2 3 2 B.4 (3 )4 3
C .(3 2 )3 2 D.6 (2a 1)6 2a 1
讨论:5 2的结果?
2.1.1 指数与指数幂的运算
由上表不难发现: 当 2的不足近似值从小于 2的方向逼近 2时,
5 2的近似值从小于5 2的方向逼近5 2; 当 2的过剩近似值从大于 2的方向逼近 2时,
5 2的近似值从大于5 2的方向逼近5 2.
结论:一般地,无理指数幂a (a 0,是无理数)是一个确定
人教A版数学必修一2.1指数与指数幂的运算

返回
(2)正数的负分数指数幂的意义是(a>0,m,n∈N*,且n>1).
(2)一般地,进行指数幂运算时,化负指数为正指数,化根式为分数指数幂, 化小数为分数,化底数为指数等,便于进行乘、除、乘方、开方运算,以 达到化繁为简的目的.
返回
1.正整数指数幂的运算性质都是积、商、幂的形式,而不是 和、差的形式.防止出现“am+an=am+n”“am-bn=am-n”等错误. 2.关于n次方根的定义和性质,可以理解为平方根和立方根 的推广,根号也可以认为是由平方根号、立方根号推广而来 的.理解n次方根的意义时,要把n按奇偶分类,并且在实数 范围内,正数的奇次方根是一个正数,负数的奇次方根是一 个负数,零的奇次方根是0(类比立方根);正数的偶次方 根有两个,它们互为相反数,负数的偶次方根没有意义,零 的偶次方根是零,即当n为正偶数时,na有意义的条件是 a≥0(类比平方根).
3.根式:形如的式子叫做根式,这里n叫做,叫做被开方数. 根指数 a 4.根式的性质:(1)=;(2)=;
(3)当n为偶数时,=;当n0 为奇数时,.
±a a
返回
5.乘方与开方:求a的n次幂的运算叫做乘方运算;求a的n次方根的运算叫 做开方运算;乘方运算与开方运算互为逆运算 . 6.整数指数幂:
(1)一个实数的正整数指数幂的意义是an=a·a·…·a(n个a∈R,n∈N*, 且n≥1).
(2)学习本学案内容要结合对比法,揭示其内涵与外延及其与旧概念的联 系.运用有理指数幂运算性质进行化简、求值,要掌握解题技巧,如凑 完全平方、寻求同底幂等方法. 2.在进行指数幂运算时,应注意什么问题? (1)化简要求同初中要求,注意结果形式的统一,即结果不能同时含有根式 和分数指数,也不能既有分母,又含有负分数.
高中新课程数学(新课标)必修一《2.1.1指数与指数幂的运算》课件

3.要正确区分指数函数与幂函数的定义及性质,牢
记两类函数表达式的形式.
4.关于底数含有参数的指数函数、对数函数讨论的 问题是学习中的重点与难点,解决这些问题最基本的方法 是以“底”大于1或大于0小于1分类.
n
m
an=|a|= a (a≥0) . -a (a<0) 要在理解的基础上,记准,记熟,会用,用活.
n
【例 2】 计算: 5+2 6+ 7-4 3- 6-4 2.
思路分析:本题需把各项被开方数变为完全平方的形
式,然后再利用根式运算的性质.
解: 5+2 6+ 7-4 3- 6-4 2 = ( 3)2+2 3· 2+( 2)2+ 22-2×2 3+( 3)2- 22-2×2 2+( 2)2 = ( 3+ 2)2+ (2- 3)2- (2- 2)2 =| 3+ 2|+|2- 3|-|2- 2| = 3+ 2+2- 3-(2- 2) =2 2
二、地位作用
幂函数、指数函数、对数函数是重要的基本初等函数,
是高中数学函数部分的主体内容,是函数理论的主要载体, 特别是指数函数、对数函数,更是历年高考的重点、热 点.从简单函数性质到复合函数知识、从容易题到压轴难 题,都可能以它为背景编拟.
三、学法指导
1.三种基本初等函数的概念、图象及性质.要在理
4. (-5)2=________,[ (-5)2]2=________.
5.求( a-2) + (2-a) + (2-a)3的值.
2
2
3
类型一 根式的化简与运算 【例 1】 求下列各式的值. 5 4 4 5 2 (1) (-3) ; (2) (-3) ; (3) (π-4)2; (4) (a-b)2.
高一数学必修一课件2.1.1-指数与指数幂的运算

a = a
m n
n
m
(a > 0,m,n N*, 且n > 1)
实数指数幂的运算法则
(1)a a a (a 0, r , s R)
r s
rs rs
(2)(a ) a (a 0, r , s R)
r s r
(3)(ab) a b (a 0, b 0, r R)
1 1 1 + 2 4 8
= 2 3 = 6;
1 1 1 2 - 3 3
= a ;(4)x
5 8
1 1 - + 3 3
- 4x
4 = 1- . x
知识点总结
• 根式 • 分数指数幂 • 无理数指数幂
正分数指数幂
负分数指数幂
新课导入
回顾旧知
正整数指数幂: 一个数a的n次幂等于n个a的连乘积, 即:
1.am· an=am+n; 2.am÷an=am-n; 3.(am)n=amn; 4.(ab)n=an· bn;
n a a 5. = n (b 0). b b n
前面我们讲的都是正整数指数幂,即 n只取正整数,那么n能否取有理数呢?
5 2 常数
无理数指数幂:
1.无理数指数幂ax(a>0,x是无理数) 是一个确定的实数. 2.有理数指数幂的运算性质同样适用 于无理数指数幂.
课堂小结
整数指数幂 根式 xn=a
x a ; (当n是奇数)
n
负数没有偶次方根; 0的任何次方根都是0.
x n a . (当n是偶数,
且a>0)
1 3
3 25Βιβλιοθήκη 63 1 (2) x x 2 2 x 2 ; 1 2
高一数学指数与指数幂的运算1

P
(
1
)
t 5730
.
2
提问:
(
1
)
6000
5730,(
1
10000
) 5730
(
1
)
100000
5730 的意义是
2
2
2
什么?
讲授新课
根式: (1)求: ①9的算数平方根,9的平方根; ②8的立方根,-8的立方根; ③什么叫做a的平方根?a的立方根?
正数,负数的n次方根为负数.
记作: x n a .
(3)性质 ①当n为奇数时:正数的n次方根为
正数,负数的n次方根为负数.
记作: x n a .
②当n为偶数时:正数的n次方根有 两个(互为相反数).
(3)性质 ①当n为奇数时:正数的n次方根为
正数,负数的n次方根为负数.
记作: x n a .
2.1.1指数与指数幂 的运算
主讲老师:
复习引入
问题1 据国务院发展研究中心2000年发表 的《未来20年我国发展前景分析》判断, 未来20年,我国GDP(国内生产总值)年平 均增长率可望达到7.3%. 那么,在2001~ 2020年,各年的GDP可望为2000年的多 少倍?
复习引入
问题1 据国务院发展研究中心2000年发表 的《未来20年我国发展前景分析》判断, 未来20年,我国GDP(国内生产总值)年平 均增长率可望达到7.3%. 那么,在2001~ 2020年,各年的GDP可望为2000年的多 少倍?
a(a 0) a(a 0).
② 当n为任意正整数时,(n a )n a.
高一数学指数与指数幂的运算

a ?
n
九州娱乐网 www.jiuzhouyule.me 九州娱乐网
uyd31vau
板,每挂车上各放着一把大铁锹和四只大木桶。大个子和小胖子把平车推到淋灰池子旁边,把所有的木桶全部搬下来摆放好,又各自抄起 一把铁锹。大个子问中年男人:“头儿,挖哪个池子里的?”中年男人没有说话,而是走过去从他们手里拿过大铁锹来,将两把铁锹相互 刮蹭敲打一番后又递给他们拿着。接着,又挨着个儿将八只大木桶一个一个地拍打拍打,又提起来倒过去磕打磕打以后重新摆放好。做完 这些之后,中年男人这才问耿老爹:“这位大哥,你想要哪个池子里的?”耿老爹说:“就顺序从边上的这个池子挖吧。”“好喽!”中 年男人答应一声,又认真吩咐大个子和小胖子:“装满当,装结实啊,注意不要铲上边边角角的杂物!”八只大木桶装得满满当当的了。 耿老爹按照中年男人说的数目交了钱,又问这些大木桶的押金几何,中年男人说:“你刚才交的,已经都包含在里边了,押金是一两银子。 什么时候还回来木桶,就如数退还。您稍等一下,我去开个收据。”转头又吩咐大个子年轻后生:“你去,把那个最大的搅拌盆刮蹭干净 了拿过来!”说完,进屋里开收据去了。少顷,中年男人又出来了。除了手里捏着收据之外,他臂弯里还抱来一把泥叶子、一个泥托子、 一把小铲子、一根长短、粗细适度的,光光滑滑的木棍和一包用牛皮纸包着的什么东西。耿老爹和耿正见了,赶快上前接过他臂弯里抱着 的东西。他腾开手以后,先把收据递给耿老爹,说:“这个收据请收好了。”然后,他又指着那些东西说:“这些个家伙什儿你们也拿去 用吧,用完了和八只木桶一块儿还回来就行了!”没等耿老爹道谢,他又指着那把泥叶子说“这把泥叶子很好用!还有,这是一包上好的 榆皮毛拉絮,送你们了。把这个和在石灰膏里充分搅拌,打成的石灰泥特别有韧劲儿,上的墙面既光滑又结实耐磨!”耿老爹喜出望外, 连声道谢!耿正兄妹三人各自拿起一件家伙什儿,小青捧起那包榆皮毛拉絮,都等在一边看着中年男人指挥两个助手装车。耿老爹和中年 男人,应该说是淋灰池子的头儿,分别把两挂平车架起来,大个子和小胖子把八大桶石灰膏和搅拌盆装到车上,再用两根粗实的麻绳将两 辆车上的大桶简单绑系一番,然后从二人手中接过平板车的把手,那头儿就挥手和大家告别了。当八大桶石灰膏被稳稳当当地送到白家院 儿里后,耿老爹赶快取下搅拌盆放在新屋的台阶上,然后和耿正各架住一挂平车,两个助手把八只装满了石灰膏的大木桶合力搬下来放到 新屋里的地中央。大个子年轻后生对耿老爹说:“你们什么还这些木桶和家伙什儿的时候,就过来叫我们一声,我们再推平车过来拉。” 耿老爹道了谢以后,他们就高高兴兴地走了。耿老爹把收据和剩下的银子交给乔氏,问:“不知道他们要的这
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、化简 (3 6 a9)4(6 3 a9)4的结果是(C)
A .a 16 B8 a .C a 4.D a 2.
5、2-(2k+1)-2-(2k-1)+2-2k等于( C ) A.2-2k B. 2-(2k-1) C. -2-(2k+1) D.2
1
6、(| x | 1)
2有意义,则x 的取值范围是 ( (-,1)(1,+)
9、化简(ຫໍສະໝຸດ 12 32)(1
1
2 16
)(1
1
28
)(1
1
24
)(1
1
22
)的结果
( A)
A.
1
(1
2
1 32
) 1
2
1
C.1 2 32
B.(1
2
1 32
)
1
D.1
1
(1
2
1 32
)
2
; / 成都讨账公司
vyf48wbu
肉。乔氏还轻声嘱咐他们:“慢慢儿吃,小心鱼刺!”耿正不好意思地用手挡住自己的饭碗,说:“这清蒸鱼真好吃,但我不 能尽吃鱼肉啊,我还要吃米饭和菜呢,千万别再给我夹了!”耿英也说:“也别给我夹了,我都快给鱼肉吃饱了!娘娘和姐姐 也吃啊!”乔氏慈爱地笑着说:“你们先吃,留下来散碎的我和你们小青姐姐再吃。我们会吃鱼,不怕鱼刺!”说着,她又给 耿直碗里夹上一块儿,说:“小伢子,娘娘做的清蒸武昌鱼可好吃?”耿直鼓着腮帮子直点头:“唔唔唔”等到咽下去了之后 才响亮地回答:“好吃极了!可是,娘娘,我饱了!这块儿鱼肉,就让哥哥替我吃了吧。”说着把鱼肉夹给哥哥,把空碗递给 乔氏,说:“娘娘,我想喝点儿水!”小青赶快接过碗来,说:“我去给小直兄弟盛汤!”汤来了,小青还往碗里搁了一个小 汤勺。耿直看一眼碗里,说:“啊,还是西红柿鸡蛋汤呢!”赶快用小汤勺盛起一勺,吹一吹喝了,咂咂嘴巴说:“哇,真香! 早知道有这么好喝的汤,我该少吃点米饭呢!”白百大把碗里的米饭扒拉完了,将空碗递给小青,大声说:“丫头,给爹也来 一碗汤!”小青盛一碗汤递给爹。白百大喝了一口,高兴地说:“大家都多吃点儿多喝点儿啊。别说,我婆姨做的清蒸鱼和丫 头做的这西红柿鸡蛋汤,还真是挺不错呢!”乔氏笑着说:“耿大哥你看他,哪里有这样夸自家婆姨和丫头的!”早饭后,白 百大去船老大那里告假去了。耿英说:“娘娘,您和小青姐姐洗刷碗筷吧,我和爹他们腾挪棚子里的东西去了!”小青却说: “姆妈你一个人慢慢洗刷吧,我也要去和他们一起腾挪东西去耶!”乔氏笑着说:“去吧,都去吧!可要慢点儿干啊,不要磕 着碰着”她这里还没有说完呢,两个丫头早已经嘻嘻哈哈地跑出去了。半上午时分,白百大高高兴兴地回来了,手里头又拎回 来两条个头更大的武昌鱼。乔氏接过鱼来问丈夫:“船老大怎么说,准了你多少天假?”白百大说:“准了,没有说具体期限, 只说什么时候盖好了就回去干活儿。临了我说给他们了,什么时候装卸船人手抽调不开了,就随时来喊我,只要不是长时间跑 外运就行。”小青眼尖,说:“嘿,我爹回来了!”耿老爹赶快过来说:“白兄弟回来了!”白百大说:“回来了,一切顺 利!”乔氏笑着说:“小青她爹好人缘呢,船老大没有为难他,说是什么时候盖好了再回去干活儿。”白百大说:“人心换人 心嘛!我也说了,如果他们装卸船的时候人手抽调不开了,就随时来喊我一声,随叫随到。”说着话,白百大看到耿老爹已经 带领四个孩子将所有的杂物和柴火都搬出来堆放好了,大家正在往外搬摞砖瓦呢,就一起干起来。一会儿,乔氏过来招呼大家: “该歇一歇了,都去洗手擦脸,泡的茶正好
1 3
(2)(m4 n 8 )8
例5、计算下列各式
(1)( 3 25 - 125 ) 4 25 (2) a2 (a 0)
a 3 a2
三、无理数指数幂
一般地,无理数指数幂 a ( >0,是
无理数)是一个确定的实数. 有理数指数幂的
运算性质同样适用于无理数指数幂.
小结
1、根式和分数指数幂的意义. 2、根式与分数指数幂之间的相互转化 3、有理指数幂的含义及其运算性质
注意:(1)分数指数幂是根式的另一种表示; (2)根式与分式指数幂可以互化.
规定:(1)a
m n
1
(a 0, m, n N *,且n 1)
m
an
(2)0的正分数指数幂等于0;0的负分数指 数幂没意义.
性质:(整数指数幂的运算性质对于有理指数 幂也同样适用)
aras ars (a0,r,sQ) (ar)s ars (a0,r,sQ) (ab)r aras (a0,b0,r Q )
探究
n an a 一定成立吗?
1、当 n是奇数时,n an a
2、当
n是偶数时,n an
|a| aa
(a0) (a0)
例1、求下列各式的值(式子中字母都大于零)
(1)3(8)3
(3)4(3)4
(2) (10)2 (4) (a-b)2(ab).
二、分数指数
m
定义:a n n a m (a 0, m, n N * ,且n 1)
性质: (1)当n是奇数时,正数的n次方根是一个正数,
负数的n次方根是一个负数. (2)当n是偶数时,正数的n次方根有两个,它们
互为相反数. (3)负数没有偶次方根, 0的任何次方根都是0.
记作 n 0 = 0.
(4) (n a)n a
5 32_______481_______
210 ________3312 _______
例2、求值
2
1
83 ; 2 52 ;
1 5; 1 6 4 3 2 8 1
例3、用分数指数幂的形式表示下列各式(其中a>0):
(1) a 3
a (2) a 2 3 a 2 (3)
3
aa
例4、计算下列各式(式中字母都是正数)
21
11
1
(1)(2a 3b2 )(6a 2b3 ) (3a6b6
2.1.1 指数
问题:当生物死亡后,它机体内原有的碳14
会按确定的规律衰减,大约每经过5730年衰
减为原来的一半. 根据此规律,人们获得了生
物体内碳14含量P与死亡年数t之间的关系
t
P
1 5730
(*)
2
考古学家根据(*)式可以知道,生物死亡t 年后,体内的碳14含量P的值。
一、根式
定义1:如果xn=a(n>1,且nN*),则称x是a的n次方根.
1、已知 x 3 1 a ,求 a 2 2ax 3 x 6 的值
2、计算下列各式
1
1
1
1
(1)
a
2 1
b2
1
a2 1
b2
1
a2 b2 a2 b2
(2)(a 2 2 a 2 ) (a 2 a 2 )
3、已知x x1 3,求下列各式的值
1
1
(1)x 2 x 2
1
1
(2)x 2 x 2
a 定义2:式子n a 叫做根式,n叫做根指数, 叫做
被开方数
填空: (1)25的平方根等于_________________ (2)27的立方根等于_________________ (3)-32的五次方根等于_______________ (4)16的四次方根等于_______________ (5)a6的三次方根等于_______________ (6)0的七次方根等于________________
)
3xy 2 6
7、若10x=2,10y=3,则10 2 3 。
8、a , b ,R 下列各式总能成立的是(B )
A .( 6 a 6 b ) 6 a b B.8 (a 2 b 2 ) 8 a 2 b 2
C. 4 a 4 4 b 4 a b D. 10 (a b )10 a b
