实验一插值方法实验
数值分析综合实验报告

一、实验目的通过本次综合实验,掌握数值分析中常用的插值方法、方程求根方法以及数值积分方法,了解这些方法在实际问题中的应用,提高数值计算能力。
二、实验内容1. 插值方法(1)拉格朗日插值法:利用已知数据点构造多项式,以逼近未知函数。
(2)牛顿插值法:在拉格朗日插值法的基础上,通过增加基函数,提高逼近精度。
2. 方程求根方法(1)二分法:适用于函数在区间内有正负值的情况,通过不断缩小区间来逼近根。
(2)Newton法:利用函数的导数信息,通过迭代逼近根。
(3)不动点迭代法:将方程转化为不动点问题,通过迭代逼近根。
3. 数值积分方法(1)矩形法:将积分区间等分,近似计算函数值的和。
(2)梯形法:将积分区间分成若干等分,用梯形面积近似计算积分。
(3)辛普森法:在梯形法的基础上,将每个小区间再等分,提高逼近精度。
三、实验步骤1. 拉格朗日插值法(1)输入已知数据点,构造拉格朗日插值多项式。
(2)计算插值多项式在未知点的函数值。
2. 牛顿插值法(1)输入已知数据点,构造牛顿插值多项式。
(2)计算插值多项式在未知点的函数值。
3. 方程求根方法(1)输入方程和初始值。
(2)选择求解方法(二分法、Newton法、不动点迭代法)。
(3)迭代计算,直到满足精度要求。
4. 数值积分方法(1)输入被积函数和积分区间。
(2)选择积分方法(矩形法、梯形法、辛普森法)。
(3)计算积分值。
四、实验结果与分析1. 插值方法(1)拉格朗日插值法:通过构造多项式,可以较好地逼近已知数据点。
(2)牛顿插值法:在拉格朗日插值法的基础上,增加了基函数,提高了逼近精度。
2. 方程求根方法(1)二分法:适用于函数在区间内有正负值的情况,计算简单,但收敛速度较慢。
(2)Newton法:利用函数的导数信息,收敛速度较快,但可能存在数值不稳定问题。
(3)不动点迭代法:将方程转化为不动点问题,收敛速度较快,但可能存在初始值选择不当的问题。
3. 数值积分方法(1)矩形法:计算简单,但精度较低。
插值法实验报告

插值法实验报告插值法实验报告一、引言插值法是一种常用的数值分析方法,用于通过已知数据点的函数值来估计在其他位置的函数值。
它在科学计算、图像处理、工程设计等领域有广泛的应用。
本实验旨在通过实际操作,深入理解插值法的原理和应用。
二、实验目的1. 掌握拉格朗日插值法和牛顿插值法的原理和计算方法;2. 通过实验比较不同插值方法的精度和效率;3. 分析插值法在实际问题中的应用。
三、实验步骤1. 收集实验数据:在实验室内设置几个测量点,记录它们的坐标和对应的函数值;2. 使用拉格朗日插值法计算其他位置的函数值:根据已知数据点,利用拉格朗日插值公式计算其他位置的函数值;3. 使用牛顿插值法计算其他位置的函数值:根据已知数据点,利用牛顿插值公式计算其他位置的函数值;4. 比较不同插值方法的精度和效率:通过计算误差和运行时间,比较拉格朗日插值法和牛顿插值法的性能差异;5. 分析插值法在实际问题中的应用:结合实验结果,探讨插值法在实际问题中的优势和局限性。
四、实验结果与分析1. 拉格朗日插值法的计算结果:根据已知数据点,利用拉格朗日插值公式计算其他位置的函数值;2. 牛顿插值法的计算结果:根据已知数据点,利用牛顿插值公式计算其他位置的函数值;3. 误差分析:比较插值结果与真实函数值之间的误差,分析误差的来源和影响因素;4. 运行时间分析:比较不同插值方法的运行时间,分析其效率和适用场景。
五、实验结论1. 拉格朗日插值法和牛顿插值法都是常用的插值方法,它们在不同场景下有各自的优势;2. 插值法在实际问题中的应用需要考虑数据的分布、函数的性质和计算效率等因素;3. 本实验结果表明,拉格朗日插值法和牛顿插值法在精度和效率上存在差异,具体选择哪种方法应根据实际需求进行权衡。
六、实验总结通过本次实验,我们深入了解了插值法的原理和应用。
实验结果表明,插值法在科学计算和工程设计中具有重要的作用。
在实际应用中,我们需要根据具体问题的要求和数据的特点选择合适的插值方法,以达到更好的效果。
插值方法

插值方法实验一:基本插值方法的比较1). 一维插值利用以下一些具体函数,考察分段线性插值﹑三次样条插值和拉格朗日多项式插值等三种插值方法的差异。
1.211x +,x Î[-5,5]; 2.sin x , x Î[0,2p]; 3.cos 10x , x Î[0,2p].注意:适当选取节点及插值点的个数;比较时可以采用插值点的函数值与真实函数值的差异,或采用两个函数之间的某种距离。
2).高维插值对于二维插值的几种方法:最邻近插值﹑分片线性插值﹑双线性插值﹑三次插值﹑组合插值等,利用如下函数进行插值计算,观察其插值效果变化,得出什么结论? (1) ())(sin ),(px t t x f -=ω,参数p =1/2000~1/200;采样步长为:t =4ms~4s ;x =5~25m.(2)⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+=εεεεy y x x y x f 1516sin 1516sin 1516sin 1516sin 103),(22参数e =1~2;x ,y Î [-1,1]。
(3) 将2中的函数推广到三维情形,进行同样的处理,体会高维插值的运用。
实验二:几何物理中的插值问题采用适当的方法求解下列问题:1). 轮船的甲板成近似半椭圆面形,为了得到甲板的面积。
首先测量得到横向最大相间8.534米;然后等间距地测得纵向高度﹑自左向右分别为:0.914, 5.060, 7.772, 8.717, 9.083, 9.144, 9.083, 8.992, 8.687, 7.376, 2.073, 计算甲板的面积。
2). 物体受水平方向外力作用,在水平直线上运动。
测得位移与受力如下表求 (1) 物体从位移为0到0.4所做的功;(2) 位移为0.4时的速度是多少?3).火车行驶的距离(路程)﹑速度数据如下,计算从静止开始20 分钟内走过的路程。
计算方法实验报告册

实验一——插值方法实验学时:4实验类型:设计 实验要求:必修一 实验目的通过本次上机实习,能够进一步加深对各种插值算法的理解;学会使用用三种类型的插值函数的数学模型、基本算法,结合相应软件(如VC/VB/Delphi/Matlab/JAVA/Turbo C )编程实现数值方法的求解。
并用该软件的绘图功能来显示插值函数,使其计算结果更加直观和形象化。
二 实验内容通过程序求出插值函数的表达式是比较麻烦的,常用的方法是描出插值曲线上尽量密集的有限个采样点,并用这有限个采样点的连线,即折线,近似插值曲线。
取点越密集,所得折线就越逼近理论上的插值曲线。
本实验中将所取的点的横坐标存放于动态数组[]X n 中,通过插值方法计算得到的对应纵坐标存放于动态数组[]Y n 中。
以Visual C++.Net 2005为例。
本实验将Lagrange 插值、Newton 插值和三次样条插值实现为一个C++类CInterpolation ,并在Button 单击事件中调用该类相应函数,得出插值结果并画出图像。
CInterpolation 类为 class CInterpolation { public :CInterpolation();//构造函数CInterpolation(float *x1, float *y1, int n1);//结点横坐标、纵坐标、下标上限 ~ CInterpolation();//析构函数 ………… …………int n, N;//结点下标上限,采样点下标上限float *x, *y, *X;//分别存放结点横坐标、结点纵坐标、采样点横坐标float *p_H,*p_Alpha,*p_Beta,*p_a,*p_b,*p_c,*p_d,*p_m;//样条插值用到的公有指针,分别存放i h ,i α,i β,i a ,i b ,i c ,i d 和i m};其中,有参数的构造函数为CInterpolation(float *x1, float *y1, int n1) {//动态数组x1,y1中存放结点的横、纵坐标,n1是结点下标上限(即n1+1个结点) n=n1;N=x1[n]-x1[0]; X=new float [N+1]; x=new float [n+1]; y=new float [n+1];for (int i=0;i<=n;i++) {x[i]=x1[i]; y[i]=y1[i]; }for (int i=0;i<=N;i++) X[i]=x[0]+i; }2.1 Lagrange 插值()()nn i i i P x y l x ==∑,其中0,()nj i j j ni jx x l x x x =≠-=-∏对于一个自变量x ,要求插值函数值()n P x ,首先需要计算对应的Lagrange 插值基函数值()i l x float l(float xv,int i) //求插值基函数()i l x 的值 {float t=1;for (int j=0;j<=n;j++) if (j!=i)t=t*(xv-x[j])/(x[i]-x[j]); return t; }调用函数l(float x,int i),可求出()n P xfloat p_l(float x) //求()n P x 在一个点的插值结果 {float t=0;for (int i=0;i<=n;i++) t+=y[i]*l(x,i); return t; }调用p_l(float x)可实现整个区间的插值float *Lagrange() //求整个插值区间上所有采样点的插值结果 {float *Y=new float [N+1]; for (int k=0;k<=N;k++) Y[k]=p_l(x[0]+k*h); return Y; } 2.2Newton 插值010()(,,)()nn i i i P x f x x x x ω==∑,其中101,0()(),0i i j j i x x x i ω-==⎧⎪=⎨-≠⎪⎩∏,0100,()(,,)()ik i nk k j j j kf x f x x x x x ==≠=-∑∏对于一个自变量x ,要求插值函数值()n P x ,首先需要计算出01(,,)i f x x x 和()i x ωfloat *f() {//该函数的返回值是一个长度为n +1的动态数组,存放各阶差商 }float w(float x, int i) {//该函数计算()i x ω }在求()n P x 的函数中调用*f()得到各阶差商,然后在循环中调用w(float x)可得出插值结果 float p_n(float x) {//该函数计算()n P x 在一点的值 }调用p_n(float x)可实现整个区间的插值 float *Newton() {//该函数计算出插值区间内所有点的值 }2.3 三次样条插值三次样条插值程序可分为以下四步编写: (1) 计算结点间的步长i hi 、i α、i β;(2) 利用i hi 、i α、i β产生三对角方程组的系数矩阵和常数向量; (3) 通过求解三对角方程组,得出中间结点的导数i m ; (4) 对自变量x ,在对应区间1[,]i i x x +上,使用Hermite 插值; (5)调用上述函数,实现样条插值。
插值运算实验报告

#### 一、实验目的1. 理解插值运算的基本概念和原理。
2. 掌握几种常见的插值方法,如拉格朗日插值、牛顿插值等。
3. 通过实验,验证插值方法在数值计算中的应用效果。
4. 培养动手能力和分析问题的能力。
#### 二、实验原理插值运算是指根据已知数据点,构造一个近似函数来描述这些数据点之间的变化规律。
常见的插值方法有拉格朗日插值、牛顿插值、分段线性插值等。
#### 三、实验内容1. 数据准备准备一组数据点,例如:```x: [1, 2, 3, 4, 5]y: [2, 4, 6, 8, 10]```2. 拉格朗日插值根据给定的数据点,构造拉格朗日插值多项式。
以三次拉格朗日插值为例,其公式如下:```L(x) = y0 ((x - x1) (x - x2) (x - x3)) / ((x0 - x1) (x0 - x2) (x0 - x3))+ y1 ((x - x0) (x - x2) (x - x3)) / ((x1 - x0) (x1 - x2) (x1 - x3))+ y2 ((x - x0) (x - x1) (x - x3)) / ((x2 - x0) (x2 - x1) (x2 - x3))+ y3 ((x - x0) (x - x1) (x - x2)) / ((x3 - x0) (x3 - x1)(x3 - x2))```将数据点代入上述公式,得到拉格朗日插值多项式。
3. 牛顿插值根据给定的数据点,构造牛顿插值多项式。
以三次牛顿插值为例,其公式如下:```N(x) = y0 + (x - x0) (y1 - y0) / (x1 - x0) + (x - x0) (x - x1) (y2 - y1) / ((x1 - x0) (x2 - x1)) + (x - x0) (x - x1) (x - x2) (y3 - y2) / ((x1 - x0) (x2 - x1) (x3 - x2))```将数据点代入上述公式,得到牛顿插值多项式。
插值运算实验报告

插值运算实验报告通过实验掌握插值运算的原理和方法,并利用插值运算技术对离散数据进行插值和逼近。
实验设备:计算机、Matlab软件实验原理:插值是利用已知数据点之间的关系,使用某种函数表达式来逼近未知点的值。
插值方法可以分为多种,如拉格朗日插值、牛顿插值等。
本次实验主要涉及的是拉格朗日插值和牛顿插值。
实验步骤:1. 采集实验数据,得到需要进行插值运算的离散数据。
2. 根据所给的离散数据,选择合适的插值方法,如拉格朗日插值或牛顿插值。
3. 利用Matlab软件进行编程,实现所选择的插值方法。
4. 运行程序,得到插值结果。
5. 根据插值结果,可以确定对未知数据点的函数值,也可以进行曲线拟合和逼近。
实验结果:经过对实验数据的处理和插值运算,得到了以下结果:1. 插值函数的形式,可以通过该函数计算未知数据点的函数值。
2. 插值曲线的图像,可以通过该曲线来拟合和逼近实验数据。
实验分析:通过实验结果的分析,可以得出以下结论:1. 插值方法的选择对结果有重要影响,不同的插值方法适用于不同的数据类型。
2. 插值运算可以有效地处理离散数据,得到连续函数的逼近值。
3. 插值运算的精度也会受到数据点分布和插值方法的影响。
实验总结:通过本次实验,我对插值运算的原理和方法有了更深入的了解。
插值运算是一种常用的数值计算方法,可以在一定程度上解决离散数据的处理问题。
插值运算不仅可以用于求解未知数据点的函数值,还可以用于曲线拟合和逼近。
不同的插值方法适用于不同类型的数据,需要根据实际情况进行选择。
插值运算的精度也会受到数据点分布和插值方法的影响,需要注意选择合适的插值方法以及优化离散数据的分布。
插值数值实验报告(3篇)

第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。
2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。
3. 分析不同插值方法的优缺点,并比较其精度和效率。
4. 通过实验加深对数值分析理论的理解和应用。
二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。
它广泛应用于科学计算、工程设计和数据分析等领域。
常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。
1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。
2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等,并且满足一定的差商条件。
三、实验内容1. 拉格朗日插值法(1)给定一组数据点,如:$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$(2)根据拉格朗日插值公式,构造插值多项式:$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$(3)计算插值多项式在不同点的函数值,并与实际值进行比较。
数值分析插值实验报告

数值分析插值实验报告引言插值是数值分析中常用的一种技术,通过已知点的函数值来推测未知点的函数值。
在实际应用中,我们经常需要根据有限的数据点来估计连续函数的值,这时插值就起到了关键作用。
本实验旨在通过插值方法来推测未知数据点的函数值,并对比不同插值方法的精度和效果。
实验目的1.了解插值的基本概念和方法;2.掌握常见的插值方法,如拉格朗日插值、牛顿插值等;3.对比不同插值方法的精度和效果,分析其优缺点。
实验步骤1.数据采集:选取一组已知数据点,作为插值的基础。
这些数据点可以是从实际场景中测量得到的,也可以是人为设定的。
2.插值方法选择:根据实验要求和数据特点,选择适合的插值方法。
常见的插值方法包括拉格朗日插值、牛顿插值、分段线性插值等。
3.插值计算:根据选定的插值方法,利用已知数据点进行计算,并得到插值结果。
4.结果分析:比较插值结果与实际数据的差异,并评估插值方法的精度和效果。
可以使用误差分析等方法进行评估。
5.优化调整:根据实验结果和需求,对插值方法进行优化调整,以提高插值的准确性和可靠性。
实验结果与讨论通过实验,我们得到了不同插值方法的结果,并进行了对比和分析。
根据实验数据和误差分析,我们可以得出以下结论:1.拉格朗日插值方法具有较高的插值精度,在一定程度上能够准确地模拟实际数据。
2.牛顿插值方法相对于拉格朗日插值方法而言,对于大量数据点的计算速度更快,但在少量数据点的情况下,两者的精度差异较小。
3.分段线性插值方法适用于数据点较为离散的情况,能够提供较为平滑的插值结果。
4.插值方法的选择应根据具体需求和数据特点进行,没有一种插值方法适用于所有情况。
实验总结通过本次实验,我们对插值方法有了更深入的了解,并掌握了常见的插值方法的原理和应用。
实验结果表明,插值方法在数值分析中起到了重要的作用,能够准确地推测未知点的函数值。
然而,在实际应用中,我们还需要考虑数据的特点、插值方法的适用性以及计算效率等因素。
实验一-插值方法实验

《计算方法》实验报告学院:信息学院专业:计算机科学与技术指导教师:班级学号:姓名:计算机科学与工程系实验一 插值方法一. 实验目的(1)熟悉数值插值方法的基本思想,解决某些实际插值问题,加深对数值插值方法的理解。
(2)熟悉Matlab 编程环境,利用Matlab 实现具体的插值算法,并进行可视化显示。
二. 实验要求用Matlab 软件实现Lagrange 插值、分段线性插值、三次Hermite 插值、Aitken 逐步插值算法,并用实例在计算机上计算和作图。
三. 实验容1. 实验题目(1)已知概率积分dx ey x x ⎰-=022π的数据表构造适合该数据表的一次、二次和三次Lagrange 插值公式,输出公式及其图形,并计算x =0.472时的积分值。
(2)将区间[-5,5]分为10等份,求作211)(xx f +=的分段线性插值函数,输出函数表达式及其图形,并计算x =3.3152时的函数值。
(3)仿照附录C 中“文件1.2 逐步插值”程序(Neville 算法,课本227页)编写相应的Aitken 逐步插值算法的程序,根据下表所给数据分别利用上述两种算法求正弦积分⎰∞-=xdt ttx f sin )(在x =0.462的值,并比较它们的结果。
(4)运行C 中“文件1.3 分段三次Hermite 插值”程序(课本228页),要求自行选择实验数据2. 设计思想(1)Lagrange 插值:Lagrange 具有累加的嵌套结构,容易编制其计算程序。
事实上,在逻辑上表现为二重循环,循环(j循环)累乘求得系数,然后再通过外循环(i循环)累加得出插值结果y。
(2)分段线性插值:分段插值是将被插值函数逐步多项式化。
分段插值的处理过程分两步,将区间分成几个子段,并在每个子段上构造插值多项式装配在一起,作为整个区间的插值函数。
在分化的每个节点给出数据,连接相邻节点得一折线,该折线函数可以视作插值问题的解。
数学实验第四章插值方法

Φ(2.3456789)≈[(Φ(2.34)+Φ(2.35))]/2=0.990485
对已知的红点按一定的规律插入的兰色点 . 这个规律叫做插值函数
插值函数一般是已知函数的线性组合或者称为
加权平均。插值操作在工程实践和科学实验中有着 非常广泛而又十分重要的应用。例如,信息技术中 的图像重建、图像放大中为避免图像的扭曲失真的 而做的插值补点、建筑工程的外观设计、物理、化 学工程实验数据与模型的分析、天文观测数据、地 理信息数据的处理(如天气预报)以及社会经济现 象的统计分析等等。
本章主要介绍插值的思想、方法和技术;如何 利用MATLAB软件作插值计算;针对实际问题,进 行建模、求解与分析;最后给出实验题目。
4.2.1 引例1:函数查表问题 标准正态分布函数值Φ(2.3456789)等于多少?
一般是通过查表的方法.先对自变量作近似, 2.3456789≈2.35,再查表得到Φ(2.35)=0.99061,所以 (2.Байду номын сангаас456789)≈Φ (2.35)=0.99061.
导言 在工程实践和科学实验中,常常需要从
一组实验观测数据 ( xi , yi ), i= 0,1,…,n,...
中揭示出自变量x与因变量y之间的解析关 系.
一般可以用一个近似的函数关系式y=f(x)来处理这 一问题。给出函数关系式的方法,因观测数据与要求的 不同而异,通常可以采用两种方法:曲线拟合和插值。
拟合主要是考虑到观测数据受随机误差的影响, 寻求整体误差最小、较好地反映观测数据的近似函 数,并不保证或追求所得到的函数一定满足yi=f(xi)。 侧重于从整体上把握问题, 拟合的方法将在第五章
实验1—插值与拟合

《计算方法》实验报告二级学院:计算机学院专业:指导教师:班级学号:姓名:实验一 插值与拟合1、 实验目的:① 通过编程和插值与拟合中的某种具体算法解决具体问题,更深一步的体会 计算方法这门课的重要性,并加深对插值与拟合公式某种具体算法的理解。
② 熟悉编程环境。
2、实验要求:实现插值与拟合中的某种具体算法编写并执行 3、实验内容:1)用牛顿法求解01553=-x 的根,取初始值为10。
2)用弦截法求解数学方程。
x*x*x-x-1=0 ,x=[1,1.5] 4、题目: 插值与拟合5、原理:(1)用牛顿法求01553=-x 的根的原理:牛顿迭代法是以微分为基础的,由于曲线不规则,微分就是用直线代替曲线, 牛顿迭代法是取x0之后,找比x0更近的方程的根,多次迭代后,找更近似 的根。
(2)用弦截法求解 x*x*x-x-1=0设x0,x1是f(x)=0的近似值,利用f(x0),f(x1)构造一次插值多项式f1,并用f1 =0作为f(x)=0的新的近似根。
其几何意义:依次用弦线代替曲线,用线性函 数的零点作为函数零点的近似值。
6、设计思想:(1)用牛顿法求01553=-x 的根的思想:用直线代替曲线,用线性函 数的零点作为函数零点的近似值。
(2)用弦截法求根思想:依次用弦线代替曲线,用线性函 数的零点作为函数零点的近似值。
7、对应程序:用牛顿法求解01553=-x 的根,取初始值为10。
#include<stdio.h> #include<math.h> void main(void) {float x0=10;float f0=x0*x0*x0-155; float f1=3*x0*x0; float x1=x0-f0/f1; while(fabs(x0-x1)>1e-6) {x0=x1;f0=x0*x0*x0-155; x1=x0-f0/f1;}printf("%.3f\n",x1); }弦截法求根 x*x*x-x-1=0 ,x=[1,1.5] #include<stdio.h> #include<math.h> void main(void) {float x0=1.5; float x1=1;float f0=x0*x0*x0-x0-1; float f1=x1*x1*x1-x1-1;float x=x0-(x1-x0)/(f1-f0)*f0; while(fabs(x-x1)>1e-6) {x1=x;f1=x1*x1*x1-x1-1;x=x0-(x1-x0)/(f1-f0)*f0; }printf("%.3f\n",x); }8、实验结果:01553=-x 的根是5.372 x*x*x-x-1=0 ,的根是 1.325 9、图形10、实验体会:通过编程,切身感到计算方法这门课绝不仅仅是数学,是图形的观察和实际计算方法的应用,从而解决一些复杂的数值问题。
实验一:插值方法

实验一:插值方法学时:41.龙格现象的发生、防止和插值效果的比较对区间[-5,5]做等距划分:xi=-5+ih(I=0,1,2….,n),h=10/n,对下列函数分别按给定方案进行插值,计算其在点xk=-5+0.25k(k=0,1,…,40)上的值,并绘出插值函数的图形(1)y=arctgx (2)y=x/(1+x4)方案1 分别取n=10,20作拉格朗日插值方案2 分别取n=10,20作分段线性插值方案3 分别取n=10,20作I型三次样条插值将计算结果用表格的形式排列,观察同一方案,不同的n的计算结果的变化状态,不同方案结果的精度比较,有无龙格现象发生2.插值法的稳定性已知y=cosx,对区间[0,1]作等距划分,结点为xi=i/n(I=0,1,…,n),试对下面两种情况分别案指定方案求cosx在0.73333点的近似值(n=10,40,160)(1)以给定节点为插值节点(2)仍以给定节点为插值节点,但在cos0.5上人为增加一个误差0.05方案1 拉格朗日插值方案2 分段线性插值方案3 I型三次样条插值试比较同一方案对不同的n、不同方案对相同的n的精度情况,分析人为增加的误差对不同方案计算结果的影响3.样条插值的应用设给定下述两种边界条件,试分别计算插值函数在点xi=50k(k=1,2,…,36)的值,并绘出飞机头部外型曲线(1)自然边界条件(2)y’(0)=1 y’(1841)=0实验二数值积分方法的使用和比较学时:2对给定的积分(1)I=∫x2e x dx (2)I=∫x5/2dx分别用下述计算方案求积分值,要求误差不超过10-6。
将每个积分的计算结果用表格排好,比较收敛速度,并讨论或说明原因方案1 复化梯形法方案2 复化辛普生法方案3 龙贝格公式方案4 复化两点高斯-勒让德公式实验三常微分方程数值解法实验学时:41.解初值问题的各种方法的比较给定初值问题y’=(2/x)y+x2e x 1<x≤2y(1)=0其准确解为y=x2(ex-e),分别案下列方案求它在节点xi=1+0.1k(k=0,1,…,10)处的数值解及误差,比价格方法的优缺点方案1 欧拉法,步长h=0.025、h=0.1方案2 改进的欧拉法,步长h=0.05、h=0.1方案3 四阶标准龙格-库塔法步长h=0.1方案4 带误差修正的哈明公式,步长h=0.12.变步长龙格-库塔法用变步长四阶标准龙格-库塔法解下列初值问题,并与准确解进行比较。
实验一函数插值方法

实验⼀函数插值⽅法《数值分析》课程设计实验报告实验⼀函数插值⽅法⼀、问题提出对于给定的⼀元函数()y f x =的n+1个节点值(),0,1,,j j y f x j n == 。
试⽤Lagrange 公式求其插值多项式或分段⼆次Lagrange 插值多项式。
数据如下:(1)求五次Lagrange 多项式5L ()x ,和分段三次插值多项式,计算(0.596)f ,(0.99)f 的值。
(提⽰:结果为(0.596)0.625732f ≈, (0.99) 1.05423f ≈)(2)试构造Lagrange 多项式6L ()x ,计算的(1.8)f ,(6.15)f 值。
(提⽰:结果为(1.8)0.164762f ≈,(6.15)0.001266f ≈)⼆、实验步骤1、利⽤Lagrange 插值公式00,()n nin k k i i k k ix x L x y x x ==≠??-= ?-??∑∏编写出插值多项式程序; function [A1,LN,L1,B1]=lagrange(X,Y) m=length(X); LN=ones(m,m); for k=1: m x1=1; for i=1:m ifk~=ix1=conv(x1,poly(X(i)))/(X(k)-X(i));endL1(k,:)=x1; B1(k,:)=poly2sym (x1)endA1=Y*L1;LN=Y*B1在主显⽰区,输⼊五次Lagrange多项式L()5x程序:>> X=[0.4 0.55 0.65 0.80 0.95 1.05];>> Y=[0.41075 0.57815 0.69675 0.90 1.00 1.25382];>> [A1,LN,L1,B1]=lagrange(X,Y)>> plot(X,A1);>> F=poly2sym(A1)运⾏后,输出五次Lagrange多项式L()5x的结果:A1 =121.6264 -422.7503 572.5667 -377.2549 121.9718 -15.0845F =(2139673480305281*x^5)/17592186044416 - (1859275536318005*x^4)/4398046511104 + (9836621836743*x^3)/17179869184 - (414796119737013*x^2)/1099511627776 + (2145751274873259*x)/17592186044416 - 1061478972867847/70368744177664拉格朗⽇插值多项式5()L x的图如下:2、给出插值多项式或分段三次插值多项式的表达式;function [f,ff] = Hermite3(x,y,y1)f = 0.0;if(length(x) == length(y))if(length(y) == length(y1))n = length(x);elsedisp('y和y的导数的维数不相等');return;endelsedisp('x和y的维数不相等! ');return;endfor i=1:nh = 1.0;a = 0.0;for j=1:nif( j ~= i)h = h*(t-x(j))^2/((x(i)-x(j))^2);a = a + 1/(x(i)-x(j));endendf = f + h*((x(i)-t)*(2*a*y(i)-y1(i))+y(i));endff = subs(f,'t');x的程序:在主显⽰区,输⼊分段三次艾尔⽶特插值多项式L()5>> x=[0.4 0.55 0.65 0.80 0.95 1.05];>> y=[0.41075 0.57815 0.69675 0.90 1.00 1.25382];>> y1=[2.3440 0.9032 1.4329 0.9903 0.9170 5.1439];>> [f,ff] = Hermite3(x,y,y1);>> ffx的输出结果:运⾏后,分段三次艾尔⽶特插值多项式L()5ff =(6400000000*(t - 4/5)^2*(t - 11/20)^2*(t - 13/20)^2*(t -19/20)^2*(t - 21/20)^2*((2240245151070481*t)/140737488355328 - 52393133567890089/8796093022208000))/184041 -(16000000*((6348013345609171*t)/140737488355328 - 85523418631741336287/1759218604441600000)*(t - 2/5)^2*(t -4/5)^2*(t - 11/20)^2*(t - 13/20)^2*(t - 19/20)^2)/169 + (16000000*((4105617466549689*t)/281474976710656 -5238387122042657959/703687441776640000)*(t - 2/5)^2*(t - 4/5)^2*(t - 13/20)^2*(t - 19/20)^2*(t - 21/20)^2)/9 - (256000000* ((35097*t)/10000 - 46347/12500)*(t - 2/5)^2*(t - 11/20)^2*(t - 13/20)^2*(t - 19/20)^2*(t - 21/20)^2)/81 - (400000000* ((13147*t)/20000 - 449611/400000)*(t - 2/5)^2*(t - 4/5)^2*(t - 11/20)^2*(t - 19/20)^2*(t - 21/20)^2)/81 - (10000000000* ((84913*t)/11000 - 1833347/220000)*(t - 2/5)^2*(t - 4/5)^2*(t - 11/20)^2*(t - 13/20)^2*(t - 21/20)^2)/9801x的图如下:分段三次艾尔⽶特插值多项式L()53、根据节点选取原则,对问题(2)⽤三点插值或⼆点插值,其结果如何;>> X=[1 2 3 4 5 6 7];>> Y=[0.368 0.135 0.050 0.018 0.007 0.002 0.001];>> [A1,LN,L1,B1]=lagrange(X,Y)>> plot(X,A1);>> F=poly2sym(A1)运⾏后,输出结果的Lagrange 多项式L ()6x 的结果:A1 =0.0001 -0.0016 0.0186 -0.1175 0.4419 -0.9683 0.9950F=(4304240283865561*x^6)/73786976294838206464- (7417128346304051*x^5)/4611686018427387904 +(223*x^4)/12000- (2821*x^3)/24000+(994976512675275*x^2)/2251799813685248-(19367*x)/20000 + 199/200Lagrange 多项式L ()6x 的图如下:4、对此插值问题⽤Newton 插值多项式其结果如何。
数值计算插值法实验报告

数值计算插值法实验报告
一、实验目标
本实验的目标是学习和掌握插值法的基本原理,通过实际操作,验证插值法的有效性,并利用插值法解决实际问题。
二、实验原理
插值法是一种数学方法,用于通过已知的离散数据点,构造一个连续的函数来近似地表示未知的函数值。
常用的插值法包括线性插值、多项式插值、样条插值等。
其中,多项式插值是一种常用的方法,其基本思想是选择一个多项式来逼近已知的数据点,从而得到未知点的近似值。
三、实验步骤
1.准备数据:收集一组已知的数据点,并将其整理成表格形式。
2.选择插值方法:根据实际情况选择适当的插值方法,如线性插值、多项式插值或样条插值等。
3.计算插值函数:根据选择的插值方法,利用已知的数据点计算插值函数的系数。
4.验证插值函数:利用已知的数据点对插值函数进行验证,检查其精度和误差。
5.应用插值函数:利用插值函数计算未知点的近似值,并将结果与实际值进行比较。
四、实验结果及分析
下面是本次实验的结果及分析:
1.已知数据点:。
实验一拉格朗日插值、分段线性插值...

实验一拉格朗日插值、分段线性插值、三次样条插值的比较一、问题提出选择函数y=exp(-x2) (-2≤x≤2),在n个节点上(n不要太大,如5~11)用拉格朗日、分段线性、三次样条三种插值方法,计算m个插值点的函数值(m要适中,如50~100)。
二、要求通过数值和图形输出,将三种插值结果与精确值进行比较。
适当增加n,在作比较,由此作初步分析。
三、问题的解答为统一起见,认为题目中的节点指的是中间节点,插值时还要考虑两端点的函数值,故原题目中有 n+2 个插值节点。
以下给出题目所需的 MATLAB 函数,其中参数 count_knot 表示题目中的n ,count_dot 表示题目中的m 。
function result=campare3inter(count_knot,count_dot)%count_knot 中间节点的个数%count_dot 拟合的函数值的个数clfknot=linspace(-2,2,count_knot+2);x=-2:0.01:2;y=exp(-x.^2);y0=exp(-knot.^2);plot(x,y,knot,y0,'ro');%,hold on;x_new=linspace(-2,2,count_dot);y_real=exp(-x_new.^2);%Lagrange 插值y_lagrange=lagrange(knot,y0,x_new);plot(x_new,y_lagrange,'k');hold on;%分段线性插值y_line=zeros(1,length(x_new))count_1=1;for j=1:count_dotfor i=1:count_knot+1if((x_new(j)>=knot(i))&((x_new(j)<=knot(i+1))))%直线的点斜式方程y_line(count_1)=((y0(i)-y0(i+1))/(knot(i)-knot(i+1)))*(x_new(j)-knot(i))+y0(i);count_1=count_1+1;break;end endendplot(x_new,y_line,'b');hold on;%三次样条插值 y_temp=[0 y0 0];pp=csape(knot,y_temp,'second');[breaks,coefs,npolys,ncoefs,dim]=unmkpp(pp);count=1;for j=1:count_dotfor i=1:count_knot+1if((x_new(j)>=knot(i))&((x_new(j)<=knot(i+1))))y_spline(count)=polyval(coefs(i,:),x_new(j)-knot(i));count=count+1;break;end endendplot(x_new,y_spline,'g');%输出原函数值和三种插值函数值的比较结果result=[y_real' y_lagrange' y_line' y_spline']图形输出(n=5,m=50)10.90.80.70.60.50.40.30.20.1-2 -1.5 -1 -0.5 0 0.5 1 1.5 2绿色:节点和exp(-x2)。
插值法实验案例范文

插值法实验案例范文插值法是一种数值分析方法,用于通过已知数据点推测未知数据点的近似值。
该方法通过在已知数据点之间进行插值计算,并利用插值多项式来描述数据点之间的曲线。
插值法在很多领域都有广泛的应用,比如图像处理、信号处理以及科学计算等领域。
下面我将为大家介绍一个插值法的实验案例。
实验目的:通过插值法来估计未知数据点的近似值。
实验材料:1.已知数据点的数据表格2.插值法计算工具实验步骤:1.收集已知数据点的数据表格,并整理该数据表格,找到未知数据点的位置。
2.将数据表格中的已知数据点用插值法进行计算,并将计算结果填入未知数据点的位置。
3.使用插值法计算工具来计算每个未知数据点的近似值。
4.对每个未知数据点进行计算,并记录计算结果。
5.用插值法计算结果与实际值进行比较,评估插值法的准确性。
实验案例:假设我们有一个关于温度变化的数据表格。
已知温度数据点如下:时间(小时)温度(摄氏度)0202254286?8?1030我们需要用插值法来计算问号处的温度值。
首先,我们可以使用拉格朗日插值法来进行计算。
拉格朗日插值法使用一个多项式来逼近所有已知数据点。
具体计算步骤如下:1.将已知数据点用拉格朗日插值多项式表示:L(x)=L0(x)*y0+L1(x)*y1+L2(x)*y2其中,L(x)为插值多项式,Li(x)为基函数,yi为已知数据点的温度值。
2.计算每个基函数Li(x):L0(x)=(x-x1)(x-x2)/(x0-x1)(x0-x2)L1(x)=(x-x0)(x-x2)/(x1-x0)(x1-x2)L2(x)=(x-x0)(x-x1)/(x2-x0)(x2-x1)3.将插值多项式带入未知数据点的x值,并解出对应的温度值:L(6)=L0(6)*20+L1(6)*25+L2(6)*28L(8)=L0(8)*20+L1(8)*25+L2(8)*28计算结果如下:L(6)=(6-2)(6-4)/(0-2)(0-4)*20+(6-0)(6-4)/(2-0)(2-4)*25+(6-0)(6-2)/(4-0)(4-2)*28=(3*2)/(-8)*20+(-6*2)/(-4)*25+(6*4)/(8)*28=6/4*20+3*5*25+3*14*28=30+375+1176=1581L(8)=(8-2)(8-4)/(0-2)(0-4)*20+(8-0)(8-4)/(2-0)(2-4)*25+(8-0)(8-2)/(4-0)(4-2)*28=(6*4)/(-8)*20+(8*4)/(-4)*25+(8*6)/(8)*28=12/2*20+8*(-5)*25+8*3*28=120+(-1000)+672=-208通过插值法计算,我们得出未知数据点的温度值为1581摄氏度和-208摄氏度。
数值分析插值与拟合实验

数值分析插值与拟合实验数值分析是一门研究利用数字计算方法解决数学问题的学科。
插值与拟合是数值分析的重要内容之一,可以用于数据分析、信号处理以及数学建模等领域。
本实验将使用MATLAB软件进行插值与拟合的实验,主要包括插值多项式与拟合曲线的构造,以及评价拟合效果的方法。
实验一:插值多项式的构造1. Lagrange插值Lagrange插值是一种构造多项式来拟合已知数据点的方法。
给定n 个数据点(xi, yi),其中xi不相等,Lagrange插值多项式可以写成:P(x) = ∑(i=0 to n) yi * l_i(x)其中l_i(x)是Lagrange基函数,定义为:l_i(x) = ∏(j=0 to n,j!=i) (x-xj)/(xi-xj)通过计算l_i(x),然后将其乘以相应的数据点yi,最后相加就可以得到插值多项式P(x)。
2. Newton插值Newton插值使用差商的概念来构造插值多项式。
首先定义差商F[x0,x1,...,xn]如下:F[x0]=f(x0)F[x0,x1]=(f(x1)-f(x0))/(x1-x0)F[x0,x1,x2]=(F[x1,x2]-F[x0,x1])/(x2-x0)...F[x0,x1,...,xn] = (F[x1,x2,...,xn] - F[x0,x1,...,xn-1])/(xn-x0)其中f(x)是已知数据点的函数。
然后,利用差商来构造插值多项式:P(x) = ∑(i=0 to n) F[x0,x1,...,xi] * ∏(j=0 to i-1) (x-xj)通过计算差商F[x0,x1,...,xi]和对应的乘积∏(x-xj),最后相加得到插值多项式P(x)。
实验二:拟合曲线的构造1.多项式拟合多项式拟合是通过构造一个多项式函数来拟合已知数据点的方法。
假设给定n个数据点(xi, yi),可以使用多项式函数来表示拟合曲线:P(x) = a0 + a1*x + a2*x^2 + ... + an*x^n其中a0, a1, ..., an是待确定的系数。
实验报告-插值法
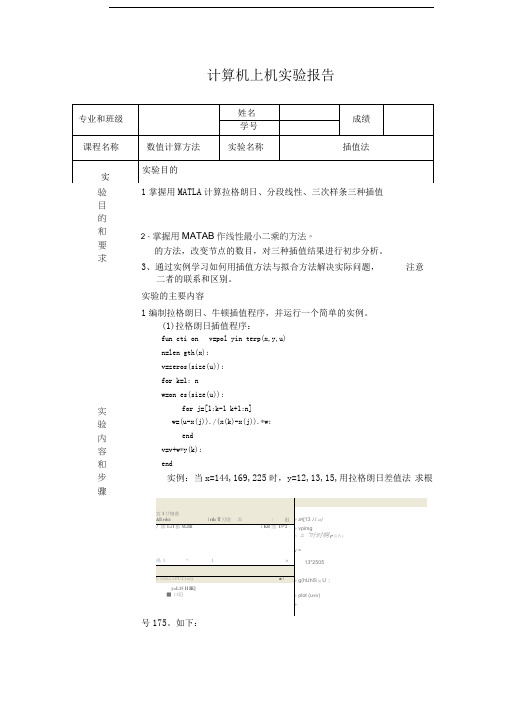
验 目 的 和 要 求2、掌握用MATAB 作线性最小二乘的方法。
实 验 内 容 和 步 骤计算机上机实验报告1掌握用MATLA 计算拉格朗日、分段线性、三次样条三种插值的方法,改变节点的数目,对三种插值结果进行初步分析。
3、通过实例学习如何用插值方法与拟合方法解决实际问题,注意二者的联系和区别。
实验的主要内容1编制拉格朗日、牛顿插值程序,并运行一个简单的实例。
(1)拉格朗日插值程序:fun cti on v=pol yin terp(x,y,u) n=len gth(x); v=zeros(size(u)); for k=1: n w=on es(size(u));for j=[1:k-1 k+1:n] w=(u-x(j))./(x(k)-x(j)).*w; end v=v+w*y(k); end实例:当x=144,169,225时,y=12,13,15,用拉格朗日差值法 求根号175。
如下:''Fl ^.kiEO- 1(2)牛顿插值程序:fun ctio n y=n ewi nterp(X,Y,x)% 牛顿插值函数m=le ngth(X);for k=2:mfor j=1:k-1Y(k)= (Y(k)- Y(j))/(X(k)-X(j));endendy=Y(m);for j=m-1:-1:1y=y.*(x-X(j))+Y(j);2、给定函数f(x)x,已知:f(2.0) .1.414214 f(2.1) .1.449138f (2.2) .1.483240 f (2.3) .1.516575 f (2.4) .1.549193 用牛顿插值法求4次Newton插值多项式在2.15处的值,以此作为函3.选择函数y=exp(-x 2) (-2 <x<2),在n个节点上(n不要太大,如5~11)用拉格朗日、分段线性、三次样条三种插值方法,计算m 个插值点的函数值(m要适中,如50~100)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《计算方法》实验报告学院:信息学院专业:计算机科学与技术指导教师:班级学号:姓名:计算机科学与工程系实验一 插值方法一. 实验目的(1)熟悉数值插值方法的基本思想,解决某些实际插值问题,加深对数值插值方法的理解。
(2)熟悉Matlab 编程环境,利用Matlab 实现具体的插值算法,并进行可视化显示。
二. 实验要求用Matlab 软件实现Lagrange 插值、分段线性插值、三次Hermite 插值、Aitken 逐步插值算法,并用实例在计算机上计算和作图。
三. 实验内容1. 实验题目(1)已知概率积分dx ey x x ⎰-=022π的数据表构造适合该数据表的一次、二次和三次Lagrange 插值公式,输出公式及其图形,并计算x =0.472时的积分值。
(2)将区间[-5,5]分为10等份,求作211)(xx f +=的分段线性插值函数,输出函数表达式及其图形,并计算x =3.3152时的函数值。
(3)仿照附录C 中“文件1.2 逐步插值”程序(Neville 算法,课本227页)编写相应的Aitken 逐步插值算法的程序,根据下表所给数据分别利用上述两种算法求正弦积分⎰∞-=xdt ttx f sin )(在x =0.462的值,并比较它们的结果。
(4)运行C 中“文件1.3 分段三次Hermite 插值”程序(课本228页),要求自行选择实验数据2. 设计思想(1)Lagrange 插值:Lagrange 具有累加的嵌套结构,容易编制其计算程序。
事实上,在逻辑上表现为二重循环,内循环(j循环)累乘求得系数,然后再通过外循环(i循环)累加得出插值结果y。
(2)分段线性插值:分段插值是将被插值函数逐步多项式化。
分段插值的处理过程分两步,将区间分成几个子段,并在每个子段上构造插值多项式装配在一起,作为整个区间的插值函数。
在分化的每个节点给出数据,连接相邻节点得一折线,该折线函数可以视作插值问题的解。
(3)Neville插值:Neville插值的基本思想和Aitken插值一样,不同的是Neville插值每次选取的两个插值节点都是上一步相邻节点插值后得到的,而不是新的插值节点,这样得到的插值函数和原函数更加接近。
Atiken逐步插值:Aitken插值是对三步插值转化为两步插值的重复,先将前两个插值点插值生成新的数据,然后与第三个插值点进行新的两点插值,不断重复这个插值过程,每一步增加一个新的节点,直到遍历所有节点为止,最终获得与原函数更加接近的插值函数。
(4)Hermite插值:Hermite插值是Lagrange插值的综合与推广,,为了保证插值函数能更好地密合原来的函数,要求“过点”,即两者在节点上有相同的函数值,而且要求“相切”,即在节点上还具有相同的导数值。
3. 对应程序(1)Lagrange插值function [y0,N]=Lagrange_eval(X,Y,x0)%X,Y是已知的差值点坐标点%x0是插值点%y0是Lagrange多项式在x0处的值%N是Lagrange插值函数的权系数m=length(X);N=zeros(m,1);y0=0;for i=1:mN(i)=1;for j=1:mif j~=iN(i)=N(i)*(x0-X(j))/(X(i)-X(j));endendy0=y0+Y(i)*N(i);end(2)分段插值syms f x;f=1/(1+x^2);N=input('请输入插值节点数N=');X=-5:10/N:5;Y=zeros(1,length(X));for i=1:(N+1)x=X(i);Y(i)=eval(f);endM = -5:0.01:5;y = zeros(1,length(M));n=1;for i=1:Nfor x=-5:0.01:5i f x<X(i+1) && x>=X(i)y(n)=Y(i)*(x-X(i+1))/(X(i)-X(i+1))+Y(i+1)*(x-X(i))/(X(i+1)-X(i)); n=n+1;ende ndendezplot(f,[-5,5])hold onx =-5:0.01:5;plot(x,y,'r');(3)Neville逐步插值function y0=Neville_eval(X,Y,x0)%X,Y是已知的插值点的坐标%x0是插值点%y0是多项式在x0处的值m=length(X);P=zeros(m,1);P1=zeros(m,1);P=Y;for i=1:mP1=P;k=1;for j=i+1:mk=k+1;P(j)=P1(j-1)+(P1(j)-P1(j-1))*(x0-X(k-1))/(X(j)-X(k-1));endif abs(P(m)-P(m-1))<10^-6;y0=P(m);return;endendy0=P(m);Atiken逐步插值function y0=Aitken_eval(X,Y,x0)%X,Y是已知的插值点的坐标%x0是插值点%y0是多项式在x0处的值m=length(X);P=zeros(m,1);P1=zeros(m,1);P=Y;for i=1:mP1=P;k=1;for j=i+1:mk=k+1;P(j)=P1(j-1)+(P1(j)-P1(1))*(x0-X(k-1))/(X(j)-X(1)); endif abs(P(m)-P(m-1))<10^-6;y0=P(m);return;endendy0=P(m);(4)Hermite插值function y0=Hermite_interp(X,Y,DY,x0)% X,Y是已知插值点向量序列% DY是插值点处的导数值% x0是插值点横坐标% y0是待求的分段三次Hemite插值多项式在x0处的值% N表示向量长度N=length(X);for i=1:Nif x0>=X(i)&x0<=X(i+1)k=i;break;endenda1=x0-X(k+1);a2=x0-X(k);a3=X(k)-X(k+1);y0=(a1/a3)^2*(1-2*a2/a3)*Y(k)+(-a2/a3)^2*(1+2*a1/a3)*Y(k+1)+(a1/a3)^2*a2*DY(k)+(-a 2/a3)^2*a1*DY(k+1);4. 实验结果列出相应的运行结果。
如果要求可视化,则同时需要给出相应的图形。
(1)Lagrange插值一次Lagrange插值:运行结果:>> X=[0.46,0.47];>> Y=[0.4846555,0.4937452];>> x0=0.472;>> [y0,N]=Lagrange_eval(X,Y,x0)y0 =0.49556314000000N =-0.200000000000001.20000000000000插值系数与作图:>> x1=0;>> [y1,N]=Lagrange_eval(X,Y,x1);>> x2=1;>> [y2,N]=Lagrange_eval(X,Y,x2);>> k=(y2-y1)/(x2-x1)k =0.90897000000001>> x=[x1,x2];>> y=[y1,y2];>> plot(x,y)二次Lagrange插值差值结果:>> X=[0.46,0.47,0.48];>> Y=[0.4846555,0.4937452,0.5027498]; >> x0=0.472;>> [y0,N]=Lagrange_eval(X,Y,x0)y0 =0.49555292800000N =-0.080000000000000.960000000000000.12000000000000插值系数与作图:>> x1=0;>> [y1,N]=Lagrange_eval(X,Y,x1);>> x2=1;>> [y2,N]=Lagrange_eval(X,Y,x2);>> k=(y2-y1)/(x2-x1)k =0.87918499999967>> x=[x1,x2];>> y=[y1,y2];>> plot(x,y)三次Lagrange插值差值结果:>> X=[0.46,0.47,0.48,0.49];>> Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x0=0.472;>> [y0,N]=Lagrange_1(X,Y,x0)>> [y0,N]=Lagrange_eval(X,Y,x0)y0 =0.49555296000000N =-0.048000000000000.864000000000000.21600000000000-0.03200000000000插值系数与作图>> x1=0;>> [y1,N]=Lagrange_eval(X,Y,x1);>> x2=1;>> [y2,N]=Lagrange_eval(X,Y,x2);>> k=(y2-y1)/(x2-x1)k =0.83708499999011>> x=[x1,x2];>> y=[y1,y2];>> plot(x,y)(2)分段差值差值结果:>> Y=interp1(x,y,3.3152,'spline')Y =0.08342312935731作图:(原函数:蓝色,插值函数:红色)>> fenduan_eval请输入插值节点数N=6(3)Neville逐步插值>> X=[0.3,0.4,0.5,0.6,0.7];>> Y=[0.29850,0.39646,0.49311,0.58813,0.68122];>> x0=0.462;>> y0=Neville_eval(X,Y,x0)y0 =0.45655811276280Aitken逐步插值>> X=[0.3,0.4,0.5,0.6,0.7];>> Y=[0.29850,0.39646,0.49311,0.58813,0.68122];>> x0=0.462;>> y0=Aitken_eval(X,Y,x0)y0 =0.77480886915945(4)分段三次Hermite插值>> X=[0.3,0.4,0.5,0.6,0.7];>> Y=log(X);>> DY=1./X;>> x0=0.462;>> y0=Hermite_interp(X,Y,DY,x0)y0 =-0.7722四.实验体会通过本次课程设计,我初步掌握了MATLAB运用,了解了matlab的基本编程思想,学会了matlab的基本语法与常用操作命令,加深了对于Lagrange插值、分段线性插值、Neville逐步插值、Aitken逐步插值、Hermite插值的理解;培养了独立工作能力和创造力;更加精进了编程的能力;综合运用专业及基础知识,解决实际数学问题的能力;深入的了解和体会了计算方法—算法设计及其matlab实现的基本原理与学习思路;在本次课程设计中,在老师的精心指导下,收益匪浅。
