吴传生 经济数学 微积分 第一章1.6 PPT
《微积分》(上下册) 教学课件 01.第1章 函数、极限、连续 高等数学第一章第9-10节
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
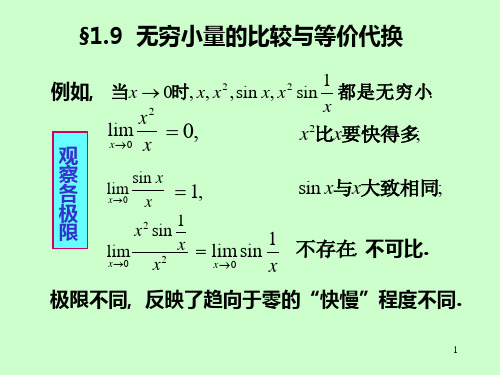
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
高中数学 第1章 导数及其应用 1.6 微积分基本定理课件 a选修22a高二选修22数学课件

第三十六页,共三十八页。
12/12/2021
第三十七页,共三十八页。
内容(nèiróng)总结
第一章 导数及其应用。解剖难点 探究(tànjiū)提高。课堂基础达标
No Image
12/12/2021
第三十八页,共三十八页。
a
12/12/2021
第五页,共三十八页。
2.微积分基本定理揭示了_导__数__(_dǎ_o_sh_ù)与_定__积__分_(_jī_fēn之) 间的内 在联系,同时它也提供了计算__定__积__分__(j_īfē_n_) __的一种有效方法.
12/12/2021
第六页,共三十八页。
12/12/2021
F(a).由此可以看出,积分运算与求导运算互为逆运算.注意: 只有 f(x)在[a,b]上连续,定积分bf(x)dx 才存在.
a
12/12/2021
第八页,共三十八页。
12/12/2021
课堂(kètáng)互动探究
归纳(guīnà)透析 触类旁通
第九页,共三十八页。
题型一 利用微积分定理求定积分 计算下列函数的定积分.
答案:76
12/12/2021
第十五页,共三十八页。
(1)计算:
x+1,x≤1,
(2)已知 f(x)=12x2,x>1,
计算2f(x)dx 的值. 0
【思路探索】 对于(1),由于 sin22x的原函数不易直接找出,
可先变形再计算;对于(2),由于 f(x)为分段函数,可按分段标准
将积分化为两段积分的和.
则e
f(x)dx
的值为(
)
0
A.43
B.2
C.1
D.23
12/12/2021
2020_2021学年高中数学第1章导数及其应用1.6微积分基本定理课件新人教A版选修2_22021

图2
图3
1.由牛顿-莱布尼茨公式,下列各式中正确的是( )
b
A.aF′(x)dx=F′(b)-F′(a) b
B.aF′(x)dx=F′(a)-F′(b) b
C.aF′(x)dx=F(b)-F(a) b
D.aF′(x)dx=F(a)-F(b)
【答案】C
2.若定积分2(ax+1)dx=4,则实数 a 的值为( ) 0
(3)原式= (1+cos x)dx=(x+sin x) =π2+1. (4)原式=10(1-x2)dx+12(x2-1)dx=x-31x310+13x3-x21=2.
定积分综合问题
【例 2】 已知函数 f(x)是二次函数,其图象过点(1,0),f′(1) =2,1f(x)dx=0,求函数 f(x)的解析式.
1.6 微积分基本定理
1.微积分基本定理 (1)定理内容: 如果函数 f(x)是区间[a,b]上的__连__续__函__数__,并且 F′(x) =__f_(x_)__,那么bf(x)dx=_F_(_b_)_-__F_(_a_) .
a
这个结论叫做微积分基本定理,又叫做_牛__顿__—__莱__布__尼__茨__公.式
(2)定理的符号表示:bf(x)dx=F(x)ba =__F_(_b_)_-__F_(a_)_. a
2.定积分和曲边梯形面积的关系 设曲边梯形在 x 轴上方的面积为 S 上,在 x 轴下方的面积为 S 下,则 (1)当曲边梯形的面积在 x 轴上方时,如图 1,则bf(x)dx=
a
__S_上___. (2)当曲边梯形的面积在 x 轴下方时,如图 2,则bf(x)dx=
A.1
B.2
C.3
D.4
【答案】A
3.设函数 f(x)=x22-,xx,∈x[∈0,11,],2],
高中数学第一章导数及其应用1.6微积分基本定理新人教A版选修

=6x-x2-x3+14x4|
3 2
=6×3-32-33+14×34-6×2-22-23+14×24
=94-4=-1.75.
(3)
3 1
x+ 1x26xdx=31x+1x+26xdx
3
= 1
(6x2+6+12x)dx
=(2x3+6x+6x2)|
3 1
=(54+18+54)-(2+6+6)
=112.
5-1f(x)dx=- 1 1x2dx+13xdx+533dx=13x3|
1-1+12x2|
31+3x|
5 3
=23+4+6=1023.
(2)f(x)=x42--x42, ,
x≥2或x≤-2, -2<x<2,
3
2
3
∴0|x2-4|dx=0(4-x2)dx+2(x2-4)dx
=4x-13x3|
20+13x3-4x|
2
[提示2] 由定积分的几何意义得0 (2x+1)dx=6.
[问题3] 求F(2)-F(0)的值. [提示3] F(2)-F(0)=4+2=6. [问题4] 你得出什么结论?
2
[提示4] 0f(x)dx=F(2)-F(0),且F′(x)=f(x).
微积分基本定理
内 如果f(x)是区间[a,b]上的__连__续___函数,并且
容 F′(x)=__f_(_x_) __,那么baf(x)dx=_F__(b_)_-__F_(_a_)__
符 号
abfxdx=Fxba=__F_(_b_)-__F__(a_)
定积分和曲边梯形面积的关系
设曲边梯形在x轴上方的面积为S上,在x轴下方的面积为S
则 下.
b
(1)当曲边梯形的面积在x轴上方时,如图①,则
最新2019-2020年人教统编高中数学第一章导数及其应用1.6微积分基本定理课件1新人教A版选修

(x),那么
b
a f (x)dx F (b) F (a)
这个结论叫做微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式 (Newton-Leibniz formula).
或记作
b a
f(x)dx
=
F(x)
b a
=
F(b)-
F(a).
b
f(x)d x
F
(
x)
b
F (b )F (a)
a
a
微积分基本定理表明:
一个连续函数在区间[a,b] 上的定积分等于它 的任意一个原函数在区间[a,b] 上的增量.
求定积分问题转化为求原函数的问题. 注意: 当 a b 时, F (x)=f(x)
1 x
3 1
9
1
1 3
1
22 3
.
例 2 计 算 下 列 定 积 分 :
π sinxdx,2π sinxdx,2π sinxdx.
0
π
0
解 因为 cos x ' sin x,
0
sin
xdx
cos
x
|0
cos
cos 0
2;
2
sin
xdx
cos
x
|2
cos
2
cos
2;
2
0
sin
xdx
cos
x
|02
cos
2
cos
0
0
.
我们发现: 定积分的值可取正值也可取负值,还可能是0;
(1)当曲边梯形位于x轴上方时,定积分的值取正值;
高等数学微积分第一章函数及其图形(共44张PPT)

如果A,B互相包含,即A B且B A,则称A与B相等,记为A=B。
如果把 y看作自变量,x 看作因变量,按照函数的定义就得到一个新的函数,这个新函数称为函数y=f(x)的反函数,记作 x=j(y)。
解: 要使函数有意义,必须x 0,且x2-4³0。
如果A,B互相包含,即A B且B A,则称A与B相等,记为A=B。
1
O
x
3.对数函数
指数函数y=ax的反函数叫做对数函数,记为
y=logax(a>0,a 1). 对数函数的定义域是区间(0,+ ).
单调性:
若a>1,则logax单调增加; 若0<a<1,则logax单调减少.
性质见书P34
y y=ax
1
O
y=logxax
a>1
4.三角函数
U(a)。 设>0,则称区间(a-, a+)为点a 的邻域,记作U(a, ),
即 U(a, ) ={x|a-<x<a+} ={x| |x-a|<}。
其中点 a 称为邻域的中心, 称为邻域的半径。
O a-
a+ x
去心邻域:
U
(a,)
={x
|0<|
x-a
|<}。
O a- a a+ x
左(右)邻域、M领域的概念见书中第七页。
bx
[a, b]={x|axb}称为闭区间。
[a, b]
Oa
bx
[a, b)={x|ax<b}及 (a, b]={x|a<xb}称为
半开区间。 [a, b)
Oa
bx
(a, b]
Oa
bx
经济数学微积分PPT课件

思考题
x
sin
1 x
,
试问函数 f ( x) 10,
5 x2 ,
x0 x 0 在x 0处
x0
的左、右极限是否存在?当x 0 时, f ( x) 的
极限是否存在?
第23页/共37页
思考题解答
lim f ( x) lim (5 x2 ) 5,
x0
x0
lim f ( x) lim x sin 1 0,
证
取
xn
1 n
,
lim
n
xn
0,
且 xn 0;
y sin 1 x
取
xn
4n
1
1
,
lim
n
xn
0,
2
且 xn 0;
第19页/共37页
而 limsin 1 limsinn 0,
n
x n n
而 limsin 1 limsin4n 1
n
xn n
2
lim1 1, n
二者不相等, 故 limsin 1 不存在.
四、讨论:函数(x) x 在 x 0 时的极限是否
x 存在?
第26页/共37页
练习题答案
一、1.0.0002; 四、不存在.
2. 397.
第27页/共37页
感谢您的观看!
第37页/共37页
第21页/共37页
过程 时刻 从此时刻以后
f (x)
n n N
x x x N
x N x N x N
f (x) A
过程 时刻 从此时刻以后
f (x)
x x0
x
x
0
0 x x0 0 x x0
最新经济数学微积分第一章函数部分

6. 【定义 1.5 】
差集 —— A B { x | x A且 x B } , A B 有时写成 A B ;
7. 【定义 1.6 】 余集 ( 补集 )
—— Ac U A ,
立身以立学为先,立学以读书为本
其中 U 为全集 . 显然: ( Ac )c A .
a A.
4. 有限集 ---- 含有有限个元素 .
无限集 ---- 含有无限个元素 .
(二)集合的表示方法
(1) 列举法——用列举全体元素表示集合的方法
.即
A { a1, a2 , , an} .
例如 A {1,2,3,4,5,6} .
(2) 描述法——用元素具有的特征表示集合的方法 A { a | a所具有的特征 } .
.即
立身以立学为先,立学以读书为本
例如 A {( x, y) | x 2 y2 1} . B { x | x2 5x 6 0} .
( 3)全集与空集 ①空集 —— 不含有任何元素的集合 . 记作 .
提问 : 0 , 是空集吗?
②全集 —— 所研究的所有事物组成的集合,记作
U.
(三)集合的关系 (包含关系) 与运算
例如:
( 1)设 A {1,2}, B {2,1}, C { x x2 3x 2 0},
则 A B C. ( 2) A x | x是大于1 而小于4 的整数 ; B x | x2 5x 6 0 则 A B .
4. 【定义 1.3 】并集
A B { x | x A或 x B } , 记作 A B .
5. 【定义 1.4 】交集
不是集合的例子:很小的数;张雨的好朋友
第一章 函数 《经济数学》PPT课件

【例1-2】自然数的全体组成一个集合.每一个自然数都是这个集合的 元素.
【例1-3】直线x+3y+3=0上所有的点组成一个集合.这里直线的每个 点是这个集合的元素.
➢ 习惯上,我们用英文大写字母 A 、B、C、X、Y等表示集合,用英文小 写字母a、b、c、x、y等表示集合的元素.如果a是集合A的元素,则记 作a∈A,读作a属于A.如果a不是集合A的元素,则记作a∉A,读作a不属 于A.
1. 2. 1 函数的概念
➢ 问题3:图1-5反映了上海证券交易所的上证指数从201×年10 月1日到201×年12月31日的60个交易日的变化情形,由此图可 以看出在这段时间中上证指数随时间的变化.
➢ 从图1-5中我们可以看到,有日期t和指数I两个变量,当变量t在某 一范围内变化时(201×年第四季度有60个交易日),指数I随着日 期t的变化而变化,并且当t取某一日期时,有唯一上证指数I与之相 对应.
➢ 补集有以下性质:A∪A ̅=I;(2)A∩A ̅=Φ . 【例1-14】设全体学生为全集I,如果男生为集合A,则A ̅表示为
女生集合.
1. 1. 5 集合的运算律
1)交换律
运 算 律
3)分配律
2)结合律
4)对偶律(德•摩根公式)
1. 1. 6
实数集
人们对数的认识从自然数发展到有理数(包括正负整数,正负分 数及零),再由有理数发展到无理数(例如e,π,√3等),如果令p,q为 整数,且q≠0,则一般有理数可用p/q表示,无理数不能用p/q表示.
1},A∩B={x|0<x≤3}. 【例1-13】 设A为全体有理数集合,B为全体无理数集合,则:A∪B为全
经济数学微积分 第一章函数部分[新版]
![经济数学微积分 第一章函数部分[新版]](https://img.taocdn.com/s3/m/00cbc47b2f60ddccda38a0f6.png)
第一章 函数教学过程:一、集合及其表示、运算(一)集合的概念1.【定义】集合—具有某种属性的事物组成的全体.用大写字母,,A B C 表示. 例如①自然数集:{0,1,2,3,4,}N =,而{1,2,3,4,}N +=; ② 整数集{0,1,2,3,}Z =±±±;③ 有理数集: Q =,,pp Z q N p q q+∈∈{且与互质};④ 实数集:R , 而{|0,}R x x x R +=>∈ .集合的例子: (1) 2009年1月2日出生的人.(2) 方程 2560x x -+=的根. (3) 全体偶数. (4) 直线 10x y +-=上所有的点. 不是集合的例子:很小的数;张雨的好朋友.2.元素——组成集合的各个事物或对象, 用小写字母c b a ,,表示.3.集合与元素的关系(从属关系)(1) a 属于A ——事物a 是集合A 的元素. 记作a A ∈;(2) a 不属于A ——事物a 不是集合A 的元素. 记作a A ∉.4.有限集----含有有限个元素.无限集----含有无限个元素. (二)集合的表示方法(1) 列举法——用列举全体元素表示集合的方法. 即},,,{21n a a a A =.例如 }6,5,4,3,2,1{=A .(2) 描述法——用元素具有的特征表示集合的方法. 即}|{所具有的特征a a A =.例如 22{(,)|1}A x y x y =+=.2{|560}B x x x =-+=.(3)全集与空集①空集——不含有任何元素的集合. 记作Φ.提问:{}{}0,Φ是空集吗?②全集——所研究的所有事物组成的集合,记作U .(三)集合的关系(包含关系)与运算 1.【定义1.1】A 是B 的子集 ——x A x B ∀∈⇒∈.记作A B ⊂.A 是B 的真子集—— A B ⊂,且A B ≠,记作 .例如: , , . 2.规定:空集为任何集合的子集. 空集为任何非空集合的真子集. 3.【定义1.2】A 与B 相等——若A B ⊂且B A ⊂,记作A B =. 例如:(1)设{1,2},A ={2,1},B =2{320},C x x x =-+=则.A B C ==(2){}|A x x =是大于1而小于4的整数;{}2|560B x x x =-+=则A B =.≠⊂Z Q ≠⊂N Z ≠⊂Q R ≠⊂A BA BB A BA4.【定义1.3】并集{|}AB x x A x B =∈∈或,记作A B .5.【定义1.4】交集{|}AB x x A x B =∈∈且,简记为A B .6.【定义1.5】差集——{|}A B x x A x B -=∈∉且,B A -有时写成A B \;7.【定义1.6】余集(补集)——cA U A =-,其中U 为全集.显然:()c cA A =. (四)集合的运算律 (1)交换律: ① AB B A =; ②A B B A =.(2)结合律: ① )()(C B A C B A =;②)()(C B A C B A =.(3)分配律: ① )()()(C B C A C B A =;② )()()(C B C A C B A =.(4)对偶原理(摩尔根原理):①()c c c AB A B =;② ()c c c A B A B =.证明:先证①. x U ∀∈,有()c x AB x A B∈⇔∉x A x B ⇔∉∉且cc c c B A x B x A x ∈⇔∈∈⇔且.① 得证.再证②.c c c c c c c c c c c c B A B A B A B A )(])()[(])[( ===.②得证.例1 某地区有100个工厂,其中,80个生产甲种机床,记为集合A ;61个生产乙种机床,记为集合B ;55个两种机床都生产.试用集合表示下列各类工厂,并计算出各类工厂的数目.(1)生产甲种机床而不生产乙种机床的工厂;(2)生产乙种机床而不生产甲种机床的工厂;(3)甲、乙两种机床中至少生产其中一种的工厂;(4)甲、乙两种机床都不生产的工厂. 解(1)此类工厂的集合为A B -,工厂数目为80-55=25(个).(2)此类工厂的集合为 B A -,工厂数目为 61-55=6(个).(3)此类工厂的集合为 A B ,工厂数目为 25+55+6=86(个).(4)此类工厂的集合为 A B ,工厂数目为 100-(25+55+6)=14(个).例2 利用集合的运算律证明:()()AB A B B =.(五)笛卡尔积1212{(,,,)|,1,2,,}n n i i A A A x x x x A i n ⨯⨯⨯=∈=.【定义1.7】设有集合:A B 和,对任意的 ,x A y B ∈∈,所有的二元有序数组(,)x y 构成的集合,称为A B 和的笛卡尔乘积(或直积),记作{}(,)|,A B x y x A y B ⨯=∈∈.平面点集 {}2(,)|,R R R x y x y R =⨯=∈.空间点集 {}3(,,)|,,R R R R x y z x y z R =⨯⨯=∈.提问:如果{3,0,2}X Y ==,求X Y ⨯.解 X Y ⨯={(3,3),(3,0),(3,2),(0,3),(0,0),(0,2),(2,3),(2,0),(2,2)}.提问:设集合1231212{,,},{,},{,}X x x x Y y y Z z z ===,求X Y Z ⨯⨯. 解 X Y Z⨯⨯x y z x y z x y z x y z =111112121121{(,,),(,,),(,,),(,,),211212221221(,,),(,,),(,,),(,,),x y z x y z x y z x y z 311312321321(,,),(,,),(,,),(,,)}x y z x y z x y z x y z .例3 设{}|02A x x =≤≤,{}|01B x y =≤≤则 A B ⨯ {}(,)|02,01x y x y =≤≤≤≤.例4 设{}{}{}0,1,1,2,3A B C ===,则{}(0,1,3),(0,2,3),(1,1,3),(1,2,3)A B C ⨯⨯=.提问:按下列要求举例: (1)一个有限集合; }4,3,2,1{=A ;(2)一个无限集合; n n k B ,12|{+=为正整数};(3)一个空集; x x x C ,01|{2=+=为实数};(4)一个集合是另一个集合的子集;}3,2,1{}2,1{21=⊂=D D提问:用集合的描述法表示下列集合:(1)圆2225x y +=内部(不包含圆周)一切点的集合;22{(,)|25,,B x y x y x y =+<均为实数};(2)抛物线2y x =与直线0x y -=的交点的集合.|),{(y x C =2x y =且y x y x ,,0=-均为实数}.提问:用列举法表示下列集合:(1)抛物线2x y =与直线0=-y x 的交点的集合;)}1,1(),0,0{(=B (2)集合5|1| |{≤-x x 的整数}.{4,3,2,1,0,1,2,3,4,5,6)}C =----.提问:下列哪些集合是空集:{|10}A x x =+=⇒∅≠A ,2{|10,B x x x =+=为实数}⇒∅=B1|{>=x x C 且}0<x ⇒∅=C ,0|{>=x x D 且}1<x ⇒∅≠D 1|),{(22=+=y x y x E 且y x y x ,,3=+为实数}⇒∅=E .提问:写出}2,1,0{=A 的一切子集.解 }2,1,0{},2,1{},2,0{},1,0{},2{},1{},0{,∅.注:空集是任何集合的子集.一般含有n 个元素的集合,其子集的个数为:12n n 0nn n n n C C C (11)C 21+++=+-=-.提问:如果}2,1{},2,1,0{==B A ,下列各种写法,哪些是对的?哪些不对?A ∈1,B ∉0,{1}A ∈,A ⊂1,A ⊂}1{,A ⊂0,A ⊂}0{,B ⊂}0{,B A =,B A ⊃,A ⊂∅,A A ⊂.提问:设},6,4,2{},5,3,1{},3,2,1{===C B A 求:解 (1)}6,5,4,3,2,1{=C B A ; (2)∅=C B A ;(3){2}A B -=.练习.如果{|35}A x x =<<,{|4}B x x =>,求:(1)A B ;(2)A B ;(3)A B -.解 (1)}3|{>=x x B A ;(2)}54|{<<=x x B A ; (3)}43|{≤<=-x x B A .练习.如果}02|),{(≥+-=y x y x A ,}0632|),{(≥-+=y x y x B ,}04|),{(≤-=x y x C ,在坐标平面上标出C B A 的区域. 解 在坐标平面上C B A 表示的区域如图15-所示.练习.如果}3,2,1{},6,5,4,3,2,1{==A U ,}6,4,2{=B求: (1)AB ;(2)A B .解 (1){1,3,4,5,6}A B =;(2){5}A B =.二、区间与邻域(一)实数与数轴 1.有理数-----有限小数或无限循环小数;2.无理数----无限不循环小数.3.实数-------有理数与无理数的总体.4.数轴-------规定了原点、正方向、单位长度的直线.5.实数集与数轴上点的集合是一一对应关系.(二)绝对值1.【定义1.8】实数x 的绝对值记作x ,且有15-图,0,0x x x x x ≥⎧=⎨-<⎩. 2. x 的几何意义:实数为x 的点到原点的距离.3.绝对值及运算性质(1)2x x =.(2)0x ≥.(3)x x =-.(4)x x x -≤≤.(5){}{}0a x x a x a x a ><=<<时,||-.(6){}{}0a x x a x x a x a >>=<>时,||-或.(7)x y x y x y -≤±≤+.(8)xy x y =⋅.(9)(0)x xy y y=≠.(三)区间区间常用I 表示. 设R ∈∀b a ,,且b a <.1.有限区间(1)开区间——}|{),(b x a x b a <<=;(2)闭区间——}|{],[b x a x b a ≤≤=;(3)半开半闭区间——}|{],(b x a x b a ≤<=;}|{),[b x a x b a <≤=.a bx a bx a b x abx2.无限区间引入记号∞+及∞-, 分别读作正无穷大和负无穷大.(1) }|{),(a x x a >=+∞;(2) }|{),[a x x a ≥=+∞;(3) }|{),(b x x b <=-∞;(4) }|{],(bx x b ≤=-∞;(5) R R =∈=+∞-∞}|{),(x x .其中:b a ,称为区间的端点;在有限区间中,a b -称为区间的长度. (四)邻域与去心邻域 点a 的邻域(称0δ>为邻域的半径) (1) 点a 的δ邻域:{}(,)|(,)U a x x a a a δδδδ=-<=-+, 简记()U a ;(2) 点a 的δ去心邻域:{}(,)|0(,)(,)U a x x a a a a a δδδδ=<-<=-+,a x a xb x O x b x δ-a δ+a xa简记()U a ;(3) 点a 的左δ邻域: (,)(,)U a a a δδ-=-, 简记()U a -;(4) 点a 的右δ邻域: (,),)U a a a δδ+=+(, 简记()U a +;4.无穷大的邻域)0(>K(1) 无穷大∞的K 邻域: ),(),(),(+∞--∞=∞K K K U,简记)(∞U ;(2) ∞-的K 邻域: ),(),(K K U --∞=-∞, 简记)(-∞U ;(3) ∞+的K 邻域: ),(),(+∞=+∞K K U, 简记)(+∞U .注:无穷大邻域中的U 也写成U ,δ-a xa δ+a xaKx0K-Kx 0xK-例如=∞),(K U),(K U ∞.三、映射*、函数关系(一)映射1.【映射定义】设B A ,是两个非空集合,若A x ∈∀,通过法则f ,|y B ∃∈与x 对应,则称f 是A 到B 的映射, 记作B A f →:.其中:(1) y 称为元素x (在映射f 下)的像,记作)(x f , 即)(x f y =;(2) x 称为元素y (在映射f 下)的原像; (3) 集合A 称为映射f 的定义域, 记作)(f D , 即)(f D A =;(4) 数集}),(|{)(A x x f y y A f ∈==称为映射f 的值域.2.特殊映射(1)满射:若()f A B =, 称映射f 为满射;(2) 单射:12,x x A ∀∈,若12x x ≠,有12()()f x f x ≠,称映射f 为单射;(3) 一一映射(双射):若映射f 既是单射,又是满射, 称映射f 为一一映射.3.逆映射:设f 是A 到B 的单射且为满射,对于)(A f y ∈∀,A x ∈∃|..t s )(x f y =,这样所确定的)(A f 到A B fA BfA B 1-fA 的映射)(y x ϕ=称为映射)(x f y =的逆映射,记作)(1y f x -=.注:(1) 逆映射)(1y f-的定义域为)(A f ,值域为A .(2) 只有双射才有逆映射.(二)函数关系1.函数概念【定义1.9】设非空数集D R ⊂,则映射:f D R →称为定义在D 上的x 的函数. 记作()y f x =,其中:(1) x 称为自变量, y 称为因变量;(2) 对于D x ∈0,称)(0x f 为函数)(x f 在点0x 处的函数值;(3) 数集D 称为函数)(x f 的定义域, 记作=()f D f D ;(4) 数集}),(|{)(D x x f y y D f ∈==称为函数)(x f 的值域. 记作()Z f 或f R .约定:用数学表达式表示的函数)(x f y =,若其定义域没有直接给出,规定()D f ={x |使表达式有意义的实数x }提问:函数有几个要素?(定义域、对应法则)例1 2arcsin(2)y x =+,2lg()y x =-,y x >是函数吗?为什么?例2 下列函数是否相同?为什么?(1)2(),()x f x x g x x==;(2)2(),()f x x g x x ==;(3)2()ln ,()2ln f x x g x x ==;(4)21(),()11x f x g x x x -==-+.例3 求下列函数的自然定义域(1)2121y x x =++-;解:⎩⎨⎧≥+≠-02012x x ⇒⎩⎨⎧-≥±≠21x x ⇒ ),1()1,1()1,2[)(+∞---= f D .(2)211arcsin 225x y x-=+-;解:121≤-x 且5x <⇒2|1|≤-x 且5x <⇒[1,3](5,5)--⇒()[1,3]D f =-.(3)ln(3)||1x y x -=-;解:⎩⎨⎧>->-01||03x x ⇒⎩⎨⎧><1||3x x ⇒)3,1()1,()( --∞=f D .(4)221arccos76x y x x -=--.解:⎪⎩⎪⎨⎧>--≤-0617122x x x ⇒⎩⎨⎧>+-≤-0)2)(3(712x x x ⇒⎩⎨⎧>-<≤≤3 243x x x 或-⇒]4,3()2,3[)( --=f D .(5)25lg 4x x y -=解: ⎪⎩⎪⎨⎧>-≥-⇒⎪⎪⎩⎪⎪⎨⎧>-≥-0)5(145045045lg 222x x x x x x x x ⎩⎨⎧<<≥+-⇒500452x x x}41|{)(≤≤=⇒x x y D ;(6)1lg(32)y x =-解: 321lg(32)021232033x x x x x x -≠⎧-≠⎧⎪⇒⇒>≠⎨⎨->>⎩⎪⎩且22(){|1}(,1)(1,)33D f x x x ⇒=>≠=+∞且.2.函数分类(1) 单值函数——R ⊂∈∀D x ,通过法则f ,R ∈∃y |与x 对应,则称函数)(x f y =是x 的单值函数. 注:除特别情况外,本课所讨论的函数均指单值函数.(2) 多值函数——R ⊂∈∀D x ,通过法则f ,R ∈∃y 与x 对应,且D x ∈∃0,通过法则f ,至少有两个不同的R ∈21,y y 与0x 对应,此时则称函数)(x f y =是x 的多值函数.例如 222r y x =+, )0(>r 是多值函数.又例如 sin arcsin ()y Arc x k x k Z π==+∈ 也是多值函数.(3)一元函数: )(x f y =自变量只有一个;(4)多元函数:(,,,)12n y f x x x =自变量有2个或2个以上的元素;(5)显函数:形如()y f x =用自变量的代数式表示因变量的函数. 225y x =-,1lg(32)y x =-,2y x 6x 7=+-,22z x y 6x 4y y =+-+等 (6)隐函数:形如(,)0F x y =,用方程表示自变量和因变量关系的函数.,sin()ln()22xy x y 4e x y 2x 5+=++=+, 1xy =,210y x +-=为隐函数.注意:隐函数不一定可以转化为显函数.不是所有的方程(,)0F x y =都可以确定隐函数,如方程2210x y ++=就不能确定隐函数.3.函数的表示法解析法、列表法、图像法.4.特殊函数(1) 绝对值函数,0,||,0.x x y x x x ≥⎧==⎨-<⎩()(,)D f =-∞+∞;()[0,)f D =+∞.(2) 符号函数1,0,sgn 0,0,1,0.x y x x x >⎧⎪===⎨⎪-<⎩()(,)D f =-∞+∞;(){1,0,1}f D =-.显然:||sgn x x x =.(3) 取整函数[]y x =, ()(,)D f =-∞+∞;Z =)(D f .其中:][x 表示不超过x 的最大 整数, 并称][x 为x 的整数部分. 例如:1]5.1[=, 2]5.1[-=-,1]2[=,0]5.0[=等等.(4) 分段函数:自变量的不同变化范围中,对应法则用不同式子表示的函数.yxO xy sgn =1-1y xO][x y =1-12-2yxy +=1xy 2=)(x f y =yxO||x y =例如:||x y =,x y sgn =,][x y =等等.例如函数⎩⎨⎧>+≤≤==.1,1,10,2)(x x x x x f y 是一个分段函数.),0[)(+∞=f D ;),0[)(+∞=D f .例如:2212)21(==f ,212)1(==f ,431)3(=+=f .提问:分段函数的定义域和值域如何确定?(5) 阶梯函数:分段取常值且增加的函数. 例如:][x y =等.(6) Dirichlet (狄利克雷)函数x QD x x R Q∈⎧=⎨∈-⎩1,()0,例4 确定下列函数的定义域并作出函数图形:(1) 1,0,()0,0,1,0.x f x x x >⎧⎪==⎨⎪<⎩(2), 1 211,()1, 2.x x f x x x ⎧-≤⎪=⎨-<<⎪⎩解 (1) ()(,)D f =-∞+∞,图形如图31-所示;(2) =)(f D }22|{<<-x x ,图形如图32-所示.例5 将函数5|21|y x =--用分段形式表示,作出函数图形.31-32-解 ⎪⎪⎩⎪⎪⎨⎧<+≥-=--=.21 ,42,21 ,26|12|5x x x x x y图形如图33-所示.例6 函数221,11,12x x y x x ⎧-<⎪=⎨-<≤⎪⎩解:1x =时函数无意义,函数定义域为[2,1)(1,1)(1,2]D =---图形如图44-所示.例7 已知函数22,02(),24x x f x xx +≤≤⎧=⎨<≤⎩,求(1)f x -.解:2(1)2,012(1)(1),214x x f x x x -+≤-≤⎧-=⎨-<-≤⎩ 21,13(1),35x x x x +≤≤⎧=⎨-<≤⎩. 例8 画出函数 []y x x =-的图像.(是周期为1的周期函数.)(三)函数的几种基本性质 1.奇偶性 :【定义1.10】给定函数()y f x =,若()D f 关于原点对称.33-(1) 偶函数()f x ——()x D f ∀∈,恒有()()f x f x -=.注: 偶函数图形关于y 轴对称.(2) 奇函数()f x ——()x D f ∀∈,恒有()()f x f x -=-.注: 奇函数图形关于原点对称.讨论函数奇偶性时,千万注意条件:()D D f =关于原点对称,即x D x D ∀∈⇒-∈.例9 判断下列函数的奇偶性(1)1y x =(奇函数);(2)31y x =+(非奇非偶函数)(3)422y x x =-(偶函数)(4)0y = (即奇又偶函数)(5)sin xy x=(偶函数).例10 判断函数10()0010x x f x x x x +<⎧⎪==⎨⎪->⎩的奇偶性.解: 10()0010x x f x x x x -+-<⎧⎪-=-=⎨⎪--->⎩100010()x x x x x f x -+>⎧⎪==⎨⎪--<⎩=- 故函数()f x 为奇函数.结论:设函数()f x 的定义域为(,)l l -,则在(,)l l -上一定存在函数奇函数()g x 与偶函数()h x ,使得()()()f x g x h x =+.即对于定义在(,)l l -上的函数,则有奇函数 ()()()2f x f xg x --=;偶函数 ()()()2f x f x h x +-=.2.周期性 设()D D f =(1)【定义1.11】 周期函数()f x —— 0,..l s t x D ∃≠∀∈,有x l D ±∈且()()f x l f x +=.其中l 称为函数()f x 的周期.注1:周期函数在)(f D 内每个长度为l 的区间上图形相同.注2:一般来说默认周期函数的周期(最小周期)是其最小正周期T .但不是所有的函数都有最小周期,例如()4f x =就是周期函数,且任何非零常数都是它的周期.又例如:狄利克雷函数 1,,()0,\.x Q D x x R Q ∈⎧=⎨∉⎩任何非零有理数均为其周期,但没有最小周期.例11 设下面所考虑的函数都是定义在区间(,)l l -上的,证明:(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数. 证 (1)①设)()()(21x f x f x f +=,其中)(1x f 与)(2x f 均为定义在区间),(l l -上的偶函数,即)()(),()(2211x f x f x f x f =-=-,则)()()()()()(2121x f x f x f x f x f x f =+=-+-=-,故)(x f 为),(l l -上的偶函数.即两个偶函数的和是偶函数.②设)()()(21x f x f x f +=,其中)(1x f 与)(2x f 均为定义在区间),(l l -上的奇函数, 即)()(),()(2211x f x f x f x f -=--=-,则)()()()()()(2121x f x f x f x f x f x f -=-+-=-+-=-,故)(x f 为),(l l -上的奇函数。
经济数学微积分吴传生PPT文档45页

51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
25、学习是劳动,是充满思想的劳动。—于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、成本函数
成本是生产一定数量产品所需要的
各种生产要素投入的价格或费用总额,
它由固定成本与可变成本两部分组成.
C 总 C 固 C 可变
支付固定生产 要素的费用 支付可变生产 要素的费用
平均成本
总成本 产量
固定成本
可变成本 产量
即 C AC
C (Q ) Q
C
1
Q
C
2
(Q )
3 Q + 4 P = 1 0 0 ,求 总 收
益和平均收益.
解
价格函数为
P
100 3 Q 4
,
100 Q 3 Q 4
100 3Q 4 .
2
所以总收益为
R (Q ) P Q
,
平均收益为
A P (Q ) P (Q )
六、利润函数
利润是生产中获得的总收益与投入的总成
q 2
,
在时间 T 内的总费用 E 为
E 1 2 C 1 Tq C Q
2
q
其中 ,
1 2
C 1 Tq 为贮存费,
C2
Q q
为进货费用
.
八、戈珀兹 (Gompertz) 曲线
戈珀兹 曲线是指数函数 y ka
在经济预测中,经常使用该曲线.
k
b
t
初始期 发展期
饱和期
当 lg a 0 , 0 b 1 时,图形如上页所示
1 .4
2.某 工 厂 对 棉 花 的 需 求 函 数 由
PQ
=0.11 给
出 ,( 1) 求 其 总 收 益 函 数 R;( 2) P(12),R(10), R(12),R(15),P(15),P(20)。 3.若 工 厂 生 产 某 种 商 品 , 固 定 成 本 200,000 元 , 每 生 产 一 单 位 产 品 , 成 本 增 加 1000 元 , 求总成本函数。
该点的横坐标称为供需平衡价格 .
供需平衡点 供需平 衡价格
Q0
E
P0
三、生产函数 生产函数刻画了一定时期内各生产
要素的投入量与产品的最大可能产量之
间的关系.一般说来,生产要素包括资金
和劳动力等多种要素 .为方便起见,我
们暂时先考虑只有一个投入变量, 与产出
4.某 厂 生 产 一 批 元 器 件 , 设 计 能 力 为 日 产 100 件 , 每 日 的 固 定 成 本 为 150 元 , 每 件 的 平 均 可 变 成 本 为 10 元 ,(1)试 求 该 厂 此 元 器 件 的 日 总 成 本 函 数 及 平 均 成 本 函 数 ;( 2) 若 每 件 售 价 14 元 , 试 写 出 总 收 入 函 数 ;( 3) 试 写 出 利 润 函 数 。
2
二次曲线需求函数:
Q a bP cP
指数需求函数:
Q Ae
bp
( 其中 a,b,c,A > 0 )
幂函数:Q kP
A
, 其中 A 0 , k 0
例 1 设某商品的需求函数为
Q aP b (a , b 0)
讨论
P 0 时的需求量和
Q 0 时的价格
总收益为
R ( Q ) P Q 20 Q
所以 L ( Q ) R ( Q ) C ( Q )
20 Q ( 20 2 Q 0 . 5 Q ) 20 18 Q 0 . 5 Q
2 2
2
L ( 10 ) ( 20 18 10 0 . 5 10 ) 110 ( 万元 ).
4 .( 1 ) C ( X ) 150 10 X ( 元 )( 0 X 100 ); C (X ) 150 X ( 2 ) R ( X ) 14 X ( 元 ( ) 0 X 100 ) ; ( 3 ) L ( X ) 150 4 X ( 元 )( 0 X 100 ); 10 ( 0 X 100 );
Q
例 3 已 知 某 种 产 品 的 总 成 本 函 数 为 C ( Q ) 1000
Q 8
2
.
求 当 生 产 100 个 该 产 品 时 的 总 成 本 和 平 均 成 本 .
解
由题意,求产量为100时的总成本
C ( 100 ) 1000 100 8
2
2250 ,
平均成本为
AC ( 100 )
5.某产品之需求函数为 Q d =20-3P,供给函数为
Qs
=5P-1,求该商品的静态均衡价格。
6.某工厂生产某产品年产量为 x 台,每台售 价为 250 元,当年产量在 600 台以内时,可 以全部售出,当年产量超过 600 台时,经广 告宣传后又可多出售 200 台,每台平均广告 费为 20 元,生产再多,本年就售不出去了。 试建立本年的销售总收入 R 与年产量 x 的关 系。
由图可见 ,曲线当 t 0 且无限增大时,
.
其无限与直线
y k 接近 ,
且始终位于该直
线 下方. 在产品销售预测中,当预测销售量充
分接近到 k 值时,表示该产品在商业流通中将
达到市场饱和 .
练习题
1.设 需 求 函 数 由 P+Q=1 给 出 , ( 1) 求 总 收 益 函 数 P;(2)若 售 出 1/3 单 位 , 求 其 总 收 益 。
Q G(P )
则 G称为供给函数.
一般地,供给函数可以用以下简单 函数近似代替: 线性函数:Q 幂函数:
aP b , 其中 a , b 0
A
Q kP
ae
, 其中 A 0 , k 0
, 其中 A 0 , b 0
指数函数:Q
bP
在同一个坐标系中作出需求曲线 D和供 给曲线 S ,两条曲线的交点称为供需平衡点,
第六节
经济学中的常用函数
一、需求函数
需求的含义:消费者在某一特定的时期内,在一 定的价格条件下对某种商品具有购买力的需要.
如果价格是决定需求量的最主要因素,
可以认为 Q 是 P的函数。记作
Q f (P )
则 f 称为需求函数.
常见的需求函数:
线性需求函数: Q a bP ,
a,b 0
本之差。即
L (Q ) R (Q ) C (Q )
例 5 设 某 种 商 品 的 总 成 本 为 C ( Q ) 20 2 Q 0 . 5 Q , 若 每 售 出 一 件 该 商 品 的 收 入 是 2 0 万 元 ,求 生 产 1 0 件的总利润.
2
解
由题意知
P 20 (万元) ,
250 x , 0 x 600 5 . R 250 600 ( 250 20 )( x 600 ), 600 x 800 250 600 230 200 , x 800 6 .Pe 21 8 ;
七、库存函数
设某企业在计划期 T 内,对某种物品总需求
量为 Q ,由于库存费用及资金占用等因素,显然
一次进货是不划算的,考虑均匀的分 n 次进货,
Q n T n
每次进货批量为 q
,进货周期为 t
. 假定
每件物品的贮存单位时间费用为 C 1 ,每次进货费 用为C 2 ,每次进货量相同,进货间隔时间不变, 以匀速消耗贮存物品,则平均库存为
.
解
P 0时 Q b ,
它表示价格为零时的
需求量为 b ,称为饱和需求量;
Q 0时 P b a ,
它表示价格为 时 ,
a
b
无人愿意购买此商品.
二、供给函数
供给的含义:在某一时间内,在一定的价格条件 下,生产者愿意并且能够售出的商品.
如果价格是决定供给量的最主要因素,
可以认为 Q 是 P 的函数。记作
2250 100
22 . 5
五、收益函数
总收益是生产者出售一定数量产品所得到 的全部收入. 用 Q 表示出售的产品数量,R 表 示总收益, R 表示平均收益,则
R R (Q ) , R R (Q ) Q
如果产品价格 P 保持不变,则
R ( Q ) PQ , R P
例
4 设某商品的需求关系是
练习题答案
1.R Q Q , R ( 2 . R 0 . 11 Q
0 .4 2
1 2
)
2 9
;
, P ( 15 ) 0 . 0025 , P ( 12 ) 0 . 0034 ,
P ( 20 ) 0 . 0017 , R ( 10 ) 0 . 044 , R ( 12 ) 0 . 041 , R ( 15 ) 0 . 037 ; 3 . C C ( Q ) 200000 1000 Q ;
g ( x ) 间的函数关系为
a
g ( x ) cx 由于
可见,当
a
g ( 2 x ) 2 cx
a 1 时,
a
2 g( x)
a
规模报酬不变; 如果投入增加一倍,产出增
当 a 1 时,
加不到一倍,即规模报酬递减;
当 a 1 时,
如果投入增加一倍,产出增
加不止一倍,即规模报酬递增 .
