双向解析光束法
双向解析摄影测量

∵ ∴
X 1Y2 − X 2Y1 Y =− 2 X 2 Z1 − X 1Z 2 Z2
BxY1 Y = − 2 N2 X 2 Z1 − X 1Z 2 Z2
Bx (Y1Y2 + Z1Z 2 ) Y22 = −( Z 2 + ) N 2 X 2 Z1 − X 1Z 2 Z2
线性化方程
∂F ∂F ∂F ∂F ∂F ∆µ + ∆ν + ∆ϕ + ∆ω + ∆κ = 0 F =F + ∂µ ∂ν ∂ϕ ∂ω ∂κ
0
∂F = Bx ( X 2 Z1 − X1Z2 ) ∂µ
∂F ≈ B xY1 X 2 ∂φ
∂F = Bx ( X 1Y2 − X 2Y1 ) ∂ν
∂F ≈ − Bx X 2 Z1 ∂κ
X2 ∂ Y 2 0 Z 2 = cos ϕ cos ω ∂κ sin ω
− cos ϕ cos ω 0 − sin ϕ cos ω
− sin ω X 2 − Y2 Y ≈ X sin ϕ cos ω 2 2 0 Z2 0
Bz Z1 = 0 Z2
X 2 x2 Y2 = R y 2 Z − f 2
连续法解析相对定向原理 连续法解析相对定向原理
1 F = Bx X 1 X2
µ
Y1 Y2
ν
Z1 = 0 Z2
∂F ∂F ∂F ∂F ∂F ∆µ + ∆ν + ∆ϕ + ∆ω + ∆κ = 0 F=F + ∂µ ∂ν ∂ϕ ∂ω ∂κ
摄影测量与遥感概论

摄影测量与遥感概论第一章绪论1.摄影测量:是利用光学或者数码摄影机获取的影像,经过处理以获取被摄物体的形状、大小、位置、性质和相互关系的一门学科。
分类:按距离远近:(1)航天摄影测量(2)航空摄影测量(3)地面摄影测量(4)近景摄影测量(5)显微摄影测量按用途:(1)地形摄影测量(2)非地形摄影测量按处理手段:(1)模拟摄影测量(2)解析摄影测量(3)数字摄影测量用途:(1)地形测量领域:各种比例尺的地形图、专题图、特种地图、正射影像图、景观图;建立各种数据库;提供地理信息系统和土地信息系统所需要的基础数据(2)非地形测量领域:生物医学;公安侦破;古文物、古建筑;建筑物变形监测2.摄影测量发展的三个阶段:模拟摄影测量(1851-1970);解析摄影测量(1950-1980);数字摄影测量(1970-现在)3.4D产品的含义:DLG(Digital Line Graphic 数字线划地图)DRG(Digital Raster Graphic 数字栅格地图)DEM(Digital Elevation Model 数字高程模型)DOM(Digital Orthpphoto Map 数字正射影像图)5.影像信息科学:是一门记录、存储、传输、量测、处理、翻译、分析和显示由非接触传感器获得的目标及其环境信息的科学、技术、和经济实体。
第二章单张航摄像片解析1.航空摄影测量的基本要求:(1)航摄倾角(相片倾角):摄影主光轴与铅垂方向的夹角α(α<3°)(2)摄影比例尺:航摄像片上的一段线l与地面上相应线段L之比视摄影像片水平、地面取平均高程时,像片上的线段l与地面上相应水平距L之比为摄影比例尺1 m =lL=fHf为摄影机主距,H为航高(3)像片的重叠度:当相邻的两张像片拍摄景区有重叠时,重叠部分占整张像片的比例要求:航向重叠度(航线相邻两张照片的重叠度)p x>53% (60%~65%)旁向重叠度(相邻航线像片的重叠度)p y>15% (15%~30%)(4)航线弯曲:把一条航线的航摄像片根据地物影像拼接起来,各张像片的主点连线不在一条直线上而呈现为弯弯曲曲的折线,称为航线弯曲。
12级摄影测量学

摄影测量学摄影测量学:利用摄影获取的影像进行测量,即利用在不同位置、不同的方向对同一个物体或地区摄影的影像进行测量、测图,是测量学科的分支。
航摄仪:航空摄影机是一种专门设计的大像幅的摄影机。
摄影比例尺:航摄像片上一线段为l的影像与地面上相应线段的水平距离L的之比,即1/m=l/L。
特点:航摄像片上的影像比例尺处处均不相等。
摄影航高:当取摄区内的平均高程面作为摄影基准面时,摄影机的物镜中心至该面的距离称为摄影航高。
绝对航高:摄影瞬间摄影机物镜中心相对于平均海平面的航高。
相对航高:摄影瞬间摄影机物镜中心相对于某一基准面或某一点的高度。
摄影基线:航线方向相邻两摄站点间的空间距离,常用B表示。
正射投影:若投影光线相互平行且垂直于投影面,称为正射投影。
中心投影:若投影光线会聚于一点,称为中心投影。
像片的方位元素:确定摄影瞬间摄影物镜与像片在地面设定的空间坐标系中的位置与姿态的参数。
内方位元素:表示摄影中心与像片之间相关位置的参数。
包括三个参数,即摄影中心S到像片的垂距(主距)f及像主点在框标坐标系中的坐标x。
、y。
外方位元素:表示摄影中心和像片在地面坐标系中的位置和姿态的参数。
包括三个直线元素Xs、Ys、Zs,三个角元素像片旋角k(偏航)、旁向倾角w(左右滚动)、航向倾角Ф(前倾后仰)。
像点位移:由于在实际航空摄影时,在中心投影的情况下,当航摄的飞机姿态出现较大倾斜或地面有起伏时,会导致地面点在航摄像片上的构象相对于理想情况下的构象所产生的位置差异。
a地面水平时,像片倾斜引起的像点位移。
b地形起伏在水平像片上引起的像点位移。
双像立体测图:是指利用一个立体像对(即在两摄站点对同一地面景物摄取有一定影像重叠的两张像片)重建地面立体几何模型,并对该几何模型进行量测,直接给出符合规定比例尺的地形图或建立数字地面模型等。
三种方法:a模拟法立体测图b解析法立体测图c影像数字化立体测图立体像对:摄影测量中,用摄影机在两摄站点对同一景物摄得的有一定重叠度的两张像片。
摄影测量学

《摄影测量学》复习提纲1、摄影测量:是利用摄影机或其他传感器采集被测对象的图像信息,经过加工处理和分析,获取有价值的可靠信息的理论和技术。
2、数字摄影测量:基于摄影测量的基本原理,通过对所获取的数字/数字化影像进行处理自动(半自动)提取被摄对象用数字方式表达的几何与物理信息,从而获得各种形式的数字化产品和目视产品。
3、摄影测量发展的三个阶段:(1)模拟摄影测量(2)解析摄影测量(3)数字摄影测量4、主光轴:透镜中心的连线。
5、航空摄影测量的要求:(1)像片倾斜角:应该小于3°;(2)航摄比例与航高:同一航线内各摄影站的航高差不得大于50米;(3)像片重叠度:航向重叠度一般规定为60%,最小不得小于53%,最大不得大于75%;旁向重叠度一般规定为30%,最小不得小于15%,最大不得大于50%;(4)航线弯曲度:通常不得大于3%;(5)像片旋偏角:一般不得大于6°,个别允许达到8°,连续三张不得超过6°。
6、透视变换中特殊的点、线、面(注意点线面之间的关系):(1)摄影方向线:过投影中心且垂直于像面的方向线;(2)像主点:摄影方向线与像面的交点;(3)地主点:摄影方向线与物面的交点;(4)像底点:过透视中心的铅垂线与像面的交点;(5)地底点:过透视中心的铅垂线与物面的交点;(6)主合点:过透视中心所做基本方向线的平行线与像面的交点;(7)像片主距:摄影机物镜后节点到像片主点的垂距;(8)等角点:过透视中心所做倾斜角a的二等分线与像(物)面的交点。
(9)迹线:像面与物面的交线。
(10)迹点:迹线上的所有点。
(11)主纵线:主垂面与像面的交线。
7、相对高度:摄影机物镜相对于某一基准面的高度。
8、绝对航高:相对于平均海平面的航高,指摄影机物镜在摄影瞬间的真实海拔高度。
9、航向重叠度:同一条航线内相邻像片间的重叠影像部分与像片边长比值的百分数。
10、旁向重叠度:相邻航线间的重叠影像部分与像片边长比值的百分数。
摄影测量整理

第一章和第二章摄影测量学:是对研究的物体进行摄影,量测和解译所获得的影像,获取被摄物体的几何信息和物理信息的一门科学和技术。
分类:按用途分为地形摄影测量、非地形摄影测量按处理手段分为模拟摄影测量、解析摄影测量、数字摄影测量按摄影机所处的位置分为地面摄影测量、航空摄影测量、航天摄影测量发展:模拟摄影测量、解析摄影测量、数字摄影测量三个阶段。
光圈号越小,光圈就越大,能通过的光线就越多,聚焦在感光物上的亮度就越高(越亮),反之,使用的光圈号数越大,影像亮度就越小。
航空摄影的基本要求:一、摄影比例尺:摄影比例尺是指航摄设计中的像片比例尺。
像片比例尺是由摄影机的主距和摄影的高度来计算的。
摄影比例尺的确定取决于成图比例尺、摄影测量成图方法和成图精度,另外考虑经济性和摄影资料的可使用性。
摄影比例尺可以分为大、中、小三种比例尺,一般都应选择小的。
二、像片重叠度:航向重叠:沿航线飞行方向两相邻像片上的影像重叠。
(60%~65%)旁向重叠:两相邻行带像片之间的影像重叠。
(15%~30%)三度重叠:一般情况下在航线方向三张相邻像片必须要有公共重叠影像,称为三度重叠。
三、航带弯曲度:不超过3%四、像片旋偏角:相邻两像片的主点连线与像幅沿航带飞行方向的两框标连线之间的夹角称为像片的旋偏角。
一般要求像片旋偏角小于6°,个别最大不应大于8°,而且不能有连续三张超过6°的情况。
航摄像片的误差:1、底片变形2、航设计物镜畸变差3、大气折光差4、地球曲率影响三原色:红、绿、蓝(三种等量相加=白)互补色:黄和蓝、红和青、绿和品红色的形成:1、加色法:将三原色按照不同的比例进行光学混合,得到其他颜色2、减色法:从白色中减去主色而获得补色第三章单张航摄像片解析中心投影:投射线会聚于一点的投影。
投射线的会聚点S称为投影中心。
中心投影的构像过程也称透视变换。
中心投影的三种方式:航摄像片是地面的中心投影,而地形图则是地面的正摄投影。
摄影测量考试复习题精编资料

摄影测量考试复习题一、名词解释:1、摄影测量学:对研究的对象进行摄影,根据所获得的构象信息,从几何方面和物理方面加以分析研究,从而对所摄对象的本质提供各种资料的一门学科。
2、解析空中三角测量:用计算的方式,根据量测的像点坐标和少量的控制点,采用较严密的数学公式,利用最小二乘原理,在计算机上解求测图所需控制点的平面坐标和高程。
3、数字摄影测量是基于数字影像与摄影测量的基本原理,应用计算计算机技术,数字影像处理,影像匹配,模拟识别等多学科的理论与方法,提取所摄对象,用数字方式表达几何与物理信息的摄影测量学的分支学科。
4、空间前方交会:由立体像对的内、外方位元素和像点坐标来确定相应地面点坐标的方法。
5、单向空间后方交会:利用航片上三个以上的像点坐标及相应的地面控制点坐标计算像片外方位元素的工作。
6、影像匹配:利用两个影像信号相关的函数,评价它们之间的相似性,以确定同名像点的过程。
7、数字影像匹配:用数字计算的方法对立体像对经数字化后所取得的灰度值,通过相关函数,探求左右影像的相似程度,以确定同名像点。
8、像片解析:利用数学分析的方法,研究被摄景物的成像规律,根据像片上的影像与所摄物体之间的数学关系式,从而建立起的像点与物点的坐标关系式。
9、双向解析摄影测量:按照立体像对与被摄物体的几何关系,以数学计算方式,通过计算机解求被摄物体的三维空间坐标的方法。
光束法:用已知的少数控制点以及待求的地面点,在立体像对内同时解求两像片的外方位元素和待定点的坐标,俗称一步定向法。
10、摄影基线:航线方向相邻两个摄站点间的空间距离。
11、相对定向:根据立体像对内在的几何关系恢复两张像片之间的相对位置和姿态,使同名光线对对相交,建立与地面相似的立体模型,即确定一个立体像对两张相片的相对位置。
12、绝对定向:用已知的地面控制点确定相对定向所建立的立体几何模型的比例尺和空间方位。
解析法绝对定向:利用已知的地面控制点,从绝对定向的关系式出发,解求七个绝对定向元素。
基于光束法双像解析的森林火点定位技术

学
学
报
Vo 1 . 4 8 No . 5 0 c t .2 0 1 3
J OU RN AL OF S OU T HW E S T J I A OT ON G UN I V ERS I T Y DOI :1 0 . 3 9 6 9 / j . i s s n . 0 2 5 8 - 2 7 2 4 . 2 0 1 3 . 0 5 . 0 1 4
b u n d l e a d j u s t me n t o f d o u b l e i m a g e s .T h e e x p e i r m e n t s s h o w e d t h a t t h e a c c u r a c y o f l o c a t i n g i f r e - p o i n t
文章编号 : 0 2 5 8 — 2 7 2 4 ( 2 0 1 3 ) 0 5 - 0 8 7 0 - 0 8
基 于光 束 法 双像 解 析 的森 林 火 点 定位 技术
段祝庚 , 肖化顺
( 1 .中南 大学地球科学 与信息物理学 院,湖南 长沙 4 1 0 0 8 3 ; 2 .中南林业科技大学理学院 , 湖南 长沙 4 1 0 0 0 4 ) 摘 要: 利用摄像机获取森林 区域立体 影像 , 以三维 电子罗盘 仪测定摄 影瞬 间摄 影机 三维姿态角 作为初始 值 ,
d o e s n o t r e q u i r e a k n o wn p o i n t t o b e a c o n t r o l p o i n t ,t h e l o c a t i o n a c c u r a c y i s d e p e n d e n t o n p a r a l l a x e r r o r o f c o r r e s p o n d i n g i ma g e p o i n t s ,p h o t o g r a p h i c b a s e l i n e l e n g t h,c o me r a n d p h o t o g r a p h i c d i s t a n c e,
摄影测量考试复习题

一、名词解释:1、摄影测量学:对研究的对象进行摄影,根据所获得的构象信息,从几何方面和物理方面加以分析研究,从而对所摄对象的本质提供各种资料的一门学科。
2、解析空中三角测量:用计算的方式,根据量测的像点坐标和少量的控制点,采用较严密的数学公式,利用最小二乘原理,在计算机上解求测图所需控制点的平面坐标和高程.3、数字摄影测量是基于数字影像与摄影测量的基本原理,应用计算计算机技术,数字影像处理,影像匹配,模拟识别等多学科的理论与方法,提取所摄对象,用数字方式表达几何与物理信息的摄影测量学的分支学科。
4、空间前方交会:由立体像对的内、外方位元素和像点坐标来确定相应地面点坐标的方法.5、单向空间后方交会:利用航片上三个以上的像点坐标及相应的地面控制点坐标计算像片外方位元素的工作。
6、影像匹配:利用两个影像信号相关的函数,评价它们之间的相似性,以确定同名像点的过程。
7、数字影像匹配:用数字计算的方法对立体像对经数字化后所取得的灰度值,通过相关函数,探求左右影像的相似程度,以确定同名像点。
8、像片解析:利用数学分析的方法,研究被摄景物的成像规律,根据像片上的影像与所摄物体之间的数学关系式,从而建立起的像点与物点的坐标关系式。
9、双向解析摄影测量:按照立体像对与被摄物体的几何关系,以数学计算方式,通过计算机解求被摄物体的三维空间坐标的方法.光束法:用已知的少数控制点以及待求的地面点,在立体像对内同时解求两像片的外方位元素和待定点的坐标,俗称一步定向法.10、摄影基线:航线方向相邻两个摄站点间的空间距离。
11、相对定向:根据立体像对内在的几何关系恢复两张像片之间的相对位置和姿态,使同名光线对对相交,建立与地面相似的立体模型,即确定一个立体像对两张相片的相对位置。
12、绝对定向:用已知的地面控制点确定相对定向所建立的立体几何模型的比例尺和空间方位。
解析法绝对定向:利用已知的地面控制点,从绝对定向的关系式出发,解求七个绝对定向元素。
名词解释
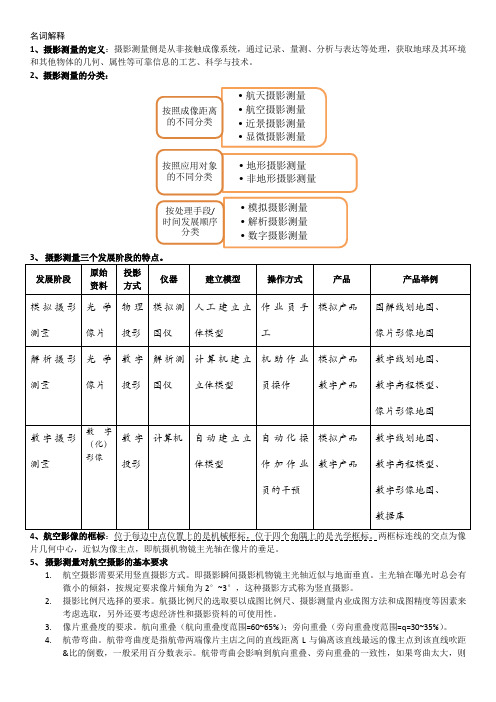
36. 解析空中三角测量:根据影像上量测的像点坐标及少量控制点的大地坐标,求出未知点的大地坐标,使得已知 点增加到每个模型中不少于四个,然后利用这些已知点求解影像的外方位元素,因而解析空中三角测量也称为 摄影测量加密。
37. 解析空中三角测量的分类。 A、 根据平差中采用的数学模型可以分为航带法、独立模型法、光束法; B、 根据平差范围的大小可以分为单模型法、单航带法、区域网法。
B. 解析空中三角测量光束法平差中基本数学模型;
C. 摄影测量中的数字投影基础;
D. 计算模拟影像数据;
E. 利用数字高程模型与共线方程制作正射影像;
F. 利用 DEM 与共线方程进行单幅影像测图,等。
16、影响内定向:数字摄影测量中,利用平面相似变换等公式,将扫描坐标系转换为像平面坐标系的过程。
17、单向空间后方交会:利用影像覆盖范围内一定数量的控制点的空间坐标与影像坐标,根据共线条件方程,反求
B、 单独像对相对定向法:以左摄影中心为原点、左主核面为 XZ 平面、摄影基线为 X 轴的右手空间直角坐标系。
24. 摄影基线:相邻两摄站的连线。
25. 立体像对:在不同摄站上对同一地区摄影取具有重叠的连续的两张像片。
26. 同名光线:同一地面点发出的两条光线。
27. 同名像点:同名光线在左、右两张影像上的构像(交点)。
28. 核面:摄影基线与某一个地面点组成的平面。
29. 同名核线:核面与左右像片面的交线。确定同名核线的方法:基于数字影像的几何纠正和基于共面条件。
30. 共面条件方程:B(R1 × R2) = 0(B、R 均为向量) 共面条件方程作用:a、确定同名核线;b、确定相对定向元素。
31. 立体像对空间前方交会:由立体像对左右两影像的内、外方位元素和同名像点的影像坐标量测值来确定该点的 物方空间坐标,称做立体像对的空间前方交会。(注:点投影系数的推导)
4D产品

摄影测量共线方程描述像点a,摄影中心s与地面点A位于一条直线上摄影中心和地面点A在地面摄影测量坐标系中的坐标分别为Xs,Ys,Zs和X,Y,Z,X,y是以像主点为原点的像点坐标双向解析结算方法后前方交会(前方交会利用后方交会获得的外方为元素和像点坐标,建立同名射线对对相交,来确定相应地面点的地面坐标)相对-绝对定向()光束法(把每张相片内所有的控制点,未知点都按共线条件式同时列误差方程式,在像对内联合进行解算,同时解求两相片的外方位元素及待定点的坐标)4D产品DOM(数字正摄影像)数字正射影像图是对航空航天像片进行数字微分纠正和镶嵌,按一定图幅范围裁剪生成的数字正射影像集。
它是同时具有地图几何精度和影像特征的图像。
DOM具有精度高、信息丰富、直观逼真、获取快捷等优点,可作为地图分析背景控制信息,也可从中提取自然资源和社会经济发展的历史信息或最新信息,为防治灾害和公共设施建设规划等应用提供可靠依据;还可从中提取和派生新的信息,实现地图的修测更新。
评价其它数据的精度、现实性和完整性都很优良。
数字正射影像图(Digital Orthophoto Map,DOM)是以航摄像片或遥感影像(单色/彩色)为基础,经扫描处理并经逐像元进行辐射改正、微分纠正和镶嵌,按地形图范围裁剪成的影像数据,并将地形要素的信息以符号、线画、注记、公里格网、图廓(内/外)整饰等形式填加到该影像平面上,形成以栅格数据形式存储的影像数据库。
它具有地形图的几何精度和影像特征。
DEM(数字高程模型)数字高程模型(Digital Elevation Model),简称DEM。
它是用一组有序数值阵列形式表示地面高程的一种实体地面模型,是数字地形模型(Digital Terrain Model,简称DTM)的一个分支,其它各种地形特征值均可由此派生。
一般认为,DTM是描述包括高程在内的各种地貌因子,如坡度、坡向、坡度变化率等因子在内的线性和非线性组合的空间分布,其中DEM是零阶单纯的单项数字地貌模型,其他如坡度、坡向及坡度变化率等地貌特性可在DEM的基础上派生。
摄影测量学总结

摄影测量学发展三个阶段:模拟/解析/数字摄影测量摄影资料的基本要求:影像色调(影像清晰,色调一致,反差适中);相片重叠(航向重叠p%=60%—65%,不小于53%;旁向重叠q%=30%—40%,不小于15%);像片倾角(不大于2度,不超过3度);航线弯曲(△L/L不大于3%);像片旋角(不超过6度,最大不超过8度))摄影测量实质:摄影测量可以被认为是研究并实现将中心投影的航摄像片转换为正射投影(地图)的科学与技术正射投影:投影光线相互平行且垂直于投影面中心投影:投影光线聚于一点航摄像片主要的点线面:像主点o、像底点n、等角点c、主合点i、朱纵线vv、合线hihi、等比线hchc、基本方向线VV。
主垂面W常用坐标系统:像方坐标系(像平面坐标系;像空间坐标系;相空间辅助坐标系);物方坐标系(地面测量坐标系;地面摄影测量坐标系)航摄像片的内外方位元素:内方位元素(表示摄影中心与像片之间相关位置的参数):f(摄影中心S到像片的垂距)、x0y0(像主点o在框标坐标系中的坐标);外方位元素(表示摄影中心和像片在地面坐标系中的位置和姿态的参数):三个直线元素:Xs、Ys、Zs(S在地面摄影测量坐标系中的值)、外方位角元素:φ(航向倾角)、ω(旁向倾角)、κ(像片旋角)立体像对:在两摄站点对同一地面景物摄取有一定影像重叠的两张像片立体像对的点线面:摄影基线B(两摄影中心S1、S2的连线)、同名像点a1、a2(地面上任一点A在左右像片上的构像)、同名射线AS1a1、AS2a2、核面WA(通过摄影基线与任意地面点A做的平面)、核线(核面与像片面的交线)、同名核线k1a1、k2a2(同一核面左右像片的核线)、核点k1、k2(基线延长线与左右像片面的交点)、左、右主核面(通过左右像片主点的两主核面)、垂核面(通过像底点的核面)重建立体模型过程:内定向(恢复像片对的内方位元素)、恢复像片对的外方位元素摄影测量双向立体测图方法:模拟法/解析法/影像数字化立体测图恢复像片对的外方位元素两个步骤:相对定向(确定一个立体像对两像片的相对位置)、绝对定向(借助地面控制点恢复或计算7个绝对定向元素)相对定向元素(5个):bv、bw(基线分量)、φ2、ω2、κ2(右像片3个角元素)绝对定向元素(7个):XS、YS、ZS(坐标原点平移量)、λ(模型缩放比例因子)、φ、Ω、Κ(方向余弦)连续像对:将左片置平,以左片的像空间坐标系作为本像对的像空间辅助坐标系的像对单向空间后方交会(角锥体法):利用至少三个已知地面控制点的坐标和其影像上对应的三个像点的影像坐标,根据共线方程,反求该像片的外方位元素立体像对前方交会:由立体像对中两张像片的内、外方位元素和像点坐标来确定相应地面点的地面坐标解析法相对定向:通过计算相对定向元素建立地面立体模型,恢复了摄像时相片之间的相对位置(解析法相对定向恢复核面,要从共面条件式出发解求5个相对定向元素,才能建立地面立体模型)连续像对相对定向至少量测五对同名像点解析法绝对定向:把模型点在像空间辅助坐标系中的坐标转化为地面摄影测量坐标(X,Y,Z)解算绝对定向公式至少需要两个平高控制点和一个高程点(三个控制点不同线),实际中在模型四个角布设四个控制点立体像对的解析摄影测量目的:求待定点的地面坐标立体像对的光束法思想:每张像片内所有的控制点、未知点都按共线条件式同时列误差方程式,在相对内联合进行结算,同时求解两像片的外方位元素及待定点坐标双向解析摄影测量的三种解算方法:后交—前交解法(已知像片外方位元素,需确定少量待定点时用)、相对定向—绝对定向解法(航带法解析空中三角测量中用)、光束法(理论严密,精度最高,光束法解析空中三角测量用)单张像片空间后方交会、解求像片外方位元素需要四个地面控制点一个立体像片对模型绝对定向需要四个地面控制点,求出7个绝对定向元素解析空中三角测量分类:按平差模型(航带法、独立模型法、光束法),按加密区域(单航带法、区域网法)三种区域网平差方法比较:航带网法区域评查方法方便,速度快,但精度不高;独立模型法区域平差解求未知数较多,仍能得到严密平差的结果;光束法区域网平差最严密,应用广泛,但计算量大DTM (Digital Terrain Model, DTM)是地形表面形态属性信息的数字表达,是带有空间位置特征和地形属性特征的数字描述。
摄影测量学5双向解析摄影测量

y1
x1
O1
X
y2
κ2
O2 x2
2021/4/21
13
1.连续法相对定向元素
在上述元素中,bz与模型的比例尺有关,是绝 对定向元素,与两片的相对关系无关,其余5个 非零元素by、bz、φ 2、ω 2 、κ 2可确定两像片的 相对位置,作为连续法相对定向的相对定向元素。
该系统的特点是以左片为基础,通过右像片相 对于左片作平移和旋转,来确定两片间的相对位 置。可以连续建立一条航线的立体模型。
2021/4/21
10
§3 立体像对的方位元素
利用立体像对摄影时同名光线成对相交 的几何关系,通过量测的像点坐标,解 求两像片的相对方位元素值的过程,称 为解析相对定向。确定相邻两像片相对 位置的参数,称为相对定向元素。相对 定向的目的是建立一个与被摄物体(地 面)相似的几何模型,解算相对定向元 素,以确定模型点的坐标。
2021/4/21
20
Z1
定向公式
由于
bbYZ
bX tg bX (bX cos ) bX
S1
共面方程可写为
Y1 b
bx
S2
bz
by X1
bX bX bX
1
F X1 Y1 Z1 bX X1 Y1 Z1 0
X 2 Y2 Z2
X 2 Y2 Z2
上式为非线性函数,将函数F按泰勒级数展开,取 至一次项,得未知数(相对定向元素)的线性方程式
解算时,把Q作为观测值, 列出如下误差方程式:
VQ
bx d
Y2 Z2
bx d
X 2Y2 Z2
N 2 d
(Z2
Y22 Z2
) N 2 d
第三章双像解析摄影测量

同名光线 同一地面点发出 的两条光线
A
核面 摄影基线与某一地 面点组成的平面
影像>采样 双像解析摄影测量>像对的前方交会公式
测绘学院 测绘学院
§ 3-2 像对的前方交会公式
z1 y1 x1 z2
二、定义
y2 S2 x2
S1
Z a1(x1,y1)
a2(x2,y2)
A(X,Y,Z) Y
由立体像对中两 张像片的内、外 方位元素和像点 坐标来确定相应 地面点在物方空 间坐标系中坐标 的方法
三、基本公式
Z1
Z2
Y2
1、点投影系数法
s1
Z1
X1
Y1
X2
X1
Zs1 Y1
Ztp
Ytp Xs1 M
(XA, YA, ZA) Ys1 Xtp
影像>采样 双像解析摄影测量>像对的前方交会公式
测绘学院 测绘学院
§ 3-2 像对的前方交会公式
摄影基线
s2 B BZ= Zs2 –Zs1 BY= Ys2 –Ys1 BX= Xs2 –Xs1
测绘学院 测绘学院
§ 3-2 像对的前方交会公式
主要内容:
◇立体像对的重要点线面 ◇立体像对前方交会定义
◇前方交会的基本公式
数字摄影测量 数字摄影测量 辽宁工程技术大学 辽宁工程技术大学
一、立体像对的重要点线面
摄影基线 相邻两摄站的连线
l1
p2
p1 S2
同名核线 核面与左右像 片面的交线
S1
同名像点 同名光线在左右 像片上的构像
人用双眼观察景物可判断其远近,得到景物的立体 效应,这种现象称为人眼的立体视觉
人 眼 立 体 视 觉
双像解析摄影测量三种方法的比较

双像解析摄影测量三种方法的比较
双像解析摄影测量是一种利用航空摄影影像进行测量和分析的技术。
该技术主要有三种方法,包括自适应光束法、DSP法
和一次平差法。
下面进行比较:
1.自适应光束法
该方法利用相机和GPS、惯性导航系统等设备获得数据,处
理过程涉及三维重建、像素级匹配等步骤。
该方法具有高精度、高效率等优点,但需要较为复杂的处理过程,而且设备的成本较高。
2.DSP法
该方法利用数字信号处理技术进行卫星影像的解析处理,然后进行三维测量。
该方法具有处理速度快、精度较高等优点,但在处理背景噪声、图像质量不同等方面存在一定局限。
3.一次平差法
该方法为传统的摄影测量方法,利用影像解析进行三维测量,然后通过平差计算获取各个特征点的坐标。
该方法成本较低,而且具有较高的精度和稳定性,但需要进行大量的数据处理,时间较长。
综上所述,三种方法各有优缺点,根据实际需求选择合适的方法进行双像解析摄影测量。
双向解析光束法

双向解析光束法光束法程序有问题,在Getelement这个函数里便出现索引超限,这个问题一直解决不了光束法的流程:1.根据同名像点对对相交理论求系数阵A,系数阵B和常数阵La11=(a1f+a3x)/Z; a12=(b1f+b3x)/Z; a13=(c1f+c3x)/Z; a14=ysin(omega)-[x/f(xcos(kappa)-ysin(kappa))+fcos(kappa)]cos(omega);a15=-fsin(kappa)-x/f(xsin(kappa)+ycos(kappa));a16=y;a21=(a2f+a3y)/Z; a22=(b2f+b3y)/Z; a23=(c2f+c3y); a24=-xsin(omega)-[x/f(xcos(kappa)-ysin(kappa))-fsin(kappa)]cos(omega)a25=-fcos(kappa)-y/f(xsin(kappa)+ycos(kappa));a26=-x;2.求方程的改化法方程求出外方位元素和物方坐标改正数3.判断改正数的值,如果小于限差则输出结果光束法是最严密的一种方法的原因:在一张相片中,待定点与控制点的像点与摄影中心及相应地面点均构成一条光束,该方法是以每张相片所组成的一束光线作为平差的基本单元,已共线条件方程作为平差的基础方程,通过各个光束在空间中的旋转和平移,使模型之间公共点的光线实现最佳交汇,并使整个区域纳入到已知的地面控制点坐标系中,所以要建立全区域统一的误差方程,整体解求全区域内每张相片的六个外方位元素及所有待定点坐标,光束法区域网平差是基于摄影时像点,物点和摄站点三点共线提出来的。
由单张相片构成区域,其平差的数学模型是共线条件方程,平差单元是单个光束,像点坐标是观测值,未知数是每张相片的外方位元素及所有待定点坐标。
误差方程直接由像点坐标的观测值列出,能对像点坐标进行系统误差改正。
光束法的程序代码为://计算像片外方位元素,架设phi=0,omega=0,kappa=0求Xs,Ys,Zs//求左片的Xs,Ys,ZsXsl = (strX[0] + strX[2]) / 2;Ysl = (strY[0] + strY[2]) / 2;L = Math.Pow(Math.Pow(strX[0] - strX[2], 2) + Math.Pow(strY[0] - strY[2], 2) + Math.Pow(strZ[0] - strZ[2], 2), 0.5);l = Math.Pow(Math.Pow(strXl[0] - strXl[2], 2) + Math.Pow(strYl[0] - strYl[2], 2),0.5);H = f * L / l;Zsl = (strZ[0] + strZ[2]) / 2 + H;//计算片左的加密点的物方坐标Class1 xyz = new Class1(8, 3, strXY);Class1 xyzt=xyz.Transpose ();//phi,omega,kappa为零,故旋转矩阵为单位阵//像空间辅助坐标系中的坐标Class1 UVW = xyzt.Multiply(H);//求地面摄影测量坐标系中的坐标for (int i = 0; i < 8; i++){UVW.SetElement(0, i, UVW.GetElement(0, i) + Xsl);UVW.SetElement(1, i, UVW.GetElement(1, i) + Ysl);UVW.SetElement(2, i, UVW.GetElement(2, i) + Zsl);}//求右片的Xs,Ys,ZsXsr = (strX[1] + strX[3]) / 2;Ysr = (strY[1] + strY[3]) / 2;L = Math.Pow(Math.Pow(strX[1] - strX[3], 2) + Math.Pow(strY[1] - strY[3], 2) + Math.Pow(strZ[1] - strZ[3], 2), 0.5);l = Math.Pow(Math.Pow(strXr[1] - strXr[3], 2) + Math.Pow(strYr[1] - strYr[3], 2),0.5);H = f * L / l;Zsr = (strZ[1] + strZ[3]) / 2 + H;//右片加密点double[] strxy;strxy = new double[24];Console.WriteLine("请输入右片加密点的相片坐标");for (int i = 0; i < 8; i++){//strxy[0 + 3 * i] = Convert.ToDouble(Console.ReadLine());//strxy[1 + 3 * i] = Convert.ToDouble(Console.ReadLine());strxy[2 + 3 * i] = -f;}for (int i = 0; i < 24; i++){strxy[i] = strxy[i] * 0.000025;}//计算片左的加密点的物方坐标Class1 XYZ = new Class1(8, 3, strxy);Class1 XYZt=XYZ .Transpose ();//phi,omega,kappa为零,故旋转矩阵为单位阵//像空间辅助坐标系中的坐标Class1 uvw = XYZt.Multiply(H);//求地面摄影测量坐标系中的坐标for (int i = 0; i < 8; i++){uvw.SetElement(0, i, (uvw.GetElement(0, i) + Xsr+UVW.GetElement(0,i))/2);uvw.SetElement(1, i, (uvw.GetElement(1, i) + Ysr+UVW.GetElement (1,i))/2);uvw.SetElement(2, i, (uvw.GetElement(2, i) + Zsr+UVW .GetElement (2,i))/2);}//从此开始循环//光束法进行平差//循环体do{//求左片旋转矩阵Rdouble[] mtrRl;mtrRl = new double[9];mtrRl[0] = Math.Cos(phil) * Math.Cos(kappal) - Math.Sin(phil) * Math.Sin(omegal) * Math.Sin(kappal);mtrRl[1] = -Math.Cos(phil) * Math.Sin(kappal) - Math.Sin(phil) * Math.Sin(omegal) * Math.Cos(kappal);mtrRl[2] = -Math.Sin(phil) * Math.Cos(omegal);mtrRl[3] = Math.Cos(omegal) * Math.Sin(kappal);mtrRl[4] = Math.Cos(omegal) * Math.Cos(kappal);mtrRl[5] = -Math.Sin(omegal);mtrRl[6] = Math.Sin(phil) * Math.Cos(kappal) + Math.Cos(phil) * Math.Sin(omegal) * Math.Sin(kappal);mtrRl[7] = -Math.Sin(phil) * Math.Sin(kappal) + Math.Cos(phil) * Math.Sin(omegal) * Math.Cos(kappal);mtrRl[8] = Math.Cos(phil) * Math.Cos(omegal);//求右片旋转矩阵Rrdouble[] mtrRr;mtrRr = new double[9];mtrRr[0] = Math.Cos(phir) * Math.Cos(kappar) - Math.Sin(phir) * Math.Sin(omegar) * Math.Sin(kappar);mtrRr[1] = -Math.Cos(phir) * Math.Sin(kappar) - Math.Sin(phir) * Math.Sin(omegar) * Math.Cos(kappar);mtrRr[2] = -Math.Sin(phir) * Math.Cos(omegar);mtrRr[3] = Math.Cos(omegar) * Math.Sin(kappar);mtrRr[4] = Math.Cos(omegar) * Math.Cos(kappar);mtrRr[5] = -Math.Sin(omegar);mtrRr[6] = Math.Sin(phir) * Math.Cos(kappar) + Math.Cos(phir) * Math.Sin(omegar) * Math.Sin(kappar);mtrRr[7] = -Math.Sin(phir) * Math.Sin(kappar) + Math.Cos(phir) *Math.Sin(omegar) * Math.Cos(kappar);mtrRr[8] = Math.Cos(phir) * Math.Cos(omegar);//求系数阵Adouble[] mtrA;mtrA = new double[576];for (int i = 0; i < 8; i++){mtrA[0 + 48 * i] = (mtrRl[0] * f + mtrRl[2] * xyz.GetElement(i, 0)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrA[1 + 48 * i] = (mtrRl[3] * f + mtrRl[5] * xyz.GetElement(i, 0)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrA[2 + 48 * i] = (mtrRl[6] * f + mtrRl[8] * xyz.GetElement(i, 0)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrA[3 + 48 * i] = xyz.GetElement(i, 1) * Math.Sin(omegal) - (xyz.GetElement(i, 0) * (xyz.GetElement(i, 0) * Math.Cos(kappal) - xyz.GetElement(i, 1) * Math.Sin(kappal) / f) + f * Math.Cos(kappal)) * Math.Cos(omegal);mtrA[4 + 48 * i] = -f * Math.Sin(kappal) - xyz.GetElement(i, 0) * (xyz.GetElement(i, 0) * Math.Sin(kappal) + xyz.GetElement(i, 1) * Math.Cos(kappal)) / f;mtrA[5 + 48 * i] = xyz.GetElement(i, 1);for (int j = 0; j < 6; j++){mtrA[j + 6 + 48 * i] = 0;}mtrA[12 + 48 * i] = (mtrRl[1] * f + mtrRl[2] * xyz.GetElement(i, 1)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrA[13 + 48 * i] = (mtrRl[4] * f + mtrRl[5] * xyz.GetElement(i, 1)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrA[14 + 48 * i] = (mtrRl[7] * f + mtrRl[8] * xyz.GetElement(i, 1)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrA[15 + 48 * i] = -xyz.GetElement(i, 0) * Math.Sin(omegal) - (xyz.GetElement(i, 0) * (xyz.GetElement(i, 0) * Math.Cos(kappal) - xyz.GetElement(i, 1) * Math.Sin(kappal)) / f - f * Math.Sin(kappal)) * Math.Cos(omegal);mtrA[16 + 48 * i] = -f * Math.Cos(kappal) - xyz.GetElement(i, 1) * (xyz.GetElement(i, 0) * Math.Sin(kappal) + xyz.GetElement(i, 1) * Math.Cos(kappal)) / f;mtrA[17 + 48 * i] = -xyz.GetElement(i, 0);for (int j = 0; j < 12; j++){mtrA[j + 18 + 48 * i] = 0;}mtrA[30 + 48 * i] = (mtrRr[0] * f + mtrRr[2] * XYZ.GetElement(i, 0)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrA[31 + 48 * i] = (mtrRr[3] * f + mtrRr[5] * XYZ.GetElement(i, 0)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrA[32 + 48 * i] = (mtrRr[6] * f + mtrRr[8] * XYZ.GetElement(i, 0)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrA[33 + 48 * i] = XYZ.GetElement(i, 1) * Math.Sin(omegar) - (XYZ.GetElement(i, 0) * (XYZ.GetElement(i, 0) * Math.Cos(kappar) - XYZ.GetElement(i, 1) * Math.Sin(kappar) / f) + f * Math.Cos(kappar)) * Math.Cos(omegar);mtrA[34 + 48 * i] = -f * Math.Sin(kappar) - XYZ.GetElement(i, 0) * (XYZ.GetElement(i, 0) * Math.Sin(kappar) + XYZ.GetElement(i, 1) * Math.Cos(kappar)) / f;mtrA[35 + 48 * i] = XYZ.GetElement(i, 1);for (int j = 0; j < 6; j++){mtrA[j + 36 + 48 * i] = 0;}mtrA[42 + 48 * i] = (mtrRr[1] * f + mtrRr[2] * XYZ.GetElement(i, 1)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrA[43 + 48 * i] = (mtrRr[4] * f + mtrRr[5] * XYZ.GetElement(i, 1)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrA[44 + 48 * i] = (mtrRr[7] * f + mtrRr[8] * XYZ.GetElement(i, 1)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrA[45 + 48 * i] = -XYZ.GetElement(i, 0) * Math.Sin(omegar) - (XYZ.GetElement(i, 0) * (XYZ.GetElement(i, 0) * Math.Cos(kappar) - XYZ.GetElement(i, 1) * Math.Sin(kappar)) / f - f * Math.Sin(kappar)) * Math.Cos(omegar);mtrA[46 + 48 * i] = -f * Math.Cos(kappar) - XYZ.GetElement(i, 1) * (XYZ.GetElement(i, 0) * Math.Sin(kappar) + XYZ.GetElement(i, 1) * Math.Cos(kappar)) / f;mtrA[47 + 48 * i] = -XYZ.GetElement(i, 0);}for (int i = 8; i < 12; i++){mtrA[0 + 48 * i] = (mtrRl[0] * f + mtrRl[2] * strXl[i - 8]) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrA[1 + 48 * i] = (mtrRl[3] * f + mtrRl[5] * strXl[i - 8]) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrA[2 + 48 * i] = (mtrRl[6] * f + mtrRl[8] * strXl[i - 8]) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrA[3 + 48 * i] = strYl[i - 8] * Math.Sin(omegal) - (strXl[i - 8] * (strXl[i - 8] * Math.Cos(kappal) - strYl[i - 8] * Math.Sin(kappal) / f) + f * Math.Cos(kappal)) * Math.Cos(omegal);mtrA[4 + 48 * i] = -f * Math.Sin(kappal) - strXl[i - 8] * (strXl[i - 8] * Math.Sin(kappal) + strYl[i - 8] * Math.Cos(kappal)) / f;mtrA[5 + 48 * i] = strYl[i - 8];for (int j = 0; j < 6; j++){mtrA[j + 6 + 48 * i] = 0;}mtrA[12 + 48 * i] = (mtrRl[1] * f + mtrRl[2] * strYl[i - 8]) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrA[13 + 48 * i] = (mtrRl[4] * f + mtrRl[5] * strYl[i - 8]) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrA[14 + 48 * i] = (mtrRl[7] * f + mtrRl[8] * strYl[i - 8]) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrA[15 + 48 * i] = -strXl[i - 8] * Math.Sin(omegal) - (strXl[i - 8] * (strXl[i - 8] * Math.Cos(kappal) - strYl[i - 8] * Math.Sin(kappal)) / f - f * Math.Sin(kappal)) * Math.Cos(omegal);mtrA[16 + 48 * i] = -f * Math.Cos(kappal) - strYl[i - 8] * (strXl[i - 8] * Math.Sin(kappal) + strYl[i - 8] * Math.Cos(kappal)) / f;mtrA[17 + 48 * i] = -strXl[i - 8];for (int j = 0; j < 12; j++){mtrA[j + 18 + 48 * i] = 0;}mtrA[30 + 48 * i] = (mtrRr[0] * f + mtrRr[2] * strXr[i - 8]) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrA[31 + 48 * i] = (mtrRr[3] * f + mtrRr[5] * strXr[i - 8]) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrA[32 + 48 * i] = (mtrRr[6] * f + mtrRr[8] * strXr[i - 8]) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrA[33 + 48 * i] = strYr[i - 8] * Math.Sin(omegar) - (strXr[i - 8] * (strXr[i - 8] * Math.Cos(kappar) - strYr[i - 8] * Math.Sin(kappar) / f) + f * Math.Cos(kappar)) * Math.Cos(omegar);mtrA[34 + 48 * i] = -f * Math.Sin(kappar) - strXr[i - 8] * (strXr[i - 8] * Math.Sin(kappar) + strYr[i - 8] * Math.Cos(kappar)) / f;mtrA[35 + 48 * i] = strYr[i - 8];for (int j = 0; j < 6; j++){mtrA[j + 36 + 48 * i] = 0;}mtrA[42 + 48 * i] = (mtrRr[1] * f + mtrRr[2] * strYr[i - 8]) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrA[43 + 48 * i] = (mtrRr[4] * f + mtrRr[5] * strYr[i - 8]) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrA[44 + 48 * i] = (mtrRr[7] * f + mtrRr[8] * strYr[i - 8]) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrA[45 + 48 * i] = -strXr[i - 8] * Math.Sin(omegar) - (strXr[i - 8] * (strXr[i - 8] * Math.Cos(kappar) - strYr[i - 8] * Math.Sin(kappar)) / f - f * Math.Sin(kappar)) * Math.Cos(omegar);mtrA[46 + 48 * i] = -f * Math.Cos(kappar) - strYr[i - 8] * (strXr[i - 8] * Math.Sin(kappar) + strYr[i - 8] * Math.Cos(kappar)) / f;mtrA[47 + 48 * i] = -strXr[i - 8];}//将数组A转化为矩阵Class1 A = new Class1(48, 6, mtrA);//求系数阵Bdouble[] mtrB;mtrB = new double[1728];for (int i = 0; i < 1728; i++){mtrB[i] = 0;//给B矩阵赋值}for (int i = 0; i < 8; i++){mtrB[0 + 147 * i] = -mtrA[0 + 48 * i];mtrB[1 + 147 * i] = -mtrA[1 + 48 * i];mtrB[2 + 147 * i] = -mtrA[2 + 48 * i];mtrB[36 + 147 * i] = -mtrA[12 + 48 * i];mtrB[37 + 147 * i] = -mtrA[13 + 48 * i];mtrB[38 + 147 * i] = -mtrA[14 + 48 * i];mtrB[72 + 147 * i] = -mtrA[30 + 48 * i];mtrB[73 + 147 * i] = -mtrA[31 + 48 * i];mtrB[74 + 147 * i] = -mtrA[32 + 48 * i];mtrB[108 + 147 * i] = -mtrA[42 + 48 * i];mtrB[109 + 147 * i] = -mtrA[43 + 48 * i];mtrB[110 + 147 * i] = -mtrA[44 + 48 * i];}//转化矩阵BClass1 B = new Class1(48, 36, mtrB);//求常数项double[] mtrL;mtrL = new double[48];for (int i = 0; i < 8; i++){mtrL[0 + 4 * i] = xyz.GetElement(i, 0) + f * (mtrRl[0] * (uvw.GetElement(0, i) - Xsl) + mtrRl[3] * (uvw.GetElement(1, i) - Ysl) + mtrRl[6] * (uvw.GetElement(2, i) - Zsl)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrL[1 + 4 * i] = xyz.GetElement(i, 1) + f * (mtrRl[1] * (uvw.GetElement(0, i) - Xsl) + mtrRl[4] * (uvw.GetElement(1, i) - Ysl) + mtrRl[7] * (uvw.GetElement(2, i) - Zsl)) / (mtrRl[2] * (uvw.GetElement(0, i) - Xsl) + mtrRl[5] * (uvw.GetElement(1, i) - Ysl) + mtrRl[8] * (uvw.GetElement(2, i) - Zsl));mtrL[2 + 4 * i] = XYZ.GetElement(i, 0) + f * (mtrRr[0] * (uvw.GetElement(0, i) - Xsr) + mtrRr[3] * (uvw.GetElement(1, i) - Ysr) + mtrRr[6] * (uvw.GetElement(2, i) - Zsr)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));mtrL[3 + 4 * i] = XYZ.GetElement(i, 1) + f * (mtrRr[1] * (uvw.GetElement(0, i) - Xsr) + mtrRr[4] * (uvw.GetElement(1, i) - Ysr) + mtrRr[7] * (uvw.GetElement(2, i) - Zsr)) / (mtrRr[2] * (uvw.GetElement(0, i) - Xsr) + mtrRr[5] * (uvw.GetElement(1, i) - Ysr) + mtrRr[8] * (uvw.GetElement(2, i) - Zsr));}for (int i = 8; i < 12; i++){mtrL[0 + 4 * i] = strXl[i - 8] + f * (mtrRl[0] * (strX[i - 8] - Xsl) + mtrRl[3] * (strY[i - 8] - Ysl) + mtrRl[6] * (strZ[i - 8] - Zsl)) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrL[1 + 4 * i] = strYl[i - 8] + f * (mtrRl[1] * (strX[i - 8] - Xsl) + mtrRl[4] * (strY[i - 8] - Ysl) + mtrRl[7] * (strZ[i - 8] - Zsl)) / (mtrRl[2] * (strX[i - 8] - Xsl) + mtrRl[5] * (strY[i - 8] - Ysl) + mtrRl[8] * (strZ[i - 8] - Zsl));mtrL[2 + 4 * i] = strXr[i - 8] + f * (mtrRr[0] * (strX[i - 8] - Xsr) + mtrRr[3] * (strY[i - 8] - Ysr) + mtrRr[6] * (strZ[i - 8] - Zsr)) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));mtrL[3 + 4 * i] = strYr[i - 8] + f * (mtrRr[1] * (strX[i - 8] - Xsr) + mtrRr[4] * (strY[i - 8] - Ysr) + mtrRr[7] * (strZ[i - 8] - Zsr)) / (mtrRr[2] * (strX[i - 8] - Xsr) + mtrRr[5] * (strY[i - 8] - Ysr) + mtrRr[8] * (strZ[i - 8] - Zsr));}//转化矩阵LClass1 LL = new Class1(48, 1, mtrL);//求改化法方程的系数Class1 N11 = A.Transpose().Multiply(A);Class1 N12 = A.Transpose().Multiply(B);Class1 N21 = B.Transpose().Multiply(A);Class1 N22 = B.Transpose().Multiply(B);Class1 u1 = A.Transpose().Multiply(LL);Class1 u2 = B.Transpose().Multiply(LL);//求外方位元素//改化法方程系数N22.InvertGaussJordan();Class1 n1 = N11.Subtract(N12.Multiply(N22).Multiply(N12.Transpose()));//常数项Class1 lt = u1.Subtract(N12.Multiply(N22).Multiply(u2));//求外方位元素改正数n1.InvertGaussJordan();Class1 t = n1.Multiply(lt);//求物方坐标改正数//改化法方程系数N22.InvertGaussJordan();N11.InvertGaussJordan();Class1 n2 = N22.Subtract(N12.Transpose().Multiply(N11).Multiply(N12));Class1 lX = u2.Subtract(N12.Transpose().Multiply(N11).Multiply(u1));//求物方坐标改正数n2.InvertGaussJordan();Class1 X = n2.Multiply(lX);count++;//改正外方位元素和物方坐标phil += t.GetElement(0, 0);omegal += t.GetElement(1, 0);kappal += t.GetElement(2, 0);Xsl += t.GetElement(3, 0);Ysl += t.GetElement(4, 0);Zsl += t.GetElement(5, 0);phir += t.GetElement(6, 0);omegar += t.GetElement(7, 0);kappar += t.GetElement(8, 0);Xsr += t.GetElement(9, 0);Ysr += t.GetElement(10, 0);Zsr += t.GetElement(11, 0);//物方坐标改正数for (int j = 0; j < 8; j++){uvw.SetElement(0, j, uvw.GetElement(0, j) + X.GetElement(0 + 3 * j, 0));uvw.SetElement(1, j, uvw.GetElement(1, j) + X.GetElement(1 + 3 * j, 0));uvw.SetElement(2, j, uvw.GetElement(2, j) + X.GetElement(2 + 3 * j, 0));}//将改正数带出作结束判断for (int j = 0; j < 12; j++){dett[j] = t.GetElement(j, 0);}for (int j = 0; j < 24; j++){detxyz[j] = X.GetElement(j, 0);}for (int i = 0; i < 12; i++){if (det1 < dett[i])det1 = dett[i];}for (int i = 0; i < 24; i++){if (det2 < detxyz[i])det2 = detxyz[i];}}while (det1 > 0.000001 && det2 > 0.000001); Console.WriteLine("count={0}", count); Console.ReadLine();。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H = f * L / l;
Zsl = (strZ[0] + strZ[2]) / 2 + H;
//计算片左的加密点的物方坐标
光束法的程序代码为:
//计算像片外方位元素,架设phi=0,omega=0,kappa=0求Xs,Ys,Zs
//求左片的Xs,Ys,Zs
Xsl = (strX[0] + strX[2]) / 2;
Ysl = (strY[0] + strY[2]) / 2;
L = Math.Pow(Math.Pow(strX[0] - strX[2], 2) + Math.Pow(strY[0] - strY[2], 2) + Math.Pow(strZ[0] - strZ[2], 2), 0.5);
a15=-fsin(kappa)-x/f(xsin(kappa)+ycos(kappa));
a16=y;
a21=(a2f+a3y)/Z; a22=(b2f+b3y)/Z; a23=(c2f+c3y); a24=-xsin(omega)-[x/f(xcos(kappa)-ysin(kappa))-fsin(kappa)]cos(omega)
l = Math.Pow(Math.Pow(strXr[1] - strXr[3], 2) + Math.Pow(strYr[1] - strYr[3], 2), 0.5);
H = f * L / l;
Zsr = (strZ[1] + strZ[3]) / 2 + H;
//右片加密点
double[] strxy;
strxy = new double[24];
Console.WriteLine("请输入右片加密点的相片坐标");
for (int i = 0; i < 8; i++)
{
//strxy[0 + 3 * i] = Convert.ToDouble(Console.ReadLine());
//strxy[1 + 3 * i] = Convert.ToDouble(Console.ReadLine());
//phi,omega,kappa为零,中的坐标
Class1 uvw = XYZt.Multiply(H);
//求地面摄影测量坐标系中的坐标
for (int i = 0; i < 8; i++)
{
uvw.SetElement(0, i, (uvw.GetElement(0, i) + Xsr+UVW.GetElement (0,i))/2);
strxy[2 + 3 * i] = -f;
}
for (int i = 0; i < 24; i++)
{
strxy[i] = strxy[i] * 0.000025;
}
//计算片左的加密点的物方坐标
Class1 XYZ = new Class1(8, 3, strxy);
Class1 XYZt=XYZ .Transpose ();
双向解析光束法
光束法程序有问题,在Getelement这个函数里便出现索引超限,这个问题一直解决不了
光束法的流程:
1.根据同名像点对对相交理论求系数阵A,系数阵B和常数阵L
a11=(a1f+a3x)/Z; a12=(b1f+b3x)/Z; a13=(c1f+c3x)/Z; a14=ysin(omega)-[x/f(xcos(kappa)-ysin(kappa))+fcos(kappa)]cos(omega);
a25=-fcos(kappa)-y/f(xsin(kappa)+ycos(kappa));
a26=-x;
2.求方程的改化法方程求出外方位元素和物方坐标改正数
3.判断改正数的值,如果小于限差则输出结果
光束法是最严密的一种方法的原因:
在一张相片中,待定点与控制点的像点与摄影中心及相应地面点均构成一条光束,该方法是以每张相片所组成的一束光线作为平差的基本单元,已共线条件方程作为平差的基础方程,通过各个光束在空间中的旋转和平移,使模型之间公共点的光线实现最佳交汇,并使整个区域纳入到已知的地面控制点坐标系中,所以要建立全区域统一的误差方程,整体解求全区域内每张相片的六个外方位元素及所有待定点坐标,光束法区域网平差是基于摄影时像点,物点和摄站点三点共线提出来的。由单张相片构成区域,其平差的数学模型是共线条件方程,平差单元是单个光束,像点坐标是观测值,未知数是每张相片的外方位元素及所有待定点坐标。误差方程直接由像点坐标的观测值列出,能对像点坐标进行系统误差改正。
for (int i = 0; i < 8; i++)
{
UVW.SetElement(0, i, UVW.GetElement(0, i) + Xsl);
UVW.SetElement(1, i, UVW.GetElement(1, i) + Ysl);
UVW.SetElement(2, i, UVW.GetElement(2, i) + Zsl);
Class1 xyz = new Class1(8, 3, strXY);
Class1 xyzt=xyz.Transpose ();
//phi,omega,kappa为零,故旋转矩阵为单位阵
//像空间辅助坐标系中的坐标
Class1 UVW = xyzt.Multiply(H);
//求地面摄影测量坐标系中的坐标
uvw.SetElement(1, i, (uvw.GetElement(1, i) + Ysr+UVW.GetElement (1,i))/2);
}
//求右片的Xs,Ys,Zs
Xsr = (strX[1] + strX[3]) / 2;
Ysr = (strY[1] + strY[3]) / 2;
L = Math.Pow(Math.Pow(strX[1] - strX[3], 2) + Math.Pow(strY[1] - strY[3], 2) + Math.Pow(strZ[1] - strZ[3], 2), 0.5);
