随机过程matlab程序(材料相关)

随机过程matlab程序

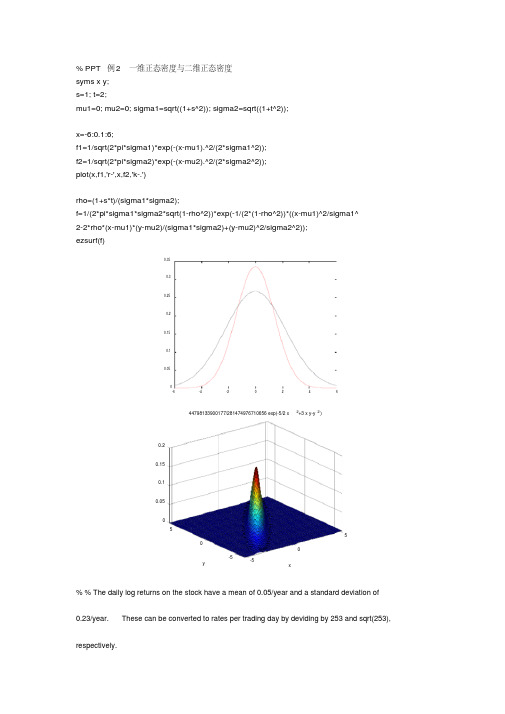
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
-6
-4
-2
0
2
4
6
44798133900177/281474976710656 exp(-5/2 x 2+3 x y-y 2 )
0.2
0.15
0.1
0.05
0
5 0
5 0
y
-5
-5
x
% % The daily log returns on the stock have a mean of 0.05/year and a standard deviation of 0.23/year. These can be converted to rates per trading day by deviding by 253 and sqrt(253), respectively.
% A=normrnd(mu,sigma,1,N)
capmu=mean(x)
tao=1 x1=A.*cos(w*(t+tao)+theta); capgamma=mean((x-capmu).*(x1-capmu))
% m time simulation clear; w=2; N=1000; mu=2; sigma=3; m=500;capmu1=[];capgamma1=[]; for i=1:m
rho=(1+s*t)/(sigma1*sigma2); f=1/(2*pi*sigma1*sigma2*sqrt(1-rho^2))*exp(-1/(2*(1-rho^2))*((x-mu1)^2/sigma1^ 2-2*rho*(x-mu1)*(y-mu2)/(sigma1*sigma2)+(y-mu2)^2/sigma2^2)); ezsurf(f)

matlab讲义

matlab讲义随机过程实验讲义刘继成华中科技大学数学与统计学院前言 (1)第一章Matlab 简介 (2)第二章简单分布的模拟 (6)第三章基本随机过程 (9)第四章Markov过程 (12)第五章模拟的应用和例子 (16)附录各章的原程序 (51)参考文献 (75)若想检验数学模型是否反映客观现实，最自然的方法是比较由模型计算的理论概率和由客观试验得到的经验频率。

不幸的是，这两件事都往往是费时的、昂贵的、困难的，甚至是不可能的。

此时，计算机模拟在这两方面都可以派上用场：提供理论概率的数值估计与接近现实试验的模拟。

模拟的第一步自然是在计算机程序的算法中如何产生随机性。

程序语言，甚至计算器，都提供了“随机”生成[0，1]区间内连续数的方法。

因为每次运行程序常常生成相同的“随机数”，因此这些数被称为伪随机数。

尽管如此，对于多数的具体问题这样的随机数已经够用。

我们将假定计算机已经能够生成[0，1]上的均匀随机数。

也假定这些数是独立同分布的，尽管它们常常是周期的、相关的、……。

……本讲义的安排如下，第一章是Matlab简介，从实践动手角度了解并熟悉Matlab环境、命令、帮助等，这将方便于Matlab的初学者。

第二章是简单随机变量的模拟，只给出了常用的Matlab 模拟语句，没有堆砌同一种变量的多种模拟方法。

对于没有列举的随机变量的模拟，以及有特殊需求的读者应该由这些方法得到启发，或者参考更详细的其他文献资料。

第三章是基本随机过程的模拟。

主要是简单独立增量过程的模拟，多维的推广是直接的。

第四章是Markov过程的模拟。

包括服务系统，生灭过程、简单分支过程等。

第五章是这些模拟的应用。

例如，计算概率、估计积分、模拟现实、误差估计，以及减小方差技术，特别给读者提供了一些经典问题的模拟，通过这些问题的模拟将会更加牢固地掌握实际模拟的步骤。

平稳过程的模拟、以及利用平稳过程来预测的内容并没有包含在本讲义之内，但这丝毫不影响该内容的重要性，这也是将会增补进来的主要内容之一。

Matlab中的随机过程建模技巧

Matlab中的随机过程建模技巧随机过程是描述随机现象随时间变化的数学模型。

它在工程、金融、生物医学等许多领域都有广泛的应用。

在Matlab中，我们可以利用其强大的数学工具箱来进行随机过程的建模和分析。

本文将介绍一些在Matlab中常用的随机过程建模技巧。

一、随机过程的基本概念在进行随机过程建模之前，我们先来回顾一下一些基本概念。

1. 马尔可夫性质马尔可夫性质是指一个随机过程在给定过去的条件下，未来与过去和未来的时间无关。

在Matlab中，可以使用markovchain对象来表示马尔可夫链，并利用其属性和方法进行分析。

2. 随机过程的平稳性如果一个随机过程的统计性质在时间平移的情况下不发生变化，那么该随机过程就是平稳的。

在Matlab中，可以使用stationary函数来判断一个随机过程是否是平稳的。

3. 随机过程的自相关函数与功率谱密度自相关函数描述了一个随机过程在不同时间点的取值之间的相关性。

功率谱密度则描述了一个随机过程在不同频率下的能量分布。

在Matlab中，可以使用xcorr 和pwelch函数分别计算随机过程的自相关函数和功率谱密度。

二、随机过程的模拟模拟随机过程是随机过程建模的重要步骤之一。

在Matlab中，可以使用rand、randn等函数生成服从特定分布的随机数序列，并利用for循环和if语句等控制结构模拟出具有特定统计性质的随机过程。

例如，我们可以使用randn函数生成服从正态分布的随机数序列，然后利用for 循环和格朗日方程生成具有平稳性的随机过程。

具体实现代码如下：```MatlabN = 1000; % 随机数序列长度X = zeros(1, N); % 存储随机过程的数组X(1) = randn; % 初始化随机过程的初始值for n = 2:NX(n) = 0.9*X(n-1) + sqrt(1 - 0.9^2)*randn;endplot(X);```通过运行上述代码，我们可以得到一个服从AR(1)过程的随机数序列，并通过绘图函数plot将其可视化。

利用MATLAB进行随机过程建模

利用MATLAB进行随机过程建模简介随机过程是一个随机变量随时间的变化过程，具有概率性质。

在许多领域，如金融、通信、生物医学等，随机过程的建模和分析是十分重要的。

MATLAB是一种功能强大、易于使用的数值计算软件，它提供了丰富的工具和函数，方便进行随机过程的建模和仿真。

本文将介绍如何利用MATLAB进行随机过程建模。

一、MATLAB中的随机变量生成在进行随机过程建模之前，首先需要生成相应的随机变量。

MATLAB提供了多种方法来生成不同分布的随机变量。

常用的包括均匀分布、正态分布、指数分布等。

例如，要生成一个均匀分布的随机变量，可以使用rand函数。

以下代码生成一个长度为1000的均匀分布的随机变量序列：```matlabrng(0); % 设置随机数种子，保证结果可复现X = rand(1, 1000); % 生成均匀分布的随机变量```同样地，通过normrnd函数可以生成正态分布的随机变量，通过exprnd函数可以生成指数分布的随机变量。

二、随机过程的建模在随机过程建模中，常用的模型包括马尔可夫过程、随机游走、泊松过程等。

利用MATLAB可以方便地进行这些模型的建模和仿真。

1. 马尔可夫过程马尔可夫过程是一种具有马尔可夫性质的随机过程，其下一个状态只依赖于当前状态。

MATLAB提供了markovchain函数用于创建马尔可夫链模型。

以下代码创建一个状态空间为{'A', 'B', 'C'}的马尔可夫链：```matlabstates = {'A', 'B', 'C'}; % 状态空间transitionMatrix = [0.5 0.2 0.3; 0.3 0.5 0.2; 0.2 0.3 0.5]; % 状态转移矩阵mc = markovchain('StateNames', states, 'TransitionMatrix', transitionMatrix); % 创建马尔可夫链模型```可以通过simulate函数模拟马尔可夫过程的状态序列。

随机过程实验报告

一、实验目的1. 理解随机过程的基本概念和性质。

2. 掌握随机过程的基本运算和性质。

3. 通过实验验证随机过程的性质和规律。

二、实验原理随机过程是指一系列随机变量按照一定规则排列而成的序列。

在现实生活中，随机过程广泛存在于自然界和人类社会，如股票价格、气象变化、生物进化等。

随机过程的研究有助于我们更好地理解和预测这些现象。

随机过程可以分为两类：离散随机过程和连续随机过程。

本实验主要研究离散随机过程。

三、实验设备与材料1. 计算机2. 随机过程模拟软件（如Matlab）3. 纸笔四、实验内容1. 随机过程的基本概念（1）随机变量的概念随机变量是指具有不确定性的变量，它可以取多个值。

在随机过程中，随机变量是基本的研究对象。

（2）随机过程的概念随机过程是由一系列随机变量按照一定规则排列而成的序列。

2. 随机过程的基本性质（1）无后效性无后效性是指随机过程的前后状态相互独立。

（2）无记忆性无记忆性是指随机过程的状态只与当前时刻有关，与过去时刻无关。

（3）马尔可夫性马尔可夫性是指随机过程的状态只与当前时刻有关，与过去时刻无关。

3. 随机过程的运算（1）随机过程的和设{Xn}和{Yn}是两个随机过程，则它们的和{Zn}定义为Zn = Xn + Yn。

（2）随机过程的差设{Xn}和{Yn}是两个随机过程，则它们的差{Zn}定义为Zn = Xn - Yn。

（3）随机过程的乘积设{Xn}和{Yn}是两个随机过程，则它们的乘积{Zn}定义为Zn = Xn Yn。

4. 随机过程的模拟利用随机过程模拟软件（如Matlab）模拟随机过程，观察其性质和规律。

五、实验步骤1. 初始化随机数生成器2. 定义随机过程（1）根据随机过程的基本性质，定义随机过程{Xn}。

（2）根据随机过程的运算，定义随机过程{Yn}。

3. 模拟随机过程（1）使用随机过程模拟软件（如Matlab）模拟随机过程{Xn}和{Yn}。

（2）观察模拟结果，分析随机过程的性质和规律。

MATLAB中的随机过程建模与求解技巧

MATLAB中的随机过程建模与求解技巧随机过程是描述随机事件在一定时间范围内的演化规律的数学模型。

在现实生活和工程实践中，随机过程的分析和建模扮演着重要的角色。

而MATLAB作为一种功能强大的数值计算和科学工程计算软件，提供了丰富的工具和函数来进行随机过程的建模与求解。

本文将介绍一些MATLAB中常用的随机过程建模与求解技巧，帮助读者更好地应用MATLAB进行相关工作。

一、概述随机过程建模随机过程建模是指根据已有的数据或者经验，通过数学模型描述随机过程的统计特性。

在MATLAB中，常用的随机过程建模方法包括：1. 随机过程的数学描述：通过定义随机过程的概率密度函数、累积分布函数、自相关函数等统计特性，来描述随机过程的数学特征。

MATLAB提供了丰富的统计函数如normpdf、normcdf、autocorr等，可以帮助用户进行随机过程的数学描述。

2. 随机过程的参数估计：对于给定的随机过程数据，通过参数估计的方法来确定随机过程的参数。

MATLAB提供了统计工具箱中的函数如gamfit、exponentialfit等，可以帮助用户进行随机过程参数的估计。

3. 随机过程的模型选择：在建模随机过程时，需要选择合适的数学模型来描述随机过程的统计特性。

MATLAB提供了丰富的概率分布和随机过程模型如正态分布、泊松分布、布朗运动等，可以帮助用户根据数据选择合适的模型进行建模。

二、随机过程建模实例为了更好地理解随机过程建模的过程和技巧，下面将通过一个具体的例子来说明。

假设某电信公司每天收到的短信数量服从泊松分布，并且每天的短信数量之间相互独立。

现有一周的短信数量数据如下：data = [10, 8, 12, 9, 11, 13, 7];我们希望通过这些数据来建立一个泊松分布的模型，以便对未来的短信数量进行预测。

首先，我们可以使用MATLAB的统计工具箱中的函数poissfit来估计泊松分布的参数。

代码如下：lambda = poissfit(data);根据估计得到的参数lambda，我们可以生成符合泊松分布的随机过程数据，代码如下：simulated_data = poissrnd(lambda, 1, 100);其中，参数lambda表示单位时间内的事件平均发生率，这里我们假设为已知的估计值。

MATLAB中的随机过程模拟与分析技巧

MATLAB中的随机过程模拟与分析技巧随机过程是描述一系列随机事件演变的数学模型，在实际问题中有广泛的应用。

MATLAB作为一款功能强大的数值计算软件，提供了丰富的工具和函数来模拟和分析随机过程。

本文将介绍在MATLAB中进行随机过程模拟与分析的一些常用技巧。

一、随机变量的生成在随机过程分析中，随机变量是基本的概念，它描述了随机事件的取值情况。

在MATLAB中，可以通过随机数生成函数来生成服从各种分布的随机变量，如均匀分布、正态分布等。

例如，可以使用rand函数生成0到1之间的均匀分布随机变量，使用randn函数生成符合标准正态分布的随机变量。

二、随机过程的模拟通过生成随机变量，可以进一步模拟随机过程。

随机过程的模拟可以通过生成一系列随机变量来实现。

例如，可以使用rand函数生成一组服从均匀分布的随机变量，并通过随机过程模型来描述这组随机变量的演变过程。

在MATLAB中，可以使用循环语句和数组来实现随机过程的模拟。

三、随机过程的统计分析在对随机过程进行模拟后，通常需要对其进行进一步的统计分析。

MATLAB提供了一系列用于随机过程统计分析的函数，如均值、方差、自相关函数、功率谱密度等。

这些函数可以帮助我们从时间域和频率域两个角度来分析随机过程的特性。

通过统计分析，我们可以得到随机过程的均值、方差、平稳性等重要信息。

四、随机过程的仿真实验MATLAB还提供了强大的仿真实验工具，可以通过模拟大量的随机过程样本来研究其统计规律。

仿真实验通常涉及到随机过程的多次模拟和统计分析。

在MATLAB中，可以使用循环语句和向量化操作来进行高效的仿真实验。

通过对仿真实验结果的分析，可以验证理论模型的正确性，评估系统的性能，以及优化系统参数等。

五、随机过程的滤波与预测在实际应用中，随机过程通常具有噪声干扰，对其进行滤波与预测是很重要的任务。

MATLAB提供了多种滤波与预测方法的函数，如卡尔曼滤波、递归最小二乘法等。

这些方法可以帮助我们提取有用信息，消除噪声干扰，并对未来的随机过程变量进行预测。

matlab 二维相关随机过程

matlab 二维相关随机过程一、简介MATLAB是一种强大的科学计算工具，常用于数据分析、仿真和可视化。

二维相关随机过程是一种随时间和空间变化的随机过程，通常用来研究信号处理、图像处理、数据压缩等领域。

本文将介绍如何使用MATLAB进行二维相关随机过程的分析与模拟。

二、MATLAB中的二维相关函数MATLAB提供了丰富的二维相关函数，用于计算二维数据的相关性。

其中最常用的函数是"corrcoef"和"xcorr2"。

1. "corrcoef"函数用于计算两个二维数据的Pearson相关系数。

它返回一个2x2的矩阵，矩阵的对角线上是两个数据的自相关系数，而矩阵的非对角线上是两个数据的互相关系数。

2. "xcorr2"函数用于计算两个二维数据的二维互相关。

它返回一个与输入数据大小相同的矩阵，矩阵中的每个元素表示对应位置的互相关值。

三、二维相关随机过程的模拟在MATLAB中，我们可以使用随机函数和相关函数来模拟二维相关随机过程。

1. 生成随机数据：可以使用MATLAB的随机函数，如"randn"函数生成服从正态分布的随机数据。

通过设定合适的均值和方差，可以生成满足实际需求的随机数据。

2. 计算相关系数：利用之前介绍的"corrcoef"函数，可以计算生成的随机数据的相关系数矩阵。

相关系数可以描述数据之间的相关性程度，从而帮助我们理解二维相关随机过程。

3. 生成二维相关随机过程：通过将随机数据传入"corrcoef"函数，然后再利用"xcorr2"函数计算互相关矩阵，我们可以生成满足相关性要求的二维相关随机过程。

可以通过调整相关系数和相关程度，来控制生成的二维数据的特性。

四、案例分析为了进一步说明如何使用MATLAB进行二维相关随机过程的分析与模拟，我们将以图像处理为例进行讲解。

哈尔滨工程大学研究生课程：随机过程大作业答案

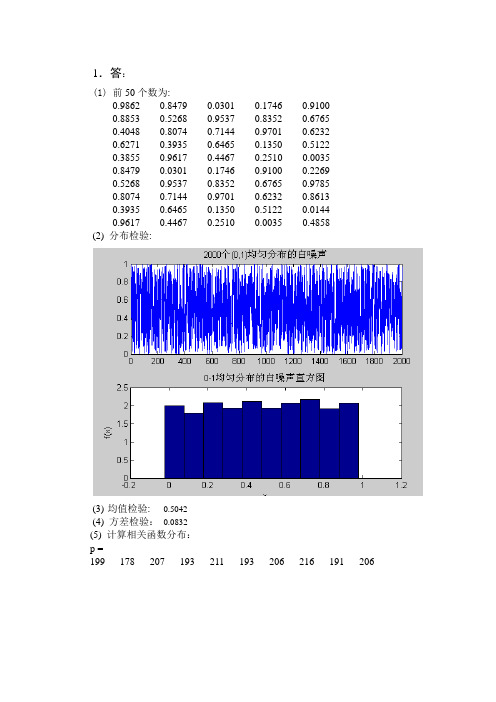
1．答：(1)前50个数为:0.9862 0.8479 0.0301 0.1746 0.91000.8853 0.5268 0.9537 0.8352 0.67650.4048 0.8074 0.7144 0.9701 0.62320.6271 0.3935 0.6465 0.1350 0.51220.3855 0.9617 0.4467 0.2510 0.00350.8479 0.0301 0.1746 0.9100 0.22690.5268 0.9537 0.8352 0.6765 0.97850.8074 0.7144 0.9701 0.6232 0.86130.3935 0.6465 0.1350 0.5122 0.01440.9617 0.4467 0.2510 0.0035 0.4858(2) 分布检验:(3)均值检验:0.5042(4) 方差检验：0.0832(5) 计算相关函数分布：p =199 178 207 193 211 193 206 216 191 206本题运用MATLAB进行编程,程序如下：for n=1:2000xt(n)=unifrnd(0,1); %产生2000个（0，1）均匀分布白序列endsubplot(2,1,1);plot(xt),title('2000个(0,1)均匀分布的白噪声');for i=1:5for j=1:10sc(j,i)=xt((i-1)*5+j);end;end;disp([sc]) %打印前50个数mx=mean(xt) %求平均数并输出dx=cov(xt) %求方差并输出subplot(2,1,2);p=hist(xt,10) %将产生的2000个随机数分为10组p=p/100; t=0.025:.1:.975; %求概率密度bar (t,p,1);title('0-1均匀分布的白噪声直方图');xlabel('x');ylabel('f(x)');[bx,i] = xcov(xt,10); %τ取-10到10Bx=bx/2000; %求自相关函数Bx(τ)figuresubplot(2,1,1);plot(i,Bx),title('自相关函数Bx分布图');xlabel('τ');ylabel('Bx(τ)');[tx,i] = xcorr(xt,10); %τ取-10到10Tx=tx/2000;subplot(2,1,2);plot(i, Tx),title('自相关函数Γx分布图');xlabel('τ');ylabel('Γx(τ)');2.答：(1)前50个数为:-0.4326 1.1909 -0.1867 0.1139 0.2944-1.6656 1.1892 0.7258 1.0668 -1.33620.1253 -0.0376 -0.5883 0.0593 0.71430.2877 0.3273 2.1832 -0.0956 1.6236-1.1465 0.1746 -0.1364 -0.8323 -0.69181.1909 -0.1867 0.1139 0.2944 0.85801.1892 0.7258 1.0668 -1.3362 1.2540-0.0376 -0.5883 0.0593 0.7143 -1.59370.3273 2.1832 -0.0956 1.6236 -1.44100.1746 -0.1364 -0.8323 -0.6918 0.5711(2) 分布检验: 如下图所示。

使用Matlab进行随机过程建模方法

使用Matlab进行随机过程建模方法随机过程建模是现代科学研究中一项重要的技术手段，它不仅在工程领域有广泛的应用，而且在金融、生物学和医学等领域也有着不可忽视的作用。

Matlab是一个强大的数值计算和科学工程计算软件，它提供了丰富的工具箱和函数，使得使用Matlab进行随机过程建模成为一项相对容易的任务。

本文将介绍使用Matlab进行随机过程建模的方法和技巧，并通过实例进行演示。

一、概述随机过程是描述随机现象随时间演化的数学模型。

它是一组随机变量的集合，这些随机变量的取值与时间相关。

随机过程的建模过程可以分为三个步骤：确定随机变量的类型、选择合适的分布函数以及确定各个随机变量之间的关系。

在Matlab中，可以利用统计工具箱中的函数来进行这些步骤的操作。

二、确定随机变量的类型在随机过程建模中，首先需要确定随机变量的类型。

常见的随机变量类型包括离散型和连续型。

离散型随机变量的取值有限或可列举，例如投掷硬币的结果；连续型随机变量的取值属于某个实数区间，例如温度的变化。

在Matlab中，可以利用符号计算工具箱中的函数来定义离散型和连续型随机变量，并进行相应的计算和操作。

三、选择合适的分布函数确定随机变量的类型后，下一步是选择合适的分布函数来描述随机变量的分布规律。

常见的分布函数包括正态分布、均匀分布和指数分布等。

在Matlab中，可以使用统计工具箱中的函数来生成符合特定分布的随机变量，并进行概率计算和仿真实验。

四、确定随机变量之间的关系随机过程中的随机变量之间通常存在某种关系，例如自相关性和互相关性等。

在Matlab中，可以利用信号处理工具箱中的函数来计算随机过程之间的相关性，并进行模拟实验。

五、案例演示为了更好地说明使用Matlab进行随机过程建模的方法和技巧，下面以船舶运行的随机过程为例进行演示。

假设船舶的速度服从正态分布，航向角度服从均匀分布，航行距离服从指数分布。

首先，利用Matlab的统计工具箱中的函数生成符合这些分布的随机变量；然后，根据随机变量之间的关系，利用信号处理工具箱中的函数计算船舶速度和位置的相关性；最后，使用Matlab的数据可视化工具进行结果展示和分析。

Matlab仿真窄带随机过程

随机过程数学建模分析任何通信系统都有发送机和接收机，为了提高系统的可靠性，即输出信噪比，通常在接收机的输入端接有一个带通滤波器，信道内的噪声构成了一个随机过程，经过该带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带随机过程的规律是重要的。

一、窄带随机过程。

一个实平稳随机过程X(t)，若它的功率谱密度具有下述性质：中心频率为ωc，带宽为△ω=2ω0，当△ω<<ωc时，就可认为满足窄带条件。

若随机过程的功率谱满足该条件则称为窄带随机过程。

若带通滤波器的传输函数满足该条件则称为窄带滤波器。

随机过程通过窄带滤波器传输之后变成窄带随机过程。

图1 为典型窄带随机过程的功率谱密度图。

若用一示波器来观测次波形，则可看到，它接近于一个正弦波，但此正弦波的幅度和相位都在缓慢地随机变化，图2所示为窄带随机过程的一个样本函数。

图1 典型窄带随机过程的功率谱密度图图2 窄带随机过程的一个样本函数二、窄带随机过程的数学表示1、用包络和相位的变化表示由窄带条件可知,窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程,从示波器观察(或由理论上可以推知):这个过程中的一个样本函数(一个实现)的波形是一个频率为ƒc且幅度和相位都做缓慢变化的余弦波。

写成包络函数和随机相位函数的形式：X(t)=A(t)*cos[ωc t+ Φ(t)]其中:A(t)称作X(t)的包络函数; Φ(t)称作X(t)的随机相位函数。

包络随时间做缓慢变化，看起来比较直观，相位的变化，则看不出来。

2、莱斯（Rice）表示式任何一个实平稳随机过程X(t)都可以表示为：X(t)=A c(t) cosωc t-A S(t) sinωc t其中同相分量：A c(t)= X(t) cosφt= X(t) cosωc t＋sinωc t=LP[X(t) *2cosωc t]正交分量：A S(t) = X(t)sinφt=cosωc t— X(t) sinωc t= LP[-X(t) *2sinωc t]（LP[A]表示取A的低频部分）。

Matlab仿真窄带随机过程

随机过程数学建模分析任何通信系统都有发送机和接收机，为了提高系统的可靠性，即输出信噪比，通常在接收机的输入端接有一个带通滤波器，信道内的噪声构成了一个随机过程，经过该带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带随机过程的规律是重要的。

一、窄带随机过程。

一个实平稳随机过程X(t)，若它的功率谱密度具有下述性质：中心频率为ωc，带宽为△ω=2ω0，当△ω<<ωc时，就可认为满足窄带条件。

若随机过程的功率谱满足该条件则称为窄带随机过程。

若带通滤波器的传输函数满足该条件则称为窄带滤波器。

随机过程通过窄带滤波器传输之后变成窄带随机过程。

图1 为典型窄带随机过程的功率谱密度图。

若用一示波器来观测次波形，则可看到，它接近于一个正弦波，但此正弦波的幅度和相位都在缓慢地随机变化，图2所示为窄带随机过程的一个样本函数。

图1 典型窄带随机过程的功率谱密度图图2 窄带随机过程的一个样本函数二、窄带随机过程的数学表示1、用包络和相位的变化表示由窄带条件可知,窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程,从示波器观察(或由理论上可以推知):这个过程中的一个样本函数(一个实现)的波形是一个频率为ƒc且幅度和相位都做缓慢变化的余弦波。

写成包络函数和随机相位函数的形式：X(t)=A(t)*cos[ωc t+ Φ(t)]其中:A(t)称作X(t)的包络函数; Φ(t)称作X(t)的随机相位函数。

包络随时间做缓慢变化，看起来比较直观，相位的变化，则看不出来。

2、莱斯（Rice）表示式任何一个实平稳随机过程X(t)都可以表示为：X(t)=A c(t) cosωc t-A S(t) sinωc t其中同相分量：A c(t)= X(t) cosφt= X(t) cosωc t＋sinωc t=LP[X(t) *2cosωc t]正交分量：A S(t) = X(t)sinφt=cosωc t— X(t) sinωc t= LP[-X(t) *2sinωc t]（LP[A]表示取A的低频部分）。

如何使用Matlab进行随机过程建模与仿真

如何使用Matlab进行随机过程建模与仿真使用Matlab进行随机过程建模与仿真随机过程是概率论的重要分支，它用于描述随机事件在时间或空间维度上的演变规律。

在工程与科学领域中，随机过程建模与仿真是十分重要的工具，它可以帮助我们预测未来的状态、优化系统设计以及进行风险评估等。

Matlab作为一种功能强大的数值计算和科学数据可视化工具，提供了丰富的函数和工具箱，使得随机过程的建模与仿真变得更加简便高效。

本文将介绍如何使用Matlab进行随机过程建模与仿真，并结合实际案例进行说明。

一、随机过程的基本概念在开始使用Matlab进行随机过程建模与仿真之前，我们首先需要了解随机过程的基本概念。

随机过程可以看作是一组随机变量的集合，它的演变具有一定的随机性。

常见的随机过程包括马尔可夫过程、泊松过程、布朗运动等。

在建模随机过程时，我们通常需要确定其状态集合、状态转移概率和初始状态等。

这些概念的理解对于后续的建模与仿真工作非常重要。

二、随机过程建模在使用Matlab建模随机过程时，我们需要选择合适的模型以及提取合适的参数。

Matlab提供了多种用于随机过程建模的函数和工具箱，例如Stochastic Process Toolbox和Statistics and Machine Learning Toolbox等。

我们可以利用这些工具来创建各种类型的随机过程模型，也可以自定义模型。

这些模型可以用来描述各种实际问题，比如金融市场的波动、传感器数据的变化等。

以布朗运动为例，我们可以使用Matlab创建一个布朗运动模型并进行仿真。

布朗运动是一种连续时间、连续状态的随机过程，其在单位时间内的状态增量是服从正态分布的。

在Matlab中，我们可以使用"brownian"函数来生成布朗运动的仿真数据。

首先，我们需要确定布朗运动的参数，例如时间步长、仿真时长、起始状态等。

然后，通过调用"brownian"函数，可以获得仿真数据，并进行可视化分析。

MATLAB随机过程与概率分布计算技巧

MATLAB随机过程与概率分布计算技巧随机过程和概率分布是数学中重要的概念，它们在许多领域中有广泛的应用，例如金融、通信、工程等。

而MATLAB作为一款功能强大的数学软件，提供了丰富的工具和函数来计算、模拟和分析随机过程以及各种概率分布。

本文将介绍一些MATLAB中常用的随机过程和概率分布计算技巧，以帮助读者更好地理解和应用这些概念。

一、随机过程的生成和仿真在MATLAB中，我们可以使用rand函数来生成服从均匀分布的随机数。

例如，rand(1,100)将生成一个包含100个0到1之间均匀分布的随机数的向量。

而randn函数可用于生成服从标准正态分布（均值为0，方差为1）的随机数。

我们可以通过设置均值和方差参数来生成服从任意正态分布的随机数。

例如，randn(1,100, mu, sigma)将生成一个含有100个服从均值为mu，方差为sigma^2的正态分布的随机数的向量。

在生成随机过程时，我们可以使用MATLAB中的cumsum函数来计算累积和。

通过对生成的随机数序列进行累积和操作，我们可以获得具有随机波动的变量。

二、概率分布的拟合与估计MATLAB提供了丰富的工具和函数来进行概率分布的拟合和参数估计。

我们可以使用histfit函数来实现对数据的直方图拟合，并得到与数据最匹配的概率分布曲线。

例如，histfit(data, bins, 'kernel')将对数据data进行直方图拟合，并以核密度估计曲线呈现。

此外，我们可以使用probplot函数来进行概率图绘制。

通过绘制数据的概率图，我们可以判断数据是否符合某种特定的概率分布。

例如，probplot(data, distribution)将绘制数据data的概率图，并与给定的概率分布进行比较。

对于参数估计，MATLAB提供了很多函数来估计概率分布的参数。

常见的估计方法包括最大似然估计和矩估计。

我们可以使用mle函数来进行最大似然估计，例如，parameters = mle(data, 'distribution', distribution)将对数据data进行最大似然估计，并返回估计得到的分布参数。

利用Matlab进行随机信号分析和随机过程建模

利用Matlab进行随机信号分析和随机过程建模随机信号在众多工程领域中起到了至关重要的作用，从通信系统到电力系统，从生物医学到金融市场，都需要对信号进行分析和建模。

Matlab作为一种功能强大且灵活易用的工具，被广泛应用于随机信号分析和随机过程建模的工作中。

本文将介绍如何利用Matlab进行随机信号分析和随机过程建模，并从实际案例中深入探讨其应用。

随机信号分析是对信号的特性进行研究的过程。

Matlab提供了丰富的函数和工具箱，可以帮助我们对随机信号进行统计分析。

其中，随机信号的概率密度函数（PDF）是一个重要的性质，可以描述信号的分布情况。

通过Matlab中的hist函数，我们可以绘制随机信号的直方图，从而直观地了解信号的分布情况。

此外，Matlab还提供了一些统计函数，如mean、var和std，可以计算信号的均值、方差和标准差等重要统计量。

除了基本的统计分析，Matlab还提供了一些进阶的分析技术，如功率谱密度（PSD）分析和自相关分析。

功率谱密度可以描述信号的频率成分和能量分布情况。

在Matlab中，我们可以使用periodogram函数来计算信号的功率谱密度，并通过绘制功率谱图来观察信号的频谱特性。

自相关分析可以分析信号与其自身之间的相关性。

Matlab中的xcorr函数可以计算信号的自相关函数，并通过绘制自相关图进行可视化分析。

在随机过程建模方面，Matlab同样提供了丰富的工具。

随机过程可以被视为一系列随机变量组成的序列。

在Matlab中，我们可以使用随机过程工具箱来建立随机过程模型，如高斯过程模型和马尔科夫过程模型。

以高斯过程模型为例，我们可以使用gp模型来建立高斯过程模型，并通过估计参数和拟合数据来进行模型训练。

随机过程的建模与分析可以帮助我们更好地理解和预测随机现象，为工程设计和决策提供依据。

在实际应用中，利用Matlab进行随机信号分析和随机过程建模具有广泛的应用前景。

例如，在通信系统中，我们可以使用Matlab对信号进行调制和解调处理，并通过随机过程建模来优化通信系统的设计。

随机过程实验报告

随机过程试验报告班级：信息与计算科学2010级1班姓名：李翠珍学号：20104609实验实验总结：本次试验熟练的掌握了三维图像的matlab 编程语句，最重要的是学习了 rnd 使x 为泊松随机数。

4实验二2o-1-228均值函数已知u=0,令自变量x的取值范围[-1,1]x=-1:0.01:1u=0;plot(x,u,'-+');方差函数var(x(t)) =2；在matlab 中用v 代替方差，同样令x=-1:0.01:1v=0;plot(x,v,'-+');-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 10.80.60.40.2-0.2-0.4-0.6-0.8-1 -1 -0.8 -0.6 -0.4 -0.2 0.2 0.4 0.6 0.8自相关函数令t 1 , t 2的范围为［0,2二］.根据已知条件编写下程序: t1=0:0.01:2;t2=0:0.01:2; t=t1-t2;w=3;r=2*cos(w*t); plot3(r,t1,t2); axis square; grid on;实验总结：本次试验，主要是借鉴了课本 2.2的课上例题，利用了随机过程中的中的相关公式求解。

3实验三实验总结：本试验主要锻炼了我们从大量信息内摘取有用信息的能力学习及理解运用新知识。

我在这方面比较欠缺，以后一定要多加练习。

3030实验成绩评阅时间评阅教师 2520151055 10 15 20 25实验内容判定一个Markov 链是否是遍历的，若是遍历的，求其极限分布。

并能从实际问题中抽象出Markov 链，并求出其极限分布，并理解其实际意义。

实验习题课本p125 5.7 将两个红球，四个白球分别放入甲乙两个盒子中。

每次从两个盒子中各取一球交换，以X n 记第n 次交换后甲盒中红球数。

(1) 说明｛ X n , n=0,1，…｝是一 Markov 链并求转移矩阵P ;(2) 试证｛ X n , n=0 , 1，…｝是遍历的；(3) 求它的极限分布；(1) 设X n 记第n 次交换后甲盒中红球数，则易见｛ X n ，n=0，1，…｝是状态空间S 二｛0,1,2｝的Markov 链，一步转移概率矩阵为:123 8 0(2) 由于状态空间S 有限，且状态互通，故｛ X n , n=0，1，-｝不可约，从而正常返，又状态1为非周期的，故｛ X n , n=0 , 1，…｝还是遍历链。

第三章_随机过程教案

第三章_随机过程教案第三章随机过程本节⾸先介绍利⽤matlab现有的库函数根据实际需要直接产⽣均分分布和⾼斯分布随机变量的⽅法，然后重点讲解蒙特卡罗算法。

⼀、均匀分布的随机数利⽤MATLAB库函数rand产⽣。

rand函数产⽣（0，1）内均匀分布的随机数，使⽤⽅法如下：1）x=rand(m)；产⽣⼀个m×m的矩阵，所含元素取值均为在（0，1）内均匀分布的随机数。

2）x=rand(m，n)；产⽣⼀个m×n的矩阵，所含元素取值均为在（0，1）内均匀分布的随机数。

3）x=rand；产⽣⼀个随机数。

举例：1、产⽣⼀个5×5服从均匀分布的随机矩阵，所含元素取值均为在（0，1）内均匀分布的随机数。

x=rand(5)2、产⽣⼀个5×3服从均匀分布的随机矩阵，所含元素取值均为在（0，1）内均匀分布的随机数。

x=rand(5,3)⼆、⾼斯分布的随机数randn函数产⽣均值为0，⽅差为1的⾼斯分布的随机数，使⽤⽅法如下：1）x=randn(m)；产⽣⼀个m×m的矩阵，所含元素都是均值为0，⽅差为1的⾼斯分布的随机数。

2）x=randn(m，n)；产⽣⼀个m×n的矩阵，所含元素都是均值为0，⽅差为1的⾼斯分布的随机数。

3）x=randn；产⽣⼀个均值为0，⽅差为1的⾼斯分布的随机数。

举例：1、产⽣⼀个5×5的矩阵，所含元素都是均值为0，⽅差为1的⾼斯分布的随机数。

x=randn(5)2、产⽣⼀个5×3的矩阵，所含元素都是均值为0，⽅差为1的⾼斯分布的随机数。

x=randn(5,3)3、产⽣⼀个5×3的矩阵，所含元素都是均值为0，⽅差为4的⾼斯分布的随机数。

x=2×randn(5,3)三、蒙特卡罗仿真1、蒙特卡罗算法蒙特卡罗估计是指通过随机实验估计系统参数值的过程。

蒙特卡罗算法的基本思想：由概率论可知，随机实验中实验的结果是⽆法预测的，只能⽤统计的⽅法来描述。

随机过程matlab程序

基本操作-5/(4.8+5.32)^2area=pi*2.5^2x1=1+1/2+1/3+1/4+1/5+1/6exp(acos(0.3))a=[1 2 3;4 5 6;7 8 9]a=[1:3,4:6,7:9]a1=[6: -1:1]a=eye(4) a1=eye(2,3) b=zeros(2,10) c=ones(2,10) c1=8*ones(3,5) d=zeros(3,2,2)；r1=rand(2, 3)r2=5-10*rand(2, 3)r4=2*randn(2,3)+3arr1=[1.1 -2.2 3.3 -4.4 5.5]arr1(3) arr1([1 4]) arr1(1:2:5)arr2=[1 2 3; -2 -3 -4;3 4 5]arr2(1,:)arr2(:,1:2:3)arr3=[1 2 3 4 5 6 7 8]arr3(5:end) arr3(end)绘图x=[0:1:10];y=x.^2-10*x+15;plot(x,y)x=0:pi/20:2*piy1=sin(x);y2=cos(x);plot(x,y1,'b-');hold on;plot(x,y2,‘k--’);legend (‘sin x’,‘cos x’);x=0:pi/20:2*pi;y=sin(x);figure(1)plot(x,y, 'r-')grid on以二元函数图 z = xexp(-x^2-y^2) 为例讲解基本操作，首先需要利用meshgrid 函数生成X-Y平面的网格数据，如下所示：xa = -2:0.2:2;ya = xa;[x,y] = meshgrid(xa,ya);z = x.*exp(-x.^2 - y.^2);mesh(x,y,z);建立M文件function fenshu( grade )if grade > 95.0disp('The grade is A.');elseif grade > 86.0disp('The grade is B.');elseif grade > 76.0disp('The grade is C.');elseif grade > 66.0disp('The grade is D.');elsedisp('The grade is F.');endendendendendfunction y=func(x)if abs(x)<1y=sqrt(1-x^2);else y=x^2-1;endfunction summ( n)i = 1;sum = 0;while ( i <= n )sum = sum+i;i = i+1;endstr = ['¼ÆËã½á¹ûÎª£º',num2str(sum)]; disp(str)end求极限syms xlimit((1+x)^(1/x),x,0,'right')求导数syms x;f=(sin(x)/x);diff(f)diff(log(sin(x)))求积分syms x;int(x^2*log(x))syms x;int(abs(x-1),0,2)常微分方程求解dsolve('Dy+2*x*y=x*exp(-x^2)','x')计算偏导数x/(x^2 + y^2 + z^2)^(1/2)diff((x^2+y^2+z^2)^(1/2),x,2)重积分int(int(x*y,y,2*x,x^2+1),x,0,1)级数syms n;symsum(1/2^n,1,inf)Taylor展开式求y=exp(x)在x=0处的5阶Taylor展开式taylor(exp(x),0,6)矩阵求逆A=[0 -6 -1; 6 2 -16; -5 20 -10]det(A)inv(A)特征值、特征向量和特征多项式A=[0 -6 -1; 6 2 -16; -5 20 -10];lambda=eig(A)[v,d]=eig(A)poly(A)多项式的根与计算p=[1 0 -2 -5];r=roots(p)p2=poly(r)y1=polyval(p,4)例子：x=[-3:3]'y=[3.03,3.90,4.35,4.50,4.40,4.02,3.26]';A=[2*x, 2*y, ones(size(x))];B=x.^2+y.^2;c=inv(A'*A)*A'*B;r=sqrt(c(3)+c(1)^2+c(2)^2)例子ezplot('-2/3*exp(-t)+5/3*exp(2*t)','-2/3*exp(-t)+2/3*exp(2*t)',[0,1]) grid on; axis([0, 12, 0, 5])密度函数和概率分布设x~ b(20,0.1),binopdf(2,20,0.1)分布函数设x~ N(1100,502) ， y~ N(1150,802) ，则有normcdf(1000,1100,50)=0.0228，1-0.0228=0.9772normcdf(1000,1150,80)=0.0304, 1-0.0304=0.9696统计量数字特征x=[29.8 27.6 28.3]mean(x)max(x)min(x)std(x)syms p k;Ex=symsum(k*p*(1-p)^(k-1),k,1,inf)syms x y;f=x+y;Ex=int(int(x*y*f,y,0,1),0,1)参数估计例：对某型号的20辆汽车记录其5L汽油的行驶里程（公里），观测数据如下：29.8 27.6 28.3 27.9 30.1 28.7 29.9 28.0 27.9 28.728.4 27.2 29.5 28.5 28.0 30.0 29.1 29.8 29.6 26.9设行驶里程服从正态分布，试用最大似然估计法求总体的均值和方差。