二阶系统动态性能分析
实验一基于MATLAB的二阶系统动态性能分析

实验一基于MATLAB的二阶系统动态性能分析二阶系统是控制系统中常见的一类系统,在工程实践中有广泛的应用。
为了对二阶系统的动态性能进行分析,可以使用MATLAB进行模拟实验。
首先,我们需要定义一个二阶系统的数学模型。
一个典型的二阶系统可以用如下的常微分方程表示:$$m\ddot{x} + b\dot{x} + kx = u(t)$$其中,$m$是系统的质量,$b$是系统的阻尼系数,$k$是系统的刚度,$u(t)$是控制输入。
在MATLAB中,我们可以使用StateSpace模型来表示二阶系统。
具体实现时,需要指定系统的状态空间矩阵,并将其转换为StateSpace模型对象。
例如:```matlabm=1;b=0.5;k=2;A=[01;-k/m-b/m];B=[0;1/m];C=[10;01];D=[0;0];sys = ss(A, B, C, D);```接下来,我们可以利用MATLAB的Simulink工具来模拟系统的响应。
Simulink提供了一个直观的图形界面,可以快速搭建系统的模型,并进行动态模拟。
我们需要使用一个输入信号来激励系统,并观察系统的响应。
例如,我们可以设计一个阶跃输入的信号,并将其作为系统的输入,然后观察系统的输出。
在Simulink中,可以使用Step函数来生成阶跃输入。
同时,我们可以添加一个Scope模块来实时显示系统的输出信号。
以下是一个简单的Simulink模型的示例:在Simulink模拟中,可以调整系统的参数,如质量、阻尼系数和刚度,以观察它们对系统动态性能的影响。
通过修改输入信号的类型和参数,还可以研究系统在不同激励下的响应特性。
另外,MATLAB还提供了一些工具和函数来评估二阶系统的动态性能。
例如,可以使用step函数来计算系统的阶跃响应,并获取一些性能指标,如峰值时间、上升时间和超调量。
通过比较不同系统的性能指标,可以选择最优的系统配置。
此外,MATLAB还提供了频域分析工具,如Bode图和Nyquist图,用于分析系统的频率响应和稳定性。
机械工程控制基础29_二阶系统的性能指标

机械工程控制基础29_二阶系统的性能指标二阶系统是指具有两个自由度的机械工程控制系统。
在控制系统理论中,衡量系统性能的指标有许多,比如超调量、调节时间、稳态误差等。
下面将详细介绍二阶系统的性能指标。
一、超调量:超调量是指过渡过程中输出量超过稳态值的最大偏离量。
对于二阶系统而言,其超调量可以通过过冲幅值与稳态值的差进行计算。
具体公式如下:超调量(%)=(过冲幅值-稳态值)/稳态值×100超调量主要反映了系统在过渡过程中的动态性能,是指标中最容易获取的。
二、调节时间:调节时间是指系统输出量从初始稳态值到达稳态值所需要的时间。
对于二阶系统而言,其调节时间通常从过渡过程的时间t1开始计算。
具体公式如下:调节时间=t2-t1其中,t2表示系统输出量进入超定态的时刻。
三、上升时间:上升时间是指系统输出量从初始稳态值到达稳态值所需要的时间,也即是调节时间的一部分。
对于二阶系统而言,上升时间是系统输出量从过渡过程的时间t1到达过冲幅值和稳态值之间的时间间隔。
四、峰值时间:峰值时间是指系统输出量达到过冲幅值或者偏离过冲幅值最远的时刻。
对于二阶系统而言,峰值时间是系统从过渡过程的时间t1到达过冲幅值的时间间隔。
五、稳态误差:稳态误差是指系统输出量在稳态下与期望输入量之间的偏差。
对于二阶系统而言,稳态误差可以通过比较系统稳态值与期望输入量来计算。
稳态误差主要反映系统的静态性能,也即系统对于不同输入的输出表现。
综上所述,二阶系统的性能指标主要包括超调量、调节时间、上升时间、峰值时间和稳态误差。
这些指标可以通过理论计算、仿真分析和实验测试等方法来获取,用于评估和比较不同二阶系统的控制性能。
在实际应用中,根据具体需求和控制要求,可以通过调整系统参数和控制策略等来改善系统的性能指标,并使系统能够更好地满足要求。
自动控制原理实验——二阶系统的动态过程分析

实验二二阶系统的动态过程分析一、 实验目的1. 掌握二阶控制系统的电路模拟方法及其动态性能指标的测试技术。
2. 定量分析二阶系统的阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
3. 加深理解“线性系统的稳定性只与其结构和参数有关,而与外作用无关”的性质。
4. 了解和学习二阶控制系统及其阶跃响应的Matlab 仿真和Simulink 实现方法。
二、 实验内容1. 分析典型二阶系统()G s 的ξ和n ω变化时,对系统的阶跃响应的影响。
2. 用实验的方法求解以下问题:设控制系统结构图如图2.1所示,若要求系统具有性能:%20%,1,p p t s σσ===试确定系统参数K 和τ,并计算单位阶跃响应的特征量d t ,r t 和s t 。
图2.1 控制系统的结构图3. 用实验的方法求解以下问题:设控制系统结构图如图2.2所示。
图中,输入信号()r t t θ=,放大器增益AK 分别取13.5,200和1500。
试分别写出系统的误差响应表达式,并估算其性能指标。
图2.2 控制系统的结构图三、实验原理任何一个给定的线性控制系统,都可以分解为若干个典型环节的组合。
将每个典型环节的模拟电路按系统的方块图连接起来,就得到控制系统的模拟电路图。
通常,二阶控制系统222()2nn nG ssωξωω=++可以分解为一个比例环节、一个惯性环节和一个积分环节,其结构原理如图 2.3所示,对应的模拟电路图如图2.4所示。
图2.3 二阶系统的结构原理图图2.4 二阶系统的模拟电路原理图图2.4中:()(),()()r cu t r t u t c t==-。
比例常数(增益系数)21RKR=,惯性时间常数131T R C=,积分时间常数242T R C=。
其闭环传递函数为:12221112()1()(1)crKU s TTKKU s T s T s K s sT TT==++++(0.1) 又:二阶控制系统的特性由两个参数来描述,即系统的阻尼比ξ和无阻尼自然频率n ω。
二阶阶跃响应动态性能指标求取

二阶阶跃响应动态性能指标求取二阶系统是控制系统中常见的一种模型,其阶跃响应动态性能指标是评估系统的性能好坏的重要指标。
本文将从二阶系统的阶跃响应的定义、特点和性能指标的求取方法等方面进行阐述。
首先,二阶系统的阶跃响应是指系统在输入为单位阶跃信号时的响应。
假设二阶系统的传递函数为:G(s)=K/(s^2+2ξω_ns+ω_n^2)其中,K为增益,ξ为阻尼比,ω_n为自然频率。
二阶系统的阶跃响应具有以下特点:1.超调量:超调量是指阶跃响应中峰值与系统最终稳定值之间的差值,用百分数表示。
超调量越小,表示系统对阶跃输入的响应越快速、平稳。
2.响应时间:响应时间是指系统从单位阶跃响应开始到稳定的时间。
响应时间越短,表示系统对阶跃输入的响应越迅速。
3.调整时间:调整时间是指系统从初始状态到达超调量指定范围内的时间,一般取超调量为5%。
调整时间越短,表示系统对阶跃输入的响应越快速、平稳。
4.峰值时间:峰值时间是指系统对阶跃输入的响应达到其最大值的时间。
5.匀稳态误差:系统在稳态下的输出与输入的差值,反映系统的控制准确性。
若单位阶跃输入的稳态输出为1,则对于系统的阶跃响应不应有静态误差。
有了以上的定义和特点之后,下面将介绍二阶系统阶跃响应动态性能指标的求取方法。
首先,根据传递函数可求得系统的特征方程:s^2+2ξω_ns+ω_n^2=0然后,通过特征方程可以求得系统的根:s_1=-ξω_n+ω_n√(ξ^2-1)s_2=-ξω_n-ω_n√(ξ^2-1)根据系统根的位置可以对系统的动态性能进行评估。
1.超调量的计算:超调量的计算公式为:MP=e^(-πξ/√(1-ξ^2))其中,MP为超调量,ξ为阻尼比。
2.响应时间的计算:响应时间的计算公式为:t_r=π/ω_d其中,t_r为响应时间,ω_d为峰值时的角频率,可通过特征方程得到:ω_d=ω_n√(1-ξ^2)3.调整时间的计算:调整时间的计算公式为:t_s=4/(ξω_n)其中,t_s为调整时间。
自控实验—二三阶系统动态分析

自控实验—二三阶系统动态分析在自控实验中,二、三阶系统动态分析是非常重要的一部分。
通过对系统的动态性能进行分析,可以评估系统的稳定性、响应速度和稳态误差等方面的性能。
本次实验将使用PID控制器对二、三阶系统进行实时控制,并通过实验数据对系统进行动态分析。
首先,我们先了解什么是二、三阶系统。
在控制系统中,系统的阶数表示系统传递函数的阶数,也可以理解为系统动态特性的复杂程度。
二阶系统由两个极点和一个零点组成,三阶系统由三个极点和一个零点组成。
二、三阶系统的动态响应特性与极点位置有关,不同的极点位置对系统的稳定性、响应速度和稳态误差等性能有着不同的影响。
在实验中,我们将使用PID控制器对二、三阶系统进行控制。
PID控制器是一种经典的比例-积分-微分控制器,可以根据误差信号进行调节,通过调整比例系数、积分时间和微分时间来控制系统的响应特性。
实验中,我们将根据二、三阶系统的实时数据进行PID参数调整,以达到控制系统的稳定和快速响应的目的。
在进行实验前,我们首先需要对二、三阶系统进行建模。
二、三阶系统的传递函数通常表示为:二阶系统:G(s) = K / (s^2 + 2ξω_ns + ω_n^2)三阶系统:G(s) = K / (s^3 + 3ξω_ns^2 + 3ω_n^2s + ω_n^3)其中,K表示系统的增益,ξ表示系统的阻尼比,ω_n表示系统的自然频率。
通过实验数据的统计和分析,我们可以估计出系统的K、ξ和ω_n的值,并据此进行PID参数的调整。
接下来,我们进行实验。
我们首先将PID控制器的参数设为初始值,然后对系统进行实时控制,并记录系统输出的数据。
通过对这些数据进行分析,我们可以得到系统的稳态误差、响应时间和超调量等性能指标。
对于二阶系统,我们将分析以下几个方面的性能:1.稳态误差:通过比较实际输出值与目标值之间的差异,可以得到系统的稳态误差。
常见的稳态误差有零稳态误差、常数稳态误差和比例稳态误差等。
二阶系统动态性能指标

代表
过阻尼二阶系统的动态表现
时化成两个一阶惯性环节串联 三、二阶系统的动态性能指标与系统参数的关系
[例] 控制系统如图,求
R(s) + -
解:
C(s)
欠阻尼系统
第五次 作业
• P134
3-9
作业三 P60 2-12 解 信号流图
1
1
梅逊公式
欠阻尼二阶系统的动态性能指标
例2(P88 例3-12)图3-24为单位反馈二阶系统的单位阶 跃响应曲线。已知性能指标为:超调量=37%,调节时间 =5s,稳态值=0.95。试确定系统的开环传函。 解 二阶系统的传函为
1
2
闭环闭环主导极点
[例] 闭环控制系统的传递函数为 ,求单位阶跃响应
解:
第六节 稳态误差分析
一、稳态误差的定义 (1)从输入端定义 (2)从输出端定义
R(s) +
C(s)
G(s)
-
H(s)
由终值定理:
开环传递函数
二、控制系统的型别
开环传递函数中积分环节的个数 上很少见
-
++
一.一阶系统的瞬态响应
-
+
=
二.一阶系统的动态性能指标
ts 是一阶系统的动态性能指标。
增大系统的开环放大系数K0 都会使T 减小,使ts 减小。
第四节 二阶系统的动态性指标
一、二阶系统的动态响应
二阶标准型
或称典型二阶系 统传递函数
P75 二阶系统的 结构图
当 ξ=0 时
Ct(t)=L -1[
当 0<ζ<1时
误差带
=37%
根据终值定理
例3(大连理工大学2001年)单位负反馈二阶系统的单位 阶跃响应曲线如图所示。试确定系统的开环传函。 解 依图可知
欠阻尼二阶系统动态性能分析与计算

1+ lim k s→0 sν r(t)=Rt R(s)=R/s2 R ess= k lim s ν s s→0 r(t)=Rt2/2 R(s)=R/s3 ess= R
lim
s→0
s2
k sν
取不同的 ν
R1(t)
0型 Ⅰ型 Ⅱ型
Rt
Rt2/2
R1(t)
Rt
Rt2/2
R 1+ k
∞
R k
∞ ∞
R k R
1 右移一位降两阶 2 每两行个数相等 3 行列式第一列不动 +8 ε -8(2ε+8)7 4 次对角线减主对角线 -7 ε 分母总是上一行第一个元素 5 2 ε 6 一行可同乘以或同除以某正数 7 第一列出现零元素 时, 用正无穷小量ε代
劳斯判据
系统稳定的必要条件: s6 1 特征方程各项系数 均大于零!
ξ ωn ωn
传递函数:
A Φ(s)= S+a
运动模态1
K(t)=Ae-at
零极点分布图:
j
-a
0 0
传递函数:
A1s+B1 Φ(s)=(S+a)2+b2
运动模态2
K(t)=Ae-atsin(bt+α)
零极点分布图:
j b -a 0 0
t
运动模态3
传递函数:
A1s+B1 Φ(s)= S2+b2
欠阻尼二阶系统动态性能分析与计算动态性能指标定义1100ba峰值时间tp间trb调节时间ts动态性能指标定义2调节时间ts上升时间tr动态性能指标定义3brabtrtpts一阶系统时域分析无零点的一阶系统ts1画图时取k1t05ht0632hh2t0865hh3t095h二阶系统单位阶跃响应定性分析21200s12212n2112ht0112ncosnt0欠阻尼二阶系统动态性能分析与计算1取其解中的最小值s121sindt欠阻尼二阶系统的tsht1ent取误差带为005则有ent005ln201235由此解出ts运动模态1ktaeat零极点分布图
3.3二阶系统的动态性能(上)解析

s 2n 1 s [( s n ) jd )][( s n ) jd ]
s 2n 1 s 2n 1 s ( s n )2 ( jd )2 s ( s n )2 d 2
at
s n n 1 s (s n )2 d 2 (s n )2 d 2 n 1 2 1 s n 1 2 2 s ( s n ) d ( s n )2 d 2
5.84 n ts 4.75 n
4、稳态误差为0,说明典型二阶系统跟踪阶跃输入信号时,无稳态误差, 系统为无静差系统。
4.过阻尼(ζ>1)状态
闭环特征方程
特征根
2 s 2 2n s n 0
s1 n n 2 1
s2 n n 2 1
nt
d
L[e at cos t ]
上式取拉氏反变换,得
y(t ) 1 e
1 1
cos d t
1
2
sa ( s a)2 2 L[e at sin t ] ( s a)2 2
ent sin d t
e nt 1 2 e
Δ 2 Δ 5
4T1 1.25 ts 3T 1
Δ 2 Δ 5
1.34
3、稳态误差为0,说明典型二阶系统跟踪阶跃输入信号时,无稳态误 Y(t) 差,系统为无静差系统。
2
4、需要说明的是,对于临界阻尼和过阻 尼的二阶系统,其单位阶跃响应都没有 振荡和超调,系统的调节时间随ζ的增加 而变大,在所有无超调的二阶系统中, 临界阻尼时,响应速度最快。
2 n 1 1 s Y ( s ) ( s ) R( s ) 2 2 2 s n s s s 2 n
自动控制原理二阶系统动态指标

自动控制原理二阶系统动态指标在自动控制原理中,二阶系统的动态特性对整个控制系统的性能至关重要。
以下是对二阶系统动态指标的详细阐述,主要包含稳定性、快速性、准确性、鲁棒性、抗干扰性、调节时间、超调量、阻尼比和频率响应等方面。
一、系统的稳定性稳定性是评估控制系统性能的重要指标。
对于二阶系统,稳定性通常通过观察系统的极点位置来判断。
如果系统的极点位于复平面的左半部分,则系统是稳定的。
此外,系统的稳定性还与阻尼比有关,阻尼比在0到1之间时,系统是稳定的。
二、系统的快速性快速性表示系统响应速度的快慢。
在二阶系统中,快速性通常通过极点的位置来决定。
极点越接近虚轴,系统的响应速度越快。
但需要注意的是,过快的响应速度可能导致系统超调量增大,因此需要综合考虑快速性和稳定性。
三、系统的准确性准确性表示系统输出与期望输出的接近程度。
对于二阶系统,可以通过调整系统的极点和零点位置来提高准确性。
一般来说,增加阻尼比可以提高准确性。
四、系统的鲁棒性鲁棒性表示系统在参数变化或干扰下保持稳定的能力。
对于二阶系统,鲁棒性可以通过调整系统的极点和零点位置来改善。
一般来说,使极点和零点距离越远,系统的鲁棒性越好。
五、系统的抗干扰性抗干扰性表示系统抵抗外部干扰的能力。
对于二阶系统,可以通过增加阻尼比来提高抗干扰性。
阻尼比增大时,系统对外部干扰的抑制能力增强。
六、系统的调节时间调节时间表示系统从受到干扰到恢复稳态所需的时间。
对于二阶系统,调节时间与阻尼比和系统增益有关。
适当增加阻尼比和系统增益可以缩短调节时间。
七、系统的超调量超调量表示系统响应超过稳态值的最大偏差量。
对于二阶系统,超调量与阻尼比有关。
阻尼比越小,超调量越大。
为了减小超调量,可以适当增加阻尼比。
八、系统的阻尼比阻尼比是衡量系统阻尼程度的参数,其值介于0和1之间。
适当的阻尼比可以保证系统具有良好的稳定性和快速性。
对于二阶系统,阻尼比与调节时间和超调量密切相关。
根据实际需求选择合适的阻尼比是关键。
实验二 二阶系统的动态特性与稳定性分析.

自动控制原理实验报告实验名称:二阶系统的动态特性与稳定性分析班级:姓名:学号:实验二 二阶系统的动态特性与稳定性分析一、实验目的1、 掌握二阶系统的电路模拟方法及其动态性能指标的测试技术过阻尼、临界阻尼、欠阻尼状态2、 分析二阶系统特征参量(ξω,n )对系统动态性能的影响;3、 分析系统参数变化对系统稳定性的影响,加深理解“线性系统稳定性至于其结构和参数有关,与外作用无关”的性质;4、 了解掌握典型三阶系统的稳定状态、临界稳定、不稳定状态;5、 学习二阶控制系统及其阶跃响应的Matlab 仿真和simulink 实现方法。
二、实验内容1、 构成各二阶控制系统模拟电路,计算传递函数,明确各参数物理意义。
2、 用Matlab 和simulink 仿真,分析其阶跃响应动态性能,得出性能指标。
3、 搭建典型二阶系统,观测各个参数下的阶跃响应曲线,并记录阶跃响应曲线的超调量%σ、峰值时间tp 以及调节时间ts ,研究其参数变化对典型二阶系统动态性能和稳定性的影响;4、 搭建典型三阶系统,观测各个参数下的阶跃响应曲线,并记录阶跃响应曲线的超调量%σ、峰值时间tp 以及调节时间ts ,研究其参数变化对典型三阶系统动态性能和稳定性的影响;5、 将软件仿真结果与模拟电路观测的结果做比较。
三、实验步骤1、 二阶系统的模拟电路实现原理 将二阶系统:ωωξω22)(22nn s G s s n++=可分解为一个比例环节,一个惯性环节和一个积分环节ωωξω)()()()(2C C C C s C C 22262154232154232154215426316320nn s s s s s G s s s C R R R R R R R R R R R R C R R R R R R R R R U U n i ++=++=++== 2、 研究特征参量ξ对二阶系统性能的影响将二阶系统固有频率5.12n =ω保持不变,测试阻尼系数ξ不同时系统的特性,搭建模拟电路,改变电阻R6可改变ξ的值当R6=50K 时,二阶系统阻尼系数ξ=0.8 当R6=100K 时,二阶系统阻尼系数ξ=0.4 当R6=200K 时,二阶系统阻尼系数ξ=0.2(1)用Matlab 软件仿真实现二阶系统的阶跃响应,计算超调量%σ、峰值时间tp 以及调节时间ts 。
二阶系统的时间响应及动态性能介绍

二阶系统的时间响应及动态性能介绍二阶系统是指具有两个自由度的动力系统,例如二阶电路、二阶机械系统等。
在控制系统和信号处理的领域中,二阶系统有着广泛的应用。
二阶系统的时间响应和动态性能是评价系统性能的重要指标之一在阶跃信号输入时,二阶系统的时间响应可以分为三个阶段:超调阶段、振荡阶段和稳定阶段。
超调阶段是指系统在初期反应过程中,输出信号的幅值超过了稳态值。
振荡阶段是指系统在超调过程之后,输出信号会出现一定的振荡现象。
稳定阶段是指系统输出信号逐渐趋于稳定的阶段。
超调量是指系统在初期反应过程中,输出信号的峰值与稳态值之间的差值,通常用百分比表示。
超调量越小,系统的动态性能越好。
调节时间是指系统从初始状态到达稳态的时间。
当输出信号接近稳态值时,调节时间结束。
调节时间越短,系统的动态性能越好。
上升时间是指系统从初始状态到达信号波形上升至稳定值的时间。
上升时间越短,系统的动态性能越好。
峰值时间是指系统输出信号达到超调量峰值的时间。
峰值时间越短,系统的动态性能越好。
除了上述指标外,二阶系统的频率响应和阶数也是评价系统性能的重要指标之一、频率响应是指系统对不同频率的输入信号的响应特性。
系统的阶数表示系统的自由度,同时也反映了系统的复杂性。
综上所述,二阶系统的时间响应和动态性能是评价系统性能的重要指标。
不同的二阶系统在时间响应和动态性能上有不同的特点和表现。
对于
不同应用场景的二阶系统,我们可以根据需要选择合适的指标和方法进行评估和优化,以提高系统的性能和效果。
实验三 二阶系统的性能分析1
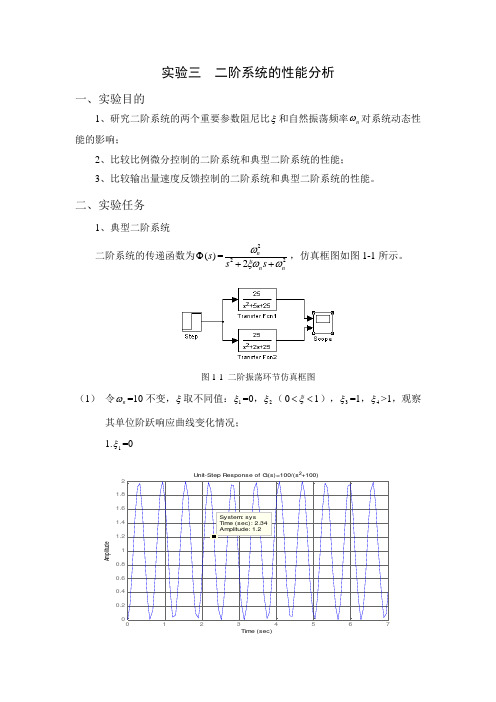
实验三 二阶系统的性能分析一、实验目的1、研究二阶系统的两个重要参数阻尼比ξ和自然振荡频率n ω对系统动态性能的影响;2、比较比例微分控制的二阶系统和典型二阶系统的性能;3、比较输出量速度反馈控制的二阶系统和典型二阶系统的性能。
二、实验任务1、典型二阶系统二阶系统的传递函数为()s Φ=2222nn ns s ωξωω++,仿真框图如图1-1所示。
图1-1 二阶振荡环节仿真框图(1) 令n ω=10不变,ξ取不同值:1ξ=0,2ξ(01ξ<<),3ξ=1,4ξ>1,观察其单位阶跃响应曲线变化情况; 1.1ξ=00.20.40.60.811.21.41.61.82U nit-Step R esponse of G(s)=100/(s 2+100)Tim e (sec)A m p l i t u d e2.2ξ=0.500.20.40.60.81 1.20.20.40.60.811.21.4Unit-Step Response of G(s)=100/(s 2+10s+100)Tim e (sec)A m p l i t u d e3.3ξ=1,00.51 1.50.10.20.30.40.50.60.70.80.91Unit-Step Response of G(s)=100/(s 2+20s+100)Tim e (sec)A m p l i t u d e4.4ξ=50.10.20.30.40.50.60.70.80.91U nit-Step R esponse of G(s)=100/(s 2+100s+100)Tim e (sec)A m p li t u d e(2)令ξ=0不变,n ω取不同值,观察其单位阶跃响应曲线变化情况; 1.n ω=50.20.40.60.811.21.41.61.82U nit-Step R esponse of G(s)=25/(s 2+25)Tim e (sec)A m p li t u d e2.n ω=200.20.40.60.811.21.41.61.82U nit-Step R esponse of G(s)=400/(s 2+400)Tim e (sec)A m p li t u d e(3)令ξ=0.2不变,n ω取不同值,观察其单位阶跃响应曲线变化情况,并计算 超调量%σ和s t ; 1.n ω=501234560.20.40.60.811.21.41.6U nit-Step R esponse of G(s)=25/(s 2+2s+25)Tim e (sec)A m p l i t u d eG=tf([0,0,25],[1,2,25]); C=dcgain(G) [y,t]=step(G); [Y ,k]=max(y);percentovershoot=100*(Y-C)/C i=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1; end setllingtime=t(i) C = 1percentovershoot = 52.6613 setllingtime =3.8810 2.n =100.20.40.60.811.21.41.6U nit-Step R esponse of G(s)=100/(s 2+4s+100)Tim e (sec)A m p l i t u d eG=tf([0,0,100],[1,4,100]); C=dcgain(G) [y,t]=step(G); [Y ,k]=max(y);percentovershoot=100*(Y-C)/C i=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1; end setllingtime=t(i) C = 1percentovershoot =52.6613 setllingtime =1.9405求超调量%σ和s t 的方法:以25425)(2++=Φs s s 为例说明。
实验一基于MATLAB的二阶系统动态性能分析

实验一 基于MATLAB 的二阶系统动态性能分析一、实验目的1、观察学习二阶控制系统的单位阶跃响应、脉冲响应。
2、记录单位阶跃响应曲线、脉冲响应曲线。
3、掌握时间响应分析的一般方法。
4、掌握系统阶跃响应曲线与传递函数参数的对应关系。
二、实验设备PC 机,MATLAB 仿真软件。
三、实验内容1、作以下二阶系统的单位阶跃响应曲线1010)(2++=s s s G 2、分别改变该系统的ζ和n ω,观察阶跃响应曲线的变化。
3、作该系统的脉冲响应曲线。
四、实验步骤1、二阶系统为1010)(2++=s s s G (1)键人程序 观察并纪录阶跃响应曲线(2)健入damp (den )计算系统的闭环根、阻尼比、无阻尼振荡频率,并作记录。
记录实际测取的峰值大小、C max (t p )、峰值时间t p 、过渡时间t s 并与理论值相比较。
2、修改参数,分别实现 ζ=1, ζ=2的响应曲线,并作记录。
程序为:n0=10;d0=[1 1 10];step (n0,d0 )%原系统ζ=0.316/2hold on%保持原曲线 n1=n0,d1=[1 6.32 10];step (n1,d1)%ζ=1n2=n0;d2=[1 12.64 10];step(n2,d2)%ζ=2修改参数,写出程序分别实现1n ω=021n ω和2n ω=20n ω的响应曲线,并作记录。
%100=n ω3、试作以下系统的脉冲响应曲线,分析结果1010)(2++=s s s G102102)(21+++=s s s s G ,有系统零点情况,即s=-5。
五、实验记录1、二阶系统为 1010)(2++=s s s G (1)键人程序 观察并纪录阶跃响应曲线(2)健入damp (den )计算系统的闭环根、阻尼比、无阻尼振荡频率,并作记录。
记录实际测取的峰值大小、Cmax (tp)、峰值时间tp、过渡时间ts并与理论值相比较。
实际值峰值 Cmax (tp)峰值时间tp过渡时间ts% 5±% 2±2、修改参数,分别实现ζ=1, ζ=2的响应曲线,并作记录。
二阶系统的动态过程分析

二阶系统的动态过程分析二阶系统是指具有两个自由度的动态系统,常见的有二阶低通滤波器、二阶惯性系统等。
在工程和控制领域中,对二阶系统的动态过程进行分析有助于了解系统的响应特性、设计控制器以及优化系统性能。
一、二阶系统的数学模型一般来说,二阶系统可以用以下微分方程来描述:$M(s)Y(s)=S(s)X(s)$其中,$M(s)$表示系统的传递函数,$X(s)$和$Y(s)$分别表示输入和输出信号的拉普拉斯变换,$s$表示复频域变量。
对于线性、时不变的二阶系统,传递函数$M(s)$可以表示为:$M(s) = \frac{K}{(s+a)(s+b)}$其中,$K$表示系统的增益,$a$和$b$分别表示系统的两个极点。
极点的位置和系统的动态响应有密切关系。
二、二阶系统的零极点分布1.两个实根:当两个极点都为实数时,系统响应会表现出一种振荡的特点。
极点的距离越小,振荡的频率越高,振荡的衰减速度越快。
2.两个共轭复根:当极点为共轭复根时,系统响应不会出现振荡,而是呈现一种渐进衰减的特性。
共轭复根的实部决定了响应的衰减速度,虚部决定了振荡的频率。
3.一个实根和一个共轭复根:这种情况下,系统的响应既会出现振荡,又会呈现渐进衰减的特点。
实根决定了振荡的频率,共轭复根的实部决定了衰减速度,虚部决定了振荡的频率。
三、二阶系统的动态响应1.响应时间:表示系统从0到达稳定状态所需要的时间。
可通过单位阶跃响应来测量。
2.超调量:表示响应曲线最大值与稳定值之间的差值。
对于二阶系统,根据极点位置不同,超调量有不同的计算方式。
3.峰值时间:指的是响应曲线达到超调量的最大值所需要的时间。
四、二阶系统的稳定性分析对于二阶系统而言,稳定性的判断可以通过极点的位置来进行。
当且仅当所有的极点实部都小于零时,系统才是稳定的。
针对具体的二阶系统,可以通过极点的特征方程来进行分析。
如果特征方程有两个负实数根,系统就是稳定的;如果有一个或两个正实数根,系统就是不稳定的。
自动控制 二阶系统性能分析

c(t1p)-1100% = e-ζπ
1-ζ
2
100%
整理ppt
第三节 二阶系统性能分析
4. 调节时间ts
c(t)=1-
e-ζ
ωnt
2
sin(ω
d
t+β
)
1-ζ
c(t)
1
误差带
可用近似公式: 0
ts =3T=ζω3n
ts
=4T=ζ
4 ωn
ζ<0.68 ζ<0.76
ts t
±5%误差带 ±2%误差带
整理ppt
第三节 二阶系统性能分析
四、带零点二阶系统单位阶跃响应
c(cФ=t=1τ)d(c=(1tsdc(s)系1(t21)=t)s+-(==2Lt统ω2ζe+)1cRC-ω=ω-ζ-12ζ1ζn结2(ω(([e1s(nsωtnns22s)t-ζ))-ζ(构s++=ωnsz+τ1n2ωsz2t11s为+[+(ζ[2ωd2nz)ω+ζ2ωω-ζdcω2nζ+ω21tn2nn(2ω)sz(τntni)=(sn)nsRs+zs2sω(+ω((i++sns1ωn)τ222ωdζ设(ω)+s)ωstωn++]2n2ζ2dβ=1n2n(ωt1+ssR)β+-+n-ωω(zse1)s+-)-ζ+n-)ω2ζdωω=c)时nnso22tds(1)sss间c+ωi(ωon闭2ζns20常(ωωd(ω<环nt数ζ+d)dβ<tC零t++1(β)βs]点)))] 设=C11-(se1)-ζ-ζ=ωn2ts2z+lω2[ζ2nzωR-ζlωn(ssn)+ωsinn2(ω则d t+βC()s+)ω=lCd c1o(ss)(ω+ dzstC+β1(s))]
二阶系统的时间响应及动态性能介绍

表 3-3 二阶系统(按阻尼比ξ )分类表
分类
特征根
ξ >1
过阻尼
ξ =1
临界阻尼
λ1,2 = −ξω n ± ω n ξ 2 − 1 λ1,2 = −ω n
特征根分布
模态
e λ1t e λ2t
e −ωnt te −ωnt
0 < ξ < 1 λ1,2 = −ξω n ± jω n 1 − ξ 2
欠阻尼
3.3 二阶系统的时间响应及动态性能
3.3.1 二阶系统传递函数标准形式及分类
常见二阶系统结构图如图 3-6(a)所示,其中 K ,T0
为环节参数。系统闭环传递函数为
Φ(s) =
K
T0s2 + s + K
为分析方便起见,常将二阶系统结构图表示成如图 3-6 (b)所示的标准形式。系统闭环传递函数标准形式为
1.欠阻尼二阶系统极点的两种表示方法
欠阻尼二阶系统的极点可以用如图 3-10 所示的两种形式表示。 z 直角坐标表示
λ1,2 = σ ± jω d = −ξω n ± j 1 − ξ 2ω n
z “极”坐标表示
(3-8)
⎧ ⎨ ⎩
λ ∠λ
= ωn =β
⎧ cos β = ξ ⎩⎨sin β = 1 − ξ 2
ξ = 1 + (T1 T2 ) = 1.25 > 1 2 T1 T2
查图 3-7 可得 ts T1 = 3.3 ,计算得 ts = 3.3T1 = 3.3 × 0.5 = 1.65s 。图 3-8 给出了系统单
位阶跃响应曲线。
当阻尼比 ξ = 1时,系统处于临界阻尼状态,此时闭环极点是一对相等的实根,即
性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
δ1%= e
ts =
−
π 1 ζ 2 1−ζ1
×100%=16%
4
ωn1ζ1
=
4 =1 s) ( 0.5×8
Monday, October 17, 2011
11
How to improve the performance of second order system
a. Derivative feedback of output
e − ζω n t 1−ζ
2
sin( ω d t + tg −1
1− ζ
2
ζ
) ≤ ∆%
for convenience
e − ζω n t s 1−ζ 2
= ∆%
2
ts = −
Monday, October 17, 2011
ln(
1−ζ
× ∆ %)
ζω
n
6
衰减振荡瞬态过程的性能指标 Transient response specification
cos β = ζ
β is damped angle
td =
Monday, October 17, 2011
1+ 0.7ξ
ωn
2
Transient response specification Peak time :t p ,for c′(t p ) = 0 when t = t p
c (t ) = 1 − e −ζω n t 1−ζ 2 sin(ω d t + β ) , t ≥ 0
Qts = 4
ωnζ
(or
3
ωnζ
),∴ωn is increased, ts . For a certain
ζ
Usually, letting ζ =0.4~0.8, then the overshoot is 25%~1.5%.
Monday, October 17, 2011
8
Example
Consider a system shown in fig.
Obtain ① ζ and ωn ; ② δ % and ts
K =16,T = 0.25
R (s )
③for δ %=16%,K=?, When T is same. Solution:① ω n = ②
K = T
−
K s(Ts + 1)
C (s )
16 1 1 = 8, ζ = = = 0 . 25 0 . 25 2 KT 2 16 × 0 . 25
R (s )
2 ωn s ( s + 2ζω n )
C (s )
-
-
τs
将输出信号的导数反馈到 系统输入端并与误差信号 比较。 比较。保持无阻尼振荡频 率不变,增大系统阻尼, 率不变,增大系统阻尼, 减小超调, 减小超调,同时减小调节 时间。 时间。
b. Proportional plus derivative of error
1− ζ 2 ωd = = tgβ thus: tg (ωd t p + β ) = ζωn ζ
故峰值时间满足的条件是 tg (ωd t p + β ) = tgβ
ωd t p = nπ (n = 0,1,2,...)
π t p is first time of peak,so n=1,we have: t p = = ωn 1−ζ 2 ωd
−
δ %×100%= e
ζ π 1− 2 ζ
×100% = 44%
4 4 = = 2s, (for∆ = 2) ω ζ 8×0.25 n ts = 3 3 = =1.5s, (for∆ = 5) ωnζ 8×0.25
③
−
ζπ
1− ζ
2
Q δ % = 16 %, ∴ 0 . 16 = e
4
衰减振荡瞬态过程的性能指标 Transient response specification
100 90 80 70 60 50 40 30 20 10 0
δ%
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Monday, October 17, 2011
ζ
5
衰减振荡瞬态过程的性能指标 Transient response specification
Settling time t s: according definition ,when t≥ts, |c(t)-c(∞)|≤ c(∞) ×∆%。 If the final value is unity, the error between the steady state and the response is equal to
Second order system and transient response specification Following shall obtain the rising time \ peak time \ maximum overshoot and settling time
c ( t ) = 1 − e − ζω n t (cos ω d t + sin ω d t ) , 1−ζ 2
−1
ζ
t≥0
c(t ) = 1 −
e −ζωnt 1− ζ
2
sin( 1 − ζ ωn t + tg
2
1− ζ 2
ζ
), t ≥ 0
rising time t r : according definition, for c ( t r ) = 1 when t = t r
c ( t ) = 1 − e − ζω n t r (cos ω d t r +
R (s )
2 ωn s ( s + 2ζω n )
Wn2 (1 + τs ) G ( s) = 2 s + (2ζWn + Wn2τ ) s + Wn2 C (s )
-
τs
+
相当于给系统增加了一个 闭环零点, 闭环零点,同时保持系统 自然频率不变, 自然频率不变,增大系统 阻尼比。 阻尼比。 Wτ ζd =ζ + n 2
Monday, October 17, ห้องสมุดไป่ตู้011
12
1
1− e −ζω n t 1−ζ 2
0
t
1−
1 1−ζ 2
ts t's
Response curve within a pair of envelope curve of
1±
Monday, October 17, 2011
e − ζω n t 1−ζ 2
7
[In Summary] Damped ratio ζ is very important parameter of second order system. It determines the performance of the system. For ζ > 1 the curve is monotonically and no oscillation and no overshoot. For ζ = 0 ,curve is oscillation for ever. For (0 < ζ < 1) ,when ζ is small, large oscillation and settling time and bad performance.
−
= 1− e
ζπ 1−ζ 2
(cos π +
ζ
1−ζ 2
sin π ) = 1 + e
−
ζπ 1−ζ 2
δ% =
c(t p ) − c(∞) c (∞ )
×100% = (c(t p ) − 1) ×100%
−
ζπ
1−ζ 2
thus: %= e δ
Monday, October 17, 2011
×100%
Monday, October 17, 2011
π
3
Transient response specification Maximum overshoot δ % :
π Substitute t p = into c(t ), hence c(t p ) = cmax ωd ζ −ζω n t p cmax = c(t p ) = 1 − e (cos ω d t p + sin ω d t p ) 2 1−ζ
1− ζ 2 where β = tg −1
ζ
c′(t ) = −
− ζωne
−ζω n t p
1−ζ 2
sin(ω d t p + β ) −
e
−ζω n t p
1−ζ 2
ωd ⋅ cos(ωd t p + β ) = 0
ζωn sin(ωd t p + β ) −ωd ⋅ cos( d t p + β ) = 0 ω
ζ
cos ω d t r +
sin ω d t r = 0 1−ζ 2
ζ
1−ζ
2
sin ω d t r ) = 1
tg ω d t r = −
Monday, October 17, 2011
1−ζ
2
ζ
thus:t r =
1
ω
tg
−1
(−
1−ζ 2
d
ζ
)
1
衰减振荡瞬态过程的性能指标 Second order system and transient response specification
