全等三角形判定SSSppt课件
合集下载
【数学课件】三角形全等的判定(SSS)

如 何 用 符 号 语 言 来 表 达 呢
A
D
B
C
E
F
在△ABC与△DEF中 AB=DE AC=DF BC=EF ∴△ABC≌△DEF(SSS)
思考:你能 用“边边边” 解释三角形 具有稳定性 吗?
例1 已知:如图,AB=AD,BC=CD, 求证:△ABC≌ △ADC
A B D
证明:在△ABC和△ADC中 AB=AD (已知) BC=CD (已知) AC = AC (公共边)
失 败
(2)一个角 (1)两边 4cm
6cm 4cm 6cm
2.给定两个条件: (2)一边一角
30º 6cm
失 败
30º 6cm
(3)两角
30º 20º 30º 20º
俗话说:失败是成功之母! 我们继续探究: 千万别泄气哦! 探究二
(1)三边 给定三个条件: (2)两边一角 (3)一边两角 (4)三角 [动手画一画]
画出一个三角形,使它的三边长分别为3cm、 4cm、6cm , 把你画的三角形与小组内画的进 行比较,它们一定全等吗?
画法: 1.画线段AB=3㎝; 2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两 弧交于点C; 3. 连接线段AC、BC.
结论:三边对应相等的两个三角形全等. 可ቤተ መጻሕፍቲ ባይዱ写为”边边边”或SSS
课堂小测
2.如图,已知 AB DC,AC DB .求证: △ABC≌△DCB.
A
D
O B C
1.课本P15习题11.2的第1、2题(一号本)
能力提升题:
课本16页第9题(一号本)
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
八年级数学三角形全等的判定 (SSS)课件

B
D
O
作法:
D′
A
C
O′
C′
B′
A′
1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB
两角一边相等
思考
情况一:三个角相等,两三角形全等吗?
不一定
两底边平行
结论: 三个内角对应相等的三角形不一定全等。
思考
情况二:三个边相等,两三角形全等吗?
画一个△AˊBˊC,使对应的三边相等?
' '
1.
画线段
B
C =BC ;
画法:
A
2. 分别以B ′ 、C ′ 为圆心,
线段AB、AC为半径画弧,
两弧交于点A′ ;
(4)∠A=∠A, (5)∠B=∠B, (6)∠C=∠C,
六个条件,可得到什么结论?
A
A
答:ΔABC ≌ ΔA′B′C′
'
三条边对
应相等
两个三角形
全等
B
B
'
C
C
'
三个角对应
相等
问题
ABC 与 Δ′ ′ ′ 满足上述六个条件中的一部分是否能保证 Δ 与
Δ′ ′ ′ 全等呢?
A
八年级数学上册
第十二章 全等三角形
三角形全等的判定 (SSS)
数学(初中)
(八年级 上)
前言
学习目标
1.掌握“边边边”条件的内容,并能初步应用“边边边”条件判定两个三角形全等 。。
全等三角形判定SSSppt课件

满足下列条件的两个三角形是一定否全等:
(1)一个条件
× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
(2)两个条件
一边一角 ×
两角
两边
三角
(3)三个条件
三边 两边一角
两角一边
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
证明:∵BD=CE ∴ BD-ED=CE-ED, B E D C
即BE=CD。 在△ AEB和△ ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌ △ ADC (sss)
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
两边
三角
(3)三个条件
三边 两边一角
两角一边
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
8cm
8cm
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
证明:在△ABC和△ADC中 A
AB=AD (已知 )
B
D
BC=CD (已知 )
AC= AC (公共边 )
∴ △ABC ≌ △ADC(SSS) C
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
全等三角形的判定SSS-获奖课件-PPT

7
大家学习辛苦了,还是要坚持
继续保持安静
8
(两角)
③如果三角形的两个内角分别是30°,45°时
30◦ 45◦
30◦
45◦
结论:两个角对应相等的两个三角形不一定全等.
9
思考1:我们通 过探究1探究2
得到的结论
思考2:如果给出三个 条件画三角形,你能说 出:哪几种可能的情况?
• 结论:只给出 1.三边
求证: ∠ A =∠ D
AD
B E
CF
16
练习3
已知: 如图,AB = DC ,AD = BC . 求证: ∠ A =∠ C
证明: 连结 BD
A
D
在△BAD 和△DCB中
AB = CD (已知)
AD = CB (已知) B
C
BD = DB (公共边)
∴ △BAD ≌ △DCB( SSS )
∴ ∠ A =∠ C (全等三角形的对应角相等)
18
全等三角形的判定SSS 获奖课件
•
1 什么叫全等三角形?
•
2 全等三角形的边角关系:
知识回顾:
2
3
探究活动1: 只有一个相等条件时
1.只有一条边相等时;
3㎝
3㎝
2.只有一个角相等;
3cm
结论:只有一 条边或一个 角对应相等 的两个三角 形不一定全 等.
45◦
45◦
45◦
4
如果给出两个条件画三角形, 你能说出有哪几种可能的情况?
的 顺
12
例题巩固,加油!
例题1
如图, △ABC 是钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD
《三角形全等的判定》课件

AD=CE,
C
D
CD=BE,
AC=CB,
B
E
∴△ACD≌△CBE(SSS).
新知探究 知识点2 用直尺和圆规作一个角等于已知角
用直尺和圆规作出一个角等于已知角.
如图,已知:∠AOB. 求作:∠A'O'B',使得∠AOB=∠A'O'B'. 作法:(1)以点O为圆心,任意长为 半径画弧,分别交OA,OB于点C,D;
如图,∠AOB是一个任意角,在边OA,OB上分别截取
OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,
N重合,过角尺顶点C的射线OC便是∠AOB的平分线,
为什么?
OM=ON,
证明:在△MOC和△NOC中,OC=OC, CM=CN, O
MA C
∴△MOC≌△NOC(SSS).
NB
∴∠MOC=∠NOC,则OC是∠AOB的平分线.
在△ABF和△ECD中,
A
E
AB=CE,
AF=ED,
BF=CD,
BDF C
∴△ABF≌△ECD(SSS).
3.已知:如图,AC=FE,AD=FB,BC=DE.求证: AC//EF,DE//BC.
证明:∵AD=FB,∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
A
C
BC=DE,
结论:两个角对应相等的两个三角形不一定全等.
画出△ABC和△A'B'C',使其满足有两个相等条件,此 时的△ABC和△A'B'C'全等吗? 3.有一条边和一个角分别对应相等的情况
结论:一条边和一个角对应相等的两个三角形 Nhomakorabea一定 全等.
全等三角形的判定PPT课件共34张

24
2024/1/30
06
判定全等三角形的注意事项
25
准确理解全等三角形的定义和性质
2024/1/30
全等三角形的定义
两个三角形如果三边及三角分别对应 相等,则称这两个三角形全等。
全等三角形的性质
全等三角形的对应边相等,对应角相 等;全等三角形的周长、面积相等; 全等三角形的对应边上的中线、高线 、角平分线分别相等。
结论
三边分别相等的两个三角 形全等,简称“SSS”。
16
SAS判定法的证明
已知条件
两边和它们的夹角分别相 等的两个三角形。
2024/1/30
证明过程
将其中一个三角形旋转至 与另一个三角形两边重合 ,由于夹角相等,因此两 个三角形全等。
结论
两边和它们的夹角分别相 等的两个三角形全等,简 称“SAS”。
示例
若三角形ABC和三角形DEF中,∠A=∠D,∠B=∠E ,BC=EF,则三角形ABC全等于三角形DEF。
2024/1/30
14
2024/1/30
04
判定方法的证明与推导
15
SSS判定法的证明
01
02
03
已知条件
三边分别相等的两个三角 形。
2024/1/30
证明过程
通过平移或旋转其中一个 三角形,使得两个三角形 的三边分别重合,从而证 明两个三角形全等。
2024/1/30
在计算三角形面积时,如果知道两个三角形全等,那么可以直接得出它们的面积相 等。
9
2024/1/30
03
全等三角形的判定方法
10
边边边判定法(SSS)
定义
三边分别相等的两个三角形全等 。
2024/1/30
06
判定全等三角形的注意事项
25
准确理解全等三角形的定义和性质
2024/1/30
全等三角形的定义
两个三角形如果三边及三角分别对应 相等,则称这两个三角形全等。
全等三角形的性质
全等三角形的对应边相等,对应角相 等;全等三角形的周长、面积相等; 全等三角形的对应边上的中线、高线 、角平分线分别相等。
结论
三边分别相等的两个三角 形全等,简称“SSS”。
16
SAS判定法的证明
已知条件
两边和它们的夹角分别相 等的两个三角形。
2024/1/30
证明过程
将其中一个三角形旋转至 与另一个三角形两边重合 ,由于夹角相等,因此两 个三角形全等。
结论
两边和它们的夹角分别相 等的两个三角形全等,简 称“SAS”。
示例
若三角形ABC和三角形DEF中,∠A=∠D,∠B=∠E ,BC=EF,则三角形ABC全等于三角形DEF。
2024/1/30
14
2024/1/30
04
判定方法的证明与推导
15
SSS判定法的证明
01
02
03
已知条件
三边分别相等的两个三角 形。
2024/1/30
证明过程
通过平移或旋转其中一个 三角形,使得两个三角形 的三边分别重合,从而证 明两个三角形全等。
2024/1/30
在计算三角形面积时,如果知道两个三角形全等,那么可以直接得出它们的面积相 等。
9
2024/1/30
03
全等三角形的判定方法
10
边边边判定法(SSS)
定义
三边分别相等的两个三角形全等 。
三角形全等的判定SSSppt课件
课堂小测
1.如图所示,在△ABC中,AB=AC,BE=CE, 则由“SSS”可以判定( )
A.△ABD≌△ACD B.△BDE≌△CDE C.△ABE≌△ACE D.以上都不对
A
E
B
D
C
本 标准适 用于已 投入商 业运行 的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
探究一
1.给定一个条件:
(1)一条边
失败
(2)一个角
(1)两边 4cm
6cm
4cm 6cm
2.给定两个条件: (2)一边一角 30º
6cm
失败
(3)两角
30º 20º
30º 6cm
30º 20º
本 标准适 用于已 投入商 业运行 的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进 行比较,它们一定全等吗?
画法: 1.画线段AB=3㎝; 2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两 弧交于点C; 3. 连接线段AC、BC.
结论:三边对应相等的两个三角形全等.
可简写为”边边边”或SSS
本 标准适 用于已 投入商 业运行 的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
12.2三角形全等的判定SSS课件

∴ AC = BD 在△AEC 和△BFD中, AC = BD(已证), ∠A = ∠B ( 已证 ), ∴ △AEC ≌ △BFD(ASA)
C F
B
OC = OD(已知)
EB
∴△ AOC ≌ △BOD(AAS)
O
D
AE = BF(已知). ∴ CE = DF
A
D =
。
E ?
?
c
= B F
。
图1
(2)∵ △ABC≌△FDE(已证) ∴ ∠C=∠E (全等三角形的对应角相等)
2.已知:△ABC的顶点和△DBC的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交于点O. 求证:OA =OD. 证明: 在△ABC和△DCB中, AB =DC(已知),AC = DB (已知), BC = CB (公共边), ∴ △ABC ≌△ DCB(SSS) ∴∠A = ∠D (全等三角形的对应角相等).
画全等三角形的另一个方法
如右上图,已知任意△ABC,画一个△A´B´C´, 使A´B´=AB, A´C´=AC, B´C´ =BC.
画法:1、画线段A´B´=AB, 如右下图
C B
A
2、分别以 A´、B´为圆心,AC、BC为半径 画弧,两弧相交于点C´ .
3、连结A´C´、 B´C´ 得 △A´B´C´. 剪下 △A´B´C´放在△ABC上, 可以看到△A´B´C´ ≌ △ABC, 由此可以得到判定两个三角形 全等的又一个公理. C
证明:∵BD=CE
∴ BD-ED=CE-ED, 即BE=CD。 在△ AEB和△ ADC中, AB=AC AE=AD BE=CD ∴ △AEB ≌ △ ADC(SSS)
B E D C
C F
B
OC = OD(已知)
EB
∴△ AOC ≌ △BOD(AAS)
O
D
AE = BF(已知). ∴ CE = DF
A
D =
。
E ?
?
c
= B F
。
图1
(2)∵ △ABC≌△FDE(已证) ∴ ∠C=∠E (全等三角形的对应角相等)
2.已知:△ABC的顶点和△DBC的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交于点O. 求证:OA =OD. 证明: 在△ABC和△DCB中, AB =DC(已知),AC = DB (已知), BC = CB (公共边), ∴ △ABC ≌△ DCB(SSS) ∴∠A = ∠D (全等三角形的对应角相等).
画全等三角形的另一个方法
如右上图,已知任意△ABC,画一个△A´B´C´, 使A´B´=AB, A´C´=AC, B´C´ =BC.
画法:1、画线段A´B´=AB, 如右下图
C B
A
2、分别以 A´、B´为圆心,AC、BC为半径 画弧,两弧相交于点C´ .
3、连结A´C´、 B´C´ 得 △A´B´C´. 剪下 △A´B´C´放在△ABC上, 可以看到△A´B´C´ ≌ △ABC, 由此可以得到判定两个三角形 全等的又一个公理. C
证明:∵BD=CE
∴ BD-ED=CE-ED, 即BE=CD。 在△ AEB和△ ADC中, AB=AC AE=AD BE=CD ∴ △AEB ≌ △ ADC(SSS)
B E D C
三角形全等的判定ppt课件

追问1:这个尺规作图的方法利用了上节课中的哪个知识点?
追问2:根据前面的操作,你能探究到什么结论?
例1. 如图,有一池塘,要测池塘两端A、B的距离,可先在平 Nhomakorabea上取一个可以
直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,
使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么?
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两
个木桩上,两个木桩离旗杆底部的距离相等吗?
解:BD=CD
在Rt△ABD 和 Rt△ACD 中,
AB=AC
AD=AD
∴Rt△ABD≌Rt△ACD(HL)
∴ BD=CD
例1.如图,AC⊥BC,BD⊥AD,AC =BD.求证:BC =AD.
(1)
AD = BC
( HL );
(2)
AC = BD
( HL );
(3) ∠DAB = ∠CBA
( AAS );
(4) ∠DBA = ∠CAB
( AAS ).
D
A
C
B
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个三
特殊方法
角形就全等了?
HL定理
SSS
一
般
方
法
SAS
AAS
AAS
直角三角形全等
问题:三角分别相等的两个三角形全等吗?
追问:证明两个三角形全等的方法有哪些?
评价3.如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.
求证:AB=AD.
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在△ABC和△ADC中,
追问2:根据前面的操作,你能探究到什么结论?
例1. 如图,有一池塘,要测池塘两端A、B的距离,可先在平 Nhomakorabea上取一个可以
直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,
使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么?
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两
个木桩上,两个木桩离旗杆底部的距离相等吗?
解:BD=CD
在Rt△ABD 和 Rt△ACD 中,
AB=AC
AD=AD
∴Rt△ABD≌Rt△ACD(HL)
∴ BD=CD
例1.如图,AC⊥BC,BD⊥AD,AC =BD.求证:BC =AD.
(1)
AD = BC
( HL );
(2)
AC = BD
( HL );
(3) ∠DAB = ∠CBA
( AAS );
(4) ∠DBA = ∠CAB
( AAS ).
D
A
C
B
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个三
特殊方法
角形就全等了?
HL定理
SSS
一
般
方
法
SAS
AAS
AAS
直角三角形全等
问题:三角分别相等的两个三角形全等吗?
追问:证明两个三角形全等的方法有哪些?
评价3.如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.
求证:AB=AD.
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在△ABC和△ADC中,
《三角形全等的判定》课件

《三角形全等的判定》
知识回顾
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
A
2.三边分别相等的两个三角形全等(可以
简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,B
C
AB=A'B',
A'
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C' (SSS). B'
C'
3.两边和它们的夹角分别相等的两个三角形全等(可以
简写成“边角边”或“SAS”).
A
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′, ∠B=∠B′, BC=B′C′,
B
C
A'
∴△ABC≌△A′B′C′(SAS). B'
C'
4.两角和它们的夹边分别相等的两个三角形全等(可以
简写成“角边角”或者“ASA”).
FE
BE=CF,
A
B
∴Rt△ABE≌Rt△DCF(HL). ∴AE=DF.
随堂练习
1.已知,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90〫,
有如下几个条件:①AC=A′C′,∠A=∠A′;②AC=A′C′, AB=A′B′;③AC=A′C′,BC=B′C′;④ AB=A′B′,
∠A=∠A′.其中,能判定Rt△ABC≌Rt△A′B′C′的条件的
需寻找的条件
可证直角与已知锐角的夹边对 应相等或者与锐角(或直角)
的对边对应相等
可证一直角边对应相等或证一 锐角对应相等
知识回顾
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
A
2.三边分别相等的两个三角形全等(可以
简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,B
C
AB=A'B',
A'
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C' (SSS). B'
C'
3.两边和它们的夹角分别相等的两个三角形全等(可以
简写成“边角边”或“SAS”).
A
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′, ∠B=∠B′, BC=B′C′,
B
C
A'
∴△ABC≌△A′B′C′(SAS). B'
C'
4.两角和它们的夹边分别相等的两个三角形全等(可以
简写成“角边角”或者“ASA”).
FE
BE=CF,
A
B
∴Rt△ABE≌Rt△DCF(HL). ∴AE=DF.
随堂练习
1.已知,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90〫,
有如下几个条件:①AC=A′C′,∠A=∠A′;②AC=A′C′, AB=A′B′;③AC=A′C′,BC=B′C′;④ AB=A′B′,
∠A=∠A′.其中,能判定Rt△ABC≌Rt△A′B′C′的条件的
需寻找的条件
可证直角与已知锐角的夹边对 应相等或者与锐角(或直角)
的对边对应相等
可证一直角边对应相等或证一 锐角对应相等
三角形全等的判定ppt课件

(2)取出四根硬纸条钉成一个四边形,拉动其中 两边,这个四边形的形状改变了吗?钉成 一个五 边形,又会怎么样?
(3)上面的现象说明了什 么?
三角形的框架,它的大小和形状是固定不变的, 三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
练一练 1.如图,已知AB=AC,AE=AD,BD=CE,试说明 △AEB △ADC.
解: BD=CE, BD-ED=CE-ED(等式的性质)
即BE=CD. 在△AEB和△ADC中,
AB=AC,(已知) AE=AD,(已知) BE=CD,(已证) △AEB △ADC(SSS)
2、如图,AB=CD,BF=DE,E,F是AC上两 点,且AE=CF.请你判断BF与DE的位置关系, 并说明理由.
有一个角对应相等的三角形 不一定全等
做一做 2. 给出两个条件画三角形时,有几种可能的情况? 每种情况下作出的三角形一定全等吗?
两个条件(两个角) (2)三角形的两个角分别是:30°,50°;
30°
不一定全等
两个条件(两条边) (3)三角形的两条边分别是:4cm,6cm.
不一定全等 两个条件不能保证三角形全等.
这节课你学到了什么?
1. 三角形全等的条件: 三边对应相等的两个三角形全等 (“边边边”或“SSS”)
2. 三角形具有稳定性。
三角形全等的条件:
三边对应相等的两个三角形全等,简 写为“边边边”或“SSS”。
数学表达式: 在△ABC和△A'B'C'中
例题 已知:如图AB=CD,AD=BC.则∠A与∠C相等 吗?为什么?
动手做一做
准备几根硬纸条
(1)取出三根硬纸条钉成一个三角形,你能拉动 其中两边,使这个三角形的形状发生变化吗?
三角形全等的判定ppt课件

∴△ABC≌△A1B1C1(AAS)
5.HL(H.L.) 在Rt△ABC与Rt△A1B1C1中,
AB=A1B1(已知)
BC=B1C1(已证) ∴△ABC≌△A1B1C1(HL)
例题精讲
例:已知:如图,点A,C,B,D在同一条直线上,
AC=BD,AM=CN,BM=DN 求证:AM∥CN,BM∥DN.
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
为BC边的中点,那么图中的全等三角形有哪几对?并选
择一对进行证明
△ABD≌△ACD
证明:∵D为BC边的中点
A
∴BD=CD
在△ABD和△ACD中
E
AB=AC
BD=CD
AD=AD
B
D
C
∴ △ABD≌△ACD(SSS)
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
证明:∵AC=BD ∴AC+CB=BD+BC 即AB=CD
M
N
在△AMB和△CND中 AM=CN
BM=DN
A
C
B
D
AB=CD
∴ △AMB≌△CND(SSS)
∴∠A=∠NCD,∠MBA=∠D ∴AM∥CN,BM∥DN
例:如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,
AE=FC
求证:△ABC≌△FDE.
(2)全等三角形对应角相等
PART II 全等三角形的判定 1.SSS(S.S.S.) 在△ABC与△A1B1C1中,
AB=A1B1(已知) BC=B1C1(已知) AC=A1C1(已证)
∴△ABC≌△A1B1C1(SSS)
5.HL(H.L.) 在Rt△ABC与Rt△A1B1C1中,
AB=A1B1(已知)
BC=B1C1(已证) ∴△ABC≌△A1B1C1(HL)
例题精讲
例:已知:如图,点A,C,B,D在同一条直线上,
AC=BD,AM=CN,BM=DN 求证:AM∥CN,BM∥DN.
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
为BC边的中点,那么图中的全等三角形有哪几对?并选
择一对进行证明
△ABD≌△ACD
证明:∵D为BC边的中点
A
∴BD=CD
在△ABD和△ACD中
E
AB=AC
BD=CD
AD=AD
B
D
C
∴ △ABD≌△ACD(SSS)
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
证明:∵AC=BD ∴AC+CB=BD+BC 即AB=CD
M
N
在△AMB和△CND中 AM=CN
BM=DN
A
C
B
D
AB=CD
∴ △AMB≌△CND(SSS)
∴∠A=∠NCD,∠MBA=∠D ∴AM∥CN,BM∥DN
例:如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,
AE=FC
求证:△ABC≌△FDE.
(2)全等三角形对应角相等
PART II 全等三角形的判定 1.SSS(S.S.S.) 在△ABC与△A1B1C1中,
AB=A1B1(已知) BC=B1C1(已知) AC=A1C1(已证)
∴△ABC≌△A1B1C1(SSS)
全等三角形的判定(SSS)精品PPT课件

有三边对应相 等的两个三角形 全等.
有两边和它们的 夹角对应相等的 两个三角形全等.
Байду номын сангаас
边 三有对角两应形角相全和等等它的.们两的个夹一应形有相个全两等角等角的所.和两对及个的其三边中对角
11
先任意画出一个△ABC,再画一个△ A’B’C’,使
A’B’= AB ,B’C’ =BC,C’ A’= CA,把画好的△ A’B’C’
接A与BC中点D的支架。求证:△ABD≌△ACD 分证析明::要∵D证是明B△CA中B点D,≌ △ACD,首 先要看这两个三角形的三条边是 否对应相∴B等D。=CD.
在△ABD和△ ACD中, AB=AC,
BD=CD,
AD=AD, ∴ △ABD ≌△ ACD(SSS).
已知AC=FE,BC=DE,点A,D,B,F在 一条
两角和夹边(ASA) 两角和一角的对边(AAS)
角角角×
SSA
\
==
两边和其中一边的对角对应相等
的两个三角形不一定全等。
可见:要使两个三角形全等, 应至少有 3 组元素对应相等。
6选3
边边边 (SSS)
两边一角 两角一边
两边和它的夹角(SAS)
两边和它一边的对角×
两角和夹边(ASA) 两角和一角的对边(AAS)
A
证明:∵AD=FB, ∴ AD-BD=FB-BD, 即AB=FD.
在 △ ABC和△ FDE中,
C BD
AC=FE,
AB=FD, BC=DE,
E
F
∴ △ ABC≌ △ FDE (SSS).
如图,AB=AD,CB=CD,∆ABC 与∆ADC全等吗?为什么?
A
C D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:求求△证证A:B:C∠≌DEC△∥=∠FBDCEE ,
证明:∵ AD=FB ∴AB=FD(等式性质)
在△ABC和△FDE 中
AC=FE(已知) BC=DE(已知)
。 A
?c
D
=
=
。B
E?
图1
F
AB=FD(已证)
∴△ABC≌△FDE(SSS)
(2)∵ △ABC≌△FDE(已证)
∴ ∠C=∠E (全等三角形的对应角相等)
× 一角
两个三角形不一定全等。
两个条件 三个条件
一边一角 × 两角 × 两边 × 三角 × 三边 √
两边一角
两角一边
只有两个条件对应相 等的两个三角形不一 定全等。
18
结论:三边对应相等的两个三角形全等. 可简写为边边边或SSS
19
A
D
如
何 用B
CE
F
符
在△ABC与△DEF中
号
语
AB=DE
言
来
AC=DF
∴ AD+DB=BF+DB
即 AB=DF
25
证明的书写步骤:
①准备条件:证全等时要用的间接 条件要先证好;
②三角形全等书写三步骤: 写出在哪两个三角形中 摆出三个条件用大括号括起来 写出全等结论
26
如图,AB=AC,AE=AD,BD=CE, A 求证:△AEB ≌ △ ADC。
证明:∵BD=CE ∴ BD-ED=CE-ED, B E D C
22
例3 如图, △ABC是一个钢架,AB=AC,AD是连接A
与BC中点D的支架,求求证证::△∠ABD=∠≌△C,ACD
A
证明:∵D是BC的中点
∴BD=CD
B
C
ቤተ መጻሕፍቲ ባይዱ
D
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C,
23
例4:已知:如图1 ,AC=FE,AD=FB,BC=DE
即BE=CD。
在△ AEB和△ ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌ △ ADC (sss)
27
练习3、如图,在四边形ABCD中, AB=CD,AD=CB,求证:∠ A= ∠ C.
你能说明AB∥CD,AD∥BC吗?
• 证明:在△ABD和△CDB中 D
C
AB=CD(已知)
AD=CB(已知) A
24
已知AC=FE,BC=DE,点A,D,B,F在 一条直线上,AD=FB(如图),要用“边边 边”证明△ABC ≌△ FDE,除了已知中的 AC=FE,BC=DE以外,还应该有什么条件? 怎样才能得到这个条件?
解:要证明△ABC ≌△ FDE, 还应该有AB=FD这个条件
∵ DB是AB与FD的公共部分, 且AD=BF
× (1)一个条件 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
(2)两个条件 (3)三个条件
一边一角 × 两角 × 两边 ×
三角 ×
三边
只有两个条件对应相 等的两个三角形不一 定全等。
两边一角
两角一边
16
8cm
8cm
17
满足下列条件的两个三角形是否一定全等:
一个条件
× 一边
只有一个条件对应相等的
B
BD=DB (公共边) ∴△ABD≌△ACD(SSS)
∴ ∠ A= ∠ C (全等三角形的对应角相等)
28
练习:1、如图,AB=AC,BD=CD,BH
§11.2 三角形全等的条件(一)
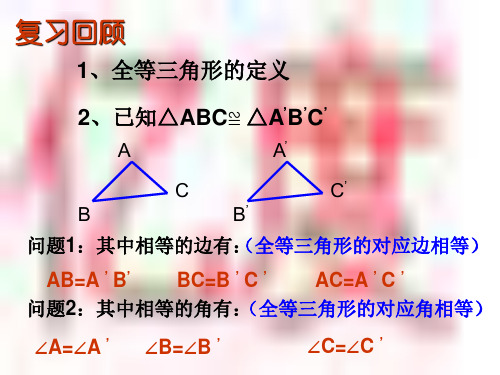
1
1、 全等三角形的定义
能够完全重合的两个三角形叫全等三角形。
2、 全等三角形有什么性质?
A
D
B
C
E
F
如图,已知△ABC≌△DEF
问题1:其中相等的边有: AB=DE, BC=EF, AC=DF (全等三角形的对应边相等)
问题2:其中相等的角有: ∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形的对应角相等)2
一边一角 ×
两角
两边
三角
(3)三个条件
三边 两边一角
两角一边
10
300
500
300
500
11
满足下列条件的两个三角形是一定否全等:
(1)一个条件
× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
(2)两个条件
一边一角 × 两角 ×
两边
三角
(3)三个条件
三边 两边一角
两角一边
12
8cm
表
达
BC=EF
呢 ∴△ABC≌△DEF(SSS)
?
20
判断两个三角形全等的推理过程,叫做证明三角形 全等。
例1 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC
证明:在△ABC和△ADC中 A
AB=AD ( 已知 )
B
D
BC=CD (已知 )
AC= AC (公共边 )
∴ △ABC ≌ △ADC(SSS) C
8cm
13
满足下列条件的两个三角形是一定否全等:
(1)一个条件 (2)两个条件
× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
× 一边一角
只有两个条件对应相
两角
× 等的两个三角形不一
两边
× 定全等。
(3)三个条件
三角 三边
两边一角
两角一边
14
65度
35度
80度
65度
35度
80度
15
满足下列条件的两个三角形是一定否全等:
(1)一个条件
× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
(2)两个条件
一边一角
两角 两边
三角
(3)三个条件
三边 两边一角
两角一边
8
300 9cm
300 9cm
9
满足下列条件的两个三角形是一定否全等:
(1)一个条件
× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
(2)两个条件
(1)一个条件 一边 一角
一边一角 (2)两个条件 两角
两边
三角
(3)三个条件 三边 两边一角
两角一边
4
8cm
8cm
5
满足下列条件的两个三角形是否一定全等:
一边 (1)一个条件
×
一角
(2)两个条件
一边一角 两角
两边
三角
(3)三个条件 三边 两边一角
两角一边
6
400
400
7
满足下列条件的两个三角形是一定否全等:
想一想
3.在△ABC 与△A'B'C'中,若AB=A'B',
BC=B'C',AC=A`C`,∠A=∠A', ∠B=∠B',
∠C=∠C',那么△ABC 与△A'B'C'全等吗?
具备三条边对应相等,三个角对应相等的两个三角形全等
A
A'
B
C
B'
C'
思考: 要使两个三角形全等,是否一定要六个条件呢?
3
满足下列条件的两个三角形是否一定全等:
21
例2. 如下图,△ABC是一个钢架,
AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD 分证析明::要∵证D是明B△CA中B点D≌, △ACD, 首先要看这两个三角形的三条边 是否对应∴相BD等=。CD.
在△ABD和△ ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD ≌△ ACD(SSS).
