结构化学第七章习题课
《结构化学》(7-10章)习题答案
《结晶学基础》习题答案目录第7章答案----------------------------------------------------------------------1第8章答案---------------------------------------------------------------------12第9章答案---------------------------------------------------------------------20第10章答案------------------------------------------------------------------251《结晶学基础》第七章习题答案7001 单晶:一个晶体能基本上被一个空间点阵的单位矢量所贯穿。
多晶:包含许多颗晶粒,这些晶粒可能为同一品种,也可能不同品种,由于各晶粒在空间取向可能不同,不能被同一点阵的单位矢量贯穿。
7002 (D) 7004 简单立方; Cs +和Cl -; 4C 37005 (1) 立方F (2) A 和 B (3) 4 个 (4) 4 组 (5) 3a (6) a /2 7007 4n 个 A, 8n 个 B, n 为自然数。
7010 d 111= 249 pm ; d 211= 176 pm ; d 100= 432 pm 7011 六方; D 3h 70127013 依次为立方,四方,四方,正交,六方。
7014 立方 P ,立方 I ,立方 F ; 四方 P ,四方 I 。
7015 旋转轴,镜面,对称中心,反轴; 旋转轴,镜面,对称中心,反轴,点阵,螺旋轴,滑移面;n =1,2,3,4,6; 32个; 七个晶系; 14种空间点阵型式; 230个空间群。
7016 (1) 四方晶系 (2) 四方 I (3) D 4 (4) a =b ≠c , α=β=γ=90° 7017 (1) 单斜晶系,单斜 P (2) C 2h (3) C 2, m , i 7018 (2a ,3b ,c ):(326); (a ,b ,c ):(111); (6a ,3b ,3c ):(122); (2a ,-3b ,-3c ):(322)。
《结构化学》(7-10章)习题
《结晶学基础》习题目录第7章------------------------------------------------------------------------------1第8章----------------------------------------------------------------------------14第9章----------------------------------------------------------------------------20第10章--------------------------------------------------------------------------28《结晶学基础》第七章习题7002 有一AB晶胞,其中A和B原子的分数坐标为A(0,0,0),B(1/2,1/2,1/2),属于:------------------------------------ ( )(A) 立方体心点阵(B) 立方面心点阵(C) 立方底心点阵(D) 立方简单点阵7004 从CsCl 晶体中能抽出________点阵,结构基元是________,所属晶系的特征对称元素是________。
7014 属于立方晶系的点阵类型有________________,属于四方晶系的点阵类型有____________。
7015 晶体宏观外形中的对称元素可有________,________,________,______四种类型;晶体微观结构中的对称元素可有________,________,________,________,________,________,______七种类型;晶体中对称轴的轴次(n)受晶体点阵结构的制约,仅限于n=_________;晶体宏观外形中的对称元素进行一切可能的组合,可得________个晶体学点群;分属于________个晶系,这些晶系总共有________种空间点阵型式,晶体微观结构中的对称元素组合可得________个空间群。
结构化学答案 chapter7

第七章 过渡金属化合物1. 对于四方配位场(7.1.1), 当点电荷与中心的距离不等, 但符合|±x |<|±y |时, 则中心原子的p 轨道和d 轨道的能级图7.3(a )及(b )将发生什么变化? 请根据你的直觉和简单分析做出最合理的判断, 画出能级图.解:当点电荷距中心距离不等时, 将导致在正四方配位场下的二维不可约表示进一步分裂为两个一维不可约表示,即 p x , p y , 和 d xz , d yz 轨道进一步分裂.若|±x |<|±y |, 则p x 将比p y 感受道更强的来至点电荷的排斥作用, 从而导致p x 能量高于p y .d xz , d yz 轨道的能量也将发生分裂, 但是由于点电荷不在轨道的最大值方向, 感受的排斥相对于p x , p y 要小. 故能级的分裂值较小, d xz 较高, d yz 较低. 能级图如下:2. 反式四配位配合物 t -MA 2B 2, 如[P t C l 2B r 2]2-及P t (NH 3)2B r 2的几何对称性为D 2h ,请以[P t C l 2B r 2]2-为对象, 给出其中的八个对称操作, 并将中心原子的原子轨道:{s , p x ,p y ,p z ,d z 2, d x 2-y 2,d xy ,d xz ,d yz }按D 2h 不可约表示分类;若按D 2h 的子群D 2分类, 结果又如何?(提示:参考特征标表)解:D 2h 的八个对称操作为 I, C 2(x ), C 2(y ), C 2(z ), i , σ(xy ), σ(yz ), σ(zx ). 特征标表为:s 轨道在所有对称操作下不变, 属于全对称表示A g .p x 轨道在I,C 2(x ), σ(xy ), σ(zx )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 1u .p y 轨道在I,C 2(y ), σ(xy ), σ(yz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于p xp yp z原子p x , p y , p zdx 2-y 2dxz dz2原子ddxydyzB 2u ;p z 轨道在I, C 2(z ), σ(xz ), σ(yz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 2u ;d z 2, d x 2-y 2轨道在在所有对称操作下不变, 属于全对称表示A g ;d xy 轨道在I,C 2(z ), i ,σ(xy )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 3g ;d xz 轨道在I,C 2(y ),i , σ(xz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 2g ; d yz 轨道在I,C 2(x ),i , σ(yz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 1g .若按D 2群分类, 所有不可约表示将不再按对称性分为 “g ” 和 “u ”, 其它与群D 2h 下的结果相同.3. 顺式四配位配合物c -MA2B2也是平面构型, 它属于什么点群? 请将中心原子的9个价原子轨道按这一点群分类. 解: 平面构型的顺式四配位配合物c -MA2B2属于C 2v 点群.本题可以采用上题同样的分析方法得到各原子轨道所属的不可约表示, 也可参见表5.1所给出的每一个不可约表示的基函数的性质, 直接得到分类结果: s , p z , d z 2, d x 2-y 2属于A 1; d xy 属于A 2; p x , d xz 属于B 1; p y , d yz 属于B 2.4. 请应用中心原子轨道为基的旋转操作的特征标公式(7-10)式,检验表7.2所列特征标数值是否正确无误; 然后由(4-40)式求出各原子轨函(l =0,1,2,3,4)在O h 配位场的约化(分裂)结果.解:根据(7-10)式, 角量子数为l 的原子轨道在绕z 轴旋转角度a 的旋转操作作用下, 特征标为:2s i n)21s i n ()(αααχ+=l ls 轨道, l =0, 12sin 21sin2sin)210sin()(==+=αααααχl,即对于所有不可约表示,特征表皆为1.p 轨道, l =1, 2sin23sin 2sin)211sin()(αααααχ=+=l所以, 321cos2123cos 23lim 21sin23sinlim)(00=⋅⋅=⋅⋅=→→ααααχααI l12121s i n2123s i n)(,03221s i n3223s i n)(,12s i n 23s i n )(432====-==ππχππχππχC C C l l l,说明表7.2中关于s , p 的两行特征标的值是正确的. 关于d , f , g 的特征标的计算过程略. 下面以f 轨道为例, 求解其在O h 群下的分裂.由于f 轨道属于 “u ”类, 所分裂出的不可约表示也将属于“u ”类,)]1(13)1(16)1(16118711[241)()(24111=-⨯⨯+-⨯⨯+-⨯⨯+⨯⨯+⨯⨯==∑R R n l RA Auuχχ1)]1(13)1()1(6)1()1(6118711[241)()(24122=-⨯⨯+-⨯-⨯+-⨯-⨯+⨯⨯+⨯⨯==∑R R n l R A Auuχχ)]1(23)1(06)1(061)1(8721[241)()(241=-⨯⨯+-⨯⨯+-⨯⨯+⨯-⨯+⨯⨯==∑R R n l RE E uuχχ1)]1()1(3)1(16)1()1(6108731[241)()(24111=-⨯-⨯+-⨯⨯+-⨯-⨯+⨯⨯+⨯⨯==∑R R n l RT Tuuχχ1)]1()1(3)1()1(6)1(16108731[241)()(24122=-⨯-⨯+-⨯-⨯+-⨯⨯+⨯⨯+⨯⨯==∑R R n l RT Tuuχχ所以f 分裂为A 2u +T 1u +T 2u .同样方法可以计算s , p , d , g 在O h 群下的分裂情况.5. 在四方配位场中, 中心原子能级(l =0, 1, 2, 3)将按D 4h 群的不可约表示类别约化(分裂)为s =a 1g , p =a 2u +e ud =a 1g +b 1g +b 2g +e g ,f =b 1u +a 2u +b 2u +2e u请按子群D 4计算各类旋转操作的特征标,证明以上结果.(提示:根据D 4h 及D 4特征标表, 仿照题4的计算处理.)解:s , p , d , f 轨道在D 4下的特征标利用(7-10)式计算得到:在D 4中约化得,Γ(s ) =a 1, Γ (p )=a 2+eΓ (d )=a 1+b 1+b 2+e , Γ (f )=b 1+a 2+b 2+2e在D 4h 中考虑原子轨道的 “g ”, “u ”对称性得:Γ (s )= a 1g , Γ (p )= a 2u +e uΓ (d )= a 1g +b 1g +b 2g +e g , Γ (f )= b 1u +a 2u +b 2u +2e u6. 当八面体场很强时, 单电子态(轨函)需按O h 群不可约表示分类, 请问组态 s 2, s 1p 1及p 2应如何表示, 相应的谱项是什么?解: 首先根据表7.2中所列s , p 轨道的特征标求出上述直积表示的O 群各操作的特征标为.再利用O 群的特征标表造出投影算符, 计算上述可约表示的约化结果. 最后得到,Γ(s2)=A1, Γ(s1p1)=T1, Γ(p2)=A1+T1+T2根据s, p轨道的“g”, “u”对称性, 再利用对称性, g×g=g, g×u=u, u×u=g, 就得到在O h 群下的约化结果:Γ(s2)=A1g, Γ(s1p1)=T1u, Γ(p2)=A1g+T1g+T2g7.[VC l6]2-的光谱吸收位置在13800c m-1, [VF6]2-的吸收峰在20120c m-1,请根据配位场理论指认它们属于何种谱项之间的跃迁: 2S+1Γ(基态)→ 2S+1Γ(激发态); 并计算出相应的∆值. 解: [VC l6]2-和[VF6]2-中, 中心原子V的d电子组态为3d1, 基态的对称性属于2t2g,激发态为2e, 光谱项反映从2t2g到2e g的跃迁.g由于上述体系中只有一个d电子,计算组态能量时不涉及库仑积分J和交换积分K, ∆值就是吸收光谱的光子能量: [VC l6]2- ∆值为13800c m-1, [VF6]2- ∆值为20120c m-1.8.正八面体三价钒配离子在可见紫外区有两个吸收峰,数据收集如下(单位:c m-1)[V(CN)6]3-22 200, 28 600;[V(NCS)6]3-16 700, 24 000;[VF6]3-14 800, 23 000;[VC l6]3-11 200, 18 020;请根据弱场方案指认, 求出∆, 排出光谱化学序列; 若采用强场方案, 指认应作何种变动? 解: 上述体系中心原子V的d的组态为d2, 基态谱相为3T1g,, 可见光区的低能量谱带属于3T→3T2g跃迁. 根据弱场方案, 3T1g,3T2g的谱项能量(在表7.4中给出), 以∆为单位分别为1g(-3/5, 1/5), 故上述体系的∆值为低能量谱带的能量乘以(5/4). 分别计算为:[V(CN)6]3-27 750;[V(NCS)6]3-20 870;[VF6]3-18 500;[VC l6]3-14 000.光谱序列为CN- > NC S> F-> C l-.若按强场方案, 3T1g,3T2g的谱项能量能量差即为∆.无需乘以系数(5/4), 所指认光谱化学序列不变.9.请按弱场方案(表7.4和图7.6( c)) ,指认下列光谱数据(单位:c m-1, 求出∆, 排出光谱化学序列.[V(H2O)]2+12 350, 18 500; [V(NCS)6]4-15 500, 22 000; [VC l6]4-7 200, 12 000; [V(NH3)6]2+14 800, 21200; [V(CN)6]4-22 300, 27 700.解:上述体系中心原子V的d的组态为d3, 基态谱相为4A2g,, 可见光区的低能量谱带属于4A→4T2g跃迁. 根据弱场方案, 4A2g,4T2g的谱项能量(在表7.4中给出), 以∆为单位分别2g为(-6/5, -2/5), 故上述体系的∆值为低能量谱带的能量乘以(5/4). 分别计算为:[V(H2O)]2+15 438; [V(NCS)6]4-19 375; [VC l6]4-9 000;[V(NH3)6]2+18 500; [V(CN)6]4-27 875.光谱序列为: CN- > NCS-> NH3 > H2O > C l-.10.请根据7.3.3的简单方法, 求出d5八面体配合物的高自旋和低自旋的能量差. 已知[F e(H2O)6]3+是高自旋, 你能否确定[F e(CN)6]3-究竟是高自旋还是低自旋?解: d5八面体配合物的高自旋组态为(t2g3e g2), 低自旋组态为(t2g5),E(t2g3e g2)=5E0+3(-2/5)∆+2(3/5)∆+10J-10K=5 E0+10J-10KE(t 2g 5)=5E 0+5(-2/5)∆ +10J -4K=5 E 0- 2∆ +10J -4K 两者能量差为E(t 2g 3e g 2) - E(t 2g 5)=2 ∆-6K.由于CN -在光谱化学序列中排在H 2O 的前面, [F e (CN)6]3-的∆要比[F e (H 2O)6]3+的大, 故如果[F e (H 2O)6]3+是高自旋, 则[F e (CN)6]3-一定是高自旋.11. 请通过你的计算, 检验表7.8的d 6与d 7八面体配合物的高自旋和低自旋能量即δ表示式. 解: d 6八面体配合物的高自旋组态为(t 2g 4e g 2), 低自旋组态为(t 2g 6),E(t 2g 4e g 2)=6E 0+4(-2/5)∆+2(3/5)∆+15J -10K=6 E 0-( 2/5) ∆ +15J -10K E(t 2g 6)=6E 0+6(-2/5)∆ +10J -6K=6 E 0-(12/5)∆ +15J -6K两者能量差为E(t 2g 4e g 2) - E(t 2g 6)=2 ∆-4K. d 7八面体配合物的高自旋组态为(t 2g 5e g 2), 低自旋组态为(t 2g 6 e g 1),E(t 2g 5e g 2)=7E 0+5(-2/5)∆+2(3/5)∆+21J -11K=7 E 0-(4/5) ∆ +21J -11K E(t 2g 6 e g 1)=7E 0+6(-2/5)∆ +(3/5)∆+21J -9K=7 E 0-(9/5)∆ +21J -9K 两者能量差为E(t 2g 4e g 2) - E(t 2g 6)= ∆-2K.12. 五配位配合物有两种稳定几何构型(图7.11(a )与(b)), 请根据图7.10中D 3h 和C 4v 能级模式讨论d 6离子为高自旋或低自旋的可能性.解: 由图7.10中所示的d 轨道在D 3h 和C 4v 下的能级分裂的情况容易判断, 在具有D 3h 对称性的双三角锥型配合物种d 6离子为高自旋, 而具有C 4v 对称性的四方锥型配合物种d 6离子为低自旋. 轨道电子填充情况如图所示:13. 在八面体配离子的J ahn -T eller 形变(O h -D 4h )中, 试简单地采用能级图7.12来分析预测, [VC l 6]2- (d 1), [VC l 6]3- (d 2), 和 [C r C l 6]4- (d 4) 的形变模式: 拉长还是压扁? 解:[VC l 6]2- (d 1) 根据图7.12, 若实现拉长形变, 一个电子填充在能量最低的e g 能级上, 总能量降低δ1/3; 若实现压扁形变, 一个电子填充在能量最低的b 2g 能级上总能量降低2δ1/3.从能量的角度看, 应当是压扁形变.[VC l 6]3-(d 2) 若实现拉长形变, 2个电子填充在能量最低的e g 能级上, 总能量降低2δ1/3; 若实现压扁形变, 2个电子填充在能量最低的b 2g 能级上总能量降低4δ1/3.从能量的角度看, 应当是压扁形变. 而且, 若实现拉长形变, 两个填充在能量最低的e g 能级上, 两个电子当取自旋相同的构型, 这样的体系仍是不稳定的还会发生畸变.[C r C l 6]4- (d 4) 若实现拉长形变, 4个电子填充在能量最低的e g 能级上, 总能量降低4δ1/3; 若实现压扁形变, 2个电子填充在能量最低的b 2g 能级上, 另2个电子填充在e g 能级上, 两者的能量升高与降低相抵, 总能量降低2δ1/3. 从能量的角度看, 应当是拉长形变.D3hC 4v14. 按照分子轨道的观点, 正八面体配离子的价电子数等于12+n, n为d电子数. 试由能级图7.15给出[VC l6]2- , [VC l6]3- , [C r C l6]4- , [F e(CN)6]3-,[C o(NH3)6]3+ ,[C o(CN)6]4-, [Ni(H2O)6]2+的基组态.解: 根据能级图7.15,所给出的能级序列, 计算出价电子数后, 可以直接得到基组态.现计算如下:n价电子数基组态[VC l6]2- 1 13 (a1g)2(t1u)6(e g)4(t2g)1[VC l6]3- 2 14 (a1g)2(t1u)6(e g)4(t2g)2[C r C l6]4- 4 16 (a1g)2(t1u)6(e g)4(t2g)4[F e(CN)6]3- 5 17 (a1g)2(t1u)6(e g)4(t2g)5[C o(NH3)6]3+ 6 18 (a1g)2(t1u)6(e g)4(t2g)6[C o(CN)6]4-7 19 (a1g)2(t1u)6(e g)4(t2g)6(e g*)1[Ni(H2O)6]2+ 8 20 (a1g)2(t1u)6(e g)4(t2g)6(e g*)215. 在正八面体配合物的能级序列(图7.15)中, t2g是非键轨道, e g*也可以近似看作非键(d z2,d x2-y2)分子轨道,因此, t2g→e g*的电子跃迁属于中心原子d→d跃迁, 不会伴随M,L之间的电荷转移;但下列跃迁: t2g→a1g*, e g*→t1u*以及e g→t2g, t1u→t2g将伴随电荷转移. 请分别指出它们之中那些属于M→L转移, 那些属于L→M的转移.解:判断电荷跃迁的方向主要根据所涉及的两个分子轨道的组成成分来判断.t2g, e g*是非键轨道, 基本由中心原子的d轨道组成. 电子由它们向其它分子轨道跃迁, 将导致M→L转移, 如t2g→a1g*, e g*→t1u*;t1u, e g是成键轨道,主要由配体原子的轨道组成. 电子由它们向其它分子轨道跃迁, 将导致L→M的转移. 如e g→t2g, t1u→t2g.16.请列举出10个单核配合物满足18电子规则, 再举出5个反例,它们均具有稳定的闭壳组态,表现为反磁性.解:满足18电子规则的例子有:[C o(NH3)6]3+,[C o(H2O)6]3+,[C o(CN)6]3-,[Zn(NH3)4]2+[F e(CN)6]4-,[F e(NCS)6]4-F e(CO)5, Ni(CO)4, F e(C5H5)2, C r(C6H6)2.不满足18电子规则的例子有:[Ni(C5H5N)4]2+, [Cu(NH3)4]2+,17.对于正四面体配合物ML4, [TiC l4, [NiC l4]2-等, 请通过群论方法,造出能级图; 指出与CH4的区别何在?解: 四个配体的轨道在T d群下分解为A1+T2, 若将四个配体原子按图5.7的CH4分子中的H原子的位置放置于立方体的相对的四个顶点, 中心原子按C原子的位置放置于立方体的中心. 造出配体的群轨道同5-8b式,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛------=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛d c b a zy z t t t a 212121212121212121212121212121212221φφφφ中心原子的轨道按对称性分类为s 属于A 1, p 属于T 2, d z 2, d x 2-y 2属于E, d xy ,d yz ,d xz 属于T 2.上述中心原子的轨道按对称性与配体原子的群轨道组合成分子轨道 能级示意图为:与CH 4相比, 中心原子除了s , p 轨道外, 还有d 轨道参加成键. HOMO -LUMO 的能隙变得很小. 从而导致可见光区的吸收光谱带的出现.配体轨道中心离子轨道配合物分子轨道3t。
江元生《结构化学》课后习题答案

第一章 量子理论1. 说明⎥⎦⎤⎢⎣⎡-=) (2cos ),(0t x a t x a νλπ及⎥⎦⎤⎢⎣⎡-=) (2sin ),(0t x a t x a νλπ都是波动方程22222),(1),(t t x a c x t x a ∂∂=∂∂的解。
提示:将),(t x a 代入方程式两端,经过运算后,视其是否相同。
解:利用三角函数的微分公式)cos()sin(ax a ax x=∂∂和)sin()cos(ax a ax x -=∂∂,将⎥⎦⎤⎢⎣⎡-=) (2c o s ),(0t x a t x a νλπ代入方程:⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡--∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-∂∂∂∂=⎥⎦⎤⎢⎣⎡-∂∂=) (2cos 2 ) (2sin 2 ) (2cos ) (2cos 2000022t x a t x x a t x x x a t x a x νλπλπνλπλπνλπνλπ左边 ()⎥⎦⎤⎢⎣⎡--=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡-∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-∂∂∂∂=⎥⎦⎤⎢⎣⎡-∂∂=) (2cos 2 ) (2sin 2 ) (2cos ) (2cos 122020200222t x c a t x x c a t x t t c a t x a t c νλππννλππννλπνλπ右边 对于电磁波νλ=c ,所以⎥⎦⎤⎢⎣⎡-=) (2cos ),(0t x a t x a νλπ是波动方程的一个解。
对于⎥⎦⎤⎢⎣⎡-=) (2sin ),(0t x a t x a νλπ,可以通过类似的计算而加以证明:⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡-∂∂=) (2sin 2) (2sin 20022t x a t x a x νλπλπνλπ左边()⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-∂∂=) (2sin 2) (2sin 12200222t x c a t x a t c νλππννλπ右边2. 试根据Planck 黑体辐射公式,推证Stefan 定律:4 T I σ=,给出σ的表示式,并计算它的数值。
结构化学习题

1.在八面体配位场中,3d 轨道分裂成几组( A)二组;(B)三组;( C)四组;( D)五组。
2.在弱八面体场中,拥有最大的配位场稳固化能的是以下的哪一个( A) d1( B) d2( C) d3( D) d43.配离子 [Mn(CN) 6]4-中 d 能级分裂状况可由以下哪一种实验测得( A)核磁共振( B)顺磁共振(C)红外光谱( D)电子能谱4.在正四周体配位场中, d 轨道将分裂成几组(A) 1(B)2(C)3(D)45.在八面体配合物中,拥有以下的哪一种电子组态的配合物可能是发生大的畸变( A) t2g5g2(B) t 2g4g2( C) t2g6g3(D) t2g4e e e[Fe( CN)6] 的磁性是以下的哪一种( A)反磁性(B)顺磁性(C)铁磁性(D)反铁磁性7.四周体配合物大多拥有以下那种性质( A)低自旋(B)高自旋(C)反旋(D)铁旋8.在正方形配合物中,若四个配位体分别位于X 轴 Y 轴上,则最高能级的 d 轨道是()。
(A) d xz( B) d z2( C) d xy( D) d x2-y29.关于配位体CN-和 F-各自形成的配位场的强弱比较结果,以下哪一种说法正确( A) CN-强于F-( B) F-强于CN-(C)同样( D)没法判断10.配位场理论是理论的发展,其本质是。
答案 :10.略第七章晶体学基础1.关于晶体的空间构造点阵型式的种类,以下哪一种说法是正确的(A)7种1. 在八面体配位场中, 3d 轨道分裂成几组? ( A )二组;( B )三组;( C )四组;( D )五组。
2. 在弱八面体场中,拥有最大的配位场稳固化能的是以下的哪一个? ( A ) d 1 ( B ) d 2 ( C ) d 3 ( D )d 43. 配离子 [Mn(CN) 6] 4- 中 d 能级分裂状况可由以下哪一种实验测得? ( A )核磁共振 (B )顺磁共振( C )红外光谱 ( D )电子能谱4. 在正四周体配位场中, d 轨道将分裂成几组?(A ) 1(B )2(C )3(D )45. 在八面体配合物中,拥有以下的哪一种电子组态的配合物可能是发生大的畸变? 5242634( A ) t 2g e g (B )t 2g e g (C ) t 2g e g ( D )t 2g6.K 4[Fe ( CN ) 6] 的磁性是以下的哪一种? ( A )反磁性( B )顺磁性( C )铁磁性( D )反铁磁性7. 四周体配合物大多拥有以下那种性质?( A )低自旋 ( B )高自旋 ( C )反旋 8. 在正方形配合物中,若四个配位体分别位于X 轴( D )铁旋Y 轴上,则最高能级的d 轨道是()。
北师大-结构化学课后习题答案

北师大 结构化学 课后习题 第一章 量子理论基础习题答案1 什么是物质波和它的统计解释?参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言,衍射强度(即波的强度)大的地方,粒子出现的数目就多,而衍射强度小的地方,粒子出现的数目就少。
对一个粒子而言,通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子,在相同的条件下重复多次相同的实验,一定会在衍射强度大的地方出现的机会多,在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释,对于单个粒子,ψψ=ψ*2代表粒子的几率密度,在时刻t ,空间q 点附近体积元τd 内粒子的几率应为τd 2ψ;在整个空间找到一个粒子的几率应为 12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件? 参考答案合格波函数的基本条件是单值,连续和平方可积。
由于波函数2ψ代表概率密度的物理意义,所以就要求描述微观粒子运动状态的波函数首先必须是单值的,因为只有当波函数ψ在空间每一点只有一个值时,才能保证概率密度的单值性;至于连续的要求是由于粒子运动状态要符合Schrödinger 方程,该方程是二阶方程,就要求波函数具有连续性的特点;平方可积的是因为在整个空间中发现粒子的概率一定是100%,所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理? 参考答案在经典理论中,一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份(如各种不同的波长和频率)。
而在量子力学中,按波函数的统计解释,态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加,使粒子部分地处于Q 1状态,部分地处于Q 2态,……。
各种态都有自己的权重(即成份)。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么? 参考答案根源就在于微观粒子的波粒二象性。
结构化学第七章习题

第七章一选择题1、KCl属于NaCl型晶体,一个晶胞中含( c )个K+ 。
A、 1B、2C、 4D、 62、CH4属于下列哪类分子点群:( a )A、TdB、D ohC、C3vD、C S3、晶包一定是一个:( c )A、八面体B、六方柱体C、平行六面体D、正方体4、(312)晶面在 a,b,c 轴上的截距分别为( c ):A、3a, b, 2cB、3a, 6b, 2cC、2a, 6b, 3cD、3a, b, c5、空间点阵中下列形式不存在的是( b )。
A 立方IB 四方C C 四方ID 正交C6、假设有一AB晶体,属于正交底心,每个晶胞中有两个A原子和2个B原子,若A原子的坐标是(000),(1/2 1/2 0),一个B原子的坐标是(1/4 1/4 1/2),则另一个B原子的分数坐标应是( d )。
A (1/2 1/2 0)B (1/2 0 1/2)C (1/2 1/2 1/2)D (3/4 3/4 1/2)7、根据正当单位选取原则,下列各组平面格子属于正当格子的组是( c)。
(1) 正方及其带心格子 (2) 六方及其带心格子(3) 平行四边行及其带心格子 (4) 矩形及其带心格子A (1)(3)(4)B (1)(2)(4) C(4) D(1)(3)8、下列说法正确的是( b ).A. 凡是八面体配合物,一定属于O h点群.B. 异核双原子分子一定没有对称中心.C. 凡是四面体构型分子,一定属于T d点群.D. 在分子点群中,对称性最低的是C1, 对称性最高的是O h群9、 空间点阵中下列形式不存在的是( b )A. 立方IB. 四方CC. 四方ID. 正交C10、 有一AB4型晶体,属立方晶系,每个晶胞中有一个A和四个B,一个A的坐标是(,,),四个B的坐标分别是(0,0,0),(,,0),(,0,),(0,,),此晶体的点阵形式是( b )A.立方IB.立方PC. 立方FD. 立方C11、已知配合物MA4B2的中心原子M是d2SP3杂化,该分子有2种构造异构体,这些异构体分别属于的点群是( a )A. B. C. D.12. 下列哪一种表述是正确的:(A )A. 各向异性是晶体区别于非晶体的一种特性.B. 各向同性是晶体区别于非晶体的一种特性.C. 晶体的所有性质都是各向异性的.13. 晶胞的两个基本要素是 (A )A. 晶胞的大小、形状及晶胞中原子的位置.B. 晶胞的质量及结构基元数目.C. 晶胞中原子的数目及位置.14. 由正当晶胞抽象出的格子必然是 ( A ) A.对称性最高. B.包含点阵点最少. C.正方体格15. 素晶胞是 ( B )A. 只包含一个原子的晶胞.B. 只包含一个结构基元的晶胞.C. 只有一种宏观对称元素的晶胞.16. 一个点阵点必然对应着晶体中的一个 ( C )A.原子B.分子C. 结构基元17. 点阵是: ( B )A.按连接其中任意两点的向量平移而能复原的有限个点.B.按连接其中任意两点的向量平移而能复原的无限多个点.C.按连接其中某些特定点的向量平移而能复原的无限多个点.18. 干冰是CO2的晶体,其中不被周期性相联系的是 ( C )A.一个结构基元与另一个结构基元.B.一个晶胞与另一个晶胞.C.CO2分子中的一个原子与另一个原子.19 . 对于金刚石与立方硫化锌,下列哪种说法是不正确的:( C )A.它们的点阵型式都是立方面心.B.它们的结构基元都包含两个原子(或离子).C.它们的结构基元内容相同.20. MgS(NaCl型)与UO2(CaF2型)晶体的不同之处是: ( B )A.正当格子形状.B.负离子堆积方式.C.点阵型式.21 . 正、负离子配位比为8:8的是下列哪一种晶体: ( A )A.CsClB.NaClC.立方ZnS22 . CeO2晶体结构属CaF2型.对于这种晶体,“简单立方”一词描述的是 ( A )A.氧负离子堆积方式.B.铈正离子堆积方式.C.点阵型式23. 有人把CaF2晶体的点阵型式误认为是点阵点处于负离子位置的立方简单点阵,错误之处就在于 ( B )A.立方简单本身违反点阵定义.B.这种立方简单无法使CaF2晶体复原.C.这样的立方简单格子比CaF2正当晶胞还要大.24. 当我们说某种离子晶体AB属于CsCl型时,意思是说 ( B )A.它由Cs和Cl两种元素组成.B.它的结构型式与CsCl晶体相同.C.它的结构基元与CsCl晶体相同.25. 布拉维格子有多少种: ( A )A. 14B. 7C. 3226. 计算立方ZnS正当晶胞中正、负离子总数的算式是: ( A )A. (1/8) ×8 +(1/2) ×6 +4B. (1/8) ×8 +(1/2) ×6C. 8 + 6 + 427. 在A1(立方面心)、A2(立方体心)、A4(金刚石型)三种金属结构中,晶胞边长与原子半径分别与下列三个关系式相符合的是: ( B )A. A1 A2 A4 B. A2 A1 A4 C. A4 A1 A228. 从点阵中一个指定的原点到点阵点mnp之间的向量为平移群T mnp=ma+nb+pc(m、n、p为整数) ,这两点之间的波程差为 ( A )A. Δ=(mh+nk+pl)λB. Δ=(m+n+p) λC. Δ=(hx+ky+lz) λ (x、y、z为分数)29. 金单晶为 A1型结构(立方面心),每个正当晶胞中原子数、 八面体空隙数、四面体空隙数分别为: ( C )A. 1、1、2B. 2、2、4C. 4、4、830. KBr晶体具有立方面心点阵,负离子形成立方最密堆积,其中的正八面体空隙全部被正离子占据.其结构型式为: ( A )A.NaCl型B.CsCl型C. 立方ZnS型31. 立方体心点阵的系统消光规律是: ( A )A. h+k+l=奇数B. h+k+l=偶数C. h、k、l奇偶混杂32. 立方底心格子不存在,是由于这种格子 ( B )A.可化为立方体心.B.破坏了立方晶系的特征对称要素.C.违反了点阵定义33. 对于二元离子晶体,下列哪一式不成立: ( C )A.n+/n-=Z-/Z+B.n-/n+= CN+/CN-C.Z-/Z+=CN+/CN-34. HMO理论适用于处理哪一种体系: ( B )A.σ体系B. π体系C. σ+π体系35. 轨道对称守恒原理表明,在加热条件下发生顺旋电环化反应的共轭烯烃衍生物具有的π电子数为 ( A )A. 4n.B. 4n+2.C. 5n+1.36. 六方晶系的晶胞形状是 ( C )A.六棱柱.B.六个顶点的八面体.C.α=β=90o,γ=120o的平行六面体37. 晶面与x、y、z轴分别相截于2、3、4,其晶面指标为 ( C )A.(234)B. (432)C. (643)38. 通过晶胞原点与晶胞中第j个原子(坐标为x j、y j、z j)的波程差为 (A )A. Δ= (hx j+ky j+lz j)λB. Δ= (ax j+by j+cz j)λC. Δ= (x j+y j+z j)λ39. 由布拉格(Bragg)方程可知,衍射级数n是 ( A )A.数目有限的几个正整数.B.数目无限的一系列正整数.C.数目有限的、介于0至1之间的几个分数.40. A1与A3金属晶体在哪方面不同: ( C )A.配位数.B. 空间占有率.C.点阵型式.41. 离子晶体中正离子配位数CN+等于6时, 离子半径比(r+/r-)的理论值应是A. 0.225≤(r+/r-)<0.414B. 0.414≤(r+/r-)<0.732C. 0.732≤(r+/r-)<1.00042、与C轴垂直的晶面的晶面指标是(d )(A)(112) (B)(100) (C)(010) (D)(001)43、反式二氯乙烯所属点群为( c )(A)C3 (B)D3d (C)C2h (D)C2v44. 下列哪种物质最不可能是晶体(B)A.金刚石 B.琥珀 C.食盐粉末45. 晶系和晶体学点群各有多少种? (A)A. 7种晶系, 32种晶体学点群B. 14种晶系, 32种晶体学点群C. 7种晶系, 14种晶体学点群46. 下列哪一式是晶体结构的代数表示——平移群:(A)A. T mnp=ma+nb+pc (m,n,p,=0,±1, ±2,……)B. r = xa+yb+zc x,y,z是零或小于1的分数C.Δ=(mh+nk+pl)λ m, n, p和 h, k, l均为整数47. 下列哪一种说法是错误的:(B)A. 属于同一晶系的晶体,可能分别属于不同的晶体学点群B. 属于同一晶体学点群的晶体,可能分别属于不同的晶系C. 属于同一晶体学点群的晶体,可能分别属于不同的空间群48. 某平面点阵在坐标轴x,y,z上的截数为3,3,5,则平面点阵指标(晶面指标)为(C)A. (335)B. (353)C.(553)49. Bragg方程中的正整数n的物理意义是(A)A.相邻平面点阵衍射波程差的波数B.晶胞中结构基元的数目C.晶胞中原子的数目50. 立方ZnS和六方ZnS晶体的CN+/CN-都是4:4,那么,它们在下列哪一点上不同?(C)A. 正离子所占空隙种类B. 正离子所占空隙分数C. 负离子堆积方式51. 为了区分素格子与复格子,空间格子中的每个顶点、棱心、面心只分别算作(B)A. 1, 1, 1B. 1/8, 1/4, 1/2C. 1, 1/2, 1/452. CuZn合金(即β黄铜)中两种金属原子的分数坐标分别为0,0,0和1/2,1/2,1/2。
结构化学课后习题答案

结构化学课后习题答案结构化化学课后习题答案一、化学键与分子结构1. 选择题a) 正确答案:D解析:选择题中,选项D提到了共价键的形成是通过电子的共享,符合共价键的定义。
b) 正确答案:B解析:选择题中,选项B提到了离子键的形成是通过电子的转移,符合离子键的定义。
c) 正确答案:C解析:选择题中,选项C提到了金属键的形成是通过金属原子之间的电子云重叠,符合金属键的定义。
d) 正确答案:A解析:选择题中,选项A提到了氢键的形成是通过氢原子与高电负性原子之间的吸引力,符合氢键的定义。
2. 填空题a) 正确答案:共价键解析:填空题中,根据问题描述,两个非金属原子之间的键称为共价键。
b) 正确答案:离子键解析:填空题中,根据问题描述,一个金属原子将电子转移到一个非金属原子上形成的键称为离子键。
c) 正确答案:金属键解析:填空题中,根据问题描述,金属原子之间的电子云重叠形成的键称为金属键。
d) 正确答案:氢键解析:填空题中,根据问题描述,氢原子与高电负性原子之间的吸引力形成的键称为氢键。
二、有机化学1. 选择题a) 正确答案:C解析:选择题中,选项C提到了烷烃是由碳和氢组成的,符合烷烃的定义。
b) 正确答案:D解析:选择题中,选项D提到了烯烃是由含有一个或多个双键的碳原子组成的,符合烯烃的定义。
c) 正确答案:B解析:选择题中,选项B提到了炔烃是由含有一个或多个三键的碳原子组成的,符合炔烃的定义。
d) 正确答案:A解析:选择题中,选项A提到了芳香烃是由芳香环结构组成的,符合芳香烃的定义。
2. 填空题a) 正确答案:醇解析:填空题中,根据问题描述,含有羟基(-OH)的有机化合物称为醇。
b) 正确答案:醚解析:填空题中,根据问题描述,含有氧原子连接两个碳原子的有机化合物称为醚。
c) 正确答案:酮解析:填空题中,根据问题描述,含有羰基(C=O)的有机化合物称为酮。
d) 正确答案:酯解析:填空题中,根据问题描述,含有羧基(-COO)的有机化合物称为酯。
《结构化学》(1-5章)习题解析

目录第一章--------------------------------------------------------------------------------------------------1 第二章-------------------------------------------------------------------------------------------------14 第三章-------------------------------------------------------------------------------------------------30 第四章-------------------------------------------------------------------------------------------------42 第五章-------------------------------------------------------------------------------------------------48第一章习题1001 首先提出能量量子化假定的科学家是:---------------------------( )(A) Einstein (B) Bohr (C) Schrodinger (D) Planck 1002 光波粒二象性的关系式为_______________________________________。
1003 德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1004 在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1005 求德布罗意波长为0.1 nm 的电子的动量和动能。
结构化学习题

结构化学习题习题类型包括:选择答案、填空、概念辨析、查错改正、填表、计算、利用结构化学原理分析问题;内容涵盖整个课程,即量子力学基础、原子结构、分子结构与化学键、晶体结构与点阵、X射线衍射、金属晶体与离子晶体结构、结构分析原理、结构数据采掘与QSAR等;难度包括容易、中等、较难、难4级;能力层次分为了解、理解、综合应用。
传统形式的习题,通常要求学生在课本所学知识范围内即可完成,而且答案是唯一的,即可以给出所谓“标准答案”。
根据21世纪化学演变的要求,我们希望再给学生一些新型的题目,体现开放性、自主性、答案的多样性,即:习题不仅与课本内容有关,而且还需要查阅少量文献才能完成;完成习题更多地需要学生主动思考,而不是完全跟随教师的思路;习题并不一定有唯一的“标准答案”,而可能具有多样性,每一种答案都可能是“参考答案”。
学生接触这类习题,有助于培养学习的主动性,同时认识到实际问题是复杂的,解决问题可能有多钟途径。
但是,这种题目在基础课中不宜多,只要有代表性即可。
以下各章的名称与《结构化学》多媒体版相同,但习题内容并不完全相同。
第一章量子力学基础1.1 选择题(1) 若用电子束与中子束分别作衍射实验,得到大小相同的环纹,则说明二者(A) 动量相同(B) 动能相同(C) 质量相同(2) 为了写出一个经典力学量对应的量子力学算符,若坐标算符取作坐标本身,动量算符应是(以一维运动为例)(A) mv (B) (C)(3) 若∫|ψ|2dτ=K,利用下列哪个常数乘ψ可以使之归一化:(A) K(B) K2 (C) 1/(4) 丁二烯等共轭分子中π电子的离域化可降低体系的能量,这与简单的一维势阱模型是一致的,因为一维势阱中粒子的能量(A) 反比于势阱长度平方(B) 正比于势阱长度(C) 正比于量子数(5) 对于厄米算符, 下面哪种说法是对的(A) 厄米算符中必然不包含虚数(B) 厄米算符的本征值必定是实数(C) 厄米算符的本征函数中必然不包含虚数(6) 对于算符Ĝ的非本征态Ψ(A) 不可能测量其本征值g.(B) 不可能测量其平均值<g>.(C) 本征值与平均值均可测量,且二者相等(7) 将几个非简并的本征函数进行线形组合,结果(A) 再不是原算符的本征函数(B) 仍是原算符的本征函数,且本征值不变(C) 仍是原算符的本征函数,但本征值改变1.2 辨析下列概念,注意它们是否有相互联系, 尤其要注意它们之间的区别:(1) 算符的线性与厄米性(2) 本征态与非本征态(3) 本征函数与本征值(4) 本征值与平均值(5) 几率密度与几率(6) 波函数的正交性与归一性(7) 简并态与非简并态1.3 原子光谱和分子光谱的谱线总是存在一定的线宽,而且不可能通过仪器技术的改进来使之无限地变窄. 这种现象是什么原因造成的?1.4 几率波的波长与动量成反比. 如何理解这一点?1.5 细菌的大小为微米量级, 而病毒的大小为纳米量级. 试通过计算粗略估计: 为了观察到病毒, 电子显微镜至少需要多高的加速电压.1.6 将一维无限深势阱中粒子的波函数任取几个, 验证它们都是相互正交的.1.7 厄米算符的非简并本征函数相互正交. 简并本征函数虽不一定正交, 但可用数学处理使之正交. 例如,若ψ1与ψ2不正交,可以造出与ψ1正交的新函数ψ’2ψ’2=ψ2+cψ1试推导c的表达式(这种方法称为Schmidt正交化方法).1.8 对于一维无限深势阱中粒子的基态, 计算坐标平均值和动量平均值, 并解释它们的物理意义.1.9 一维无限深势阱中粒子波函数的节点数目随量子数增加而增加. 试解释: 为什么节点越多, 能量越高. 再想一想: 阱中只有一个粒子, 它是如何不穿越节点而出现在每个节点两侧的?1.10 下列哪些函数是d2/dx2的本征函数: (1) e x (2) e2x(3) 5sin x(4) sin x+cos x(5)x3. 求出本征函数的本征值.1.11 对于三维无限深正方形势阱中粒子, 若三个量子数平方和等于9, 简并度是多少?1.12 利用结构化学原理,分析并回答下列问题:纳米粒子属于介观粒子,有些性质与宏观和微观粒子都有所不同. 不过,借用无限深势阱中粒子模型,对纳米材料中的“量子尺寸效应”还是可以作一些定性解释.例如: 为什么半导体中的窄能隙(<3eV)在纳米颗粒中会变宽, 甚至连纳米Ag也会成为绝缘体?第二章原子结构2.1 选择题(1) 对s、p、d、f 原子轨道进行反演操作,可以看出它们的对称性分别是(A) u, g, u, g (B) g, u, g, u (C) g, g, g, g(2) H原子的电离能为13.6 eV, He+的电离能为(A) 13.6 eV (B) 54.4 eV (C) 27.2 eV(3) 原子的轨道角动量绝对值为(A) l(l+1)2(B) (C) l(4) p2组态的原子光谱项为(A) 1D、3P、1S(B) 3D、1P、3S(C) 3D、3P、1D(5) Hund规则适用于下列哪种情况(A) 求出激发组态下的能量最低谱项(B) 求出基组态下的基谱项(C) 在基组态下为谱项的能量排序(6) 配位化合物中d→d跃迁一般都很弱,因为这种跃迁属于:(A) g←/→g(B) g←→u(C) u←/→u(7) Cl原子基态的光谱项为2P,其能量最低的光谱支项为(A) 2P3/2(B) 2P1/2(C) 2P02.2 辨析下列概念,注意它们的相互联系和区别:(1) 复波函数与实波函数(2) 轨道与电子云(3) 轨道的位相与电荷的正负(4) 径向密度函数与径向分布函数(5)原子轨道的角度分布图与界面图(6)空间波函数、自旋波函数与自旋-轨道(7)自旋-轨道与Slater行列式(8)组态与状态2.3 请找出下列叙述中可能包含着的错误,并加以改正:原子轨道(AO)是原子中的单电子波函数,它描述了电子运动的确切轨迹. 原子轨道的正、负号分别代表正、负电荷. 原子轨道的绝对值平方就是化学中广为使用的“电子云”概念,即几率密度. 若将原子轨道乘以任意常数C,电子在每一点出现的可能性就增大到原来的C2倍.2.4(1) 计算节面对应的θ;(2) 计算极大值对应的θ;(3) 在yz平面上画出波函数角度分布图的剖面, 绕z轴旋转一周即成波函数角度分布图. 对照下列所示的轨道界面图,从物理意义和图形特征来说明二者的相似与相异.2.5 氢原子基态的波函数为试计算1/r的平均值,进而计算势能平均值<V>, 验证下列关系:<V> = 2E= -2<T>此即量子力学维里定理,适用于库仑作用下达到平衡的粒子体系(氢原子基态只有一个1s电子,其能量等于体系的能量) 的定态, 对单电子原子和多电子原子具有相同的形式.2.6 R. Mulliken用原子中电子的电离能与电子亲合能的平均值来定义元素电负性. 试从原子中电子最高占有轨道(HOMO)和最低空轨道(LUMO)的角度想一想,这种定义有什么道理?2.7 原子中电子的电离能与电子亲合能之差值的一半, 可以作为元素化学硬度的一种量度(硬度较大的原子,其极化率较低).根据这种定义,化学硬度较大的原子,其HOMO与LUMO之间的能隙应当较大还是较小?2.8 将2p+1与2p-1线性组合得到的2p x与2p y, 是否还有确定的能量和轨道角动量z分量?为什么?2.9 原子的轨道角动量为什么永远不会与外磁场方向z重合, 而是形成一定大小的夹角? 计算f轨道与z轴的所有可能的夹角.为什么每种夹角对应于一个锥面, 而不是一个确定的方向?2.10 快速求出P原子的基谱项.2.11 Ni2+的电子组态为d8, 试用M L表方法写出它的所有谱项, 并确定基谱项. 原子光谱表明, 除基谱项外, 其余谱项的能级顺序是1D<3P<1G<1S, 你是否能用Hund规则预料到这个结果?2.12 d n组态产生的谱项, 其宇称与电子数n无关, 而p n组态产生的谱项, 其宇称与电子数n有关. 为什么?2.13 试写出闭壳层原子Be的Slater行列式.2.14 Pauli原理适用于玻色子和费米子, 为什么说Pauli不相容原理只适用于费米子?第三章双原子分子结构与化学键理论3.1 选择题(1) 用线性变分法求出的分子基态能量比起基态真实能量,只可能(A) 更高或相等(B) 更低(C) 相等(2) N2、O2、F2的键长递增是因为(A) 核外电子数依次减少(B) 键级依次增大(C) 净成键电子数依次减少(3) 下列哪一条属于所谓的“成键三原则”之一:(A) 原子半径相似(B) 对称性匹配(C) 电负性相似(4) 下列哪种说法是正确的(A) 原子轨道只能以同号重叠组成分子轨道(B) 原子轨道以异号重叠组成非键分子轨道(C) 原子轨道可以按同号重叠或异号重叠,分别组成成键或反键轨道(5) 氧的O2+ , O2 , O2- , O22-对应于下列哪种键级顺序(A) 2.5,2.0, 1.5, 1.0(B) 1.0, 1.5,2.0, 2.5(C) 2.5,1.5, 1.0 2.0(6) 下列哪些分子或分子离子具有顺磁性(A) O2、NO (B) N2、F2(C) O22+、NO+(7) B2和C2中的共价键分别是(A)π1+π1,π+π(B)π+π,π1+π1 (C)σ+π,σ3.2 MO与VB理论在解释共价键的饱和性和方向性上都取得了很大的成功, 但两种理论各有特色. 试指出它们各自的要点(若将两种理论各自作一些改进, 其结果会彼此接近).3.3 考察共价键的形成时, 为什么先考虑原子轨道形成分子轨道, 再填充电子形成分子轨道上的电子云, 而不直接用原子轨道上的电子云叠加来形成分子轨道上的电子云?3.4 “成键轨道的对称性总是g, 反键轨道的对称性总是u”. 这种说法对不对? 为什么?3.5 一般地说, π键要比σ键弱一些. 但在任何情况下都是如此吗? 请举实例来说明.3.6 N2作为配位体形成配合物时, 通常以2σg电子对去进行端基配位(即N ≡ N→), 而不以1πu电子对去进行侧基配位。
结构化学课后习题及答案
01.量子力学基础知识【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm ,这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的,试计算该红光的频率、波数以及以k J·mol -1为单位的能量。
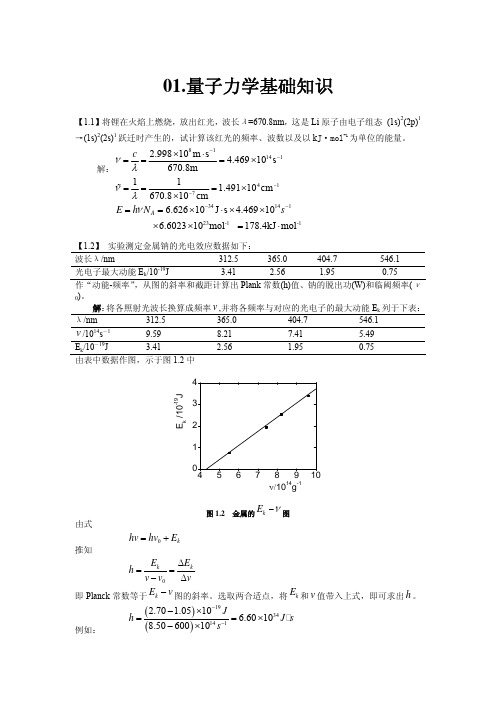
解:811412.99810m s 4.46910s 670.8m cνλ−−×⋅===× 41711 1.49110cm 670.810cm νλ−−===××%3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν−−==×⋅××××=⋅【1.2】 实验测定金属钠的光电效应数据如下:波长λ/nm 312.5 365.0 404.7 546.1 光电子最大动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”,从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。
解:将各照射光波长换算成频率,并将各频率与对应的光电子的最大动能E k 列于下表:v λ/nm 312.5 365.0 404.7 546.1v /1014s -19.59 8.21 7.41 5.49E k /10-19J 3.41 2.56 1.95 0.75 由表中数据作图,示于图1.2中E k /10-19Jν/1014g-1图1.2 金属的kE ν−图由式 0k hv hv E =+推知0k kE E h v v v Δ==−Δ即Planck 常数等于图的斜率。
选取两合适点,将和v 值带入上式,即可求出h 。
例如: k E −v k E ()()19341412.708.50 1.0510 6.601060010J h J s s −−−×==×−×图中直线与横坐标的交点所代表的即金属的临界频率,由图可知,。
结构化学课后答案

一、练习题1.立方势箱中的粒子,具有的状态量子数,是A. 211 B. 231 C. 222 D. 213。
(参考答案)解:(C)。
2.处于状态的一维势箱中的粒子,出现在处的概率是多少?A.B.C.D.E.题目提法不妥,以上四个答案都不对。
(参考答案)解:(E)。
3.计算能量为100eV光子、自由电子、质量为300g小球的波长。
( )(参考答案)解:光子波长自由电子300g小球。
4.根据测不准关系说明束缚在0到a范围内活动的一维势箱中粒子的零点能效应。
(参考答案)解:。
5.链状共轭分子在波长方向460nm处出现第一个强吸收峰,试按一维势箱模型估计该分子的长度。
(参考答案)解:6.设体系处于状态中,角动量和有无定值。
其值是多少?若无,求其平均值。
(参考答案)解:角动量角动量平均值7.函数是不是一维势箱中粒子的一种可能的状态?如果是,其能量有没有确定值?如有,其值是多少?如果没有确定值,其平均值是多少?(参考答案)解:可能存在状态,能量没有确定值,8.求下列体系基态的多重性。
(2s+1) (1)二维方势箱中的9个电子。
(2)二维势箱中的10个电子。
(3)三维方势箱中的11个电子。
(参考答案)解:(1)2,(2)3,(3)4。
9.在0-a间运动的一维势箱中粒子,证明它在区域内出现的几率。
当,几率P怎样变?(参考答案)解:10.在长度l的一维势箱中运动的粒子,处于量子数n的状态。
求 (1)在箱的左端1/4区域内找到粒子的几率?(2)n为何值,上述的几率最大?(3),此几率的极限是多少?(4)(3)中说明什么?(参考答案)解:11.一含K个碳原子的直链共轭烯烃,相邻两碳原子的距离为a,其中大π键上的电子可视为位于两端碳原子间的一维箱中运动。
取l=(K-1)a,若处于基组态中一个π电子跃迁到高能级,求伴随这一跃迁所吸收到光子的最长波长是多少?(参考答案)解:12.写出一个被束缚在半径为a的圆周上运动的质量为m的粒子的薛定锷方程,求其解。
结构化学练习(4-7章)

结构化学练习(4-7章)第四章练习(1)I3和I6不是独立的对称元素,因为I3= ,I6= 。
(2)下列等式成立的是A S3=C3+B S3=C6+σhC S3=C3+iD S3=C6+i(3)如果图形中有对称元素S6,那么该图形中必然包含A C6, σhB C3,C C3,iD C6,i(4)下列说法错误的是A 分子中有S n轴,则此分子必然同时存在C n轴和σh。
B 反映面σd一定也是反映面。
C I4是个独立的对称元素。
D 分子既有C n轴又有垂直于C n轴的σh,此分子必有Sn轴。
(5)对称元素C2与σh组合得到,C n轴与垂直于它的C2轴组合可得到。
(6)写出如下点群所具有的全部对称元素及其对称操作:(1)C2h (2)D3 (3)C3i(7)已知配合物MA2B4的中心原子M是d2sp3杂化,该分子中有多少种构造异构体,这些异构体各属于什么点群。
(8)下列说法正确的是A 凡是八面体配合物一定属于Oh点群B 异核双原子分子一定没有对称中心C 凡是四面体构型分子一定属于Td点群D 在分子点群中,对称性最低的是C1,对称性最高的是Oh(9)下列分子具有偶极矩,而不属于C nv群的是A H2O2B NH3C CH2Cl2D H2C=CH2(10)下列各组分子中有极性,但无旋光性的是(1)N3- (2)I3- (3)O3A (1),(2)B (2),(3)C (1),(2),(3)D (3)(11)下列具有相同阶的分子是(1)B2H6 (2)BrCl5 (3)SiF4A (1),(2)B (2),(3) B (1),(3) D 都不同(12)下列分子的点群不是16个群元素的是A CCl4B XeO4C S8D Ni(CN)4(13)(1)SO42- (2)PO43- (3)ClO4-三者中不是T d点群的是A (1)B (2)C (3)D 都是T d点群(14)下列空格中打上“+”或“-”分别表示对与错。
结构化学课后习题答案

结构化学课后习题答案结构化学是化学学科中的一个重要分支,它主要研究原子、分子以及晶体的结构和性质。
课后习题是帮助学生巩固和深化课堂知识的重要手段。
以下是一些结构化学课后习题的答案示例,请注意,这些答案仅为示例,具体习题的答案需要根据实际的习题内容来确定。
习题一:原子轨道的基本概念1. 描述s、p、d、f轨道的基本形状和特征。
- s轨道:球形,对称性高,只有一个轨道。
- p轨道:哑铃形,有两个主瓣,对称性较低,有三个轨道。
- d轨道:具有更复杂的形状,如四叶草形等,有五个轨道。
- f轨道:形状更为复杂,有七个轨道。
2. 解释原子轨道的量子数。
- 主量子数n:决定电子层,n越大,电子离原子核越远。
- 角量子数l:决定轨道形状,l的不同值对应不同的轨道类型。
- 磁量子数m:决定轨道在空间的取向。
- 自旋量子数s:描述电子自旋状态。
习题二:分子几何结构1. 描述价层电子对互斥理论(VSEPR)的基本原理。
- VSEPR理论基于电子对的排斥作用,认为电子对会尽可能地分布在原子周围,以减少排斥力,从而形成稳定的分子几何结构。
2. 根据VSEPR理论,预测CO2分子的几何形状。
- CO2分子中,碳原子有两个双键氧原子,没有孤对电子,根据VSEPR理论,分子呈线性结构。
习题三:晶体结构1. 解释晶体的布拉维格子和晶系。
- 布拉维格子:描述晶体中原子排列的几何结构,有简单立方、体心立方、面心立方等。
- 晶系:根据晶体的对称性,晶体可以分为立方晶系、四方晶系、六方晶系等。
2. 描述面心立方(FCC)晶体的特点。
- FCC晶体中,每个原子周围有12个相邻原子,形成紧密堆积结构,具有较高的对称性和密堆积度。
习题四:化学键1. 区分离子键、共价键和金属键。
- 离子键:由正负离子之间的静电吸引形成。
- 共价键:由原子间共享电子对形成,常见于非金属元素之间。
- 金属键:由金属原子与自由电子云之间的相互作用形成。
2. 描述氢键的特点及其在分子间作用中的影响。
王顺荣编高教版社结构化学习题答案第7章
A
s
。程方格拉布出正推�况情的直垂�*l*k*h�组面晶与阵点线直对.81
’5 ’8 ’1 ’4 6 5 8 1 4 7 2 3 8 7 4 3 ’2 ’6 ’7
’3
5 6 1 2
。之释解并�来起系联式公或程方么什过通别分�系联 何有者二�么什是素要二的射衍中射衍体晶在线射 X�么什是素要二的胞晶.02
。替代心体方四由可心面方四为因�示所图如 �式型阵点心面方四无而�式型阵点心面方立有么什为.5 。格晶或子 格间空为称 �格网线直套一得获�分划线连位单体面六行平的定确照按阵点间空 。式形何几的性期周构结体晶应反是阵点。原复够能都移平行进�量矢的定决所 点两何任中其接连 �质性的同共个一有都们它但�同相定一不式形阵点的应对所 �同不的体晶 。阵点了成构就 �复重期周� 列排律规定一按间空在点何几些这 �答 �事回一同是还系关应对是格晶与子格间空�系关应对何有体晶与构结阵点.4 。构结的列排置并胞晶有成形成形�的成组所线色红择选可胞晶 。胞晶是不形矩的中图 � �线接连有没方下点 B �线接连有没方上点 A� �同不境环 围周的点 B 和点 A 于由�元基构结个一表代形矩个每若�图如。境环的同相着 有点的上点定胞晶证保能才�有共胞晶个 4 为应点定胞晶�构结维二于对�析解
4= �2/1�×6+�8/1�×8 : �lC 4=1+�4/1�×21� aN + 。标指面晶的面晶个三的影阴 带出求推并�数子粒 lCaN 和数�lC、�aN 中胞晶算计试�示所图如胞晶 lCaN.11 bn+am=nmT 述所上综。面平个一定确以可线直条两的行平
�下如�
0,2�,1� � )n \ �2( soc 2
。心底方立在存不以所�盾矛相素元称对征特的有拥所系晶方 立与这�轴次 3 个 4 在存不它知可图由则�心底方立在存设假�示所 3 图如 。替代阵点单简方四由可心底方四�示所 2 图如 。替代来阵点单简交正由能不心底交正�示所 1 图如 。式型心底方立和心底方 四无而�心底交正有中式型阵点间空种 41 明证图绘�求要的胞晶当正据根.51 .6�4�3�2�1=n�明证经已 1 2 5.0 1 0 0 5.01121 6 4 3 2 n
结构化学课件第七章

a1g,a*1g eg,e*g
3dxy 3dxy 3dyz
t1u,t*1u
t2g
配位化合物分子轨道能级图 M ML6
t*1u a*g
6L
np
ns (n-1)d
e*g t2g eg
Δo
不同电子组态的 LFSE 的数值( Δo ) d电子 数目 HS (弱场) e*g LFSE LS (强场) e*g LFSE
t2g
t2g
0
1 2
0
0.4 0.8
0
0.4 0.8
3
4 5
1.2
0.6 0
1.2
1.6 2.0
6
7 8 9 10
0.4
0.8 1.2 0.6 0
2.4
1.8 1.2 0.6 0
4. 配位化合物的热力学稳定性
●配位化合物的稳定性常用稳定常数来表示。 在水溶液中金属离子和水结合在一起,形成水合离子,加入配位体 L
时,发生置换 H2O 的反应,逐级平衡常数为:
M(H2O)n + L ……
M(H2O)Ln-1 + L
M(H2O)n-1L + H2O
K1=
[M(H2O)n-1L] [M(H2O)n][L]
: s,p x,p y,p z,d x : d xy,d yz,d xz
2
y2
,d z 2
配位体L按能与中心原子生 成σ键或π键轨道分别组合 成新的群轨道,使与M的 中心原子轨道及配体的群轨道 原子轨道对称性匹配。 设处在x,y,z 3个正向的L的σ轨道分别是σ1、σ2、σ3 ,负向的σ4、σ5、σ6 。 这些轨道组成和中心原子σ 轨道对称性匹配的群轨道(如下表) 。而中心原子 的各个轨道以及和它对称性匹配的配位体群轨道的图形如上图。 由于M的dxy,dyz,dxy轨道的极大值方向正好和L的σ轨道错开,基本不受影响, 是非键轨道。M的6个轨道和6 个配位体轨道组合得到12个离域分子轨道,一 半为成键轨道,一半为反键轨道。
北师大_结构化学课后习题答案

北师大 结构化学 课后习题第一章 量子理论基础习题答案1 什么是物质波和它的统计解释?参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言,衍射强度(即波的强度)大的地方,粒子出现的数目就多,而衍射强度小的地方,粒子出现的数目就少。
对一个粒子而言,通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子,在相同的条件下重复多次相同的实验,一定会在衍射强度大的地方出现的机会多,在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释,对于单个粒子,ψψ=ψ*2代表粒子的几率密度,在时刻t ,空间q 点附近体积元τd 内粒子的几率应为τd 2ψ;在整个空间找到一个粒子的几率应为12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件?参考答案合格波函数的基本条件是单值,连续和平方可积。
由于波函数2ψ代表概率密度的物理意义,所以就要求描述微观粒子运动状态的波函数首先必须是单值的,因为只有当波函数ψ在空间每一点只有一个值时,才能保证概率密度的单值性;至于连续的要求是由于粒子运动状态要符合Schrödinger 方程,该方程是二阶方程,就要求波函数具有连续性的特点;平方可积的是因为在整个空间中发现粒子的概率一定是100%,所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理?参考答案在经典理论中,一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份(如各种不同的波长和频率)。
而在量子力学中,按波函数的统计解释,态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加,使粒子部分地处于Q 1状态,部分地处于Q 2态,……。
各种态都有自己的权重(即成份)。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么?参考答案根源就在于微观粒子的波粒二象性。
结构化学 第七章练习题DOC

第七章 晶体的点阵结构和晶体的性质1. (东北师大98)简答(1)讨论晶体的周期性结构用什么理论,(2)在A 1,A 2,A 3型密堆积中,哪种空间利用率低。
解:(1) 用点阵理论(2) 空间利用率:A 1(74.05%), A 2(68.02%), A 3(74.05%) 2.东北师大98(1)用0.579Ǻ的X 衍射得某立方晶体衍射指标为111的衍射角为5.1度,计算该晶体的晶胞参数a.(2)钨属于立方体心结构, 每个晶胞可以摊到几个钨原子, 分数坐标为什么?若钨的晶胞的大小为a=3.165Ǻ, 求其原子半径。
解:(1) 2 d hkl sin θ = λ222222222222sin () () 44sin h k l a h k l aλλθθ=++=++a=5.641 Ǻ(2) 每个晶胞可以摊到2个钨原子,分数坐标为(0, 0, 0)(1/2, 1/2, 1/2) ,W 原子半径: 4 1.37r r === Ǻ 3. 东北师大99已知CsCl 晶体中正负离子半径分别为1.69 Ǻ 和1.81 Ǻ ,试确定该晶体的配位数和结构形式。
解:0.732 < r +/r -=0.9337 <1.0, 配位数为8,配位多面体为立方体,体心为Cs+, 顶点为Cl 。
晶体的结构形式为简单立方。
4.东北师大2000某金属单晶为立方P 晶格, 在戴维逊-革末实验中测得该晶体(100)晶面上的一级反射型衍射的布拉格角为30。
,若已知晶格常数a=250pm ,求金属半径和加速电子电压。
解:立方P, r=a/2=125 pm, d hkld 100=250/1=250 pm,2d h*k*l* sin θ=n λ 2d hkl sin θ=λ 2×250×sin30。
=λ λ=250 pm2k =E 2p ev p m==h p λ== 5.(清华)S 8分子可形成单斜S 和正交S, 用X 射线衍射法(CuK 2线)测得某正交晶体的参数a=1048pm,b=1292pm,c=2455pm, λ=1.542 Ǻ, 已知密度为2.07g/cm 3,原子质量S=32, 求(a)每个晶胞中S 8的分子数目,(b)计算224衍射的Bragg 角θ。
结构化学习题解答解析

习题选解第一章1.1 E = 1.988⨯10-18Jp = 6.626⨯10-27kg ⋅m ⋅s -1 1.2 h = 6.442⨯10-34J ⋅s w = 5.869⨯10-19J ν0 = 9.11⨯1014s -1 1.4 光子能量21.24eV ;电子动能 5.481eV 1.5 70.8pm1.9 (1)1/4;(2)2.63⨯10-5;(3)2/l ;(4)01.10 3个,E 1 = h 2/(8ml 2);E 2 = 4h 2/(8ml 2);E 3 = 9h 2/(8ml 2) 1.13 301.5 nm 1.16 0.14 nm 1.17 86.2nm1.20 (1)无,l /2;(2)无,0;(3)有,2224n h l ;(4)有,2228n h ml 1.21 (1)是,能量无确定值,22513h E mL =;(2) 是,能量无确定值,2297104h E mL = 1.22 (1) 2222k E mr =,i k φψ, k =0, ±1, ±2, …;(2) 136pm 1.23 (1) h 2/(8ml 2);(2) l /2,2/l ;(3)01.24 n x =3, n y =1, n z =2;n x =3, n y =2, n z =1;n x =2, n y =1, n z =3;n x =2, n y =3, n z =1;n x =1, n y =2, n z =3;n x =1, n y =3, n z =2 1.25 (1)不是,x →∞时,ψ→∞不满足平方可积;(2)不是,x →-∞时,ψ→∞不满足平方可积;(3)不是,在x =0处一阶微商不连续;(4)不是,ψ不满足平方可积;(5) 不是,ψ不满足平方可积,在x =0处一阶微商不连续;(6) 是 1.27 11πsin 42π2n n -;n =3;1/4;说明当n →∞时,一维势箱中运动的粒子,其概率分布与经典力学相同 1.28 (1)1ψ=;(2) ψ=(3) i m φψ=;(4) 0/r a ψ-=1.29 (1)是;(2) 是;(3) 不是;(4) 是;(5) 不是1.31 (1) 是d/d x 和d 2/d x 2的本征函数,本征值分别为a 、a 2(2) 不是d/d x 和d 2/d x 2的本征函数(3) 不是d/d x 的本征函数,是d 2/d x 2的本征函数,本征值为-a 2 (4) 不是d/d x 的本征函数,是d 2/d x 2的本征函数,本征值为-a 2 (5) 不是d/d x 和d 2/d x 2的本征函数 (6) 不是d/d x 和d 2/d x 2的本征函数1.34 无确定值,2258h E ml =1.351.36 (a /2, a /4, a /2),(a /2, 3a /4, a /2);y = a /2 1.37 (1) 是;(2) 是;(3) 不是;(1) 不是 1.38 |p |=nh /2l第二章 2.1 3a 0/2 2.5 22.6 (1) ()22212349R C C C ⎡⎤-++⎣⎦;(2)21C ;;(4)1;(5) 2223()C C - ;(6)0 2.14 (1) -3.4eV ;(2) ;(3)0;(4)r /a 0(5)(6)2.15 (1);(2) n =2, l =1, m =0;(3) E =-3.4eV ,|M | =0,M z = 02.16 (1) 1111(1)(1)(1)(1)(2)(2)(1)(2)s s s s αψβΦαψβ=;(2) E = -78.6eV2.17 (1) 112112112(1)(1)(1)(1)(3)(3)(2)(2)(2)(2)(3)(3)(3)(3)(3)(3)(3)(3)s s s s s s s s s αψβψαΦαψβψααψβψα=或112112112(1)(1)(1)(1)(3)(3)(2)(2)(2)(2)(3)(3)(3)(3)(3)(3)(3)(3)s s s s s s s s sαψβψβΦαψβψβαψβψβ=; (2) E = -204.03eV2.18 (1) 3P 0;(2) 3P 2;(3) 4S 3/2;(4) 6S 5/2;(5) 3F 2;(6) 3F 4;(7) 4F 3/2;(8) 4F 9/2;(9) 5D 4 2.19 (1) 1S(1S 0);(2) 2P(2P 3/2 2P 1/2);(3) 1S(1S 0), 3P(3P 2, 3P 1, 3P 0), 1D(1D 2);(4) 1S(1S 0), 3P(3P 2, 3P 1, 3P 0), 1D(1D 2), 3F(3F 4, 3F 3, 3F 2), 1G(1G 4); (5) 1P(1P 1),3P(3P 2, 3P 1, 3P 0);(6)1S(1S 0), 3S(3S 1), 1P(1P 1),3P(3P 2, 3P 1, 3P 0), 1D(1D 2), 3D(3D 3, 3D 2, 3D 1) 2.21 第一种2.22 未成对电子数:2l +1 基支项:2212l l S ++2.24 (1) 4S 、2D 、2P(2) 4D 、4P 、4S 、2D(2)、2P(2)、2S(2) (3) 4P 、2D 、2P 、2S(4) 4P 、4D 、4F 、2S 、2P(2)、2D(3)、2F(2)、2G (5)1S 3P 1D 1S 1S 3P 1D 3P 3P 5D, 5P,5S, 3D, 3P, 3S, 1D, 1P, 1S3F, 3D,3P1D 1D 3F, 3D, 3P 1G,1F, 1D, 1P,1S3 F 3F 5G, 5F , 5D, 3G, 3F , 3D, 1G, 1F , 1D 3H, 3G, 3F, 3D,3P1G 1G 3H, 3G, 3F 1I, 1H, 1G,1F,1D2.25 I 1= 11.46eV2.26 (1)5;(2)15;(3)4;(4)45;(5)675;(6)1350 ;;(4) 2, 1, 0, -1, -2;(5)5 2.29 (1)A, C ;(2)A, B ;(3)B, C 2.31 2个节面2.32 (1))122z s s p ψψψψ=++;(2) 无,<E>=-6.8eV ,1/3; (3) 3 ,2/3; (4) 有,0,0第三章3.7 (1)OF :(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)3,一个σ键,一个三电子π键,键级3/2,顺磁性(2)NO :(1σ)2(2σ)2(3σ)2(4σ)2(1π)4 (5σ)2(2π)1,1σ,1π,一个三电子π键,键级5/2,顺磁性 (3)CO :(1σ)2(2σ)2(3σ)2(4σ)2(1π)4 (5σ)2,一个σ键,二个π键,键级3,反磁性(4)CN :(1σ)2(2σ)2(3σ)2(4σ)2(1π)4 (5σ)1,一个单电子σ键,二个π键,键级5/2,顺磁性 (5)HF :(1σ)2(2σ)2(3σ)2(1π)4,一个σ键,键级1,反磁性3.8 (1) O 2:2*22*2222*1*1112222222s s s s pz px py px py σσσσσππππ;O 2+:2*22*2222*111222222s s s s pz px py px σσσσσπππ;O 2-:2*22*2222*2*1112222222s s s s pz px py px py σσσσσππππ;键级:O 2+ > O 2 > O 2-;键长:O 2+ < O 2 < O 2- (2) OF :(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)3;OF +:(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)2;OF -:(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)4;键级:OF + > OF > OF -;键长:OF + < OF < OF -3.10 (1)得电子变为AB -型负离子后比原来中性分子键能大的分子:C 2,CN(2)失电子变为AB +型正离子后比原来中性分子键能大的分子:O 2,F 2,NO 3.12 p x -d xy (否);p y -d yz (π);d x 2-y 2-d x 2-y 2(δ);d z 2-d z 2(σ);p x -p x (π) 3.13原子轨道3s 3p z 3p x 3p y 3d z 23d zx 3d yz 3d xy 3d x 2-y 2沿z 轴对称类型(节面数) 0 0 1 10 1 1 2 2 有14对轨道对符合对称性匹配:原子轨道对 3s -3s 3s -3p z 3s -3d z 2 3p z -3p z 3p z -3d z 23d z 2-3d z 2 3p x -3p x 分子轨道类型 σ σ σ σσσπ原子轨道对 3p x -3d xz 3p y -3p y 3p y -3d yz 3d xz -3d xz 3d yz -3d yz 3d xy -3d xy 3d x 2-y 2-3d x 2-y 2分子轨道类型 π π π ππδδ3.14 (1) E I <E 1<E 2<E II ;(2) 222112/()a a a +;(3) 222112/()b b b +;(4) ψI 含φ1(A)原子轨道的成份多一些,ψII 含φ2(B)原子轨道的成份多一些;(5) 这个化学键的电子云会偏向A 原子3.15 1122x s p ψψ=+;21263x y s p p ψψψψ=-+;312662x y z s p p p ψψψψψ=--+;412662x y z s p p p ψψψψψ=---3.17 (1)0.73;(2)0.71;(3)0.683.23 NF :1σ22σ23σ24σ25σ21π42π2,键级:2,顺磁性;NF +:1σ22σ23σ24σ25σ21π42π1,键级:2.5,顺磁性;NF -:1σ22σ23σ24σ25σ21π42π3,键级:1.5,顺磁性第四章4.1 (1)π34,(2)π78,(3) π78,(4) π88,(5) π910,(6) π78,(7) π34,(8) π34,(9)无,(10) π1414,(11) π44,(12) π34(2个),(13) π34(2个),(14) π34(2个),(15)无,(16) π34(2个),(17) π34,(18) π46,(19) π46,(20)π46,(21) π344.6 (1) 1E α=,E 2 = α,3E α=;(2) ()112312φψψ=++)213φψψ-()312312φψψ=-+; (3) -0.828β;(4) C C C0.51.00.7074.8 (1) E 1=α+2β,E 2=E 3=α-β(2) 环丙烯正离子、自由基和负离子的离域能分别为-2β、-β和0(3) )1123φψψψ++,)21232φψψψ=--,)323φψψ=-(4) 4.11 (1) 2个π34,(2) E 1=α+2β, E 2=α+β,E 3=α-β(3) α+2βα+βα-β(4) 离域能为-1.528β 4.14 6α+5.656β第六章6.2 存在对称中心i : C 2h C 4h C 6h D 2h D 4h D 6h D 3d D 5d S 2 S 6存在垂直于主轴的镜面σh :C 2h C 3h C 4h C 5h C 6h D 2h D 3h D 4h D 5h D 6h S 3 S 5 6.3(1) CO —C ∞v ,CO 2—D ∞h ,NO 2+—D ∞h ,乙炔—D ∞h ,H 2S —C 2v ,NH 3—C 3v ,CH 3Cl —C 3v ,HOCl —C s ,H 2O 2—C 2,NO 2—C 2v ,CH 4—T d ,SF 6—O h(2) 重叠式乙烷—D 3h ,交叉式乙烷—D 3d ,椅式环己烷—D 3d ,船式环己烷—C 2v ,丙二烯—D 2d ,CHCl 2Br —C s ,CH 2=C=CCl 2—C 2v ,CHCl=C=CHCl —C 2,CH 3-CCl 3(交叉式)—C 3v , CH 3-CCl 3(重叠式)—C 3v(3) 顺式(重叠式)二茂铁—D 5h ,反式(交叉式)二茂铁—D 5d ,[Co(NH 2–CH 2–CH 2–NH 2)3]3+—D 3,1,3,5,7四甲基–环辛四烯—S 4(4) [PtCl 4]2-—D 4h ,HCHO —C 2v ,顺式二氯乙烯—C 2v ,反式二氯乙烯—C 2h ,CH 2=CCl 2—C 2v ,苯分子—D 6h ,萘分子—D 2h ,对二氯苯—D 2h ,邻二氯苯—C 2v ,间二氯苯—C 2v , BCl 3—D 3h ,[CO 3]2-—D 3h6.4B N B N B N H H H H H HD 3h ,B B BNH 2NH 2H 2ND 3hFH HFHHC 2h , H FF HHH C 2h, HHHHFFC2h ,CC FC 2h ,6.5 (1)D 2h (2)D 2d (3)D 26.6 (1) 去掉2个球有以下3种情况:2vvd (2) 去掉3个球有以下3种情况:s s 3v6.7⑴正三角形D 3h ⑵正方形 D 4h ⑶正六边形D 6h ⑷长方形 D 2h ⑸中国国旗上的一个五角星 D 5h ⑹正三棱锥 C 3v ⑺正三棱柱D 3h ⑻正四棱锥C 4v ⑼正四棱柱 D 4h ⑽双正四棱锥D 4h ⑾正六棱柱D 6h ⑿正四面体T d ⒀正八面体 O h⒁正六面体(即立方体)O h⒂圆锥体C ∞v ⒃园柱体D ∞h6.8 XX XXXXXXXX XXX XXX X XXXXXXX XXXXXX XXX XX Y XXY XYXYYXX YC s C 2D 2dC 2vC i C 1C 2hC s C sC 2vD 2hC 2hC 2hC 4v C 2C 2v第七章 7.1点阵点数目1 1 1 1每个点阵点代表的内容 白1、黑2白1、黑1白1、黑1白3 黑球和白球的数目 白1、黑2白1、黑1白1、黑1白37.7(1)0,0,0; 1/2,1/2,0; 1/2,0,1/2; 0,1/2,1/2; 1/4,1/4,1/4; 1/4,3/4,3/4; 3/4,1/4,3/4; 3/4,3/4,1/4;(2)154.5pm 7.8 (右图)7.9 d 110=233.8pm ;d 220=143.2pm7.10 201pm7.11 (100)与(010):90°;(100)与(001):90°;(100)与(210):26.56°7.14 (1)C 2v ,正交;(2) C 2h ,单斜;(3)D 2h ,正交;(4) D 4h ,四方; (5)D 6h ,六方;(6)C 3v ,三方;(7)C 3i ,三方(8)C 3h ,六方;(9)D 3h ,六方; (10)S 4,四方;(11)C s ,单斜;(12) O h ,立方;(13)T d ,立方; (14) D 2d ,四方;(15)O ,立方;(16) C 6h ,六方;(17) D 3,三方; (18) T ,立方;(19) D 3d 三方;(20)T h ,立方 7.157.17(100)(010)(120)(230)第八章8.1 28.0748.2 21.453gcm-3r=138.7pm8.3 a=b=328pm,c=536pm;3.187gcm-38.4 r =185.8pm,0.967gcm-3,d=303pm8.8 a=352.4pm,8.908gcm-3,r=124.6pm8.14 r=146pm8.17 CaS:正负离子配位数皆为6,正八面体,A1,晶体结构型式为cF;CsBr:正负离子配位数皆为8,立方体,立方简单,晶体结构型式为cP8.18 (2) 154pm;(3) 1.53gcm-3;(4) 274pm8.20 cF;分数坐标:0,0,0; 1/2,1/2,0; 1/2,0,1/2; 0,1/2,1/2;80.99%8.22 (1)Ti4+:000;Ba2+:1/2,1/2,1/2;O2-:0,0,1/2; 0,1/2,0; 1/2,0,0(2) BaTiO3 (3)cP(4)与Ba2+离子配位的O2-负离子数为12;与Ti4+离子配位的O2-负离子数为6(6) A1第九章9.2 cF,a=359pm9.5 (1) a=415.8pm;(2) x = 0.92,(NiO)76(Ni2O3)8;(3) A1,正八面体空隙,92%;(4) 294pm9.8 (1) 21.45gcm-3,r = 186.7pm;(2)有两个,分别来自200和4009.9 (1)19.356gcm-3;(2) 共有7对粉末线,衍射指标依次为(110), (200), (211), (220), (310), (222) (321) 9.10 (1) r = 128pm;(2) 仅有(200)和(400)的衍射峰;(3) (200)与(400)衍射峰对应的2L值分别为50.4mm和116.8mm9.11 (1) a=565.9pm;(2)cF;(3)n = 49.12 (1) r=137.0pm;(2)2级9.16 106.6pm9.17 141.9pm9.18 k1/k2=1.7149.19 11MHz9.26 λ1,λ3,λ5由HCl产生,HCl核间距129pm;λ2,λ4,λ6由HBr产生,HBr核间距143pm9.28 131pm;477.7Nm−19.30 64.32⨯1012s−1;1.5547⨯10−14s;1859.7 Nm−1;12.83kJ;3.859cm−1附录III 模型实习实习一、分子的对称性目的:1. 掌握寻找分子中独立对称元素、判断分子点群的方法;2. 根据分子所属点群判断分子有无偶极矩3. 根据分子所属点群判断分子有无旋光性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为衍射级数 对于立方晶系 a=b=c, Bragg方程可写成: a 2 sin θ hkl = nλ 2 2 2 h * + k * +l *
n
二、衍射强度与晶胞中原子的分布: 衍射强度与晶胞中原子的分布: 衍射强度与晶胞中原子的分布 衍射强度 IC
I c = I e FHKL
2
设 晶胞中含有A1,A2,。。。,AN 个原子,如果A 散射因子为fj ,坐标为(x j, y j, z j),则 结构因子 FHKL =
j =1 N i 2π ( Hx j + Ky j + Lz j )
原子的
j
∑ f je
∴
I c ∝ FHKL
2
f j —散射因子,由原子的性质所决定;
H , K , L —衍射指标; x j , y j , z j —第 j个原子的坐标.
通过上式用衍射强度,可测出原子的坐标 x j , y j , z j
.a .
b
.
a
3、空间点阵:三维点阵
β α
c
γ b a
平行六面体单位+结构基元 = 晶胞
三.晶胞
空间点阵是晶体结构的数学抽象,对于实际的三维晶体,选 择三个不相平行的、能满足周期性的单位向量a,b,c,可 将晶体划分成一个个完全相同的平行六面体,它代表晶体 结构的基本重复单位,叫晶胞。 晶胞的基本要素:一个是晶胞的大小和形状,可用晶胞参数 (a,b,c,α ,β ,γ )表示;另一个是晶胞中原子的位置, 通常用分数坐标(x,y,z)表示。
21. 在面心结构中,每个晶胞含四个原子,其分数坐标为:
(0,0,0)
1 1 (0, , ) 2 2 1 1 ( , ,0) 2 2
1 1 ( ,0, ) 2 2
F hkl
2
= [ f cos 2 π ( 0 ⋅ h + 0 ⋅ k + 0 ⋅ l ) + f cos 2 π ( 0 ⋅ h +
k l + ) 2 2
n=1、2、3…
19.
d h* k * l * =
404.9 2 +0 +0
2 2 2
a h +k +l
2 2 2
d 200 =
= 202.45( pm)
d111 =
404.9 1 +1 +1
2 2 2
= 233.77( pm)
d 220 =
404.9 2 +2 +0
2 2 2
= 143.15( pm)
h k h l + + 0 ⋅ l ) + f cos 2 π ( + 0 ⋅ k + )] 2 2 2 2 2 k l + [ f sin 2 π ( 0 ⋅ h + 0 ⋅ k + 0 ⋅ l ) + f sin 2 π ( 0 ⋅ h + + ) 2 2 h k h l + f sin 2 π ( + + 0 ⋅ l ) + f sin 2 π ( + 0 ⋅ k + )] 2 2 2 2 2 2 = f 2 [1 + cos π ( k + l ) + cos π ( k + h ) + cos π ( h + l ) ] + f cos 2 π (
习题课
12.01.04
第七章 晶体结构的点阵理论
• 定义:晶体的外部多是有规则的多面体。内部结构微粒 (原子、分子、离子等)在空间有规则有周期性排列的固 体物质。
结构的周期性:是指同一种微粒在空间排列上每隔一定距 离重复出现。
二、晶体的点阵结构 晶体的点阵结构
由于晶体具有周期性结构,可以把结构基元抽象成点,形成 点阵 晶体结构 = 点阵+结构基元 点阵:按连接其中任意两点的向量进行平移后,均能复原的 一组点。 1、直线点阵:一维点阵 2、平面点阵:二维点阵
= d sin θ + d sin θ = 2d sin θ = nλ , n = 0,±1,L
2d h* k * l * sin θ nh*nk *nl* = nλ
*
θ
N M N+1
O θθ O’
θ
n=1、2、3… n=1 2 3…
* **
N
上式为Bragg 方程,式中 dh k l 为晶面间距
θ nh nk nl 为Bragg角—衍射角
9. 不论该晶体属于哪一个晶系,均为体心点阵(I),结构基元为AB
11. Na+:4个;Cl-:4个;NaCl:4个
1:(101)2:(201)3:(001)
18
2d 光程差∆= MB+BN= 2d h* k * l * sinθ nh*nk*nl*
∆必为波长的整数倍
2d h* k * l * sin θ nh*nk *nl* = nλ
若h,k,l均为奇数或偶数时,k+l, h+k, h+l均是偶数
Fhkl
2
= f 2 (1 + 1 + 1 + 1) 2 = 16 f
2
若h,k,l奇偶混杂,则k+l, h+k, h+l中必有二奇一偶Fra bibliotekFhkl
2
= f 2 (1 − 1 − 1 + 1) 2 = 0
系统消光
z
4c
倒易截数之比:1/2:1/3:1/4 = 6:4:3
cb
a
1 1 1 符号化—倒易截数之比: : : = h : k : l r s t
∴ hkl 为晶面指标
2a
x
3b
y
(643)
晶面指标较小的平面点阵,其面间距较大,每面的密度较大。
晶
带心
晶胞类型:晶系 晶系(七个) 晶系
特 征 对 称 元 素
空间点阵形式(十四种) 空间点阵形式
与 微 观 对 称 元 素 组 合 形
类型:点 点
( 个)
空间
(
个)
§7-3 X 射线晶体结构分析原理
1.劳埃方程 劳埃方程 2.布拉格方程 布拉格方程
一、衍射方向与晶胞参数
二、衍射强度与晶胞中原子的分布
1、Lane 方程: 直线点阵衍射:素向量 a
α 设 s0 和 s 分别为入射、衍射X 射线的单位矢量 α 0入射角, 衍射角
四.分数坐标
晶胞中任一原子的位置可用向量表示
r r r OP = X a + Yb + Z c
Q X ,Y , Z ≤ 1
五、晶面指标(符号)和有理指数定律: 晶面指标(符号) 晶面指标
用晶面表示不同的平面点阵组,那晶面在三个晶轴上的倒易截 数之比——晶面指标。 截距 截数 倒易截数
2a , 3b , 4c 2 1 2 3 1 3 4 1 4
若按虚线划出格子,违背了平移向量间的夹角最好是90°的要求
对于正方形:
若有带心型式,按虚线连接后,格子仍为正方形,可减少点阵点。故不可能存在正 方形带心格子。
对于六方格子: 同上,同理。带心六方可被矩形代替
对于平行四边形格子: 带心平行四边形可被简单平行四边形代替
5. 对于立方面心点阵型式符合立方晶系的对称性,从中不可能取出更小且对称 性与原同的格子。只能取较小的菱面体。显然对称性降低了,所以立方面心格子 存在。而四方面心格子可取出体积更小且对称类型相同的四方体心格子。故四方 面心不存在。(P221)
光程差(∆)=PA-BO 若用矢量表示:
= a cos α − a cos α 0 = a(cos α − cos α 0 )
= hλ , h = 0 ,±1,L s
A
∆ = a( s − so ) = hλ , h = 0 ,±1,L
同样,三维情况
a ⋅ ( s − s o ) = hλ b ⋅ ( s − so ) = kλ c ⋅ ( s − so ) = lλ
式中
a(cos α − cos α 0 ) = hλ b(cos β − cos β 0 ) = kλ c(cos γ − cos γ ) = lλ s0 0
. α P
α0
.O
B
a
.
h , k ,l = 0,±1,L 为衍射指标
∆ 光程差必为整数倍,这满足次生射线的衍射条件。
2、Bragg 方程: 平面点阵的衍射 空间点阵可以分解成一组组平面点阵,且间距相等 如图 N和N+1 层的光程差 ∆=MO’+NO’
系统消光:由Lane和Bragg方程应产生的部分衍射而系统消失 的现象。 由消光规律可以确定晶体所属的空间群 点阵型式 体心I 面心F 底心C 简单P 系统消光条件 H+K+L=奇数 H,K,L奇偶混杂 H+K=奇数 无消光现象
2. 正当格子的要求是:对称性高,点阵点少。 对于矩形: 带心型式不可能用更高对称性或更少点阵点的格子来代替
