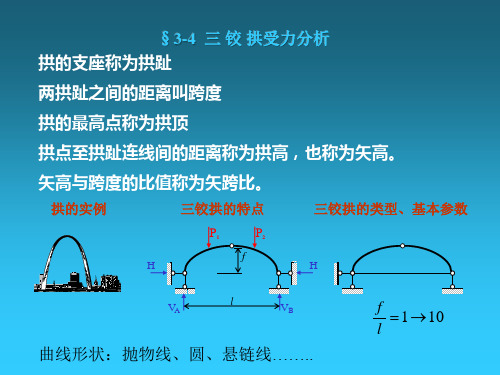
结构力学 第三章 三铰拱
合集下载
第3章静定结构受力分析三铰拱

将以上两式代入上方程得 :
FN FQ0 sin FH cos
FQ FQ0 cos FH sin
(2)
M M 0 FH y
概念:
上式即为用相应简支梁的内力 表示的拱的内力式。当将上式 用作拱的内力计算公式时,可 以叫做公式法。
3.拱的内力图特征和制作
分析
由式2可知,在竖向荷载作用 下静定拱内力与相应简支梁
例1 图(a)所示三铰拱的拱轴 为半圆形。计算截面K1、K2的 内力。
FP=10kN
R=4m
(a)
解 1)求支座反力
竖 MA 0
向 FBy
1 [q R 2R
R 2
FP (R
R cos )] 11.33kN()
反 MB 0
力 FAy
1 [q R 2R
力与前规定相同;弯矩以使 拱的下侧受拉为正;
以图示三铰刚架为例说明拱的内 力计算的一般方法。
FH F Ay
FH
F By FN0
解:
截开指定截面K,取左侧为隔 离体,见下页图(c)(d),截 面上的内力均按规定的正方 向示出 。
M FN
FH
FQ
FAy
(c)
M0 0
FQ0
(d)
在轴力和剪力的两个正交方 向上建立投影方程,并建立 关于截面形心的力矩方程, 即得:
内力及拱水平反力有关。其
中拱水平反力对应确定的荷
载是一常数。此外,拱轴力
和剪力还与所计算截面外法
线与x轴的夹角a有关。
结论
拱轴上内力有以下3个特点:
1
不管是在均布荷载下还是在集 中荷载下,拱的三个内力图都 是曲线图形。
FN FQ0 sin FH cos
FQ FQ0 cos FH sin
(2)
M M 0 FH y
概念:
上式即为用相应简支梁的内力 表示的拱的内力式。当将上式 用作拱的内力计算公式时,可 以叫做公式法。
3.拱的内力图特征和制作
分析
由式2可知,在竖向荷载作用 下静定拱内力与相应简支梁
例1 图(a)所示三铰拱的拱轴 为半圆形。计算截面K1、K2的 内力。
FP=10kN
R=4m
(a)
解 1)求支座反力
竖 MA 0
向 FBy
1 [q R 2R
R 2
FP (R
R cos )] 11.33kN()
反 MB 0
力 FAy
1 [q R 2R
力与前规定相同;弯矩以使 拱的下侧受拉为正;
以图示三铰刚架为例说明拱的内 力计算的一般方法。
FH F Ay
FH
F By FN0
解:
截开指定截面K,取左侧为隔 离体,见下页图(c)(d),截 面上的内力均按规定的正方 向示出 。
M FN
FH
FQ
FAy
(c)
M0 0
FQ0
(d)
在轴力和剪力的两个正交方 向上建立投影方程,并建立 关于截面形心的力矩方程, 即得:
内力及拱水平反力有关。其
中拱水平反力对应确定的荷
载是一常数。此外,拱轴力
和剪力还与所计算截面外法
线与x轴的夹角a有关。
结论
拱轴上内力有以下3个特点:
1
不管是在均布荷载下还是在集 中荷载下,拱的三个内力图都 是曲线图形。
§3-8 三铰拱

f/l:矢跨比、高跨比。高跨比对拱的主要性能有比较大的影响 (1-1/10)。若f-0,三铰共线或接近共线,瞬变体系 平拱:两拱趾在同一水平线上的拱 斜拱:两拱趾不在同一水平线上的拱
二、竖向荷载作用下三铰拱的计算
1、支座反力的计算
1)公式
F AV = F
0 AV
∑ Pb =
i
i
0 F BV = F BV =
例2:设三铰拱承受均匀水压力作用,求其合理轴线
例3:设三铰拱承受上表面水平的填土重量下三铰拱的合理轴线。
M =M
0
− FH y
F S = F S0 cos ϕ − F H sin ϕ
F N = F S0 sin ϕ + F H cos ϕ
2)结论 ①由于水平推力的存在,三铰拱 横截面上的弯矩要比相应简支梁 的弯矩小 ②在竖向荷载作用下,三铰拱的 内力主要为轴力,且为压力 ③三铰拱的内力值不但与荷载及 三个铰的位置有关,而且与各铰 间拱轴线的形状有关。
∑
l Pi a i
l
F AH = F BH
2)结论
M c0 = f
①在竖向荷载作用下,三铰拱的 竖向反力与相当梁的竖向力相同, 与拱轴形状及拱高无关;
相应简支梁
②在竖向荷载作用下,水平推力FH等于相应梁C截面的弯矩除以拱高而 得。FH仅与荷载及三个铰的位置有关,而与拱轴无关。
2、内力的计算
1)公式
3、拱内力图的绘制
1)描点法 ①沿拱轴将拱截成为若干相等的小段 ②计算各截面处的y,tan,sin,cos ③利用公式逐一计算各截面的M、FS、FN值 ④逐点描绘
近似法
作拱的内力图,用水平线代替拱轴线,用截面法求出一系列截面的 内力,在水平线上用描点法作出 2)内力的计算公式推算三铰拱内力图的一些特点 ① M=M0-FH•y集中力偶作用处,M图发生突变 ②集中力作用处,三铰拱的FN、Fs图将发生突变 ③在FS=0的截面上M将出现极值,在集中力作用处由于FS发生突变, M图将出现尖角。 dM FS = dx cos ϕ
结构力学5三铰拱课件

拱架搭设
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
3-5 三铰拱

P2a2
MB 0
VA
1 l
P1b1
P2b2
HB x 0
HA HB H
VA
l1
l2 lLeabharlann VBP1 dc
MC 0
VB VB VA VA
P1
P2
H
c
V
A
x
VA
VB
f l1
VA l1 P1 d H f 0
M
C
H
f
院
VA
P1
Qo
Q Q cos H sin
Mo
N Q sin H cos
H
受力V特A 点
(1)在竖向荷载作用下有水平反力 H;
(2)由拱截面弯矩计算式可见,比相应简支梁小得多;
(3)拱内有较大的轴向压力N.
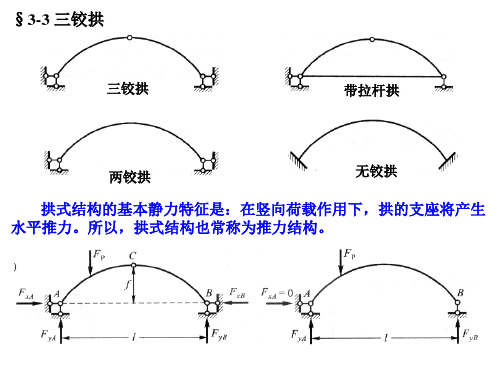
第3章 静定结构的受力分析
q=2kN .m
P=8kN
例、三铰拱及其所受荷
dy dx
x3
4f l
1
2x l
x3
44 12
1
2123
Q2
Q2 cos2 H sin2 11 2 3 0.832
7.5 0.555 0.0025kN 0.003kN
0.667
N2 Q2 sin2 H cos2 11 230.555
其缺点是:拱对基础或下部结构施加水平推力,增加了下 部结构的材料用量;拱具有曲线形状,施工不方便。
第3章 静定结构的受力分析
防
为了消除拱对支座的水平推力,可采用带拉
结构力学-三铰拱

曲梁
拱
拱 (arch)
一、概述
2.拱的受力特点 拱的受力特点 拱
曲梁
P
拱比梁中的弯矩小
拱 (arch)
一、概述
3.拱的分类 拱的分类
超静定拱
静定拱
两铰拱
三铰拱 拉杆 拉杆拱
高差h 高差
超静定拱
无铰拱 斜拱
拱 (arch)
一、概述
4.拱的有关名称 拱的有关名称 顶铰 拱肋 拱趾铰 跨度 拱肋 拱趾铰 矢高
1 l l a1 b1 不再顶部,或 铰C不再顶部 或 不再顶部 FH = [Y A × − P1 ( − a1 )] f 2 2 0 b a2右边的结2 YB0 YA不是平拱 不是平拱,右边的结 l l
M c0 = [Y A0 × − P1 ( − a1 )]
YB=YB YA=YA0 XA=XB =FH
二、三铰拱的数解法 ----支反力计算 支反力计算 P1 三铰拱的竖向反 P2 C 力与其等代梁的 XB 反力相等 水平反 f FH 反力相等;水平反 A B 力与拱轴线形状0 XA Mc YA l/2 l/2 无关.荷载与跨度 无关 荷载与跨度 YB YA l 一定时, 一定时,水平推 YA0 等代梁 P1 P2 A C 力与矢高成反比. 力与矢高成反比 B 请问:有水平荷载 有水平荷载,或 请问 有水平荷载 或
32kN.m C C 32kN.m
8m B 4m 4m 2kN 2kN A 4m 4m
8m B 2kN
A 2kN
32kN.m
16kN.m
16kN.m
16kN.m
水平反力的作用:使相应水平代梁弯矩 水平反力的作用:使相应水平代梁弯矩MC0 降至为零。 降至为零。
结构力学 三铰拱

4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中, F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中,M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤,可求出各等分截面的内力,作出内力图。
三、三较拱的合理轴线
在给定荷载作用下,三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化,f 的值对内力有 很大影响。
工程实例
拱桥 (无铰拱)
超静定拱
世界上最古老的铸铁拱桥(英国科尔布鲁克代尔桥)
万县长江大桥:世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº =12.5kN QK左 A 12.5kN
结构力学三铰拱宣讲

三铰位置拟定,合理拱轴唯一拟定
设计时只能根据主要荷载选择近似合理拱轴 一种合理轴线只相应一种荷载,荷载布置变化,合理拱轴 亦变化。
第四节 三铰拱旳合理轴线
a. 三铰拱在均匀水压力作用下,合理轴线为一圆弧
R FN const q
第四节 三铰拱旳合理轴线
b. 在填土重量作用下,三铰拱旳合理轴线是一悬链线
第三部分 三铰拱
学习内容
三铰拱旳构成特点及其优缺陷; 三铰拱旳反力和内力计算及内力图旳绘制; 三铰拱旳合理拱轴线。
学习目旳和要求
目旳:实际工程中拱旳形式越来越多,了解拱旳受力特征, 对指导设计和构造选型是非常必要旳。
要求:熟练掌握三铰拱旳反力和内力计算。 了解三铰拱旳内力图绘制旳环节。 掌握三铰拱合理拱轴旳形状及其特征。
第三节 竖向荷载作用下三铰拱旳内力特点
绘弯矩图
36
40 48 40
M
0 K
FH y
MK
M
0 K
FH y
综合弯矩图是两种弯矩图叠加旳成果(注意是竖标旳叠加, 或称代数叠加),即两个曲线所夹部分,可见弯矩很小。三 铰拱弯矩下降旳原因完全是因为推力造成旳。
第三节 竖向荷载作用下三铰拱旳内力特点
三铰拱在竖向荷载作用下旳弯矩由两部分构成,水平反力 产生负弯矩,能够抵消一部分正弯矩,与简支梁相比拱旳弯 矩、剪力较小,轴力较大(压力),应力沿截面高度分布较均 匀。
FAx=FBx =FH • 荷载与跨度一定时,水平推力与矢高成反
比,且总是正旳,故称内推力。扁拱旳水
FH= MC0 / f 平推力不小于陡拱。
• 该组结论仅适合于平拱,且承受竖向荷载。
2 竖向荷载作用下拱内力计算
截面旳外法线(即该处切线)与水平方向旳倾角φk要求左 半拱为正,右半拱为负。拱截面弯矩一般以内侧受拉为正,
设计时只能根据主要荷载选择近似合理拱轴 一种合理轴线只相应一种荷载,荷载布置变化,合理拱轴 亦变化。
第四节 三铰拱旳合理轴线
a. 三铰拱在均匀水压力作用下,合理轴线为一圆弧
R FN const q
第四节 三铰拱旳合理轴线
b. 在填土重量作用下,三铰拱旳合理轴线是一悬链线
第三部分 三铰拱
学习内容
三铰拱旳构成特点及其优缺陷; 三铰拱旳反力和内力计算及内力图旳绘制; 三铰拱旳合理拱轴线。
学习目旳和要求
目旳:实际工程中拱旳形式越来越多,了解拱旳受力特征, 对指导设计和构造选型是非常必要旳。
要求:熟练掌握三铰拱旳反力和内力计算。 了解三铰拱旳内力图绘制旳环节。 掌握三铰拱合理拱轴旳形状及其特征。
第三节 竖向荷载作用下三铰拱旳内力特点
绘弯矩图
36
40 48 40
M
0 K
FH y
MK
M
0 K
FH y
综合弯矩图是两种弯矩图叠加旳成果(注意是竖标旳叠加, 或称代数叠加),即两个曲线所夹部分,可见弯矩很小。三 铰拱弯矩下降旳原因完全是因为推力造成旳。
第三节 竖向荷载作用下三铰拱旳内力特点
三铰拱在竖向荷载作用下旳弯矩由两部分构成,水平反力 产生负弯矩,能够抵消一部分正弯矩,与简支梁相比拱旳弯 矩、剪力较小,轴力较大(压力),应力沿截面高度分布较均 匀。
FAx=FBx =FH • 荷载与跨度一定时,水平推力与矢高成反
比,且总是正旳,故称内推力。扁拱旳水
FH= MC0 / f 平推力不小于陡拱。
• 该组结论仅适合于平拱,且承受竖向荷载。
2 竖向荷载作用下拱内力计算
截面旳外法线(即该处切线)与水平方向旳倾角φk要求左 半拱为正,右半拱为负。拱截面弯矩一般以内侧受拉为正,
第3章 三铰拱

(二) 对称三铰拱的数解法
1. 计算支座反力
图示三铰拱中,共有 四个反力: VA、HA、VB、HB。 根据整体的平衡 条件可建立三个 平衡方程: ∑MA=0 ∑MB=0 ∑X=0 再取中间铰一侧隔离 体, ∑ MC=0, 由这四个方程可 解出四个反力。
由∑MB= 0,得: VAl-P1b1- P2b2-…= 0 VA= (P1b1 + P2b2 + …)/ l V0A 由∑MA= 0,得: VB= (P1a1+ P2a2+…)/ l V0B 把两个竖向反力VA 、VB与相应简支梁支座反力V0A 、 V0B 相比,可知竖向荷载作用下,对称三铰拱的竖向反力与 其相应简支梁的反力完全相同。
两个投影方程可用拱轴在该点的法线n和切线t为 投影轴。
∑n = 0 ,得: QD = VA cosφD -P1 cosφD -P2 cosφD -H sinφD = (V0A-P1-P2) cosφD -H sinφD
= Q0D cosφD -H sinφD
∑t = 0 ,得: ND = VA sinφD - P1 sinφD -P2 sinφD +H cosφD = (V0A-P1-P2) sinφD +H cosφD
由∑X= 0,得: HA= HB = H 中间铰左侧隔离体 ∑MC=0 得:
∑ MC =
VAl1-P1(l1 - a1) - P2(l1 - a2) - P3(l1 - a3)- H f = 0 得: H=[VAl1-P1(l1 - a1)- P2(l1 - a2)- P3(l1 - a3)] / f 因 VA = V0A ,得:H= M0C / f M0C为相应简支梁截面C的弯矩。
最后根据本例的已知条件,进行具体计算。
VA=VB= V0A = q l / 2= 4× 16 / 2 = 32kN H = (q l 2 / 8) / f = (4× 162 / 8) / 4 = 32kN
结构力学 第三章 三铰拱

B
②剪力、轴力计算公式
FQFQ 0co-sFHsin
F0yA φ FP1
M0
F0yB
FNFQ 0sin-FHcos
KM
FN
F
0 Q
—相应简支梁对应截面上的剪力
φ φ—截面处拱轴切线倾角,在左半拱
FH A
y φ FQ
为正(右半拱为负)
φ
x
FVA φ
◆ 拱截面轴力较大,且一般为压力
例3-5 作图示三铰拱的内力图,拱轴为抛物线,其方程为
1kN/m C
f=4m x
FQ0L 1kN
FV A l1=8m
4m
l=16m
4kN
D
B FH B
4m
FV B
FQ0R 5kN
1kN/m
A
C
4kN B
F0yA
F0yB
F QLF Q 0L co-sFHsin 1 0 .89 6 ( 4 0 .44 ) 4 1 .7 7k 8 2 N
F Q RF Q 0c R o -sF Hsin 5 0 .8 9 6 ( 0 4 .44 ) 4 1 7 .7k 2 8N 9
四 三铰拱的合理拱轴线(reasonable axis of arch) 1 合理拱轴线的概念 在给定荷载作用下,使拱处于无弯矩状态的拱轴线,称 为拱的合理拱轴线
2 合理拱轴线的确定 根据荷载作用下,任一截面弯矩为零条件确定。如竖向 荷载作用下的三铰拱:
MM0FHy0 y M0
FH
通过由调此整可拱见的,轴当线拱,上使荷拱载在为确已定知荷时载,作只用要下求各出截相面应上简的支弯梁 矩值的为弯零矩,方这程时,拱除截以面支上座只水有平通推过力截FH面,形即心可的求轴得向合压理力拱作轴 用,的其轴压线应方力程沿截面均匀分布,此时的材料使用最为经济
结构力学§3-8 三铰拱.

0 C
FH
f
0
FH
M
0 C
f
竖向反力: FVA
FPibi L
FV0A
FVB
FP i ai L
FV0B
水平反力:
FHA
FHB
FH
M
0 C
f
由前面计算可见: ●竖向反力与相应简支梁的相同;
●水平反力FH与拱高f成反比,与拱轴的曲线形式无关;
M
0不变时,
C
f小,则FH大;
QC
1050.832 82.50.555 41.6kN
FN左D FQ0D左SinD FHCosD
MD0 D
FQ0左D
1050.555 82.50.832 127kN
d) 求D右剪力、轴力:
100kN
FQ右D FQ0D右CosD HSinD
(105 100) 0.832 82.5 0.555 41.6kN
核心区
(2)合理拱轴线
d/3 d/3 d/3
M
K
FNK
RK
ek
K0
——在给定荷载下,适当选取拱轴线,使拱仅有轴力,而M=0, 拱轴线与压力线与完全重合,这样的拱轴线称为合理拱轴线。
数解法求合理拱轴பைடு நூலகம்:
已知:
Mk
M
0 k
Hyk
令:
Mk
M
0 k
Hyk
0
则有:
yk
M
0 k
H
[例3] 求图示对三铰拱在均布荷载作用下的合理拱轴线。
MD
F右 ND
D F右
第3章 三铰拱

1 1 2 1 M qlx qx ql x x 2 ql x x 8f l 2
M = M0 -Hy = 0 可见,拱内无弯矩。
(3) 任一截面的剪力
dy 4 f 8 f 4f 2 x 由于 y 2 l x x dx l l l dy 4f 8f sin tg cos cos 2 x cos dx l l Q Q 0 cos H sin
1 ql 2 ql x x y 2 8f
令 M= 0,
1 ql 2 ql x x y0 2 8f
得合理拱轴方程: 4f y 2 l x x l
可见,合理拱轴方程是二次抛物线,与前 例所给的拱轴方程完全一致。 要使拱处于无弯矩状态,只有在恒载作用 情况下才有可能做到。工程实际中的结构,往 往同时受恒载和活载的共同作用,而活载是时 而出现,时而消失的(如人群、风雪荷载等), 或是移动的(如吊车、车辆荷载等),这就很难 使拱内完全不出现弯矩。 设计中以正常使用情况下经常出现的荷载 为依据,选择一个拱轴,使之弯矩尽量减少。
例中,已知二次抛物线拱在全跨受竖向均布 荷载作用下,各截面均无弯矩。现假设拱轴方程y 为未知,但三个铰的位置已定,铰C在拱顶处, 如图示。 现按照上述方法,求其合理拱轴方程。
由平衡条件可求出三铰拱的反力。 任一截面的弯矩为:
2 1 1 ql M M 0 Hy ( qlx qx2 ) y 2 2 8f
两个投影方程可用拱轴在该点的法线n和切线t为 投影轴。
∑n = 0 ,得: QD = VA cosφD -P1 cosφD -P2 cosφD -H sinφD = (V0A-P1-P2) cosφD -H sinφD
= Q0D cosφD -H sinφD
M = M0 -Hy = 0 可见,拱内无弯矩。
(3) 任一截面的剪力
dy 4 f 8 f 4f 2 x 由于 y 2 l x x dx l l l dy 4f 8f sin tg cos cos 2 x cos dx l l Q Q 0 cos H sin
1 ql 2 ql x x y 2 8f
令 M= 0,
1 ql 2 ql x x y0 2 8f
得合理拱轴方程: 4f y 2 l x x l
可见,合理拱轴方程是二次抛物线,与前 例所给的拱轴方程完全一致。 要使拱处于无弯矩状态,只有在恒载作用 情况下才有可能做到。工程实际中的结构,往 往同时受恒载和活载的共同作用,而活载是时 而出现,时而消失的(如人群、风雪荷载等), 或是移动的(如吊车、车辆荷载等),这就很难 使拱内完全不出现弯矩。 设计中以正常使用情况下经常出现的荷载 为依据,选择一个拱轴,使之弯矩尽量减少。
例中,已知二次抛物线拱在全跨受竖向均布 荷载作用下,各截面均无弯矩。现假设拱轴方程y 为未知,但三个铰的位置已定,铰C在拱顶处, 如图示。 现按照上述方法,求其合理拱轴方程。
由平衡条件可求出三铰拱的反力。 任一截面的弯矩为:
2 1 1 ql M M 0 Hy ( qlx qx2 ) y 2 2 8f
两个投影方程可用拱轴在该点的法线n和切线t为 投影轴。
∑n = 0 ,得: QD = VA cosφD -P1 cosφD -P2 cosφD -H sinφD = (V0A-P1-P2) cosφD -H sinφD
= Q0D cosφD -H sinφD
第三章 静定结构--三铰拱

拱结构的缺点:由于推力的存在,所以对基础的要求较高; 拱轴的曲线形状不便于施工(有时为减轻拱对基础的压力, 常使用拉杆布置)
4、 三铰拱的合理轴线
使拱在给定荷载下各截面弯矩都等于零的拱轴线,被称为
与该荷载对应的合理拱轴
M M 0 FH y 0
y
M0 FH
M0 MC0
f
只限于三铰平拱受 竖向荷载作用
FAy AF0 AyFra biblioteka1 P1
a2 C
f
l1 l
P1
C
X 0
b1 P2
x l2
P2
b2 F l Pb Pb 0
Ay
11
22
FAy
P1 b1
l
P2b2
B FBx
FBy
Pibi l
F0 Ay
mA 0
FBy
Piai l
F0 By
B
mc 0
F0 By
FH
•
•
内力图均不再为直线; 集中力作用处,剪力图将发 生突变; 集中力偶作用处,弯矩图将 发生突变; 上述公式仅适合于平拱,且 承受竖向荷载情况; 拱的内力仍然有FS=dM/ds
例题:三铰拱所受荷载如图所示,拱的轴线为抛物线方程
y
4f l2
xl
x
计算其反力并绘制内力图
q=2kN·m C
3、竖向荷载作用下三铰拱的内力特点
三铰拱在竖向荷载作用下的弯矩由两部分组成,水平反 力产生负弯矩,可以抵消一部分正弯矩,与简支梁相比拱的 弯矩、剪力较小,轴力较大(压力),应力沿截面高度分布 较均匀。
4、 三铰拱的合理轴线
使拱在给定荷载下各截面弯矩都等于零的拱轴线,被称为
与该荷载对应的合理拱轴
M M 0 FH y 0
y
M0 FH
M0 MC0
f
只限于三铰平拱受 竖向荷载作用
FAy AF0 AyFra biblioteka1 P1
a2 C
f
l1 l
P1
C
X 0
b1 P2
x l2
P2
b2 F l Pb Pb 0
Ay
11
22
FAy
P1 b1
l
P2b2
B FBx
FBy
Pibi l
F0 Ay
mA 0
FBy
Piai l
F0 By
B
mc 0
F0 By
FH
•
•
内力图均不再为直线; 集中力作用处,剪力图将发 生突变; 集中力偶作用处,弯矩图将 发生突变; 上述公式仅适合于平拱,且 承受竖向荷载情况; 拱的内力仍然有FS=dM/ds
例题:三铰拱所受荷载如图所示,拱的轴线为抛物线方程
y
4f l2
xl
x
计算其反力并绘制内力图
q=2kN·m C
3、竖向荷载作用下三铰拱的内力特点
三铰拱在竖向荷载作用下的弯矩由两部分组成,水平反 力产生负弯矩,可以抵消一部分正弯矩,与简支梁相比拱的 弯矩、剪力较小,轴力较大(压力),应力沿截面高度分布 较均匀。
结构力学——组合结构-三铰拱ppt课件

(A,B,C三铰在一直线上,成为几何瞬变体。)
.
②拱内力计算:
QM
P1
N
D
HA
VA
弯矩:受拉侧做弯矩图; 剪力:垂直于拱轴线的切线(顺时针为正); 轴力:平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩:
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点:方便,简单; 缺点:截面仍有弯矩。
.
②三铰曲拱:
f MM0Hy (HM c0/ f)
优点:截面弯矩很小或无弯矩; 缺点:曲线杆件施工复杂。
.
③桁架: 上弦、下弦承受弯矩;腹杆承受剪力。
其中:M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力:
其中:
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
(由水平向逆时针为正)
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力:
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力:
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0
.
②拱内力计算:
QM
P1
N
D
HA
VA
弯矩:受拉侧做弯矩图; 剪力:垂直于拱轴线的切线(顺时针为正); 轴力:平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩:
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点:方便,简单; 缺点:截面仍有弯矩。
.
②三铰曲拱:
f MM0Hy (HM c0/ f)
优点:截面弯矩很小或无弯矩; 缺点:曲线杆件施工复杂。
.
③桁架: 上弦、下弦承受弯矩;腹杆承受剪力。
其中:M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力:
其中:
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
(由水平向逆时针为正)
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力:
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力:
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0
第三章-静定结构----三铰拱
∑ M0 = 0 N D ⋅ R − N E ( R + dR ) = 0 ND = NE = N
这表明拱在法向均布荷载作用下处于无弯矩状态时,截面的轴力为一常数。
∑y=0
q ⋅ dS + 2 N ⋅ sin
dϕ =0 2 N = − qR
q ⋅ Rd ϕ + N ⋅ d ϕ = 0
R=−
N q
因N为一常数,q也为一常数,所以任一点的曲率半径R也是常数,即拱轴为圆弧。
绘制内力图
0
y
13.300 10.958 9.015 7.749 7.500 7.433 6.796 11.235 11.665 11.700 1.421 3.325 3.331 1.060 0.600 0.472 1.000 0.003 0.354
0.600
0.000
A
1
1.125 1.500 1.125
P2
f H
VA
VB
f = 1 → 10 l
曲线形状:抛物线、圆、悬链线……..
三铰拱的支座反力和内力 一、支座反力 与同跨度同荷载对应简支梁比较 支座反力
a1
d P1 a2
D
b1
c
f l2 l
b2
P2
HB
∑ MAP2 a2 ) 1 l
VB = VBo
o VA = VA
2
y2
q=2kN .m
6m x
0.000 0.375 4.500
3
ϕ2
4 5
6m
6
0.375
7 B 8
P=8kN
0.000
M图 kN.m
N图 kN
Q图 kN
拱的合理轴线 在固定荷载作用下,使拱处于无弯矩状态的轴线称为合理 轴线。由上述可知,按照压力曲线设计的拱轴线就是合理轴线。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。
这表明拱在法向均布荷载作用下处于无弯矩状态时,截面的轴力为一常数。
∑y=0
q ⋅ dS + 2 N ⋅ sin
dϕ =0 2 N = − qR
q ⋅ Rd ϕ + N ⋅ d ϕ = 0
R=−
N q
因N为一常数,q也为一常数,所以任一点的曲率半径R也是常数,即拱轴为圆弧。
绘制内力图
0
y
13.300 10.958 9.015 7.749 7.500 7.433 6.796 11.235 11.665 11.700 1.421 3.325 3.331 1.060 0.600 0.472 1.000 0.003 0.354
0.600
0.000
A
1
1.125 1.500 1.125
P2
f H
VA
VB
f = 1 → 10 l
曲线形状:抛物线、圆、悬链线……..
三铰拱的支座反力和内力 一、支座反力 与同跨度同荷载对应简支梁比较 支座反力
a1
d P1 a2
D
b1
c
f l2 l
b2
P2
HB
∑ MAP2 a2 ) 1 l
VB = VBo
o VA = VA
2
y2
q=2kN .m
6m x
0.000 0.375 4.500
3
ϕ2
4 5
6m
6
0.375
7 B 8
P=8kN
0.000
M图 kN.m
N图 kN
Q图 kN
拱的合理轴线 在固定荷载作用下,使拱处于无弯矩状态的轴线称为合理 轴线。由上述可知,按照压力曲线设计的拱轴线就是合理轴线。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。
结构力学-三铰拱

关于内力
关于内力
第二节 竖向荷载作用下三铰拱的受力分析 竖向荷载作用下拱反力计算 竖向荷载作用下指定截面内力计算 内力图均不再为直线; 集中力作用处,剪力图将发生突变; 集中力偶作用处,弯矩图将发生突变; 上述公式仅适合于平拱,且承受竖向荷载情况; 拱的内力仍然有FS=dM/ds
竖向荷载作用下指定截面内力计算
B
A
C
P1
P2
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算
FBy=YBy0
FAy=YAy0
FH= MC0 / f
FAx=FBx =FH
拱的竖向反力与其相应简支梁的竖向反力相等; 水平反力只与三个铰的位置有关而与拱轴线形状无关; 荷载与跨度一定时,水平推力与矢高成反比,且总是正的。 该组结论仅适合于平拱,且承受竖向荷载。
竖向荷载作用下拱反力计算 第二节 竖向荷载作用下三铰拱的受力分析
拱的内力图 由于拱轴线是弯曲的,所以内力图都是曲线形的,内力图要通过逐点描图的方法绘制,总的规律仍符合荷载和内力的微分关系。
01
03
02
FP=8kN
q=2kN·m
C
A
B
l=16m
f=4m
1、支座反力计算
例题:三铰拱所受荷载如图所示,拱的轴线为抛物线方程
[解]
FAy
FAx
FBx
FBy
计算其反力并绘制内力图
第二节 竖向荷载作用下三铰拱的受力分析
[解]
2、求截面 3 内力
FP=8kN
C
A
B
l=16m
f=4m
q=2kN·m
FP2=8kN
q=2kN·m
3
10
关于内力
第二节 竖向荷载作用下三铰拱的受力分析 竖向荷载作用下拱反力计算 竖向荷载作用下指定截面内力计算 内力图均不再为直线; 集中力作用处,剪力图将发生突变; 集中力偶作用处,弯矩图将发生突变; 上述公式仅适合于平拱,且承受竖向荷载情况; 拱的内力仍然有FS=dM/ds
竖向荷载作用下指定截面内力计算
B
A
C
P1
P2
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算
FBy=YBy0
FAy=YAy0
FH= MC0 / f
FAx=FBx =FH
拱的竖向反力与其相应简支梁的竖向反力相等; 水平反力只与三个铰的位置有关而与拱轴线形状无关; 荷载与跨度一定时,水平推力与矢高成反比,且总是正的。 该组结论仅适合于平拱,且承受竖向荷载。
竖向荷载作用下拱反力计算 第二节 竖向荷载作用下三铰拱的受力分析
拱的内力图 由于拱轴线是弯曲的,所以内力图都是曲线形的,内力图要通过逐点描图的方法绘制,总的规律仍符合荷载和内力的微分关系。
01
03
02
FP=8kN
q=2kN·m
C
A
B
l=16m
f=4m
1、支座反力计算
例题:三铰拱所受荷载如图所示,拱的轴线为抛物线方程
[解]
FAy
FAx
FBx
FBy
计算其反力并绘制内力图
第二节 竖向荷载作用下三铰拱的受力分析
[解]
2、求截面 3 内力
FP=8kN
C
A
B
l=16m
f=4m
q=2kN·m
FP2=8kN
q=2kN·m
3
10
第3章-5三铰拱

3.拱常受压,M:内侧受拉+,Q:顺时针+,N:压+。 拱轴倾角,左+,右- 4.拱内力图:计算控制截面内力,拱轴线水平投影为基 线,标内力竖标,连接曲线。
5.合理三铰拱轴线依据M=0这一条件确定,只产生轴力。 反力与三铰位置有关,与拱轴形状无关;但内力与位置 和拱轴线形状都有关。
H= MC0 / f
二、三铰拱的数解算法 y P 1
K
A
x
y f
l/2 l x l/2
C
拱轴线倾角 φ: P2 左半跨:+ 右半跨:-
P1
QK M K NK P1
0 MK
B
XB
XA
XA YA
P1 A a1 YA0
YA
YB
P2
Y
0 A
0 QK
0 M K M K Hy
K
C b1
B b2 YB0
拱的主要力 学性能与高 跨比有关
二、三铰拱的数解法 ----支反力计算 P1 P
C
2
A
f
B
XB
H YA
YA0 Mc0
XA
YA
等代梁 P1
A
l/2
l
C
l/2
YB P2
B
a1
b1 a2 b2
YA0
YB=YB0 XA=XB =H
YA=YA0
1 l l H [YA P ( a1 )] 1 f 2 2 0 YB l l 0 0 M c [YA P ( a1 )] 1 2 2
一、概述 起拱线 三铰拱 拉杆 跨度 拱趾 拉杆拱
3.拱的分类
超静定拱
静定拱
两铰拱
超静定拱
平拱
无铰拱
3-3三铰拱(结构力学第3章)
证:可先考虑半圆形三铰拱的情况。作用 于圆弧上的径向均布荷载q 可以用两 个垂直方向上等值的均布荷载等效替 代。
恰好等于沿竖向和水平方向的两种 均布荷载 q 作用于微段时产生的竖 向分力和水平分力。
qRd cos 竖向分力: dFy qRd sin
水平分力: dFx
例3-9 试证圆弧线是三铰拱拱轴线法线 方向均布压力作用下的合理拱轴线。
26.8kN
0 MK MK FH yK
0 MC FH f
例3-6 绘制图示三铰拱的内力图。 4f y 2 x( l x ) 拱轴线方程: l 解:求支座反力。
0 FyA FyA 28kN , 0 FyB FyB 20kN 0 MC 20kN 8m 16kN 4m 96kN m 0 M C 96 FH 24kN f 4
3-3-3 合理拱轴线 在给定的荷载作用下,能使拱体所有截面上弯矩为零的拱轴 线称为合理拱轴线。 0 弯矩: MK MK FH yK 令:
M M 0 FH y 0 M0 y 得: FH
例3-7 求图示三铰拱的合理拱轴线。 解:相应简支梁的弯: FH f 8 f M0 4 f x l x 合理拱轴线: y 2 FH l
0 MC (推力计算公式 ) FH f
相当梁
⑴在给定荷载作用下,三铰拱的支座反力仅与三个铰的位置有 关,而与拱轴的形状无关。 ⑵在竖向荷载作用下,三铰平拱的支座竖向反力与相应简支梁 反力相同,而水平推力与拱高成反比。拱的高跨比(矢跨比) 愈大则推力愈小;反之,则推力愈大。 0 MC FH f
例3-6 绘制图示三铰拱的内力图。 4f y 2 x( l x ) 拱轴线方程: l 解:求支座反力。
恰好等于沿竖向和水平方向的两种 均布荷载 q 作用于微段时产生的竖 向分力和水平分力。
qRd cos 竖向分力: dFy qRd sin
水平分力: dFx
例3-9 试证圆弧线是三铰拱拱轴线法线 方向均布压力作用下的合理拱轴线。
26.8kN
0 MK MK FH yK
0 MC FH f
例3-6 绘制图示三铰拱的内力图。 4f y 2 x( l x ) 拱轴线方程: l 解:求支座反力。
0 FyA FyA 28kN , 0 FyB FyB 20kN 0 MC 20kN 8m 16kN 4m 96kN m 0 M C 96 FH 24kN f 4
3-3-3 合理拱轴线 在给定的荷载作用下,能使拱体所有截面上弯矩为零的拱轴 线称为合理拱轴线。 0 弯矩: MK MK FH yK 令:
M M 0 FH y 0 M0 y 得: FH
例3-7 求图示三铰拱的合理拱轴线。 解:相应简支梁的弯: FH f 8 f M0 4 f x l x 合理拱轴线: y 2 FH l
0 MC (推力计算公式 ) FH f
相当梁
⑴在给定荷载作用下,三铰拱的支座反力仅与三个铰的位置有 关,而与拱轴的形状无关。 ⑵在竖向荷载作用下,三铰平拱的支座竖向反力与相应简支梁 反力相同,而水平推力与拱高成反比。拱的高跨比(矢跨比) 愈大则推力愈小;反之,则推力愈大。 0 MC FH f
例3-6 绘制图示三铰拱的内力图。 4f y 2 x( l x ) 拱轴线方程: l 解:求支座反力。
结构力学之三铰拱课件

桥梁工程
三铰拱广泛应用于桥梁工程中, 如公路桥、铁路桥和立交桥等。
100%
工业建筑
三铰拱适用于工业建筑中的大型 厂房、仓库等结构,能够承受较 大的竖向荷载和水平荷载。
80%
公共建筑
三铰拱也适用于公共建筑中,如 体育馆、会展中心等大型建筑, 能够提供大跨度和高承载能力的 结构体系。
02
三铰拱的力学分析
定位与调整
在吊装完成后,对三铰拱的位 置和角度进行调整,确保其符 合设计要求三铰拱的各个部件连接牢 固、可靠。
防腐与涂装
在施工完成后,对三铰拱进行 防锈蚀处理和涂装,提高其耐 久性和美观度。
施工安全
安全措施
在施工过程中,采取一系列安全措施,如设置安全警示标志、配 备安全带和安全帽等,确保施工人员的安全。
在基础上按照设计要求拼装三铰拱的各个部件,确保 拱体的几何尺寸和位置准确。
04
固定与调整
通过焊接或螺栓连接等方式将拱体固定在基础上,并 进行必要的调整,确保拱体的稳定性和承载能力。
05
施工监测
在施工过程中,对三铰拱的各项参数进行监测,确保 施工质量和安全。
安装技术
01
02
03
04
吊装方法
根据三铰拱的重量和尺寸,选 择合适的吊装机械和吊装方法 ,确保吊装过程中的安全和质 量。
三铰拱的特点
稳定性好
由于三铰拱具有静定结构的特点,因此其稳定性较 好,不易发生侧向失稳或扭转失稳。
承载能力强
三铰拱的承载能力较强,能够承受较大的竖向荷载 和水平荷载。
适用范围广
三铰拱适用于各种类型的建筑结构,如桥梁、厂房 、仓库等,尤其适用于需要承受较大荷载和跨度的 结构。
三铰拱的应用场景
三铰拱广泛应用于桥梁工程中, 如公路桥、铁路桥和立交桥等。
100%
工业建筑
三铰拱适用于工业建筑中的大型 厂房、仓库等结构,能够承受较 大的竖向荷载和水平荷载。
80%
公共建筑
三铰拱也适用于公共建筑中,如 体育馆、会展中心等大型建筑, 能够提供大跨度和高承载能力的 结构体系。
02
三铰拱的力学分析
定位与调整
在吊装完成后,对三铰拱的位 置和角度进行调整,确保其符 合设计要求三铰拱的各个部件连接牢 固、可靠。
防腐与涂装
在施工完成后,对三铰拱进行 防锈蚀处理和涂装,提高其耐 久性和美观度。
施工安全
安全措施
在施工过程中,采取一系列安全措施,如设置安全警示标志、配 备安全带和安全帽等,确保施工人员的安全。
在基础上按照设计要求拼装三铰拱的各个部件,确保 拱体的几何尺寸和位置准确。
04
固定与调整
通过焊接或螺栓连接等方式将拱体固定在基础上,并 进行必要的调整,确保拱体的稳定性和承载能力。
05
施工监测
在施工过程中,对三铰拱的各项参数进行监测,确保 施工质量和安全。
安装技术
01
02
03
04
吊装方法
根据三铰拱的重量和尺寸,选 择合适的吊装机械和吊装方法 ,确保吊装过程中的安全和质 量。
三铰拱的特点
稳定性好
由于三铰拱具有静定结构的特点,因此其稳定性较 好,不易发生侧向失稳或扭转失稳。
承载能力强
三铰拱的承载能力较强,能够承受较大的竖向荷载 和水平荷载。
适用范围广
三铰拱适用于各种类型的建筑结构,如桥梁、厂房 、仓库等,尤其适用于需要承受较大荷载和跨度的 结构。
三铰拱的应用场景
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二 三铰拱支座反力和内力
a1
1 支座反力
MB 0
MA0
ห้องสมุดไป่ตู้
FH A
A
FP1 a2
FP2
b1
C f
b2
B FH B
FX 0
l1
l2
F VA F P 1b1 lF P2b2
F Pbii l
FV A
l
FP1
FP2
FV B
F
0 yA
F VB F P 1a1 lF P2a2
F Paii l
A
B
F
0 yB
F0yA
B
②剪力、轴力计算公式
FQFQ 0co-sFHsin
F0yA φ FP1
M0
F0yB
FNFQ 0sin-FHcos
KM
FN
F
0 Q
—相应简支梁对应截面上的剪力
φ φ—截面处拱轴切线倾角,在左半拱
FH A
y φ FQ
为正(右半拱为负)
φ
x
FVA φ
◆ 拱截面轴力较大,且一般为压力
例3-5 作图示三铰拱的内力图,拱轴为抛物线,其方程为
四 三铰拱的合理拱轴线(reasonable axis of arch) 1 合理拱轴线的概念 在给定荷载作用下,使拱处于无弯矩状态的拱轴线,称 为拱的合理拱轴线
2 合理拱轴线的确定 根据荷载作用下,任一截面弯矩为零条件确定。如竖向 荷载作用下的三铰拱:
MM0FHy0 y M0
FH
通过由调此整可拱见的,轴当线拱,上使荷拱载在为确已定知荷时载,作只用要下求各出截相面应上简的支弯梁 矩值的为弯零矩,方这程时,拱除截以面支上座只水有平通推过力截FH面,形即心可的求轴得向合压理力拱作轴 用,的其轴压线应方力程沿截面均匀分布,此时的材料使用最为经济
F Q(F V AF P 1)co-F sH sin
FQ 0cos-FHsin
F N (F V A F P 1 )si-n F H cos
FVA φ
FQ 0sin-FHcos
FP1 K
φ
C
FP2
2内力计算
FH
A
y x
①弯矩计算公式
B
FH
MM0 FHy
FV A
A
F
0 Q
FP1
FP2
FV B
①弯矩计算公式
B
FH MM0FHy
F
0 Q
②剪力、轴力计算公式
FV A
FP1
FP2
FV B
A
B
◆ 由于推力的存在,三铰拱截面弯矩比跨度、荷载相同的
简支梁弯矩小
F0yA φ FP1
M0
FH A
KM FN
φ y φ FQ
φ
x
F0yB
M [F V x A F P 1 (x a 1 ) ] F H y
1kN/m C
f=4m x
FQ0L 1kN
FV A l1=8m
4m
l=16m
4kN
D
B FH B
4m
FV B
FQ0R 5kN
1kN/m
A
C
4kN B
F0yA
F0yB
F QLF Q 0L co-sFHsin 1 0 .89 6 ( 4 0 .44 ) 4 1 .7 7k 8 2 N
F Q RF Q 0c R o -sF Hsin 5 0 .8 9 6 ( 0 4 .44 ) 4 1 7 .7k 2 8N 9
F0yB
◆ 竖向荷载作用下,三铰拱的竖向支座反力与相应简支梁的 竖向支座反力相等
二 三铰拱支座反力和内力
FP1 a2
FP2
b2
a1
b1
1 支座反力
C
FVAFP1b1lFP2b2 Fy0A FH A
A
f
B FH B
◆F F VH B 轴三A F 线铰P F 1a H 形拱1 B l 状的FF P无水2H a2关平,推Fy0当力B 载只荷与F和荷V A 拱载的及跨三度个Fl1P1一铰l定的时位,置FP2水有l2平关推,力与F与拱V B
FNL FQ 0L sin-FHcos ( 1 ) ( 0 .4) 4 6 0 7 .82 9 5 .8 4 k 1 4 N 4 FNR FQ 0R sin-FHcos ( 5 ) ( 0 .4) 4 6 0 7 .82 9 7 .6 4 k 0 4 N 2
3 绘内力图
考虑拱中高间f成铰反C处比弯矩为零:
A
C
B
M C F V l 1 A F P 1 ( l 1 a 1 ) F H f 0 F0yaA1 FP1
M
0 C
C FXC
F0yB
FHFVA l1FP f1(l1a1)
M
0 C
f
FH A FV A
f FyC l1
FP1 K
φ
C
FP2
2内力计算
FH
A
y x
结构力学 第三章 三铰拱
赵州桥又名安济桥,该桥为空腹敞肩式坦拱桥,桥长64.4m,净 跨37.02m,桥宽9m,净矢高7.23m,桥面纵坡6.5% ,拱由28圈 拱石平行砌筑,每圈有拱石43块;为加强拱石间的结合,拱石各 面均凿有相当细密斜纹,另外还在拱石间设置X形锚铁和铁锚杆
万县长江大桥:世界上跨度最大的混凝土拱桥420m
A
C
B
y
4f l2
x(l x)
416241243m
F0yA
F0yB
tgd dx y x 1m 24 l2 f(l 2 x)x 1m 2 0 .5 -26034'
sin -0.4472 cos 0.8944
例3-5 作图示三铰拱的内力图
MM0 FHy
y
5 4 6 3 2 kN m FH A A
y
4f L2
x(Lx)
1kN/m
4kN
C
解 1 求支座反力
FVA Fy0A
y
FH A A
D
f=4m
B FH B
181 2447kN ()
x
16
FV B
Fy0B
184412 5kN () 16
FV A
l1=8m
4m
l=16m
4m
FV B
FH
M
0 C
f
781846kN 4
1kN/m
4kN
2 内力计算 x=12m
A A+
A
C B
C+
-
-
1.0
+B
6.0
C
B
M图 (kN.m)
FQ图 (kN)
FN图 (kN)
三 三铰拱的压力线
在确定荷载作用下,三铰拱的任意截面三个内力分量可
以用合力FR代替,由三铰拱各截面合力作用点组成的多
边形,称为三铰拱的压力线
FR
k
C
A
k
B
对于材料抗拉强度低的砖石、混凝土拱,通常要求各个截 面不出现拉应力,因此压力线不应超出截面的核心
