三角函数特殊角值表

三角函数特殊角值表75587

三角函数特殊值1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：sin30°=cos60°=21 sin45°=cos45°=22tan30°=cot60°=33tan 45°=cot45°=12、列表法：30˚13145˚121603说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从0变化，其余类似记忆．3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ．4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为2m 形式，正切、余切值可表示为3m 形式，有关m的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．巧记特殊角的三角函数值初学三角函数，记忆特殊角三角函数值易错易混。

若在理解掌握的基础上，经过变形，使其呈现某种规律，再配以歌诀，则可浅显易记，触目成诵。

仔细观察表1，你会发现重要的规律。

表1表1中，三角函数值的前三行，分子被开方数排列特征依次为“1，2，3，3，2，1，3，9，27”。

“一二三，三二一，三九二十七”。

记此歌诀即可。

观察表2也可发现重要的规律。

三角函数特殊角值表

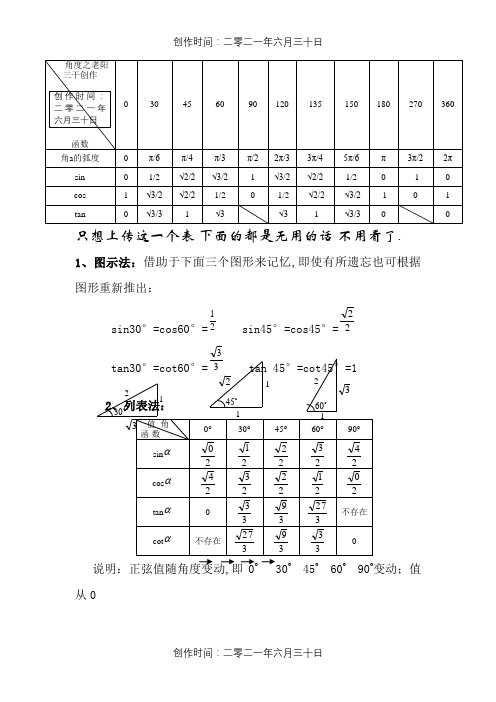
只想上传这一个表下面的都是无用的话不用看了.
1、图示法：借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出：
sin30°=cos60°=2
1
sin45°=cos45°=
22
说明：正弦值随角度变动,即0˚ 30˚ 45˚ 60˚ 90˚变动；值从0
变动,其余类似记忆．
3、规律记忆法：观察表中的数值特征,可总结为下列记忆规律：
① 有界性：（锐角三角函数值都是正值）即当
0°＜α＜90°时,
则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0. ②增减性：（锐角的正弦、正切值随角度的增年夜而增年夜；余弦、余切值随角度的增年夜而减小）,即当0＜A ＜B ＜90°时,则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°,则sin A ＜cos A ；tan A ＜cot A 若45°＜A ＜90°,则sin A ＞cos A ；tan A ＞cot A ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可暗示为
2
m 形式,正切、余切值可暗示为
3
m 形式,
有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．。

(完整版)三角函数特殊角值表

角度函数 0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出： sin30°=cos60°=21，sin45°=cos45°=22， tan30°=cot60°=33， tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法：说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从02122 23 1变化，其余类似记忆．3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A 若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为2m 形式，正切、余切值可表示为3m 形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．30˚ 123145˚ 1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin（A）=a/c余弦函数cos（A）=b/c正切函数tan（A）=a/b余切函数cot（A）=b/a其中a为对边，b为邻边，c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=-2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--化asinα ±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式）22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定，φ角的值由tan ba φ=确定六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

特殊角三角函数值表Word版

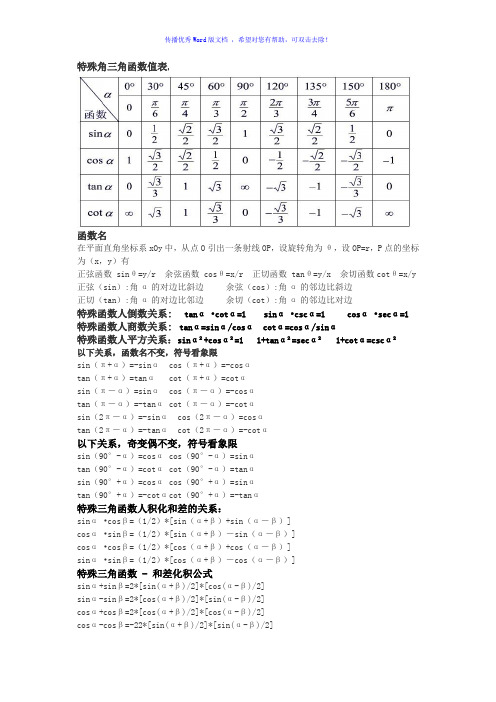
特殊角三角函数值表：函数名在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y 正弦（sin）:角α的对边比斜边余弦（cos）:角α的邻边比斜边正切（tan）:角α的对边比邻边余切（cot）:角α的邻边比对边特殊函数人倒数关系: tanα •cotα=1sinα •cscα=1cosα •secα=1特殊函数人商数关系:tanα=sinα/cosαcotα=cosα/sinα特殊函数人平方关系：sinα²+cosα²=11+tanα²=secα²1+cotα=cscα²以下关系，函数名不变，符号看象限sin（π+α）=-sinα cos（π+α）=-cosαtan（π+α）=tanα cot（π+α）=cotαsin（π－α）=sinα cos（π－α）=-cosαtan（π－α）=-tanα cot（π－α）=-cotαsin（2π－α）=-sinα cos（2π－α）=cosαtan（2π－α）=-tanα cot（2π－α）=-cotα以下关系，奇变偶不变，符号看象限sin（90°-α）=cosα cos（90°-α）=sinαtan（90°-α）=cotα cot（90°-α）=tanαsin（90°+α）=cosα cos（90°+α）=sinαtan（90°+α）=-cotαcot（90°+α）=-tanα特殊三角函数人积化和差的关系：sinα •cosβ=（1/2）*[sin（α+β）+sin（α－β）]cosα •sinβ=（1/2）*[sin（α+β）－sin（α－β）]cosα •cosβ=（1/2）*[cos（α+β）+cos（α－β）]sinα •sinβ=（1/2）*[cos（α+β）－cos（α－β）]特殊三角函数 - 和差化积公式sinα+sinβ=2*[sin(α+β)/2]*[cos(α-β)/2]sinα-sinβ=2*[cos(α+β)/2]*[sin(α-β)/2]cosα+cosβ=2*[cos(α+β)/2]*[cos(α-β)/2]cosα-cosβ=-22*[sin(α+β)/2]*[sin(α-β)/2]特殊三角函数 - 两角和与差的三角函数公式sin（α+β）=sinαcosβ+cosαsinβcos（α+β）=cosαcosβ-sinαsinβtan（α+β）==(tanα+tanβ )/(1－tanα •tanβ) sin（α-β）=sinαcosβ-cosαsinβcos（α-β）=cosαcosβ+sinαsinβtan（α－β）=(tanα-tanβ )/(1+tanα •tanβ)。

三角函数特殊角值表75872

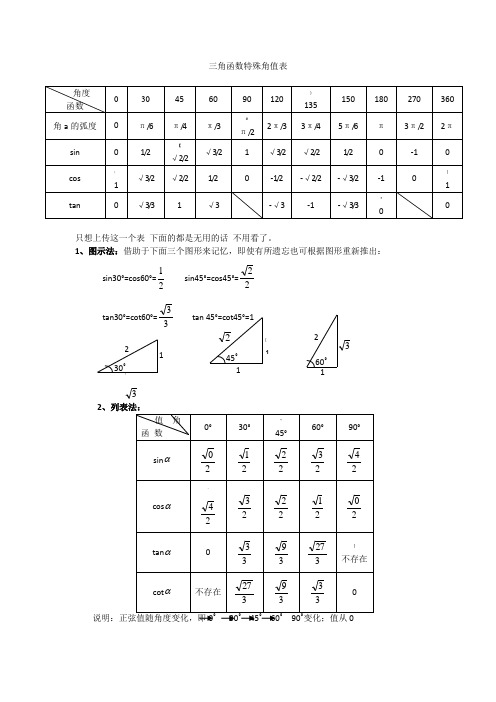
三角函数特殊角值表
只想上传这一个表下面的都是无用的话不用看了。

1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出： sin30°=cos60°=
2
1
sin45°=cos45°=22
tan30°=cot60°=3
3
tan 45°=cot45°=1
2说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 30˚ 1
2
）
3
1
45˚ [
1
2 1
2 60˚ 3
23 1变化，其余类似记忆．
3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：
① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，
则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A 若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为
2m 形式，正切、余切值可表示为3
m 形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．。

三角函数特殊角值表

只想上传这一个表下面的都是无用的话不必看了。

1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：
sin30°=cos60°=21 sin45°=cos45°=2
2
说明：正弦值随角度变更，即0˚ 30˚ 45˚ 60˚ 90˚变更；值从0
1
变更，其余类似记忆．
3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：
① 有界性：（锐角三角函数值都是正值）即当
0°＜α＜90°时，
则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sinA ＜sinB ；tanA ＜tanB ； cosA ＞cosB ；cotA ＞cotB ；特别地：若0°＜α＜45°，则sinA ＜cosA ；tanA ＜cotA
若45°＜A ＜90°，则sinA ＞cosA ；tanA ＞cotA ． 4、口决记忆法：观察表中的数值特征正弦、余弦值可暗示为
2
m
形式，正切、余切值可暗示为
3
m 形式，
有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．。

三角函数特殊角值表

三角函数特殊角值表1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：in30°=co60°=12in45°=co45°=22tan30°=cot60°=221tan45°=cot45°=132213451601说明：正弦值随角度变化，即030456090变化；值从031变化，其余类似记忆．23、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：①有界性：（锐角三角函数值都是正值）即当0°＜＜90°时，则0＜in＜1；0＜co＜1；tan＞0；cot＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A＜B＜90°时，则inA＜inB；tanA＜tanB；coA＞coB；cotA＞cotB；特别地：若0°＜＜45°，则inA＜coA；tanA＜cotA若45°＜A＜90°，则inA＞coA；tanA＞cotA．4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为m形式，正切、余切值可表示为形式，有关m的值可归纳成23顺口溜：一、二、三；三、二、一；三九二十七．巧记特殊角的三角函数值初学三角函数，记忆特殊角三角函数值易错易混。

若在理解掌握的基础上，经过变形，使其呈现某种规律，再配以歌诀，则可浅显易记，触目成诵。

仔细观察表1，你会发现重要的规律。

表1中，三角函数值的前三行，分子被开方数排列特征依次为“1，2，3，3，2，1，3，9，27”。

“一二三，三二一，三九二十七”。

记此歌诀即可。

观察表2也可发现重要的规律。

表2中，弦函数分子被开方数分别为1，2，3，3，2，1，分母都是2；切函数分子的幂指数分别是1，2，3，3，2，1，分母都是3。

据此概括歌诀为：“一二三，三二一，弦内切外莫忘记。

三角函数特殊角值表

只念上传那一个表底下的皆是无用的话没有必瞅了.
1、图示法：借帮于底下三个图形去影象，纵然有所遗记也可根据图形沉新推出：
sin30°=cos60°=2
1 sin45°=cos45°=
2
2
证明：正弦值随角度变更，即0˚ 30˚ 45˚ 60˚ 90˚变更；值从0
1变更，其余类似影象．
3、逆序影象法：瞅察表中的数值特性，可归纳为下列影象逆序：
① 有界性：（钝角三角函数值皆是正值）即当
0°＜α＜90°时，
则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0. ②删减性：（钝角的正弦、正切值随角度的删大而删大；余弦、余切值随角度的删大而减小），即当0＜A ＜B ＜90°时，则sinA ＜sinB ；tanA ＜tanB ； cosA ＞cosB ；cotA ＞cotB ；特天天：若0°＜α＜45°，则sinA ＜cosA ；tanA ＜cotA 若45°＜A ＜90°，则sinA ＞cosA ；tanA ＞cotA ．
4、心决影象法：瞅察表中的数值特性正弦、余弦值可表示为
2
m
形式，正切、余切值可表示为
3
m 形式，有闭m 的值可归纳成逆心溜：一、两、三；三、两、一；三九两十七．。

三角函数特殊角值表75794

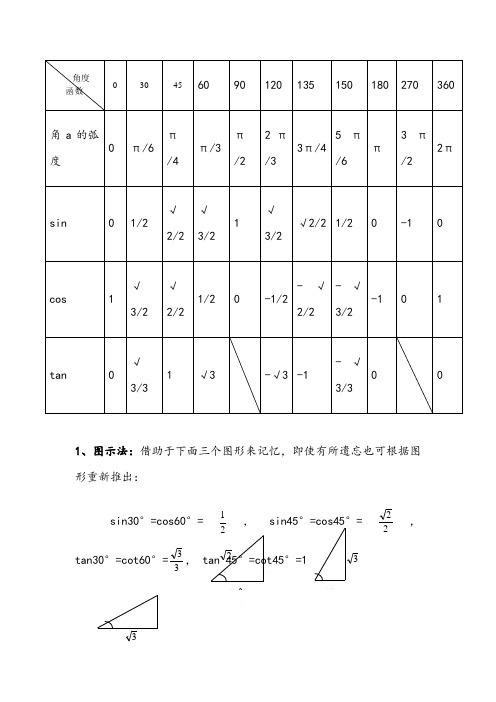
1、图示法：借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出：sin30°=cos60°=21，sin45°=cos45°=22，tan30°=cot60°=33， tan 45°=cot45°=130˚13145˚12 1603正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法：说明：正弦值随角度变化，即0˚ 30˚ 45˚ 60˚ 90˚变化；值从0212223 1变化，其余类似记忆． 3、规律记忆法：观察表中的数值特征，可总结为下列记忆规律：① 有界性：（锐角三角函数值都是正值）即当0°＜α＜90°时，则0＜sin α＜1； 0＜cos α＜1 ； tan α＞0 ； cot α＞0。

②增减性：（锐角的正弦、正切值随角度的增大而增大；余弦、余切值随角度的增大而减小），即当0＜A ＜B ＜90°时，则sin A ＜sin B ；tan A ＜tan B ； cos A ＞cos B ；cot A ＞cot B ；特别地：若0°＜α＜45°，则sin A ＜cos A ；tan A ＜cot A若45°＜A ＜90°，则sin A ＞cos A ；tan A ＞cot A ．4、口决记忆法：观察表中的数值特征正弦、余弦值可表示为2m 形式，正切、余切值可表示为3m 形式，有关m 的值可归纳成顺口溜：一、二、三；三、二、一；三九二十七．函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc 正弦函数sin （A ）=a/c 余弦函数cos （A ）=b/c 正切函数tan （A ）=a/b 余切函数cot （A ）=b/a其中a 为对边，b 为邻边，c 为斜边三角函数对照表sin sin 2sin cos 22sin sin 2cos sin 22cos cos 2cos cos 22cos cos 2sin sin 22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 化asinα ±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式）22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定，φ角的值由tan ba φ=确定六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点。

特殊角的三角函数值表格

特殊角的三角函数值表格
在三角学中，特殊角的三角函数值是非常重要的知识点。

特殊角是指常见的角度值，如0度、30度、45度、60度和90度，它们的三角函数值是固定的，具有特殊性。

下表列出了这些特殊角的正弦、余弦和正切函数值：
角度正弦（sin）余弦（cos）正切（tan）
0度010
30度1/2√3/21/√3
45度√2/2√2/21
60度√3/21/2√3
90度10无穷大
这些特殊角的三角函数值是在解决三角函数问题时经常会用到的基本数值，对于计算各种三角函数式子和题目的解答都具有很大的帮助。

熟练掌握这些数值可以提高解题效率，并对理解三角函数的概念和性质有很大帮助。

特殊角度三角函数值表

特殊角度三角函数值表特殊角度三角函数值表三角函数特殊角值表只想上传这一个表下面的.都是无用的话不用看了。

1、图示法:借助于下面三个图形来记忆，即使有所遗忘也可根据图形重新推出:sin30°=cos60°= sin45°=cos45°=12、列表法:1变化，其余类似记忆.3、规律记忆法:观察表中的数值特征，可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<<90°时，则00 ; cot>0。

②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小)，即当0cosB;cotA>cotB;特别地:若0°<<45°，则sinA若45°cosA;tanA>cotA.4、口决记忆法:观察表中的数值特征正弦、余弦值可表示为形式，正切、余切值可表示为形式，有关m的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.特殊角的三角函数值表0度sina=0,cosa=1,tana=030度sina=0,cosa=√3/2,tana=√3/345度sina=√2/2,cosa=√2/2,tana=160度sina=√3/2,cosa=1/2,tana=√390度sina=1,cosa=0,tana不存在120度sina=√3/2,cosa=-1/2,tana=-√3150度sina=1/2,cosa=-√3/2,tana=-√3/3180度sina=0,cosa=-1,tana=0270度sina=-1,cosa=0,tana不存在360度sina=0,cosa=1,tana=0。

三角函数特殊角值表

三角函数特殊角值表75587

三角函数特殊角值表

(完整版)三角函数特殊角值表

特殊角三角函数值表Word版

三角函数特殊角值表75872

三角函数特殊角值表

三角函数特殊角值表

三角函数特殊角值表

三角函数特殊角值表75794

特殊角的三角函数值 表格

特殊角度三角函数值表

特殊角的三角函数值表格