导体切割磁感线产生感应电动势的计算(15-2-4)板
电动势的计算

(B⊥L) 2、当以导体棒的中点为轴转动时 E=0 (B⊥L)
3、当以导体棒上任意一点为轴转动时 (B⊥L) 【说明】:L1与L2是导体棒的两段长度,且L1>L2)
例3、 如图所示为法拉第圆盘发电机。半径为r的导体圆 盘绕竖直轴以角速度ω旋转,匀强磁场B竖直向上,电 刷a与圆盘表面接触,接触点距圆心为r/2 ,电刷b与圆 盘边缘接触,两电刷间接有阻值为R的电阻,忽略圆盘 电阻与接触电阻,求通过电阻R的电流强度的大小和方 向。
例4、如图所示,边长为L的正方形 线框abcd的面积为S=0.1m2,匝数为 N=100匝,线框绕ad边的中点和bc边 的中点的连线由图所示位置开始以 ω=100πrad/S做匀速转动,磁感应 强度为B=0.1T。线圈内电阻不计与外 电阻R=10πΩ构成闭合电路,求: (1)感应电动势的峰值; (2)闭合电路电流的瞬时表达式; (3)若在A、B两点接入一理想电压 表,则电压表的读数为多少?
例4【解析】(1)()(3)(交流电)
一、定义式:
1、当B变,S不变时
(适用于求平均感应电动势)
2、当S变,B不变时,
注意
当B和S都变化时
例1、有一面积为S=100cm2的金属环,电阻为R=0.1Ω, 环中磁场变化规律如图所示,磁场方向垂直环面向里,则在 0.1s-0.2s内金属环中产生的感应电动势 、通过金 属环的电流 、通过金属环的电荷量为________.
例2【解析】
(1)棒ab上产生的感应电动势: E=BLV
(2)通过电阻R的电流:I
E BLV Rr Rr
,
BLV R ab间的电压: U IR Rr
(3)金属棒ab所受安培力: 所加外力为:
考点32 导体棒切割磁感线产生感应电动势的计算

考点3.2 导体切割磁感线产生感应电动势的计算1.公式E=Blv的使用条件(1)匀强磁场.(2)B、l、v三者相互垂直.2.“瞬时性”的理解(1)若v为瞬时速度,则E为瞬时感应电动势.(2)若v为平均速度,则E为平均感应电动势.3.“相对性”的理解E=Blv中的速度v是相对于磁场的速度,若磁场也运动,应注意速度间的相对关系.4. 公式中l为有效长度,即导线的首尾两端连线在沿垂直速度方向上的投影长度.5. 感应电动势的计算及电势高低的判断1.导体棒平动速度均为v,产生电动势为BLv的是(D)2.如图所示,六根形状各异的导线处在匀强磁场中,每根导线只有两个端点与MN、PQ两导轨良好接触,导线的其他部分外层涂有绝缘材料,MN、PQ相互平行.所有导线在同一平面内,若各导线运动的速度大小相同,方向沿虚线(虚线与MN、PQ平行)下列说法正确的是(C)A.因为②号导线最短:所以感应电动势最小B .②③④⑤号导线的感应电动势相同但比①⑥号小C .六根导线的感应电动势相同D .①⑥号导线形状不规则,并超过导轨宽度,无法与其他四根导线产生的感应电动势进行比较3. 如图所示,平行导轨间距为d ,一端跨接一个电阻R ,匀强磁场的磁感应强度为B ,方向垂直于平行金属导轨所在平面,一根金属棒与导轨成θ角放置,金属棒与导轨的电阻均不计,当金属棒沿垂直于棒的方向以恒定的速度v 在金属导轨上滑行时,通过电阻R 的电流是( D )A.Bdv RB.Bdv sin θRC.Bdv cos θRD.Bdv R sin θ4. 一根导体棒ab 在水平方向的匀强磁场中自由下落,并始终保持水平方向且与磁场方向垂直.如图所示,则有( C )A.U ab =0B.U ab 保持不变C.U ab 越来越大D.U ab 越来越小5. 如图所示,金属棒ab 、金属导轨和螺线管组成闭合回路,金属棒ab 在匀强磁场B 中沿导轨向右运动,则( C )A . ab 棒不受安培力作用B . a b 棒所受安培力的方向向右C . a b 棒向右运动速度越大,所受安培力越大D . 螺线管产生的磁场,A 端为N 极6. (多选)半径为a 、右端开小口的导体圆环和长为2a 的导体直杆,单位长度电阻均为R 0.圆环水平固定放置,整个内部区域分布着垂直纸面向里的匀强磁场,磁感应强度为B .直杆在圆环上以速度v 平行于直径CD 向右做匀速直线运动,直杆始终有两点与圆环良好接触,从圆环中心O 开始,直杆的位置由θ确定,如图3所示.则( AD )A. θ=0时,直杆产生的电动势为2BavB. θ=π3时,直杆产生的电动势为3BavC. θ=0时,直杆受的安培力大小为2B 2av (π+2)R 0D. θ=π3时,直杆受的安培力大小为3B 2av (5π+3)R 07. 如图所示,用铝制成⊃型框,将一质量为m 的带电小球用绝缘细线悬挂在框的上方,使整体在匀强磁场中沿垂直于磁场的方向向左以速度v 匀速运动,悬挂拉力为F ,则( A )A .F =mgB .F >mgC .F <mgD .无法确定8. 如图所示,水平地面上方有正交的匀强电场E 和匀强磁场B ,电场方向竖直向下,磁场方向垂直纸面向外,等腰三角形的金属框由底边呈水平位置开始沿竖直平面在电磁场中由静止开始下落,下落过程中三角形平面始终在竖直平面内,不计阻力,a ,b 落到地面的次序是( A )A .a 先于bB .b 先于aC .a ,b 同时落地D .无法判断9. 如图所示,在磁感应强度为B 、方向垂直纸面向里的匀强磁场中,金属杆MN 在平行金属导轨上以速度v 向右匀速滑动,MN 中产生的感应电动势为E 1;若磁感应强度增为2B ,其他条件不变,MN 中产生的感应电动势变为E 2.则通过电阻R 的电流方向及E 1与E 2之比E 1∶E 2分别为( C )A.c →a ,2∶1B.a →c ,2∶1C.a →c ,1∶2D.c →a ,1∶210. (多选)如图所示,AB 、CD 是两根固定的足够长的平行金属导轨,放置在水平面上,电阻不计,间距为L ,MN 是一根电阻为R 、长度为L 的金属杆,导轨间加垂直于纸面向里的匀强磁场,AC 间有一电阻r =R 2.现用力拉MN 以恒定的速度向右匀速运动,当开关S 断开时,MN 两点间电势差为U 1;当开关S 闭合时,MN 两点间电势差为U 2,则正确的是( BD )A.U 1=0,U 2≠0B.U 1≠0,U 2≠0C.U 1∶U 2=3∶2D.U 1∶U 2=3∶111. 在匀强磁场中,a 、b 是两条平行金属导轨,而c 、d 为串有电流表、电压表的两金属棒,如图所示,两棒以相同的速度向右匀速运动,则以下结论正确的是( )A .电压表有读数,电流表没有读数B .电压表有读数,电流表也有读数C .电压表无读数,电流表有读数D .电压表无读数,电流表也无读数12. 如图所示,两根相距为l 的平行直导轨ab 、cd ,b 、d 间连有一固定电阻R ,导轨电阻可忽略不计.MN 为放在ab 和cd 上的一导体杆,与ab 垂直,其电阻也为R .整个装置处于匀强磁场中,磁感应强度的大小为B ,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN 施力使它沿导轨方向以速度v 做匀速运动.令U 表示MN 两端的电压的大小,则( A )A .U =12Bl v ,流过固定电阻R 的感应电流由b 到d B .U =12Bl v ,流过固定电阻R 的感应电流由d 到b C .U =Bl v ,流过固定电阻R 的感应电流由b 到dD .U =Bl v ,流过固定电阻R 的感应电流由d 到b13. 粗细均匀的电阻丝围成的正方形框置于有界匀强磁场中,磁场方向垂直于线框平面,其边界与正方形线框的边平行.现使线框以同样大小的速度沿四个不同方向平移出磁场,如下图所示,则在移出过程中线框的一边ab 两点间电势差绝对值最大的是( B )14. 如图,由某种粗细均匀的总电阻为3R 的金属条制成的矩形线框abcd ,固定在水平面内且处于方向竖直向下的匀强磁场B 中.一接入电路电阻为R 的导体棒PQ ,在水平拉力作用下沿ab 、dc 以速度v 匀速滑动,滑动过程PQ 始终与ab 垂直,且与线框接触良好,不计摩擦.在PQ 从靠近ad 处向bc 滑动的过程中( C )A . PQ 中电流先增大后减小B . P Q 两端电压先减小后增大C . P Q 上拉力的功率先减小后增大D . 线框消耗的电功率先减小后增大15. (多选)如图所示,金属三角形导轨COD 上放有一根金属棒MN ,MN ⊥OD ,拉动MN 使它从O 点以速度v 在匀强磁场中向右匀速平动,若导轨和金属棒都是粗细相同的均匀导体,它们的电阻率相同,则在MN 运动过程中闭合电路的( AC )A.感应电动势逐渐增大B.感应电流逐渐增大C.感应电流将保持不变D.感应电流逐渐减小。
导体切割磁感线产生感应电动势的计算
【名师支招】电路闭合,且穿过闭合电路的磁通量发生变化,是产生感应电 流的条件。
1
如图9-1-3所示,开始时矩形线框与匀强磁 场的方向垂直,且一半在磁场内,一半在 磁场外。若要使线框中产生感应电流,下 AB 列办法中可行的是 ( C ) A.将线框向左拉出磁场 B.以ab边为轴转动(小于90°) C.以ad边为轴转动(小于60°) D.以bc边为轴转动(小于60°)
图9-1-5
热点三
楞次定律的推广含义
【例3】如图9-1-6所示,光滑固定导轨m、n水平放置,两根导体棒p、q平行放于导轨上,形成一个闭合回路, 当一条形磁铁从高处下落靠近回路时( ) A.p、q将互相靠拢 B.p、q将互相远离 C.磁铁的加速度仍为g D.磁铁的加速度小于g 图9-1-6
AD
【解析】在磁铁下落过程中,p、q是相互靠拢,还是相互远离, 取决于p、q中的感应电流所受到的磁铁的作用力方向,而磁铁的加 速度是否大于g,则取决于闭合回路对磁铁的作用力的方向。 解法一:先判断感应电流方向,再判断安培力方向。在磁铁下 落过程中,穿过 闭合回路的磁通量向下,并且不断增大,根据楞次定律可判知, 回路中感应电流的 图9-1-7 图9-1-8 磁场应向上,其中感应电流沿逆时针方向。据左手定则可判知,磁铁对p、q棒的安培力方向如图9-1-7所示,故p、q 相互靠拢。 将闭合电路的磁场等效成如图9-1-8所示条形磁铁N′S′,由此可知,磁铁下落时,闭合电路对磁铁产生向上的排斥力, 故磁铁加速下落的加速度a<g。 可见本题正确选项为A、D。 解法二:应用楞次定律的推广含义判断。 磁铁下落时,闭合电路中产生感应电流,由楞次定律的推广含义知,感应电流的产生必然阻碍导致产生感应电流的原 因——磁铁下落,故而磁铁下落时,必然受到向上的排斥力。磁铁下落的加速度a<g,故D选项正确;另一方面,磁铁下 落时,穿过闭合电路的磁通量增大,若p、q两导体棒相互远离,这会加剧磁通量的增大,这与楞次定律的含义——感应电 流阻碍磁通量的变化矛盾,故p、q棒应相互靠近,即A选项正确。
导体切割磁感线产生电动势的计算

导体切割磁感线产生电动势的计算
首先,我们来看一下导体切割磁感线产生电动势的基本原理。
根据法拉第电磁感应定律,当导体以速度v在磁感应强度为B的磁场中运动时,它在两端将产生电动势ε,其大小可以由以下公式计算得出:
ε = B l v sin(θ)。
其中,ε为导体上的感应电动势,B为磁感应强度,l为导体在磁场中的长度,v为导体在磁场中的速度,θ为磁场方向与导体运动方向的夹角。
接下来,我们通过一个例子来具体计算导体切割磁感线产生的电动势。
假设一个导体以速度v=5 m/s在磁感应强度为B=0.2 T的磁场中运动,导体的长度为l=10 m,磁场方向与导体运动方向的夹角为θ=30°,那么根据上述公式,我们可以计算出导体上的感应电动势ε的大小为:
ε = 0.2 T 10 m 5 m/s sin(30°) = 5 V.
这表明当导体以给定速度在磁场中运动时,会在导体两端产生5V的电动势。
在实际应用中,导体切割磁感线产生的电动势常常被用于发电机、电动机等设备中,利用这一原理可以将机械能转化为电能,实现能量的转换和传输。
因此,对导体切割磁感线产生电动势的计算和理解,对于电磁学的学习和工程技术的应用具有重要意义。
总之,导体切割磁感线产生电动势是一种重要的物理现象,通过对其计算和理解,我们可以更好地应用这一原理,实现能量的转换和利用,推动科学技术的发展。
法拉第电磁感应定律
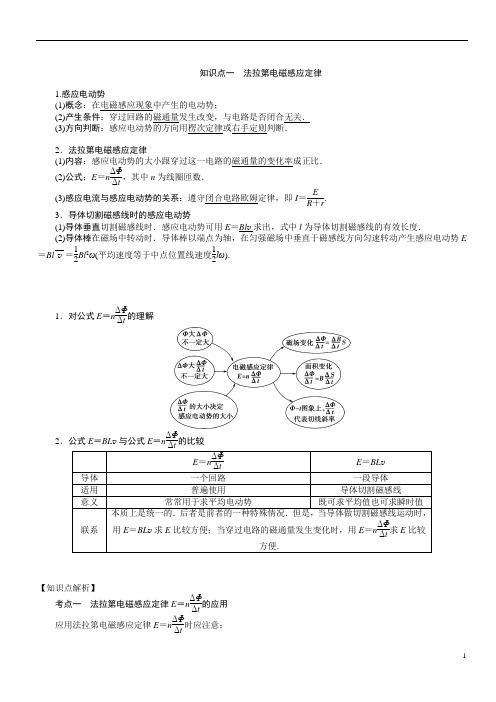
知识点一 法拉第电磁感应定律1.感应电动势(1)概念:在电磁感应现象中产生的电动势;(2)产生条件:穿过回路的磁通量发生改变,与电路是否闭合无关. (3)方向判断:感应电动势的方向用楞次定律或右手定则判断.2.法拉第电磁感应定律(1)内容:感应电动势的大小跟穿过这一电路的磁通量的变化率成正比.(2)公式:E =n ΔΦΔt,其中n 为线圈匝数.(3)感应电流与感应电动势的关系:遵守闭合电路欧姆定律,即I =ER +r.3.导体切割磁感线时的感应电动势(1)导体垂直切割磁感线时.感应电动势可用E =Bl v 求出,式中l 为导体切割磁感线的有效长度.(2)导体棒在磁场中转动时.导体棒以端点为轴,在匀强磁场中垂直于磁感线方向匀速转动产生感应电动势E=Bl v =12Bl 2ω(平均速度等于中点位置线速度12lω).1.对公式E =n ΔΦΔt的理解2.公式E =BL v 与公式E =n ΔΦΔt的比较E =nΔΦΔt E =BL v 导体 一个回路 一段导体 适用 普遍使用 导体切割磁感线意义 常常用于求平均电动势 既可求平均值也可求瞬时值联系 本质上是统一的.后者是前者的一种特殊情况.但是,当导体做切割磁感线运动时,用E =BL v 求E 比较方便;当穿过电路的磁通量发生变化时,用E =n ΔΦΔt求E 比较方便.【知识点解析】考点一 法拉第电磁感应定律E =n ΔΦΔt 的应用应用法拉第电磁感应定律E =n ΔΦΔt时应注意:(1)研究对象:E =n ΔΦΔt 的研究对象是一个回路,而不是一段导体;(2)物理意义:E =n ΔΦΔt求的是Δt 时间内的平均感应电动势,当Δt ―→0时,则E 为瞬时感应电动势;(3)E =n ΔΦΔt求得的电动势是整个回路的感应电动势,而不是回路中某段导体的电动势.整个回路的电动势为零,其回路中某段导体的感应电动势不一定为零;(4)用公式E =nS ΔBΔt求感应电动势时,S 为线圈在磁场范围内的有效面积.例 如图9-2-5甲所示,一个电阻值为R ,匝数为n 的圆形金属线圈与阻值为2R 的电阻R 1连接成闭合回路,线圈的半径为r 1,在线圈中半径为r 2的圆形区域内存在垂直于线圈平面向里的匀强磁场,磁感应强度B 随时间t 变化的关系图线如图9-2-5乙所示,图线与横、纵轴的截距分别为t 0和B 0.导线的电阻不计,求0至t 1时间内,图9-2-5(1)通过电阻R 1上的电流大小和方向;(2)通过电阻R 1上的电荷量q 及电阻R 1上产生的热量.习题小结(1)计算通过导线横截面的电荷量一定要用平均电流乘以时间. (2)由q =I ·Δt ,I =ER 总,E =n ΔΦΔt ,可导出电荷量q =n ΔΦR 总.考点二 导体切割磁感线产生感应电动势的计算对于导体平动切割磁感线产生感应电动势的计算式E =Bl v ,应从以下几个方面理解和掌握 .(1)公式使用条件:本公式是在一定条件下得出的,除了磁场是匀强磁场外,还需B 、l 、v 三者相互垂直.实际问题中当它们不相互垂直时,应取垂直的分量进行计算,公式可为E =Bl v sin θ,θ为B 与v 方向间的夹角.(2)使用范围:导体平动切割磁感线时,若v 为平均速度,则E 为平均感应电动势,即E =Bl v .若v 为瞬时速度,则E 为相应的瞬时感应电动势.(3)有效性:公式中的l 为有效切割长度,即导体与v 垂直的方向上的投影长度.图中有效长度分别为:甲图:l =cd sin β;乙图:沿v 1方向运动时,l =MN ;沿v 2方向运动时,l =0.丙图:沿v 1方向运动时,l =2R ;沿v 2方向运动时,l =0;沿v 3方向运动时,l =R例2 如图9-2-7所示,水平放置的三条光滑平行金属导轨abc ,相距均为d =1 m ,导轨ac 间横跨一质量为m =1 kg 的金属棒MN ,棒与导轨始终良好接触,棒的电阻r =2 Ω,导轨的电阻忽略不计.在导轨bc 间接一电阻为R =2 Ω的灯泡,导轨ac 间接一理想电压表.整个装置 放在磁感应强度B =2T 的匀强磁场中,磁场方向垂直导轨平面向下,现对棒MN 施加一水平向右的拉力F ,使棒从静止开始运动,试求:图9-2-7(1)若施加的水平恒力F =8 N ,则金属棒达到稳定时速度为多少?(2)若施加的水平外力功率恒定,棒达到稳定时速度为1.5 m/s ,则此时电压表的读数为多少?(3)若施加的水平外力功率恒为P =20 W ,经历t =1 s 时间,棒的速度达到2 m/s ,则此过程中灯泡产生的热量是多少?练习 如图9-2-8所示,一导线弯成闭合线圈,以速度v 向左匀速进入磁感应强度为B 的匀强磁场,磁场方向垂直平面向外.线圈总电阻为R ,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( ).图9-2-8A .感应电流一直沿逆时针方向B .线圈受到的安培力先增大,后减小C .感应电动势的最大值E =Br vD .穿过线圈某个横截面的电荷量为B (r 2+πr 2)R电磁感应中的“杆+导轨”模型单杆水平式匀强磁场与导轨垂直,磁感应强度为B ,棒ab 长为L ,质量为m ,初速度为零,拉力恒为F ,水平导轨光滑,除电阻R 外,其他电阻不计设运动过程中某时刻棒的速度为v ,由牛顿第二定律知棒ab 的加速度为a =F m -B 2L 2vmR,a 、v 同向,随速度的增加,棒的加速度a 减小,当a =0时,v 最大,I =BL vR恒定例 如图9-2-11所示,质量m 1=0.1 kg ,电阻R 1=0.3 Ω,长度l =0.4 m 的导体棒ab 横放在U 型金属框架上.框架质量m 2=0.2 kg ,放在绝缘水平面上,与水平面间的动摩擦因数μ=0.2.相距0.4 m 的MM ′、NN ′相互平行,电阻不计且足够长.电阻R 2=0.1 Ω的MN 垂直于MM ′.整个装置处于竖直向上的匀强磁场中,磁感应强度B =0.5 T .垂直于ab 施加F =2 N 的水平恒力,ab 从静止开始无摩擦地运动,始终与MM ′、NN ′保持良好接触.当ab 运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力,g 取10 m/s 2.(1)求框架开始运动时ab 速度v 的大小;(2)从ab 开始运动到框架开始运动的过程中,MN 上产生的热量Q =0.1 J ,求该过程ab 位移x 的大小.单杆倾斜式匀强磁场与导轨垂直,磁感应强度为B ,导轨间距L ,导体棒质量m ,电阻R ,导轨光滑,电阻不计棒ab 释放后下滑,此时a =g sin α,棒ab 速度v ↑→感应电动势E =BL v ↑→电流I =ER↑→安培力F =BIL ↑→加速度a ↓,当安培力F =mg sin α时,a =0,v 最大例 如图9-2-12所示,电阻可忽略的光滑平行金属导轨长s =1.15 m ,两导轨间距L =0.75 m ,导轨倾角为30°,导轨上端ab 接一阻值R =1.5 Ω的电阻,磁感应强度B =0.8 T 的匀强磁场垂直轨道平面向上.阻值r =0.5 Ω,质量m =0.2 kg 的金属棒与轨道垂直且接触良好,从轨道上端ab 处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Q 1=0.1 J .(取g =10 m/s 2)求:图9-2-12(1)金属棒在此过程中克服安培力的功W 安; (2)金属棒下滑速度v =2 m/s 时的加速度a .(3)为求金属棒下滑的最大速度v m ,有同学解答如下:由动能定理,W 重-W 安=12m v m 2,…….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.【课堂练习】1针对性练习(tnE ∆∆Φ=).图中a ~d 所示分别为穿过某一闭合回路的磁通量Φ随时间t 变化的图象,关于回路中产生的感应电动势下列论述正确的是( ).A .图a 中回路产生的感应电动势恒定不变B .图b 中回路产生的感应电动势一直在变大C .图c 中回路在0~t 1时间内产生的感应电动势小于在t 1~t 2时间内产生的感应电动势D .图d 中回路产生的感应电动势先变小再变大 2.闭合回路由电阻R 与导线组成,其内部磁场大小按B -t 图变化,方向如图9-2-4所示,则回路中( ).图9-2-4A .电流方向为逆时针方向B .电流强度越来越大C .磁通量的变化率恒定不变D .产生的感应电动势越来越大图9-2-13针对性练习(导体棒在磁场中以端点为轴转动w Bl v Bl E 221==).如图9-2-1所示,半径为r 的金属圆盘在垂直于盘面的匀强磁场B 中,绕O 轴以角速度ω沿逆时针方向匀速转动,则通过电阻R 的电流的方向和大小是(金属圆盘的电阻不计)A .由c 到d ,I =Br 2ωRB .由d 到c ,I =Br 2ωRC .由c 到d ,I =Br 2ω2RD .由d 到c ,I =Br 2ω2R图9-2-24针对性练习(S tB nE ∆∆=).在匀强磁场中,有一个接有电容器的单匝导线回路,如图9-2-2所示,已知C =30 μF ,L 1=5 cm ,L 2=8 cm ,磁场以5×10-2 T/s 的速率增加,则( ).A .电容器上极板带正电,带电荷量为6×10-5 CB .电容器上极板带负电,带电荷量为6×10-5C C .电容器上极板带正电,带电荷量为6×10-9 CD .电容器上极板带负电,带电荷量为6×10-9 C5针对性练习(能量转化).如图9-2-3所示为一光滑轨道,其中MN 部分为一段对称的圆弧,两侧的直导轨与圆弧相切,在MN 部分有如图所示的匀强磁场,有一较小的金属环如图放置在P 点,金属环由静止自由释放,经很多次来回运动后,下列判断正确的有( ).A .金属环仍能上升到与P 等高处B .金属环最终将静止在最低点C .金属环上升的最大高度与MN 等高D .金属环上升的最大高度一直在变小【课后作业】一、公式E =Bl v 的应用1.某地的地磁场磁感应强度的竖直分量方向向下,大小为4.5×10-5T .一灵敏电压表连接在当地入海河段的两岸,河宽100 m ,该河段涨潮和落潮时有海水(视为导体)流过.设落潮时,海水自西向东流,流速为2 m/s.下列说法正确的是( ).A .电压表记录的电压为5 mVB .电压表记录的电压为10 mVC .河南岸的电势较高D .河北岸的电势较高图9-2-132.如图9-2-13所示,空间存在两个磁场,磁感应强度大小均为B ,方向相反且垂直纸面,MN 、PQ 为其边界,OO ′为其对称轴.一导线折成边长为l 的正方形闭合回路abcd ,回路在纸面内以恒定速度v 0向右运动,当运动到关于OO ′对称的位置时,下列说法错误的是( ).A .穿过回路的磁通量为零B .回路中感应电动势大小为2Bl v 0C .回路中感应电流的方向为顺时针方向D .回路中ab 边与cd 边所受安培力方向相同图9-2-143.如图9-2-14,空间某区域中有一匀强磁场,磁感应强度方向水平,且垂直于纸面向里,磁场上边界b 和下边界d 水平.在竖直面内有一矩形金属线圈,线圈上下边的距离很短,下边水平.线圈从水平面a 开始下落.已知磁场上下边界之间的距离大于水平面a 、b 之间的距离.若线圈下边刚通过水平面b 、c (位于磁场中)和d 时,线圈所受到的磁场力的大小分别为F b 、F c 和F d ,则( ).A .F d >F c >F bB .F c <F d <F bC .F c >F b >F dD .F c <F b <F d二、法拉第电磁感应定律E =n ΔΦΔt的应用4.一矩形线框置于匀强磁场中,线框平面与磁场方向垂直.先保持线框的面积不变,将磁感应强度在1 s 时间内均匀地增大到原来的两倍.接着保持增大后的磁感应强度不变,在1 s 时间内,再将线框的面积均匀地减小到原来的一半.先后两个过程中,线框中感应电动势的比值为( ).A.12B .1C .2D .45.半径为r 带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d ,如图9-2-15甲所示.有一变化的磁场垂直于纸面,规定向内为正,变化规律如图9-2-15乙所示.在t =0时刻平板之间中心有一重力不计,电荷量为q 的静止微粒.则以下说法正确的是( ).图9-2-15A .第2秒内上极板为正极B .第3秒内上极板为负极C .第2秒末微粒回到了原来位置D .第2秒末两极板之间的电场强度大小为0.2πr 2d6.将闭合多匝线圈置于仅随时间变化的磁场中,线圈平面与磁场方向垂直,关于线圈中产生的感应电动势和感应电流,下列表述正确的是( ).A .感应电动势的大小与线圈的匝数无关B .穿过线圈的磁通量越大,感应电动势越大C .穿过线圈的磁通量变化越快,感应电动势越大D .感应电流产生的磁场方向与原磁场方向始终相同图9-2-167.如图9-2-16所示,足够长的U 型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN 与PQ 平行且间距为L ,导轨平面与磁感应强度为B 的匀强磁场垂直,导轨电阻不计.金属棒ab 由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab 棒接入电路的电阻为R ,当流过ab 棒某一横截面的电量为q 时,棒的速度大小为v ,则金属棒ab 在这一过程中( ).A .运动的平均速度大小为12vB .下滑的位移大小为qRBLC .产生的焦耳热为qBL vD .受到的最大安培力大小为B 2L 2vRsin θ。
【第37课时法拉第电磁感应定律】考点二 导体切割磁感线产生感应电动势的计算

考点二导体切割磁感线产生感应电动势的计算(高频55)1.公式E=Blv的使用条件(1) 匀强磁场.(2)B、l、v三者相互垂直.2.“瞬时性”的理解(1)若v为瞬时速度,则E为瞬时感应电动势.(2)若v为平均速度,则E为平均感应电动势.3.切割的“有效长度”公式中的l为有效切割长度,即导体在与v垂直的方向上的投影长度.图中有效长度分别为:甲图:沿v1方向运动时,l=cd;沿v2方向运动时,l=cd·sin β;乙图:沿v1方向运动时,l=MN;沿v2方向运动时,l=0 ;丙图:沿v1方向运动时,l=2R;沿v2方向运动时,l=0 ;沿v3方向运动时,l=R.4.“相对性”的理解E=Blv中的速度v是相对于磁场的速度,若磁场也运动,应注意速度间的相对关系.【温馨提示】E=n ΔΦΔt、E=Blv的比较(1)区别:E=n ΔΦΔt常用于求平均感应电动势;E=Blv既可求平均值,也可以求瞬时值.(2)联系:E=Blv是E=n ΔΦΔt的一种特殊情况.当导体做切割磁感线运动时,用E=Blv求E比较方便,当穿过电路的磁通量发生变化时,用E=n ΔΦΔt求E比较方便.命题点1 平动切割类3.如图,水平面(纸面)内间距为l的平行金属导轨间接一电阻,质量为m、长度为l的金属杆置于导轨上.t=0时,金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动.t 0时刻,金属杆进入磁感应强度大小为B 、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.杆与导轨的电阻均忽略不计,两者始终保持垂直且接触良好,两者之间的动摩擦因数为μ.重力加速度大小为g .求:(1)金属杆在磁场中运动时产生的电动势的大小; (2)电阻的阻值.【解析】 (1)对金属杆由牛顿第二定律:F -μmg =ma 匀加速直线运动:v =at 0 动生电动势:E =Blv 解得:E =Blt 0⎝ ⎛⎭⎪⎫F m -μg .(2)金属杆进磁场后匀速运动:F =μmg +BIl 由欧姆定律:I =E R得:R =B 2l 2t 0m.【答案】 (1)Blt 0⎝ ⎛⎭⎪⎫F m -μg(2)B 2l 2t 0m4.如图所示,两条相距d 的平行金属导轨位于同一水平面内,其右端接一阻值为R 的电阻.质量为m 的金属杆静置在导轨上,其左侧的矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下.当该磁场区域以速度v0匀速地向右扫过金属杆后,金属杆的速度变为v.导轨和金属杆的电阻不计,导轨光滑且足够长,杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:(1)MN刚扫过金属杆时,杆中感应电流的大小I;(2)MN刚扫过金属杆时,杆的加速度大小a;(3)PQ刚要离开金属杆时,感应电流的功率P.【解析】(1)MN刚扫过金属杆时,金属杆的感应电动势E=Bdv0①回路的感应电流I=E R ②由①②式解得I=BdvR.③(2)金属杆所受的安培力F=BId④由牛顿第二定律得,对金属杆F=ma⑤由③④⑤式得a=B2d2v0 mR.⑥(3)金属杆切割磁感线的相对速度v′=v0-v⑦感应电动势E=Bdv′⑧感应电流的电功率P=E2 R⑨由⑦⑧⑨式得P=B2d2v-v2R⑩【答案】(1)BdvR(2)B2d2vmR(3)B2d2v-v2R命题点2 转动切割类5.半径分别为r和2r的同心圆形导轨固定在同一水平面内,一长为r、质量为m且质量分布均匀的直导体棒AB置于圆导轨上面,BA的延长线通过圆导轨中心O,装置的俯视图如图所示.整个装置位于一匀强磁场中,磁感应强度的大小为B,方向竖直向下.在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻(图中未画出).直导体棒在水平外力作用下以角速度ω绕O逆时针匀速转动,在转动过程中始终与导轨保持良好接触.设导体棒与导轨之间的动摩擦因数为μ,导体棒和导轨的电阻均可忽略.重力加速度大小为g.求:(1)通过电阻R的感应电流的方向和大小;(2)外力的功率.【思路点拨】 1.由右手定则可判断导体电流方向(电源内部电流方向)→通过R 的电流方向;2.由法拉第电磁感应定律→感应电动势→欧姆定律求电流;3.能的转化和守恒→确定各部分的功率.【解析】(1)在Δt时间内,导体棒扫过的面积为:ΔS=12ωΔt[(2r)2-r2]①根据法拉第电磁感应定律,导体棒产生的感应电动势大小为:E=BΔS Δt②根据右手定则,感应电流的方向是从B端流向A端,因此流过电阻R的电流方向是从C 端流向D 端;由欧姆定律:I =E R③ 联立①②③可得:I =3ωBr 22R ④(2)在竖直方向有:mg -2F N =0⑤式中,由于质量分布均匀,内、外圆导轨对导体棒的正压力相等,其值为F N ,两导轨对运动的导体棒的滑动摩擦力均为:F f =μF N ⑥在Δt 时间内,导体棒在内、外圆导轨上扫过的弧长分别为:l 1=rωΔt ⑦l 2=2rωΔt ⑧克服摩擦力做的总功为:W f =F f (l 1+l 2)⑨在Δt 时间内,消耗在电阻R 上的功为:W R =I 2R Δt ⑩ 根据能量转化和守恒定律,外力在Δt 时间内做的功为:W =W f +W R ⑪ 外力的功率为:P =W Δt⑫由④~⑫式可得:P =32μmgωr +9ω2B 2r 44R .【答案】 (1)C 端流向D 端 3ωBr 22R(2)32μmgωr +9ω2B 2r 44R求解感应电动势大小的计算方法(1)试求上题中的金属棒AB转动一周的过程中AB棒和电阻R产生的热量以及通过导体棒截面的电荷量各是多少?(2)若圆形导轨单位长度的电阻为R,导体棒的电阻不计.试求导体棒AB在转动一周过程中U CD的取值范围.【探究提示】(1)T=2πω,AB棒与导轨间由于摩擦产生的热量Q1=P f·T=32μmgωr·2πω=3πμmgr;电阻R上产生的焦耳热Q2=P R·T=9B2ω2r44R·2πω=9πB2ωr42R ;通过AB棒截面的电荷量q=It=3Br2ω2R·2πω=3πBr2R(2)当AB棒转到与C、D两点对称处时电路总阻值最大,等效电路如下图所示:其中R′=πrR,R″=2πrRUCD的最小值为:RπrR 2+πrR+R·32Br2ω=3Br2ω3πr+2当AB棒转到与C、D两点重合时U CD最大为32Br2ω故3Br2ω3πr+2≤U CD≤32Br2ω。
导体切割磁感线产生的感应电动势-2019届高考物理---精校解析 Word版

(3)相对性:E=Blv中的速度v是相对于磁场的速度,若磁场也运动时,应注意速度间的相对关系。
2. 转动切割当导体在垂直于磁场的平面内,绕一端以角速度ω如图所示。
如图所示,长为l的金属棒ab,绕b端在垂直于匀强磁场的平面内以角速度小为B,ab棒所产生的感应电动势大小可用下面两种方法推出。
方法一:棒上各处速率不同,故不能直接用公式正比,故可用棒的中点的速度作为平均切割速度代入公式计算。
ωlA.磁感应强度的大小为0.5 TB.导线框运动的速度的大小为0.5 m/sC.磁感应强度的方向垂直于纸面向外(1)根据法拉第电磁感应定律(2)已知B=0.2 T,L=A.回路电流I1∶B.产生的热量A .因右边面积减少B .因右边面积减少A.θ=0时,杆产生的感应电动势为B.θ=π3时,杆产生的感应电动势为C.θ=0时,杆受到的安培力大小为A .感应电流方向始终沿顺时针方向不变B .CD 段直导线始终不受安培力A .I =Br 2ωR ,由c C .I =Br 2ω2R ,由cA.C点电势一定高于B.圆盘中产生的感应电动势大小为C.电流表中的电流方向为由D.若铜盘不转动,使所加磁场磁感应强度均匀增大,在铜盘中可以产生涡旋电流A.B2ω2r2RB.C.B2ω2r4D.A.金属棒中电流从BB.金属棒两端电压为C.电容器的M板带负电A.若圆盘转动的角速度恒定,则电流大小恒定B.若从上向下看,圆盘顺时针转动,则电流沿C.若圆盘转动方向不变,角速度大小发生变化,则电流方向可能发生变化A.U a >U c ,金属框中无电流B.U b >U c ,金属框中电流方向沿C.U bc =-12Bl由力的平衡可知由动能定理可得故D,则感应电动势最大值为届江西省红色七校高三第一次联考)A. R1中无电流通过错误;感应电动势为:的电压为:ab克服安培力做的功等于电阻棒经过环心时所受安培力的大小为棒运动过程中产生的感应电流在棒中由A流向Cat,故=,故=正确。
4. 导体切割磁感线产生感应电动势的计算

导体切割磁感线产生感应电动势的计算1.公式E=Bl v的使用条件(1)匀强磁场.(2)B、l、v三者相互垂直.(3)如不垂直,用公式E=Bl v sin θ求解,θ为B与v方向间的夹角.2.“瞬时性”的理解若v为瞬时速度,则E为瞬时感应电动势.若v为平均速度,则E为平均感应电动势,即E=Bl v.3.切割的“有效长度”公式中的l为有效切割长度,即导体在与v垂直的方向上的投影长度.图10中有效长度分别为:图10甲图:l=cd sin β;乙图:沿v1方向运动时,l=MN;沿v2方向运动时,l=0.丙图:沿v1方向运动时,l=2R;沿v2方向运动时,l=0;沿v3方向运动时,l=R. 4.“相对性”的理解E=Bl v中的速度v是相对于磁场的速度,若磁场也运动,应注意速度间的相对关系.对点练习1. 如图所示,两根相距为l的平行直导轨ab、cd.b、d间连有一定值电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向纸面内).现对MN施力使它沿导轨以速度v做匀速运动.令U表示MN两端电压的大小,则()图11A.U=12v Bl B.U=13v BlC.U=v Bl D.U=2v Bl2. 如图所示,两光滑平行金属导轨间距为L,直导线MN垂直跨在导轨上,且与导轨接触良好,整个装置处在垂直于纸面向里的匀强磁场中,磁感应强度为B.电容器的电容为C,除电阻R外,导轨和导线的电阻均不计.现给导线MN一初速度,使导线MN向右运动,当电路稳定后,MN以速度v向右做匀速运动时()图12A.电容器两端的电压为零B.电阻两端的电压为BL vC.电容器所带电荷量为CBL vD.为保持MN匀速运动,需对其施加的拉力大小为B2L2v R(2020年教材) 1. 如图所示,在竖直向下的匀强磁场中,将一水平放置的金属棒ab以水平速度v0抛出.设整个过程中棒的方向不变,且不计空气阻力,则金属棒运动过程中产生的感应电动势的大小变化情况应是()A.越来越大B.越来越小C.保持不变D.无法判断如图所示,两根相距为L的竖直平行金属导轨位于磁感应强度为B. 方向垂直纸面向里的匀强磁场中,导轨电阻不计,另外两根与上述光滑导轨保持良好接触的金属杆ab、cd质量均为m,电阻均为R.若要使cd静止不动,则ab杆应沿导轨向___运动,速度大小为___,作用于ab杆上竖直拉力的大小为___.2. 如图所示,P、Q是两根竖直且足够长的金属杆(电阻忽略不计),处在垂直纸面向里的匀强磁场B中,MN是一个螺线管,它的绕线方式没有画出,P、Q的输出端a、b和MN的输入端c、d之间用导线相连,A是在MN的正下方水平放置在地面上的金属圆环。
热点突破导体切割磁感线产生感应电动势的计算

热点突破导体切割磁感线产生感应电动势的计算导体切割磁感线产生感应电动势是电磁感应的基本原理之一,它在许多实际应用中起着重要的作用。
本文将介绍导体切割磁感线所产生的感应电动势的计算方法。
电磁感应原理依据法拉第电磁感应定律,即导体切割磁感线时,会产生感应电动势,其大小与导体切割磁感线的速度以及磁感线的强度有关。
对于导体在磁场中作直线运动的情况,感应电动势的计算公式可以用法拉第电磁感应定律表示为:ε=-N*ΔΦ/Δt其中,ε表示感应电动势,N表示导线的匝数,ΔΦ表示磁感线的磁通量,Δt表示时间的变化量。
这个公式表明,当导体切割的磁感线的磁通量变化时,会产生感应电动势。
对于导体在磁场中作回路运动的情况,感应电动势的计算公式可以用柯尔赛定律表示为:ε=-N*ΔΦ/Δt其中,N表示回路的匝数,ΔΦ表示穿过回路的磁感线的磁通量,Δt表示时间的变化量。
这个公式与直线运动的情况类似,都是表示导体切割磁感线产生的感应电动势。
在实际应用中,为了计算导体切割磁感线产生的感应电动势,可以根据具体的实验条件和系统特性进行计算。
一种常见的方法是利用楞次定律和奥姆定律。
楞次定律表明,当导体切割磁场时,电流将会在导体中产生,而该电流产生的电磁场会抵消掉原始磁场。
根据楞次定律,可以计算出感应电动势。
奥姆定律则表明,导体中的电流产生的电压与电流成正比。
根据奥姆定律,可以计算出感应电动势。
通过对楞次定律和奥姆定律的应用,我们可以计算导体切割磁感线所产生的感应电动势。
具体的计算方法包括:1.确定导体切割的磁感线的速度和磁感线的强度。
这些参数可以通过实验测定或者通过计算得到。
2.确定导体的几何形状和导体上的电流的分布情况。
这些参数也需要通过实验测定或者通过计算得到。
3.利用楞次定律和奥姆定律,计算出导体切割磁感线所产生的感应电动势。
需要注意的是,以上的计算方法是针对导体作直线或者回路运动的情况。
在实际应用中,还会存在其他复杂情况,如导体的弯曲、磁场的非均匀性等因素,这些因素的存在会对感应电动势的计算产生影响。
热点突破导体切割磁感线产生感应电动势的计算PPT学习教案

第17页/共22页
转解析
五、真题演 练
➢5.真题演练
第19页/共22页
【真题】 (2013·海南卷,6)如图,水平桌面上固定有一半径为 R 的金属细圆环,环面水平,圆环每单位长度的电阻为 r,空间有一 匀强磁场,磁感应强度大小为 B,方向竖直向下;一长度为 2R、电 阻可忽略的导体棒置于圆环左侧并与环相切,切点为棒的中点. 棒在拉力的作用下以恒定加速度 a 从静止开始向右运动,运动过 程中棒与圆环接触良好.下列说法正确的是( ). A.拉力的大小在运动过程中保持不变 B.棒通过整个圆环所用的时间为 2R/a C.棒经过环心时流过棒的电流为 B 2aR/πr
【变式训练 3】 [转动切割](2015·新课标全国卷Ⅱ,15)如图,直角三 角形金属框 abc 放置在匀强磁场中,磁感应强度大小为 B,方向平行于 ab 边向上。当金属框绕 ab 边以角速度 ω 逆时针转动时,a、b、c 三点 的电势分别为 Ua、Ub、Uc。已知 bc 边的长度为 l。下列判断正确的是( ) A.Ua>Uc,金属框中无电流 B.Ub>Uc,金属框中电流方向沿 a-b-c-a C.Ubc=-12Bl2ω,金属框中无电流 D.Ubc=12Bl2ω,金属框中电流方向沿 a-c-b-a
D.棒经过环心时所受安培力的大小为 8B2R 2aR/πr
a
审题 (12)导体棒在经运过动圆过心程时中,速受此变刻化两?侧运的动总过电程阻遵为从多哪少些?怎物样理求规此律刻?流为过什棒么的?电流
及棒所受安培力?
转解析
第20页/共22页
第12页/共22页
转解析
四、跟踪训 练
➢4.跟踪训练
第14页/共22页
【跟踪训练】 如图所示,水平放置的 U 形框架上接一个阻值为
模型21 单杆切割模型(解析版)

模型21 单杆切割(解析版)导体切割磁感线产生的感应电动势(1)导体切割磁感线产生的感应电动势:①当导体棒垂直于磁场运动,B、l、v两两垂直时,E=Blv。
②当导线的运动方向与导线本身垂直,但与磁感线方向夹角为θ时,E=Blv sin θ。
(2)用公式E=计算的感应电动势是平均电动势,只有在电动势不随时间变化的情况下平均电动势才等于瞬时电动势。
用公式E=BLv计算电动势时,如果v是瞬时速度,那么电动势是瞬时值;如果v是平均速度,那么电动势是平均值。
(3)公式E=是计算感应电动势的普遍适用的公式,公式E=BLv则是E=的一个特例。
公式E=BLv成立的条件是L、v、B三者两两垂直。
如果不是两两垂直,那么L取导线在垂直于B方向的有效长度,v取垂直于B方向的分速度。
(4)E=是求整个回路的总电动势,并且求出的是Δt时间内的平均感应电动势,而公式E=BLv求出的只是切割磁感线的那部分导体中的感应电动势,不一定是回路中的总感应电动势,并且它一般用于求某一时刻的瞬时感应电动势。
【典例1】如图,一直导体棒质量为m、长为l、电阻为r,其两端放在位于水平面内间距也为l的光滑平行导轨上,并与之密接;棒左侧两导轨之间连接一可控制的负载电阻(图中未画出);导轨置于匀强磁场中,磁场的磁感应强度大小为B,方向垂直于导轨所在平面。
开始时,给导体棒一个平行于导轨的初速度v0。
在棒的运动速度由v0减小至v1的过程中,通过控制负载电阻的阻值使棒中的电流强度I保持恒定。
导体棒一直在磁场中运动。
若不计导轨电阻,求此过程中导体棒上感应动势的平均值和负载电阻上消耗的平均功率。
【解析】导体棒所受的安培力为F=IlB①该力大小不变,棒做匀减速运动,因此在棒的速度从v 0减小到v 1的过程中,平均速度为 011()2v v v =+ ② 当棒的速度为v 时,感应电动势的大小为E=lvB ③棒中的平均感应电动势为E lvB = ④由②④式得011()2E l v v B =+ ⑤ 导体棒中消耗的热功率为21P I r = ⑥负载电阻上消耗的平均功率为21P EI P =- ⑦由⑤⑥⑦式得22011()2P l v v BI I r =+- ⑧ 【变式训练1】如图,两根相距L =0.4m 、电阻不计的平行光滑金属导轨水平放置,一端与阻值R =0.15Ω的电阻相连。
导体切割磁感线产生电动势的计算

导体切割磁感线产生电动势的计算导体切割磁感线产生电动势是电磁感应现象的一种重要表现。
当导体在磁场中运动或者磁场发生变化时,会产生感应电流,这个现象可以用法拉第电磁感应定律来描述。
在本文中,我们将讨论如何计算导体切割磁感线产生的电动势。
首先,让我们来看看法拉第电磁感应定律的数学表达式:\[ \mathcal{E} = -\frac{d\Phi}{dt} \]其中,$\mathcal{E}$代表感应电动势,$\Phi$代表磁通量,$t$代表时间。
这个公式告诉我们,感应电动势的大小与磁通量的变化率成正比。
现在,假设一个导体以速度$v$在磁感线方向上移动,磁感应强度为$B$,导体的长度为$l$。
在时间间隔$\Delta t$内,导体切割磁感线的磁通量的变化量可以用以下公式来表示:\[ \Delta \Phi = B \cdot l \cdot \Delta x \]其中,$\Delta x$代表导体在时间间隔$\Delta t$内切割的磁感线的长度。
因此,感应电动势$\mathcal{E}$可以表示为:\[ \mathcal{E} = -\frac{\Delta \Phi}{\Delta t} = -B\cdot l \cdot \frac{\Delta x}{\Delta t} \]根据导体的速度$v$的定义,我们知道$\frac{\Deltax}{\Delta t} = v$,所以感应电动势可以进一步表示为:\[ \mathcal{E} = -B \cdot l \cdot v \]这个公式告诉我们,当导体以速度$v$在磁感线方向上移动时,感应电动势的大小与磁感应强度$B$、导体长度$l$和速度$v$都成正比。
综上所述,我们可以通过上述公式来计算导体切割磁感线产生的电动势。
这个计算对于理解电磁感应现象和应用于电磁感应相关的问题具有重要意义。
导体棒切割磁感线产生感应电动势公式

导体棒切割磁感线产生感应电动势公式
当导体棒切割磁感线时,会在导体内部产生感应电动势。
这是基
于法拉第电磁感应定律的原理,即磁通量的变化会导致感应电动势的
产生。
具体来说,当导体棒以速度v沿着磁场方向运动时,磁感线就会
随着导体棒的运动而切割导体棒,这样就会导致磁通量发生变化。
而
根据法拉第电磁感应定律,这个磁通量的变化就会在导体内部产生一
个感应电动势E,其大小与磁通量变化速率的乘积成正比。
具体来说,根据电动势的定义公式E=Blv,其中B代表磁场强度,
l代表导体棒的长度,v代表导体棒相对于磁场的运动速度。
因此,可
以发现,当导体棒的速度越大或者导体棒越长,磁场强度越大时,感
应电动势也会相对更大。
此外,还需要注意的是,运动方向所产生的电势方向由电磁感应
定律中的楞次定律确定。
如果导体在平行磁场中运动,则电势方向与
磁场线方向垂直,且当导体运动速度越大时,感应电动势也会相对更大;如果导体垂直于磁场运动,则感应电动势的大小与导体的速度有关,且其方向按右手定则决定。
这些细微的区别需要我们在实际使用时加
以注意。
总之,导体棒切割磁感线产生感应电动势公式是一个重要的基本
物理公式,我们需要在实际运用时灵活掌握,以便更好地应用于实际
问题中,从而使我们的研究和应用更具成效。
导体切割磁感线产生感应电动势的计算

导轨匀速下滑时,将该微粒沿原
来的中心线水平射入金属板间,
若微粒最后碰到金属板并被吸收.
求微粒在金属板间运动的时间t.
(1)棒匀速下滑,有
回路中的电流
将R=3r代入棒下滑的速率
金属板间的电压
带电微粒在板间匀速运动,有
联立解得带电微粒的质量
导体棒沿导轨匀速下滑,回路电流
保持不变,金属板间的电压
体棒MN垂直于导轨放置,质量为0.2 kg,接
入电路的电阻为1 Ω,两端与导轨接触良好,
与导轨间的动摩擦因数为0.5.在导轨间存在着
垂直于导轨平面的匀强磁场,磁感应强度为
0.8 T.将导体棒MN由静止释放,运动一段时
间后,小灯泡稳定发光,此后导体棒MN的运
动速度以及小灯泡消耗的电功率分别为 (
).
A.2.5 m/s 1 W
电压增大使微粒射入后向上偏转,有
联立解得微粒在金属板间运动的时间
【典例4】 如图,水平桌面上固定有一半
径为R的金属细圆环,环面水平,圆环每单位
长度的电阻为r,空间有一匀强磁场,磁感应
强度大小为B,方向竖直向下;一长度为2R、
电阻可忽略的导体棒置于圆环左侧并与环相
切,切点为棒的中点.棒在拉力的作用下以恒
1 2
=
,A 错、B 对;由功能关系得 Fd= mv +Q+Qμ,C
2
R0+r
2BLd
错;此过程中平均感应电流为 I =
,通过电阻 R0 的电
R0+rΔt
2BLd
荷量为 q= I Δt=
,D 对.
R0+r
答案
BD
6.如图所示,质量为M的导体棒ab,垂直放在
导体切割磁感线产生感应电动势的计算

导体切割磁感线产生感应电动势的计算ε=-ΔΦ/Δt其中,ε是感应电动势,ΔΦ是磁通量的变化量,Δt是时间的变化量。
首先,我们先了解一些基本概念。
磁通量(Φ)是磁感线穿过一些表面的数量度量,单位是韦伯(Wb)。
感应电动势(ε)是导体中产生的电压,单位是伏特(V)。
时间(t)的单位是秒(s)。
当导体与磁场的相对运动会导致磁通量的变化。
为了计算感应电动势,我们需要知道磁通量的变化量。
通常情况下,磁通量(Φ)通过以下公式计算:Φ = B * A * cosθ其中,B是磁感应强度,A是被磁感线穿过的面积,θ是磁感线和法线之间的夹角。
在导体切割磁感线的过程中,磁通量会发生变化,因此会产生感应电动势。
假设一个导体切割磁感线穿过一个导线的圆环。
假设磁感应强度是B,圆环的半径是r,圆环中心和磁场方向之间的夹角是θ。
导体在时间Δt内旋转角度Δϴ。
在这种情况下,磁通量的变化量可以表示为:ΔΦ = B * A * (cos(θ+Δϴ) - cosθ)导线上的感应电动势可以表示为:ε=-ΔΦ/Δt将ΔΦ的表达式代入,可以得到:ε = - (B * A * (co s(θ+Δϴ) - cosθ)) / Δt为了计算方便,可以根据夹角的小角度近似(cosθ≈1 - θ^2/2)来简化公式。
ε≈-(B*A*((1-(θ+Δϴ)^2/2)-(1-θ^2/2)))/Δt化简后可得:ε≈-(B*A*(θ^2/2-(θ+Δϴ)^2/2))/Δt进一步化简:ε≈-(B*A*(θ^2/2-(θ^2+2θΔϴ+Δϴ^2)/2))/Δtε≈-(B*A*(θΔϴ+Δϴ^2/2))/Δt最后,如果Δϴ趋近于0,可以忽略Δϴ^2项,得到近似公式:ε≈-(B*A*θΔϴ)/Δt这就是导体切割磁感线产生感应电动势的近似计算公式。
需要注意的是,这仅适用于小角度的情况,磁感应强度、面积和角度必须以SI单位计算,公式中的除法应该使用正常的数学除法运算。
通过计算感应电动势,我们可以了解磁场和导体之间的相互作用,并在实际的电磁设备中应用这个原理。
【2018新课标 高考必考知识点 教学计划 教学安排 教案设计】高二物理:导体切割磁感线产生感应电动势的计算

一、导体平动切割磁感线对于导体平动切割磁感线产生感应电动势的计算式E =Blv ,应从以下几个方面理解和掌握。
(1)正交性本公式是在一定条件下得出的,除了磁场是匀强磁场,还需B 、l 、v 三者相互垂直。
实际问题中当它们不相互垂直时,应取垂直的分量进行计算,公式可为E =Blv sin θ,θ为B 与v 方向间的夹角。
(2)平均性导体平动切割磁感线时,若v 为平均速度,则E 为平均感应电动势,即E Blv 。
(3)瞬时性若v 为瞬时速度,则E 为相应的瞬时感应电动势。
(4)有效性公式中的l 为有效切割长度,即导体与v 垂直的方向上的投影长度。
图中有效长度分别为:甲图:l =cd sin β(容易错算成l =ab sin β)。
乙图:沿v 1方向运动时,l =MN ;沿v 2方向运动时,l =0。
丙图:沿v 1方向运动时,l =2R ;沿v 2方向运动时,l =0;沿v 3方向运动时,l =R 。
(5)相对性E =Blv 中的速度v 是相对于磁场的速度,若磁场也运动时,应注意速度间的相对关系。
二、导体转动切割磁感线当导体在垂直于磁场的平面内,绕一端以角速度ω匀速转动时,产生的感应电动势为E=Bl v =12Bl 2ω,如图所示。
例题1 如图所示,一段导线弯曲成半径为R 的半圆形闭合回路。
虚线MN 、PQ 间有磁感应强度为B 的匀强磁场,磁场的宽度等于R ,方向垂直于回路所在的平面。
现让回路以速度v 向右匀速穿过磁场,直径CD 始终与MN 垂直。
关于此过程,下列结论正确的是( )A. 穿过的过程中回路中感应电流一直不为零B. 感应电流的方向一直不变C. 感应电动势先增大后减小再增大再减小D. 感应电动势最大值E m =2BRv解析:当回路的圆心到磁场的中间时,(切割磁感线的有效长度为0),回路中的感应电动势为零,电流为零,A 项错误;磁通量先向里增大,后向里减小,根据楞次定律,感应电流的方向先沿逆时针方向后沿顺时针方向,B 项错误;当回路的圆心到MN 或PQ 上时,切割磁感线的有效长度最长,感应电动势最大为BRv ,D 项错误;在穿过磁场的过程中,回路切割磁感线的有效长度先变大,后变小,再变大,再变小,因此感应电动势先增大后减小再增大再减小,C 项正确。
导体切割磁感线产生感应电动势的理解与例题分析

导体切割磁感线产⽣感应电动势的理解与例题分析导体切割磁感线产⽣感应电动势的理解与例题分析⼀、知识概观1.导体切割磁感线时产⽣感应电动势那部分导体相当于电源。
在电源内部,电流从负极流向正极。
不论回路是否闭合,都设想电路闭合,由楞次定律或右⼿定则判断出感应电流⽅向,根据在电源内部电流从负极到正极,就可确定感应电动势的⽅向。
2. 导体棒平动切割公式:E=BLv ,由法拉第电磁感应定律可以证明。
公式的⼏点说明:(1)公式仅适⽤于导体棒上各点以相同的速度切割匀强的磁场的磁感线的情况。
如匀强磁场和⼤⼩均匀的辐向磁场。
(2)公式中的B 、v 、L 要求互相两两垂直,即L ⊥B ,L ⊥v 。
⽽v 与B成θ夹⾓时,可以将导体棒的速度v 分解为垂直于磁场⽅向的分量和沿磁场⽅向的分量,如图1所⽰,显然对感应电动势没有贡献。
所以,导体棒中感应电动势为θsin BLv BLv E ==⊥。
(3)公式中v 为瞬时速度,E 为瞬时感应电动势, v 为平均速度,E 为平均感应电动势。
(4)若导体棒是曲线,则公式中的L 为切割磁感线的导体棒的有效长度,有效长度的长度为曲线两端点的边线长度。
3. 导体棒转动切割长为L 的导体棒在磁感应强度为B 的匀强磁场中以ω匀速转动,产⽣的感应电动势:4.线圈匀速转动切割n 匝⾯积为S 的线圈在B 中以⾓速度ω绕线圈平⾯内的任意轴,产⽣的感应电动势:线圈平⾯与磁感线平⾏时,感应电动势最⼤:(n 为匝数)。
线圈平⾯与磁感线垂直时,E=0线圈平⾯与磁感线夹⾓为θ时,θωsin nBs E =(与⾯积的形状⽆关)。
⼆、例题分析【例题1】如图2所⽰,将均匀电阻丝做成的边长为l 的正⽅形线圈abcd 从磁感应强度为B 的匀强磁场中以速度v 向右匀速拉出的过程中,线圈中产⽣了感应电动势。
相当于电源的是边,端相当于电源的正极,ab 边上产⽣的感应电动势E = 。
ab 边两端的电压为,另3边每边两端的电压均为。
导体切割磁感线产生感应电动势的计算(15-2-4)

导体切割磁感线产生感应电动势的计算1.公式E =BLv 的使用条件(1)匀强磁场.(2)B 、L 、v 三者相互垂直.(3)如不垂直,用公式E =BLv sin θ求解,θ为B 与v 方向间的夹角.2.“瞬时性”的理解若v 为瞬时速度,则E 为瞬时感应电动势.若v 为平均速度,则E 为平均感应电动势,即E =BL v . 3.切割的“有效长度”公式中的L 为有效切割长度,即导体与v 垂直的方向上的投影长度.图中有效长度分别为:4.“相对性”的理解E =BLv 中的速度v 是相对于磁场的速度,若磁场也运动,解决电磁感应中的电路问题三步曲1.确定电源.切割磁感线的导体或磁通量发生变化的回路将产生感应电动势,该导体或回路就相当于电源,利用E =n ΔΦΔt 或E =BLv sin θ求感应电动势的大小,利用右手定则或楞次定律判断电流方向.2.分析电路结构(内、外电路及外电路的串、并联关系),画出等效电路图.3.利用电路规律求解.主要应用欧姆定律及串、并联电路的基本性质等列方程求解.1.如图所示,在一匀强磁场中有一U 型导线框bacd ,线框处于水平面内,磁场与线框平面垂直,R 为一电阻,ef 为垂直于ab 的一根导体杆,它可以在ab 、cd 上无摩擦地滑动,杆ef 及线框中导体的电阻都可不计.开始时,给ef 一个向右的初速度,则( ) A .ef 将减速向右运动,但不是匀减速B .ef 将匀减速向右运动,最后静止C .ef 将匀速向右运动D .ef 将做往复运动 解析:杆ef 向右运动,所受安培力F =BIl =Bl Bl v R =B 2l 2v R,方向向左,故杆做减速运动;v 减小,F 减小,杆做加速度逐渐减小的减速运动,A 正确.答案:A2、如图所示,金属杆ab 、cd 可以在光滑导轨PQ 和RS 上滑动,匀强磁场方向垂直纸面向里.当ab 、cd 分别以速度v 1和v 2滑动时,发现回路感生电流方向为逆时针方向,则v 1和v 2的大小、方向可能是A.v 1>v 2,v 1向右,v 2向左 B .v 1>v 2,v 1和v 2都向左C.v 1=v 2,v 1和v 2都向右D.v 1=v 2,v 1和v 2都向左3.(2014·无锡模拟)如图所示,在竖直向下的匀强磁场中,将一水平放置的金属棒ab 以水平初速度v 0抛出,设在整个过程棒的方向不变且不计空气阻力,则在金属棒运动过程中产生的感应电动势大小变化情况是( )A .越来越大B .越来越小C .保持不变D .无法判断解析:金属棒ab 切割磁感线,产生感应电动势而不产生感应电流,没有安培力产生,在重力作用下做平抛运动,垂直于磁感线方向速度不变,始终为v 0,由公式E =BL v 知,感应电动势为BL v 0不变,故A 、B 、D 错误,C 正确.答案:C4.如图所示,竖直平面内有一金属环,半径为a ,总电阻为R (指拉直时两端的电阻),磁感应强度为B 的匀强磁场垂直穿过环平面,在环的最高点A 用铰链连接长度为2a 、电阻为R 2的导体棒AB ,AB 由水平位置紧贴环面摆下,当摆到竖直位置时,B 点的线速度为v ,则这时AB 两端的电压大小为( )A.Ba v 3B.Ba v 6 C .2Ba v 3 D .Ba v 解析:摆在竖直位置时,AB 切割磁感线的瞬时感应电动势E =B ·2a ·12v =Ba v .由闭合电路欧姆定律得,U AB =E R 2+R 4·R 4=13Ba v ,故A 正确. 答案:A5、(10山东卷)21.(多选)如图所示,空间存在两个磁场,磁感应强度大小均为B ,方向相反且垂直纸面,MN 、PQ 为其边界,OO ′为其对称轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导体切割磁感线产生感应电动势的计算
公式E=BLv的使用条件
解决电磁感应中的电路问题
1.确定电源.
2.分析电路结构(内、外电路及外电路的串、并联关系),画出等效电路图.
3.利用电路规律求解.主要应用欧姆定律及串、并联电路的基本性质等列方程求解.
1.如图所示,在一匀强磁场中有一U型导线框bacd,线框处于水平面内,磁场与线框平面垂直,R为一电阻,ef为垂直于ab的一根导体杆,它可以在ab、cd上无摩擦地滑动,杆ef及线框中导体的电阻都可不计.开始时,给ef 一个向右的初速度,则()
A.ef将减速向右运动,但不是匀减速
B.ef将匀减速向右运动,最后静止
C.ef将匀速向右运动
D.ef将做往复运动
2、如图所示,金属杆ab、cd可以在光滑导轨PQ和RS上滑动,匀强磁场方向垂直纸面向里.当ab、cd分别以速度v1和v2滑动时,发现回路感生电流方向为逆时针方向,则v1和v2的大小、方向可能是
A.v1>v2,v1向右,v2向左
B.v1>v2,v1和v2都向左
C.v1=v2,v1和v2都向右
D.v1=v2,v1和v2都向左
3.(2014·无锡模拟)如图所示,在竖直向下的匀强磁场中,将一水平放置的金属棒ab 以水平初速度v 0抛出,设在整个过程棒的方向不变且不计空气阻力,则在金属棒运动过程中产生的感应电动势大小变化情况是( )
A .越来越大
B .越来越小
C .保持不变
D .无法判断
4.如图所示,竖直平面内有一金属环,半径为a ,
总电阻为R (指拉直时两端的电阻),磁感应强度为B 的
匀强磁场垂直穿过环平面,在环的最高点A 用铰链连
接长度为2a 、电阻为R 2
的导体棒AB ,AB 由水平位置
紧贴环面摆下,当摆到竖直位置时,B 点的线速度为v ,
则这时AB 两端的电压大小为( )
A.Ba v 3
B.Ba v 6 C .2Ba v 3
D .Ba v
5、(10山东卷)21.(多选)如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直纸面,MN、PQ为其边界,OO′为其对称轴。
一导线折成边长为l的正方形闭合回路abcd,回路在纸面内以恒定速度v0向右运动,当运动到关于OO′对称的位置时()
A.穿过回路的磁通量为零
B.回路中感应电动势大小为2B l
C.回路中感应电流的方向为顺时针方向
D.回路中ab边与cd边所受安培力方向相同
6、(10新课标卷)21.如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直。
让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为E1,下落距离为0.8R时电动势大小为E2,忽略涡流损耗和边缘效应.关于E1、E2的大小和铜棒离开磁场前两端的极性,下列判断正确的是() A、
E>2E,a端为正
1
B、
E>2E,b端为正
1
C、
E<2E,a端为正
1
D、
E<2E,b端为正
1
7、(07山东理综) 16、用相同导线绕制的边长为L 或2L 的四个闭合导体线框,以相同的速度匀速进入右侧匀强磁场,如图所示。
在每个线框进入磁场的过程中,M 、N 两点间的电压分别为U a 、U b 、U c 和U d 。
下列判断正确的是
( )
A .U a <U b <U c <U d
B .
U a <U b <U d <U c C .U a =U b <U c =U d
D .U b <U a <U d <U c
8.如图所示,正方形线框的左半侧处在磁感应强度为B 的匀强磁场中,磁场方向与线框平面垂直,线框的对称轴MN 恰与磁场边缘平齐.若第一次将线框从磁场中以恒定速度v 1向右匀速拉出,第二次让线框绕轴MN 以线速度v
2匀速转过90°.若两次操作过程中线框产生的平均感应电动势相等,则( )
A .v 1∶v 2=2∶π
B .v 1∶v 2=π∶2
C .v 1∶v 2=1∶2
D .v 1∶v 2=2∶1
N a b c d
9. (2012·新课标全国卷)如图所示,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0。
使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流。
现使线框保持图中所示位置,磁感应强度大小随时间线性变化。
为了产生与线框转动半周过程中同样大
小的电流,磁感应强度随时间的变化率ΔB
Δt的大小应为()
A.4ωB0
π B.
2ωB0
π
C.ωB0
π D.
ωB0
2π
10.(多选)如图所示,两个足够长的平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动.两金属棒ab、cd的质量之比为2∶1.用一沿导轨方向的恒力F 水平向右拉金属棒cd,经过足够长时间以后
()
A.金属棒ab、cd都做匀速运动
B.金属棒ab上的电流方向由b向a
C.金属棒cd所受安培力的大小等于2F/3
D.两金属棒间距离保持不变。
