相似三角形的综合应用
平面几何中的相似三角形的综合应用的综合应用

平面几何中的相似三角形的综合应用的综合应用在平面几何中,相似三角形是一种常见的几何形状,它们有着相似的内部角度以及对应边长的比例关系。
相似三角形具有广泛的综合应用,涉及到各个领域的问题解决和计算。
本文将介绍相似三角形的基本性质和应用,并通过实际问题探索其综合应用。
一、相似三角形的基本性质相似三角形是指具有相同形状但不一定相同大小的三角形。
两个相似三角形的对应角度相等,而对应边长之间的比例保持一致。
在两个相似三角形ABC和DEF中,我们可以得到以下关系:1. 角度相等:∠A = ∠D,∠B = ∠E,∠C = ∠F2. 边长比例:AB/DE = BC/EF = AC/DF二、相似三角形的应用场景相似三角形的性质使得它们在实际问题的求解中具有广泛的应用。
以下是几个常见的应用场景:1. 测量高度问题在无法通过直接测量的情况下,可以利用相似三角形的性质求解对象的高度。
通过测量已知物体的高度和距离,以及观察者与物体的垂直角度,可以利用相似三角形的比例关系计算出未知物体的高度。
2. 倾斜角度计算当无法直接测量物体的倾斜角度时,可以利用相似三角形的性质进行计算。
通过在已知角度下测量物体的高度和距离,以及物体上两点的水平距离,可以建立相似三角形,从而计算出物体的倾斜角度。
3. 长度比例计算相似三角形的比例关系还可以应用于求解长度比例问题。
例如,在地图上测量两地的实际距离,然后通过相似三角形的比例关系计算出地图上表示的距离。
4. 面积比例计算相似三角形的面积比例也是重要的应用之一。
通过相似三角形的边长比例,可以推导出面积比例。
这在建筑设计等领域中经常使用,用于估算或设计房屋、地块等物体的面积。
5. 圆的相似性在圆的几何学中,相似三角形也有重要的应用。
两个圆可以通过相似三角形的性质进行比较,从而判断其相似性或相等性。
这对于建模、制图和计算圆的属性非常关键。
三、相似三角形综合应用示例为了更好地理解相似三角形的综合应用,以下是一个实际问题的求解示例:问题:一根高塔竖直安放在地面上。
相似三角形的应用

相似三角形的应用相似三角形是指具有相同形状但大小不同的两个或多个三角形。
相似三角形之间存在一种特殊的比例关系,通过这种比例关系,我们可以运用相似三角形解决各种实际问题。
本文将重点介绍相似三角形的应用领域及其在数学和几何中的具体运用。
一、相似三角形在实际问题中的应用1. 测量高度和距离:相似三角形的应用在测量高度和距离方面非常常见。
例如,在无法直接测量建筑物或树木的高度时,可以通过相似三角形的比例关系,利用已知的高度和距离来计算未知的高度。
类似地,当无法直接测量两个物体之间的距离时,可以利用相似三角形的比例关系来推算出距离。
2. 图像的放大和缩小:在艺术和设计领域中,相似三角形的应用非常重要。
当我们需要将一幅图像进行放大或缩小时,可以利用相似三角形的性质来确定新图像与原图像的比例关系,从而实现图像的变形。
3. 建筑设计与规划:在建筑设计与规划中,相似三角形的应用也非常普遍。
通过相似三角形可以计算出建筑物的高度、宽度、长度等尺寸信息,从而帮助设计师进行准确的规划和设计。
二、相似三角形在数学中的应用1. 比例和比值的计算:相似三角形的比例关系可以用来计算不同长度之间的比例和比值。
通过相似三角形的性质,我们可以建立起各种数学关系式,进行比例和比值的计算,从而解决许多实际和抽象的问题。
2. 三角函数的定义和性质:在三角函数的定义和性质中,相似三角形也扮演着重要角色。
例如,在定义正弦、余弦和正切函数时,就需要利用相似三角形的性质来推导出它们的数学表示式。
相似三角形的运用使得三角函数的计算和应用更加简便和灵活。
3. 几何图形的相似性判定:相似三角形的性质在判定几何图形的相似性方面起着至关重要的作用。
根据相似三角形的比例关系,我们可以通过对角、边长比较等方法来判断两个图形是否相似,并进一步推导出它们之间的其他性质。
总结:相似三角形在实际问题、数学和几何中都有着广泛的应用。
通过运用相似三角形的比例关系,我们可以解决测量、计算和设计等问题,在数学和几何中推导出各种定理和性质。
相似三角形的性质及应用用

通过将相似三角形组合起来,可以创 造出各种具有对称性和美感的几何图 案。这些图案在建筑设计、装饰艺术 和纺织品设计中都有广泛应用。
利用相似三角形解决实际问题
总结词
相似三角形的性质在解决实际问题中具有广泛的应用,如工程测量、航海、航空等。
详细描述
在工程测量中,可以利用相似三角形来计算物体的高度、长度等参数。在航海和航空领域,可以利用相似三角形 来计算航行距离、高度和方向等数据。这些应用都基于相似三角形的性质,能够提供精确和可靠的测量结果。
相似比
相似三角形对应边的比值称为相 似比。
性质
对应角相等
面积比等于相似比的平方
相似三角形的对应角相等,即$angle A_1 = angle A_2, angle B_1 = angle B_2, angle C_1 = angle C_2$。
相似三角形的面积比等于其相似比的 平方,即$frac{S_1}{S_2} = (frac{a_1}{a_2})^2$。
相似三角形的对应边长之比是一个常数,这个常数被称为 相似比。
总结相似三角形的性质和应用
• 面积比等于相似比的平方:相似三角形的面积之比等于其 相似比的平方。
总结相似三角形的性质和应用
测量
在几何测量中,相似三角形是解 决实际问题的重要工具,如计算
建筑物的高度、河的宽度等。
建筑设计
在建筑设计领域,相似三角形可用 于确定建筑物的比例和尺寸,以实 现美观和功能性的平衡。
对应边成比例
相似三角形的对应边成比例,即 $frac{a_1}{a_2} = frac{b_1}{b_2} = frac{c_1}{c_2}$。
相似三角形的判定条件
01
02
相似三角形的应用举例

相似三角形的应用举例相似三角形是指在形状相似的两个三角形中,对应的角度相等,而对应的边长成比例关系。
这一性质使得相似三角形在实际生活中有着广泛的应用。
本文将举例介绍相似三角形在地理测量、影视制作和建筑设计等领域的具体应用。
一、地理测量中的相似三角形应用地理测量中常常使用相似三角形原理来测量高处物体的高度以及难以直接测量的距离。
以测量一座建筑物的高度为例,通过在平面上选择两个不同位置,测量出与地平线夹角相同的两个点,再利用三角形相似原理计算出建筑物的高度。
这样的测量方法可以避免测量过程中的误差和测量的困难,提高测量的准确性和效率。
二、影视制作中的相似三角形应用在影视制作中,相似三角形的应用尤为重要。
例如,在电影中要制作一个逼真的远景特写,如果直接拍摄远处的景象,可能会因为远离拍摄现场而导致细节无法清晰展现。
为了解决这个问题,可以利用相似三角形的原理,在近距离拍摄一个类似的模型或者画面,然后通过电脑生成与实景相似的远景效果。
这种利用相似三角形的方法可以在节约成本的同时,制作出逼真的远景特写效果。
三、建筑设计中的相似三角形应用相似三角形在建筑设计中有着广泛的应用,特别是在设计高层建筑时更是如此。
以设计一座摩天大楼为例,建筑师需要保证高楼的结构坚固稳定,同时也要满足美学上的要求。
在设计过程中,利用相似三角形的原理可以根据大楼的比例尺度,在小模型上进行实际尺寸的计算和预测。
这种预测方法不仅可以方便地展示设计方案,还可以在施工前发现和修正设计中的不足之处,提高整体设计质量。
通过上述几个具体例子,我们可以看到相似三角形在地理测量、影视制作和建筑设计中的重要应用。
相似三角形原理的运用,使得我们能够更加准确地进行测量、制作出逼真的特效和设计出稳固美观的建筑物。
这一应用不仅提高了工作效率,还为我们提供了更多实际问题的解决方案。
因此,相似三角形的学习与应用在我们的生活中具有重要的意义。
总结生活中相似三角形的应用

总结生活中相似三角形的应用在生活中,相似三角形是一种非常常见的几何形状。
它们在各个领域的应用非常广泛,包括建筑、工程、美术等等。
本文将总结生活中相似三角形的应用,并探讨它们在不同领域中的实际应用案例。
1. 建筑领域中的相似三角形应用在建筑设计中,相似三角形被广泛运用于建筑物的设计与构造。
以摩天大楼为例,工程师会使用相似三角形原理,根据比例关系来确定大楼的高度、宽度和两侧的倾斜度。
这不仅可以确保大楼的外观美观,还可以为建筑提供更好的结构稳定性。
此外,在房屋设计中,相似三角形也被用来计算尺寸比例。
比如,在设计家具时,设计师会考虑到房屋的整体比例,并运用相似三角形的原理来确定家具的大小和形状,以保证整体空间的和谐统一。
2. 工程领域中的相似三角形应用在工程领域,相似三角形被广泛应用于测量和勘探工作。
例如,在制作地图时,相似三角形原理可以用于测量地表的高度和坡度。
勘测人员可以利用利用光学仪器,通过测得的角度和距离,推导出不同地点的高度,并绘制出精确的地图。
此外,在电力工程中,相似三角形也被用来计算电线杆之间的高度和距离。
根据相似三角形的比例关系,工程师可以通过测量电线杆顶部到地面的高度和距离,推导出其他电线杆之间的高度和距离,以确保电线的牢固性和安全性。
3. 美术领域中的相似三角形应用相似三角形在美术领域中也有重要的应用。
艺术家们利用相似三角形的比例关系来捕捉和表达物体的形状和透视。
例如,在人物素描中,艺术家可以通过观察和绘制物体的相似三角形来准确地表达人物的体型和比例。
此外,在景观绘画中,艺术家也会利用相似三角形的原理来描绘山脉、树木和其他自然景观的远近和大小。
通过运用相似三角形的比例关系,艺术家可以在绘画中准确地再现现实中的景观。
总结:相似三角形作为一种常见的几何形状,在生活中有着广泛的应用。
在建筑中,相似三角形帮助保证建筑物的结构稳定和外观美观;在工程中,相似三角形用于测量和勘测工作,确保工程的精确性和安全性;在美术中,相似三角形被用来准确表达物体形状和透视。
相似三角形的应用

相似三角形的应用在几何学中,相似三角形是一种非常重要的概念。
相似三角形是指具有相同形状但大小不同的三角形。
本文将探讨相似三角形的应用,并介绍在现实生活中如何使用相似三角形进行测量和求解问题。
一、地图测量地图是我们在日常生活中常用的工具之一。
地图上的距离和大小都是通过测量获得的。
由于地球是一个球体,所以将其展示在平面地图上会引起形状的改变。
利用相似三角形的性质,我们可以通过测量地图上的两条边和它们对应的实际距离,来计算其他位置的距离。
例如,假设我们知道地图上两个城市之间的距离为10厘米,而实际距离为100公里。
如果我们需要计算其他两个城市之间的距离,可以利用相似三角形的比例关系,设这两个城市之间的距离为x公里,则可以得到以下比例关系:10厘米/100公里 = x厘米/x公里。
通过解这个比例关系,我们就可以计算出实际距离。
二、建筑测量在建筑领域,使用相似三角形可以帮助我们测量高处的物体或建筑物的高度。
如果我们无法直接测量高度,但可以测量到某个位置的斜边长度和水平距离,那么我们可以利用相似三角形的性质来计算物体的高度。
以测量一栋建筑物的高度为例,我们可以在地面上选取一个合适的位置,测量从这个位置到建筑物顶部的斜边长度为10米,而与地面垂直的水平距离为5米。
我们可以设建筑物的高度为h米,则可以得到相似三角形的比例关系:10米/5米= h米/x米。
通过解这个比例关系,我们就可以计算出建筑物的高度。
三、影视特效影视特效制作中,相似三角形也起到了关键的作用。
例如,在拍摄特技镜头时,为了保证画面的连贯性,摄影师和特效制作人员需要准确计算出角色与背景之间的相对位置。
通过利用相似三角形的性质,可以测量出摄影机与角色的距离和角度,进而确定背景的大小和位置。
这样,在特效制作时,就可以根据这些信息来合成或添加特效,使得特技镜头看起来更加真实和自然。
总结:相似三角形的应用非常广泛,不仅限于地图测量、建筑测量和影视特效等领域。
相似三角形在现实生活中的应用场景

相似三角形在现实生活中的应用场景
相似三角形的判定在现实生活中有广泛的应用,以下是一些常见的应用场景:
1.建筑和工程领域:在建筑设计和工程计算中,相似三角形的判定被用于解
决各种实际问题。
例如,工程师会利用相似三角形原理来计算建筑物的缩放比例,以确定建筑物的外观和尺寸是否符合设计要求。
此外,在桥梁、道路和水利工程的设计和建设中,工程师也需要用到相似三角形的概念来测量斜坡的斜率和角度等参数。
2.地图和导航领域:在地图和导航中,利用相似三角形的原理可以精确地测
量距离和角度。
例如,在地图上测量两点之间的距离时,可以利用相似三角形来计算实际距离。
此外,在导航中,飞行员和船员也需要用到相似三角形的概念来测量飞行或航行的角度和距离,以确保安全飞行或航行。
3.科学实验和观测:在科学实验和观测中,相似三角形的判定也被广泛用于
各种测量和计算。
例如,物理实验中常常需要测量物体的速度、加速度等物理量,这时可以利用相似三角形来测量或计算所需参数。
此外,在天文观测中,天文学家也会用到相似三角形的原理来测量天体的位置和距离。
4.日常生活中的应用:在日常生活中,我们也会遇到一些与相似三角形相关
的应用场景。
例如,摄影时需要调整相机的角度和高度,这时可以利用相似三角形的原理来计算所需的参数。
另外,在测量物体的尺寸或角度时,我们也可以利用相似三角形的概念来进行粗略的估算。
总之,相似三角形的判定在现实生活中有广泛的应用,涉及到建筑、工程、科学实验、导航、摄影等领域。
通过掌握相似三角形的原理和应用技巧,我们可以更好地解决各种实际问题,提高生活和工作的效率和质量。
相似三角形应用举例

相似三角形应用举例在我们的日常生活和学习中,相似三角形的应用无处不在。
相似三角形是指对应角相等,对应边成比例的两个三角形。
通过利用相似三角形的性质,我们可以解决许多实际问题,下面就让我们一起来看看一些具体的例子。
一、测量物体的高度假设我们想要测量一棵大树的高度,但又无法直接测量。
这时候,相似三角形就派上用场了。
我们可以在同一时刻,在大树旁边立一根已知长度的杆子,然后分别测量杆子的影子长度和大树的影子长度。
因为在同一时刻,太阳光线的角度是相同的,所以杆子和它的影子以及大树和它的影子分别构成了两个相似三角形。
假设杆子的高度为h1,杆子影子的长度为 s1,大树影子的长度为 s2,大树的高度为 h2。
根据相似三角形的性质,我们可以得到:h1 / s1 = h2 / s2通过已知的 h1、s1 和 s2,就可以计算出大树的高度 h2。
例如,杆子高度为2 米,影子长度为15 米,大树影子长度为9 米。
那么:2 / 15 = h2 / 915h2 = 2 × 915h2 = 18h2 = 12 米所以,这棵大树的高度约为 12 米。
二、计算河的宽度当我们面对一条河流,想要知道它的宽度,但又无法直接跨越测量时,相似三角形同样能帮助我们解决问题。
我们可以在河的一侧选择一个点A,然后在河的对岸选择一个点B,使得 A、B 两点与河岸基本在同一直线上。
接着,在河的这一侧,沿着河岸选定一个点 C,使得 AC 垂直于河岸,并测量出 AC 的长度。
然后,我们再沿着 AC 的方向向前走一段距离,到达点 D,使得点 D、A、B 三点在同一直线上,并且测量出 CD 的长度。
由于三角形 ABC 和三角形 ADC 有一个共同的角∠A,并且∠ACB=∠ACD = 90°,所以这两个三角形相似。
假设河宽为AB =x,AC =a,CD =b。
根据相似三角形的性质,我们有:AC / AB = CD / AC即 a / x = b / a通过已知的 a 和 b,就可以计算出河的宽度 x。
相似三角形的应用

相似三角形的应用相似三角形是指两个或更多个三角形的对应角相等,对应边成比例。
在数学和几何学中,相似三角形具有广泛的应用,本文将探讨相似三角形在实际问题中的应用和意义。
一、地理测量地理测量是相似三角形应用的典型领域。
在实际测量过程中,我们经常会遇到难以直接测量的地理距离或高度。
通过使用相似三角形的原理,我们可以利用已知的尺寸测量未知的尺寸。
举例来说,当我们想要测量一座高山的高度时,可以在水平地面上测量该高山的基座与观测点的距离,并同时测量观测点与该高山的顶点的夹角。
然后,我们可以构造一个与已知角度相等且具有比例关系的三角形,如此,我们就可以通过比例计算出高山的真实高度。
二、建筑设计相似三角形在建筑设计中也扮演着重要的角色。
当建筑师设计建筑物的平面图时,通常需要考虑到各种限制条件,如建筑物所在地的面积、材料的成本和现有建筑的布局。
相似三角形的应用可以帮助建筑师在平面图中精确计算出各个部分的尺寸。
举例来说,当建筑师需要设计一个大厦的外墙高度时,可以先测量周围已有建筑物的高度,然后利用相似三角形的原理创建一个比例,从而计算出大厦外墙的高度。
三、影视制作在影视制作领域,相似三角形的应用同样不可或缺。
特效动画、绿幕合成和特殊镜头的制作都需要准确的测量和计算。
相似三角形可以帮助摄影师和特效团队准确地计算出场景中各个元素的尺寸和位置关系。
举例来说,当制作一个动画场景时,摄影师可以首先测量实际场景中各个元素的尺寸和位置,然后通过相似三角形的原理将这些尺寸和位置比例应用到动画场景中,从而创造出逼真且准确的效果。
四、遥感技术遥感技术利用卫星或飞机上的传感器来获取地球表面的信息,然后通过相似三角形的应用来测量地球表面的高度、距离和坐标。
相似三角形在遥感图像处理中扮演着重要的角色,可以帮助科学家和地理学家研究地球表面的变化和特征。
举例来说,当科学家想要测量一片森林的总面积时,可以先使用遥感图像获取该森林的部分面积,并且可以测量出图像上的距离。
相似三角形应用举例

相似三角形的判定
(1) 定义法
(2)通过平行线.(A型 X型)
(3)三边对应成比例.
(4)两边对应成比例且夹角相等 .
(5)两角相等.
(6)直角三角形
相似三角形的性质 (1)对应边的比相等,对应角相等. (2)对应高的比,对应中线的比、对应角平分 线的比都等于相似比. (3)周长的比等于相似比. (4)面积的比等于相似比的平方.
一题多解
还可以有其他方法测量吗?
B E
┐ F
△ABO∽△AEF
平面镜
A
OB
OA
=
EF
AF
┐ O
OA ·EF OB =
AF
利用三角形相似可以解决一些不能直接测 量的物体的长度的问题
例5. 如图,为了估算河的宽度,我们可以在河对岸选 定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直 线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适 当的点T,确定PT与点Q且垂直PS的直线b的交点R.如果测 得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
分析:如图,设观察者眼睛的位置(视点)为点F(EF近似为人 的身高),画出观察者的水平视线FG ,它交AB、 CD于点H 、 K.视线FA、 FG的夹角∠ AFH是观察点A的仰角.能看到C 点.类似地, ∠ CFK是观察点C时的仰角,由于树的遮挡,区 域Ⅰ和Ⅱ都在观察者看不到的区域(盲区)之内.再往前走就 根本看不到C点了.
乐山大佛
世界上最高的树 —— 红杉
怎样测量这些非常高 大物体的高度?
台湾最高的楼 ——台北101大楼
怎样测量河宽?
世界上最宽的河 ——亚马孙河
利用三角形的相似,可以解决一些不能直接测量 的物体的长度问题,下面请看几个例子.
部编数学九年级下册专项32相似三角形射影定理综合应用(2种类型)(解析版)含答案

专项32 相似三角形-射影定理综合应用(2种类型) 一、射影定理 直角三角形斜边上的高是它分斜边所得两条线段的比例中项;且每条直角边都是它在斜边上的射影和斜边的比例中项。
如图(1):Rt△ABC中,若CD为高,则有CD2=BD•AD、BC2=BD•AB或AC2=AD•AB。
(证明略)二、变式推广 1.逆用 如图(1):若△ABC中,CD为高,且有DC2=BD•AD或AC2=AD•AB或BC2=BD•AB,则有∠DCB=∠A或∠ACD=∠B,均可等到△ABC为直角三角形。
2.一般化,若△ABC不为直角三角形,当点D满足一定条件时,类似地仍有部分结论成立。
(后文简称:射影定理变式(2)) 如图(2):△ABC中,D为AB上一点,若∠CDB=∠ACB,或∠DCB=∠A,则有△CDB∽△ACB,可得BC2=BD•AB;反之,若△ABC中,D为AB上一点,且有BC2=BD•AB,则有△CDB∽△ACB,可得到∠CDB=∠ACB,或∠DCB=∠A。
【类型1:直角三角形中射影定理】【典例1】(2021秋•南京期末)如图,在Rt△ABC中,∠ACB=90°,点D在AB上,且=.(1)求证△ACD∽△ABC;(2)若AD=3,BD=2,求CD的长.【解答】(1)证明:∵=,∠A=∠A,∴△ACD∽△ABC;(2)解:∵△ACD∽△ABC,∴∠ACD=∠B,∵∠ACB=90°,∴∠A+∠B=90°,∴∠A+∠ACD=90°,∴∠ADC=90°,∴∠ADC=∠BDC,∵∠ACD=∠B,∴△ACD∽△CBD,∴=,∴=,∴CD=.【变式1-1】(2022•义乌市校级开学)如图,在△ABC中,∠ACB=90°,CD⊥AB,若AD=4,BD=8,则CD的长为( )A.4B.4C.4D.【答案】A【解答】解:∵∠ACB=90°,∴∠A+∠B=90°,∵CD⊥AB,∴∠DCB+∠B=90°,∴∠A=∠DCB,∵∠ADC=∠CDB=90°,∴△ADC∽△CDB,∴=,即=,解得:CD=4,故选:A.【变式1-2】(2021秋•漳州期末)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,CD=4,则BD的长为( )A.B.C.D.2【答案】A【解答】解:∵∠BAC=90°,∴∠B+∠C=90°,∵AD⊥BC,∴∠DAC+∠C=90°,∠ADB=∠ADC=90°,∴∠B=∠DAC,∴△BDA∽△ADC,∴=,∵AD=3,CD=4,∴=,解得:BD=,故选:A.【变式1-3】(2020秋•梁平区期末)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )A.AC2=AD•AB B.CD2=CA•CB C.CD2=AD•DB D.BC2=BD•BA 【答案】B【解答】解:∵∠ACB=90°,CD⊥AB于点D,∴AC2=AD•AB,CD2=DA•DB,BC2=BD•BA.故选:B.【变式1-4】(2015•黄冈中学自主招生)将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )A.3B.8C.D.2【答案】A【解答】解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.【类型2:非直角三角形中射影定理】【典例2】如图,已知∠A=70°,∠APC=65°,AC2=AP•AB,则∠B的度数为( )A.45°B.50°C.55°D.60°【答案】A【解答】解:∵∠A=70°,∠APC=65°,∴∠ACP=180°﹣70°﹣65°=45°.∵AC2=AP•AB,∴=.∵∠B=∠B,∴△BAC∽△CPA.∴∠B=∠ACP=45°.故选:A.【变式2-1】如图,在△ABC中,点D在边AB上,若∠ACD=∠B,AD=3,BD=4,则AC的长为( )A.2B.C.5D.2【答案】B【解答】解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴,∵AD=3,BD=4,∴AB=AD+BD=3+4=7,∴,∴AC=或﹣(舍去),故选:B.【变式2-2】如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.(1)求证:△ABC∽△ACD;(2)若AD=2,AB=6.求AC的长.【解答】(1)证明:∵∠ABC=∠ACD,∠A=∠A,∴△ABC∽△ACD;(2)解:∵△ABC∽△ACD,∴,∴AC2=2×6=12,∴AC=2.【典例3】如图,在△ABC中,∠A=90°,点D、E分别在AC、BC边上,BD=CD=2DE,且∠C+∠CDE=45°,若AD=6,则BC的长为 .【答案】8【解答】解:∵∠A=90°,∴∠ABD+∠ADB=90°,∵BD=CD,∴∠DBC=∠C,∴∠ADB=∠DBC+∠C=2∠C,∵∠C+∠CDE=45°∴2∠C+∠CDE=90°,∴∠ADB+∠CDE=90°,∴∠BDE=90°,作DF⊥BC于F,如图所示:则BF=CF,△DEF∽△BED∽△BDF,∴===,设EF=x,则DF=2x,BF=CF=4x,∴BC=8x,DE=x,∴CD=BD=2x,AC=6+2x,∵∠DFC=∠A=90°,∠C=∠C,∴△CDF∽△CBA,∴=,即=,解得:x=,∴BC=8;故答案为:8.【变式3】如图,在锐角△ABC中,BD⊥AC于D,DE⊥BC于E,AB=14,AD=4,BE:EC=9:2,则CD= .【答案】2【解答】解:∵BD⊥AC,∴∠ADB=90°,∴BD2=AB2﹣AD2=142﹣42=180,设BE=9x,EC=2x,∵DE⊥BC,∴BD2=BE•BC,即180=9x(9x+2x),解得x2=,∵CD2=CE•CB=2x•11x=22×=40,∴CD=2.1.(2022秋•义乌市月考)如图,小明在A时测得某树的影长为3m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.A.B.C.6D.【答案】B【解答】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=3m;∵∠E+∠F=90°,∠E+∠ECD=90°,∴∠ECD=∠F,∴△EDC∽△CDF,∴=,即DC2=ED•FD=2×3=6,解得CD=m.故选:B.2.(2012•麻城市校级自主招生)如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2,AC=3,BC=6,则⊙O的半径是( )A.3B.4C.4D.2【答案】D【解答】解:延长EC交圆于点F,连接DF.则根据90°的圆周角所对的弦是直径,得DF是直径.∵DE∥BC,∴△ADE∽△ABC.∴.则DE=4.在直角△ADF中,根据射影定理,得EF==4.根据勾股定理,得DF==4,则圆的半径是2.故选:D.3.(2022春•周村区期末)如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 .【答案】6【解答】解:∵∠BAC=90°,AD⊥BC,∴AD2=CD•BD=36,∴AD=6,故答案为:6.4.(2021春•汉阴县期中)如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD 交于O,且BE:ED=1:3,AD=6cm,则AE= cm.【答案】3【解答】解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x (3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.5.(2022•武汉模拟)在矩形ABCD中,BE⊥AC交AD于点E,G为垂足.若CG=CD=1,则AC的长是 .【答案】【解答】解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.6.(2021秋•滦州市期中)已知关于x的方程x2﹣2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.(1)试判断△ABC的形状,并说明理由;(2)若CD是AB边上的高,AC=2,AD=1,求BD的长.【解答】解:(1)∵两根相等,∴可得:4(a+b)2﹣4(c2+2ab)=0,∴a2+b2=c2,∴△ABC是直角三角形;(2)由(1)可得:AC2=AD×AB,∵AC=2,AD=1,∴AB=4,∴BD=AB﹣AD=3.7.如图,点D在△ABC的边BC上,∠ADC+∠BAC=180°,AB=4,BC=8,求BD的长.【解答】解:∵∠ADC+∠BAC=180°,∠ADC+∠ADB=180°,∴∠ADB=∠BAC,又∵∠B=∠B,∴△BAD∽△BCA,∴=,∴BA2=BD•BC,∵AB=4,BC=8,∴BD=2.即AC⋅CF=CB⋅DF.8.(盐城校级模拟)【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E 在CD上,过点C作CF⊥BE,垂足为F,连接OF,(1)试利用射影定理证明△BOF∽△BED;(2)若DE=2CE,求OF的长.【解答】【问题情境】证明:如图1,∵CD⊥AB,∴∠ADC=90°,而∠CAD=∠BAC,∴Rt△ACD∽Rt△ABC,∴AC:AB=AD:AC,∴AC2=AD•AB;【结论运用】(1)证明:如图2,∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,∴BC2=BO•BD,∵CF⊥BE,∴BC2=BF•BE,∴BO•BD=BF•BE,即=,而∠OBF=∠EBD,∴△BOF∽△BED;(2)方法一:∵BC=CD=6,而DE=2CE,∴DE=4,CE=2,在Rt△BCE中,BE==2,在Rt△OBC中,OB=BC=3,∵△BOF∽△BED,∴=,即=,∴OF=.方法二:将△OFC绕O顺时针旋转90度得到△OGB,如图3,由△BOF∽△BED得到∠OFB=45°,∴∠OGB=∠OFC=45°+90°=135°,∵OG=OF,∴△OGF为等腰直角三角形,∴∠OGF=45°,∴G点在BE上,∵BG=CF=,∴GF=,∴OF=GF=.。
相似三角形的判定及应用

相似三角形的判定及应用相似三角形是指具有相同形状但不一定相同大小的两个三角形。
判定两个三角形是否相似可以通过以下几种方法,同时这些方法也可以应用于解决实际问题:1. AAA判定法:若两个三角形的对应角度相等,则它们是相似三角形。
即若两个三角形的三个角分别对应相等,则它们是相似三角形。
这种判定法可以应用于解决实际问题如测量倾斜物体的高度等。
2. AA判定法:若两个三角形的两个对应角相等,则它们是相似三角形。
即若两个三角形的两个角分别对应相等,则它们是相似三角形。
这种判定法可以应用于解决实际问题如计算山坡的斜率等。
3. SAS判定法:若两个三角形的一个角相等,且两个对应边的比例相等,则它们是相似三角形。
即若两个三角形的一个角相等,且两条与该角相对应的边的比例相等,则它们是相似三角形。
这种判定法可以应用于解决实际问题如计算高塔的阴影长度等。
4. SSS判定法:若两个三角形的三个对应边的比例相等,则它们是相似三角形。
即若两个三角形的三条边的比例相等,则它们是相似三角形。
这种判定法可以应用于解决实际问题如计算建筑物的缩放比例等。
相似三角形的应用在几何学和现实生活中都非常广泛。
以下是一些应用示例:1. 建筑和工程:通过相似三角形的概念,可以计算建筑物的缩放比例,包括建筑物的高度、宽度和深度等。
这对于设计和规划新建筑物或改建现有建筑物非常有用。
2. 地形测量:利用相似三角形的原理,可以测量山坡的斜率、高塔的阴影长度等。
这对于地理测量和地形分析非常重要,可以用于制作地形图和地图。
3. 倾斜物体测量:对于无法直接测量的高物体(如高塔、山峰等),可以利用相似三角形的原理,通过测量影子长度和角度,计算物体的高度。
这在地理测量和旅行中很常见。
4. 统计学:在统计学中,相似三角形的概念可以被用于创建样本的代理数据集,从而更好地理解和解释真实数据集的特征和趋势。
5. 生物学:在生物学中,相似三角形的原理可以应用于研究和分析动物和植物的形态特征以及它们之间的关系。
部编数学九年级下册专项33相似三角形一线三等角模型综合应用(解析版)含答案
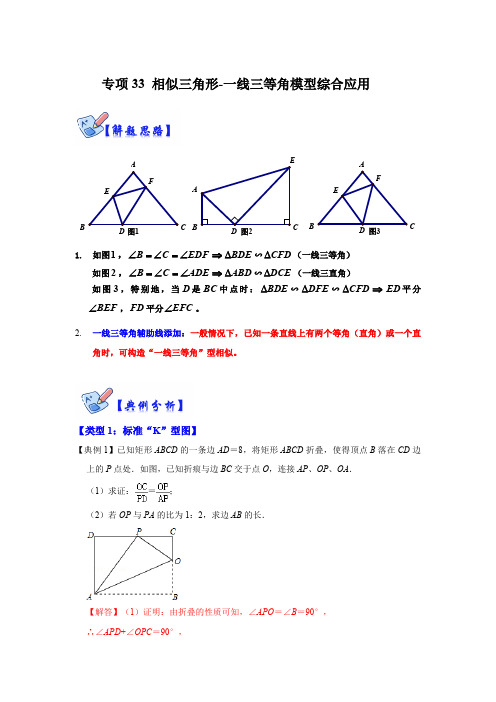
专项33 相似三角形-一线三等角模型综合应用1.如图1,BDE EDF C B ∆⇒∠=∠=∠∽CFD ∆(一线三等角)如图2,ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆(一线三直角)如图3,特别地,当D 是BC 中点时:BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠,FD 平分EFC ∠。
2.一线三等角辅助线添加:一般情况下,已知一条直线上有两个等角(直角)或一个直角时,可构造“一线三等角”型相似。
【类型1:标准“K ”型图】【典例1】已知矩形ABCD 的一条边AD =8,将矩形ABCD 折叠,使得顶点B 落在CD 边上的P 点处.如图,已知折痕与边BC 交于点O ,连接AP 、OP 、OA .(1)求证:=;(2)若OP 与PA 的比为1:2,求边AB 的长.【解答】(1)证明:由折叠的性质可知,∠APO =∠B =90°,∴∠APD +∠OPC =90°,CB BC A A∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠POC+∠OPC=90°,∴∠APD=∠POC,∴△OCP∽△PDA,∴=;(2)解:∵△OCP∽△PDA,∴,∵OP与PA的比为1:2,AD=8,∴,∴PC=4,设AB=x,则DC=x,AP=x,DP=x﹣4,在Rt△APD中,AP2=AD2+PD2,∴x2=82+(x﹣4)2,解得:x=10,∴AB=10.【变式1-1】如图,正方形ABCD中,点E在BC边上,且AE⊥EF,若BE=2,CF=,求正方形ABCD的边长.【解答】解:∵∠AEB+∠CEF=90°,∠BAE+∠AEB=90°,∴∠BAE=∠CEF,又∵∠B=∠C=90°,∴△BAE∽△CEF,∴=,∵AB=BC,∴,∴,∴CE=4,∴BC=CE+BE=4+2=6,∴正方形ABCD的边长为6.【变式1-2】如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.(1)求证:△ABM∽△MCF;(2)若AB=4,BM=2,求△DEF的面积.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,BC∥AD,∴∠BAM+∠AMB=90°,∵ME⊥AM,∴∠AME=90°,∴∠AMB+∠FMC=90°,∴∠BAM=∠FMC,∴△ABM∽△MCF;(2)解:∵AB=4,∴AB=BC=CD=4,∵BM=2,∴MC=BC﹣BM=4﹣2=2,由(1)得:△ABM∽△MCF,∴=,∴=,∴CF=1,∴DF=CD﹣CF=4﹣1=3,∵BC∥AD,∴∠EDF=∠MCF,∠E=∠EMC,∴△DEF∽△CMF,∴=,∴=,∴DE=6,∴△DEF的面积=DE•DF=×6×3=9,答:△DEF的面积为9【类型2:做辅助线构造“K”型图】【典例2】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.(1)如图1,填空:当点G在CD上,且DG=1,AE=2,则EG= ;(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:∠AEF=∠FEN;(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MN•MD.【解答】(1)解:∵∠EFG=90°,∴∠AFE+∠DFG=90°,∵∠AEF+∠AFE=90°,∴∠AEF=∠DFG,又∵∠A=∠D=90°,EF=FG,∴△AEF≌△DFG(AAS),∴AE=FD=2,∴FG=,∴EG=FG=,故答案为:;(2)证明:延长EA、NF交于点M,∵点F为AD的中点,∴AF=DF,∵AM∥CD,∴∠M=∠DNF,∠MAD=∠D,∴△MAF≌△NDF(AAS),∴MF=FN,∵EF⊥MG,∴ME=GE,∴∠MEF=∠FEN;(3)证明:如图,过点G作GP⊥AD交AD的延长线于P,∴∠P=90°,同(1)同理得,△AEF≌△PFG(AAS),∴AF=PG,PF=AE,∵AE=AD,∴PF=AD,∴AF=PD,∴PG=PD,∵∠P=90°,∴∠PDG=45°,∴∠MDG=45°,在Rt△EFG中,EF=FG,∴∠FGE=45°,∴∠FGE=∠GDM,∵∠GMN=∠DMG,∴△MGN∽△MDG,∴,∴MG2=MN•MD.【变式2-1】(2021春•永川区期末)如图,在边长为6的正方形ABCD中,E为BC上一点,CE=2BE,将△ABE沿AE折叠得到△AFE,连接DF,则线段DF的长为 .【解答】解:过点F作FN⊥BC,垂足为N,延长NF交AD于点M,∵四边形ABCD是正方形,∴AB=BC=AD=6,∠B=90°,AD∥BC,∴FM⊥AD,∴∠AMF=∠FNE=∠DMF=90°,∴四边形ABNM是矩形,∴AM=BN,∵CE=2BE,∴BE=BC=2,由折叠得:BE=FE=2,AB=AF=6,∠B=∠AFE=90°,∴∠AFM+∠EFN=90°,∵∠FEN+∠EFN=90°,∴∠FEN=∠AFM,∴△ENF∽△FMA,∴===,设EN=x,则FM=3x,∴AM=BN=BE+EN=2+x,在Rt△AFM中,AM2+FM2=AF2,∴(2+x)2+(3x)2=36,∴x=或x=﹣2(舍去),∴AM=2+x=,FM=3x=,∴DM=AD﹣AM=,在Rt△DMF中,DF===,故答案为:.【变式2-2】(2022秋•皇姑区校级月考)已知,如图,矩形ABCD中,AB=5,AD=3,点E是射线BC上一动点,将矩形ABCD沿直线AE翻折,点B落在点F处.(1)若点F恰好落在CD边上,如图1,求线段BE的长;(2)若BE=1,如图2,直接写出点F到BC边的距离;(3)若△CEF为直角三角形,直接写出CE所有值.【解答】解:(1)∵四边形ABCD是矩形,∴CD=AB=5,BC=AD=3,∠B=∠C=∠D=90°,由折叠的性质得:BE=FE,AF=AB=5,∴DF===4,∴CF=CD﹣DF=5﹣4=1,设BE=FE=x,则CE=BC﹣BE=3﹣x,在Rt△CEF中,由勾股定理得:CF2+CE2=FE2,即12+(3﹣x)2=x2,解得:x=,即线段BE的长为;(2)如图2,过F作FG⊥BC于G,延长GF交AD于H,则∠FGE=90°,四边形ABGH是矩形,∴HG=AB=5,BG=AH,∠AHF=90°=∠FGE,由折叠的性质得:AF=AB=5,∠AFE=∠B=90°,FE=BE=1,∴∠AFH+∠EFG=90°,∵∠AFH+∠FAH=90°,∴∠EFG=∠FAH,∴△EFG∽△FAH,∴==,∴AH=5FG,设FG=x,则BG=AH=5x,∴EG=BG﹣BE=5x﹣1,在Rt△EFG中,由勾股定理得:x2+(5x﹣1)2=12,解得:x=或x=0(不符合题意舍去),∴FG=,即点F到BC边的距离为;(3)分三种情况:①∠CFE=90°时,如图3,∵∠AFE=90°,∴∠AFE+∠CFE=180°,∴A、F、C三点共线,∵四边形ABCD是矩形,∴CD=AB=5,∠B=∠D=90°,AD∥BC,∴∠ECF=∠CAD,AC===,由折叠的性质得:AF=AB=5,FE=BE,∠AFE=∠B=90°,∴∠CFE=90°=∠D,CF=AC﹣AF=﹣5,∴△CEF∽△ACD,∴=,即=,解得:CE=;②点F在CD上,∠ECF=90°时,如图4,由(1)可知,BE=,∴CE=BC﹣BE=3﹣=;③∠CEF=90°时,如图5,由折叠的性质得:∠AEB=∠AEF=45°,∴△ABE是等腰直角三角形,∴BE=AB=5,∴CE=BE﹣BC=5﹣3=2;④点F在CD延长线上,∠ECF=90°时,如图6,由折叠的性质得:AF=AB=5,∠AFE=∠B=90°,∵∠ADF=180°﹣∠ADC=90°,∴DF===4,∴CF=CD+DF=5+4=9,∵∠CFE+∠CEF=90°,∠CFE+∠DFA=90°,∴∠CEF=∠DFA,∵∠ECF=∠ADF=90°,∴△CEF∽△DFA,∴===3,∴CE=3DF=12;综上所述,若△CEF为直角三角形,则CE的值为或或2或12.【类型2:特殊“K”型图】【典例3】(2021秋•通许县期中)感知:(1)数学课上,老师给出了一个模型:如图1,∠BAD=∠ACB=∠AED=90°,由∠1+∠2+∠BAD=180°,∠2+∠D+∠AED=180°,可得∠1=∠D;又因为∠ACB=∠AED =90°,可得△ABC∽△DAE,进而得到= .我们把这个数学模型称为“一线三等角”模型.应用:(2)实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.若BC=a,AB=b,求CE的长度(用含a,b的代数式表示).拓展:(3)创新组突发奇想,将此模型迁移到平行四边形中,如图3,在▱ABCD中,E为边BC上的一点,F为边AB上的一点.若∠DEF=∠B.求证:AB•FE=BE•DE.【解答】(1)解:∵△ABC∽△DAE,∴,故答案为:;(2)解:∵∠B=∠ADE=∠C,∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,∴∠EDC=∠BAD,∵DA=DE,在△ADB与△DEC中,,∴△ADB≌△DEC(AAS),∴EC=BD,AB=DC=b,∴BD=BC﹣DC=a﹣b,即CE=a﹣b;(3)解:∵∠DEF=∠B,∴∠BFE+∠BEF=∠BEF+∠DEC,∴∠BFE=∠DEC,作CG∥FE交DE于点G,如图:∴∠DEF=∠EGC,∴∠B=∠EGC,∴△FBE∽△EGC,∴,∵四边形ABCD是平行四边形,∴∠B+∠BCD=180°,∵∠EGC+∠DGC=180°,∵∠B=∠EGC,∴∠DGC=∠BCD,∵∠EDC=∠CDG,∴△DGC∽△DCE,∴,∴,∴DC•FE=BE•DE,∵四边形ABCD是平行四边形,∴AB=DC,∴AB•FE=•BE•DE.解法二:延长BC到M,使得DC=DM.∵DC=DM,∵DC∥AB,∴∠DCM=∠B,∴∠B=∠M,∵∠BFE=∠DEM,∴△BFE∽△MED.∴=,∵AB=CD=DM,∴AB•FE=•BE•DE.【变式3-1】如图,AB=9,AC=8,P为AB上一点,∠A=∠CPD=∠B,连接CD.(1)若AP=3,求BD的长;(2)若CP平分∠ACD,求证:PD2=CD•BD.【解答】(1)解:∵AB=9,AC=3,∴BP=AB﹣AP=9﹣3=6,∵∠A=∠CPD,∠ACP+∠APC=180°﹣∠A,∠APC+∠BPD=180°﹣∠CPD,∴∠ACP=∠BPD,∵∠A=∠B,∴△ACP∽△BPD,∴=,∴=,∴BD=,∴BD的长为;(2)证明:∵CP平分∠ACD,∴∠PCD=∠ACP,∴∠PCD=∠DPB,∵∠CPD=∠B,∴△CPD∽△PBD,∴=,∴PD2=CD•BD.【变式3-2】(2022春•定海区校级月考)【基础巩固】(1)如图1,在△ABC中,∠ACB=90°,直线l过点C,分别过A、B两点作AE⊥l,BD⊥l,垂足分别为E、D.求证:△BDC∽△CEA.【尝试应用】(2)如图2,在△ABC中,∠ACB=90°,D是BC上一点,过D作AD的垂线交AB 于点E.若BE=DE,,AC=20,求BD的长.【拓展提高】(3)如图3,在平行四边形ABCD中,在BC上取点E,使得∠AED=90°,若AE=AB,,CD=,求平行四边形ABCD的面积.【解答】(1)证明:∵∠ACB=90°,∴∠BCD+∠ACE=90°,∵AE⊥CE,∴∠AEC=90°,∴ACE+∠CAE=90°.∴∠BCD=∠CAE.∵BD⊥DE,∴∠BDC=90°,∴∠BDC=∠AEC.∴△BDC∽△CEA.(2)解:过点E作EF⊥BC于点F.由(1)得△EDF∽△DAC.∴.∵AD⊥DE,,AC=20,∴,∴DF=16.∵BE=DE,∴BF=DF.∴BD=2DF=32.(3)解:过点A作AM⊥BC于点M,过点D作DN⊥BC的延长线于点N.∴∠AMB=∠DNC=90°.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠B=∠DCN.∴△ABM≌△DCN(AAS).∴BM=CN,AM=DN.∵AB=AE,AM⊥BC,∴BM=ME,∵,设AM=b,BE=4a,EC=3a.∴BM=ME=CN=2a,EN=5a.∵∠AED=90°,由(1)得△AEM∽△EDN.∴,∴,∴,∵,∴(2a)2+b2=14,∴a=1,.∴平行四边形ABCD的面积=.1.(2021秋•南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE ⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )A.4B.C.D.5【答案】B【解答】解:∵EF⊥FG,∴∠EFB+∠GFC=90°,∵四边形ABCD为矩形,∴∠A=∠B=∠C=90°,AB=CD,∴∠GFC+∠FGC=90°,∴∠EFB=∠FGC,∴△EFB∽△FGC,∴,∵BE=3,BF=2,FC=6,∴,∴CG=4,同理可得△DAE∽△EBF,∴,∴,∴AE=,∴BA=AE+BE=+3=,∴DG=CD﹣CG=﹣4=.故选:B.2.(2022秋•二道区月考)如图,在△ABC中,AB=AC=9,BC=12,D,E分别是BC,AB上的动点(点D与B,C不重合),且2∠ADE+∠BAC=180°,若BE=4,则CD 的长为 .【答案】6【解答】解:∵AB=AC,∴∠C=∠B,∴∠C+∠B+∠BAC=2∠C+∠BAC=180°,又∵2∠ADE+∠BAC=180°,∴∠C=∠ADE,又∵∠BDE+∠ADC=180°﹣∠ADE,∠CAD+∠ADC=180°﹣∠C,∴∠BDE=∠CAD,∴△BDE∽△CAD,∴=,即=,解得CD=6.故答案为:6.3.(2022•杭州模拟)如图,点E是矩形ABCD边BC上一点,沿AE折叠,点B恰好落在CD边上的点F处.设=x(x>1),(1)若点F恰为CD边的中点,则x= .(2)设=y,则y关于x的函数表达式是 .【解答】解:(1)∵点F为CD边的中点,∴DC=2DF,∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=∠D=90°,∴∠FEC+∠EFC=90°,由折叠得:BE=EF,AB=AF,∠B=∠AFE=90°,∴AB=AF=DC=2DF,∵∠EFC+∠AFD=90°,∴∠AFD=∠FEC,∴△AFD∽△FEC,∴==2,∴=2,∴x=2,故答案为:2;(2)由(1)可得AB=AF=DC=DF+CF,∵△AFD∽△FEC,∴=,∴=,∴x=,∴x=1+,∴x=1+,∴y=,故答案为:y=.4.(2021•海州区校级二模)如图,△DEF的三个顶点分别在等边△ABC的三条边上,BC =4,∠EDF=90°,=,则DF长度的最小值是 .【答案】【解答】解:过点F作FH⊥BC,垂足为H,∵∠EDF=90°,tan∠EFD==,∴∠EFD=60°,∴∠AFE+∠DFC=120°,∵△ABC是等边三角形,∴∠C=∠A=60°,AC=BC=4,∴∠AFE+∠AEF=120°,∴∠AEF=∠DFC,∴△AEF∽△CFD,∴=,∵∠EDF=90°,∠EFD=60°,∴cos∠EFD==,∴=2,∴设CD=a,则AF=2a,∴CF=AC﹣AF=4﹣2a,在Rt△CFH中,∠C=60°,∴CH=CF=2﹣a,∴FH=CH=2﹣a,∴DH=CD﹣CH=a﹣(2﹣a)=2a﹣2,在Rt△DFH中,DF2=DH2+FH2=(2a﹣2)2+(2﹣a)2=7a2﹣20a+16=7(a﹣)2+,∴DF2的最小值为,∴DF的最小值为:.5.如图,在等边三角形ABC中,点E,D分别在BC,AB上,且∠AED=60°,求证:△AEC∽△EDB.【解答】证明:∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠EDB+∠BED=120°,∠CAE+∠AEC=120°∵∠AED=60°,∴∠BED+∠AEC=180°﹣60°=120°,∴∠BED=∠CAE,∴△AEC∽△EDB.6.如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,点D、E分别在边BC、AC上,连接AD、DE,有∠ADE=45°.(1)证明:△BDA∽△CED.(2)若BC=6,当AE=ED时,求BD的长.【解答】(1)证明:∵∠AED=∠C+∠EDC=45°+∠EDC,而∠ADC=∠ADE+∠EDC.∵∠ADE=45°,∴∠ADC=45°+∠EDC,∴∠AED=∠ADC.∴∠DEC=∠ADB(等角的补角相等).而∠B=∠C=45°,∴△ABD∽△DCE.故△ABD∽△DCE得证.(2)解:当AE=DE时,∴∠ADE=∠DAE,∵∠ADE=45°,∴∠ADE=∠DAE=45°,∵∠BAC=90°,∠BAD=∠EAD=45°,∴AD平分BAC,∴AD垂直平分BC,∴BD=3.7.(2022•安徽三模)如图,在四边形ABCD中,∠A=∠D=90°,AD=AB,以BC为直径的半⊙O与边AD相切于点E.(1)求证:∠BCE=∠DCE;(2)若,求DE的长.【解答】(1)证明:连接OE,∵半⊙O与边AD相切于点E,∴∠OEA=90°,∵∠D=90°,∴∠D=∠OEA=90°,∴OE∥CD,∴∠ECD=∠OEC,∵OE=OC,∴∠OEC=∠OCE,∴∠BCE=∠DCE;(2)解:连接BE,∵BA⊥AD,OE⊥AD,CD⊥AD,∴AB∥CD∥OE,∵OB=OC,∴AE=DE,设DE=AE=x,则AD=AB=2x,∵BC为⊙O的直径,∴∠BEC=90°,∴∠DEC+∠AEB=180°﹣∠BEC=90°,∵∠A=∠D=90°,∴∠ABE+∠AEB=90°,∴∠ABE=∠DEC,∴△ABE∽△DEC,∴,∴,解得:,∴DE的长为.8.(2022•钦州一模)已知下列各图中,△ABC是直角三角形,∠ABC=90°.【基本模型感知】如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N.求证:△ABM∽△BCN;【基本模型应用】如图2,点P是边BC上一点,∠BAP=∠C,,求tan C的值;【灵活运用】如图3,点D是边CA延长线上一点,AE=AB,∠DEB=90°,,,请直接写出tan∠BEC的值.【解答】(1)证明:∵AM⊥MN,CN⊥MN,∴∠AMB=∠BNC=90°.∴∠BAM+∠ABM=90°.∵∠ABC=90°,∴∠ABM+∠CBN=90°.∴∠BAM=∠CBN.又∵∠AMB=∠CNB,∴△ABM∽△BCN.(2)解:如图2,过点P作PF⊥AP交AC于点F,过点F作FQ⊥BC交BC于点Q,在Rt△AFP中,tan∠PAC===,与(1)同理得,△ABP∽△PQF.∴===.设AB=a,PQ=2a(a>0),∵∠BAP=∠C=∠FPQ,∴PF=CF,且FQ⊥BC.∴PQ=CQ=2a.∴BC=BP+PQ+CQ=BP+2a+2a=4a+BP.∵∠BAP=∠C,∠B=∠B=90°,∴△ABP∽△CBA.∴=.∴BP⋅BC=AB2,即BP⋅(4a+BP)=.∴BP=a,BC=5a,在Rt△ABC中,tan C==.(3)解:在Rt△ABC中,sin∠BAC==,如图3,过点A作AG⊥BE于点G,过点C作CH⊥BE交EB的延长线于点H,∵∠DEB =90°,∴CH ∥AG ∥DE .∴==.与(1)同理得,△ABG ∽△BCH∴===.设BG =4m ,CH =3m ,AG =4n ,BH =3n ,∵AB =AE ,AG ⊥BE ,∴EG =BG =4m .∴GH =BG +BH =4m +3n .∴=.∴n =2m .∴EH =EG +GH =4m +4m +3n =8m +3n =8m +6m =14m .在Rt △CEH 中,tan ∠BEC ==.9.(2021•坪山区一模)如图,抛物线y =x 2+bx +c 与x 轴交于点A (﹣3,0)、B ,与y 轴交于点C (0,﹣3).(1)求抛物线的解析式;(2)在抛物线上求点P ,使S △BCP =2S △BCO ,求点P 的坐标;(3)如图2,直线y =x +3交抛物线于第一象限的点M ,若N 是抛物线y =x 2+bx +c 上一点,且∠MAN =∠OCB ,求点N 的坐标.【解答】解:(1)将C (0,﹣3)代入到抛物线解析式中得,c =﹣3,将B (﹣3,0)代入到抛物线解析式中得,9﹣3b ﹣3=0,∴b =2,∴抛物线解析式为:y =x 2+2x ﹣3;(2)令y =0,则x 2+2x ﹣3=0,解得x 1=﹣3,x 2=1,∴B (1,0),∴,∵S △BCP =2S △BCO ,∴S △BCP =3,如图1,过P 作PM ∥BC 交x 轴于M ,连接MC ,则S △MBC =S △BCP =3,∴,∴MB =2,∴M (﹣1,0),设直线BC 为y =k 1x ﹣3,代入点B (1,0)得,k 1=3,∴直线BC 为:y =3x ﹣3,则直线PM 设为:y =3x +b ,代入点M (﹣1,0)得,b =3,∴直线PM 为:y =3x +3,联立,解得,,∴P(3,12)或(﹣2,﹣3);(3)∵直线y=x+3交抛物线于第一象限的点M,∴联立,解得,,∴A(﹣3,0),M(2,5),在Rt△OBC中,tan∠OCB=,∴,①如图2,当N在AM下方时,过A作y轴平行线,过M作x轴平行线,两线交于点G过M作MQ⊥AM交AN于Q,过Q作y轴平行线交GM于H,∴∠AGM=∠MHQ=90°,∴∠AMG+∠GAM=90°,又AM⊥MQ,∴∠AMQ=90°,∴∠AMG+∠HMQ=90°,∴∠GAM=∠HMQ,又∠AGM=∠MHQ=90°,∴△AGM∽△MHQ,∴=,∵A(﹣3,0),M(2,5),∴AG=5,GM=5,∴MH=HQ=,∴Q(),设直线AQ为:y=k2(x+3),代入点Q,得,∴直线AQ为,联立,化简得,2x2+3x﹣9=0,解得x=或﹣3,当x=时,y=,∴N(),②当N在AM上方时,同理可得,N(3,12),∴N()或(3,12).。
相似三角形在现实生活中的应用

应用比例解题
边长比例+对应角相等
1.使用相似三角形解决实际问题,需要掌握边长比例和对应角相等的概念,并且需要注意确定哪些角度以及哪些边是对应的。
2.当两个三角形相似时,我们可以利用边长比例+对应角相等,通过知道一个确定的边长或角度,来求出其他未知的边长或角度。这种方法常用于建筑工程计算、地图比例尺计算等实际生活中的问题解决。
直角三角形与比例
直角三角形的一条直角边上的中线等于斜边的一半,这可以用于构建相似三角形。
在相似三角形中,两个三角形的对应边的比例相等,可以利用这个性质求解一些实际问题。例如,可以用直角三角形的勾股定理和相似三角形的比例关系求出高度、边长等参数。
相似三角形可以用于估计远处物体的高度、距离等,例如在测量电线塔高度、建筑物高度等方面有广泛应用。
2023/6/1
目录
CONTENTS
相似三角形面积比例为边比例平方
根据公式,可以在实际应用中解决许多与比例相关的问题,例如测量高楼建筑物的高度或深度、估算远离我们的大型物体的大小或形状,以及计算三角形的面积等。此外,通过掌握相似三角形的解题技巧,我们还可以更好地理解几何学中的概念,提高我们的数学素养和应用能力。
1. 通过对应角相等,可以推导出平行线之间的性质。当两条平行线被一条横线所切分时,所形成的对应角相等的三角形也是相似的。这可以帮助我们推导出平行线的基本性质,如平行线上的相邻角互补,平行线之间的距离相等等。
2. 对应角相等还可以用于解决三角形的问题。当两个三角形中对应角相等时,这两个三角形是相似的。利用相似三角形的性质,我们可以解决一些涉及到三角形的问题,如求解三角形的面积、周长等。同时,相似三角形的性质也可以帮助我们推导出勾股定理、正弦定理、余弦定理等三角函数公式。
(详细版)相似三角形的性质和应用

(详细版)相似三角形的性质和应用
1. 相似三角形的性质
相似三角形是指具有相同形状但尺寸不同的三角形。
相似三角形的性质如下:
- 对应角相等性质:如果两个三角形的对应角相等,则它们是相似三角形。
- 对应边成比例性质:相似三角形的对应边的长度成比例。
2. 相似三角形的应用
相似三角形的性质在实际生活和数学问题中有广泛的应用,以下是一些常见的应用场景:
- 测量高度:通过相似三角形的性质,我们可以利用测量出的一个三角形的高度来计算另一个相似三角形的高度。
这在实际中可以用于测量高楼、山峰等的高度。
- 图形设计:相似三角形的性质可以用于图形设计中的缩放问题。
通过改变三角形的大小来实现图形的缩放效果。
- 工程测量:在土木工程中,相似三角形的性质可以用于测量地形的坡度、直角三角形的边长等。
3. 实例分析
为了更好地理解相似三角形的性质和应用,以下是一个实际问题的分析:
假设有一根高大的电线杆,测得其高度为30米。
为了确定杆子的阴影长度,我们利用测量出的相似三角形来推算。
测量阴影的长度为10米,而测量器与杆子的距离为4米。
根据相似三角形的性质,可以建立如下比例关系:(30高度/4距离) = (阴影长度/10距离)。
通过解这个比例关系,我们可以计算出杆子的阴影长度为75米。
以上是相似三角形的性质和应用的一些简要介绍,通过理解和运用相似三角形的性质,我们可以解决许多实际问题,提高数学和几何的应用能力。
(Word count: 229 words)。
数学相似三角形应用举例

数学相似三角形应用举例相似三角形是指具有相似形状但不一定相等大小的三角形。
数学中,在相似三角形之间存在着各种有意义的关系,这些关系在实际中有广泛的应用。
下面我将为大家举例说明相似三角形的应用。
首先,相似三角形在地图比例尺的确定中起到了重要的作用。
地图上的距离是实际距离的缩放版本,而这个缩放比例就是通过相似三角形来确定的。
我们可以通过测量地图上两个地点的距离,然后测量这两个地点的实际距离,通过相似三角形的比例关系,就可以计算出地图的比例尺,从而准确地测量其他地点的距离。
其次,相似三角形在工程测量中也有广泛的应用。
例如,在建筑设计中,我们常常需要测量高楼大厦的高度。
然而,直接测量高楼大厦的高度是非常困难的,而且也不安全。
这时,我们可以利用相似三角形的原理。
我们可以在地面上选择一个安全的位置,测量出到高楼大厦的距离和自己的高度,然后再测量出到高楼大厦顶部的夹角。
通过相似三角形的比例关系,可以计算出高楼大厦的高度。
此外,相似三角形还可以用于计算塔尖的高度。
在船舶导航中,我们需要确定灯塔的高度,以便进行航行计划。
然而,由于灯塔通常会建在陡峭的悬崖上,直接测量灯塔的高度非常困难。
这时,我们可以借助相似三角形的原理。
我们可以在海面上选择一个远离灯塔的位置,测量出到灯塔的距离和自己的水平高度,然后再测量出到灯塔塔尖的仰角。
通过相似三角形的比例关系,可以计算出灯塔的高度。
最后,相似三角形还在数学教育中有着重要的应用。
通过相似三角形,我们可以对学生进行数学思维的培养和训练。
让学生通过实际问题的解决,去发现数学中的规律和关系,培养学生的逻辑思维能力和创新能力。
总之,相似三角形在地图比例尺确定、工程测量、船舶导航和数学教育中都有广泛的应用。
通过相似三角形的原理,我们可以准确地测量距离、确定高度,并培养学生的数学思维能力。
相似三角形不仅是数学的重要概念,也是实际问题解决的有力工具。
通过深入理解相似三角形的应用,我们可以更好地应用数学知识解决实际问题,为我们的生活和工作带来便利。
相似三角形应用举例课件

优化建筑布局
在建筑布局设计中,可以利用相 似三角形原理来优化空间布局, 提高建筑的使用效率和舒适度。
航海中的应用
确定航向
导航定位
在航海过程中,可以利用相似三角形 原理来计算船只与目标之间的角度, 从而确定正确的航向。
在导航定位过程中,可以利用相似三 角形原理来计算船只的位置和航速, 确保航行安全和准确到达目的地。
相似三角形应用举例课件
目录
CONTENTS
• 相似三角形的基本概念 • 相似三角形在生活中的应用 • 相似三角形在数学问题中的应用 • 相似三角形在实际问题中的解决策略 • 相似三角形的综合应用举例
01 相似三角形的基本概念
CHAPTER
相似三角形的定义
01
02
03
相似三角形
如果两个三角形对应的角 相等,则这两个三角形相 似。
如果两个三角形有一个对 应的角相等和一组对应的 边成比例,则这两个三角 形相似。
02 相似三角形在生活中的应用
CHAPTER
测量中的应用
测量建筑物高度
利用相似三角形原理,通过测量 建筑物的影长或其他已知高度的 物体,可以计算出建筑物的高度。
测量河流宽度
在河流两岸分别设置标杆,利用相 似三角形原理,可以计算出河流的 宽度。
示例
证明两条线段相等,可以通过构造两个三角形,使它们相似,然后利用对应边成比例的性 质来证明线段相等。
在代数问题中的应用
01
总结词
利用相似三角形的性质,解决代数方程或不等式问题。
02 03
详细描述
在代数问题中,有时需要通过解方程或不等式来求解未知数。通过构造 相似三角形,可以利用相似三角形的性质,如对应边成比例、对应角相 等,来转化方程或不等式,从而简化求解过程。
相似三角形的比例与应用

相似三角形的比例与应用相似三角形是中学数学中的重要概念,它涉及到几何学的多个方面,并在实际生活中有着广泛的应用。
相似三角形指的是两个三角形的形状相同但大小不一定相同,它们的对应角度相等,对应边的比例相等。
相似三角形的判定条件有两个:1.两个三角形的对应角相等。
2.两个三角形的对应边的比例相等。
相似三角形的性质有以下几点:1.相似三角形的对应角相等。
2.相似三角形的对应边的比例相等。
3.相似三角形的面积比等于对应边长比的平方。
相似三角形在实际应用中有着广泛的作用,例如在测量、建筑、工程等领域。
下面介绍相似三角形在实际中的应用:1.测量:在测量土地面积或距离时,常常遇到三角形。
通过测量三角形的某些边长和角度,可以利用相似三角形的性质计算出未知的边长或角度。
2.建筑:在建筑设计中,常常需要根据实际尺寸和比例关系进行设计。
利用相似三角形的性质,可以计算出建筑物的不同部分的比例和尺寸。
3.工程:在工程领域,例如桥梁、塔架等结构的设计和建造中,常常需要根据相似三角形的性质进行计算和设计。
相似三角形是中学数学中的重要概念,通过学习和掌握相似三角形的性质和应用,可以帮助学生更好地理解和解决实际问题。
习题及方法:1.习题:判断两个三角形是否相似。
已知:三角形ABC和三角形DEF,其中∠A = ∠D = 90°,AB = 10cm,DE =12cm。
由于∠A = ∠D = 90°,所以三角形ABC和三角形DEF都是直角三角形。
直角三角形的两个直角边成比例,则两个直角三角形相似。
因此,根据题目给出的信息,可以得出三角形ABC和三角形DEF相似。
2.习题:计算两个相似三角形的对应边长比例。
已知:三角形ABC和三角形DEF相似,且AB = 6cm,BC = 8cm,DE = 9cm,EF = 12cm。
由于三角形ABC和三角形DEF相似,根据相似三角形的性质,它们的对应边长比例相等。
设AB与DE的比例为k,则BC与EF的比例也为k。
第34讲 相似三角形的性质及应用(解析版)

第34讲 相似三角形的性质及应用一、相似三角形的性质1.相似三角形的对应角相等,对应边的比相等.2. 相似三角形中的重要线段的比等于相似比.相似三角形对应高,对应中线,对应角平分线的比都等于相似比.要点:要特别注意“对应”两个字,在应用时,要注意找准对应线段.3. 相似三角形周长的比等于相似比∽,则由比例性质可得:4. 相似三角形面积的比等于相似比的平方∽,则分别作出与的高和,则要点:相似三角形的性质是通过比例线段的性质推证出来的.二、三角形的重心三角形三条中线的交点叫做三角形的重心,三角形的重心分每一条中线成1:2的两条线段.即12O D O E O F O A O B O C === .要点:21122=1122ABCA B C BC AD k B C k A D S k S B C A D B C A D ¢¢¢¢¢¢¢××××==¢¢¢¢¢¢¢¢¢××△△1.测量高度测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点:测量旗杆的高度的几种方法:平面镜测量法影子测量法手臂测量法标杆测量法2.测量距离测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。
1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长.2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长.要点: 1.比例尺:表示图上距离比实地距离缩小的程度,比例尺= 图上距离/ 实际距离; 2.太阳离我们非常遥远,因此可以把太阳光近似看成平行光线.在同一时刻,两物体影子之比等于其对应高的比; 3.视点:观察事物的着眼点(一般指观察者眼睛的位置);4. 仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角.例1.已知V ABC∽V DEF,若AB:DE=1:2,则V ABC与V DEF的面积之比是( )A.1:3B.1:4C.1:9D.1:16【答案】B【解析】【分析】根据相似三角形的性质:相似三角形的面积之比等于相似比的平方,即可求出答案.解:∵△ABC ∽△DEF ,2(,ABC DEF S AB S DED D \=∵ AB :DE =1:2,,∴△ABC 与△DEF 的面积比211.24æöç÷==ç÷èø故选:B .【点睛】本题考查了相似三角形的性质的应用,注意:相似三角形的面积之比等于相似比的平方,而不等于相似比,题目比较典型,难度不大.例2.已知ABC DEF ∽△△,12AB DE =,若2BC =,则EF =( )A .4B .6C .8D .16【答案】A【解析】【分析】根据相似三角形的性质得到AB BC DE EF =,代入求解即可.解:∵ABC DEF ∽△△,∴12AB BC DE EF ==,即212EF =,解得4EF =.故选:A .【点睛】此题考查了相似三角形的性质,解题的关键是熟练掌握相似三角形性质.相似三角形性质:相似三角形对应边成比例,对应角相等.相似三角形的相似比等于周长比,相似三角形的相似比等于对应高,对应角平分线,对应中线的比,相似三角形的面积比等于相似比的平方.例3.如图,AB ∥CD ,34AE ED =,AB =2,则CD 的长为( )A.98B.83C.3D.4【答案】B 【解析】【分析】通过证明△ABE∽△DEC,可得AB AECD ED=,即可求解.解:∵AB CD∥,∴△ABE∽△DEC,∴AB AECD ED=,而34AEED=,AB=2,∴23,4 CD=∴83 CD=,故选:B.【点睛】本题考查了相似三角形的判定和性质,证明三角形相似是解题的关键.例4.如图,小明从路灯下A处,向前走了5米到达D处,在D处发现自己在地面上的影子长DE 是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是()米.A.4.6B.5.6C.7.5D.8.5【答案】B【解析】【分析】根据相似三角形对应边成比例可解.解:∵AD=5,DE=2,∴AE=7,∵AB⊥AE,CD⊥AE,∴△ABE∽△DCE,∴AB AE CD DE=,∴71.6 5.62AEAB CDDE=×=´=(米).故选:B.【点睛】此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.例5.如图:在△ABC中,AB=AC,D是AC上的一点,且∠A=∠DBC=36°,则下列结论不成立的是( )A.BC=AD B.点D是AC的黄金分割点C.AB CDBC BD=D.BC2=AC•CD【答案】C 【解析】【分析】由等腰三角形的判定、相似三角形的判定与性质分别对各个选项进行判断即可.解:A 、∵AB =AC ,∠A =36°,∴∠ABC =∠C 12=(180°﹣∠A )12=´(180°﹣36°)=72°,∵∠DBC =36°,∴∠ABD =∠ABC ﹣∠DBC =36°,∴∠BDC =∠A +∠ABD =72°,∴∠BDC =∠C ,∴BC =BD ,∵∠A =∠ABD =36°,∴BD =AD ,∴BC =AD ,故选项A 成立,不符合题意;∵∠A =∠DBC ,∠C =∠C ,∴△ABC ∽△BDC ,∴AB :BD =BC :DC ,∴AB :AD =AD :DC ,∴点D 是AC 的黄金分割点,AB :BC =BD :CD ,故选项B 成立,选项C 不成立;D 、∵AD 2=AB •CD ,AD =BC ,∴BC 2=AB •CD ,故选项D 成立;故选:C .【点睛】本题考查了黄金分割、等腰三角形的判定与性质、相似三角形的判定与性质等知识,熟练掌握等腰三角形的判定与性质,证明三角形相似是解题的关键.例6.如图,ABC V 中,点D 、E 分别在AB 、AC 上,且2AD AE DB EC==,下列结论错误的是( )A .DE BC∥B .:2:3DE BC =C .ADE V 与ABC V 的面积比为4:9D .ADE V 与ABC V 的周长比为1:2【答案】D【解析】【分析】根据题中成比例线段证ABC ADE D D :,从而即可进行判断;解:∵2AD AE DB EC ==,∴23AD AE AB AC ==,∵∠A =∠A ,∴ABC ADE D D :,∴ABC ADE Ð=Ð,:2:3DE BC =;故B 不符合题意;∴DE BC ∥,故A 不符合题意;∵23AD AE AB AC ==,∴ADE D 与ABC D 的周长比为2:3;故D 符合题意;∴249ADE ABC S AD S AB D D æö==ç÷èø,故C 不符合题意;故选:D .【点睛】本题主要考查相似三角形的性质及证明,掌握相关知识并灵活应用是解题的关键.例7.如图,在△ABC 中,中线BE ,CD 相交于点O ,连接DE ,下列结论:①12DE BC =;②12DOE COB S S D D =;③AD OE AB OB =;④13ODE ADC S S D D =,其中正确的个数有( )A .1个B .2个C .3个D .4个【答案】C【解析】【分析】由BE 、CD 是△ABC 的中线, 可得1,2DE BC = 即12DE BC =,从而可判断①;由DE 是△ABC 的中位线,可得△DOE ∽△COB ,从而可判断②;由△ADE ∽△ABC 与△DOE ∽△COB ,利用相似三角形的性质可判断③;由△ABC 的中线BE 与CD 交于点O .可得点O 是△ABC 的重心,根据重心性质,BO =2OE ,△ABC 中BC 上的高=△BOC 中BC 上的高的3倍,且△ABC 与△BOC 同底(BC ),可得3ABC BOC S S =V V ,由②和③知,13,44ODE COB ADE BOC S S S S ==V V V V ,从而可判断④.解:①∵BE 、CD 是△ABC 的中线,即D 、E 是AB 和AC 的中点,∴DE 是△ABC 的中位线,∴1,2DE BC = 即12DE BC =,故①正确;②∵DE 是△ABC 的中位线,∴DE ∥BC ,∴△DOE ∽△COB ,∴221124DOE COB S DE S BC æöæö===ç÷ç÷èøèø△△,故②错误;③∵DE ∥BC ,∴△ADE ∽△ABC ,∴AD DE AB BC=,∵△DOE ∽△COB ,OE DE OB BC \=, ∴AD OE AB OB=,故③正确;④∵△ABC 的中线BE 与CD 交于点O ,∴点O 是△ABC 的重心,根据重心性质,BO =2OE ,△ABC 中BC 上的高=3△BOC 中BC 上的高,且△ABC 与△BOC 同底(BC ),∴3ABC BOC S S =V V ,由②和③知,14ODE COB S S =V V ,1=2AD DE AB BC =,∴221124DAE BAC S AD S AB æöæö===ç÷ç÷èøèøV V ,∴34ADE BOC S S =V V ,∴13ODEADE S S =V V .故④正确.综上,①③④正确.故选C .【点睛】本题考查的三角形的中线与三角形的中位线的性质,三角形的重心的性质,相似三角形的判定与性质,掌握利用以上知识解决三角形的面积问题是解题的关键.例8.如图,D 、E 分别是ABC V 的边AB 、BC 上的点,且//DE AC ,若:1:3BDE CDE S S =V V ,则DOE AOC S S V V :的值( )A .13B .14C .19D .116【答案】D【解析】【分析】证明:1:3=BE EC ,得出:1:4BE BC =;证明BDE BAC D D ∽,DOE AOC D D ∽,得到14DE BE AC BC ==,由相似三角形的性质即可解决问题.解::1:3BDE CDE S S D D =Q ,:1:3BE EC \=;:1:4BE BC \=;//DE AC Q ,BDE BAC \D D ∽,DOE AOC D D ∽,\14DE BE AC BC ==,21:(16DOE AOC DE S S AC D D \==.故选:D .【点睛】本题主要考查了相似三角形的判定及其性质的应用问题,解题的关键是灵活运用相似三角形的判定及其性质来分析、判断、推理或解答.例9.ABC D 的边上有D 、E 、F 三点,各点位置如图所示.若B FAC Ð=Ð,BD AC =,BDE C Ð=Ð,则根据图中标示的长度,求四边形ADEF 与ABC D 的面积比为何?( )A .1:3B .1:4C .2:5D .3:8【答案】D【解析】【分析】先证明ΔΔCAF CBA ∽,再利用相似三角形的性质求出AC =ΔΔ:5:16ACF ACB S S =,再证明BDE BCA D D ∽,求出ΔΔ:5:16BDE ABC S S =,即可求出答案.解:C C Ð=ÐQ ,CAF B Ð=Ð,ΔΔCAF CBA \∽,\CA CF CB CA=,2CA CF CB \=×,251680CA \=´=,0AC >Q ,AC \=\AC CB ==ΔΔ:5:16ACF ACB S S \=,同法可证BDE BCA D D ∽,BD AC =Q\BD BC =ΔΔ:5:16BDE ABC S S \=,()Δ:1655:163:8ABC ADEF S S \=--=四边形,故选:D .【点睛】本题考查相似三角形的判定和性质,解题的关键是正确寻找相似三角形解决问题,属于中考选择题中的压轴题.例10.如图,在平面直角坐标系xOy 中,半径为2的⊙O 与x 轴的正半轴交于点A ,点B 是⊙O 上一动点,点C 为弦AB 的中点,直线y =34x ﹣3与x 轴、y 轴分别交于点D 、E ,则△CDE 面积的最小值为( )A.3.5B.2.5C.2D.1.2【答案】C【解析】【分析】连接OC,得到∠ACO=90°,确定点C在以OA为直径的圆上(点O、A除外),以OA为直径作⊙P,过P 点作直线PH⊥DE于H,交⊙P于M、N,求出点E(0,﹣3),D(4,0),利用勾股定理求出DE=5,证明△DPH∽△DEO,求出PH=95,得到S△NED=12×5×45=2,S△MED=12×5×245=7,设△CDE面积为S,由此得到当C点与M点重合时,S最大;C点与N点重合时,S最小,由此确定答案解:连接OC,如图,∵点C为弦AB的中点,∴OC⊥AB,∴∠ACO=90°,∴点C在以OA为直径的圆上(点O、A除外),以OA为直径作⊙P,过P点作直线PH⊥DE于H,交⊙P于M、N,当x=0时,y=34x﹣3=﹣3,则E(0,﹣3),当y=0时,34x﹣3=0,解得x=4,则D(4,0),∴OD=4,∴DE,∵A(2,0),∴P(1,0),∴OP=1,∴PD=OD﹣OP=3,∵∠PDH=∠EDO,∠PHD=∠EOD,∴△DPH∽△DEO,∴PH:OE=DP:DE,即PH:3=3:5,解得PH=95,∴MP=PH+1=145,NH=PH﹣1=45,∴S△NED=12×5×45=2,S△MED=12×5×245=7,设△CDE面积为S,当C点与M点重合时,S最大;C点与N点重合时,S最小,∴S的范围为2≤S≤7,∴△CDE面积的最小值为2.故选:C.【点睛】此题考查垂径定理,勾股定理,一次函数图象与坐标轴的交点坐标,相似三角形的判定及性质,这是一道图形类的综合题,综合掌握各知识点并熟练应用解决问题是解题的关键.例11.如图,是小莹设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD BD^.且测得 1.4AB=米, 2.1PB=米,PD=12米,那么该古墙的高度是__________米.【答案】8【解析】【分析】由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到AB BPCD PD=代入数值求解即可.解:∵AB ⊥BD ,CD ⊥BD ,∴∠ABP =∠CDP =90°,∵∠APB =∠CPD ,∴△ABP ∽△CDP ∴AB BP CD PD=,即1.42.112CD = 解得:CD =8米.故答案为:8.【点睛】本题考查了相似三角形的应用:利用入射与反射的原理构建相似三角形,然后利用相似三角形的性质即相似三角形的对应边的比相等解决.例12.如图,已知CA DB ^,DE AB ^,AC 、ED 交于F ,3BC =,1FC =,5BD =,则AC =________.【答案】6【解析】【分析】由题意在Rt △CDF 中可求得DF =△CDF ∽△EDB ,可得CF DF BE BD =,可求得BE ,由勾股定理可求得DE ,进一步可求得EF ,再证明△BDE ∽△BAC ,可得到BE DE BC AC =,进而分析即可求得AC .∵CA ⊥DB ,DE ⊥AB ,∴∠DCF =∠BED ,且∠D =∠D ,∴△CDF ∽△EDB ,∴CF DF BE BD=,∵BC =3,BD =5,∴CD =2,且FC =1,在Rt △CDF 中,DF ==,∴1BE =解得BE =在Rt △BDE 中,BD =5,BE =DE =,同理可证得△BDE ∽△BAC ,∴BE DE BC AC =,=,解得AC =6.故答案为:6.【点睛】本题主要考查相似三角形的判定和性质,熟练掌握相似三角形的判定方法以及勾股定理是解题的关键.例13.如图,在Rt △ABC 中,∠A =90°,AB =AC =,点E 为AC 的中点,点F 在底边BC 上,且FE ⊥BE ,则CF 长__.【解析】【分析】作EH ⊥BC 于H ,如图,利用等腰直角三角形的性质得BC =∠C =45°,再计算出EH =CH =BH =BE 后根据射影定理计算出BF ,然后计算BC−BF 即可.作EH ⊥BC 于H ,如图,∵∠A =90°,AB =AC =,∴BC ==∠C =45°,∵点E 为AC 的中点,∴AE =CE =,∵△CEH 为等腰直角三角形,∴EH =CH ==∴BH =在Rt △ABE 中,BE ==在Rt △BEF 中,∵EH ⊥BF ,∴BE 2=BH•BF ,即BF =∴CF =BC ﹣BF ==.【点睛】本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了等腰直角三角形的性质.例14.如图,在四边形ABCD 中,对角线AC 与BD 相交于点O ,OA OC =,在AB 的延长线上取一点E ,连接OE 交BC 于点F 已知,,AB m BC n BF k ===,则BE =___.(用含m 、n 、k 的代数式表示)【答案】2mkn k -【解析】【分析】作//OM AB 交BC 于点M ,首先证明OM 是△ABC 的中位线,求出OM ,FM ,再根据△OMF ∽△EBF ,可得BE BF OM FM=,由此求出BE 即可.解:如图,过点O 作//OM AB 交BC 于点M .∵,//OA OC OM AB =,∴1122BM CM BC n ===,∴1122OM AB m ==,∵BF k =,∴12FM BM BF n k =-=-,∵//OM BE ,∴EBF OMF V V ∽,∴BE BF OM FM =,即1122BE k m n k =-,解得2mk BE n k =-.故答案为2mk n k-.【点睛】此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.例15.已知Rt △ABC ≌Rt △DEF 中,∠C =∠F =90°,BC =6,AC =8,点D 是边AB 的中点,∠FDE 的两边分别与AC 交于点G 、H .当△BDH 与△ADG 相似时,CH 的长为__.【答案】74【解析】【分析】根据勾股定理求出AB 的长,然后分为三种情况讨论:当△BDH 与△ADG 相似时,①∠A =∠DBH ,②∠A =∠BHD ,③∠A =∠HDB ,对于①∠A =∠DBH ,②∠A =∠BHD 利用三角形相似的性质即可求解,③根据外角的性质判断出不存在.∵∠C =90°,BC =6,AC =8,∴AB =10,①当△BDH 与△ADG 相似时,∠A =∠DBH ,∴AH =BH ,∵点D 是边AB 的中点∴HD ⊥AB∴∠ADH =∠C =90°∴△ADH ∽△ACB ∴AD AC AH AB =∴58AH 10=∴AH 425=∴CH =AC ﹣AH =825744-=;②当△BDH 与△ADG 相似时,∠A =∠BHD∵∠ABH =∠DBH∴△ABH ∽△HBD ∴BD BH BH AB=∴BH ===∴CH ===③当△BDH 与△ADG 相似时,∠A =∠HDB∵HDB 是△ADH 的外角∴∠HDB >∠A∴这种情况不存在.故答案为74【点睛】本题考查了三角形相似的判定和性质,勾股定理,根据题意选择适当的方法证明两三角形相似,并利用三角形相似的性质解答是本题的关键.例16.如图,在边长为2个单位长度的正方形ABCD 中,E 是AB 的中点,点P 从点D 出发沿射线DC 以每秒1个单位长度的速度运动,过点P 作PF ⊥DE 于点F ,当运动时间为______秒时,以P 、F 、E 为顶点的三角形与△AED 相似.【答案】1或52【解析】【分析】分两种情形:①如图,当△PFE ∽△EAD 时,②如图,当△EFP ∽△EAD 时,分别求解即可.解:①如图,当△PFE ∽△EAD 时,∴∠ADE =∠FEP ,∴AD ∥PE ,∴PE ⊥CD ,∴四边形AEPD 是矩形,∵四边形ABCD 是正方形,E 是AB 的中点,∴t =DP =AE =1;②如图,当△EFP ∽△EAD 时,∴∠ADE =∠FPE ,∠AED =∠FEP ,∵DC ∥AB ,∴∠AED =∠CDE ,∴∠FEP =∠CDE ,∴PD =PE ,∴PF 是DE 的垂直平分线,∴F 为DE 中点,DE =EF =DF =12DE∵DA DE PF EP =,解得t =DP =52,综上所述,满足条件的t 的值为1s 或52s .故答案为:1或52.【点睛】本题考查了相似三角形的性质、正方形的性质等知识,解题的关键是学会用分类讨论的思想思考问题.一、单选题1.在△ABC 中,三条边的长分别为2、3、4,△A′B′C′的两边长分别为1、1.5,要使△ABC ∽△A′B′C′,那么△A′B′C′的第三边长应该是( )A .2B C .4D .【答案】A【解析】根据相似三角形对应边成比例,得:△A′B′C′的三边比为2:3:4,由于两边长为1和1.5,即2:3,则第三边为1.5423´=,故选A.2.在RT △ABC 中,∠ACB=90°,CD ⊥AB 于D ,则下列等式中错误的是( )A .AC ﹒BC=AB ﹒CDB .AC ﹒BD=BC ﹒AD C .AC 2=AB ﹒ADD .CD 2=AD ﹒BD【答案】B【解析】【分析】如图,根据△ABC 面积的两种计算方法可以判断A 成立,根据△ACD~△CBD 可以判断B 错误、D 正确,根据△ACD~△ABC 可以判断C 正确.解:如图,A 、根据△ABC 面积的两种计算方法可知等式成立,正确;B 、由题意可知△ACD~△CBD,所以AC CD CB BD =,所以AC ﹒BD=BC ﹒CD ,错误;C 、由题意可知△ACD~△ABC,所以AC AD AB AC=,所以AC 2=AB ﹒AD ,正确;D 、由题意可知△ACD~△CBD, 所以AD CD CD BD=,所以CD 2=AD ﹒BD ,正确.故选B .【点睛】本题考查直角三角形的应用,熟练掌握直角三角形被斜边上高分成若干相似三角形是解题关键.3.如图,△ABC 中,AE 交BC 于点D ,∠C=∠E ,AD=4,BC=8,BD :DC=5:3,则DE 的长等于 ( )A .203B .174C .163D .154【答案】D【解析】试题分析:在△BDE 和△ADC 中,∠C=∠E ,∠BDE=∠ADC∴△BDE ∽△ADC ∴AD CD BD DE=∵BC=8,BD :DC=5:3,∴BD=5,CD=3∴DE=154故选D.考点:相似三角形的判定与性质.4.如图,在ABC V 中,90ACB Ð=°,MN 垂直平分AC ,延长BC 至点D ,使12CD BC =,连接.DN 若5DN =,则AB 等于( )A .6B .8C .10D .12【答案】C【解析】【分析】根据垂直平分线的性质证明AMN ABC V :V ,可得到12MN BC =,即可得到MN CD =,得到△△R t A M N R t N D C @,即可得到结果;由题意知:MN 垂直平分AC ,∴12A N C N A C ==,90ANM Ð=°,∵90ACB Ð=°,∴MN BC P ,90ACD Ð=°,∴AMN ABC V :V ,90A N M A C B Ð=Ð=°,∴12A N A M N M A C AB BC ===,∴12MN BC =,∵12CD BC =,∴MN CD =,在Rt △AMN 和Rt△NDC 中,A N N C NM C D ì=í=î,∴△△R t A M N R t N D C @,∴AM DN =,∵5DN =,∴5AM =,512A B =,∴10AB =.故选:C .【点睛】本题主要考查了全等三角形性质和判定及相似三角形的判定和性质,准确计算是解题的关键.5.如图,已知在ABC V 中,∥DE BC ,EF AB ∥,则下列比例式中正确的个数为( )①DE AE BC EC = ②AD AB B CE C = ③CE CA CF CB = ④AD AE AB AC =A .1个B .2个C .3个D .4个【答案】C【解析】【分析】利用相似三角形的判定及性质分析结论即可.解:∵∥DE BC ,∴ADE ABC △△∽,∴=DE AE BC AC,故①错误;∵ADE ABC △△∽,∴=AD AE AB AC ,故④正确;由=AD AE AB AC 可得:--AB BD AC CE AB AC =,即11--BD CE AB AC =,∴=BD CE AB AC,故②正确;∵EF AB ∥,∴CEF CAB ∽△△,∴CE CA CF CB=,故③正确;综上所述:正确的有②③④.故选:C【点睛】本题考查相似三角形的判定及性质,解题的关键是掌握相似三角形的判定及性质.6.如图,BD 、CE 是ABC V 的两条高,BD 、CE 相交于O ,则下列结论不正确的是( ).A .ADE V ∽ABCV B .DOE △∽COB △C .BOE △∽COD△D .BOE △∽BDEV 【答案】D【解析】【分析】根据相似三角形的判定定理,找出图中的全等三角形,即可得到答案.∵BD 、CE 是△ABC 的高,∴∠ADB=∠AEC=90°,又∵∠A=∠A∴△ADB ∽△AEC ∴AD AB =AE AC又∵∠A=∠A∴△ADE ∽△ABC ,故A 正确;∵BD 、CE 是△ABC 的高,∴∠OEB=∠ODC=90°,又∵∠EOB=∠DOC∴△BOE ∽△COD ,故C 正确;∵△BOE ∽△COD ∴OE OB =OD OC又∵∠DOE=∠COB∴△DOE ∽△COB ,故B 正确;无法判定△BOE ∽△BDE ,故D 错误;故选D.【点睛】本题考查相似三角形的判定与性质,熟练掌握相似三角形的判定定理是解决本题的关键.7.如图,已知ABC V 的面积是12,6BC =,点E ,I 分别在边AB ,AC 上,在边BC 上依次作了n 个全等的小正方形,DEFG ,GFMN ,L ,KHIJ ,则每个小正方形的边长为( )A .1211B .1223n -C .125D .1223n +【答案】D【解析】【分析】设正方形的边长为x ,根据正方形的性质以及相似三角形性质先求出相应情况下的正方形边长,然后进一步寻求规律即可.当作了1个正方形时,如图所示,过A 作AM ⊥BC ,垂足为M ,交GH 于N ,∴∠AMC=90°,∵四边形EFGH 为正方形,∴GH ∥BC ,GH=GF ,GF ⊥BC ,∴∠AGH=∠B ,∠ANH=∠AMC=90°,∵∠GAH=∠BAC ,∴△AGH~△ABC ,∴AN:AM=GH:BC ,∵△ABC 面积为12,BC 为6,∴1161222ABC s BC AM AM D ===n n n ,∴AM=4,设GH=x ,∵GF=NM=GH ,∴AN=AM−NM=AM−GH=4x -,∴464x x -=,∴125x =,同理,当2n =时,根据正方形性质可得:DN=2DE ,∴244DN DE BC -=,∴127DN =,以此类推,当为第n 个正方形时,每个小正方形边长为:1223n +,故选:D.【点睛】本题主要考查了正方形性质以及相似三角形性质的综合运用,熟练掌握相关概念是解题关键.8.如图,矩形ABCD 中,5AB =,12AD =,点P 在对角线BD 上,且BP BA =,连接AP 并延长,交DC 的延长线于点Q ,连接BQ ,则BQ 的长为( )A B .C .D .【答案】C【解析】【分析】根据矩形的性质可求BD ,ABP QDP D D :,从而得到QC ,由勾股定理即可求解;解:∵在矩形ABCD 中,5AB =,12AD =,∴13BD ===∵AB ∥CD ,∴ABP QDPÐ=Ð∵APB QPDÐ=Ð∴ABP QDPD D :∵5BP BA ==∴1358DQ PD BD BP ==-=-=∴853QC DQ CD =-=-=∴BQ ==故选:C .【点睛】本题主要考查三角形的相似、矩形的性质、勾股定理,掌握相关知识并灵活应用是解题的关键.9.如图,将⊙O 的圆周分成五等分(分点为A 、B 、C 、D 、E ),依次隔一个分点相连,惊讶于图形的奇妙,于是对图形展开了研究,M 也是线段NE 、AH 的黄金分割点.在以下结论中,不正确的是( )A .MN AM =B .FD AD =C .BN =NM =MED .∠A =36°【答案】C【解析】【分析】由A 、B 、C 、D 、E 是⊙O 上的5等分点,连接CO 、OD 求得∠COD =72°根据圆周角定理得到∠CAD =36°;连接CD 、AE ,得出AM =EM ,再根据黄金分割的定义和相似三角形的性质判断即可.连接CO 、OD 、CD 、AE ,∵A 、B 、C 、D 、E 是⊙O 上的5等分点,∴∠COD =3605°=72°,∴∠CAD =36°;D 正确,不符合题意;同理可得,∠BEA =∠DAE =∠BDC =∠ECD =∠ADB =36°;∴AM =EM ,∠AMN =72°;∴AM ≠MN ,C 错误,符合题意;∵M∴MN EM =MN AM =A 正确,不符合题意;∵∠ADC =∠ADB +∠BDC =72°;∴△,∴CD AD =同理∠ACD =∠ADC =72°;∴∠ACD =∠DFC =72°;∴DC =∴FD AD =B 正确,不符合题意;故选:C【点睛】本题考查了圆周角定理、黄金分割和相似三角形,解题关键是根据圆周角定理求出角度,利用黄金分割和相似三角形解决问题.10.如图,直角三角形ABC 中,90ACB Ð=°,CD AB ^于D ,DE AC ^于E ,则下列说法中正确的有( )个.①图中有4个三角形与ACB △相似;②2DE AE EC =×;③A BCD CDE Ð=Ð=Ð;④AD CE AC BD=;⑤若4AC =,3BC =,则163CD =;⑥AE AD EC DB =.A .2个B .3个C .4个D .5个【答案】D【解析】【分析】根据题意,对选项逐一分析,即可得出结论.解:因为CD AB ^,DE AC ^,所以AED DEC ADC Ð=Ð=Ð =90°,A ACD Ð+Ð=90°,所以A ADE Ð+Ð=90°,可得ACD ADE Ð=Ð,所以AED DEC V :V ,所以AE DE DE CE=,即2DE AE EC =×,故选项②正确;由题意90ACB Ð=°,CD AB ^于D ,DE AC ^于E ,所以A B Ð+Ð=90°,90A ADE Ð+Ð=°,90A ACD Ð+Ð=°,90B BCD Ð+Ð=°,由相似的判定可知图中有4个三角形与ACB △相似,分别是ACD △、CDB △、ADE V 、DEC V ,故选项①正确;因为90ACB Ð=°,所以∠A 与∠B 互余,CD AB ^于D ,DE AC ^于E ,∠BCD 与∠B 互余,∠CDE 与∠DCE 互余,∠DCE 与∠BCD 互余,所以A BCD CDE Ð=Ð=Ð,故选项③正确;因为90ACB Ð=°,CD AB ^于D ,DE AC ^于E ,根据③中结论A BCD CDE Ð=Ð=Ð,所以ACD CBD V :V ,AD CD CD BD =,因为ACD DCE :△△,所以CD CE AC CD =,两式相乘即可得AD CE AC BD=,故选项④正确;若4AC =,3BC =,由勾股定理可得AB =5,利用等面积可得341255CD ´==,故选项⑤错误;因为DE ∥BC ,所以AE AD EC DB =,故选项⑥正确;5个正确,故答案为:D .【点睛】本题考查了相似三角形的判定和性质,勾股定理的应用,余角的性质,熟练掌握相似三角形的判定和性质是解题的关键.二、填空题11.如图,△ABC 中,点 D 在边 AB 上,满足∠ACD =∠ABC ,若 AC =2,AD =1,则 DB =________.【答案】3【解析】【分析】由题意,在△ABC 中,点D 在边AB 上,满足∠ACD =∠ABC ,可证△ABC ∽△ACD ,再根据相似三角形对应边成比例来解答即可.解:∵∠ACD =∠ABC ,∠A =∠A ,∴△ABC ∽△ACD ,∴=AB AC AC AD,∵AC =2,AD =1,∴1+221DB =,解得DB =3.故答案为:3.【点睛】本题主要考查相似三角形的性质及对应边长成比例,难点在于找对应边.12.如图,四边形ABCD 中,AD BC ∥,1AD =,3BC =,AC 与BD 相交于点O ,AOD △的面积为3,则BOC V 的面积是______.【答案】27【解析】【分析】首先证明△AOD ∽△COB ,然后根据面积之比等于相似比的平方即可求出BOC V 的面积.解:∵AD BC ∥,∴△AOD ∽△COB ,∴219AOD BOC S AD S BC æöç÷==ç÷èøV V ,∵AOD △的面积为3,∴BOC V 的面积是27,故答案为:27.【点睛】本题考查了相似三角形的判定和性质,熟知相似三角形的面积比等于相似比的平方是解题关键.13.在同车道行驶的机动车,后车应当与前车保持一定的安全距离.如图,在一个路口,一辆长为10m 的大巴车遇红灯后停在距交通信号灯20m 处,小林驾驶一辆小轿车,距大车尾xm ,若大巴车车顶高于小林的水平视线0.8m ,红灯下沿高于小林的水平视线3.2m ,若小林能看到整个红灯,则x 的最小值为_____.【答案】10m【解析】【分析】根据平行证出ECD EAB :V V ,列出比例式即可求出x 的最小值.解:如下图,当红灯,大巴车车车顶和小张的眼睛三点共线时,x 最小,由题意可知CD AB P ,∴ECD EAB:V V ∴ED CD EB AB=即0.82010 3.2x x =++,解得10x =.∴x 的最小值为10m.故答案为:10m.【点睛】此题考查的是相似三角形的应用,掌握利用平行证相似及相似三角形的性质是解决此题的关键.14.如图,四边形ABCD 中,AC 、BD 相交于O ,若AO DO CO BO=,8AO =,12CO =,15BC =,则AD =______.【答案】10【解析】【分析】首先证明△AOD ∽△COB ,然后根据相似三角形的性质求解即可.解:∵AO DO CO BO=,∠AOD=∠BOC ,∴△AOD ∽△COB ,∴AO AD CO BC =,即81215AD =,∴AD=10,故答案为10.【点睛】本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定定理是解题关键.15.如图,在ABC D 中,D ,E 分别是AB ,AC 上的点,AF 平分BAC Ð,交DE 于点G ,交BC 于点F ,若AED B Ð=Ð,且:3:2AG GF =,则:DE BC =_______.【答案】3:5【解析】【分析】根据题意利用相似三角形的性质即相似三角形的对应角平分线的比等于相似比即可解决问题.解:∵∠DAE=∠CAB ,∠AED=∠B ,∴△ADE ∽△ACB ,∵GA ,FA 分别是△ADE ,△ABC 的角平分线,∴DE AG BC AF=(相似三角形的对应角平分线的比等于相似比),AG :FG=3:2,∴AG :AF=3:5,∴DE :BC=3:5,故答为3:5.【点睛】本题考查相似三角形的判定和性质、解题的关键是灵活运用所学知识解决问题,属于中考常考题型,难度一般.16.如图,在Y ABCD 中,点E 在CD 边上运动(不与C ,D 两点重合),连结AE 并延长与BC 的延长线交于点F.连结BE ,DF ,若△BCE 的面积为8,则△DEF 的面积为________.【答案】8【解析】试题解析:::.BCE CEF S S BC CF =V V Q:::.DEF CEF S S DE CE AD CF ==V V.AD BC =Q :::.DEF CEF BCE CEF S S S S BC CF \==V V V V8.DEF BCE S S \==V V 故答案为8.17.如图,△ABC 中,AB =8cm ,AC =16cm ,点P 从A 出发,以每秒1厘米的速度向B 运动,点Q 从C 同时出发,以每秒2厘米的速度向A 运动.其中一个动点到达端点时,另一个也相应停止运动.那么,当以A 、P 、Q 为顶点的三角形与△ABC 相似时,运动时间是_____.【答案】325秒或4秒【解析】【分析】分两种情况讨论,利用相似三角形的性质求解即可.设运动时间是t 秒∵点P 从A 出发,以每秒1厘米的速度向B 运动,点Q 从C 同时出发,以每秒2厘米的速度向A 运动,2,162AP t CQ t AQ t\===-由题意可得:当8t =时,点P 运动到端点B ,此时点Q 正好运动到端点A ,均停止运动则要使A 、P 、Q 三点能构成三角形,t 的取值范围为08t <<BAC PAQ Ð=ÐQ ,且以A 、P 、Q 为顶点的三角形与ABC D 相似∴AP AQ AC AB =或AP AQ AB AC=即162168t t -=或162816t t -=∴325t =或4t =故答案为:325秒或4秒.【点睛】本题考查了相似三角形的性质,依据题意将三角形相似分两种情况讨论是解题关键.18.如图,边长为6的正方形ABCD 中,点E 是BC 上一点,点F 是AB 上一点.点F 关于直线DE 的对称点G 恰好在BC 延长线上,FG 交DE 于点H .点M 为AD 的中点,若MH =EG =_____.【答案】5【解析】【分析】连接DF ,DG ,过H 作HP ⊥AB 于P ,HQ ⊥AD 于Q ,由点F ,点G 关于直线DE 的对称,得到DF=DG ,根据正方形的性质得到AD=CD ,∠ADC=∠A=∠BCD=90°,推出Rt △AFD ≌Rt △CDG ,证得△FDG 是等腰直角三角形,推出四边形APHQ 是矩形,证得△HPF ≌△DHQ ,根据全等三角形的性质得到HP=HQ ,证得APHQ 为正方形,利用正方形性质联系题中所给数据计算出正方形边长,然后再利用△FPH ∽△EHG 求得EG 长.解:连接DF ,DG ,过H 作HP ⊥AB 于P ,HQ ⊥AD 于Q ,∵点F ,点G 关于直线DE 的对称,∴DF=DG ,正方形ABCD 中,∵AD=CD ,∠ADC=∠A=∠BCD=90°,∴∠GCD=90°,又在Rt △AFD 与Rt △CDG 中,AD CD DF DG=ìí=î∴Rt △AFD ≌Rt △CDG ,∴∠ADF=∠CDG ,∴∠FDG=∠ADC=90°,∴△FDG 是等腰直角三角形,∵DH ⊥CF ,12DH FH FG \==∵HP ⊥AB ,HQ ⊥AD ,∠A=90°,∴四边形APHQ 是矩形,∴∠PHQ=90°,∵∠DHF=90°,∴∠PHF=∠DHQ ,又在△PFF 与△DQH 中有:90HPF HQD PHF DHQHF HD °ìÐ=Ð=ïÐ=Ðíï=î∴△HPF ≌△DHQ ,∴HP=HQ ,所以矩形APHQ 是正方形;设正方形APHQ 边长为a ,则在Rt △MQH 中,有(a-3)2+a 2=17,解得a=4;∴FP=QD=AD-AQ=6-4=2,又易证△FPH ∽△EHG ,则有EG GH FH PH =,即2FH EG PH=,又FH 2=22+42=20,PH=4,∴EG=5故答案为5.【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,勾股定理,正确的作出辅助线是解题的关键.三、解答题19.根据图中所注的条件,判断图中两个三角形是否相似,并求出x 和y 的值.【答案】(1)相似,4x =,10y =;(2)相似,124x =,33y =【解析】【分析】(1)由题得,1290G I Ð=ÐìíÐ=Ð=°î,根据两角对应相等的两个三角形相似可得,FGH JIH V :V ,由相似三角形的性质得,5386x y ==,解出x ,y 即可;(2)由90FHG GHK KHJ GHK Ð+Ð=°=Ð+Ð,从而得出,FHG JHK Ð=Ð,由7248348322==,根据两边成比例且夹角相等的两个三角形相似可得,FGH JKH V :V ,由相似三角形的性质可解出x ,y .在图(1)中,1290G I Ð=ÐìíÐ=Ð=°îQ ,FGH JIH \V :V ,GH FH GF IH JH IJ\==,5386x y \==,解得:4x =,10y =;在图(2)中,90FHG GHK KHJ GHK \Ð+Ð=°=Ð+Ð,FHG JHK \Ð=Ð,7248348322FH GH JH KH ====Q ,FGH JKH \V :V ,124x G \=Ð=°,3222y = ,124x \=°,33y =.【点睛】本题考查了相似三角形,解题关键是熟练掌握相似三角形的性质与判定.20.如图,ABC V 与A B C ¢¢¢V 相似,AD ,BE 是ABC V 的高,A D ¢¢,B E ¢¢是A B C ¢¢¢V 的高,求证AD BE A D B E =¢¢¢¢.【答案】见解析【解析】【分析】由△ABC 与△A ′B ′C ′相似可得∠ABD =∠A ′B ′D ′,可证明△ABD ∽△A ′B ′D ,可得AB AD A B A D =¢¢¢¢,同理可证明AB BE A B B E =¢¢¢¢,可得出结论.证明:∵△ABC 与∽A ′B ′C ′,∴∠ABD =∠A ′B ′D ′,∵AD 和A ′D ′是高,∴∠ADB =∠A ′D ′B ′,∴△ABD ∽△A ′B ′D ,∴AB AD A B A D =¢¢¢¢,同理可得AB BE A B B E =¢¢¢¢,∴AD BE A D B E =¢¢¢¢.【点睛】本题主要考查了相似三角形的判定和性质,掌握相似三角形的对应角相等、对应边成比例是解题的关键.21.如图,在ABC V 中,点D ,E 分别在边AB 和AC 上,且//DE BC .(1)若:1:1AD DB =,则:ADE DBCE S S V 四边形等于多少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
1
B xD
y
E
C
尝试练习
已知:如图,D在△ABC的边AC上,且DE∥BC, 交AB于E,F在AE上,且AE2=AF×AB, 求证: △AFD∽ △AEC.
A
F
E
D
B
C
挑战自我
如图,三角形ABC中,BE,CD是两边上的高, 问题1、图中有相似三角形吗?并说明理由 问题2、连接DE,说明∠AED=∠ABC
问:你能画出符合条件的直线吗?
A
D
B
C
1、平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似
2、有两角对应相等的两个三角形相似
如图,每个小正方形边长均为1,则下 列图中的三角形(阴影部分)与左图 中△ABC相似的是( )
A
B
C
A.
B.
C.
D.
3、两边对应成比例,且夹角相等的两三角形相似 4、三边对应成比例的两三角形相似
P
AC
D
B
例3、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D 是BC边上的一个动点(不与B、C重合),在AC上取一点E, 使∠ADE=45°
(1)求证:△ABD∽△DCE (2)设BD=x,AE=y,求y关于x的函数关系式及自变量x 的取值范围,并求出当BD为何值时AE取得最小值
22.2 相似三角形的判定 综合应用
教学目标:
1、熟练掌握相似三角形的判定定理 2、了解常见的相似三角形的类型 3、灵活应用相似三角形的判定
教学重点:相似三角形判定的应用 教学难点:相似三角形判定的应用
如图,在△ABC中,AB>AC,D为AC边上异于A、C 的一点,过D点作一直线与AB相交于点E,使所得 到的新三角形与原△ABC相似.
A
A
Q Q
B
B
P
C
P
C
例1、如图,已知:AB⊥DB于点B ,CD⊥DB于 点D,AB=6,CD=4,BD=14.问:在DB上是否存 在P点,使以C、D、P为顶点的三角形与以P、B、 A为顶点的三角形相似?如果存在,计算出点P的 位置;如果不存在,请说明理由。
A
C
6 4
D
14
B
2.如图,△PCD是等边三角形,A、C、D、B在同 一直线上,且∠APB=120°. 求证:⑴△PAC∽△BPD;⑵AC·BD=CD2.
(2)如图2,∠1= ∠2= ∠3,则图中相似三角形的组数为 ________.
A
D
E
B
C
F
如图(1)
A
D1 E
2
B3 如图(2) C
渐入佳境
2.在平面直角坐标系,B(1,0), A(3,-3), C(3,0), 点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与 △ABC相似,则点P的坐标是__________________.
A
D E
B
C
自主探究
练习.如图,先把一矩形纸片ABCD对折,设折痕为MN, 再把B点叠在折痕线上,得到△ABE,过B点折纸片使D
点叠在直线AD上,得折痕PQ。
1、求证:△PBE∽△QAB;
2、你认为△PBE和△BAE相似吗? 如果相似给出证明,是否能叠在直线EC上?
为什么?
B
C
EP
C
M
N
M
B
N
A
DA
Q
D
根据下列条件能否判定Rt△ABC与Rt△A`B`C`相似? 为什么?
<B=900 , BC=3 ,AC=5 <B`=900, A`B`=12 ,A`C`= 15
A`
A
5
12
15
B
3C
B`
C`
5、两直角三角形斜边、直角边对应成比例,两 三角形相似
相似三角形的基本类型
渐入佳境
1.找一找:
(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有 _____对三角形相似.
y
O B· ·C
x
·A
渐入佳境
3. 如图:在⊿ABC中, ∠C= 90°,BC=8,AC=6.点P从点B 出发,沿着BC向点C以2cm/秒的速度移动;点Q从点C出 发,沿着CA向点A以1cm/秒的速度移动。如果P、Q分 别从B、C同时出发,问:
经过多少秒时以C、P、Q为顶点的三角形恰好
与⊿ABC相似?
