第五章异方差与自相关问题
计量经济学第五章

Variables-Likelihood Ratio • 出现对话框时,写入删除变量名--OK • 对比删除前后的AIC与SC信息值,信息
值小的结论是应采纳的。
9
用Eviews的误设定检验3
• 第一,估计出简单(单纯)方程 • 第二,在命令窗口上写入genr v_hat=resid 或者 Procs/Generate Series中 v_hat=resid 发现 v_hat • 第三,估计出新的回归方程
无约束模型(U)
有约束模型(K) (general to simple)
计算统计量F
F=(RSSK-RSSu)/J RSSu/(n-k-1)
~F(J, n-k)
J 为表示约束条件数, K 为表示自变量数 或者 应估计的参数数, n 为表示样本数(obs)
4
2. LM检验(Lagrange Multiplier
多重共线性多出现在横截面资料上。
16
三、异方差性的检验及对策
Var(ℇi)≠Var(ℇj) (i≠j)时, ℇi中存在异方差性(Herteroskedasticity)。 即随机项中包含着对因变量的影响因素。 异方差性多发生在横截面资料上。
17
异方差性的检验
1.图示检验法 如模型为Yi=0+1X1i+2X2i+…+ℇi 时,
7
用Eviews的误设定检验1
• 首先估计出简单(单纯)方程 • View/Coefficient Tests/Omitted
Variables-Likelihood Ratio • 出现对话框时,写入新变量名 OK • 检验结果出现在上端,如果P值很小时, 拒
第五章异方差与自相关问题

X11 f (X j1) X12 f (X j2 ) M X1n f (X jn )
L L M L
Xk1 f (X j1) Xk2 f (X j2 ) M Xkn f (X jn )
~ Y=
Y f (X j )
Xi ~ Xi = f (X j )
~ X0 =
2
§5.3 异方差模型的估计
(一)广义最小平方估计对于异方差模型的意义
1 2 d 1 − 1 Ω = 1 2 dn
O
~ − ~ 1 ~ ~~ ′ ~ ~~ = (Y − Xβ)′Ω 1(Y − Xβ) = ∑ 2 ei2 (Y − Xβ) (Y − Xβ) di
2 n )的观测值。再对模型中的其余变量,以 c= 4
∑ei2
A
A
∑ei2
B
2 2 B
(c)构造统计量 F = ∑ei ∑ei或
F = ∑ei2
B
∑ei2;
A
(d)根据显著性水平 α,以及双自由度 n −c −(k +1 ,查取 F 分布临 ) 界值 F 。若经比较 F > F ,则接受模型存在单调形式的异方差,否 α α 则拒绝异方差。
D−W =1.980
F =14.747
20
Residual
Fitted
§5.3 异方差模型的估计
的广义最小平方估计: 例5.1 的广义最小平方估计:
~ Y = −0.637 + 0.072X
(-2.087)(6.636)
广义最小平方估计的残差平方和:
~ ~2 = (Y −Y )2 = 43.046 ei ∑ i ∑ i
1 X11 1 X12 M M 1 X1n
计量经济学题库第5章异方差

第5章异 方 差习 题一、单项选择题1. 回归模型中具有异方差性时,仍用OLS 估计模型,则以下说法正确的是( )A. 参数估计值是无偏非有效的B. 参数估计量仍具有最小方差性C. 常用F 检验失效D. 参数估计量是有偏的 2.更容易产生异方差的数据为 ( )A. 时序数据B. 修匀数据C. 横截面数据D. 年度数据 3.在具体运用加权最小二乘法时, 如果变换的结果是则Var(u)是下列形式中的哪一种?( )A. B. C. D.4. 在异方差性情况下,常用的估计方法是( )A .一阶差分法 B. 广义差分法 C .工具变量法 D. 加权最小二乘法 5. 在异方差的情况下,参数估计值的方差不能正确估计的原因是( )A. B.C. D. 6. 设,则对原模型变换的正确形式为( )7. 下列说法不正确的是( )A.异方差是一种随机误差现象B.异方差产生的原因有设定误差C.检验异方差的方法有F 检验法D.修正异方差的方法有加权最小二乘法8. 如果回归模型违背了同方差假定,最小二乘估计是( )A .无偏的,非有效的 B. 有偏的,非有效的011yx ux x x x ββ=++2x σ22xσσ2log x σ22()i E u σ≠()0()i j E u u i j ≠≠()0i i E x u ≠()0i E u ≠)()(,2221i i i i i i x f u Var u x y σσββ==++=01212222212...()()()().()()()()i i i i i i i i i i i i i i i i i A y x u B y x u C f x f x f x f x D y f x f x x f x u f x βββββββ=++=+=++=++C .无偏的,有效的 D. 有偏的,有效的 9. 在检验异方差的方法中,不正确的是( )A. Goldfeld-Quandt 方法B. ARCH 检验法C. White 检验法D. DW 检验法10. 在异方差的情况下,参数估计值仍是无偏的,其原因是( )A.零均值假定成立B.序列无自相关假定成立C.无多重共线性假定成立D.解释变量与随机误差项不相关假定成立11. 在修正异方差的方法中,不正确的是( )A.加权最小二乘法B.对原模型变换的方法C.对模型的对数变换法D.两阶段最小二乘法 12. 下列说法正确的是( )A.异方差是样本现象B.异方差的变化与解释变量的变化有关C.异方差是总体现象D.时间序列更易产生异方差二、多项选择题1. 如果模型中存在异方差现象,则会引起如下后果( )A. 参数估计值有偏B. 参数估计值的方差不能正确确定C. 变量的显著性检验失效D. 预测精度降低E. 参数估计值仍是无偏的2. Goldfeld-Quandt 检验法的应用条件是( )A. 将观测值按解释变量的大小顺序排列B. 样本容量尽可能大C. 随机误差项服从正态分布D. 将排列在中间的约1/4的观测值删除掉 E .除了异方差外,其它假定条件均满足三、计算题1.根据某城市1978——1998年人均储蓄(y)与人均收入(x)的数据资料建立了如下回归模型x y6843.1521.2187ˆ+-=se=(340.0103)(0.0622)下面取时间段1978——1985和1991——1998,分别建立两个模型(括号内为t 值), 模型1:模型2:计算F 统计量,即,对给定的,查F 分布表,得临界值。
第讲异方差与自相关

▪ 3.异方差检验 ▪ 对模型进行回归并不是本章的知识,然而回归是一个基础,即做
异方差检验之前必须做回归,下面将会详细介绍异方差检验的基 本方法。 ▪ (1)残差图观察法 ▪ 做完模型的基本回归后,运用Stata绘制残差图来观察异方差是 否存在。 ▪ 在命令窗口中输入如下(rúxià)两个命令中的任意一个即可 ▪ rvfplot (residual-versus-fitted plot) ▪ rvpplot varname (residual-versus-predictor plot) ▪ 第一个命令语句的作用是绘制默认形式的残差图,第二个命令语 句的作用是绘制残差与某个解释变量的散点图,varname可以换 做认为合理的解释变量。
精品文档
▪ 在前面的章节中,已经介绍过作残差图的各种命令,所作出的各种 图形虽然有些差异,但是(dànshì)所展示的信息是基本一致的。图 8.2中显示残差的方差是变化的,从一开始时分散程度很大(方差 大),然后逐渐变得紧凑(方差变小),这样一来很显然的否定了 球形扰动项的假设。即通过残差图观察法,得出的结论是此模型存 在异方差问题。
精品文档
▪ reg y x1 x2… [aweight=invvar] ▪ 输入此命令语句对模型加上得出的权重(quán zhònɡ)进行修
正回归,这样就基本完成了FGLS法回归,可以得到一个修 正回归后的结果。 ▪ 那么在本实验中,使用FGLS方法来对模型进行修正回归的 操作如下: ▪ predict u, residuals ▪ gen lnu2=ln(u^2) ▪ 然后进行回归,并得到拟合值, ▪ quietly reg lnu2 lnq lnpl lnpf lnpk ▪ predict g, xb ▪ 找到权重(quán zhònɡ),对模型加上权重(quán zhònɡ)进行 回归就可以得到图8.13的回归结果图。 ▪ gen h=exp(g) ▪ gen invvar=1/h ▪ reg lntc lnq lnpl lnpf lnpk [aweight=invvar]
异方差与自相关问题

a
与 b 。 a 与 b 的线性相关系数,称为
q
z
的等级相关系数 。
(ai a )(bi b ) rs (ai a ) 2 (bi b ) 2
6 (ai bi ) 2 rs 1 n(n 2 1)
§5.2
等级相关检验
异方差问题
(a) 完成模型的OLS估计,获取残差数据
X 11 f ( X j1 ) X 12 f ( X j2 ) X 1n f ( X jn )
X k1 f ( X j1 ) X k2 f ( X j2 ) X kn f ( X jn )
~ Y
Y f (X j )
~ Xi
Xi f (X j )
1 1 1
X 11 X 12 X 1n
Y1 X k 1 f ( X j1 ) Y2 X k2 f ( X j2 ) Y n X kn f ( X jn )
1 f ( X j1 ) 1 f ( X j2 ) 1 f ( X jn )
第五章
异方差与自相关问题
除了本章讨论所涉及的同方差性与不自相关性以外,
关于线性回归模型的其它假定在本章中都成立。 ——广义最小平方估计; ——异方差模型及其估计; ——自相关模型及其估计; ——异方差模型、自相关模型的预测。
§5.1
广义最小平方法
同方差且不自相关
cov(U ) 2 I cov(U ) 2
ei ;
(b) 选择可能与异方差有关的解释变量 rs ( j ),计算变量 X j与变
量
e 的等级相关系数
(c) 计算统计量
自相关和异方差处理顺序

自相关和异方差处理顺序引言自相关和异方差是时间序列分析中常见的两种问题,它们影响了模型的准确性和可靠性。
在进行时间序列建模时,需要处理这些问题,以确保模型的有效性。
本文将深入探讨自相关和异方差处理的顺序,并讨论不同处理顺序的影响。
什么是自相关和异方差自相关自相关是指时间序列中当前观测值与之前观测值之间的相关性。
它衡量的是时间序列中各个观测值之间的依赖关系。
自相关可以用自相关函数(ACF)图来表示,通过观察ACF图,可以判断时间序列是否存在自相关。
异方差异方差是指时间序列中方差不稳定的特征。
在时间序列中,方差可能随着时间的推移发生变化,这会导致模型的拟合不准确。
异方差可以用方差函数(VCF)图来表示,通过观察VCF图,可以判断时间序列是否存在异方差。
自相关和异方差处理的重要性自相关和异方差对时间序列建模的准确性和可靠性有重要影响,它们需要被处理以获得可靠的模型结果。
•自相关的存在会导致参数估计不准确,预测结果失真。
如果存在自相关,模型会无法捕捉到序列的真实动态,导致预测结果不准确。
•异方差使得模型的残差不符合正态分布,违背了建模的基本假设。
这会使得模型的显著性检验和置信区间估计不可靠,影响模型的有效性。
因此,为了获得可靠的模型结果,需要对自相关和异方差进行处理。
自相关和异方差处理顺序的影响自相关和异方差的处理顺序会对最终的模型结果产生影响。
不同的处理顺序可能导致不同的模型结构和参数估计。
先处理自相关后处理异方差如果先处理自相关再处理异方差,可能会导致如下影响:1.自相关处理可能会改变时间序列的动态特征。
当我们去除自相关时,可能会削弱序列中的一些重要信息,导致模型无法准确捕捉到序列的动态变化。
2.异方差处理可能会影响自相关的结构。
当我们对残差进行异方差处理时,可能会改变残差序列的结构,从而使得自相关的估计失真。
先处理异方差后处理自相关如果先处理异方差再处理自相关,可能会产生如下影响:1.异方差处理可能改变原始序列的动态特征。
异方差与自相关

七、 异方差与自相关一、背景我们讨论如果古典假定中的同方差和无自相关假定不能得到满足,会引起什么样的估计问题呢?另一方面,如何发现问题,也就是发现和检验异方差以及自相关的存在性也是一个重要的方面,这个部分就是就这个问题进行讨论。
二、知识要点1、引起异方差的原因及其对参数估计的影响2、异方差的检验(发现异方差)3、异方差问题的解决办法4、引起自相关的原因及其对参数估计的影响5、自相关的检验(发现自相关)6、自相关问题的解决办法 (时间序列部分讲解) 三、要点细纲1、引起异方差的原因及其对参数估计的影响原因:引起异方差的众多原因中,我们讨论两个主要的原因,一是模型的设定偏误,主要指的是遗漏变量的影响。
这样,遗漏的变量就进入了模型的残差项中。
当省略的变量与回归方程中的变量有相关关系的时候,不仅会引起内生性问题,还会引起异方差。
二是截面数据中总体各单位的差异。
后果:异方差对参数估计的影响主要是对参数估计有效性的影响。
在存在异方差的情况下,OLS 方法得到的参数估计仍然是无偏的,但是已经不具备最小方差性质。
一般而言,异方差会引起真实方差的低估,从而夸大参数估计的显著性,即是参数估计的t 统计量偏大,使得本应该被接受的原假设被错误的拒绝。
2、异方差的检验 (1)图示检验法由于异方差通常被认为是由于残差的大小随自变量的大小而变化,因此,可以通过散点图的方式来简单的判断是否存在异方差。
具体的做法是,以回归的残差的平方2i e 为纵坐标,回归式中的某个解释变量i x 为横坐标,画散点图。
如果散点图表现出一定的趋势,则可以判断存在异方差。
(2)Goldfeld-Quandt 检验Goldfeld-Quandt 检验又称为样本分段法、集团法,由Goldfeld 和Quandt 1965年提出。
这种检验的思想是以引起异方差的解释变量的大小为顺序,去掉中间若干个值,从而把整个样本分为两个子样本。
用两个子样本分别进行回归,并计算残差平方和。
第五章-异方差性-答案说课讲解

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T )二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B )A. B. C. D. 7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模型时,应将模型变换为( C )。
异方差与自相关
1.5 假定条件的不成立用OLS 法得到的估计模型通过统计检验后,还要检验摸型是否满足假定条件。
由1.3 节知,只有模型的4个假定条件都满足时,用OLS 法得到的估计量才具有最佳线性无偏特性。
当一个或多个假定条件不成立时,OLS 估计量将丧失上述特性。
本节讨论当假定条件不成立时,对参数估计带来的影响以及相应的补救措施。
以下讨论都是在某一个假定条件被违反,而其他假定条件都成立的情况下进行。
分为5个步骤。
(1)回顾假定条件。
(2)假定条件不成立对模型参数估计带来的影响。
(3)定性分析假定条件是否成立。
(4)假定条件是否成立的检验(定量判断)。
(5)假定条件不成立时的补救措施。
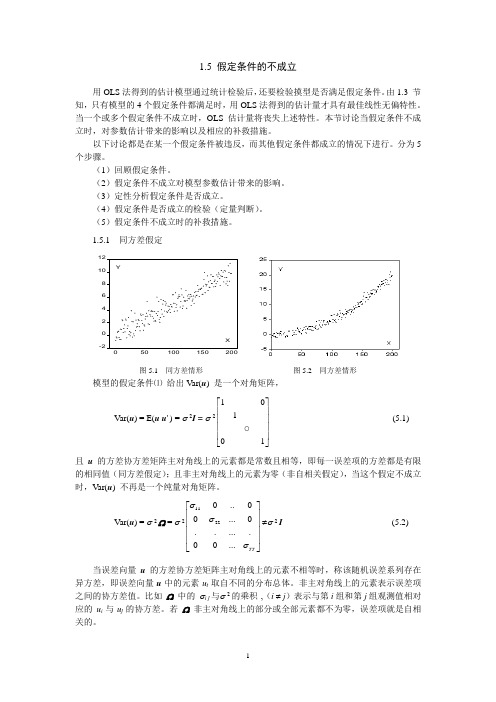
1.5.1 同方差假定-224681012050100150200XY图5.1 同方差情形 图5.2 同方差情形模型的假定条件⑴ 给出V ar(u ) 是一个对角矩阵, Var(u ) = E(u u ' ) = σ 2I = σ 21011⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(5.1) 且u 的方差协方差矩阵主对角线上的元素都是常数且相等,即每一误差项的方差都是有限的相同值(同方差假定);且非主对角线上的元素为零(非自相关假定),当这个假定不成立时,Var(u ) 不再是一个纯量对角矩阵。
Var(u ) = σ 2 Ω = σ 211220..00...0 00...TT σσσ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦≠σ 2 I (5.2)当误差向量u 的方差协方差矩阵主对角线上的元素不相等时,称该随机误差系列存在异方差,即误差向量u 中的元素u t 取自不同的分布总体。
非主对角线上的元素表示误差项之间的协方差值。
比如 Ω 中的 σi j 与σ 2的乘积 ,(i ≠ j )表示与第i 组和第j 组观测值相对应的u i 与 u j 的协方差。
若 Ω 非主对角线上的部分或全部元素都不为零,误差项就是自相关的。
本节讨论异方差。
下一节讨论自相关问题。
异方差自相关共线性

检验解释变量之间是否存在多重共线性的 常见方法有以下几种: (1)相关系数检验法 (2)辅助回归模型检验 (3)方差膨胀因子检验 (4)特征值检验 下面介绍如何利用Eviews6.0软件进行 相关系数检验和方差膨胀因子检验。
①相关系数检验 下面分析我国居民家庭电力消耗量(单位:千瓦 小时)与居住面积x1(单位:平方米)及可支配 收入x2(1978=100)的关系,以预测居民家庭电 力的需求量,原始数据如下图:
这里n R2的值明显变小了
3、自相关
自相关违背了经典线性回归假设中对随 机误差项无序列相关的要求。即随机误差项 之间存在着自相关性或者序列相关。 自相关的影响有:模型参数估计值不具有 最优性;随机误差的方差一般会低估;模型 的统计检验失效;区间估计和预测区间的精 度降低。
自相关性的检验方法主要有以下几种: (1)图示法; (2)德宾—沃森(DW)检验; (3)高阶自相关性检验; (4)回归检验法。 下面将介绍如何利用Eviews6.0软件进 行DW检验与高阶自相关性检验。
异方差的解决方法有: (1)模型变换法; (2)加权最小二乘法; (3)模型的对数变换; (4)广义最小二乘法。 其中最常见的是加权最小二乘法。下面 就介绍如何用Eviews6.0进行加权最小二乘 法的实现。
加权最小二乘法估计 模型的方法为:在方 程窗口中单击 Quick→Estimate Equation→Options, 并在权数变量栏输入 加权变量,这里选取 1/x为权数,点击确定, 就可以得到估计结果。
滞后阶数的选择, 一般会根据样本选 择默认的滞后阶数
检验的进入步骤
得到的检验结果表示残差与滞后各期的 相关系数与偏相关系数。(这里在时间序 列ARMA模型里面会介绍)。通过自相关系 数和偏自相关系数图,可以得到,残差序 列存在一阶和二阶自相关。
计量经济学课后思考题答案

计量经济学课后思考题答案第五章异⽅差性思考题5.1 简述什么是异⽅差?为什么异⽅差的出现总是与模型中某个解释变量的变化有关?答:设模型为,如果其他假定均不变,但模),....,,(....n 21i X X Y i i 33i 221i =µ+β++β+β=型中随机误差项的⽅差为,则称具有异⽅差性。
由于异⽅差性),...,,()(n 21i Var 2i i =σ=µi µ指的是被解释变量观测值的分散程度是随解释变量的变化⽽变化的,所以异⽅差的出现总是与模型中某个解释变量的变化有关。
5.2 试归纳检验异⽅差⽅法的基本思想,并指出这些⽅法的异同。
答:各种异⽅差检验的共同思想是,基于不同的假定,分析随机误差项的⽅差与解释变量之间的相关性,以判断随机误差项的⽅差是否随解释变量变化⽽变化。
其中,⼽德菲尔德-跨特检验、怀特检验、ARCH 检验和Glejser 检验都要求⼤样本,其中⼽德菲尔德-跨特检验、怀特检验和Glejser 检验对时间序列和截⾯数据模型都可以检验,ARCH 检验只适⽤于时间序列数据模型中。
⼽德菲尔德-跨特检验和ARCH 检验只能判断是否存在异⽅差,怀特检验在判断基础上还可以判断出是哪⼀个变量引起的异⽅差。
Glejser 检验不仅能对异⽅差的存在进⾏判断,⽽且还能对异⽅差随某个解释变量变化的函数形式进⾏诊断。
5.3 什么是加权最⼩⼆乘法?它的基本思想是什么?答:以⼀元线性回归模型为例:12i i i Y X u ββ=++经检验存在异⽅差,公式可以表i µ⽰为22var()()i i i u f X σσ==。
选取权数,当越⼩时,权数越⼤。
当 i w 2i σi w 越⼤时,权数越⼩。
将权数与残差平⽅相乘以后再求和,得到加权的残差平⽅和:2i σi w ,求使加权残差平⽅和最⼩的参数估计值。
这种2i 21i 2i i X Y w e w )(**β-β-=∑∑**??21ββ和求解参数估计式的⽅法为加权最⼩⼆乘法。
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
第五讲异方差和自相关精制课件

reg lny lnk lnl 检查是否具有异方差
精制课件
16
4。use nerlove,clear reg lntc lnq lnpl lnpf lnpk 检验是否具有异方差
对于经典计量模型,我们的基本假设有:
假设 对于解释变量的所有观测值,随机误差项
有相同的方差。
Var(i
)
E
(
2 i
)
2
i 1, 2,...n
Var(U ) E[U E(U )][U E(U )]' E(UU ')
E(μμ )
E
1
1
n
12 E
1 n
n
n
1
2 n
其二,可能的情况下对变量取自然对数。变量取对 数降低了变量的变化程度,因此有助于消除异方差。
精制课件
26
自相关
经典假设 随机误差项彼此之间不相关 Cov(i , j ) E(i j ) 0 i j i, j 1,2,, n • 如果存在自相关,则:
COV (ui,uj) 0
• 时间序列数往往存在着自相关,即:
精制课件
17
异方差的处理
1。使用“OLS+异方差稳健标准误”(robust standard error):这是最简单,也是目前比较 流行的方法。只要样本容量较大,即使在异方差 的情况下,只要使用稳健标准误,则所有参数估 计、假设检验均可照常进行。
sysuse nlsw88, clear
reg wage ttl_exp race age industry hours
自相关和异方差处理顺序

自相关和异方差处理顺序在统计学和计量经济学中,自相关和异方差是两个常见的问题,需要进行相应的处理才能保证模型的准确性和可靠性。
本文将以人类的视角,采用准确的中文进行描述,详细介绍自相关和异方差的处理顺序及其重要性。
一、自相关处理自相关是指时间序列数据中观测值之间存在的相关性。
当序列中的观测值之间存在一定的相关性时,会导致统计模型的参数估计不准确,假设检验无效,预测结果不可靠。
因此,需要进行自相关的处理。
自相关处理的一种常见方法是使用自相关函数(ACF)和偏自相关函数(PACF)进行分析。
ACF表示观测值与不同滞后期的观测值之间的相关性,PACF表示观测值与滞后期观测值之间的相关性,探究观测值之间的相关性结构。
在进行自相关处理时,可以采取以下步骤:1. 绘制时间序列图,观察序列的趋势和波动性。
2. 进行序列的平稳性检验,确保序列满足平稳性的要求。
3. 绘制ACF和PACF图,分析观测值之间的相关性结构。
4. 根据ACF和PACF的图形特征,选择合适的自回归移动平均模型(ARMA模型)。
5. 估计模型参数,进行模型拟合。
6. 检验模型的残差序列是否存在自相关,如果存在,则返回第3步,重新选择模型。
通过以上步骤,可以有效地处理自相关问题,提高模型的准确性和可靠性。
二、异方差处理异方差是指随着自变量的变化,因变量的方差也发生变化。
当存在异方差时,会导致模型的参数估计不准确,假设检验无效,预测结果不可靠。
因此,需要进行异方差的处理。
异方差处理的一种常见方法是使用加权最小二乘法(Weighted Least Squares, WLS)。
WLS是一种在回归分析中常用的方法,通过对误差项进行加权,降低异方差对回归结果的影响。
在进行异方差处理时,可以采取以下步骤:1. 绘制残差图,观察残差的分布特征。
2. 进行异方差检验,判断是否存在异方差。
3. 如果存在异方差,可以使用加权最小二乘法进行回归估计。
4. 根据异方差的特点,选择合适的加权函数,对误差项进行加权。
自相关和异方差处理顺序

自相关和异方差处理顺序自相关和异方差是统计学中常见的两个问题,它们在数据分析和建模中起着重要的作用。
在本文中,我们将讨论自相关和异方差的处理顺序,并介绍一些常用的方法和技巧。
一、自相关的处理自相关是指同一时间序列数据中不同时间点之间的相关性。
在时间序列分析中,我们经常会遇到自相关的问题,这会影响到模型的准确性和可靠性。
为了解决自相关问题,我们可以采取以下几种方法:1. 平稳化处理:对于非平稳的时间序列数据,我们可以通过差分、对数变换或者其他方法来使其变得平稳。
平稳化后的数据能够更好地满足模型的假设条件,从而减小自相关的影响。
2. 引入滞后项:在建立模型时,我们可以引入滞后项来考虑时间序列数据中不同时间点之间的相关性。
常用的方法有自回归(AR)模型和移动平均(MA)模型等。
3. 模型诊断:在建立模型后,我们需要对模型进行诊断,检验是否存在自相关。
常用的方法有自相关图和部分自相关图等。
如果发现存在自相关,我们可以进一步调整模型的参数或者引入其他变量来解决自相关问题。
二、异方差的处理异方差是指同一时间序列数据中不同时间点之间方差不相等的现象。
异方差会导致模型的预测结果不准确,因此需要进行处理。
以下是一些处理异方差的方法:1. 变换方法:对于存在异方差的数据,我们可以通过对数变换、平方根变换或者倒数变换等方法来使其变得更加稳定。
变换后的数据能够更好地满足模型的假设条件,从而减小异方差的影响。
2. 加权最小二乘法:在建立模型时,我们可以采用加权最小二乘法来解决异方差问题。
加权最小二乘法能够根据不同时间点的方差大小来调整模型的参数,从而减小异方差的影响。
3. 残差诊断:在建立模型后,我们需要对模型的残差进行诊断,检验是否存在异方差。
常用的方法有残差图和方差稳定性检验等。
如果发现存在异方差,我们可以进一步调整模型的参数或者引入其他变量来解决异方差问题。
自相关和异方差是统计学中常见的问题,它们在数据分析和建模中起着重要的作用。
第5讲 自相关与异方差

绘制1:y轴为残差平方,x轴为y的拟合值
绘制2:y轴为残差平方,x轴为某个解释变量
绘制3:y轴为被解释变量,X轴为某个解释变 量
2-14
如何检验异方差:方法2white和bp检 验
适用于:误差项方差的变化连续 White检验步骤: 1、OLS回归,得到残差 2、残差取平方,然后对所有解释变量,解释 变量的平方,解释变量的交互进行回归 3、零假设:同方差。此时所有斜率项系数应 为0,大样本下有
2-19
如何检验异方差:方法3 Goldfeld– Quandt检验
SSRL SSRS (5) Relabel the groups as L and S , such that nL k nS k SSRL nL k Compute G SSRS nS k (6) Compare G to the critical value for an F -statistic with ( nL k ) and ( nS k ) degrees of freedom.
ˆ X ) ( X ' X )1 X ' E( X ) E(
ˆ E E ˆ X E X
2-9
异方差下的OLS2:不是最小方差
• 高斯马尔科夫定理(四个假定都用上) ,OLS估计量是方差最小(最优)的线 性无偏估计量BLUE。异方差下:
思路:仍然用OLS无偏估计 处理:重新正确估计方差,white稳健方差
此时OLS仍然不是BLUE,但无偏,
2-34
多元回归DGP:高斯马尔科夫假定4
• 4b无自相关假定
cov(i , j | X ) 0 E(i j | X ) E (i | X )E ( j | X ) E(i j | X ) 0
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(c) 计算统计量
Tj
rs ( j) n 2 1 rs2 ( j)
;
(d)T j 近似服从自由度为n 2 的 t 分布。根据显著性水平
t 及自由度 n 2,查取
分布临界值 t 。如果 2
Tj
t ,则判定 2
模型存在单调形式的异方差,否则拒绝异方差。
§5.2 异方差问题
3. F 检验
(a)选择可能与异方差有关的解释变量 X j 。将 X j的样本观测值由小到
X kn
f f f
( X j1 ) Y2
(X j2) Yn
(X jn )
1
f ( X j1 ) 1
f (X j2) 1
f (X jn )
X 11
f ( X j1 )
X 12
f (X j2)
X 1n
f (X jn )
X k1
f ( X j1 )
X k2
f (X j2)
f
X kn (X jn
几种常见的可供参考的函数形式:
e 0 1X j
e
0
1X
1 j
e 0 1 X j
取 d 为函数 f ( X j ) 中的可变部分 : X j
X
1 j
Xj
§5.3 异方差模型的估计
(三)异方差模型的广义最小平方估计
Y1 Y2 Yn
1 1 1
X 11 X 12
X 1n
Y1
X k1 X k2
等级相关检验表明模型存在递增形式的异方差。
例5.1 异方差性的 F 检验
按照销售收入水平的排序,从中心删去第9-12号样本点,形成
两个子样本A与B:
ei2 1.451
FA
ei2 37.169
B
ei2
F B 25.616
ei2
A
检验表明模型存在递增形式的异方差。
§5.3 异方差模型的估计
Y X U PPI
Y~ X~ U~ (~)
——(~)模型满足关于线性回归模型的全部基本假定,(~)模型
的普通最小平方估计将给出系数 的线性无偏最小方差估计。
~ (X 1 X )1 X 1Y
§5.1 广义最小平方法
三个所谓协方差矩阵
(a)OLS估计 ˆ 的协方差矩阵
cov(ˆ) 2( X X )1 X X ( X X )1
z 与 的等级相关系数 。
rs
(ai a)(bi b ) (ai a)2 (bi b )2
rs
1
6 (ai
n(n 2
bi )2 1)
§5.2 异方差问题
等级相关检验
(a) 完成模型的OLS估计,获取残差数据 ei ;
(b) 选择可能与异方差有关的解释变量rs ( j),计算变量 X j与变 量 e 的等级相关系数 X j ;
)
Y~ Y f (X j)
X~i
Xi f (X j)
X~0
1 f (X j)
Y~
0 X~0
1
~ X1
k X~k
U~
i 1,, k
§5.3 异方差模型的估计
(四)异方差模型示例5.1
设 Y 表示商场利润总额,X表示商场销售收入。北京市20家最大
的百货商店的销售资料 ,商场按照销售收入规模从大到小排序。
第五章 异方差与自相关问题
除了本章讨论所涉及的同方差性与不自相关性以外, 关于线性回归模型的其它假定在本章中都成立。 ——广义最小平方估计; ——异方差模型及其估计; ——自相关模型及其估计; ——异方差模型、自相关模型的预测。
§5.1 广义最小平方法
同方差且不自相关 cov(U ) 2I
异方差或自相关 cov(U ) 2 正定
(b)广义最小平方估计 ~ 的协方差矩阵 cov(~) 2 ( X 1X )1
(c)伪协方差矩阵
2 ( X X )1
§5.2 异方差问题
(一)异方差概念
var(Ui )
EU
2 i
i2
2 i
(i 1,2,, n)不全相同
var(Yi ) var(Ui )
异方差概念理解
(二)异方差的检测
Ui Yi (0 1 X1i k X ki ) ei Yi (ˆ0 ˆ1 X1i ˆk X ki )
Yˆ 0.5160 0.0668 X
15
残差图提示递增
10
形式的异方差。
4
5
2
0
0
-2
-4 2
4 6 8 10 12 14 16 18 20
ቤተ መጻሕፍቲ ባይዱResidual
Actual
Fitted
§5.3 异方差模型的估计
例5.1 异方差性的等级相关检验
rs 0.5594
T 2.8632
t 2.101 2
大进行排列,然后从这一排列的中心删去约 n c 的观测值,并使剩余的
两个子列具有相同数目(
c n
2
)的观测值。再对模型中的其余变量,以
4
的观测值序号为准,进行相应的删与留,形成A、B两个子样本;
(b)两个子样本分别进行OLS估计,获取两个残差平方和:
ei2
A
ei2
B
(c)构造统计量 F ei2 ei2或 F ei2 ei2;
(Y
X~)1(Y
X~)
1 di2
ei2
对于与具有较小方差相应的残差,给以较大的权数,使其在确定回
归函数时,起较为重要的作用。或者说使回归函数主要参照那些对应
较小方差的样本点而被决定。
§5.3 异方差模型的估计
(二)参数 d i 的估计
P
1 d1
1 d
n
散点图( X ji , ei ) e f ( X j ) V
A
B
B
A
(d)根据显著性水平 ,以及双自由度 n c (k 1) ,查取 F 分布临 2
界值 F 。若经比较 F F ,则接受模型存在单调形式的异方差,否
则拒绝异方差。
§5.3 异方差模型的估计
(一)广义最小平方估计对于异方差模型的意义
1
1 d12
1 d
2 n
(Y~
X~~)(Y~
X~~)
1. 图示法 ( X ji,Yi )
( X ji, ei )
§5.2 异方差问题
2. 等级相关检验 : 等级相关系数
设变量 q 与 z有 n 组观测值,
{qi , zi }
i 1,, n
按照某种性能,同方向分别指定各观测值的等级:
{ai , bi } i 1,, n
并由此产生等级变量 a 与 b 。a 与 b 的线性相关系数,称为 q
Y~ˆ 0.637 X~0 0.072 X~1
例5.1 的广义最小平方估计
试探性考虑异方差的 e X 形式, 1 。经过若干次试验最
后选取
e f ( X ) X 1.7
4
3
ABSE
2
1
0
0
50
100
150
200
X
§5.3 异方差模型的估计
施实变换
Y~ YX 1.7
X~1 X 0.7
X~0 X 1.7
(~)模型的OLS估计结果: 0.008
