旋转体的体积试题解析——高数常考题目
完整)高等数学考试题库(附答案)

完整)高等数学考试题库(附答案)高数》试卷1(上)一.选择题(将答案代号填入括号内,每题3分,共30分)。
1.下列各组函数中,是相同的函数的是()。
A)f(x)=ln(x^2)和g(x)=2lnxB)f(x)=|x|和g(x)=x^2C)f(x)=x和g(x)=x^2/xD)f(x)=2|x|和g(x)=1/x答案:A2.函数f(x)=ln(1+x)在x=0处连续,则a=()。
A)1B)0C)-1D)2答案:A3.曲线y=xlnx的平行于直线x-y+1=0的切线方程为()。
A)y=x-1B)y=-(x+1)C)y=(lnx-1)(x-1)D)y=x答案:C4.设函数f(x)=|x|,则函数在点x=0处()。
A)连续且可导B)连续且可微C)连续不可导D)不连续不可微答案:A5.点x=0是函数y=x的()。
A)驻点但非极值点B)拐点C)驻点且是拐点D)驻点且是极值点答案:A6.曲线y=4|x|/x的渐近线情况是()。
A)只有水平渐近线B)只有垂直渐近线C)既有水平渐近线又有垂直渐近线D)既无水平渐近线又无垂直渐近线答案:B7.∫f'(1/x^2)dx的结果是()。
A)f(1/x)+CB)-f(x)+CC)f(-1/x)+CD)-f(-x)+C答案:C8.∫ex+e^(-x)dx的结果是()。
A)arctan(e^x)+CB)arctan(e^(-x))+CC)ex-e^(-x)+CD)ln(ex+e^(-x))+C答案:D9.下列定积分为零的是()。
A)∫π/4^π/2 sinxdxB)∫0^π/2 xarcsinxdxC)∫-2^1 (4x+1)/(x^2+x+1)dxD)∫0^π (x^2+x)/(e^x+e^(-x))dx答案:A10.设f(x)为连续函数,则∫f'(2x)dx等于()。
A)f(1)-f(0)B)f(2)-f(0)C)f(1)-f(2)D)f(2)-f(1)答案:B二.填空题(每题4分,共20分)。
大学高等数学上下考试题库(及答案)

高数试题1(上)及答案一.选择题(将答案代号填入括号内,每题3分,共30分).1.下列各组函数中,是相同的函数的是( ).(A )()()2ln 2ln f x x g x x == 和 (B )()||f x x = 和 ()g x =(C )()f x x = 和 ()2g x =(D )()||x f x x=和 ()g x =1 2.函数()00x f x a x ≠=⎨⎪=⎩ 在0x =处连续,则a =( ).(A )0 (B )14(C )1 (D )23.曲线ln y x x =的平行于直线10x y -+=的切线方程为( ).(A )1y x =- (B )(1)y x =-+ (C )()()ln 11y x x =-- (D )y x = 4.设函数()||f x x =,则函数在点0x =处( ).(A )连续且可导 (B )连续且可微 (C )连续不可导 (D )不连续不可微5.点0x =是函数4y x =的( ).(A )驻点但非极值点 (B )拐点 (C )驻点且是拐点 (D )驻点且是极值点6.曲线1||y x =的渐近线情况是( ). (A )只有水平渐近线 (B )只有垂直渐近线 (C )既有水平渐近线又有垂直渐近线 (D )既无水平渐近线又无垂直渐近线 7.211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是( ). (A )1f C x ⎛⎫-+ ⎪⎝⎭(B )1f C x ⎛⎫--+ ⎪⎝⎭(C )1f C x ⎛⎫+ ⎪⎝⎭(D )1f C x ⎛⎫-+ ⎪⎝⎭8.x x dxe e -+⎰的结果是( ).(A )arctan xe C + (B )arctan xeC -+ (C )x x e e C --+ (D )ln()x x e e C -++9.下列定积分为零的是( ).(A )424arctan 1x dx x ππ-+⎰ (B )44arcsin x x dx ππ-⎰ (C )112x xe e dx --+⎰ (D )()121sin x x x dx -+⎰ 10.设()f x 为连续函数,则()12f x dx '⎰等于( ).(A )()()20f f - (B )()()11102f f -⎡⎤⎣⎦(C )()()1202f f -⎡⎤⎣⎦(D )()()10f f -二.填空题(每题4分,共20分)1.设函数()2100x e x f x x a x -⎧-≠⎪=⎨⎪=⎩在0x =处连续,则a =.2.已知曲线()y f x =在2x =处的切线的倾斜角为56π,则()2f '=.3.21xy x =-的垂直渐近线有条. 4.()21ln dxx x =+⎰.5.()422sin cos xx x dx ππ-+=⎰.三.计算(每小题5分,共30分) 1.求极限①21lim xx x x →∞+⎛⎫⎪⎝⎭ ②()20sin 1lim x x x x x e →-- 2.求曲线()ln y x y =+所确定的隐函数的导数x y '. 3.求不定积分 ①()()13dx x x ++⎰②()0a > ③x xe dx -⎰四.应用题(每题10分,共20分) 1. 作出函数323y x x =-的图像.2.求曲线22y x =和直线4y x =-所围图形的面积.《高数》试卷1参考答案一.选择题1.B 2.B 3.A 4.C 5.D 6.C 7.D 8.A 9.A 10.C 二.填空题1.2-2.33-3.24.arctan ln x c+5.2三.计算题1①2e②162.11xyx y'=+-3. ①11ln||23xCx+++②22ln||x a x C-++③()1xe x C--++四.应用题1.略2.18S=《高数》试卷2(上)一.选择题(将答案代号填入括号内,每题3分,共30分) 1.下列各组函数中,是相同函数的是( ).(A) ()f x x =和()g x = (B) ()211x f x x -=-和1y x =+(C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =2.设函数()()2sin 21112111x x x f x x x x -⎧<⎪-⎪⎪==⎨⎪->⎪⎪⎩,则()1lim x f x →=( ). (A) 0 (B) 1 (C) 2 (D) 不存在3.设函数()y f x =在点0x 处可导,且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为{ }. (A) 0 (B)2π(C) 锐角 (D) 钝角 4.曲线ln y x =上某点的切线平行于直线23y x =-,则该点坐标是( ). (A) 12,ln2⎛⎫⎪⎝⎭(B) 12,ln 2⎛⎫- ⎪⎝⎭ (C)1,ln 22⎛⎫⎪⎝⎭ (D) 1,ln 22⎛⎫- ⎪⎝⎭5.函数2xy x e-=及图象在()1,2内是( ).(A)单调减少且是凸的 (B)单调增加且是凸的 (C)单调减少且是凹的 (D)单调增加且是凹的6.以下结论正确的是( ).(A) 若0x 为函数()y f x =的驻点,则0x 必为函数()y f x =的极值点. (B) 函数()y f x =导数不存在的点,一定不是函数()y f x =的极值点. (C) 若函数()y f x =在0x 处取得极值,且()0f x '存在,则必有()0f x '=0. (D) 若函数()y f x =在0x 处连续,则()0f x '一定存在. 7.设函数()y f x =的一个原函数为12xx e ,则()f x =( ).(A) ()121xx e - (B) 12x x e - (C) ()121x x e + (D) 12xxe 8.若()()f x dx F x c =+⎰,则()sin cos xf x dx =⎰( ).(A) ()sin F x c + (B) ()sin F x c -+ (C) ()cos F x c + (D) ()cos F x c -+ 9.设()F x 为连续函数,则12x f dx ⎛⎫' ⎪⎝⎭⎰=( ). (A) ()()10f f - (B)()()210f f -⎡⎤⎣⎦ (C) ()()220f f -⎡⎤⎣⎦ (D) ()1202f f ⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦10.定积分badx ⎰()a b <在几何上的表示( ).(A) 线段长b a - (B) 线段长a b - (C) 矩形面积()1a b -⨯ (D) 矩形面积()1b a -⨯ 二.填空题(每题4分,共20分)1.设 ()()2ln 101cos 0x x f x xa x ⎧-⎪≠=⎨-⎪=⎩, 在0x =连续,则a =________.2.设2sin y x =, 则dy =_________________sin d x . 3.函数211xy x =+-的水平和垂直渐近线共有_______条. 4.不定积分ln x xdx =⎰______________________.5. 定积分2121sin 11x x dx x -+=+⎰___________. 三.计算题(每小题5分,共30分)1.求下列极限:①()10lim 12xx x →+ ②arctan 2lim 1x x xπ→+∞-2.求由方程1yy xe =-所确定的隐函数的导数x y '. 3.求下列不定积分:①3tan sec x xdx ⎰②)0a > ③2x x e dx ⎰ 四.应用题(每题10分,共20分) 1.作出函数313y x x =-的图象.(要求列出表格)2.计算由两条抛物线:22,y x y x ==所围成的图形的面积.《高数》试卷2参考答案一.选择题:CDCDB CADDD二填空题:1.-2 2.2sin x 3.3 4.2211ln 24x x x c -+ 5.2π 三.计算题:1. ①2e ②1 2.2yx e y y '=- 3.①3sec 3xc + ②()22ln x a x c +++ ③()222x x x e c -++四.应用题:1.略 2.13S =《高数》试卷3(上)一、 填空题(每小题3分, 共24分)1. 函数219y x=-的定义域为________________________.2.设函数()sin 4,0,0xx f x x a x ⎧≠⎪=⎨⎪=⎩, 则当a =_________时, ()f x 在0x =处连续.3. 函数221()32x f x x x -=-+的无穷型间断点为________________.4. 设()f x 可导, ()xy f e =, 则____________.y '=5. 221lim _________________.25x x x x →∞+=+- 6. 321421sin 1x xdx x x -+-⎰=______________. 7. 20_______________________.x t d e dt dx -=⎰ 8. 30y y y '''+-=是_______阶微分方程.二、求下列极限(每小题5分, 共15分)1. 01lim sin xx e x →-; 2. 233lim 9x x x →--; 3. 1lim 1.2xx x -→∞⎛⎫+ ⎪⎝⎭三、求下列导数或微分(每小题5分, 共15分)1. 2xy x =+, 求(0)y '. 2. cos x y e =, 求dy . 3. 设x y xy e +=, 求dydx .四、求下列积分 (每小题5分, 共15分)1. 12sin x dx x ⎛⎫+ ⎪⎝⎭⎰. 2.ln(1)x x dx +⎰.3.120xedx ⎰五、(8分)求曲线1cos x t y t=⎧⎨=-⎩在2t π=处的切线与法线方程.六、(8分)求由曲线21,y x =+ 直线0,0y x ==和1x =所围成的平面图形的面积, 以及此图形绕y 轴旋转所得旋转体的体积. 七、(8分)求微分方程6130y y y '''++=的通解.八、(7分)求微分方程x yy e x'+=满足初始条件()10y =的特解. 《高数》试卷3参考答案一.1.3x< 2.4a = 3.2x = 4.'()x x e f e5.126.07.22x xe -8.二阶二.1.原式=0lim 1x xx→= 2.311lim36x x →=+ 3.原式=112221lim[(1)]2x x e x--→∞+= 三.1.221','(0)(2)2y y x ==+2.cos sin x dy xe dx =-3.两边对x 求写:'(1')x y y xy e y +==+'x y x y e y xy yy x e x xy++--⇒==-- 四.1.原式=lim 2cos x x C -+2.原式=2221lim(1)()lim(1)[lim(1)]22x x x d x x d x x +=+-+⎰⎰=22111lim(1)lim(1)(1)221221x x x x dx x x dx x x+-=+--+++⎰⎰=221lim(1)[lim(1)]222x x x x x C +--+++3.原式=1221200111(2)(1)222x x e d x e e ==-⎰五.sin 1,122dy dy tt t y dx dx ππ=====且 切线:1,1022y x y x ππ-=---+=即 法线:1(),1022y x y x ππ-=--+--=即六.12210013(1)()22S x dx x x =+=+=⎰11224205210(1)(21)228()5315V x dx x x dxx x x ππππ=+=++=++=⎰⎰七.特征方程:2312613032(cos 2sin 2)xr r r iy e C x C x -++=⇒=-±=+八.11()dxdxxx x y ee edx C -⎰⎰=+⎰1[(1)]x x e C x=-+ 由10,0y x C ==⇒=1xx y e x-∴=《高数》试卷4(上)一、选择题(每小题3分) 1、函数 2)1ln(++-=x x y 的定义域是( ).A []1,2-B [)1,2-C (]1,2-D ()1,2- 2、极限xx e ∞→lim 的值是( ).A 、 ∞+B 、 0C 、∞-D 、 不存在 3、=--→211)1sin(limx x x ( ).A 、1B 、 0C 、 21-D 、21 4、曲线 23-+=x x y 在点)0,1(处的切线方程是( ) A 、 )1(2-=x y B 、)1(4-=x y C 、14-=x y D 、)1(3-=x y 5、下列各微分式正确的是( ).A 、)(2x d xdx = B 、)2(sin 2cos x d xdx = C 、)5(x d dx --= D 、22)()(dx x d = 6、设⎰+=C xdx x f 2cos 2)( ,则 =)(x f ( ).A 、2sinxB 、 2sin x -C 、 C x +2sinD 、2sin 2x -7、⎰=+dx xx ln 2( ).A 、C x x++-22ln 212 B 、 C x ++2)ln 2(21C 、 C x ++ln 2lnD 、 C x x++-2ln 18、曲线2x y = ,1=x ,0=y 所围成的图形绕y 轴旋转所得旋转体体积=V ( ). A 、⎰14dx x π B 、⎰1ydy πC 、⎰-1)1(dy y π D 、⎰-104)1(dx x π9、⎰=+101dx e e xx( ). A 、21lne + B 、22ln e + C 、31ln e + D 、221ln e + 10、微分方程 xe y y y 22=+'+'' 的一个特解为( ).A 、x e y 273=* B 、x e y 73=* C 、x xe y 272=* D 、x e y 272=*二、填空题(每小题4分)1、设函数xxe y =,则 =''y ; 2、如果322sin 3lim 0=→x mx x , 则 =m .3、=⎰-113cos xdx x ;4、微分方程 044=+'+''y y y 的通解是 .5、函数x x x f 2)(+= 在区间 []4,0 上的最大值是 ,最小值是 ;三、计算题(每小题5分) 1、求极限 x x x x --+→11lim 0; 2、求x x y sin ln cot 212+= 的导数;3、求函数 1133+-=x x y 的微分; 4、求不定积分⎰++11x dx ;5、求定积分⎰eedx x 1ln ; 6、解方程21xy xdx dy -=;四、应用题(每小题10分)1、 求抛物线2x y = 与 22x y -=所围成的平面图形的面积.2、 利用导数作出函数323x x y -= 的图象.参考答案一、1、C ; 2、D ; 3、C ; 4、B ; 5、C ; 6、B ; 7、B ; 8、A ; 9、A ; 10、D ;二、1、xe x )2(+; 2、94 ; 3、0 ; 4、xe x C C y 221)(-+= ; 5、8,0三、1、 1; 2、x 3cot - ; 3、dx x x 232)1(6+ ;4、C x x +++-+)11ln(212;5、)12(2e- ; 6、C x y =-+2212 ; 四、1、38; 2、图略《高数》试卷5(上)一、选择题(每小题3分) 1、函数)1lg(12+++=x x y 的定义域是( ).A 、()()+∞--,01,2B 、 ()),0(0,1+∞-C 、),0()0,1(+∞-D 、),1(+∞- 2、下列各式中,极限存在的是( ).A 、 x x cos lim 0→ B 、x x arctan lim ∞→ C 、x x sin lim ∞→ D 、xx 2lim +∞→3、=+∞→xx xx )1(lim ( ). A 、e B 、2e C 、1 D 、e1 4、曲线x x y ln =的平行于直线01=+-y x 的切线方程是( ). A 、 x y = B 、)1)(1(ln --=x x y C 、 1-=x y D 、)1(+-=x y 5、已知x x y 3sin = ,则=dy ( ).A 、dx x x )3sin 33cos (+-B 、dx x x x )3cos 33(sin +C 、dx x x )3sin 3(cos +D 、dx x x x )3cos 3(sin + 6、下列等式成立的是( ).A 、⎰++=-C x dx x 111ααα B 、⎰+=C x a dx a xx ln C 、⎰+=C x xdx sin cos D 、⎰++=C xxdx 211tan 7、计算⎰xdx x e x cos sin sin 的结果中正确的是( ).A 、C ex+sin B 、C x e x +cos sinC 、C x ex+sin sin D 、C x e x +-)1(sin sin8、曲线2x y = ,1=x ,0=y 所围成的图形绕x 轴旋转所得旋转体体积=V ( ). A 、⎰14dx x π B 、⎰1ydy πC 、⎰-1)1(dy y π D 、⎰-104)1(dx x π9、设 a ﹥0,则=-⎰dx x a a22( ).A 、2a B 、22a πC 、241a 0 D 、241a π 10、方程( )是一阶线性微分方程.A 、0ln2=+'xyy x B 、0=+'y e y x C 、0sin )1(2=-'+y y y x D 、0)6(2=-+'dy x y dx y x二、填空题(每小题4分)1、设⎩⎨⎧+≤+=0,0,1)( x b ax x e x f x ,则有=-→)(lim 0x f x ,=+→)(lim 0x f x ;2、设 xxe y = ,则 =''y ;3、函数)1ln()(2x x f +=在区间[]2,1-的最大值是 ,最小值是 ;4、=⎰-113cos xdx x;5、微分方程 023=+'-''y y y 的通解是 .三、计算题(每小题5分) 1、求极限 )2311(lim 21-+--→x x x x ;2、求 x x y arccos 12-= 的导数;3、求函数21xx y -=的微分;4、求不定积分⎰+dx xxln 21 ;5、求定积分 ⎰eedx x 1ln ;6、求方程y xy y x =+'2满足初始条件4)21(=y 的特解.四、应用题(每小题10分)1、求由曲线 22x y -= 和直线 0=+y x 所围成的平面图形的面积.2、利用导数作出函数 49623-+-=x x x y 的图象.参考答案(B 卷)一、1、B ; 2、A ; 3、D ; 4、C ; 5、B ; 6、C ; 7、D ; 8、A ; 9、D ; 10、B.二、1、 2 ,b ; 2、xe x )2(+ ; 3、 5ln ,0 ; 4、0 ; 5、xxeC e C 221+.三、1、31 ; 2、1arccos 12---x x x ; 3、dx xx 221)1(1-- ; 4、C x ++ln 22 ; 5、)12(2e- ; 6、x e x y 122-= ;四、1、 29; 2、图略《高等数学》试卷1(下)一.选择题(3分⨯10)1.点1M ()1,3,2到点()4,7,22M 的距离=21M M ( ).A.3B.4C.5D.62.向量j i b k j i a+=++-=2,2,则有( ).A.a ∥bB.a ⊥bC.3,π=b aD.4,π=b a3.函数1122222-++--=y x y x y 的定义域是( ).A.(){}21,22≤+≤y x y x B.(){}21,22<+<y x y xC.(){}21,22≤+<y xy x D (){}21,22<+≤y x y x4.两个向量a 与b垂直的充要条件是( ).A.0=⋅b aB.0 =⨯b aC.0 =-b aD.0 =+b a5.函数xy y x z 333-+=的极小值是( ). A.2 B.2- C.1 D.1- 6.设y x z sin =,则⎪⎭⎫ ⎝⎛∂∂4,1πyz=( ).A.22B.22-C.2D.2-7.若p 级数∑∞=11n p n 收敛,则( ). A.p 1< B.1≤p C.1>p D.1≥p8.幂级数∑∞=1n nnx 的收敛域为( ).A.[]1,1- B ()1,1- C.[)1,1- D.(]1,1-9.幂级数nn x ∑∞=⎪⎭⎫⎝⎛02在收敛域内的和函数是( ).A.x -11 B.x -22 C.x -12 D.x-21 10.微分方程0ln =-'y y y x 的通解为( ). A.xce y = B.xe y = C.xcxe y = D.cxe y = 二.填空题(4分⨯5)1.一平面过点()3,0,0A 且垂直于直线AB ,其中点()1,1,2-B ,则此平面方程为______________________.2.函数()xy z sin =的全微分是______________________________.3.设13323+--=xy xy y x z ,则=∂∂∂yx z 2_____________________________.4.x+21的麦克劳林级数是___________________________. 5.微分方程044=+'+''y y y 的通解为_________________________________. 三.计算题(5分⨯6)1.设v e z usin =,而y x v xy u +==,,求.,yz x z ∂∂∂∂ 2.已知隐函数()y x z z ,=由方程05242222=-+-+-z x z y x 确定,求.,yz x z ∂∂∂∂ 3.计算σd y x D⎰⎰+22sin ,其中22224:ππ≤+≤y x D . 4.如图,求两个半径相等的直交圆柱面所围成的立体的体积(R 为半径).5.求微分方程xe y y 23=-'在00==x y条件下的特解.四.应用题(10分⨯2)1.要用铁板做一个体积为23m 的有盖长方体水箱,问长、宽、高各取怎样的尺寸时,才能使用料最省?2..曲线()x f y =上任何一点的切线斜率等于自原点到该切点的连线斜率的2倍,且曲线过点⎪⎭⎫⎝⎛31,1,求此曲线方程 .《高数》试卷2(下)一.选择题(3分⨯10)1.点()1,3,41M ,()2,1,72M 的距离=21M M ( ). A.12 B.13 C.14 D.152.设两平面方程分别为0122=++-z y x 和05=++-y x ,则两平面的夹角为( ). A.6π B.4π C.3π D.2π 3.函数()22arcsin yx z +=的定义域为( ).A.(){}10,22≤+≤y x y x B.(){}10,22<+<y x y xC.()⎭⎬⎫⎩⎨⎧≤+≤20,22πy x y x D.()⎭⎬⎫⎩⎨⎧<+<20,22πy x y x 4.点()1,2,1--P 到平面0522=--+z y x 的距离为( ). A.3 B.4 C.5 D.6 5.函数22232y x xy z --=的极大值为( ). A.0 B.1 C.1- D.216.设223y xy x z ++=,则()=∂∂2,1xz ( ).A.6B.7C.8D.9 7.若几何级数∑∞=0n nar是收敛的,则( ).A.1≤rB. 1≥rC.1<rD.1≤r8.幂级数()nn xn ∑∞=+01的收敛域为( ).A.[]1,1-B.[)1,1-C.(]1,1-D. ()1,1- 9.级数∑∞=14sin n n na是( ). A.条件收敛 B.绝对收敛 C.发散 D.不能确定 10.微分方程0ln =-'y y y x 的通解为( ). A.cxe y = B.xce y = C.xe y = D.xcxe y = 二.填空题(4分⨯5)1.直线l 过点()1,2,2-A 且与直线⎪⎩⎪⎨⎧-==+=t z t y t x 213平行,则直线l 的方程为__________________________.2.函数xye z =的全微分为___________________________. 3.曲面2242y x z -=在点()4,1,2处的切平面方程为_____________________________________. 4.211x+的麦克劳林级数是______________________. 5.微分方程03=-ydx xdy 在11==x y 条件下的特解为______________________________.三.计算题(5分⨯6)1.设k j b k j i a32,2+=-+=,求.b a ⨯2.设22uv v u z -=,而y x v y x u sin ,cos ==,求.,y z x z ∂∂∂∂ 3.已知隐函数()y x z z ,=由233=+xyz x 确定,求.,yz x z ∂∂∂∂ 4.如图,求球面22224a z y x =++与圆柱面ax y x 222=+(0>a )所围的几何体的体积.5.求微分方程023=+'+''y y y 的通解. 四.应用题(10分⨯2) 1.试用二重积分计算由x y x y 2,==和4=x 所围图形的面积.2.如图,以初速度0v 将质点铅直上抛,不计阻力,求质点的运动规律().t x x =(提示:g dt x d -=22.当0=t 时,有0x x =,0v dtdx=)《高等数学》试卷3(下)一、选择题(本题共10小题,每题3分,共30分) 1、二阶行列式 2 -3 的值为( )4 5A 、10B 、20C 、24D 、222、设a=i+2j-k,b=2j+3k ,则a 与b 的向量积为( ) A 、i-j+2k B 、8i-j+2k C 、8i-3j+2k D 、8i-3i+k3、点P (-1、-2、1)到平面x+2y-2z-5=0的距离为( ) A 、2 B 、3 C 、4 D 、54、函数z=xsiny 在点(1,4π)处的两个偏导数分别为( ) A 、,22 ,22 B 、,2222- C 、22- 22- D 、22- ,22 5、设x 2+y 2+z 2=2Rx ,则yzx z ∂∂∂∂,分别为( ) A 、z y z R x --, B 、z y z R x ---, C 、zyz R x ,-- D 、zyz R x ,- 6、设圆心在原点,半径为R ,面密度为22y x +=μ的薄板的质量为( )(面积A=2R π)A 、R 2AB 、2R 2AC 、3R 2AD 、A R 2217、级数∑∞=-1)1(n nnn x 的收敛半径为( )A 、2B 、21C 、1D 、3 8、cosx 的麦克劳林级数为( )A 、∑∞=-0)1(n n)!2(2n x n B 、∑∞=-1)1(n n )!2(2n x n C 、∑∞=-0)1(n n )!2(2n x n D 、∑∞=-0)1(n n)!12(12--n x n9、微分方程(y``)4+(y`)5+y`+2=0的阶数是( ) A 、一阶 B 、二阶 C 、三阶 D 、四阶 10、微分方程y``+3y`+2y=0的特征根为( ) A 、-2,-1 B 、2,1 C 、-2,1 D 、1,-2 二、填空题(本题共5小题,每题4分,共20分) 1、直线L 1:x=y=z 与直线L 2:的夹角为z y x =-+=-1321___________。
《经济数学-微积分》旋转体的体积

旋转体定义
一个平面图形绕着它所在的平面 内的一条定直线旋转所形成的曲 面围成的几何体称为旋转体。
旋转体分类
根据旋转轴的不同,旋转体可以 分为绕x轴旋转的旋转体和绕y轴 旋转的旋转体。
体积计算公式推导
01
圆柱体体积公式推导
02
圆锥体体积公式推导
03
圆球体体积公式推导
圆柱体可以看作是一个矩形绕其一边 旋转而成的,因此其体积可以通过矩 形的面积与旋转的高度的乘积来计算 。
多重积分概念与性质
了解多重积分的概念和性质,如二重积分、三重积分等。
在旋转体体积求解中应用
对于复杂形状的旋转体,可以通过多重积分进行求解,如球体、椭 球体等。
求解步骤与技巧
掌握多重积分的求解步骤和技巧,如选择合适的坐标系、确定积分 顺序等。
数值近似解法介绍
01
数值近似解法概念
当无法直接通过积分公式求解旋 转体体积时,可以采用数值近似 解法进行估算。
04 积分法在求解旋转体体积 中应用
定积分求解旋转体体积基本原理
旋转体体积的定积分表示
通过截面面积函数对定区间进行积分,得到旋转体体积的公式。
几何意义与物理应用
定积分求解旋转体体积的方法在几何和物理领域有广泛应用,如计 算圆柱、圆锥等体积。
求解步骤与技巧
掌握定积分的求解步骤和技巧,如确定积分区间、选择合适的积分 变量等。
物理应用
旋转体体积的计算公式在物理学中也 有广泛应用,例如在计算物体的质量 、密度、浮力等方面都需要用到体积 的计算公式。
常见问题及解决方法
问题1
如何判断一个几何体是否为旋转体?
解决方法
观察几何体的形状和特征,看其是否符合旋转体的定义和 性质。
大一高等数学练习题及答案解析

大一高等数学练习题及答案解析 11.2.limx?0xx?.1?1x?1?x2005??ex?e?x?dx?x?y2.3.设函数y?y由方程?1xe?tdt?xdy确定,则dxx?0tfdt?ff?1fx14. 设可导,且,,则f?x??5.微分方程y4y??4y?0的通解为 .二.选择题1.设常数k?0,则函数个; 个; 1个; 0个.2.微分方程y4y?3cos2x 的特解形式为.y?Acos2x; y?Axcos2x;f?lnx?x?ke在内零点的个数为.y?Axcos2x?Bxsin2x;y?Asin2x..下列结论不一定成立的是.*f?x?dx??f?x?dxc,d?a,bca若,则必有;f?x?dx?0a,bf?0a若在上可积,则;若f?x?是周期为T的连续函数,则对任意常数a都有 xba?Taf?x?dx??f?x?dxT;tf?t?dtfx0若可积函数为奇函数,则也为奇函数. f?x??4. 设1?e1x1x2?3e, 则x?0是f的.连续点; 可去间断点;跳跃间断点; 无穷间断点. 三.计算题 1 .计算定积分x3e?xdx2.2.计算不定积分xsinxcos5x.xxa,t2处的切线的方程. .求摆线?y?a,在4. 设F??cosdt,求F?.5.设四.应用题 1.求由曲线y?xn?nlimxnn,求n??.x?2与该曲线过坐标原点的切线及x轴所围图形的面积.222.设平面图形D由x?y?2x与y?x所确定,试求D绕直线x?旋转一周所生成的旋转体的体积.ta?1,f?a?at在内的驻点为 t. 问a为何值时t最小?并求3. 设最小值.五.证明题设函数f在[0,1]上连续,在内可导且1ff=?1试证明至少存在一点??, 使得f?=1. 一.填空题: 11..limx?x?0e.4e.dy确定,则dxx?0121?1x?1?x2005??ex?e?x?dx?x?y3.设函数y?y由方程?1e?tdt?x?e?1.12x24. 设f?x?可导,且x1tfdt?f,f?1,则f?x??e2x.5.微分方程y4y??4y?0的通解为y?e二.选择题: .1.设常数k?0,则函数个; 个; 1个; 0个.2.微分方程y4y?3cos2x 的特解形式为y?Acos2xy; ?Axcos2x; ?y?Axcos2x?Bxsin2x; y?Asin2x.下列结论不一定成立的是f?lnx?x?k内零点的个数为. e 在若?c,da,b?,则必有dcf?x?dx??f?x?dxabb;f?x?dx?0a,bf?0a若在上可积,则;若f?x?是周期为T的连续函数,则对任意常数a都有a?Taf?x?dx??f?x?dxT;xtf?t?dtfx0 若可积函数为奇函数,则也为奇函数. f?x??1?e1x1x2?3e, 则x?0是f的.. 设连续点; 可去间断点;跳跃间断点; 无穷间断点. 三.计算题: 1.计算定积分?0 解:2x3e?xdx202.2设x2?t,则?x3e?xdx??1?t12tedttde?t0220-------221??t22?t?te??edt?002?? -------22131e?2?e?te?2022--------22.计算不定积分解:xsinx5cosx.xsinx111?xdx?dx?xd??4?cos5x?cos4x?4?cos4x4??cosx?--------3 x1dtanx44cosx4x113tanx?tanx?C4cos4x1-----------?xa,t2处的切线的方程..求摆线?y?a,在,a)2解:切点为 -------2k?dyasint?s)t??dxt??a即y?x?a.-------24. 设.设F??cosdt22F2xcosxcos. ,则xn?nn?1)?limxnn,求n??.1nilnxn??ln1ni?1n ---------解:n1i1limlnxn?lim?ln??lndx0n??n??nni?1--------------12ln2101?x =------------22ln2?1e?limxne 故 n??=xln10??x1四.应用题 1.求由曲线y?x?2与该曲线过坐标原点的切线及x轴所围图形的面积.解:大一高等数学期末考试试卷一、选择题2ex,x0,1. 若f??为连续函数,则a的值为.ax,x01 3-12. 已知f??2,则limh?0f?f的值为.h13-113. 定积分?2?的值为. ?20-2124. 若f在x?x0处不连续,则f在该点处.必不可导一定可导可能可导必无极限二、填空题1.平面上过点,且在任意一点处的切线斜率为3x2的曲线方程为 .2. ?dx? . ?113. limx2sinx?01= . x4. y?2x3?3x2的极大值为三、计算题1. 求limx?0xln. sin3x22. 设y?求y?.. 求不定积分?xlndx.4. 求?30?x,x?1,? fdx,其中f??1?cosx?ex?1,x?1.?5. 设函数y?f由方程?edt??costdt?0所确定,求dy. 00ytx6. 设?fdx?sinx2?C,求?fdx.3??7. 求极限lim?1??. n2n?四、解答题1. 设f??1?x,且f?1,求f. n2. 求由曲线y?cosxx??与x轴所围成图形绕着x轴旋转一周2??2所得旋转体的体积.3. 求曲线y?x3?3x2?24x?19在拐点处的切线方程.4. 求函数y?x[?5,1]上的最小值和最大值.五、证明题设f??在区间[a,b]上连续,证明bafdx?b?a1b[f?f]??f??dx.2a标准答案一、 1 B; C; D; A.二、 1 y?x?1;2; 0;0.三、 1 解原式?limx?5x5分 x?03x21分2分 x??lxn2d分 ?212x?[lndx2分21?x1?[ln?x2]?C1分解令x?1?t,则分03fdx1fdt 1分122t1??1dt 1分 1?cost1分 ?0?[et?t]1e2e1 1分两边求导得ey?y??cosx?0,分ycosx 1分 ye?cosx 1分 sinx?1cosx?dy?dx分 sinx?1解 ?fdx?12?fd2?C4分3??lim1?解原式=??n2n?322n3?32分 =e2分四、1 解令lnx?t,则x?et,f??1?et, 分 f??dt=t?et?C.2分 ?f?1,?C?0, 分fxex. 1分解 Vx2??2??cosxdx分 ?2202cos2xdx2分 ?解 ?22. 分 6x?1分 y??3x2?6x?24,y令y0,得x?1. 1分当x?1时,y0; 当1?x时,y0,分 ?为拐点, 1分该点处的切线为y?3?21. 分解y??1??2分令y??0,得x3?. 1分435y52.55,y,y1,分 ?4?435y5y最大值为. 分 ?最小值为?4?4五、证明bafdf?分 ab[f]aaf[2xdx分a[2x?df分 bbb[2x?]f?a?2?afdx分[f?f]?2?afdx,分移项即得所证分 bbb大一高数试题及答案一、填空题________ 11.函数y=arcsin√1-x+────── 的定义域为_________ √1-x2_______________。
高数上册之立体的体积

一系列圆柱形薄壳组成的, 以此柱壳的体积作为体积元素,
当dx很小时,此小柱体的高看作f(x),
即为圆柱薄壳
8
y
在区间 [ x , x dx] 上
柱壳体的体积元素为
绵 阳
师 范 学 院
y f (x)
dV 2x dx f ( x )
V dV 2 xf ( x )dx
a a
b
o
a
x
b
4
x
图1
y
绵 同理,如旋转体由图2的曲边梯 阳 师 范 学 d 形绕y轴形成. x=(y) d 2 c 则体积为 V [ ( y )] dy 院
c
例3 求如图直角三角形绕x轴 旋转而成的圆锥体的体积.
解 可求得过点O及P(h,r)的直线方程为
r y x h
o
2 3 2
o
x
例4 求阿基米德螺线r=a(a>0)上 相应于从0到2的一段弧长. 解
s
b
r ( ) r ( )d a
2 2
2
1 2 d
0
a [2 1 4 2 ln(2 1 4 2 )] 2
14
1
绵 阳
师 范 学 院
解
如图,过x的截面是直角三角形,
边长分别为y和ytan .因此
1 2 A( x ) ( R x 2 ) tan ,-R 2 o R 1 x y 2 2 V ( R x ) tandx R R 2 x 1 2 1 3 2 3 R ( R x x ) tan | R R tan 2 3 3
o
b
x
解 圆的方程为 ( x b) 2 y 2 a 2 ,则所求体积可视为
旋转体(圆柱、圆锥、圆台)-高中数学知识点讲解(含答案)

旋转体(圆柱、圆锥、圆台)(北京习题集)(教师版)一.选择题(共6小题)1.(2019春•西城区校级期中)若圆柱的轴截面是一个正方形,其面积为4S ,则它的一个底面面积是 () A .4SB .4S πC .S πD .2S π2.(2019•西城区校级模拟)用一块圆心角为240︒、半径为R 的扇形铁皮制成一个无底面的圆锥容器(接缝忽略不计),则该容器的体积为( )ABCD3.(2018春•西城区期末)圆柱的侧面展开图是一个边长为2的正方形,那么这个圆柱的体积是( ) A .2πB .1πC .22π D .21π4.(2017春•丰台区期中)直角三角形的两条直角边的长度分别是3,4,以直角三角形的斜边所在直线为旋转轴,旋转一周形成几何体的体积是( ) A .12πB .1445πC .485πD .48π5.(2015秋•西城区校级期中)下列命题中错误的是( ) A .圆柱的轴截面是过母线的截面中面积最大的一个B .圆锥的轴截面是所在过顶点的截面中面积最大的一个C .圆台的所有平行于底面的截面都是圆面D .圆锥所有的轴截面是全等的等腰三角形6.(2014秋•西城区校级期中)在ABC ∆中,4AB =,3BC =,90ABC ∠=︒,若使ABC ∆绕直线BC 旋转一周,则所形成的几何体的体积是( ) A .36πB .28πC .20πD .16π二.填空题(共8小题)7.(2017秋•西城区期末)在ABC ∆中,3AB =,4BC =,AB BC ⊥.以BC 所在的直线为轴将ABC ∆旋转一周,则旋转所得圆锥的侧面积为 .8.(2018春•西城区校级期中)圆台两底面半径分别是2和5,母线长是,则它的轴截面的面积是 . 9.(2017秋•东城区期末)一个横放的圆柱形水桶,桶内的水占底面周长的四分之一,那么当桶直立时,水的高度与桶的高度的比为 .10.(2017秋•东城区期末)圆22(1)2x y -+=绕直线0kx y k --=旋转一周所得的几何体的表面积为 . 11.(2017秋•海淀区校级期中)用一张48cm cm ⨯的矩形硬纸卷成圆柱的侧面,则圆柱轴截面的面积为 2cm (接头忽略不计).12.(2017春•丰台区期中)已知圆柱底面半径是2,高是3,则圆柱的表面积是 .13.(2015秋•昌平区期末)已知一个圆柱的底面半径为2,体积为16π,则该圆柱的母线长为 ,表面积为 . 14.(2016秋•昌平区月考)四边形ABCD 四顶点的坐标分别为(0,0)A ,(1,0)B ,(2,1)C ,(0,3)D ,将四边形绕y 轴旋转一周得到一几何体,则此几何体的表面积为 . 三.解答题(共1小题)15.(2015秋•海淀区校级期中)如图,AB 是圆O 的直径,点C 是半圆的中点,PA ⊥平面ABC ,PA AB =,6PB D =是PB 的中点,E 是PC 上一点. (Ⅰ) 若DE PB ⊥,求PEEC的值; (Ⅱ)若点Q 是平面ABC 内一点,且||2||QA QC =,求点Q 在ABC ∆内的轨迹长度.旋转体(圆柱、圆锥、圆台)(北京习题集)(教师版)参考答案与试题解析一.选择题(共6小题)1.(2019春•西城区校级期中)若圆柱的轴截面是一个正方形,其面积为4S ,则它的一个底面面积是 () A .4SB .4S πC .S πD .2S π【分析】根据圆柱的轴截面是正方形,且轴截面面积是4S ,出圆柱底面圆的直径,代入面积公式计算. 【解答】解:圆柱的轴截面是一个正方形,且此正方形的面积为4S ,故此正方形的边长为故此圆柱的底面直径为,故圆柱的底面面积为:S π, 故选:C .【点评】本题考查的知识点是旋转体,其中熟练掌握圆柱的几何特征是解答的关键.2.(2019•西城区校级模拟)用一块圆心角为240︒、半径为R 的扇形铁皮制成一个无底面的圆锥容器(接缝忽略不计),则该容器的体积为( )ABCD【分析】根据题意求出扇形围成的圆锥底面圆半径和高,再计算圆锥的体积. 【解答】解:扇形的圆心角为42403π︒=,半径为R ; 设扇形围成的圆锥底面半径为r ,高为h ; 则423r R ππ=,解得23Rr =;h =, 则该圆锥的体积为221454339R V r h R ππ===. 故选:A .【点评】本题考查了圆锥的结构特征与体积计算问题,是基础题.3.(2018春•西城区期末)圆柱的侧面展开图是一个边长为2的正方形,那么这个圆柱的体积是( ) A .2πB .1πC .22π D .21π【分析】由题意求出圆柱的高和底面圆半径,再求圆柱的体积. 【解答】解:如图所示,圆柱的侧面展开图是一个边长为2的正方形, 则圆柱的高为2h =, 底面圆的周长为22r π=, 解得1r π=,∴圆柱的体积是2212()2V r h ππππ===.故选:A .【点评】本题考查了圆柱的侧面展开图和体积的计算问题,是基础题.4.(2017春•丰台区期中)直角三角形的两条直角边的长度分别是3,4,以直角三角形的斜边所在直线为旋转轴,旋转一周形成几何体的体积是( ) A .12πB .1445πC .485πD .48π【分析】由已知中,3AC =,4BC =,5AB =,可得三角形ABC 为直角三角形,我们可以判断出以斜边AB 为轴旋转一周,所得旋转体的形状是AB 边的高CO 为底面半径的两个圆锥组成的组合体,计算出底面半径及两个圆锥高之和,代入圆锥体积公式,即可求出旋转体的体积;【解答】解:以该直角三角形的斜边所在直线为旋转轴旋转一周形成的几何体是两个圆锥的组合体, 其中圆锥的底面半径为125,高的和为5, 所以该几何体的体积211248()5355V ππ=⨯⨯⨯=.故选:C .【点评】题考查的知识点是旋转体,圆锥的体积和表面积,其中根据已知判断出旋转所得旋转体的形状及底面半径,高,母线长等关键几何量,是解答本题的关键. 5.(2015秋•西城区校级期中)下列命题中错误的是( ) A .圆柱的轴截面是过母线的截面中面积最大的一个B .圆锥的轴截面是所在过顶点的截面中面积最大的一个C .圆台的所有平行于底面的截面都是圆面D .圆锥所有的轴截面是全等的等腰三角形【分析】对于A ,B ,计算出截面面积与轴截面面积比较大小即可判断,对于C ,D ,利用旋转体的结构特征进行分析判断.【解答】解:对于A ,设圆柱的底面半径为r ,高为h ,设圆柱的过母线的截面四边形在圆柱底面的边长为a ,则截面面积2S ah rh =.∴当2a r =时截面面积最大,即轴截面面积最大,故A 正确.对于B ,设圆锥SO 的底面半径为r ,高为h ,过圆锥定点的截面在底面的边长为AB a =,则O 到AB 的距离为,∴截面三角形SAB ∴截面面积22221)(222h r h r S ++==.故截面的最大面积为222h r hr +.故B 错误.对于C ,由圆台的结构特征可知平行于底面的截面截圆台,所得几何体仍是圆台,故截面为圆面,故C 正确. 对于D ,由于圆锥的所有母线长都相等,轴截面的底面边长为圆锥底面的直径,故圆锥所有的轴截面是全等的等腰三角形,故D 正确. 故选:B .【点评】本题考查了旋转体的结构特征,属于中档题.6.(2014秋•西城区校级期中)在ABC ∆中,4AB =,3BC =,90ABC ∠=︒,若使ABC ∆绕直线BC 旋转一周,则所形成的几何体的体积是( ) A .36πB .28πC .20πD .16π【分析】使ABC ∆绕直线BC 旋转一周,则所形成的几何体是一个底面半径为4,高为3的一个圆锥,代入圆锥体积公式,可得答案.【解答】解:将ABC ∆绕直线BC 旋转一周, 得到一个底面半径为4,高为3的一个圆锥, 故所形成的几何体的体积2143163V ππ=⨯⨯⨯=,故选:D .【点评】本题考查的知识点是旋转体,其中分析出旋转得到的几何体形状及底面半径,高等几何量是解答的关键. 二.填空题(共8小题)7.(2017秋•西城区期末)在ABC ∆中,3AB =,4BC =,AB BC ⊥.以BC 所在的直线为轴将ABC ∆旋转一周,则旋转所得圆锥的侧面积为 15π .【分析】以BC 所在的直线为轴将ABC ∆旋转一周,形成的旋转体是底面半径为3r AB ==,高为4BC =的圆锥,由此能求出旋转所得圆锥的侧面积.【解答】解在ABC ∆中,3AB =,4BC =,AB BC ⊥.229165AC AB BC ∴=+=+=, 以BC 所在的直线为轴将ABC ∆旋转一周,形成的旋转体是底面半径为3r AB ==,高为4BC =的圆锥,∴旋转所得圆锥的侧面积:S rl AB AC ππ==⨯⨯ 3515ππ=⨯⨯=故答案为:15π.【点评】本题考查过圆锥的侧面积的求法,考查圆锥、旋转体等基础知识,考查运算求解能力、空间想象能力,数形结合思想,是中档题.8.(2018春•西城区校级期中)圆台两底面半径分别是2和5,母线长是310,则它的轴截面的面积是 63 . 【分析】圆台的轴截面为等腰梯形,求出梯形的高,即可求出轴截面的面积. 【解答】解:由题意,圆台的轴截面为等腰梯形, 圆台两底面半径分别是2和5,母线长是310∴22(310)(52)9--,∴轴截面的面积是1(410)9632⨯+⨯=.故答案为:63.【点评】本题考查轴截面的面积,考查学生的计算能力,确定梯形的高是关键.9.(2017秋•东城区期末)一个横放的圆柱形水桶,桶内的水占底面周长的四分之一,那么当桶直立时,水的高度与桶的高度的比为 (2):4ππ- .【分析】直接求出水桶两种放置时,水的体积相等,即可得到水的高度与桶的高度的比值. 【解答】解:横放时水桶底面在水内的面积为221142R R π-.221142V R R h π⎛⎫=- ⎪⎝⎭水,直立时2V R x π=水,:(2):4x h ππ∴=-故答案为:(2):4ππ-【点评】本题考查简单几何体和球的知识,考查空间想象能力,计算能力.10.(2017秋•东城区期末)圆22(1)2x y -+=绕直线0kx y k --=旋转一周所得的几何体的表面积为 8π . 【分析】由题意知圆22(1)2x y -+=的圆心在直线0kx y k --=上, 圆绕直线旋转一周所得的几何体是球, 由球的表面积公式求解即可.【解答】解:圆22(1)2x y -+=的圆心坐标为(1,0) 而直线0kx y k --=过定点(1,0),∴圆22(1)2x y -+=绕直线0kx y k --=的球,其表面积为24(2)8S ππ==. 故答案为:8π.【点评】本题考查了球的结构特征以及球表面积公式的计算问题,是基础题.11.(2017秋•海淀区校级期中)用一张48cm cm ⨯的矩形硬纸卷成圆柱的侧面,则圆柱轴截面的面积为 32π2cm (接头忽略不计).【分析】以4为高卷起,则28r π=,82r π=;若以8为高卷起,则24R π=,42R π=,由此能求出轴截面面积.【解答】解:以4为高卷起,则28r π=,82r π∴=,∴轴截面面积为232cm π.若以8为高卷起,则24R π=, 42R π∴=,∴轴截面面积为232cm π.故答案为:232cm π.【点评】本题考查轴截面面积的求法,考查分类讨论的数学思想,属于中档题.12.(2017春•丰台区期中)已知圆柱底面半径是2,高是3,则圆柱的表面积是 20π .【分析】利用圆柱的表面积公式直接计算. 【解答】解:由题意,圆柱的底面积是228r ππ=, 侧面积4312ππ=⨯=,故圆柱的表面积81220S πππ=+=. 故答案为:20π.【点评】本题考查的知识点是旋转体,熟练掌握圆柱的表面积公式,是解答的关键.属于基础题.13.(2015秋•昌平区期末)已知一个圆柱的底面半径为2,体积为16π,则该圆柱的母线长为 4 ,表面积为 . 【分析】代入体积和表面积公式计算.【解答】解:由圆柱的体积公式2V r h π=得164h ππ=,∴圆柱的高4h =,∴圆柱的母线长4l h ==;圆柱的表面积22222222424S r rl πππππ=+=⨯+⨯⨯=. 故答案为4,24π.【点评】本题考查了圆柱的结构特征,圆柱的体积,表面积计算,属于基础题.14.(2016秋•昌平区月考)四边形ABCD 四顶点的坐标分别为(0,0)A ,(1,0)B ,(2,1)C ,(0,3)D ,将四边形绕y 轴旋转一周得到一几何体,则此几何体的表面积为 (721)π+ .【分析】过C 作y 轴的垂线交y 轴于E ,则三角形DCE 是直角三角形,四边形ABCE 是直角梯形,进而可得四边形ABCD 绕y 轴旋转一周所得几何体是一个圆锥和一个圆台的组合体,结合圆台和圆锥的表面积公式,可得答案.【解答】解:过C 作y 轴的垂线交y 轴于E ,则三角形DCE 是直角三角形,四边形ABCE 是直角梯形, 四边形ABCD 绕y 轴旋转一周所得几何体是一个圆锥和一个圆台的组合体,易求得1AB =,2BC ,2CD =,1AE =,2ED =,22DC =, 所得旋转体的表面积是21(12)2222(721)S ππππ=+++=. 故答案为(721)π+.【点评】本题考查的知识点是旋转体,熟练掌握圆台和圆锥表面积公式是解答的关键. 三.解答题(共1小题)15.(2015秋•海淀区校级期中)如图,AB 是圆O 的直径,点C 是半圆的中点,PA ⊥平面ABC ,PA AB =,6PB D=是PB 的中点,E 是PC 上一点. (Ⅰ) 若DE PB ⊥,求PEEC的值; (Ⅱ)若点Q 是平面ABC 内一点,且||2||QA QC =,求点Q 在ABC ∆内的轨迹长度.【分析】(1)由PA ⊥平面ABC 可得PA BC ⊥,又BC AC ⊥,故而BC ⊥平面PAC ,于是BC PC ⊥,又DE PB ⊥故~PDE PCB ∆∆,利用勾股定理和相似比求出PE ,CE 得出比值;(2)在平面ABC 上建立平面直角坐标系,求出Q 点的轨迹为圆,利用弧长公式计算点Q 在ABC ∆内的轨迹长度. 【解答】解:()I AB 为直径,AC BC ∴⊥,PA ⊥平面ABC ,BC ⊂平面ABC ,PA BC ∴⊥,又AC PA A =,AC ⊂平面PAC ,PA ⊂平面PAC ,BC ∴⊥平面PAC ,PC ⊂平面PAC ,BC PC ∴⊥,6PB =,PA AB =,∴232PA AB ==,23AC BC ==, 222233PC PA AC PB AB +=-=132PD PB ==.在Rt PBC ∆中,DE PB ⊥,~PDE PCB ∴∆∆,∴PD PEPC PB=, ∴2333PB PD PE PC ===33233EC PC PE =-=, ∴2323PE EC ==. ()II 以点C 为坐标原点,OB 所在直线为x 轴,OA 所在直线为y 轴建立如图所示的面直角坐标系,则(0,3)A ,(0,0)C . 设动点Q 的坐标为(,)x y ,则22||(3)QA x y =+-22||QC x y +,∴2222(3)2x y x y +-+整理可得:22(1)4x y ++=,即Q 的轨迹是以(0,1)P -为圆心,以2为半径的圆,设Q 的轨迹与x 轴,y 轴的交点分别为M ,N ,则(3M ,0),(0,1)N . 连结PM ,PN ,则3sin MC MPN PM ∠==,3MPN π∴∠=. ∴点Q 在ABC ∆内的轨迹长度2233MN ππ=⨯=.【点评】本题考查了线面垂直的判定,轨迹方程,弧长公式,属于中档题.。
2020年广东省专插本考试《高等数学》真题+答案

广东省2020年普通高等学校本科插班生招生考试《高等数学》试题本试卷共2⻚,20⻚题,满分100分。
考试时间120一、单项选择题(本大题共5小题,每小题3分,共15分。
每小题只有一个符合题目要求)1.设lim x→0[cos x −f(x)]=1, 则下列等式正确的是( )A.lim x→0f(x)=1 B.lim x→0f(x)cos x =1C.lim x→0f(x)=−1 D.lim x→0[f(x)+cos x ]=12.函数f(x)=2x 3−3x 2的极小值点为( ) A.x =−1 B.x =0 C.x =1 D.x =23.已知3x 是函数f(x)的一个原函数,则f(x)=( ) A.3x B.3x ln 3 C.x3xD.3x ln 34.设平⻚区域D ={(x,y )|x 2+y 2≤1,y ≥0},则∬(x 2+y 2)4dσD( ) A.π10 B.π9 C.π5 D.2π95.设级数∑a n ∞n=1 满⻚0≤a n ≤15n ,则下列级数发散的是( )A.∑3a n ∞n=1B. ∑a n ∞n=1+3C.∑(a n ∞n=1+√n23) D.∑(a n ∞n=1−√n3) 二、填空题。
6.若函数f(x)={(1+a )x 2, x ≤1a (x −2)3+3, x >1 在x=1处连续,则常数a= . 7.曲线x 22+y 2=3在点(2,−1)处的切线方程为y= . 8.微分方程 y n +3y ’−4y =0的通解为y= .9.设二元函数f (x,y )在点(0,0)的某个邻域内有定义,且当x ≠0时,f(x,0)−f(0,0)x=3x +2,则f ’x (0,0)= 。
10.设函数f(x)在(−∞,+∞)内可导,且满足f(x)=f ‘(x),f(0)=m ,如果∫f(x)e xdx =81−1,则m=____________。
三、计算题。
11.求极限limx→0∫tarctantdtx0x 312.已知y 是x的函数,且y ′=ln √x +√ln x +2ln 2,求d 2y dx 2|x =e13.求不定积分∫(cos x −x sin x 2)dx14.设函数f(x)={x 31+x 2, x ≤1x, x >1,求定积分∫f(x +2)dx 0−315.求二元函数z =3xy 2+x 2y的全微分dz ,并求ð2zðxðy16.计算∬ydσD ,其中D 是由直线y =x,y =−2与y =0,y =2x 围成的有界闭区域。
高等数学考试题库(含答案解析)

范文范例参考《高数》试卷1(上)一.选择题(将答案代号填入括号内,每题 3 分,共 30 分).1.下列各组函数中,是相同的函数的是().(A )f x ln x2和 g x2ln x( B)(C )f x x 和g x2x(D )f x| x | 和g x x2f x| x |g x1和xsin x 4 2x02.函数f x ln 1x在 x 0 处连续,则a() .a x0(A )0( B)1(D)2(C)143.曲线y x ln x 的平行于直线 x y 1 0 的切线方程为() .(A )y x 1( B)y( x 1)(C )y ln x 1x 1(D)y x 4.设函数f x| x |,则函数在点x0 处() .(A )连续且可导( B)连续且可微( C )连续不可导( D)不连续不可微5.点x0 是函数y x4的().(A )驻点但非极值点(B)拐点(C)驻点且是拐点(D)驻点且是极值点6.曲线y1) .的渐近线情况是(| x |(A )只有水平渐近线( B)只有垂直渐近线( C )既有水平渐近线又有垂直渐近线(D )既无水平渐近线又无垂直渐近线7.f11). x x2dx 的结果是((A )1C1C1C (D) f1f( B)f( C )f C x x x x8.dxxe e x的结果是().(A )arctane xC()arctan exC(C)xexC(D)xex)CB e ln( e9.下列定积分为零的是() .(A )4arctanx dx(B)4x arcsin x dx (C) 1e x e x1x2x sin x dx 1x212dx (D)44110 .设f x为连续函数,则1f 2x dx 等于() . 0(A )f 2f0(B)1f 11 f 0 (C)1f 2 f 0 (D) f 1 f 0 22二.填空题(每题 4 分,共 20 分)f x e 2x1x0在 x 0处连续,则 a1.设函数x.a x02.已知曲线 y f x在 x 2 处的切线的倾斜角为5,则 f2. 6x3. y的垂直渐近线有条.x 2 14.dx. x 1ln2 x5.2x4 sin x cosx dx.2WORD 格式整理范文范例参考三.计算(每小题 5 分,共 30分)1.求极限12 xx sin x① lim x② limx x e x2x x 012.求曲线y ln x y 所确定的隐函数的导数y x.3.求不定积分①dx②dx a0③ xe x dxx1x 3x2a2四.应用题(每题10 分,共 20 分)1.作出函数y x33x2的图像.2.求曲线y22x 和直线 y x 4 所围图形的面积.WORD 格式整理范文范例参考《高数》试卷 1 参考答案一.选择题1.B 2.B 3.A 4.C 5.D 6.C 7. D 8.A 9.A 10. C二.填空题1. 22 .3 24. arctanln x c5.23.3三.计算题1① e 2② 12. y x16 xy 13. ① 1 ln |x 1| C ② ln | x 2a 2x | C③ e x x 1 C2x 3四.应用题1.略2.S 18《高数》试卷2(上)一. 选择题 ( 将答案代号填入括号内 ,每题 3 分,共 30 分 )1.下列各组函数中 ,是相同函数的是 ().(A)f xx 和 g xx 2(B)f xx 2 1 和 y x 1x 1(C)f xx 和 g xx(sin 2 x cos 2 x)(D)f xln x 2 和 g x2ln xsin 2 x 1x1 x12.设函数 fx2x 1,则 limf x().x 2x11x1(A) 0(B)1(C)2(D) 不存在3.设函数 y f x 在点 x 0 处可导,且 fx >0, 曲线则 yf x 在点 x 0 , f x 0处的切线的倾斜角为 {}.(A)0 (B)2(C)锐角(D)钝角4.曲线 y ln x 上某点的切线平行于直线 y 2x 3 ,则该点坐标是 ().(A)2,ln1(B)2, ln1(C)1,ln 2(D)1 , ln 222225.函数y x2e x及图象在1,2 内是().(A) 单调减少且是凸的(B)单调增加且是凸的(C) 单调减少且是凹的(D) 单调增加且是凹的6.以下结论正确的是 ().(A)若 x0为函数y f x的驻点 ,则x0必为函数y f x的极值点 .(B)函数 y f x 导数不存在的点,一定不是函数 y f x的极值点 .(C)若函数 y f x在 x0处取得极值,且f x0存在,则必有 f x0=0.(D)若函数 y f x在 x0处连续,则f x0一定存在 .WORD 格式整理范文范例参考17.设函数 y f x的一个原函数为x2e x,则f x=().1111(A) 2 x 1 e x(B)2x e x(C)2x 1 e x(D)2xe x8.若 f x dx F x c ,则 sin xf cosx dx().(A) F sin x c(B)F sin x c(C)F cos x c(D)F cos x c9.设 F x1f xdx =().为连续函数 , 则2(A) f1f0(B) 2f1f0(C)2 f 2f0 (D) 2 f1f0210. 定积分ba b 在几何上的表示(). dxa(A) 线段长b a(B)线段长 a b (C)矩形面积a b 1 (D)矩形面积b a1二.填空题 (每题 4 分,共 20 分)ln1x2x 0, 在x01.设 f x1cos x连续 ,则a =________.a x02.设 y sin 2x ,则 dy_________________ d sin x .3.函数 yx1的水平和垂直渐近线共有_______条 . x214.不定积分x ln xdx______________________.5.定积分1x2 sin x1___________. 11x2dx三.计算题 (每小题 5 分,共 30分 )1.求下列极限 :① lim12x 1② lim2arctanxx1x 0xx2.求由方程 y1xe y所确定的隐函数的导数y x.3.求下列不定积分 :① tan x sec3xdx②dx a0③x2e x dxx2a2四.应用题 (每题 10 分,共 20 分)1.作出函数 y1x3x 的图象.(要求列出表格)32.计算由两条抛物线:y2x, y x2所围成的图形的面积.WORD 格式整理范文范例参考《高数》试卷 2 参考答案一.选择题: CDCDB CADDD二填空题: 1. -2 2. 2sin x 3.3 4.1x2 ln x1x2c 5.242三. 计算题: 1.2②1 2.y e y① ex y23.① sec3 x c② ln x2a2x c③ x22x 2 e x c3四.应用题: 1.略 2.S 13《高数》试卷3(上)一、填空题 (每小题 3分,共 24分)1.函数 y1的定义域为 ________________________.9x22.设函数 f x sin 4x , x0则当 a =_________时, f x 在 x0处连续 .x,a,x03.函数 f (x)x2x21的无穷型间断点为 ________________. 3x24.设 f ( x) 可导,y f (e x ) ,则 y____________.5.limx21_________________. 2x2x5x6.1x3 sin 2 x dx =______________.1 x4x217.d x2e t dt_______________________.dx 08.y y y30 是_______阶微分方程.二、求下列极限 ( 每小题 5 分,共15分)xx 1x311.lim e;2.lim;3.lim12.x 0sin x x 3x9x2x 三、求下列导数或微分 (每小题 5分, 共15分)1.yx x,求 y (0) . 2.y e cos x ,求 dy . 2求dy.3.设 xy e x y ,dx四、求下列积分(每小题 5分, 共15分)1.12sin x dx . 2.x ln(1x)dx . x3.1e2x dx五、 (8 分 )求曲线xtcost在 t处的切线与法线方程 . y12WORD 格式整理范文范例参考六、 (8 分 )求由曲线 yx 21, 直线 y 0, x 0 和 x 1所围成的平面图形的面积 , 以及此图形绕 y 轴旋转所得旋转体的体积 .七、 (8 分 )求微分方程 y 6 y13 y 0 的通解 .八、 (7 分 )求微分方程 yy e x 满足初始条件 y 10的特解.x《高数》试卷 3 参考答案一. 1. x 32. a 43. x 24. e x f '(e x )5.16.07. 2 xe x 28. 二阶2二 .1.原式 = lim x1x 0x2. lim11 x 3 x3 63.原式 = lim[(11 11)2 x ] 2 e 2x2x三 .1.2.y'212)2, y '(0)(x2dysin xe cos x dx3.两边对 x 求写: yxy ' e x y (1 y ')e x yyxy yy 'e x yx xyx四.1.原式 = lim x2cos x Cx2212.原式 = lim(1)xx)2x)]x)d (lim(1 2x d [lim(12x= x22lim(1 x)1 1 x dx x lim(1 x) 1 ( x 11 ) dx22 x 2 21 x=x22lim(1 x) 1 [ xx lim(1 x)]C22 23.原式 =11 2 x2 x 1 1 20 e d (2 x) 1 e 0( e 1)222五.dysin tdy t1 且 t2 , y 1dxdx2切线: y1 x,即 y x 122法线: y1( x),即 y x 122六. S11 21320 ( x1)dx ( xx) 022V11)2dx12x21)dx(x2( x4( x 52 x 2 x) 10 285 315七.特征方程 : r 2 6r 13 0r 3 2iye 3 x (C 1 cos2 x C 2 sin 2 x)11dxxdx八. y e xdx C )( e e x1 xC ][ (x 1e)x由 y x 1 0,C0y x 1 e xx《高数》试卷4(上)WORD 格式整理范文范例参考一、选择题(每小题 3 分)1、函数 y ln(1 x) x 2 的定义域是() . A2,1B2,1C 2,1D2,12、极限 lim e x的值是() .xA 、B 、C 、D 、 不存在3、 limsin(x 1) ( ) .x 1 1 x 2 1 1A 、 1B 、 0C 、2D 、24、曲线 y x 3x 2 在点 (1,0) 处的切线方程是()A 、 y2( x1)B 、 y 4( x 1)C 、 y 4x 1D 、 y 3( x 1)5、下列各微分式正确的是( ) .A 、 xdx d (x 2 )B 、 cos 2xdx d(sin 2x)C 、 dx d (5 x)D 、 d (x 2 ) (dx) 26、设f (x)dx2 cosxC ,则f ( x) () .2A 、 sin xB 、22 ln x ) .7、dx (xxxxsinC 、 sinC D 、 2 sin222A 、2 1ln 2x CB 、 1( 2 ln x) 2Cx 2 22C 、 ln 2 ln xC1 ln xCD 、x 28、曲线 y x 2 , x 1 , y0 所围成的图形绕y 轴旋转所得旋转体体积 V() .1 x 4dx1ydyA 、B 、1(1y) dy1(1 x 4)dxC 、D 、1e xdx9、e x() .11 e2 e1 e1 2eA 、 ln2B 、 lnC 、 lnD 、 ln23210 、微分方程 yy y2e 2 x 的一个特解为() .A 、 y3 e 2x B 、 y3 e x C 、 y2 xe 2 x D 、 y2 e 2 x7777二、填空题(每小题4 分)1、设函数 y xe x ,则 y;2 、如果 lim3sin mx2 , 则 m .x 0 2x313cos xdx3、 x;14、微分方程 y 4 y 4 y0 的通解是.5、函数 f ( x) x 2 x在区间0,4上的最大值是,最小值是;三、计算题(每小题 5 分)1、求极限lim 1 x 1 x ; 2 、求y 1cot 2 x ln sin x 的导数;x 0x2 WORD 格式整理范文范例参考x314 、求不定积分dx;3、求函数y的微分;xx3111eln x dx ;dy x5、求定积分6、解方程1;e dx y 1 x2四、应用题(每小题10 分)1、求抛物线y x 2与y 2 x 2所围成的平面图形的面积.2、利用导数作出函数y 3x2x3的图象.参考答案一、 1、C;2、D;3、C ;4、B;5、C ;6、B;7、B;8、A ;9、A ;10、D;二、 1、(x2)e x; 2 、4;3、0; 4 、y(C1 C 2 x)e 2 x;5、8,0 9三、1、 1 ; 2 、cot 3 x ; 3 、 6 x2dx ; 4 、2 x 1 2 ln(1x 1) C ;5、2(21) ;6、y2 2 1 x2 C ;( x31) 2e四、1、8;32、图略《高数》试卷5(上)一、选择题(每小题 3 分)1、函数 y2x1的定义域是() . lg( x 1)A 、2,10,B、1,0( 0,)C 、(1,0)(0,)D、( 1,)2、下列各式中,极限存在的是() .A 、x B、lim arctan x C 、lim sin x D 、lim 2x l i mc o sx0x x x3、 lim (x) x() .x 1 xA 、e B、e2 C 、1 D 、1e4、曲线 y x ln x 的平行于直线x y 1 0 的切线方程是() .A 、y x B、y(ln x1)( x1)C 、y x1D、y(x1)5、已知 y xsin 3x,则 dy() .A 、( cos3x3sin 3x)dx B、(sin 3x3x cos3x)dxC 、(cos 3x sin 3x)dxD 、(sin 3x x cos3x)dx6、下列等式成立的是() .WORD 格式整理范文范例参考A 、x dx1x 1 CB 、 a x dx a x ln x C11C 、cosxdxsin x CD 、 tan xdxCx 217、计算e sin x sin xcos xdx 的结果中正确的是() .A 、 e sin x CB 、 e sin x cos x CC 、 e sin x sin x CD 、 e sin x (sin x 1) C8、曲线 yx 2 , x1 , y0 所围成的图形绕 x 轴旋转所得旋转体体积 V().1x 4dx1A 、B 、ydy1 (1 y) dy1 (1 x 4)dxC 、D 、a a 2x 2dx () . 9、设 a ﹥ 0 ,则A 、 a2B 、 a2C 、 1a2D 、 1a 224410 、方程()是一阶线性微分方程 .A 、 x 2ylnyB 、 y e x y 0xC 、 (1x 2 ) yy sin yD 、 xy dx ( y 2 6x)dy 0二、填空题(每小题 4 分)1、设 f ( x)e x 1, x, lim f ( x);,则有 lim f (x)ax b, xx 0 x 02、设 y xe x ,则 y;3、函数 f ( x)ln(1x 2 ) 在区间1,2 的最大值是,最小值是;14、 x 3cos xdx;15、微分方程y 3 y 2 y 0 的通解是.三、计算题(每小题 5 分)1、求极限 lim (11 x23 ) ; x 1x x 22、求y1 x2 arccosx 的导数;3、求函数 yx 的微分;1 x 24、求不定积分1dx ;x 2ln x5、求定积分eln x dx ;1e6、求方程x2y xy y 满足初始条件y( 1 ) 4 的特解.2WORD 格式整理范文范例参考四、应用题(每小题10 分)1、求由曲线y 2 x2和直线x y 0 所围成的平面图形的面积.2、利用导数作出函数y x 36x 29x 4的图象.参考答案( B 卷)一、 1、B;2、A;3、D;4、C ;5、B;6、C ;7、 D;8、 A;9、D;10、B.二、 1、 2 , b ; 2 、( x2)e x; 3 、ln 5 , 0 ;4、 0 ;5、C1e x C 2 e2x.三、1、1; 2 、arccos1; 3 、1dx;x x3 1 x2(1 x2 ) 1 x 24、2 2 ln x C ;1);2215、2(2 6 、y e x;e x四、 1、92、图略;2WORD 格式整理。
新高考新试卷结构立体几何与旋转体有关的题型

新高考新试卷结构立体几何与旋转体有关的题型考点一:求直线和平面所成的角如图,设直线l 的方向向量为e ,平面α的法向量为n ,直线与平面所成的角为φ,e 与n 的角为θ,则有sin ϕ=|cos θ|=|e ⋅n ||e |⋅|n |.(易错点)考点二:求二面角如图,若PA ⊥α于A ,PB ⊥β于B ,平面PAB 交l 于E ,则∠AEB 为二面角α-l -β的平面角,∠AEB +∠APB =180°.若n 1 ,n 2 分别为面α,β的法向量,cos n 1 ,n 2 =n 1 ⋅n 2n 1 ⋅n 2,则二面角的平面角∠AEB =n 1 ,n 2 或π-n 1 ,n 2,即二面角θ等于它的两个面的法向量的夹角或夹角的补角.①当法向量n 1 与n 2 的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于n 1 ,n 2 的夹角n 1 ,n 2的大小.②当法向量n 1 ,n 2 的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于n 1 ,n 2 的夹角的补角π-n 1 ,n 2的大小.③已知n 1 和n 2分别是二面角α−l −β的半平面α,β的法向量,记二面角的大小为θ,若P ∈半平面α,Q ∈半平面β(P ∉l ,Q ∉l ),则当PQ ⋅n 1 与PQ ⋅n 2 同号时,二面角θ的大小等于n 1 ,n 2 的夹角n 1 ,n 2的大小.当PQ ⋅n 1 与PQ ⋅n 2 异号时,二面角θ的大小等于n 1 ,n 2 的夹角的补角π-n 1 ,n 2 的大小.【精选例题】1如图,四边形ABCD 是圆柱OQ 的轴截面,圆柱OQ 的侧面积为63π,点P 在圆柱OQ 的底面圆周上,且△OPB 是边长为3的等边三角形,点G 是DP 的中点.(1)求证:AG ⊥平面PBD ;(2)求二面角A -PG -O 的正弦值.【答案】(1)证明见解析;(2)105【详解】(1)∵点P 在圆柱OQ 的底面圆周上,∴AP ⊥BP ,∵四边形ABCD 是圆柱OQ 的轴截面,∴AD ⊥平面APB ,因PB ⊂平面APB ,∴AD ⊥PB ,∵AP ∩AD =A ,AP ,AD ⊂平面ADP ,∴PB ⊥平面ADP ,而AG ⊂平面ADP ,∴AG ⊥PB ①.∵△OPB 是边长为3的等边三角形,∠APB =90°,∴AP =PB tan ∠ABP =3tan60°=3.∵圆柱OQ 的侧面积为63π,即2π⋅OB ⋅AD =23π⋅AD =63π,则AD =3=AP ,又点G 是DP 的中点,∴AG ⊥PD ②.又PD ∩PB =P ,PD ,PB ⊂平面PBD ,由①②可得AG ⊥平面PBD .(2) 以P 为坐标原点,以PB ,PA 及过点P 与AD 平行的直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系.则A 0,3,0 ,O 32,32,0 ,D 0,3,3 ,G 0,32,32 ∴PO =32,32,0 ,PG =0,32,32.设平面OPG 的法向量为n =x ,y ,z ,则PO ⋅n =32x +32y =0PG ⋅n =32y +32z =0,令z =1,得x =3,y =-1,∴n=3,-1,1 .由(1)知,PB ⊥平面ADP ,故PB =3,0,0 是平面APG 的一个法向量.由图知二面角A -PG -O 为锐角,设为α,则cos α=cos PB ,n =PB ⋅nPB ⋅ n=33×5=155,∴sin α=105,即二面角A -PG -O 的正弦值为105.2如右图,已知Rt △ABC 的直角边AB =6,BC =4,点F 1,F 2是BC 从左到右的四等分点(非中点).已知椭圆Γ所在的平面⊥平面ABC ,且其左右顶点为B ,C ,左右焦点为F 1,F 2,点P 在Γ上.(1)求三棱锥A -F 1F 2P 体积的最大值;(2)证明:二面角F 1-AP -F 2不小于60°.取BC 中点O ,在AC 上取一点Q 使得OQ ⊥BC ,【详解】以O 为坐标原点,OC 为x 正方向,BC 的中垂线l 的方向向量u 为y 轴正方向,OQ为z 轴正方向,建立空间直角坐标系Oxyz .(1)设点P x 0,y 0 .椭圆Γ的方程为x 2a 2+y 2b2=1a >b >0 .由题意,易知OB=OC =12BC =2,OF 1=OF 2=14BC =1,则a =OC =2,c =OF 1=a 2-b 2=1,解得b =3,所以Γ:x 24+y 23=1.V A -F 1F 2P =13·h ·S △F 1F 2P =S △F 1F 2P =12·F 1F 2 ·y 0 =y 0 ≤b =3故三棱锥A -F 1F 2P 体积的最大值是3.(2)易知A -2,0,3 ,F 10,-1,0 ,F 20,1,0 ,设P 3cos θ,2sin θ,0 cos θ≠0 ,则AF 1 =0,1,-3 ,F 1P =3cos θ,2sin θ+1,0 ,设平面APF 1的一个法向量n 1=x ,y ,z ,则n 1·AF 1=y -3z =0n 1·F 1P =3x cos θ+2sin θ+1 y =0 令y =3cos θ,则x =-32sin θ+1 ,z =cos θ,所以平面APF 1的一个法向量n 1=-32sin θ+1 ,3cos θ,cos θ ,同理可求得平面APF 2的一个法向量n 2=-2sin θ-1 ,3cos θ,cos θ ,令t =sin θ+1,则(化简后得)cos <n 1,n 2>=n 1·n 2n 1 ·n 2=33-4t 4-16t 3+12t 2+73t +27(I )当t ∈0,54 时,则83-32t 23>0,所以-4t 4-16t 3+12t 2+73t +27<-4t 4-803t 3+12t 2+72t +1643,令f t =-4t 4-803t 3+12t 2+72t +1643,f t =-8t -1 2t 2+6t +9 ,因为t ∈0,54,所以2t 2+6t +9>0,令f t =0得t =1,当t ∈0,1 时,f t >0,f t 单调递增;当t ∈1,54时,ft <0,f t 单调递减.(II )当t ∈54,2 时,令g t =-4t 4-16t 3+12t 2+73t +27,g t =-16t 3-48t 2+24t +72,g t =24-2t 2-4t +1 <0,所以g t 单调递减,所以g t <g 54<0,即g t 单调递减,g t <g 54 =606364<108,综上,-4t 4-16t 3+12t 2+73t +27<108对t ∈0,2 成立,即cos <n 1,n 2>>33108=12,即<n 1,n 2>>π3,故二面角F 1-AP -F 2不小于60°得证.3如图所示,圆台的上、下底面圆半径分别为4cm 和6cm ,AA 1,BB 1为圆台的两条不同的母线.(1)求证:A 1B 1⎳AB ;(2)截面ABB 1A 1与下底面所成的夹角大小为60°,且截面截得圆台上底面圆的劣弧A 1B 1的长度为8π3,求截面ABB 1A 1的面积.【答案】(1)证明见解析;(2)103cm 2【详解】(1)因为圆台可以看做是由平行于圆锥底面的平面去截圆锥而得到,所以圆台的母线也就是生成这个圆台的圆锥相应母线的一部分.可知母线AA 1与母线BB 1的延长线必交于一点,即A ,A 1,B ,B 1四点共面,又因为圆面O 1∥圆面O ,且平面ABB 1A 1∩圆面O 1=A 1B 1,平面ABB 1A 1∩圆面O =AB ,所以A 1B 1∥AB .(2)解法一:因为劣弧A 1B 1的长度为8π3,则∠A 1O 1B 1=23π,由△A 1O 1B 1∽△AOB ,可得∠AOB =23π.如图,建立空间直角坐标系O -xyz ,设OO 1 =t (t >0),则A 6,0,0 ,B -3,33,0 ,A 14,0,t ,可得AA 1 =-2,0,t ,AB =-9,33,0 ,设平面ABB 1A 1的一个法向量为n 1=x ,y ,z ,则n ⋅AA 1=-2x +tz =0n ⋅AB=-9x +33y =0,令x =1,则y =3,z =2t ,可得n 1=1,3,2t,由题意可知:底面的一个法向量n 2=0,0,t ,因为截面与下底面所成的夹角大小为60°,则cos60°=cos n 1,n 2 =n 1⋅n 2 n 1 ⋅n 2 =2t ⋅1+3+4t2=1t 2+1=12,解得t =3,即OO 1 =3,可得BB 1=7,在等腰梯形ABB 1A 1中,A 1B 1=43,AB =63,可得等腰梯形ABB 1A 1的高h =2,所以S 梯形ABB 1A 1=1243+63 ⋅2=103cm 2.解法二:如图,分别取AB ,A 1B 1的中点为C ,C 1,连结O 1C 1,CC 1,OC ,由题意可得:OC ⊥AB ,CC 1⊥AB ,所以∠OCC 1为截面ABB 1A 1与底面所成夹角,即∠OCC 1=60°,过点C 1作C 1D ⊥OC 于点D ,由O 1C 1=2,OC =3,得CD =1,则CC 1 =2(即梯形的高),所以S 梯形ABB 1A 1=1243+63 ⋅2=103cm 2.4已知椭圆C :x 2a 2+y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,离心率为12,经过点F 1且倾斜角为θ0<θ<π2的直线l 与椭圆交于A 、B 两点(其中点A 在x 轴上方),△ABF 2的周长为8.(1)求椭圆C 的标准方程;(2)如图,将平面xOy 沿x 轴折叠,使y 轴正半轴和x 轴所确定的半平面(平面AF 1F 2)与y 轴负半轴和x 轴所确定的半平面(平面BF 1F 2)互相垂直.①若θ=π3,求三棱锥A -BF 1F 2的体积,②若θ=π3,异面直线AF 1和BF 2所成角的余弦值;③是否存在θ0<θ<π2 ,使得△ABF 2折叠后的周长为与折叠前的周长之比为1516?若存在,求tan θ的值;若不存在,请说明理由.【答案】(1)x 24+y 23=1;(2)①35;②1328;③存在,tan θ=33514【详解】(1)由椭圆的定义知:AF 1 +AF 2 =2a ,BF 1 +BF 2 =2a ,所以△ABF 2的周长L =4a =8,所以a =2,又椭圆离心率为12,所以c a =12,所以c =1,b 2=a 2-c 2=3,由题意,椭圆的焦点在x 轴上,所以椭圆的标准方程为x 24+y 23=1;(2)①由直线l :y -0=3x +1 与x 24+y 23=1,由y -0=3(x +1)x 24+y 23=1 得x =0,y =3 或x =-85y =-353,所以A 0,3 (因为点A 在x 轴上方)以及B -85,-353 ,AF 1 =2,BF 1 =65,V =13⋅12BF 1‖F 1F 2 sin120°AF 1 sin60°=35②O 为坐标原点,折叠后原y 轴负半轴,原x 轴,原y 轴正半轴所在直线为x ,y ,z 轴建立空间直角坐标系,则F 10,-1,0 ,A 0,0,3 ,B 353,-85,0 ,F 20,1,0 ,F 1A =0,1,3 ,BF 2 =-353,135,0 .记异面直线AF 1和BF 2所成角为φ,则cos φ=cos F 1A ,BF 2 =F 1A ⋅BF2 F 1A BF 2 =1328;③设折叠前A x 1,y 1 ,B x 2,y 2 ,折叠后A ,B 在新图形中对应点记为A ,B ,A x 1,y 1,0 ,B x 2,0,-y 2 ,折叠前△ABF 2周长是8,则折叠后△A B F 2周长是152,由A 'F 2 +B 'F 2 +A 'B ' =152,AF 2 +BF 2 +AB =8,故AB -A 'B ' =12,设l 方程为my =x +1,由my =x +1x 24+y 23=1,得3m 2+4 y 2-6my -9=0,y 1+y 2=6m 3m 2+4,y 1y 2=-93m 2+4,在折叠后的图形中建立如图所示的空间直角坐标系(原x 轴仍然为x 轴,原y 轴正半轴为y 轴,原y 轴负半轴为z 轴);A 'B ' =x 1-x 22+y 12+y 22,AB =x 1-x 22+y 1-y 2 2,所以AB -A 'B ' =x 1-x 22+y 1-y 2 2-x 1-x 2 2+y 21+y 22=12,(ⅰ)又-2y 1y 2x 1-x 22+y 1-y 2 2+x 1-x 2 2+y 21+y 22=12,所以x 1-x 12+y 1-y 2 2+x 1-x 22+y 21+y 21=-4y 1y 2,(ⅱ)由(ⅰ)(ⅱ)可得x 1-x 22+y 1-y 2 2=14-2y 1y 2,因为x 1-x 2 2+y 1-y 2 2=1+m 2 y 1-y 2 2=14-2y 1y 22,所以1+m 2 6m 3m 2+42+363m 2+4=14+183m 2+42,即1441+m3m 2+42=14+183m 2+42,所以12+12m 23m 2+4=14+183m 2+4,解得m 2=2845,因为0<θ<π2,所以tan θ=1m =33514.5如图,在圆锥SO 中,AB 是圆O 的直径,且△SAB 是边长为4的等边三角形,C ,D 为圆弧AB 的两个三等分点,E 是SB 的中点.(1)证明:DE ⎳平面SAC ;(2)求平面SAC 与平面SBD 所成锐二面角的余弦值.【答案】(1)证明见解析;(2)15【详解】(1)证明:取SA 的中点F ,连接CF ,EF ,CD .因为C ,D 为圆弧AB 的两个三等分点,所以CD ⎳AB ,CD =12AB .因为E ,F 分别为SB ,SA 的中点,所以EF ⎳AB ,EF =12AB ,则CD ⎳EF ,EF =CD ,从而四边形CDEF 为平行四边形,故DE ⎳CF .因为DE ⊄平面SAC ,CF ⊂平面SAC ,所以DE ⎳平面SAC .(2)解:以O 为坐标原点,OB ,OS的方向分别为y ,z 轴的正方向,建立如图所示的空间直角坐标系.因为AB =SA =4,所以A 0,-2,0 ,B 0,2,0 ,C 3,-1,0 ,D 3,1,0 ,S 0,0,23 ,则AC =3,1,0 ,AS =0,2,23 ,BD=3,-1,0 ,BS =0,-2,23 .设平面SAC 的法向量为m=x 1,y 1,z 1 ,则m ⋅AC=3x 1+y 1=0,m ⋅AS=2y 1+23z 1=0,令x 1=1,得m=1,-3,1 .设平面SBD 的法向量为n=x 2,y 2,z 2 ,则n ⋅BD=3x 2-y 2=0,n ⋅BS =-2y 2+23z 2=0,令x 2=1,得n =1,3,1 .设平面SAC 与平面SBD 所成锐二面角为θ,则cos θ=|cos ‹m ,n ›|=|m ⋅n||m ||n |=15.故平面SAC 与平面SBD 所成锐二面角的余弦值为15.6如图,AB 是半球O 的直径,AB =4,M ,N 依次是底面AB上的两个三等分点,P 是半球面上一点,且∠PON =60°.(1)证明:PB ⊥PM ;(2)若点P 在底面圆上的射影为ON 中点,求直线PM 与平面PAB 所成的角的正弦值.【答案】(1)证明见解析;(2)105【详解】(1)连接AM ,OM ,MN ,PN ,因为M ,N 依次是底面AB上的两个三等分点,所以四边形OMNB 是菱形,设MB ∩ON =Q ,则Q 为ON 中点,且ON ⊥MB ,又因为OP =ON ,∠PON =60°,故△OPN 是等边三角形,连接PQ ,则ON ⊥PQ ,又因为MB ,PQ ⊂面PMB ,MB ∩PQ =Q ,所以ON ⊥面PMB ,因为PB ⊂面PMB ,所以ON ⊥PB ,因为M ,N 依次是底面AB上的两个三等分点,所以ON ⎳AM ,所以AM ⊥PB ,又因为AB 是半球O 的直径,P 是半球面上一点,所以PB ⊥PA ,因为AM ,PA ⊂面PAM ,AM ∩PA =A ,所以PB ⊥面PAM ,又因为PM ⊂面PAM ,所以PB ⊥PM (2)因为点P 在底面圆上的射影为ON 中点,所以PQ ⊥面AMB ,因为QM ,QN⊂面AMB ,所以PQ ⊥QM ,PQ ⊥QN ,又因为QM ⊥QN ,所以以QM ,QN ,QP 为正交基底建立如图所示的空间直角坐标系,所以P 0,0,3 ,M 3,0,0 ,B -3,0,0 ,A 3,-2,0 ,所以PM =3,0,-3 ,PA=3,-2,-3 ,BA =23,-2,0 ,设平面PAB 的法向量n=x ,y ,z ,则n ⋅PA=3x -2y -3z =0n ⋅BA=23x -2y =0,令x =1,则n =1,3,-1 ,设直线PM 与平面PAB 所成角为θ0≤θ≤π2 ,则sin θ=cos PM ,n =PM ⋅nPM ⋅n =236×5=105所以直线PM 与平面PAB 所成角的正弦值为105【跟踪训练】1如图所示,用平面BCC 1B 1表示圆柱的轴截面,BC 是圆柱底面的直径,O 为底面圆心,E 为母线CC 1的中点,已知AA 1为一条母线,且AB =AC =AA 1=4.(1)求证:平面AEO ⊥平面AB 1O ;(2)求平面AEB 1与平面OAE 夹角的余弦值.【答案】(1)证明见解析;(2)66.【详解】(1)依题意可知AB ⊥AC ,则△ABC 是等腰直角三角形,故AO ⊥BC ,由圆柱的特征可知BB 1⊥平面ABC ,又AO ⊂平面ABC ,BB 1⊥AO ,因为BB 1∩BC =B ,BB 1、BC ⊂平面BCC 1B 1,则AO ⊥平面BCC 1B 1,而B 1O ⊂平面BCC 1B 1,则AO ⊥B 1O ,因为AB =AC =AA 1=4,则BC =2AB =42,∴B 1O 2=B 1B 2+BO 2=24,OE 2=OC 2+CE 2=12,B 1E 2=E 1C 2+B 1C 21=36=B 1O 2+OE 2,所以B 1O ⊥OE ,因为B 1O ⊥OE ,AO ⊥B 1O ,AO ∩OE =O ,AO 、OE ⊂平面AEO ,所以B 1O ⊥平面AEO ,因为B 1O ⊂平面AB 1O ,所以平面AEO ⊥平面AB 1O ;(2)由题意及(1)知易知AA1,AB ,AC 两两垂直,如图所示建立空间直角坐标系,则B 14,0,4 ,E 0,4,2 ,O 2,2,0 ,所以AB 1 =4,0,4 ,AE =0,4,2 ,B 1O=-2,2,-4 ,由(1)知B 1O 是平面AEO 的一个法向量,设n=x ,y ,z 是平面AB 1E 的一个法向量,则有n ⋅AB 1=4x +4z =0n ⋅AE=4y +2z =0,取z =-2⇒x =2,y =1,所以n=2,1,-2 ,设平面AEB 1与平面OAE 的夹角为θ,所以cos θ=cos n ,B 1O =n ⋅B 1O n ⋅B 1O =6324=66.即平面AEB 1与平面OAE 夹角的余弦值为66.2如图,四边形ABCD 是圆柱OQ 的轴截面,圆柱OQ 的侧面积为63π,点P 在圆柱OQ 的底面圆周上,且△OPB 是边长为3的等边三角形,点G 是DP 的中点.(1)求证:AG ⊥平面PBD ;(2)求二面角A -PG -O 的正弦值.【答案】(1)证明见解析;(2)105【详解】(1)∵点P 在圆柱OQ 的底面圆周上,∴AP ⊥BP ,∵四边形ABCD 是圆柱OQ 的轴截面,∴AD ⊥平面APB ,因PB ⊂平面APB ,∴AD ⊥PB ,∵AP ∩AD =A ,AP ,AD ⊂平面ADP ,∴PB ⊥平面ADP ,而AG ⊂平面ADP ,∴AG ⊥PB ①.∵△OPB 是边长为3的等边三角形,∠APB =90°,∴AP =PB tan ∠ABP =3tan60°=3.∵圆柱OQ 的侧面积为63π,即2π⋅OB ⋅AD =23π⋅AD =63π,则AD =3=AP ,又点G 是DP 的中点,∴AG ⊥PD ②.又PD ∩PB =P ,PD ,PB ⊂平面PBD ,由①②可得AG ⊥平面PBD .(2)以P 为坐标原点,以PB ,PA 及过点P 与AD 平行的直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系.则A 0,3,0 ,O 32,32,0,D 0,3,3 ,G 0,32,32 ,∴PO =32,32,0 ,PG =0,32,32.设平面OPG 的法向量为n=x ,y ,z ,则PO ⋅n=32x +32y =0PG ⋅n =32y +32z =0,令z =1,得x =3,y =-1,∴n=3,-1,1 .由(1)知,PB ⊥平面ADP ,故PB=3,0,0 是平面APG 的一个法向量.由图知二面角A -PG -O 为锐角,设为α,则cos α=cos PB ,n =PB ⋅nPB ⋅ n =33×5=155,∴sin α=105,即二面角A -PG -O 的正弦值为105.3如图所示的几何体是由一个直三棱柱和半个圆柱拼接而成.其中,∠FAB =90°,AB =AF =2,点G 为弧CD 的中点,且C ,G ,D ,E 四点共面.(1)证明:D ,G ,B ,F 四点共面;(2)若平面BDF 与平面ABG 夹角的余弦值为216,求AD 长.【答案】(1)证明见解析;;(2)AD =5.【详解】(1)连接DG ,因为AB ⊥AF ,AF =AB ,所以直棱柱的底面为等腰直角三角形,∠DCE =45°,在半圆DGC 上,G 是弧CD 中点,所以∠GDC =45°,所以DG ⎳EC ,又EC ⎳FB ,所以DG ⎳FB ,所以B ,F ,D ,G 四点共面.(2)法1:直棱柱中AB ⊥AF ,以A 为原点,建立如图空间直角坐标系,设AD =h ,F 2,0,0 ,B 0,2,0 ,D 0,0,h ,则FD =-2,0,h ,BF=2,-2,0 ,设面BFD 的法向量为n =x ,y ,z ,则n ⋅FD=-2x +hz =0n ⋅BF=2x -2y =0,取z =2,所以n=h ,h ,2 ,A 0,0,0 ,B 0,2,0 ,G -1,1,h ,AB =0,2,0 ,AG=-1,1,h ,设面ABG 的法向量为m =r ,s ,t ,则m ⋅AB=2s =0m ⋅AG=-r +s +ht =0,取t =1,所以m=h ,0,1 ,平面BDF 与平面ABG 所成夹角,即n 与m 夹角或其补角,所以cos n ,m=h 2+22h 2+4h 2+1=216,解得h =5,所以AD =5法2:设AD =h ,由(1)知B ,F ,D ,G 四点共面,则面BDF ∩面ABG =BG .取BF 中点N ,连接AN ,DN ,则AN ⊥BF ,而AD ⊥面ABF ,BF ⊂面ABF ,故AD ⊥BF ,AN ∩AD =A ,AN ,AD ⊂面ADN ,则BF ⊥平面ADN ,过A 作AO ⊥DN 于O ,又BF ⊥AO ,DN ∩BF =N ,DN ,BF ⊂平面BDF ,所以AO ⊥平面BDF ,过O 作OM ⊥BG 于M ,连接AM ,则AM ⊥BG ,又∠AMO 是锐角.所以∠AMO 是平面BDF 与平面ABG 所成的夹角,则cos ∠AMO =216,所以在Rt △AOM 中,sin ∠AMO =156=AO AM ,在Rt △DAN 中,根据等面积法AO =AD ⋅AN DN =h ⋅2h 2+2,在△ABG 中,AG =BG =h 2+2,AB =2.所以AM =AB ⋅sin ∠ABG =AB ⋅BG 2-AB2 2BG=2h 2+2-1h 2+2.所以sin ∠AMO =156=2⋅h h 2+22⋅h 2+1h 2+2=h 2h 2+2,解得h 2=5,h >0,即h =5,所以AD = 5.4如图,矩形BCC 1B 1是圆柱OO 1的一个轴截面,O 1、O 分别为上下底面的圆心,E 为CO 1的中点,BC =8,BB 1=4.(1)当点A 为弧BC 的中点时,求证:AO ⊥平面BB 1C 1C ;(2)若点A 为弧BC 的靠近C 点的三等分点,求直线AE 与平面AOB 1所成角的正弦值.【答案】(1)证明见解析;(2)217.【详解】(1)结合题意:易知底面是以O 为圆心,以BC 为直径的半圆,因为点A 为弧BC 的中点,所以AO ⊥BC ,因为矩形BCC 1B 1是圆柱OO 1的一个轴截面,所以BB 1⊥面ABC ,因为OA ⊂面ABC ,所以BB 1⊥AO ,因为BB 1∩BC =B ,且BB 1,BC ⊂平面BB 1C 1C ,所以AO ⊥平面BB 1C 1C .(2)取弧BC 的中点A 1连接OA 1,由(1)问可知:A 1O ⊥平面BB 1C 1C ,且易得A 1O ⊥O 1O,O 1O ⊥BC ,A 1O ⊥BC ,故以O 坐标原点,以OC ,OA 1,OO 1所在的直线分别为x ,y ,z 轴建立空间直角坐标系如图所示:因为BC =8,BB 1=4,点A 为弧BC 的靠近C 点的三等分点,所以O 0,0,0 ,B 1-4,0,4 ,O 10,0,4 ,C 4,0,0 ,A 2,23,0 ,所以OB 1 =-4,0,4 ,OA =2,23,0 ,因为E 为CO 1的中点,所以E 2,0,2 ,所以AE=0,-23,2 ,设平面AOB 1的法向量为n=x ,y ,z ,则n ⊥OAn ⊥OB 1,即n ⋅OA=2x +23y =0n⋅OB 1 =-4x +4z =0,令x =3,则n=3,-1,3 ,所以直线AE 与平面AOB 1所成角的正弦值为sin θ=cos n,AE =n ⋅AE n AE=0×3+-23 ×-1 +2302+-23 2+22×3 2+1+32=217.5如图所示,圆台的上、下底面圆半径分别为2cm 和3cm ,AA 1,BB 1为圆台的两条不同的母线.O 1,O 分别为圆台的上、下底面圆的圆心,且△OAB 为等边三角形.(1)求证:A 1B 1⎳AB ;(2)截面ABB 1A 1与下底面所成的夹角大小为60°,求异面直线AA 1与B 1O 1所成角的余弦值.【答案】(1)证明见解析;(2)1313【详解】(1)证明∵圆台可以看做是由平行于圆锥底面的平面去截圆锥而得到,所以圆台的母线也就是生成这个圆台的圆锥相应母线的一部分.∴母线AA 1与母线BB 1的延长线必交于一点,∴A ,A 1,B ,B 1四点共面.∵圆面O 1⎳圆面O ,且平面ABB 1A 1∩圆面O 1=A 1B 1,平面ABB 1A 1∩圆面O =AB .∴A 1B 1⎳AB .(2)∵△ABO 为等边三角形,∴∠AOB =π3,如图建立空间直角坐标系O -xyz ,设OO 1 =t (t >0).A 3,0,0 ,B 32,332,0,A 12,0,t .AA 1 =-1,0,t ,AB =-32,332,0 ,设平面ABB 1A 1的一个法向量n 1=x ,y ,z .则有:-x +tz =0,-32x +332y =0. ,令x =3,则y =1,z =3t ,∴n 1=3,1,3t.底面的一个法向量n 2=0,0,1 ,因为截面与下底面所成的夹角大小为60°,所以cos60°=cos n 1,n2 =3t ⋅4+3t2=33+4t2=12,∴t =32,∴AA 1 =-1,0,32 ,又A 1B 1 =23AB =-1,3,0 ,∴B 1坐标为1,3,32.∴O 1B 1 =1,3,0 ,cos AA 1 ,O 1B 1 =AA 1 ⋅O 1B 1AA 1 O 1B 1 =-1132⋅2=-1313.∴异面直线AA 1与O 1B 1所成角的余弦是1313.6如图,线段AA 1是圆柱OO 1的母线,BC 是圆柱下底面圆O 的直径.(1)弦AB 上是否存在点D ,使得Q 1D ⎳平面A 1AC ,请说明理由;(2)若BC =2,∠ABC =30°,A 1A =2,求二面角C -A 1B -A 的余弦值.【答案】(1)存在,当点D 为AB 中点时,理由见解析.(2)25719【详解】(1)当点D 为AB 的中点时,O 1D ⎳平面A 1AC ,证明如下:取AB 的中点D ,连接OD ,∵O ,D 分别为BC ,AB 的中点,则OD ⎳AC ,又OD ⊄平面A 1AC ,AC ⊂平面A 1AC ,∴OD ⎳平面A 1AC ,又∵OO 1⎳AA 1,OO 1⊄平面A 1AC ,AA 1⊂平面A 1AC ,∴OO 1⎳平面A 1AC ,O 1O ∩OD =O ,O 1O ,OD ⊂平面OO 1D ,∴平面OO 1D ⎳平面A 1AC ,由于O 1D ⊂平面OO 1D ,故O 1D ⎳平面A 1AC ;(2)∵BC 是⊙O 的直径,可得∠BAC =90°,即AB ⊥AC ,且BC =2,∠ABC =30°,故AB =3,AC =1,如图,以点A 为原点建立空间直角坐标系,则A 0,0,0 ,B 3,0,0 ,C 0,1,0 ,A 10,0,2 ,得A 1B=3,0,-2 ,A 1C =0,1,-2 ,设n=x ,y ,z 为平面A 1BC 的一个法向量,则n ⋅A 1B=3x -2z =0n ⋅A 1C=y -2z =0,令x =2,则y =23,z =3,可得n=2,23,3 ,因为y 轴⊥平面A 1AB ,则可取平面A 1AB 的一个法向量为m =0,1,0 ,设二面角C -A 1B -A 为θ,则cos θ=cos m ,n =m ⋅nm n=231×19=25719,所以二面角C-A 1B -A 的余弦值为25719.7如图,圆台O 1O 2的轴截面为等腰梯形A 1ACC 1,AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点(1)若P 是线段BC 的中点,求证:C 1P ⎳平面A 1AB(2)若AB =BC ,设直线l 为平面A 1AB 与平面C 1CB 的交线,点Q ∈l ,BC 1与平面QAC 所成角为α,求sin α的最大值.【答案】(1)证明见解析;(2)144【详解】(1)取AB 中点H ,连接A 1H ,PH ,如图,因为P 为BC 中点,所以PH ⎳AC ,PH =12AC ,在等腰梯形A 1ACC 1中,A 1C 1⎳AC ,A 1C 1=12AC ,所以HP ⎳A 1C 1,HP =A 1C 1,所以四边形A 1C 1PH 为平行四边形,所以C 1P ⎳A 1H ,又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB ,所以C 1P ⎳平面A 1AB ;(2)延长AA 1,CC 1交于点O ,作直线BO ,则直线BO 即为直线l ,∵AB =BC ,则O 2B ⊥AC ,以直线O 2A ,O 2B ,O 2O 分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,在等腰梯形A 1ACC 1中,AC =2AA 1=2A 1C 1=4,此梯形的高为h =AA 21-AC -A 1C 122=3,因为A 1C 1=12AC ,A 1C 1⎳AC ,所以A 1C 1为△OAC 的中位线,则O 20,0,0 ,O 0,0,23 ,A 2,0,0 ,B 0,2,0 ,C 1-1,0,3 ,所以BC 1 =-1,-2,3 ,AB =-2,2,0 ,BO =0,-2,23 ,O 2A =2,0,0 ,设BQ =λBO ,则AQ =AB +BQ =AB +λBO=-2,2-2λ,23λ ,设平面QAC的一个法向量为n=x ,y ,z ,则n ⋅O 2A=2x =0n ⋅AQ=-2x +2-2λ y +23λz =0,令y =3λ,得n =0,3λ,λ-1 ,则有:sin α=cos n,BC 1 =n ⋅BC 1 n BC 1=-2×3λ+3λ-1 3λ 2+λ-1 2×-1 2+-2 2+3 2=3λ+1 22×4λ2-2λ+1,令t =λ+1,则sin α=3t22×4t 2-10t +7,当t =0时,sin α=0,此时λ=-1,当t ≠0时,0<sin α=322×7t 2-10t+4=322×71t -57 2+37≤144,当且仅当t =75,即λ=25时取等号,综上所述,sin α的最大值为144.。
高等数学考试题库(附答案解析)

《高数》试卷1(上)一.选择题(将答案代号填入括号内,每题3分,共30分).1.下列各组函数中,是相同的函数的是( ).(A )()()2ln 2ln f x x g x x == 和 (B )()||f x x = 和 ()g x =(C )()f x x = 和 ()2g x =(D )()||x f x x=和 ()g x =1 2.函数()00x f x a x ≠=⎨⎪=⎩ 在0x =处连续,则a =( ).(A )0 (B )14(C )1 (D )23.曲线ln y x x =的平行于直线10x y -+=的切线方程为( ).(A )1y x =- (B )(1)y x =-+ (C )()()ln 11y x x =-- (D )y x = 4.设函数()||f x x =,则函数在点0x =处( ).(A )连续且可导 (B )连续且可微 (C )连续不可导 (D )不连续不可微5.点0x =是函数4y x =的( ).(A )驻点但非极值点 (B )拐点 (C )驻点且是拐点 (D )驻点且是极值点6.曲线1||y x =的渐近线情况是( ). (A )只有水平渐近线 (B )只有垂直渐近线 (C )既有水平渐近线又有垂直渐近线 (D )既无水平渐近线又无垂直渐近线 7.211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是( ). (A )1f C x ⎛⎫-+ ⎪⎝⎭(B )1f C x ⎛⎫--+ ⎪⎝⎭(C )1f C x ⎛⎫+ ⎪⎝⎭(D )1f C x ⎛⎫-+ ⎪⎝⎭8.x x dxe e -+⎰的结果是( ).(A )arctan xe C + (B )arctan xe C -+ (C )x x e e C --+ (D )ln()x x e e C -++9.下列定积分为零的是( ).(A )424arctan 1x dx x ππ-+⎰ (B )44arcsin x x dx ππ-⎰ (C )112x xe e dx --+⎰ (D )()121sin x x x dx -+⎰ 10.设()f x 为连续函数,则()12f x dx '⎰等于( ).(A )()()20f f - (B )()()11102f f -⎡⎤⎣⎦(C )()()1202f f -⎡⎤⎣⎦(D )()()10f f -二.填空题(每题4分,共20分)1.设函数()2100x e x f x x a x -⎧-≠⎪=⎨⎪=⎩在0x =处连续,则a =.2.已知曲线()y f x =在2x =处的切线的倾斜角为56π,则()2f '=.3.21xy x =-的垂直渐近线有条. 4.()21ln dxx x =+⎰.5.()422sin cos xx x dx ππ-+=⎰.三.计算(每小题5分,共30分) 1.求极限①21lim xx x x →∞+⎛⎫⎪⎝⎭ ②()20sin 1lim xx x x x e →-- 2.求曲线()ln y x y =+所确定的隐函数的导数x y '. 3.求不定积分 ①()()13dxx x ++⎰ ②()220dx a x a >-⎰ ③x xe dx -⎰四.应用题(每题10分,共20分) 1. 作出函数323y x x =-的图像.2.求曲线22y x =和直线4y x =-所围图形的面积.《高数》试卷1参考答案一.选择题1.B 2.B 3.A 4.C 5.D 6.C 7.D 8.A 9.A 10.C 二.填空题 1.2- 2.- 3. 2 4.arctanln x c + 5.2 三.计算题 1①2e ②162.11xy x y '=+- 3. ①11ln ||23x C x +++②ln ||x C + ③()1x e x C --++四.应用题1.略 2.18S =《高数》试卷2(上)一.选择题(将答案代号填入括号内,每题3分,共30分) 1.下列各组函数中,是相同函数的是( ).(A) ()f x x =和()g x = (B) ()211x f x x -=-和1y x =+(C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =2.设函数()()2sin 21112111x x x f x x x x -⎧<⎪-⎪⎪==⎨⎪->⎪⎪⎩,则()1lim x f x →=( ). (A) 0 (B) 1 (C) 2 (D) 不存在3.设函数()y f x =在点0x 处可导,且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为{ }.(A) 0 (B)2π(C) 锐角 (D) 钝角 4.曲线ln y x =上某点的切线平行于直线23y x =-,则该点坐标是( ). (A) 12,ln2⎛⎫ ⎪⎝⎭ (B) 12,ln 2⎛⎫- ⎪⎝⎭ (C) 1,ln 22⎛⎫ ⎪⎝⎭ (D) 1,ln 22⎛⎫- ⎪⎝⎭5.函数2xy x e-=及图象在()1,2内是( ).(A)单调减少且是凸的 (B)单调增加且是凸的 (C)单调减少且是凹的 (D)单调增加且是凹的6.以下结论正确的是( ).(A) 若0x 为函数()y f x =的驻点,则0x 必为函数()y f x =的极值点. (B) 函数()y f x =导数不存在的点,一定不是函数()y f x =的极值点. (C) 若函数()y f x =在0x 处取得极值,且()0f x '存在,则必有()0f x '=0. (D) 若函数()y f x =在0x 处连续,则()0f x '一定存在.7.设函数()y f x =的一个原函数为12xx e ,则()f x =( ). (A) ()121x x e - (B)12x x e - (C) ()121x x e + (D) 12xxe8.若()()f x dx F x c =+⎰,则()sin cos xf x dx =⎰( ).(A) ()sin F x c + (B) ()sin F x c -+ (C) ()cos F x c + (D) ()cos F x c -+ 9.设()F x 为连续函数,则12x f dx ⎛⎫' ⎪⎝⎭⎰=( ). (A) ()()10f f - (B)()()210f f -⎡⎤⎣⎦ (C) ()()220f f -⎡⎤⎣⎦ (D) ()1202f f ⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦10.定积分badx ⎰()a b <在几何上的表示( ).(A) 线段长b a - (B) 线段长a b - (C) 矩形面积()1a b -⨯ (D) 矩形面积()1b a -⨯ 二.填空题(每题4分,共20分)1.设 ()()2ln 101cos 0x x f x xa x ⎧-⎪≠=⎨-⎪=⎩, 在0x =连续,则a =________.2.设2sin y x =, 则dy =_________________sin d x . 3.函数211xy x =+-的水平和垂直渐近线共有_______条. 4.不定积分ln x xdx =⎰______________________.5. 定积分2121sin 11x x dx x -+=+⎰___________. 三.计算题(每小题5分,共30分)1.求下列极限:①()10lim 12xx x →+ ②arctan 2lim 1x x xπ→+∞-2.求由方程1yy xe =-所确定的隐函数的导数x y '.3.求下列不定积分: ①3tan sec x xdx ⎰ ②()220dx a x a>+⎰③2x x e dx ⎰ 四.应用题(每题10分,共20分) 1.作出函数313y x x =-的图象.(要求列出表格)2.计算由两条抛物线:22,y x y x ==所围成的图形的面积.《高数》试卷2参考答案一.选择题:CDCDB CADDD二填空题:1.-2 2.2sin x 3.3 4.2211ln 24x x x c -+ 5.2π三.计算题:1. ①2e ②1 2.2yx e y y '=- 3.①3sec 3xc +②)ln x c + ③()222x x x e c -++四.应用题:1.略 2.13S =《高数》试卷3(上)一、 填空题(每小题3分, 共24分)1.函数y =的定义域为________________________.2.设函数()sin 4,0,0xx f x x a x ⎧≠⎪=⎨⎪=⎩, 则当a =_________时, ()f x 在0x =处连续.3. 函数221()32x f x x x -=-+的无穷型间断点为________________.4. 设()f x 可导, ()xy f e =, 则____________.y '=5. 221lim _________________.25x x x x →∞+=+- 6. 321421sin 1x xdx x x -+-⎰=______________. 7. 20_______________________.x td e dt dx -=⎰8. 30y y y '''+-=是_______阶微分方程.二、求下列极限(每小题5分, 共15分)1. 01lim sin xx e x →-; 2. 233lim 9x x x →--; 3. 1lim 1.2xx x -→∞⎛⎫+ ⎪⎝⎭三、求下列导数或微分(每小题5分, 共15分)1. 2xy x =+, 求(0)y '. 2. cos x y e =, 求dy . 3. 设x y xy e +=, 求dydx .四、求下列积分 (每小题5分, 共15分)1. 12sin x dx x ⎛⎫+ ⎪⎝⎭⎰. 2. ln(1)x x dx +⎰.3.120xedx ⎰五、(8分)求曲线1cos x t y t=⎧⎨=-⎩在2t π=处的切线与法线方程.六、(8分)求由曲线21,y x =+ 直线0,0y x ==和1x =所围成的平面图形的面积, 以及此图形绕y 轴旋转所得旋转体的体积. 七、(8分)求微分方程6130y y y '''++=的通解. 八、(7分)求微分方程x yy e x'+=满足初始条件()10y =的特解. 《高数》试卷3参考答案一.1.3x< 2.4a = 3.2x = 4.'()x x e f e5.126.07.22x xe -8.二阶二.1.原式=0lim 1x xx→= 2.311lim36x x →=+ 3.原式=112221lim[(1)]2x x e x--→∞+= 三.1.221','(0)(2)2y y x ==+2.cos sin x dy xe dx =-3.两边对x 求写:'(1')x y y xy e y +==+'x y x y e y xy yy x e x xy++--⇒==--四.1.原式=lim 2cos x x C -+2.原式=2221lim(1)()lim(1)[lim(1)]22x x x d x x d x x +=+-+⎰⎰=22111lim(1)lim(1)(1)221221x x x x dx x x dx x x +-=+--+++⎰⎰=221lim(1)[lim(1)]222x x x x x C +--+++3.原式=1221200111(2)(1)222x x e d x e e ==-⎰五.sin 1,122dy dy tt t y dx dx ππ=====且 切线:1,1022y x y x ππ-=---+=即 法线:1(),1022y x y x ππ-=--+--=即六.12210013(1)()22S x dx x x =+=+=⎰11224205210(1)(21)228()5315V x dx x x dxx x x ππππ=+=++=++=⎰⎰七.特征方程:2312613032(cos 2sin 2)xr r r iy e C x C x -++=⇒=-±=+八.11()dxdxxx x y e e edx C -⎰⎰=+⎰1[(1)]x x e C x=-+ 由10,0y x C ==⇒=1xx y e x-∴=《高数》试卷4(上)一、选择题(每小题3分) 1、函数 2)1ln(++-=x x y 的定义域是( ).A []1,2-B [)1,2-C (]1,2-D ()1,2- 2、极限xx e ∞→lim 的值是( ).A 、 ∞+B 、 0C 、∞-D 、 不存在 3、=--→211)1sin(limx x x ( ).A 、1B 、 0C 、 21-D 、214、曲线 23-+=x x y 在点)0,1(处的切线方程是( ) A 、 )1(2-=x y B 、)1(4-=x y C 、14-=x y D 、)1(3-=x y 5、下列各微分式正确的是( ).A 、)(2x d xdx = B 、)2(sin 2cos x d xdx =C 、)5(x d dx --=D 、22)()(dx x d =6、设⎰+=C xdx x f 2cos 2)( ,则 =)(x f ( ). A 、2sin x B 、 2sin x- C 、 C x +2sin D 、2sin 2x -7、⎰=+dx xx ln 2( ).A 、C x x++-22ln 212 B 、 C x ++2)ln 2(21C 、 C x ++ln 2lnD 、 C xx++-2ln 1 8、曲线2x y = ,1=x ,0=y 所围成的图形绕y 轴旋转所得旋转体体积=V ( ). A 、⎰14dx x π B 、⎰1ydy πC 、⎰-1)1(dy y π D 、⎰-104)1(dx x π9、⎰=+101dx e e xx( ). A 、21lne + B 、22ln e + C 、31ln e + D 、221ln e + 10、微分方程 xe y y y 22=+'+'' 的一个特解为( ).A 、x e y 273=* B 、x e y 73=* C 、x xe y 272=* D 、x e y 272=*二、填空题(每小题4分)1、设函数xxe y =,则 =''y ; 2、如果322sin 3lim 0=→x mx x , 则 =m .3、=⎰-113cos xdx x;4、微分方程 044=+'+''y y y 的通解是 .5、函数x x x f 2)(+= 在区间 []4,0 上的最大值是 ,最小值是 ;三、计算题(每小题5分) 1、求极限 x x x x --+→11lim; 2、求x x y sin ln cot 212+= 的导数;3、求函数 1133+-=x x y 的微分;4、求不定积分⎰++11x dx;5、求定积分⎰eedx x 1ln ; 6、解方程21xy xdx dy -=;四、应用题(每小题10分)1、 求抛物线2x y = 与 22x y -=所围成的平面图形的面积.2、 利用导数作出函数323x x y -= 的图象.参考答案一、1、C ; 2、D ; 3、C ; 4、B ; 5、C ; 6、B ; 7、B ; 8、A ; 9、A ; 10、D ;二、1、xe x )2(+; 2、94 ; 3、0 ; 4、xe x C C y 221)(-+= ; 5、8,0三、1、 1; 2、x 3cot - ; 3、dx x x 232)1(6+ ; 4、C x x +++-+)11ln(212; 5、)12(2e - ; 6、C x y =-+2212 ; 四、1、38; 2、图略《高数》试卷5(上)一、选择题(每小题3分) 1、函数)1lg(12+++=x x y 的定义域是( ).A 、()()+∞--,01,2B 、 ()),0(0,1+∞-C 、),0()0,1(+∞-D 、),1(+∞- 2、下列各式中,极限存在的是( ).A 、 x x cos lim 0→B 、x x arctan lim ∞→C 、x x sin lim ∞→D 、xx 2lim +∞→3、=+∞→xx xx )1(lim ( ). A 、e B 、2e C 、1 D 、e1 4、曲线x x y ln =的平行于直线01=+-y x 的切线方程是( ). A 、 x y = B 、)1)(1(ln --=x x y C 、 1-=x y D 、)1(+-=x y 5、已知x x y 3sin = ,则=dy ( ).A 、dx x x )3sin 33cos (+-B 、dx x x x )3cos 33(sin +C 、dx x x )3sin 3(cos +D 、dx x x x )3cos 3(sin + 6、下列等式成立的是( ).A 、⎰++=-C x dx x 111ααα B 、⎰+=C x a dx a x x ln C 、⎰+=C x xdx sin cos D 、⎰++=C xxdx 211tan 7、计算⎰xdx x e x cos sin sin 的结果中正确的是( ).A 、C ex+sin B 、C x e x +cos sinC 、C x ex+sin sin D 、C x e x +-)1(sin sin8、曲线2x y = ,1=x ,0=y 所围成的图形绕x 轴旋转所得旋转体体积=V ( ). A 、⎰14dx x π B 、⎰1ydy πC 、⎰-1)1(dy y π D 、⎰-104)1(dx x π9、设 a ﹥0,则=-⎰dx x a a22( ).A 、2a B 、22a πC 、241a 0D 、241a π 10、方程( )是一阶线性微分方程. A 、0ln2=+'xyy x B 、0=+'y e y x C 、0sin )1(2=-'+y y y x D 、0)6(2=-+'dy x y dx y x二、填空题(每小题4分)1、设⎩⎨⎧+≤+=0,0,1)( x b ax x e x f x ,则有=-→)(lim 0x f x ,=+→)(lim 0x f x ;2、设 xxe y = ,则 =''y ;3、函数)1ln()(2x x f +=在区间[]2,1-的最大值是 ,最小值是 ;4、=⎰-113cos xdx x;5、微分方程 023=+'-''y y y 的通解是 .三、计算题(每小题5分) 1、求极限 )2311(lim 21-+--→x x x x ;2、求 x x y arccos 12-= 的导数;3、求函数21xx y -=的微分;4、求不定积分⎰+dx xxln 21 ;5、求定积分 ⎰eedx x 1ln ;6、求方程y xy y x =+'2满足初始条件4)21(=y 的特解.四、应用题(每小题10分)1、求由曲线 22x y -= 和直线 0=+y x 所围成的平面图形的面积.2、利用导数作出函数 49623-+-=x x x y 的图象.参考答案(B 卷)一、1、B ; 2、A ; 3、D ; 4、C ; 5、B ; 6、C ; 7、D ; 8、A ; 9、D ; 10、B.二、1、 2 ,b ; 2、xe x )2(+ ; 3、 5ln ,0 ; 4、0 ; 5、xxeC e C 221+.三、1、31 ; 2、1arccos 12---x xx ; 3、dx x x 221)1(1-- ;4、C x ++ln 22 ;5、)12(2e- ; 6、x e x y 122-= ;四、1、 29; 2、图略。
高中数学必修二 8 简单几何体的表面积与体积(精讲)(含答案)

8.3 简单几何体的表面积与体积(精讲)考点一 旋转体的体积【例1】(2021·山东莱西·高一期末)在ABC 中,2AB =,32BC =,120ABC ∠=︒,若将ABC 绕BC 边所在的直线旋转一周,则所形成的面围成的旋转体的体积是______. 【答案】32π 【解析】依题意可知,旋转体是一个大圆锥去掉一个小圆锥,所以sin 602OA AB =︒==,1cos60212OB AB =︒=⨯=,所以旋转体的体积:()21332V OC OB ππ=⋅⋅-=故答案为:32π. 【一隅三反】1.(2021·湖南省邵东市第三中学高一期中)圆台上、下底面面积分别是π、4π积是( )A B .C D 【答案】D【解析】由题意1(4)3V ππ=+=.故选:D .2.(2021·山东任城·高一期中)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周六尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为6尺,米堆的高为5尺,问堆放的米有多少斛?”已知1斛米的体积约为1.6立方尺,圆周率约为3,估算出堆放的米约有_______斛.【答案】12.5【解析】设圆柱的底面半径为r 尺,则14⨯2πr =6,∴r ≈4,∴圆锥的体积V =21134543⨯⨯⨯⨯=20立方尺,∴堆放的米约有201.6=12.5斛. 故答案为:12.5.3.(2021·上海市七宝中学)已知圆锥的侧面展开图是半径为2的半圆,则圆锥的体积为________.【解析】由题意圆锥的母线长为2l =,设圆锥底面半径为r ,则22r ππ=,1r =,所以高为h体积为2211133V r h ππ==⨯=..考点二 旋转体的表面积【例2】(2021·吉林·延边二中高一期中)如图,圆锥的底面直径和高均是4,过PO 的中点O '作平行于底面的截面,以该截面为底面挖去一个圆柱,(1)求剩余几何体的体积 (2)求剩余几何体的表面积【答案】(1)103π;(2)8π+. 【解析】(1)由题意知,因为O '为PO 的中点,所以挖去圆柱的半径为1,高为2,剩下几何体的体积为圆锥的体积减去挖去小圆柱的体积, 所以22110241233V πππ=⋅⨯⨯-⨯⨯=.(2)因为圆锥的底面直径和高均是4,所以半径为2,母线l =所以圆锥的表面积为2122(4S πππ=⨯+⨯⨯+, 挖去的圆柱的侧面积为:22124S ππ=⨯⨯=,所以剩余几何体的表面积为12(4+4+8S S S πππ==+=+. 【一隅三反】1.(2021·广东·仲元中学高一期中)已知一个母线长为1的圆锥的侧面展开图的圆心角等于240︒,则该圆锥的侧面积为( )A B .881πCD .23π【答案】D【解析】将圆心角240︒化为弧度为:43π,设圆锥底面圆的半径为r 由圆心角、弧长和半径的公式得:4213r ππ=⨯,即23r = 由扇形面积公式得:22133S ππ=⨯⨯=所以圆锥的侧面积为23π.故选:D.2.(2021·全国·高一课时练习)已知圆台的上、下底面半径分别为10和20,它的侧面展开图的扇环的圆心角为180°,则这个圆台的侧面积为( ) A .600π B .300π C .900π D .450π【答案】A【解析】圆台的上底面圆半径10r '=,下底面圆半径20r =,设圆台的母线长为l ,扇环所在的小圆的半径为x ,依题意有:220()210l x x ππππ⨯=+⎧⎨⨯=⎩,解得2020x l =⎧⎨=⎩,所以圆台的侧面积20()()1020600+S r r l πππ'=⨯=+=. 故选:A3(2021·全国·高一课时练习)圆台的上、下底面半径和高的比为1:4:4,若母线长为10,则圆台的表面积为________. 【答案】168π【解析】圆台的轴截面如图所示,设上底面半径为r ,下底面半径为R ,高为h 则4h R r ==,则它的母线长为510l r =, 所以2r,8R =.故()(82)10100S R r l πππ=+=+⨯=侧,22100464168S S r R ππππππ=++=++=表侧.故答案为:168π考点三 多面体的体积【例3-1】(2021·全国·高一课时练习)如图所示,正方体ABCD-A 1B 1C 1D 1的棱长为1,则三棱锥D-ACD 1的体积是( )A .16B .13C .1 2D .1【答案】A【解析】三棱锥D-ACD 1的体积等于三棱锥D 1-ACD 的体积,三棱锥D 1-ACD 的底面ACD 是直角边长为1的等腰直角三角形,高D 1D=1,∴三棱锥D-ACD 1的体积为V=1132⨯×1×1×1=16.故选:A【例3-2】(2021·全国·高一课时练习)若正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14,则棱台的高度为( ) A .8 B .4C .2D .【答案】C【解析】如图,设棱台的上、下底面边长分别为2x ,8x ,斜高h '为5x ,则棱台的高h x ,由棱台的体积公式1()3V S S h '=得:2224161)31(6444++x x x x ⋅=,解得12x =,棱台的高为h =4x =2. 故选:C 【一隅三反】1.(2021·全国·高一课时练习)设四棱锥的底面是对角线长分别为2和4的菱形,四棱锥的高为3,则该四棱锥的体积为( ) A .12 B .24 C .4 D .30【答案】C【解析】所求的体积为11324432⨯⨯⨯⨯=,故选:C.2.(2021·全国·高一课时练习)棱台的上、下底面面积分别是2,4,高为3,则棱台的体积等于( )A .6B .3+C .6+D .6【答案】C【解析】依题意,棱台的上底面面积2S '=,下底面面积4S =,高为3h =,故由公式可知,棱台的体积是()()11243633V S S h '==⨯⨯=+ 故选:C.3.(2021·全国·高一课时练习)若一个四棱锥的底面的面积为3,体积为9,则其高为( ) A .13B .1C .3D .9【答案】D【解析】设四棱锥的高为h ,则由锥体的体积公式得:13×3h =9,解得h =9,所以所求高为9. 故选:D4.(2021·广东·仲元中学高一期中)如图所示,在长方体ABCD A B C D ''''-中,用截面截下一个棱锥C A DD '''-则棱锥C A DD '''-的体积与剩余部分的体积之比为( )A .1:5B .1:4C .1:3D .1:2【答案】A【解析】由图知:13C A DD A DD V C D S'''''-''=⋅⋅,ABCD A B C D A D DA V C D S ''''''-''=⋅,而2A D DA A DD S S''''=,∴剩余部分的体积为53ABCD A B C D C A DD A DD V V C D S'''''''''--''-=⋅,∴棱锥C A DD '''-的体积与剩余部分的体积之比为1:5.故选:A考点四 多面体的表面积【例4】(2021·全国·高一课时练习)正六棱柱的底面边长为2,最长的一条对角线长为积为()A .4)B .2)C .1)D .8)【答案】B【解析】正六棱柱的底面边长为2,最长的一条对角线长为12BB =,它的表面积为)16=2622sin 6222412223S S S π=+⨯⨯⨯⨯⨯+⨯⨯==表面积底面积矩形.故选:B. 【一隅三反】1.(2021·全国·高一课时练习)若六棱柱的底面是边长为3的正六边形,侧面为矩形,侧棱长为4,则其侧面积等于( ) A .12 B .48 C .64 D .72【答案】D【解析】六棱柱的底面是边长为3的正六边形, 故底面周长6318C =⨯=, 又侧面是矩形,侧棱长为4, 故棱柱的高4h =,∴棱柱的侧面积72S Ch ==,故选:D2.(2021·全国·高一课时练习)如图,在正方体ABCD -A 1B 1C 1D 1中,三棱锥D 1AB 1C 的表面积与正方体的表面积的比为( )A .1∶1B .1C .1D .1∶2【答案】C【解析】设正方体的边长为a ,则表面积216S a =,因为三棱锥11D AB C -的各面均是正三角形,其边长为正方体侧面对角线.,三棱锥D 1AB 1C 的表面积)222142S =⨯⨯=,所以2221::6S S a ==故选:C3(2021·全国·高一课时练习)长方体同一顶点上的三条棱长分别为2,2,3,则长方体的体积与表面积分别为( ) A .12,32 B .12,24 C .22,12 D .12,11【答案】A【解析】长方体的体积为22312⨯⨯=,表面积为()222+23+2332⨯⨯⨯=, 故选:A.4.(2021·全国·高一课时练习)(多选)正三棱锥底面边长为3,侧棱长为则下列叙述正确的是( )A .正三棱锥高为3 BC D 【答案】ABD【解析】设E 为等边三角形ADC 的中心,F 为CD 的中点,连接,,PF EF PE , 则PE 为正三棱锥的高,PF 为斜高,又PF ==32EF ==,故3PE ==, 故AB 正确.而正三棱锥的体积为1393⨯=,侧面积为1332⨯⨯=故C 错误,D 正确. 故选:ABD.5(2021·全国·高一课时练习)(多选)在正方体1111ABCD A B C D -中,三棱锥11D AB C -的表面积与正方体的表面积的比不可能是( )A .1:1B .C .D .1:2【答案】ABD【解析】设正方体1111ABCD A B C D -的棱长为a ,则正方体1111ABCD A B C D -的表面积为226S a =.三棱锥11D AB C -的正四面体,其中一个面的面积为212S ==,则三棱锥11D AB C -的表面积为2214S ==所以三棱锥11D AB C -的表面积与正方体的表面积的比为22126S S a ==::故选:ABD.考点五 有关球的计算【例5-1】(2021·全国·高一课时练习)长方体的三个相邻面的面积分别是2,3,6,这个长方体的顶点都在同一个球面上,则这个球的表面积为( ) A .72π B .56π C .14π D .16π【答案】C【解析】设长方体的三条棱长分别为a ,b ,c ,由题意得236ab ac bc =⎧⎪=⎨⎪=⎩,得123a b c =⎧⎪=⎨⎪=⎩∴2414S R ππ球==. 故选:C【例5-2】(2021·广东高州·高一期末)已知正四面体ABCD的表面积为A 、B 、C ,D 四点都在球O 的球面上,则球O 的体积为( ) A. BCD .3π【答案】C【解析】正四面体各面都是全等的等边三角形,设正四面体的棱长为a ,所以该正四面体的表面积为2142S a =⨯⨯=,所以a =1, 所以正方体的外接球即为该正四面体的外接球,O 的体积为343π⨯=⎝⎭. 故选:C. 【一隅三反】1.(2021·全国·高一课时练习)表面积为16π的球的内接轴截面为正方形的圆柱的体积为( )A .B .C .16πD .8π【答案】A【解析】由题意可知,4πR 2=16π,所以R =2,即球的半径R =2.设圆柱的底面圆半径为r 2R =,即2816r =,所以r ,∴V 圆柱=πr 2·2r =2π·π.故选:A.2.(2021·全国·高一课时练习)若一个正方体内接于表面积为4π的球,则正方体的表面积等于( )A .B .8C .D .【答案】B【解析】设正方体棱长为x ,球半径为R ,则24π4πS R ==球,解得1R =,22R ==,解得x =所以该正方体的表面积为22668S x ==⨯=正.故选:B.3.(2021·全国·高一课时练习)(多选)我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知半球内有一个方锥,方锥的底面内接于半球的底面,方锥的顶点在半球的球面上,若方锥的体积为18,则半球的说法正确的是( ) A .半径是3 B .体积为18π C .表面积为27π D .表面积为18π【答案】ABC【解析】如图,PAC △是正四棱锥的对角面,设球半径为r ,AC 是半圆的直径,,棱锥体积为2312)1833V r r =⨯⨯==,3r =,半球体积为332231833V r πππ==⨯=,表面积为2223327S πππ=⨯+⨯=, 故选:ABC .4.(2021·全国·高一课时练习)一个球内有相距9cm 的两个平行截面,它们的面积分别为249cm π和2400cm π2,求球的体积和表面积.【答案】球的表面积为22500cm π,球的体积为362500cm 3π. 【解析】(1)当截面在球心的同侧时,如图①所示为球的轴截面,由截面性质知12AO //BO ,1O ,2O 为两截面圆的圆心,且11OO AO ⊥,22OO BO ⊥,①设球的半径为R ,因为2249O B ππ=,所以27cm O B =,同理得120cm O A =.设1cm OO x =,则2(9)cm OO x =+, 在1Rt O OA 中,22220R x =+,① 在2Rt OO B 中,2227(9)R x =++,② 联立①②可得15x =,25R =.所以2242500cm S R ππ==球,33462500cm 33V R ππ==球.(2)当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,12O A//O B ,1O ,2O 分别为两截面圆的圆心,且11OO O A ⊥,22OO O B ⊥.②设球的半径为R ,因为2249O B ππ⋅=,所以27cm O B =.因为21400O A ππ⋅=,所以120cm O A =.设1cm O O x =,则2(9)cm OO x =-. 在1Rt OO A △中,22400R x =+,在2Rt OO B 中,22(9)49R x =-+, 所以22400(9)49x x +=-+, 解得15x =-(不合题意,舍去) 综上所述,球的表面积为22500cm π. 球的体积为362500cm 3π. 考点六 综合运用【例6】(2021·全国·高一课时练习)一块边长为12cm 的正三角形薄铁片,按如图所示设计方案,裁剪下三个全等的四边形(每个四边形中有且只有一组对角为直角),然后用余下的部分加工制作成一个“无盖”的正三棱柱(底面是正三角形的直棱柱)形容器.(1)请将加工制作出来的这个“无盖”的正三棱柱形容器的容积V 表示为关于x 的函数,并标明其定义域; (2)若加工人员为了充分利用边角料,考虑在加工过程中,使用裁剪下的三个四边形材料恰好拼接成这个正三棱柱形容器的“顶盖”.请指出此时x 的值(不用说明理由),并求出这个封闭的正三棱柱形容器的侧面积S .【答案】(1)323(012)82x V x x =-+<<;(2)6cm x =,2S =侧.【解析】(1)结合平面图形数据及三棱柱直观图,求得三棱柱的高6cm 2x h ⎫=-⎪⎝⎭,其底面积22cm S =,则三棱柱容器的容积232236624282x x x x V Sh x x ⎫⎛⎫==-=-=-+⎪ ⎪⎝⎭⎝⎭, 即所求函数关系式为323(012)82x V x x =-+<<;(2)此时6cm x =,而相应棱柱的高h ,故侧面积为236S =⨯=. 【一隅三反】1.(2021·安徽镜湖·高一期中)如图所示,在边长为5的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M ,N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥的底面,围成一个圆锥,求该圆锥的表面积与体积.【答案】表面积10π. 【解析】设圆的半径为r ,扇形的半径为R ,由题意,得(522R r Rr ππ⎧+=⎪⎨=⎪⎩,解得r R ⎧=⎪⎨=⎪⎩所以围成的圆锥的母线长为l =r =h ∴圆锥的表面积210S rl r πππ=+=;∴圆锥的体积为213V r h π==.2.(2021·全国·高一课时练习)有一塔形几何体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,求该塔形的表面积(含最底层正方体的底面面积).【答案】36【解析】易知由下向上三个正方体的棱长依次为2,1.考虑该几何体在水平面的投影,可知其水平投影面积等于下底面最大正方体的底面面积.∴S 表=2S 下+S 侧=2×22+4×[22+2+12]=36, ∴该几何体的表面积为36.3.(2021·全国·高一课时练习)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m ,高为4 m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大4 m (高不变);二是高度增加4 m (底面直径不变). (1)分别计算按这两种方案所建的仓库的体积; (2)分别计算按这两种方案所建的仓库的表面积; (3)哪个方案更经济些?【答案】(1)2563π(m 3),96π(m 3);(m 2),60π(m 2);(3)方案二比方案一更加经济. 【解析】(1)若按方案一,仓库的底面直径变成16 m ,则仓库的体积为V 1=13S ·h=13×π×2162⎛⎫⎪⎝⎭×4=2563π(m 3).若按方案二,仓库的高变成8 m ,则仓库的体积为V 2=13S ·h=13×π×2122⎛⎫⎪⎝⎭×8=96π(m 3).(2)若按方案一,仓库的底面直径变成16 m ,半径为8 m.圆锥的母线长为l 1m ),则仓库的表面积为S 1=π×8×(m 2). 若按方案二,仓库的高变成8 m.圆锥的母线长为l 210(m ), 则仓库的表面积为S 2=π×6×10=60π(m 2).(3)由(1)、(2)知,V 1<V 2,S 2<S 1,故方案二体积更大,表面积更小,所需耗材更少,即方案二比方案一更加经济.。
旋转体的体积试题解析——高数常考题目

B x = x2( y)
可看作平面图OABC 与OBC
x = x1( y) o
A
2a x
分别绕 y轴旋转构成旋转体的体积之差.
Vy =
2a
0
x
2
2
(
y)dy
-
2a 0
x
2
1
(
y
)dy
= a2 (t - sin t)2 a sin tdt 2 - a2 (t - sin t)2 a sin tdt 0
构成旋转体的体积.
y( x)
解 绕 x轴旋转的旋转体体积
Vx =
2a y2 ( x)dx
0
a 2a
= 2 a2 (1 - cos t)2 a(1 - cos t)dt 0
= a3
2
(1 - 3cos t
3cos2
t
- cos3
t )dt
=
52a3 .
0
绕 y轴旋转的旋转体体积
y
2a C
直线 x = a 、 x = b及x 轴所围成的曲边梯形绕
x 轴旋转一周而成的立体,体积为多少?
取积分变量为 x ,
y
y = f (x)
x [a,b]
在[a, b]上任取小区 o
x x dx
x
间[ x, x dx],
取以dx 为底的窄边梯形绕x 轴旋转而成的薄
片的体积为体积元素, dV = [ f ( x)]2 dx
•
6、意志坚强的人能把世界放在手中像 泥块一 样任意 揉捏。 2020年 12月11 日星期 五上午 4时42 分51秒0 4:42:51 20.12.1 1
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月上午 4时42 分20.12. 1104:4 2December 11, 2020
旋转体的体积试题解析高数常考题目

可看作平面图OABC 与OBC
x = x1( y) o
A
2a x
分别绕y 轴旋转构成旋转体的体积之差.
Vy =
2a
x
2
2
(
y)dy
-
0
2a
x
2
1
(
y
)dy
0
= a2 (t - sin t)2 a sin tdt 2 - a2 (t - sin t)2 a sin tdt 0
= a3 2 (t - sin t)2 sin tdt = 63a3 . 0
例 7 求由曲线 y = 4 - x2及 y = 0所围成的图形 绕直线 x = 3旋转构成旋转体的体积.
解 取积分变量为y , y [0,4]
体积元素为
P
dy Q M
dV = [PM 2 - QM 2 ]dy 3 = [(3 4 - y)2 - (3 - 4 - y)2]dy
= 12 4 - ydy,
i =1
S(x)dx
a
例 1 一平面经过半径为 R的圆柱体的底圆中心,
并与底面交成角 ,计算这平面截圆柱体所得立
体的体积.
解 取坐标系如图
-R
底圆方程为
o
y
x2 y2 = R2
x
R
垂直于x 轴的截面为直角三角形
x
截面面积 A( x) = 1 (R2 - x2 )tan ,
2
立体体积 V = 1 R (R2 - x2 )tandx = 2 R3 tan .
二、旋转体的体积
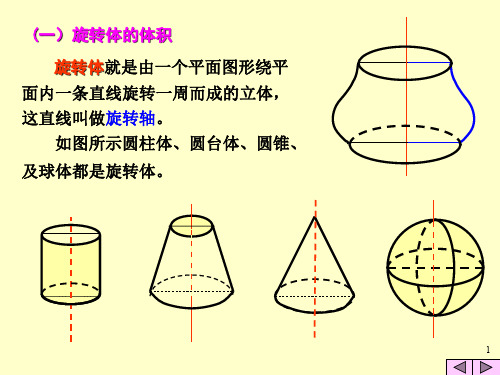
旋转体就是由一个平面图形饶这平面内 一条直线旋转一周而成的立体.这直线叫做 旋转轴.
圆柱
圆锥
圆台
(完整版)大一第一学期期末高等数学(上)试题及答案

第一学期期末高等数学试卷一、解答下列各题(本大题共16小题,总计80分)1、(本小题5分)求极限 lim x x x x x x →-+-+-23321216291242、(本小题5分) .d )1(22x x x ⎰+求3、(本小题5分) 求极限limarctan arcsinx x x →∞⋅14、(本小题5分)⎰-.d 1x x x 求5、(本小题5分) .求dt t dx d x ⎰+2021 6、(本小题5分)⎰⋅.d csc cot 46x x x 求7、(本小题5分) .求⎰ππ2121cos 1dx x x8、(本小题5分) 设确定了函数求.x e t y e ty y x dy dx t t ==⎧⎨⎪⎩⎪=cos sin (),229、(本小题5分) .求dx x x ⎰+301 10、(本小题5分)求函数 的单调区间y x x =+-42211、(本小题5分) .求⎰π+202sin 8sin dx x x 12、(本小题5分).,求设 dx t t e t x kt )sin 4cos 3()(ωω+=-13、(本小题5分) 设函数由方程所确定求.y y x y y x dy dx =+=()ln ,226 14、(本小题5分)求函数的极值y e e x x =+-215、(本小题5分) 求极限lim ()()()()()()x x x x x x x →∞++++++++--121311011011112222Λ16、(本小题5分) .d cos sin 12cos x x x x ⎰+求二、解答下列各题(本大题共2小题,总计14分)1、(本小题7分),,512沿一边可用原来的石条围平方米的矩形的晒谷场某农场需建一个面积为.,,才能使材料最省多少时问晒谷场的长和宽各为另三边需砌新石条围沿2、(本小题7分) .8232体积轴旋转所得的旋转体的所围成的平面图形绕和求由曲线ox x y x y ==三、解答下列各题 ( 本 大 题6分 )设证明有且仅有三个实根f x x x x x f x ()()()(),().=---'=1230一学期期末高数考试(答案)一、解答下列各题(本大题共16小题,总计77分)1、(本小题3分)解原式:lim =--+→x x x x 22231261812 =-→lim x x x 261218 =22、(本小题3分) ⎰+x x x d )1(22 ⎰++=222)1()1d(21x x =-++12112x c .3、(本小题3分) 因为arctan x <π2而limarcsin x x →∞=10故limarctan arcsin x x x →∞⋅=10 4、(本小题3分) ⎰-x x x d 1 x x x d 111⎰----= ⎰⎰-+-=x x x 1d d =---+x x c ln .1 5、(本小题3分)原式=+214x x6、(本小题4分) ⎰⋅x x x d csc cot 46⎰+-=)d(cot )cot 1(cot 26x x x=--+171979cot cot .x x c7、(本小题4分) 原式=-⎰cos ()1112x d x ππ=-sin 112x ππ=-1 8、(本小题4分) 解: dy dx e t t e t t t t t =+-22222(sin cos )(cos sin ) =+-e t t t t t t (sin cos )(cos sin )2222 9、(本小题4分)令 1+=x u 原式=-⎰24122()u u du=-2535312()u u =11615 10、(本小题5分) ),(+∞-∞函数定义域 01)1(222='=-=-='y x x x y ,当 (][)+∞<'>∞->'<,1011,01函数的单调减区间为,当函数单调增区间为, 当y x y x 11、(本小题5分)原式=--⎰d x x cos cos 9202π=-+-163302ln cos cos x x π=162ln12、(本小题6分) dx x t dt ='()[]dt t k t k e kt ωωωωsin )34(cos )34(+--=- 13、(本小题6分) 2265yy y y x '+'='=+y yx y 315214、(本小题6分) 定义域,且连续(),-∞+∞ '=--y e e x x 2122()驻点:x =1212ln 由于''=+>-y e e x x 20 22)21ln 21(,,=y 故函数有极小值 15、(本小题8分) 原式=++++++++--→∞lim ()()()()()()x x x x x x x 1121311011011112222Λ =⨯⨯⨯⨯=101121610117216、(本小题10分) dx x x dx x x x ⎰⎰+=+2sin 2112cos cos sin 12cos :解⎰++=x x d 2sin 211)12sin 21(=++ln sin 1122x c 二、解答下列各题(本大题共2小题,总计13分)1、(本小题5分)设晒谷场宽为则长为米新砌石条围沿的总长为 x xL x x x ,,()51225120=+> '=-=L x x 2512162 唯一驻点 ''=>=L x x 10240163 即为极小值点 故晒谷场宽为米长为米时可使新砌石条围沿所用材料最省165121632,,= 2、(本小题8分)解 :,,.x x x x x x 232311288204====V x x dx x x dx x =-⎡⎣⎢⎤⎦⎥=-⎰⎰ππ()()()223204460428464=⋅-⋅π()1415164175704x x π=-π=35512)7151(44三、解答下列各题( 本 大 题10分 ) 证明在连续可导从而在连续可导:()(,),,[,];,.f x -∞+∞03又f f f f ()()()()01230====则分别在上对应用罗尔定理得至少存在[,],[,],[,](),011223f x ξξξξξξ1231230112230∈∈∈'='='=(,),(,),(,)()()()使f f f 即至少有三个实根'=f x (),0,,,0)(它至多有三个实根是三次方程又='x f由上述有且仅有三个实根'f x ()高等数学(上)试题及答案一、 填空题(每小题3分,本题共15分)1、.______)31(lim 20=+→x x x 。
高中数学必修二 8 简单几何体的表面积与体积(精练)(含答案)

8.3 简单几何体的表面积与体积(精练)【题组一 旋转体的体积】1.(2021·吉林·延边二中高一期中)阿基米德(Archimedes ,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球(如图所示),该球与圆柱的两个底面及侧面均相切,圆柱的底面直径与高都等于球的直径.若该球的体积为36π,则圆柱的体积为 ( )A .36πB .45πC .54πD .63π【答案】C 【解析】因为该球的体积为36π,设球的半径为R ,则34363R ππ=,解得3R =。
所以圆柱的体积为:23654V ππ=⨯⨯=,故选:C.2.(2021·河北·保定市第二十八中学高一月考)唐朝的狩猎景象浮雕银杯如图1所示,其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度)如图2所示,设酒杯上部分(圆柱)的体积为1V ,下部分(半球)的体积为2V ,若122V V =,则半球的半径与圆柱的高之比为( )A .4:3B .3:4C .1:2D .5:3【答案】B 【解析】设圆柱的高为h ,半径为r ,则圆柱的体积为21=V r h π.而半球的体积为332412==323V r r ππ⨯. 因为122V V =,所以324=3r r h ππ,所以3=4r h . 故选:B3(2021·全国·高一课时练习)如图所示,半径为R 的半圆内(其中∠BAC =30°)的阴影部分以直径AB 所在直线为轴,旋转一周得到一个几何体,则该几何体的表面积为_____,体积为_____.2R 356R π 【解析】如图所示,过C 作CO 1⊥AB 于O 1,在半圆中可得∠BCA =90°,又∠BAC =30°,AB =2R ,∴AC ,BC =R ,CO 1,∴1AO S 圆锥侧=π=32πR 2,1BO S 圆锥侧=π×R R 2,∴S 几何体表=S 球+11AO BO S S +=圆锥侧圆锥侧R 2,πR 2. 又V 球=43πR 3,∴V 几何体=V 球-(11AO BO V V +圆锥圆锥)=43πR 3-13×AB ×π×C 2143O =πR 3-22536R π⎫⨯=⎪⎪⎝⎭πR 3.2R ;356R π4.(2021·全国·高一课时练习)若圆锥的侧面展开图为一个半径为2的半圆,则圆锥的体积是__________.【解析】设圆锥的底面半径为r ,则22ππ=r ,所以1r =,圆锥的高h = 所以圆锥的体积213V r h π=5.(2021·全国·高一课时练习)若一个圆锥的底面直径和高都与一个球的直径相等,那么这个圆锥的体积与球的体积之比为________. 【答案】12【解析】解析:设球体的半径为R 2312=2=33R V R R ππ⋅圆锥,343V R π球=,33213==423R V R V ππ圆锥球. 故答案为:12【题组二 旋转体的表面积】 1.(2021·全国·高一课时练习)如图,在四边形ABCD 中,∠DAB=90°,∠ADC=135°,AB=5,CD=AD=2,则四边形ABCD 绕AD 所在直线旋转一周所成几何体的表面积为( )A .(60+πB .(60+)π C .(56+πD .(56+)π【答案】A 【解析】四边形ABCD 绕AD 所在直线旋转一周所成的几何体为一个圆台挖去一个圆锥,如图所示:因为25r AB ==,所以圆台下底面面积125S π=,又因为CD =,135ACD ∠=,所以12ED r ==,25l ==,所以圆台的侧面积()()212225535S r r l πππ=+=+⨯=.圆锥的侧面积3111122222S r l ππ=⨯⨯=⨯⨯⨯.所以几何体的表面积为(123253560S S S S πππ=++=++=+.故选:A2.(2021·山东邹城·高一期中)如图是底面半径为3的圆锥,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点S 滚动,当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了3周,则( )A .圆锥的母线长为18B .圆锥的表面积为27πC .圆锥的侧面展开图扇形圆心角为60°D .圆锥的体积为【答案】D【解析】设圆锥的母线长为l ,以S 为圆心,SA 为半径的圆的面积为2S l π=,又圆锥的侧面积3S rl l ππ==圆锥侧,因为圆锥在平面内转到原位置时,圆锥本身滚动了3周,所以233l l ππ=⨯,解得9l =,所以圆锥的母线长为9,故选项A 错误;圆锥的表面积239336S S S πππ=+=⨯⨯+⨯=圆锥侧底,故选项B 错误;因为圆锥的底面周长为236ππ⨯=,设圆锥的侧面展开图扇形圆心角为α,则69πα=⋅,解得23πα=, 所以圆锥的侧面展开图扇形圆心角为120°,故选项C 错误;圆锥的高h =所以圆锥的体积为2133V π=⨯⨯⨯=,故选项D 正确. 故选:D .3.(2021·重庆·垫江第五中学校高一月考)如图,圆锥的母线长为4,点M 为母线AB 的中点,从点M 处拉一条绳子,绕圆锥的侧面转一周达到B 点,这条绳子的长度最短值为则此圆锥的表面积为__________【答案】5π【解析】将圆锥侧面沿母线AB 剪开,其侧面展开图为扇形,如图,从点M 处拉一条绳子,绕圆锥的侧面转一周达到B 点,最短距离即为线段BM 长,则有BM = 而M 是线段AB '中点,又母线长为4,于是得22220AM AB BM +==,即2BAB π'∠=,设圆锥底面圆半径为r ,从而有:242r ππ=⋅,解得1r =,所以圆锥的表面积为25S r r AB πππ=+⋅=.故答案为:5π4(2021·全国·高一课时练习)已知一块正方形薄铁片的边长为8cm ,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),若用这块扇形铁片围成一个无底的圆锥,则这个无底的圆锥的表面积为多少平方厘米?【答案】()216cm π 【解析】由已知,可得这个无底的圆锥的母线长为8cm ,设圆锥的底面半径为cm r ,则282r ππ=⨯,所以2cm r =,所以圆锥的表面积即侧面积()22816cm S rl πππ==⨯=侧. 【题组三 多面体的体积】1.(2021·上海外国语大学闵行外国语中学高二期中)在三棱锥P ABC -中,已知5PA BC PB AC PC AB ======,则该三棱锥的体积为___________.【答案】8【解析】如图,设长方体的三条棱长为,,a b c ,由题得22220a b +==;2213a c +=;222525b c +==, 解之得2224,16,9a b c ===.所以2,4,3a b c ===. 所以该三棱锥的体积为112344243=832⨯⨯-⨯⨯⨯⨯⨯.故答案为:82(2021·全国·高一课时练习)已知一个空间几何体的所有棱长均为1 cm ,其表面展开图如图所示,则该空间几何体的体积V =________cm 3.【答案】【解析】依题意,原几何体是由一个正方体上面接一个正四棱锥组成,其中正方体的棱长为1cm ,正方体的体积为1cm 3,正四棱锥的底面边长和侧棱长均为1cm ,体积为2113⨯=3),所以该空间几何体的体积为(1V =cm 3.故答案为:3.(2021·全国·高一课时练习)球O 的球心为点O ,球O 3的圆锥,三棱锥V ABC -内接于球O ,已知,OA OB AC BC ⊥⊥,则三棱锥V ABC -的体积的最大值为_______.【解析】=O 的半径为r=,解得1r =, ,1OA OB OA OB ⊥==,AB ∴=AC BC ⊥,∴C 在以AB 为直径的圆上,∴平面OAB ⊥平面ABC ,∴O 到平面ABC 2,故V 到平面ABC 1+,又C 到AB∴三棱锥V ABC -的体积的最大值为,111)32⨯4.(2021·全国·高一课时练习)如图所示,△ABC 和△A ′B ′C ′的对应顶点的连线AA ′,BB ′,CC ′交于同一点O ,且12AO BO CO A O B O C O =''==',则O ABC O A B C V V --'''=___________. 【答案】18【解析】如题干图,12AO BO CO A O B O C O =''==', 可证AB //A ′B ′,AC //A ′C ′,BC //B ′C ′.所以平面//ABC 平面A B C '''三棱锥O ABC -和三棱锥O A B C '''-高之比也为12,由等角定理得∠CAB =∠C ′A ′B ′,∠ACB =∠A ′C ′B ′,所以△ABC ∽△A ′B ′C ′, 由12AO BO CO A O B O C O =''==', 可得211()24ABC A B C S S '''==, 所以O ABC O A B C V V --'''==111428⨯=. 故答案为:185.(2021·山东·日照神州天立高级中学有限责任公司高一月考)如图是边长为1的正方体,H 、G 、F 分别是棱AB 、AD 、1AA 的中点,现在沿三角形GFH 所在平面锯掉正方体的一个角,问锯掉的这块的体积是原正方体的______.【答案】148【解析】1111113222248A FGH V -=⨯⨯⨯⨯=,所以148A FGH V V -=正方体, 故答案为:148. 6.(2021·黑龙江·哈师大附中高一期中)如图,在四面体ABCD 中作截面PQR ,其中14AR AD =,13AP AC =,12AQ AB =,则:A PQR D BCPQ V V --=______.【答案】1:20【解析】作RG ⊥平面ABC ,作DH ⊥平面ABC ,则GH 共线,由14AR AD =,则14RG DH =, 由12AQ AB =,13AP AC =,则16APQ ABC S S =, 所以15APQBCPQ S S =, 所以11113:154203APQ R APQA PQR D BCPQ D BCPQ BCPQ S RG V V V V S DH ----⋅===⨯=⋅,故答案为:1:20【题组四 多面体的表面积】1.(2021·上海市控江中学高二期中)若正四棱台的上底边长为2,下底边长为8,高为4,则它的侧面积为___________.【答案】100【解析】因正四棱台的上底边长为2,下底边长为8,高为4,则该正四棱台上底、下底面边心距分别为1,4,而正四棱台的高、斜高、两底面对应边心距构成直角梯形,于是得斜高5h '=, 因此,侧面积28451002S +=⨯⨯=, 所以所求的侧面积为100.故答案为:1002(2021·上海外国语大学闵行外国语中学高二期中)已知正三棱锥O ABC -的底面边长为4,高为2,则此三棱锥的侧面积为___________.【答案】【解析】由题意作出图形如图:因为三棱锥P ABC -是正三棱锥,顶点在底面上的射影D 是底面的中心,在三角PDF 中, 2PD =,DF =,PF ∴==则这个棱锥的侧面积为1342⨯⨯=故答案为:3.(2021·全国·高一课时练习)已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________.【答案】80+【解析】如图,在四棱台1111ABCD A B C D -中,过点1B 作1B F BC ⊥,垂足为点F ,在1Rt B FB 中1(84)22BF =⨯-=,18B B =,故1B F =所以111(84)2BB C C S =⨯+⨯=梯形故四棱台的侧面积4S =⨯=侧,所以448880S =⨯+⨯=+表故答案为:80+4.(2021·全国·高一课时练习)已知正四棱台两底面边长分别为4cm,8cm ,侧棱长为8cm ,则它的侧面积为_______2cm .【答案】【解析】作出正四棱台的一个侧面如图,设,E F 分别为,AD BC 的中点,过D 作DG BC ⊥于点G .由题知4cm,8cm,8cm AD BC CD ===,得2cm,4cm DE FC ==,解得2cm GC =,在Rt DGC △中,DG =,即斜高为,所以所求侧面积为)21(1632)cm 2⨯+⨯=.答案:5.(2021·全国·高一课时练习)若五棱台11111ABCDE A B C D E -的表面积是30,侧面积是25,则两底面面积的和为______.【答案】5【解析】S S S =+表侧两底,则30255S S S =-=-=两底表侧.故答案为:5.6(2021·全国·高一课时练习)如图,已知正三棱锥S ABC -的侧面积是底面积的2倍,正三棱锥的高3SO =,则此正三棱锥的表面积为___________.【答案】【解析】如图,设正三棱锥的底面边长为a ,斜高为h ',侧面积、底面积分别为12,S S ,过点O 作OE AB ⊥,与AB 交于点E ,连接SE ,则,SE AB SE h '⊥=.由21 2S S =,即21322a h '⋅⋅=⨯,可得a '.由SO OE ⊥,则222SO OE SE +=,即2223h ⎫''+=⎪⎪⎝⎭.h '∴=6a =.222 6S ∴=== 1 S =∴表面积 1 2 S S S =+==故答案为:【题组五 有关球的计算】1.(2021·新疆·新和县实验中学高一期末)若三个球的表面积之比是1:2:3,则它们的体积之比是( )A .1:B .1:C .2:4:9D .【答案】A【解析】设三个球的半径分别为1R ,2R ,3R ,因为三个球的表面积之比为1:2:3,所以2221234π:4π:4π1:2:3R R R =,所以123::R R R =所以它们的体积之比为3333331231234π4π4π::::1:333R R R R R R == 故选:A.2.(2021·山东邹城·高一期中)已知长方体1111ABCD A B C D -的长、宽、高分别为2、1、1,且其顶点都在球面上,则该球的体积是( )AB .6πC .36πD .【答案】A【解析】长方体1111ABCD A B C D -=长方体1111ABCD A B C D -343π⨯=⎝⎭. 故选:A .3.(2021·全国·高一课时练习)两个半径为1的实心铁球,熔化成一个大球,这个大球的半径是________.【解析】设大球的半径为R ,则有3334421,233R R ππ=⨯⨯=,所以R =4.(2021·全国·高一课时练习)一个底面直径是32cm 的圆柱形水桶装入一些水,将一个球放入桶内完全淹没,水面上升了9cm 且无溢出,则这个球的表面积是________.【答案】2576cm π【解析】由题意,上升的水的体积即为球的体积,若球的半径为R ,即23324923R ππ⎛⎫⨯= ⎪⎝⎭,解得12R =, 故这个球的表面积224412576S R πππ=⨯=⨯=.故答案为:2576cm π5.(2021·全国·高一课时练习)如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为3,则该半球的表面积为________.【答案】6π【解析】如图,连接AC ,BD 交点为O ,设球的半径为r ,由题意知:SO AO OC OD OB r =====.则AB =,四棱锥的体积为21)3V r =⨯⨯=r = ∴该半球的表面积为22214362S r r r ππππ=⨯+==.故答案为:6π6.(2021·全国·高一课时练习)在四棱锥S ABCD -中,底面ABCD 是边长为为【答案】48π【解析】因为四棱锥S ABCD -中,底面ABCD 是边长为 所以该四棱锥是正四棱锥,取正方形ABCD 的中心1O ,连接1SO ,AC ,则点1O 为AC 的中点,如图,则球心O 在1SO 上,因为正方形ABCD 边长为6AC ==,所以13AO =,因为SA =,所以1SO ==设四棱锥S ABCD -外接球的半径为r ,则11OO SO SO r =-,在1Rt AOO 中,22211AO AO OO =+,即)2223r r =+,解得:r =所以该四棱锥外接球的表面积为(224π4π48πr =⨯=.【题组六 综合运用】1(2021·全国·高一课时练习)如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x 的圆柱.(1)求出此圆锥的侧面积;(2)用x 表示此圆柱的侧面积表达式;(3)当此圆柱的侧面积最大时,求此圆柱的体积.【答案】(1);(2)224(02)S x x x ππ=-+<<圆柱侧;(3)π.【解析】(1)圆锥的底面半径R 与高H 均为2,则圆锥的母线长为L =2S RL ππ==⨯⨯=圆锥侧.(2)设圆柱的半径为r , 则222r x -=,解得2r x =-,且02x <<; 所以圆柱的侧面积为222(2)24(02)S rx x x x x x ππππ==-=-+<<圆柱侧.(3)22242(1)1S x x x πππ⎡⎤=-+=--+⎣⎦圆柱侧,02x <<;当1x =时,S 圆柱侧取得最大值为2π,此时1r =,圆柱的体积为2211V r x πππ==⋅⋅=圆柱.2.(2021·贵州·高一月考)在长方体1111ABCD A B C D -中,AB =6,BC =8,16AA =.(1)求三棱锥1D ABC -的体积;(2)在三棱柱111ABC A B C -内放一个体积为V 的球,求V 的最大值.【答案】(1)48;(2)323π. 【解析】(1)由长方体的几何特征知,1D 到平面ABC 的距离为116DD AA ==, 又1242ABC S AB BC =⋅=,所以11112464833D ABC ABC V S DD -=⋅=⨯⨯=; (2)设球的半径为R ,若该球与三棱柱111ABC A B C -的三个侧面均相切,则R 为ABC 的内切圆的半径,则()1242R AB AC BC ++=, 又=6+10+8=24AB AC BC ++,此时2R =;若该球与三棱柱111ABC A B C -的上下底面均相切,此时126R AA ==,3R =;所以在三棱柱111ABC A B C -内放一个体积为V 的球,该球半径最大为2,3max 4=2=3323V ππ⨯.3.(2021·浙江路桥·高一月考)如图所示,在平面五边形ABCDE 中,2AB AE CD ===,1BC =,DE =90ABC ∠=︒,90AED ∠=︒,分别沿AC ,AD 将ABC 与ADE 折起使得B ,E 重合于点P .试求:(1)三棱锥A PCD -的体积;(2)三棱锥A PCD -的外接球的表面积.【答案】(2)8π.【解析】(1)PD =1PC =,2CD =,则222 PC PD CD PC PD +=⇒⊥,又AP PD ⊥,AP PC ⊥,PC PD D ⋂=,AP ⊥平面PCD .所以111111233232A PCD PCD V S AP PC PD PA -=⋅=⨯⋅⋅⋅=⨯⨯=△ (2)将三棱锥补成长方体知三棱锥A PCD -的外接球的直径即为长方体的体对角线长,即2R R ==,所以球的表面积为24π8πR =. 4.(2021·河北定州·高一期中)定州市某广场设置了一些多面体形或球形的石凳供市民休息.如图(1)的多面体石凳是由图(2)的正方体石块截去八个相同的四面体得到,且该石凳的体积是3160000cm 3(1)求正方体石块的棱长;(2)为争创全国文明城市,现将表面脏污,棱角轻微磨损的多面形石凳(图(1))打磨成一个球形的石凳,并用一种环保底漆全面粉刷.已知这种底漆一瓶的净含量为235克,可粉刷21.5m 左右,求此球形石凳最大时,一瓶环保底漆大约可以粉刷几个球形石凳?(精确到1)(π按3.14算)【答案】(1)40cm ;(2)3个.【解析】(1)设正方体石块的棱长为a , 则每个截去的四面体的体积为3113222248a a a a ⨯⨯⨯⨯=. 由题意可得331600008483a a ⨯+=, 解得40a =.故正方体石块的棱长为40cm ;(2)当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大.此时正方体的棱长正好是球的直径,∴球形石凳的表面积224041600cm 2S ππ⎛⎫=⨯= ⎪⎝⎭. 41.51031600π⨯≈, 所以一瓶环保底漆大约可以粉刷3个球形石凳.5.(2021·湖北孝感·高一期中)如下图1,一个正三棱柱形容器中盛有水,底面三角形ABC 的边长为2cm ,侧棱14cm AA =,若侧面11AA B B 水平放置时(如下图2),水面恰好过AC ,BC ,11A C ,11B C 的中点.(1)求容器中水的体积;(2)当容器底面ABC 水平放置时(如图1),求容器内水面的高度.【答案】(1))3cm ;(2)3cm .【解析】(1)在图2中,水所占部分为四棱柱.四棱柱底面积为)222112sin 601sin 6022S cm =⨯⨯︒-⨯⨯︒=,又高为4cm所以水的体积为)34V cm ==,(2)设图1中水高度为cm h ,则212sin 602V h =⨯⨯︒⨯=3h =. 所以当容器底面ABC 水平放置时,容器内水面的高度为3cm .6.(2021·福建宁德·高一期中)如图所示是在圆锥内部挖去一正四棱柱所形成的几何体,该正四棱柱上底面的四顶点在圆锥侧面上,下底面落在圆锥底面内,已知圆锥侧面积为15π,底面半径为3r =.(Ⅰ)若正四棱柱的底面边长为a =(Ⅱ)求该几何体内正四棱柱侧面积的最大值.【答案】(Ⅰ)16123π-;(Ⅱ)【解析】设圆锥母线长为l ,高为h ,正四棱柱的高为1h(Ⅰ)由S rl π=圆锥侧,有315l ππ=,故5l =,由222h r l +=,故4h =,所以圆锥体积为2211341233V r h πππ==⨯⨯=圆锥由a =2, 由图可得11h r h r -=,所以11318433r h h r --==⨯=, 故正四棱柱的体积为21816233V a h ==⨯=正四棱柱 所以该几何体的体积为16123V V π-=-圆锥正四棱柱 (Ⅱ)由图可得12r h h r =,即13243h =,即1312h +=由13h +≥,当且仅当136h ==时左式等号成立,有112h a ⇒≤12h =,a =故正四棱柱侧面积14S h a =≤侧12h =,a =所以该几何体内正四棱柱侧面积的最大值为7.(2021·福建福州·高一期中)如图所示的圆锥,顶点为O ,底面半径是5cm ,用一与底面平行的平面截得一圆台,圆台的上底半径为2.5cm ,这个平面与母线OA 交于点B ,线段AB 的长为10cm .(提示:本题的数据有长度单位)(1)求圆台的体积和圆台的侧面积;(2)把一根绳从线段AB 的中点M 开始到点A ,沿着侧面卷绕.使它成为最短时候,求这根绳的长度;【答案】cm 3,75πcm 2;(2)25cm. 【解析】(1)作出圆锥的轴截面和沿OA 剪开的侧面展开图,如下图由下底面半径是5cm ,上底半径为2.5cm ,AB 的长为10 cm ,可得:10OB =cm ,因此圆台的体积为:223115 2.5(33cm )V ππ=⨯⨯⨯=, 侧面积为:2520 2.510)75cm (S πππ=⨯⨯-⨯⨯=.(2)由圆锥的底面周长可得侧面展开图的弧长为10π, 所以,侧面展开图的圆心角为2π,在直角三角形MOA '中15OM =,可得25(cm)MA '=,所以最短时候,绳长为25cm。
小结旋转体的体积绕x轴旋转绕y轴旋转二
OP 的直线方程为: y r x
y
h
于是所求圆锥体的体积为:
V
h
r
0 h
x 2 dx
r 2
h2
x3
3
h
0
r 2h
3
O
x
P(h,r)
r
h
x
当然这个题可以用元素法来解。 3
例2
计算由椭圆
x2 y2 1
a2 b2
所围成的图形绕x轴旋转而成的旋转体
-R
X
O
xR
则底圆的方程为: x2 y2 R2
过 x轴上的点 x 作垂直于 x 轴的平面,截正劈锥体得等腰三角形。
这截面的面积为: A( x) h y h R2 x 2
于是所求正劈锥体得体积为:
R
R
V A( x)dx h
R2 x 2 dx
R
R
2R 2h
a 2 1 4 2 ln 2 1 4 2 2
15
小结
一、旋转体的体积
绕x轴旋
转
V
b
f ( x) 2 dx利用曲线参数方程时 b y 2dx
a
a
绕y轴旋转
按照x (t)换限
V
d
( y)
dy 2 利用曲线参数方程时
于是所求弧长为 s b 1 y'2 dx a
10
例1Biblioteka 计算曲线 y2
3
x2
上相应于
x
从
a
到
b的一段弧的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 b 2 (a 2 x - x 3 ) a 4 ab2 。 连接坐标原点O 及点 P(h, r)的直线、直线
x h及 x轴围成一个直角三角形.将它绕 x轴旋
转构成一个底半径为r 、高为h的圆锥体,计算圆
锥体的体积.
y
P
解 直线 OP方程为
r
o
y x
h
r
h
x
17
§2由平行截面面积求体积
一、平行截面面积为已知的立体的体积 二、旋转体的体积
三、小结
1
一、已知平行截面面积的立体的体积
设一立体在x轴上的投影区间为[a, b] ,过x点垂直于x轴 的截面面积S(x)是x的连续函数,求此立体的体积。
(1) 在[a, b]内插入分点: a=x0<x1<x2< <xn-1<xn=b,
2 a2 (1 - cos t)2 a(1 - cos t)dt 0
a3
2
(1 -
3cos t
3 cos2
t
- cos3
t )dt
52a3 .
0
14
绕 y轴旋转的旋转体体积
y
2a C
B x x2( y)
可看作平面图OABC 与OBC
x x1( y) o
A
2a x
分别绕y 轴旋转构成旋转体的体积之差.
取积分变量为x , x [0, h]
在[0, h]上任取小区间[ x, x dx],
10
以dx 为底的窄边梯形绕x 轴旋转而成的薄片的
体积为
y
dV
r h
x
2
dx
o
P
r
h
x
圆锥体的体积
V
h 0
r h
x
2
dx
r 2 h2
x3 h 3 0
hr2 3
.
11
2
2
2
例 5 求星形线 x 3 y 3 a 3 (a 0)绕 x轴旋转
解 取积分变量为y , y [0,4]
体积元素为
P
dy Q M
dV [PM 2 - QM 2 ]dy 3 [(3 4 - y)2 - (3 - 4 - y)2]dy
12 4 - ydy,
4
V 120 4 - ydy 64.
16
三、小结
绕 x轴旋转一周
旋转体的体积
绕 y轴旋转一周
平行截面面积为已知的立体的体积
直线x a 、x b 及x 轴所围成的曲边梯形绕
x 轴旋转一周而成的立体,体积为多少?
取积分变量为x ,
y
y f (x)
x [a,b]
在[a,b]上任取小区 o
x x dx
x
间[ x, x dx],
取以dx 为底的窄边梯形绕x 轴旋转而成的薄
片的体积为体积元素, dV [ f ( x)]2 dx
2 -R
3
4
例 2 求以半径为 R的圆为底、平行且等于底圆
直径的线段为顶、高为h的正劈锥体的体积.
解 取坐标系如图
y
底圆方程为
x2 y2 R2,
o x Rx
垂直于x 轴的截面为等腰三角形
截面面积 A( x) h y h R2 - x2
立体体积
V
h R -R
R2 - x2dx 1 R2h. 2
i 1
S(x)dx
a
3
例 1 一平面经过半径为 R的圆柱体的底圆中心,
并与底面交成角 ,计算这平面截圆柱体所得立
体的体积.
解 取坐标系如图
-R
底圆方程为
x2 y2 R2
o
y
x
R
垂直于x 轴的截面为直角三角形
x
截面面积 A( x) 1 (R2 - x2 )tan ,
2
立体体积 V 1 R (R2 - x2 )tandx 2 R3 tan .
5
二、旋转体的体积
旋转体就是由一个平面图形饶这平面内一 条直线旋转一周而成的立体.这直线叫做旋 转轴.
圆柱
圆锥
圆台
6
旋转体:
由连续曲线 yf (x)、直 线 xa 、ab 及 x 轴所围成 y 的曲边梯形绕 x轴旋转一周
而成的立体。
讨论:
Oa
旋转体的体积怎样求?
yf (x) bx
7
一般地,如果旋转体是由连续曲线 y f ( x) 、
旋转体的体积为 V b [ f ( x)]2 dx a
8
曲线y=f(x)绕
x
轴旋转而成的立体体积:V
b
a
[f(x)]2dx。
例3
求椭圆 x 2 a2
y2 b2
1
绕x轴旋转产生的旋转体的体
b y y b a2 - x2 a
积。
解:椭圆绕 x 轴旋转产生
O
ax
的旋转体的体积:
a
Vx 2 0
y2dx 2 a b 2 (a 2 -x 2 )dx
体积为
y
V d [ ( y)]2 dy c
d
x ( y)
c
o
x
13
例 6 求摆线 x a(t - sin t),y a(1 - cos t)的
一拱与 y 0所围成的图形分别绕 x轴、y 轴旋转
构成旋转体的体积.
y( x)
解 绕x 轴旋转的旋转体体积
Vx
2a y2 ( x)dx
0
a 2a
Vy
2a
x
2
2
(
y)dy
-
0
2a
x
2
1
(
y
)dy
0
a2 (t - sin t)2 a sin tdt 2 - a2 (t - sin t)2 a sin tdt 0
a3 2 (t - sin t)2 sin tdt 63a3 . 0
15
例 7 求由曲线 y 4 - x2及 y 0所围成的图形 绕直线 x 3旋转构成旋转体的体积.
构成旋转体的体积.
y
2
2
2
解 y3 a3 - x3,
y2
2 a 3
-
2
x3
3
-a
x [-a, a]
o
ax
旋转体的体积
V
-aa
a
2 3
-
2
x3
3
dx
32 105
a3 .
12
类似地,如果旋转体是由连续曲线
x ( y) 、直线 y c 、 y d 及y 轴所围
成的曲边梯形绕y 轴旋转一周而成的立体,
O a x1
xi-1 xi
xn b x
2
(2)过xi(i=1, 2, , n-1)且垂直于x轴的平面,把立体分割成n 个小薄片,第i个小薄片体积的近似值S(xi)Dxi。
将n个小薄片体积的近似值相加得立体体积的近似值
n
V S(i)xi。
i1
(3) 立体体积为
n
b
V
lim
T 0
S(xi )
