水面曲线计算
天然河道水面曲线计算问题说课材料

Wh g V Z g V Z ++=+22211222αα推求法计算天然河道水面曲线的局限性 和解决办法---暴雨洪水的水力学模型及其应用程序张校正(新疆水利厅 新疆乌鲁木齐 830000)【摘 要】 天然河道水面曲线计算的‘推求法’使用中是有很多限制的,很多情况下不便应用,应该与‘比降法’配合使用,解决天然河道水面曲线计算问题。
【关键词】 天然河道 水面曲线 推求法 比降法 水力学模型 应用程序2012年,暴雨洪水给我国很多地方造成了生命财产的重大损失,引起了防洪部门的重视,纷纷加大了防洪工程的投入。
因而防洪工程的水力学计算,尤显重要。
怎样计算天然河道的水面曲线?应该不是问题,但一些设计单位确实出现过这个问题,问题是从使用推求法计算天然河道水面曲线时产生的。
在我国的有关防洪工程的规范中,大量的篇幅,是有关工程措施的规定,水力学计算部分内容很少,没有具体的公式。
虽然规范没有详细的公式,但是在旧版的《水工设计手册》以及水力学教科书中,却有‘天然河道水面曲线’的详细论述和方法讲解。
大家都是按照这些常规算法,解决天然河道水面曲线计算问题。
新版的《水工设计手册》也有‘天然河道水面曲线的计算’的章节。
武汉大学水利水电学院出版的《水力计算手册》中也有“河道恒定流水面曲线计算”章节。
对于天然河道的各种水力要素的计算,有着详尽的规定。
上面所说的这些书中的方法是暴雨洪水的一种水力学模型,是一种一维静态的水力学模型,它就是所谓‘推求法’,是从已知水位推求未知水位的计算方法。
本文从这个方法的使用过程中产生的问题,就暴雨洪水的一维静态的其它的水力学模型进行一些研讨。
《水利水电工程设计计算程序集》为天然河道的水力计算提供了两个程序,一个是“D-14A 推求法计算天然河道水面曲线程序”;一个是“D-14B 比降法计算天然河道水面曲线程序”。
一、D-14A 推求法计算天然河道水面曲线程序的使用情况这个程序的方法,是求解下面的基本方程(过去叫做柏努立方程):这是一个在河道上解决非均匀流从已知水位推求未知水位的公式。
水面线计算示例

水面线计算示例注:水面线计算是水利设计的一部分,作为水工设计人员是必须掌握的。
下面以《水力学》第四版 吴持恭编p241的例子进行计算演算开始:1 判定水面曲线形式 a 临界水深求解:m 27.11081.945322322=⨯==gb aQ h k b 正常水深求解因为梯形断面,故正常水深需用迭代法计算(迭代法原理非常简单,首先定一数,代入,求解,再代入,直至误差满足要求)步骤:明渠均匀流流量公式Ri AC Q =;h mh b A )(+=;212m h b ++=X ;X=AR ;611R n C =得mh b m h b inQ h +++=52253))1(2()(迭代开始:kk k mh b m h b i nQ h +++=+522531))1(2()((k=0,1,2,3……….) 取h 0=0;得h 1=8.149;取h 1=8.149;得h 2=1.594;取h 2=1.594;得h 3=1.981;取h 3=1.981;得h 4=1.959;取h 4=1.959;得h 5=1.959,迭代停止,得正常水深为1.96m 。
c 判定陡坡还是缓坡 计算临界坡需同时满足两个公式1 满足临界流: kk B A g aQ 32=(1) 2 满足均匀流 k k k k i R C A Q = (2) 联立(1)、(2)式: 得kk k k k k k k B aC g B R aC gA i 2X ==;6.14122=++=X m h b k k ;16.15)(=+=k k k k h mh b A ;04.1=X =k k k A R ;75.45161==k k R nC ;得i k =0.0068>0.0009=i ,故为缓坡。
d 判定急流还是缓流因正常水深h 0=1.96>1.27=hk (临界水深),故可知为缓流,而末端水深h 为3.4>1.96=h 0(正常水深);可知为壅水曲线。
水力学综合计算说明书(设计水面曲线)

水利计算综合练习计算说明书学校:SHUI YUAN系别:水利工程系班级: 水工班姓名: mao学号:指导老师:XXX2013年06月22日目录一、水力计算资料 2公式中的符号说明 3二、计算任务 4任务一: 4绘制陡坡段水面曲线 4⑴.按百年一遇洪水设计 41、平坡段:(坡度i=0) 4① 水面曲线分析 4② 分段求和计算Co型雍水曲线 52、第一陡坡段(坡度i=0.1) 6① 判断水面曲线类型 6② 按分段求和法计算水面曲线 73、第二陡坡段(坡度 i=1/3.02) 8① 判断水面曲线类型 8② 按分段求和法计算水面曲线 8⑵.设计陡坡段边墙 9⑶.按千年一遇洪水校核 111、水平坡段(坡度i=0) 12① 水面曲线分析 12② 分段求和计算Co型雍水曲线 132、第一陡坡段(坡度i=0.1) 14① 判断水面曲线类型 14②按分段求和法计算水面曲线 143、第二陡坡段(坡度 i=1/3.02) 16① 判断水面曲线类型 16② 按分段求和法计算水面曲线 16① 千年校核的掺气水深 17② 比较设计边墙高度与千年校核最高水深的大小 19⑷.绘制水面曲线及边墙 21任务二: 24绘制正常水位至汛前限制水位~相对开度~下泄流量的关系曲线 24 任务三: 26绘制汛前限制水位以上的水库水位~下泄流量的关系曲线 26三、总结 29、水力计算资料:某水库以灌溉为主,结合防洪、供电和发电、设带弧形闸门的驼峰堰开敞式河岸溢洪道。
1.水库设计洪水标准:百年一遇洪水(P=1%)设计相应设计泄洪流量Q=633.8 m^3/s相应闸前水位为25.39 m相应下游水位为4.56 m千年一遇洪水(P=0.1%)校核相应设计泄洪流量Q=752.5 m^3/s相应闸前水位为26.3 m相应下游水位为4.79 m正常高水位为24.0 m,汛前限制水位22.9 m。
2.溢洪道的有关资料:驼峰剖面选用广东省水科所1979年提出的形式(参阅武汉水院水力学教研室编的水力计算手册,P156图3-2-16a)。
流体力学7-6水面曲线分析

一、概述
棱柱形渠道恒定非均匀渐变流 水面曲线的分析
明渠非均匀流水深沿程变化,自由水面线是和渠底不 h f (s) 平行的曲线,称为水面曲线
1、根据沿程v、h变化程度不同 非均匀渐变流
非均匀急变流
2、定性分析
壅水曲线:h沿程增加,dh/ds>0 降水曲线:h沿程减少,dh/ds<0 均匀流: h沿程不变,dh/ds=0
dh Q dh i B J 0 3 ds gA ds
2
3
棱柱形渠道非均匀渐 变流微分方程
dh ds
iJ 1
Q2
gA
3
B
iJ 1 Fr
上式是在顺坡(i>0)的情况下得出的,是分析计
算水面曲线的理论基础。
三、水面曲线分析的二线三区
水面曲线的变化决定于式中分子、分母的正负变化。 分子i-J=0 对应两条直线将水面曲线 分成变化规律不同三个曲域 分母1-Fr =0 分析i-J/(1-Fr)的正负(单调增减性),便可得到水面 曲线沿程变化的趋势及两端极限情况
2
3 曲线 S1
S2
S3
hc > h> h0 急流
hc >h0 > h 急流
+ - -
+
下凹的降水曲线
上凸的壅水曲线
S2
S3
上游渐近线 下游渐近线 工程实例 水跃h→hc 水平线h→∞ 修挡水建筑物 dh/ds→∞正交 dh/ds→i 静止 水跌h→hc N-N线h→h0 dh/ds→-∞正交 dh/ds→0 均匀流 由缓坡入急坡 受出流条件限制 挡水建筑物下泄 同上
4
1、分界线h0、hc 正常水深线:N-N(分子为零)
水面曲线教程

4、无压圆管均匀流的水力计算
这里主要介绍城市下水道的水力计算。
1)无压圆管均匀流的水流特征:
①属明渠均匀流:J=Jp=i;
② Q=Qmax 发生在满流之前。
即水力最优断面的充满度
mh/d0.95
第二十四页,共79页。
6-2 明渠恒定均匀流
(1)几个概念
第六章 明渠水流水力计算
充满度h/d
最大流速充满度V=Vmax
h/d0.81 25.75
第二十六页,共79页。
第六章 明渠水流水力计算
6-2 明渠恒定均匀流 2) 无压圆管水力计算
① 校核过流能力:已知d, n, 和i, 求Q
② 设计底坡:已知Q, d, n, 求 i
i Q2 / K2
③ 设计d:已知Q, n, i和 求d
这类问题必须试算。
①连续方程
②谢才(Chezy)公式 ③曼宁(Manning)公式
第十一页,共79页。
第六章 明渠水流水力计算
6-2 明渠恒定均匀流
3.水力最优断面和允许流速
1)水力最优断面:给定渠道断面 形状、尺寸、断面面积A、n 、i,
能通过的Q=Qmax。(或通过给定流 量,A=Amin )。
以梯形断面为例:当A=const, 欲 使Q=Qmax,
第六章 明渠水流水力计算
是最常见的人工渠道。其基本几何参数为水深h、底
宽b和边坡系数m。
边坡系数 定。
,由土壤的力学性质决
过水断面面积
水面宽
湿周
水力半径
。当m=0,为矩形断面。
第六页,共79页。
6-1 概述
第六章 明渠水流水力计算
推算水面曲线

0.003093 0.002911 0.002744 0.002592 0.002451 0.002322 0.002203
2 Q 2 A p 1
2
2 2 Q n 2 4 A R p 1 p
/ 3 1
渠道水面线的计算 非棱柱形渠道,输入假设分段长度后,按“水深计算”按钮即可) 流量 不均匀系数 糙率 底坡 断面比能 比能损失 ES △ES Q α n i 1 1 1 1 1 1 1 1 1 1 1.05 1.05 1.05 1.05 1.05 1.05 1.05 1.05 1.05 1.05 0.014 0.001 0.014 0.001 0.014 0.001 0.014 0.001 0.014 0.001 0.014 0.001 0.014 0.001 0.014 0.001 0.014 0.001 0.014 1.329347 1.349295 -0.01995 1.369245 -0.01995 1.389199 -0.01995 1.409156 -0.01996 1.429115 -0.01996 1.449076 -0.01996 1.469039 -0.01996 1.489005 -0.01997 1.508387 -0.01938
渠道水面线的计算 (假设水深,推求分段长度,适用于棱 断面面积 流量 A Q 1.610793606 1.650774935 1.690724234 4.4 4.4 4.4
2 0.97 3 1.65
1.06
1.65 4 2.40 5 3.23 6 4.13 7 5.13 8 6.24 9 7.47 10 1.20 31.57 1 1.968113373 4.4 1.18 24.10 1 1.928842714 4.4 1.16 17.86 1 1.889425648 4.4 1.14 12.73 1 1.849878898 4.4 1.12 8.60 1 1.810219023 4.4 1.10 5.38 1 1.770462438 4.4 1.08 2.97 1 1.730625442 4.4
水面曲线计算
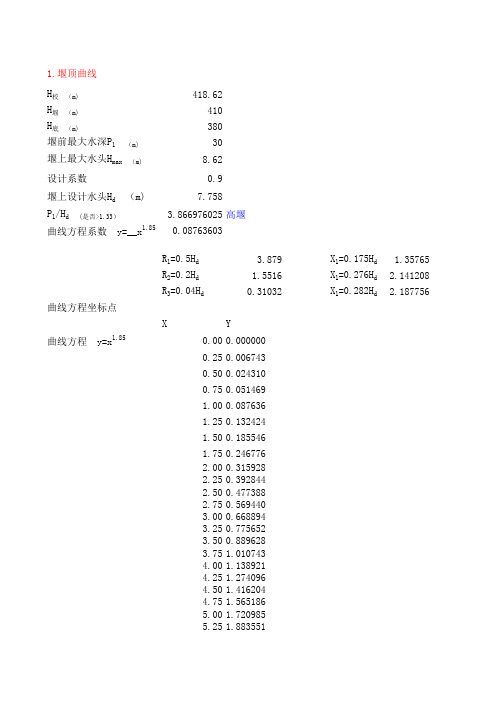
X1=0.175Hd X1=0.276Hd X1=0.282Hd
1.35765 2.141208 2.187756
5.50 2.052833 5.75 2.228785 6.00 2.411363 6.25 2.600523 6.50 2.796227 6.75 2.998435 7.00 3.207112 7.25 3.422221 7.50 3.643729 7.75 3.871603 8.00 4.105813 8.25 4.346328 8.50 4.593119 8.75 4.846158 9.00 5.105418 9.25 5.370873 9.50 5.642497 9.75 5.920266 10.00 6.204156 10.25 6.494143 10.50 6.790205 10.75 7.092321 11.00 7.400468 11.25 7.714626 11.50 8.034775 11.75 8.360895 12.00 8.692966 12.25 9.030971 12.50 9.374891 12.75 9.724707 13.00 10.080403 13.25 10.441961 13.50 10.809365 13.75 11.182597 14.00 11.561643 14.25 11.946486 14.50 12.337112 14.75 12.733504 15.00 13.135649 15.25 13.543531 15.50 13.957137 15.75 14.376452 16.00 14.801464 16.25 15.232157 16.50 15.668521 16.75 16.110540 17.00 16.558203
1.75 0.246776
4.2 水面线计算

4.3下细坑涌河道水面线计算
由于本项目的建设为对现状下细坑涌长115m (2号涌)进行整治,因此,需对整治后下细坑涌的过流能力进行计算,采用水面线公式计算。
4.3.1 计算方法
采用渠道恒定渐变流水面曲线的计算,需要求解明槽恒定渐变流的微分方程:
J i ds
dE s
-= (4-8)
式中:J 、i ——渠道的水力坡度和底坡; s ——渠道沿流动方向的沿程坐标,m ; E s ——明槽过水断面的断面比能,m 。
小底坡渠道的断面比能表达式为:
2
2
2
22gA
Q h g
v h E s αα+
=+
= (4-9)
式中:Q ——流量,m 3/s ; g ——重力加速度,m/s 2; α——动能修正系数; h ——水深,m ; v ——流速,m/s ; A ——过水断面面积,m 2;
4.2.2 设计水面线计算
1)起始断面的水位
本文以下细坑涌河口处的针咀水闸闸前水位,作为下细坑涌设计水面线计算的起始水位。
已知2号涌设计洪峰流量为3.859m3/s,由起始断面的水位流量关系得出起始水位为4.22m。
2)河道糙率
本设计河涌护岸和河底材料为现浇C30砼,根据《水力计算手册》(第二版),本设计河涌糙率n采用0.017。
3)设计水面线成果
以前述起始断面的水位作控制,根据整治后下细坑涌横断面及河道糙率,采用式4-8、4-9推求20年一遇洪水时的水面线,成果见表4-7。
表4-7 整治后下细坑涌设计水面线成果表。
立新水库溢洪道水面曲线计算
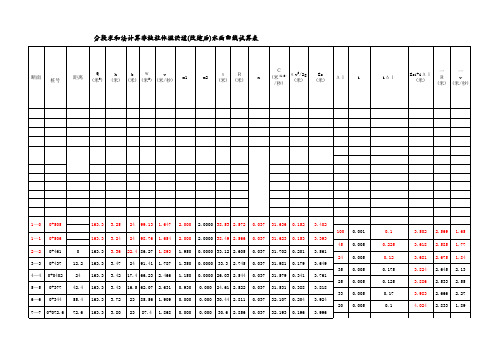
一 Es2+JΔ l (米) 0.247 2.264 1.907 2.040 2.219 3.067 4.097 0.1444 0.36575 0.91 1.153846 0.176582 0.385
0.3116
50.328 45.433 41.567 41.235 39.301 38.101
0.00090 0.005 0.00215 0.026 0.00300 0.038 0.00453 0.080 0.01616 0.210 0.03702 0.637
36.64 2.026
#REF!
#REF! 0.937
124.9 13.44 2.479 2.79
0.01454
19.251 0.938
125.68 6.27
0.36
一 C (1/2)一 Es2+JΔ l (米)
分析和绘制水面曲线时,缓流应从下 游的控制断面向上游推算,而急流应 从上游控制断面向下游推算
临界坡度按公式ik=gχ k/(α C2Bk)计算,再与实际坡度相比,判别是否是急流. 0.001604
一 C (1/2) (米 /秒)
一 J
一 JΔ l (米)
一 Es2+JΔ l (米) 2.331 2.205 2.228 2.260 5.518 #DIV/0! 0.75 118.85 缓流 118.86
0.22278481 0.87 1.146666667 0.76
2.225 3.006 3.932 4.059
1.203 0.923 0.759 0.802
3.04 4.71 6.15 6.59
可能有2个水深符合 单宽流量 4.2375 50.85/12 临界水深1.22367 POWER(L54*L54/9.8,1/3)
天然河道水面曲线的推求方法

工作探索2018年第01期1520%、40%、60%、80%和100%共5个点。
参考文献:[1] 秦海峰,刘永录,王磊.扭矩扳子校准结果的不确定评定方法[J].计测技术,2011,31(6):45-47.[2] 史文渤.扭矩扳子测量不确定度评定[J].计量与测试技术,2014, 41(6):88.随着近几年暴雨洪水灾难的产生,需要各个部门对其更为重视。
所以,对防洪工程进行计算十分必要。
基于推求方法得使用,是一种暴雨洪水水力学模型,在整体上为静态式,基于存在的水位推求未知水位计算方法,因此,要对其进行积极探讨。
1 推求方法的利用推求方法的使用,是对河道上的非均匀流进行分析,基于存在的水位推求,分析未知的水位。
当还没有计算机年代下,对其计算将面对较大困难,在整体上也更为困难。
后期,随着对计算机的使用,一些技术人员开始基于计算机编程工作,重点对其存在的问题进行解决。
但是,计算后获得的结果还不够合理。
经过人们在工作中对各个程序的检查和分析,得出一些合理方法。
当计算水库回水曲线的时候,能获得更为合理的结果。
但是,如果将其应用到山区河流中,或者应用到还没有产生大洪水河流地区、季节性干涸河流地区的时候,将产生各个问题。
针对实际应用效果发现,该方法的使用需要具备一些条件。
其表现在三个方面。
第一,对起始断面水深进行计算期间,要为其提供合理依据,不能随意设定。
第二,还需要保证断面之间的水流,分析其具备的性质。
第三,断面之间的距离也不能太长,保证能满足一定的计算要求。
如果这些条件无法满足,将无法保证计算效果,也不能对其有效应用。
起始断面水深,是基于河道的延伸,为断面水位。
但是,在河流中,特别是小河流中还未产生大洪水河流。
当处于季节性干涸河流的时候,也无法确定出已知水位。
在该情况下,将对其随意设定,无法满足水力学要求,也不能确保计算结果的准确性。
所以说,起始断面水深度存在一些问题。
因此,对水库回水曲线进行计算的时候,可以分析正常水位,利用推求方法保证计算结果更合理、更可靠。
基于Excel的水面曲线计算程序编制

基于Excel的水面曲线计算程序编制张家锐王敏(云南省水利水电勘测设计研究院,云南昆明650021)摘要:工程实际中,解决水力学问题时,正常水深、临界水深、水面线等高次隐函数,难以直接求解。
传统方法是利用查图表求解或用试算法求解,也可利用编程求解,但都不太方便。
利用Excel单变量求解功能可快捷、精准地解决水力学计算中高次隐函数方程问题。
配合宏的运用,编写出了可求变底坡,变断面渠道任意位置水深的水面曲线推求程序。
本文介绍了单变量求解功能在求解高次隐函数中的运用,并介绍宏在水面曲线推求过程中对多次求解的集成功能。
关键词: 水力学;高次隐函数;水面曲线;Excel;单变量求解;宏Compilation methods based on Excel for calculation program of watersurface profileZHANG Jia-rui,WANG Min, YU Rui-li(Yunnan Institute of Water & Hydropower Engineering Investigation ,Design And Research, Kunming650021,China)Abstract: In engineering practice, some hydraulic problems such as normal depth, critical depth and water surface profile, which are higher implicit functions, are difficult to solve directly. Traditional methods solved them by “trial method” and “graph method” or by programming, but all of them are not convenient. Using goal seek in Excel, the higher implicit function equations of hydraulic calculation can be solved quickly and accurately. With the use of macros, a water surface profile calculation program which can solve water depth at any position of channel with variable slop or section size was written. This paper introduces the application of solving higher implicit function by goal seek and integration of multiple solving by macros in water surface profile calculation.Key words: hydraulic; higher implicit function; water surface profile; Excel; goal seek; macros在工程实际中,解决水力学问题,难以避免地会遇到正常水深、临界水深、水面线等求解问题,这些待求量往往是高次隐函数,难以直接求解。
05 非棱柱体渠道水面线计算

专题5. 非棱柱体渠道水面线计算对实际工程中的非棱柱体渠道的水面曲线的计算,其基本计算原理与棱柱体渠道相似,但非棱柱体渠道没有临界水深、临界底坡等,断面形状随流程发生变化,故不能完全采用棱柱体渠道的计算方法。
这种情况下,应首先确定断面位置,然后想办法求出断面水深。
基本公式如下:Ji E E Ji E l s s s --=-∆=∆12 (5-1)式中:1s E 、2s E 分别表示流段上、下游断面的断面比能;J 表示流段内的平均水力坡度;i 表示渠道的底坡;l ∆为流段长度。
流段的平均水力坡度J 一般采用以下方法计算:)(2121J J J +=(5-2) 22KQ J =(5-3)流量模数平均值K 或2K 可用以下三种方法之一计算:(1) R C A K = (5-4)式中:)(2121A A A +=,)(2121C C C +=,)(2121R R R += (2) )(2122212K K K += (5-5)(3))1(21122212K K K+=(5-6) 具体步骤如下:(1)将非棱柱体的渠道分成若干断面,并确定各断面之间的间距i l ∆。
(2)从控制断面起,以控制断面为断面1-1,对断面1-1和断面2-2之间的流段,即第一个流段进行分析,使用试算法确定断面2-2处的水深。
用试算法确定断面2-2水深的基本方法是,先给断面2-2假定一个水深2h ,用这个假定的水深确定断面2-2的断面尺寸和水力参数。
将这个断面上的假定的水力参数与断面1-1的相关参数结合,代入公式5-1计算第一流段的长度1l ∆,若1l ∆与实际分段的长度相等,则假设的水深2h 即断面2-2的实际水深;反之,则不是所求水深,重新给断面2-2水深赋值计算。
(3)依照第一个流段分析的方法,依次计算断面3-3、断面4-4、……,直至计算最远处的断面水深。
需要注意的是,与棱柱体水面线的计算方法一样,分段越多,精度也越高,但计算量也越大。
天然河道水面曲线计算问题

天然河道水面曲线计算问题新疆水利厅张校正在水力学教科书中,论述天然河道水面曲线计算的方法时,一般都是对河道相邻两断面列出伯努立方程,从已知断面水位,依次求解此方程,得出未知断面的水位,这些断面的水位的连线,就认为是河道的水面曲线。
《程序集》中的D-14A就是按照这个原理编制的。
一、D-14A的程序功能已知天然河道各横断面的地形点坐标及糙率,从起始断面水位开始,按照伯努里方程,逐段向上游或者向下游推算,求出各断面的水位。
计算结果输出地形点坐标,绘出河道横断面图,标出水位,打印流量、平均流速值。
1,河床的糙率可以随地形点的不同而变化。
2,局部阻力系数可随不同河段选用不同值。
3,程序采用二分法,优选试算,从而加快了收敛。
二、D-14A的计算原理1,水面曲线计算原理:Wh gV Z gV Z ++=+22211222αα如图示,根据伯努里方程:-------------(1)式中:Z 1、V 1 -- 断面1的水位和流速; Z 2、V 2 -- 断面2的水位和流速;h W = h y + h j -- 断面1到断面2之间的水头损失;h y = j ×ΔL -- 沿程水头损失; j = V 2/(C 2R) -- 沿程摩阻坡度;V C ,R -- 断面1和断面2的平均流速、平均流速系数、平均水力半径;ΔL -- 两断面间的距离; h j =-ξ(V 12/2g-V 22/2g)—局部水头损失;ξ -- 河段的局部阻力系数,在顺直河段及收缩河段ξ=0,()022222121=∆⨯+⎪⎪⎭⎫⎝⎛--+-L j g V g V Z Z ξα()022222121=∆⨯+⎪⎪⎭⎫⎝⎛--+-=L j g V g V Z Z K ξα逐步扩散河段ξ=(0.3~0.5), 急剧扩散河段ξ=(0.5~1.0)。
将(1)式移项:--------------(2)方程 (2) 中,Z 1,V 1,α,ξ,ΔL 均为已知,采用二分法试算求解Z 2。
分段求和法计算天然河道水面曲线

1 1 6 2 0 0 )
要】 人们对水情 的观察 , 主要是研究水位 的变化 , 因此 天然河道 水面 曲线的计算便 成为 河道规 划设计 中的
重 要 环 节 。 本 文 以太 阳河 河段 为例 , 采 用 分 段 求和 法 推 求 该 河 段 的水 面 曲 线 。 计 算 过 程 及 相 关 理 论 可 为 类 似 工 程 计算提供参考 。
为了正确反映河道 的实 际情况 , 提高计算 精度 , 对 天然河道分段应遵循 以下原则 : a .每个计算 流段 内, 过 水断 面形状 、 尺寸 、 粗 糙 系
数及底坡变化不要太大 。 b .在 一 个 计 算 流 段 内 , 上游 、 下游 水 位 差不 要太
不得不采 用某 种平均值 作为计算依据 。人们 对水情 的 观察 , 首 先关注 的是 水位 , 因此研 究河 道水 面 曲线 时 ,
Ke y wo r d s :n a t u r a l r i v e r c h a n n e l ;wa t e r s u r f a c e c u v e;s r u b s e c t i o n s u mma t i o n me t h o d ;h y d r a u l i c e l e me n t s
r i v e r s e c t i o n .T h e c a l c u l a t i o n p r o c e s s a n d r e l a t e d t h e o r y c a n p r o v i d e r e f e r e n c e o f r c a l c u l a t i o n i n s i m i l a r p r o j e c t s .
分段求和法计算天然河道水面曲线

分段求和法计算天然河道水面曲线鞠福勇【摘要】人们对水情的观察,主要是研究水位的变化,因此天然河道水面曲线的计算便成为河道规划设计中的重要环节.本文以太阳河河段为例,采用分段求和法推求该河段的水面曲线.计算过程及相关理论可为类似工程计算提供参考.【期刊名称】《水利建设与管理》【年(卷),期】2017(037)005【总页数】4页(P28-31)【关键词】天然河道;水面曲线;分段求和法;水力要素【作者】鞠福勇【作者单位】大连市普兰店区河道管理处,辽宁大连 116200【正文语种】中文【中图分类】TV131天然河道的过水断面一般极为不规则,粗糙系数、底坡沿流程都有变化,可视为非棱柱形明渠。
在河道中修建桥梁、闸、坝等建筑物时,必然会遇到建筑物建成后所引起的有关水面曲线的一些问题,如:护岸设计高度、雍水淹没范围等。
在天然河道中,估算建筑物建成后新的水面曲线最大的困难在于天然河道中水力要素变化急剧,因而不得不采用某种平均值作为计算依据。
人们对水情的观察,首先关注的是水位,因此研究河道水面曲线时,主要研究水位的变化,这样天然河道水面曲线的设计便自成系统。
虽然它与人工渠道水面曲线的计算不同,但无本质区别。
天然河道水面曲线的计算方法很多,第一类是分段求和法,第二类是将不规则的天然河道人为地简化为具有平均底坡的棱柱形渠道,以此代替天然河道水面曲线的计算。
第一类在工程中较为常用,故本文利用分段求和法计算天然河道水面曲线。
为了正确反映河道的实际情况,提高计算精度,对天然河道分段应遵循以下原则:a.每个计算流段内,过水断面形状、尺寸、粗糙系数及底坡变化不要太大。
b.在一个计算流段内,上游、下游水位差不要太大,平原河流一般Δz取0.2~1.0m,山区河流一般Δz取1.0~3.0m。
c.计算流段内不要有支流汇入或流出。
若有支流存在,必须把支流放在计算流段的起始端或末端,对汇入的支流一般放在流段的起始端,对流出的支流一般放在流段的末端。
