【数学】1.5.1 平行关系的判定----平面与平面平行的判定 课件 (北师大版必修2)
合集下载
平面与平面平行的判定PPT
平面与平面平行的判定PPT简介本文档将会介绍如何通过PPT进行平面与平面平行的判定。
该PPT将针对学生群体，以简单明了的方式讲解平面与平面平行的概念，并通过实例演示如何进行判定操作。
本文中的PPT操作与示例均基于PowerPoint 2016版本。
平面与平面平行平面是由无限多个点构成的二维图形，可以用一条或多条直线作为基本元素进行描述。
平面经常被用来描述三维空间中的物体表面，通过平面的交角可以判断物体间的位置关系。
平面平行指的是两个平面之间没有任何交点。
如果有交点，则称两个平面不平行。
平面平行是一种十分常见的几何关系，在工程、建筑等领域中也有广泛应用。
在三维空间中，平面与平面平行的判定操作是一项基本的几何操作，在很多实际问题中都具有重要意义。
下面将介绍如何利用PPT进行平面与平面平行的判定。
平面与平面平行的判定步骤1.平面方程平面方程是平面的一种标准化表示方法，通过一些参数来描述平面的特征。
常见的平面方程有点法式方程和截距式方程等。
在本文中，我们选择点法式方程来表示平面。
点法式方程可以表示为：Ax+By+Cz+D=0含义为平面上一点的坐标为(x,y,z)，法向量为(A,B,C)，D为常数。
2.法向量平面的法向量是垂直于平面的一条向量，可以根据平面方程求解。
法向量是判定平面与平面平行关系的重要基础。
求解法向量的方法可以通过计算两条平面的向量积得到：n = (a1b2 - a2b1, a2b0 - a0b2, a0b1 - a1b0)其中，(a0,a1,a2)和(b0,b1,b2)分别为两条平面的系数。
3.平行判定找到两个平面的法向量后，只需要判断两个法向量是否平行即可。
法向量平行意味着两个平面平行，反之则不平行。
两个向量平行的判定方法可以通过计算两个向量的夹角得到：如果夹角为0，则两个向量平行；如果夹角为180度，则两个向量相反。
在具体操作中，我们可以利用PPT来展示必要的计算过程，并通过示例演示判定过程。
【全国百强校】江西省鹰潭市第一中学高一数学课件：北师大版 必修二 1.5.1平行关系的判定(共20张PPT)
授课人：宁美芳
【课例名称：《平行关系的判定》(第一课 时）】 【学段：高中】
【学科：数学】 【年级：高一】 【版本：北师大版（必修二）】
知识回顾: 在空间中直线与平面有几种位置关系？
线在面外
α
位置关系
符号表示 交点个数
a
a
α
A
a
α
线在面内
相交
平行
a
无数个
a ∩α =A
一个
a //α
0个
定理运用:
例3 空间四边形ABCD中,E,F分别为AB,AD的中点， 求证：EF//平面BCD.
证明：连接BD 在ABD中,E, F分别是
AB, AD的中点, EF//BD EF 平面BCD
BD 平面BCD EF // 平面BCD
A
E F D B
C
分析：解决此题的关键是 能在平面BCD内找(作)一 条与直线EF平行的直线.
问题概括：
如何用语言表述（或定义）直线与平面平行呢？
定义：一条直线和一个平面没有公共点，
叫做直线与平面平行.
a
(a //α)
A
B
新知探究： 怎样判定直线与平面平行呢？ 根据定义，判定直线与平面是否平行，只 需判定直线与平面有无公共点.但是直线是无限 延伸的，平面是无限延展的，用有无公共点来 判断不大方便，因此有必要寻找一个便捷、可 行的判断直线和平面平行的方法.
变式训练:
(2)在例3基础上，若H
成立
CH CG HB GD BC, G DC, H , G满足 _______
(1)若将例3条件改为：AE : EB AF : FD, 结论成立吗？
条件; 使得HG // 平面ABD，此时，E, F , H , G共面吗？
【课例名称：《平行关系的判定》(第一课 时）】 【学段：高中】
【学科：数学】 【年级：高一】 【版本：北师大版（必修二）】
知识回顾: 在空间中直线与平面有几种位置关系？
线在面外
α
位置关系
符号表示 交点个数
a
a
α
A
a
α
线在面内
相交
平行
a
无数个
a ∩α =A
一个
a //α
0个
定理运用:
例3 空间四边形ABCD中,E,F分别为AB,AD的中点， 求证：EF//平面BCD.
证明：连接BD 在ABD中,E, F分别是
AB, AD的中点, EF//BD EF 平面BCD
BD 平面BCD EF // 平面BCD
A
E F D B
C
分析：解决此题的关键是 能在平面BCD内找(作)一 条与直线EF平行的直线.
问题概括：
如何用语言表述（或定义）直线与平面平行呢？
定义：一条直线和一个平面没有公共点，
叫做直线与平面平行.
a
(a //α)
A
B
新知探究： 怎样判定直线与平面平行呢？ 根据定义，判定直线与平面是否平行，只 需判定直线与平面有无公共点.但是直线是无限 延伸的，平面是无限延展的，用有无公共点来 判断不大方便，因此有必要寻找一个便捷、可 行的判断直线和平面平行的方法.
变式训练:
(2)在例3基础上，若H
成立
CH CG HB GD BC, G DC, H , G满足 _______
(1)若将例3条件改为：AE : EB AF : FD, 结论成立吗？
条件; 使得HG // 平面ABD，此时，E, F , H , G共面吗？
平面与平面平行的判定课件
12
1面.线面面平平行行的是判否定可定用理其它条件代替？ 变式探究
如果一个平面内有两条 相交直线分别 平行于另一个平面，那么这两个平面平行。
a ?? , b?? a? b=P a // ?
b //
?
? // ? ?
?
a ?b
a'
可用什么 条件代替？
2020年1月14日
线面平行 转 化 线线平行？ 13
2020年1月14日
1
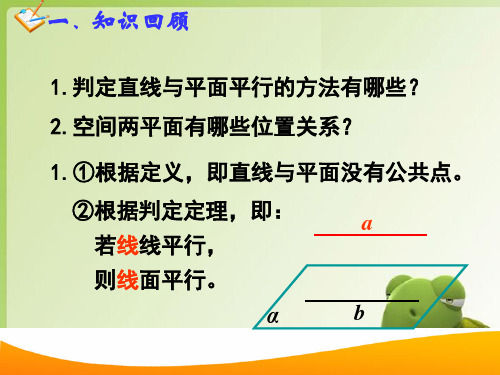
一、知识回顾
1.判定直线与平面平行的方法有哪些？ 2.空间两平面有哪些位置关系？
1.①根据定义，即直线与平面没有公共点。
②根据判定定理，即：
a
若线线平行，
则线面平行。
α
b
2020年1月14日
2
一、知识回顾
1.判定直线与平面平行的方法有哪些？ 2.空间两平面有哪些位置关系？
相交
面β, 则α∥ β吗?
直观
感受
2020年1月14日
8
二、新知探究
问题3 平面α内有两条相交直线 a , b
平行平面β, 则α∥ β吗?
C
B
动手 体验
?
A
当三角板ABC的两条边BC、
AB都平行桌面? 时，ABC所
在的平面是否平行桌面? ？
2020年1月14日
9
问题3 平面α内有两条相交直线 a , b 平行平
求证：平面AB1D1∥平面C1BD.
变探式究::已知正方体ABCD-A1B1C1D1（如图），
P求A,1证QP=,：AR分平1Q别面=A为P1QRAR1(A∥P,,Q平A,R1面B在1,CA正1B1DD方1.体的的中棱点上 )
D
平面与平面平行的判定ppt正式完整版
AC、BC、SC的中 ∴平面EFG∥平面ABC.
本节学习难点：平行关系的相互转化．
点，试
判断SG与
平面DEF的
位置关系，
∴PA∥平面D1BQ.
并给予证明． 观察图形可以看出：连结CG与DE相交于H，连结FH，FH就是适合题意的直线．
∵P，Q分别为DD1，CC1的中点，
[解析] 当Q为CC1的中点时，平面D1BQ∥平面PAO.
[例2] 已知点S是正三角形ABC所在平面外的一点，
(2)依判定定理通过一平面内有两相交直线与另一平面平行来判定两平面平行(线面平行⇒面面平行)．
∵[点E评F⊄] 平应面且用SA定SB理，A时S＝B，⊂一平S定面B要S＝A把B定，S理C的条，件找S全G. 为△SAB边AB上的高，D、E、F分别是
又PQ∩QR＝Q，EF∩FG＝F，PQ，QR⊂平面PQR，EF，FG⊂平面EFG，∴平面PQR∥平面EFG.
c⊂β，d⊂β⇒α∥β
.
3．α∥β，a⊂α⇒ a∥β .
本节学习重点：平面与平面平行的判定定理． 本节学习难点：平行关系的相互转化．
1．由面面平行的定义知，若α∥β，则α与β无公共点， 若a⊂α，则a与β无公共点，从而a∥β.这样我们可以由“面 面平行”得到“线面平行”．
应用判定定理时，应特别注意“两相交直线”这个条 件，否则如右图α∩β＝a，a1∥a，a2∥a，……，a1、a2…… 都与α平行，但显然α不与β平行．
[分析2] 由题设条件中，D、E、F都是棱的中点，不 难得出DE∥AB，DF∥SA，从而平面DEF∥平面SAB，
又SG⊂平面SAB，从而得出SG∥平面DEF. [证法2] ∵EF为△SBC的中位线， ∴EF∥SB. ∵EF⊄平面SAB，SB⊂平面SAB， ∴EF∥平面SAB. 同理：DF∥平面SAB，EF∩DF＝F， ∴平面SAB∥平面DEF， 又∵SG⊂平面SAB，∴SG∥平面DEF.
平面与平面平行的判定课件ppt
1.线面平行是否可用其它条件代替？
变式探究
如果一个平面内有两条 相交 直线分别 平行于另一个平面，那么这两个平面平行。
a , b ab=P a // b //
a
//
b
a'
a∥a ' , a' 线面平行 转 化 线线平行？
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
a , b ab=P a // b //
符号语言
线不在多 贵在/相/ 交
P
a b
图形语言
面面平行 转 化 线面平行 转 化 线线平行？
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
问题3
平面α内有两条相交直线 a , b 平行平
面β, 则α∥ β吗?
模型 验证
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
面面平行的判定定理
如果一个平面内有两条 相交 直线分别 平行于另一个平面，那么这两个平面平行。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
小结
1.通过本节课的学习,你学会了 哪些判定面面平行的方法?
2.上述判定面面平行的方法体 现了什么思想?
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
变式探究
如果一个平面内有两条 相交 直线分别 平行于另一个平面，那么这两个平面平行。
a , b ab=P a // b //
a
//
b
a'
a∥a ' , a' 线面平行 转 化 线线平行？
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
a , b ab=P a // b //
符号语言
线不在多 贵在/相/ 交
P
a b
图形语言
面面平行 转 化 线面平行 转 化 线线平行？
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
问题3
平面α内有两条相交直线 a , b 平行平
面β, 则α∥ β吗?
模型 验证
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
面面平行的判定定理
如果一个平面内有两条 相交 直线分别 平行于另一个平面，那么这两个平面平行。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
小结
1.通过本节课的学习,你学会了 哪些判定面面平行的方法?
2.上述判定面面平行的方法体 现了什么思想?
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
高中数学北师大版必修第一章《平面与平面平行的判定》课件
ａ ，ｂ ，ａ ｂ＝Ｐ，ａ
，ｂ
与 平行；
∴与D1长平C1行∥方；AB，体D1C1模＝AB型， ，平面ABCD中直线AD平行平面
如图，AD∥PQ，AD∥平面BCC’B’，PQ∥BCC’B’，但平面ABCD与平面BCC’B’不平行。
如果平面β内的两条直线是相交的直线，两个平面会不会一定平行？
BCC'B'，但平面ABCD与平面BCC'B'不平行。 同理 D1B1∥平面C1BD,又 D1A∩D1B1=D1,
求证：平面MNG∥平面ACD。
B
N· ·G
M·
A
D
C
行；
判断下列命题是否正确，并说明理由．
求证：平面DEF∥平面ABC。
如果平面β内的两条直线是平行直线，平面α与平面β不一定平行。
与 平行；
生活中有没有平面与平面平行的例子呢?
（3）平行于同一直线的两个平面平行；
第一步：在一个平面内找出两条相交 如图，AD∥PQ，AD∥平面BCC’B’，PQ∥BCC’B’，但平面ABCD与平面BCC’B’不平行。
平面与平面有几种位置关系？分别是什么？
（2）直线与平面平行的判定定理：
如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行
3、面面平行判定定理的应用：要证面面平行，只要证线面平行，而要证线面平行，只要证线线平行。
所以 D1C1∥A1B1，D1C1＝A1B1
（2）直线与平面平行的判定定理：
ａ ，ｂ ，ａ ｂ＝Ｐ，ａ
，ｂ
求证：平面DEF∥平面ABC。
同理 D1B1∥平面C1BD,又 D1A∩D1B1=D1,
如图，AD∥PQ，AD∥平面BCC’B’，PQ∥BCC’B’，但平面ABCD与平面BCC’B’不平行。
北师大必修平行关系的判定课件
北师大必修平行关系的判定课件
学习目标 1.理解直线与平面平行、平面与平面平行判定定 理的含义(重点)；2.会用图形语言、文字语言、符号语言准 确描述直线与平面平行、平面与平面平行的判定定理，并知 道其地位和作用(重点)；3.能运用直线与平面平行的判定定 理、平面与平面平行的判定定理证明一些空间线面关系的简 单问题(重、难点)．
课堂达标
1．直线a，b为异面直线，过直线a 与直线b平行的平面( )
A．有且只有一个
B．有无数多个
C．至多一个
D．不存在
解析 在直线a上任选一点A，过点A作b′∥b，则b′是唯一
的，因a∩b′＝A，所以a与b′确定一平面并且只有一个平面，
故选A.
答案 A
2．平面α与平面β平行的条件可以是
()
A．α内的一条直线与β平行
课堂小结 1．判定直线与平面平行的方法：
(1)定义法：直线与平面没有公共点则线面平行； (2)判定定理：(线线平行⇒线面平行)，
a⃘α
b α ⇒a∥α.
a∥b
2．用定理证明线面平行时，在寻找平行直线可以通过三角 形的中位线、梯形的中位线、平行线的判定等来完成．
3．证明面面平行的方法： (1)面面平行的定义； (2)面面平行的判定定理：如果一个平面内有两条相交直 线都平行于另一个平面，那么这两个平面平行； (3)两个平面同时平行于第三个平面，那么这两个平面平 行.
中，底面ABCD为平行四边形，点M， N，Q分别在PA，BD，PD上，且 PM∶MA＝BN∶ND＝PQ∶QD.求证： 平面MNQ∥平面PBC.
证明 因为PM∶MA＝BN∶ND＝PQ∶QD， 所以MQ∥AD，NQ∥BP. 因为BP 平面PBC，NQ 平面PBC， 所以NQ∥平面PBC. 又因为底面ABCD为平行四边形， 所以BC∥AD，所以MQ∥BC. 因为BC 平面PBC，MQ 平面PBC， 所以MQ∥平面PBC. 又因为MQ∩NQ＝Q， 所以根据平面与平面平行的判定定理，得平面MNQ∥平面PBC.
学习目标 1.理解直线与平面平行、平面与平面平行判定定 理的含义(重点)；2.会用图形语言、文字语言、符号语言准 确描述直线与平面平行、平面与平面平行的判定定理，并知 道其地位和作用(重点)；3.能运用直线与平面平行的判定定 理、平面与平面平行的判定定理证明一些空间线面关系的简 单问题(重、难点)．
课堂达标
1．直线a，b为异面直线，过直线a 与直线b平行的平面( )
A．有且只有一个
B．有无数多个
C．至多一个
D．不存在
解析 在直线a上任选一点A，过点A作b′∥b，则b′是唯一
的，因a∩b′＝A，所以a与b′确定一平面并且只有一个平面，
故选A.
答案 A
2．平面α与平面β平行的条件可以是
()
A．α内的一条直线与β平行
课堂小结 1．判定直线与平面平行的方法：
(1)定义法：直线与平面没有公共点则线面平行； (2)判定定理：(线线平行⇒线面平行)，
a⃘α
b α ⇒a∥α.
a∥b
2．用定理证明线面平行时，在寻找平行直线可以通过三角 形的中位线、梯形的中位线、平行线的判定等来完成．
3．证明面面平行的方法： (1)面面平行的定义； (2)面面平行的判定定理：如果一个平面内有两条相交直 线都平行于另一个平面，那么这两个平面平行； (3)两个平面同时平行于第三个平面，那么这两个平面平 行.
中，底面ABCD为平行四边形，点M， N，Q分别在PA，BD，PD上，且 PM∶MA＝BN∶ND＝PQ∶QD.求证： 平面MNQ∥平面PBC.
证明 因为PM∶MA＝BN∶ND＝PQ∶QD， 所以MQ∥AD，NQ∥BP. 因为BP 平面PBC，NQ 平面PBC， 所以NQ∥平面PBC. 又因为底面ABCD为平行四边形， 所以BC∥AD，所以MQ∥BC. 因为BC 平面PBC，MQ 平面PBC， 所以MQ∥平面PBC. 又因为MQ∩NQ＝Q， 所以根据平面与平面平行的判定定理，得平面MNQ∥平面PBC.
《平面与平面平行的判定(二)》教学课件(北师大版)
例1、已知正方体ABCD-A1B1C1D1，求证：平面AB1D1∥平面C1BD。 证明：
随堂练习
棱长为a的正方体AC1中,设M、N、E、F分别为棱A1B1、A1D1、 C1D1、 B1C1的中点. (1)求证：E、F、B、D四点共面；
(2)求证：面AMN∥面EFBD.
D1
N A1
M
E
C1
F B1
D A
G
∴DE∥MN,DF∥MG，∴ DE//平 面ABC,DF//平面ABC，
M
N
B
又DE∩DF=D, ∴平面DEF//平面ABC
小结：
平面与平面平行的判定定理： 一个平面内的两条相交直线与另一个平面平行，则这两
个平面平行。 定理的推论：
如果一个平面内有两条相交直线分别平行于另一个平 面内的两条直线，那么这两个平面平行。
思考3: （1）平面β内有一条直线与平面α平行，α，β平行吗？
（2）平面β内有两条直线与平面α平行，α，β平行吗？
思考5:通过上述分析，我们可以得到判定平面与平面平行的 一个定理，你能用文字语言表述出该定理的内容吗？
定理 一个平面内的两条相交直线与另一个平面平行，则 这两个平面平行.
思考5:上述定理通常称为平面与平面平行的判定定理，该定 理用符号语言可怎样表述？
C B
例2 在三棱锥P-ABC中，点D、E、F分别是△PAB、△PBC、 △PAC的重心，求证：平面DEF//平面ABC.
证明：连PD,PE,PF并延长，
P
分别交AB,BC,AC于点M,N,G,
连MN,MG,NG,
F
∵点D、E、F分别是△PAB、 △PBC、△PAC的重心，
A
D
E C
∴PD:DM=PE:EN=PF:FG=2:1,
随堂练习
棱长为a的正方体AC1中,设M、N、E、F分别为棱A1B1、A1D1、 C1D1、 B1C1的中点. (1)求证：E、F、B、D四点共面；
(2)求证：面AMN∥面EFBD.
D1
N A1
M
E
C1
F B1
D A
G
∴DE∥MN,DF∥MG，∴ DE//平 面ABC,DF//平面ABC，
M
N
B
又DE∩DF=D, ∴平面DEF//平面ABC
小结：
平面与平面平行的判定定理： 一个平面内的两条相交直线与另一个平面平行，则这两
个平面平行。 定理的推论：
如果一个平面内有两条相交直线分别平行于另一个平 面内的两条直线，那么这两个平面平行。
思考3: （1）平面β内有一条直线与平面α平行，α，β平行吗？
（2）平面β内有两条直线与平面α平行，α，β平行吗？
思考5:通过上述分析，我们可以得到判定平面与平面平行的 一个定理，你能用文字语言表述出该定理的内容吗？
定理 一个平面内的两条相交直线与另一个平面平行，则 这两个平面平行.
思考5:上述定理通常称为平面与平面平行的判定定理，该定 理用符号语言可怎样表述？
C B
例2 在三棱锥P-ABC中，点D、E、F分别是△PAB、△PBC、 △PAC的重心，求证：平面DEF//平面ABC.
证明：连PD,PE,PF并延长，
P
分别交AB,BC,AC于点M,N,G,
连MN,MG,NG,
F
∵点D、E、F分别是△PAB、 △PBC、△PAC的重心，
A
D
E C
∴PD:DM=PE:EN=PF:FG=2:1,
平面与平面平行的判定公开课课件
法向量法注意事项
法向量的方向
在计算法向量时需要注意其方向，通常 选择指向平面外部的方向为正方向。
VS
共线向量的处理
当两个平面的法向量共线时，需要注意它 们所代表的平面是否重合或平行。如果重 合，则两个平面不平行；如果平行，则它 们可能是同一个平面或者相距一定距离的 两个平行平面。
CHAPTER 05
例2
已知平面α和直线l，若l上任意一点到α的距离都相等，则l与α平行。
距离相等法注意事项
注意1
距离相等法适用于任意两平面，但需 注意判断距离是否处处相等。
注意2
注意3
当两平面存在公共点时，距离相等法 无法直接判定平面平行，需结合其他 方法进行判断。
在实际应用中，可结合其他判定方法 （如法向量平行等）以提高准确性。
具备发现、分析和解 决与平面与平面平行 相关的问题的能力。
掌握利用判定定理证 明两个平面是否平行 的方法和步骤。
下一步学习计划安排
深入学习平面与直线的位置关系，包括平行、相交、垂直等，为进一步学习空间几 何打下基础。
学习空间向量的基本概念和性质，掌握空间向量的运算和应用，为解决空间几何问 题提供新的方法和工具。
通过大量的练习和实际问题解决，加深对平面与平面平行相关知识的理解和掌握。
THANKS
[ 感谢观看 ]
CHAPTER 04
判定方法二：法向量法
法向量法原理
法向量定义
平面上的一个非零向量，与平面 垂直，称为该平面的法向量。
法向量性质
两个平面平行的充要条件是它们 的法向量平行（共线）。
法向量计算
给定平面上不共线的三点A、B、 C，可以计算该平面的法向量 n=(B-A)×(C-A)。
高中数学北师大版必修二课件：第一章 立体几何初步§5 5-1
返回首页
下一页
【解析】 当平面 β 与平面 ABC 重合时，有 MN β； 当平面 β 与平面 ABC 不重合时， 则 β∩平面 ABC＝BC. ∵M，N 分别为 AB，AC 的中点，∴MN∥BC. 又 MN⊆/ β，BC β，∴MN∥β.
【答案】 A
上一页
返回首页
下一页
[质疑·手记] 预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流： 疑问 1： _____________________________________________________ 解惑： _______________________________________________________ 疑问 2： _____________________________________________________ 解惑： _______________________________________________________ 疑问 3： ______________________________________________________ 解惑： _______________________________________________________
阶
阶
段
段
一
三
§5 平行关系
5.1 平行关系的判定
学
阶 段 二
业 分 层 测
评
上一页
返回首页
下一页
1．理解直线与平面平行、平面与平面平行的判定定理的含义，会判断线面、 面面平行．(重点)
2．会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与 平面平行的判定定理，并知道其地位和作用．(重点、易错点)
1.5.1 平行关系的判定 课件(北师大必修2)
同理MG∥平面ACD，
MG∩MN＝M，
∴平面MNG∥平面ACD.
MG BG 2 (2)由(1)可知： PH ＝BH＝ ， 3 2 ∴MG＝ PH. 3 1 1 又 PH＝ AD，∴MG＝ AD. 2 3 1 1 同理 NG＝ AC，MN＝ CD， 3 3 ∴△MNG∽△ACD，其相似比为 1∶3， 故 S△MNG∶S△ADC＝1∶9.
N，E，F分别是棱A1B1，A1D1，B1C1，C1D1的中点．求证：
平面AMN∥平面EFDB.
[自主解答]
如图所示，连接MF.
∵M，F分别是A1B1，C1D1的中点，且四边形A1B1C1D1为正 方形， ∴MF∥A1D1且MF＝A1D1.
又∵A1D1＝AD且AD∥A1D1，
∴MF＝AD且MF∥AD. ∴四边形AMFD是平行四边形． ∴AM∥DF.
平面内的两条相交直线，则两个平面平行．
[通一类] 2．如图所示，三棱柱ABC－A1B1C1，D是BC上一点，且
A1B∥平面AC1D，D1是B1C1的中点，求证：平面A1BD1∥
平面AC1D.
证明：连接A1C交AC1于点E，
∵四边形A1ACC1是平行四边形， ∴E是A1C的中点．连接ED， ED是△A1BC的中位线， ∴ED∥A1B. ∵ED 平面A1BD1，A1B Þ 平面A1BD1，∴ED∥平面A1BD1. ∵C1D1 綊 BD，∴四边形BDC1D1是平行四边形，
[悟一法] 证明面面平行，转化为证明线面平行，而要证线面平行， 转化为证明线线平行．在立体几何中，通过线线、线面、面 面间的位置关系相互转化，使问题顺利得到解决．熟练掌握 这种转化的思想方法，就能找到解题的突破口．这是高考重 点考查证明平行的方法，应引起重视．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
α β
知识探究(二):平面与平面平行的判定定理 思考1:对于平面α 、β ，你猜想在什么条件 下可保证平面α 与平面β 平行？ 思考2:设a，b是平面α 内的两条相交直线，且 a//β ，b//β . 在此条 件下，若α ∩β =l ，则 直线a、b与直线l 的位置 关系如何？
α
b a
β
l
思考3:通过上述分析，我们可以得到判 定平面与平面平行的一个定理，你能用 文字语言表述出该定理的直线与桌面平行，这个三 角板所在平面与桌面平行吗？
A
思考4：三角板的两条边所在直线分别与桌 面平行，三角板所在平面与桌面平行吗？
思考5: 建筑师如何检验屋顶平面与水平面 是否平行？
思考6：一般地，如果平面α内有一条直线 平行于平面β，那么平面α与平面β一定平 行吗？如果平面α内有两条直线平行于平面 β，那么平面α与平面β一定平行吗？
定理5.2 如果一个平面内有两条相交直 线都平行于另一个平面，那么这两个平
思考4:上述定理通常称为平面与平面平行的 判定定理，该定理用符号语言可怎样表述？
b a P
α
β
a , b , a b P,且 a // , b // //
思考5:在直线与平面平行的判定定理中， “a∥α ,b∥β ” ，可用什么条件替代？ 由此可得什么推论？ 推论 如果一个平 面内有两条相交直 线分别平行于另一 个平面内的两条直 线，那么这两个平 面平行.
第一章 立体几何初步
5.1 平行关系的判定---平面与平面平行的判定
问题提出
1.空间两个不同平面的位置关系有哪几 种情况？
α
β
2.两个平面平行的基本特征是什么？ 有什么简单办法判定两个平面平行呢？
知识探究(一):平面与平面平行的背景分析
思考1：根据定义，判定平面与平面平行 的关键是什么？ 思考2: 若一个平面内的所有直线都与另 一个平面平行，那么这两个平面的位置 关系怎样？若一个平面内有一条直线与 另一个平面有公共点，那么这两个平面 的位置关系又会怎样呢？
知识探究(二):平面与平面平行的判定定理 思考1:对于平面α 、β ，你猜想在什么条件 下可保证平面α 与平面β 平行？ 思考2:设a，b是平面α 内的两条相交直线，且 a//β ，b//β . 在此条 件下，若α ∩β =l ，则 直线a、b与直线l 的位置 关系如何？
α
b a
β
l
思考3:通过上述分析，我们可以得到判 定平面与平面平行的一个定理，你能用 文字语言表述出该定理的直线与桌面平行，这个三 角板所在平面与桌面平行吗？
A
思考4：三角板的两条边所在直线分别与桌 面平行，三角板所在平面与桌面平行吗？
思考5: 建筑师如何检验屋顶平面与水平面 是否平行？
思考6：一般地，如果平面α内有一条直线 平行于平面β，那么平面α与平面β一定平 行吗？如果平面α内有两条直线平行于平面 β，那么平面α与平面β一定平行吗？
定理5.2 如果一个平面内有两条相交直 线都平行于另一个平面，那么这两个平
思考4:上述定理通常称为平面与平面平行的 判定定理，该定理用符号语言可怎样表述？
b a P
α
β
a , b , a b P,且 a // , b // //
思考5:在直线与平面平行的判定定理中， “a∥α ,b∥β ” ，可用什么条件替代？ 由此可得什么推论？ 推论 如果一个平 面内有两条相交直 线分别平行于另一 个平面内的两条直 线，那么这两个平 面平行.
第一章 立体几何初步
5.1 平行关系的判定---平面与平面平行的判定
问题提出
1.空间两个不同平面的位置关系有哪几 种情况？
α
β
2.两个平面平行的基本特征是什么？ 有什么简单办法判定两个平面平行呢？
知识探究(一):平面与平面平行的背景分析
思考1：根据定义，判定平面与平面平行 的关键是什么？ 思考2: 若一个平面内的所有直线都与另 一个平面平行，那么这两个平面的位置 关系怎样？若一个平面内有一条直线与 另一个平面有公共点，那么这两个平面 的位置关系又会怎样呢？