MATLAB在非线性曲线拟合中的应用研究
matlab各类拟合曲线代码

标题:探索MATLAB中各类拟合曲线的代码应用在MATLAB中,拟合曲线是数据分析和模型建立中常用的技术之一。
通过拟合曲线,我们可以了解数据之间的关联性并建立预测模型,为进一步分析和应用数据奠定基础。
本文将深入探讨MATLAB中各类拟合曲线的代码应用,帮助读者更深入地理解该主题。
一、线性拟合曲线1. 使用MATLAB进行线性拟合曲线的代码示例在MATLAB中,使用polyfit函数可以进行线性拟合。
对一组数据点(x, y)进行线性拟合,代码如下:```matlabx = [1, 2, 3, 4, 5];y = [2, 3.5, 5, 7, 8.5];p = polyfit(x, y, 1);```其中,x为自变量,y为因变量,1表示进行一次线性拟合。
通过polyfit函数,可以得到线性拟合的系数p。
2. 线性拟合曲线的应用和特点线性拟合曲线适用于线性关系较为明显的数据,例如物理实验数据中的直线关系。
通过线性拟合,可以获得各项系数,对数据进行预测和建模。
二、多项式拟合曲线1. 使用MATLAB进行多项式拟合曲线的代码示例在MATLAB中,使用polyfit函数同样可以进行多项式拟合。
对一组数据点(x, y)进行二次多项式拟合,代码如下:```matlabx = [1, 2, 3, 4, 5];y = [1, 4, 9, 16, 25];p = polyfit(x, y, 2);```其中,x为自变量,y为因变量,2表示进行二次多项式拟合。
通过polyfit函数,同样可以得到多项式拟合的系数p。
2. 多项式拟合曲线的应用和特点多项式拟合曲线适用于数据中存在曲线关系的情况,通过选择合适的最高次数,可以灵活地拟合各种曲线形状。
三、非线性拟合曲线1. 使用MATLAB进行非线性拟合曲线的代码示例在MATLAB中,使用fit函数可以进行非线性拟合。
对一组数据点(x, y)进行指数函数拟合,代码如下:```matlabx = [1, 2, 3, 4, 5];y = [2.1, 7.4, 16.1, 29.3, 48.2];f = fit(x', y', 'exp1');```其中,x为自变量,y为因变量,'exp1'表示进行指数函数拟合。
基于MATLAB的非线性曲线拟合

基于MATLAB的非线性曲线拟合一、本文概述随着科技的不断进步,数据分析和处理在各个领域中都发挥着越来越重要的作用。
非线性曲线拟合作为一种重要的数据处理方法,被广泛应用于科学研究、工程实践以及日常生活等多个领域。
MATLAB作为一款强大的数学计算和数据分析软件,为非线性曲线拟合提供了便捷的工具和丰富的函数库。
本文旨在介绍基于MATLAB的非线性曲线拟合方法,包括非线性模型的建立、参数估计、模型验证等步骤,并通过具体实例展示MATLAB在非线性曲线拟合中的应用。
本文首先简要介绍了非线性曲线拟合的基本概念和研究背景,阐述了非线性曲线拟合在实际应用中的重要性。
接着,详细介绍了MATLAB 中非线性曲线拟合的实现过程,包括非线性模型的构建、数据预处理、参数估计方法的选择、模型拟合和评估等方面。
在此基础上,通过实例分析,展示了MATLAB在非线性曲线拟合中的实际应用,并对拟合结果进行了分析和讨论。
对全文进行了总结,指出了非线性曲线拟合在实际应用中的潜在价值和未来研究方向。
通过本文的学习,读者可以了解非线性曲线拟合的基本原理和方法,掌握MATLAB在非线性曲线拟合中的应用技巧,提高数据处理和分析能力,为相关领域的研究和实践提供有力支持。
二、非线性曲线拟合基础在数据分析和科学研究中,我们经常遇到需要通过一组离散的数据点来寻找其潜在的非线性关系。
非线性曲线拟合就是这样一个过程,它旨在找到最能描述数据点之间关系的非线性函数。
与线性拟合不同,非线性拟合的模型函数通常包含非线性参数,这些参数需要通过一定的优化算法来求解。
MATLAB作为一款强大的数学软件,提供了多种非线性曲线拟合的工具和函数。
在MATLAB中,非线性曲线拟合通常通过lsqcurvefit、lsqnonlin或fit等函数实现。
这些函数允许用户定义自己的非线性模型函数,并通过迭代优化算法来寻找最佳拟合参数。
在进行非线性曲线拟合时,选择合适的模型函数至关重要。
Matlab中的数据拟合与曲线拟合技巧

Matlab中的数据拟合与曲线拟合技巧在科学研究和工程应用中,数据拟合和曲线拟合是常见的任务。
Matlab作为一种强大的数值计算和数据分析工具,提供了丰富的函数和工具箱来进行数据拟合和曲线拟合。
本文将介绍一些常用的数据拟合和曲线拟合技巧,让读者能够更好地利用Matlab来处理自己的数据。
首先,我们来看一下最常用的数据拟合技术之一——多项式拟合。
Matlab提供了polyfit函数来进行多项式拟合。
这个函数接受两个输入参数:x和y,分别为要拟合的数据点的横坐标和纵坐标。
我们可以根据实际需求选择合适的多项式阶数,然后调用polyfit函数,即可得到拟合后的多项式系数。
可以使用polyval函数来根据多项式系数计算拟合后的y值。
这样,我们就可以在Matlab中方便地进行数据拟合和预测了。
除了多项式拟合,Matlab还提供了其他常见的数据拟合方法,如指数拟合、对数拟合和幂函数拟合等。
这些方法在Matlab中的实现也非常简单,大部分都可以通过调用相关函数实现。
对于指数拟合,可以使用fit函数和exp2fit函数来进行拟合。
对于对数拟合,可以使用fit函数和log2fit函数来进行拟合。
对于幂函数拟合,可以使用fit函数和powerfit函数来进行拟合。
这些函数的使用方法大体相同,都需要提供拟合的数据点x和y,然后调用相应的函数即可得到拟合后的结果。
另外,Matlab还提供了一些高级的数据拟合和曲线拟合方法,如非线性最小二乘拟合和样条插值拟合。
非线性最小二乘拟合是一种非常灵活的拟合方法,可以拟合各种非线性函数。
Matlab提供了lsqcurvefit函数来实现非线性最小二乘拟合。
这个函数需要提供一个函数句柄,表示要拟合的函数模型,然后根据拟合的数据点进行拟合。
通过修改函数模型和参数的初始值,可以得到不同的拟合结果。
样条插值拟合是一种光滑曲线的拟合方法,可以更好地拟合离散数据点。
Matlab提供了spline函数来进行样条插值拟合。
在Matlab中进行数据拟合和曲线拟合的方法

在Matlab中进行数据拟合和曲线拟合的方法在科学研究或工程应用中,数据拟合和曲线拟合是常见的计算任务之一。
Matlab作为一种强大的数值计算软件,提供了丰富的工具和函数,方便我们进行数据拟合和曲线拟合的操作。
本文将介绍在Matlab中进行数据拟合和曲线拟合的几种方法。
一、线性回归线性回归是最简单的数据拟合方法之一,常用于建立变量之间的线性关系模型。
在Matlab中,可以使用polyfit函数进行线性回归拟合。
该函数可以根据输入数据点的横纵坐标,拟合出一条直线,并返回直线的斜率和截距。
例如,以下代码演示了如何使用polyfit函数进行线性回归拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];coefficients = polyfit(x, y, 1);slope = coefficients(1);intercept = coefficients(2);```在上述代码中,数组x和y分别表示数据点的横纵坐标。
polyfit函数的第三个参数1表示拟合的直线为一阶多项式。
函数返回的coefficients是一个包含斜率和截距的数组,可以通过coefficients(1)和coefficients(2)获取。
二、多项式拟合在实际应用中,线性模型并不适用于所有情况。
有时,数据点之间的关系可能更复杂,需要使用更高阶的多项式模型来拟合。
Matlab中的polyfit函数同样支持多项式拟合。
我们可以通过调整多项式的阶数来拟合不同次数的曲线。
以下代码展示了如何使用polyfit函数进行二次多项式拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 6, 10, 16, 24];coefficients = polyfit(x, y, 2);a = coefficients(1);b = coefficients(2);c = coefficients(3);```在上述代码中,polyfit的第三个参数2表示拟合的多项式为二阶。
基于MATLAB的非线性曲线拟合

vefit,确定模型 (2)中的参数 c1 , c2 , c3 。求解过程为 :
先编写一个 M - 函数文件 Examp le2_1
M - file: function f = Examp le2_1 ( c, tdata)
f = c (1 ) 3 ( exp ( - c ( 2 ) 3 tdata) - exp ( - c ( 3 ) 3 tda2
17
先编写 M - 函数文件 Examp le2_2
M - file: function f = Examp le2_2 ( c, tdቤተ መጻሕፍቲ ባይዱta, ydata)
tdata = [ 0. 25 0. 5 0. 75 1 1. 5 2 2. 5 3 3. 5 4 4. 5 5 6 7 8 9
10 11 12 13 14 15 16 ];
legend ( ′实验数据 ′, ′一次拟合 ′, ′二次拟合 ′) ; 故一次 、二次拟合多项式分别为 :
y3 = 2. 2516x + 2. 0131 和 y3 = 0. 0313x2 + 2. 2516x + 2. 0001,拟合曲线图见图 1。
图 1 例 1多项式曲线拟合图
(2)非线性数据拟合函数 lsqcurvefit和 lsqnonlin。 MATLAB 提供了两个求解最小二乘非线性数据 拟合问题的命令 lsqcurvefit和 lsqnonlin。两者都要事 先定义 M - 函数文件 。 ① c = lsqcurvefit ( ′fun′, x0, xdata, ydata) 其中‘fun’为拟合函数的 M - 函数文件名 , x0为 初始向量 , xdata, ydata为参与曲线拟合的实验数据 。 函数返回值 c为非线性函数‘fun’的拟合系数 。 例 2: 2004年全国大学生数学建模竞赛 C题 (酒 后驾车 )中给出某人在短时间内喝下两瓶啤酒后 ,间 隔一定的时间 t测量他的血液中酒精含量 y (毫克 /百 毫升 ) ,得到数据如表 1所示 。
matlab非线性拟合

matlab非线性拟合
Matlab非线性拟合是一种使用Matlab软件调用内置非线性拟合功能的数据处理方法。
由于Matlab具有强大的数学建模和仿真功能,因此,
在许多科学和工程应用中,都通常将其用于数据拟合。
Matlab非线性
拟合可以有效地对各种形式的数据进行拟合,而无需显式的模型表达式。
Matlab非线性拟合可以采用多种算法来实现,包括拟牛顿算法、梯度
下降算法、最小二乘算法和全局最优化算法等。
Matlab非线性拟合可
以帮助我们准确地拟合数据,具有很高的精度和高效率,而且不需要
太多的参数即可实现。
例如,如果我们需要优化一个复杂的多元函数,我们可以使用Matlab非线性拟合来找出最佳的解。
此外,Matlab非线性拟合还可以用来处理不确定性数据和随机噪声。
这些不确定的变量和噪声可以通过拟合技术来解决,这样可以使得拟
合结果更加准确。
此外,Matlab非线性拟合还可以应用于多个变量间
的相关性分析,从而帮助我们更好地了解数据的规律,并提高拟合的
准确性。
因此,Matlab非线性拟合能有效解决我们的实际问题,它具有很高的
精度和高效率,也可以有效处理不确定性和噪声数据,是一种有效的
数据拟合方法。
通过正确使用Matlab非线性拟合,可以有效地提高拟
合的准确性,为解决科研问题和工程实践提供有效的解决方案。
MATLAB实例:多元函数拟合(线性与非线性)

MATLAB实例:多元函数拟合(线性与⾮线性)MATLAB实例:多元函数拟合(线性与⾮线性)作者:凯鲁嘎吉 - 博客园更多请看:之前写过⼀篇博⽂,是。
现在⽤拟合多元函数,实现线性拟合与⾮线性拟合,其中⾮线性拟合要求⾃定义拟合函数。
下⾯给出三种拟合⽅式,第⼀种是多元线性拟合(回归),第⼆三种是多元⾮线性拟合,实际中第⼆三种⽅法是⼀个意思,任选⼀种即可,推荐第⼆种拟合⽅法。
1. MATLAB程序fit_nonlinear_data.mfunction [beta, r]=fit_nonlinear_data(X, Y, choose)% Input: X ⾃变量数据(N, D), Y 因变量(N, 1),choose 1-regress, 2-nlinfit 3-lsqcurvefitif choose==1X1=[ones(length(X(:, 1)), 1), X];[beta, bint, r, rint, states]=regress(Y, X1)% 多元线性回归% y=beta(1)+beta(2)*x1+beta(3)*x2+beta(4)*x3+...% beta—系数估计% bint—系数估计的上下置信界% r—残差% rint—诊断异常值的区间% states—模型统计信息rcoplot(r, rint)saveas(gcf,sprintf('线性曲线拟合_残差图.jpg'),'bmp');elseif choose==2beta0=ones(7, 1);% 初始值的选取可能会导致结果具有较⼤的误差。
[beta, r, J]=nlinfit(X, Y, @myfun, beta0)% ⾮线性回归% beta—系数估计% r—残差% J—雅可⽐矩阵[Ypred,delta]=nlpredci(@myfun, X, beta, r, 'Jacobian', J)% ⾮线性回归预测置信区间% Ypred—预测响应% delta—置信区间半⾓plot(X(:, 1), Y, 'k.', X(:, 1), Ypred, 'r');saveas(gcf,sprintf('⾮线性曲线拟合_1.jpg'),'bmp');elseif choose==3beta0=ones(7, 1);% 初始值的选取可能会导致结果具有较⼤的误差。
应用MATLAB进行非线性回归分析

应用MATLAB进行非线性回归分析摘要早在十九世纪,英国生物学家兼统计学家高尔顿在研究父与子身高的遗传问题时,发现子代的平均高度又向中心回归大的意思,使得一段时间内人的身高相对稳定。
之后回归分析的思想渗透到了数理统计的其他分支中。
随着计算机的发展,各种统计软件包的出现,回归分析的应用就越来越广泛。
回归分析处理的是变量与变量间的关系。
有时,回归函数不是自变量的线性函数,但通过变换可以将之化为线性函数,从而利用一元线性回归对其进行分析,这样的问题是非线性回归问题。
下面的第一题:炼钢厂出钢水时用的钢包,在使用过程中由于钢水及炉渣对耐火材料的侵蚀,使其容积不断增大。
要找出钢包的容积用盛满钢水时的质量与相应的实验次数的定量关系表达式,就要用到一元非线性回归分析方法。
首先我们要对数据进行分析,描出数据的散点图,判断两个变量之间可能的函数关系,对题中的非线性函数,参数估计是最常用的“线性化方法”,即通过某种变换,将方程化为一元线性方程的形式,接着我们就要对得到的一些曲线回归方程进行选择,找出到底哪一个才是更好一点的。
此时我们通常可采用两个指标进行选择,第一个是决定系数,第二个是剩余标准差。
进而就得到了我们想要的定量关系表达式。
第二题:给出了某地区1971—2000年的人口数据,对该地区的人口变化进行曲线拟合。
也用到了一元非线性回归的方法。
首先我们也要对数据进行分析,描出数据的散点图,然后用MATLAB编程进行回归分析拟合计算输出利用Logistic模型拟合曲线。
关键词:参数估计,Logistic模型,MATLAB正文一、一元非线性回归分析的求解思路:•求解函数类型并检验。
•求解未知参数。
可化曲线回归为直线回归,用最小二乘法求解;可化曲线回归为多项式回归。
二、回归曲线函数类型的选取和检验1、直接判断法2、作图观察法,与典型曲线比较,确定其属于何种类型,然后检验。
3、直接检验法(适应于待求参数不多的情况)4、表差法(适应于多想式回归,含有常数项多于两个的情况)三、化曲线回归为直线回归问题用直线检验法或表差法检验的曲线回归方程都可以通过变量代换转化为直线回归方程,利用线性回归分析方法可求得相应的参数估计值。
关于采用matlab进行指定非线性方程拟合的问题

关于采用matlab进行指定非线性方程拟合的问题(1)※1。
优化工具箱的利用函数描述LSQLIN 有约束线性最小二乘优化LSQNONNEG 非负约束线性最小二乘优化问题当有约束问题存在的时候,应该采用上面的方法代替Polyfit与反斜线(\)。
具体例子请参阅优化工具箱文档中的相应利用这两个函数的例子。
d. 非线性曲线拟合利用MATLAB的内建函数函数名描述FMINBND 只解决单变量固定区域的最小值问题FMINSEARCH 多变量无约束非线性最小化问题(Nelder-Mead 方法)。
下面给出一个小例子展示一下如何利用FMINSEARCH1.首先生成数据>> t=0:.1:10;>> t=t(:);>> Data=40*exp(-.5*t)+rand(size(t)); % 将数据加上随机噪声2.写一个m文件,以曲线参数作为输入,以拟合误差作为输出function sse=myfit(params,Input,Actural_Output)A=params(1);lamda=params(2);Fitted_Curve=A.*exp(-lamda*Input);Error_Vector=Fitted_Curve-Actural_Output;%当曲线拟合的时候,一个典型的质量评价标准就是误差平方和sse=sum(Error_Vector.^2);%当然,也可以将sse写作:sse=Error_Vector(:)*Error_Vector(:);3.调用FMINSEARCH>> Strarting=rand(1,2);>> options=optimset('Display','iter');>> Estimates=fiminsearch(@myfit,Strarting,options,t,Data);>> plot(t,Data,'*');>> hold on>> plot(t,Estimates(1)*exp(-Estimates(2)*t),'r');Estimates将是一个包含了对原数据集进行估计的参数值的向量。
实验五 用Matlab数据拟合

2. 已知观测数据点如表所示 x 1.6 2.7 1.3 4.1 3.6 2.3 y 17.7 49 13.1 189.4 110.8 34.5
0.6
4
4.9
409.1
3
65
2.4
36.9
求a, b, c的值, 使得曲线 f(x)=aex+bsin x+c lnx 与已知数据 点在最小二乘意义上充分接近.
例4 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17 求三个参数 a, b, c的值, 使得曲线 f(x)=aex+bx2+cx3 与 已知数据点在最小二乘意义上充分接近.
1.55
500 106
2.47
2. 93
3. 03
2.89
1000 106 1500 106 2000 106 2375 106
3 1.953 103 1.517 103 1.219 10
/ / N / m 2 3.103 103 2.465 103
解: 描出散点图, 在命令窗口输入: t=[0:1:16] y=[30.0 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8 24.0] plot(t,y,'*')
a=polyfit(t,y,1) a= -0.3012 29.3804 hold on
beta
= 3.0022 4.0304 0.9404
matlab中的lsqcurvefit使用

matlab中的lsqcurvefit使⽤转⾃:⾮线性曲线拟合是已知输⼊向量xdata和输出向量ydata,并且知道输⼊与输出的函数关系为ydata=F(x, xdata),但不知道系数向量x。
今进⾏曲线拟合,求x使得输出的如下最⼩⼆乘表达式成⽴:min Σ(F(x,xdatai)-ydatai)^2函数 lsqcurvefit格式 x = lsqcurvefit(fun,x0,xdata,ydata)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)[x,resnorm] = lsqcurvefit(…)[x,resnorm,residual] = lsqcurvefit(…)[x,resnorm,residual,exitflag] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output,lambda,jacobian] =lsqcurvefit(…)参数说明:x0为初始解向量;xdata,ydata为满⾜关系ydata=F(x, xdata)的数据;lb、ub为解向量的下界和上界lb≤x≤ub,若没有指定界,则lb=[ ],ub=[ ];options为指定的优化参数;fun为待拟合函数,计算x处拟合函数值,其定义为 function F = myfun(x,xdata)resnorm=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平⽅和;residual=fun(x,xdata)-ydata,即在x处的残差;exitflag为终⽌迭代的条件;output为输出的优化信息;lambda为解x处的Lagrange乘⼦;jacobian为解x处拟合函数fun的jacobian矩阵。
如何使用Matlab进行线性回归与非线性回归

如何使用Matlab进行线性回归与非线性回归使用Matlab进行线性回归与非线性回归简介:线性回归和非线性回归是统计分析中常用的两种回归模型。
线性回归假设自变量与因变量之间存在线性关系,而非线性回归则假设二者之间存在非线性关系。
本文将介绍如何使用Matlab进行线性回归和非线性回归分析,并分析其应用领域和优缺点。
一、线性回归分析线性回归是一种最基本的回归分析方法,广泛应用于统计学、经济学、金融学等领域。
在Matlab中,可以使用fitlm函数进行线性回归分析。
回归模型的基本形式如下所示:Y = β0 + β1X1 + β2X2 + ... + ε其中Y是因变量,X1,X2等是自变量,β0,β1,β2等是回归系数,ε是误差项。
线性回归模型的参数估计可以采用最小二乘法。
在Matlab中,可以使用fitlm 函数进行参数估计和显著性检验。
显著性检验可以帮助我们确定回归系数的是否显著不等于零,从而判断自变量对因变量的影响是否显著。
二、非线性回归分析在某些情况下,变量之间的关系不是线性的,而是呈现出曲线的形式。
这时,我们需要使用非线性回归模型进行分析。
在Matlab中,可以使用cftool函数进行非线性回归分析。
cftool是一个交互式的拟合工具箱,通过界面操作可以方便地进行曲线拟合。
用户可以选择不同的拟合模型,并根据数据点进行拟合。
cftool提供了各种常见的非线性回归模型,如指数模型、幂函数模型、对数模型等。
用户可以根据实际需求选择合适的模型进行分析。
非线性回归模型的参数估计可以使用最小二乘法、最大似然估计等方法。
在Matlab的cftool中,可以直接进行参数估计,并生成相应的拟合曲线。
三、线性回归与非线性回归的应用领域线性回归和非线性回归分析在各个领域都有广泛的应用。
线性回归常用于预测、趋势分析、经济建模等方面。
非线性回归则更适用于描述非线性关系的数据,常用于生物医学、环境科学、物理学等领域。
以医学领域为例,线性回归可以用于预测患者的生存时间、评估药物的剂量-效应关系等。
matlab中拟合曲线的算法

一、引言在科学和工程领域中,拟合曲线是一种重要的数学工具,它用于寻找一条曲线,使得该曲线最好地描述已知的数据点或者模拟实验结果。
MATLAB作为一种强大的数学计算软件,拥有丰富的拟合曲线的算法和工具。
本文将介绍MATLAB中拟合曲线的算法,包括常见的线性拟合、多项式拟合、非线性拟合等。
二、线性拟合1. 线性拟合是指采用线性方程来拟合已知数据点的方法。
在MATLAB 中,可以使用polyfit函数来实现线性拟合。
该函数的基本语法如下: p = polyfit(x, y, n),其中x和y分别代表已知数据点的横坐标和纵坐标,n代表拟合多项式的阶数。
函数返回一个长度为n+1的向量p,其中p(1)、p(2)分别代表拟合多项式的系数。
2. 通过polyfit函数可以实现对数据点的线性拟合,得到拟合曲线的系数,并且可以使用polyval函数来计算拟合曲线在指定点的取值。
该函数的基本语法如下:yfit = polyval(p, x),其中p代表拟合曲线的系数向量,x代表待求取值的点,yfit代表拟合曲线在该点的取值。
三、多项式拟合1. 多项式拟合是指采用多项式方程来拟合已知数据点的方法。
在MATLAB中,可以使用polyfit函数来实现多项式拟合,和线性拟合类似。
不同之处在于,可以通过调整多项式的阶数来适应不同的数据特性。
2. 除了使用polyfit函数进行多项式拟合外,MATLAB还提供了Polytool工具箱,它是一个方便的图形用户界面,可以用于拟合已知数据点并可视化拟合曲线。
使用Polytool工具箱,用户可以直观地调整多项式的阶数和观察拟合效果,非常适合初学者和快速验证拟合效果。
四、非线性拟合1. 非线性拟合是指采用非线性方程来拟合已知数据点的方法。
MATLAB中提供了curvefitting工具箱,其中包含了众多非线性拟合的工具和算法,例如最小二乘法、最大似然法、拟合优度计算等。
通过该工具箱,用户可以方便地进行各种复杂数据的非线性拟合。
Matlab与Mathematica在非线性拟合中的应用比较

( 02 , 0} 0 5 6 } O7 , 5} { . 5 3 ,{ . 8 ,{ .5 7 , { , 2 , { ., 2} 2 7 ,{ ., 8} 18 ) 1 8 ,{ , 7} 25 6 , 5 { , 8) 35 5 ,{ , 1 , { ., 0) 3 6 ,{ ., 8) 4 5 ) 4 5 5 , f , 1 ,f , 8 , { , 5) { , 8 , 5 4 } 6 3 ) 73 , 82 } { , 5} { 0 1 ,{ 1 1 , 9 2 , 1 , 8) 1 , 5} { 2 l , ( 3 1 , { 4 7} l , 2} 1 , 0) 1 , ,
时 间 (JH ,I ,
p = i Po d t] g Ls ll a t t a 就 可以输 出的带坐标 的散点 图。 当数 据 需手 动输 入 时 ,Mah maia te t 可 c 以 随 时 将 录 入 错 误 的 数 据 加 以 修 正 ,而 在 M alb 令 窗 口中 ,如 果 需 要修 正 数 据 , t 命 a 就 必 须 调 出 已输 入 过 的 数 据 再 加 以 修 改 , 查 找起 来 不  ̄ Mah maia 便 。作 图时 N t e tc 方 Maa 使用绘 图命令po tb l l t= ( ,Y 口 ) t , ,而 Mah mai 用Ls lt aa,两 种软件 绘 图 t e t a i P o[ t ] c t d 操 作都很 方便 。 其次 ,利 用软 件的 内建 函数对 此数据 进 行 非线性拟 合 。做 出比较 。 用Mal 的 内 建函数 对参 数求 解 ,可调 tb a 用 最小二乘拟 合 函 ̄l cret ,先 定义非 s uvf() q i 线性 函数t . 文件 : i i m n fnt n u co Y= f (,t i ua ) n Y = ( }x (a1 t *x (a ) ) a ) p一 (}) ep一 ( ) 3e ) 一 2 t 这 里a1 o,a ) p,a ) () L ( 为 为 2 ( 代表A,即 3 为y A e = ( Le ) - 。 在 命令窗 口中运 行以下 命令 : >> t= [ .5 .,0 7 ,1 .,2 0 2 ,O 5 .5 ,15 ,
matlab_多元与非线性回归即拟合问题regressnlinfit

回归(拟合)自己的总结(20100728)1:学三条命令:polyfit(x,y,n)---拟合成一元幂函数(一元多次) regress(y,x)----可以多元,nlinfit(x,y,’fun ’,beta0) (可用于任何类型的函数,任意多元函数,应用范围最主,最万能的)2:同一个问题,可能这三条命令都可以使用,但结果肯定是不同的,因为拟合的近似结果,没有唯一的标准的答案。
相当于咨询多个专家。
3:回归的操作步骤:(1) 根据图形(实际点),选配一条恰当的函数形式(类型)---需要数学理论与基础和经验。
(并写出该函数表达式的一般形式,含待定系数)(2) 选用某条回归命令求出所有的待定系数所以可以说,回归就是求待定系数的过程(需确定函数的形式)配曲线的一般方法是: (一)先对两个变量x 和y 作n 次试验观察得n i y x ii,...,2,1),,( 画出散点图,散点图(二)根据散点图确定须配曲线的类型. 通常选择的六类曲线如下:(1)双曲线xb a y +=1 (2)幂函数曲线y=a bx , 其中x>0,a>0(3)指数曲线y=a bx e 其中参数a>0.(4)倒指数曲线y=a xb e/其中a>0,(5)对数曲线y=a+blogx,x>0(6)S 型曲线x be a y -+=1(三)然后由n 对试验数据确定每一类曲线的未知参数a 和b.一、一元多次拟合polyfit(x,y,n)一元回归polyfit多元回归regress---nlinfit(非线性)二、多元回归分析(其实可以是非线性,它通用性极高)对于多元线性回归模型:e x x y p p ++++=βββ 110设变量12,,,p x x x y的n 组观测值为12(,,,)1,2,,i i ip i x x x y i n=.记 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=np n n p p x x x x x x x x x x 212222111211111,⎪⎪⎪⎪⎪⎭⎫⎝⎛=n y y y y 21,则⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=p ββββ 10 的估计值为排列方式与线性代数中的线性方程组相同()拟合成多元函数---regress 使用格式:左边用b=或[b, bint, r, rint, stats]= 右边用regress(y, x) 或regress(y, x, alpha)---命令中是先y 后x,---须构造好矩阵x(x 中的每列与目标函数的一项对应) ---并且x 要在最前面额外添加全1列/对应于常数项 ---y 必须是列向量---结果是从常数项开始---与polyfit 的不同。
matlab:最小二乘法线性和非线性拟合
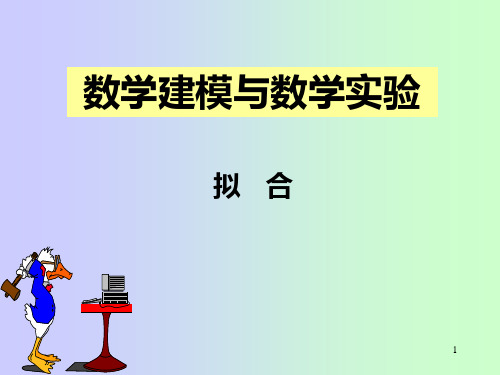
x f 1 1.5 2 3.9 4 6.6 7 11.7 9 15.6 12 13 18.8 19.6 15 20.6 17 21.1
MATLAB(cn)
7
最临近插值、线性插值、样条插值与曲线拟合结果:
25
0 0 2 4 6 8 10 12 14 16 18
MATLAB(zxec2)
%作出数据点和拟合曲线的图形 20.1293 -0.0317
2)计算结果: A = -9.8108
f ( x) 9.8108x 2 20.1293x 0.0317
17
用MATLAB作非线性最小二乘拟合
Matlab的提供了两个求非线性最小二乘拟合的函数: lsqcurvefit和lsqnonlin。两个命令都要先建立M-文件fun.m, 在其中定义函数f(x),但两者定义f(x)的方式是不同的,可参 考例题. 1. lsqcurvefit 已知数据点: xdata=(xdata1,xdata2,…,xdatan), ydata=(ydata1,ydata2,…,ydatan) lsqcurvefit用以求含参量x(向量)的向量值函数
最小。 其中 fi(x)=f(x,xdatai,ydatai) =F(x,xdatai)-ydatai
20
输入格式为: 1) x=lsqnonlin(‘fun’,x0); 2) x= lsqnonlin (‘fun’,x0,options); 3) x= lsqnonlin (‘fun’,x0,options,‘grad’); 4) [x,options]= lsqnonlin (‘fun’,x0,…); 5) [x,options,funval]= lsqnonlin 说明: x= lsqnonlin (‘ fun’ x0 ,…); (‘fun’,x0,options); fun是一个事先建立的 定义函数f(x)的M-文件, 自变量为x 选项见无 迭代初值 约束优化
matlab 拟合曲线 计算峰面积

《Matlab拟合曲线与计算峰面积》一、引言在科学研究和工程应用中,曲线拟合和峰面积计算是常见的数据处理和分析方法。
Matlab作为一种强大的科学计算软件,提供了丰富的工具和函数来实现曲线拟合和峰面积计算。
本文将深入探讨Matlab中的曲线拟合方法和峰面积计算算法,并结合具体案例进行详细讲解。
二、曲线拟合方法1. 线性拟合线性拟合是一种最简单的曲线拟合方法,适用于自变量和因变量之间存在线性关系的情况。
在Matlab中,可以使用polyfit函数进行线性拟合,该函数可以得到拟合直线的斜率和截距,从而实现对实验数据的线性拟合。
2. 非线性拟合非线性拟合适用于自变量和因变量之间存在非线性关系的情况。
Matlab提供了curve fitting工具箱,包括lsqcurvefit、nlinfit等函数,可以实现对实验数据的非线性拟合。
通过选择合适的模型和参数,可以得到最佳拟合曲线,从而更好地描述数据间的关系。
3. 分段拟合有时候实验数据可能存在多个阶段或分段的趋势,这种情况下可以采用分段拟合的方法。
Matlab中的分段线性拟合和分段非线性拟合函数可以帮助我们实现对复杂数据的有效拟合,从而更全面地理解数据的变化规律。
三、峰面积计算算法1. 峰的识别与定位在进行峰面积计算之前,首先需要对数据中的峰进行识别和定位。
Matlab中的findpeaks函数可以帮助我们找到数据中的峰,并确定其位置、高度和宽度,为后续的面积计算奠定基础。
2. 面积计算方法对于已定位的峰,可以采用多种方法来计算其面积,如梯形法则、辛普森法则等。
Matlab中的trapz和integral函数可以帮助我们方便地实现对峰面积的计算。
对于非常规形状的峰,还可以利用数值积分的方法来更精确地计算峰面积。
四、案例分析以某光谱实验数据为例,我们将结合实际数据,使用Matlab进行拟合曲线和计算峰面积的案例分析。
我们将使用线性拟合方法对数据进行初步拟合,然后采用非线性拟合的方法进一步优化拟合效果。
MATLAB在曲线拟合中的应用

汪 禹
( 中南大学 土木工程学院 , 南 长沙 4 0 0 ) 湖 10 4
摘 要 : 绍 了 曲线拟 合 的 最 小二 乘 原理 和 M T A 曲线拟 舍 的 方 法 , 介 A LB 并通 过 实例 说 明 了 多项 式 拟合 和 既 定 函数 拟 合 的 M tb a a l 实现 过程 。 关键 词 : T A ; 线拟合 ; 小二乘 法 MA L B 曲 最
al e r f( u ' O xY ( ) =a uv i " n, ,,) 4 q e tf a
式 中 , 0为拟合 系数 a a 的初始 向量 ,, 为实测 数据 向量 , n 为 xy f u 式 中, ,为实测数 据向量 ,i xy n为拟合多项 式的最 高次数 ,a 为函 拟 合函数 ,为 函数 fn a u 的拟合系数 。 数返回值, 即拟合多项式的系数向量( 按降幂排列) 。 例 2 某化 学反 应 中, 得生物 浓度 y ) 时间 t i 的数 据如 表 测 与 (n m ) 多项式在 x 处的值 Y 以利用 函数 ypl aa) 可 =oy l, 计算 。 v (x 2 示, Y t 所 求 与 的近似 函数 关系。 般对于 同一组原始数 据 ,可 以用 高一 阶或低 一 阶多 项式拟合 曲 表 2 生物 浓度 与化 学 反应 时间 关 系 线, 但实践证明并不是阶次越高拟合越好 , 有时会发生阶 高越不精 t l 2I 6 8 l l l l 0 2 4 6 1 4 确 的情况 , 因为一些 高阶项往往对 Y 影响很小 。 一般 总是先从低 阶开始 y I0 4 8 6l8 . 9 4 . 5 . 0 0 n 0 . 9 9 - . l l l 1 5 . 2 4 6 拟合, 然后根 据曲线是 否平滑 , 点之 间是 否 出现较 大的纹 波来决定 数据 是 否需要提高 阶数进行 曲线拟 合 ,对于 n个数 据点的拟合 曲线最 高阶 由 观测数据 应 化趋势可见 , 反应初期浓度增加很决, 一段时间后 趋 于定值 。下 面的两个简单模 型具有这种性 质日 。 次 不能超过 n1 _。 例 1现有 如表 1 所示 的试 验数据 , 求分别用 2 、 阶多项式 拟 要 阶 8 a l t
MATLAB实现非线性曲线拟合最小二乘法
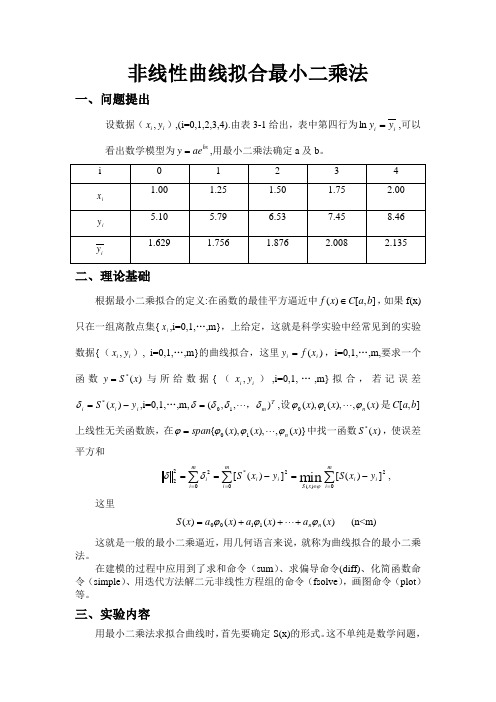
非线性曲线拟合最小二乘法一、问题提出设数据(i i y x ,),(i=0,1,2,3,4).由表3-1给出,表中第四行为i i y y =ln ,可以看出数学模型为bx ae y =,用最小二乘法确定a 及b 。
二、理论基础根据最小二乘拟合的定义:在函数的最佳平方逼近中],[)(b a C x f ∈,如果f(x)只在一组离散点集{i x ,i=0,1,…,m},上给定,这就是科学实验中经常见到的实验数据{(i i y x ,), i=0,1,…,m}的曲线拟合,这里)(i i x f y =,i=0,1,…,m,要求一个函数)(*x S y =与所给数据{(i i y x ,),i=0,1,…,m}拟合,若记误差i i i y x S -=)(*δ,i=0,1,…,m,T m ),,(10δδδδ, =,设)(,),(),(10x x x n ϕϕϕ 是],[b a C 上线性无关函数族,在)}(,),(),({10x x x span n ϕϕϕϕ =中找一函数)(*x S ,使误差平方和∑∑∑===∈-=-==m i m i mi i i x S i i iy x S y x S 02)(2*222])([])([min ϕδδ,这里)()()()(1100x a x a x a x S n n ϕϕϕ+++= (n<m)这就是一般的最小二乘逼近,用几何语言来说,就称为曲线拟合的最小二乘法。
在建模的过程中应用到了求和命令(sum )、求偏导命令(diff)、化简函数命令(simple )、用迭代方法解二元非线性方程组的命令(fsolve ),画图命令(plot )等。
三、实验内容用最小二乘法求拟合曲线时,首先要确定S(x)的形式。
这不单纯是数学问题,还与所研究问题的运动规律及所得观测数据(i i y x ,)有关;通常要从问题的运动规律及给定数据描图,确定S(x)的形式,并通过实际计算选出较好的结果。
在Matlab中进行数据拟合与曲线拟合的基本方法

在Matlab中进行数据拟合与曲线拟合的基本方法数据拟合是一种通过数学函数描述和预测现有数据集的方法,而曲线拟合则是一种特定形式的数据拟合。
在实际应用中,数据拟合和曲线拟合广泛用于物理学、工程学、经济学等领域。
而Matlab是一个功能强大的数学计算软件,其中有许多用于数据拟合和曲线拟合的工具和函数。
一、数据拟合的基本方法1. 线性拟合线性拟合是最简单的数据拟合方法之一。
在Matlab中,可以使用polyfit函数进行线性拟合。
假设我们有一组数据点,可以使用polyfit函数拟合出一个一次多项式(直线),该多项式可以最小化与实际数据之间的距离。
2. 多项式拟合多项式拟合是数据拟合中常用的方法之一。
可以使用polyfit函数进行多项式拟合。
该函数可以拟合出一个n次多项式,n为用户设定的拟合阶数。
3. 曲线拟合曲线拟合是更一般的数据拟合方法。
它可以拟合各种形式的曲线,包括指数、对数等。
Matlab中提供了curvefit函数用于曲线拟合。
该函数可以使用非线性最小二乘法拟合各种形式的曲线。
二、曲线拟合的基本方法1. 直线拟合直线拟合是曲线拟合中最简单的方法之一。
在Matlab中,可以使用polyfit函数进行直线拟合。
和数据拟合中的线性拟合类似,直线拟合也可以求出最小二乘拟合的直线方程。
2. 非线性拟合非线性拟合可以拟合各种复杂的曲线。
在Matlab中,可以使用fit函数进行非线性拟合。
该函数可以拟合任意的自定义模型。
3. 傅里叶拟合傅里叶拟合是一种将信号分解为一系列基本谐波的方法,并根据基本谐波的振幅和相位进行拟合的方法。
在Matlab中,可以使用fft函数进行傅里叶拟合。
三、实例演示下面通过一个实例演示在Matlab中进行数据拟合与曲线拟合的基本方法。
假设我们有一组实际测量的温度数据,并希望拟合出一个合适的曲线来描述这组数据。
1. 首先,我们可以将实际数据点绘制在图上,以便观察数据的分布和趋势。
2. 接下来,我们可以使用polyfit函数进行线性拟合,拟合出一个最小二乘拟合的直线方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB 在非线性曲线拟合中的应用小结
摘要:归纳总结了非线性曲线拟合的方法、求解步骤和上机操作过程 关键词:曲线拟合非线性MATLAB
正文:
1.曲线拟合的基本原理
已知一组测定的数据(例如N 个点(xi,yi )去求得自变量x 和因变量y 的一个近似解析表达式y=φ(x )。
若记误差δi=φ(xi )-yi ,i=1,2,…N ,则要使误差的平方和最小,即要求:
∑==N
i i
Q 1
2
δ
为最小,这就是常用的最小二乘法原理。
2 .MATLAB 曲线拟合的相关方法 2.1.函数形式:
(1)多项式拟合函数polyfit ,调用格式为: p=polyfit (x,y,n )
其中x ,y 为参与曲线拟合的实验数据,n 为拟合多项式的次数,函数返回值为拟合多项式的系数(按降幂排列)。
n=1时,就为线性拟合。
例1:给出表1数据,试用最小二乘法求一次和二次拟合多项式。
表1 数据
在MATLAB 命令窗口中输入: clear; close; x=-1:0.25:1;
y=[-0.2209,0.3295,0.8826,1.4392,2.0003,2.5645,3.1334,3.7061,4.2836] p1=polyfit(x,y,1) p2=polyfit(x,y,2) y1=polyval(p1,x); y2=polyval(p2,x);
plot(x,y,'+',x,y1,'r:',x,y2,'k-.') 运行结果:
拟合多项式为:y*=2.0516+2.0131和y*=0.0313x2+2.2516x+2.20001 (2)非线性数据拟合函数lsqcurvefit 调用格式为: c=lsqcurvefi (t'fun',x0,xdata,ydata )
其中'fun'为拟合函数的M -函数文件名,x0为初始向量,xdata,ydata 为参与曲线拟合的实验数据。
函数返回值c 为非线性函数fun 的拟合系数。
例2:2004年全国大学生数学建模竞赛C 题(酒后驾车)中给出某人在短时间内喝下两瓶啤酒后,间隔一定的时间测量他的血液中酒精含量y (毫克/百毫升),得到数据如表2。
表2 酒精含量与饮酒时间的实验数据
通过建立微分方程模型得到短时间内喝酒后血液中 酒精浓度与时间的关系为:
)(321t c t c e e c y ---= (2)
根据实验数据,利用非线性拟合函数lsqcurvefit ,确定模型(2)式中的参数c1,c2,c3。
求解过程为:
先编写一个M -函数文件Example2_1: function f=Example2_1(c,tdata)
f=c(1)*(exp(-c(2)*tdata)-exp(-c(3)*tdata)); 保存后,在命令窗口中输入: clear
tdata=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16]; ydata=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 8 15 12 10 7 7 4]; c0=[1 1 1];
for i=1:50;
c=lsqcurvefit('Example2_1',c0,tdata,ydata); c0=c; end
得到最优解为:c= 117.05,0.1930,1.9546 从而得出拟合曲线:
)(05.1179546.11930.0t t e e y -= 2.2.图形窗口形式
(1)利用多项式拟合的交互图命令(GUI )polytool ,调用格式为:polytoo (lx,y ) 其中x,y 分别为实验数据构成的向量,例如利用polytool 求解例1的MATLAB 命令如下: x=-1:0.25:1
y=[-0.2209,0.3295,0.8826,1.4392,2.0003,2.5645,3.1334,3.7061,4.2836]; polytool (x,y )
打开多项式拟合的交互式界面,由于要拟合的函数为线性函数,因此在多项式拟合交互式界面中的Degree 中输入1,点击导出数据Export ,出现保存对话框ExporttoWorkspace ,选中Parameters (参数),Residuals (残差)后点击OK ,在MATLAB 的Workspace 窗口中可以看到参数为:2.2516和2.0131,即拟合函数为 Y*=2.2516x+2.0131。
同样如果拟合的函数为二次函数,则只要在Degree 中输入2,其它步骤相同,可得拟合函数为:
Y*=0.0313x2+2.2516x+2.0001
通过查看Residuals (残差)值,可以发现二次函数拟合的残差值比线性函数的要小一些,从拟合的效果看,可以选择二次函数作为拟合函数,但由于线性函数较简单,残差值也很小,从简单出发,也可选择线性函数作为拟合函数。
(2)基本拟合界面
MATLAB 提供了一个方便简洁的拟合界面。
具有拟合快速和操作简便的优势,只能拟合多项式。
例如用基本拟合界面求解例1的过程如下: clear; close; x=-1:0.25:1;
y=[-0.2209,0.3295,0.8826,1.4392,2.0003,2.5645,3.1334,3.7061,4.2836]; plot(x,y,'+'); 运行结果:
在散点图的图形窗口上分别点击菜单档中的ToolsBasic Fitting,在Plots Fits中分别选中linear、quadratic、Show equations、plot residuals、show norm of residuals,所得拟合直线方程为:y*=2.3x+2;
拟合二次多项式为:
Y*=0.031x2+2.3x+2
(3)曲线拟合工具界面cftool
曲线拟合工具界面cftool是一个可视化的图形界面,具有强大的图形拟合功能,下面通过一个具体例子来介绍cftool的用法。
例3某生化系学生为研究嘌呤霉素在某项酶促反应中对反应速度与底物浓度之间关系的影响,设计了一个实验,所得的实验数据见表3。
根据问题的背景和数据建立一个合适的数学模型,来反映这项酶促反应的速度与底物浓度之间的关系。
表3 嘌呤霉素实验中的反应速度与底物浓度数据
酶促反应的速度y与底物浓度x之间的关系可用下面两个简单模型描述:
Michaelis-Menten模型:
y=f (x,β)=
x
x ++32
1βββ (4)
指数增长模型:y=f(x,β)=β1(1-e x β,) (5)
使用曲线拟合工具界面cftool 来确定模型(4)和(5)中的参数,并比较模型(4)、(5)的拟合效果。
在MATLAB 命令窗口中输入以下语句: clear; close;
x=[0.02 0.02 0.06 0.06 0.11 0.11 0.22 0.22 0.56 0.56 1.10 1.10]; y=[76 47 97 107 123 139 159 152 191 201 207 200]; cftool(x,y);
在″Curve Fitting Tool ″对话框中单击″Fitting ″,打开″Fitting ″对话框,点击″New fit ″,在″Fit Name :″中输入″有理函数″,在″Type of fit ″中选中″Rational ″,在″Numerator ″中选中″linear polynomial ″,在″Denominator ″中选中″linear polynomi al ″,然后点击″Apply ″,完成有理函数拟合。
然后,再次点击″New fit ″,在″Fit Name:″中输入″指数函数″,在″Type of fit ″中选中″Custom Equation ″,点击″New equation ″,打开用户自定义方程对话框,点击″General Equation ″,在″Equation ″中输入″y=a*(1-exp(-b*x))″,点击″Ok ″后回到拟合窗口,点击″Apply ″,完成指数函数拟合,参数计算结果见表4。
表4 模型(4)、(5)计算结果
拟合图为:
通过表4可以看出,有理函数(Michaelis-Menten模型)ys=221.7x+3.318x+0.1047拟合剩余标准差较小,R-square较大(越接近1越好),故用有理函数ys=221.7x+3.318x+0.1047拟合数据比用指数函数ys=192.1(1-e-11.38x)拟合的效果好。
3结束语
利用MATLAB的绘图功能和曲线拟合功能,可以很方便地进行多项式拟合和其它非线性曲线拟合,并可以通过比较剩余标准差和可决系数R2的大小,来对比不同曲线的拟合效果。
从而在不知数学模型情况下,也能根据数据的散点图找出较优的曲线来拟合数据。
参考文献:
[1]徐萃薇,孙绳武,计算方法引论[M].北京:高等教育出版社,2002-01:62-85.
[2]苏金明,张莲花,等.MATLAB工具箱应用[M].北京:电子工业出版社,2004-01:489-512.
[3]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2003-08:308-316.。
