三角函数 诱导公式专项练习(含答案)
三角函数的诱导公式练习题含答案

三角函数的诱导公式练习题(1)1. tan225∘的值为()A.1B.√22C.−√22D.−12. 已知3sin(θ+π2)+sin(θ+π)=0,θ∈(−π,0),则sinθ=( )A.−3√1010B.−√1010C.3√1010D.√10103. 若sin(π3−α)=−13,则cos(α+π6)=( )A.−13B.13C.−2√23D.2√234. 已知sin(α+π4)=35,则cos(π4−α)=( )A.4 5B.−45C.−35D.355. 已知α是第二象限角,若sin(π2−α)=−13,则sinα=()A.−2√23B.−13C.13D.2√236. 已知函数f(x)={1x,x0,log2x−3,x0,则f(−12)⋅f(16)=()A.3B.1C.−1D.−27. (5分)已知x∈R,则下列等式恒成立的是( )A.sin(−x)=sin xB.sin(3π2−x)=cos xC.cos(π2+x)=−sin x D.cos(x−π)=−cos x8. sin 14π3−cos (−25π4)=________.9. 已知sin α=45,则cos (α+π2)=________. 10. cos 85∘+sin 25∘cos 30∘cos 25∘等于________11. 已知cos θ=−35,则sin (θ+π2)=________.12. 已知cos (π−α)=35,α∈(0,π),则tan α=________.13. 已知f (α)=sin (α−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π),其中α≠12kπ(k ∈Z ).(1)化简f (α);(2)若f (π2+β)=−√33,且角β为第四象限角,求sin (2β+π6)的值.14. 已知α为第二象限角,且sin α+cos α=−713,分别求tan α,sin 2α−2sin αcos α的值.15. 如图,四边形ABCD 中,△ABC 是等腰直角三角形,其中AC ⊥BC ,AB =√6,又CD//AB ,cos ∠ABD =√63.(1)求BD 的长;(2)求△ACD的面积.参考答案与试题解析三角函数的诱导公式练习题(1)一、选择题(本题共计 6 小题,每题 5 分,共计30分)1.【答案】A【考点】运用诱导公式化简求值【解析】原式中的角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果.【解答】解:原式=tan(180∘+45∘)=tan45∘=1,故选A.2.【答案】A【考点】同角三角函数间的基本关系诱导公式【解析】利用诱导公式,同角三角函数基本关系式即可求解.【解答】解:∵sin(θ+π2)=sinθcosπ2+cosθsinπ2=cosθ,sin(θ+π)=sinθcosπ+cosθsinπ=−sinθ,∴ 3cosθ−sinθ=0,∴cosθ=13sinθ,由于sin2θ+cos2θ=1,而θ∈(−π,0),∴sinθ<0,∴109sin2θ=1.∴sinθ=−3√1010.故选A.3.【答案】A【考点】运用诱导公式化简求值【解析】观察所求角和已知角可得cos(α+π6)=cos[π2−(π3−α)],再利用诱导公式即可求解.【解答】解:∵ (α+π6)+(π3−a)=π2,∴ cos (α+π6)=cos [π2−(π3−α)]=sin (π3−α)=−13.故选A .4.【答案】 D【考点】运用诱导公式化简求值 【解析】由题意利用利用诱导公式化简三角函数式的值,可得结果. 【解答】解:∵ sin (α+π4)=35, ∴ cos (π4−α)=sin [π2−(π4−α)] =sin (π4+α)=35. 故选D . 5. 【答案】 D【考点】同角三角函数间的基本关系 运用诱导公式化简求值【解析】直接利用诱导公式以及同角三角函数基本关系式转化求解即可. 【解答】α是第二象限角,若sin (π2−α)=−13 可得cos α=−13,所以sin α=√1−cos 2α=2√23. 6.【答案】 D【考点】 求函数的值 分段函数的应用 函数的求值 【解析】推导出f(−12)=1−12=−2,f(16)=log 216−3=4−3=1,由此能求出f(−12)⋅f(16)的值. 【解答】∵ 函数f(x)={1x,x0,log 2x −3,x0,∴ f(−12)=1−12=−2,f(16)=log 216−3=4−3=1, ∴ f(−12)⋅f(16)=(−2)×1=−2.二、 多选题 (本题共计 1 小题 ,共计5分 ) 7.【答案】 C,D【考点】运用诱导公式化简求值 【解析】 此题暂无解析 【解答】解:A ,sin (−x )=−sin x ,故 A 不成立; B ,sin (3π2−x)=−cos x ,故B 不成立; C ,cos (π2+x)=−sin x ,故C 成立;D ,cos (x −π)=−cos x ,故D 成立. 故选CD .三、 填空题 (本题共计 5 小题 ,每题 5 分 ,共计25分 ) 8.【答案】√3−√22【考点】运用诱导公式化简求值 【解析】本题考查利用诱导公式求值. 【解答】 解:sin14π3−cos (−25π4)=sin (4π+2π3)−cos (−6π−π4) =sin 2π3−cos π4=√3−√22. 故答案为:√3−√22.−4 5【考点】运用诱导公式化简求值【解析】原式利用诱导公式化简,将sinα的值代入计算即可求出值.【解答】解:∵sinα=45,∴cos(π2+α)=−sinα=−45.故答案为:−45.10.【答案】12【考点】三角函数的恒等变换及化简求值【解析】把cos85∘化为cos(60∘+25∘),由两角和的余弦公式化简即可.【解答】cos85∘+sin25∘cos30∘cos25∘=cos(60∘+25∘)+sin25∘cos30∘cos25∘=12cos25∘−√32sin25∘+√32sin25∘cos25∘=12.11.【答案】−3 5【考点】三角函数的恒等变换及化简求值【解析】由已知利用诱导公式即可化简求值得解.【解答】∵cosθ=−35,∴sin(θ+π2)=cosθ=−35.−43【考点】同角三角函数间的基本关系 运用诱导公式化简求值【解析】由诱导公式可得cos a 的值,及α的范围,利用同角三角函数间的基本关系求出tan α的值即可. 【解答】解: ∵ cos (π−α)=−cos α=35,α∈(0,π), ∴ cos α=−35<0,则α∈(π2,π),则sin α=√1−cos 2α=45, ∴ tan α=sin αcos α=45−35=−43.故答案为:−43.四、 解答题 (本题共计 3 小题 ,每题 5 分 ,共计15分 ) 13.【答案】 解:(1) f(α)=sin (a−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)=(−cos α)⋅sin α⋅(−tan α)(−tan α)⋅sin α=−cos α.(2)由f (π2+β)=−cos (π2+β)=−√33,得sin β=−√33, 又角β为第四象限角,所以cos β−√63, sin 2β=−2√23,cos 2β=13,所以sin (2β+π6)=sin 2βcos π8+cos 2βsin π6 =(−2√23)⋅√32+13⋅12=1−2√66. 【考点】运用诱导公式化简求值同角三角函数间的基本关系 【解析】 此题暂无解析 【解答】 解:(1) f(α)=sin (a−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)=(−cos α)⋅sin α⋅(−tan α)(−tan α)⋅sin α=−cos α.(2)由f (π2+β)=−cos (π2+β)=−√33,得sin β=−√33, 又角β为第四象限角,所以cos β−√63, sin 2β=−2√23,cos 2β=13,所以sin (2β+π6)=sin 2βcos π8+cos 2βsin π6=(−2√23)⋅√32+13⋅12=1−2√66. 14. 【答案】解:因为sin α+cos α=−713,所以(sin α+cos α)2=sin 2α+2sin αcos α+cos 2α=49169, 整理得2sin αcos α=−120169,则(sin α−cos α)2=1−2sin αcos α=289169. 因为α为第二象限角,所以sin α−cos α=1713,解得sin α=513,cos α=−1213. 所以tan =sin αcos α=−512, sin 2α−2sin αcos α=25169−(−120169)=145169. 【考点】同角三角函数间的基本关系 三角函数的恒等变换及化简求值 【解析】 【解答】解:因为sin α+cos α=−713,所以(sin α+cos α)2=sin 2α+2sin αcos α+cos 2α=49169, 整理得2sin αcos α=−120169,则(sin α−cos α)2=1−2sin αcos α=289169.因为α为第二象限角,所以sin α−cos α=1713, 解得sin α=513,cos α=−1213. 所以tan =sin αcos α=−512,sin 2α−2sin αcos α=25169−(−120169)=145169.15.【答案】解:(1)因为CD // AB ,AC ⊥BC ,△ABC 是等腰直角三角形, 所以∠ABC =∠CA =∠ACD =12×(180∘−90∘)=45∘, 所以∠BCD =90∘+45∘=135∘.所以sin ∠BDC =sin ∠ABD =√1−(√63)2=√33, 在△ABC 中,BC =AC =√3, 在△BCD 中,由正弦定理得, BD =BC⋅sin ∠BCD sin ∠BDC=√3×√22√33=3√22.(2)在△BCD 中,由正弦定理可得, CD =BC ⋅sin (45∘−∠ABD)sin ∠BDC=√3×√22×(√63−√33)√33=2√3−√62. 所以S △ACD =12AC ⋅CD ⋅sin ∠ACD =12×√3×2√3−√62×√22=3(√2−1)4. 【考点】正弦定理同角三角函数间的基本关系【解析】(1)由题意可求∠BCD =135∘,在△BCD 中,由正弦定理可得BD 的值.(2)在△BCD 中,由正弦定理可得CD 的值,根据三角形的面积公式即可求解. 【解答】解:(1)因为CD // AB ,AC ⊥BC ,△ABC 是等腰直角三角形, 所以∠ABC =∠CA =∠ACD =12×(180∘−90∘)=45∘, 所以∠BCD =90∘+45∘=135∘.所以sin ∠BDC =sin ∠ABD =(√63)=√33, 在△ABC 中,BC =AC =√3, 在△BCD 中,由正弦定理得, BD =BC⋅sin ∠BCD sin ∠BDC=√3×√22√33=3√22.(2)在△BCD 中,由正弦定理可得,CD=BC⋅sin(45∘−∠ABD)sin∠BDC=√3×√22×(√63−√33)√33=2√3−√62.所以S△ACD=12AC⋅CD⋅sin∠ACD=12×√3×2√3−√62×√22=3(√2−1)4.试卷第11页,总11页。
02三角函数诱导公式(含经典例题+答案)
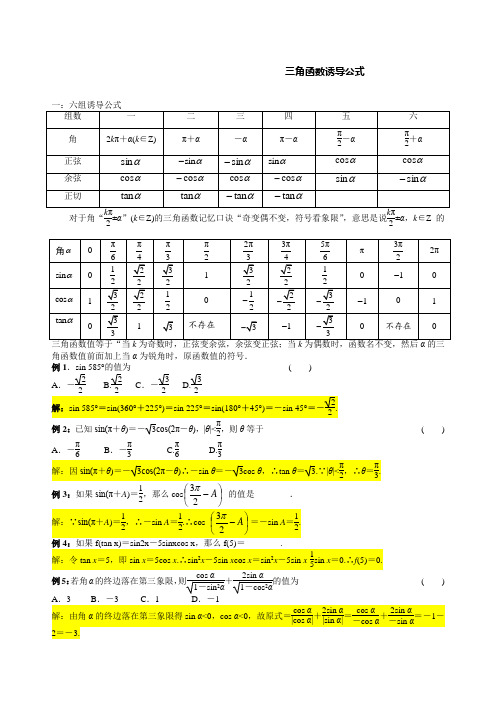
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
三角函数诱导公式练习题集附答案解析

三角函数诱导公式练习题一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数2、点P(cos2009°,sin2009°)落在()A、第一象限B、第二象限C、第三象限D、第四象限3、已知,则=()A、B、C、D、4、若tan160°=a,则sin2000°等于()A、B、C、D、﹣5、已知cos(+α)=﹣,则sin(﹣α)=()A、﹣B、C、﹣D、6、函数的最小值等于()A、﹣3B、﹣2C、D、﹣17、本式的值是()A、1B、﹣1C、D、8、已知且α是第三象限的角,则cos(2π﹣α)的值是()A、B、C、D、9、已知f(cosx)=cos2x,则f(sin30°)的值等于()A、B、﹣C、0 D、110、已知sin(a+)=,则cos(2a﹣)的值是()A、B、C、﹣D、﹣11、若,,则的值为()A、B、C、D、12、已知,则的值是()A、B、C、 D、13、已知cos(x﹣)=m,则cosx+cos(x﹣)=()A、2mB、±2mC、D、14、设a=sin(sin20080),b=sin(cos20080),c=cos(sin20080),d=cos(cos20080),则a,b,c,d的大小关系是()A、a<b<c<dB、b<a<d<cC、c<d<b<aD、d<c<a<b15、在△ABC中,①sin(A+B)+sinC;②cos(B+C)+cosA;③tan tan;④,其中恒为定值的是()A、②③B、①②C、②④D、③④16、已知tan28°=a,则sin2008°=()A、B、C、D、17、设,则值是()A、﹣1B、1C、D、18、已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2007)=5,则f(2008)=()A、3B、5C、1D、不能确定19、给定函数①y=xcos(+x),②y=1+sin2(π+x),③y=cos(cos(+x))中,偶函数的个数是()A、3B、2C、1D、020、设角的值等于()A、B、﹣C、D、﹣21、在程序框图中,输入f0(x)=cosx,则输出的是f4(x)=﹣csx()A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题(共9小题)22、若(﹣4,3)是角终边上一点,则Z的值为.23、△ABC的三个内角为A、B、C,当A为°时,取得最大值,且这个最大值为.24、化简:=25、化简:=.26、已知,则f(1)+f(2)+f(3)+…+f(2009)=.27、已知tanθ=3,则(π﹣θ)=.28、sin(π+)sin(2π+)sin(3π+)…sin(2010π+)的值等于.29、f(x)=,则f(1°)+f(2°)+…+f(58°)+f(59°)=.30、若,且,则cos(2π﹣α)的值是.答案与评分标准一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
三角函数诱导公式练习题 答案

三角函数的引诱公式1一.选择题1.假如|cosx|=cos (x+π),则x 的取值聚集是()A .-2π+2kπ≤x≤2π+2kπ B.-2π+2kπ≤x≤2π3+2kπC .2π+2kπ≤x≤2π3+2kπ D.(2k+1)π≤x≤2(k+1)π(以上k∈Z)2.sin (-6π19)的值是()A .21 B .-21 C .23D .-233.下列三角函数:①sin(nπ+3π4);②cos(2nπ+6π);③sin(2nπ+3π);④cos[(2n+1)π-6π];⑤sin[(2n+1)π-3π](n∈Z).个中函数值与sin 3π的值雷同的是()A .①②B .①③④C .②③⑤D .①③⑤ 4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为()A .-36B .36 C .-26 D .265.设A.B.C 是三角形的三个内角,下列关系恒成立的是()A .cos (A+B )=cosCB .sin (A+B )=sinC C .tan (A+B )=tanCD .sin 2B A +=sin 2C6.函数f (x )=cos 3πx (x∈Z)的值域为()A .{-1,-21,0,21,1} B .{-1,-21,21,1}C .{-1,-23,0,23,1} D .{-1,-23,23,1}二.填空题7.若α是第三象限角,则)πcos()πsin(21αα---=_________.8.sin21°+sin22°+sin23°+…+sin289°=_________.三.解答题9.求值:sin (-660°)cos420°-tan330°cot(-690°).10.证实:1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ. 11.已知cosα=31,cos (α+β)=1,求证:cos (2α+β)=31.12.化简:︒+︒︒︒+790cos 250sin 430cos 290sin 21.13.求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tanθ.14.求证:(1)sin (2π3-α)=-cosα; (2)cos (2π3+α)=sinα.参考答案1一.选择题1.C 2.A 3.C 4.B 5.B 6.B 二.填空题7.-sinα-cosα 8.289三.解答题 9.43+1.10.证实:左边=θθθθ22sin cos cos sin 2-1-- =-θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++,右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--,左边=右边,∴原等式成立.11.证实:∵cos(α+β)=1,∴α+β=2kπ.∴cos(2α+β)=cos (α+α+β)=cos (α+2kπ)=cosα=31.12.解:︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21=︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1.13.证实:左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tanθ=右边,∴原等式成立.14证实:(1)sin (2π3-α)=sin [π+(2π-α)]=-sin (2π-α)=-cosα.(2)cos (2π3+α)=cos [π+(2π+α)]=-cos (2π+α)=sinα.三角函数的引诱公式2一.选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为() A. 21B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为() A.23 B. 21C. 23±D. —233.化简:)2cos()2sin(21-•-+ππ得()2 C.sin2-cos2 D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中准确的是()A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD.cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于(),A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4)二.填空题: 6.cos(π-x)= 23,x∈(-π,π),则x 的值为.7.tanα=m,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ.8.|sinα|=sin(-π+α),则α的取值规模是. 三.解答题: 9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos2(65π-x )的值. 11.求下列三角函数值:(1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);12.求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5;(2)sin [(2n+1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.参考答案21.C 2.A 3.C 4.C 5.A 6.±65π 7.11-+m m 8.[(2k-1) π,2k π]9.原式=)cos (·sin()cos()n s (sin αα)παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sinα 10.161111.解:(1)sin 3π7=sin (2π+3π)=sin 3π=23.(2)cos 4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23.(4)sin (-765°)=sin [360°×(-2)-45°]=sin (-45°)=-sin45°=-22.注:应用公式(1).公式(2)可以将随意率性角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.12.解:(1)sin 3π4·cos 6π25·tan 4π5=sin (π+3π)·cos(4π+6π)·tan(π+4π)=(-sin 3π)·cos 6π·tan 4π=(-23)·23·1=-43.(2)sin [(2n+1)π-3π2]=sin (π-3π2)=sin 3π=23.13.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++---=θθθθθcos cos 22)1(cos cos )1(cos 223++--- =θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cosθ-1,∴f(3π)=cos 3π-1=21-1=-21.三角函数公式1. 同角三角函数根本关系式sin2α+cos2α=1 sinαcosα =ta nαtanαcotα=12. 引诱公式 (奇变偶不变,符号看象限)(一)sin(π-α)=sinα sin(π+α)=-sinαcos(π-α)=-cosα cos(π+α)=-cosα tan(π-α)=-tanα tan(π+α)=tanα sin(2π-α)=-sinα sin(2π+α)=sinα cos(2π-α)=cosα cos(2π+α)=cosα tan(2π-α)=-tanα tan(2π+α)=tanα(二) sin(π2 -α)=cosα sin(π2+α)=cosαcos(π2 -α)=sinα cos(π2 +α)=- sinαtan(π2 -α)=cotα tan(π2 +α)=-cotαsin(3π2 -α)=-cosα sin(3π2 +α)=-cosαcos(3π2 -α)=-sinα cos(3π2 +α)=sinαtan(3π2 -α)=cotα tan(3π2+α)=-cotαsin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα3. 两角和与差的三角函数cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ sin (α+β)=sinαcosβ+cosαsinβ s in (α-β)=sinαcosβ-cosαsinβ tan(α+β)= tanα+tanβ1-tanαtanβtan(α-β)= tanα-tanβ1+tanαtanβ4. 二倍角公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2α tan2α=2tanα1-tan2α5. 公式的变形 (1)升幂公式:1+cos2α=2cos2α 1—cos2α=2sin2α (2)降幂公式:cos2α=1+cos2α2 sin2α=1-cos2α2(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)(4)全能公式(用tanα暗示其他三角函数值)sin2α=2tanα1+tan2α cos2α=1-tan2α1+tan2α tan2α=2tanα1-tan2α6. 拔出帮助角公式asinx +bcosx=a2+b2 sin(x+φ) (tanφ= ba )特别地:sinx±cosx= 2 sin(x±π4)7. 熟习情势的变形(若何变形)1±sinx±cosx 1±sinx 1±cosx tanx+cotx 1-tanα1+tanα 1+tanα1-tanα若A.B 是锐角,A+B =π4,则(1+tanA )(1+tanB)=28. 在三角形中的结论若:A +B +C=π , A+B+C 2 =π2则有tanA +tanB +tanC=tanAtanBtanCtan A 2 tan B 2 +tan B 2 tan C 2 +tan C 2 tan A2=1。
三角函数诱导公式专项练习(含答案)

三角函数 诱导公式专项练习学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.sin (−600∘)=( ) A . −√32 B . −12C . 12D .√322.cos 11π3的值为( ) A . −√32B . −12 C .√32D . 123.已知sin(30°+α)=√32,则cos (60°–α)的值为A . 12 B . −12 C .√32 D . –√324.已知 cos (π2+α)=−35,且 α∈(π2,π),则tan (α−π)=( ) A . −34 B . −43 C . 34 D . 435.已知sin(π-α)=-23,且α∈(-π2,0),则tan(2π-α)的值为( )A .2√55B . -2√55C . ±2√55 D .√526.已知cos(π4−α)=√24,则sin(α+π4)=( )A . −34B . 14C . √24D .√1447.已知sinα=35,π2<α<3π2,则sin(7π2−α)=( ) A . 35B . −35C . 45D . −458.已知 tanx =−125, x ∈(π2,π),则cos(−x +3π2)=( )A .513B . -513C .1213D . -12139.如果cos(π+A)=−12,那么sin(π2+A)= A . -12 B . 12 C . 1 D . -1 10.已知cos(π2−α)−3cosαsinα−cos (π+α)=2,则tanα=( ) A . 15 B . −23 C . 12 D . −5 11.化简cos480∘的值是( )A.12B.−12C.√32D.−√3212.cos(−585°)的值是()A.√22B.√32C.−√32D.−√2213.已知角α的终边经过点P(−5,−12),则sin(3π2+α)的值等于()A.−513B.−1213C.513D.121314.已知cos(π+α)=23,则tanα=()A.√52B.2√55C.±√52D.±2√5515.已知cosα=15,−π2<α<0,则cos(π2+α)tan(α+π)cos(−α)tanα的值为()A.2√6B.−2√6C.−√612D.√61216.已知sinα=13,α∈(π2,π)则cos(−α)=()A.13B.−13C.2√23D.−2√2317.已知sin(π+α)=45,且α是第四象限角,则cos(α−2π)的值是( )A.−35B.35C.±35D.4518.已知sin=,则cos=( ) A.B.C.-D.-19.已知cos α=k,k∈R,α∈,则sin(π+α)=( ) A.-B.C.±D.-k20.=( )A.sin 2-cos 2B.sin 2+cos 2C.±(sin 2-cos 2)D.cos 2-sin 221.sin585∘的值为A.√22B.−√22C.√32D.−√3222.sin(−1020°)=()A.12B.−12C.√32D.−√3223.若α∈(0,π),sin(π−α)+cosα=√23,则sinα−cosα的值为( )A .√23B . −√23C . 43 D . −4324.已知α∈(π2,π)且sin (π+α)=−35,则tan α=( ) A . −34B . 43C . 34D . −4325.已知sin (π2+θ)+3cos (π−θ)=sin (−θ),则sinθcosθ+cos 2θ=( )A . 15B . 25C . 35 D .√5526.若sinθ−cosθ=43,且θ∈(34π,π),则sin(π−θ)−cos(π−θ)=( ) A . −√23B .√23C . −43D . 4327.已知sin (π2+θ)+3cos (π−θ)=sin (−θ),则sinθcosθ+cos 2θ=( ) A . 15 B . 25 C . 35 D . √5528.已知sin(2015π2+α)=13,则cos(π−2α)的值为( )A . 13 B . -13 C . 79 D . −79 29.若α∈(0,π),sin(π−α)+cosα=√23,则sinα−cosα的值为( )A .√23B . −√23C . 43 D . −4330.已知a =tan (−π6),b =cos (−23π4),c =sin25π3,则a,b,c 的大小关系是( )A . b >a >cB . a >b >cC . c >b >aD . a >c >b 31.cos7500= A .√32B . 12C . −√32D . −1232.sin (−236π)的值等于( )A .√32B . −12 C . 12 D . −√3233.sin300°+tan600°+cos (−210°)的值的( ) A . −√3 B . 0 C . −12+√32D . 12+√3234.已知α∈(π2,3π2),tan(α−π)=−34,则sinα+cosα等于( ). A . ±15 B . −15 C . 15 D . −75 35.已知sin1100=a ,则cos200的值为( )A . aB . −aC . √1−a 2D . −√1−a 2 36.点A (cos2018∘,tan2018∘)在直角坐标平面上位于( ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 37.如果sin (π−α)=13,那么sin (π+α)−cos (π2−α)等于( ) A . −23B . 23C .2√23 D . −2√2338.已知角α的终边过点(a,−2),若tan (π+α)=3,则实数a = A . 6 B . −23C . −6D . 2339.cos (2π+α)tan (π+α)sin (π−α)cos (π2−α)cos (−α)=A . 1B . −1C . tan αD . −tan α 40.已知sin (−α)=−√53,则cos (π2+α)的值为( )A . √53B . −√53C . 23 D . −23参考答案1.D【解析】【分析】直接运用诱导公式,转化为特殊角的三角函数值求解。
三角函数诱导公式练习题-带答案

三角函数的诱导公式(1)一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A .-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k π C . 2π+2k π≤x ≤2π3+2k π D .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z ) 2.sin (-6π19)的值是( ) A . 21 B .-21 C .23 D .-23 3.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π]; ⑤sin [(2n +1)π-3π](n ∈Z ). 其中函数值与sin3π的值相同的是( ) A .①② B .①③④ C .②③⑤ D .①③⑤4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为( ) A .-36 B .36 C .-26 D .26 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )A .cos (A +B )=cosC B .sin (A +B )=sin C C .tan (A +B )=tan CD .sin2A B +=sin 2C 6.函数f (x )=cos3πx (x ∈Z )的值域为( ) A .{-1,-21,0,21,1} B .{-1,-21,21,1} C .{-1,-23,0,23,1} D .{-1,-23,23,1} 二、填空题7.若α.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).11..12、求证:tan(2π)sin(2π)cos(6π)cos(π)sin(5π)q q qq q-----+=tanθ.三角函数的诱导公式(2)一、选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A. 21 B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A. 23 B. 21 C. 23± D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD. cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4) 二、填空题:6.cos(π-x)= 23,x ∈(-π,π),则x 的值为 . 7.tanα=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ . 8.|sinα|=sin (-π+α),则α的取值范围是 .三、解答题:9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5; (2)sin [(2n +1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.。
三角函数的诱导公式的练习题及答案

三角函数的诱导公式在ABC ∆中,若()()0sin sin =--+-+C A B C B A ,试判断ABC ∆的形状。
()()()[]()[]()()()CB C B B C B C B C B C B B C C C A B C B A ==+∴=-+-=∴=--∴=-+-∴=--+--∴=--+-+或或2222202sin 2sin 02sin 2sin 0sin sin 0sin sin πππππππππ ∴ABC ∆为直角三角形或等腰三角形。
2、设()()(),cos sin βπαπ+++=x b x a x f 其中βα,,,b a 都是非零实数,若(),12010-=f 则()=2011f 。
()()()()()()()()()()()[]()[]()()().1cos sin cos sin 2010cos 2010sin 2011cos 2011sin 20111cos sin 12010cos 2010sin 2010;12010,cos sin =+-=+++=+++++=+++=∴-=+∴-=+++=∴-=+++=βαβπαπβππαππβπαπβαβπαπβπαπb a b a b a b a f b a b a f f x b x a x f3、已知α是第三象限()()()()()αππαπααπαπ-+-+---=3sin tan )2tan(2cos sin x f (1)、化简();αf (2)、若;53sin -=α求();αf(3)、若,1860︒-=α();αf(1)、()()()()()αππαπααπαπ-+-+---=3sin tan )2tan(2cos sin x f()()ααααααsin sin tan tan cos sin =--= (2)、α是第三象限,;54cos ;53sin -=∴-=αα ()54-=∴αf(3)、()()()︒+︒⨯-=︒-=︒-3003606cos 1860cos 1860f().2160cos 60360cos 300cos =︒=︒-︒=︒=4.设()()()()()()⎪⎩⎪⎨⎧≥--<=⎩⎨⎧≥+-<=)21(11)21(cos 0110sin x x g x x x g x x f x x x f ππ 求)43()65()41()31(f g g f +++的值。
(完整版)三角函数诱导公式练习题__答案(最新整理)

13.证明:左边=
tan( ) sin( ) cos( ) ( cos )( sin )
( tan )( sin ) cos cos sin
=tanθ=右边,
∴原等式成立.
14 证明:(1)sin( 3π -α)=sin[π+( π -α)]=-sin( π -α)=-cosα.
2
2
2
(2)cos( 3π +α)=cos[π+( π +α)]=-cos( π +α)=sinα.
22 22 22
8
3
4
6
12. 求下列三角函数值:
(1)sin 4π ·cos 25π ·tan 5π ;
3
6
4
(2)sin[(2n+1)π- 2π ]. 3
13.设
f(θ)=
2 cos3 2
sin2 (2π ) sin(π 2
2cos2 (π ) cos( )
)
3
,求
f( π 3
)的值.
4
参考答案 1
8.sin21°+sin22°+sin23°+…+sin289°=_________. 三、解答题 9.求值:sin(-660°)cos420°-tan330°cot(-690°).
1
10.证明:
2sin(π ) cos 1 2 sin2
1
tan(9π ) 1 tan(π ) 1
.
11.已知 cosα= 1 ,cos(α+β)=1,求证:cos(2α+β)= 1 .
2
π tan( +α)=-cotα
2
3π sin( -α)=-cosα
诱导公式练习题答案

诱导公式练习题答案诱导公式是三角函数中常用的公式,主要用于将正弦、余弦等三角函数的角转换为锐角,从而简化计算。
以下是一些诱导公式的练习题及其答案。
# 练习题1:求 \(\sin(90^\circ - x)\) 的值。
答案:根据诱导公式,我们知道 \(\sin(90^\circ - x) = \cos(x)\)。
# 练习题2:计算 \(\cos(180^\circ - x)\)。
答案:根据诱导公式,\(\cos(180^\circ - x) = -\cos(x)\)。
# 练习题3:给出 \(\tan(270^\circ - x)\) 的表达式。
答案:\(\tan(270^\circ - x) = -\cot(x)\)。
# 练习题4:求 \(\sin(360^\circ - x)\) 的值。
答案:\(\sin(360^\circ - x) = -\sin(x)\)。
# 练习题5:计算 \(\cos(90^\circ + x)\)。
答案:\(\cos(90^\circ + x) = -\sin(x)\)。
# 练习题6:给出 \(\tan(180^\circ + x)\) 的表达式。
答案:\(\tan(180^\circ + x) = \tan(x)\)。
# 练习题7:求 \(\sin(270^\circ + x)\) 的值。
答案:\(\sin(270^\circ + x) = -\cos(x)\)。
# 练习题8:计算 \(\cos(360^\circ + x)\)。
答案:\(\cos(360^\circ + x) = \cos(x)\)。
这些练习题涵盖了诱导公式的基本应用,通过这些练习,学生可以更好地理解和掌握诱导公式,提高解决三角函数问题的能力。
高一三角函数诱导公式练习题(带详解答案)

1.全国Ⅱ)若sin α<0且tan α>0,则α是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角2.(07·湖北)tan690°的值为( )A .-33 B.33C. 3 D .- 3 3.f (sin x )=cos19x ,则f (cos x )=( )A .sin19xB .cos19xC .-sin19xD .-cos19x4.设f (x )=a sin(πx +α)+b cos(πx +β),其中a ,b ,α,β∈R ,且ab ≠0,α≠k π(k ∈Z).若f (2009)=5,则f (2010)等于( )A .4B .3C .-5D .55.(09·全国Ⅰ文)sin585°的值为( )A .-22 B.22 C .-32 D.326.函数y =5sin ⎝ ⎛⎭⎪⎫25x +π6的最小正周期是( ) A.25π B.52π C.π3 D .5π7.(2010·重庆文,6)下列函数中,周期为π,且在[π4,π2]上为减函数的是( ) A .y =sin(2x +π2) B .y =cos (2x +π2) C .y =sin(x +π2) D .y =cos(x +π2) 8.函数y =-2tan ⎝ ⎛⎭⎪⎫3x +π4的单调递减区间是________.三角函数诱导公式(答案)1.[答案] C2.[答案] A[解析] tan690°=tan(-30°+2×360°)=tan(-30°)=-tan30°=-33,选A. 3.[答案] C[解析] f (cos x )=f (sin(90°-x ))=cos19(90°-x )=cos(270°-19x )=-sin19x .4.[答案] C[解析] ∵f (2009)=a sin(2009π+α)+b cos(2009π+β)=-a sin α-b cos β=5, ∴a sin α+b cos β=-5.∴f (2010)=a sin α+b cos β=-5.5.[答案] A[解析] sin585°=sin(360°+225°)=sin225°=sin(180°+45°)=-sin45°=-22. 6.[答案] D[解析] T =2π25=5π. 7.[答案] A[解析] 选项A :y =sin(2x +π2)=cos2x ,周期为π,在[π4,π2]上为减函数; 选项B :y =cos(2x +π2)=-sin2x ,周期为π,在[π4,π2]上为增函数; 选项C :y =sin(x +π2)=cos x ,周期为2π; 选项D :y =cos(x +π2)=-sin x ,周期为2π.故选A. 8. [答案] ⎝ ⎛⎭⎪⎫k π3-π4,k π3+π12(k ∈Z) [解析] 求此函数的递减区间,也就是求y =2tan ⎝ ⎛⎭⎪⎫3x +π4的递增区间,由k π-π2<3x +π4<k π+π2,k ∈Z 得:k π3-π4<x <k π3+π12, ∴减区间是⎝ ⎛⎭⎪⎫k π3-π4,k π3+π12,k ∈Z.。
(完整版)三角函数诱导公式练习题__答案.doc

三角函数的诱导公式一、1.如果 |cosx|=cos ( x+π), x 的取 集合是()ππ+2k π B .- π3 πA .- +2k π≤x ≤+2k π≤x ≤+2k π2 2 22C .π+2k π≤x ≤3π+2k πD .( 2k+1) π≤x ≤2( k+1 ) π(以上 k ∈ Z )222.sin (-19π)的 是( )6A .1B .-13 3C .D .-22223.下列三角函数:4π π ππ]; ① sin ( n π+);② cos ( 2n π+ );③ sin ( 2n π+ );④ cos [( 2n+1) π-6 363⑤ sin [( 2n+1) π- π]( n ∈Z ).3其中函数 与sinπ的 相同的是()3A .①②B .①③④C .②③⑤D .①③⑤ 4.若 cos ( π+α) =-10 ,且 α∈(- π, 0), tan (3π+α)的 ( )5 2266C .-6D .6 A .-B .223 35. A 、B 、 C 是三角形的三个内角,下列关系恒成立的是()A . cos ( A+B ) =cosCB . sin ( A+B ) =sinCA B C C . tan ( A+B ) =tanC D . sin2=sin26.函数 f ( x ) =cosπx( x ∈ Z )的 域 ( )3A . { - 1,- 1 , 0, 1, 1}B . { - 1,- 1 , 1, 1}2 222C . { - 1,-3, 0,3, 1}D . { - 1,-3 , 3, 1}2222二、填空7.若 α是第三象限角,1 2sin(π ) cos(π ) =_________ .21°+sin 2228.sin 2°+sin 3° +⋯ +sin89°=_________ .三、解答9.求 : sin (- 660 °) cos420 °- tan330 cot °(- 690 °).10.证明:2 sin(π) cos 1 tan(9 π) 1 .1 2 sin 2 tan(π) 111.已知 cosα= 1 , cos(α+β) =1,求证: cos( 2α+β) = 1.3 312.化简: 1 2 sin 290 cos 430 .sin 250 cos79013、求证:tan(2 π) sin( 2 π) cos(6π) =tanθ.cos(π) sin( 5 π)3π14.求证:( 1) sin(-α)=-cosα;(2) cos(3π+α)=sinα. 2参考答案 1 一、选择题1.C 2. A 3. C 4. B 5. B6. B二、填空题7.- sinα-cosα 8.892三、解答题3+1.9.410.证明:左边 =2sin coscos2 sin 2=-(sin cos )2 sin cos,)(cos sin ) sin cos(cossin右边 = tan tan sin cos ,tan tan sin cos左边 =右边,∴原等式成立.11.证明:∵ cos(α+β) =1,∴α+β=2kπ.∴cos(2α+β) =cos(α+α+β)=cos(α+2kπ) =cosα=1.31 2 sin 290 cos43012.解:cos 790sin 2501 2 sin( 70 360 ) cos(70 360 )=70 ) cos(70 2 360 )sin(1801 2 sin 70 cos 70=sin 70cos 70(sin 70 cos70 )2=sin 70cos 70sin 70 cos70- 1.= =cos70 sin 70 13.证明:左边 = tan() sin( ) cos( ) ( tan )( sin ) cos =tanθ=右边,( cos )( sin ) cos sin∴原等式成立.14证明:( 1) sin (3π-α) =sin[π+(π-α)]=- sin(π-α) =- cosα.22 2(2) cos(3π+α) =cos[π+(π+α)] =- cos(π+α) =sinα.22 2三角函数的诱导公式 2一、选择题:π +α )=3,则 sin(3π-α)值为(1.已知 sin( )424A.1 B. —1C.3 D. —322222.cos(+α )= 1 , 3π <α<,sin(2 -α ) 值为()— 2 22A.31C. 3D. —32B.2223.化简: 1 2 sin( 2) ? cos( 2) 得()A.sin2+cos2B.cos2-sin2C.sin2-cos2D. ±(cos2-sin2)4.已知 α和 β的终边关于 x 轴对称,则下列各式中正确的是()A.sin α =sin2βC.cos α =cos β D. cos( 2-α ) =-cos β β B. sin( - α ) =sin 5.设 tan θ=-2, π2θ +cos(- θ )的值等于(),θ <0,那么 sin 22A.1( 4+ 5 ) B.1(4-5 ) C. 1( 4± 5 )D.1 ( 5 -4)5 555二、填空题:6.cos(-x)=3, x ∈( - , ),则 x 的值为.27.tan α =m ,则 sin(α 3 ) cos(π α).sin( α) π α- cos( )8.|sin α |=sin (- +α),则 α的取值范围是.三、解答题:π α) si n() cos( π α9. sin(2) .π α)π αsin(3·cos( )π ) = 1,求 sin ( π x) +cos 2(5π-x )的值.10.已知: sin ( x+7646611. 求下列三角函数值:( 1) sin 7 π;( 2) cos 17 π ;(3) tan (- 23 π);3 4 612. 求下列三角函数值:( 1) sin 4π·cos 25π·tan 5 π;3 6 4( 2) sin [( 2n+1) π-2π] .32 cos3 sin 2 ( 2π ) π) 3sin(π)的值 .13.设 f ( θ)= 2cos 2(π ) 2,求 f ( 2 cos( )3参考答案 21.C 2. A 3. C 4. C 5. A5π m 1,2k ]6.±7.8. [(2k-1)6m 19.原式 = sin α( sin ) cos(π α) sin 2α( cos α)11 π α) α= α = sin α10.α 16sin( ·( cos )sin ?( cos )7ππ ) =sin π 311.解:( 1) sin =sin ( 2π+3 =.3 32( 2) cos 17 π=cos ( 4π+ π ) =cos π = 2 .4 4 42(3) tan (- 23π) =cos (- 4π+ π )=cos π=3 . 66 62(4) sin (- 765°) =sin [ 360°×(- 2)- 45°] =sin (- 45°) =- sin45 °=-2 .2注:利用公式( 1)、公式( 2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值 .12.解:( 1) sin 4π 25π ·tan 5 π ππ π 3 ·cos 6 =sin ( π+ ) ·cos ( 4π+ ) ·tan ( π+ )4 36 4=(- sin π) ·cos π·tan π =(- 3 ) · 3 ·1=- 3 .3 64 2 2 4(2) sin [( 2n+1) π- 2π] =sin ( π- 2π)=sin π = 3 .333213.解: f ( θ)=2 cos 3sin 2cos32 2 cos 2 cos=2 cos 31 cos2cos32 2 cos 2cos2 cos3 2 (cos 2cos )=2 cos 2cos22(cos 3 1) cos (cos 1)=2 cos 2cos22(cos 1)(cos 2cos1) cos (cos 1)=2 2 cos 2cos(cos1)(2 cos 2 cos2)=2 cos2cos2= c os θ- 1,∴ f ( π) =cos π- 1= 1 - 1= - 1 .3 3 2 2三角函数公式1. 同角三角函数基本关系式sin 2 α+ cos 2 α=1sin αcos α =tan αtan α cot α =1 2. 诱导公式(奇变偶不变,符号看象限 )(一) sin( π-α )= sin αsin( π +α )= -sin α cos(π-α )= -cos αcos(π +α )= -cos α tan( π-α )= -tan α tan( π +α )= tan α sin(2 π-α )= -sin α sin(2π +α )= sin α cos(2π-α )= cos α cos(2π +α )= cos α tan(2 π-α )= -tan αtan(2 π +α )= tan αππ (二) sin( 2 -α )= cos α sin( 2 +α )= cos αππcos( 2 -α )= sin αcos( 2 +α )= - sin αππ tan( 2 -α )= cot α tan( 2 +α )= -cot α 3π3π sin( 2 -α )= -cos αsin( 2 +α )= -cos α3π3πcos( 2 -α )= -sin α cos( 2 +α )= sin α tan( 3π -α )= cot α tan( 3π+α )= -cot α 2 2sin( -α )=- sin αcos(-α )=cos αtan( -α )=- tan α3. 两角和与差的三角函数cos(α +β )=cos α cos β- sin α sin β cos(α-β )=cos α cos β+ sin α sin β sin ( α +β )=sin α cos β+ cos α sin β sin ( α-β )=sin αcos β- cos α sin βtan α +tan β tan( α +β )=1- tan α tan βtan α- tan β tan( α-β )=1+ tan α tan β4. 二倍角公式sin2α =2sin α cos αcos2α =cos 2α- sin 2α= 2 cos 2α- 1= 1- 2 sin 2α2tan αtan2 α =1- tan 2α5. 公式的变形( 1) 升幂公式: 1+ cos2α= 2cos 2α1—cos2α= 2sin 2α ( 2) 降幂公式: cos 2α=1+ cos2α sin 2α= 1- cos2α2 2 ( 3) 正切公式变形: tan α +tan β= tan( α +β )( 1- tan α tan β)tan α- tan β= tan( α-β )( 1+ tan α tan β )( 4) 万能公式(用 tan α表示其他三角函数值)2tan α 1- tan 2α2tan α sin2α=1+tan 2αcos2α=1+tan 2αtan2α=1- tan 2α6. 插入辅助角公式asinx + bcosx= a 2+b 2sin(x+ φ ) (tan φ = b) a 特殊地: sinx ± cosx = 2πsin(x ±)47. 熟悉形式的变形(如何变形)1± sinx ± cosx 1± sinx1± cosxtanx + cotx1- tan α1+ tan α 1+ tan α1- tan απ若 A 、 B 是锐角, A+B =,则( 1+ tanA ) (1+tanB)=248. 在三角形中的结论若: A + B + C= π ,A+B+C π2= 2 则有 tanA + tanB + tanC=tanAtanBtanCAB BCC Atan 2 tan 2 + tan 2 tan 2 + tan 2 tan 2 = 1。
三角函数的诱导公式习题及答案解析

三角函数的诱导公式1. 任意角α的正弦、余弦、正切是怎样定义的?2. 2kπ+α(k∈Z)与α的三角函数之间的关系是什么?3.你能求750°和930°的值吗?4.利用公式一,可将任意角的三角函数值,转化为00~3600范围内的三角函数值.其中锐角的三角函数是我们熟悉的,而对于900~3600范围内的三角函数值,能否转化为锐角的三角函数值,这就是我们需要研究和解决的问题.同名三角函数的诱导公式思考:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?根据三角函数定义:对比α,α,α的值,π+α的三角函数与α的三角函数有什么关系?思考:对于任意给定的一个角α,-α的终边与α的终边有什么关系?设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?利用π-α=π+(-α),结合公式二、三,你能得到什么结论?公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,再放上将α当作锐角时原函数值的符号.即函数同名,象限定号.利用诱导公式一~四,可以求任意角的三角函数,其基本思路是:例3 求下列各三角函数的值:1,求下列各式的值:例4 已知(π+x)=3(1)(2π-x);(2)(π-x). 例5 化简:异名三角函数的诱导公式思考:若α为一个任意给定的角,那么απ-2的终边与角α的终边有什么对称关系?点P1(x ,y )关于直线对称的点P2的坐标如何? 设角α的终边与单位圆的交点为P 1(x ,y ),则απ-2的终边与单位圆的交点为P 2(y ,x ),根据三角函数的定义,你能获得哪些结论? 公式五思考2:απ+2与απ-2有什么内在联系?公式六证明下列等式三角形中的三角函数问题三角函数的化简求值.(A)第一象限(B)第二象限(C)第三象限(D)第四象限(A)f(1)<f(2)<f(3) (B)f(2)<f(1)<f(3) (C)f(2)<f(3)<f(1) (D)f(3)<f(2)<f(1)三角函数的诱导公式练习一、选择题(本大题共12个小题,每小题5分,共60分. 在每小题给出的四个选择中,只有一项是符合题目要求的.) 1、与-463°终边相同的角可表示为( ) A .k·360°+436°(k ∈Z ) B .k·360°+103°(k ∈Z )C .k·360°+257°(k ∈Z )D .k·360°-257°(k ∈Z ) 2、下列四个命题中可能成立的一个是( ) A 、21cos 21sin ==αα且 B 、1cos 0sin -==αα且C 、1cos 1tan -==αα且D 、α是第二象限时,αααcos tan sia -=3、若54sin =α,且α是第二象限角,则αtan 的值为( ) A 、34- B 、43 C 、43± D 、34± 4、若2cos sin =+αα,则ααcot tan +等于( )A 、1B 、2C 、-1D 、-2 1、 ︒︒+450sin 300tan 的值为( )A 、31+B 、31-C 、31--D 、31+-5、若A 、B 、C 为△的三个内角,则下列等式成立的是( )A 、A CB sin )sin(=+ B 、AC B cos )cos(=+ C 、A C B tan )tan(=+D 、A C B cot )cot(=+ 6、)2cos()2sin(21++-ππ等于 ( )A .2-2B .2-2C .±(2-2)D .227、αα=81,且4π<α<2π,则α-α的值为( )A .23 B .23-C .43D .43-8、在△中,若最大角的正弦值是22,则△必是( )A 、等边三角形B 、直角三角形C 、钝角三角形D 、锐角三角形9、下列不等式中,不成立的是( ) A 、︒︒>140sin 130sin B 、︒︒>140cos 130cos C 、︒︒>140tan 130tan D 、︒︒>140cot 130cot10、已知函数2cos )(x x f =,则下列等式成立的是( ) A 、)()2(x f x f =-π B 、)()2(x f x f =+πC 、)()(x f x f -=-D 、)()(x f x f =-11、若θsin 、θcos 是关于x 的方程0242=++m mx x 的两个实根,则m 值为( )A 、⎪⎭⎫⎢⎣⎡-∈0,34m B 、51-=m C 、51±=m D 、51+=m12、已知()sin()cos()4f x a x b x παπβ=++++(,,,a b αβ为非零实数), (2011)5f = 则(2012)f =( )A .1B .3C .5D .不能确定 二、填空题(本大题共4个小题,每小题5分,共20分.将答案填在题中横线上)13、化简=+-+βαβαβα222222cos cos sin sin sin sin . 14、若0cos 3sin =+αα,则ααααsin 3cos 2sin 2cos -+的值为 .15、=-︒)945cos( . 16、=⋅⋅⋅⋅⋅⋅︒︒︒︒89tan 3tan 2tan 1tan .三、解答题(本大题共6道小题,共70分.解答应写出文字说明,证明过程或演算步骤)17、求值22sin 120cos180tan 45cos (330)sin(210)︒+︒+︒--︒+-︒18、 化简:)(cos )tan()2tan()cos()(sin 32πααππααππα--⋅+--+⋅+.19、已知21)sin(=+απ,求απααπcos )tan()2sin(⋅-+-的值.20、已知54sin -=α. 求ααtan cos 和的值 .21、(10分)已知α是第三角限的角,化简ααααsin 1sin 1sin 1sin 1+---+22、已知1)sin(=+βα,求证 0tan )2tan(=++ββα参考答案一、选择题(每小题4分,共48分)题号 1 2 3 4 5 6 7 8 9 10 11 12 总分答案B AC B B A C B CD B B二、填空题(每小题4分,共16分) 13、1. 14、115-15、22- 16、1三、解答题(本大题共5道小题,共36分.解答应写出文字说明,证明过程或演算步骤)17、提示:[]1cos tan cot cos sin )cos (tan cot )cos (sin )(cos tan )2cot()cos ()sin (323232-=⋅-⋅⋅=-⋅⋅-⋅=+⋅+-⋅-⋅-=αααααααααααπααπαα原式18、提示:利用诱导公式,原式=219、提示:54sin -=α ,∴角α在第三、四象限,(1) 当α在第三象限,则34tan ,53cos =-=αα(2) 当α在第四象限,则34tan ,53cos -==αα20、提示:右边左边=-=+-=--=ααααααααααααcos sin cos sin cos sin sin 1cos 1sin cos cos sin 22故等式成立 21、提示:)(22,1)sin(Z k k ∈+=+∴=+ππβαβα)(22Z k k ∈-+=∴βππα,0tan tan tan )tan(tan )4tan(tan )24tan(tan )22(2tan tan )2tan(=+-=+-=+-+=++-+=+⎥⎦⎤⎢⎣⎡+-+=++ββββπββππβββππβββππββαk k k0tan )2tan(=++∴ββα。
三角函数诱导公式练习题附答案

三角函数诱导公式练习题一、选择题〔共21小题〕1、函数f〔x〕=sin,g〔x〕=tan〔π﹣x〕,那么〔〕A、f〔x〕与g〔x〕都是奇函数B、f〔x〕与g〔x〕都是偶函数C、f〔x〕是奇函数,g〔x〕是偶函数D、f〔x〕是偶函数,g〔x〕是奇函数2、点P〔cos2021°,sin2021°〕落在〔〕A、第一象限B、第二象限C、第三象限D、第四象限3、,那么=〔〕A、B、C、D、4、假设tan160°=a,那么sin2000°等于〔〕A、B、C、D、﹣5、cos〔+α〕=﹣,那么sin〔﹣α〕=〔〕A、﹣B、C、﹣D、6、函数的最小值等于〔〕A、﹣3B、﹣2C、D、﹣17、本式的值是〔〕A、1B、﹣1C、D、8、且α是第三象限的角,那么cos〔2π﹣α〕的值是〔〕A、 B、C、D、9、f〔cosx〕=cos2x,那么f〔sin30°〕的值等于〔〕A、B、﹣C、0 D、110、sin〔a+〕=,那么cos〔2a﹣〕的值是〔〕A、B、C、﹣D、﹣11、假设,,那么的值为〔〕A、B、C、D、12、,那么的值是〔〕A、B、C、 D、13、cos〔x﹣〕=m,那么cosx+cos〔x﹣〕=〔〕A、2mB、±2mC、D、14、设a=sin〔sin20210〕,b=sin〔cos20210〕,c=cos〔sin20210〕,d=cos〔cos20210〕,那么a,b,c,d的大小关系是〔〕A、a<b<c<dB、b<a<d<cC、c<d<b<aD、d<c<a<b15、在△ABC中,①sin〔A+B〕+sinC;②cos〔B+C〕+cosA;③tan tan;④,其中恒为定值的是〔〕A、②③B、①②C、②④D、③④16、tan28°=a,那么sin2021°=〔〕A、B、C、D、17、设,那么值是〔〕A、﹣1B、1C、D、18、f〔x〕=asin〔πx+α〕+bcos〔πx+β〕+4〔a,b,α,β为非零实数〕,f〔2007〕=5,那么f 〔2021〕=〔〕A、3B、5C、1D、不能确定19、给定函数①y=xcos〔+x〕,②y=1+sin2〔π+x〕,③y=cos〔cos〔+x〕〕中,偶函数的个数是〔〕A、3B、2C、1D、020、设角的值等于〔〕A、B、﹣C、D、﹣21、在程序框图中,输入f0〔x〕=cosx,那么输出的是f4〔x〕=﹣csx〔〕A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题〔共9小题〕22、假设〔﹣4,3〕是角终边上一点,那么Z的值为.23、△ABC的三个角为A、B、C,当A为°时,取得最大值,且这个最大值为.24、化简:=25、化简:=.26、,那么f〔1〕+f〔2〕+f〔3〕+…+f〔2021〕=.27、tanθ=3,那么〔π﹣θ〕=.28、sin〔π+〕sin〔2π+〕sin〔3π+〕…sin〔2021π+〕的值等于.29、f〔x〕=,那么f〔1°〕+f〔2°〕+…+f〔58°〕+f〔59°〕=.30、假设,且,那么cos〔2π﹣α〕的值是.答案与评分标准一、选择题〔共21小题〕1、函数f〔x〕=sin,g〔x〕=tan〔π﹣x〕,那么〔〕A、f〔x〕与g〔x〕都是奇函数B、f〔x〕与g〔x〕都是偶函数C、f〔x〕是奇函数,g〔x〕是偶函数D、f〔x〕是偶函数,g〔x〕是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
(完整版)三角函数诱导公式练习题附答案.doc

三角函数诱导公式练习题一、选择题(共21 小题)1、已知函数 f( x)=sin , g(x) =tan(π﹣ x),则()A、 f( x)与 g( x)都是奇函数B、 f( x)与 g( x)都是偶函数C、 f ( x)是奇函数, g(x)是偶函数D、 f( x)是偶函数, g( x)是奇函数2、点 P( cos2009 ,° sin2009 )°落在()A、第一象限B、第二象限C、第三象限D、第四象限3、已知,则=()A、B、C、D、4、若 tan160 =a°,则 sin2000 等°于()A、B、C、D、﹣5、已知 cos(+α)=﹣,则 sin(﹣α) =()A、﹣B、C、﹣D、6、函数的最小值等于()A、﹣ 3B、﹣ 2C、D、﹣ 17、本式的值是()A、 1B、﹣ 1C、D、8、已知且α是第三象限的角,则cos( 2π﹣α)的值是()A、B、C、D、9、已知 f(cosx) =cos2x,则 f ( sin30 )°的值等于()A、B、﹣C、 0 D、110、已知 sin( a+ ) = ,则 cos( 2a﹣)的值是()A、B、C、﹣D、﹣11、若,,则的值为()A、B、C、D、12、已知,则的值是()A、B、C、D、13、已知 cos( x﹣) =m,则 cosx+cos( x﹣) =()A 、 2mB 、 ± 2mC 、D 、14、设 a=sin ( sin20080),b=sin ( cos20080),c=cos ( sin20080),d=cos ( cos20080),则 a ,b , c , d 的大小关系是()A 、 a <b <c < dB 、 b < a <d < cC 、 c < d < b < aD 、 d < c < a < b15 、在△ ABC 中,① sin ( A+B )+sinC ;② cos (B+C )+cosA ;③tantan ;④,其中恒为定值的是()A 、②③B 、①②C 、②④D 、③④16 、已知 tan28 =a °,则 sin2008 =°( )A 、B 、C 、D 、17、设 ,则 值是( )A 、﹣ 1B 、 1C 、D 、18、已知 f ( x ) =asin (π x+ α)+bcos ( π x+)β+4(a , b , α,β 为非零实数),f ( 2007) =5,则 f ( 2008 ) =()A 、 3B 、 5C 、 1D 、不能确定19 、给定函数① y=xcos ( +x ),② y=1+sin 2( π+x ),③ y=cos ( cos ( +x ))中,偶函数的个数是()A 、 3B 、 2C 、 1D 、 020 、设角的 值等 于()A 、B 、﹣C 、D 、﹣21 、在程序框图中,输入 f 0( x ) =cosx ,则输出的是 f 4( x )=﹣ csx ()A 、﹣ sinxB 、 sinxC 、 cosxD 、﹣ cosx二、填空题(共 9 小题)22、若(﹣ 4,3)是角终边上一点, 则Z 的值为 .23、△ ABC 的三个内角为 A 、B 、 C ,当 A 为°时, 取得最大值,且这个最大值为 .24、化简:=25 、化:= .26 、已知, f( 1)+f( 2) +f( 3) +⋯ +f( 2009 )= .27 、已知tan θ =3,(π θ)= .28 、sin(π+) sin(2π+) sin( 3π+)⋯ sin( 2010 π+)的等于.29 、f( x)= , f( 1°)+f(2°)+⋯ +f( 58°)+f( 59°) = .30 、若,且, cos(2π α)的是.答案与评分标准一、选择题(共21 小题)1、已知函数f( x)=sin,g(x)=tan(π﹣x),则()A、 f( x)与 g( x)都是奇函数B、 f( x)与 g( x)都是偶函数C、 f ( x)是奇函数, g(x)是偶函数D、 f( x)是偶函数,g( x)是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
(完整版)三角函数诱导公式练习题附答案

三角函数诱导公式练习题一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数2、点P(cos2009°,sin2009°)落在()A、第一象限B、第二象限C、第三象限D、第四象限3、已知,则=()A、B、C、D、4、若tan160°=a,则sin2000°等于()A、B、C、D、﹣5、已知cos(+α)=﹣,则sin(﹣α)=()A、﹣B、C、﹣D、6、函数的最小值等于()A、﹣3B、﹣2C、D、﹣17、本式的值是()A、1B、﹣1C、D、8、已知且α是第三象限的角,则cos(2π﹣α)的值是()A、B、C、D、9、已知f(cosx)=cos2x,则f(sin30°)的值等于()A、B、﹣C、0 D、110、已知sin(a+)=,则cos(2a﹣)的值是()A、B、C、﹣D、﹣11、若,,则的值为()A、B、C、D、12、已知,则的值是()A、B、C、D、13、已知cos(x﹣)=m,则cosx+cos(x﹣)=()A、2mB、±2mC、D、14、设a=sin(sin20080),b=sin(cos20080),c=cos(sin20080),d=cos(cos20080),则a,b,c,d的大小关系是()A、a<b<c<dB、b<a<d<cC、c<d<b<aD、d<c<a<b15、在△ABC中,①sin(A+B)+sinC;②cos(B+C)+cosA;③tan tan;④,其中恒为定值的是()A、②③B、①②C、②④D、③④16、已知tan28°=a,则sin2008°=()A、B、C、D、17、设,则值是()A、﹣1B、1C、D、18、已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2007)=5,则f(2008)=()A、3B、5C、1D、不能确定19、给定函数①y=xcos(+x),②y=1+sin2(π+x),③y=cos(cos(+x))中,偶函数的个数是()A、3B、2C、1D、020、设角的值等于()A、B、﹣C、D、﹣21、在程序框图中,输入f0(x)=cosx,则输出的是f4(x)=﹣csx()A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题(共9小题)22、若(﹣4,3)是角终边上一点,则Z的值为.23、△ABC的三个内角为A、B、C,当A为°时,取得最大值,且这个最大值为.24、化简:=25、化简:=.26、已知,则f(1)+f(2)+f(3)+…+f(2009)=.27、已知tanθ=3,则(π﹣θ)=.28、sin(π+)sin(2π+)sin(3π+)…sin(2010π+)的值等于.29、f(x)=,则f(1°)+f(2°)+…+f(58°)+f(59°)= .30、若,且,则cos(2π﹣α)的值是.答案与评分标准一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
三角函数 诱导公式专项练习(含答案)

三角函数诱导公式专项练习(含答案) 三角函数诱导公式专项练一、单选题1.sin(-600°)的值为()A。
-√3/2B。
-1C。
1D。
√3/22.cos(11π/3)的值为()A。
-√3/2B。
-13/2C。
√2D。
23.已知sin(30°+α)=√3/2,则cos(60°-α)的值为A。
1/2B。
-1/2C。
√3/2D。
-√3/24.已知cos(π/3+α)=-5/2,且α∈(2π/5,π),则XXX(α-π)=()A。
-34/4B。
-3C。
4D。
35.已知sin(π-α)=-2/√3,且α∈(-2,0),则tan(2π-α)的值为A。
2√5/5B。
-2√5/2√5C。
±5D。
√5/26.已知cos(π/4-α)=√2/2,则sin(α+π/4)=()A。
-3B。
1C。
√2D。
√14/47.已知sinα=3/5,2<α<π/2,则sin(2-α)=()A。
3/5B。
-3/5C。
4/5D。
-4/58.已知tanx=-12/5π,x∈(π/2,π),则cos(-x+3π/2)=()A。
5/13B。
-5/12C。
13D。
-12/139.如果cos(π+A)=-1,那么sin(π/2+A)=A。
-1/2B。
2C。
1D。
-110.已知cos(π/2-α)-3cosα/(sinα-cos(π+α))=2,则tanα=()A。
12/5B。
-3C。
1/2D。
-511.化简cos480°的值是()A。
1B。
-1C。
√3/2D。
-√3/212.cos(-585°)的值是()A。
√2/2B。
√3/2C。
-√3/2D。
-√2/213.已知角α的终边经过点P(-5,-12),则sin(3π/2+α)的值等于()A。
-5B。
-12/13C。
13D。
12/1314.已知cos(π+α)=2/3,则tanα=()A。
√55/2B。
2√5/52.已知cosα=2/5,-2/5<α<0,则tan(α+α)cos(-α)tanα的值为()答案:D解析:由cosα=2/5可得sinα=-√(21)/5,代入公式可得tan(α+α)cos(-α)tanα=-1/√3=-√3/3,故选D。
三角函数诱导公式练习题,带答案

三角函数诱导公式练习题,带答案1.全国Ⅱ)若sinα0,则α是A.第一象限角B.第二象限角C.第三象限角D.第四象限角2.tan690°的值为A.-3.f=cos19x,则f=A.sin19x4.设f=asin+bcos,其中a,b,α,β∈R,且ab≠0,α≠kπ.若f=5,则f等于A.B.C.- D.55.sin585°的值为A.-2π?6.函数y=5sin??5+6?的最小正周期是π C.D.5π22C.- D.2B.cos19x C.-sin19xD.-cos19xB.C.3D33ππ7.下列函数中,周期为π,且在[,上为减函数的是2ππA.y=sin B.y=cos =tan=-tan30°=-3.[答案] C[解析] f=f)=cos19=cos=-sin19x.4.[答案] C[解析] ∵f=asin+bcos=-asinα-bcosβ=5,∴asinα+bcosβ=-5.∴f=asinα+bcosβ=-5.5.[答案] A[解析] sin585°=sin=sin225°=sin=-sin45°=-6.[答案] D[解析] T=2π5π.5.3,选A.7.[答案] Aπππ[解析] 选项A:y=sin=cos2x,周期为π,在[,上为减函数;42πππ选项B:y=cos=cosx,周期为2π;选项D:y=cosπππ3x+的递增区间,由kπ-x+[解析] 求此函数的递减区间,也就是求y=2tan?4?24kππkπππ kππkππ?∴减区间是??34312?,k∈Z.三角函数诱导公式检测题1.全国Ⅱ)若sinα0,则α是A.第一象限角B.第二象限角C.第三象限角D.第四象限角2.tan690°的值为A.-3.f=cos19x,则f=A.sin19x4.设f=asin+bcos,其中a,b,α,β∈R,且ab≠0,α≠kπ.若f=5,则f等于A.B.C.- D.55.sin585°的值为A.-2π?6.函数y=5sin??5+6?的最小正周期是π C.D.5π22C.- D.2B.cos19x C.-sin19xD.-cos19xB.C.3D33ππ7.下列函数中,周期为π,且在[,上为减函数的是2ππA.y=sin B.y=cos =tan=-tan30°=-3.[答案] C[解析] f=f)=cos19=cos=-sin19x.4.[答案] C[解析] ∵f=asin+bcos=-asinα-bcosβ=5,∴asinα+bcosβ=-5.∴f=asinα+bcosβ=-5.5.[答案] A[解析] sin585°=sin=sin225°=sin=-sin45°=-6.[答案] D[解析] T=2π5π.5.3,选A.7.[答案] Aπππ[解析] 选项A:y=sin=cos2x,周期为π,在[,上为减函数;42πππ选项B:y=cos=cosx,周期为2π;选项D:y=cosπππ3x+的递增区间,由kπ-x+[解析] 求此函数的递减区间,也就是求y=2tan?4?24kππkπππ kππkππ?∴减区间是??34312?,k∈Z.三角函数定义及诱导公式练习题2015-05-171.将120o化为弧度为?2?3?5?A.B. C.D.34632.代数式sin120cos210的值为 A.?3431 C.? D.43.tan120?? A..4.已知角α的终边经过点,则sin α+cos α等于1717A. B. C.-D.-5555.已知扇形的面积为2cm2,扇形圆心角θ的弧度数是4,则扇形的周长为 2cm4cm6cm8cm6.若有一扇形的周长为60 cm,那么扇形的最大面积为 A.500 cmB.60 cm C.22cm2D.30 cm2?3?cossin257.已知f?,则f的值为costan3A.11 B.- C.223?3??,且??,则sin?2224433A、 B、? C、 D、?55558.已知tan?9.若角?的终边过点,则sin??_______.10.已知点P在第二象限,则角α的终边在第________象限. 11.若角θ同时满足sinθ sin?sin12.已知tan??2,则的值为.3cos?cos2?13.已知??,cos??,则sin?_____________.sincos2?_________. 14.已知tan??2,则sinsin?2?4sin2??3sin?cos??. 15.已知tan?=3,则4cos2??sin?cos?16.已知tanα=?,求证: ?sina??cosa?=-;sina?cosa??sin2α+sinαcosα=.?17.已知tan??2.3sin??2cos?求的值;sin??cos??3?coscossin求的值;sinsincos若?是第三象限角,求cos?的值.18.已知sin=2cos,求sin+5cos的值.?3??2sin?-??-sin?2?参考答案1.B2?.考点:弧度制与角度的相互转化..A.试题分析:??180,故120?oo试题分析:由诱导公式以可得,sin120°cos210°=sin60°×??tan60??C. 考点:诱导公式..A试题分析:r?55?,sin??考点:三角函数的定义.C设扇形的半径为R,则R2θ=2,∴R2=1?R=1,∴扇形的周长为2R+θ·R=2+4=6..C设扇形的圆心角为?,弧长为lcm,由题意知,l?2R?60 11∴S?lR?R?30R?R2??2?22522y431?,cos,?sin??cos??.故选A. r555∴当R?15cm时,扇形的面积最大;这个最大值为225cm2. 应选C..A试题分析:f?s??i??c?o?n??s??c?ocos,sanf=cos=cos?=cos?8???=cos=.3323??3??考点:诱导公式..B33?3??tan??.又因为??,所以?为三象限的角,4422?4sin?cos.选B.25考点:三角函数的基本计算. tan?试题分析: 9.?20,试题分析:点?sin?sin??cos??tan??1?2?1sin??cos?tan??12?1cos?cos213.5?试题分析:因为α是锐角所以sin=sinα考点:同角三角函数关系,诱导公式. 14.?3sins??c?o?2co?s222??试题分析:,又sinsinncos??sin?1?cos?1?tans?i??2?tan??,则原式2=?2.考点:三角函数的诱导公式.15.4试题分析:已知条件为正切值,所求分式为弦的齐次式,所以运用弦化切,即将分子分母同除以cos2?得4sin2??3sin?cos?4tan2??3tan?4?9?3?345.4cos??sin?cos?4?tan?4?3考点:弦化切sina??cosa??=-.sin2α+sinαcosα=.sina?cosa??原式可以分子分母同除以cosx,达到弦化切的目的.然后将tanx=2代入求值即可.16.证明:把”1”用cos2x?sin2x替换后,然后分母也除以一个”1”,再分子分母同除以cos2x,达到弦化切的目的.?sina??cosatana证明:由已知tanα=.===-.?sina?cosatanasina?sinacosatana?tana????=?. si n2α+sinαcosα===??sin?a?cos?atan?a117.8;?;2?试题分析:因为已知分子分母为齐次式,所以可以直接同除以cosa转化为ata2?,只含tana的式子即可求得;用诱导公式将已知化简即可求得;有n得sin??2cos?,再利用同角关系sin2?+cos2??1,又因为?是第三象限角,所以cosa?0;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数 诱导公式专项练习学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.sin (−600∘)=( ) A . −√32 B . −12C . 12D .√322.cos 11π3的值为( ) A . −√32B . −12 C .√32D . 123.已知sin(30°+α)=√32,则cos (60°–α)的值为A . 12 B . −12 C .√32 D . –√324.已知 cos (π2+α)=−35,且 α∈(π2,π),则tan (α−π)=( ) A . −34 B . −43 C . 34 D . 435.已知sin(π-α)=-23,且α∈(-π2,0),则tan(2π-α)的值为( )A .2√55B . -2√55C . ±2√55 D .√526.已知cos(π4−α)=√24,则sin(α+π4)=( )A . −34B . 14C . √24D .√1447.已知sinα=35,π2<α<3π2,则sin(7π2−α)=( ) A . 35B . −35C . 45D . −458.已知 tanx =−125, x ∈(π2,π),则cos(−x +3π2)=( )A .513B . -513C .1213D . -12139.如果cos(π+A)=−12,那么sin(π2+A)= A . -12 B . 12 C . 1 D . -1 10.已知cos(π2−α)−3cosαsinα−cos (π+α)=2,则tanα=( ) A . 15 B . −23 C . 12 D . −5 11.化简cos480∘的值是( )A.12B.−12C.√32D.−√3212.cos(−585°)的值是()A.√22B.√32C.−√32D.−√2213.已知角α的终边经过点P(−5,−12),则sin(3π2+α)的值等于()A.−513B.−1213C.513D.121314.已知cos(π+α)=23,则tanα=()A.√52B.2√55C.±√52D.±2√5515.已知cosα=15,−π2<α<0,则cos(π2+α)tan(α+π)cos(−α)tanα的值为()A.2√6B.−2√6C.−√612D.√61216.已知sinα=13,α∈(π2,π)则cos(−α)=()A.13B.−13C.2√23D.−2√2317.已知sin(π+α)=45,且α是第四象限角,则cos(α−2π)的值是( )A.−35B.35C.±35D.4518.已知sin=,则cos=( ) A.B.C.-D.-19.已知cos α=k,k∈R,α∈,则sin(π+α)=( ) A.-B.C.±D.-k20.=( )A.sin 2-cos 2B.sin 2+cos 2C.±(sin 2-cos 2)D.cos 2-sin 221.sin585∘的值为A.√22B.−√22C.√32D.−√3222.sin(−1020°)=()A.12B.−12C.√32D.−√3223.若α∈(0,π),sin(π−α)+cosα=√23,则sinα−cosα的值为( )A .√23B . −√23C . 43 D . −4324.已知α∈(π2,π)且sin (π+α)=−35,则tan α=( ) A . −34B . 43C . 34D . −4325.已知sin (π2+θ)+3cos (π−θ)=sin (−θ),则sinθcosθ+cos 2θ=( )A . 15B . 25C . 35 D .√5526.若sinθ−cosθ=43,且θ∈(34π,π),则sin(π−θ)−cos(π−θ)=( ) A . −√23B .√23C . −43D . 4327.已知sin (π2+θ)+3cos (π−θ)=sin (−θ),则sinθcosθ+cos 2θ=( ) A . 15 B . 25 C . 35 D . √5528.已知sin(2015π2+α)=13,则cos(π−2α)的值为( )A . 13 B . -13 C . 79 D . −79 29.若α∈(0,π),sin(π−α)+cosα=√23,则sinα−cosα的值为( )A .√23B . −√23C . 43 D . −4330.已知a =tan (−π6),b =cos (−23π4),c =sin25π3,则a,b,c 的大小关系是( )A . b >a >cB . a >b >cC . c >b >aD . a >c >b 31.cos7500= A .√32B . 12C . −√32D . −1232.sin (−236π)的值等于( )A .√32B . −12 C . 12 D . −√3233.sin300°+tan600°+cos (−210°)的值的( ) A . −√3 B . 0 C . −12+√32D . 12+√3234.已知α∈(π2,3π2),tan(α−π)=−34,则sinα+cosα等于( ). A . ±15 B . −15 C . 15 D . −75 35.已知sin1100=a ,则cos200的值为( )A . aB . −aC . √1−a 2D . −√1−a 2 36.点A (cos2018∘,tan2018∘)在直角坐标平面上位于( ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 37.如果sin (π−α)=13,那么sin (π+α)−cos (π2−α)等于( ) A . −23B . 23C .2√23 D . −2√2338.已知角α的终边过点(a,−2),若tan (π+α)=3,则实数a = A . 6 B . −23C . −6D . 2339.cos (2π+α)tan (π+α)sin (π−α)cos (π2−α)cos (−α)=A . 1B . −1C . tan αD . −tan α 40.已知sin (−α)=−√53,则cos (π2+α)的值为( )A . √53B . −√53C . 23 D . −23参考答案1.D【解析】【分析】直接运用诱导公式,转化为特殊角的三角函数值求解。
【详解】sin(−6000)=sin(−7200+1200)=sin1200=√32【点睛】本题考查诱导公式及特殊角的三角函数值,关键要牢记公式及特殊角的三角函数值,属于基础题。
2.D【解析】【分析】根据诱导公式,结合特殊角的三角函数即可得结果.【详解】化简cos11π3=cos(4π−π3)=cos(−π3)=cosπ3=12,故选D.【点睛】本题主要考查诱导公式的应用以及特殊角的三角函数,属于简单题.对诱导公式的记忆不但要正确理解“奇变偶不变,符号看象限”的含义,同时还要加强记忆几组常见的诱导公式,以便提高做题速度.3.C【解析】【分析】首先观察30°+α与60°–α的关系,再运用诱导公式即可。
【详解】cos(60°–α)=sin[90°–(60°–α)]=sin(30°+α)=√32,故选C.【点睛】本题考查诱导公式,属于基础题,比较容易。
4.A【解析】【分析】由诱导公式可得sinα,再由同角基本关系式可得结果.【详解】∵cos(π2+α)=−35,且α∈(π2,π),∴sinα=35,cosα=−45∴tan(α−π)=tanα=sinαcosα=−34故选:A【点睛】本题考查利用诱导公式与同角基本关系式化简求值,属于基础题. 5.A【解析】【分析】先由诱导公式得到sinα=-23,同角三角函数关系得cosα=√53,再计算tan(2π-α)。
【详解】因为sin(π-α)=-23所以sinα=-23,因为α∈(-π2,0),所以cosα=√1−sin2α=√53tan(2π-α)=−tanα=−sinαcosα=-23√53=2√55。
答案选A。
【点睛】本题考查了诱导公式,同角三角函数关系及三角函数在各象限内的符号等知识点,都属于基本知识,比较容易,但在求三角函数的值时,较容易出现符号错误,需要注意。
6.C【解析】由诱导公式可得sin (α+π4)=sin [π2−(π4−α)]=cos(π4−α),再由条件求得结果 【详解】sin (α+π4)=sin [π2−(π4−α)]=cos(π4−α)=√24故选C 【点睛】本题主要考查了诱导公式的应用,注意角之间的转化,属于基础题。
7.C 【解析】 【分析】利用同角基本关系得到cosα,再利用诱导公式化简所求即可. 【详解】∵sinα=35,π2<α<3π2,∴cosα=−45∴sin (7π2−α)=sin (3π2−α)=−cosα=45 故选:C 【点睛】本题考查了同角基本关系式及诱导公式,考查了计算能力,属于基础题. 8.D 【解析】 【分析】由已知条件利用同角关系求出sinx ,再利用诱导公式可得结果. 【详解】∵tanx =−125, x ∈(π2,π)∴sinx =1213∴cos (−x +3π2)=−sinx =−1213 故选:D . 【点睛】本题考查了同角基本关系式,考查了诱导公式,考查运算能力及推理能力,属于基础题. 9.B【分析】由题意结合诱导公式求解sin(π2+A)的值即可. 【详解】由诱导公式可得:cos (π+A ) =−cosA =−12,则cosA =12, 则sin (π2+A)=cosA =12. 本题选择B 选项. 【点睛】本题主要考查诱导公式及其应用,意在考查学生的转化能力和计算求解能力. 10.D 【解析】 【分析】利用三角函数的诱导公式和化弦为切,化简得tana−3tana+1=2,解方程即可. 【详解】∵cos (π2−α)−3cosαsinα−cos(π+α)=2, ∴sina−3cosa sina+cosa=tana−3tana+1=2,解得tana =−5,故选D . 【点睛】本题考查三角函数的诱导公式和同角三角函数的商数关系,属于基础题. 11.B 【解析】 【分析】利用终边相同的角同名函数相同,可转化为求120°的余弦值即可. 【详解】cos480°=cos(360°+120°)=cos120°=−12.故选B. 【点睛】本题主要考查了三角函数中终边相同的角三角函数值相同及特殊角的三角函数值,属于容易题.12.D【解析】【分析】根据三角函数的诱导公式,化为锐角的三角函数,即可求出答案.【详解】cos(−585°)=cos(−2×360°+135°)=cos135°=cos(180°−45°)=−cos45°=−√22;故选D.【点睛】本题考查利用三角函数的诱导公式求三角函数值,关键是熟练掌握诱导公式和特殊角的三角函数值.利用诱导公式解决“给角求值”问题的步骤:(1)“负化正”,负角化为正角;(2)“大化小”,大角化为[0°,360°)之间的角;(3)“小化锐”,将大于90°的角转化为锐角;(4)“锐求值”,化成锐角的三角函数后求值.13.C【解析】【分析】首先求得cosα的值,然后结合诱导公式整理计算即可求得最终结果.【详解】由三角函数的定义可得:cosα=√(−5)2+(−12)2=−513,则sin(3π2+α)=−cosα=513.本题选择C选项.【点睛】本题主要考查终边相同的角的三角函数定义,诱导公式及其应用等知识,意在考查学生的转化能力和计算求解能力.14.C【解析】分析:利用诱导公式以及同角三角函数关系式即可.详解:∵cos(π+α)=23,∴cosα=−23,则α为第二或第三象限角,∴sinα=±√1−cos2α=±√53.∴tanα=sinαcosα=±√53−23=±√52.故选:C.点睛:熟练运用诱导公式和同角三角函数基本关系,注意象限角对三角函数符号的影响,尤其是利用平方关系在求三角函数值时,进行开方时要根据角的象限或范围,判断符号后,正确取舍.15.D【解析】【分析】利用诱导公式化简所求不等式,然后求解表达式的值.【详解】已知cosα=15,−π2<α<0,∴sinα=−√1−cos2α=−2√65,则cos(π2+α)tan(α+π)cos(−α)tanα=−sinαtanα⋅cosα⋅tanα=−1tanα=−cosαsinα=√612.故选D.【点睛】本题考查诱导公式,同角三角函数基本关系式,属基础题.16.D【解析】【分析】利用诱导公式、同角三角函数的平方关系和象限角的符号,即可求得答案.【详解】∵sinα=13,α∈(π2,π)∴cosα<0, cos(−α)=cosα=−√1−sin2α=−2√23.故选D.【点睛】本题考查三角函数的诱导公式、同角三角函数的平方关系以及三角函数的符号与位置关系,属于基础题.17.B【解析】【分析】先化简已知得到sinα=−45,再化简cos(α−2π)=cosα,再利用平方关系求值得解.【详解】因为sin(π+α)=45,所以sinα=−45,因为cos(α−2π)=cosα,α是第四象限角,所以cosα=35.故答案为:B【点睛】(1)本题主要考查诱导公式和同角的平方关系,意在考查学生对这些知识的掌握水平和分析推理计算能力.(2)利用平方关系sin2α+cos2α=1求三角函数值时,注意开方时要结合角的范围正确取舍“±”号.18.B【解析】【分析】用已知角α+π3去表示未知角π6−α,再利用诱导公式化简即可.【详解】因为sin=,所以cos=sin=sin=.故选B.【点睛】用已知角去表示未知角是求三角值常见的一种处理技巧,巧用角之间的和差、以及特殊角的关系进行配凑从而简化计算,三角诱导公式的口诀为:奇变偶不变,符号看象限.19.A【解析】【分析】由已知及同角三角函数基本关系的运用可求sinα,从而由诱导公式即可得解.由cos α=k,α∈得sin α=,∴sin(π+α)=-sin α=-.故选A.【点睛】题主要考查了同角三角函数基本关系的运用,运用诱导公式化简求值,属于基本知识的考查.20.A【解析】【分析】根据诱导公式及三角函数同角关系进行化简,从而可得答案.【详解】===|sin 2-cos 2|=sin 2-cos 2.故选A.【点睛】本题主要考查了三角函数的化简求值问题,其中解答中熟记三角函数的诱导公式和同角三角函数的基本关系式化简三角函数式是解答的关键,注意最后化简的符号,这是解答的一个易错点,着重考查了推理与运算能力.21.B【解析】【分析】由诱导公式,化简即可得到sin585∘的值。
