数学物理方法答案_梁昆淼编_(第四版)
数学物理方法(梁昆淼)chapt7

x0
x0
( x)
1 1 x at u ( x, t ) [ ( x at ) ( x at )] ( )d 2 2a x at
x (t ) a
1 1 x at 1 at x u ( x, t ) [ ( x at ) (at x)] ( )d ( )d 2 2a 0 2a 0
n
xl
f (t )
u f (t ) (Ys ) x x l
ux
k
x l
ux
二齐
x l
f (t ) Ys
若为自由振动 f (t ) 0 例2 细杆导热问题
f (t )
xl
0
流出 流入
u f (t ) x x l u k f (t ) x x l
端点绝热 f (t ) 0
utt a2uxx 0在x0无意义
u1x ( x0 ) u2 x ( x0 )
例 均匀细杆长为 l , x 0 固定,
(1)另一端受着沿杆方向的力 Q ,如果开始的一瞬间 t 0 突然停止力的作用,求杆纵振动的定解条件。
振动方向
t0
x0 xl
t 0 时, Q 沿杆长方向加于杆的另一 (2)处于静止状态中, 端,写出定解条件 力从 t 0 开始作用在 x l
x (t ) a
4
utt a uxx 0
2
(0 x , t 0)
半无界区间内的一维自由振动
u x0 f (t )
u t 0 ( x)
ut t 0 ( x)
非奇非 偶延拓
一非齐
(0 x )
精选数学物理方法第四版梁昆淼期末总结讲义

设函数 f(z)在回路 l 所围区域 B上除有限个孤
立奇点b1,b2,…,bn外解析,在闭区域 B 上除b1,
b2,…,bn外连续,则f(z)沿l正向积分 l f (z)dz 之值
等于f(z)在l所围区域内各奇点的留数和的2 i倍.
n
l
f
( z )dz
2 i
Re sf
j 1
1 cos 2 2
u v 1 sin sin
2 2
22
第14页,共84页。
u 1 cos 2 2
u sin 2 2
将上面第二式对 积分, 视作参数,有
u
u
d
R(
)
sin d R()
22
2
sin
2
d
R(
)
2 cos R()
2
其中 R() 为 的任意函数。 将上式两边对 求导,
0 arg z 2 ,
辐角:Argz arg z 2k (k 0,1,2,)
共轭复数: z x iy z* x iy
第2页,共84页。
2、复数的运算: 加、减、乘、除、乘方、开方 (1)、加法和减法
z1 x1 iy1 z2 x2 iy2
z1 z2 (x1 x2 ) i( y1 y2 ) (2)、乘法和除法
2kπ n
i sin
2kπ n
i 2k
n e n
( k 0, 1, 2, , n 1 )
复数的乘、除、乘方和开方运算,采用三角式
或指数式往往比代数式来得方便。
第5页,共84页。
二、六种初等复变函数:
1. 幂函数 w z n
2 .指数函数 w e z
数学物理方法第四版课后习题答案

数学物理方法第四版课后习题答案《数学物理方法第四版课后习题答案》数学物理方法是一门涉及数学和物理学的交叉学科,它的研究对象是如何利用数学方法来解决物理学中的问题。
《数学物理方法第四版》是一本经典的教材,它涵盖了许多重要的数学物理方法,如傅里叶分析、复变函数、分析力学等。
在这本教材中,每一章都包含了大量的习题,这些习题旨在帮助学生加深对所学知识的理解,并提高他们的解题能力。
然而,对于许多学生来说,这些习题可能会带来一定的困难,因此他们需要及时地查阅习题答案来核对自己的解答。
本文将以《数学物理方法第四版课后习题答案》为标题,探讨数学物理方法这门学科的重要性以及这本教材对学生学习的帮助。
首先,数学物理方法在物理学中具有重要的地位。
许多物理学问题都可以通过数学方法来解决,比如利用微分方程来描述物理系统的演化,利用傅里叶分析来分析信号的频谱等。
因此,学习数学物理方法对于物理学专业的学生来说是至关重要的。
其次,这本教材提供了大量的习题,并且每一章都附带了习题答案。
学生可以通过做这些习题来巩固所学知识,并且及时地查阅答案来核对自己的解答。
这样一来,学生可以更好地理解课程内容,提高解题能力。
最后,数学物理方法这门学科对于培养学生的数学思维和物理直觉具有重要意义。
通过学习这门学科,学生可以培养自己的抽象思维能力和逻辑推理能力,同时也可以提高对物理现象的理解和分析能力。
总之,《数学物理方法第四版课后习题答案》这本教材对于学生学习数学物理方法这门学科具有重要的帮助。
它提供了丰富的习题和详细的答案,可以帮助学生更好地理解课程内容,提高解题能力,培养数学思维和物理直觉。
希望学生们能够充分利用这本教材,努力学习,取得更好的成绩。
数学物理方法梁昆淼答案

数学物理方法梁昆淼答案【篇一:第五章傅里叶变换数学物理方法梁昆淼】>?t1.函数 f(t)???0?12. 函数 f(t)???03.设(|t|?1)(|t|?1)的傅里叶变换为2(?cos??sin?/?)/(??)(|t|?1)(|t|?1)的傅里叶变换为f(?)?2sin?/??。
的傅立叶变换像函数,的傅立叶变换像函数为 _______________________ 。
4.?2012?2011excosx??(x??) dx?[sinx??(x??e??。
5. ?12009?6 ?2008) ]dx? 6.?xsinx?(x? ?1?3) dx?。
7. ?xsinx?(x?) dx? ?128.?[(x2?1)tan(sinx)??(x?)] dx? 。
?201038?911??9.?x3 ?(x?3) dx?-27 。
?tf(t)?10.函数 ??0(|t|?1)(|t|?1)的傅里叶变换为2(?cos??sin?/?)/(??)。
(0?t?1)?1?(?1?t?0)的傅里叶变换为。
11. f(t)???1?0(|t|?1)?12. 在(??,?)这个周期上,f(x)?x。
其傅里叶级数展开为?k?1?2sinkx k13.当0?x?2时,f(x)??1;当?2?x?0时,f(x)?1;当|x|?2时,f(x)?0。
则函数的f(x)傅里叶变换为b(?)?2??(1?cos2?)1?14已知函数f(x)的傅里叶变换为f(?),试证明f(ax)的傅里叶变换为f()。
af[f(ax)]?1?2????f(ax)e?i?xdx【令x?y/a】?1?2????f(y)e?i?aydya【令y?x】?1?f(x) ?i?ax2????aedx?1?af(a)a---(2分) ---(2分) ---(2分) ---(2分) 证明:【篇二:8000份课程课后习题答案与大家分享~~】> 还有很多,可以去课后答案网(/bbs)查找。
第四章 留数定理 习题梁昆淼数学物理方法

第四章 留数定理1. 函数z ze z f /1)(=在0=z 的奇点类型为 本性奇点 ,其留数为 1/2 。
2. 设n m ,为整数,则=⋅⎰-dx nx mx )cos (sin ππ0 。
3.函数23)(22+++=z z z z z f 有____1___个极点,为_____1____阶极点,在极点处的留数为____________-2____________。
4.为的单极点,则为__________________。
5.函数sin /()z z f z e =在0=z 的奇点类型为 可去奇点 ,其留为 06.函数43)(22-+-=z z zz z f 有________个极点,为__________阶极点;在极点处的留数 为________________________。
7.为的 。
A) 单极点 B) 二阶极点C) 三阶极点 D) 四阶极点8.已知函数,试判断是的几阶极点,然后计算、和在的留数,再利用所得结果给出在的邻域上洛朗展开级数的前三项。
(注意:此题亦可用的泰勒展开直接求出的洛朗展开的前几项,然后利用所得结果求出留数。
)9.求函数的奇点所在的位置,然后计算积分。
10.用留数定理计算复积分⎰=-+=2/3||22)2)(1(z z z dzI 。
解: 回路内有两个一阶极点.,21i z i z -== (2分)其留数为分)(350/)34(])2(2/[1])2)(/[(1lim )]()[(lim )(Re 22221i i i z i z z f i z z sf iz iz -=-=-+=-=→→分)(350/)34(])2(2/[1])2)(/[(1lim )]()[(lim )(Re 22222i i i z i z z f i z z sf iz iz +=---=--=+=→-→25/8))(Re )((Re 221i z sf z sf i I ππ=+= (2分)。
梁昆淼-数学物理方法

xat
2d
2
2a xat
cos x cos at 2t
( x)
u0
x1
x2
x1 x2
2
u(x,t) t0 (x)
例:求定解问题
utt a2uxx 0
ut (x,t) t0 0
2u0
x x1 x2 x1
x1
x
x1
2
x2
2u0
x2 x x2 x1
x1
x2 2
x
x2
0
x x1, x x2
u(x,t) 1 [(x at) (x at)]
2
u(x,t) 1 [(x at) (x at)]
2
u0
x1
x2
t 0
t t1 t t2
(二)、端点反射
utt a2uxx 0
u(x,t) t0 (x) ut (x,t) t0 (x)
Hu0
0 2
例2:一根导热杆由两段构成,两段热传导系数、比热、密
度分别为kI, cI, I, kII, cII, II, 初始温度为u0, 然后保持两端
温度为零,写出热传导问题的定解方程。
解:
第一段
ut I
kI
cI I
uxx I
0
x1
x
x2
x3
uI t0 u0
at)
1 2
(x
at)
1 2a
xat
(
)d
C
x0
2
u 1 [(x at) (x at)] 1
数学物理方法第1章复变函数-2016解答

【解】 设方根为 w k ,根据上面公式有
wk
1 e n
i 2kπ n
k 0,1,2,…,n 1
当 n=2 时,其根为 1. 对应于单位圆与实轴
的两交点.
22
当 n 3 时,各根分别位于单位圆 z 1的内接正多边
形的顶点处,其中一个顶点对应着主根: w0 1 , (k 0 ) .
面上的一个矢量, 为矢量长度,
为幅角 。记
z ei
z=x+iy=2k 幅角主值:0 Arg z 2 , Arg z ,
(z 0, ; k 0,1,2,...)
注:arg :argument (幅角、宗量,自变量)
数学物理方程(方法)
共60学时,3学分.
(以课堂讲授为主,加强课前和课后练习)
考试时间:暂定11月30日下午 考核方式:30%作业+70%期末考试
主要参考书目:
1. 梁昆淼 《数学物理方法》(第四版)高等教育出版社. 2. 吴崇试,《数学物理方法》,北京大学出版社 3. 冉扬强,《数学物理方法》, 科学出版社。 4. 王友年等《数学物理方法》,大连理工大学出版社
等式,对于 x 0 ,其辐角不满足要求.
24
1.2 复变函数 (一) 复变函数的定义
在复平面上一点集 E 中每一点z ,都有一个或几个 复数w与之对应,称w为 z 的函数,E 为定义域,记 w =f(z),z E 。z有时称为宗量(argument) 或自变量。 实函数: y=f(x)= ± x^(1/2), x>=0 多值
17
N
A’
A
S
球的南极与复数平面的原 点相切,平面上任意点 A 与球的北极由一条直线相 连,直线与球相交于 A’ 。 由此,每一有限的复数 投 影到球上一点 。这个投影 叫测地投影,这个球叫复 数球。
数学物理方法第(梁昆淼)部分知识点

1.复变函数 .................................................................................................................................................................. 2 1.1 复数与复数运算 ........................................................................................................................................... 2 1.2 复变函数 ....................................................................................................................................................... 2 1.3 导数 ............................................................................................................................................................... 2 1.4 解析函数 ..........................................................................................................................
数学物理方法(梁昆淼)总复习

ut a2uxx 0
ux x0 0 ux xl 0 u (x)
t 0
通解
u( x, t )
C0
n1
C e
n2 2
l2
a2
n
t
cos
n
l
x
系数
C0
1 l
l
( x)dx
0
Cn
2 l
l (x) cos n x dx
0
l
3. 边界条件为“ 混齐”
F (x)eimxdx
0
2
i{F (z)eimz在上半平面所有奇点留数之和}
1
G(x)sin mxdx
G(x)eimxdx
0Leabharlann 2i {G( z )eimz 在上半平面所有奇点留数之和}
八 奇函数和偶函数的傅立叶级数
奇函数
f
(x)
k 1
bk
sin
k
u f (t) x xa Ys
例2 细杆导热问题 f (t)
xa
u
k
f (t)
x xa
k u f (t) x xa
流出 流入
达朗贝尔公式适用的问题
1 utt a2uxx 0
u (x) t 0
ut t0 (x)
齐次的泛定方程
( x ,t 0)
n
l f (z)dz 2 i Re sf (bj )
.bn
j 1
全平面的留数定理:
函数 f (z) 在全平面上所有各点
的留数之和为零
.
.b1
.b2
.
数理方法题解 梁昆淼
∂u ∂ρ
=
1 ρ
∂v ∂ϕ
1
ρ
∂u ∂ϕ
=
−
∂v ∂ρ
第18页 2 .已知解析函数f (z)的实部u(x, y)或虚部v(x, y), 求该解析函数 以下题目可以有多种解法 这里只列其中之一
(1) u(x, y) = e x sin y
解 已知实部或虚部 一般意味它们已经是调和函数 可以验证
=
x2
x +
y2
=2
得
x2
+
y2
−
x 2
=
0
即
x −
1 4
2
+
y2
=
1 16
=
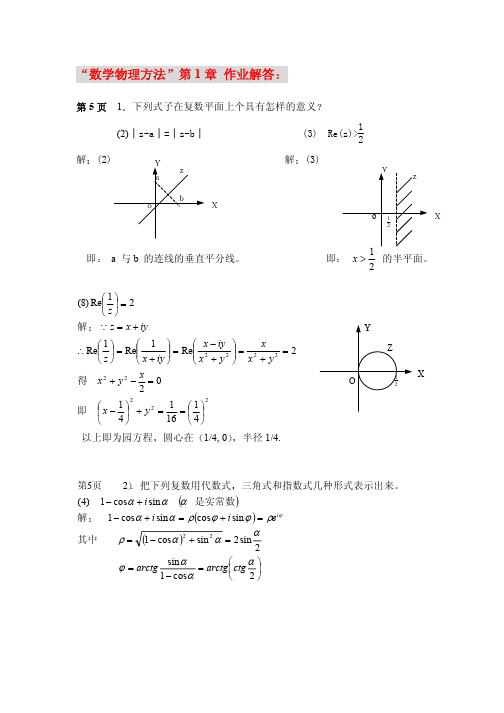
1 4
2
以上即为园方程 圆心在 1/4, 0 半径 1/4.
o1
2
即
x
>
1 2
的半平面
Y Z
O
1
X
2
第5页 2 . 把下列复数用代数式 三角式和指数式几种形式表示出来
(4) 1 − cosα + i sinα (α 是实常数)
其中
ρ = x2 + y2
ϕ
=
arctg
y x
(6) e1−i
解 e1+i = e × ei = e(cos1 + i sin1)
第9页 2 .计算下列数值 a和b为实常数 x为实变数
(3) ln(−1)
[ ] 解 ln(−1) = ln 1ei(π +2nπ ) = ln1 + i(2n + 1)π = i(2n + 1)π
解 1 − cosα + i sinα = ρ(cosϕ + i sinϕ ) = ρeiϕ
数学物理方法第四版(梁昆淼)期末总结ppt

f ( z) 2i ( n ) dz f ( ) (2) 利用柯西公式 l n 1 n! (z )
来计算积分.
19
例1.
c
sin(
z) 4 dz, 其中c : ( x 1) 2 y 2 1 z2 1
y
sin( z ) 4 dz I z 1 z 1 c
v 2 x ( y ) y
( y) y
1 2 y C 2 1 v 2 xy ( y 2 x 2 ) C 2 1 f ( z ) u iv x 2 y 2 xy i[2 xy ( y 2 x 2 )] iC 2 1 ( x iy ) 2 i ( x iy ) 2 iC 2 1 z 2 i z 2 iC 2 ( y )
0 (l不包围 ) 1 l z dz 2 i (l包围 )
z
1 1 1 1 dz ( dz 2 z z 1 z z 1 dz ) z 1 2 1 (2 i 2 i ) 2 0
21
第三章
一、收敛半径
或虚部,通过C—R条件求出该解析函数的虚部或
实部,从而写出这个解析函数。
① 算偏导
② u或v 的全微分
③ 求积分
④ 表成 f ( z )
10
例 3:已知解析函数 f (z ) 的实部u( x, y) x2 y2 xy, f (0) 0 , 求虚部和这个解析函数。
解:
u u 2 x y, x 2 y x y
17
4、柯西公式
f ( z) l z dz 2 if ( )
高阶导数的柯西公式
梁昆淼数学物理方法

Copyright 2004-2011 Aspose Pty Ltd.
u(x) tt0
2h
(l x) [l / 2,l]
l
速度满足 ut (x, y, z,t) tt0 0
二、边界条件
第一类边 界条件
u(x, y, z,t) x0 y0 z0 f (x0,Байду номын сангаасy0, z0,t)
第二类边
(Yu
Copyright
x xa )S
2004-2011
f (t)
AsposuexPxtyaLtdf.Y(St
)
如杆端自由 f(t)=0
ux xa 0
B)、热传导
如细杆热传导端
点有热量流出 0
x a
eaqtexdxwaithCAosppkyorusigen.hSxtl2Eiad0ve0as4luf-o2akrt0i.1oN1nuExAoTnsxpl3yo..a5seCPlitfeyn(Lt)tPdr.ofile 5.2.0
( a )( a )u 0 t x t x
令: x a( )
t
eated with Aspose.tSlEitdveaslufxoarti.oxNnEoTntl3y..5aClxient Profile 5.2.0
( x )
Client Profile 5.2.0
Copyriguht 2f010(x4-2a0t1)1Afs2p(oxseaPtt)y Ltd.
求导有 ut af1'(x at) af2'(x at)
f1(x) f2(x) (x)
af1'(x) af2 '(x) (x)
