钢环分离锥式无级变速器弹流润滑膜厚的计算
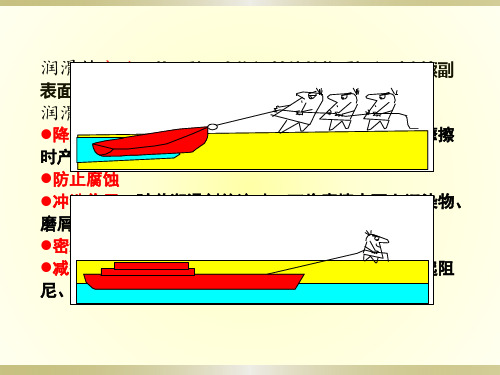
流体润滑(弹流润滑)
几种摩擦的界限常以膜厚比来大致估计:
hmin R R
2 q1 2 q2
式中:hmin——最小公称油膜厚度,m
Rq1 ——接触表面轮廓的均方根偏差,m
Rq2 ——接触表面轮廓的均方根偏差,m
≤0.4,干摩擦 ≤1,边界摩擦; =1~3,混合摩擦; >3,流体摩擦
不同润滑状态下的摩擦因数
总结:粘压效应和弹性变形效应有利于提高润滑膜的承载能力。
前面所讨论的流体动压润滑理论及计算,是假定两个润滑表面相对运 动时仍保持完全的刚性,未产生弹性变形,这在低副接触时是正确的。但是, 对于高副接触,如齿轮、滚动轴承等,其比压很大,运用流体动压润滑理论 就不再合适了。 低副 (面接触) 润滑表面刚性 流体动压润滑理论 高副 (点、线接触) 润滑表面弹性变形 弹性流体动压润滑理论 定义一:相对运动表面的弹性变形与流体动压作用都对润滑油的润滑性 能起着重要作用的一种润滑状态。 定义二:弹性流体动力润滑是指流体进入在两个相互运动的固体摩擦接 触表面后,受到接触表面产生的巨大接触压力而发生的性状改变,以分 割固体摩擦接触表面,减少摩擦。 从广义上说:凡是表面弹性变形量和最小油膜厚度处在同一量级上的 润滑问题,都属于弹流问题。 弹性流体动压润滑理论是流体动压润滑理论的重要发展,可以说弹性流 体动力润滑是流体膜润滑的一种特殊形式。它主要研究名义上是点、线 接触的摩擦副润滑问题(如齿轮副、滚动轴承等)。
两个弹性圆柱的接触,可等效于一当量圆柱和一刚性平面的接触问题,因此 在弹流润滑的研究中,可以将接触区视为平面。
等效圆柱
刚性平面
为了分析弹性流体动压润滑机理,首先观察一下对偶表面干接触时的情况。 如图所示模型是弹性圆柱体与一刚性平面干接触的情况。在载荷作用下,弹性 圆柱体发生弹性变形,使线接触变成了小面积接触,载荷所造成的接触压力常 称为赫兹压力,其分布情况是在接触区域内成抛物线形分布,中间的压力最高 而至边缘降低为零。
钢环分离锥式无级变速器设计

目录第一章绪论 (1)1.1无级变速器的介绍 (1)1.2摩擦式无级变速器 (1)1.3摩擦式无级变速器运动原理 (1)1.4钢环分离锥式无级变速器的优点 (3)1.5本次课题设计任务 (3)第二章钢环分离锥式无级变速器设计方案 (4)2.1钢环分离锥式无级变速器简图 (4)2.2传动零件尺寸 (4)2.3钢环分离锥式无级变速器受力分析 (5)2.4强度验算 (7)2.4.1恒功率传动情况时 (8)2.4.2恒扭矩传动情况时 (10)2.4.3钢环强度效验计算 (11)第三章钢环分离锥式无级变速器的计算 (13)3.1计算锥轮的尺寸和参数 (13)3.2钢环的设计 (14)3.3轴系零件设计 (14)3.4调速操纵机构设计 (16)3.4.1确定齿轮的参数 (16)3.4.2确定齿条的参数 (17)3.4.3计算螺杆 (16)3.5设计箱体 (18)第四章强度校核 (19)4.1刚换强度验算 (19)4.2校验轴的强度 (20)设计总结 (22)致谢 (23)参考文献 (24)附录:英文文献翻译及原文 (25)摘要钢环分离锥锥轮无级变速器是机械摩擦式的一种变速器,它以钢环为中间原件,以改变主、从动锥轮的工作半径来实现无级变速。
它能实现对称变速而且无需再设加压装,结构简单,时常将这种变速器应用在传动系统的高速级。
首先查找变速器相关资料,了解其传动原理及设计要求和计算公式,选择材料。
通过已知给定参数先求出变速器主要零件钢环和主从锥轮的相关尺寸,再根据已算出的数据和配合关系选定其主要配合原件轴承型号,然后确定锥轮各段长度和大小。
再进行轴的设计,通过公式选取轴的最少直径,再结合与锥轮配合关系确定轴的各段长度及选取键和轴键等相关尺寸,根据设计手册选取有关尺寸的配合公差,选取设计调速操作机构,再由已知的零件尺寸和配合关系,根据设计手册确定箱体和端盖的基本尺寸,其后对轴和钢环进行强度校核,以确定尺寸是否满足要求。
面接触润滑测量系统油膜厚度自动计算方法

面接触润滑测量系统油膜厚度自动计算方法白清华;郭峰;田鹏晖【摘要】To overcome the low efficiency in artificial estimation of the film thickness in an optical slider-on-disc lubricating film tester,a robust algorithm was proposed to recognize interference intensity variation and its order change,which enables automatic measurement of film thickness.Theoretical and experimental results show that the multi-beam interference principle can be applied to the film thickness measurement in the slider-on-disc contact,and the interference intensity profile can be divided into regions Ⅰ and Ⅱ within one film thickness period.Freeman chain code and simple moving average filter technique were used to smooth the data.A normalization algorithm based on threshold value was proposed for determining in which region the data are,and the interference order can be obtained accurately.A template matching method was used to infer the shape of the start and the end areas.This approach was applied to process measured data in the experiments,and results were in good agreement with the oit film thickness calculated by the old method.%为了解决面接触润滑油膜光干涉测量系统人工计算油膜厚度效率低下的问题,提出光强数据的高效处理算法,实现油膜厚度的自动计算.通过理论和实验验证多光束干涉理论应用于滑块-玻璃盘面接触副的可行性.对整周期内的光强分布进行区域定义,应用Freeman方向链码和均值滤波对数据曲线进行分段光滑,设计基于阈值的归一算法,通过模板对比算法,得到光强曲线的始末端形态,自动计算出光强数据所属区域Ⅰ和Ⅱ的数量,实现干涉级次的准确计算;以该方法编写程序应用于实际测量,结果与手动计算的油膜厚度有很好的一致性.【期刊名称】《润滑与密封》【年(卷),期】2017(042)001【总页数】7页(P34-40)【关键词】光干涉;油膜厚度;Freeman方向链码;模板对比【作者】白清华;郭峰;田鹏晖【作者单位】青岛理工大学计算机工程学院山东青岛266520;青岛理工大学机械工程学院山东青岛266520;青岛理工大学机械工程学院山东青岛266520;青岛理工大学机械工程学院山东青岛266520【正文语种】中文【中图分类】TH117摩擦副表面之间形成一定厚度的流体润滑油膜可以减少或避免磨损,降低摩擦阻力。
滚动轴承点接触弹流油膜厚度及摩擦力矩的分析计算

滚动轴承的摩擦力矩问题涉及到弹性力学 、 接触力学 、摩擦 、润滑等学科 , 且各种因素相互影 响 ,相互作用 ,使摩擦力矩的精确分析计算不易进 行 。新的摩擦力矩计算公式可以定量地分析轴承 弹流油膜厚度与摩擦力矩的关系 , 也可以应用于 轴承的设计和工艺 ,提高轴承的性能 , 进而增强机 械设备的可靠性 ,增加设备利用率 。
(1
-
e ) - 0. 68k
(3)
材料参数 G′=αE′
(4)
E1′=
1 21 (-源自ν2 1E1+
1
-
ν2 2
)
E2
速度参数 U ′=ηE0′RUx
(5)
U
π =
(Dp2w
-
Dw2 co sβ)
120Dpw
| ne
-
ni
|
载荷参数W
′=
W
E ′R2x
(6)
W = Fa / Z sinβ
椭圆率 k = 1. 03 ( Ry ) 0. 64
(1. 河南科技大学 机电工程学院 ,河南 洛阳 471003; 2. 洛阳轴承研究所 ,河南 洛阳 471039)
摘要 :点接触弹流润滑的实际计算较为复杂 ,对点接触弹流油膜厚度及摩擦力矩的计算进行了详细分析并给出 了计算实例 。同时对弹流油膜厚度与轴承摩擦力矩的关系进行了探讨 ,提出了新的摩擦力矩经验计算公式 。 关键词 :滚动轴承 ;点接触 ;弹流润滑 ;油膜厚度 ;摩擦力矩 中图分类号 : TH133. 33; TH117 文献标志码 : B 文章编号 : 1000 - 3762 (2008) 04 - 0010 - 03
对试验所得的数据进行整理分析 , 提出了新 的摩擦力矩经验计算公式为
金属带式无级变速器钢带环弹性特性及其造成的能量损失

金属带式无级变速器钢带环弹性特性及其造成的能量损失张武1,2 刘凯1 崔亚辉1 原园1 赵桐1【摘要】摘要:基于弹性力学理论,建立了金属带式无级变速器钢带环伸长模型。
在圆弧段上,钢带环被简化为组合薄壁圆筒模型,在直线段上被简化为单向拉伸模型。
模型计算结果显示:随着传动比的增大,应力应变在主动轮上不断增大,在从动轮上先减小后增大;径向位移在主动轮上先减小后增大,在从动轮上不断增大;当传动比一定时,最内层钢带环的应力应变和径向位移最大,最外层最小;钢带环总的伸长量随着传动比的增大而增大,但当传动比为1时有所减小;钢带环线应变范围是0.04% ~0.08%。
功率损失分析表明:钢带环应变能功率损失范围为27.15~86.73W,当传动比为1时,总功率损失为34.85W。
【期刊名称】中国机械工程【年(卷),期】2012(023)021【总页数】7【关键词】关键词:钢带环;金属带;无级变速器;伸长量0 引言金属带式无级变速器(MB-CVT)作为最成功的无级变速器之一,具有节省燃料、操控简单、驾驶平顺舒适和低排放等优点。
最新研究显示:在相同的工作状态下,装备MB-CVT的汽车较装备自动挡的汽车节油7% ~15%[1]。
MB-CVT 属于摩擦传动系统,因此其传递动力的能力受到一定限制。
Kong等[1]以单个钢带环为基础建立了MBCVT动力学模型,研究了带轮与最内层钢带环以及钢带环之间的相互作用及每层钢带环在传递动力方面的负载分布状况,并且认为一层或多层钢带环过早断裂是变速器失效的一个重要原因。
Kuwabara等[2]在研究中忽略了钢带环之间的相互作用,并将其假设为一个整体。
Kim等[3]完全忽略MB-CVT各部件间的相互作用,且进一步认为两组钢带环和数以百计的金属块是一个连续体。
Akehurst等[4]假设所有的钢带环都具有相同的圆弧段,且每组钢带环是由数层钢带环组合而成,但是对于每层钢带环承载力矩的能力却没有研究。
弹流润滑数值计算方法-赵江

弹流润滑数值计算方法1.1等温线接触弹流润滑数值计算方法与程序等温点接触弹流润滑的基本方程包括:Reynolds 方程、膜厚方程、变形方程、粘压方程、密压方程和载荷平衡方程,主要形式如下Reynolds 方程:xρh 12μ=x p ηρh x 3d )d()d d (d d s (1) 膜厚方程)(+2R+=)(20x υx h x h (2)变形方程∫ex +d ln(2-=x c s x -s x p Eπx υ))()( (3)粘压方程{}])()[.(z p p ηηη000+1+1-679+ln exp = (4)密压方程)..ppρρ71+160+1=0( (5)载荷平衡方程∫0=d -0ex x x x p ω)( (6)计算程序计算工况参数 节点数:N=30量纲一花起始点坐标:X0=-4.0 量纲一花终止点坐标:XE=1.5 载荷:W=1.0E5综合弹性模量E1=2.2E11 初始粘度:EDA0=0.05 圆柱半径:R=0.05 速度:US=1.5 主程序:FORGRAM LINEEHLCOMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DH/COM2/EDA0/COM4/X0,XE/COM3/E1,PH,B,RDATA PAI,Z,P0/3.14159565,0.68,1.96E8/DATA N,X0,XE,W,E1,EDA0,R,US/130,-4.0,1.5,1.0E5,2.2E11,0.05,0.05,1.5/OPEN(8,FILE=’OUT.DAT’,STA TUS=’UNKNOWN’)W1=W/(E1*R)C W无量纲公式,PH=E1*SQRT(0.5*W1/PAI)C PH为最大hertz接触应力Ph,单位paA1=(ALOG(EDA0)+9.67)C 粘度公式计算时的参数A2=PH/P0C 粘度公式计算时的参数A3=0.59/(PH*1.E-9)C 密度公式计算时参数B=4.*R*PH/E1C B为HERTZ接触区半宽,单位mALFA=Z*A1/P0 C粘度系数G=ALFA*E1 C材料参数U=EDA0*US/(2.*E1*R)C 苏联人提出的入口区分析解中定义的CC1=SQRT(2.*U)AM=2.*PAI*(PH/E1)**2/CC1ENDA=3.*(PAI/AM)**2/8C ENDA量钢化reynolds中的栏目达HM0=1.6*(R/B)**2*G**0.6*U**0.7*W1**(-0.13)C hm0最小膜厚,公式为最小膜厚公式WRITE(*,*)N,X0,XE,W,E1,EDA0,R,USCALL SUBAK(N)CALL EHL(N)STOPENDSUBROUTINE EHL(H)C 弹流润滑子程序DIMENSION X(1100),P(1100),H(1100),RO(1100),EPS(1100),EDA(1100),V(1100)C X P压力、H膜厚、RO密度、EPS雷诺方程中的E、EDA粘度、V弹性变形COMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DH/COM4/X0,XEC ENDA量钢化reynolds中的栏目达, hm0最小膜厚COMMON/COM3/E1,PH,B,RRC E1当量弹性模量E,PH为最大hertz接触应力ph,B为HERTZ接触区半宽,RRMK=1DX=(XE-X0)/(N-1.0)C DX等距节点间距DO 10 I=1,NX(I)=X0+(I-1)*DXIF(ABS(X(I)).GE,1.0)P(I)=0.0C 压力分布为抛物线形式,IF(ABS(X(I)).LT,1.0)C 压力分布为抛物线形式10 CONTINUECALL HREE(N,KK,DX,X,P,H,RO,EPS,EDA,V)CALL FZ(N,P,POLD)C 对应于框图中,调用HREE子程序计算个节点膜厚,密度ro,和粘度EDA,C 并调用子程序VI计算个节点的弹性变形C 调用子程序FZ将P(I)的值赋给POLD,POLD第i个节点的前一次迭代压力值14 KK=19CALL ITER(N,KK,DX,X,P,H,RO,EPS,EDA,V)C 调用ITER子程序进行雷诺方程迭代,重新计算hree压力分布下的节点膜厚/粘度/密度MK=MK+1CALL ERROP(N,P,POLD,ERP)C 调用ERROP子程序计算迭代前后的压力差并输出WRITE(*,*)’ERP=’,ERPIF(ERP.GT.1.E-5.AND.DH.GT.1.E-6)THENC .GT.大于IF(MK.GE.50)THENMK=1DH=0.5*DHENDIFGOTO14ENDIFC 判断ERP和DH是否满足条件IF(DH.LE.1.E-6)WRITE(*,*)’pressure are not convergent’H2=1.E3P2=0.0DO 106 I=1,NIF(H(I).LT.H2)H2=H(I)IF(P(I).GT.P2)P2=P(I)C 找出最小膜厚H2和最大压力P2,量纲一化并输出106 CONTINUEH3=H2*B*B/RRP3=P2*PHC 这个地方还不是很懂,可能是获得最小的值然后量纲计算出有单位的值110 FORMAT(6(1X,E12.6))C 格式化输出1X把输出位置向右跳过n个位置C E12.6以12个字符宽输出指数类型的浮点数,小数部分占6个字符宽120 CONTINUEWRITE(*,*)‘P2,H2,P3,H3=’,P2,H2,P3,H3CALL OUTHP(N,X,P,H)RETURNSUBROUTINE OUTHP(N,X,P,H)C 输出子程序DIMENSION X(N),P(N),H(N)DO 10 I=1,NWRITE(8,20)X(I),P(I),H(I)10 CONTINUE20 FORMA T(1X,6(E12,6,1X))RETURNENDSUBROUTINE HREE(N,DX,X,P,H,RO,EPS,EDA,V)DIMENSION X(N),P(N),H(N),RO(N),EPS(N),EDA(N),V(N)COMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DH/COM2/EDA0/COMAK/AK(0:1100)DATA KK,PAI1,G0/0,0.318309886,1.570796325/IF(KK.NE.0)GOTO3H00=0.03 W1=0.0DO 4 I=1,N4 W1=W1+P(I)C3=(DX*W1)/G0DW=1.-C3C 不是很懂CALL VI(N,DX,P,V)HMIN=1.E3DO 30 I=1,NH0=0.5*X(I)*X(I)+V(I)C 和膜厚公式有关IF(H0.LT.HMIN) HMIN=H0H(I)=H030 CONTINUEIF(KK.NE.0)GOTO 32KK=1DH=0.005*HM0C 逐步减小法H00=-HMIN+HM032 IF(DW.LT.0.0)H00=H00+DHIF(DW.GT.0.0)H00=H00-DHDO 60 I=1,NH(I)=H00+H(I)EDA(I)=EXP(A1*(-1.+(1.+A2*P(I)**Z))C 就是粘压公式RO(I)=(A3+1.35*P(I))/(A3+P(I))EPS(I)=RO(I)*H(I)**3/(ENDA*EDA(I))C 求出了雷诺方程中的一副三拉,为后面雷诺方程的迭代计算做基础60 CONTINUERETURNSUBROUTINE ITER(N,KK,DX,X,P,H,RO,EPS,EDA,V)C 雷诺方程中的迭代DIMENSION X(N),P(N),H(N),RO(N),EPS(N),EDA(N),V(N)COMMON/COMAK/AK(0:1100)DATA PAI1/0.318309886/DO 100 K=1,KKD2=0.5*(EPS(1)+EPS(2))D3=0.5*(EPS(2)+EPS(3))DO 70 I=2, N-1D1=D2D2=D3IF(I.NE.N-1)D3=0.5*(EPS(I+1)+EPS(I+2))D8=RO(I)*AK(0)*PAI1D9=RO(I-1)*AK(1)*PAI1D10=1.0/(D1+D2+(D9-D8)*DX)D11=D1*P(I-1)+D2*P(1+1)D12=(RO(I)*H(I)-RO(I-1)*H(I-1)+(D8-D9)*P(I))*DXP(I)=(D11-D12)*D10IF(P(I).LT.0.0)P(I)=0.0C 计算雷诺差分方程个系数,计算节点压力,并保证节点压力不小于0(这里还要仔细考虑)70 CONTINUECALL HREE(N,DX,X,P,H,RO,EPS,EDA,V)C 调用HREE方程重新计算各节点的膜厚,100 CONTINUERETURNENDSUBROUTINE VI(N,DX,P,V)DIMENSION P(N),V(N)COMMON/COMAK/AK(0:1100)PAI1=0.318309886C=ALOG(DX)DO 10 I=1,NV(I)=0.0DO 10 J=1,NIJ=IABS(I-J)10 V(I)=V(I)+(AK(IJ)+C)*DX*P(J)DO I=1,NV(I)=-PAI1*V(I)ENDDORETURNENDSUBROUTINE SUBAK(MM)COMMON/COMAK/AK(0:1100)DO 10 I=1,MM10 AK(I)=(I+0.5)*(ALOG(ABS(I+0.5))-1.)-(I-0.5)*(ALOG(ABS(I-0.5))-1.)ENDSUBROUTINE FZ(N,P,POLD)DIMENSION P(N),POLD(N)DO 10 I=1,N10 POLD(I)=P(I)RETURNENDSUBROUTINE ERROP(N,P,POLD,ERP)DIMENSION P(N),POLD(N)SD=0.0SUM=0.0DO 10 I=1,NSD=SD+ABS(P(I)-POLD(I))10 SUM=SUM+P(I)ERP=SD/SUMRETURENENDFORGRAM LINEEHLCOMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DH/COM2/EDA0COMMON/COM4/X0,XE/COM3/E1,PH,B,RDATA PAI,Z,P0/3.14159565,0.68,1.96E8/DATA N,X0,XE,W,E1,EDA0,R/130,-4.0,1.5,1.0E5,2.2E11,0.05,0.05/ DATA US/1.5/OPEN(8,FILE=’OUT.DAT’,STATUS=’UNKNOWN’)W1=W/(E1*R)C W无量纲公式,PH=E1*SQRT(0.5*W1/PAI)C PH为最大hertz接触应力Ph,单位paA1=(ALOG(EDA0)+9.67)C 粘度公式计算时的参数A2=PH/P0C 粘度公式计算时的参数A3=0.59/(PH*1.E-9)C 密度公式计算时参数B=4.*R*PH/E1C B为HERTZ接触区半宽,单位mALFA=Z*A1/P0 C粘度系数G=ALFA*E1 C材料参数U=EDA0*US/(2.*E1*R)C 苏联人提出的入口区分析解中定义的CC1=SQRT(2.*U)ENDA=3.*(PAI/AM)**2/8C ENDA量钢化reynolds中的栏目达HM0=1.6*(R/B)**2*G**0.6*U**0.7*W1**(-0.13)C hm0最小膜厚,公式为最小膜厚公式WRITE(*,*)N,X0,XE,W,E1,EDA0,R,USCALL SUBAK(N)CALL EHL(N)STOPENDSUBROUTINE EHL(H)C 弹流润滑子程序DIMENSION X(1100),P(1100),H(1100),RO(1100),EPS(1100),EDA(1100)DIMENSION V(1100)C X P压力、H膜厚、RO密度、EPS雷诺方程中的E、EDA粘度、V弹性变形COMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DH/COM4/X0,XEC ENDA量钢化reynolds中的栏目达, hm0最小膜厚COMMON/COM3/E1,PH,B,RRC E1当量弹性模量E,PH为最大hertz接触应力ph, B为HERTZ接触区半宽,RRMK=1DX=(XE-X0)/(N-1.0)C DX等距节点间距DO 10 I=1,NX(I)=X0+(I-1)*DXC 定位X(I)的位置,对应于框图中的计算个节点X(I),和hertz压力值IF(ABS(X(I)).GE,1.0)P(I)=0.0C 压力分布为抛物线形式,IF(ABS(X(I)).LT,1.0)C 压力分布为抛物线形式10CONTINUECALL HREE(N,KK,DX,X,P,H,RO,EPS,EDA,V)CALL FZ(N,P,POLD)C 对应于框图中,调用HREE子程序计算个节点膜厚,密度ro,和粘度EDA,C 并调用子程序VI计算个节点的弹性变形C 调用子程序FZ将P(I)的值赋给POLD,POLD第i个节点的前一次迭代压力值14 KK=19CALL ITER(N,KK,DX,X,P,H,RO,EPS,EDA,V)C 调用ITER子程序进行雷诺方程迭代,重新计算hree压力分布下的节点膜厚/粘度/密度 MK=MK+1CALL ERROP(N,P,POLD,ERP)C 调用ERROP子程序计算迭代前后的压力差并输出WRITE(*,*)’ERP=’,ERPIF(ERP.GT.1.E-5.AND.DH.GT.1.E-6)THENC .GT.大于IF(MK.GE.50)THENMK=1ENDIFGOTO14ENDIFC 判断ERP和DH是否满足条件IF(DH.LE.1.E-6)WRITE(*,*)’pressure are not convergent’H2=1.E3P2=0.0DO 106 I=1,NIF(H(I).LT.H2)H2=H(I)IF(P(I).GT.P2)P2=P(I)C 找出最小膜厚H2和最大压力P2,量纲一化并输出106CONTINUEH3=H2*B*B/RRP3=P2*PHC 这个地方还不是很懂,可能是获得最小的值然后量纲计算出有单位的值110FORMAT(6(1X,E12.6))C 格式化输出1X把输出位置向右跳过n个位置C E12.6以12个字符宽输出指数类型的浮点数,小数部分占6个字符宽120CONTINUEWRITE(*,*)‘P2,H2,P3,H3=’,P2,H2,P3,H3CALL OUTHP(N,X,P,H)RETURNENDSUBROUTINE OUTHP(N,X,P,H)C 输出子程序DIMENSION X(N),P(N),H(N)DO 10 I=1,NWRITE(8,20)X(I),P(I),H(I)10CONTINUE20FORMAT(1X,6(E12,6,1X))RETURNENDSUBROUTINE HREE(N,DX,X,P,H,RO,EPS,EDA,V)DIMENSION X(N),P(N),H(N),RO(N),EPS(N),EDA(N),V(N)COMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DH/COM2/EDA0/COMAK/AK(0:1100)DATA KK,PAI1,G0/0,0.318309886,1.570796325/IF(KK.NE.0)GOTO3H00=0.03 W1=0.0DO 4 I=1,N4 W1=W1+P(I)C3=(DX*W1)/G0DW=1.-C3C 不是很懂HMIN=1.E3DO 30 I=1,NH0=0.5*X(I)*X(I)+V(I)C 和膜厚公式有关IF(H0.LT.HMIN) HMIN=H0H(I)=H030CONTINUEIF(KK.NE.0)GOTO 32KK=1DH=0.005*HM0C 逐步减小法H00=-HMIN+HM032IF(DW.LT.0.0)H00=H00+DHIF(DW.GT.0.0)H00=H00-DHDO 60 I=1,NH(I)=H00+H(I)EDA(I)=EXP(A1*(-1.+(1.+A2*P(I)**Z))C 就是粘压公式RO(I)=(A3+1.35*P(I))/(A3+P(I))EPS(I)=RO(I)*H(I)**3/(ENDA*EDA(I))C 求出了雷诺方程中的一副三拉,为后面雷诺方程的迭代计算做基础60CONTINUERETURNENDSUBROUTINE ITER(N,KK,DX,X,P,H,RO,EPS,EDA,V)C 雷诺方程中的迭代DIMENSION X(N),P(N),H(N),RO(N),EPS(N),EDA(N),V(N)COMMON/COMAK/AK(0:1100)DATA PAI1/0.318309886/DO 100 K=1,KKD2=0.5*(EPS(1)+EPS(2))D3=0.5*(EPS(2)+EPS(3))DO 70 I=2, N-1D1=D2D2=D3IF(I.NE.N-1)D3=0.5*(EPS(I+1)+EPS(I+2))D8=RO(I)*AK(0)*PAI1D9=RO(I-1)*AK(1)*PAI1D10=1.0/(D1+D2+(D9-D8)*DX)D11=D1*P(I-1)+D2*P(1+1)D12=(RO(I)*H(I)-RO(I-1)*H(I-1)+(D8-D9)*P(I))*DXP(I)=(D11-D12)*D10IF(P(I).LT.0.0)P(I)=0.0C 计算雷诺差分方程个系数,计算节点压力,并保证节点压力不小于0(这里还要仔细考虑) 70CONTINUEC 调用HREE方程重新计算各节点的膜厚,100CONTINUERETURNENDSUBROUTINE VI(N,DX,P,V)DIMENSION P(N),V(N)COMMON/COMAK/AK(0:1100)PAI1=0.318309886C=ALOG(DX)DO 10 I=1,NV(I)=0.0DO 10 J=1,NIJ=IABS(I-J)10 V(I)=V(I)+(AK(IJ)+C)*DX*P(J)DO I=1,NV(I)=-PAI1*V(I)ENDDORETURNENDSUBROUTINE SUBAK(MM)COMMON/COMAK/AK(0:1100)DO 10 I=1,MM10 AK(I)=(I+0.5)*(ALOG(ABS(I+0.5))-1.)-(I-0.5)*(ALOG(ABS(I-0.5))-1.)RETURNENDSUBROUTINE FZ(N,P,POLD)DIMENSION P(N),POLD(N)DO 10 I=1,N10 POLD(I)=P(I)RETURNENDSUBROUTINE ERROP(N,P,POLD,ERP)DIMENSION P(N),POLD(N)SD=0.0SUM=0.0DO 10 I=1,NSD=SD+ABS(P(I)-POLD(I))10 SUM=SUM+P(I)ERP=SD/SUMRETURNENDPROGRAM MAINWRITE(*,*) 'HELLO'WRITE(*,*)1'HELLO'100WRITE(*,*)'HELLO'10STOPEND1.2等温点接触弹流润滑数值计算方法与程序Program pointehlCOMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DHDATA PAI,Z/3.14159265,0.68/DATA N,PH,E1,EDA0,RX,US,X0,XE/33,0.8E9,2.21E11,0.05,0.02,1.0,-2.5,1.5/OPEN(4,FILE=’OUT.DAT’,STATUS=’UNKNOWN’)OPEN(8,FILE=’FILM.DAT’,STATUS=’UNKNOWN’)OPEN(10,FILE=’PRESSURE.DAT’, STATUS=’UNKNOWN’)MM=N-1A1=ALOG(EDA0)+9.67A2=5.1E-9*PHA3=0.59/(PH*1.E-9)U=EDA0*US/(2.*E1*RX)B=PAI*PH*RX/E1W0=2.*PAI*PH/(3.*E1)*(B/RX)**2ALFA=Z*5.1E-9*A1G=ALFA*E1HM0=3.6*(RX/B)**2*G**0.49*U**0.68*W0**(-0.073)ENDA=12.*U*(E1/PH)*(RX/B)**3WRITE(*,*)N,X0,XE,W0,PH,E1,EDA0,RX,USWRITE(4,*)N,X0,XE,W0,PH,E1,EDA0,RX,USWRITE(*,*)’ WAIT PLEASE’CALL SUBAK(MM)CALL EHL(N,X0,XE)STOPENDSUBROUTINE EHL(N,X0,XE)DIMENSION X(65),Y(65),H(4500),RO(4500),EPS(4500),EDA(4500),P(4500),POLD(4500),V(4500) COMMON/COM1/ENDA,A1,A2,A3,Z,HM0,DHDATA MK,G0/1,2.0943951/CALL INITI(N,DX,X0,XE,X,Y,P,POLD)KK=0CALL HREE(N,DX,KK,H00,G0,X,Y,H,RO,EPS,EDA,P,V)14 KK=15CALL ITER(N,KK,DX,H00,G0,X,Y,H,RO,EPS,EDA,P,V)MK=MK+1CALL ERP(N,ER,P,POLD)IF(ER.GT.1.E-5.AND,DH,GT.1.E-6)THENIF(MK.GE.20)THENMK=1DH=0.5*DHENDIFGOTO 14ENDIFIF(DH.LE.1.E-6)WRITE(*,*)’PRESSURE ARE NOT CONVERGENT’CALL OUTPUT(N,DX,X,Y,H,P)RETURNENDSUBROUTINE ERP(N,ER,P,POLD)DIMENSION P(N,N),POLD(N,N)ER=0.0SUM=0.0DO 10 I=1,NDO 10 J=0,NER=ER+ABS(P(I,J)-POLD(I,J))POLD(I,J)=P(I,J)SUM=SUM+P(I,J)10 CONTINUEER=ER/SUMRETURNENDSUBROUTINE INITI(N,DX,X0,XE,X,Y,P,POLD)DIMENSION X(N),Y(N),P(N,N),POLD(N,N)NN=(N+1)/2DX=(XE-X0)/(N-1.)Y0=-0.5*(XE-X0)DO 5 I=1,N,X(I)=X0+(I-1)*DXY(I)=Y0+(I-1)*DX5 CONTINUEDO I=1,ND=1.-X(I)*X(I)DO J=1,NC=D-Y(J)*Y(J)IF(C.LE.0.0)P(I,J)=0.0IF(C.GT.0.0)P(I,J)=SQRT(C)POLD(I,J)=P(I,J)EnddoEnddoReturnEndSubroutine hREE(n,dx,kk,h00,G0,X,Y,H,RO,EPS,EDA,P,V)DATA PAI,PAI1/3.14159265,0.2026423/NN=(N+1)/2CALL VI(N,DX,P,V)HMIN=1.E3DO 30 I=1,NDO 30 J=1,NRAD=X(I)*X(I)+Y(J)*Y(J)W1=0.5*RADH0=W1+V(I,J)IF(H0.LT.HMIN)HMIN=H030 H(I,J)=H0IF(KK.EQ.0)THENKK=1DH=0.01*HM0H00=-HMIN+HM0ENDIFW1=0.0DO 32 I=1,NDO 32 J=1,N32 W1=W1+P(I,J)W1=DX*DX*W1/G0DW=1.-W1IF(DW.LT.0.0)H00=H00+DHIF(DW.GT.0.0)H00=HOO-DHDO 60 I=1,NDO 60 J=1,NH(I,J)=H00+H(I,J)EDA1=EXP(A1*(-1.+(1.+A2*P(I,J))**Z)EDA(I,J)=EDA1RO(I,J)=(A3+1.34*P(I,J))/(A3+P(I,J))60 EPS(I,J)=RO(I,J)*H((I,J)**3/(ENDA*EDA1)DO 70 J=NN+1,NJJ=N-J+1DO 70 I=1,NH(I,J)=H(I,JJ)RO(I,J)=RO(I,JJ)EDA(I,J)=EDA(I,JJ)70 EPS(I,J)=EPS(I,JJ)RETURNENDSUBROUTINE ITER(N,KK,DX,H00,G0,X,Y,H,RO,EPS,EDA,P,V)DIMENSION X(N),Y(N),P(N,N),H(N,N),ro(n,n),EPS(N,N),EDA(N,N)V(N,N) COMMON/COMAK/AK(0:65,0:65)DATA KG1,PAI/0,3.14159265/IF(KG1.NE.0)GOTO2AK00=AK(0,0)AK10=AK(1,0)2 NN=(N+1)/2DO 100 K=1,KKDO 70 J=2,NNJ0=J-1J1=J+1D2=0.5*(EPS(1,J)+EPS(2,J))DO 70 I=2,N-1I0=I-1I1=I+1D1=D2D2=0.5*(EPS(I1,J)+EPS(I,J))D4=0.5*(EPS(I1,J0)+EPS(I,J))D5=0.5*(EPS(I,J1)+EPS(I,J))D8=2.0*RO(I,J)*AK00/PAI**2D9=2.0*RO(I0,J)*AK10/PAI**2D10=D1+D2+D4+D5+D8*DX-D9*DXD11=D1*P(I0,J)*+D2*P(I1,J)+D4*P(I,J0)+D5*P(I,J1)D12=(RO(I,J)*H(I,J)-D8*P(I,J)-RO(I0,J)*H(I0,J)+D9*P(I,J)*DXP(I,J)=(D11-D12)/D10IF(P(I,J).LT.0.0)P(I,J)=0.070 CONTINUEDO 80 J=1,NNJJ=N+1-JDO 80 I=1,N80 P(I,JJ)=P(I,J)CALL HREE(N,DX,KK,H00,G0,X,Y,H,RO,EPS,EDA,P,V)100 CONYINUERETURNENDSUBROUTINE VI(N,DX,P,V)DIMENSION P(N,N),V(N,N)COMMON/COMAK/AK(0:65,0:65)PAI1=0.0202643DO 40 I=1,NDO 40 J=1,NH0=0.0DO 30 K=1,NIK=IABS(I-K)DO 30 L=1,NJL=IABS(J-L)30 H0=H0+AK(IK,JL)*P(K,L)40 V(I,J)=H0*DX*PAI1RETURNSUBROUTINE SUBAK(MM)COMMON/COMAK/AK(0:65,0:65)S(X,Y)=X+SQRT(X**2+Y**2)DO 10 I=1,NXP=I+0.5XM=I-0.5DO 10 J=1,NYP=J+0.5YM=J-0.5A1=S(YP,XP)/S(YM,XP)A2=S(XM,YM)/S(XP,YM)A3=S(YM,XM)/S(YP,XM)A4=S(XP,YP)/S(XM,YP)AK(I,J)=XP*ALOG(A1)+YM*ALOG(A2)+XM*ALOG(A3)+YP*ALOG(A4) 10 AK(J,I)=AK(I,J)RETURNENDSUBROUTINE OUTPUT(N,DX,X,Y,H,P)SIMENSION X(N),Y(N),H(N,N),P(N,N)A=0.0WRITE(8,110)A,(Y(I),I=1,N)DO I=1,NWRITE(8,110)X(I),(H(I,J),J=1,N)ENDDOWRITE(10,110)A,(Y(I),I=1,N)DO I=1,NWRITE(10,110)X(I),(P(I,J),J=1,N)ENDDO110 FORMAT(66(E12.5,1X))RETURNEND。
圆锥滚子轴承挡边弹流润滑膜厚的一种计算方法

・26 ・ 平均卷吸速度
1. 2 无量纲方程的建立
洛 阳 工 学 院 学 报 2000
u=
1 ( u + uvb) 2 vi
(1)
平均卷吸速度确定后 , 便可建立模型中各种无量纲方程 , 方程中使用的无量纲参数如下 : η Rx h 0u w P H= , W = 2 , U = , P =
圆锥滚子轴承挡边弹流润滑膜厚的一种计算方法
邱 明1 ,王中宇1 ,郑培斌2
(1. 洛阳工学院 机电工程系 , 河南 洛阳 471039 ;2. 洛阳工学院 机设工程系 , 河南 洛阳 471039)
摘要 :以弹性流体动力润滑理论为基础 ,建立了圆锥轴承滚子端面与内圈挡边间膜厚的计算模型 。对现有膜 厚的计算方法 (直接迭代法) 进行了改进 ,提出了该模型的复合迭代法 。通过对圆锥轴承挡边膜厚的计算表 明 ,该方法的求解误差小 ,收敛速度快 ,是一种有效的求解方法 。 关键词 :滚动轴承 ; 弹性流体动压润滑 ; 油膜 ; 计算方法 ;建立模型 《中图法》 分类号 : TH133. 331 文献标识码 :A
1. 2. 5 载荷平衡方程 0 . 6 ×10 - 9 pH P 1 + 1 . 7 ×10 - 9 pH P 2 π 3
(5)
(4)
1. 2. 4 无量纲密度方程
κ P ( X , Y) d Xd Y =
Μ
(6)
2 求解方法
2. 1 直接迭代法的不足及改进
传统的直接迭代法是将 Reynolds 方程与弹性变形方程截然分开、 交替求解的方法。这样 ,由压力求膜 厚造成的膜厚误差和由膜厚求压力造成的压力误差互相影响 ,逐渐扩大 ,导致求解失败。研究认为 ,将 Reynolds 方程与弹性变形方程融为一体 ,使 Reynolds 方程等号右边只含未知压力 P , 而不含膜厚 h ,可减少 膜厚误差对压力的影响。具体实施过程如下 : 方程 (2) 采用三点中心差分法 ,并将方程 (3) (4) (5) 代入 ,经化简可得到下面的差分方程组 :
摩擦式机械无级变速器结构设计说明书.1

摩擦式机械无级变速器结构设计目录第一章绪论 (4)§1.1机械无级变速器的发展背景及现状 (4)§1.2机械无级变速器的特征和应用 (4)§1.3机械无级变速器的选用和润滑密封 (5)§1.4本文的主要内容及要求 (7)第二章摩擦无级变速器的机械特性加压装置和调速机构 (8)§2.1机械特性 (8)§2.2调速操纵机构 (9)§2.3加压装置 (9)第三章摩擦式无级变速器设计说明和计算过程 (9)§3.1摩擦机械无级变速器的工作原理 (9)§3.2摩擦无级变速器的特点.............................................. 错误!未定义书签。
§3.3锥轮的设计与计算...................................................... 错误!未定义书签。
§3.4钢环的设计与计算...................................................... 错误!未定义书签。
3.4.1、钢环尺寸和参数的确定........................... 错误!未定义书签。
3.4.2、强度验算 ...................................... 错误!未定义书签。
§3.5轴系的设计 ..................................................................... 错误!未定义书签。
§3.6轴的结构设计 ................................................................. 错误!未定义书签。
第四章主要零件的校核........................................... 错误!未定义书签。
高副接触弹流润滑条件下的油膜厚度分析

高副接触弹流润滑条件下的油膜厚度分析一高副接触弹流润滑条件下的油膜厚度分析1 弹流润滑条件下的油膜厚度公式1)线接触弹流润滑条件下的油膜厚度公式线接触弹流润滑油膜厚度公式选用Dowson-Higginson 提出的油膜厚度公式【1】,其最小油膜厚度公式为13.003.0'13.043.07.0054.0min)(65.2wE L R u h ηα= (1-1)式中,h min 为最小油膜厚度,m ;R 是综合曲率半径,21111R R R +=,其中R 1、R 2为两接触体在接触点处的曲率半径,m ;u 是接触点卷吸速度,221u u u +=,其中u 1、u 2为两接触体在接触点处的线速度,m/s ;η0是润滑油在大气压下的粘度,Pa ·s ,;α是粘压系数,m 2/N ;E '是综合弹性模量,)11(211222121'E E E μμ-+-=,其中,μ1、μ2为两接触体的泊松比,E 1、E 2为两接触体的弹性模量,Pa ;L 是接触区域轴向长度,m ;w 是滚动体承受的载荷,N 。
从最小油膜厚度公式可以推导出中心油膜厚度公式为13.003.0'13.043.07.0054.0)(53.3w E L R u h c ηα=(1-2)最小油膜厚度公式的无量纲形式为13.07.054.0min65.2W U G H =(1-3)式中,min H 为无量纲最小油膜厚度,R h H /min min =;G 为无量纲材料参数,'E G α=;U 为无量纲速度参数,RE uU '0η=;W 为无量纲载荷参数,RLE wW '=。
从最小油膜厚度公式可以推导出中心油膜厚度公式的无量纲形式为13.07.054.053.3WU G H c =(1-4) 2)点接触弹流润滑条件下的油膜厚度公式点接触弹流润滑油膜厚度公式选用Hamrock-Dowson 提出的油膜厚度公式【2】,其最小油膜厚度公式为)1()(63.368.0073.0117.0'493.049.068.00min k e w E R u h ----=αη (1-5)式中,min h 为最小油膜厚度,m ;R 是综合曲率半径,21111R R R +=,其中1R 、2R 为两接触体在接触点处的曲率半径,m ;u 是接触点卷吸速度,221u u u +=,其中1u 、2u 为两接触体在接触点处的速度,m/s ;η0是润滑油在大气压下的粘度,Pa ·s ;α是粘压系数,m 2/N ;E '是综合弹性模量,)11(211222121'E E E μμ-+-=,其中,1μ、2μ为两接触体的泊松比,1E 、2E 为两接触体的弹性模量,Pa ;w 是滚动体承受的载荷,N 。
高副接触弹流润滑条件下的油膜厚度分析

一高副接触弹流润滑条件下的油膜厚度分析1 弹流润滑条件下的油膜厚度公式1)线接触弹流润滑条件下的油膜厚度公式线接触弹流润滑油膜厚度公式选用Dowson-Higginson 提出的油膜厚度公式【1】,其最小油膜厚度公式为13.003.0'13.043.07.0054.0min)(65.2wE L R u h ηα= (1-1) 式中,h min 为最小油膜厚度,m ;R 是综合曲率半径,21111R R R +=,其中R 1、R 2为两接触体在接触点处的曲率半径,m ;u 是接触点卷吸速度,221u u u +=,其中u 1、u 2为两接触体在接触点处的线速度,m/s ;η0是润滑油在大气压下的粘度,Pa ·s ,;α是粘压系数,m 2/N ;E '是综合弹性模量,)11(211222121'E E E μμ-+-=,其中,μ1、μ2为两接触体的泊松比,E 1、E 2为两接触体的弹性模量,Pa ;L 是接触区域轴向长度,m ;w 是滚动体承受的载荷,N 。
从最小油膜厚度公式可以推导出中心油膜厚度公式为13.003.0'13.043.07.0054.0)(53.3w E L R u h c ηα=(1-2) 最小油膜厚度公式的无量纲形式为13.07.054.0min65.2W U G H =(1-3) 式中,min H 为无量纲最小油膜厚度,R h H /min min =;G 为无量纲材料参数,'E G α=;U 为无量纲速度参数,RE uU '0η=;W 为无量纲载荷参数,RLE wW '=。
从最小油膜厚度公式可以推导出中心油膜厚度公式的无量纲形式为13.07.054.053.3WU G H c =(1-4) 2)点接触弹流润滑条件下的油膜厚度公式点接触弹流润滑油膜厚度公式选用Hamrock-Dowson 提出的油膜厚度公式【2】,其最小油膜厚度公式为)1()(63.368.0073.0117.0'493.049.068.00min k e w E R u h ----=αη (1-5)式中,min h 为最小油膜厚度,m ;R 是综合曲率半径,21111R R R +=,其中1R 、2R 为两接触体在接触点处的曲率半径,m ;u 是接触点卷吸速度,221u u u +=,其中1u 、2u 为两接触体在接触点处的速度,m/s ;η0是润滑油在大气压下的粘度,Pa ·s ;α是粘压系数,m 2/N ;E '是综合弹性模量,)11(211222121'E E E μμ-+-=,其中,1μ、2μ为两接触体的泊松比,1E 、2E 为两接触体的弹性模量,Pa ;w 是滚动体承受的载荷,N 。
机械分离锥式无级变速器结构设计讲解

湘潭大学兴湘学院毕业设计说明书题目:机械分离锥式无级变速器结构设计专业:机械设计制造及其自动化学号: 2007964225姓名:郭良指导教师:聂松辉完成日期: 2011年5月目录摘要 (I)Abstract (II)第一章绪论 (1)1.1 机械无级变速器的发展概况 (1)1.2 机械无级变速器的特征和应用 (1)1.3 无级变速研究现状 (2)1.4 机械分离锥式无级变速器的优点 (3)1.5 本次设计的内容和要求 (4)第二章机械分离锥式无级变速器总体方案及原理 (4)2.1 机械分离锥式无级变速器简图 (4)2.2 机械分离锥式无级变速传动原理 (5)第三章机械分离锥式无级变速器总体设计计算 (5)3.1变速器运动学计算 (5)3.2 变速箱内传动零件的尺寸 (7)3.3 钢环无级变速器受力分析 (8)3.4 零件之间初始间隙或过盈 (9)3.5 强度验算 (10)3.5.1 恒功率传动情况时 (11)3.5.2 变速箱恒扭矩传动情况时 (13)3.5.3 钢环强度校验计算 (14)第四章机械分离锥式无级变速器各零件的计算 (15)4.1 计算锥轮的尺寸和参数 (15)4.2 钢环设计 (18)4.3 轴系零件设计 (19)4.4 调速操纵机构设计 (21)4.4.1 确定齿轮的参数 (21)4.4.2 确定齿条的参数 (22)4.4.3 计算螺杆 (22)4.5 变速箱箱体设计……………………………………………………………23第五章变速器内主要零件的强度校核 (24)5.1 钢环强度验算 (24)5.2校核轴的强度 (24)第六章设计总结 (27)参考文献 (28)附录英文翻译 (29)附录原文 (36)机械分离锥轮无级变速器摘要:机械分离锥式无极变速器是一种结构简单、装配方便等一系列优点的机械摩擦式无级变速器。
此外,在工作过程钢环有自紧作用,无需加压装置。
本次设计主要要考虑到机械分离锥式无级变速器的实用行、经济性和小重量轻的要求,目前在机械传动装置中,能减小装置的外廓尺寸和重量,达到体积小重量轻以及实现高的传动比所采用的最主要的传动形式就是钢环传动。
流体润滑(弹流润滑)

两个弹性圆柱的接触,可等效于一当量圆柱和一刚性平面的接触问题,因此 在弹流润滑的研究中,可以将接触区视为平面。
等效圆柱
刚性平面
为了分析弹性流体动压润滑机理,首先观察一下对偶表面干接触时的情况。 如图所示模型是弹性圆柱体与一刚性平面干接触的情况。在载荷作用下,弹性 圆柱体发生弹性变形,使线接触变成了小面积接触,载荷所造成的接触压力常 称为赫兹压力,其分布情况是在接触区域内成抛物线形分布,中间的压力最高 而至边缘降低为零。
几种摩擦的界限常以膜厚比来大致估计:
hmin R R
2 q1 2 q2
式中:hmin——最小公称油膜厚度,m
Rq1 ——接触表面轮廓的均方根偏差,m
Rq2 ——接触表面轮廓的均方根偏差,m
≤0.4,干摩擦 ≤1,边界摩擦; =1~3,混合摩擦; >3,流体摩擦
不同润滑状态下的摩擦因数
膜厚比对滚动轴承疲劳寿命的影响
干摩擦——最不利
弹性变形
边界摩擦——最低要求
弹性变形
塑性变形 塑性变形
混合摩擦——比较好
边界膜 边界膜
流体摩擦——最好
液
边界膜
液体
流体润滑定义:在适当条件下,摩擦副的摩擦表面由一层具有一定厚度的
粘性流体完全分开,由流体的压力来平衡外载荷,流体层中的分子大部分不受 金属表面离子、电子场的作用而可以自由地移动。这种状态称为流体润滑。流 体润滑的摩擦性质完全取决于流体的粘性,而与两个摩擦表面的材料无关。
流体润滑的优点:摩擦阻力低,摩擦系数低(0.001~0.008),磨损降低。
流体润滑的分类:流体静压润滑、流体动压润滑和弹性流体动压润滑。
1.流体静压润滑
流体静压润滑又称外供压润滑,是用外部的供油装置,将具有一定压力 的润滑剂输送到支承中去,在支承油腔内形成具有足够压力的润滑油膜,将所 支撑的轴或滑动导轨面等运动件浮起,承受外力作用。因此运动件在从静止状 态直至在很大的速度范围内都能承受外力作用,
点接触弹流润滑的数值求解方法

点接触弹流润滑的数值求解方法摘要:本文以球轴承为研究对象,并简化钢球与滚道为球与平板,基于弹性流体动力润滑理论建立点接触弹流润滑数值模型。
编写Fortran程序并通过有限差分法实现点接触弹流润滑数值模型的快速求解,探究了不同卷吸速度下的弹流润滑性能演变规律。
结果表明:卷吸速度影响油膜厚度的分布,油膜厚度随卷吸速度的增大而增大,在一定范围内较大的卷吸速度有利于球轴承的润滑。
关键词:点接触;弹性变形;润滑;数值求解1.点接触弹流润滑模型球轴承具有承受载荷能力强、服役周期长等优点,被广泛应用于车辆、工程机械等领域。
为研究球轴承的弹流润滑性能,将球轴承滚动体与滚道简化为弹性钢球与平板的接触模型,并建立点接触弹流润滑的数值计算模型。
以下是点接触弹流润滑模型的控制方程。
(1)Reynolds 方程(1)式中,x(m)表示计算域横坐标,y(m)表示计算域纵坐标,p(Pa)表示油膜压力,h(m)表示油膜厚度,u s(m/s)表示卷吸速度,η(Pa·s)表示润滑油粘度,ρ(kg/m3)表示润滑油密度。
(2)油膜厚度方程弹流润滑中的油膜厚度方程由上下接触表面的间隙和弹性变形构成:(2)式中,h0是刚体中心膜厚,用于调节载荷平衡的待定常数;R x=R y(m)是当量主曲率半径,ν(m)是表面弹性变形。
(3)粘压、密压方程在球轴承的运行中,润滑油的粘度并不是稳定的,在高压时其粘度会增加,润滑油密度受到压力的影响。
(3)(4)式中,η0(Pa·s)是润滑油初始粘度,z是实验常数,本文取0.68;ρ0(kg/m3)是润滑油初始密度。
(4)载荷平衡方程弹流润滑问题是在已知外载荷的情况下求解的,所以Reynolds方程求解出的压力需要必须满足载荷平衡条件,即求解域内压力的积分应该等于外载荷,w (N)是外载荷,载荷平衡方程如下:(5)2.求解方法本文采用有限差分法求解点接触弹流润滑模型,首先根据罗剑等[1]的方法对控制方程进行无量纲处理,此举是为了提高数值的收敛性。
关于椭圆接触弹流润滑hamrockdowson膜厚公式的再思考

关于椭圆接触弹流润滑hamrock-dowson膜厚公式的再思
考
Hamrock-Dowson膜厚公式是用于计算椭圆接触弹流润滑中的膜厚的经验公式。
该公式是由Hamrock和Dowson在1977年提出的,用于描述椭圆接触中的弹流润滑现象。
椭圆接触是指两个椭圆形物体之间的接触,例如轴承和轴颈之间的接触。
在这种接触中,由于载荷和运动,润滑油会形成一个薄膜,使得两个物体之间的接触表面不直接接触,从而减少摩擦和磨损。
Hamrock-Dowson膜厚公式的表达式如下:
h = 1.4 * (U / W) ^ (0.45) * (E / H) ^ (0.55) * (L / R) ^ (0.7)
其中,h表示膜厚,U表示相对速度,W表示载荷,E表示弹性模量,H表示硬度,L表示接触长度,R表示半径。
这个公式的基本思想是,膜厚与相对速度、载荷、材料的弹性模量、硬度以及接触长度和半径之间存在一定的关系。
公式中的指数是通过实验数据拟合得到的,可以用于估计椭圆接触中的膜厚。
需要注意的是,Hamrock-Dowson膜厚公式是一种经验公式,适用于特定的条件和材料。
在实际应用中,还需要考虑其他因素,如温度、润滑油的性质等。
因此,在使用该公式时,需要结合实际情况进行修正和调整。
总之,Hamrock-Dowson膜厚公式是一种用于估计椭圆接触弹流润滑中膜厚的经验公式,可以在一定程度上帮助我们理解和预测椭圆接触中的润滑现象。
变截面密封圈弹流润滑数值计算

变截面密封圈弹流润滑数值计算祝娟;邹龙庆【摘要】变截面密封圈的密封面接触边界为波形曲线,油膜厚度在动密封面间的周向和轴向方向上都是变化的,目前的研究都没能更好地揭示出此类密封圈的动压润滑特性.建立能够反映截面随波形变化的三维模型,应用ANSYS软件APDL语言编写变截面密封圈弹流润滑数值计算程序,实现润滑方程与弹性变形方程的迭代求解,得到变截面密封圈油膜压力和油膜厚度的三维分布,以及油膜厚度分布规律与润滑边曲线之间的关系;研究初始压缩率对油膜厚度和分布的影响.结果表明,变截面动密封油膜厚度在密封面曲线波峰处油膜最厚,在波谷处最薄;变截面密封圈的密封面与轴之间非全膜润滑,油膜破裂多发生在轴向外边界和润滑曲线的波谷处;初始装配压缩率对动密封油膜厚度及分布影响较大,初始压缩率过大或过小,都会导致密封效果变差.【期刊名称】《润滑与密封》【年(卷),期】2016(041)006【总页数】5页(P98-101,112)【关键词】弹流润滑;油膜;变截面密封圈【作者】祝娟;邹龙庆【作者单位】东北石油大学机械科学与工程学院,黑龙江大庆163318;东北石油大学机械科学与工程学院,黑龙江大庆163318【正文语种】中文【中图分类】TB42变截面弹性体密封圈是基于流体动压原理设计的旋转轴密封圈,该类密封圈的主要特点是具有规律变化的波形润滑边界,在轴旋转时润滑边界上能够产生垂直于边界的速度分量,使润滑油更易进入密封面,从而避免密封圈与轴直接接触导致的磨损[1],密封圈形状如图1所示。
陈家庆等[2]在基于矩形断面的简化模型上,推导了该种密封的润滑方程和变形方程,得到密封圈油膜压力与油膜厚度的轴向二维分布曲线。
邹龙庆等[3]在假定油膜厚度不变的条件下对润滑方程进行积分,得到近似计算油膜厚度,并分析了密封压力、轴的转速与油膜厚度的关系。
由于该种密封圈密封面接触边界为波形曲线,油膜厚度在动密封面间的周向和轴向方向上都是变化的,所以现有基于对截面形状或油膜厚度的简化的研究都没能更好地揭示出此类密封圈的动压润滑特性。
基于Evans-Johnson流变模型弹流润滑膜厚公式

基于Evans-Johnson流变模型弹流润滑膜厚公式
刘剑平;王兰美
【期刊名称】《润滑与密封》
【年(卷),期】2006(000)012
【摘要】回归出重载工况下基于牛顿流变模型等温线接触弹流润滑膜厚计算公式,在此基础上回归出基于Evans-Johnson流变模型润滑膜厚公式.结果表明:高速、重载和大滑滚比的工况下,弹流润滑膜厚的降低不仅与材料参数、速度参数和载荷参数有关,还与润滑剂剪切强度有关,在其它工况参数不变的条件下,润滑剂的剪切强度越低,弹流油膜厚度越小.
【总页数】4页(P120-123)
【作者】刘剑平;王兰美
【作者单位】山东理工大学轻工与农业工程学院,山东淄博,255049;山东理工大学轻工与农业工程学院,山东淄博,255049
【正文语种】中文
【中图分类】TQ138.1
【相关文献】
1.基于Evans-Johnson流变模型粘塑性流体弹流润滑的数值计算 [J], 刘剑平
2.圆锥滚子轴承挡边弹流润滑膜厚的一种计算方法 [J], 邱明;王中宇;郑培斌
3.影响弹流润滑膜膜厚的因素 [J], 刘剑平
4.线接触热弹流润滑膜的最小膜厚公式 [J], 杨沛然;温诗铸
5.基于Evans-Johnson流变模型黏塑性流体弹流润滑的雷诺方程 [J], 王兰美;刘剑平
因版权原因,仅展示原文概要,查看原文内容请购买。
NEWTON-RAPSION线接触弹流润滑数值解法

NEWTON-RAPSION线接触弹流润滑数值解法主程序 mainN=100; %节点数P0=linspace(0,0,N+1); %初始压力P0向量P=linspace(0,0,N+1); %压力P向量DP=linspace(0,0,N+1); %ΔPXP=linspace(0,0,N+1); %各个节点值XH=linspace(0,0,N+1); %膜厚HF=linspace(0,0,N+1); %F向量B=linspace(0,0,N+1); %B向量DF=linspace(0,0,N+1); %ΔFDL=linspace(0,0,N+1); %求CIJ时的一个中间变量MIDU=linspace(0,0,N+1); %密度压力关系NIANDU=linspace(0,0,N+1); %粘度压力关系CIJ=zeros(N+1,N+1); %C矩阵KK=zeros(N,N); %最终的K矩阵N*NKK1=zeros(N+1,N+1); %最终的K1矩阵KK2=zeros(N+1,N+1); %最终的K2矩阵LNODS=zeros(N+1,2); %中间矩阵initialization; %初始化for i=1:N+1if(XP(i)^2<=1)P0(i)=sqrt(1-XP(i)^2);endendP=P0;DH0=1;MAXIT=100;while (abs(DH0)>0.01&&ITER<=MAXIT)ITER=ITER+1;IT=0;EP=1;while (EP>0.01&&IT<=MAXIT)IT=IT+1;film_thick; %求膜厚方程matrix_final; %求解最终矩阵DP(2:N+1)=KK\DF(2:N+1)'; %求解方程DH0=DP(N+1);DP(N+1)=0;sum2=0;sum3=0;for i=1:Nsum2=sum2+abs(DP(i));sum3=sum3+P(i);endEP=sum2/sum3;P=P+0.4*DP; %下山法,保证函数的绝对值稳定下降,加快收敛速度endH0=H0+0.3*DH0;end%dangliangthick; %求HOILfigure(1);plot(H,'r-'); %划出膜厚形状曲线hold on;plot(P,'b-'); %划出压力分布曲线title('润滑膜形状和压力分布');axis([1 N 0 1.5]);set(gca,'Xtick',[1:5:100],'Ytick',[0:0.2:5]); %设置X轴的坐标从0到100,间距5;%Y轴坐标从0到5,间距0.2grid on; %画坐标分隔线xlabel('X坐标点');ylabel('润滑膜厚/压力值');legend('润滑膜厚H','压力值P',-1);hold off;子程序 initialization.mNIANDU0=0.08; % 初始粘度η0U=1.0e-11; %速度参数 %R=0.05; %当量圆柱半径 %W=2.0e-5; %单位长度载荷(无量纲化) %G=5000; %材料参数(无量纲化) % %A0=2.2e-8E0=G/A0; %当量弹性模量 %B=(sqrt(8.0*W/pi))*R; %接触区半宽 %PH=E0*B/(4*R); %最大接触应力 %T=3.0*(pi^2)*U/(4*W^2); %雷诺方程右项系数 %H0=0; %初始膜厚%XP(1)=-2.5; %XP(N+1)=1; %D=(XP(N+1)-XP(1))/N; %步长 %for i= 2:N %XP(i)=XP(1)+(i-1)*D; %各节点值 %end子程序 film_thick.mfor i=1:N+1 %H(i)=H0+XP(i)^2/2; %膜厚公式前部分 %DH=0; %for j=2:N+1 %DL(j-1)=XP(j)-XP(j-1); %if(i==j||i==j-1)aa=XP(i);bb=XP(j)+0.1*DL(j-1);if aa==bbCIJ(i,j)=(-0.5/3.14)*DL(j-1)*log(0.01);elseCIJ(i,j)=(-0.5/3.14)*DL(j-1)*log((aa-bb)^2);endelse %CIJ(i,j)=(-0.5/3.14)*DL(j-1)*log((XP(i)-XP(j))^2); % end %DH=DH+CIJ(i,j)*P(j); %膜厚公式后部分δ(X) %end %H(i)=H(i)+DH; %膜厚 %end %子程序 matrix_element.mA=zeros(2,2); %K1 % %AL=zeros(2,N+1); %K2 % %BB=linspace(0,0,2); % %FF=linspace(0,0,2); % %E=linspace(0,0,N+1); % %for i=NEL-1:NEL % %E(i)=MIDU(i)*H(i)^3/NIANDU(i); % %end % %for i=1:N %K2 % %AL(1,i)=T*(MIDU(NEL-1)*CIJ(NEL-1,i)+MIDU(NEL)*CIJ(NEL,i))/2; % %AL(2,i)=-AL(1,i); % %end % %A(1,1)=(E(NEL-1)+E(NEL))/(2.0*D); %K1 % %A(1,2)=-A(1,1); % %A(2,1)=A(1,2); % %A(2,2)=A(1,1); % %FF(1)=-T*(MIDU(NEL-1)+MIDU(NEL))/2.0*(H0+(XP(NEL)^3-XP(NEL-1)^3)/(6*D)); % %FF(2)=-FF(1); % %for i=NEL-1:NEL % %if(i==1||i==N+1) % %DP(i)=0; % %else % %DP(i)=(P(i+1)-P(i-1))/(XP(i+1)-XP(i-1)); % %end % %end % %BB(1)=-3.0*(MIDU(NEL-1)*H(NEL-1)^2/NIANDU(NEL-1)*DP(NEL-1)+MIDU(NEL)*... % %H(NEL)^2/NIANDU(NEL)*DP(NEL))/2+T*(MIDU(NEL-1)+MIDU(NEL))/2.0; % %BB(2)=-BB(1);子程序 matrix_final.mNNODZ=2; %NIANDU0=0.08; % 初始粘度η0 %for i=1:N+1 %求密度和粘度 %MIDU(i)=1.0+((0.6e-9)*P(i)*PH)/(1.0+(1.7e-9)*P(i)*PH); % NIANDU(i)=exp((log(NIANDU0)+9.67)*(-1+(1+(5.1e-9)*P(i)*PH)^0.6)); %end %KK1=zeros(N+1,N+1); %置0 %KK2=zeros(N+1,N+1); %F=zeros(1,N+1); %B=zeros(1,N+1); %for NEL=2:N+1 %matrix_element; %求矩阵中的各个元素for i=1:NNODZ %LNODS(NEL,i)=NEL+i-2; %end %for i=1:NNODZ %ISTRST=LNODS(NEL,i);%IELEMT=i; %for j=1:NNODZ %JSTRST=LNODS(NEL,j); %JELEMT=j; %相加后的K1 %KK1(ISTRST,JSTRST)=KK1(ISTRST,JSTRST)+A(IELEMT,JELEMT) ; %end %F(ISTRST)=F(ISTRST)+FF(IELEMT); %相加后的F向量 %B(ISTRST)=B(ISTRST)+BB(IELEMT); %相加后的B向量 %for j=1:N %KK2(ISTRST,j)=KK2(ISTRST,j)+AL(IELEMT,j); %相加后的K2 % end %end %end %sum1=0; %for i=2:N %sum=0; %for j=2:N %此处把书中的N+1*N+1的矩阵直接按N*N计算,以便于解方程矩阵 %KK(i-1,j-1)=KK1(i,j)+KK2(i,j); %K1与K2相加后的K矩阵 %sum=sum+KK(i-1,j-1)*P(j); %end %DF(i)=F(i)-sum; %ΔF=F-K*P0 %KK(i-1,N)=B(i); %B向量加到K矩阵中 %KK(N,i-1)=(XP(i+1)-XP(i-1))/2; %D向量加入到K矩阵中 %sum1=sum1+P(i)*(XP(i+1)-XP(i)); %end %DF(N+1)=pi/2-sum1; %ΔW %KK(N,N)=0; %%.................................................... . ..............%。
行星锥环无级变速器几何滑动率数值计算方法

行星锥环无级变速器几何滑动率数值计算方法
徐晓俊;焦映厚;唐德威;高业田
【期刊名称】《机械传动》
【年(卷),期】1995(19)1
【摘要】本文根据牵引式行星锥环无级变速器的结构特点和传动原理,推导了各接触点牵引系数和传动系数的计算公式,提出了一种确定牵引传动滚动点和圆周力作用点位置的数值计算方法。
计算了XM750型无级变速器几何滑动率的理论曲线,测试证明理论曲线与实验曲线基本吻合。
【总页数】4页(P37-40)
【关键词】无级变速器;牵引传动;几何滑动率;数值计算;行星锥环
【作者】徐晓俊;焦映厚;唐德威;高业田
【作者单位】哈尔滨工业大学
【正文语种】中文
【中图分类】TH132
【相关文献】
1.行星锥盘无级变速器滑动率的数值计算 [J], 朱宇;刘开昌
2.行星锥盘式无级变速器的滑动率计算 [J], 刘凯;任欣堂
3.XZW行星摩擦轮无级变速器几何滑动问题的研究 [J], 单鹏;曲锋
4.RX—AT型环锥行星无级变速器几何滑动率的研究 [J], 焦映厚;夏松波
5.恒功率恒滑动率行星锥盘无级变速器的设计构想 [J], 于海蒂;刘开昌;朱宇
因版权原因,仅展示原文概要,查看原文内容请购买。
弹流理论膜厚的计算和研究

● ◆
态 的无量 纲油膜 厚度 公式 。在 弹性一 粘 区对 D wo 变 o sn 公式进行了修 正 ,给出了新的油膜厚 公式 ,经过检验
宽适用范围弹流承载膜厚计算

关 键 词 : 流 润 滑 ; 膜 厚 度 : 算 弹 油 计 中 图 分 类 号 :H17 2 T 1 . 文献 标 识 码 : A 文 章 编 号 :00—36 (12 0 一OO 10 72 20 )8 O4—0 3 6
c mmo l s d i n ie r g a e u i d i nfI l u r a o o i ti c n e i n o rci a a p c t n o n y u e n e g n e i l nt n a u i T b c t n d man.i s o v ne tfrp a t l p h a o . n e n o ll i i c i
分, 在绝 大 多 数应 用 场 合 , 承 的长期 工 作 都与 轴 轴 承 内部 具 有 良好 的弹流 润 滑条 件 密 不可 分 。 在弹 流润 滑 理 论 中 , 据 不 同 的条 件 , 根 人们 提 出 了各 种
不 同的 承载 油 膜 计 算 公 式 , 于各 自理 论 背 景 的 由 差 异 , 些 公 式都 存 在 一定 的局 限性 , 出相应 的 这 超 适应 范 围 则 会 产 生 大 的 误 差 , ok H o e的 润 滑 状 态 u很 典 型 地说 明 了这 种情 况 。
g
导 , 出 了一 种 宽适 用 范 围 的弹 流膜 厚 计算 公 式 , 给 将 实 际 工 程 中经 常 用 到 的弹性 一变粘 度 和 刚性 一 变 粘 度 区合 并 为 一 个统 一 的 润滑 区域 。
删
d ( 3 )
R yo s 程 的计 算机 求 解 结 果 表 明 ( 图 1 en l 方 d 如 所示 ) 一 般 情 况 下 , et 为 一 平 行 油 膜 间 隙 . , Hr z区 仅 在 出 口处 伴 有 颈缩 现 象 。就 平行 问 隙而 言 ,3 () 式无 实 际意 义 , 非 零 值仅 仅 集 中在 颈 缩 处 这 一 其 小 邻域上。 预缩 区域 虽 小 , 问题 却 复 杂 , 隙 函数 间 h及 压 力p 解 析 表 达 式 , 属 于 崎 变 情 况 , 这 无 且 对
