第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
第二十届华杯赛解答

(B) 12 分
(24 ´ 60) ´ 66 = 1452 720 分钟,所以比标准 11
时间 24 小时对应的 24 ´ 60 = 1440 分钟多了 1452-1440=12 分钟,即慢了 12 分钟
6. 在右图的 6× 6 方格内, 每个方格中只能填 A, B, C, D, E, F 中的某个字母,要求每行、每列、每个 3 长方形的六个字母均不能重复.那么, 标有粗线的 2× 第四行除了首尾两个方格外, 中间四个方格填入的字母
【答案】630 【题型】几何:一半模型 【解析】
A A ①② F ③ D⑫ ④ ⑪ P ⑤ ⑩ ⑨ ⑧⑦ ⑥ C B E C
D P B E
F
S3 = S4 , S5 = S6 , S7 = S8 , S9 = S10 , S11 = S12 ; 过点 P 作 AB , AC , BC 的平行线, 则 S1 = S2 ,
第二十届华罗庚金杯少年数学邀请赛
初赛 A 卷解析(小学高年级组)
总分:150 分时间:60 分钟
一、选择题. (每小题 10 分,共 60 分.以下每题的四个选项中,仅 有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号 内. )
1.
现在从甲、 乙、 丙、 丁四个人中选出两个人参加一项活动. 规定: 如果甲去, 那么乙也去;如果丙不去,那么乙也不去;如果丙去,那么丁不去.最后去 参加活动的两个人是() . (A)甲、乙 (B)乙、丙 (C)甲、丙 (D)乙、丁
1 1 2 所以 S阴影 =S白 = S△ABC = 2028 = 1014cm ,则 S△PCF = 1014 - 192 2 = 630cm2 2 2
9. 自然数 2015 最多可以表示成________个连续奇数的和.
第20届华杯赛小中组答案详解a卷

第二十届华罗庚金杯少年数学邀请赛初赛 A 卷(小学中年级组)总分:100 分时间:60分钟一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.森林里举行比赛,要派出狮子、老虎、豹子和大象中的两个动物去参加.如果派狮子去,那么也要派老虎去;如果不派豹子去,那么也不能派老虎去;要是豹子参加的话,大象可不愿意去.那么,最后能去参加比赛的是().(A)狮子、老虎(B)老虎、豹子(C)狮子、豹子(D)老虎、大象【答案】B【题型】逻辑推理、逆否命题【解析】在逻辑推理中,原命题成立,则逆否命题也成立.从题意出发:(1)狮子去则老虎去,逆否命题:老虎不去则狮子也不去(2)不派豹子则不派老虎,逆否命题:派老虎则要派豹子(3)派豹子则大象不愿意去,逆否命题:大象去则不能派豹子从(2)出发可以看出答案为 B.题目要求有两个动物去,可以使用假设法,若狮子去,则老虎去,老虎去则豹子也去.三个动物去,矛盾,所以狮子不去.若豹子不去则老虎不去,那么只有大象去,矛盾,所以豹子去.豹子去则大象不去,由两种动物去得到结论,老虎要去.所以答案是 B,豹子和老虎去.2.小明有多张面额为 1 元、2 元和 5 元的人民币, 他想用其中不多于 10 张的人民币购买一只价格为 18 元的风筝, 要求至少用两种面额的人民币,那么不同的付款方式有()种.(A)3(B)9(C)11(D)8【答案】C【题型】奇数:列表枚举【解析】5 元 2 元 1 元总张数3 0 3 63 1 1 52 4 0 62 3 2 72 2 4 82 1 6 9 2 0 8 10 1 6 1 8 1 53 9 145 10 08210共11 种.3. 如右图,在由 1 1 的正方形组成的网格中,写有 2015 四个数字(阴影部分).其边线要么是水平或竖直的直线段、要么是连接11 的正方形相邻两边中点的线段,或者是 1 1 的正方形的对角线. 则图中 2015 四个数字(阴影部分)的面积是().(A )47(B ) 471(C )48(D ) 48122【答案】B 【题型】几何:割补【解析】将小三角形移到空白处补成完整正方形再数正方形个数即可,共47.5 个.4.新生入校后,合唱队、田径队和舞蹈队共招收学员 100 人.如果合唱队招收的人数比田径队多一倍,舞蹈队比合唱队多 10 人,那么舞蹈队招收()人.(注:每人限加入一个队)(A )30(B )42(C )46(D )52【答案】C 【题型】几何:割补【解析】设田径队员为a 人,则合唱队员2a 人,舞蹈队员(2a +10)人,2a +a +2a +10=100,则a = 18,所以舞蹈队员18 2 + 10 = 46人.5.一只旧钟的分针和时针每重合一次,需要经过标准时间66 分.那么,这只旧钟的24 小时比标准时间的 24 小时().(A )快 12 分(B )快 6 分(C )慢 6 分(D )慢 12 分【答案】D 【题型】时钟问题【解析】时针速度为每分钟 0.5 度,分针速度为每分钟6 度.分钟每比时针多跑一圈,即多跑 360 度,360720时针分针重合一次.经过6-0.511 分钟,旧钟时针分针重合一次,需要经过标准时间66分钟;则旧钟的 24 小时,相当于标准时间的(24 60) 661452分钟,所以比标准时间 24 小时对应的7201124 60 1440 分钟多了1452-1440=12分钟,即慢了12分钟6.一次考试共有 6 道选择题,评分规则如下:每人先给 6 分,答对一题加 4 分,答错一题减 1 分,不答得 0 分.现有 51 名同学参加考试,那么, 至少有()人得分相同.(A)3(B)4(C)5(D)6【答案】A【题型】组合:抽屉原理【解析】设答对 x 题,答错y题,x y≤6;当x 6时,得分30分;当x 5时,y0,1,对应得分26, 25;当x 4时,y0,1, 2,对应得分22, 21, 20;当x 3时,y0,1,2,3,对应得分18,17,16,15;当x 2时,y0,1, 2,3,4,对应得分14,13,12,11,10;当x 1时,y0,1,2,3,4,5,对应得分10,9,8, 7, 6,5;当x 0时,y0,1,2,3,4,5,6,对应得分6,5, 4,3, 2,1, 0;共计 25 种得分,51252???1,则至少213人得分相同.二、填空题 (每小题 10 分, 共 40 分)7.计算:(1000 15 314) (201 360 110) (1000 - 201 - 360 - 110) (15 314) ________.【答案】1000000【题型】计算:换元法【解析】令 a 15314, b 201360110;则1000 15 314 201 360 110 1000 - 201 - 360 - 110 15 314=1000 a b1000 -b a1000 a ab 1000b-ab1000 a b1000 15 314 201 360 11010000008. 角可以用它的两边上的两个大写字母和顶点的字母表示,如右图的∠AOB 符号(“∠”表示角),也可以用∠O 表示(顶点处只有一个角时).下图的三角形 ABC 中,∠BAO∠CAO,∠CBO∠ABO,∠ACO ∠BCO ,∠AOC 110,则∠CBO ________.【答案】20【题型】几何:角度2 ∠CAO∠ACO∠CBO 180,解得∠CBO 20.【解析】由题意得,∠ CAO ∠ ACO ∠ AOC 180∠ AOC 1109.张叔叔和李叔叔两人年龄和是 56 岁,当张叔叔是李叔叔现在年龄的一半时,李叔叔当时的年龄是张叔叔现在的年龄.那么张叔叔现在有________岁.【答案】24【题型】应用题:年龄问题【解析】设张叔叔现在 x 岁,张叔叔减少y岁后是李叔叔年龄的一半,则李叔叔现在年龄为2 x - y岁,张叔叔是李叔叔现在年龄的一半时李叔叔为 2 x-y-y岁,则56 y 8x 2 x - y,解得,即张叔叔现在 24 岁.x - y- yx 2 x 24此题亦可运用线段图的解法,同学们可以自己思考!10.妈妈决定假期带小花驾车去 10 个城市旅游,小花查完地图后惊奇地发现:这 10 个城市的任意三个城市之间或者都开通了高速公路,或者只有两个城市间没有开通高速路.那么这 10 个城市间至少开通了________条高速公路.(注:两个城市间最多只有一条高速公路)【答案】40【题型】组合:最值构造【解析】 (1) 将 10 个城市设为A1,A2,???,A10这 10 个点,两个城市间的高速路视为连接两个点的线段,则任意三点间至少连接两条线段.(2)先将 10 个点两量相连,共C10245条线段(中年级不会组合公式的同学可以想想怎么得出 45 条线段).(3)现在考虑最多能去掉多少条线段?先任意去掉一条,不妨记为 A1 A2这一条,则线段 A1 A i或 A2 A(j i 3, 4,???,10; j 3, 4,???,10)均不能去掉,否则 A1, A2, A i或 A1, A2, A j三个点中只有一条线段.即只能在 A3, A4,???, A10这8个点的连线中去掉一条,记为 A3 A4;同理可再去掉 A5 A6, A7 A8, A9 A10,故最多可去掉5条线段.(4)因此至少连接45 - 5=40 条线段,即至少开通了 40 条高速公路.。
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
2012年-2017年华罗庚金杯少年数学邀请赛初赛真题合集(小高组)附答案

目录第二十二届华罗庚金杯少年数学邀请赛 (1)第二十一届华罗庚金杯少年数学邀请赛 (3)第二十一届华罗庚金杯少年数学邀请赛 (5)第二十届华罗庚金杯少年数学邀请赛 (7)第二十届华罗庚金杯少年数学邀请赛 (9)第十九届华罗庚金杯少年数学邀请赛 (11)第十九届华罗庚金杯少年数学邀请赛 (13)第十八届华罗庚金杯少年数学邀请赛 (15)第十八届华罗庚金杯少年数学邀请赛 (17)第十七届华罗庚金杯少年数学邀请赛 (19)第十七届华罗庚金杯少年数学邀请赛 (21)第二十二届华罗庚金杯少年数学邀请赛答案 (23)第二十一届华罗庚金杯少年数学邀请赛答案 (24)第二十一届华罗庚金杯少年数学邀请赛答案 (25)第二十届华罗庚金杯少年数学邀请赛答案 (26)第二十届华罗庚金杯少年数学邀请赛答案 (27)第十九届华罗庚金杯少年数学邀请赛答案 (28)第十九届华罗庚金杯少年数学邀请赛答案 (29)第十八届华罗庚金杯少年数学邀请赛答案 (30)第十八届华罗庚金杯少年数学邀请赛答案 (31)第十八届华罗庚金杯少年数学邀请赛答案 (32)第十七届华罗庚金杯少年数学邀请赛答案 (33)第十七届华罗庚金杯少年数学邀请赛答案 (34)A B 第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)(时间 2016 年 12 月 10 日 10:00-11:00)一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 两个有限小数的整数部分分别是 7 和 10,那么这两个有限小数的积的整数部分有( )种可能的取值.A .16B .17C .18D .192. 小明家距学校,乘地铁需要 30 分钟,乘公交车需要 50 分钟,某天小明因故先乘地铁,再换乘公交车,用了 40 分钟到达学校,其中换乘过程用了 6 分钟,那么这天小明乘坐公交车用了( )分钟. A .6 B .8 C .10 D .123. 将长方形 ABCD 对角线平均分成 12 段,连接成右图,长方形 ABCD 内部空白部分面积总和是 10 平方厘米,那么阴影部分面积总和是( )平方厘米.A .14B .16C .18D .204.请在图中的每个方框中填入适当的数字,使得乘法竖式成立.那么乘积是( ).A .2986B .2858C .2672D .27545. 在序列 20170……中,从第 5 个数字开始,每个数字都是前面 4 个数字和的个位数,这样的序列可以一直写下去.那么从第 5 个数字开始,该序列中一定不会出现的数组是( )A .8615B .2016C .4023D .20176. 从 0 至 9 选择四个不同的数字分别填入方框中的四个括号中,共有( )种填法使得方框中话是正确的.× 71 0 2罗华金杯ABG FHDEC二、填空题.(每小题 10 分,共 40 分)7. 若( 1 5 245 3— )× 9 2 5 7 ÷ 2 +2.25=4,那么A 的值是 .3 34 1A8. 右图中,“华罗庚金杯”五个汉字分别代表 1-5 这五个不同的数字,将各线段两端点的数字相加得到五个和,共有 种情况使得这五个和恰为五个连续自然数.9. 右图中,ABCD 是平行四边形,E 为 CD 的中点,AE 和 BD 的交点为 F ,AC 和 BE 的交点为 H ,AC 和BD 的交点为 G ,四边形 EHGF 的面积是 15 平方厘米,则 ABCD 的面积是平方厘米.10. 若 2017,1029 与 725 除以 d 的余数均为 r ,那么 d -r 的最大值是 .庚第二十一届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组A 卷) (时间:2015 年 12 月 12 日 10:00~11:00一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内) 1. 算式999 9 × 999 9 的结果中含有( )个数字 0.2016个92016个9A .2017B .2016C .2015D .20142. 已知 A ,B 两地相距 300 米.甲、乙两人同时分别从 A 、B 出发,相向而行,在距 A 地 140 米处相遇;如果乙每秒多行 1 米,则两人相遇处距 B 地 180 米.那么乙原来的速度是每秒( )米.A . 2 2B . 2 4C .3D . 3 15 5 53. 在一个七位整数中,任何三个连续排列的数字都构成一个能被 11 或 13 整除的三位数,则这个七位数最大是( )A .9981733B .9884737C .9978137D .98717734. 将 1,2,3,4,5,6,7,8 这 8 个数排成一行,使得 8 的两边各数之和相等,那么共有( )种不同的排法. A .1152B .864C .576D .2885. 在等腰梯形 ABCD 中,AB 平行于 CD ,AB =6,CD =14,∠AEC 是直角,CE =CB ,则 AE 2 等于( )A .84B .80C .75D .646. 从自然数 1,2,3,…,2015,2016 中,任意取 n 个不同的数,要求总能在这 n 个不同的数中找到 5个数,它们的数字和相等.那么 n 的最小值等于( ). A .109 B .110 C .111 D .112EABD C二、填空题.(每小题 10 分,共 40 分)AP M O7. 两个正方形的面积之差为 2016 平方厘米,如果这样的一对正方形的边长都是整数厘米,那么满足上述条件的所有正方形共有对.8. 如下图,O ,P ,M 是线段 AB 上的三个点,AO = 4 AB ,BP = 2AB ,M 是 AB 的中点,且 OM =2,那5 3么 PM 长为 .9. 设 q 是一个平方数.如果 q -2 和 q +2 都是质数,就称 q 为 p 型平方数.例如,9 就是一个 p 型平方数.那么小于 1000 的最大 p 型平方数是 .10. 有一个等腰梯形的纸片,上底长度为 2015,下底长度为 2016.用该纸片剪出一些等腰梯形,要求剪出的梯形的两底边分别在原来梯形的底边上,剪出的梯形的两个锐角等于原来梯形的锐角,则最多可以剪出 个同样的等腰梯形.第二十一届华罗庚金杯少年数学邀请赛初赛试卷 B (小学高年级组)(时间:2015 年 12 月 12 日 10:00~11:00)一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内) 1. “凑 24 点”游戏规则是:从一副扑克牌中抽去大小王剩下 52 张,(如果初练也可只用 1 至 10 这 40 张牌)任意抽取 4 张牌(称牌组),用加、减、乘、除(可加括号)把牌面上的数算成 24.每张牌必须用一次且只能用一次,并不能用几张牌组成一个多位数,如抽出的牌是 3,8,8,9,那么算式为(9- 8)×8×3 或(9-8÷8)×3 等.在下面 4 个选项中,唯一无法凑出 24 点的是( ). A .1,2,2,3 B .1,4,6,7 C .1,5,5,5 D .3,3,7,72. 有一种数,是以法国数学家梅森的名字命名的,它们就是形如 2n -1( n 为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如:22-1=3 就是一个梅森质数.第一个梅森合数是( ).A .4B .15C .127D .20473. 有一种饮料包装瓶的容积是 1.5 升.现瓶里装了一些饮料,正放时饮料高度为 20 厘米,倒放时空余部分的高度为 5 厘米,如下图.那么瓶内现有饮料( )升.A .1B .1.2C .1.25D .1.3754. 已知 a ,b 为自然数, 4 = 1 + 1,那么 a +b 的最小值是( ).15 a bA .16B .20C .30D .65. 如下图,平面上有 25 个点,每个点上都钉着钉子,形成 5×5 的正方形钉阵.现有足够多的橡皮筋,最多能套出( )种面积不同的正方形.A .4B .6C .8D .106. 在一个七位整数中,任何三个连续排列的数字都构成一个能被 11 或 13 整除的三位数,那么这个七位数最大是( ).A .9981733B .9884737C .9978137D .9871773二、填空题.(每小题 10 分,共 40 分)华 杯 赛 三 十 年× 杯 杯今 年 认 真 赛 好今 年 认 真 赛 好 三 十 年 华 杯 赛 好7. 计算:20152+20162-2014×2016-2015×2017= .8. 在下边的算式中,相同汉字代表相同数字,不同汉字代表不同数字.当杯代表 5 时,“华杯赛”所代表的三位数是 .9. 于 2015 年 10 月 29 日闭幕的党的十八届五中全会确定了允许普遍二孩的政策.笑笑的爸爸看到当天的新闻后跟笑笑说:我们家今年的年龄总和是你年龄的 7 倍,如果明年给妳添一个弟弟或妹妹,我们家 2020 年的年龄总和就是你那时年龄的 6 倍.那么笑笑今年 岁.10. 教育部于 2015 年 9 月 21 日公布了全国青少年校园足球特色学校名单,笑笑所在的学校榜上有名.为 了更好地备战明年市里举行的小学生足球联赛,近期他们学校的球队将和另 3 支球队进行一次足球友 谊赛.比赛采用单循环制(即每两队比赛一场),规定胜一场得 3 分,负一场得 0 分,平局两队各得 1分;以总得分高低确定名次,若两支球队得分相同,就参考净胜球、相互胜负关系等决定名次.笑笑学校的球队要想稳获这次友谊赛的前两名,至少要得 分.第二十届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2015 年 3 月 14 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 现在从甲、乙、丙、丁四个人中选出两个人参加一项活动,规定:如果甲去,那么乙也去;如果丙不去,那么乙也不去;如果丙去,那么丁不去.最后去参加活动的两个人是( )A .甲、乙B .乙、丙C .甲、丙D .乙、丁2. 以平面上任意 4 个点为顶点的三角形中,钝角三角形最多有( )个.A .5B .2C .4D .33. 桌上有编号 1 至 20 的 20 张卡片,小明每次取出 2 张卡片,要求一张卡片的编号是另一张卡片的 2 倍多 2,则小明最多取出( )张卡片. A .12B .14C .16D .184. 足球友谊比赛的票价是 50 元,赛前一小时还有余票,于是决定降价,结果售出的票增加了三分之一, 而票房收入增加了四分之一,那么每张票售价降了( )元.A .10B . 25C . 50D .25235. 一只旧钟的分针和时针每重合一次,需要经过标准时间 66 分,那么,这只旧钟的 24 小时比标准时间的 24 小时( ).A .快 12 分B .快 6 分C .慢 6 分D .慢 12 分6. 在下图的 6×6 方格内,每个方格中只能填 A 、B 、C 、D 、E 、F 中的某个字母,要求每行、每列、每个标有粗线的 2×3 长方形的六个字母均不能重复.那么,第四行除了首尾两个方格外,中间四个方格填入的字母从左到右的顺序是( ).A .E 、 C 、 D 、 FB .E 、D 、C 、FC .D 、 F 、 C 、E D .D 、C 、F 、EB CA B D ABCE二、填空题(每小题 10 分,共 40 分) - - - = AFDPBEC7. 计算4811 + 265 1 + 904 129 41 55184160 7036 12 2030 42 568. 过正三角形 ABC 内一点 P ,向三边作垂线,垂足依次为 D 、E 、F ,连接 AP 、BP 、CP .如果正三角形ABC 的面积是 2028 平方厘米,三角形 PAD 和三角形 PBE 的面积都是 192 平方厘米,则三角形 PCF的面积为平方厘米.9. 自然数 2015 最多可以表示成 个连续奇数的和.10. 由单位正方形拼成的 15×15 网格,以网格的格点为顶点作边长为整数的正方形,则边长大于 5 的正方形有 个.第二十届华罗庚金杯少年数学邀请赛A BED H C 初赛 C 试卷(小学高年级组)(时间:2015 年 3 月 14 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 计算:( 9 - 11 + 13 - 15 + 17 )×120- 1 ÷ 1=( )20 30 42 56 72 3 4A .42B .43C .15 1D .16 2332. 如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成 45 度角.最高的小树高 2.8 米,最低的小树高 1.4 米,那么从左向右数第 4 棵树的高度是( )米.A .2.6B .2.4C .2.2D .2.03. 春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生,事后,甲、乙、丙、丁 4 位同学有如下的对话: 甲:“丙、丁之中至少有 1 人捐了款.” 乙:“丁、甲之中至多有 1 人捐了款.” 丙:“你们 3 人中至少有 2 人捐了款.” 丁:“你们 3 人中至多有 2 人捐了款.” 已知这 4 位同学说的都是真话且其中恰有 2 位同学捐了款,那么这 2 位同学是( ).A .甲、乙B .丙、丁C .甲、丙D .乙、丁4. 六位同学数学考试的平均成绩是 92.5 分,他们的成绩是互不相同的整数,最高的 99 分,最低的 76分,那么按分数从高到低居第三位的同学的分数至少是( ). A .94 B .95 C .96D .975. 如图,BH 是直角梯形 ABCD 的高,E 为梯形对角线 AC 上一点;如果△DEH 、△BEH 、△BCH 的面积依次为 56、50、40,那么△CEH 的面积是( ).A .32B .34C .35D .366. 一个由边长为 1 的小正方形组成的n n 的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的 4 个角上的小正方形不全同色,那么正整数 n 的最大值是( ).A .3B .4C .5D .645°二、填空题(每小题10 分,共40 分)7.在每个格子中填入1 至6 中的一个,使得每行、每列及每个2×3 长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是3 月 1 4相约华杯8.整数n 一共有10 个约数,这些约数从小到大排列,第8 个数是n.那么整数n 的最大值是39.在边长为300 厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是厘米.(π取3.14)10.A 地、B 地、C 地、D 地依次分布在同一条公路上,甲、乙、丙三人分别从A 地、B 地C 地同时出发,匀速向D 地行进.当甲在C 地追上乙时,甲的速度减少40%;当甲追上丙时,甲的速度再次减少40%;甲追上丙后9 分钟,乙也追上了丙,这时乙的速度减少25%;乙追上丙后再行50 米,三人同时到D 地.已知乙出发时的速度是每分钟60 米,那么甲出发时的速度是每分钟米,A、D 两地间的路程是米.第十九届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2014 年 3 月 15 日 8:00—9:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行.A .0B .2C .3D .42. 某次考试有 50 道试题,答对一道题得 3 分,答错一道题扣 1 分,不答题不得分.小龙得分 120 分,那么小龙最多答对了( )道试题.A .40B .42C .48D .503. 用左下图的四张含有 4 个方格的纸板拼成了右下图所示的图形.若在右下图的 16 个方格分别填入 1、3、5、7(每个方格填一个数),使得每行、每列的四个数都不重复,且每个纸板内四个格子里的数也不重复,那么 A 、B 、C 、D 四个方格中数的平均数是( ).A . 4B . 5C D .74. 小明所在班级的人数不足 40 人,但比 30 人多,那么这个班男、女生人数的比不可能是( ).A .2︰3B .3︰4C .4︰5D .3︰75. 某学校组织一次远足活动,计划 10 点 10 分从甲地出发,13 点 10 分到达乙地,但出发晚了 5 分钟, 却早到达了 4 分钟.甲、乙两地之间的丙地恰好是按照计划时间到达的,那么到达丙地的时间是( ). A .11 点 40 分 B .11 点 50 分 C .12 点 D .12 点 10 分6. 如图所示,AF =7cm ,DH =4cm ,BG =5cm ,AE =1cm .若正方形 ABCD 内的四边形 EFGH 的面积为78 平方厘米,则正方形的边长为( )cm .A .10B .11C .12D .13ABA EDHF BC二、填空题(每小题 10 分,共 40 分)甲 乙7. 五名选手 A 、B 、C 、D 、E 参加“好声音”比赛,五个人站成一排集体亮相.他们胸前有每人的选手编号牌,5 个编号之和等于 35.已知站在 E 右边的选手的编号和为 13;站在 D 右边的选手的编号和为 31;站在 A 右边的选手的编号和为 21;站在 C 右边的选手的编号和为 7.那么最左侧与最右侧的选手编号之和是 .8. 甲、乙同时出发,他们的速度如下图所示,30 分钟后,乙比甲一共多行走了米.9. 四个黑色 1×1×1 的正方体和四个白色 1×1×1 的正方体可以组成方体(经过旋转得到相同的正方体视为同一种情况).种不同的 2×2×2 的正10. 在一个圆周上有 70 个点,任选其中一个点标上 1,按顺时针方向隔一个点的点上标 2,隔两个点的点上标 3,再隔三个点的点上标 4,继续这个操作,直到 1,2,3,…,2014 都被标记在点上.每个点可 能不止标有一个数,那么标记了 2014 的点上标记的最小整数是分分5 10 15 202530 5 10 15 202530第十九届华罗庚金杯少年数学邀请赛初赛 B 试卷(小学高年级组)(时间:2014 年 3 月 15 日 8:00—9:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行.A .0B .2C .3D .42. 在下列四个算式中: AB ÷ CD =2,E ×F =0,G -H =1,I +J =4,A ~J 代表 0~9 中的不同数字,那么两位数 AB 不可能是( ). A .54 B .58 C .92 D .963. 淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是( ).A .淘气的剪法利用率高B .笑笑的剪法利用率高C .两种剪法利用率一样D .无法判断4. 小华下午 2 点要到少年宫参加活动,但他的手表每个小时快了 4 分钟,他特意在上午 10 点时对好了表.当小华按照自己的表于下午 2 点到少年宫时,实际早到了( )分钟.A .14B .15C .16D .175. 甲、乙、丙、丁四个人今年的年龄之和是 72 岁.几年前(至少一年)甲是 22 岁时,乙是 16 岁.又知道,当甲是 19 岁的时候,丙的年龄是丁的 3 倍(此时丁至少 1 岁).如果甲、乙、丙、丁四个人的年龄互不相同,那么今年甲的年龄可以有( )种情况.A .4B .6C .8D .106. 有七张卡片,每张卡片上写有一个数字,这七张卡片摆成一排,就组成了七位数 2014315.将这七张卡片全部分给了甲、乙、丙、丁四人,每人至多分 2 张.他们各说了一句话: 甲:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 8 的倍数.” 乙:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数仍不是 9 的倍数.” 丙:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 10 的倍数.” 丁:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 11 的倍数.” 已知四个人中恰好有一个人说了谎,那么说谎的人是( ).A .甲B .乙C .丙D .丁甲 乙二、填空题(每小题 10 分,共 40 分)13 ÷ 3 + 3 ÷ 2 1 + 17. 算式 1007× 4 44 3 ÷19 的计算结果是 .(1 + 2 + 3 + 4 + 5)⨯ 5 - 228. 海滩上有一堆栗子,这是四只猴子的财产,它们想要平均分配,第一只猴子来了,它左等右等别的猴子都不来,便把栗子分成四堆,每堆一样多,还剩下一个,它把剩下的一个顺手扔到海里,自己拿走了四堆中的一堆.第二只猴子来了,它也没有等到别的猴子,于是它把剩下的栗子等分成四堆,还剩下一个,它又扔掉一个,自己拿走一堆.第三只猴子也是如此,等分成四堆后,把剩下的一个扔掉, 自己拿走一堆;而最后一只猴子来,也将剩下的栗子等分成了四堆,扔掉多余的一个,取走一堆.那 么这堆栗子原来至少有 个.9. 甲、乙二人同时从 A 地出发匀速走向 B 地,与此同时丙从 B 地出发匀速走向 A 地.出发后 20 分钟甲与丙相遇,相遇后甲立即掉头;甲掉头后 10 分钟与乙相遇,然后甲再次掉头走向 B 地.结果当甲走到 B 地时,乙恰走过 A 、B 两地中点 105 米,而丙离 A 地还有 315 米.甲的速度是乙的速度的 倍,A 、B 两地间的路程是 米.10. 从 1,2,3,…,2014 中取出 315 个不同的数(不计顺序)组成等差数列,其中组成的等差数列中包含 1 的有 种取法;总共有 种取法.第十八届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2013 年 3 月 23 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 2012.25×2013.75-2010.25×2015.75=( )A .5B .6C .7D .82. 2013 年的钟声敲响了,小明哥哥感慨地说:这是我有生以来第一次将要渡过一个没有重复数字的年份.已知小明哥哥出生的年份是 19 的倍数,那么 2013 年小明哥哥的年龄是( )岁.A .16B .18C .20D .223. 一只青蛙 8 点从深为 12 米的井底向上爬,它每向上爬 3 米,因为井壁打滑,就会下滑 1 米,下滑 1 米的时间是向上爬 3 米所用时间的三分之一.8 点 17 分时,青蛙第二次爬至离井口 3 米之处,那么青蛙从井底爬到井口时所花的时间为( )分钟.A .22B .20C .17D .164. 一个盒子里有黑棋子和白棋子若干粒,若取出一粒黑子,则余下的黑子数与白子数之比为 9︰7,若放回黑子,再取出一粒白子,则余下的黑子数与白子数之比为 7︰5,那么盒子里原有的黑子数比白子数多( )个.A .5B .6C .7D .85. 图 ABCD 是平行四边形,M 是 DC 的中点,E 和 F 分别位于 AB 和 AD 上,且 EF 平行于 BD .若三角形 MDF 的面积等于 5 平方厘米,则三角形 CEB 的面积等于( )平方厘米.A .5B .10C .15D .206. 水池 A 和 B 同为长 3 米,宽 2 米,深 1.2 米的长方体.1 号阀门用来向 A 池注水,18 分钟可将无水的A 池注满;2 号阀门用来从 A 池向B 池放水,24 分钟可将 A 池中满池水放入 B 池.若同时打开 1 号和2 号阀门,那么当 A 池水深 0.4 米时,B 池有( )立方米的水.A .0.9B .1.8C .3.6D .7.2D F MCAEB二、填空题(每小题 10 分,共 40 分)D E AFB7. 小明、小华、小刚三人分 363 张卡片,他们决定按年龄比来分.若小明拿 7 张,小华就要拿 6 张;若小刚拿 8 张,小明就要拿 5 张.最后,小明拿了 张;小华拿了张.张;小刚拿了8. 某公司的工作人员每周都工作 5 天休息 2 天,而公司要求每周从周一至周日,每天都至少有 32 人上班,那么该公司至少需要名工作人员.9. 如图,AB 是圆 O 的直径,长 6 厘米,正方形 BCDE 的一个顶点 E 在圆周上,∠ABE =45°.那么圆 O中非阴影部分的面积与正方形 BCDE 中非阴影部分面积的差等于 平方厘米(取 π=3.14)10. 圣诞老人有 36 个同样的礼物,分别装在 8 个袋子中.已知 8 个袋子中礼物的个数至少为 1 且各不相 同.现要从中选出一些袋子,将选出的袋子中的所有礼物平均分给 8 个小朋友,恰好分完(每个小朋 友至少分得一个礼物).那么,共有 种不同的选择.第十八届华罗庚金杯少年数学邀请赛AB 初赛 B 试卷(小学高年级组)(时间:2013 年 3 月 23 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 一个四位数,各位数字互不相同,所有数字之和等于 6,并且这个数是 11 的倍数,则满足这种要求的四位数共有( )个.A .6B .7C .8D .92. 2+2×3+2×3×3+……+2× 3 ⨯ 3 ⨯⨯ 3 个位数字是( ). 9个3A .2B .8C .4D .63. 在下面的阴影三角形中,不能由下图中左面的阴影三角形经过旋转、平移得到的是图( )中的三角形.ABCD4. 某日,甲学校买了 56 千克水果糖,每千克 8.06 元.过了几日,乙学校也需要买同样的 56 千克水果糖,不过正好赶上促销活动,每千克水果糖降价 0.56 元,而且只要买水果糖都会额外赠送 5%同样的水果糖.那么乙学校将比甲学校少花( )元.A .20B .51.36C .31.36D .10.365. 甲、乙两仓的稻谷数量一样,爸爸、妈妈和阳阳单独运完一仓稻谷分别需要 10 天、12 天和 15 天.爸爸、妈妈同时开始分别运甲、乙两仓的稻谷,阳阳先帮妈妈,后帮爸爸,结果同时运完两仓稻谷.那么阳阳帮妈妈运了( )天. A .3B .4C .5D .66. 如图,将长度为 9 的线段 AB 分成 9 等份,那么图中所有线段的长度的总和是( ).A .132B .144C .156D .165二、填空题(每小题10 分,共40 分)7.将乘积0.2˙43˙×0.32˙5233˙化为小数,小数点后第2013 位的数字是.8.一只青蛙8 点从深为12 米的井底向上爬,它每向上爬3 米,因为井壁打滑,就会下滑1 米,下滑1 米的时间是向上爬3 米所用时间的三分之一.8 点17 分时,青蛙第二次爬至离井口3 米之处,那么青蛙从井底爬到井口时所花的时间为分钟.9.一个水池有三个进水口和一个出水口.同时打开出水口和其中的两个进水口,注满整个水池分别需要6 小时、5 小时和4 小时;同时打开出水口和三个进水口,注满整个水池需要3 小时.如果同时打开三个进水口,不打开出水口,那么注满整个水池需要小时.10.九个同样的直角三角形卡片,用卡片的锐角拼成一圈,可以拼成类似下图所示的平面图形.这种三角形卡片中的两个锐角中较小的一个的度数有种不同的可能值.(下图只是其中一种可能的情况)第十七届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2012 年 3 月 17 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 计算:[(0.8+ 1 )×24+6.6]÷ 9-7.6=( ).5 14A .30B .40C .50D .602. 以平面上 4 个点为端点连接线段,形成的图形中最多可以有( )个三角形.A .3B .4C .6D .83. 一个奇怪的动物庄园里住着猫和狗,狗比猫多 180 只.有 20%的狗错认为自己是猫;有 20%的猫错认为自己是狗.在所有的猫和狗中,有 32%认为自己是猫,那么狗有( )只.A .240B .248C .420D .8424. 下图的方格纸中有五个编号为 1,2,3,4,5 的小正方形,将其中的两个涂上阴影,与图中阴影部分正好组成正方体的展开图,这两个正方形的编号可以是( )A .1,2B .2,3C .3,4D .4,55. 在下图所示的算式中,每个字母代表一个非零数字,不同的字母代表不同的数字,则和的最小值是( ) A .369B .396C .459D .5496. 下图是由相同的正方形和相同的等腰直角三角形构成,则正方形的个数为( )A .83B .79C .72D .651 253 4A B C + D E F H IJ二、填空题(每小题 10 分,共 40 分)百十个百 十 个A EC HFB7. 如图的计数器三个档上各有 10 个算珠,将每档算珠分成上下两部分,得到两个三位数.要求上面部分是各位数字互不相同的三位数,且是下面三位数的倍数,则上面部分的三位数是.8. 四支排球队进行单循环比赛,即每两队都要赛一场,且只赛一场.如果一场比赛的比分是 3:0 或 3:1.则胜队得 3 分,负队得 0 分;如果比分是 3:2,则胜队得 2 分,负队得 1 分.比赛的结果各队得分恰好是四个连续的自然数,则第一名的得分是 分.9. 甲、乙两车分别从 A 、B 两地同时出发,且在 A 、B 两地往返来回匀速行驶.若两车第一次相遇后,甲车继续行驶 4 小时到达 B ,而乙车只行驶了 1 小时就到达 A ,则两车第 15 次(在 A ,B 两地相遇次数不计)相遇时,它们行驶了 小时.10. 正方形 ABCD 的面积为 9 平方厘米,正方形 EFGH 的面积为 64 平方厘米.如图所示,边 BC 落在 EH上.己知三角形 ACG 的面积为 6.75 平方厘米,则三角形 ABE 的面积为 平方厘米.。
第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小中组b卷)

2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小中组B卷)一、填空题(每小题10分,共80分)1.(10分)计算:3752÷(39×2)+5030÷(39×10)=.2.(10分)如图中,∠A+∠B+∠C+∠D+∠F+∠G 等于度.3.(10分)商店以每张2角1分的价格进了一批贺年卡,共卖14.57元.若每张的售价相同,且不超过买入价格的两倍,则商店赚了角.4.(10分)两个班植树,一班每人植3棵,二班每人植5棵,共植树115棵.两班人数之和最多为.5.(10分)某商店第一天卖出一些笔,第二天每支笔降价1元后多卖出100支,第三天每支笔比前一天涨价3元后比前一天少卖出200支.如果这三天每天卖得的钱相同,那么第一天每支笔售价是元.6.(10分)一条河上有A,B两个码头,A在上游,B在下游.甲、乙两人分别从A,B同时出发,划船相向而行,4小时后相遇.如果甲、乙两人分别从A,B同时出发,划船同向而行,乙16小时后追上甲.已知甲在静水中划船的速度为每小时6千米,则乙在静水中划船每小时行驶千米.7.(10分)某个两位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,那么这个两位数是.8.(10分)在三个给词语“尽心尽力”、“力可拔山”和“山穷水尽”中,每个汉字代表1至8之间的数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字,如果每个词语的汉字所代表的数字之和都是19,且“尽”>“山”>“力”,则“水”最大等于.二、简答题(每小题15分,共60分,要求写出简要过程)9.(15分)有一批作业,王老师原计划每小时批改6本,批改了2小时后,他决定每小时批改8本,结果提前3小时批改完,那么这批作业有多少本?10.(15分)用五种不同的颜色涂正方体的六个面.如果相邻的两个面不能涂同种颜色,则共有多少种不同的涂色方法?(将正方体任意翻转后仍然不同的涂色方法才被认为是不同的)11.(15分)如图所示,有一个圆圈填了数字1.请在空白圆圈内填上2,3,4,5,6中的一个数字,要求无重复数字,且相邻圆圈内的数字的差至少为2.问共有几种不同的填法?12.(15分)边长分别为8cm和6cm的两个正方形ABCD与BEFG如图并排放在一起.连接DE交BG于P,则图中阴影部分APEG的面积是多少?2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小中组B卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)计算:3752÷(39×2)+5030÷(39×10)=61 .【分析】根据除法的性质,原式=3752÷2÷39+5030÷10÷39=1876÷39+503÷39=(1876+503)÷39=2379÷39=61,据此解答即可.【解答】解:3752÷(39×2)+5030÷(39×10)=3752÷2÷39+5030÷10÷39=1876÷39+503÷39=(1876+503)÷39=2379÷39=61;故答案为:61.2.(10分)如图中,∠A+∠B+∠C+∠D+∠F+∠G 等于360 度.【分析】连接CD,有∠G+∠F=∠EDC+∠ECD,这样就转化成四边形的内角和了,四边形的内角和是360度.【解答】解:连接CD,有∠G+∠F=∠EDC+∠ECD,所以,∠A+∠B+∠C+∠D+∠F+∠G=∠A+∠B+∠C+∠D+∠EDC+∠ECD=四边形ABCD的内角和,180×(4﹣2)=180×2=360(度)答:∠A+∠B+∠C+∠D+∠F+∠G 等于 360度.故答案为:360.3.(10分)商店以每张2角1分的价格进了一批贺年卡,共卖14.57元.若每张的售价相同,且不超过买入价格的两倍,则商店赚了47 角.【分析】将14.57元化为整数是1457分,售价应是不超过42的奇数,容易试出答案.【解答】1457分解质因数是1457=31×47,47超过了21的2倍,31符合条件,所以售价是31分,进而数量是47张,47×(31﹣21)=470分=47角故答案为:47.4.(10分)两个班植树,一班每人植3棵,二班每人植5棵,共植树115棵.两班人数之和最多为37 .【分析】设一班a人,二班b人,则有3a+5b=115,求两班人数最多,算式转化成:3(a+b)+2b=115,a+b最大,b尽可能的小,b=2时,a+b =37.【解答】解:设一班a人,二班b人,则3a+5b=115,3(a+b)+2b=115,a+b最大,b尽可能的小,b=1时,得出a不是整数,b=2时,3(a+2)+2×2=1153a+6+4=1153a=105a=35a+b=35+2=37(人)答:两班人数之和最多的是37人.故答案为:37.5.(10分)某商店第一天卖出一些笔,第二天每支笔降价1元后多卖出100支,第三天每支笔比前一天涨价3元后比前一天少卖出200支.如果这三天每天卖得的钱相同,那么第一天每支笔售价是 4 元.【分析】设第一天每支笔售价x元,卖出y支,那么根据总价=单价×数量可知:第一天卖出的钱数就是xy元,第二天的单价就是x﹣1元,卖出的支数是y+100支,第二天卖出的总价就是(x﹣1)(y+100);同理得出第三天卖出的总价,再分别根据第一天卖出的钱数与第二天和第三天卖出的钱数分别相等列出方程组,再化简求解.【解答】解:设第一天的单价为x元,数量为y只,那么有:化简得:解得:答:第一天每支笔售价是 4元.故答案为:4.6.(10分)一条河上有A,B两个码头,A在上游,B在下游.甲、乙两人分别从A,B同时出发,划船相向而行,4小时后相遇.如果甲、乙两人分别从A,B同时出发,划船同向而行,乙16小时后追上甲.已知甲在静水中划船的速度为每小时6千米,则乙在静水中划船每小时行驶10 千米.【分析】在流水行船问题中,两船相遇的速度即两船的速度和,两船追及速度即两船的速度差.相向而行两船所行的路程是A、B两个码头之间的距离,同向而行两船的距离差也为A、B两个码头之间的距离,因此根据路程相等,设乙船的速度是x千米/小时,列出方程(x+6)×4=(x﹣6)×16,解决问题.【解答】解:设乙船的速度是每小时x千米,(x+6)×4=(x﹣6)×164x+24=16x﹣9612x=120x=10答:乙在静水中划船每小时行驶10千米.故答案为:10.7.(10分)某个两位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,那么这个两位数是62 .【分析】根据2、3、5的倍数的特征:个位上是0、2、4、6、8的数都是2的倍数;各位上的数字之和是3的倍数,这个数一定是3的倍数;个位上是0或5的数都是5的倍数;据此解答即可.【解答】解:2、3、4、5的最小公倍数是:2×3×2×5=60,已知这个两位数是偶数,在60~70之间5的倍数是65,又知这个两位数加上3是5的倍数,所以这个两位数是65﹣3=62,答:这个两位数是62.故答案为:62.8.(10分)在三个给词语“尽心尽力”、“力可拔山”和“山穷水尽”中,每个汉字代表1至8之间的数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字,如果每个词语的汉字所代表的数字之和都是19,且“尽”>“山”>“力”,则“水”最大等于7 .【分析】通过分析可知:由“尽心尽力”、“力可拔山”和“山穷水尽”三个词语中每个词语的汉字所代表的数字之和都是19,可得方程:可得3尽+心+2力+可+拔+2山+穷+水=19×3=57而1~8的和是36,则有2尽+1力+1山=57﹣36=21,与(1)比较得山﹣心=2.“尽”>“山”>“力”,“力”尽可能大,“尽”才最小,假定“力”、“山”、“尽”是连续自然数,有2(力+2)+力+1+力=21 “力”为4,此时山=5,心=3,尽=6;(1)式满足:6+3+6+4=19;(3)式:5+穷+水+6=19穷水,水此时最大为7,穷为1,来推倒2式:(2)式:4+可+拔+5=19可拔,而现在只剩下2和8了,满足条件.此时水最大为7若水最大取8时,有但此时6(尽)、4(山)、5(力),不满足“尽”>“山”>“力”,所以不符合要求.故水最大为7.据此解答即可.【解答】解:由“尽心尽力”、“力可拔山”和“山穷水尽”三个词语中每个词语的汉字所代表的数字之和都是19,可得方程:(1)+(2)+(3)可得:3尽+心+2力+可+拔+2山+穷+水=19×3=57而1~8的和是36,则有2尽+1力+1山=57﹣36=21,与(1)比较得山﹣心=2.“尽”>“山”>“力”,“力”尽可能大,“尽”才最小,假定“力”、“山”、“尽”是连续自然数,有2(力+2)+力+1+力=21 “力”为4,此时山=5,心=3,尽=6;(1)式满足:6+3+6+4=19;(3)式:5+穷+水+6=19穷水,水此时最大为7,穷为1,来推倒2式:(2)式:4+可+拔+5=19可拔,而现在只剩下2和8了,满足条件.此时水最大为7若水最大取8时,有但此时6(尽)、4(山)、5(力),不满足“尽”>“山”>“力”,所以不符合要求.故水最大为7.故答案为:7.二、简答题(每小题15分,共60分,要求写出简要过程)9.(15分)有一批作业,王老师原计划每小时批改6本,批改了2小时后,他决定每小时批改8本,结果提前3小时批改完,那么这批作业有多少本?【分析】根据题意知道,这批作业的总数本变,即工作总量一定,那么计划与实际的工作效率与工作时间成反比例,据此设出原计划x小时批改完,列出方程先求出原计划用的小时数,再根据工作效率×工作时间=工作量进而得解.【解答】解:设原计划x小时批改完,由题意得:6×2+8(x﹣3﹣2)=6x12+8x﹣40=6x8x﹣6x=282x=28x=14.6×14=84(本);答:这批作业有84本.10.(15分)用五种不同的颜色涂正方体的六个面.如果相邻的两个面不能涂同种颜色,则共有多少种不同的涂色方法?(将正方体任意翻转后仍然不同的涂色方法才被认为是不同的)【分析】用五种不同的颜色涂正方体的六个面.先确定1种颜色染一组对面,剩下的4种颜色(用a、b、c、d表示)有abcd、acdb、acbd,3种染色方法,有•3=15种;据此解答即可.【解答】解:根据分析可得,•3=5×3=15(种);答:共有15种不同的涂色方法.11.(15分)如图所示,有一个圆圈填了数字1.请在空白圆圈内填上2,3,4,5,6中的一个数字,要求无重复数字,且相邻圆圈内的数字的差至少为2.问共有几种不同的填法?【分析】可以按照数字找位置来分析,数字2不能在1附近,数字3有不在2附近,可以根据数字的位置枚举出来进行分析即可.【解答】解:相邻两个圆圈内的数字的差至少为2,设如图所示字母为a,b,c,d,e所以2只能填在d和e.(1)d处填2,2的周围不能有3.所以3只能填在a处.3的周围不能填4,4只能填在c和e.,5、6不能在一起,所以5填在b.6和4可以在c 和e交换,此时2种填法;(见中图)(2)e处填2,3填a或者b处.3填a处,4、5、6必有两个相邻,没有满足条件的填法;3填b处,4只能填入c处,5只能填入a处,6填入d处.1种填法;(见右图)故共2+1=3种填法.答:共有3种不同的方法.12.(15分)边长分别为8cm和6cm的两个正方形ABCD与BEFG如图并排放在一起.连接DE交BG于P,则图中阴影部分APEG的面积是多少?【分析】首先需要将阴影部分和已知的正方形的边长的关系找到,可根据△APG转换成同底等高的△DPG,然后再根据等积变形的原理与边长为6的正方形联系起来即可解决.【解答】解:依题意可知:将△APG移到△DPG(如上面中图),连接DB,DB与GE平行.△DGE等于△BGE的面积(如上面右图).S阴=6×6÷2=18cm2.答:影部分APEG的面积是18cm2.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 11:00:15;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第20届华杯赛小高组答案详解

3
二、填空题 (每小题 10 分,共 40 分)
1 1 1 29 41 55 7. 计算: 481 + 265 + 904 − 184 − 160 − 703 =________. 6 12 20 30 42 56
【答案】 600
3 8
【题型】凑整、分数裂项 【解析】
1 1 1 1 1 1 + + − (1 − ) − (1 − ) − (1 − ) 6 12 20 30 42 56 1 1 1 1 1 1 + + + ) = (481 + 265 + 904 − 184 − 160 − 703 − 1 − 1 − 1) + ( + + 6 12 20 30 42 56 1 1 1 1 1 1 1 1 1 1 1 1 = 600 + ( − ) + ( − ) + ( − ) + ( − ) + ( − ) + ( − ) 2 3 3 4 4 5 5 6 6 7 7 8 1 1 = 600 + − 2 8 3 = 600 8 = 481 + 265 + 904 − 184 − 160 − 703 +
4.
足球友谊比赛的票价是 50 元,赛前一小时还有余票,于是决定降价.结果售出的票 增加了三分之一,而票房收入增加了四分之一,那么每张票售价降了( )元. 25 50 (A)10 (B) (C) (D)25 2 3
【答案】B 【题型】方程 【解析】设共有 x 张票,赛前一小时的余票降价 y 元. 1 25 1 由题意得: × ( x × 50) = × [ x × (50 − y)], y = 3 2 4
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案

1 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
2 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
3 / 12
ห้องสมุดไป่ตู้
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
4 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
5 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
11 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
12 / 12
6 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
7 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
8 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
9 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
10 / 12
第二十届华罗庚金杯少年数学邀请赛决赛试题及答案
第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组c卷)

2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组C卷)一、填空题(每小题10分,共80分)1.(10分)计算:+=.2.(10分)将自然数1至8分为两组,使两组的自然数各自之和的差等于16,共有种不同的分法.3.(10分)将2015的十位、百位和千位的数字相加,得到的和写在2015个位数字之后,得到一个自然数20153;将新数的十位、百位和千位数字相加,得到的和写在20153个位数字之后,得到201536;再次操作2次,得到201536914,如此继续下去,共操作了2015次,得到一个很大的自然数,这个自然数所有数字的和等于.4.(10分)如图,四边形ABCD是边长为11厘米的正方形,G在CD上,四边形CEFG是边长为 9 厘米的正方形,H在AB上,∠EDH是直角,三角形EDH的面积是平方厘米.5.(10分)如图是网格为3×4的长方形纸片,长方形纸片正面是灰色,反面是红色,网格是相同的小正方形.沿网格线将长方形裁剪为两个形状相同的卡片,如果形状和正反面颜色相同,则视为相同类型的卡片,则能裁剪出种不同类型的卡片.6.(10分)一个长方体,棱长都是整数厘米,所有棱长之和是 88 厘米,问这个长方体总的侧面积最大是平方厘米.7.(10分)[x﹣]=3x﹣5,这里[x]表示不超过x的最大整数,则x =.8.(10分)右边是一个算式,9个汉字代表数字1至9,不同的汉字代表不同的数字,则该算式可能的最大值是.二、解答下列各题(每小题10分,共40分,要求写出简要过程)9.(10分)已知C地为A,B两地的中点.上午7点整,甲车从A出发向B 行进,乙车和丙车分别从B和C出发向A行进.甲车和丙车相遇时,乙车恰好走完全程的,上午10点丙车到达A地,10点30分当乙车走到A 地时,甲车距离B地还有84千米,那么A和B两地距离是多少千米?10.(10分)将2015个分数,,…,,化成小数,共有多少个有限小数?11.(10分)a,b 为正整数,小数点后第3位经四舍五入后,式子+=1.51,求a+b=?12.(10分)已知算式abcd=aad×e,式中不同字母代表不同的数码,问四位数abcd最大值是多少?三、解答下列各题(每题15分,共30分,要求写出详细过程)13.(15分)在图中,ABCD是平行四边形,F在AD上,△AEF的面积=8cm2,△DEF的面积=12cm2,四边形BCDF的面积=72cm2,求出△CDE的面积?14.(15分)将530本书分给48名学生,至少有几名学生分到的数量相同?2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组C卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)计算:+= 1 .【分析】把繁分数的分子分母中的算式分别化简,然后根据分数的基本性质解答即可.【解答】解:+=+=+=1;故答案为:1.2.(10分)将自然数1至8分为两组,使两组的自然数各自之和的差等于16,共有8 种不同的分法.【分析】根据题意,分成的两组之和为(1+8)×8÷2=36,因为两组的自然数各自之和的差等于16,因此和较大的一组等于(36+16)÷2=26,较小的一组是36﹣26=10,由此即可解答.【解答】解:分成的两组之和为:(1+8)×8÷2=9×8÷2=36和较大的一组等于:(36+16)÷2=52÷2=26较小的一组是:36﹣26=10因为10=2+8=3+7=4+6=1+2+7=1+3+6=1+4+5=2+3+5=1+2+3+4相应地26=1+3+4+5+6+7=1+2+4+5+6+8=1+2+3+5+7+8=3+4+5+6+8=2+4+5+7+8=2+3+6+7+8=1+4+6+7+8=5+6+7+8所以共有8种不同的分法故答案为:8.3.(10分)将2015的十位、百位和千位的数字相加,得到的和写在2015个位数字之后,得到一个自然数20153;将新数的十位、百位和千位数字相加,得到的和写在20153个位数字之后,得到201536;再次操作2次,得到201536914,如此继续下去,共操作了2015次,得到一个很大的自然数,这个自然数所有数字的和等于8479 .【分析】按题设条件,操作16次后,如上图,发现数字的规律为:从7次开始数字为11、3、3、5、7,从第12次开始为11、3、3、5、7,这5个数字重复出现.根据整个规律,推出操作了2015次,得到的数,再求和即可.【解答】解:按题设条件,操作16次后,如下:数字的规律为:从7次开始数字为11、3、3、5、7,从第12次开始为11、3、3、5、7,这5个数字重复出现,则操作2015次:(2015﹣6)÷5=401…4,则2015次操作的对应的数字是5;则所有自然数和为:前4位:2+0+1+5=8,后6为:3+6+9+1+4+1+6+6=36,重复的数字和为:1+1+1+3+3+5+7=21,重复401次后,和为401×21=8421,余数4,对应数字的和为:1+1+1+3+3+5=14,以上数字相加即为所有自然数和=8+36+8421+14=8479.故:应该填:8479.4.(10分)如图,四边形ABCD是边长为11厘米的正方形,G在CD上,四边形CEFG是边长为 9 厘米的正方形,H在AB上,∠EDH是直角,三角形EDH的面积是101 平方厘米.【分析】1、延长EF、AD交于点K;2、将△DEK和△ADH面积相等,所以,HB=2;3、S阴影=S ABEK﹣S DEK﹣S ADH﹣S BHE【解答】根据上述分析故答案是:S阴影=S ABEK﹣S DEK﹣S ADH﹣S BHE=11×(11+9)﹣0.5×9×11﹣0.5×9×11﹣0.5×2×(11+9)=1015.(10分)如图是网格为3×4的长方形纸片,长方形纸片正面是灰色,反面是红色,网格是相同的小正方形.沿网格线将长方形裁剪为两个形状相同的卡片,如果形状和正反面颜色相同,则视为相同类型的卡片,则能裁剪出8 种不同类型的卡片.【分析】可首先分析向左的减法,然后根据左右对称情况得出向右的剪法,减去重合的剪法,从而得出总的不同剪法.【解答】解:先考虑从正面剪,中间那条粗线是一定要剪开的,剪开后,从点1有三种选择,向上向左向右;1、向上:,属于第1种类型;2、向左:剪至点3,又有3种选择,向上向左向下,(1)向上(黑线):,红线是和黑线对称的情况,但按红线剪出的图形旋转后和黑线相同,属于第2种类型;(2)向左:,按红线剪出的图形旋转后和黑线不同,是两种不同的类型,属于第3、4种类型;(3)向下:向下剪至点6,有两种选择,向左,向下,①向左:,按红线剪出的图形旋转后和黑线不同,是两种不同的类型,属于第5、6种类型;②向下:,按红线剪出的图形旋转后和黑线不同,是两种不同的类型,属于第7、8种类型;综上可得,总共有8种类型.故答案是:8.6.(10分)一个长方体,棱长都是整数厘米,所有棱长之和是 88 厘米,问这个长方体总的侧面积最大是224 平方厘米.【分析】长宽高的和是:88÷4=22厘米,长方体的总侧面积最大,长宽高的长度必须最接近,即22=8+7+7,然后再利用长方体的侧面积公式,也就是用底面周长乘高,据此解答即可.【解答】解:长宽高的和是:88÷4=22(厘米),长方体的总侧面积最大,长宽高的长度必须最接近,即22=8+7+7,(7+7)×2×8=28×8=224(平方厘米);答:这个长方体的总侧面积最大是224平方厘米.故答案为:224.7.(10分)[x﹣]=3x﹣5,这里[x]表示不超过x的最大整数,则x=2 .【分析】按题意,要使原式成立,则[x﹣]≤x﹣,⇒3x﹣5≤x﹣,而3x﹣5为整数,不难求得x=2.【解答】解:根据分析,要使原式成立,则[x﹣]≤x﹣,⇒3x﹣5≤x﹣,⇒x≤,∵3x﹣5≥0∴x=2而3x﹣5为整数,不难求得x=2.故答案是:28.(10分)右边是一个算式,9个汉字代表数字1至9,不同的汉字代表不同的数字,则该算式可能的最大值是8569 .【分析】观察这个算式,要使这个算式的值最大,那么两位数与两位数的乘积就要尽可能的大,所以天空=96,则湛蓝=87;同理,两位数与一位数的乘积也要尽可能的大,所以翠绿=43,则树=5;那么盼=1,望=2;据此解答即可.【解答】解:根据分析可得,1×2+43×5+96×87=2+215+8352=8569;故答案为:8569.二、解答下列各题(每小题10分,共40分,要求写出简要过程)9.(10分)已知C地为A,B两地的中点.上午7点整,甲车从A出发向B 行进,乙车和丙车分别从B和C出发向A行进.甲车和丙车相遇时,乙车恰好走完全程的,上午10点丙车到达A地,10点30分当乙车走到A 地时,甲车距离B地还有84千米,那么A和B两地距离是多少千米?【分析】首先根据甲丙相遇走完全程的一半,乙走完全程的即可列出一组甲乙丙速度的关系式,再根据丙3小时走一半路程,乙3.5小时走完全程可以列出乙丙的速度关系式.重点求出甲乙的速度比,根据甲车距离B 地84千米,求得对应的份数,即可求出所求.【解答】解:根据题意可知,当甲丙相遇时走完全程的一半,乙走完全程的,即(V甲+V丙)=V乙.①再根据丙3小时走了全程的一半,乙3.5小时走完全程,即6V丙=3.5V乙.②根据①②得:V甲:V乙=3:4.所以甲乙路程之比就是3:4.一份量是:84÷(4﹣3)=84千米.全程是:84×4=336千米.故答案为:336千米.10.(10分)将2015个分数,,…,,化成小数,共有多少个有限小数?【分析】先找出分母中只有因数2,5,同时有2和5的数的个数,即可得出结论.【解答】解:在2015个分数,,…,,的分母中,只有因数2的数有2,4,8,16,32,64,128,256,512,1024共10个数,只有因数5的数有5,25,125,625共4个数,既有因数2,也有因数5的数有10,20,40,50,80,100,160,200,250,320,400,500,640,800,1000,1250,1280,1600,2000共19个数,所以总有10+4+19=33个有限小数,答:共有33个有限小数.11.(10分)a,b 为正整数,小数点后第3位经四舍五入后,式子+=1.51,求a+b=?【分析】根据条件,代入验证,求出a,b,即可得出结论.【解答】解:由题意,a=7,则取b=1,+=1.4+0.143≈1.54,不符合题意;a=6,则取b=3,+=1.2+0.429≈1.63,不符合题意;a=5,则取b=4,+=1+0.571≈1.57,不符合题意;a=4,则取b=5,+=0.8+0.714≈1.51,符合题意;∴a+b=9.12.(10分)已知算式abcd=aad×e,式中不同字母代表不同的数码,问四位数abcd最大值是多少?【分析】aad×e=abcd中,d×e的个位数仍为d(1~9)×1=(1~9)(2、4、6、8)×6=(12、24、36、48)5×(3、5、7、9)=(15、25、35、45)【解答】解:从上面的分析可以看出e可能为1、6、(3、5、7、9)设:e为9,希望得最大值,则d为5从a=(1~9)检测,得115×9=1035225×9=2025335×9=3015…通过检测,∴abcd的最大值为3015答:这个四位数最大是3015.三、解答下列各题(每题15分,共30分,要求写出详细过程)13.(15分)在图中,ABCD是平行四边形,F在AD上,△AEF的面积=8cm2,△DEF的面积=12cm2,四边形BCDF的面积=72cm2,求出△CDE的面积?【分析】连接BD(如下图),若△AEF以AF为底、△EFD以FD为底,他们的高相等,则底边比等于面积比,可以求出AF:DF=2:3;若△ABF、△BFD分别以AF、FD为底,他们高相同,则S△ABF=0.2×S▱ABCD、而S△BDF=0.6×S△ABD=0.3×S▱ABCD;S△BCDF=S△BFD+S△BCD,求出S▱ABCD;由S△ABF=0.2×S▱ABCD,求出S△ABF;,根据S△AEB=S△ABF﹣S△AEF,可以S△AEB;S△AEB与S△ECD之和为平行四边形面积的一半,可以求出S△ECD.【解答】解:连接BD(如上图),根据△AEF的面积=8cm2,△DEF的面积=12cm2,求出AF:DF=8:12=2:3;S△BCDF=S△BFD+S△BCD=0.5S▱ABCD+0.3S▱ABCD=0.8S▱ABCD=72,所以:S▱ABCD=90;S△ABF=0.2S▱ABCD=18,S△ABE=S△ABF﹣S△AEF=10;S△ABE+S△ECD=0.5×S▱ABCD=45;故S△ECD=45.答:S△ECD的面积为45cm2.14.(15分)将530本书分给48名学生,至少有几名学生分到的数量相同?【分析】①若48名学生分到的数量互不相同,则至少要:0+1+2+3+…+47=1128>530,不满足条件;②若只有2名学生分到的书数量相同,则至少要:(0+1+2+3+…+23)×2=552>530,不满足条件;③若只有3名学生分到的书数量相同,则至少要:(0+1+2+3+…+15)×3=360<530,满足条件;所以至少3名学生分到的书数量相同,据此解答即可.【解答】解:①若48名学生分到的数量互不相同,则至少要:0+1+2+3+…+47=1128>530,不满足条件;②若只有2名学生分到的书数量相同,则至少要:(0+1+2+3+…+23)×2=552>530,不满足条件;③若只有3名学生分到的书数量相同,则至少要:(0+1+2+3+…+15)×3=360<530,满足条件;所以至少3名学生分到的书数量相同.答:至少3名学生分到的书数量相同.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:59:44;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第二十届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组c卷)

2015年第二十届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组C卷)一、选择题(每小题10分,共60分).1.(10分)计算:(﹣+﹣+)×120﹣÷()A.42 B.43 C.15D.162.(10分)如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成45度角,最高的小树高2.8米,最低的小树高峰1.4米,那么从左向右数第4棵树的高度是()米.A.2.6 B.2.4 C.2.2 D.2.03.(10分)春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、丙、丁4位同学有如下对话:甲:“丙,丁之中至少有1人捐了款”乙:“丁,甲之中至多有1人捐了款”丙:“你们3人之中至少有2人捐了款”丁:“你们3人之中至多有2人捐了款”已知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这2位同学是()A.甲,乙B.丙,丁C.甲,丙D.乙,丁4.(10分)六位同学数学考试的平均成绩是92.5分,他们的成绩是互不相同的整数,最高的99分,最低的76分,那么按分数从高到低居第3位的同学的分数至少是()A.94 B.95 C.96 D.975.(10分)如图,BH是直角梯形ABCD的高,E为梯形对角线AC上一点,如果△DEH、△BEH、△BCH的面积依次为56、50、40,那么△CEH的面积是()A.32 B.34 C.35 D.366.(10分)一个由边长为1的小正方形组成的n×n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个角上的小正方形不全同色,那么正整数n的最大值是()A.3 B.4 C.5 D.6二、填空题:(每小题10分,满分40分)7.(10分)在每个格子中填入1﹣6中的一个,使得每行、每列及每个2×3长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数“相约华杯”是.8.(10分)整数n一共有10个因数,这些因数从小到大排列,第8个是.那么整数n的最大值是.9.(10分)在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是厘米.(π取3.14)10.(10分)A地,B地,C地,D地依次分布在同一条公路上.甲,乙,丙三人分别从A地,B地,C地同时出发,匀速向D地行进.当甲在C地追上乙时,甲的速度减少40%,当甲追上丙时,甲的速度再次减少40%,甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少25%;乙追上丙后再行50米,三人同时到D地.已知乙出发时的速度是每分钟60米,那么甲出发时的速度是每分钟米,A、D两地间的路程是米.2015年第二十届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组C卷)参考答案与试题解析一、选择题(每小题10分,共60分).1.(10分)计算:(﹣+﹣+)×120﹣÷()A.42 B.43 C.15D.16【分析】首先对(﹣+﹣+)进行拆分,然后用所得的结果减去除以所得的商,求出算式的值是多少即可.【解答】解:(﹣+﹣+)×120﹣÷=(+﹣﹣++﹣﹣++)×120﹣=(+)×120﹣=30+×120﹣=42故选:A.2.(10分)如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成45度角,最高的小树高2.8米,最低的小树高峰1.4米,那么从左向右数第4棵树的高度是()米.A.2.6 B.2.4 C.2.2 D.2.0【分析】因为∠A=45°,最高的小树高2.8米,所以AC=2.8米,又因为树根成一条直线,树顶也成一条直线,所以所有的树都互相平行,所以AB=1.4米,BC=AC﹣AB=1.4米,因为这排树的间距相同,则每个间距是1.4÷7=0.2米,则从左向右数第4棵树的高度:0.2×4+1.4,据此解答即可.【解答】解:因为:树根成一条直线,树顶也成一条直线,∠A=45°,最高的小树高2.8米,最低的小树高峰1.4米,所以AC=2.8米,AB=1.4米,BC=AC﹣AB=1.4米,又因为:这排树的间距相同,所以:1.4÷7=0.2(米)0.2×4+1.4=0.8+1.4=2.2(米)答:那么从左向右数第4棵树的高度是2.2米.故选:C.3.(10分)春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、丙、丁4位同学有如下对话:甲:“丙,丁之中至少有1人捐了款”乙:“丁,甲之中至多有1人捐了款”丙:“你们3人之中至少有2人捐了款”丁:“你们3人之中至多有2人捐了款”已知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这2位同学是()A.甲,乙B.丙,丁C.甲,丙D.乙,丁【分析】因为有2位同学捐了款,所以根据:丙:“你们3人之中至少有2人捐了款,说明捐款的只能是甲乙丁中的两个人,而丙没捐钱;甲:“丙,丁之中至少有1人捐了款”因为丙没捐钱,所以只能是丁捐款;乙:“丁,甲之中至多有1人捐了款”只能是丁,所以甲没捐款;这恰好印证了丁:“你们3人之中至多有2人捐了款”是正确的.据此解答即可.【解答】解:根据分析可得:丙:“你们3人之中至少有2人捐了款,说明捐款的只能是甲乙丁中的两个人,而丙没捐钱;甲:“丙,丁之中至少有1人捐了款”因为丙没捐钱,所以只能是丁捐款;乙:“丁,甲之中至多有1人捐了款”只能是丁,所以甲没捐款;这恰好印证了丁:“你们3人之中至多有2人捐了款”是正确的,只有乙和丁捐了款.故选:D.4.(10分)六位同学数学考试的平均成绩是92.5分,他们的成绩是互不相同的整数,最高的99分,最低的76分,那么按分数从高到低居第3位的同学的分数至少是()A.94 B.95 C.96 D.97【分析】要求第三名同学至少要考多少分,知道六名同学的总平均分,能求出总成绩,用总成绩﹣最高分﹣最低分=另四名同学的总成绩,要想第3个同学成绩最小,则第2个同学成绩取最大值为:98,进而求出另三位同学的总成绩,进而根据“总成绩÷总人数=平均分”能求出另三名同学的平均分,继而分析、推导得出所求问题的答案.【解答】解:92.5×6﹣99﹣76=380(分),由于最高分是99分,所以第二个的最好成绩最多是:98剩余三人成绩和为:380﹣98=282(分),第3个同学成绩最小,第4、5个同学的成绩尽可能接近第三个同学的成绩,则这3个数相差为1,282÷3=94(分),则第三位同学至少是:94+1=95(分).答:第三名至少得95分.故选:B.5.(10分)如图,BH是直角梯形ABCD的高,E为梯形对角线AC上一点,如果△DEH、△BEH、△BCH的面积依次为56、50、40,那么△CEH的面积是()A.32 B.34 C.35 D.36【分析】如下图所示:分别过点E作EF⊥DC,EG⊥BH,连接AF,BF,BD,由等底等高的三角形面积相等,可得S△BDF=S△ADF,S△ADC=S△BDC,因此有:SS△ADC﹣S△ADE=S△BDC﹣S△BDF=S△BFC,而S△BFC=S△BFH+S△BCH=S△BEH+S△BCH=90;△CDE=因此S△CHE=S△EDC﹣S△HDE=90﹣56=34,据此即可解决.【解答】解:如上图所示,分别过点E作EF⊥DC,EG⊥BH,连接AF,BF,BD,则S△BDF=S△ADF,S△ADC=S△BDC,所以S△CDE=S△ADC﹣S△ADE=S△BDC﹣S△BDF=S△BFC,又因为S△BFC=S△BFH+S△BCH=S△BEH+S△BCH=90,所以S△CHE=S△EDC﹣S△HDE=90﹣56=34.故选:B.6.(10分)一个由边长为1的小正方形组成的n×n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个角上的小正方形不全同色,那么正整数n的最大值是()A.3 B.4 C.5 D.6【分析】此题要充分利用抽屉原理和假设推理.根据题目所给的选项不妨选一个中间的数5为假设n的值,进行一步步地推理,进而推出与题目要求矛盾.从而得出n的取值范围,即得出答案.【解答】解:①假设n=5,(由抽屉原理知)第一行中至少有3个格子颜色相同.不妨设前3格为黑色(如图1).在这3个黑格下方可以分割为4个横着的3×1的长方形,若其中有一个中有2个黑格(如图2),则存在着图中的粗线长方形4个角上的小正方形都是黑格;所以这4个横着的3×1的长方形中,每个至多1个黑格.②假设这4个横着的3×1的长方形中,有两个对应格子颜色都一样(如图3),则一样存在图中的粗线长方形4个角上的小正方形都是白格;而3×1的长方形中至多1个黑格的只有如图4的这4种.如果这4种都存在的话如图5,则同样存在图中粗线长方形4个角上的小正方形都是白格;这均与题目要求的矛盾.所以,n<5,正整数n的最大值是4.而图6给出了n=4的一种构造.故选:B.二、填空题:(每小题10分,满分40分)7.(10分)在每个格子中填入1﹣6中的一个,使得每行、每列及每个2×3长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数“相约华杯”是4123 .【分析】如图:因为第三行存在1、3、4,所以A为2,5,6之一,而3与A的和是质数,所以A为2.在A所在的长方形中,还剩下1、4、5、6没有使用.而3与“相”的和是质数,所以“相”是4.“相”与“约”的和为质数,“约”为1,“约”与“月”的和为质数,“月”为6,剩下的C为5.第三行只剩下数字5,所以B为5;在B所在的长方形中,还剩下2、3、6没有使用.而4与“杯”的和是质数,所以“杯”为3,“杯”与”“华”的和为质数,所以“华”为2,剩下的D就是6;所以四位数“相约华杯”是4123,据此解答即可.【解答】解:如图:因为第三行存在1.、3、4,所以A为2,5,6之一,而3与A的和是质数,所以A为2.在A所在的长方形中,还剩下1、4、5、6没有使用.而3与“相”的和是质数,所以“相”是4.“相”与”“约”的和为质数,“约”为1,“约”与”“月”的和为质数,“月”为6,剩下的C为5.第三行只剩下数字5,所以B为5;在B所在的长方形中,还剩下2、3、6没有使用.而4与“杯”的和是质数,所以“杯”为3,“杯”与”“华”的和为质数,所以“华”为2,剩下的D就是6;所以四位数“相约华杯”是4123.故答案为:4123.8.(10分)整数n一共有10个因数,这些因数从小到大排列,第8个是.那么整数n的最大值是162 .【分析】由于整数的因数都是成对出现,则这10个约数必然是1、、3、、、、、、、n,立即可以填出1、2、3、、、、、、、n,也就是说n必然含有质因数2和3,然后结合因数个数定理可求解.【解答】解:根据分析可知10个因数分别为1、2、3、、、、、、、n,根据因数个数定理10=1×(9+1)=(1+1)×(4+1),由于含质因数2和3,则n应为21×34或24×31,其中21×34=162更大.故答案为:162.9.(10分)在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是15975 平方厘米,两块阴影部分的周长差是485 厘米.(π取3.14)【分析】(1)如图:扇形ABC的面积=①+②+③,扇形BCD的面积=②+③+④,正方形ABCD 的面积=①+②+③+④+⑤,所以扇形ABC的面积+扇形BCD的面积﹣正方形ABCD的面积=②+③﹣⑤,据此可求出两块阴影部分面积的差是多少;(2)连结BE、CE,因BC=BE=CE,所以三角形BCE是等边三角形,所以扇形BCE的圆心角是60°,扇形CED的圆心角是30°,据此可分别阴影部分的周长是多少,再相减即可.【解答】解:(1)S扇形ABC=①+②+③S扇形BCD=②+③+④S正方形ABCD=①+②+③+④+⑤,S扇形ABC+S扇形BCD﹣S正方形ABCD的=②+③﹣⑤③﹣⑤=S扇形ABC+S扇形BCD﹣S正方形ABCD的﹣②=3.14×3002÷4+3.14×3002÷4﹣300×300﹣3.14×(300÷2)2÷2=3.14×90000÷4+3.14×90000÷4﹣300×300﹣3.14×22500÷2=70650+70650﹣90000﹣35325=15975(平方厘米)(2)连结BE、CE阴影部分③的周长是×3.14×300×2+3.14×300÷2=628+471=1099(厘米)阴影部分⑤的周长是×3.14×300×2+300=314+300=614(厘米)1099﹣614=485(厘米)答:两块阴影部分的面积差是 15975平方厘米,两块阴影部分的周长差是485厘米.故答案为:15975,485.10.(10分)A地,B地,C地,D地依次分布在同一条公路上.甲,乙,丙三人分别从A地,B地,C地同时出发,匀速向D地行进.当甲在C地追上乙时,甲的速度减少40%,当甲追上丙时,甲的速度再次减少40%,甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少25%;乙追上丙后再行50米,三人同时到D地.已知乙出发时的速度是每分钟60米,那么甲出发时的速度是每分钟125 米,A、D两地间的路程是1880 米.【分析】由于同时到达,所以甲追上丙后二者速度相等,乙追上丙后二者速度相等.乙出发时的速度是每分钟60米,遇到丙后速度变为60×(1﹣25%)=45(米/分),所以丙的速度为45米/分,可以推知甲在追上丙后的速度变为45米/分,在追上乙后追上丙之前速度为45÷(1﹣40%)=75米/分,甲出发时的速度为75÷(1﹣40%)=125(米/分).甲在C地追上乙,设在此时起追上丙花了t分钟,则在乙追上丙时也追上了甲,此时甲走的路程为(75t+45×9)米,乙走的路程为60×(t+9)米,列方程为:75t+45×9=60×(t+9),解得t=9.由于此后又走了50米到达D地,所以CD的距离为75t+45×9+50=1130(米).由于甲从C地花了9分钟追上乙,所以此时丙到C的距离为75×9﹣45×9=270(米),即甲从A地到C地,丙走了270÷45=6(分钟),那么AC的距离为125×6=750(米),所以AD得距离为1130+750=1880(米).【解答】解:遇到丙后速度变为:60×(1﹣25%)=60×0.75=45(米/分)甲在追上乙后追上丙之前速度为:45÷(1﹣40%)=45÷0.6=75(米/分)甲出发时的速度为:75÷(1﹣40%)=75÷0.6=125(米/分)甲在C地追上乙,设在此时起追上丙花了t分钟,得:75t+45×9=60×(t+9)75t+405=60t+54015t=135t=9CD的距离为:75t+45×9+50=75×9+405+50=1130(米)甲从C地花了9分钟追上乙,所以此时丙到C的距离为:75×9﹣45×9=(75﹣45)×9=270(米)甲从A地到C地,丙走了:270÷45=6(分钟),那么AC的距离为:125×6=750(米),所以AD得距离为1130+750=1880(米).答:甲出发时的速度是每分钟125米,A、D两地间的路程是1880米.故答案为:125,1880.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 11:00:31;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第二十届华罗庚金杯少年数学邀请赛

第二十届华罗庚金杯少年数学邀请赛决赛试题解答(初二组)(时间:2015年 月 日)一、填空题 (每小题10分,共80分)1.21-,52-中较大的是______.【答案】21-.【解答】 估值判断21-较大.要证2152->-,即215+>,3225+>,只需证222>,即21>,显然成立,故21-较大. 解法二:12121-=+, 15252-=+,通过估值得2152+<+,所以2152->-,故21-较大.2.记13520132462014N =⨯⨯⨯⨯+⨯⨯⨯⨯,N 除以2015的余数等于______.【答案】0.【解答1】因为 2015=5×13×31,而1352013⨯⨯⨯⨯含有因数5,13,31,所以1352013⨯⨯⨯⨯被2015整除;又2462014⨯⨯⨯⨯中含有因数10=2×5,26=2×13,62=2×31,所以2462014⨯⨯⨯⨯也被2015整除.【解答2】由于nn n N ⨯=⨯+-+⨯⨯⨯⨯⨯=⨯+-⨯⨯---+⨯⨯⨯⨯=-⨯⨯---+⨯⨯⨯⨯=⨯⨯⨯⨯+⨯⨯⨯⨯=20152015])1(1[20135312015)1()2009)(2011)(2013(2013531)12015()20092015)(20112015)(20132015(2013531201464220135311007 其中n 为某整数,因此 N 是2015的倍数,所以余数是0. 3.如图,在矩形OABC 中,OA =6,OC =5.反比例函数xy 7=的图象装订线总分分别与AB 和BC 交于E 和F 点.那么三角形OEF 与三角形BEF 的面积差等于______. 【答案】30115. 【解答】由已知:)5,0(),5,6(),0,6(C B A ,)5,57(),67,6(F E所以75752167621=⨯⨯+⨯⨯=+∆∆OCF OAE s S6052952362321)576()675(21=⨯⨯=-⨯-⨯=∆BEF S 故 (30)OEF BEF OAE OCF BEF BEF S S S S S S ∆∆∆∆∆∆-=----=30115. 4. A 和n 都是自然数,且(7)(8)A n n =-+.如果A 是平方数,那么n 的最大可能值是______. 【解答1】设(7)n -和(8)n +的最大公约数是d ,则有).)((15)(,8;72222x y x y d x y d dy n dx n +-==-=+=-由此,我们有;56,7,8,15,1,1)1====+=-=n x y x y x y d ;8,1,4,5,3,1)2====+=-=n x y x y x y d )3d=3,y -x=1,y+x=5,y=3,x=2,n=19;4)d=5,y -x=1,y+x=3,y=2,x=1,n=8. 所以,n 的最大可能值是56.【解答2】 设2A x =, 则2221225(7)(8)56()24x A n n n n n ==-+=+-=+-,即22151()()22A n +=+.又知A 是一个完全平方数, 由勾股定理可知, x , 152, 12n +是某一个直角三角形的三边, 且 12n +是斜边, 欲使n 最大就是使x 最大, 由于它们围起一个直角三角形, 所以x n ≤, 取x n =, 则21514n -=, 所以56n =. 此解是整数满足题意,本题的解是56n =.5.用][x 表示不超过实数x 的最大整数,方程05][32=--x x 的所有根的乘积等于______.【答案】238. 【解答】21,013[] 5. 1.x x x x <->>-≥+∴≥-若210,123[] 5.0.0x x x x x -≤<≤<=+∴≥≥若当时,设 m x =][,m 为整数.则 5][32+=x x .由222222222[]35 0,1,2,3,4 (1)([]1)(1)35(1) 4 (2)12x x m m m m x x m m m m m ≥=⇒+≥⇒=<+=+⇒+<+⇒>+将()代入(),得到 3m =或4.当 3=m 时,1414532=⇒=+=x m x ;当 4=m 时,1717532=⇒=+=x m x .所以两根的乘积等于238.6.如图,直角三角形ABC 中,三角形ADF , 三角形BED 和三角形CFE 分别是以A ,B ,C 为顶点的等腰三角形,AC =17厘米,BC =15厘米,那么三角形DEF 的面积是______平方厘米.【答案】71117. 【解答】由勾股定理,AB=2217158-=(厘米),三角形ABC 的面积=60平方厘米. 设AD AF x ==厘米,BE BD y ==厘米,CF CE z ==厘米,由题目条件有:81517x y y z z x +=⎧⎪+=⎨⎪+=⎩, 解上述方程组,可得:5, 3, 12x y z ===.连接BF ,由于当2个三角形高相等时,其面积比等于底边比。
第20届华杯赛决赛试题B(小高组)试题及详解
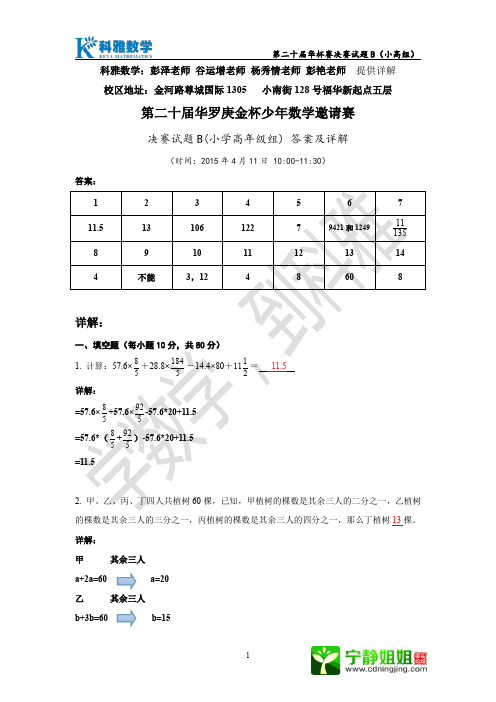
6. 由四个互不相同的非零数字组成的没有重复数字的所有四位数之和为 106656,则这些四 位数中最大的是 9421 ,最小的是 1249。 详解: 设这四个数字为 abcd 共 A 4 =4*3*2*1=24 个 以 a 开头=以 b 开头=以 c 开头=以 d 开头的个数=24/4=6 个
4
2
第二十届华杯赛决赛试题 B(小高组) 百位,十位,个位每个字母都出现 6 次 和为 b(a+b+c+d)*1111=106656 a+b+c+d=16 abcd 最大为 9421,最小为 1249
9421 和 1249
7
11 135
14 8
13 60
详解:
一、填空题(每小题 10 分,共 80 分) 1. 计算:57.6× +28.8× 详解:
8 92 =57.6× +57.6× -57.6*20+11.5 5 5 8 5 184 1 -14.4× 80+ 11 = 5 2
ห้องสมุดไป่ตู้
11.5
=57.6*( + =11.5
6
详解 ①
由上图所标份数可知
S M E D =
1 S ABCD 12
②易知:MB:CF=2:3
5
第二十届华杯赛决赛试题 B(小高组)
由上图所标份数可知:
S FCG =
所以
3 9 S ABCD = S ABCD 10 30 3 1 )=60cm 2 10 12
S ABCD =13/(
14. 设“一家之言”、“言扬行举”、“举世皆知”、“知行合一”四个成语中的每个汉字代表 11 个 连续的非零自然数中的一个,相同的汉字代表相同的数,不同的汉字代表不同的数。如 果每个成语中四个汉字所代表的数之和都是 21,则“行”可以代表的数最大是多少? 详解: 11 个连续自然数的和+言+一+行+知+举=21*4=84 11 个连续自然数的和是 11 的倍数,只能是 66 此时,言+一+行+知+举=84-66=18 要使行最大,言+一+知+举=1+2+3+4=10,此时行=8 所以“行”可以代表的数最大是 8,下面构造满足条件的情况: 一 4 言 1 举 2 知 3 家 7 扬 10 世 5 行 8 之 9 行 8 皆 11 合 6 言 1 举 2 知 3 一 4
第10~21届全国华罗庚金杯少年数学邀请赛试题

第十届“华罗庚金杯”少年数学邀请赛初赛试题1、2005年是中国伟大航海家郑和首次下西洋600周年,西班牙伟大航海家歌伦布首次远洋航行是在1492年。
问这两次远洋航行相差多少年?2、从冬至之日起每九天分为一段,依次称之为一九,二九,……,九九,2004年的冬至为12月21日,2005年的立春是2月4日。
问立春之日是几九的第几天?3、右下方是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形。
问这个直三棱柱的体积是多少?4、爸爸、妈妈、客人和我四人围着圆桌喝茶。
若只考虑每人左邻的情况,问共有多少种不同的入座方法?5、在奥运会的铁人三项比赛中,自行车比赛距离是长跑的4倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米。
求三项的总距离。
6、如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形。
其中最小的三角形顶点的个数(重合的顶点只计一次)依次为:3,6,10,15,21,……问这列数中的第9个是多少?7、一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示。
若用甲容器取水来注满乙容器,问:至少要注水多少次?8、100名学生参加社会实践,高年级学生两人一组,低年级学生三人一组,共有41组。
问:高、低年级学生各多少人?9、小鸣用48元钱按零售价买了若干练习本。
如果按批发价购买,每本便宜2元,恰好多买4本。
问:零售价每本多少元?10、不足100名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈。
问最多有多少名同学?11、输液100毫升,每分钟输2.5毫升。
请你观察第12分钟时吊瓶图像中的数据,回答整个吊瓶的容积是多少毫升?12、两条直线相交所成的锐角或直角称为两条直线的“夹角”。
现平面上有若干条直线,它们两两相交,并且“夹角”只能是30°,60°或90°。
【小中组】第20届华杯赛决赛

第二十届华罗庚金杯少年数学邀请赛决赛(A )卷【小中组】1. 森林里举行比赛,要派出狮子、老虎、豹子和大象中的两个动物去参加,如果派狮子去,那么也要派老虎取;如果不派豹子去,那么也不能派老虎去;要是豹子参加的话,大象可不愿意去,那么,最后能去参加比赛的是( )A. 狮子、老虎B.老虎、豹子C.狮子、豹子D.老虎、大象2. 小明有多张面额为1元,2元和5元的人民币,他想用其中不多于10张的人民币购买一只价格为18元的风筝,要求至少用两种面额的人民币,那么不同的付款方式有( )种. A.3 B.9 C.11 D.83. 如右图,在有1×1的正方形组成的网格中,写有2015四个数字(阴影部分),其边线要么是水平,要么是竖直的直线段,要么是连接1×1正方形相邻两边中点的线段,或者是1×1的正方形的对角线,则图中2015四个数字(阴影部分)的面积是( ) A.47 B.2147C.48D.21484. 新生入校后,合唱队,田径队,舞蹈队共招收学员100人,如果合唱队招收的人数比田径队多一倍,舞蹈队比合唱队多10人,那么舞蹈队招收( )人.(注:每人限加入一个队) A.30 B.42 C.46 D.525.一只旧钟的时针和分针每重合一次,需要经过标准时间66分钟,那么这只旧钟的24小时比标准时间的24小时()A.快12分B.快6分C.慢6分D.慢12分6.一次考试共有6道选择题,评分规则如下:每人先给6分,答对一题加4分,答错一题减一分,不答得0分,现有51名同学参加考试,那么,至少有()人得分相同.A.3B.4C.5D.67.计算:_____(=⨯+314-151000+++.⨯)-+-+)110(15(314360)360201201110)1000(8.角可以用它的两边上的两个大写字母和顶点的字母表示,(如右图的AOB∠表示,∠,也可以用0顶点处只有一个角时),下面的三角形ABC中,οBCO∠ACO=∠AOCABOBAO,则_____CAO∠CBO,,==110∠,∠∠∠=∠CBO.=9.张叔叔和李叔叔的年龄和是56岁,当张叔叔的年龄是李叔叔现在年龄的一半时,李叔叔当时的年龄是张叔叔现在的年龄,那么张叔叔现在有______岁.10.妈妈决定假期带小花驾车去10个城市旅游,小花查完地图后惊奇地发现:10个城市的任意三个城市之间或者都开通了高速公路,或者只有两个城市间没有开通高速路,那么这10个城市间至少开通了______条高速公路.(注:两个城市间最多只有一条高速公路)第二十届华罗庚金杯少年数学邀请赛决赛(A )卷参考答案【小中组】1.解析:【知识点】逻辑推理假设派狮子去,那么老虎也去,那么豹子就不去,这样老虎也不能去,矛盾,A 排除; 假设派狮子去,那么老虎也去,C 排除; 不派豹子去,那么也不能派老虎去,D 排除; 故只能派老虎和豹子去,答案选B 2.解析:【知识点】计数,枚举 付款方式有以下几种:3×5+1×2+1×1=18,3×5+1×3=18,2×5+4×2=18,2×5+3×2+2×1=18,2×5+2×2+4×1=18, 2×5+1×2+6×1=18,2×5+8×1=18,1×5+6×2+1×1=18,1×5+5×2+3×1=18,1×5+4×2+5×1, 8×2+2×1=18;总共11种,答案选C 。
2020年第二十届“无悔金杯”少年数学邀请赛决赛试卷(小高组b卷)

树
棵.
3.(10 分)某个三位数是 2 的倍数,加 1 是 3 的倍数,加 2 是 4 的倍数,加 3 是 5 的倍数,
加 4 是 6 的倍数,那么这个数最小为
.
4.(10 分)贝塔星球有七个国家,每个国家恰有四个友国和两个敌国,没有三个国家两两
都是敌国,对于一种这样的星球局势,共可以组成
个两两都是友国的三国联盟.
11.(10 分)两人进行乒乓球比赛,三局两胜制,每局比赛中,先得 11 分且对方少于 10 分 者胜,10 平后多得 2 分者胜.两人的得分总和都是 31 分,一人赢了第一局并且赢得了比 赛,那么第二局的比分共有多少种可能?
三、解答下列各题(每小题 15 分,共 30 分,要求写出详细过程) 12.(15 分)如图所示,点 M 是平行四边形 ABCD 的边 CD 上的一点,且 DM:MC=1:2,
x 的长方体(x,y 为整数),余下部分的体积为 120,求 x 和 y.
第 1页(共 12页)
10.(10 分)圆形跑道上等距插着 2015 面旗子,甲与乙同时同向从某个旗子出发,当甲与 乙再次同时回到出发点时,甲跑了 23 圈,乙跑了 13 圈.不算起始点旗子位置,则甲正 好在旗子位置追上乙多少次?
第 2页(共 12页)
2015 年第二十届“华罗庚金杯”少年数学邀请赛决赛试 卷(小高组 B 卷)
参考答案与试题解析
一、填空题(每小题 10 分,共 80 分) 1.(10 分)计算:57.6× +28.8× ﹣14.4×80+10 .
【分析】把算式中的 28.8× 变成 57.6× ,14.4×80 变成 57.6×20,然后根据乘法 的分配律简算. 【解答】解:57.6× +28.8× ﹣14.4×80+10
全国“华罗庚金杯”决赛试卷(五年级组)

全国“华罗庚金杯”少年数学邀请赛决赛试卷(五年级组)(时间:(时间: 10:00~11:30 )一、填空题(每题10分,共80分)1、计算:)195167248(66.698.19)75.4285412375.2247816(-´´´´+´= 2、一次数学竞赛满分是100分,某班前六名同学的平均得分是95.5分,排名第六的同学的得分是89分,每人得分是互不相同的整数,那么排名第三的同学至少得至少得 分。
分。
3、在下面的等式中,相同的字母表示同一数字,若abcd -dcba =□997,那么,那么 □ 中 应填应填 。
4、在梯形ABCD 中,上底长5厘米,下底长10厘米,20=D BOC S 平方厘米,则梯形ABCD 的面积是的面积是平方厘米。
平方厘米。
5、已知:10△3=14, 8△7=2, 43△141=,根据这几个算式找规律,如果,根据这几个算式找规律,如果85△x =1,那么x = . 6、右图中共有、右图中共有 个三角形。
个三角形。
7、有一个自然数,除以2余1,除以3余2,除以4余3,除以5余4,除以6余5,则这个数最小是,则这个数最小是 。
8、A 是乘积为2007的5个自然数之和,B 是乘积为2007的4个自然数之和。
那么A 、B 两数之差的最大值是两数之差的最大值是 。
装订线全国“华罗庚金杯”少年数学邀请赛决赛试题参考答案(五年级组)一、填空题(每题10分,共80分)分)题号题号 1 2 3 4 5 6 7 8 答案答案 3 96 2 45 8124 59 1781 1~8题答案提示:题答案提示:1、3 解:原式=÷øöçèæ-´´úûùêëé´÷øöçèæ++´÷øöçèæ+1951679666.698.19419285412819247816 =19528953419285441912819247881916´÷øöçèæ´+´+´+´=195289531515713138´÷øöçèæ+++=195289531952895´÷øöçèæ+=3 2、96 解:要想排名第三的同学得分尽量低,则其它几人的得分就要尽量的高,故第一名应为100分,第二名应为99分,因此第三、四、五名的总分为:分,因此第三、四、五名的总分为: 95.5×95.5×66-100-99-89=285(分) 故第三、四、五名的平均分为故第三、四、五名的平均分为 285÷3=95(分),因此第三名至少要得96分。
第二十届华杯初赛小学高级组C卷(含解析)

第二十届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级C 卷)(时间:2014 年 3 月 14 日 10:00〜11:00)一、选择题(每小题10分,满分60分•以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内 )『9 11 13 1517 )1 11120 一30 42 5672 丿 3 43.春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、 下的对话:甲:“丙、丁之中至少有1人捐了款” 乙:“丁、甲之中至多有1人捐了款” 丙:“你们3人中至少有2人捐了款” 丁: “你们3人中至多有2人捐了款” 己知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这 4位同学是()A .甲、乙 B.丙、丁 C.甲、丙D.乙、丁4.六位同学数学考试的平均成绩是 92.5分,他们的成绩是互不相同的整数,最高的那么按分数从高到低居第三位的同学的分数至少是().A. 94 B . 95 C. 96D . 975.如图,BH 是直角梯形ABCD 的高,E 为梯形对角线 AC 上一点;如果 DEH 、•汨EH 、厶BCH 的面积 依次为56、50、40,那么 CEH 的面积是(). A. 32B . 34C. 35D. 366.—个由边长为1的小正方形n n 的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的 4个用上的小正方形不全同色,那么正整数的最大值是(). A . 3 B. 4 C. 5D. 6二、填空题(每小题10分,满分40分.)7.在每个格子中填入1〜6中的一个,使得每行、每列及每个 2 3长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯 是 __________ .&整数n —共有10个约数,这些约数从小到大排列.笫 8个是-.那么整数的最大值是=(20 A. 42B. 43C.2.如图, 有一排间距相同但高度不等的小树,1 2 15— D. 1633这两条直线成45度角.最高的小树高2.8米,最低的小树高1.4米, 那么从左向右数第 4棵树的高度是()米.A . 2.6 B. 2.4 C. 2.2 D. 2.0丙、丁 4位同学有如99分,最低的76分,39.在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是 _____________ 厘米.(二取3.14)10. A 地、B 地、C 地依次分布在同一条公路上,甲、乙、丙三人分别从 A 地、B 地、C 地同时出发,匀 速向D 地行进.当甲在 C 地追上乙时,甲的速度减少 40% ;当甲追上丙时,甲的速度再次减少 40% ;甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少 25% ;如乙追上丙后再行 50米,三人同时到 D地•已知乙出发时的速度是每分钟 60米,那么甲出发时的速度是每分钟 _______ 米,A 、D 两地间的路程是 ___________ 米.第二十届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级C 卷)参考答案参考解析【考点】速算巧算【考点】等差数列 【难度】☆☆ 【答案】C【解析】如右图,AB =2.8-1.4 =1.4 (米),AC =1.4'7 3=0.6 (米)因此,第四高的小树为 2.8-0.6=2.2 (米).3. 春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、下的对话:甲:“丙、丁之中至少有1人捐了款”一、选择题 (每小题10分,满分60分•以下每题的四个选项中,仅有一个是正确的,请将表示正确答案 的英文字母写在每题的圆括号内『9 Il L 131 ———-—20 30 42d 卫56 72120一3 =(A. 42B. 43C.115 3D. 163【答案】Af 1【解析】原式=寸2.如图,有一排间距相同但高度不等的小树,IL 8 9树根成一条直线, 120 3 4 1竺=42 .3树顶也成一条直线.这两条直线成45度角.最高的小树高2.8米,最低的小树高1.4米, 那么从左向右数第 4棵树的高度是()米.A . 2.6B. 2.4C. 2.2D. 2.0丙、丁 4位同学有如乙:“丁、甲之中至多有1人捐了款”丙:“你们3人中至少有2人捐了款”丁:“你们3人中至多有2人捐了款”己知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这4位同学是()•A.甲、乙B.丙、丁C.甲、丙D.乙、丁【考点】逻辑推理【难度】☆☆☆【答案】D【解析】因为恰有2位同学捐了款,据丙所说知甲、乙、丁就至少2人捐款,所以丙没捐款;再据甲所说知丙、丁之中至少有1人捐了款,现在丙没捐款,所以丁一定捐款了;再据乙所说知丁、甲之中至多有1人捐了款,现在丁捐款了,所以甲一定没捐款;恰有2位同学捐了款,即恰有2位同学没捐款,现在甲、丙都没捐款,所以乙、丁都捐款了.4.六位同学数学考试的平均成绩是92.5分,他们的成绩是互不相同的整数,最高的99分,最低的76分,那么按分数从高到低居第三位的同学的分数至少是().A. 94B. 95C. 96D. 97【考点】最值问题【难度】☆☆☆【答案】B【解析】“至少”的含义是:第三位同学的得分若低于这个分数,不论其它同学得多少分,平均分都不会达到92.5分.要想使第三位同学的得分尽可能的少,应使第二位同学的得分尽可能的多;同时,第四位、第五位的同学得分与第4位同学的得分尽可能的接近.由此,可先求出第三位、第四位、第五位同学的平均分,再对三位同学的分数进行调整即可解决问题.由己知,第三、四、五三位同学的平均分是(92.5 6 -99 -76 -98)十3 = 282 “ 3 = 94 (分),故第三位同学的得分至少是94 •仁95 .5.如图,BH是直角梯形ABCD的高,E为梯形对角线AC上一点;如果DEH、•汨EH、厶BCH的面积依次为56、50、40,那么CEH的面积是().A. 32B. 34C. 35D. 36【考点】几何【难度】☆☆☆【答案】B【解析】因为S DEH ' S.AEH =S ABCD ' 2 = S ABC ~ S.BCE ' S AEB 所以S~ S DEH =56 ;所以,S .CEH = S BEH S BCH _ S BCE = 50 40- 56 = 34 .6.—个由边长为1的小正方形n n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个用上的小正方形不全同色,那么正整数的最大值是().A. 3B. 4C. 5D. 6【考点】最值问题【难度】☆☆☆☆【答案】B【解析】假设n =5 ,笫1行中至少有3个格子颜色相同,不妨设前3格为黑色(如图1).在这3个黑格下方可以分割为4个横着的3 1的长方形,若其中有一个中有2个黑格(如图2),则存在巷图中的粗线长方形4个角上的小正方形都是黑格;所以这4个横着的3 1的长方形中,每个至多1个黑格.假设这4个横着的3 1的长方形中,有两个对应格子颜色都一样(如图3),则一样存在图中的粗线长方形4个角上的小正方形都是白格.而3 1的长方形中至多1个黑格的只有如图4的这4种.如果这4种都存在的话(如图5),则同样存在图中的粗线长方形4个角上的小正方形都是白格•矛盾!所以n <5.而图6给出了n =4的一种构造•所以,正整数n的最大值是4 .二、填空题(每小题10分,满分40分.)7•在每个格子中填入1〜6中的一个,使得每行、每列及每个 2 3长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是___________ .【考点】数阵图【难度】☆☆☆☆【答案】4123【解析】如下左图,因为A 3为质数且A =4 ,所以A =2 ;因为“月”1为质数且“月”-2、4 ,所以“月” =6 ;从而C=5 ;因为“杯”4为质数且“杯”-1 ,所以“杯” =3 ;从而C =5 ;因为D 3为合数且D =2或6 ,所以D =6 ;从而“华” =2 ;因为“相”3为质数且“相”-2 ,所以“相” -4 ;因为B 4为合数且D =1或5 ,所以B =5 ;从而“约”=1 ;所以,相约华杯=4123(如下中图)•实际上其它格子中的数也能唯一确定(如下右图)&整数n—共有10个约数,这些约数从小到大排列•笫8个是-•那么整数的最大值是3 ----------【考点】数论【难度】☆☆☆【答案】162【解析】n有10个约数,由于第8个是-,而第10个必然是n ,所以第9个只能是-•所以n有质因子2和3 23 •所以n可能是24 3或者34 2 •而最大是34 2 =162 .9•在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是_ 平方厘米,两块阴影部分的周长差是_____________ 厘米.(二取3.14)【考点】几何基本概念【难度】☆☆☆【答案】①15975 :②485 .【解析】①QS阴影ABE -S l影CDE =S扇形ABD S扇形ABC —SE方形ABCD —S半圆AB②因为ABE为等边三角形,所以∙EAB =. E B A=60 ,从而∙DAE =. CBE=30 ;阴影CDE的周长=弧CE 弧DE CD =2二300^12 2 300 =100二300 ;阴影ABE的周长二弧AE •弧BE •弧AB =2二300-:-6 2 • 300-:-2 = 350二;所以,的周长差=350二_(100二300)=250二_300 : 485 .10. A地、B地、C地依次分布在同一条公路上,甲、乙、丙三人分别从A地、B地、C地同时出发,匀速向D地行进.当甲在C地追上乙时,甲的速度减少40% ;当甲追上丙时,甲的速度再次减少40% ;甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少25% ;如乙追上丙后再行50米,三人同时到D地•已知乙出发时的速度是每分钟60米,那么甲出发时的速度是每分钟________ 米,A、D两地间的路程是 __________ 米.【考点】行程问题【难度】☆☆☆☆【答案】①125 :②1880 .【解析】①因为三人同时到D地,所以甲、乙最后的速度和丙相同;所以丙速为60 (1 -25%)=45(米/分);甲减速一次后的速度为45 “(1 - 40%)=75 (米/分),甲出发时的速度为75 “(1 -40%)=125(米/分).②如下图,设甲在E地追上丙,乙在F地追上丙,因为甲、乙出发时的速度比为125:60 =25:12 , 所以AB:BC =25:12 ;设AC为25份,则BC为12份;因为乙、丙出发时的速度比为60: 45=4:3 ,所以BF :CF =4:3 ,从而CF 为12“(4-3) 3=36 份,AF 为25 *36=61 份.因为甲减速一次后与丙的速度比为75: 45 = 5:3 ,而甲原速行AC这25份时,相当于以75米/分行25 60% =15份;所以CE=15"(5-3) 3=22.5 份,从而EF =36-22.5 =13.5 份;而EF是丙9分钟所行的路程,为45 9 =405(米),所以每份405 "13.5 =30(米),从而AF =30 61 H 1830 (米),所以AD =1830 50 -1880 (米).。
华罗庚金杯赛数学试题与答案[第1至15届]
![华罗庚金杯赛数学试题与答案[第1至15届]](https://img.taocdn.com/s3/m/be6d1522bb68a98271fefabf.png)
华罗庚金杯赛数学试题与答案[第1至15届]目录第1届华罗庚金杯赛数学试题与答案 (1)第2届华罗庚金杯赛数学试题与答案 (6)第3届华罗庚金杯赛数学试题与答案 (14)第4届华罗庚金杯赛数学试题与答案 (21)第5届华罗庚金杯赛数学试题与答案 (26)第6届华罗庚金杯赛数学试题与答案 (31)第7届华杯赛初赛试题及解答 (38)第8届华杯赛初赛试题及解答 (41)第9届华杯赛初赛试题及解答 (45)第10届华杯赛初赛试题及解答 (49)第11届华杯赛初赛试题及解答 (53)第12届华杯赛初赛试题及解答 (60)第13届华杯赛少年邀请赛初赛摸拟试卷 (64)第14届华罗庚金杯少年数学邀请赛 (66)第15届华杯赛决赛真题及答案解析 (68)第1届华罗庚金杯赛数学试题与答案1、甲班和乙班共83人,乙班和丙班共86人,丙班和丁班共88人。
问甲班和丁班共多少人?2、一笔奖金分一等奖、二等奖、三等奖,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍。
如果评一、二、三等奖各两人,那么每个一等奖的奖金是308元;如果一个一等奖,两个二等奖,三个三等奖,那么一等奖的奖金是多少元?3、一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩。
问另一个长方形的面积是多少亩?4、在一条公路上,每隔一百公里有一个仓库,共有五个仓库。
一号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。
现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输一公里需要0.5元的运费,那么最少要花多少运费才行?5、有一个数,除以3余数是2,除以4余数是1。
问这个数除以12余数是几?6、四个一样的长方形和一个小的正方形(如图)拼成了一个大正方形。
大正方形的面积是49平方米,小正方形的面积是4平方米。
问长方形的短边长度是几米?7、有两条纸带,一条长21厘米,一条长13厘米,把两条纸带剪下同样长的一段以后,发现短纸带剩下的长度是长纸带的长度的八分之十三。
