数值分析模拟题3
半导体器件模拟及数值分析(PDF)

主要内容2.12.22.32.1 器件模拟的基本方程组2.1.3 载流子输运的基本方程2.1.3.2小尺寸半导体器件的载流子输运方程(a) (b)图2.1 半导体中的载流子过冲. (a) GaAs材料, (b) Si材料2.1 器件模拟的基本方程组2.1.6光波导方程由Maxwell 方程组同样可以导出在半导体材料中传输的光波的电场分量E 所满足的方程:式中n 为材料的折射率,k 0 =2π/λ,λ是波长。
对于沿z 方向传播的波,式中β是波沿z 方向的传播常数,可得到Helmholtz 方程为,2022=+∇E E k n )(exp ),,(),,,(z t j E E E t z y x z y x βω−=E 222/,/ββ−=∂∂−=∂∂z j z 所以,)(22022=−+∇E E βk n T 式中,22222//y x T ∂∂+∂∂=∇2.3 半导体器件的分级模拟2.3.1 问题目的提出判断一个半导体器件模拟软件优劣的指标是功能全、精度高、速度快和便于用户使用。
功能全主要指能处理问题面广,便于用户使用则主要指程序输入参数形式简单,并以交互或对话方式工作。
实际开发半导体器件模拟软件时要考虑这两点,但这不是衡量半导体器件模拟方法本身优劣的指标。
衡量半导体器件模拟方法优劣的指标是速度快、精度高。
在半导体器件的计算机模拟中,除了从指标要求出发选取好的方法外,在给定精度的条件下,还经常使用分级模拟技术以减少计算时间和提高计算速度。
2.3 半导体器件的分级模拟2.3.3 分级模拟的意义随着工件条件的变化,模型方程的复杂性越来越高,相应地,模拟的复杂性也越来越高。
对于复杂的模拟问题,往往需要采用分级模拟的方法,该方法包括两点:(1)根据具体的工作条件,选用级别较低的模型方程,以在保证精度的条件下大大减少计算时间。
(2)利用低一级的解作为初值。
由于低一级的解是本级的很好近似,这样做将有效减少计算时间。
数值分析模拟试卷1,2,3

数值分析模拟试卷1一、填空(共30分,每空3分) 1 设⎪⎪⎭⎫⎝⎛-=1511A ,则A 的谱半径=)(a ρ______,A 的条件数)(1A cond =________.2 设,2,1,0,,53)(2==+=k kh x xx f k ,则],,[21++n n n x x x f =________,],,[321+++n n n n x x x x f ,=________.3 设⎪⎩⎪⎨⎧≤≤-++≤≤+=21,1210,)(2323x cx bx x x x x x S ,是以0,1,2为节点的三次样条函数,则b=________,c=________.4 设∞=0)]([k k x q 是区间[0,1]上权函数为x x =)(ρ的最高项系数为1的正交多项式族,其中1)(0=x q ,则⎰=10)(dx x xq k ________,=)(2x q ________.5 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=11001aaa a A ,当∈a ________时,必有分解式,其中L 为下三角阵,当其对角线元素)3,2,1(=i L ii 满足条件________时,这种分解是唯一的.二、(14分)设49,1,41,)(21023====x x x x x f ,(1)试求)(x f 在]49,41[上的三次Hermite 插值多项式)(x H 使满足2,1,0),()(==i x f x H i i ,)()(11x f x H '='.(2)写出余项)()()(x H x f x R -=的表达式.三、(14分)设有解方程0cos 2312=+-x x 的迭代公式为n n x x cos 3241+=+,(1) 证明R x ∈∀0均有∙∞→=x x n x lim (∙x 为方程的根);(2) 取40=x ,用此迭代法求方程根的近似值,误差不超过,列出各次迭代值;(3)此迭代的收敛阶是多少?证明你的结论.四、(16分) 试确定常数A ,B ,C 和,使得数值积分公式有尽可能高的代数精度. 试问所得的数值积分公式代数精度是多少?它是否为Gauss 型的?五、(15分) 设有常微分方程的初值问题⎩⎨⎧=='00)(),(y x y y x f y ,试用Taylor 展开原理构造形如)()(11011--++++=n n n n n f f h y y y ββα的方法,使其具有二阶精度,并推导其局部截断误差主项.六、(15分) 已知方程组b Ax =,其中⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=21,13.021b A , (1) 试讨论用Jacobi 迭代法和Gauss-Seidel 迭代法求解此方程组的收敛性. (2) 若有迭代公式)()()()1(b Axa xxk k k ++=+,试确定一个的取值范围,在这个范围内任取一个值均能使该迭代公式收敛. 七、(8分) 方程组,其中,A 是对称的且非奇异.设A 有误差,则原方程组变化为,其中为解的误差向量,试证明.其中1λ和2λ分别为A 的按模最大和最小的特征值.数值分析模拟试卷2填空题(每空2分,共30分)1. 近似数231.0=*x 关于真值229.0=x 有____________位有效数字; 2. 设)(x f 可微,求方程)(x f x =根的牛顿迭代格式是_______________________________________________;3. 对1)(3++=x x x f ,差商=]3,2,1,0[f _________________;=]4,3,2,1,0[f ________;4. 已知⎪⎪⎭⎫⎝⎛-='-=1223,)3,2(A x ,则=∞||||Ax ________________,=)(1A Cond______________________ ;5. 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根所在区间为_________,进行二步后根所在区间为_________________;6. 求解线性方程组⎪⎩⎪⎨⎧=+=+04511532121x x x x 的高斯—赛德尔迭代格式为_______________________________________;该迭代格式迭代矩阵的谱半径=)(G ρ_______________;7. 为使两点数值求积公式:⎰-+≈111100)()()(x f x f dx x f ωω具有最高的代数精确度,其求积节点应为=0x _____ , =1x _____,==10ωω__________. 8. 求积公式)]2()1([23)(30f f dx x f +≈⎰是否是插值型的__________,其代数精度为___________。
17Game游戏策划数值分析员招聘笔试试题

17Game 游戏筹划数值分析员招聘笔试试题17Game 游戏筹划-数值分析员招聘试题:一、ARPG游戏理论题目01. 1点体质=3点HP,1点力量=1点HP。
请问一个具有17点体质和28点力量的角色,有多少HP?〔2分〕02. 某款游戏中,设定对怪物造成多少比例的伤害,那么获得相应比例的EXP。
现设定山丘巨人具有10000点生命,200点EXP。
一个勇士手持利刃,一刀砍掉了山丘巨人500的生命,请问他获得多少EXP?〔5分〕03. DiabloII中,野蛮人的旋风每等级提升的伤害如下表所示,请推算数值的关系:〔8分〕 Level 1 2 3 4 5 6 7 8 9 10 Damage % -50 -42 -34 -26 -18 -10 -2 +6 +14 +2204. DnD(龙与地下城)系统中,判断命中时投掷一个20面的骰子(随机得到1~20的数字),当得到的数字大于或等于攻击目标的AC(防御等级)时,那么表示命中了目标。
那么,攻击AC=16的目标,命中几率是多少?(结果可用分数表示)〔9分〕05. DiabloII的物理攻击命中公式为:Chance to Hit for Melee Attacks: 100 * AR / (AR + DR) * 2 * alvl / (alvl + dlvl)。
其中AR = Attack Rating(命中值); DR = Defense Rating(闪躲值); alvl = Level of Attacker; dlvl = Level of Defender。
现假定AR的取值范围是:100~1000;DR的取值范围是50~500;level的取值范围是1~99。
请计算物理攻击命中几率结果的取值范围?(结果可用分数表示)〔10分〕06. ARPG中角色常用属性中根本都有力量、敏捷、智慧。
请说明你认为它们所具有的含义。
〔12分〕07. 列举5个ARPG中的属性(比方:命中、闪躲、伤害、防御),并请说明你认为它们所具有的含义。
数值分析原理习题答案

数值分析原理习题答案数值分析原理习题答案【篇一:数值分析习题】学号班级习题主要考察点:有效数字的计算、计算方法的比较选择、误差和误差限的计算。
1 若误差限为0.5?10,那么近似数0.003400有几位有效数字?(有效数字的计算)2 ??3.14159?具有4位有效数字的近似值是多少?(有效数字的计算)3 已知a?1.2031,b?0.978是经过四舍五入后得到的近似值,问a?b,a?b有几位有效数字?(有效数字的计算)4 设x?0,x的相对误差为?,求lnx的误差和相对误差?(误差的计算)**5测得某圆柱体高度h的值为h?20cm,底面半径r的值为r?5cm,已知5|h?h*|?0.2cm,|r?r*|?0.1cm,求圆柱体体积v??rh的绝对误差限与相对误差限。
(误差限的计算)6 设x的相对误差为a%,求y?xn的相对误差。
(函数误差的计算)7计算球的体积,为了使体积的相对误差限为1%,问度量半径r时允许的相对误差限为多大?(函数误差的计算)128 设in?e1nxx?edx,求证: 0(1)in?1?nin?1(n?0,1,2?)(2)利用(1)中的公式正向递推计算时误差逐步增大;反向递推计算时误差逐步减小。
(计算方法的比较选择)第二章插值法姓名学号班级习题主要考察点:拉格朗日插值法的构造,均差的计算,牛顿插值和埃尔米特插值构造,插值余项的计算和应用。
1 已知f(?1)?2,f(1)?1,f(2)?1,求f(x)的拉氏插值多项式。
(拉格朗日插值)2 已知y?x,x0?4,x1?9,用线性插值求7的近似值。
(拉格朗日线性插值)3 若xj(j?0,1,...n)为互异节点,且有lj(x)?试证明(x?x0)(x?x1)?(x?xj?1)(x?xj?1)?(x?xn)(xj?x0)(xj?x1)?(xj?xj?1)(xj?xj?1)?(xj?xn)xlj?0nkjj(拉格朗日插值基函数的性质) (x)?xk(k?0,1,...n)。
岩土工程数值分析试卷试题及参考(附答案)

岩土工程数值分析试题一、简答题(40分)1.简述梁单元、杆单元、连续梁单元、平面三角形常量单元和四边形等参单元的特点(10分)。
答:1)梁单元是由两个节点组成,每一个节点都具有三个方向的线性移动位移和三个方向的旋转位移,因而每个节点具有6个自由度,梁单元具有拉,压,剪,弯,扭的变形刚度。
计算理论成熟,建模方便,计算量小,在工程结构有限元分析中得到广泛的应用,适用于各种截面形式的杆件分析。
2)由有限个构件以一定方式连接起来所形成的结构,在同一平面内的杆系结构,其所受的外力作用线位于该平面内,在杆系中,每一个杆件可视为一个单元,每个单元的端点成为结点。
3)对于每跨各自等截面的连续梁,以每跨为一个单元。
结点编号和单元编号一般是从连续梁的左端顺序编到右端。
由于连续梁各单元的轴线方向一致,各单元坐标系与结构坐标系的方向相同,因此在矩阵位移法的计算过程中无须进行坐标变换,在单元坐标系和结构坐标系中单元刚度矩阵的表达式是相同的。
4) 平面三角形单元具有适应性强的优点,较容易进行网络划分和逼近边界形状,应用比较灵活。
其缺点是它的位移模式是线性函数,单元应力和应变都是常数,精度不够理想。
5) 四边形等参单元能更好地反映物体内的应力变化,适应曲线边界,常使用于弹性力学平平面问题的分析。
八结点单元一共有16个已知的结点位移分量。
2.除有限单元法外,岩土工程常用到哪些数值方法,并对比其优缺点(10分)。
答:岩土工程常用的数值方法包括:有限差分法、边界元法、离散元法、颗粒元法、不连续变形分析法、流形元法、模糊数学方法、概率论与可靠度分析方法、灰色系统理论、人工智能与专家系统、神经网络方法、时间序列分析法。
有限单元法的优缺点:有限单元法的理论基础是虚功原理和基于最小势能的变分原理,它将研究域离散化,对位移场和应力场的连续性进行物理近似。
有限单元法适用性广泛,从理论上讲对任何问题都适用,但计算速度相对较慢。
即,物理概念清晰、灵活、通用、计算速度叫慢。
数值分析课程第五版课后习题答案(李庆扬等)

数值分析课程第五版课后习题答案(李庆扬等)数值分析课程第五版课后习题答案(李庆扬等)第一章:数值分析导论1. 解答:数值分析是一门研究如何使用计算机来解决数学问题的学科。
它包括了从数学理论到计算实现的一系列技术。
数值分析的目标是通过近似的方式求解数学问题,其结果可能不是完全精确的,但是能够满足工程或科学应用的要求。
2. 解答:数值分析在实际应用中起着重要的作用。
它可以用于求解复杂的数学方程、计算机模拟及建模、数据的统计分析等等。
数值分析是科学计算和工程计算的基础,对许多领域都有着广泛的应用,如物理学、经济学、生物学等。
3. 解答:数值方法指的是使用数值计算的方式来求解数学问题。
与解析方法相比,数值方法一般更加灵活和高效,可以处理一些复杂的数学问题。
数值方法主要包括了数值逼近、插值、数值积分、数值微分、线性方程组的求解、非线性方程的求根等。
4. 解答:计算误差是指数值计算结果与精确解之间的差异。
在数值计算中,由于计算机的有限精度以及数值计算方法本身的近似性等因素,都会导致计算误差的产生。
计算误差可以分为截断误差和舍入误差两种。
第二章:数值误差分析1. 解答:绝对误差是指实际值与精确值之间的差异。
例如,对于一个计算出的数值近似解x和精确解x_0,其绝对误差为| x - x_0 |。
绝对误差可以衡量数值近似解的精确程度,通常被用作评估数值计算方法的好坏。
2. 解答:相对误差是指绝对误差与精确解之间的比值。
对于一个计算出的数值近似解x和精确解x_0,其相对误差为| (x - x_0) / x_0 |。
相对误差可以衡量数值近似解相对于精确解的精确度,常用于评估数值计算方法的收敛速度。
3. 解答:舍入误差是由于计算机的有限精度而引起的误差。
计算机中使用的浮点数系统只能表示有限的小数位数,因此在进行数值计算过程中,舍入误差不可避免地会产生。
舍入误差会导致计算结果与精确结果之间存在差异。
4. 解答:误差限度是指对于给定的数值计算问题,所能容忍的误差范围。
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
强夯加固饱和地基土的数值模拟_周世良

Δ Δ N=
Ni 0
0 Ni
Nj 0
0 Nj
Nm 0
0 Nm
… …
为形函数
矩阵,i,j,m……为单元结点。
矩阵B軒 中BL0和BL1均是与△ae无关的矩阵,且 B 在 L0 形式上与小变形的应变转换矩阵相同,而矩 阵BL1则反映了增量应变的初始位移效应。
对于轴对称问题,式 (13) 中的L,A和G表达
(2)
克希荷夫应力张量的物质导数S觶 ij和屈斯笛尔
塄(T)
应力率 τ ij满足如下关系式[3]:
S觶 ij= J
坠Xi 坠xp
坠Xj 坠xq
塄(T)
τ qp
(3)
由式 (2) 和式 (3) 可得:
S觶 ij= J
坠Xi 坠Xj 坠xp 坠xq
[DpqklVkl+τpqVkk-τpkVkq-τqkVkp]
·142·
水运工程
2009 年
式如下:
坠 坠r
1 r L= 0
1·坠 2 坠z
坠
坠r 0
1
r
0
坠
,G=
坠 坠z
坠z 0
1·坠 2 坠r
0
0
0
0 N, 坠 坠r 坠 坠z
坠u 坠r
00
坠ω 坠r
0
0
A=
1 2
0
u r
0
0 坠u
0 0
0 坠ω
坠z
坠z
12·坠坠uz 0
1 2
·坠坠ur
1 2
·坠坠ωz
1 2
(21b)
u咬(s 0)=u咬 0s, u咬(f 0)=u咬 0f
(21c)
西安电子科技大学数值分析
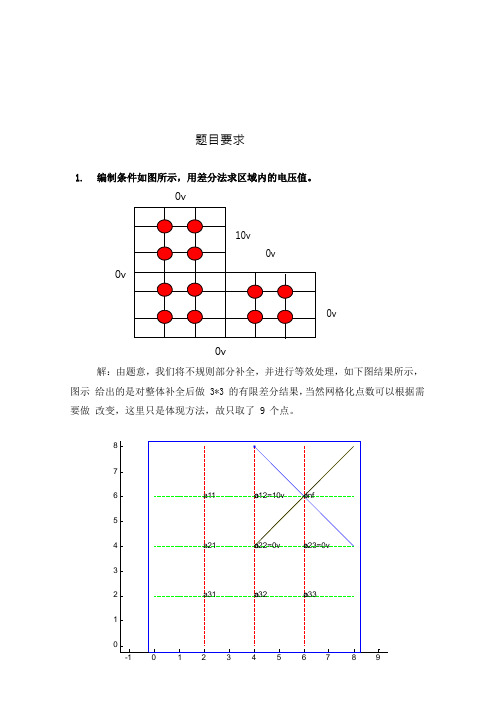
题目要求1. 编制条件如图所示,用差分法求区域内的电压值。
0v10v0v0v0v0v解:由题意,我们将不规则部分补全,并进行等效处理,如下图结果所示,图示给出的是对整体补全后做3*3 的有限差分结果,当然网格化点数可以根据需要做改变,这里只是体现方法,故只取了 9 个点。
876 a11o a12=10v o-inf54 a21o a22=0v o a23=0v32 a31o a32o a331-1 0 1 2 3 4 5 6 7 8 9根据拉普拉斯 5 点差分原理,可知得到关于电压变量 a(i, j 1, 2, 3) 的i , j方程如下:4a 1,1 a 2,110;a 1,1 4a 2,1 a 3,1 0; a 2,1 4a 3,1 a 3,2 0; a 3,1 4a 3,2 a 3,3 0; a 3,2 4a 3,30.4 1 0 0 0 10 1 4 1 00 0 写成矩阵的形式: Ax b ; 其中, A 0 1 4 10 , b 0 。
0 0 1 41 0编写程序可以求得0 01 4a , a , a , a , a , 2.6790.7180.1920.0513 0.0132. 在区域一边有个源,边界为 PML 边界,用 FDTD 法求所研究区域的场分布。
建模说明:二维 TE 波在空间传播,采用 PML 边界吸收,点辐射源验证。
FDTD 基本差分方程Yee 采用矩形网格进行空间离散,将每个节点进行编号,节点的编号和其空 间坐标位置按照下面的方式对应起来()(),,,,i j k i x j y k z =∆∆∆ (2-1) 而该点的任意函数()x,y,z,F t 在时刻n t ∆的值可以表示为:()(),,,,,n F i j k F i x j y k z n t =∆∆∆∆ (2-2)式中x ∆、y ∆、z ∆分别为沿,,x y z 方向上离散的空间步长,t ∆是时间步长。
数值分析模拟题

1. (10分)利用Gauss-Legendre 求积公式 ⎰-++-≈11)7746.0(5556.0)0(8889.0)7746.0(5556.0)(f f f dx x f 导出求积分3()f x dx-⎰的三点高斯型求积公式。
2. (15分)写出求解线性代数方程组 123121322531272x x x x x x x -+=⎧⎪-+=-⎨⎪+=⎩的Gauss-Seidel 迭代格式,并分析此格式的敛散性。
3. (15分)设矩阵21011000201010A ⎡⎤⎢⎥⎢⎥=⎢⎥⎥⎥⎦, (1)试计算||||A ∞。
(2)用Householder 变换阵H 将A 相似约化为上Hessenberg 阵,即HAH 为上Hessenberg 阵。
4. (10分) 求关于点集{}1,2,3,4的正交多项式{}012(),(),()x x x ϕϕϕ。
5. (10分)用最小二乘法确定一条经过原点的二次曲线,使之拟合下列数据1.02.03.04.00.8 1.5 1.8 2.0i ix y ⎧⎨⎩6. (20分)给出数据点: 013419156i i x y =⎧⎨=⎩(1)用012,,x x x 构造二次Lagrange 插值多项式2()L x ,并计算 1.5x =的近似值2(1.5)L 。
(2)用123,,x x x 构造二次Newton 插值多项式2()N x ,并计算 1.5x =的近似值2(1.5)N 。
(3)用事后误差估计方法估计2(1.5)L 、2(1.5)N 的误差。
7.(10分) 设矩阵A 可逆,A δ为A 的误差矩阵,证明:当11A Aδ-<时,A A δ+也可逆。
8.(10分)设()f x 四阶连续可导,0,0,1,2.i x x ih i =+=试建立如下数值微分公式 ''01212()2()()()f x f x f x f x h -+≈,并推导该公式的截断误差。
建筑朝向对室内自然通风影响的数值模拟

通风可以改善居住建筑的室内空气条件,保护人们的身体健康。
自然通风是利用自然风动力和存在的温差的空气循环动力进行通风,不需要消耗机械动力,是一种经济的通风方式[1]。
建筑室内的气流分布、温度分布可通过合理的自然通风组织得到有效调节,较大的提高室内热环境的满意度。
自然通风作为一种被动式的节能策略,可以在不消耗能源的情况下降低室内温度,降低建筑能耗,同时更大限度地为人们提供健康舒适的室内环境,符合绿色建筑的发展趋势。
自然通风的应用效果较大程度上受制于建筑的平面布局、朝向等,主要由于其实现是一种依赖于建筑设计的被动式方法[2]。
本文拟通过对建筑的不同朝向室内自然通风的数值模拟,得出建筑设计朝向与室内自然通风及室内热舒适性的相互关系,为建筑师在对如何加强室内自然通风及室内实际通风效果的设计上提供数据支撑。
1研究对象研究对象为南京市的1栋层高为3.00m,总层数为30层的居住建筑。
本文选取其中的一个户型进行研究,具体户型如图1所示,套内面积为122.92m2。
2工况分析利用风玫瑰图[3],给出频率最多的风速风向情况,确定为当地平均风速,作为模拟区域的输入条件。
确定南京市过建筑朝向对室内自然通风影响的数值模拟夏俊,徐丹(江苏省建筑设计研究院有限公司,江苏南京210019)[摘要]建筑朝向设计对于室内自然通风有很大影响,因建筑设计的不同,自然通风有多种形式如:被动风井通风、穿堂风、风塔、拔风井等。
建筑及气候特点的合理设计,能更多地利用自然通风来改善室内的热舒适环境。
为了比较建筑设计朝向变化与室内自然通风效果的相互关系,以南京市某居住小区为例,利用数值分析的方法,对该小区内某一户型在不同建筑朝向的设计情况下,对其进行室内速度场、温度场和室内空气龄的评价分析。
通过对比分析结果,室内产生的最大气流随着建筑朝向的改变从1.5m/s提高到2.5m/s,室内的自然通风效果得到较大的改善;室内换气次数可由原20次/h~36次/h提高到40次/h~60次/h,通风效果更好。
《数值分析》课程论文参考选题

《数值分析》课程论文参考选题1.插值与拟合方法在×××问题解决中的应用论文提纲: 1引言(提出问题)、2插值与拟合方法介绍(知识准备)、3×××问题的插值模型(必须附相应的MATLAB求解程序)、4×××问题的拟合模型(必须附相应的MATLAB求解程序)、5检验与分析2.几种插值方法在解决×××问题中的比较研究论文提纲: 与上面的类似3.高次插值逼近效果分析论文提纲: 1引言(提出问题)、2插值方法介绍(知识准备)、3应用实例一(必须附相应的MATLAB求解程序,无龙格现象)、4应用实例二(必须附相应的MATLAB求解程序,有龙格现象)、5结果分析4.Romberg算法及其MATLAB实现与应用论文提纲: 1引言(提出问题)、2 Romberg算法及其MA TLAB程序、3应用实例一(必须附相应的MATLAB求解程序)、4应用实例二(必须附相应的MATLAB求解程序)、5结果分析5.常见数值求积公式的MATLAB实现与应用论文提纲: 1引言(提出问题)、2 常见数值求积公式及其MA TLAB程序、3应用实例一(必须附相应的MA TLAB求解程序)、4应用实例二(必须附相应的MA TLAB求解程序)、5结果分析6.Richardson外推加速法在数值微分公式设计中的应用论文提纲: 1 Richardson外推加速法介绍、2 某具体的数值微分公式的Richardson外推加速与MA TLAB实现(必须推出相应的算法公式,并附MATLAB通用程序)、3应用举例7.解线性方程组的迭代方法介绍及数值实验8.解非线性方程的几种迭代法的收敛性分析与数值实验9.用NEWTON迭代法解代数方程的算法设计及MATLAB实现10.解非线性方程的迭代函数的求法与应用11.解非线性方程的迭代方法的加速技巧与应用12.常微分方程数值求解方法的MA TLAB与应用13.一类×××模型(微分方程模型)的数值模拟研究14.×××算法的改进与数值实验1 / 1。
数值分析模拟试题(XAUT)(15套)

模拟试题一一、填空(每小题3分,共30分)1. 设2.40315x *=是真值 2.40194x =的近似值,则x *有 位有效数字。
2. 牛顿—柯特斯求积公式的系数和()0nn k k c =∑ 。
3 已知 12,()_________01A A ∞⎛⎫== ⎪⎝⎭则条件数cond 。
4 若332x -1x 1S(x)=1(x -1)+a(x -1)+b(x -1)+c 1x 220⎧≤≤⎪⎨≤≤⎪⎩是三次样条函数,则a =_______, b =______, c =______.5 以n + 1个 整 数 点k ( k =0,1,2,…,n ) 为 节 点 的 Lagrange 插 值 基函 数 为()k l x ( k =0,1,2,…,n ),则 nk k=0kl (x)=_____.∑6 序列{}n n=0y ∞满足递推关系:n n-1y =10y -1,(n =1,2,...),若0y 有误差, 这个计算过程____________稳定.7 若42f(x)=2x +x -3, 则f[1,2,3,4,5,6]=_____. 8 数值求积公式10311f(x)dx f()+f(1)434=⎰的代数精度是____________. 9.当x很大时,为防止损失有效数字,应该使 .10.已知A =⎢⎢⎢⎣⎡761 852 ⎥⎥⎥⎦⎤943,x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111,则=1Ax . 二、(10分) 用最小二乘法确定一条经过原点的二次曲线,使之拟合下列数据x 0 1.0 2.0 3.0 y 0.2 0.5 1.0 1.2三、(10分)2011A =050,b =3,203-1⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭用迭代公式(1)()()()(0,1,2,)k k k x x Ax b k α+=+-=求解,Ax b =问取什么实数α可使迭代收敛,什么α可使迭代收敛最快。
四、(10)设()f x 四阶连续可导,0,0,1,2,,i x x ih i =+= 试建立如下数值微分公式''01212()2()()()f x f x f x f x h -+≈并推导该公式的截断误差。
高速公路路基沉降数值模拟分析

高速公路路基沉降数值模拟分析摘要:目前,随着高速公路的快速发展,路基沉降问题已成为高速公路施工技术部分的重要难题,一旦路基出现不均匀沉降,甚至超过规范要求,都会造成巨大的损失。
本文以某高速公路填方路段进行现场路基沉降试验观测,运用Marc软件进行数值模拟分析路基沉降规律,从而确定高填方路基沉降主要由初始沉降、固结沉降和次固结沉降组成,随时间的推移,路基最终沉降量趋于一个定值。
关键词:路基沉降;现场试验;沉降组成;数值模拟在经济快速发展的当今,高速公路建设显得尤为重要。
然而在修建高速公路的同时,路基问题也相应的出现,如路基裂缝、路基边坡滑塌、冲刷严重等路基灾害现象。
影响高速公路使用质量的重要因素主要有路基稳定性和沉降,而路基沉降处理措施的合理性直接影响到施工的进度和质量。
因此,对路基沉降的研究有一定的现实意义。
1 路基沉降计算方法目前,路基沉降计算方法主要有:有限元分析法、分层总和法、沉降预估法和应力路径法等。
本文主要介绍有限元分析法和分层总和法。
1.1 有限元分析法有限元分析法的原理是指将整个固体分为有限个离散单元,并对其施加荷载,经过选取对应的实际参数计算出路基各点的应力和位移,而所求最终路基的沉降量便是由竖向位移引起的沉降量。
这种方法不仅考虑到了路基的二维甚至是三维变形,而且还顾及到与实际情况相符的边界条件、路基与路堤之间的力学特性、土体应力应变特性等,从而使得计算的最终沉降量更接近实测结果。
1.2 分层总和法分层总和法一般取基底中心下地基附加应力来计算各层土的竖向压缩量,认为基础的平均沉降量s为各土层竖向压缩量si之和,即:式中:n为沉降计算深度范围内的层数。
而计算△si时,假设地基土只在竖向发生压缩变形,没有侧向变形,故可利用室内侧限压缩试验成果进行计算。
对地基土分层时,分层厚度不宜小于0.4b(b为基底宽度);确定地基沉降计算深度时,一般取地基附加应力等于自重应力的20%深度处作为沉降计算深度的限值;若在该深度以下为高压缩性土,则应取地基附加应力等于自重应力的10%深度处作为沉降计算深度的限值。
数值分析试题

, , , ,于是有
(10分)
, , , ,于是有
(14分)
所求为 , (15分)
四、证明题(本题10分)
15.已知函数表
0
1
2
3
4
5
-7
-4
5
26
65
128
求证由此构造的牛顿插值多项式的最高次幂的系数为1.
证明:作均差表
一阶均差
二阶均差
三阶均差
0
-7
1
-4
3
2
5
9
3
3
26
21
6
1
(6分)
4
65
39
9
1
5
128
63
12
1
因为三阶均差均为常数1,可见该函数表的牛顿插值多项式最高次幂为3次,
(7分)
且其系数为1.(10分)
一、单项选择题(每小题3分,共15分)
1.数值 的近似值 ,若满足 (D),则称x有4位有效数字.
(A) (B) (C) (D)
2. 设矩阵 ,那么以A为系数矩阵的线性方程组 的雅可比迭代矩阵为(A)
(A) (B) (C) (D)
3. 已知 的均差 , , , ,那么均差 (C)
(A) (B) (C) (D)
于是,代入函数 ,本题有迭代公式
(7分)
,不满足精度要求.(11分)
当 时, ,
,满足精度要求.所求方程的解为 (15分)
14.用四阶龙格-库塔法求解初值问题 ,取 ,求 时的数值解.要求写出由 直接计算 的迭代公式。计算过程保留3位小数.已知四阶龙格-库塔法斜率值公式为 , , ,
解: ,
三维热传导问题温度场分布的数值分析

02
导热微分方程及定解条件
02
导热微分方程及定解条件
02
导热微分方程及定解条件
定解条件
02
导热微分方程及定解条件
通过无限大平壁的导热
02
02
(二)用傅里叶定律求解
03
导热问题的数值 求解基础
03
导热问题的数值求解基础
原则上,导热问题的求解就是对导热微分方程 方程式在规定的边界和初 始条件下求解。这种解法称为分析解法。但从前面的分析看出,分析解法只 能求解一些导热体的几何形状或边界条件简单的导热问题。 对于工程技术中遇到的许多几何形状或边界条件复杂的导热问题,由于 数学上的困难还无法得出其分析解。
线不会相交.
• 观察一物体内温度为t及t+Δ t的两个不同温度的等温面,沿等温面法线方向上 的温度增量Δ t与法向距离Δ n比值的极限称为温度梯度,用符号gradt表示
Δt t gradt n lim n Δ n 0Δ n n
01
热传导及导热的基本定律
四、热导率及傅里叶定律
A
04
各种数值解法的介绍
• 定义:一种将连续体离散化为若干个有限大小的单元体的集合,以求解 连续体力学问题的数值方法。 • 有限元法:是将连续的求解域离散为一组单元的组合体,用在每个单 元内假设的近似函数来分片的表示求解域上待求的未知场函数,近似 函数通常由未知场函数及其导数在单元各节点的数值插值函数来表 达。从而使一个连续的无限自由度问题变成离散的有限自由度问题。
03
导热问题的数值求解基础
节点方Байду номын сангаас组的求解
03
导热问题的数值求解基础
高斯-赛德尔迭代法:用最新值进行迭代计算
西安理工大学研究生《数值分析》复习题

.。
x y
(4)设 I ( f )
则其 2 次 Lagrange 插值多项式为
.,2 次拟合多项式为 。
.。
1
0
1 e x dx ,则用梯形公式所得近似值为
y f ( x, y ), y (a) a xb
(5)求解常微分方程处值问题
6 4 2
b 的经验公式。 x
四、利用矩阵的三角分解法,解方程组 五 给定方程 x Lnx 2 0 。 (1)分析该方程存在几个根,找出每个根所在的区间; (2)构造求近似根 的迭代公式,并证明所用的迭代公式是收敛的。
1 1 1 2 1 3 1 x1 1 x2 六 求解矛盾方程组 2 5 2 1 x3 2 3 1 5
ax 2 bx ,求证:用欧拉法以 h 为步长所得近似解 2
yn 的整体截断误差为 n y( xn ) yn
八 给定线性方程组 Ax b ,其中 A
1 ahxn 。 2
3 2 3 , b ,用迭代公式 x(k 1) x(k ) (b Ax(k ) ) 1 2 1
b 的经验公式。 x
ax 2 bx ,求证:用欧拉法以 h 为步长所得近似解 2
yn 的整体截断误差为 n y( xn ) yn
八 给定线性方程组 Ax b ,其中 A
1 ahxn 。 2
(k 0,1,2 )
3 2 3 , b ,用迭代公式 x( k 1) x( k ) (b Ax( k ) ) 1 2 1
x2
. 试在 M
数值分析在气象学中的应用例题和知识点总结

数值分析在气象学中的应用例题和知识点总结气象学是一门研究大气现象和过程的科学,它对于预测天气、应对气候变化以及保障人类的生产生活具有重要意义。
在气象学的研究和实践中,数值分析方法发挥着至关重要的作用。
通过对大气物理过程进行数学建模,并利用数值方法求解这些模型,我们能够更加深入地理解大气的行为,并做出更准确的气象预测。
数值分析在气象学中的应用十分广泛,以下我们将通过一些具体的例题来展示其应用,并总结相关的知识点。
一、气象学中的数值分析例题例题 1:天气预报中的数值模式假设我们要预测未来几天某个地区的气温变化。
首先,我们需要建立一个描述大气热传递过程的数学模型。
这个模型可能包括太阳辐射的吸收、地表的热交换、大气的对流和传导等因素。
然后,使用数值方法(如有限差分法或有限元法)将这个偏微分方程在空间和时间上进行离散化,并求解得到不同时刻和地点的温度值。
例如,对于一维的热传导方程:$\frac{\partial u}{\partial t} =\alpha \frac{\partial^2 u}{\partial x^2}$其中,$u(x,t)$表示温度,$\alpha$ 是热扩散系数。
我们可以将空间区间$0,L$ 分成$N$ 个等距的网格点,时间步长为$\Deltat$ 。
使用有限差分法,可以得到以下的差分格式:$u_{i}^{n+1} = u_{i}^{n} +\frac{\alpha \Delta t}{(\Delta x)^2}(u_{i+1}^{n} 2u_{i}^{n} + u_{i-1}^{n})$通过不断迭代计算,就可以得到未来各个时刻的温度分布。
例题 2:大气环流模型中的数值解法大气环流是指大气在全球范围内的大规模运动。
为了模拟大气环流,我们需要建立一个复杂的方程组,包括动量方程、质量守恒方程、能量方程等。
以二维的不可压缩流体动量方程为例:$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} =\frac{1}{\rho}\frac{\partial p}{\partial x} +\nu (\frac{\partial^2 u}{\partial x^2} +\frac{\partial^2 u}{\partial y^2})$$\frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} =\frac{1}{\rho}\frac{\partial p}{\partial y} +\nu (\frac{\partial^2 v}{\partial x^2} +\frac{\partial^2 v}{\partial y^2})$其中,$u$ 和$v$ 分别是水平和垂直方向的速度分量,$p$ 是压力,$\rho$ 是密度,$\nu$ 是粘性系数。
数值分析9-3(龙格-库塔方法)

总结词
除了Python和MATLAB,还有许多其他编 程语言可以用于实现龙格-库塔方法。
详细描述
例如C、Java和R等编程语言也提供了相应 的数值计算库或框架,可以实现龙格-库塔 方法。使用这些语言实现龙格-库塔方法需 要一定的编程基础和对相应语言的数值计算 库的了解。
龙格-库塔方法可以用于求解偏微分方程的数值解,通过将偏微分方程转化为常微分方程组,利用龙格 -库塔方法进行迭代求解,能够得到较为精确的结果。
积分方程的数值解
积分方程是描述函数与积分之间的关 系的数学模型,常见于物理、工程等 领域。
VS
龙格-库塔方法也可以用于求解积分 方程的数值解,通过将积分方程转化 为常微分方程组,利用龙格-库塔方 法进行迭代求解,能够得到较为精确 的结果。
重要性及应用领域
龙格-库塔方法是数值分析中非常重要的内容, 它为解决常微分方程提供了一种有效的数值方 法。
在科学、工程和经济学等领域中,许多问题都 可以转化为求解常微分方程的问题,因此龙格库塔方法具有广泛的应用价值。
例如,在物理学、化学、生物学、金融学等领 域中,龙格-库塔方法被广泛应用于模拟和预测 各种动态系统的行为。
数值分析9-3:龙格-库塔方法
目录
• 引言 • 龙格-库塔方法概述 • 龙格-库塔方法在数值分析中的应用 • 龙格-库塔方法的实现与编程 • 龙格-库塔方法的改进与优化 • 结论与展望
01 引言
主题简介
龙格-库塔方法是一种用于求解常微 分方程的数值方法。
它通过构造一个离散化的时间序列来 逼近微分方程的解,并利用已知的离 散点来计算新的离散点,逐步逼近微 分方程的真实解。
02 龙格-库塔方法概述
定义与原理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟题3
一、填空题:(4×15分)
1.使3的近似值的绝对误差限精确到11021-⨯,21021-⨯,3102
1
-⨯时,其值分别
为 , , 。
2.若x 的相对误差为2%,则n x 的相对误差为 。
3.经测量得正方形的边长*x =100cm ,用*x 的值计算其面积,误差不超过1cm 2,由此可知,*x 的误差限为 cm 。
4.计算函数值)(x f 问题的条件数p C 是指 ,当 时,问题是病态的。
5.设)5,4,3,2,1,0(=i x i 为互异节点,)(x l i 为对应的5次Lagrange 插值基函数,则
=+++∑=5
345
)()12(i i i i i x l x x x。
6.13)(2+=x x f ,则=]3,2,1[f ,=]4,3,2,1[f 。
7.i x x x f i 2
1
,1)(5=
+=,其中i=0,1,2,3,…,则=∆06f ,=∆22f 。
8.满足条件2)2(,1)1(,0)0()0(==='=P P P P 的三次插值多项式
=)(3x P 。
9.一元函数逼近是指“ ”。
10.x x f 2
sin
)(π
=在[0,1]上的伯恩斯坦多项式=),(2x f B 。
11.x e x f =)(在[0,1]上的最佳一次逼近多项式=)(1x P 。
12.13)(34-+=x x x f 在区间[-1,1]上的三次最佳一致逼近多项式
=)(3x P 。
(188)(244+-=x x x T ) 13.根据积分中值定理,在积分区间[a ,b]内存在一点ξ,使得
)()()(ξf a b dx x f b
a
-=⎰
因此,机械求积方法是 其特点是 。
14.用辛普森公式计算=⎰1
0dx e x ,其误差≤)(f R 。
15.求积公式)1()0()1()(3211
1
f A f A f A x f ++-≈⎰-至少具有 次代数精度,其
中A 1= ,A 2= ,A 3= 。
二、证明两点三次Hermite 插值余项是
!
4)())(()(2
12)4(3+--=k k x x x x f x R ξ ),(1+∈k k x x ξ
并由此求出分段三次Hermite 插值的误差限。
(10分)
三、已知函数)(x f 是一个多项式,完成下面的差商表,并按差商表求)(x f 。
(10
分)
四、求函数[0,1]
x
f关于}
=x e
(∈
x,
)
Φ的最佳平方逼近多项式。
(10
=
,1{x
span
分)
五、观测物体的直线运动,得出以下数据:
求运动方程。
(10分)。
