随机信号分析(常建平,李林海)课后习题答案第三章 习题讲解
随机信号分析课后习题答案

1第一次作业:练习一之1、2、3题1.1 离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=i i i x X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他0201)](2π[cos 2)()(x x A dx x dF x f 由1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P1.3 试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x (2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x x x x F (3)0)]()([)(>--=a a x u x u a xx F (4)0)()()(>---=a a x u axa x u a x x F2解:(1)⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x 当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数; 1)(0≤≤x F 成立;)()(x F x F =+也成立。
随机信号分析课后习题答案

第一次作业:练习一之1、2、3题1.1离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-000e1)(2x x x F x (2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F(3)0)]()([)(>--=a a x u x u ax x F (4)0)()()(>---=a a x u ax a x u a x x F解:(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数;1)(0≤≤x F 成立; )()(x F x F =+也成立。
随机信号分析[常建平 李海林]习题答案解析
![随机信号分析[常建平 李海林]习题答案解析](https://img.taocdn.com/s3/m/126bfdd87c1cfad6195fa7b4.png)
1-9 已知随机变量X 的分布函数为20,0(),011,1X x F x kx x x <⎧⎪=≤≤⎨⎪>⎩求:①系数k ; ②X 落在区间(0.3,0.7)内的概率; ③随机变量X 的概率密度。
解:第①问 利用()X F x 右连续的性质 k =1第②问{}{}{}()()0.30.70.30.70.70.30.7P X P X F P X F =<<=<≤-=-第③问 201()()0X X xx d F x f x elsedx ≤<⎧==⎨⎩1-10已知随机变量X 的概率密度为()()xX f x kex -=-∞<<+∞(拉普拉斯分布),求:①系数k ②X 落在区间(0,1)内的概率 ③随机变量X 的分布函数 解:第①问 ()112f x dx k ∞-∞==⎰ 第②问 {}()()()211221x x P x X x F x F x f x dx <≤=-=⎰随机变量X 落在区间12(,]x x 的概率12{}P x X x <≤就是曲线()y f x =下的曲边梯形的面积。
{}{}()()1010101112P X P X f x dxe -<<=<≤==-⎰第③问()102102xx e x f x e x -⎧≤⎪⎪=⎨⎪>⎪⎩()00()110022111010222xx xxx x x x F x f x dxe dx x ex e dx e dxx e x -∞-∞---∞=⎧⎧≤≤⎪⎪⎪⎪==⎨⎨⎪⎪+>->⎪⎪⎩⎩⎰⎰⎰⎰1-11 某繁忙的汽车站,每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001,若每天有1000辆汽车进出汽车站,问汽车站出事故的次数不小于2的概率是多少?,(01)p q λ→∞→→∞→−−−−−−−−→−−−−−−−−→−−−−−−−−→n=1n ,p 0,np=n 成立,0不成立-分布二项分布泊松分布高斯分布汽车站出事故的次数不小于2的概率()()P(2)101k P k P k ≥=-=-= 答案0.1P(2)1 1.1k e -≥=-100.1n p ≥≤实际计算中,只需满足,二项分布就趋近于泊松分布()np!k e P X k k λλλ-===1-12 已知随机变量(,)X Y 的概率密度为(34)0,0(,)0x y XY kex y f x y -+⎧>>⎪=⎨⎪⎩,,其它求:①系数k ?②(,)X Y 的分布函数?③{01,02}P X X <≤<≤?第③问 方法一:联合分布函数(,)XY F x y 性质:若任意四个实数1212,,,a a b b ,满足1212,a a b b ≤≤,则121222111221{,}(,)(,)(,)(,)XY XY XY XY P a X a b Y b F a b F a b F a b F a b <≤<≤=+--{01,02}(1,2)(0,0)(1,0)(0,2)XY XY XY XY P X Y F F F F ⇒<≤<≤=+--方法二:利用(){(,)},XY DP x y D f u v dudv∈∈⎰⎰)(210{01,02},XY P X Y f x y dxdy <≤<≤=⎰⎰1-13 已知随机变量(,)X Y 的概率密度为101,(,)0x y xf x y ⎧<<<=⎨⎩,,其它 ①求条件概率密度(|)X f x y 和(|)Y f y x ?②判断X 和Y 是否独立?给出理由。
随机信号分析(第3版)课后习题解答

随机信号分析(第3版)课后习题解答《随机信号分析》课程(32学时)—— 2007年教学内容建议1 概率论基础 1.12 随机信号2.1 两条样本函数为:0)(0=t X 、wt t X cos 21)(1=;1)0,(=x f X 、2)4,(=w x f X π;)(0-)2,(x wx f X δπ= 2.2 3103532)2,(=++=X E 、)()()(5-313-312-31)2,(x x x x F X εεε++= 2.3 )()(1-2121)21,(x x x F X εε+=、)()(2-21121)1,(x x x F X εε++=;)()()()(2-,1411,1412-,411,41)1,21,,(21x x x x x x x x x x F X -++-+++=εεεε2.4 略2.5 )()(1-1.09.0)5,(x x x F X εε+=;)()(y x y x y x F ,11.0,9.0)0025.0,0,,(-+=εε;0因为其概率为0.9;1的概率为1(样本函数),它是可预测的,就是样本函数。
2.6 略 2.7 略 2.8 )()(121121),(-++=x x n x f X δδ、0121)1(21)(=?+-?=n X E 、{})()]()([)]()()][()([),(2121221121n n n X n X E n m n X n m n X En n Cov X X -==--=δ;不可预测2.9 (2.19)10103523)()(),(2111=?==t t t t Cov σσρ、所以(X,Y )满足10103;5,2;2,2的高斯分布。
其概率密度函数为:-+--?--?-=-+--?----=5)2(5)2)(2(32)2(5exp215)2(10)2)(2(1010322)2()10/91(21exp 21),(2222y y x x y y x x y x f XY ππ;特征函数为:++-+=)6)(5)(2(21)22(exp ),(21222121v v v v v v j y x XY φ3 平稳性与功率谱密度3.1 kk k u t t u u f-=)4exp(2*21),,;,,(211π ;因为k 阶概率密度函数与绝对时间无关,所以为严格平稳过程。
随机信号分析(常建平李海林)习题答案解析

完美 WORD 格式1-9 已知随机变量X的分布函数为0 , x 02F (x) kx , 0 x 1X1 , x 1求:①系数 k;②X落在区间(0.3,0.7) 内的概率;③随机变量X的概率密度。
解:第①问利用F X (x) 右连续的性质k =1P 0.3 X 0.7 P 0.3 X 0.7 P X 0.7 第②问F 0.7 F 0.3第③问f (x)Xd F(x)Xdx2x 0 x 10 else专业知识分享完美 WORD 格式x1-10 已知随机变量X 的概率密度为( ) ( )f x ke xX(拉普拉斯分布),求:①系数k ②X落在区间 (0,1)内的概率③随机变量 X的分布函数解:第①问f x dx 1 k12第②问x2P x X x F x F x f x dx1 2 2 1x1随机变量 X落在区间( x1 , x2 ] 的概率 P{ x1 X x2} 就是曲线y f x 下的曲边梯形的面积。
1P 0 X 1 P 0 X 1 f x dx1 2 1 e1第③问12 f x12xe xxe xxF x f ( x)dx1 1x x xe dx x 0 e x 02 20 1 1 1xx x xe dx e dx x 0 1 e x 02 0 2 2专业知识分享完美 WORD 格式1-11 某繁忙的汽车站,每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001,若每天有1000 辆汽车进出汽车站,问汽车站出事故的次数不小于 2 的概率是多少?n=1- 分布 (0 1)n ,p 0,np=二项分布泊松分布n 成立,0不成立, p q高斯分布实际计算中,只需满足,二项分布就趋近于泊松分布n 10 p 0.1P X kk e==np k!汽车站出事故的次数不小于 2 的概率P(k 2) 1 P k 0 P k 10.1P(k 2) 1 1.1e 答案专业知识分享完美 WORD 格式1-12 已知随机变量 (X,Y)的概率密度为f (x, y) XY(3 x 4 y),ke x 0, y 0, 其它0求:①系数k?②( X ,Y)的分布函数?③P{0 X 1,0 X 2} ?第③问方法一:联合分布函数F XY (x, y) 性质:若任意四个实数 a ab b ,满足1, 2, 1, 2a a bb ,满足a1 a2,b1 b2 ,则P{a X a ,b Y b}F XY(a ,b ) F XY(a ,b) F XY(a ,b ) F XY(a ,b)1 2 1 2 2 2 1 1 1 2 2 1P{0X 1,0 Y 2} F XY(1,2) F XY(0,0) F XY(1,0) F XY(0,2)方法二:利用P{( x, y) D } f XY u,v dudvD2 1P{0X 1,0 Y 2} f XY x,y dxdy0 0专业知识分享完美 WORD 格式1-13 已知随机变量(X,Y) 的概率密度为f (x, y)1, 0 x 1, y x0 , 其它①求条件概率密度 f X (x| y)和f Y ( y | x) ?②判断X 和Y 是否独立?给出理由。
随机信号分析(常建平,李林海)课后习题答案第三章 习题讲解

、随机过程 X(t)=A+cos(t+B),其中A 是均值为2,方差为1的高斯变量,B 是(0,2π)上均匀分布的随机变量,且A 和B 独立。
求(1)证明X(t)是平稳过程。
(2)X(t)是各态历经过程吗?给出理由。
(3)画出该随机过程的一个样本函数。
(1)(2)3-1 已知平稳过程()X t 的功率谱密度为232()(16)X G ωω=+,求:①该过程的平均功率? ②ω取值在(4,4)-范围内的平均功率?解[][]()[]2()cos 211,cos 5cos 22X E X t E A E t B A B R t t EA τττ=++=⎡⎤⎣⎦+=+=+与相互独立()()()21521()lim2TT T E X t X t X t X t dt AT-→∞⎡⎤=<∞⇒⎣⎦==⎰是平稳过程()()[]()()4112211222222242'4(1)24()()444(0)41132(1)224414414(2)121tan 13224X X XE X t G d RFG F e R G d d d arc x x ττωωωωωππωωπωωπωπωω∞----∞∞-∞-∞∞--∞∞⎡⎤⨯⎡⎤==⋅=⋅⎢⎥+⎣⎦====+==⎛⎫+ ⎪==⎣⎦=++⎝⎭=⎰⎰⎰⎰⎰P P P P 方法一()方:时域法取值范围为法二-4,4内(频域的平均率法功)2d ω=3-7如图3.10所示,系统的输入()X t 为平稳过程,系统的输出为()()()Y t X t X t T =--。
证明:输出()Y t 的功率谱密度为()2()(1cos )Y X G G T ωωω=-[][]:()[()()]{()()}{()(}2()()()()()()()()2(()[)()(()()]()())Y X X X Y X X Y Y Y X X X Y Y j T j T R E Y t Y t E X t X t T X t X t T R R R R E Y t Y t G F R T T e e G R G R G G G G ωωτττττωτωττωττττωωωω-⇒⇒=+=--+-+-=--=+=-⇔⇔∴=-+-=已知平稳过程的表达式利用定义求利用傅解系统输入输出立叶平变稳换的延时特性2()2()22()(1cos )j T j T X X X e e G G G T ωωωωωω-⎡⎤+-⎢⎥⎣⎦=-3-9 已知平稳过程()X t 和()Y t 相互独立,它们的均值至少有一个为零,功率谱密度分别为216()16X G ωω=+22()16Y G ωωω=+令新的随机过程()()()()()()Z t X t Y t V t X t Y t =+⎧⎨=-⎩ ①证明()X t 和()Y t 联合平稳; ②求()Z t 的功率谱密度()Z G ω? ③求()X t 和()Y t 的互谱密度()XY G ω? ④求()X t 和()Z t 的互相关函数()XZ R τ? ⑤求()V t 和()Z t 的互相关函数()VZ R τ 解:()()4124(1)()()()2[()]()0[()]0()2[()]0()()(,)[()][()]0()()(2)()()()()[()()][()()][()X X X Y XY Z X t Y t R F G e E X t R E X t R eE Y t X t Y t R t t E X t E Y t X t Y t Z t X t Y t R E Z t Z t E X t Y t X t τττωτδττττττ---==∞=⇒=⎡⎤⎣⎦=-⇒=∴+=⋅+=⇒=+=+=++、都平稳=与与联合独平立稳[][]{}2214||()]()()()()()0()()()16()()()116(3)()0()0(4)()[()()]()()()()()()[()]2(5)(X YX XY Y XY Z X Y Z X Y XY XY XZ X XY X X VZ Y t R R R R R R R R G G G R G R E X t Z t E X t X t Y t R R R F G e R ττττττττττωωωωωτωτττττττωτ--++=+++=∴=++∴=+==+=→==+=+++=+==={}4||)[()()][()()][()()]()()()4X Y E V t Z t E X t Y t X t Y t R R e ττττττδτ-=+=-+++=-=+-3-11 已知可微平稳过程()X t 的自相关函数为2()2exp[]X R ττ=-,其导数为()()Y t X t '=。
随机信号分析常建平李林海课后习题答案第二章习题讲解

随机信号分析常建平李林海课后习题答案第⼆章习题讲解2-1 已知随机过程0()cos X t A t ω=,其中0ω为常数,随机变量A 服从标准⾼斯分布。
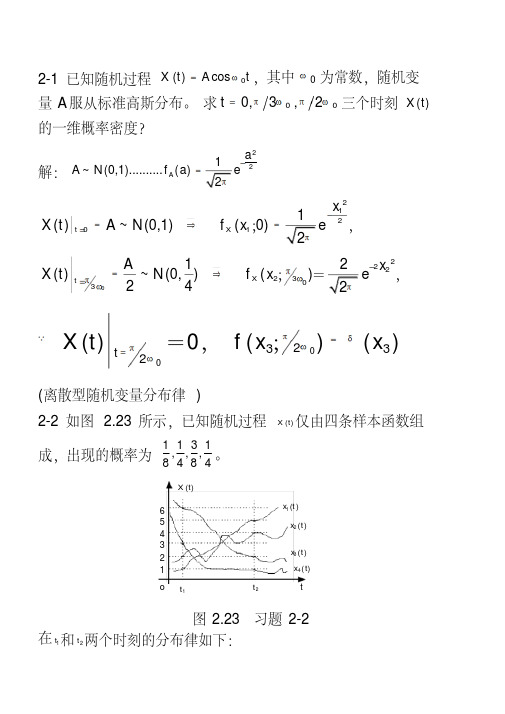
求000,3,2t πωπω=三个时刻()X t 的⼀维概率密度?解:221~(0,1)..........()2A a A N f a π-=21211()~(0,1)(0)2t X x X t A N f x eπ-==?=;,2223203A 12()~(0,)()242X t x X t N f x e πωπωπ-==?;=, 002323()0()()t X t f x x πωπωδ===,;(离散型随机变量分布律)2-2 如图所⽰,已知随机过程()X t 仅由四条样本函数组成,出现的概率为1131,,,8484。
t()X t 1t 1()x t 2()x t 3()x t 4(x t o图习题2-2在1t 和2t 两个时刻的分布律如下:1ζ2ζ3ζ4ζ1()X t 1 2 6 3 2()X t54211212(,)k k p t t 1/8 1/4 3/8 1/4求1212[()],[()],[()()]E X t E X t E X t X t ()41129[()]8k k k E X t x p t ===∑221[()]8E X t =()()(){}121212121122[()()],,X k k E X t X t R t t k k p X t k X t k ====∑∑[][][]()()()22221212221121222()cos cos ()()()()cos cos cos cos 12(,)cos cos cos cos cos cos 1cos c 232o X XYD aE X t E A t XH t EA XHD X tE X t E X t D X t D A t XH D A t D XH tt DA R t t E A t XH X a D X b D Y abC EA EA A t XH t t XH t t XH t =+=?+??=-??=+=+=?=+++==+=+++公式:+b =Y⽅法:()2212s cos cos 2XH t t t XH +++()()()()22cos 022~,322cos 022~,cos 0()2122,cos 2cos cos cos c 21322,(;)cos o 2s 2X k t k t tX t U XH XH k t k t t X t U XH XH t k t X t XHk t k XH x XH t k t k XH x XH f x t t x X t t t t ππππππππππππππππππδ-+<<+>+<<+<=+==-+<<+<<-++<<+<+++<=-对某⼀固定时刻对某⼀固定时刻概率密度⽤冲激函数表⽰()=+=2-4 已知随机过程()X t A Bt =+,其中,A B 皆为随机变量。
随机信号分析(第3版)第三章 习题答案

Z (t )的均值: E[ Z (t )] = E[ A ⋅ X (t ) ⋅ Y (t )] = E[ A] ⋅ E[ X (t )] ⋅ E[Y (t )] = 2 E[ X (t )] ⋅ E[Y (t )]
2 mX = RX (∞) = lim
2 cos ω0τ = 0 → mX = 0 τ →∞ eτ
⎡ 2 1.3 0.4 __ ⎤ ⎢ __ 2 1.2 0.8⎥ ⎢ ⎥ ⎢ 0.4 1.2 __ 1.1 ⎥ ⎢ ⎥ ⎣ 0.9 __ __ 2 ⎦ 3.12 解:根据广义平稳随机信号过程的自相关函数矩阵的对称性,得到: ⎛ 2 1.3 0.4 0.9 ⎞ ⎜ 1.3 2 1.2 0.8 ⎟ ⎟ C= ⎜ ⎜ 0.4 1.2 2 1.1 ⎟ ⎜ ⎟ ⎝ 0.9 0.8 1.1 2 ⎠ 3.13
= E[100 sin 2 (ω 0 t + θ ) ×100 sin 2 (ω 0 t + ω 0τ + θ ) ] = 2500 E[1 − cos(2ω 0τ ) − cos(4ω 0 t + 2ω 0τ + 4θ )] = 2500 E[1 − cos(2ω 0τ ) ] ∴ R Z (τ ) 仅与 τ 有关,且均值为常数,故 Y(t ) 是平稳过程。
3.6 给定随机过程 X ( t ) = A cos (ω 0t ) + B sin (ω 0t ) ,其中 ω 0 是常数, A 和 B 是 两个任意的不相关随机变量,它们均值为零,方差同为 σ 2 。证明 X ( t ) 是广义平 稳而不是严格平稳的。 3.6 证明:Q m X (t ) = E[X(t )] = E[ A cos(ω 0 t ) + B sin(ω 0 t) ] = 0
随机信号分析(常建平李海林)习题答案解析

y
y
0
1
1
e
e
y
3
2
1
0
else
1-17 已知随机变量 X,Y 的联合分布律为
P X m,Y n
m ne 5
32
, m,n 0,1,2,
m! n!
***
求: ① 边缘分布律
***
P X m (m 0,1,2, ) 和
②条 件分布律 P X m |Y
和 n
PY
n|X
m?
专业 知识分享
P Y n (n 0,1,2,
0.0001 ,若每天有 1000 辆汽车进
出汽车站,问汽车站出事故的次数不小于
2 的概率是多少?
二项分布
n=1
- 分布 (0 1)
n
,p 0,np=
泊松分布
n
成立 , 0 不成立
,p q
高斯分布
实际计算中,只需满足
,二项分布就趋近于泊松分布 n 10 p 0.1
ke PX k =
k!
= np
汽车站出事故的次数不小于
X
3
6
7
求: ①X 的分布函数
P 0.2 0.1 0.7 ② 随机变量 Y 3X 1 的分布律
1-15 已知随机变量 X 服从标准高斯分布。 求:①随机变量 Z X 的概率密度? 的概率密度? ② 随机变量
分析 : ① f Y (y)
h '(y)
f X h( y)
② f Y ( y) | h' 1 (y) | f X [h 1 ( y)]
第③问
fx Fx
1x 2e
0 x
1x
e 2
0 x
随机信号分析课后习题答案

1第一次作业:练习一之1、2、3题1.1 离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3 试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x2(2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F (3)0)]()([)(>--=a a x u x u ax x F (4)0)()()(>---=a a x u ax a x u a x x F解:(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数;1)(0≤≤x F 成立; )()(x F x F =+也成立。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解
A与 B独立 , f AB (a, b) f A (a) fB (b)
X (t) A Bt Y(t) A
A Y(t) X (t) Y (t)
B t
01 J1 1 1
t tt
1
xy 1
xy
f XY (x, y; t ) J f AB (a,b) t f AB ( y, t ) t f A ( y) f B ( t )
E X (t) E A cost XH cost EA XH
D X (t) E X 2 (t ) E2 X (t )
方法 2:
D X (t)
D Acost XH D Acost cos2 t DA cos2 t
12
D XH
公式: D aX+ bY a2 D X b2 D Y 2abC XY
RX (t1, t2 )=E Acost1 XH A cost2 XH
f X (x1;0)
1
x12 e 2,
2Байду номын сангаас
A
1
X (t)
~ N (0, )
t 30
2
4
f X ( x2; 3
)=
0
2 2
e
2
x2
2
,
X (t) t
=0,
f ( x3;2
)
0
20
( x3)
(离散型随机变量分布律 )
2-2 如图 2.23 所示,已知随机过程 X (t) 仅由四条样本函数组
成,出现的概率为
数 RX (t1, t2 ) ?②若已知随机变量相 A, B 互独立,
它们的概率密度分别为 f A (a) 和 f B (b) ,求 X (t) 的一
随机信号分析(常建平-李林海)课后习题答案第二章习题讲解

2-1 已知随机过程0()cos X t A t ω=,其中0ω为常数,随机变量A 服从标准高斯分布。
求000,3,2t πωπω=三个时刻()X t 的一维概率密度?解:221~(0,1)..........()A a A N f a -=21211()~(0,1)(0)t X x X t A N f x e-==⇒=;,2223203A 12()~(0,)()24X t x X t N f x e πωπω-==⇒;, 002323()0()()t X t f x x πωπωδ===,;(离散型随机变量分布律)2-2 如图2.23所示,已知随机过程()X t 仅由四条样本函数组成,出现的概率为1131,,,8484。
t()X t 1234561t 2t 1()x t 2()x t 3()x t 4(x t o图2.23 习题2-2在1t 和2t 两个时刻的分布律如下:求? 1212[()],[()],[()()]E X t E X t E X t X t ()41129[()]8k k k E X t x p t ===∑221[()]8E X t =()()(){}121212121122[()()],,X k k E X t X t R t t k k p X t k X t k ====∑∑2-23[][]12()cos (0,1)(;),()()(,)X X X t A t XH A U f x t E X t D X t R t t =+~随机过程,其中(均匀分布)。
求,,?[][][][][][][][][][][]()()()22221212221121222()cos cos ()()()()cos cos cos cos 12(,)cos cos cos cos cos cos 1cos c 232o X XYD aE X t E A t XH t EA XHD X tE X t E X t D X t D A t XH D A t D XH tt DA R t t E A t XH X a D X b D Y abC EA EA A t XH t t XH t t XH t =+=⋅+⎡⎤=-⎣⎦=+=+=⋅=++⎡⎤⎣⎦+==+=+++公式:+b =Y方法:()2212s cos cos 2XH t t t XH +++()()()()22cos 022~,322cos 022~,cos 0()2122,cos 2cos cos cos c 21322,(;)cos o 2s 2X k t k t tX t U XH XH k t k t t X t U XH XH t k t X t XHk t k XH x XH t k t k XH x XH f x t t x X t t t t ππππππππππππππππππδ-+<<+>+<<+<=+==-+<<+<<-++<<+<+++<=-对某一固定时刻对某一固定时刻概率密度用冲激函数表示(),20H t k x XH else ππ⎧⎪⎪⎪⎪⎨⎪=+=⎪⎪⎪⎩2-4 已知随机过程()X t A Bt =+,其中,A B 皆为随机变量。
随机信号分析基础第三章习题

首先讨论平稳性,由题可知
E [ X (t )] 1 T
T 0
S (t )
1 T
d
tT t
S ( ) d
co n st
R X (t 1 , t 2 ) E [ X (t 1 ) X (t 2 )]
T 0
S (t 1 )S (t 2 )
2
T 0
S (t )
2
1 T
d
tT t
S ( )d
2
• 综合以上讨论,该随相周期过程是宽平稳的
现在讨论各态历经性:
X (t ) lim 1 T 1 T 1 2T
T
T T
s(t ) d t
T 0 T 0
s(t ) d t s( ) d
E [ X (t )]
X (t ) X (t ) lim lim 1 T 1 2T 1 2T
T 0
T
T T T T
x (t ) x (t ) d t s(t )s(t ) d t
T
s( )s( ) d
R X ( )
m X lim 4 e
2
co s 0
2
E [ X (t )] m X 5
2 2
R X ( ) 4 e
1
co s co s 3
2
R X ( ) R X ( )
• 噪声分量 • 信号分量
PN R X (0 ) 4
1
PS R X (0 ) 1
随机信号分析基础第三章课后答案

da cos 0 t1 cos 0 t 2
0
2
a 2 e
0 2
2
2 2
d(
a de
0
a2 2 2
1 1 cos 0 t 2 t1 cos 0 t1 t 2 2 d 2 2 a2 a2 2 1 2 2 2 1 cos 0 t 2 t1 a e e 2 da 2 cos 0 t 2 t1 0 2 2 0 2 2 cos 0 t 2 t1 2 cos 0 t 2 t1 2 2
第三章 Chapter 3 ========================================== 3.2 随 机 过 程
t 为 t A cos 0 t 式 中 , A 具 有 瑞 利 分 布 , 其 概 率 密 度 为
a2 2 2
PA a
R Z 26e
2 3 2 cos 9 e
2 Z R Z 0 R Z 260
3.14 设 X(t)是雷达的发射信号,遇到目标后的回波信号 aX (t ), a 1, 1 是信号返回 时间,回报信号必然伴有噪声,计为 N(t), 于是接收到的全信号为:
R( t , t ) E A 2 cos( 0 t ) cos( 0 ( t ) ) E A 2 E cos( 0 t ) cos( 0 ( t ) )
E A2 E cos(( 2 0 t 0 ) 2 ) cos( 0 ) 2 E A2 cos( 0 ) 2
随机信号与系统课第三章习题部分答案

第三章 习题3-1 设某一随机过程的样本为{x 1,x 2,…,x k },设k 时刻的样本均值和方差分别为21111(),(1)1kkk ik i k i i x x s x x k k k ====-≠-∑∑和 假定新的观测值为x k+1,试推导样本均值x k+1和样本方差s k+1的更新公式。
解:111k k k kx x x k +++=+. ∵ 121111()k k i k i s x x k +++==-∑,而211()1k k i k i s x x k ==--∑,所以 112211111222111111122112211()()111211 ()()()()11111 0()()(1)(1) k k k k k k k i i k i i k k k k k k k k k i k i k k i i i k k k k kkx x x x s x x x k k k k x x x x kx x x x x x x k k k k k k k k k s x x x x k k k +++++==++++===+++-=-=--++--+=---++-+++-=-+-+-++∑∑∑∑∑2111 ().1k k k k s x x k k +-=+-+∴ 更新公式为11111k k k k x x x k k ++=+++, 21111()1k k k k k s s x x k k ++-=+-+.3-2 设某一随机过程样本由x k =a+bk+v k 描述,其中,v k ~N (0,σ2);a 和b 是待定的未知参数。
试求估计量a ˆ,b ˆ的CR 下界。
解:未知参数向量为θ=[a ,b ]T 。
首先计算Fisher 信息矩阵,即222222ln (|)ln (|)[][]()ln (|)ln (|)[][]p x p x E E a a b p x p x E E b a b ⎡⎤∂∂--⎢⎥∂∂∂⎢⎥=⎢⎥∂∂⎢⎥--⎢⎥∂∂∂⎣⎦θθI θθθ (3.1.31) 依题意,似然函数可写成22/22111(|)exp[()](2π)2NkN k p x xa bk σσ==---∑θ对上式等号两边取自然对数,并分别对A 和B 求偏导,得到21ln (|)1()Nkk p x xa bk a σ=∂=--∂∑θ21ln (|)1()Nkk p x xa bk kb σ=∂=--∂∑θ容易验证,以上二式的数学期望为零,满足正则条件(3.1.25)。
随机信号分析基础课后练习题含答案

随机信号分析基础课后练习题含答案第一部分随机变量和概率分布练习题1设离散随机变量X的概率分布函数为:X0 1 2 3 4P X0.05 0.15 0.35 0.30 0.15求E(X)和D(X)。
答案1根据概率分布函数的公式有:$$E(X)=\\sum_{i=1}^n x_i P_X(x_i) = 0 \\times 0.05 + 1\\times 0.15 + 2 \\times 0.35 + 3 \\times 0.30 + 4 \\times 0.15 = 2.25$$$$D(X)=\\sum_{i=1}^n (x_i-E(X))^2P_X(x_i) = 0.710625$$ 练习题2已知随机变量X的概率密度函数为:$$f_X(x) = \\begin{cases} \\frac{1}{3}e^{-\\frac{x}{3}} & x \\geq 0 \\\\ 0 & x < 0 \\end{cases}$$求E(X)和D(X)。
答案2根据概率分布函数的公式有:$$E(X)=\\int_{-\\infty}^{+\\infty}xf_X(x)dx =\\int_{0}^{+\\infty}x\\frac{1}{3}e^{-\\frac{x}{3}}dx=3$$ $$D(X)=E(X^2)-(E(X))^2=\\int_{-\\infty}^{+\\infty}x^2f_X(x)dx-(E(X))^2=\\int_{0}^{+\\infty}x^2\\frac{1}{3}e^{-\\frac{x}{3}}dx-9=\\frac{27}{4}$$第二部分随机过程练习题3设二阶矩有限的离散时间随机过程X n的均值序列为m n,自相关函数为R n(i,j)=E(X i−m i)(X j−m j),其中 $0 \\leq i,j \\leq N$。
若m n=n2,R n(i,j)=ij(i+j),求 $E(\\sum_{n=0}^N X_n)$。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解资料

2-1 已知随机过程0()cos X t A t ω=,其中0ω为常数,随机变量A 服从标准高斯分布。
求000,3,2t πωπω=三个时刻()X t 的一维概率密度?解:221~(0,1)..........()2A a A N f a e π-=21211()~(0,1)(0)2t X x X t A N f x eπ-==⇒=;,2223203A 12()~(0,)()242X t x X t N f x e πωπωπ-==⇒;=, 002323()0()()t X t f x x πωπωδ===,;(离散型随机变量分布律)2-2 如图2.23所示,已知随机过程()X t 仅由四条样本函数组成,出现的概率为1131,,,8484。
t()X t 1234561t 2t 1()x t 2()x t 3()x t 4()x t o图2.23 习题2-2在1t 和2t 两个时刻的分布律如下:1ζ2ζ3ζ4ζ1()X t 1 2 6 3 2()X t54211212(,)k k p t t 1/8 1/4 3/8 1/4求 ? 1212[()],[()],[()()]E X t E X t E X t X t ()41129[()]8k k k E X t x p t ===∑221[()]8E X t =()()(){}121212121122[()()],,X k k E X t X t R t t k k p X t k X t k ====∑∑2-23[][]12()cos (0,1)(;),()()(,)XXX t A t XH A U f x t E X t D X t R t t =+~随机过程,其中(均匀分布)。
求,,?[][][][][][][][][][][]()()()22221212221121222()cos cos ()()()()cos cos cos cos 12(,)cos cos cos cos cos cos 1cos c 232o X XYD aE X t E A t XH t EA XHD X tE X t E X t D X t D A t XH D A t D XH tt DA R t t E A t XH X a D X b D Y abC EA EA A t XH t t XH t t XHt =+=⋅+⎡⎤=-⎣⎦=+=+=⋅=++⎡⎤⎣⎦+==+=+++公式:+b =Y方法:()2212s cos cos 2XH t t t XH +++()()()()22cos 022~,322cos 022~,cos 0()2122,cos 2cos cos cos c 21322,(;)cos o 2s 2X k t k t tX t U XH XH k t k t t X t U XH XH t k t X t XHk t k XH x XH t k t k XH x XH f x t t x X t t t t ππππππππππππππππππδ-+<<+>+<<+<=+==-+<<+<<-++<<+<+++<=-对某一固定时刻对某一固定时刻概率密度用冲激函数表示(),20H t k x XH else ππ⎧⎪⎪⎪⎪⎨⎪=+=⎪⎪⎪⎩2-4 已知随机过程()X t A Bt =+,其中,A B 皆为随机变量。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解

2-1 已知随机过程0()cos X t A t ω=,其中0ω为常数,随机变量A 服从标准高斯分布。
求000,3,2t πωπω=三个时刻()X t 的一维概率密度?解:221~(0,1)..........()2A a A N f a e π-=21211()~(0,1)(0)2t X x X t A N f x eπ-==⇒=;,2223203A 12()~(0,)()242X t x X t N f x e πωπωπ-==⇒;=, 002323()0()()t X t f x x πωπωδ===,;(离散型随机变量分布律)2-2 如图2.23所示,已知随机过程()X t 仅由四条样本函数组成,出现的概率为1131,,,8484。
t()X t 1234561t 2t 1()x t 2()x t 3()x t 4()x t o图2.23 习题2-2在1t 和2t 两个时刻的分布律如下:1ζ 2ζ 3ζ 4ζ1()X t 1 2 6 3 2()X t 5 4 2 1 1212(,)k k p t t1/8 1/4 3/8 1/4求 ? 1212[()],[()],[()()]E X t E X t E X t X t ()41129[()]8k k k E X t x p t ===∑221[()]8E X t =()()(){}121212121122[()()],,X k k E X t X t R t t k k p X t k X t k ====∑∑2-23[][]12()cos (0,1)(;),()()(,)X X X t A t XH A U f x t E X t D X t R t t =+~随机过程,其中(均匀分布)。
求,,?[][][][][][][][][][][]()()()22221212221121222()cos cos ()()()()cos cos cos cos 12(,)cos cos cos cos cos cos 1cos c 232o X XYD aE X t E A t XH t EA XHD X tE X t E X t D X t D A t XH D A t D XH tt DA R t t E A t XH X a D X b D Y abC EA EA A t XH t t XH t t XH t =+=⋅+⎡⎤=-⎣⎦=+=+=⋅=++⎡⎤⎣⎦+==+=+++公式:+b =Y方法:()2212s cos cos 2XH t t t XH +++()()()()22cos 022~,322cos 022~,cos 0()2122,cos 2cos cos cos c 21322,(;)cos o 2s 2X k t k t tX t U XH XH k t k t t X t U XH XH t k t X t XHk t k XH x XH t k t k XH x XH f x t t x X t t t t ππππππππππππππππππδ-+<<+>+<<+<=+==-+<<+<<-++<<+<+++<=-对某一固定时刻对某一固定时刻概率密度用冲激函数表示(),20H t k x XH else ππ⎧⎪⎪⎪⎪⎨⎪=+=⎪⎪⎪⎩2-4 已知随机过程()X t A Bt =+,其中,A B 皆为随机变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、随机过程 X(t)=A+cos(t+B),其中A 是均值为2,方差为1的高斯变量,B 是(0,2π)上均匀分布的随机变量,且A 和B 独立。
求
(1)证明X(t)是平稳过程。
(2)X(t)是各态历经过程吗?给出理由。
(3)画出该随机过程的一个样本函数。
(1)
(2)
3-1 已知平稳过程()X t 的功率谱密度为
2
32
()(16)
X G ωω=
+,求:①该过程的平均功率? ②ω取值在(4,4)-范围内的平均功率?
解
[][]()[]2
()cos 2
11
,cos 5cos 22
X E X t E A E t B A B R t t EA τττ
=++=⎡⎤⎣⎦+=+=+与相互独立
()()()2
1521()lim
2T
T T E X t X t X t X t dt A
T
-→∞⎡⎤=<∞
⇒⎣⎦==⎰是平稳过程
()()[]()
()41122
11222222
2
4
2'
4(1)24()()444(0)4
1132
(1
)2244144
14(2)121tan 132
24X X X
E X t G d R
F
G F e R G d d d arc x x τ
τωωωωω
ππωωπωωπ
ω
π
ωω∞
----∞∞
-∞-∞∞--∞∞
⎡⎤⨯⎡⎤==⋅=⋅⎢⎥+⎣⎦
====+==⎛⎫+ ⎪==
⎣⎦=
++⎝⎭
=⎰
⎰⎰⎰⎰P P P P 方法一()
方:时域法取值范围为法二-4,4内(频域的平均率法功)
2
d ω
=
3-7如图3.10所示,系统的输入()X t 为平稳过程,系统的输出为()()()Y t X t X t T =--。
证明:输出()Y t 的功率谱密度为()2()(1cos )Y X G G T ωωω=-
[][]:
()[()()]
{()()}{()(}2()()()
()()()()
()2(()[)()(()()]()())Y X X X Y X X Y Y Y X X X Y Y j T j T R E Y t Y t E X t X t T X t X t T R R R R E Y t Y t G F R T T e e G R G R G G G G ωωτττττωτωττωττττωωωω-⇒⇒=+=--+-+-=--=+=-⇔⇔∴=-+-=已知平稳过程的表达式
利用定义求利用傅解系统输入输出立叶平变稳
换的延时特性
2()2()22()(1cos )
j T j T X X X e e G G G T ωωωωωω-⎡⎤
+-⎢⎥⎣⎦=-
3-9 已知平稳过程()X t 和()Y t 相互独立,它们的均值至少有一个为零,功率谱密度分别为
2
16
()16
X G ωω=+
22()16
Y G ωωω=
+
令新的随机过程
()()()()()()
Z t X t Y t V t X t Y t =+⎧⎨=-⎩ ①证明()X t 和()Y t 联合平稳; ②求()Z t 的功率谱密度()Z G ω ③求()X t 和()Y t 的互谱密度()XY G ω ④求()X t 和()Z t 的互相关函数()XZ R τ ⑤求()V t 和()Z t 的互相关函数()VZ R τ 解:
()()4124(1)()()()2[()]()0[()]0()2[()]0
()()(,)[()][()]0()()(2)()()()
()[()()]
[()()][()X X X Y XY Z X t Y t R F G e E X t R E X t R e
E Y t X t Y t R t t E X t E Y t X t Y t Z t X t Y t R E Z t Z t E X t Y t X t τ
τ
τωτδττττττ---==∞=⇒=⎡⎤⎣⎦=-⇒=∴+=⋅+=⇒=+=+=++、都平稳=与与联合独平立
稳
[][]{}
2214||
()]()()()()()0
()()()
16
()()()1
16
(3)()0()0
(4)()[()()]()()()()()
()[()]2(5)(X YX XY Y XY Z X Y Z X Y XY XY XZ X XY X X VZ Y t R R R R R R R R G G G R G R E X t Z t E X t X t Y t R R R F G e R ττττττττττωωωωωτωτττττττωτ--++=+++=∴=++∴=+==+=→==+=+++=+==={}4||
)[()()]
[()()][()()]()()()4X Y E V t Z t E X t Y t X t Y t R R e ττττττδτ-=+=-+++=-=+-
3-11 已知可微平稳过程()X t 的自相关函数为
2()2exp[]X R ττ=-,其导数为()()Y t X t '=。
求互谱密
度()XY G ω和功率谱密度()Y G ω? Ⅰ.平稳过程 维纳-辛钦定理
()
1
()F X X F G R ωτ-
Ⅱ.2-17 已知平稳过程()X t 的均方可导,()()Y t X t '=。
证明
(),()X t Y t 的互相关函数和()Y t 的自相关函数分别为
Ⅲ.傅立叶变换的微分性质
2
2
2222
2222
222
27928exp 24
:()[()][2]4
()()()()4
()()()()2)(X X XY X XY X Y X
Y X t e e
e
t P G F R F e R j j R G G e R R G G e τωττσωωτσωωττωωωωττωωσωω-⎛⎫
⎛⎫-- ⎪ ⎪⎝⎭
⎝⎭
⇔⎧⎫⎧⎫
-⇔-⎨⎬⎨-
===-
'===⋅-
''=-=-⎬
⎩⎭⎩⎭
⋅高斯脉冲表第解利用傅立叶变换的=个微分特性22()
()
()()X
X XY Y dR d R R R d d τττττ
τ
==-
3-17 已知平稳过程()X t 的物理功率谱密度为
()4X F ω=,
①求()X t 的功率谱密度()X G ω和自相关函数
()X R τ画出(),(),()X X X F G R ωωτ的图形。
②判断过程()X t 是白噪声还是色噪声?给出理由
()(1
()()2,)22
()2()
[()]()()0()X X X X X X G F R E X t X G R t F U ωωωδτωτωω-∞=
===±∞<=⋅∴<∞
=物理功率谱密度 定义式,是白噪声。
白噪声的定义
若平稳随机过程的均值为零,功率谱密度在整个频率轴(,)-∞+∞上均
匀分布,满足 错误!未找到引用源。
其中0N 为正实常数,则称此过程为白噪声过程,简称白噪声。
01
()2
N G N ω=。
