接触问题的非线性有限元分析
基于有限元的滚动轴承非线性接触分析
麓 翳
基 于 有 限元 的 滚 动 轴 承 非 线 性 接 触 分析
崔 波 程 珩
太原 00 2 ) 3 0 4 ( 原理工大学 机 械电子工程研 究所 山西 太
摘
要: 基于有 限元 分析软件A ss NY ,对滚 动轴承进 行非 线性接触 分析 ,得到其 受载过程 中的应 力和应 变分布情 况 将 计算结 果同赫 兹解 比较 ,二者较 为接
式 中, :00 3 3 . 6 p, 2
、
y是接 触 区尺寸 ,可 通过 图 表查 出 。对于轴 承钢 可 取值 为 l 。
赫 兹接触 应 力计算 式 表述 如下 : 最 大赫兹 接触 应 力:
p一
考
=
⑤
图1 边 界条件 及 加载模 型 3 4 非线性 有 限元 求解结 果分 析
cn at 7单 元 。 ot c 14
其 中 为接触 体 的 主 曲率 ,分 别 为半 径 , h,听2 , 对于轴 承沟 道 的凸面 取正 值 ,凹面 取 负值 。
3 3 施 加边界 条件 及载 荷 .
根 据赫 兹接 触理 论 ,接触 面椭 圆的 长 半轴瘌 短半 轴b 算式为 ; 计 a e£ 1E ③ , b=
本 文 网格划 分 采用 8 节点 离散 三维 实 体单元 s ld5 o i4 。轴承 的 内外 圈采 用 L IE S Z 定义线 长 ,扫略 生成 网格 ;滚 动体 不能 直接 扫略 生成 网格 ,处理 方
法 是 : 中 问 和 两边 的球 体 分 别通 过 球 心 切 分 为 形状 大 小 相 同 的 四份 和 两 份 , 定义 各 自的源 面 和 目标 面扫 略分 网,这 样 能获得 比通过 直接 自由划 分 的 方法 较 为均 匀 的网 格 。同 时为 了节 省 资源 和提 高计 算 精度 ,采 用接 触 部 位 细 化 网 格 的 方 法 。划 分完 网格 后 模 型 共 有 40 5 单元 ,46 5 节 点 5 5个 96 个
非线性有限元 第5章接触问题的非线性问题

PAi PBi
(i= x , y , z )
(5.8) (5.9)
Az Bz 0 z
Ai Bi
(i= x , y )
同时要满足沿接触面的切平面方向不滑动的条件:
PBz 0 和 PB2x PB2y f PBz
以上式中, 0 z 是接触面在 z 方向的初始间隙,f 是接触面之间的滑动摩擦系数。 (2) 滑动接触条件
Q
向接触力是不可逆的。 因此,凡是考虑接触面切向摩擦力的接触问题,都应当按复杂加载过程来研究,即通过 增量的方式求解。对于不考虑摩擦的可逆过程,是一种简单加载过程,可以一步加载完成求 解。 5.3 弹性接触问题有限元基本方程和柔度法求解 假设 A、B 是相互接触的两个物体,为了研究的方便,将它们分开,代之以接触力 PA B 和 P ,如图 5.4 所示。然后建立各自的有限元支配方程:
K 2δ 2 R2
(5.2)
再由式(5.2)解得δ 2 ,进一步计算接触力 P2 ,将δ 2 和 P2 代入接触条件,验算接触条件是
否满足。这样不断的迭代循环,直至δ n 和 Pn 满足接触条件为止,此时得到的解答就是真实 接触状态下的解答。 在以上的研究中, 没有考虑接触面的摩擦力。 不考虑摩擦力的接触过程是一种可逆的过 程,即最终结果与加载途径无关。此时,只需要进行一次加载,就能得到最终稳定的解。如 果考虑接触面的摩擦力,接触过程就是不可逆的,必须采用增量加载的方法进行接触分析。 1973 年,Tusta 和 Yamaji 的文章详细讨论了接触过程的可逆性和不可逆性。 从 Wilson 和 Parsons 的方法可看出, 每一次接触状态的改变, 都要重新形成整体劲度矩 阵,求解全部的支配方程,既占内存,又费机时。实际上,接触状态的改变是局部的,只有 与接触区域有关的一小部分需要变动,为此又提出一些改进的方法。 1975 年, Francavilla 和 Zienkiewicz 提出相对简单的柔度法。 图 5.1 示出两个相互接触的物体 A 和 B,假定 A 上有外力 R 作用,B 有固定边界。接触面作用在 A 上的接触力是 PJ ,作用在 B 上的接 触力是 PJ ,对于二维问题,
桩-土-桩相互作用有限元接触分析

桩-土-桩相互作用有限元接触分析摘要:桩土体作为一个共同工作的系统,广泛存在于土木工程实践中,是典型的接触问题之一,对桩-土-桩相互作用的研究也是工程十分关心的,其中桩身摩阻力的分布更是关键所在。
本文基于有限元数值分析方法软件对此进行了深入研究。
关键词:有限单元法;接触非线性;桩土相互作用;桩侧摩阻力中图分类号:TU43 文献标识码:A 文章编号:1006-4311(2010)11-0108-020 引言桩土相互作用问题的实质是固体力学中不同介质的接触问题,具体表现为材料非线性、接触非线性等。
目前,有限单元法是解决复杂空间结构静、动力问题、弹塑性问题最有效的数值方法之一。
本文对桩土相互作用中接触问题进行分析时主要采用接触非线性有限元法,利用ABAQUS有限元软件进行研究。
1 ABAQUS软件概述ABAQUS是功能强大的有限元法软件[1,2],提供了广泛的功能且使用起来十分简明。
对于非线性分析,ABAQUS能自动选择合适的荷载增量和收敛精度,且拥有十分丰富的、可模拟任意实际形状的单元库。
2 ABAQUS桩土接触分析中需解决的问题2.1 单元类型的选择在接触模拟中采用二阶单元会引起接触面上等效节点力的计算出现混淆,因此接触面两侧的单元一般不宜采用二阶单元,只能采用线性单元。
2.2 主从接触面的建立可以通过定义接触面(surface)来模拟接触问题,本文所涉及的桩土体之间的接触面主要有两类:①桩侧单元构成的柔性接触面(桩侧土体表面)或刚性接触面(桩表面);②桩底土体一般采用节点构成的接触面,选取桩底土体节点时,不包含己定义在柔性接触面上的节点。
在模拟过程中,接触方向总是主面的法线方向,从面上的节点不会穿越主面,但主面上的节点可以穿越从面。
一般遵循以下原则:①应选择刚度较大的面作为主面,对于刚度相似的两个面,应选择网格较粗的面作为主面;②主面不能是由节点构成的面,并且必须是连续的;③如果接触面在发生接触的部位有很大的凹角或尖角,应该将其分别定义为两个面;④如果两个接触面之间的相对滑动小于接触面单元尺寸的20%,选用小滑动,否则选用有限滑动。
有限元非线性分析

下表简要列出了线性和非线性有限元分析之间的主要不同。关于荷载-位移关系、应力-应变关系、应力-应变度量 等主要不同将在本章详细介绍。
序号 1.
特征 荷载-位移关系
2.
应力-应变关系
3.
比例缩放
4.
线性叠加
5.
可逆性
6.
求解序列
7.
计算时间
8.
用户与软件的交互
13.3 非线性的类型
2)对数应变和真实应力 对数应变/自然应变/真实应变是度量大应变的方法,计算公式如下:
它是非线性应变的度量,因此是关于最终长度的非线性函数。与线性应变相比,对数应变(或真实应变)是可加
的。考虑一个初始长度为1m的杆经过下面3步的变形: 第1步: 从1m 变形至1.2m 第2步:从1.2m 变形至1.5m 第3步:从1.5m变形至2m 在下表中我们比较了工程应变和真实应变。可以清楚地看到,只有真实应变是可加的,因此在非线性分析中应该
13.6 非线性静力分析的一般流程
一个典型的非线性静力分析项目需要以下步骤:
网格划分:有限元模型的创建是有限元分析一个非常重要的步骤,不论进行什么样的分析。在第4-7章已经讨论过对 于某些应用的如何选择适当的单元类型。FEA小组会得到零件的几何数据,需要对这些几何进行网格划分以得到零件 网格。当装配中所有的零件划分网格后,使用适当的连接单元把它们都连接在一起如CWELD或CBUSH。一般来说, 四边形单元和六面体单元优于三角形单元、楔形单元和四面体单元。应该注意模型中的关键特征,比如圆角、孔和倒 角。如果在两个平行表面之间有紧固件或焊接,应该尽量在两个面上创建相似的网格。这将有助于焊接单元或刚性单 元垂直于表面而不破坏壳单元。然而,许多有限元分析(FEA)代码支持不依赖于节点焊接,而是基于绑定接触。这 允许用户在两个焊接零件之间创建不依赖于节点的连接单元。建议首先对复杂零件进行网格划分,然后对简单或平面 几何进行网格划分以保证良好的单元质量。需要用适当的方式来模拟夹紧、铰接和焊接以在结构中正确地传递荷载。 为单元定义适当的刚度和预荷载以得到更高的精度。如果荷载从结构上的某个面传递到另一个面上,应该在两个面间 定义接触。每个FEA代码都有自己的接触参数输入格式。一个典型的接触定义需要主从节点或单元,摩擦系数,接触 面间的间隙和接触算法。
第18章接触问题有限元分析技术

第18章接触问题的有限元分析技术第1节基本知识接触问题是一种高度非线性行为,需要较大的计算资源,为了进行准确而有效的计算,理解问题的特性和建立合理的模型是很重要的。
接触问题存在两个较大的难点:其一,在求解问题之前,不知道接触区域,表面之间是接触或分开是未知的、突然变化的,这些随载荷、材料、边界条件和其它因素而定;其二,大多数的接触问题需要计算摩擦,有几种摩擦和模型可供挑选,它们都是非线性的,摩擦使问题的收敛性变得困难。
一、接触问题分类接触问题分为两种基本类型:刚体─柔体的接触和半柔体─柔体的接触。
在刚体─柔体的接触问题中,接触面的一个或多个被当作刚体,(与它接触的变形体相比,有大得多的刚度),一般情况下,一种软材料和一种硬材料接触时,问题可以被假定为刚体─柔体的接触,许多金属成形问题归为此类接触;另一类,柔体─柔体的接触,是一种更普遍的类型,在这种情况下,两个接触体都是变形体(有近似的刚度)。
ANSYS支持三种接触方式:点─点、点─面和平面─面。
每种接触方式使用的接触单元适用于某类问题。
二、接触单元为了给接触问题建模,首先必须认识到模型中的哪些部分可能会相互接触,如果相互作用的其中之一是一点,模型的对立应组元是一个节点。
如果相互作用的其中之一是一个面,模型的对应组元是单元,例如梁单元,壳单元或实体单元。
有限元模型通过指定的接触单元来识别可能的接触匹对,接触单元是覆盖在分析模型接触面之上的一层单元。
下面分类详述ANSYS使用的接触单元和使用它们的过程。
1.点─点接触单元点─点接触单元主要用于模拟点─点的接触行为,为了使用点─点的接触单元,需要预先知道接触位置,这类接触问题只能适用于接触面之间有较小相对滑动的情况(即使在几何非线性情况下)。
如果两个面上的节点一一对应,相对滑动又以忽略不计,两个面挠度(转动)保持小量,那么可以用点─点的接触单元来求解面─面的接触问题,过盈装配问题是一个用点─点的接触单元来模拟面─与的接触问题的典型例子。
第8章 接触问题的有限元法

18
小滑动和有限滑动 当选用小滑动公式时,ABAQUS从模拟开始就
建立从属表面和主控表面的关系。ABAQUS确定主 控表面的哪个部分与从属表面的每一个节点发生关 系。这种关系在整个分析中保持不变。如果分析包 括几何非线性,小滑动公式需要考虑主控表面的任 何转动与变形对接触力的影响。如果不包括几何非 线性问题,可忽略主控表面的任何转动和变形,认 为加载路径是固定的。
一对接触面的法线方向应该相反,如果法线方向 错误,ABAQUS理解为过盈接触,因此无法收敛。
17
从属表面和主控表面
ABAQUS采用主控—从属接触算法:从属表面 的节点不能穿透主控表面的任何部分。这种算法对 主控表面没有限制,它可以穿透从属表面。为了获 得接触模拟的最好结果,必须认真和准确地定义从 属和主控表面:
力引起的等效节点力向量
和罚系数有关的矩阵
F 'k+1 = −Λ'T T N cd c − Λ'd '
整体坐标系下接触力等效节点力向量
对称阵 F k+1 = −(N c )T T Λ'T T N cd c − (N c )T T Λ'd '
F k+1 = −Kcd c + F̃ k+1 --系统的等效节点接触力向量
采用有限元法分析接触问题时,需要分别对接触 物体进行有限元网格剖分,并规定在初始接触面上, 两个物体对应节点的坐标位置相同,形成接触对。整 体和局部坐标系下,两个物体由于接触载荷引起的等 效节点力矢量分别记为
3
{ } F Ι = F1Ι , F2Ι , F3Ι T
机械设计中有限元分析的几个关键问题

机械设计中有限元分析的几个关键问题机械设计中有限元分析是一种重要的工程分析方法,通过对机械结构进行有限元分析,可以评估结构的强度、刚度、稳定性等性能,为设计提供依据,提高产品的可靠性和安全性。
在进行有限元分析时,有一些关键问题需要特别注意,本文将就机械设计中有限元分析的几个关键问题进行探讨。
一、材料特性的选择在进行有限元分析时,首先需要确定材料的特性,例如弹性模量、屈服强度、断裂韧性等参数。
这些参数的选择对于有限元分析结果的准确性有着重要的影响。
在实际工程中,材料的特性往往是不确定的,因此需要根据实际情况进行合理的选择。
对于复合材料等非均质材料,其材料特性更为复杂,需要进行更为精细的分析和计算。
二、网格的生成和质量有限元分析是通过将结构划分为有限个小单元来进行分析计算的,这些小单元即为网格单元。
网格的生成和质量直接关系到分析结果的准确性。
不合理的网格划分可能会导致计算结果的误差,甚至影响到整个分析的可靠性。
合理的网格生成和质量的控制是进行有限元分析时的关键问题之一。
三、边界条件的确定在进行有限元分析时,需要明确结构的边界条件,包括约束边界和加载边界。
边界条件的确定关系到分析结果的可靠性和准确性。
合理的边界条件能够更好地模拟实际工况,得到真实的分析结果。
不合理的边界条件可能导致分析结果的失真,甚至无法得到可靠的结论。
四、材料非线性和接触非线性在实际工程中,材料的行为往往是非线性的,包括弹塑性、损伤、断裂等。
在一些结构的分析中,考虑到接触的影响也需要考虑到接触非线性。
这些非线性因素对于分析结果有着重要的影响,需要在有限元分析中予以充分考虑。
五、模态分析和稳定性分析除了结构的强度和刚度等静态性能外,对于一些关键结构还需要进行模态分析和稳定性分析。
模态分析用于评估结构的振动特性,稳定性分析则用于评估结构在受到外部载荷时的稳定性。
这些分析对于确保机械结构的安全性和可靠性至关重要。
六、敏感性分析和可靠度分析在进行有限元分析时,还需要进行敏感性分析和可靠度分析。
橡胶O形密封圈的非线性有限元分析

收稿日期:2004-08-11作者简介:王伟(1971-),男,硕士,主要从事轮胎和橡胶制品结构有限元分析及其应用的研究1E 2mail:wdavid1@1631com 1橡胶O 形密封圈的非线性有限元分析王 伟 赵树高(青岛科技大学高分子科学与工程学院橡塑材料与工程教育部重点实验室 山东青岛266042)摘要:借助于大型非线性有限元分析软件M S C 1MARC,建立了橡胶O 形圈与沟槽接触的非线性有限元分析模型,分析了橡胶O 形圈在安装和使用中的接触变形、接触宽度和密封界面上的接触应力分布规律,从而为进一步可靠设计、优化橡胶O 形圈提供了理论依据。
关键词:橡胶O 形密封圈;接触问题;非线性有限元中图分类号:T Q33611 文献标识码:A 文章编号:0254-0150(2005)4-106-2Nonli n ear F i n ite Ele m ent Ana lysis of Rubber O 2sea li n g Ri n gW a ng W e i Zhao S hugao(Key Laborat ory of Rubber 2p lastics ofM inistry of Educati on,School of Poly mer Science &Engineering,Q ingdao University of Science &Technol ogy,Q ingdao 266042,China )Abstract:W ith the help of commercial nonlinear finite element analysis code,MSC .MARC,a nonlinear finite elementmodel for rubber O 2sealing ring and its groove were set up.The contact defor mation,contact width and the distributi on of contact stress within the sealing interface were discussed 1It puts for ward a theory base on designing and op ti m izing rubber O 2sealing ring .Keywords:rubber O 2sealing ring;contact p r oblem;nonlinear finite element 橡胶密封件广泛应用于机械设备中,其性能直接影响设备的正常工作,密封件失效有时甚至会引起重大事故。
ANSYS非线性接触问题分析汇总

ANSYS 分线性接触问题分析汇总接触非线性是一门复杂的学科,ANSYS 关于计算非线性接触的设置选项多只又多,很多人摸不到头脑,本文就基于ANSYS 模拟过的几个接触实例,研究了相关设置选项对接触结果的影响。
实例1:橡胶密封圈配合接触研究—非线性求解设置对结果的影响密封圈配合模型简图见图1,左右两端为刚体,中间圆部分为橡胶密封圈,将刚体2沿刚体1方面移动,从而实现橡胶圈密封作用,采用plane182单元,设置轴对称行为,建立橡胶密封圈与刚体接触模型,见图2。
图1 密封圈配合模型简图 图2 密封圈配合有限元模型图接触对采用默认设置,摩擦系数取0.10,研究非线性求解器设置对收敛方面的影响,大变形静态(Large Displacement Static )效应打开,自动时间步长(Automatic time stepping )打开,子步数(Number of substeps )设置为50,线性搜索(Line search )打开。
1 收敛准则对结果的影响此实例收敛准则默认采用力收敛结合力矩收敛准则(基于L2范数),收敛容差(Tolerance )默认为0.001,工程上认为0.05的收敛容差足够满足要求。
表 1 收敛容差对计算结果的影响收敛容差 最大应力/ MPa报错与否? 0.001 4.12364报错 0.05 4.12785 报错 0.14.12996报错查看报错信息,见图3,表示单元过于扭曲,建议提高子步数或降低时间步长,需要提高网格质量,也要考虑材料属性,接触对及约束方程的合理性,若在第一步迭代就如此,需要预先执行单元形状检查。
图3 报错信息刚体1刚体2密封圈橡胶密封圈配合Von Mises应力云图见图4。
图4 橡胶密封圈配合Von Mises应力2 子步数对结果的影响此实例子步数设置为50、100、200、500,收敛容差(Tolerance)默认为0.001,研究子步数对收敛的影响。
ANSYS非线性接触问题分析汇总

ANSYS 分线性接触问题分析汇总接触非线性是一门复杂的学科,ANSYS 关于计算非线性接触的设置选项多只又多,很多人摸不到头脑,本文就基于ANSYS 模拟过的几个接触实例,研究了相关设置选项对接触结果的影响。
实例1:橡胶密封圈配合接触研究—非线性求解设置对结果的影响密封圈配合模型简图见图1,左右两端为刚体,中间圆部分为橡胶密封圈,将刚体2沿刚体1方面移动,从而实现橡胶圈密封作用,采用plane182单元,设置轴对称行为,建立橡胶密封圈与刚体接触模型,见图2。
图1 密封圈配合模型简图 图2 密封圈配合有限元模型图接触对采用默认设置,摩擦系数取0.10,研究非线性求解器设置对收敛方面的影响,大变形静态(Large Displacement Static )效应打开,自动时间步长(Automatic time stepping )打开,子步数(Number of substeps )设置为50,线性搜索(Line search )打开。
1 收敛准则对结果的影响此实例收敛准则默认采用力收敛结合力矩收敛准则(基于L2范数),收敛容差(Tolerance )默认为0.001,工程上认为0.05的收敛容差足够满足要求。
表 1 收敛容差对计算结果的影响收敛容差 最大应力/ MPa报错与否? 0.001 4.12364报错 0.05 4.12785 报错 0.14.12996报错查看报错信息,见图3,表示单元过于扭曲,建议提高子步数或降低时间步长,需要提高网格质量,也要考虑材料属性,接触对及约束方程的合理性,若在第一步迭代就如此,需要预先执行单元形状检查。
图3 报错信息刚体1刚体2密封圈橡胶密封圈配合Von Mises应力云图见图4。
图4 橡胶密封圈配合Von Mises应力2 子步数对结果的影响此实例子步数设置为50、100、200、500,收敛容差(Tolerance)默认为0.001,研究子步数对收敛的影响。
非线性有限元

(三)混合法 如对同一非线性方程组混合使用增量
法和迭代法,则称为混合法或逐步迭代法。 一般在总体上采用Euler增量法,而在
同一级荷载增量内,采用迭代法。
Ki-1
刚度的取值可根据给定的应力-应变曲 线导出。若每级计算都采用上一级增量计算 终了时的刚度值,则称为始点刚度法。
Ki-1
始点刚度法类似于解微分方程初值问题 的欧拉(Euler)折线法,计算方法简单但计算 精度较低,容易“漂移”。
若采用中点刚度法则可以提高精度。该 法类似于解常微分方程初值问题的龙格-库塔 (Runge-Kutta)法,包括中点切线刚度法 和中点平均刚度法。
(1) 直接迭代法 对非线性方程组
设其初始的近似解为 ,由此确定近似的
矩阵
可得出改进的近似解
重复这一过程,以第i次近似解求出第i+1 次近似解的迭代公式为直接迭代法
对非线性方程组
直到 变得充分小,即近似解收敛时,终止迭代。
在迭代过程中,得到的近似解一般不会满足 作为对平衡偏离的一种度量,称为失衡力。
q-Newton—Raphson迭代法的计算过程
(2)初应力法 如果在弹性材料内确实存在初应力 ,则材料的应力应变关系为
由上式及虚功原理可导出单元的结点力为
集合单元得出以下的有限元方程 式中, 为由初应力 引起的等效结点荷载
初应力法就是将初应力看作是变化的, 以此来反映应力和应变之间的非线性关系。 通过不断地调整初应力,使线弹性解逼近非 线性解。
接触非线性 由于接触体的变形和接触边界的摩擦作用,
使得部分边界条件随加载过程而变化,且不 可恢复。这种由边界条件的可变性和不可逆 性产生的非线性问题,称为接触非线性。
材科非线性有限元法 材料非线性是由本构关系的非线性引
浅谈结构有限元分析中的接触问题
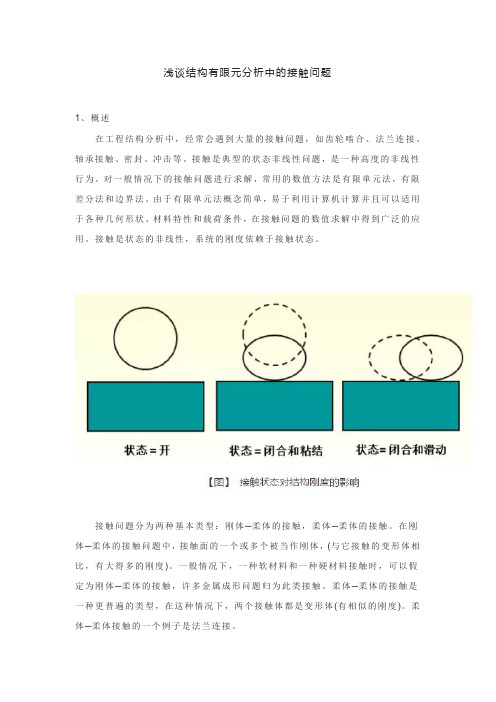
浅谈结构有限元分析中的接触问题1、概述在工程结构分析中,经常会遇到大量的接触问题,如齿轮啮合、法兰连接、轴承接触、密封、冲击等。
接触是典型的状态非线性问题,是一种高度的非线性行为。
对一般情况下的接触问题进行求解,常用的数值方法是有限单元法,有限差分法和边界法。
由于有限单元法概念简单,易于利用计算机计算并且可以适用于各种几何形状、材料特性和载荷条件,在接触问题的数值求解中得到广泛的应用。
接触是状态的非线性,系统的刚度依赖于接触状态。
接触问题分为两种基本类型:刚体─柔体的接触,柔体─柔体的接触。
在刚体─柔体的接触问题中,接触面的一个或多个被当作刚体,(与它接触的变形体相比,有大得多的刚度)。
一般情况下,一种软材料和一种硬材料接触时,可以假定为刚体─柔体的接触,许多金属成形问题归为此类接触。
柔体─柔体的接触是一种更普遍的类型,在这种情况下,两个接触体都是变形体(有相似的刚度)。
柔体─柔体接触的一个例子是法兰连接。
2、接触算法介绍接触问题可描述为求区域内位移场U,使得系统的势能在接触边界条件的约束下达到最小,即式中K、U、F分别为通常有限元位移法中的刚度矩阵、未知结点位移向量和结点荷载向量,为两物体间的穿透量。
接触约束算法就是通过对接触边界约束条件的适当处理,将上式所示的约束优化问题转化为无约束优化问题求解。
根据无约束优化方法的不同,主要可分为罚函数方法、Lagrange乘子法及增广Lagrange乘子法等。
(1)罚函数法数学上要求有限的穿透量在交界面处产生接触力。
保持系统平衡需要此接触力。
为了平衡,必须大于零。
然而,实际的接触体相互不穿透。
因此,为了最高的精度,应使发生在接触界面处的穿透量最小,这意味着,理想的接触刚度应该是个非常大的值。
然而,值太大会引起收敛困难。
如果接触刚度太大,一个微小的穿透将会产生一个过大的接触力,在下一次迭代中可能会将接触面推开,用太大的接触刚度通常会导致收敛振荡,并且常会发散。
接触问题分析-10

经典的接触问题求解方法(2/3)
定解条件:
四类接触状态,对应的定解条件为:
1)开式
Fal Fl Fbl Fbl 0
Байду номын сангаас
l x, y, z
2
引言(2/5)
研究内容:
接触模式问题:描述两接触体间的力的传递、描述不同载荷 下接触状态的变化;(解决如何描述的问题)
几何约束问题:表示接触面上两物体位移所要满足的条件; (解决到底以什么具体形式来描述、即怎样描述?)
摩擦定律问题:反映接触面上力与位移或压力与切向力之间 的关系;
求解方法问题:建立数学方程并加以求解。
6
经典的接触问题求解方法(1/3)
一般采用三个假设: 接触表面是凸的、连续的; 接触表面服从库仑摩擦定律; 接触模式是点-点接触模式。
z(法向)
A
y
B
x (切平面)
(a)
(b)
可能接触区
接触的A、B两物体
(a) 可能接触区;(b) 接触区局部坐标系
r表示接触点对间的间隙
2021/7/5
边界的接触状态(判定性条件) 分别为:
1 2
ij
ij
1 T
2
D
位移场中,真实解使得系统的总势 能取最小值。
find
min
ui (ui )
H
ui ui ui , on u
s.t.n 0
2021/7/5
12
数学规划方法求解接触问题(4/17)
接触问题的势能变分原理及其等价形式(续)
有限元接触分析

第五章接触问题的非线性有限元分析5.1引言在工程结构中,经常会遇到大量的接触问题。
火车车轮与钢轨之间,齿轮的啮合是典型的接触问题。
在水利和土木工程中,建筑物基础与地基,混凝土坝分缝两侧,地下洞室衬砌与围岩之间,岩体结构面两侧都存在接触问题。
对于具有接触面的结构,在承受荷载的过程中,接触面的状态通常是变化的,这将影响接触体的应力场。
而应力场的改变反过来又影响接触状态,这是一个非线性的过程。
由于接触问题对工程实践的重要性,本章将作为专门问题进行研究。
最早对接触问题进行系统研究的是H. Hertz,他在1882年发表了《弹性接触问题》一书中,提出经典的Hertz弹性接触理论。
后来Boussinesg 等其他学者又进一步发展了这个理论。
但他们都是采用一些简单的数学公式来研究接触问题,因而只能解决形状简单(如半无限大体)、接触状态不复杂的接触问题。
二十世纪六十年代以后,随着计算机和计算技术的发展,使应用数值方法解决复杂接触问题成为可能。
目前,分析接触问题的数值方法大致可分为三类:有限元法、边界元法和数学规划法。
数学规划法是一种优化方法,求解接触问题时,根据接触准则或变分不等式建立数学模型,然后采用二次规划或罚函数方法给出解答。
边界元方法也被用来求解接触问题,1980年和1981年,Anderson先后发表两篇文章,用于求解无摩擦弹性接触和有摩擦弹性接触问题。
近年来虽有所发展,但仍主要用于解决弹性接触问题。
就目前的发展水平来看,数学规划法和边界元法只适合于解决比较简单的弹性接触问题。
对于相对复杂的接触非线性问题,如大变形、弹塑性接触问题,还是有限元方法比较成熟、比较有效。
早在1970年,Wilson和Parsons提出一种位移有限元方法求解接触问题。
Chan和Tuba,Ohte等进一步发展了这类方法。
它的基本思想是假定接触状态,求出接触力,检验接触条件,若与假定的接触状态不符,则重新假定接触状态,直至迭代计算得到的接触状态与假定状态一致为止。
接触问题的有限元分析

U
1 2
λT
E
p
1
λ
6.1 接触边界的有限元算法
(2)接触约束算法
2) Lagrange 乘子法与增广Lagrange 乘子法
U
1 2
λT
E p
1
λ
min
U,
λ
1 2
UT
K
U
UT
F
g
U
T
λ
1 2
λT
Ep
λ
U
1 2
λT
Ep
1
λ
解收敛于
min U, λ 1 UT K UUT F g U T λ 解
虚力法:用沿边界的虚拟等效压力来模拟接触状态, 这样在每次迭代中并不重新形成刚度矩阵,所做的只是 回代工作。
有限元混合法:以结点位移和接触力为未知量,并 采用有限元形函数插值,将接触区域的位移约束条件和 接触力约束条件均反映到刚度矩阵中去,构成有限元混 合法控制方程
6.1 接触边界的有限元算法
(1)直接迭代法
惩罚函数法对接触约束条件的处理是通过在势能泛函中
增加一个惩罚势能。
p
U
1 2
P T
EP
P
惩罚因子
嵌入深度,是节点位移的函数
接触问题就等价于无约束优化问题:
min U U p U
K K U FF
p
p
6.1 接触边界的有限元算法
(2)接触约束算法
1)罚函数方法
K K U FF
p
6.1 接触边界的有限元算法
(2)接触约束算法 2) Lagrange 乘子法与增广Lagrange 乘子法
min U, λ 1 UT K UUT F g U T λ
工程有限元方法接触非线性讲义PPT(30页)

反向,使得解的过程不稳定
4 接触问题的有限元方程
• 4.1 接触界面的离散处理
– 接触块
接触块(或线):单元上处于接触面上的面(或边)
二维问题的主被动接触线
– 接触点对
罚函数法
惩罚因子
z* x, y. 2x2 2xy y2 18x 6y x y2
z* 4x 2 y 18 2 x y 0
x
z* 2x 2 y 6 2 x y 0
y
x 12 ; y 12 15 / 11/
y 12
3 接触问题的求解方案
原问题中不包含 接触约束条件的
3. 利用接触面上和上述等式约束所对应的动力学或运动学的不等式 约束条件作为校核条件对解的结果进行检查 ➢ 若不违反接触条件,则完成本步求解并转入下一增量步 ➢ 否则转入1再次进行搜寻和迭代求解,直到每一点的解都满足 校核条件
3 接触问题的求解方案
• 3.2 接触面的定解条件和校核条件
接触状态
定解条件
有限元方法与
• 接触非线性概述 • 接触界面条件 • 接触问题的求解方案 • 接触问题的有限元方程 • 有限元方程的求解方法
1 接触非线性概述
接触非线性的来源:由随时间发生变化的接触状态引起,主要 包括
(1) 接触界面的区域大小和相互位置以及接触状态不仅事先未知,且都随时 间发生变化,需要在求解过程中确定
2 接触界面条件
• 2.3 切向接触条件
– (1) 无摩擦模型
若两个物体的接触面是绝对光滑的,或 者相互间的摩擦可以忽略,则采用无摩 擦模型
ABAQUS接触问题浅析_宫龙颖

煤炭科技#机电与信息化ABAQUS接触问题浅析宫龙颖(煤炭科学研究总院检测研究分院,北京市朝阳区,100013)摘要分别讨论了在ABAQU S两种求解器下解决接触问题的方法,并就其中容易引起分析结果不正确或者不收敛之处予以重点阐述,力图最大限度减少在分析此类问题时出现的错误,并加深对它的理解。
关键词接触非线性有限元ABAQU S中图分类号T D40文献标识码BOn the use of ABAQUS for analyzing the problem of contactsGong Lo ng ying(T est Br anch of China Co al R esear ch Institute,Q ing niang ou Dong lu5,Beijing100013,China)Abstract Discussing t he methods to solve the problem o f contact s under2different solvers o f ABA QU S,this pa per fo cuses on t he points w her e w r ong r esult s o r abort ive analy sis ma y cro p out.T his paper also aims at minim-i zing the po ssibility of mistakes during the course of analyzing and acquir ing a deepened co mpr ehension abo ut the use of finit e element as a to ol for analysis and the problem o f contacts pr oper.Key words contact,no n-linear,finite element,A BAQ U S1概述在工程技术中,接触问题的应用十分普遍。
