第八章 绕流运动
合集下载
8第八章-边界层理论基础和绕流运动
8第⼋章-边界层理论基础和绕流运动第⼋章边界层理论基础和绕流运动8—1 设有⼀静⽌光滑平板宽b ＝1m ，长L ＝1m ，顺流放置在均匀流u ＝1m/s 的⽔流中，如图所⽰，平板长边与⽔流⽅向⼀致，⽔温t ＝20℃。
试按层流边界层求边界层厚度的最⼤值δmax 和平板两侧所受的总摩擦阻⼒F f 。
解：20℃⽔的运动粘度ν＝1.003?10-6 m 2/s 密度3998.2/kg m ρ=6119970091.00310ν-?===?L uLRe 因为 56310997009310?<=按层流边界层计算。
max 1/25.4470.0055m Re L L δ===3f 1/21.46 1.4610-===?L C Re 223998.2122 1.461011N 1.46N 22f ff u F C A ρ-?=== 8—2 设有极薄的静⽌正⽅形光滑平板，边长为a ，顺流按⽔平和铅垂⽅向分别置放于⼆维恒定均速u 的⽔流中，试问：按层流边界层计算，平板两种置放分别所受的总摩擦阻⼒是否相等，为什么？解：因为两种置放情况的物理模型和数学模型及其分析、推导所得计算公式是相同的，所以两种情况平板所受的总摩擦阻⼒相等。
8—3 设有⼀静⽌光滑平板,如图所⽰,边长1m,上宽0.88m,下宽0.38m,顺流铅垂放置在均匀流速u =0.6m/s 的⽔流中，⽔温t=15℃。
试求作⽤在平板两侧的总摩擦阻⼒F f 。
注：若为层流边界层，C f 按式（8—24）计算。
解：由表1—1查得，15℃时⽔的密度ρ=999.13/kg m ，运动粘度ν=1.139×10-6m 2/s 。
⾸先判别流态，计算平板上宽雷诺数560.60.884635655101.13910-?===Re ，按层流边界层计算。
设z 轴铅垂向上,平板宽度x 为0.38+0.5z ，阻⼒系数C f 按式（8-24）计算,即12f 60.6(0.380.5)1.328 1.13910--?+??==z C1521.328 5.2677810(0.380.5)z -轾=创?犏臌总摩擦阻⼒F f 按式(8—20)计算，f f12012(0.380.5)d 2F C u z z r =?ò11522 1.328 5.2677810(0.380.5)z -轾=创创+犏臌ò题8-1图21999.10.6(0.380.5)d 2z z 创创+ 110.658(0.380.5)d z z =ò。
第8章 边界层理论基础及绕流运动
ux
∂ux ∂x
+ uy
∂ux ∂y
=
−
1 ρ
∂p ∂x
+
ν
∂ 2u x ∂y 2
∂ux ∂x
+
∂uy ∂y
=
0
边界条件： y =∞（或y = δ），ux = U0 y = 0，ux = 0， uy = 0
其中 U0 = U0(x) =边界层外界限上外部流动的流速 且 p = p(x) = 边界层外界限上外部流动的压强
=
1 2
δ
∫ ∫ δ2 =
δ 0
ux u0
⎜⎜⎝⎛1 −
ux u0
⎟⎟⎠⎞dy
=
δ
1η(1− η)dη = 1 δ
0
6
∫ ∫ ( ) δ3 =
δ 0
ux u0
⎜⎜⎝⎛1 −
ux 2 u0 2
⎟⎟⎠⎞dy
=
δ
1η 1− η2
0
dη = 1 δ 4
10
8.2 边界层微分方程
——利用边界层的性质对粘性流体基本方程（纳维－斯托克斯方 程）的简化。
⎟⎠⎞
=
−δ
dp dx
− τ0
其中: dp/dx和u0应由外部流动求出 → 三个未知量：τ0、δ、ux
应用动量积分方程求解边界层问题的步骤： (1) 补充 ux (x, y)、τ0(δ)关系式，积分方程转变为δ的常微分方程
（2）求解方程 → δ(x) →τ0(x) → 总阻力→ 计算位移厚度等其他 参数。
∫ ∫∫ ∑ 积分形式的动量方程
∂ ∂t
ρurdV
cv
+
cs
ρurundA
流体力学第八章 绕流运动
2 2
由此得 24 Cd Re
（8-70）
二、悬浮速度 设在上升的气流中，小球的密度为 m，大于气体的密 度 , 即 m 。小球受力情况如下。 方向向上的力有： u 0 2 1 2 2 F C A C d u 绕流阻力 d d 0 1 3 D 2 8 FB d g 浮力 6 方向向下的力有： 1 重力 G d 3 m g
绕流物体的摩擦阻力作用，主要表现在附面层 内流速的降低，引起动量的变化。
附面层的动量方程为 d d dp 2 u x dy U u x dy 0 dx 0 dx 0 dx
、 p、 u x、 U 和 0。 附面层动量方程有五个未知数： dp 其中U可以用理想流体的势流理论求得， 可
u y
为平面无旋流动。
u x x y
平面无旋流动的速度势函数为 d u x dx u y dy 并满足拉普拉斯方程：
2 2 2 0 2 x y
义一个函数 , 令u x ,uy y x 满足上式的函数称为流函数。
由不可压缩流体平面流动的连续性方程可以定
第八章 绕流运动
第一节 无旋流动 第二节 平面无旋流动 第三节 几种简单的平面无旋运动 第四节 势流叠加 第五节 绕流运动与附面层基本概念 第六节 附面层动量方程 第七节 平板上层流附面层的近似计算 第八节 平板上紊流附面层的近似计算 第九节 曲面附面层的分离现象与卡门涡街 第十节 绕流阻力和升力
因此，无旋流动的前提条件是
u z u y y z u x u z z x u y u x x y 由不可压缩流体的连续性方程 u x u y u z 0 x y z 得出拉普拉斯方程 2 2 2 2 2 0 2 x z y
由此得 24 Cd Re
（8-70）
二、悬浮速度 设在上升的气流中，小球的密度为 m，大于气体的密 度 , 即 m 。小球受力情况如下。 方向向上的力有： u 0 2 1 2 2 F C A C d u 绕流阻力 d d 0 1 3 D 2 8 FB d g 浮力 6 方向向下的力有： 1 重力 G d 3 m g
绕流物体的摩擦阻力作用，主要表现在附面层 内流速的降低，引起动量的变化。
附面层的动量方程为 d d dp 2 u x dy U u x dy 0 dx 0 dx 0 dx
、 p、 u x、 U 和 0。 附面层动量方程有五个未知数： dp 其中U可以用理想流体的势流理论求得， 可
u y
为平面无旋流动。
u x x y
平面无旋流动的速度势函数为 d u x dx u y dy 并满足拉普拉斯方程：
2 2 2 0 2 x y
义一个函数 , 令u x ,uy y x 满足上式的函数称为流函数。
由不可压缩流体平面流动的连续性方程可以定
第八章 绕流运动
第一节 无旋流动 第二节 平面无旋流动 第三节 几种简单的平面无旋运动 第四节 势流叠加 第五节 绕流运动与附面层基本概念 第六节 附面层动量方程 第七节 平板上层流附面层的近似计算 第八节 平板上紊流附面层的近似计算 第九节 曲面附面层的分离现象与卡门涡街 第十节 绕流阻力和升力
因此，无旋流动的前提条件是
u z u y y z u x u z z x u y u x x y 由不可压缩流体的连续性方程 u x u y u z 0 x y z 得出拉普拉斯方程 2 2 2 2 2 0 2 x z y
绕流运动详解
第八章 绕流流动
本章主要讨论绕流问题，即外流问题。 首先将介绍粘性流体的运动微分方程， 然后将给出边界层的概念及其控制方 程，最后针对绕流流动现象的一些具 体问题进行了讨论。
第一节 边界层的概念
边界层：物体壁面附近存在大的速度梯度的薄层。
图7－1 绕平板的边界层示意图
我们可以用图7－1所示的绕平板的流动情况说明边层 层的概念。
对于某固定断面 是定值可提到积分号之外，v∞沿x方向
不变，可以提到对x的全导数之外，最后得到 沿x方向的变化
关系式
1 v 2 xC 15 2
当 x 0 ， 0 时， C0 ，因此
1 v 2 x 15 2
上式化简为
5.477 x
v
（4）
方程（4）是平板边界层厚度沿s方向的变化关系式。
把（4）代入（3）
即
Cf
1.46 1.46
vL
vL
Cf
1.46
1 ReL
（8）
ReL是以板长L为特征长度的Re数
二 平板紊流边界层的计算
假定整个平板上都是紊流边界层，首先补充边界层流速
分布关系式，紊流边界层内的流速分布用圆管中紊流光
滑区的速度分布，即
v
r vmax( r0
1
)7
应用到紊流边界层，速度分布为
vx
v
(y
边界层分离：边界层脱离壁面 1.分离现象 圆柱后部 在顺压梯度区（BC)：流体加速 在逆压梯度区（CE)：CS段减速S点停止 SE段倒流。 2.分离的原因 — 粘性 3.分离的条件 — 逆压梯度 4.分离的实际发生 — 微团滞止和倒流
图7－7
层流和湍流边界层都会发生分离，其本质是一致的，但不同 流态时在给定的曲面上的分离点位置差别很大。层流流动时， 速度较快的外层流体与内层流体的动量交换是通过粘性切应 力作用而产生的，紧靠壁面处的流体质点速度慢，动量小， 不能在逆压梯度下长时间的紧靠壁面，边界层在较前的位置 就发生了分离。相反，当边界层转变为湍流后，快速移动的 外层流体与内层流体强烈混合，使紧靠壁面的流体质点的平 均流速大大增加了，结果湍流边界层的分离点向下游移动。
本章主要讨论绕流问题，即外流问题。 首先将介绍粘性流体的运动微分方程， 然后将给出边界层的概念及其控制方 程，最后针对绕流流动现象的一些具 体问题进行了讨论。
第一节 边界层的概念
边界层：物体壁面附近存在大的速度梯度的薄层。
图7－1 绕平板的边界层示意图
我们可以用图7－1所示的绕平板的流动情况说明边层 层的概念。
对于某固定断面 是定值可提到积分号之外，v∞沿x方向
不变，可以提到对x的全导数之外，最后得到 沿x方向的变化
关系式
1 v 2 xC 15 2
当 x 0 ， 0 时， C0 ，因此
1 v 2 x 15 2
上式化简为
5.477 x
v
（4）
方程（4）是平板边界层厚度沿s方向的变化关系式。
把（4）代入（3）
即
Cf
1.46 1.46
vL
vL
Cf
1.46
1 ReL
（8）
ReL是以板长L为特征长度的Re数
二 平板紊流边界层的计算
假定整个平板上都是紊流边界层，首先补充边界层流速
分布关系式，紊流边界层内的流速分布用圆管中紊流光
滑区的速度分布，即
v
r vmax( r0
1
)7
应用到紊流边界层，速度分布为
vx
v
(y
边界层分离：边界层脱离壁面 1.分离现象 圆柱后部 在顺压梯度区（BC)：流体加速 在逆压梯度区（CE)：CS段减速S点停止 SE段倒流。 2.分离的原因 — 粘性 3.分离的条件 — 逆压梯度 4.分离的实际发生 — 微团滞止和倒流
图7－7
层流和湍流边界层都会发生分离，其本质是一致的，但不同 流态时在给定的曲面上的分离点位置差别很大。层流流动时， 速度较快的外层流体与内层流体的动量交换是通过粘性切应 力作用而产生的，紧靠壁面处的流体质点速度慢，动量小， 不能在逆压梯度下长时间的紧靠壁面，边界层在较前的位置 就发生了分离。相反，当边界层转变为湍流后，快速移动的 外层流体与内层流体强烈混合，使紧靠壁面的流体质点的平 均流速大大增加了，结果湍流边界层的分离点向下游移动。
同济大学流体力学(下) 朱立明 课件
流函数(?)、势函数性质
等流函数线与流线的关系； 等势函数线代表“等高线”的概念，流速为等高 线的梯度(速度方向)； 流体是从“低处向高处”流动。
流网：等流函数线和等势函数线
两线正交（证明）
0
§8-2、平面无旋流动
流函数与流量的关系
dq ux dy u y dx d
结果一样
M u v0 (1 ) sin 2 r 2 v0 r
§8-4、势流叠加
圆柱表面的速度分布： 圆柱表面的压强分布：
u r 0 u 2v sin 0
po
cp
2
v p
2 0
2
v2
p p0 2
2 v0
有限元法(任意微分方程)
用”区域”平均满足方程代替”点”满足的方 程
有限简单基本解法(无旋流体)
势流叠加（未知数少）
补充
复数变换
有一变换将z平面变换到 平面
1 z z
如在z平面上有一圆（r=1）
1 1 1 re i (r ) cos i(r ) sin r r re
Q AB Q CD Q AB dx x
2 Px u x dy dx U u x dy dx x 0 x 0
K AB dx x
K AC QACU
§8-7、附面层动量方程
p Px dx o dx x
2 0
v u 0 x y
2 i 0
无旋流
存在速度势Φ
u ,v x y
平面势流
平面流 不可压缩
等流函数线与流线的关系； 等势函数线代表“等高线”的概念，流速为等高 线的梯度(速度方向)； 流体是从“低处向高处”流动。
流网：等流函数线和等势函数线
两线正交（证明）
0
§8-2、平面无旋流动
流函数与流量的关系
dq ux dy u y dx d
结果一样
M u v0 (1 ) sin 2 r 2 v0 r
§8-4、势流叠加
圆柱表面的速度分布： 圆柱表面的压强分布：
u r 0 u 2v sin 0
po
cp
2
v p
2 0
2
v2
p p0 2
2 v0
有限元法(任意微分方程)
用”区域”平均满足方程代替”点”满足的方 程
有限简单基本解法(无旋流体)
势流叠加（未知数少）
补充
复数变换
有一变换将z平面变换到 平面
1 z z
如在z平面上有一圆（r=1）
1 1 1 re i (r ) cos i(r ) sin r r re
Q AB Q CD Q AB dx x
2 Px u x dy dx U u x dy dx x 0 x 0
K AB dx x
K AC QACU
§8-7、附面层动量方程
p Px dx o dx x
2 0
v u 0 x y
2 i 0
无旋流
存在速度势Φ
u ,v x y
平面势流
平面流 不可压缩
工程流体力学第八章--粘性流体绕物体的流动
4
v
2 f
2
vf
4 gd s 3 CD
在实际应用中，根据雷诺数的范围用下列三个公式求得
（1）当 Re 1
vf
1 18
g v
s
d2
（2）当 Re 10 ~ 1000
vf
( 4 39
g v 0.5
s
2
)3
d
（3）当 Re 1000 ~ 2105
共有九个分量 三个是法向应力 六个是切向应力
第一节 不可压缩粘性流体的运动微分方程
一、微元体的受力分析和运动微分方程的推导
作用于微元体各面上的x轴方向的应力
把作用于控制体上x方向的力叠加起来，得到作用 在微元体上的表面力在x方向的分量为：
x dxdydz yx dydxdz zx dzdxdy
①风洞实验技术。 ②机翼理论。 ③湍流理论。
一、边界层的概念
由于流体的易 变形性，流体与固 壁可实现分子量级 的粘附作用。通过 分子内聚力使粘附 在固壁上的流体质 点与固壁一起运动。
壁面不滑移条件
二、边界层的厚度d
y
U0
Ue
0.99Ue
Ue
o
边界层流动δ
Ue
dx) ux,y)
L
y
外部势流 u
2vz z 2
)
如果流动是不可压缩流体，则连续性方程为
vx v y vz 0 x y z
将式（8－6）依次求 2 p 、 2 p、 2 p ，然后相加，
x 2 y 2 z 2
并结合连续性方程，即得 2 p 2 p 2 p 2 p 0 x2 y 2 z 2
v
2 f
2
vf
4 gd s 3 CD
在实际应用中，根据雷诺数的范围用下列三个公式求得
（1）当 Re 1
vf
1 18
g v
s
d2
（2）当 Re 10 ~ 1000
vf
( 4 39
g v 0.5
s
2
)3
d
（3）当 Re 1000 ~ 2105
共有九个分量 三个是法向应力 六个是切向应力
第一节 不可压缩粘性流体的运动微分方程
一、微元体的受力分析和运动微分方程的推导
作用于微元体各面上的x轴方向的应力
把作用于控制体上x方向的力叠加起来，得到作用 在微元体上的表面力在x方向的分量为：
x dxdydz yx dydxdz zx dzdxdy
①风洞实验技术。 ②机翼理论。 ③湍流理论。
一、边界层的概念
由于流体的易 变形性，流体与固 壁可实现分子量级 的粘附作用。通过 分子内聚力使粘附 在固壁上的流体质 点与固壁一起运动。
壁面不滑移条件
二、边界层的厚度d
y
U0
Ue
0.99Ue
Ue
o
边界层流动δ
Ue
dx) ux,y)
L
y
外部势流 u
2vz z 2
)
如果流动是不可压缩流体，则连续性方程为
vx v y vz 0 x y z
将式（8－6）依次求 2 p 、 2 p、 2 p ，然后相加，
x 2 y 2 z 2
并结合连续性方程，即得 2 p 2 p 2 p 2 p 0 x2 y 2 z 2
流体力学(第二版) 龙天渝 第八章 绕流运动习题答案
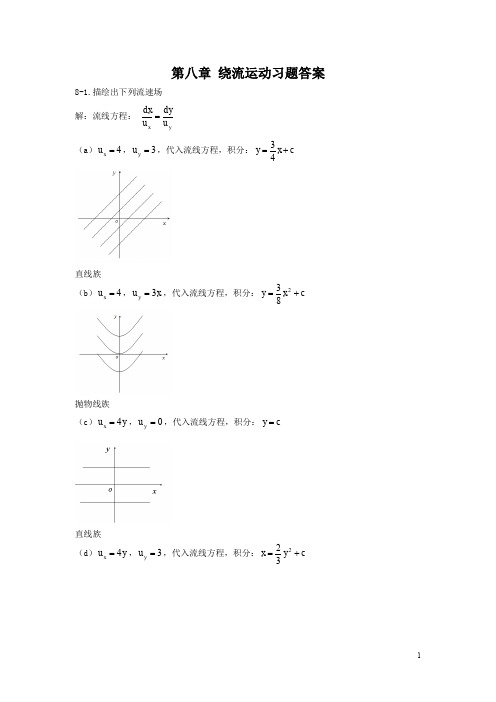
直线族 （d） u x 4 y ， u y 3 ，代入流线方程，积分： x
2 2 y c 3
1
抛物线族 （e） u x 4 y ， u y 3x ，代入流线方程，积分： 3x 2 4 y 2 c
椭圆族 （f） u x 4 y ， u y 4 x ，代入流线方程，积分： x 2 y 2 c
5
u0 X k
（查表知 t=20ºC， 1.007 106 m / s ）
Xk=
Re xk =0.1m<30m u0
可认为是紊流附面层：Re= 采用 C f
u0 X
=1.49×10
8
0.445 -3 ，则： C f =1.963×10 2.58 (lg Re )
2 u 0
u0 X k
,知
Xk=0.55m
8
（2）根据： =0.37 (
u0 x
) x，知 =0.0572m=57.2mm
1 5
（3） 根据：Re= 则： C f =
vx 6 知 Re =2.75×10 .
0.074 1700 -3 =3.196×10 1 Re Re 5
2 u 0
根据： D f C f A
解：叠加前
ux
Q y y (arctg arctg ) 2 xa xa
Q xa xa ( ) y 2 y 2 ( x a) 2 y 2 ( x a) 2 Q y y ( 2 2 ) 2 x 2 y ( x a) y ( x a) 2 uy Qy (y2 a2 )
Q y y (arctg arctg ) 2 xa xa
水力学 第八章 边界层理论基础与绕流运动
3
2、边界层的厚度（Boundary Layer Thickness）
（1）边界层名义厚度
自固体边界表面沿其外法线到纵向流速 ux 达到主流速U0的99%处的距离。 边界层的厚度顺流增大，所以δ 是 x 的函数，即：δ （x）。
8-1 边界层的基本概念
4
（2）边界层位移厚度d（流量亏损厚度、排挤厚度）
第八章
§8 — 1 §8 — 2 §8 — 3 §8 — 4 §8 — 5 §8 — 6 §8 — 7
第八章
边界层理论基础和绕流运动
边界层的基本概念 边界层微分方程•普朗特边界层方程 边界层的动量积分方程 平板上的层流边界层 平板上的湍流边界层 边界层的分离现象和卡门涡街 绕流运动
1
边界层理论基础和绕流运动
3 10 Re xcr
5
教材中取： （2）边界层厚度
Re xcr 5.0 10
U 0xcr 3 106 v
5
1）层流边界层： 5 x Re 1x/ 2
8-1 边界层的基本概念
10
0.381x 2）紊流边界层： /5 Re1 x
2、管流或明渠流的边界层
进口处没有特别干扰的光 滑圆管流，进口段或起始段 长度为
8-1 边界层的基本概念
7
3、层流边界层与紊流边界层
当边界层厚度较小时，流速梯度很大，粘滞应力也很大，边界层内 的流动属于层流，这种边界层称为层流边界层（Laminar Boundary Layer）。 当雷诺数达到一定数值时，边界层内的流动经过一过渡段后转变为湍 流，成为湍流边界层（Turbulence Boundary Layer） 。
如图所示，可知： ρU δ δd 也可表示为：
2、边界层的厚度（Boundary Layer Thickness）
（1）边界层名义厚度
自固体边界表面沿其外法线到纵向流速 ux 达到主流速U0的99%处的距离。 边界层的厚度顺流增大，所以δ 是 x 的函数，即：δ （x）。
8-1 边界层的基本概念
4
（2）边界层位移厚度d（流量亏损厚度、排挤厚度）
第八章
§8 — 1 §8 — 2 §8 — 3 §8 — 4 §8 — 5 §8 — 6 §8 — 7
第八章
边界层理论基础和绕流运动
边界层的基本概念 边界层微分方程•普朗特边界层方程 边界层的动量积分方程 平板上的层流边界层 平板上的湍流边界层 边界层的分离现象和卡门涡街 绕流运动
1
边界层理论基础和绕流运动
3 10 Re xcr
5
教材中取： （2）边界层厚度
Re xcr 5.0 10
U 0xcr 3 106 v
5
1）层流边界层： 5 x Re 1x/ 2
8-1 边界层的基本概念
10
0.381x 2）紊流边界层： /5 Re1 x
2、管流或明渠流的边界层
进口处没有特别干扰的光 滑圆管流，进口段或起始段 长度为
8-1 边界层的基本概念
7
3、层流边界层与紊流边界层
当边界层厚度较小时，流速梯度很大，粘滞应力也很大，边界层内 的流动属于层流，这种边界层称为层流边界层（Laminar Boundary Layer）。 当雷诺数达到一定数值时，边界层内的流动经过一过渡段后转变为湍 流，成为湍流边界层（Turbulence Boundary Layer） 。
如图所示，可知： ρU δ δd 也可表示为：
《流体力学》第八章绕流运动
这时速度势函数全微分为：
duxdxuydy
对应的拉普拉斯方程为： 2 2 0
H
x2 y2
8
在平面流动中，流线微分方程为：
dx dy ux uy
uxdy(uydx)0
二元流动 连续性方程为：
ux x
u y y
0
ux x
(uy ) y
由全微分理论，由于存在条件 ux (u y )
x y
则 uxdy(uydx) 必是某函数的全微分，即：
Q 2
环
流
ur =0
u
2 r
ln x2 y2 2
ln r 2
势流叠加演示 H
Q ln x2 y2 2 Q ln x2 y2 2
arctg y 2 x
Q ln r 2 Q ln r 2
2
15
第六节 绕流运动与附面层基本概念
在绕流中，流体作用在物体的力可分为两分量： ➢ 升力：垂直于来流方向的作用力。 ➢ 阻力：平行于来流方向的作用力。
本章主要讨论绕流阻力
摩擦阻力：空气、水等粘性小的流体在绕过物体 运动时，其摩擦阻力主要发生在附面层内（紧靠物 体表面的流速梯度很大的流体薄层）。
形状阻力：流体绕曲面体或具有锐缘棱角的物体
流动时，附面层要发生分离，从而产生涡旋所造成
的阻力。
H
16
u
u
u 紊流边界层
层流边界层
xx l
δ δ
附 层流底层 面
流函数存在的条件则是不可压缩流体，以 及流动是平面问题，与流动是否无旋，是 否恒定和是否具有粘性无关。当流动又是 无旋时，则流函数也满足拉普拉斯方程。
H
13
第三节 几种简单的平面无旋流动
第八章 绕流问题
如果上式恰好是某函数的全微分，积分就相当简单，即：
d
d udx vdy wdz (8 - 2)
积分得：
dx dy udx vdy 0 x y
（8－8）
（8－7）
x, y c
x, y 就称为流函数。式（8-8）表示一簇流线。当积分常数的 值一定时，它表示一条确定的流线。显然，在同一流线上，流函数值 不变。
u a, v b
d udy vdx ady bdx
d udx vdy adx bdy
将以上两式积分，得平行流的流函数和势函数分别为：
ay bx ax by
(8-12)
8.1.2 几种简单的平面势流
8.1.2 几种简单的平面势流
8.1 势流理论基础
8.1.1 势函数和流函数 势函数 现引入一个函数。如果它的偏导数和速度之间存在如下关系：
u, u, w x y z
(8 - 1)
d udx vdy wdz
(8 - 2)
,存在着势函数的流动 ,称为有势流动 , 则称函数 x , y , z 为流场的速度势函数 简称势流。 可以证明，当流动为无旋时，势函数必存在。
EXIT
1
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
足球运动的香蕉球
输船在大海中航行
EXIT
EXIT
经过近80年的研究和改进，汽车阻力系数从0.8 降至0.137，减少到原来的1/5。
8.1.1
势函数和流函数
8.1.1
流体力学第八章绕流运动
流体⼒学第⼋章绕流运动第⼋章绕流运动⼀、应⽤背景1、问题的⼴泛存在性：在⾃然界和⼯程实际中，存在着⼤量的流体绕物体的流动问题（绕流问题），如：飞机在空⽓中的飞⾏、河⽔流过桥墩、⼤型建筑物周围的空⽓流动、植物护岸（消浪，船⾏波），粉尘颗粒在空⽓中的飞扬和沉降，⽔处理中固体颗粒污染物在⽔中的运动。
（⼀种：流体运动；另外⼀种：物体运动），我们研究，将坐标系固结于物体上，将物体看成静⽌的，讨论流体相对于物体的运动。
2、问题的复杂性上⼀章的内容中可以看出，流体⼒学的问题可以归结为求解在⼀定边界条件和初始条件下偏微分⽅程组的求解。
但描述液体运动的⽅程式⾮常复杂的：⼀⽅⾯，是⽅程的⾮线性性质，造成⽅程求解的困难；另⼀⽅⾯，复杂的边界条件和初始条件都给求解流体⼒学造成了很多⿇烦。
迄今为⽌，只有很少数的问题得到了解决。
平⾯泊萧叶流动，圆管coutte流动等等。
⽽我们所要解决的绕流问题正是有着⾮常复杂的边界条件。
3、问题的简化及其合理性流体⼒学对此的简化则是，简化原⽅程，建⽴研究理想液体的势流理论。
实际液体满⾜势流运动的条件：粘性不占主导地位，或者粘性还没有开始起作⽤。
正例：远离边界层的流体绕流运动、地下⽔运动、波浪运动、物体落⼊静⽌⽔体中，⽔的运动规律研究。
反例：研究阻⼒规律、能量损失、内能转换等等。
圆柱绕流（经典之⼀）半⽆限长平板绕流（经典之⼆）分成两个区域：⼀个区域是远离边界的地⽅，此区域剪切作⽤不明显，⽽且流体惯性⼒的影响远远⼤于粘性⼒的影响（理想液体）（引导n-s⽅程）；另⼀个是靠近边界的地⽅（附⾯层，粘性底层），此区域有很强烈的剪切作⽤，粘性⼒的影响超强，据现代流体⼒学的研究表明，此区域是产⽣湍流的重要区域，有强烈的剪切涡结构，但此区域只有⾮常薄的厚度。
此区域对绕流物体的阻⼒、能量耗损、扩散、传热传质都产⽣重要影响。
4、本章的主要研究内容（1）外部：理想液体，（简化⽅法，求解⽅式）、（2）内部：附⾯层理论，（简化⽅法，求解⽅式，求解内容，现象描述）（3）两者的衔接。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、形状阻力：
流体绕经物体时，物体受到流体所给予的阻力主要包括两部分 即摩擦阻力和形状阻力(或称压差阻力，尾涡阻力)，这两部分之和称 绕流阻力。其中的形状阻力大小取决于漩涡区的大小，即分离点的 位置。
分离点后移，漩涡区减小，则形状阻力减少，摩擦阻力增大；在高 Re时形状阻力比摩擦阻力大许多。因此，工程上减少了形状阻力便 减少了绕流阻力。
c 取不同值，得不同的势函数等值线，称为等势线 c 同理
c 取不同值，得不同的流函数等值线，即流线
对比二函数与流速的关系
ux x y
二式交叉相乘
uy y x
等势线与流线正交
0 x x y y
0
2 ux dy dx
微元体三个面上的平均压强
固体壁面对流体的切力
p pCD p dx x 1 p pAC p dx 2 x
TBD 0dx
pAB p
各表面力在 x 方向的合力
p 1 p p dx d + p dx ds sin 0dx Fsx p x 2 x
汇流流动与源流相反，势函数与流函数则均取负值 Q 称为源（汇）流强度
□ 8.3.3 环流（势涡） 速度环量
y
r θ
2 ru
分速度
ur 0 u 2 r
势函数
x
ur dr u rd 2
流函数
ur rd udr ln r 2
z
将速度势函数带入不可压缩流体的连续性方程：
ux u y uz 0 x y z
2 2 2 2 2 0 2 x y z
拉普拉斯方程，满足此方程的 函数称为调和函数。拉普拉斯 函数本身就是不可压缩流体无 旋流动的连续性方程。
8.2 平面无旋流动
u0 x Re x
当雷诺数达到一定数值时，附面层内的流动经过一过渡段后转变为紊流， 成为紊流附面层。由层流附面层转变为紊流附面层的点称为称为转捩点，其 雷诺数为临界雷诺数Reδk 。对于光滑平板来说，Reδk范围为2700~8500；
2、管道进口段附面层： 不仅绕流存在附面层，内流也存在附面层。
x
□ 8.3.2 源流与汇流 源流 分速度
y
r θ
QV ur 2 r u 0
x
势函数
QV QV ur dr u rd ln r ln x 2 y 2 2 2 流函数 QV QV y ur rd udr arctan 2 2 x
在流场中，相互正交的等势线与流线组成的网格称为流网 φ1 ψ1 ψ2 ψ3 流网的性质 等势线与流线相互正交 相邻两流线的流函数之差等于两流线间的单宽流量 φ2 φ3
流网中每一网格的相邻边长维持一定比例
8.3 几种简单的平面势流
□ 8.3.1 均匀流 分速度 y
ux a
势函数
uy b d ux dx uy dy adx bdy
假设速度以均匀速度流入，则在入口段的始端将保持均匀的速度 分布。 由于管壁的作用，靠近管壁的流体将受阻滞而形成附面层，其厚 度 δ 将随离入口的距离的增加而增加。当附面层发展到管轴，流 体的运动都处于附面层内，自此以后流动将保持这个状态不变， 才成为均匀流动。
u0
xE
对于层流 对于紊流
xE 0.028Re d xE 50 d
uz uy y z
1 ux uz y 0 2 z x
1 uy ux z 0 2 x y
ux uz z x
uy x ux y
根据全微分理论，上式是某空间位置函数φ(x、y、z)存在的充要条件
□ 8.3.4 直角内的流动 设速度势 分速度
y
a x2 y 2
ux 2ax uy 2ay
流函数
x
2axy
流线为双曲线
零流线
0
或为 x = 0，或为 y = 0，坐标轴相当于固体壁面
8.5 绕流运动与附面层基本概念
边界层理论是普朗特在1904年开始创立的，它的发展 主要是与研究流体绕经物体时的阻力问题有关。它为解 决边界复杂的实际流体运动的问题开辟了途径，对流体 力学的发展有着极其重要的意义。
在实际流体流经固体时，不管流动的雷诺 数多大，固体边界上的流速必为零，称无 滑移条件。由于这个条件在固体边界的外 法线方向上，流体速度从零迅速增大。这 样，在边界附近的流区存在着相当大的流 速梯度，在这个流区内粘性的作用就不能 忽略。边界附近的这个流区就称为附面层 边或称界层。其外，粘性可以忽略按理想 流体运动处理。
L h
振动频率：
fd 19.7 0.198(1 ) (250 Re 2 105 ) u0 Re
8.8 绕流阻力与升力
8.8.1 绕流阻力 分离点下游形成的旋涡区又称为尾流 流体绕过物体时，机械能消耗包括两部分 流体与固体表面摩擦，摩擦阻力耗能 尾流旋涡区的能量消耗， 尾流耗能导致绕流物体前后形 成 压强差，因此而产生的阻力称绕流物体的形状阻力 一般情况下，形状阻力远大于摩擦阻力 旋涡区是出现形状阻力的主要原因 改变物体边界形状，使之不出现边界层分离，消除旋涡 区，这种形状的物体称为流线型物体
根据平面流动连续性微分方程
ux uy 0 x y
得
uy ux x y
上式是使 ux dy uy dx 成为某函数ψ全微分的充分与必要条件
d ux dy uy dx
ψ的全微分又可以写成
d dx dy x y ux y
uy x
x
ax by
流函数
d ux dy uy dx ady bdx
ay bx
当流动平行于 y 轴时
y
ux 0
势函数 流函数
by
x y
bx
uy 0
当流动平行于 x 轴时
势函数 流函数
ax
ay
若按极坐标表示
ar cos ar sin
u dy dx
0 x
通过微元体三个面的单宽动量流量
2 K AB ux dy 0 K AB 2 K CD K AB dx ux dy 0 x x K AC u0QmAC u0 ux dy dx 0 x
对比二式 ψ称为流函数
将流速与流函数的关系代入平面无旋流的条件中
uy x
得拉普拉斯方程
ux 0 y
2 0
2 2 2 0 2 x y
以极坐标形式表示
ur r
u r
在平面流动中 令 得
d ux dx uy dy 0 c
d ux dx u y dy u zdz
函数φ称为速度势函数。
存在速度势函数的流动，称为有势流动，简称势流。 那么，无旋流动必然是有势流动。 φ的全微分又可以写成
对比二式
d dx dy dz x y z
ux x
uy
y
uz
1、平板附面层：
u0
层流附面层
紊流附面层
u0 0.99u0
u0 （1）平板附面层的描述： 根据无滑移条件和流体的 层流底层 δ 粘性作用，与平板接触的流体 质点的流速都要降为零。而沿 xk 壁面的法线方向流速很快增大 l 到u0。由此可见，该流场存在 两个区，贴近壁面很薄的一层内，dux/dy很大，粘性不可忽略，即附面 层。其外， dux/dy≈0，相当于理想流体运动。 （2）附面层的厚度 自固体边界表面，沿其外法线到纵向流速ux达到主流速u0的 99%处， 这段距离称为附面层厚度。附面层的厚度顺流增大，即δ是x的函数。
对于平面流动，仅有
1 uy ux z 0 2 x y
平面无旋流动的势函数为：
或
uy x
ux y
d ux dx uy dy
拉普拉斯方程为：
2 2 2 0 2 x y
以极坐标形式表示
2 0
u ur r r 2 2 1 2 2+ 0 2 r r r r
第八章 绕流运动
阐述势流理论的基本内容，不可压缩流体
平面流动的流函数、不可压缩流体平面无 旋流动的速度势函数和流函数的关系、附 面层的概念、曲面附面层的分离现象和平 板附面层的计算。
8.1 无旋运动
当流动为无旋流动时： 指流体微团运动分析中的旋转角速度为零的流体运动
1 uz uy x 0 2 y z
3、卡门涡街
液流通过一个非流线型的障碍物体时，在物体两侧便会周期性的 产生两列内漩的交替出现的漩涡。当两列漩涡的间距 h 与同列两个 相邻漩涡之间的距离L之比满足于h/L≤0.281时，此时所产生的漩涡是 稳定的，经得起微扰动的影响，是稳定的，称为卡门涡街。 当Re≈90时，涡街产生；当Re较大时，涡街就消失了。
为层流而其余部分是紊流。
8.6 附面层动量方程
取附面层微元段 假设 不计质量力
恒定平面流动 根据动量定理 y A C
F
sx
KCD KAB KAC
B
x dx
D
通过微元体三个面的单宽质量流量
Qmபைடு நூலகம்B ux dy
0
QmAB QmCD QmAB dx ux dy 0 x x QmAC QmCD QmAB ux dy dx 0 x
8.7 曲面附面层的分离现象和卡门涡街