第七章 非平稳时间序列模型
非平稳时间序列建模步骤

非平稳时间序列建模步骤介绍非平稳时间序列是指其统计特性在时间上发生变化的序列。
在实际应用中,我们经常面临非平稳时间序列的建模问题,如股票价格、气温变化等。
本文将探讨非平稳时间序列建模的步骤和方法。
为什么要建立模型非平稳时间序列在其统计特性的变化中存在一定的规律性,因此建立模型可以帮助我们理解和预测序列的行为。
模型可以从数据中提取有用的信息,揭示序列的规律和动态特征。
步骤一:观察时间序列的特性在建立模型之前,我们首先需要观察时间序列的特性,包括趋势、周期性、季节性和随机性等。
这些特性是决定时间序列模型选择的重要因素。
步骤二:平稳化处理由于非平稳时间序列的统计特性随时间变化,不利于建模和分析。
因此,我们需要对时间序列进行平稳化处理。
常用的平稳化方法包括差分法和变换法。
2.1 差分法差分法是通过计算相邻两个观测值的差异来实现序列的平稳化。
一阶差分是指相邻观测值之间的差异,二阶差分是指一阶差分的差异,以此类推。
差分法可以有效地去除序列的趋势和季节性,使序列平稳。
2.2 变换法变换法是通过对时间序列进行数学变换,将非平稳序列转化为平稳序列。
常用的变换方法包括对数变换、平方根变换和 Box-Cox 变换等。
变换法可以改变序列的分布特性,使序列满足平稳性的要求。
步骤三:选择模型平稳化处理后,我们需要选择合适的模型进行建模。
常用的时间序列模型包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)、季节性自回归移动平均模型(SARIMA)和指数平滑模型等。
3.1 自回归移动平均模型(ARMA)ARMA 模型是描述时间序列随机变动的经典模型,其包括自回归和移动平均两个部分。
自回归部分考虑了序列的历史值对当前值的影响,移动平均部分考虑了序列的误差对当前值的影响。
ARMA 模型适用于没有趋势和季节性的平稳序列。
3.2 自回归积分移动平均模型(ARIMA)ARIMA 模型是在 ARMA 模型基础上引入了积分项,用于处理非平稳序列。
第7章 平稳时间序列模型预测

et l
xˆt l
预测误差
预测值
特别当 l=1时有 Xt1 t1 xˆt 1 ,即 t1 Xt1 xˆt 1
MA(q)序列的预测
当预测步长l大于等于MA模型的阶数q,即l >q时, Xt+l可以分解为:
X tl tl 1tl1 2tl2 L qtlq
即一期修正后第 l 步预测方差就等于修正前第 l 1步预测
方差。它比修正前的同期预测方差减少了Gl21 2,提高了预
测精度。
一般情况
假设获得k个新的观察值 Xt1,L , Xtk 1 k l ,则
X tl 的修正预测值为
Xˆ tk (l k ) Gl-k t+k L Gl1t+1 Glt Gl1t1 L
其中t+1=Xt1 Xˆt 1 是Xt+1的一步预测误差。
修正预测误差为 et1 (l 1) G0 tl Gl2 t2
修正预测原理
预测方差为
var[et1(l 1)] (G02 L
G2 l2
)
2
var et l 1
1
Xˆ
t
l
1
2
Xˆ
t
l
2
L
p Xˆ t l p
q
i tli , l q
il
1Xˆ t l 1 2 Xˆ t l 2 L p Xˆ t l p,
lq
例7.4
已知ARMA(1,1)模型为:
X t 0.8X t1 t 0.6t1, 2 0.0025
解: (1) 预测值计算
非平稳时间序列模型

非平稳时间序列模型非平稳时间序列模型是用来描述时间序列数据中存在趋势、季节性或其他波动的模型。
这些模型通常用于预测未来的数值或分析数据中的特征。
其中一个常见的非平稳时间序列模型是趋势模型。
趋势模型用来描述数据中存在的长期趋势。
例如,如果一个公司的销售额在过去几年里呈现稳定的增长趋势,那么趋势模型可以帮助预测未来几年的销售额。
另一个常见的非平稳时间序列模型是季节性模型。
季节性模型用来描述数据中存在的周期性变动。
例如,如果一个餐厅的每周客流量在周末较高,在工作日较低,那么季节性模型可以用来预测未来每周的客流量。
此外,还有其他非平稳时间序列模型,如自回归移动平均模型(ARMA)、自回归综合滑动平均模型(ARIMA)等。
这些模型结合了自身过去时刻的观测值和过去时刻的误差,用来预测未来的数值。
非平稳时间序列模型的建立和拟合通常包括多个步骤。
首先,需要对原始数据进行处理,例如去除趋势和季节性。
然后,选择适当的模型来拟合剩余数据。
最后,根据模型来预测未来的数值,并进行评估模型的准确性和可靠性。
总之,非平稳时间序列模型是一种描述和分析时间序列数据中存在趋势、季节性或其他波动的模型。
这些模型可以帮助我们理解数据的特征,并预测未来的趋势和变化。
非平稳时间序列模型是用来描述和分析时间序列数据中存在趋势、季节性或其他波动的模型。
这些模型通常用于预测未来的数值或分析数据中的特征。
非平稳时间序列模型在许多领域中都有广泛的应用,包括经济学、金融学、气象学等。
在经济学中,非平稳时间序列模型被广泛应用于经济预测和决策制定。
例如,GDP增长率是一个典型的非平稳时间序列数据,它受到许多因素的影响,如技术进步、政府政策等。
通过建立一个趋势模型,可以预测未来的经济增长趋势,从而提供政府和企业的决策参考。
在金融学中,非平稳时间序列模型被广泛应用于股票价格预测和风险管理。
股票价格是一个非平稳时间序列,它受到市场供需关系、公司盈利情况等多个因素的影响。
ARIMA模型

二阶差分 2 xt xt xt 1
1 t t 1 ( 1 t 1 t 2 ) t 2 t 1 t 2
第七章 ARIMA模型
前面的章节我们围绕着平稳时间序列的问题进行讨论。 但是,在实际应用中,我们经常会遇见不满足平稳性的时 间序列,尤其在经济领域和商业领域中的时间序列都是非 平稳的。例如,美国1961年1月—1985年12月16-19岁失 业女性的月度数据。
大量的非平稳时间使我们不禁提出这样的疑问: 1.遇到非平稳时间序列怎么办? 我们知道平稳序列有许多好的性质,便于我们进行建 模、检验与预测 。因此,我们引入了差分方法,希望 通过差分能使非平稳时间序列转化为平稳时间序列。 2.差分方法如何使非平稳时间序列转化为平稳时间序列? 我们将通过直观上观察与理论证明分析差分对一个非 平稳时间序列的作用。
这时因为,过多阶数的差分导致信息损失,从而降低了估计 的精度 。
7.6 ARIMA模型分析
1.确定差分的阶数 通过观察差分后的时序图、自相关图、偏相关图。
2.观察时序图和自相关图,确定模型形式 3.拟合模型 若为确定性趋势模型,直接根据最小二乘法拟合。 若为随机趋势模型,则需要通过自相关图、偏相关图定阶。
t ~ WN (0, 2 )
当a k 0, 且k 1时
一阶差分
xt xt xt 1 a1[t (t 1)] ak 1[t k 1 (t 1) k 1 ] a k [t k (t 1) k ] t t 1
d阶差分
xt (1 B) xt (1)
潘省初计量经济学——第七章

潘省初计量经济学——第七章
协整
协整分析被认为是上世纪八十年代中期以来计量 经济学领域最具革命性的进展。
简单地说,协整分析涉及的是一组变量,它们各自 都是不平稳的(含义是随时间的推移而上行或下行), 但它们一起漂移。这种变量的共同漂移使得这些变量 之间存在长期的线性关系,因而使人们能够研究经济 变量间的长期均衡关系。如果这些长时间内的线性关 系不成立,则对应的变量被称为是“非协整的” 。
潘省初计量经济学——第七章
一. 单位根 考察(7.8)式的一阶自回归过程,即
Xt=φXt-1+εt
(7.11)
其中εt为白噪声,此过程可写成
Xt-φXt-1=εt 或(1-φL)Xt = εt (7.12)
其中L为滞后运算符,其作用是取时间序列的滞后, 如Xt 的一期滞后可表示为L(Xt),即
L(Xt)= Xt-1
ΔXt=εt
(7.6)
这个一阶差分新变量ΔXt是平稳的,因为它就等 于白燥声εt,而后者是平稳时间序列。
潘省初计量经济学——第七章
3、带漂移项的随机漫步 (Random walk with drift)
Xt=μ+Xt-1+εt
(7.7)
其中μ是一非0常数,εt为白燥声。
μ之所以被称为“漂移项”,是因为(7.7)式的 一阶差分为
例7.1 检验某国私人消费时间序列的平稳性。
潘省初计量经济学——第七章
潘省初计量经济学——第七章
用表7.2中的私人消费(Ct)时间序列数据,估计 与(7.16)和(7.17)相对应的方程,分别得到如下
七章非平稳时间序列

第七章非平稳时间序列时间序列数据被广泛地运用于计量经济研究。
经典时间序列分析和回归分析有许多假定前提,如序列的平稳性、正态性等,,如果直接将经济变量的时间序列数据用于建模分析,实际上隐含了这些假定。
在这些假定成立的条件下,进行的t检验、F检验与2 等检验才具有较高的可靠度。
但是,越来越多的经验证据表明,经济分析中所涉及的大多数时间序列是非平稳的。
那末,如果直接将非平稳时间序列当作平稳时间序列来进行分析,会造成什么不良后果?如何判断一个时间序列是否为平稳序列?当我们在计量经济分析中涉及到非平稳时间序列时,应作如何处理呢?这就是本章要讨论的基本内容。
第一节伪回归问题经典计量经济学建模过程中,通常假定经济时间序列是平稳的,而且主要以某种经济理论或对某种经济行为的认识来确立计量经济模型的理论关系形式,借此形式进行数据收集、参数估计以及模型检验,这是20世纪70年代以前计量经济学的主导方法。
然而,这种方法所构建的计量经济模型在20世纪70年代出现石油危机后引起的经济动荡面前却失灵了。
这里的失灵不是指这些模型没能预见石油危机的出现,而是指这些模型无法预计石油危机的振荡对许多基本经济变量的动态影响。
因此引起了计量经济学界对经典计量经济学方法论的反思,并将研究的注意力转向宏观经济变量非平稳性对建模的影响。
人们发现,由于经济分析中所涉及的经济变量数据基本上是时间序列数据,而大多数经济时间序列是非平稳的,如果直接将非平稳时间序列当作平稳时间序列进行回归分析,则可能会带来不良后果,如伪回归问题。
所谓“伪回归”,是指变量间本来不存在有意义的关系,但回归结果却得出存在有意义关系的错误结论。
经济学家早就发现经济变量之间可能会存在伪回归现象,但在什么条件下会产生伪回归现象,长期以来无统一认识。
直到20世纪70年代,Grange、Newbold研究发现,造成“伪回归”的根本原因在于时间序列变量的非平稳性。
他们用Monte Carlo模拟方法研究表明,如果用传统回归分析方法对彼此不相关联的非平稳变量进行回归,t检验值和F检验值往往会倾向于显著,从而得出“变量相依”的“伪回归结果”。
时间序列的平稳非平稳协整格兰杰因果关系

时间序列的平稳、非平稳、协整、格兰杰因果关系步骤:先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。
若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。
如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
1.单位根检验是序列的平稳性检验,如果不检验序列的平稳性直接OLS容易导致伪回归。
常用的ADF检验包括三个模型方程。
在李子奈的《高级计量经济学》上有该方法的全部步骤,即从含趋势项、截距项的方程开始,若接受原假设,则对模型中的趋势项参数进行t 检验,若接受则进行对只含截距项的方程进行检验,若接受,则对一阶滞后项的系数参数进行t检验,若接受,则进行差分后再ADF检验;若拒绝,则序列为平稳序列。
2.当检验的数据是平稳的(即不存在单位根),要想进一步考察变量的因果联系,可以采用格兰杰因果检验,但要做格兰杰检验的前提是数据必须是平稳的,否则不能做。
3.当检验的数据是非平稳(即存在单位根),并且各个序列是同阶单整(协整检验的前提),想进一步确定变量之间是否存在协整关系,可以进行协整检验,协整检验主要有EG两步法和JJ检验:(1)EG两步法是基于回归残差的检验,可以通过建立OLS模型检验其残差平稳性;(2)JJ检验是基于回归系数的检验,前提是建立VAR模型(即模型符合ADL模式)。
4.当变量之间存在协整关系时,可以建立ECM进一步考察短期关系,Eviews这里还提供了一个Wald-Granger检验,但此时的格兰杰已经不是因果关系检验,而是变量外生性检验,请注意识别。
5.格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。
时间序列分析第七章趋势性时间序列模型王振龙第二版

20000
0.4 0.3
15000
0.2
10000
0.1 0.0
5000
-0.1
XFP 0 55 60 65 70 75 80 85 90
DLNXFP -0.2 55 0.3 60 65 70 75 80 85 90
10
9
0.2
8
0.1
7
0.0
6 LNXFP 55 60 65 70 75 80 85 90
第二步,计算均值序列或方差序列的逆序总数。
A Ai
i 1
M 1
第三步,计算统计量进行检验 在原假设条件下,A具有以下期望与方差
1 E ( A) M ( M 1) 4 M (2 M 2 3M 5) D( A) 72
其中,M为数据个数。
统计量
1 [ A E ( A)] 2 Z D ( A)
d d 1 d 2 d 2 d d
例:对温度序列作一阶差分。 原序列图
15 10 5 0 -5 -10 -15 25 50 75 100 125 tempreture 150 175 200
一阶差分序列图
8
4
0
-4
-8 25 50 75 100 125 150
DWD 175 200
过差分
• 足够多次的差分运算可以充分地提取原 序列中的非平稳确定性信息 • 但过度的差分会造成有用信息的浪费
30
20
10
0
-10 85
DGY 86 87 88 89 90 91 92 93
gy
• 对数变换与差分运算的结合运用
如果时间序列含有指数趋势,可以通过取对数将 指数趋势转化为线性趋势。
非平稳时间序列

首先定义序列 yt 的拟差分序列如下:
d ( yt
|
a)
yt yt
ayt 1
if t 1 if t 1
并且构造如下回归方程:
t = 1, 2, , T
d ( yt | a) d ( xt | a) δ(a) ut t = 1, 2, , T (5.3.14)
§5. 3 非平稳时间序列建模
前述的AR(p)、MA(q) 和ARMA(p,q) 三个模型只适 用于刻画一个平稳序列的自相关性。一个平稳序列的数 字特征,如均值、方差和协方差等是不随时间的变化而 变化的,时间序列在各个时间点上的随机性服从一定的 概率分布。也就是说,对于一个平稳的时间序列可以通 过过去时间点上的信息,建立模型拟合过去信息,进而 预测未来的信息。
其中: = -1。
(5.3.10)
14
其中: = -1,所以原假设和备选假设可以改写为
H0 H1
: :
0 0
可以通过最小二乘法得到 的估计值ˆ,并对其进行
显著性检验的方法,构造检验 ˆ 显著性的 t 统计量。
但是,Dickey-Fuller研究了这个t 统计量在原假设下 已经不再服从 t 分布,它依赖于回归的形式(是否引进了 常数项和趋势项) 和样本长度T 。
16
2. ADF检验
考虑 yt 存在p阶序列相关,用p阶自回归过程来修正,
yt a 1 yt1 2 yt2 p yt p ut
在上式两端减去 yt-1,通过添项和减项的方法,可得
其中
p 1
Δ yt a yt1 i Δ yti ut i 1
11
第七章非平稳时间序序列的特征与检验

逆序检验方法
检验原理 检验步骤
四、游程检验
游程的概念
游程检验
第三节 时间序列非平稳性的单位根检验法 本节基本内容: 单位根过程 单位根过程检验基础 DF单位根检验法 PP单位根检验法与ADF单位根检验法 其它高效的单位根检验法简介
一、单位根过程
时间序列 y 称为随机漫步过程,如果有:
H 0 : 1;
情 形 四 : 假 设 数 据 由 ( 真 实 过 程 ) (7.30) 产 生 , 在 回 归 模 型
yt yt 1 t t 中检验假设: H 0 : 1; 0
(一) 情形一的DF检验法
回归模型(7.29)系数 的OLS估计为:
例子: 平稳AR(1)的自相关图
(a) yt 0.5 yt 1 t , t
i.i.d. N (0,1) 的样本自相关图
例子: 非平稳过程的样本自相关图
(b) yt yt 1 t , t
i.i.d . N (0,1) 的样本相关图
三、逆序检验法
逆序数的定义
t t t 1 t
三、非平稳时间序列的统计特征
对单位根过程而言,有
k
1 k / t 2 2 V a r () y a r ( y ) t ( t k ) t V tk
C o v (, y ) ty tk
2 ( t k )
可以看出,随着时间长度的增加,相关系数趋近于常数1;在小样本条件下, 随着滞后期k的增加,相关系数会不断衰减。
0
2
t
i y e r e + r y = r e å t= t+ t -1 t -i 2 t -2 i = 0
非平稳金融时间序列模型

张成思
► 最简单的线性确定性趋势模型可以写成
yt ctut t 1,2,L
(6.1)
其中表示均值为0的平稳随机变量。
对(6.1)两边同取期望,可得
E(yt)ct
(6.2)
(6.2)说明,只要系数不为0,则序列的 均值随时间推移而不断增大。正因为这个
特点,确定性趋势模型也称为“均值非平 稳”过程
4
2
0
-2 10 20 30 40 50 60 70 80 90 100
6
4
AR(1): alpha=0.9
2
0
-2
-4
-6 10 20 30 40 50 60 70 80 90 100
1.00 0.75 0.50 0.25 0.00 -0.25
0
ACF: Random Walk
5
10
15
20
25
于随机游走过程的一次差分 y t是一
个平稳的随机时序变量,因为 t 等于
平稳白噪音过程。
图6-4 RWD及其 一次差分后序列
200 y(t)=2+y(t-1)+e
160
120
80
40
0
25
50
75
100
5
first difference 4
3
2
1
0
-1
25
50
75
100
以上处理方法很容易拓展到高阶 单整序列。例如,假设 y t 是一个I(2) 过程,那么对其二次差分就可以获得 平稳序列,即:
E(t2j
2 tj1
L
12)
(t j)2
进而,可以获得自相关函数的表达式:
第七章 非平稳时间序列模型

y t = α 0 + α 1 y t − q + α 2 y t − q −1 + L + υ t
随机序列,若 lim τ = Var ( yt )
q →∞ 2 q
page 4
2011年3月21日星期一 2011年 21日星期一
对于任何一个离散平稳过程{xt } 它都可以分解为两个 不相关的平稳序列之和,其中一个为确定性的,另一 个为随机性的,不妨记作
xt = Vt + ξ t ∞ ξ {V 为确定性序列, t } {ξ 为随机序列, t = ∑ ϕ j ε t − j 其中: t } j =0
它们需要满足如下条件 ∞ (1)ϕ 0 = 1, ∑ ϕ 2 < ∞ (2){ε t } ~ WN (0, σ ε2 ) j
安徽财经大学统计与应用数学学院
案例一:中国人口时间序列模型(file:5b2c1)(怎样建 立AR 模型)
13 12 11 10 9
8 7 6 5 50 55 60 65 70 75 80 85 90 95 00 -.1 -.2 50 55 60 65 70 75 80 85 90 95 00 .2 .1 .0 .4 DY
一、ARIMA模型结构 模型结构
使用场合 差分平稳序列拟合 模型结构
Φ ( B)∇ d xt = Θ( B)ε t E (ε t ) = 0,Var (ε t ) = σ ε2 , E (ε t ε s ) = 0, s ≠ t Ex ε = 0, ∀s < t s t
page 13 2011年3月21日星期一 2011年 21日星期一
∇ d x t = (1 − B ) d x t =
非平稳时间序列分析
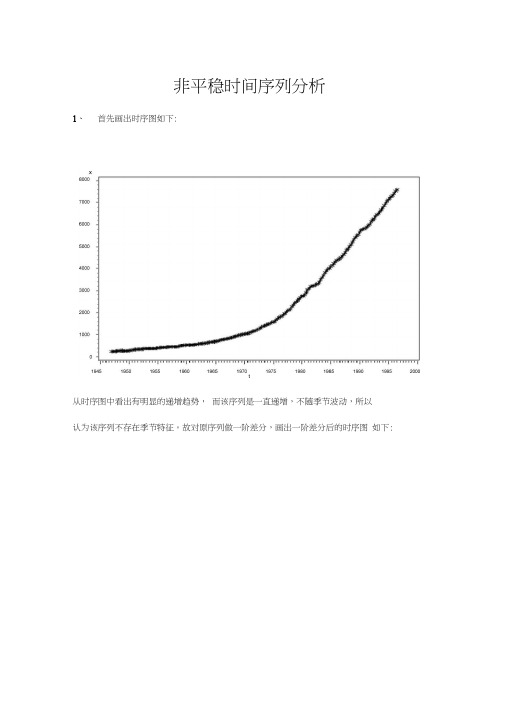
非平稳时间序列分析1、首先画出时序图如下:t从时序图中看出有明显的递增趋势,而该序列是一直递增,不随季节波动,所以认为该序列不存在季节特征。
故对原序列做一阶差分,画出一阶差分后的时序图如下:difx140 130 120 110 100 90 80 70 60 50 40 30 20 10 0 -10从中可以看到一阶差分后序列仍然带有明显的增长趋势,再做二阶差分:dif2x90 80 70 60 50 40 30 20 10 0 -10 -20 -30 -40 -50 -60 -70 -80 -90 -100 -110做完二阶差分可以看到,数据的趋势已经消除,接下来对二阶差分后的序列进行194519501945 19551960196519701975198019851990199520001950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000检验:AutocorrelationsLag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error0 577.333 1.00000 | |********************| 01 -209.345 -.36261 | *******| . | 0.0712472 -52.915660 -.09166 | .**| . | 0.0800693 9.139195 0.01583 | . | . | 0.0806004 15.375892 0.02663 . |* . | 0.0806155 -59.441547 -.10296 .**| . | 0.0806606 -23.834489 -.04128 | . *| . | 0.0813247 100.285 0.17370 | . |*** | 0.0814318 -146.329 -.25346 | *****| . | 0.0832909 52.228658 0.09047 | . |**. | 0.08711810 21.008575 0.03639 | . |* . | 0.08759311 134.018 0.23213 | . |***** | 0.08767012 -181.531 -.31443 | ******| . | 0.09073613 23.268470 0.04030 | . |* . | 0.09610814 71.112195 0.12317 | . |** . | 0.09619415 -105.621 -.18295 | ****| . | 0.09699116 37.591996 0.06511 . |* . | 0.09872717 23.031506 0.03989 | . |* . | 0.09894518 45.654745 0.07908 | . |** . | 0.09902719 -101.320 -.17550 | ****| . | 0.09934720 127.607 0.22103 | . |**** | 0.10090821 -61.519663 -.10656 | . **| . | 0.10333722 35.825317 0.06205 | . |* . | 0.10389323 -93.627333 -.16217 | .***| . | 0.10408124 55.451208 0.09605 | . |** . |从其自相关图中可以看出二阶差分后的序列自相关系数很快衰减为零,且都在两倍标准差范围之内,所以认为平稳,白噪声检验结果:Autocorrelation Check for White NoiseTo Chi- Pr >Lag Square DF ChiSq------------------- Autocorrelations -------------------6 30.70 6 <.0001 -0.363 -0.092 0.016 0.027 -0.103 -0.04112 84.54 12 <.0001 0.174 -0.253 0.090 0.036 0.232 -0.31418 97.98 18 <.0001 0.040 0.123 -0.183 0.065 0.040 0.07924 126.99 24 <.0001 -0.175 0.221 -0.107 0.062 -0.162 0.096P 值都小于 0.05 ,认为不是白噪声。
平稳性和非平稳时间序列分析

β1 + β 3 Xt 如果我们作下列变换 ecmt = Yt − 1− β2 α = β2 − 1 ,那么模型变为:
,
∆Yt = β 0 + β1∆X t + αecmt −1 + ε t
误差修正模型的自动调整机制类似于适应性预 期模型。如果误差修正项的系数 α 在统计上 是显著的,它将告诉我们 Y 在一个时期里的失 衡,有多大一个比例部分可在下一期得到纠正。 或者更应该说“失衡”对下一期 水平变化的 Y 影响的大小)。
6
1、基本的DF检验方法 (1)检验时间序列{ Yt }是否属于最基本的 单位根过程,也就是随机游走过程 Yt = Yt −1 + ε t ,其中 ε t 为白噪声过程。 (2)检验思路 首先 Yt 服从如下的自回归模型 Yt = δYt −1 + ε t
7
如果其中 δ = 1 ,或者变换成如下的回归 模型 ∆Yt = λYt −1 + ε t 中的 λ = 0 ,那么时间序列{ Yt }就是最基 本的单位根过程 Yt = Yt −1 + ε t ,肯定是非平 稳的。 对上述差分模型中的显著性检验,就是 检验时间序列是否存在上述单位根问题。
25
ˆ 3、把 ut −1 作为误差修正项,代入前述ECM 模型。因为 Yt 和 X t 有协整关系,ECM模 型各项都平稳,因此可直接用OLS法估计 参数。最后再进行相关检验和进行应用 分析等。
26
15
四、时间序列的协积性 (一)定义 如果一组时间序列都 X 1 ,L, X n 是同阶单积 的( I (d ) ),并且存在向量 ( β1 ,L, β n ) 使加权组合 β1 X 1 + L + β n X n 为平稳序列 (I (0)),则称这组时间序列为“协积的 协积的” 协积的 (Cointegrated),其中 ( β1 ,L, β n ) 称为 “协积向量”。
平稳性和非平稳时间序列分析

28
随机游走一直围绕最初出发点为中心前后左右移动,但随着游走 时间次数增加,围绕最初出发点的来回的距离(方差)越来越远。
29
随机游走模型。 它最早于1905年7月由卡尔〃皮尔逊(Karl Pearson)在 《自然》杂志上作为一个问题提出: 假如有一个醉汉醉得非常严重,完全丧失方向感,把他放 在荒郊野外,一段时间之后再去找他,在什么地方找到他 的概率最大呢?
奖级
中奖条件 红球 蓝球
说明
单注奖金
一等奖
●●● ●●●
●
当奖池资金低于 1亿元时,奖金 总额为当期高等 选6+1中6+1 奖奖金的70%与 奖池中累积的奖 金之和。
---------时间序列的动态特性 时间序列模型:时间序列各观测值之间的关系。
从系统的观点来看,某一时刻进入系统的输入 对系统后继行为的影响
与t无关,与 有关的有限值
60
ARMA(p,q)模型的平稳性条件
•
宽平稳时间序列(week stationary)—指序列的 统计性质只要保证序列的二阶矩平稳就能保证序 列的主要性质近似稳定。
5
时间序列的平稳性定义
如果在任取时间 t 、 s 和 k 时,时间序列 X t 满足如下三个条件:
EXt2
EX t
E( X t t )( X s s ) E( X k k )( X k st k st )
t 1 j t j
类似
阶数增加,越来越复杂!
53
一般情况?
cov( zt , zt ) E zt mt zt mt E zt zt
E (at 1at 1 j at j )(at 1at 1 j at j )
第七章-时间序列分析

第一节 时间序列分析的基本概念 第二节 平稳性检验 第三节 协整 第四节 误差修正模型
第一节 时间序列分析的基本概念
一、平稳性的定义 二、几种有用的时间序列模型 三、单整的时间序列
经济分析通常假定所研究的经济理论中涉及的
变量之间存在着长期均衡关系。按照这一假定,在 估计这些长期关系时,计量经济分析假定所涉及的 变量的均值和方差是常数,不随时间而变。
△x t=α+δx t-1+εt (7.14) 和 △x t=α+βt+δx t-1+εt (7.15)
二者的τ临界值分别记为τμ和τT。尽管三种 方程的τ临界值有所不同,但有关时间序列平 稳性的检验依赖的是Xt-1的系数δ,而与α、β无 关。
3.增项的单位根检验(ADF检验)
ADF 检 验 的 全 称 是 扩 展 的 迪 奇 - 福 勒 检 验 (Augmented Dickey-Fuller test),它是 DF检验的扩 展AD,F适与用DF于检扰验动的项区εt别是服在从(平7稳.12的)A式R(中P)增过加程若的干情形个。 △要回x t 归的的滞方后程项变△为x t-j(j=1,2,…,p)作为解释变量,即
一、 平稳性(Stationarity)
1. 严格平稳性
如果一个时间序列Xt的联合概率分布不随时 间而变,即对于任何n和k,X1,X2,…,Xn的联 合概率分布与X1+k,X2+k,…Xn+k 的联合分布相同, 则称该时间序列是严格平稳的。
2. 弱平稳性(宽平稳)
由于在实践中上述联合概率分布很难确定,我 们用随机变量Xt(t=1,2,…)的均值、方差和协方 差代替之。 如果一个时间序列满足下列条件:
经济统计学中的非平稳数据分析

经济统计学中的非平稳数据分析引言:经济统计学是研究经济现象的数量化方法和技术的学科。
在经济统计学中,数据分析是非常重要的一环。
然而,经济数据往往呈现出非平稳的特征,这给数据分析带来了一定的困难。
本文将探讨经济统计学中非平稳数据的分析方法和技巧。
一、什么是非平稳数据非平稳数据是指在时间序列中,数据的均值和方差不随时间保持恒定,呈现出明显的趋势或波动性。
与平稳数据相比,非平稳数据更具有挑战性,因为它们不符合许多经典统计方法的假设。
二、非平稳数据的特征1. 趋势性:非平稳数据往往呈现出明显的趋势,可以是上升趋势、下降趋势或周期性趋势。
2. 季节性:非平稳数据可能存在季节性的波动,如销售额在节假日期间的增加或减少。
3. 突变性:非平稳数据可能会受到外部因素的干扰,导致突变,如经济危机或政策调整。
三、非平稳数据的分析方法1. 差分法:差分法是一种常用的非平稳数据分析方法。
通过对数据进行一阶或多阶差分,可以将非平稳数据转化为平稳数据。
差分法的基本思想是通过消除趋势性和季节性,使数据更符合平稳性的假设。
2. 移动平均法:移动平均法是一种平滑时间序列数据的方法。
通过计算一段时间内的平均值,可以减少数据的波动性,使其更具平稳性。
移动平均法常用于消除季节性和趋势性的影响。
3. 时间序列模型:时间序列模型是一种用来描述和预测时间序列数据的方法。
常用的时间序列模型包括ARIMA模型、ARCH模型和GARCH模型等。
这些模型可以对非平稳数据进行建模,从而提供预测和分析的依据。
四、非平稳数据的应用1. 宏观经济分析:非平稳数据在宏观经济分析中有着广泛的应用。
例如,GDP、通货膨胀率和失业率等经济指标往往呈现出非平稳的特征,通过对这些数据进行分析,可以了解经济的发展趋势和变化。
2. 金融市场分析:金融市场中的股票价格、汇率和利率等数据通常也是非平稳的。
通过对这些数据的分析,可以帮助投资者和决策者做出更准确的预测和决策。
3. 企业经营分析:企业经营数据中的销售额、利润和市场份额等指标也常常是非平稳的。
非平稳和季节时间序列模型分析方法

非平稳和季节时间序列模型分析方法非平稳时间序列是指在时间序列数据中,均值、方差、自相关函数等统计性质随时间变化的数据。
这种时间序列模型常常由于其自身的特性而较难进行分析和预测。
不过,季节时间序列是非平稳时间序列的一种特殊类型,其特点是在数据中存在明显的季节性变化。
对于这种时间序列,可以采用不同的分析方法进行预测和建模。
一、非平稳时间序列分析方法:1.差分法:差分法是通过对序列数据进行相邻时间点的差分,使得序列转变为平稳时间序列。
差分法有一阶差分、二阶差分等。
通过差分法可以使得序列的单位根等统计性质得到稳定。
2.滑动平均法:滑动平均法基于序列的平均值,将序列转化为平稳时间序列。
该方法通过计算序列的滑动平均值来消除序列的变化趋势。
3.指数平滑法:指数平滑法是一种通过加权平均的方法来消除序列的变化趋势。
指数平滑法可以根据实际情况选择不同的权重系数来进行计算。
4.回归分析:对于非平稳时间序列,通过引入自变量,建立回归模型来描述序列的变化。
回归分析可以通过多个变量的关系来解释序列的变动。
二、季节时间序列分析方法:1.季节分解法:季节分解法是将季节时间序列分解为长期趋势、季节性和随机成分的组合。
这种方法可以将季节性的变动独立出来,从而更好地进行建模和预测。
2.季节移动平均法:季节移动平均法通过计算时间序列在相邻季节的平均值,消除序列的季节性变动。
这种方法可以降低季节时间序列的变化趋势。
3.季节差分法:季节差分法是将季节时间序列转化为其相邻时间点的差分。
通过差分法可以去除序列的季节性变化,使得序列更为平稳。
4.季节ARIMA模型:季节ARIMA模型是一种结合了季节差分和ARIMA 模型的方法。
该方法可以同时考虑序列的季节性变化和非平稳性,通过建立ARIMA模型来进行预测和分析。
以上所述是常用的非平稳和季节时间序列模型分析方法。
根据实际情况,我们可以选择合适的方法来分析和预测时间序列数据,以提高分析的准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
引言:前面我们讨论的是平稳时间序列的建模和预测方法,即所讨论的时间序列都是宽平稳的。
一个宽平稳的时间序列的均值和方差都是常数,并且它的协方差有时间上的不变性。
但是许多经济领域产生的时间序列都是非平稳的。
对协方差过程,非平稳时间序列会出现各种情形,如它们具有非常数的均值μt ,或非常数的二阶矩,如非常方差σt 2,或同时具有这两种情形的非平稳序列。
第七章非平稳时间序列模型第七章非平稳时间序列模型第一节非平稳时间序列模型的种类第二节非平稳性的检验第三节求和自回归滑动平均模型(ARIMA)第一节非平稳时间序列模型的种类一、均值非平稳过程二、方差和自协方差非平稳过程一、均值非平稳过程均值非平稳过程指随机过程的均值随均值函数的变化而变化。
我们可以引进两种非常有用的均值非平稳过程:确定趋势模型和随机趋势模型。
(一)确定趋势模型当非平稳过程均值函数可由一个特定的时间趋势表示时,一个标准的回归模型曲线可用来描述这种现象。
.,::,,1010模型来描述前面介绍的可以用程是一个零均值的平稳过其中趋势模型表示如下则原序列可用确定的有服从线性趋势若均值例如ARMA y y t x t t tt t t ++=+=ααααμμtt t y t t x t t +++=++=22102210:,ααααααμ原序列可用下式表示对二次均值函数此外,均值函数还可能是指数函数、正弦—余弦波函数等,这些模型都可以通过标准的回归分析处理。
处理方法是先拟合出μt 的具体形式,然后对残差序列y t ={x t -μt }按平稳过程进行分析和建模。
(二)随机趋势模型随机趋势模型又称齐次非平稳ARMA模型。
为理解齐次非平稳ARMA模型,可先对ARMA模型的性质作一回顾。
.1)(1)(:)()(:),(221221为白噪声序列其中模型如下假设有一个t qq ptt a BB B B B B B B a B x B q p ARMA θθθθϕϕϕϕθϕ----=----== .,,0)(.0)(:,就是非平稳的么那的根不都在单位圆外如果根都在单位圆外的则必须有为满足平稳性t x B B ==ϕϕtt d d a B x B B B B B d B )()1)((:)1)(()(:,,0)(θϖϖϕϕ=--==于是原模型可写为则可令而其它根都在单位圆外个根落在单位圆上恰有现假设.)()()(:,)1(.,运算后可变为平稳序列差分次程经过若干次可见一个齐次非平稳过则令称为齐次性的阶为齐次非平稳过程这时我们就称d a B w B x B w d x tt t dt t θϖ=-=可见我们所能分析处理的仅是一些特殊的非平稳序列,即齐次非平稳序列。
由于齐次非平稳序列模型恰有d个特征根在单位圆上,即有d个单位根,因此齐次非平稳序列又称单位根过程。
二、方差和自协方差非平稳过程一个均值平稳过程不一定是方差和自协方差平稳过程,同时一个均值非平稳过程也可能是方差和自协方差非平稳过程。
不是所有的非平稳问题都可以用差分方法解决,还有期望平稳和方差非平稳序列,为了克服这个问题,我们需要适当进行方差平稳化变换。
⎪⎩⎪⎨⎧≠-==010ln :,)(λλλλλt t t x x x 表示如下稳一般用幂变换使方差平这个变换最早由BOX 和COX 于1964年提出,因此称作BOX —COX 变换。
其中λ为变换参数。
第二节非平稳性的检验一、通过时间序列的趋势图来判断二、通过自相关函数(ACF)判断三、特征根检验法四、用非参数检验方法判断序列的平稳性五、随机游走的单位根检验一、通过时间序列的趋势图来判断这种方法通过观察时间序列的趋势图来判断时间序列是否存在趋势性或周期性。
优点:简便、直观。
对于那些明显为非平稳的时间序列,可以采用这种方法。
缺点:对于一般的时间序列是否平稳,不易用这种方法判断出来。
二、通过自相关函数(ACF)判断平稳时间序列的自相关函数(ACF)要么是截尾的,要么是拖尾的。
因此我们可以根据这个特性来判断时间序列是否为平稳序列。
若时间序列具有上升或下降的趋势,那么对于所有短时滞来说,自相关系数大且为正,而且随着时滞k的增加而缓慢地下降。
若序列无趋势,但是具有季节性,那末对于按月采集的数据,时滞12,24,36……的自相关系数达到最大(如果数据是按季度采集,则最大自相关系数出现在4,8,12,……),并且随着时滞的增加变得较小。
若序列是有趋势的,且具有季节性,其自相关函数特性类似于有趋势序列,但它们是摆动的,对于按月数据,在时滞12,24,36,……等处具有峰态;如果时间序列数据是按季节的,则峰出现在时滞4,8,12,……等处。
三、特征根检验法(P146).1;,1:,,,:则该序列就是非平稳的如果的则可以认为序列是平稳即件都满足平稳性条若所有的特征根特征根组成的特征方程的求由该适应模型的参数然后先拟合序列的适应模型基本思想≥<λλλ根据拟合出的时序模型参数检验(P146)基本思想:时间序列模型的平稳性条件不仅可以用特征根来表示,也可以用模型的自回归参数表示,因此要检验一个序列是否平稳,可以先拟合适应的模型,然后再根据求出的自回归参数来检验序列是否平稳。
检验方法:参见课本146;,.1:),(111:,),2(1,),1(,.21212211如果满足则需要列原序列肯定为非平稳序那么即如果上述条件不满足种便捷的途径是否平稳提供了一这为我们判断时间序列都有如下必要条件模型要满足平稳性一般的平稳性条件为模型平稳性条件为模型如例如时间序列模型较为方便归阶数较低的这种检验方法对于自回<+++⎪⎩⎪⎨⎧<<-<+<p q p ARMA q ARMA q ARMA ϕϕϕϕϕϕϕϕϕ四、用非参数检验方法判断序列的平稳性(一)什么是参数检验和非参数检验?参数检验:参数检验是这样一种检验,它的模型对抽出研究样本的总体的分布作了限制性假定。
如果对总体的分布不知道或了解很少,则参数检验方法就不可靠,甚至会发生较大偏差。
非参数检验:非参数检验是一种不依赖于总体分布知识的检验方法。
由于非参数检验不对总体分布加以限制性假定,所以它也称为自由分布检验。
非参数检验与参数检验相比有如下优点:a.检验条件比较宽松,适应性强。
b.参数检验对样本容量的要求极低。
c.检验方法灵活,用途更广泛。
非参数检验主要用顺序统计量进行检验,因此它既可检验定距数据和定比数据,又可以检验定类数据和定序数据;而参数检验只能处理定距数据和定比数据。
因为这些优点,非参数检验比参数检验应用更广泛。
d.非参数检验计算相对简单,易于理解。
非参数检验的缺点:如果参数统计模型的所有假设在数据中事实上都能满足,而且测量达到了所要求的水平(定距数据或定比数据),那么用非参数检验就浪费了数据中的信息。
也就是说此时非参数检验的功效不如参数检验高。
(二)非参数检验方法在检验序列平稳性中的应用1.游程检验方法(1)什么是游程一个游程定义为一个具有相同符号的连续串,在它前后相接的是与其不同的符号或完全无符号。
例如,观察的结果用加、减标志表示,得到一组这样的记录顺序:++---+----++-+这个样本的观察结果共有7个游程。
(2)用游程检验方法检验时间序列平稳性的基本思想..,"","",},{程数并可求出这个序列的游序列这样就形成了一个符号号的观察值记为大比号小的观察值记为对序列中比设其样本均值为对于一个时间序列+-x x x x t 如果符号序列是随机的,那么“+”和“-”将随机出现,因此它的游程数既不会太多,又不会太少;反过来说如果符号序列的游程总数太少或太多,我们就可以认为时间序列存在某种趋势性或周期性。
.)1,0()()(:)15()1()12(2)(12)(::"""",,212212121212121服布渐近服从有大于或在大样本情况下的期望和方差分别如下数游程总明,对于随机序列可以证总数为出现的次数,游程与为记号序列中分别和设序列长度为N r D r E r Z N N N N N N N N r D N N N N r E r r N N N N N N -=--=++=-++=(3)检验方法a.小样本情况零假设:H0:加号和减号以随机的方式出现检验方法:取显著性水平α(一般取0.05),查单样本游程检验表,得出抽样分布的临界值r L、r U判定:若r L<r< r U则不能拒绝零假设,即不能拒绝序列是平稳的;若r> r L或r< r U 则拒绝零假设,序列是非平稳的。
b.大样本情况零假设:H 0:加号和减号以随机的方式出现检验方法:给定显著性水平α(一般取0.05)查标准正态分布表,得出抽样分布的临界值-z α,+z α。
并计算统计量:)()(r D r E r Z -=判定:若-z α<z<+z α,则不能拒绝零假设,即不能拒绝序列是平稳的;否则拒绝零假设,序列是非平稳的。
(例见P151例6.5)非参数检验可以很方便的通过SPSS软件进行,游程检验可见操作。
实例:用游程检验S&T数据的平稳性;步骤如下:1.打开SPSS输入数据2.依次单击Analyze—Nonparmetric Tests—Runs;打开Runs对话框。
3.在源变量对话框中选择“stpoor”进入“Test Variable list”栏内4.选中“cut point”栏中“mean”选项5.单击“OK”按纽,开始进行统计分析。
输出结果分析:因为P值(sig.)极小,所以拒绝零假设,故原序列是非平稳的。
也可以通过其它的非参数检验方法来判断序列是否平稳,如Spearman等级相关系数,Kendall τ相关系数等。
五、随机游走的单位根检验(Unit root test)在第三章我们已经讲过,随机游走是一种非平稳过程,其实随机游走一种特殊的齐次非平稳过程。
检验序列是否为随机游走,通常利用David Dickey和Wayne Fuller的单位根检验。
单位根的含义和检验原理如下:返回本节首页下一页上一页.,,1:..),,,(:11间序列序列就叫做随机游走时一个有位单位根的时间根有一个单位那么就说随机变量并确实发现如果我们作如下回归非平稳的情况它是一种的单位根问题这时我们就遇到了所谓无自相关恒定方差点零均值为白噪声其中可由下式描述假设序列t tt t t tt t t y u y y u u y y y =+=+=--ρρ)(.)(.,0ˆ.;,,0ˆ,ˆ)1(:11检验由此得名统计量进行检验算的计和这时需要根据分布不服从值并通常计算的下然而要在原假设序列是平稳的否则它是非平稳的是随机游走过程则如果检验出对上述模型作回归下等价形式随机游走模型可写成如DF tau Fuller Dickey t t y u y u y y t tt tt t τδδδρ==+=+-=∆--检验时:如果所计算的τ统计量的绝对值(即|τ|)大于DF分布表中临界值的绝对值,则拒绝δ=0的假设,原序列是平稳的;否则,如果它小于临界值,则时间序列是非平稳的。
