(完整)2019高考数学专题十四外接球
高考数学中的内切球和外接球问题(附习题)-精选.pdf

一、 有关外接球的问题
如果一个多面体的各个顶点都在同一个球面上, 那么称这个多面
体是球的内接多面体,这个球称为多面体的外接球 . 有关多面体外接
球的问题, 是立体几何的一个重点, 也是高考考查的一个热点 . 考查
学生的空间想象能力以及化归能力 .研究多面体的外接球问题,既要
学习 .
五 .确定球心位置法
例 5 在矩形 ABCD 中, AB 4, BC 3,沿 AC 将矩形 ABCD 折成一
个直二面角 B AC D ,则四面体 ABCD 的外接球的体积为
125
A. 12
125
B. 9
125
C. 6
125
D. 3
D
A
O
C
图4 B
解 设矩形对角线的交点为 O ,则由矩形对角线互相平分,可知
例 2 一个正方体的各顶点均在同一球的球面上,若该正方体的
表面积为 24 ,则该球的体积为 ______________.4 3 . 2、求长方体的外接球的有关问题
例 3 一个长方体的各顶点均在同一球面上, 且一个顶点上的三条
棱长分别为 1,2,3 ,则此球的表面积为
.14 .
例 4、已知各顶点都在一个球面上的正四棱柱高为 4,
只是希望能有个人,在我说没事的时候,知道我不是真的没事;能有个人,在我强颜欢笑的时候,知道我不是真的开心。 ——张小娴
OA OB OC OD .∴点 O 到四面体的四个顶点 A、B、C、D 的距离相
等,即点 O 为四面体的外接球的球心,如图 2 所示 .∴外接球的半径
5 R OA
V 球 4 R3 125
2 .故
3
6 .选 C.
高中数学空间几何体的外接球专题(附经典例题与解析)
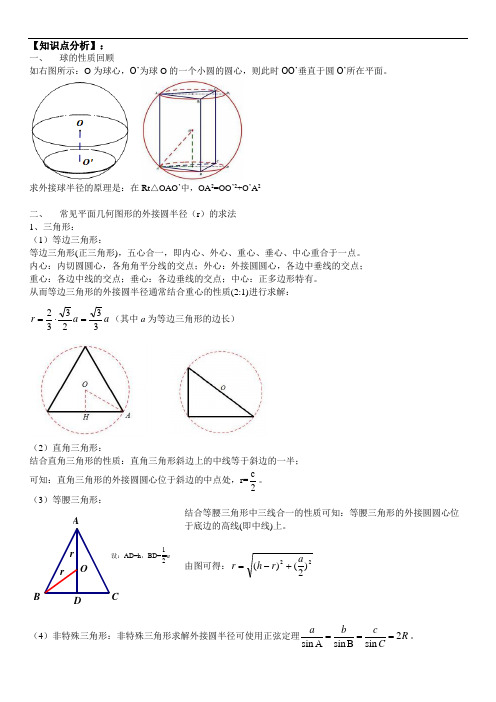
【知识点分析】: 一、 球的性质回顾如右图所示:O 为球心,O’为球O 的一个小圆的圆心,则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是:在Rt △OAO ’中,OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径(r )的求法1、三角形:(1)等边三角形:等边三角形(正三角形),五心合一,即内心、外心、重心、垂心、中心重合于一点。
内心:内切圆圆心,各角角平分线的交点;外心:外接圆圆心,各边中垂线的交点;重心:各边中线的交点;垂心:各边垂线的交点;中心:正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解:a a r 332332=⋅=(其中a 为等边三角形的边长)(2)直角三角形:结合直角三角形的性质:直角三角形斜边上的中线等于斜边的一半;可知:直角三角形的外接圆圆心位于斜边的中点处,r=2c 。
(3)等腰三角形: 结合等腰三角形中三线合一的性质可知:等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得:22)2()(a r h r +-=(4)非特殊三角形:非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ,BD=12a B CO2、四边形常见具有外接圆的四边形有:正方形、矩形、等腰梯形,其中正方形与长方形半径求解方法转化为直角三角形,等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点;外接球球心则是球心到几何体各个顶点距离相同的点。
结论:几何体的外接球球心与底面外心的连线垂直于底面,(也即球心落在过底面外心的垂线上,)简单称之为:球心落在底面外心的正上方。
【相似题练习】2.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【知识点分析】:类型一:直(正)棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直,从而球心O 必位于上下两底面外心连线的中点处,即121'AA OO =,从而R 可求.【相似题练习】1.三棱柱ABC ﹣A 1B 1C 1中,底面ABC 是边长为2的正三角形,侧棱AA 1垂直于底面ABC ,且AA 1=4,则此三棱柱外接球的表面积为( )A .B .C .D .【知识点分析】:类型二:侧棱垂直底面的三棱锥,法一:补形法:该几何体可由正三棱柱沿平面PBC 切割得来,故可转化为原三棱柱的外接球;法二:先确定底面三角形ABC 的外心O’,从而球心位于O’的正上方,即OO’ ⊥平面ABC ,同时:OP=OA ,故,过O 作OM ⊥PA 于M ,此时M 必为PA 中点,从而四边形OMAO’为矩形,所以PA AM OO 21'==,在直角三角形OO’A 中有:222'OO r R +=.【相似题练习】2.已知在三棱锥P ﹣ABC 中,△ABC 是边长为2的正三角形,若PA ⊥底面ABC 且PA =2,则该三棱锥的外接球的表面积为( )A .32πB .28πC .24πD .20π3.在三棱锥P ﹣ABC 中,PA ⊥平面ABC ,PA =2,AB =4,AC =3,∠BAC =,则三棱锥P ﹣ABC 的外接球的半径R =( )A .B .C .D .【知识点分析】:类型三:正三棱锥:由底面正三角形边长可得r ,在直角三角形OO’A 中,222'OO r R +=,故只需确定OO’的长度即可,结合图形,OO’=PO’-OP=H-R ,代入222)(R H r R -+=即可求解.【相似题练习】3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 .2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )【知识点分析】:类型四:侧面垂直于底面的三棱锥:设△ABC和△PAB的外心分别为O’,O’’,则PM⊥AB,球心设为O,则OO’ ⊥平面ABC,OO’’⊥平面PAB,从而四边形OO’MO’’是矩形,可得:OO’=O’’M,在Rt△OO’C中用勾股定理求解.【讲透例题】1.在四面体A﹣BCD中,AB=5,BC=CD=3,DB=2,AC=4,∠ACD=60°,则该四面体的外接球的表面积为.解析:如图:取AB的中点O,在△ACD中,由余弦定理得:AD2=AC2+CD2﹣2×AC×CD cos60°=13,在△ABD中,∵AB2=BD2+AD2,∴∠ADB=90°,∴OA=OB=OD,在△ABC中,∵AB2=BC2+AC2,∴∠ACB=90°,∴OA=OB=OC,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心,其半径R=AB=,∴S球=4πR2=4π()2=25π.故答案为:25π.【相似题练习】4.在三棱锥P-ABC中,面PAB⊥面ABC,三角形ABC和三角形PAB均为等边三角形,且AB=3,求该几何体外接球半径.2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为.5、如图,在四棱锥P﹣ABCD中,底面ABCD为长方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.7、如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π课后作业:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.参考答案与解析12.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π【解答】解:由题意可知图形如图:⊙O1的面积为4π,可得O1A=2,则AO1=AB sin60°,,∴AB=BC=AC=OO1=2,外接球的半径为:R==4,球O的表面积:4×π×42=64π.故选:A.1.1.一个几何的三视图如图所示,它们都是腰长为1的等腰直角三角形,则该几何体的外接球的体积等于()A.B.C.πD.2π解析:由三视图可知:该几何体是一个如图所示的三棱锥,其中底面是一个两直角边都为1的直角三角形,PC⊥底面ABC,且PC=1.将此三棱锥恢复为棱长为1的正方体,可知该正方体的外接球的直径即为正方体的对角线,∴V外接球==.故选:B.1.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【解答】解:三棱锥P﹣ABC中,PA=PB=PC=2,AB=AC=BC,如图,过点p作PM⊥平面ABC的垂足为M,则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上,∵球O的半径为2,∴OB=OP=2,∴由余弦定理得cos∠BPM==∴∠BPM=30°,∴在Rt△PMB中,∠PBM=60°,∴PM=PB sin∠PBM=3.故选:D.1.三棱柱ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为()A.B.C.D.【解答】解:∵正三棱柱ABC﹣A1B1C1的中,底面边长为2,高为4,由题意可得:三棱柱上下底面中心连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,∴正三棱柱ABC﹣A1B1C1的外接球的球心为O,外接球的半径为r,表面积为:4πr2.球心到底面的距离为2,底面中心到底面三角形的顶点的距离为:=,所以球的半径为r==.外接球的表面积为:4πr2=π故选:D.2.已知在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,若PA⊥底面ABC且PA=2,则该三棱锥的外接球的表面积为()A.32πB.28πC.24πD.20π【解答】解:由正弦定理可知,正△ABC的外接圆的直径为,∵PA⊥平面ABC,所以,该三棱锥的外接球的直径为,则.因此,该三棱锥的外接球的表面积为4πR2=20π.故选:D.3.在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC=,则三棱锥P﹣ABC的外接球的半径R=()A.B.C.D.【解答】解:∵AC=3,AB=4,∠BAC=,∴由余弦定理可得BC=,∴△ABC外接圆的半径r=,设球心到平面ABC的距离为d,则d=PA=1.由勾股定理可得R =,故选:D .3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 1 . 【解答】解:过点P 作PH ⊥平面ABC 于H ,则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角,得∠PAH =60°, ∴Rt △PAH 中,AH =PA cos60°=,PH =PA sin60°=设三棱锥外接球的球心为O ,∵PA =PB =PC ,∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得,外接球心O 必定在PH 上,连接OA 、OB 、OC ∵△POA 中,OP =OA , ∴∠OAP =∠OPA =30°,可得PA =OA =,∴三棱锥外接球的半径R =OA =1故答案为:1.2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )A .16πB .12πC .9πD .8π【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为等腰直角三角形,高为2的三棱锥体. 如图所示:所以该三棱锥体的外接球的球心为O ,外接球的半径为OA =r ,则:,解得.故S =.故选:C .4.在三棱锥P-ABC 中,面PAB ⊥面ABC ,三角形ABC 和三角形PAB 均为等边三角形,且AB=3,求该几何体外接球半径.由题可得:333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.【解答】解:∵在边长为2的菱形ABCD中,;如图,由已知可得,△ABC与△ACD均为等边三角形,取AC中点G,连接BG,DG,则BG⊥AC,∴DG=⇒cos∠GDA=⇒∠GDA=⇒∠ADC=;∵二面角B﹣AC﹣D为直二面角,则BG⊥平面ACD,分别取△BCD与△ABD的外心E,F,过E,F分别作两面的垂线,相交于O,则O为三棱锥A﹣BCD的外接球的球心,由△BCA与△ACD均为等边三角形且边长为2,可得OE=OF=DG=.∴DE=DG﹣GE=.∴OD===.∴三棱锥A﹣BCD的外接球的表面积为4π×R2=4π×()2=.故选:C.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为10π.【解答】解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,根据球的性质,球心一定在垂线l,∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,在△PBC中,由余弦定理得cos B=,⇒sin B=,由正弦定理得:,解得R=,∴三棱锥P﹣ABC外接球的表面积为s=4πR2=10π,故答案为:10π.1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD 中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.【解答】证明:(1)∵PA⊥底面ABCD,AB⊂底面ABCD,∴PA⊥AB,又∵底面ABCD为矩形,∴AB⊥AD,PA∩AD,又PA⊂平面PAD,AD⊂平面PAD,∴AB⊥平面PAD,又PD⊂平面PAD,∴AB⊥PD,AD=AP,E为PD中点,∴AE⊥PD,AE∩AB=A,AE⊂平面ABE,AB⊂平面ABE,∴PD⊥平面ABE.解:(II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由已知BD===4,设C为BD中点,∴AM=2,OM=AP=1,∴OA===3,∴四棱锥P﹣ABCD外接球的体积是=36π.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.【解答】(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.又因为AB⊄平面PDE,DE⊂平面PDE,所以AB∥平面PDE.因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,所以AB∥FG.(2)解:连接AD,EM,相交于O′,易得AO′=,PO′=.由正四棱锥P﹣AMDE的对称性,得正四棱锥P﹣AMDE得外接球球心在线段PO′上,不妨设为O点.设OA=OP=R,则OO′=﹣R,∵AO2=AO′2+OO′2,∴R2=2+(﹣R)2,∴R=∴S=4πR2=,∴正四棱锥P﹣AMDE的外接球的表面积为.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.【解答】解:(I)∵四边形ABCD是矩形,∴AD⊥CD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,∴CD⊥平面PAD,∵CD⊂平面PCD,∴平面PAD⊥平面PCD.(II)过P作PE⊥AD,垂足为E,∵△PAD是等腰直角三角形,∠APD=90°,∴PE==1.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PE⊂平面PAD,PE⊥AD,∴PE⊥平面ABCD,∴V棱锥P﹣ABD=S△ABD•PE=••2•4•1=.(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,连接AM,则AM==.∵PE⊥平面ABCD,∴MN∥PE.∵四棱锥P﹣ABCD内接于球,,∴OA==.∴S⊙O=4πOA2=20π.∴E为外心,∴OM=1.如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π【解答】解:几何体的直观图如图:是长方体的一部分,上底面PCD的外接圆的半径:O1D==,几何体的外接球的半径为:OD==,该四棱锥的外接球的表面积是:4=π.故选:A.课后作业答案:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π【解答】解:设正三棱柱的外接球的半径为R,则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为=1,∵正三棱柱的高为2∴正三棱柱的外接球的半径为=∴正三棱柱的外接球的表面积等于4π×=8π故选:C.2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π【解答】解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长=.∴此四面体的外接球的表面积为表面积==3π.故选:B.3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π【解答】解:由题意可知,几何体的直观图如图:是四棱锥D1﹣ABCD,是棱长为1的正方体的一部分,外接球奇数正方体的外接球,取得直径是体对角线,r=,外接球的表面积为:4=3π.故选:A.4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.【解答】证明:(1)设AD的中点为E,则∵PA=PD,∴PE⊥AD,∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD,∵PA在平面ABCD内的射影为AE,AE⊥CD,∴PA⊥CD,∵PA⊥PD,CD∩PD=D,∴PA⊥平面PCD∴PA⊥PC;解:(2)连接AC交BD于F,球心O在底面的射影必为点F,取截面PEF,PE=,EF=1.假设OF=x,则由OA2=x2+4=1+得x=0,∴球的半径为2,∴四棱锥P﹣ABCD的外接球的体积为=.。
2019届高考数学专题十四外接球精准培优专练理201811081151

培优点十四 外接球1.正棱柱,长方体的外接球球心是其中心例 1:已知各顶点都在同一球面上的正四棱柱的高为 4 ,体积为16,则这个球的表面积是 ()A .16πB . 20πC . 24πD .32π【答案】C 【解析】Va 2h 16, a 2 , 4R 2 a 2 a 2 h 2 4 4 16 24 , S 24π ,故选 C .2.补形法(补成长方体)PPPPO 2ccAbCCa bAAaB aBBbc C AaB bcC图 1 图 2 图 3 图 4例 2:若三棱锥的三个侧面两两垂直,且侧棱长均为 3 ,则其外接球的表面积是 .【答案】9π 【解析】 4R 23 3 3 9 , S 4πR 2 9π .3.依据垂直关系找球心 例 3:已知三棱锥 PABC 的四个顶点均在同一个球面上,底面△ABC 满足BA BC,π 6ABC,若该三棱锥体积的最大值为 3,则其外接球的体积为2()16 3A .8πB .16πC .πD . 32 3π【答案】D1 【解析】因为△ABC 是等腰直角三角形,所以外接球的半径是 r,设外接球的 12 32半径是R,球心O到该底面的距离d,如图,则11V S h 6h 3△,ABC361S△63,BD 3,由题设ABC21最大体积对应的高为SD h3,故R2d23,即233R R,解之得R2,2所以外接球的体积是4π332πR,故答案为D.33对点增分集训一、单选题1.棱长分别为2、3、5的长方体的外接球的表面积为()A.4πB.12πC.24πD.48π【答案】B2 222【解析】设长方体的外接球半径为R,由题意可知:2R235,则:R23,该长方体的外接球的表面积为S4πR24π312π.本题选择B选项.2.设三棱柱的侧棱垂直于底面,所有棱的长都为23,顶点都在一个球面上,则该球的表面积为()A.12πB.28πC.44πD.60π【答案】B【解析】设底面三角形的外接圆半径为r,由正弦定理可得:2r23sin60,则r2,2设外接球半径为R,结合三棱柱的特征可知外接球半径R23227,外接球的表面积S4πR228π.本题选择B选项.3.把边长为3的正方形ABCD沿对角线AC对折,使得平面ABC平面ADC,则三棱锥2D ABC的外接球的表面积为()A.32πB.27πC.18πD.9π【答案】C【解析】把边长为3的正方形ABCD沿对角线AC对折,使得平面ABC 平面ADC,则三棱锥D ABC的外接球直径为AC 32,外接球的表面积为4πR218π,故选C.4.某几何体是由两个同底面的三棱锥组成,其三视图如下图所示,则该几何体外接球的面积为()A.a2πB.2a2πC.3a2πD.4a2π【答案】C【解析】由题可知,该几何体是由同底面不同棱的两个三棱锥构成,其中底面是棱长为2a的正三角形,一个是三条侧棱两两垂直,且侧棱长为a的正三棱锥,另一个是棱长为2a的正四面体,如图所示:该几何体的外接球与棱长为푎的正方体的外接球相同,因此外接球的直径即为正方体的体对角线,所以222233R a a aa Ra,所以该几何体外接球面积22232S 4πR 4πa3aπ2,故选C.5.三棱锥A BCD的所有顶点都在球O的表面上,AB 平面BCD,BC BD 2,3AB 2CD 4 3 ,则球 O 的表面积为() A .16π B .32πC . 60πD . 64π【答案】D22 22 3122【解析】因为 BC BD 2 ,CD 2 3 ,所以CBDcos2 2 22,2πCBD,3因此三角形 BCD 外接圆半径为1 CD 2sin CBD2,设外接球半径为 R ,则2R2 =22 +4 12 16 ,S =4πR 264π ,故选D .AB26.如图 ABCD A B C D 是边长为 1的正方体, SABCD 是高为 1的正四棱锥,若点S ,1 1 1 1A ,B 1 ,C 1 ,D 1 在同一个球面上,则该球的表面积为()19 A . 16 π25 16 B .π49 16 C .π81 D . π16【答案】D【解析】如图所示,连结A C,B1D1,交点为M,连结SM,11易知球心O在直线SM上,设球的半径R OS x,在R t△OMB中,由勾股定理有:142222OMB MB O ,即:22 22 xx ,解得: 1129x ,则该球的表面积82SR4π 4ππ .本题选择 D 选项.29 81 8167.已知球 O 的半径为 R , A , B , C 三点在球 O 的球面上,球心 O 到平面 ABC 的距离为1 2R ,AB AC 2 , BAC 120,则球 O 的表面积为( )16 9 A . π 16 3 B . πC .649 π D . 64 3 π 【答案】D【解析】由余弦定理得: BC4 4 222cos1202 3 ,设三角 ABC 外接圆半径为 r ,由正弦定理可得: 2 3 sin1202r,则 r2,又 R 21 R2 4 ,解得: R 216 ,则球的表面积 4π 2 64 π SR.本题选择 D 选项.4338.已知正四棱锥 P ABCD (底面四边形 ABCD 是正方形,顶点푃在底面的射影是底面的中心) 的各顶点都在同一球面上,底面正方形的边长为 10 ,若该正四棱锥的体积为 50 3,则此球的 体积为( )A .18πB .8 6C .36πD .32 3π【答案】C 【解析】如图,设正方形 ABCD 的中点为 E ,正四棱锥 P ABCD 的外接球心为 O ,底面正方形的边长为10,EA5,正四棱锥的体积为5031250,V10PE,P ABCD335则 PE 5 ,OE 5 R ,在△AOE中由勾股定理可得:VR5 R5 R ,解得 R3 ,4 π336π 22球,故选 C .39.如图,在△ABC 中, AB BC 6 , ABC 90 ,点 D 为 AC 的中点,将△ABD 沿 BD折起到 △PBD 的位置,使 PC PD ,连接 PC ,得到三棱锥 P BCD .若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )A . 7πB .5πC .3πD . π【答案】A【解析】由题意得该三棱锥的面 PCD 是边长为 3 的正三角形,且 BD 平面 PCD ,设三棱锥 P BDC 外接球的球心为 O , △PCD 外接圆的圆心为O ,则OO 1 面 PCD ,∴四边形OO 1DB 为直角梯形,17由 BD 3 ,O D ,及OB OD ,得OB,∴外接球半径为1 1 2∴该球的表面积4π 2 4π 7 7π S R.故选 A .47 R,210.四面体 A BCD 中, ABCABDCBD 60 , AB3 ,CB DB2 ,则此四面体外接球的表面积为( ) 19 2 A . π 19 38π B .2417 17π C .17πD .6【答案】A 【解析】由题意,△BCD中,CB DB2,CBD60,可知△BCD是等边三角形,BF3,6∴△BCD 的外接圆半径 FE, r 2 3BE ,3 33∵ ABCABD 60,可得 AD AC7 ,可得 AF6 ,∴ AFFB ,∴ AFBCD ,∴四面体 A BCD 高为 AF6 .设外接球 R , O 为球心,OEm ,可得: r 2 m 2 R 2 ……①,2226πEFR ……②由①②解得:SR.故选 A .R 19 .四面体外接球的表面积:4π219 π 8211.将边长为 2的正 △ABC 沿着高 AD 折起,使 BDC 120 ,若折起后 A 、B 、C 、D 四点都在球 O 的表面上,则球 O 的表面积为( )A . 7 2 π13 B . 7πC . π213 D . π3【答案】B【解析】△BCD 中, BD1,CD1, BDC120 ,底面三角形的底面外接圆圆心为 M ,半径为 r ,由余弦定理得到 BC 3 ,再由正弦定理得到3 sin1202r r1,见图示:AD 是球的弦, DA 3 ,将底面的圆心 M 平行于 AD 竖直向上提起,提起到 AD 的高度的一3半,即为球心的位置 O ,∴OM ,在直角三角形OMD 中,应用勾股定理得到OD ,OD 2即为球的半径.37OD.该球的表面积为 4πOD 27π ;故选 B .∴球的半径14212.在三棱锥A BCD中,AB CD6,AC BD AD BC5,则该三棱锥的外接球的表面积为()7A .43 43π 24 B .43 43π 6 C .43π 2D . 43π【答案】D【解析】分别取 AB ,CD 的中点 E , F ,连接相应的线段CE , ED , EF , 由条件, ABCD4 , BCACAD BD5 ,可知, △ABC 与△ADB ,都是等腰三角形,AB 平面 ECD ,∴ AB EF ,同理CD EF ,∴ EF 是 AB 与CD 的公垂线,球心G 在 EF 上,推导出△AGB ≌△CGD ,可以证明G 为 EF 中点,DE 25 9 4 , DF3, EF 16 9 7 ,∴GF7 ,球半径 7 9 43 2 4 2故选 D .二、填空题13.棱长均为 6的直三棱柱的外接球的表面积是_________. 【答案】84π16 1 6 【解析】由正弦定理可知底面三角形的外接圆半径为r2 sin6023 22 3 ,2则外接球的半径R 32 391221 ,2则外接球的表面积为 S4πR 24π 21 84π .14.已知棱长都相等正四棱锥的侧面积为16 3 ,则该正四棱锥内切球的表面积为________.【答案】32 16 3π【解析】设正四棱锥的棱长为 a ,则 43216 3 a,解得 a 4 .4于是该正四棱锥内切球的大圆是如图△PMN的内切圆,8其中MN 4,PM PN 23.∴PE 22.设内切圆的半径为r,由△PFO △PEN,得FO PO,即r 22r,EN PN22322解得r 6231,2 ∴内切球的表面积为Sr2.4π4π6232163π15.已知三棱柱A BC A B C的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为1113,AB 2,AC 1,BAC 60,则此球的表面积等于______.【答案】8π【解析】∵三棱柱A BC A B C的侧棱垂直于底面,棱柱的体积为3,AB 2,AC1,1111BAC 60,21sin603,,AA AA1 212BC2AB2AC22AB ACcos60412,BC 3,BC设△ABC外接圆的半径为R,则=2R ,R 1,sin602∴外接球的半径为112,∴球的表面积等于4π28π.故答案为8π.16.在三棱锥A BCD中,AB AC,DB DC,AB DB 4,AB BD,则三棱锥A BCD外接球的体积的最小值为_____.82π【答案】3【解析】如图所示,三棱锥A BCD的外接圆即为长方体的外接圆,外接圆的直径为长方体的体对角线AD,9设 AB AC x ,那么 DB DC 4 x , AB BD ,所以 ADAB 2 DB 2 .由题意,体积的最小值即为AD 最小, 24AD xx ,所以当 x 2 时, AD 的最小值为 2 2 ,所以半径为 2 ,28 2π 故体积的最小值为3.10。
(完整版)高考数学中的内切球和外接球问题.

(完整版)高考数学中的内切球和外接球问题.高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______________ .例2一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为______________.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为.例4已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为().A. 16πB. 20πC. 24πD. 32π3.求多面体的外接球的有关问题例5一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为8 9,底面周长为3,则这个球的体积为 .解设正六棱柱的底面边长为x ,高为h ,则有==h x x 24368936==213x h ∴正六棱柱的底面圆的半径21=r ,球心到底面的距离23=d .∴外接球的半径22d r R +=. 体积:334R V π=. 小结本题是运用公式222d r R +=求球的半径的,该公式是求球的半径的常用公式.二、构造法(补形法) 1、构造正方体例5 若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是_______________.例3 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 .故其外接球的表面积ππ942==r S .小结:一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为c b a ,,,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2222c b a R ++=. 出现“墙角”结构利用补形知识,联系长方体。
高考数学立体几何专题:外接球

b2
1 a2 3
PO1
b2
1 a2 3
OO1
PO1
PO
b2 1 a2 R ; 3
在 RtOO1A 中:根据勾股定理得到:
OO12 AO12 AO2 (
b2 1 a2 R)2 ( 3 a)2 R2 b2 1 a2 2
第二部分:柱体的外接球半径 【计算步骤】 第一步:计算底面的外接圆的半径。 第二步:计算直柱体的外接球的半径。 直柱体的外接球的球心:上下底面的外接圆圆心连线的中点为球心。如下图所示:
第3页共8页
其中: O1 为下底面的外接圆的圆心, O2 为上底面的外接圆的圆心, O 为 O1O2 的中点(直柱体外接球的球心); r 为上下底面的外接圆的半径, R 为直柱体的外接球的半径。
2
训练:求下列图形的外接圆半径。
(Ⅰ)在 ABC 中: AB AC , AB 3 , AC 4 ; (Ⅱ)在 ABC 中: AB AC 3 , BC 2 5 ; (Ⅲ)在正 ABC 中: AB 3 ;
3 (Ⅳ)在 ABC 中, AB 2 , BC 3, AC 2 ; (Ⅴ)在矩形 ABCD 中: AB 6 , BC 3 ; (Ⅵ)在正方形 ABCD 中: AB 2 。
根据勾股定理得到: R2 r 2 ( h )2 r 2 h2 R r 2 h2 。
2
4
4
【训练一】:已知:在直三棱柱 ABC A1B1C1 中: AB AC , AB AC 2 , AA1 2 。 求解:直三棱锥 ABC A1B1C1 的外接球的半径。
【训练二】:已知:在正三棱柱 ABC A1B1C1 中: AB 3 , BB1 2 3 。 求解:直三棱锥 ABC A1B1C1 的外接球的半径。
(完整版)高考外接球内切球专题练习

高考外接球与内接球专题练习(1)正方体,长方体外接球1. 如图所示,已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,长为2的线段MN 的一个端点M 在棱DD 1上运动,另一端点N 在正方形ABCD 内运动,则MN 的中点的轨迹的面积为( )A. 4πB. 2πC. πD. 2π 2. 正方体的内切球与其外接球的体积之比为( ) A. 1:3 B. 1:3 C. 1:33 D. 1:93. 长方体ABCD ﹣A 1B 1C 1D 1的8个顶点在同一个球面上,且AB=2,AD=3,AA 1=1, 则该球的表面积为( )A. 4πB. 8πC. 16πD. 32π4. 底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一球面上,则该球的体积为A. 323π B. 4π C. 2π D. 43π 5. 已知正三棱锥P ﹣ABC ,点P ,A ,B ,C 都在半径为3的球面上,若P A ,PB ,PC 两两垂直,则球心到截面ABC 的距离为 _________ .6. 在三棱椎A ﹣BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ADB 的 面积分别为22,32,62,则该三棱椎外接球的表面积为( ) A. 2π B. 6π C. 46π D. 24π7. 设A 、B 、C 、D 是半径为2的球面上的四点,且满足AB ⊥AC 、AD ⊥AC 、AB ⊥AD , 则S △ABC +S △ABD +S △ACD 的最大值为( )A. 4B. 8C. 12D. 168. 四面体ABCD 中,已知AB=CD=29,AC=BD=34,AD=BC=37,则四面体的 外接球的表面积为( )A. 25πB. 45πC. 50πD. 100π9. 如图,在三棱锥S ﹣ABC 中,M 、N 分别是棱SC 、BC 的中点,且MN ⊥AM ,若AB=22,则此正三棱锥外接球的体积是A. 12πB. 43πC. 433π D. 123π 10. 已知三棱锥P ABC -的顶点都在同一个球面上(球O ),且2,6PA PB PC ===, 当三棱锥P ABC -的三个侧面的面积之和最大时,该三棱锥的体积与球O 的体积的比值为( )A. 316πB. 38πC. 116πD. 18π (2)直棱柱外接球11. 已知三棱柱ABC ﹣A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC , AA 1=12,则球O 的半径为A. 3172B. 210C. 132D. 310 12. 设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面 积为( )A. 2a πB. 273a πC. 2113a π D. 25a π 13. 直三棱柱ABC ﹣A 1B 1C 1的各顶点都在同一球面上,若AB=AC=AA 1=2,∠BAC=120°, 则此球的表面积等于_________ .14. 三棱锥S ﹣ABC 的所有顶点都在球O 的表面上,SA ⊥平面ABC ,AB ⊥BC ,又SA=AB=BC=1,则球O 的表面积为( )A. 32πB. 32π C. 3π D. 12π 15. 已知球O 的面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA=AB=BC=3, 则球O 的体积等于 _________ .(3)正棱锥外接球16. 棱长均相等的四面体ABCD 的外接球半径为1,则该四面体的棱长为___________17. 如图,在等腰梯形ABCD 中,AB=2DC=2,∠DAB=60°,E 为AB的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B重合于点P ,则P ﹣DCE 三棱锥的外接球的体积为( )A. 4327πB. 62π C. 68π D. 624π 18. 已知三棱锥P ABC -的所有顶点都在表面积为28916π的球面上,底面ABC 是边长为 3的等边三角形,则三棱锥P ABC -体积的最大值为__________19. 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积 为( )A. 814π B. 16π C. 9π D. 274π 20. 已知正三棱锥P ﹣ABC 的顶点均在球O 上,且P A=PB=PC=25,AB=BC=CA=23, 则球O 的表面积为( )A. 25πB. 1256πC. 52π D. 20π21. 在球O 的表面上有A 、B 、C 三个点,且3AOB BOC COA π∠=∠=∠=,△ABC 的外接圆半径为2,那么这个球的表面积为( ) A. 48π B. 36π C. 24π D. 12π 22. 半径为2的半球内有一内接正六棱锥P ﹣ABCDEF ,则此正六棱锥的侧面积是 ____.23. 表面积为23的正八面体的各个顶点都在同一个球面上,则此球的体积为( )A. 23πB. 3π C. 23π D. 223π 24. 正四棱锥P ﹣ABCD 底面的四个顶点A 、B 、C 、D 在球O 的同一个大圆上,点P 在球面 上,如果163P ABCD V -=,则求O 的表面积为( ) A. 4π B. 8π C. 12π D. 16π(4)棱锥外接球25. 已知A ,B ,C ,D 在同一个球面上,AB ⊥平面BCD ,BC ⊥CD ,若AB=6,213AC =, AD=8,则此球的体积是 _________ .26. 在矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B ﹣AC ﹣D , 则四面体ABCD 的外接球的体积为( )A. 12512πB. 1259πC. 1256πD. 1253π 27. 点A ,B ,C ,D 在同一个球的球面上,AB=BC=2,AC=22,若四面体ABCD 体积 的最大值为43,则该球的表面积为( ) A. 163π B. 8π C. 9π D. 12π 28. 四棱锥S ﹣ABCD 的底面ABCD 是正方形,侧面SAB 是以AB 为斜边的等腰直角三角 形,且侧面SAB ⊥底面ABCD ,若AB=23,则此四棱锥的外接球的表面积为( )A. 14πB. 18πC. 20πD. 24π29. 三棱锥S ﹣ABC 的四个顶点都在球面上,SA 是球的直径,AC ⊥AB ,BC=SB=SC=2, 则该球的表面积为( )A. 4πB. 6πC. 9πD. 12π30. 已知四棱锥V ﹣ABCD 的顶点都在同一球面上,底面ABCD 为矩形,AC∩BD=G ,VG ⊥平面ABCD ,AB=3,AD=3,VG=3,则该球的体积为( )A. 36πB. 9πC. 123πD. 43π(5)内接球31. 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A. 1B. 2C. 3D. 432. 在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6,8AB BC ==,13AA =,则V 的最大值为A. 4πB. 92πC. 6πD. 323π 33. 已知球O 与棱长为4的正四面体的各棱相切,则球O 的体积为( ) A. 823π B. 833π C. 863π D. 1623π 34. 把一个皮球放入一个由8根长均为20的铁丝接成的四棱锥形骨架内,使皮球的表面 与8根铁丝都有接触点(皮球不变形),则皮球的半径为( )A. 103B. 10C. 102D. 3035. 棱长为23的正四面体内切一球,然后在正四面体和该球形成的空隙处各放入一个小 球,则这些球的最大半径为( )A. 2B. 22C. 24D. 2636. 如图,在四面体ABCD 中,截面AEF 经过四面体的内切球球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A ﹣BEFD 与三棱锥A ﹣EFC的表面积分别是S 1,S 2,则必有( )A. S 1<S 2B. S 1>S 2C. S 1=S 2D. S 1,S 2的大小关系不能确定(6)球的截面问题37. 平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为,则此球的体 积为( )A. 6πB. 43πC. 46πD. 63π38. 已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形, SC 为球O 的直径,且SC=2,则此棱锥的体积为( )A. 26B. 36C. 23D. 2239. 高为2的四棱锥S ﹣ABCD 的底面是边长为1的正方形,点S ,A ,B ,C ,D 均在半 径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为( )A. 102B. 232+C. 32D. 240. 已知三棱锥S ﹣ABC 的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,AC =,则球的体积与三棱锥体积之比是( )A. πB. 2πC. 3πD. 4π41. 在半径为13的球面上有A ,B ,C 三点,AB=6,BC=8,CA=10,则(1)球心到平面ABC 的距离为 _________ ;(2)过A ,B 两点的大圆面与平面ABC 所成二面角为(锐角)的正切值为 ____.42. 设A 、B 、C 、D 是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到 该平面的距离是球半径的一半,则球的体积是( )A. B. C. D.43. 已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2, 则球面面积是( ) A. 169π B. 83π C. 4π D. 649π 44. 已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M . 若圆M 的面积为3π,则球O 的表面积等于 _________ .45. 三棱锥P ﹣ABC 的各顶点都在一半径为R 的球面上,球心O 在AB 上,且有P A=PB=PC , 底面△ABC 中∠ABC=60°,则球与三棱锥的体积之比是 _________ .46. 已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截 球O 所得截面的面积为π,则球O 的表面积为__________(7)旋转体的外接内切47. 半径为4的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面 积之差是 _________ .48. 将4个半径都是R 的球体完全装入底面半径是2R 的圆柱形桶中,则桶的最小高度 是 _________ .1. D ;2. C ;3. B ;4. D ;5. 3; 6. B ; 7. B ; 8. C ; 9. B ;10. A ; 11. C ; 12. B ; 13. 20π; 14. C ; 15. 92π; 16. ;17. C ; 19. A ; 20. A ; 21. A ; 22. ; 23. A ; 24. D ; 25. 2563π; 26. C ; 27. C ; 28. D ; 29. B ; 30. D ; 31. B ; 32. B ; 33. A ; 34. B ; 35. C ; 36. C ; 37. B ; 38. A ; 39. A ; 40. D ;41. 12;3;42. A;43. D;44. 16π;45.3;46.92π47. 30π;48.(2R+;。
高中数学空间几何体的外接球专题(附经典例题与解析)

高中数学空间几何体的外接球专题(附经典例题与解析)球的性质回顾:球心O和小圆O'的连线OO'垂直于圆O'所在平面。
外接球半径的求法是利用直角三角形的勾股定理,在Rt△OAO'中,OA^2=OO'^2+O'A^2.常见平面几何图形的外接圆半径(r)的求法:1.三角形:1) 等边三角形:内心、外心、重心、垂心、中心重合于一点。
外接圆半径通常结合重心的性质(2:1)进行求解:r=a*(2/3)^(1/2) (其中a为等边三角形的边长)。
2) 直角三角形:外接圆圆心位于斜边的中点处,r=斜边/2.3) 等腰三角形:外接圆圆心位于底边的高线(即中线)上。
r=a/(2sin(A/2)) (其中A为顶角)。
4) 非特殊三角形:可使用正弦定理求解,XXX)。
2.四边形:常见具有外接圆的四边形有正方形、矩形、等腰梯形。
其中正方形与长方形半径求解方法转化为直角三角形。
几何体的外接球球心与底面外心的连线垂直于底面,即球心落在过底面外心的垂线上。
练:2.半径为2的球的内接三棱锥P-ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为3.1.三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为8π。
本文介绍了三棱锥的外接球的求解方法,其中包括侧棱垂直底面的三棱锥、正三棱锥和侧面垂直于底面的三棱锥三种类型。
对于侧棱垂直底面的三棱锥,可以采用补形法或通过确定底面三角形的外心来求解外接球的半径。
补形法是指将该几何体转化为原三棱柱的外接球,从而求出外接球的半径。
而通过确定底面三角形的外心,则可以通过勾股定理求解外接球的半径。
对于正三棱锥,可以通过底面正三角形的边长来求解内切球的半径,然后再利用勾股定理求解外接球的半径。
对于侧面垂直于底面的三棱锥,则需要确定△ABC和△PAB的外心分别为O’和O’’,并通过勾股定理求解OO’的长度,从而求解外接球的半径。
2019-2020学年高三下学期高考数学之空间几何体的外接球专题课件

│课堂互动│
空间几何体的外接球问题
类型一:补形为正方体、长方体的类型(学生做,完成后直接对答案)
1.棱长为 2 2 的正四面体的顶点在同一球面上,则该球面的表面积为
A.12 B. 32 C.8 D. 4
3
【详解】 如图,将正四面体补成正方体 ,
设正方体的棱长为 a ,
则 a2 a2 (2 2)2,a 2 .
该外接球的半径 R 1 PB 1 PD2 AB2 AD2 1
2
2
2
∴该外接球的体积V
4 3
R
3
4 3
33
36 ,
11 9 16 3 ,
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│课堂互动│
空间几何体的外接球问题
类型一:补形为正方体、长方体的类型(学生做,完成后直接对答案)
学情分析: 空间几何体的外接球问题是历年常考的题型,是热点知识点, 本专题由浅入深,分类型突破,清晰的为学生解读了空间几何体的 外接球的几种常见的类型!
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│新课引入│
空间几何体的外接球问题
知识引入:
(1)球的性质(如图)___R__2__=___r_2__+__d__2____;
4.直三棱柱 ABC A1B1C1 的 6 个顶点在球O 的球面上.若 AB 3 ,
AC 4 . AB AC , AA1 12 ,则球O 的表面积为( )
A.169 B.169 C. 288 D. 676
4
【详解】
解:将直三棱柱补形为长方体 ABEC A1B1E1C1 , 所以体对角线 BC1 的长为球O的直径.
2019届高考数学专题十四-外接球总结-练习题及答案

【解析】由余弦定理得: BC 4 4 2 2 2cos120 2 3 ,
设三角 ABC 外接圆半径为 r ,由正弦定理可得: 2 3 2r ,则 r 2,
sin120
又 R2 1 R2 4 ,解得: R2 16 ,则球的表面积 S 4πR2 64 π .本题选择
4
3
3
D 选项.
42
12.在三棱锥 A BCD 中, AB CD 6 , AC BD AD BC 5 ,则该三棱
锥的外接球的表面积为( )
A. 43 43π
24
【答案】D
B. 43 43π
6
C. 43π
2
D. 43π
【解析】分别取 AB , CD 的中点 E , F ,连接相应的线段 CE , ED,
EF ,
△PCD 外接圆的圆心为 O1 ,则 OO1 面 PCD ,∴四边形 OO1DB 为直角梯 形,
由 BD
3 , O1D 1 ,及 OB OD ,得 OB
7 ,∴外接球半径为 R
2
7,
2
∴该球的表面积 S 4πR2 4π 7 7π .故选 A.
4
10.四面体 A BCD 中, ABC ABD CBD 60, AB 3 , CB DB 2 ,
则此四面体外接球的表面积为( )
A. 19 π
2
【答案】A
B. 19 38π
24
C.17π
D. 17 17π
6
【解析】
由题意,△BCD 中, CB DB 2 , CBD 60 ,可知△BCD 是等边三角 形, BF 3 ,
9
∴ △BCD 的外接圆半径 r 2 3 BE , FE 3 ,
将△ABD沿 BD折起到△PBD的位置,使 PC PD ,连接 PC ,得到三棱锥
高中数学 空间几何体外接球问题课件(共27张PPT)

A
B
C
7
合作探究一:
(2)已知三棱锥 P-ABC 的四个顶点都在球 O 的表面 上,PA⊥面 ABC,AB⊥BC,如何求这个球的半径?
P
A
B
C
8
合作探究一:
(3)已知正四面体A-BCD,所有棱长都相等,点 A, B,C ,D都在球O 的表面上,如何求这个球的半径?
B
C
D
D
A
9
合作探究一:
(3)已知正四面体A-BCD,所有棱长都相等,点 A, B,C ,D都在球O 的表面上,如何求这个球的半径?
P
A
B
D
C
阳马( PA⊥面ABCD(矩形) )
22
课堂小结:
一、长方体外接球直径为 其体对角线
二、可补
B
C
AB、AC、AD两两垂直(墙角)鳖臑(四个面都为直角三角形)
P
B A
A
B
C
D
C
D
阳马( PA⊥面ABCD(矩形) )
对棱相等
23
课堂小结:
三、正棱锥
O O'
24
课堂小结:
已知正方体ABCD-A1B1C1D1的长、宽、高分别为a、 b、c且它的8个顶点都在球面上,求这个球的半径?
a2 b2 c2
c
a2 b2 b a
长方体外接球的直径等于长方体的体对角线。
2R a2 b2 c2
3
合作探究一:
(1)已知三棱锥 P-ABC 的四个顶点都在球 O 的表 面上,PA⊥面 ABC,AB⊥AC,如何求这个球的半径?
空间几何体外接球问题
1
几何体与球的组合问题,一种是内切球,一种 是外接球。纵观高考题,这种位置关系在高考中 既是考查的热点,也是考查的难点,这是因为与 球有关的几何体能很好地考察学生的空间想象能 力以及化归能力。下面就常见几何体的外接球问 题进行分析,找出规律,以便同学们更好地迎接 高考。
外接球、内切球模型总结专题课件-高三数学二轮复习备考课件

把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球
其直径为 =
=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2
1
2 + 2 + 2
半径为
6
2
4
球 = ×
找三条两两垂直的线段,直接用公式 2
即2 = 2 + 2 + 2 ,求出
2
= 2 + 2 + 2 ,
例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7
1
C.
10
3
D.
40
3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘
=7
= 7
中
的外接球直径为
7 2 7
=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体,这个球是这个多面体的内切球.
高中数学立体几何之外接球与内切球问题常见模型归纳(完整版)
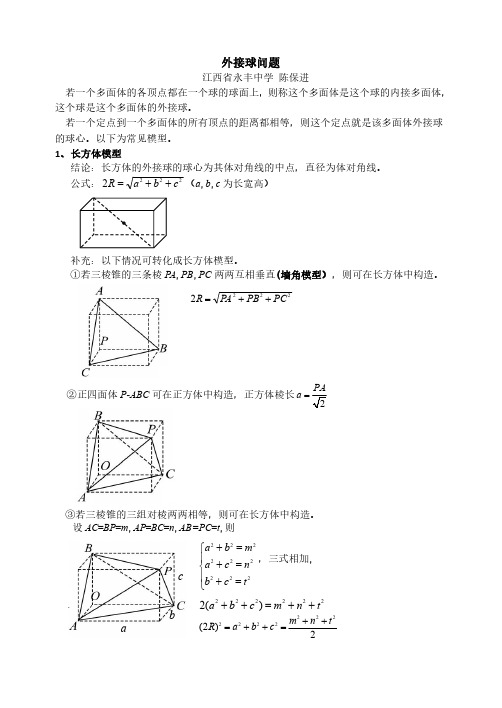
外接球问题江西省永丰中学陈保进若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
若一个定点到一个多面体的所有顶点的距离都相等,则这个定点就是该多面体外接球的球心。
以下为常见模型。
1、长方体模型结论:长方体的外接球的球心为其体对角线的中点,直径为体对角线。
公式:2222c b a R ++=(a ,b ,c 为长宽高)补充:以下情况可转化成长方体模型。
①若三棱锥的三条棱PA ,PB ,PC 两两互相垂直(墙角模型),则可在长方体中构造。
2222PC PB P A R ++=②正四面体P -ABC 可在正方体中构造,正方体棱长2=PA a ③若三棱锥的三组对棱两两相等,则可在长方体中构造。
设AC =BP =m ,AP =BC =n ,AB=PC =t ,则⎪⎩⎪⎨⎧=+=+=+222222222t c b n c a m b a ,三式相加,222222)(2t n m c b a ++=++2)2(2222222t n m c b a R ++=++=abc2、直三棱柱模型结论:直三棱柱外接球的球心是上、下底面外心连线的中点,222()2hR r =+r 为底面三角形外接圆的半径,可用正弦定理求,h 为直三棱柱的高。
补充:有一条侧棱垂直底面的三棱锥可补成直三棱柱,如图P -ABC 中,PA ⊥平面ABC ,则可补成直三棱柱PB 1C 1-ABC ,外接球半径公式同上。
提醒:底面具有外接圆的直棱柱才有外接球,比如正棱柱,且球心在上、下底面外心连线的中点,底面无外接圆的直棱柱,以及所有斜棱柱均无外接球。
3、共斜边模型四面体D-ABC 中,DC AD ⊥,BC AB ⊥,AC 为公共的斜边,O 为AC 的中点,则O 为四面体D-ABC 外接球的球心。
4、正棱锥模型外接球的球心在正棱锥的高所在直线上,如图正三棱锥A-BCD 中,作AO 1⊥平面BCD ,则易得BO 1=CO 1=DO 1,所以O 1为△BCD 的外心,设O 为其外接球球心,半径为R ,则BO =AO =R ,设AO 1=h ,BO 1=r ,则由BO 2=BO 12+OO 12,得R 2=r 2+(h-R )2。
2019届高考数学专题14外接球

培优点十四 外接球1.正棱柱,长方体的外接球球心是其中心例1:已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ) A .16π B .20πC .24πD .32π【答案】C【解析】162==h a V ,2=a ,24164442222=++=++=h a a R ,24πS =,故选C .2.补形法(补成长方体)图2图3例2:若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 .【答案】9π【解析】933342=++=R ,24π9πS R ==.3.依据垂直关系找球心例3:已知三棱锥P ABC -的四个顶点均在同一个球面上,底面ABC △满足BA BC ==π2ABC ∠=,若该三棱锥体积的最大值为3,则其外接球的体积为( ) A .8π B .16π C .16π3 D .32π3【答案】D【解析】因为ABC △是等腰直角三角形,所以外接球的半径是12r ==的半径是R ,球心O 到该底面的距离d ,如图,则1632ABC S =⨯=△,BD =116336ABC V S h h ==⨯=△,最大体积对应的高为3SD h ==,故223R d =+,即()2233R R =-+,解之得2R =,所以外接球的体积是3432ππ33R =,故答案为D .一、单选题1.棱长分别为235的长方体的外接球的表面积为( ) A .4π B .12π C .24π D .48π【答案】B【解析】设长方体的外接球半径为R ,由题意可知:()(22222235R =++,则:23R =,该长方体的外接球的表面积为24π4π312πS R ==⨯=.本题选择B 选项.2.设三棱柱的侧棱垂直于底面,所有棱的长都为23面积为( ) A .12π B .28π C .44π D .60π【答案】B【解析】设底面三角形的外接圆半径为r ,由正弦定理可得:232r =2r =, 设外接球半径为R ,结合三棱柱的特征可知外接球半径222327R =+=,对点增分集训外接球的表面积24π28πS R ==.本题选择B 选项.3.把边长为3的正方形ABCD 沿对角线AC 对折,使得平面ABC ⊥平面ADC ,则三棱锥D ABC -的外接球的表面积为( ) A .32π B .27πC .18πD .9π【答案】C【解析】把边长为3的正方形ABCD 沿对角线AC 对折,使得平面ABC ⊥平面ADC , 则三棱锥D ABC -的外接球直径为32AC =,外接球的表面积为24π18πR =,故选C . 4.某几何体是由两个同底面的三棱锥组成,其三视图如下图所示,则该几何体外接球的面积为( )A .2πaB .22πaC .23πaD .24πa【答案】C【解析】由题可知,该几何体是由同底面不同棱的两个三棱锥构成,其中底面是棱长为2a 的正三角形,一个是三条侧棱两两垂直,且侧棱长为a 的正三棱锥,另一个是棱长为2a 的正四面体,如图所示:该几何体的外接球与棱长为的正方体的外接球相同,因此外接球的直径即为正方体的体对角线,所以222323R a a a a R a =++=⇒=,所以该几何体外接球面积22234π4π3πS R a a ⎛⎫==⨯= ⎪ ⎪⎝⎭,故选C .5.三棱锥A BCD -的所有顶点都在球O 的表面上,AB ⊥平面BCD ,2BC BD ==,243AB CD ==,则球O 的表面积为( )A .16πB .32πC .60πD .64π【答案】D【解析】因为2BC BD ==,23CD =,所以()22222231cos 2222CBD +-∠==-⨯⨯,2π3CBD ∴∠=, 因此三角形BCD 外接圆半径为122sin CDCBD=∠,设外接球半径为R ,则222=2+412162AB R ⎛⎫=+= ⎪⎝⎭,2=4π64πS R ∴=,故选D .6.如图1111ABCD A B C D -是边长为1的正方体,S ABCD -是高为1的正四棱锥,若点S ,1A ,1B ,1C ,1D 在同一个球面上,则该球的表面积为( )A .9π16B .25π16C .49π16D .81π16【答案】D【解析】如图所示,连结11A C ,11B D ,交点为M ,连结SM ,易知球心O 在直线SM 上,设球的半径R OS x ==,在1Rt OMB △中,由勾股定理有:22211OM B M B O +=,即:()222222x x ⎛⎫-+= ⎪ ⎪⎝⎭,解得:98x =,则该球的表面积229814π4ππ816S R ⎛⎫==⨯= ⎪⎝⎭.本题选择D 选项.7.已知球O 的半径为R ,A ,B ,C 三点在球O 的球面上,球心O 到平面ABC 的距离为12R ,2AB AC ==,120BAC ∠=︒,则球O 的表面积为( ) A .16π9B .16π3C .64π9D .64π3【答案】D【解析】由余弦定理得:44222cos12023BC =+-⨯⨯︒=,设三角ABC 外接圆半径为r ,由正弦定理可得:232r =,则2r =,又22144R R =+,解得:2163R =,则球的表面积2644ππ3S R ==.本题选择D 选项.8.已知正四棱锥P ABCD -(底面四边形ABCD 是正方形,顶点在底面的射影是底面的中心)的各顶点都在同一球面上,10若该正四棱锥的体积为503,则此球的体积为( ) A .18π B .86C .36πD .323π【答案】C 【解析】如图,设正方形ABCD 的中点为E ,正四棱锥P ABCD -的外接球心为O , 底面正方形的边长为10,5EA ∴=, 正四棱锥的体积为503,()21501033P ABCD V PE -∴=⨯⨯=, 则5PE =,5OE R ∴=-,在AOE △中由勾股定理可得:()2255R R -+=,解得3R =,34π36π3V R ∴==球,故选C .9.如图,在ABC △中,6AB BC ==,90ABC ∠=︒,点D 为AC 的中点,将ABD △沿BD 折起到PBD △的位置,使PC PD =,连接PC ,得到三棱锥P BCD -.若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )A .7πB .5πC .3πD .π【答案】A【解析】由题意得该三棱锥的面PCD 3BD ⊥平面PCD , 设三棱锥P BDC -外接球的球心为O ,PCD △外接圆的圆心为1O ,则1OO ⊥面PCD ,∴四边形1OO DB 为直角梯形, 由3BD 11O D =,及OB OD =,得7OB =7R =∴该球的表面积274π4π7π4S R ==⨯=.故选A . 10.四面体A BCD -中,60ABC ABD CBD ∠=∠=∠=︒,3AB =,2CB DB ==,则此四面体外接球的表面积为( ) A .19π2B .1938πC .17πD .1717π【答案】A 【解析】由题意,BCD △中,2CB DB ==,60CBD ∠=︒,可知BCD △是等边三角形,3BF =, ∴BCD △的外接圆半径23r BE ==,3FE ∵60ABC ABD ∠=∠=︒,可得7AD AC ==可得6AF =∴AF FB ⊥,∴AF BCD ⊥, ∴四面体A BCD -高为6AF =设外接球R ,O 为球心,OE m =,可得:222r m R +=……①,)2226πEF R +=……②由①②解得:19R =2194ππ2S R ==.故选A . 11.将边长为2的正ABC △沿着高AD 折起,使120BDC ∠=︒,若折起后A B C D 、、、四点都在球O 的表面上,则球O 的表面积为( ) A .7π2B .7πC .13π2D .13π3【答案】B【解析】BCD △中,1BD =,1CD =,120BDC ∠=︒,底面三角形的底面外接圆圆心为M ,半径为r ,由余弦定理得到3BC =321r r =⇒=,见图示:AD 是球的弦,3DA =,将底面的圆心M 平行于AD 竖直向上提起,提起到AD 的高度的一半,即为球心的位置O ,∴3OM =,在直角三角形OMD 中,应用勾股定理得到OD ,OD 即为球的半径. ∴球的半径3714OD =+=.该球的表面积为24π7πOD ⨯=;故选B . 12.在三棱锥A BCD -中,6AB CD ==,5AC BD AD BC ====,则该三棱锥的外接球的表面积为( ) A .4343πB .4343πC .43π2D .43π【答案】D【解析】分别取AB ,CD 的中点E ,F ,连接相应的线段CE ,ED ,EF ,由条件,4AB CD ==,5BC AC AD BD ====,可知,ABC △与ADB △,都是等腰三角形,AB ⊥平面ECD ,∴AB EF ⊥,同理CD EF ⊥,∴EF 是AB 与CD 的公垂线,球心G 在EF 上,推导出AGB CGD △≌△,可以证明G 为EF 中点, 2594DE =-=,3DF =,1697EF =-=,∴7GF =,球半径74394DG =+=,∴外接球的表面积为24π43πS DG =⨯=. 故选D .二、填空题13.棱长均为6的直三棱柱的外接球的表面积是_________.【答案】84π【解析】由正弦定理可知底面三角形的外接圆半径为16123 2sin6023r=⨯=⨯=︒,则外接球的半径()2232391221R=+=+=,则外接球的表面积为24π4π2184πS R==⨯=.14.已知棱长都相等正四棱锥的侧面积为163,则该正四棱锥内切球的表面积为________.【答案】()32163π-【解析】设正四棱锥的棱长为a,则234163a⎛⎫=⎪⎪⎝⎭,解得4a=.于是该正四棱锥内切球的大圆是如图PMN△的内切圆,其中4MN=,23PM PN==22PE=.设内切圆的半径为r,由PFO PEN≅△△,得FO POEN PN=,即22223r r-=,解得226231r==+∴内切球的表面积为(224π4π6232163πS r===-.15.已知三棱柱111ABC A B C-的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积32AB=,1AC=,60BAC∠=︒,则此球的表面积等于______.【答案】8π【解析】∵三棱柱111ABC A B C-32AB=,1AC=,60BAC ∠=︒,1121sin 6032AA ∴⨯⨯⨯︒⨯=,12AA ∴=,2222cos60412BC AB AC AB AC =+-⋅︒=+-,3BC ∴=,设ABC △外接圆的半径为R ,则2sin 60BCR ︒=,1R ∴=, ∴外接球的半径为112+=,∴球的表面积等于()24π28π⨯=.故答案为8π.16.在三棱锥A BCD -中,AB AC =,DB DC =,4AB DB +=,AB BD ⊥,则三棱锥A BCD -外接球的体积的最小值为_____. 【答案】82π3【解析】如图所示,三棱锥A BCD -的外接圆即为长方体的外接圆,外接圆的直径为长方体的体对角线AD ,设AB AC x ==,那么4DB DC x ==-,AB BD ⊥,所以22AD AB DB =+积的最小值即为AD 最小,()224AD x x =+-2x =时,AD 的最小值为222故体积的最小值为82π3.。
高三数学专题外接球

高三数学专题外接球高三数学专题:外接球1.正棱柱和长方体的外接球的球心是其中心。
例1:一个正四棱柱的高为4,体积为16,其外接球的表面积是多少?解:由于正四棱柱的底面是一个正方形,所以它的体积为$V=\frac{1}{3}hS=16$,其中 $h=4$,$S$ 是正方形的面积。
解得 $S=12$。
正方形的对角线长为 $d=\sqrt{2}S=2\sqrt{6}$,所以外接球的半径为 $R=\frac{d}{2}=\sqrt{6}$,表面积为$S=4\pi R^2=24\pi$。
因此,答案为 C。
2.补形法(补成长方体)。
例2:一个三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是多少?解:将三棱锥补成长方体,如下图所示。
长方体的对角线长为 $d=\sqrt{3^2+3^2+3^2}=3\sqrt{3}$,所以外接球的半径为$R=\frac{d}{2}=\frac{3\sqrt{3}}{2}$,表面积为 $S=4\piR^2=27\pi$。
因此,答案为 B。
3.依据垂直关系找球心。
例3:一个三棱锥P-ABC 的四个顶点均在同一个球面上,底面△ABC 满足 BA=BC=6,∠ABC=π,若该三棱锥体积的最大值为3,则其外接球的体积为多少?解:根据垂直关系,三棱锥的外接球的球心位于底面△ABC 的垂心 H 上。
设球心为 O,底面中心为 M,则$OM=OH-R$,其中 $R$ 是外接球的半径。
根据勾股定理,$AH=\sqrt{AP^2-PH^2}=\sqrt{R^2-\frac{1}{4}BC^2}$,$BM=MC=\frac{1}{2}BC=3$,所以 $OM=\sqrt{OH^2-HM^2}=\sqrt{R^2-(AH+BM)^2}=\sqrt{R^2-\left(R^2-\frac{1}{4}BC^2+9\right)}=\frac{\sqrt{3}}{2}$。
由于三棱锥的体积最大值为3,所以 $AH\cdot BC=6\sqrt{3}$,解得$R=\frac{3\sqrt{3}}{2}$,体积为$V=\frac{1}{3}Ah=\frac{1}{3}\cdot 6\sqrt{3}\cdotR=9\sqrt{3}\pi$。
高考数学中的内切球和外接球问题(附习题)

高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.考查学生的空间想象能力以及化归能力•研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为_________________ 27—例2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为_________________ 3届.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为 _________ .14.例4、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为().CA. 16兀B. 20兀C. 24兀D. 32兀3•求多面体的外接球的有关问题例5. 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知 8,底面周长为3,则这个球的体积为的半径的常用公式.二、构造法(补形法) 1、构造正方体例5若三棱锥的三条侧棱两两垂直,且侧棱长均为 ' 3,则其外 接球的表面积是 __________________ 护.例3若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外 接球的表面积是 ________ .2故其外接球的表面积S=4「:R =9二.小结:一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分 别为a 、b 、c,则就可以将这个三棱锥补成一个长方体, 于是长方体的 体对角线的长就是该三棱锥的外接球的直径•设其外接球的半径为R ,该六棱柱的顶点都在同一个球面上, 且该六棱柱的体积为 解 设正六棱柱的底面边长为x ,咼为h,则有6x =3, 9 3 2U 6 x h,841 x ,2_ h = . 3.二正六棱柱的底面圆的半径 接球的半径R ^-:r 2d 2.体积:小结本题是运用公式R 2 1r = 2 ,球心到底面的距离4兀3VR 3. 3d 2求球的半径的,该公式是求球则有 2R 二、•. a 2 b 2 c 2 .出现“墙角”结构利用补形知识,联系长方体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
培优点十四 外接球1.正棱柱,长方体的外接球球心是其中心例1:已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ) A .16π B .20πC .24πD .32π【答案】C【解析】162==h a V ,2=a ,24164442222=++=++=h a a R ,24πS =,故选C .2.补形法(补成长方体)图2图3例2:若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 .【答案】9π【解析】933342=++=R ,24π9πS R ==.3.依据垂直关系找球心例3:已知三棱锥P ABC -的四个顶点均在同一个球面上,底面ABC △满足BA BC ==π2ABC ∠=,若该三棱锥体积的最大值为3,则其外接球的体积为( ) A .8π B .16π C .16π3 D .32π3【答案】D【解析】因为ABC △是等腰直角三角形,所以外接球的半径是12r ==的半径是R ,球心O 到该底面的距离d ,如图,则1632ABC S =⨯=△,BD =116336ABC V S h h ==⨯=△,最大体积对应的高为3SD h ==,故223R d =+,即()2233R R =-+,解之得2R =,所以外接球的体积是3432ππ33R =,故答案为D .一、单选题1.棱长分别为235的长方体的外接球的表面积为( ) A .4π B .12π C .24π D .48π【答案】B【解析】设长方体的外接球半径为R ,由题意可知:()(22222235R =++,则:23R =,该长方体的外接球的表面积为24π4π312πS R ==⨯=.本题选择B 选项.2.设三棱柱的侧棱垂直于底面,所有棱的长都为23面积为( ) A .12π B .28π C .44π D .60π【答案】B【解析】设底面三角形的外接圆半径为r ,由正弦定理可得:232r =2r =, 设外接球半径为R ,结合三棱柱的特征可知外接球半径222327R =+=,对点增分集训外接球的表面积24π28πS R ==.本题选择B 选项.3.把边长为3的正方形ABCD 沿对角线AC 对折,使得平面ABC ⊥平面ADC ,则三棱锥D ABC -的外接球的表面积为( ) A .32π B .27πC .18πD .9π【答案】C【解析】把边长为3的正方形ABCD 沿对角线AC 对折,使得平面ABC ⊥平面ADC , 则三棱锥D ABC -的外接球直径为32AC =,外接球的表面积为24π18πR =,故选C . 4.某几何体是由两个同底面的三棱锥组成,其三视图如下图所示,则该几何体外接球的面积为( )A .2πaB .22πaC .23πaD .24πa【答案】C【解析】由题可知,该几何体是由同底面不同棱的两个三棱锥构成,其中底面是棱长为2a 的正三角形,一个是三条侧棱两两垂直,且侧棱长为a 的正三棱锥,另一个是棱长为2a 的正四面体,如图所示:该几何体的外接球与棱长为的正方体的外接球相同,因此外接球的直径即为正方体的体对角线,所以222323R a a a a R a =++=⇒=,所以该几何体外接球面积22234π4π3πS R a a ⎛⎫==⨯= ⎪ ⎪⎝⎭,故选C .5.三棱锥A BCD -的所有顶点都在球O 的表面上,AB ⊥平面BCD ,2BC BD ==,243AB CD ==,则球O 的表面积为( )A .16πB .32πC .60πD .64π【答案】D【解析】因为2BC BD ==,23CD =,所以()22222231cos 2222CBD +-∠==-⨯⨯,2π3CBD ∴∠=, 因此三角形BCD 外接圆半径为122sin CDCBD=∠,设外接球半径为R ,则222=2+412162AB R ⎛⎫=+= ⎪⎝⎭,2=4π64πS R ∴=,故选D .6.如图1111ABCD A B C D -是边长为1的正方体,S ABCD -是高为1的正四棱锥,若点S ,1A ,1B ,1C ,1D 在同一个球面上,则该球的表面积为( )A .9π16B .25π16C .49π16D .81π16【答案】D【解析】如图所示,连结11A C ,11B D ,交点为M ,连结SM ,易知球心O 在直线SM 上,设球的半径R OS x ==,在1Rt OMB △中,由勾股定理有:22211OM B M B O +=,即:()222222x x ⎛⎫-+= ⎪ ⎪⎝⎭,解得:98x =,则该球的表面积229814π4ππ816S R ⎛⎫==⨯= ⎪⎝⎭.本题选择D 选项.7.已知球O 的半径为R ,A ,B ,C 三点在球O 的球面上,球心O 到平面ABC 的距离为12R ,2AB AC ==,120BAC ∠=︒,则球O 的表面积为( ) A .16π9B .16π3C .64π9D .64π3【答案】D【解析】由余弦定理得:44222cos12023BC =+-⨯⨯︒=,设三角ABC 外接圆半径为r ,由正弦定理可得:232r =,则2r =,又22144R R =+,解得:2163R =,则球的表面积2644ππ3S R ==.本题选择D 选项.8.已知正四棱锥P ABCD -(底面四边形ABCD 是正方形,顶点在底面的射影是底面的中心)的各顶点都在同一球面上,10若该正四棱锥的体积为503,则此球的体积为( ) A .18π B .86C .36πD .323π【答案】C 【解析】如图,设正方形ABCD 的中点为E ,正四棱锥P ABCD -的外接球心为O , Q 底面正方形的边长为10,5EA ∴=, Q 正四棱锥的体积为503,()21501033P ABCD V PE -∴=⨯⨯=, 则5PE =,5OE R ∴=-,在AOE △中由勾股定理可得:()2255R R -+=,解得3R =,34π36π3V R ∴==球,故选C .9.如图,在ABC △中,6AB BC ==,90ABC ∠=︒,点D 为AC 的中点,将ABD △沿BD 折起到PBD △的位置,使PC PD =,连接PC ,得到三棱锥P BCD -.若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )A .7πB .5πC .3πD .π【答案】A【解析】由题意得该三棱锥的面PCD 3BD ⊥平面PCD , 设三棱锥P BDC -外接球的球心为O ,PCD △外接圆的圆心为1O ,则1OO ⊥面PCD ,∴四边形1OO DB 为直角梯形, 由3BD 11O D =,及OB OD =,得7OB =7R =∴该球的表面积274π4π7π4S R ==⨯=.故选A . 10.四面体A BCD -中,60ABC ABD CBD ∠=∠=∠=︒,3AB =,2CB DB ==,则此四面体外接球的表面积为( ) A .19π2B .1938πC .17πD .1717π【答案】A 【解析】由题意,BCD △中,2CB DB ==,60CBD ∠=︒,可知BCD △是等边三角形,3BF =, ∴BCD △的外接圆半径23r BE ==,3FE ∵60ABC ABD ∠=∠=︒,可得7AD AC ==可得6AF =∴AF FB ⊥,∴AF BCD ⊥, ∴四面体A BCD -高为6AF =设外接球R ,O 为球心,OE m =,可得:222r m R +=……①,)2226πEF R +=……②由①②解得:19R =2194ππ2S R ==.故选A . 11.将边长为2的正ABC △沿着高AD 折起,使120BDC ∠=︒,若折起后A B C D 、、、四点都在球O 的表面上,则球O 的表面积为( ) A .7π2B .7πC .13π2D .13π3【答案】B【解析】BCD △中,1BD =,1CD =,120BDC ∠=︒,底面三角形的底面外接圆圆心为M ,半径为r ,由余弦定理得到3BC =321r r =⇒=,见图示:AD 是球的弦,3DA =,将底面的圆心M 平行于AD 竖直向上提起,提起到AD 的高度的一半,即为球心的位置O ,∴3OM =,在直角三角形OMD 中,应用勾股定理得到OD ,OD 即为球的半径. ∴球的半径3714OD =+=.该球的表面积为24π7πOD ⨯=;故选B . 12.在三棱锥A BCD -中,6AB CD ==,5AC BD AD BC ====,则该三棱锥的外接球的表面积为( ) A .4343πB .4343πC .43π2D .43π【答案】D【解析】分别取AB ,CD 的中点E ,F ,连接相应的线段CE ,ED ,EF ,由条件,4AB CD ==,5BC AC AD BD ====,可知,ABC △与ADB △,都是等腰三角形,AB ⊥平面ECD ,∴AB EF ⊥,同理CD EF ⊥,∴EF 是AB 与CD 的公垂线,球心G 在EF 上,推导出AGB CGD △≌△,可以证明G 为EF 中点, 2594DE =-=,3DF =,1697EF =-=,∴7GF =,球半径74394DG =+=,∴外接球的表面积为24π43πS DG =⨯=. 故选D .二、填空题13.棱长均为6的直三棱柱的外接球的表面积是_________.【答案】84π【解析】由正弦定理可知底面三角形的外接圆半径为16123 2sin6023r=⨯=⨯=︒,则外接球的半径()2232391221R=+=+=,则外接球的表面积为24π4π2184πS R==⨯=.14.已知棱长都相等正四棱锥的侧面积为163,则该正四棱锥内切球的表面积为________.【答案】()32163π-【解析】设正四棱锥的棱长为a,则234163a⎛⎫=⎪⎪⎝⎭,解得4a=.于是该正四棱锥内切球的大圆是如图PMN△的内切圆,其中4MN=,23PM PN==22PE=.设内切圆的半径为r,由PFO PEN≅△△,得FO POEN PN=,即22223r r-=,解得226231r==+∴内切球的表面积为(224π4π6232163πS r===-.15.已知三棱柱111ABC A B C-的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积32AB=,1AC=,60BAC∠=︒,则此球的表面积等于______.【答案】8π【解析】∵三棱柱111ABC A B C-32AB=,1AC=,60BAC ∠=︒,1121sin 6032AA ∴⨯⨯⨯︒⨯=,12AA ∴=,2222cos60412BC AB AC AB AC =+-⋅︒=+-Q ,3BC ∴=,设ABC △外接圆的半径为R ,则2sin 60BCR ︒=,1R ∴=, ∴外接球的半径为112+=,∴球的表面积等于()24π28π⨯=.故答案为8π.16.在三棱锥A BCD -中,AB AC =,DB DC =,4AB DB +=,AB BD ⊥,则三棱锥A BCD -外接球的体积的最小值为_____. 【答案】82π3【解析】如图所示,三棱锥A BCD -的外接圆即为长方体的外接圆,外接圆的直径为长方体的体对角线AD ,设AB AC x ==,那么4DB DC x ==-,AB BD ⊥,所以22AD AB DB =+积的最小值即为AD 最小,()224AD x x =+-2x =时,AD 的最小值为222故体积的最小值为82π3.。
