相平衡和相图 (7)
合集下载
热力学7相平衡
a x1 b x1
7.3 汽液平衡的计算
7.3.1 汽液平衡的准则和计算方法 汽液平衡的准则 ˆi v ˆi l f f
i 1,2,, N
计算方法有两种：
1. 活度系数法
ˆ v y v P ˆ fi i i
Vi l ( P Pi s ) ˆ l x f l x s P s exp fi i i i i i i i RT
s
7.3.4.3 等温露点计算
已知T与{ yi }，求P与 { xi }。 计算与等压泡点计算相同，γi与xi有关，开始时需假定γi=1由相
平衡关系式计算xi，在重新计算γi。
未知，需假定p的初值，而后判断
yi Ki xi
y1＝0.237 y2＝0.514 y3＝0.249
7.3.4 利用活度系数法进行汽液平衡计算
Vi l ( P Pi s ) ˆ yiiv P xi iis Pi s exp RT Vi l ( P Pi s ) i is exp i RT ˆv
等温泡点计算 已知体系温度T与液相组成xi，求泡点 压力P与汽相组成 yi 。 等压泡点计算 已知体系压力P与液相组成xi，求泡点 温度T与汽相组成 yi 。 等温露点计算 已知体系温度T与汽相组成yi，求露点 压力P与液相组成 xi 。 等压露点计算 已知体系压力P与汽相组成yi，求露点 温度T与液相组成 xi 。
是否第一 次迭代？
是
y
i
变化吗 ？
计算 yi
否
7.3.4.2 等温泡点计算
已知T与{ xi }，求P与 { yi }。
计算步骤:
①已知T,由Antoine方程求 Pi s ②已知T,选择合适的状态方程计算 i ③已知xi，由活度系数方程求γi
7.3 汽液平衡的计算
7.3.1 汽液平衡的准则和计算方法 汽液平衡的准则 ˆi v ˆi l f f
i 1,2,, N
计算方法有两种：
1. 活度系数法
ˆ v y v P ˆ fi i i
Vi l ( P Pi s ) ˆ l x f l x s P s exp fi i i i i i i i RT
s
7.3.4.3 等温露点计算
已知T与{ yi }，求P与 { xi }。 计算与等压泡点计算相同，γi与xi有关，开始时需假定γi=1由相
平衡关系式计算xi，在重新计算γi。
未知，需假定p的初值，而后判断
yi Ki xi
y1＝0.237 y2＝0.514 y3＝0.249
7.3.4 利用活度系数法进行汽液平衡计算
Vi l ( P Pi s ) ˆ yiiv P xi iis Pi s exp RT Vi l ( P Pi s ) i is exp i RT ˆv
等温泡点计算 已知体系温度T与液相组成xi，求泡点 压力P与汽相组成 yi 。 等压泡点计算 已知体系压力P与液相组成xi，求泡点 温度T与汽相组成 yi 。 等温露点计算 已知体系温度T与汽相组成yi，求露点 压力P与液相组成 xi 。 等压露点计算 已知体系压力P与汽相组成yi，求露点 温度T与液相组成 xi 。
是否第一 次迭代？
是
y
i
变化吗 ？
计算 yi
否
7.3.4.2 等温泡点计算
已知T与{ xi }，求P与 { yi }。
计算步骤:
①已知T,由Antoine方程求 Pi s ②已知T,选择合适的状态方程计算 i ③已知xi，由活度系数方程求γi
相平衡与相图
液相线 B的熔点
A的熔点
A和B的二元低共熔点
4个相区： 固相线 L、L+A、 L+B、A+B
特点： 两个组分在液态时能以任何比例互溶，形成单相溶液；但在 固态时则完全不互溶，二个组分各自从液相中分别结晶。 组分间无化学作用，不生成新的化合物
杠杆规则
如果一个相分解为2个相，则生成的2个相的数量与原始
65
35
35
1450
725
铁碳平衡图
铁碳平衡图 （iron-carbon equilibrium diagram ）， 又称铁碳相图或铁碳状态图。它以温度为纵坐标，碳含量 为横坐标,表示在接近平衡条件（铁-石墨）和亚稳条件
（铁－碳化铁）下（或极缓慢的冷却条件下）以铁、碳为
组元的二元合金在不同温度下所呈现的相和这些相之间的 平衡关系。
4
二元系统
C=2，一般情况下，凝聚系统中的相律：
一、二元相图表示方法
F=C+P+1=3-P
当P=1时，F=2
当P=2时，F=1
当γ =3时，F=0 相数最大为3，自由度最大为2，对于浓度：A+B=A'%+B'%=100% 任意确定一个，则另一个确定相图为T组成图
二 具有一个低共熔点的简单二元相图
相平衡与相图
主要内容
发展历史 相图基础知识 单元系相图 二元系相图 三元系相图
1 相图发展历史
一 理论基础
平衡图的理论基础是吉布斯（J W Gibbs）的相律 ，他于1876年创建相律。
二 发展历程 1990年：罗泽朋（Bakhuis Roozeboom）发表了《用相律的观点来
看复相平衡》巨著的第一部分。
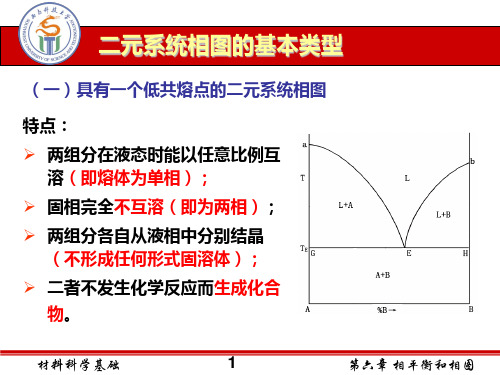
A的熔点
A和B的二元低共熔点
4个相区： 固相线 L、L+A、 L+B、A+B
特点： 两个组分在液态时能以任何比例互溶，形成单相溶液；但在 固态时则完全不互溶，二个组分各自从液相中分别结晶。 组分间无化学作用，不生成新的化合物
杠杆规则
如果一个相分解为2个相，则生成的2个相的数量与原始
65
35
35
1450
725
铁碳平衡图
铁碳平衡图 （iron-carbon equilibrium diagram ）， 又称铁碳相图或铁碳状态图。它以温度为纵坐标，碳含量 为横坐标,表示在接近平衡条件（铁-石墨）和亚稳条件
（铁－碳化铁）下（或极缓慢的冷却条件下）以铁、碳为
组元的二元合金在不同温度下所呈现的相和这些相之间的 平衡关系。
4
二元系统
C=2，一般情况下，凝聚系统中的相律：
一、二元相图表示方法
F=C+P+1=3-P
当P=1时，F=2
当P=2时，F=1
当γ =3时，F=0 相数最大为3，自由度最大为2，对于浓度：A+B=A'%+B'%=100% 任意确定一个，则另一个确定相图为T组成图
二 具有一个低共熔点的简单二元相图
相平衡与相图
主要内容
发展历史 相图基础知识 单元系相图 二元系相图 三元系相图
1 相图发展历史
一 理论基础
平衡图的理论基础是吉布斯（J W Gibbs）的相律 ，他于1876年创建相律。
二 发展历程 1990年：罗泽朋（Bakhuis Roozeboom）发表了《用相律的观点来
看复相平衡》巨著的第一部分。
第八章-相平衡与相图原理
f 1 单变量体系
F 3 三相共存
f 0 无变量体系
单组分体系的自由度最多为2，双变量体系 的相图可用平面图表示。
2024/7/17
单组分体系的相图
相点 表示某个相状态（如相态、组成、温度 等）的点称为相点。 物系点 相图中表示体系总状态的点称为物系点。 在T-x图上，物系点可以沿着与温度坐标平行的垂线 上、下移动；在水盐体系图上，随着含水量的变化， 物系点可沿着与组成坐标平行的直线左右移动。
2024/7/17
照片为亚共晶Pb-Sn合金的显微组织照片， 图中块状深色组织为先共晶相，其余黑白相间的基体为共晶组织。
2024/7/17
气体，不论有多少种气体混合，只有一个气相。 液体，按其互溶程度可以组成一相、两相或三 相共存。 固体，一般有一种固体便有一个相。两种固体粉 末无论混合得多么均匀，仍是两个相（固体溶液 除外，它是单相）。
2024/7/17
三相点与冰点的区别
三相点是物质自身的特性，不能加以改变，如H2O 的三相点。 T 273.16 K , p 610.62 Pa . 冰点是在大气压力下，水、冰、气三相共存。当大 气压力为105 Pa时，冰点温度为 273.15 K ，改变外 压，冰点也随之改变。
2024/7/17
2024/7/17
• 二组元在液态和固态都能够完全相互溶解，所 有成分(Ni: 0~100%)的合金在固态只有一种晶 体结构，相图中只有一个固相区。
• 因此，能够形成匀晶合金系的两种组元必须具 有相同的晶体结构，相同的原子价，原子半径 接近(相差不超过15％)，相互不形成化合物。
2024/7/17
设合金的平均成分为x，合金的总量为Q，在温度T1时液、 固 质两量相为平QS衡。，则液有相：的成分为xL、质量为QL，固相的成分为xS、
相平衡与相图原理
室温组织:
F + P，500×
(4)过共析钢 ( C % = 1.2 % )结晶过程
各组织组成物的相对量：
Fe3CII % = ( 1.2 – 0.77 ) / ( 6.69 – 0.77 )
≈7% P % ≈ 1 – 7 % = 93 % 各相的相对量：
Fe3CII % ≈ 1.2 / 6.69 = 18 % F % ≈ 1 – 18 % = 82 %
室温组织:
P + Fe3CII 400×
(5)共晶白口铁 ( C % = 4.3 % )结晶过程
室温组织: （低温）莱氏体 Le′ （P + Fe3CII + 共晶 Fe3C ）, 500×
莱氏体 Le′的性能：硬而脆
(６)亚共晶白口铁 ( C % = 3 % )结晶过程
室温组织:
Le′+ P + Fe3CII
亚共晶白口铁 ＜ 4.3 % 共晶白口铁 ＝ 4.3 % 过共晶白口铁 ＞ 4.3 %
几种 常见 碳钢
类型 钢号 碳质量分数／％
亚共析钢 20 45 60 0.20 0.45 0.60
共析钢 T8 0.80
过共析钢
T10
T12
1.00 1.20
(1)工业纯铁 ( C % ≤ 0.0218 % )结晶过程
20
液固两相区
40 60 Ni%
Ni 80 100
匀晶合金的结晶过程
L
T,C
T,C
L
1500
1455
L
1400 1300
c
a
L+
匀晶转变 L
1200d
1100 1000 1083
第六章 相平衡和相图
材料科学基础
31/156
第六章 相平衡和相图
2）硅质耐火材料的生产和使用
硅砖生产：97~98％天然石英或砂岩 2~3％的CaO（作矿化剂） 粉碎成一定颗粒级配，混合成型，经高温烧成。 【要求】含有尽可能多鳞石英，而方石英晶体越少 越好，以获得稳定致密的制品。
材料科学基础
32/156
第六章 相平衡和相图
b. 水热合成法
材料科学基础
30/156
第六章 相平衡和相图
恰克洛斯法（即直拉法）: α- 方石英转变为 β- 方石英时有较 大体积效应（△ V ＝ 2.8％），室 温下β-方石英为亚稳相。 水热合成法： 底部温度高，无定形 SiO2 ，溶解 度大，溶解的 SiO2 随热对流上升， 上部温度低，溶解度过饱和，在 籽晶周围析出 SiO2 单晶。由于在 573℃以下进行（虽压力是40MPa， 但 α- 石英和 β- 石英的转变曲线是 向高温方向偏斜），生长出的单 晶一定是β-石英。
F=0 无变量 系统
材料科学基础
9/156
第六章 相平衡和相图
（5）相律（1876年，Gibbs）：多相平衡系统的普通规律 吉布斯相律：F = C - P + n
式中：F---自由度数。 系统中组分数C越多，则自由度数F越大；
C---独立组分数，即构成平衡系统所有各相组成所需 相数P越多，自由度数F越小；
就有热效应的产生，曲线就有突变或转折。但如果相变的
热效应很小，在曲线上就不易体现出来，为了测量出这种 相变过程的微小热效应，通常采用差热分析法。
材料科学基础
14/156
第六章 相平衡和相图
材料科学基础
15/156
第六章 相平衡和相图
注意：热分析法(动态法)中， 只测得了相变所对应的温度以 及热效应，而没有测得系统相 变前后的相组成、数量和分布， 要想得到这些信息还需借助于 其它手段
31/156
第六章 相平衡和相图
2）硅质耐火材料的生产和使用
硅砖生产：97~98％天然石英或砂岩 2~3％的CaO（作矿化剂） 粉碎成一定颗粒级配，混合成型，经高温烧成。 【要求】含有尽可能多鳞石英，而方石英晶体越少 越好，以获得稳定致密的制品。
材料科学基础
32/156
第六章 相平衡和相图
b. 水热合成法
材料科学基础
30/156
第六章 相平衡和相图
恰克洛斯法（即直拉法）: α- 方石英转变为 β- 方石英时有较 大体积效应（△ V ＝ 2.8％），室 温下β-方石英为亚稳相。 水热合成法： 底部温度高，无定形 SiO2 ，溶解 度大，溶解的 SiO2 随热对流上升， 上部温度低，溶解度过饱和，在 籽晶周围析出 SiO2 单晶。由于在 573℃以下进行（虽压力是40MPa， 但 α- 石英和 β- 石英的转变曲线是 向高温方向偏斜），生长出的单 晶一定是β-石英。
F=0 无变量 系统
材料科学基础
9/156
第六章 相平衡和相图
（5）相律（1876年，Gibbs）：多相平衡系统的普通规律 吉布斯相律：F = C - P + n
式中：F---自由度数。 系统中组分数C越多，则自由度数F越大；
C---独立组分数，即构成平衡系统所有各相组成所需 相数P越多，自由度数F越小；
就有热效应的产生，曲线就有突变或转折。但如果相变的
热效应很小，在曲线上就不易体现出来，为了测量出这种 相变过程的微小热效应，通常采用差热分析法。
材料科学基础
14/156
第六章 相平衡和相图
材料科学基础
15/156
第六章 相平衡和相图
注意：热分析法(动态法)中， 只测得了相变所对应的温度以 及热效应，而没有测得系统相 变前后的相组成、数量和分布， 要想得到这些信息还需借助于 其它手段
相平衡与相图
17
5.5 -6 80 327 271 451 657 1412
-26 -71 60 246 144 306 578 1090
50 24 64 88 55 69 89 32
合金体系"热分析"原理
热分析法研究固液平衡体系相图主要是依据体系发生相变时伴随着相变潜热的吸 收或放出，导致体系冷却速度的变化，来研究相变过程的规律。由实验数据所绘 制的温度(T)与时间(t)的曲线，称为“步冷曲线”，由步冷曲线斜率的变化可提 供相的产生、消失、和达成相平衡的信息。
4
610.62
273.16
水的相图
2.2 单组分体系的两相平衡- 克拉贝龙(Clapeyron)方程式
可适用于任何纯物质体系的各类两相平衡，如气～液、气～固、液～固或固～固 晶型转变等。
如气～液、气～固、液～固或固～固晶型转变等。如果 α、β 两相中有一相是气相（设 β 为气相），则因气体体积远大于液体和固体的体积，即 Vm(g)》Vm(l) 或 Vm(s) 。对比之 下可略去液相或固相的体积，而
可得 Φ = 1 ，f = 3 Φ = 2 ，f = 2 Φ = 3 ，f = 1 Φ = 4 ，f = 0
即"三变量体系" 即"二变量体系" 即"单变量体系" 即"无变量体系"
通常情况下，描述体系状态时以温度（T）、压力（p）和组成 （浓度 x1 或 x2 ）三个变量为坐标构成的立体模型图。
固定 T 就得 p～x 图，固定 p 就得 T～x 图对工业上的提纯、分离、精馏、分馏 分面很有实用价值
6
三、二级相变
一类相变称之为一级相变（first order phase transition），特点是，如果改变体系的独 立强度变量（例如 pVT 系统的 t，p，x1，x2，……，xr ），一旦这些变量或其中之一 达到相变能发生的值时，从宏观上看相变将突然发生。它是一种不连续的突变现象，表 现出在确定的强度变量值时发生，同时体积、熵、焓等热力学量发生不连续的但有限的 突变。我们通常所见的气、液、固态的相变都属于这类相变。
5.5 -6 80 327 271 451 657 1412
-26 -71 60 246 144 306 578 1090
50 24 64 88 55 69 89 32
合金体系"热分析"原理
热分析法研究固液平衡体系相图主要是依据体系发生相变时伴随着相变潜热的吸 收或放出，导致体系冷却速度的变化，来研究相变过程的规律。由实验数据所绘 制的温度(T)与时间(t)的曲线，称为“步冷曲线”，由步冷曲线斜率的变化可提 供相的产生、消失、和达成相平衡的信息。
4
610.62
273.16
水的相图
2.2 单组分体系的两相平衡- 克拉贝龙(Clapeyron)方程式
可适用于任何纯物质体系的各类两相平衡，如气～液、气～固、液～固或固～固 晶型转变等。
如气～液、气～固、液～固或固～固晶型转变等。如果 α、β 两相中有一相是气相（设 β 为气相），则因气体体积远大于液体和固体的体积，即 Vm(g)》Vm(l) 或 Vm(s) 。对比之 下可略去液相或固相的体积，而
可得 Φ = 1 ，f = 3 Φ = 2 ，f = 2 Φ = 3 ，f = 1 Φ = 4 ，f = 0
即"三变量体系" 即"二变量体系" 即"单变量体系" 即"无变量体系"
通常情况下，描述体系状态时以温度（T）、压力（p）和组成 （浓度 x1 或 x2 ）三个变量为坐标构成的立体模型图。
固定 T 就得 p～x 图，固定 p 就得 T～x 图对工业上的提纯、分离、精馏、分馏 分面很有实用价值
6
三、二级相变
一类相变称之为一级相变（first order phase transition），特点是，如果改变体系的独 立强度变量（例如 pVT 系统的 t，p，x1，x2，……，xr ），一旦这些变量或其中之一 达到相变能发生的值时，从宏观上看相变将突然发生。它是一种不连续的突变现象，表 现出在确定的强度变量值时发生，同时体积、熵、焓等热力学量发生不连续的但有限的 突变。我们通常所见的气、液、固态的相变都属于这类相变。
相图与相平衡基础知识
推导过程
假设一个平衡系统中有C个组分，P个相， 如果C个组分在每个相中都存在，那么对每 一个相来讲，只要任意指定（C－1）个组分 的浓度就可以表示出该相中所有组分的浓度， 因为余下的一个组分的浓度可以从100中减去 （C－1）个组分的浓度之和求得。由于系统 有P个相，所以需要指定的浓度数总共有P （C－1）个，只要才能确定体系中各相浓度。
相律 吉布斯根据前人的实验素材，用严谨的热力学作 为工具，于1876年导出了多相平衡系统中，系统的 自由度数（F），独立组元数（C），相数（P）和 对系统的平衡状态能够发生影响的外界影响因素 （n）之间的关系，相律的数学表达式为： F＝C－P＋n 一般情况下，只考虑温度和压力对系统的平衡状态的 影响，即n＝2，则相律表达式为 F＝C－P＋2
总之，气相只能一个相，无论多少种气体混在一起 都一样，形成一个气相，液体可以是一个相，也可 以是两个相（互溶程度有限时）。固体如果是连续 固溶体为一相；其他情况下，一种固体物质是一个 相。
一个系统中所含有相的数目，叫做相数，以符号P 表示，按照相数的不同，系统可分为单相系统 （P=1），二相系统（P=2），三相系统（P=3）等。 含有两个相以上的系统，统称为多相系统。
第六章 相平衡和相图
什么是相图
相图的研究方法有哪些 相图的应用
相图的定义
在一个多相体系中，随温度、压力和浓度的
变化，相的种类、数量及含量都要相应地发 生变化，对于变化情况可用几何图形来描绘， 这个图形就可以反映出该系统在一定组成、 温度和压力下，达到平衡时所处的状态，这 个几何图形就是相图，也叫相平衡图、状态 图。
相平衡研究方法
动态法 热分析法 差热分析法（DTA） 溶解度法 静态法(淬冷法)
相平衡和相图
材料科学基础
30
第六章 相平衡和相图
C 例：根据下列相图 (1) 用连线规则划分副三角形。 (2) 用箭头标出界线上温度变化方向及界线性质。 C (3) 判断S、S1、S2化合物的性质。 (4) 写出各无变量点的性质及反应式。 (5)在相图下侧画出A－B二元系统相图。 u v (6) 分析熔体M1、M2的析晶路程。 S (M1在SO连线上)
第六章 相平衡和相图
13
3、背向线规则
在浓度三角形中，一个三元系统的组成点愈靠近某个顶点，
该顶点所代表的组分的含量就愈高；反之，愈少。
C 若熔体在冷却时析出某一
顶点所代表的组元，则液
相中组成点必定沿着该顶 点与熔体组成点的连线向 背离该顶点的方向 A
材料科学基础
D
B
第六章 相平衡和相图
14
4、杠杆规则
C C
b L .2 N
a
e2
K
1
.
B
x B
z y
熔体1
L LB 1[B，(B)] a[B，B+(A)] f=3 f=2
L B+N f=1
L B＋A K[x，B+A+(N)] f=1
e1
L＋AB＋N f=0
K[y(A消失),N＋B]
LN＋B＋C L[z,N+B+(C)] f=0
L(液相消失)[1,N+B+C]
所谓一致熔融化合物是一种稳定 的化合物。它与正常的纯物质一 样具有固定的熔点，融化时，所
产生的液相与固相的化合物组成 相同，故称一致熔融
材料科学基础
2
第六章 相平衡和相图
2、不一致熔融化合物： 一种不稳定的化合物，加热这种 化合物到某一温度便发生分解， 分解产物是一种液相和一种晶相， 二者组成与原来化合物组成完全 不同。 点：纯物质熔点；低共熔点； 转熔点等 线：液相线（3条）固相线等；
30
第六章 相平衡和相图
C 例：根据下列相图 (1) 用连线规则划分副三角形。 (2) 用箭头标出界线上温度变化方向及界线性质。 C (3) 判断S、S1、S2化合物的性质。 (4) 写出各无变量点的性质及反应式。 (5)在相图下侧画出A－B二元系统相图。 u v (6) 分析熔体M1、M2的析晶路程。 S (M1在SO连线上)
第六章 相平衡和相图
13
3、背向线规则
在浓度三角形中，一个三元系统的组成点愈靠近某个顶点，
该顶点所代表的组分的含量就愈高；反之，愈少。
C 若熔体在冷却时析出某一
顶点所代表的组元，则液
相中组成点必定沿着该顶 点与熔体组成点的连线向 背离该顶点的方向 A
材料科学基础
D
B
第六章 相平衡和相图
14
4、杠杆规则
C C
b L .2 N
a
e2
K
1
.
B
x B
z y
熔体1
L LB 1[B，(B)] a[B，B+(A)] f=3 f=2
L B+N f=1
L B＋A K[x，B+A+(N)] f=1
e1
L＋AB＋N f=0
K[y(A消失),N＋B]
LN＋B＋C L[z,N+B+(C)] f=0
L(液相消失)[1,N+B+C]
所谓一致熔融化合物是一种稳定 的化合物。它与正常的纯物质一 样具有固定的熔点，融化时，所
产生的液相与固相的化合物组成 相同，故称一致熔融
材料科学基础
2
第六章 相平衡和相图
2、不一致熔融化合物： 一种不稳定的化合物，加热这种 化合物到某一温度便发生分解， 分解产物是一种液相和一种晶相， 二者组成与原来化合物组成完全 不同。 点：纯物质熔点；低共熔点； 转熔点等 线：液相线（3条）固相线等；
chap7 相平衡
T-x1 0 x1,y1 1
17
P
等温 P-x1
P1s
2.一般负偏差体系 当恒温时的P~x曲线低于拉 乌尔定律的P~x直线，此体 系为负偏差体系。 γi<1
P2s 0 T
P-y1
x1,y1 等压 T-y1 T-x1
1
0
x1,y1
1
18
P
3. 最大正偏差体系
当正偏差较大时, 在P~x曲线上就可以 出现极大值， γ1> 1 ； 在这一点上，x=y, 此点称为共沸点； 由于这一点压力最大，温度最低，所 以称为最大压力（或最低温度）共沸 点； 对于这种体系，用一般精馏法是不能 将此分离开的，必须要采用特殊分离 法。 0 0 T
i
xi Pi ③ yi = P
s
28
2. 等温露点计算
已知T与{ yi }，求P与 { xi }
yi P = xi Pi yi P xi = s Pi
i i i
s
(i = 1,2,L , N )
yi P =1 s Pi
∑x =∑
1 P= s ∑ yi / Pi
i
29
计算步骤 ① 由Antoine方程求 Pi
Y ⑤ T T0 ≤ ε N 转6 T → T0 , 返回2
37
⑥
Bi Pi = exp Ai T + Ci
s
yi P xi = s Pi
将xi 值归一化
(i = 1,2,L , N )
xi
xi =
输出T和各xi
∑x
i
38
例7-1 丙酮(1)，乙腈(2)和硝基甲烷(3)体系可按完全
等温 共沸点
x1,y1 等压
第六章 相平衡和相图
•如果加热速度很慢，则在870℃转变为－鳞石英。
如果加热速度过快，则－石英过热而在1600℃时熔融。
鳞石英
117 163 230
573
870
1200～1350
1470 1600 1670 1713 ℃
•－鳞石英缓慢加热，在1470℃时转变为－方石英，继续加热 到1713℃熔融。 •－鳞石英在加热较快时，过热到1670℃时熔融。 •当缓慢冷却时，在870℃仍可逆地转变为－石英；当迅速冷却 时，沿虚线变化
p=3 , f=0 ,无变量系统
冰的饱和蒸汽压曲线（升华曲线）
三相点与冰点是一 回事吗
二、具有多晶转变的单元系统相图
E F
β型
α型
实线部分： 四个单相区：1相 五条界线：2相共存
两个三相点：B,C
晶体的升华曲线（或延长线）与液体的蒸发曲线（或延长线） 的交点是该晶体的熔点。如C点，实际是三相点。 两种晶型的升华曲线（或延长线）的交点是两种晶型的晶型转 变点。如B点，实际是三相点。
化合物
固溶体 同质多晶
二、相律 根据Gibbs相律 F= C－P＋2
平衡时最多 有几个相
F－ 自由度数
C－ 独立组元数
P－ 相数
2 － 温度和压力外界因素
盐水系统
建立多相系统中自由度数、独立组元数、相数之间的关系
二、相律
假设一系统中有S种化学物质，在平衡条件下形成P种物相， 每种相中都有S种化学物质。 则总变量数：P（S-1）+2
120 163 230
573
870
1200～1350
1470 1600 1670 1713 ℃
采 取 的 措 施
① 在870℃适当保温，促使鳞石英生成； ② 在1200～1350℃加快升温速度避免生成α- 方石英; ③ 在配方中加入Fe2O3或CaO等矿化剂。在1000℃左右产生一定 量的液相，石英、方石英在此液相中的溶解度大，而鳞石英的溶 解度小，因而石英、方石英不断溶入液相，而鳞石英则不断从液 相中析出。
5 《材料科学基础》第五章 相平衡和相图
( p -T 图)
自由
一、水的相图
冰的熔融曲线 水的饱和蒸汽压曲线（蒸发曲线）
3个相区：
p=1, f=2 ,双变量系统(T、P) 3条界线： p=2 , f= 1,单变量系统(T或P) 1个无变量点(三相点)：
T
p=3 , f=0 ,无变量系统
冰的饱和蒸汽压曲线（升华曲线）
？？
注意：
•冰点和三相点O
第五章
第五章
§5.1
相平衡和相图
基本知识
§5.2
§5.3
单元系统
二元系统
§5.4
三元系统
§5.1
相平衡与相图的基本知识
一、相平衡的基本概念 二、相律 三、相平衡的研究方法
一、相平衡的基本概念
相平衡：是研究一个多组分（或单组分）多相系统中相的平
衡问题，即多相系统的平衡状态(包括相的个数、各相的状态、
二、二元凝聚系统相图的基本类型
三、复杂二元相图的分析步骤
四、二元系统专业相图
要求
一、二元系统相图的表示方法及杠杆规则
1、作为特种陶瓷的重要原料
由于7％～9％的体积效应，常加适量CaO或Y2O3稳定剂。
在>1500℃以上与四方型ZrO2形成立方晶型固溶体，称稳定
化立方ZrO2 。
2、熔点高(2680℃)，作耐火材料 3、利用导氧导电性能，作氧敏传感器元件 4、利用体积效应，对陶瓷材料进行相变增韧。
增韧机理: 微裂纹增韧
实线部分： 四个单相区： 五条界线：
两个无变量点：
晶体的升华曲线（或延长线）与液体的蒸发曲线（或延长线） 的交点是该晶体的熔点。 两种晶型的升华曲线（或延长线）的交点是两种晶型的晶型转 变点。
材料科学基础课件第六章--相平衡与相图
F = C－P＋n
自由 度数
独立组 元数
F = C－P＋2
对凝聚态体系， 压力恒定或影响 较小，其相律为:
F = C－P＋1
组元数C多，自 由度F大；相数P 多，自由度小
6.1.3 相平 衡研究方法
动态法
静态法 (淬冷法)
热分 析法
差热分 析法
T/℃
(1ቤተ መጻሕፍቲ ባይዱ 热分析法
1
2
3
原理：根据系统在冷却
ab c
100 80Bi 60Bi 20Bi 100 Bi 20Cd 40Cd 80Cd Cd
T/℃
ab c d e
t/s
Bi-Cd合金冷却曲线
546.15K
596.15K
L
L+Bi(s) ●
L+Cd(s)
20 40 Bi(s)+Cd(s) 80
0 Bi
WCd/%
100 Cd
Bi-Cd系统相图
液相线：由凝固开始温度连接起来的相界线 固相线：由凝固终结温度连接起来的相界线
元系统相图
P ●：熔点
■：转变点
2
L
●
Ⅱ
3
■
1
●
Ⅰ
O T0 T2 T1 T3
T
图 6-7 具有不可逆多晶转变的
单元系统相图
晶体I T3 晶体II
晶体Ⅰ 晶体Ⅱ 液相
(1) 晶体I、Ⅱ有稳定区 (2) 转变温度T3<T1 、T2(熔点)
T1 液 相 T2
（1）晶体Ⅱ无稳定区 （2）T3>T1、T2
6.2.2 单元系统专业相图
G
E
H
A+B
A
相平衡和相图(共294张PPT)
C＝1，称为单元系统； C＝2，称为二元系统； C＝3，称为三元系统学反响，那么： 独立组元数＝物种数〔即组元数〕
〔2〕如果系统中存在化学反响并建立了平衡，
那么： 独立组元数＝物种数一独立化学反响数
〔指独立化学平衡关系式数〕
例如，由CaCO3、CaO、CO2组成 的系统，在高温下存在下述反响：
〔1〕稳定相平衡局部〔即实线局部〕 相区： FCD是液相区； ABE是β-晶型的相区； EBCF是α-晶型的相区， 在ABCD以下是气相区。
相界线：
CD线：是液相和气相两相平衡共存线，即液相
的蒸发曲线； BC线：是α-晶型和气相两相平衡共存线，即α-
晶型的升华曲线；
AB线：是β-晶型和气相两相平衡共存线，即β晶型的升华曲线；
〔或延长线〕的交点是该晶体的熔点。
②两种晶型的升华曲线的交点是两种晶型的多晶转 变点。
③在同一温度下，蒸气压低的相更加稳定。所以， 介稳平衡的虚线，总是在稳定平衡的实线上方 。
④交汇于三相点的三条平衡曲线互相之间 的位置遵循下面两条准那么：
a、每条曲线越过三相点的延长线必定在另 外两条曲线之间。
b、同一温度时，在三相点附近比容差最大 的两相之间的单变量曲线或其介稳延长 线居中间位置。
假设该反响能够到达平衡，那么有 一个独立的化学反响平衡常数。
此时，虽然组元数＝3，但独立组元 数C＝3－1＝2。
4、自由度 在一定范围内，可以任意改变而不
引起旧相消失或新相产生的独立变量称 为自由度，平衡系统的自由度数用F表示。
这些变量主要指组成〔即组分的浓 度〕、温度和压力等。
5、外界影响因素 影响系统平衡状态的外界因素包括：温度、压力、电
主要区别在于固-液平衡的熔融曲线OC线倾斜
〔2〕如果系统中存在化学反响并建立了平衡，
那么： 独立组元数＝物种数一独立化学反响数
〔指独立化学平衡关系式数〕
例如，由CaCO3、CaO、CO2组成 的系统，在高温下存在下述反响：
〔1〕稳定相平衡局部〔即实线局部〕 相区： FCD是液相区； ABE是β-晶型的相区； EBCF是α-晶型的相区， 在ABCD以下是气相区。
相界线：
CD线：是液相和气相两相平衡共存线，即液相
的蒸发曲线； BC线：是α-晶型和气相两相平衡共存线，即α-
晶型的升华曲线；
AB线：是β-晶型和气相两相平衡共存线，即β晶型的升华曲线；
〔或延长线〕的交点是该晶体的熔点。
②两种晶型的升华曲线的交点是两种晶型的多晶转 变点。
③在同一温度下，蒸气压低的相更加稳定。所以， 介稳平衡的虚线，总是在稳定平衡的实线上方 。
④交汇于三相点的三条平衡曲线互相之间 的位置遵循下面两条准那么：
a、每条曲线越过三相点的延长线必定在另 外两条曲线之间。
b、同一温度时，在三相点附近比容差最大 的两相之间的单变量曲线或其介稳延长 线居中间位置。
假设该反响能够到达平衡，那么有 一个独立的化学反响平衡常数。
此时，虽然组元数＝3，但独立组元 数C＝3－1＝2。
4、自由度 在一定范围内，可以任意改变而不
引起旧相消失或新相产生的独立变量称 为自由度，平衡系统的自由度数用F表示。
这些变量主要指组成〔即组分的浓 度〕、温度和压力等。
5、外界影响因素 影响系统平衡状态的外界因素包括：温度、压力、电
主要区别在于固-液平衡的熔融曲线OC线倾斜
第七章相平衡与相图A
研制开发新材料确定材料成分制订材料生产加工和热处理工艺分析平衡态的组织和可能的非平衡态组织变化预测材料的性能进行材料失效分析一相平衡概念和相律一个结构的相转变为另一种结构相的过程称为相变相变
第7章 相平衡与相图
教学内容
1.相、相平衡、相图等基本概念 2.单元系相图 3.二元系中的相平衡 4.共晶相图 5.包晶相图 6.偏晶相图 7.复杂相图 8.包含固-固反应的相平衡 9.三元系中的相平衡
体系为单相 相点落在线上: f = 1 自由度为1
两相平衡 相点落在交点: f = 0 自由度为0
三相共存
举例：
举例：
7.3 二元系中的相平衡
一、成分的描述 质量分数和摩尔分数。 如A组元的质量分数为wA、摩尔分数为xA， 其相对原子量为MA；B组元的质量分数为wB、 摩尔分数为xB，其相对原子量为MB，则： xA=(wA/MA)/(wA/MA + wB/MB) xB=(wB/MB)/(wA/MA + wB/MB)
相组成物是指组成合金 显微组织的基本相。
组织组成物是指合金在 结晶过程中，形成的具
有特定形态特征的独立 组成部分。
α
β
19
61.9
97.5
M
%
97.5 61.9 97.5 19
100%
45.4%
亚共晶合金 19%＜Sn% ＜61.9 % 过共晶合金 61.9 %＜Sn% ＜97.5%
L 匀 晶 转变 L多 共晶转变 脱溶转变 ( ) II ( )
相界线
在相图上将各相区分隔开的线叫相界线， 由于相界线的特性不同，可区分为： ①液相线：其上全为液相，线下有固相出现， 可以表示为L/L+。 ②固相线：其下全为固相，可表示为L+/L。
第7章 相平衡与相图
教学内容
1.相、相平衡、相图等基本概念 2.单元系相图 3.二元系中的相平衡 4.共晶相图 5.包晶相图 6.偏晶相图 7.复杂相图 8.包含固-固反应的相平衡 9.三元系中的相平衡
体系为单相 相点落在线上: f = 1 自由度为1
两相平衡 相点落在交点: f = 0 自由度为0
三相共存
举例：
举例：
7.3 二元系中的相平衡
一、成分的描述 质量分数和摩尔分数。 如A组元的质量分数为wA、摩尔分数为xA， 其相对原子量为MA；B组元的质量分数为wB、 摩尔分数为xB，其相对原子量为MB，则： xA=(wA/MA)/(wA/MA + wB/MB) xB=(wB/MB)/(wA/MA + wB/MB)
相组成物是指组成合金 显微组织的基本相。
组织组成物是指合金在 结晶过程中，形成的具
有特定形态特征的独立 组成部分。
α
β
19
61.9
97.5
M
%
97.5 61.9 97.5 19
100%
45.4%
亚共晶合金 19%＜Sn% ＜61.9 % 过共晶合金 61.9 %＜Sn% ＜97.5%
L 匀 晶 转变 L多 共晶转变 脱溶转变 ( ) II ( )
相界线
在相图上将各相区分隔开的线叫相界线， 由于相界线的特性不同，可区分为： ①液相线：其上全为液相，线下有固相出现， 可以表示为L/L+。 ②固相线：其下全为固相，可表示为L+/L。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学前指导将学习到的知识点：
知识点094.具有一个低温分解、高温稳定二元化合物的三元
系统相图
6.4.3.6 具有一个低温稳定、高温分解的二元
化合物的三元系统相图
●化合物S的组成点在AB边上，化合物在
T R温度以下才能稳定存在，温度高于T R，
则分解为A、B两种晶相。
●由于其分解温度低于A、B两组元的低共
熔温度，因而不可能从A、B二元的液相
线A′e3′和B′e3′直接析出 S晶体，即S晶体
的初晶区不会与AB边相接触。
E和R，但只能划分出与P和E对应的两个副三
角形。
●P点在对应的△ASC外的交叉位置，是双升点。
E点在对应的△BSC内的重心位置，是低共熔
●R点周围的三个初晶区是（A）、（S）、
（B），对应的三种晶相的组成点A、S、B在
一条直线上，不能形成一个副三角形。
在R点上进行的过程是化合物的形成或分解过程，即: A＋B<-> S（A m B n）。
●这种无变量点称为过渡点。
从R点周围三条界
线上的温降方向看，类似于双降点，所以R点
●在过渡点上由于F=0。
系统的温度不变，液相
组成在R点上不变，实际上液相量也不变，这
个情况和前面介绍的各种无变量点有所不同。
●M点在副三角形SBC内，对应的无变量点E，
最终析晶产物为晶相B、S、C
●M的初晶区在A内，冷却先析出A，P=2，
F=2，液相组成沿着AM背向线变化，固相组成在A，
●液相组成到达界线Re3上的a后析出A和B，
P=3，F=1，液相组成沿着界线aR变化，固相组成离开A沿着AB变化。
●液相组成到R点，固相组成在D点， A+B->S，
P=4，F=0,系统不能继续降温，直到A消失。
●液相组成才沿RE界线变化，不断析出B、S。
P=3，F=1，固相离开D，向G变化，固相组
成为B、S
●最后在E点，液相中同时析出B、S、C，固相
组成由G离开AB边进入三角形内部，当固相
组成与M重合，液相消耗完毕，析晶结束。
液相刚到R点时，固相组成在D点，这时的固相由A、B两种晶相组成。
根据杠杆规则，系统中的液相量为：
当A晶相消失，液相组成要离开R点时，固相组成仍在D点，但这时的固相是由B、S两种晶相组成的，系统中的液相量仍为：
液相量没有变化。
因此在R点进行化合物的形成或分解过程时，液相只起介质作用。
过渡点一定不是结晶的结束点。
合物的三元系统相图
●化合物在高于T P温度是稳定的，它有自己的
初晶区，也可以由二元熔体直接析晶得到，但在低于T P温度时不稳定，要分解为A、B两
种晶相。
●P点同样没有对应的副三角形，P点周围三个
初晶区所对应的晶相组成点A、S、B在一条直线上，因此P点也是个过渡点。
合物的三元系统相图
●由于它形似双升点，便称为双升点形式的过
渡点。
●在P点的相平衡关系为，
P＝4，F＝0。
同样是化合物的分解与形成过
程。
在此过程进行时，液相只起介质作用。
●因此，如果无变量点周围三个初晶区所对
应的晶相组成点在一条直线上，无变量点没
有对应的副三角形，该无变量点便是过渡点。
这是判断过渡点的方法。