温度应力计算

大体积混凝土温度应力实用计算方法及控裂工程实例

大体积混凝土温度应力实用计算方法及控裂工程实例嘿，咱今儿就来聊聊大体积混凝土温度应力实用计算方法和控裂工程实例这档子事儿。

你想想看，那大体积混凝土，就好像是一个大块头，它可不简单呐！温度应力就像是藏在它身体里的小怪兽，要是不把这小怪兽给搞定，那可就要出大乱子啦！那怎么计算这个温度应力呢？这可不是随随便便就能搞定的事儿。

咱先来说说计算方法。

就好比咱要去量一个人的身高体重一样，得有一套靠谱的办法。

计算大体积混凝土温度应力也有它的门道。

咱得考虑好多因素呢，像混凝土的材料特性啦，环境温度啦，施工过程啦等等。

这就像是解一道复杂的谜题，得一步步慢慢来，不能着急。

比如说，咱得知道这混凝土在不同温度下会有啥变化，就像人在不同天气穿不同衣服一样。

然后呢，根据这些信息来算出温度应力有多大。

这可不是拍拍脑袋就能想出来的，得有真功夫才行！再来说说控裂工程实例。

你看那些高楼大厦、大桥大坝，它们可都是用大体积混凝土建起来的。

要是不做好控裂，那可不得了，说不定哪天就裂出个大口子来。

就好比有个大坝，那可是关系着好多人的生命财产安全呐！要是大坝因为温度应力裂了，那后果简直不堪设想。

所以啊，在工程中就得特别小心地处理这个问题。

他们会采取各种办法来控制温度应力，比如用合适的材料，调整施工工艺，做好养护工作等等。

就像照顾一个小婴儿一样，得精心呵护。

你想想，要是建个房子，没几年就裂得不成样子，那多难看呐，还不安全。

所以啊，这个大体积混凝土温度应力实用计算方法和控裂工程实例可太重要啦！咱平常生活中可能不太会注意到这些，但这些可都是建筑工程里的关键啊！没有这些，那些宏伟的建筑怎么能建得起来呢？总之，大体积混凝土温度应力实用计算方法就像是一把钥匙，能打开解决问题的大门；而控裂工程实例则是一面镜子，让我们看到实际应用中的成功与失败。

我们得好好研究它们，让我们的建筑更加坚固、美观、安全。

难道不是吗？你说要是没有这些，那我们的城市会变成什么样呢？。

温度应力计算·

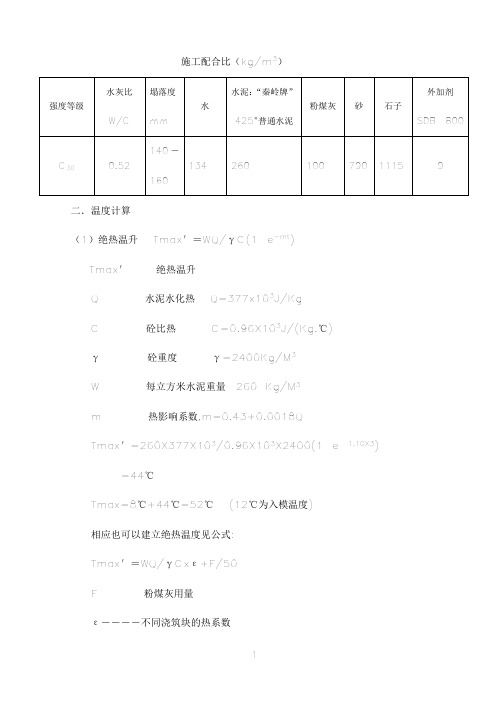
施工配合比（kg/m3）二．温度计算（1）绝热温升Tmax′＝WQ/γC(1-e-mt) Tmax′---绝热温升Q-----水泥水化热Q=377x103J/KgC-----砼比热C=0.96X103J/(Kg.℃)γ-----砼重度γ=2400Kg/M3W-----每立方米水泥重量260 Kg/M3m-----热影响系数,m=0.43+0.0018QTmax′=260X377X103/0.96X103X2400(1-e-1.10X3) =44℃Tmax=8℃+44℃=52℃(12℃为入模温度)相应也可以建立绝热温度见公式:Tmax′＝WQ/γCxε+F/50F-----粉煤灰用量ε――――不同浇筑块的热系数Tmax′＝260X377X103/Tmax=8+55=63℃取Tmax＝63℃三. 温应力计算1.将砼的收缩随时间的进程换算成当量温度计算：Ty(t)= εy(t)/αα=1x10-5砼线膨胀系数εy(t)=ε0M1M2M3······M10(1-e0.01t)Ty(t)------当量温度εy(t)----任意时间的收缩(mm/mm)M1-----水泥品种为普通水泥,取1.0M2-----水泥细度为4000孔，取1.35M3-----骨料为石灰石，取1.00M4-----水灰比为0.52,取1.64M5-----水泥浆量为0.2,取1.00M6------自然养护30天，取0.93M7------环境相对湿度为50%,取0.54M8------水里半径倒数为0.4,取1.2M9------机械振捣，取1.00M10------含筋率为8%,取0.9ε0--ε∞---最终收缩，在标准状态下ε0=3.24X10-4εy(30)=1.01x10-4Ty(30)=10.1℃εy(27)=0.92 x10-4Ty(27)=9.2℃εy(24)=0.83 x10-4Ty(24)=8.3℃εy(21)=0.73 x10-4 Ty(21)=7.3℃εy(18)=0.64 x10-4Ty(18)=6.4℃εy(15)=0.54 x10-4Ty(15)=5.4℃εy(12)=0.439 x10-4 Ty(12)=4.39℃εy(9)=0.335 x10-4 Ty(9)=3.35℃εy(6)=0.226 x10-4 Ty(6)=2.26℃εy(3)=0.114 x10-4 Ty(3)=1.14℃计算中心温度当量温差:△T6=2.26-1.14=1.12℃△T9=3.35-2.26=1.09℃△T12=4.39-3.35=1.04℃△T15=5.4-4.39=1.01℃△T18=6.4-5.4=1.0℃△T21=7.3-6.4=0.9℃△T24=8.3-7.3=1.0℃△T27=9.2-8.3=0.9℃△T30=10.1-9.2=0.9℃2.计算中心温度砼基础施工时处于散热条件，考虑上下表面及侧面的散热条件,当体积厚达3m时,,散热影响系数取0.97；当中心浇筑完第四天后，水化热达峰值。

第十五章工程结构温度应力计算方法

图15.2 砖混组合体胀缩变形关系图
图15.3 墙板边界变形条件的建立注：1. 顶板；2. 墙体；3. 底板。
第十五章工程结构温度应力计算方法
砖混结构温度应力实用计算方法
将钢筋混凝土顶板与墙体分离，放松相互之间的约束力，则顶板及墙体在温差及干湿影响下，其自由应变量分别为 c1 ac (T1 T ) c1 (15-1) (15-2) 根据变形协调条件，墙与板接触面纤维的应变方程如图15.2所示 c1 b1 ec1 eb1 (15-3) 同样，将钢筋混凝土底板与上、下层墙体分离，则有 (15-4) c 2 ac (T3 T ) c 2
b2 b b b
Q1 Q2
(Q1 Q2 )h
将式(15-7)至式(15-10)代入式(15-3)、式(15-6)得
15.11
第十五章工程结构温度应力计算方法
砖混结构温度应力实用计算方法
( 1 1 h 1 h )Q1 ( )Q2 Ac1 2Z c1 Ec bhEb 2Z b Eb bhEb 2Z b Eb
15.9
第十五章工程结构温度应力计算方法
砖混结构温度应力实用计算方法
顶板 y T1 墙板 T2 Q3 Q2 T3 Q2 Q2 Q2 (c) 底板 Q1 Q1 Q3 Q1 Q11 Q1 (b) 顶板底板 Q2 Q2 Q1 Q1
δ
Q1 Q1 Q3
Q1
h
Q3 Q2
δ
Q2 Q2 底板 (a) 组合体
a
第十五章工程结构温度应力计算方法
砖混结构温度应力实用计算方法
c1 b1、 c 2、 b 2 应先按当量温差法， (实际上如果考虑干湿胀缩影响时，、将干湿胀缩影响因素考虑到计算温度中去，使计算过程简化。) 于是得 Q1 [(2 Ac1Zc1ZbbhEb Ec ) (2Zb bh2 )( Ac1Ec Zc1 )Q2 ]/ (15-16) Q2 [ (2 Ac 2 EcbhEb Zb ) (2 Ac1bhZc1Zb Eb Ec )(2Zb bh2 ) Ac 2 E]/ [(4bhEb Zb ) (2 Ac 2 Eb Zb Ac 2 Ecbh2 ) (2Zb bh2 )2 Ac1Ec2Zc1 Ac 2 ](15-17) 需要说明的是，以上计算考虑了墙板偏心受拉(压)的弯曲作用，与墙板底边被嵌固的实际情况仍有出入。

2019年温度场和温度应力计算.doc

附计算书3：温度场和温度应力计算一、温度场计算计算以本工程1.2m 厚底板为例，用差分法计算底板28d 水化热温升曲线。

计算中各参数的取值如下：W ——每m 3胶凝材料用量，440kg/ m 3；Q ——胶凝材料水化热总量（kJ/kg ）；，本例采用实测值260kJ/kg ；c ——混凝土的比热，取1.0kJ/ (kg ∙C )；ρ——混凝土的质量密度，取2400kg/ m 3；α——导温系数，取0.0035m 2/h ；m ，取0.5。

混凝土的入模温度取10C ，地基温度为18C ，大气温度为18C 。

温度场计算差分公式如下：1,1,,1,,222(21)2n k n kn k n kn k T T t t T aT a T x x -+++∆∆=∙--+∆∆∆ （B.4.2-1）⑴试算t ∆、x ∆，确定2x t∆∆α。

取t ∆ = 0.5天 = 12小时，x ∆ = 0.4m ，即分3层则412625.04.0120035.022≈=⨯=∆∆x t α，可行。

代入该值得出相应的差分法公式为k k n kn k n k n T T T T T ∆+⋅++⋅=+-+,,1,11,475.02525.0⑵画出相应的计算示意图，并进行计算。

底板厚1.2m ，分3层，每层0.4m ，相应的计算示意如下图。

从上至下各层混凝土的温度分别用1T 、2T 、3T 表示，相应k 时刻各层的温度即为k T ,1、k T ,2、k T ,3。

混凝土与大气接触的上表面边界温度用0T 表示，与地基接触的下表面边界温度用0'T 表示。

k = 0，即第05.00=⋅=∆⋅t k 天，上表面边界0T ，取大气温度，0T = 18C 各层混凝土温度取入模温度，即0,1T =0,2T = 0,3T = 10C下表面边界0'T ，取地基温度，0'T = 18C ；k = 1，即第5.05.01=⋅=∆⋅t k 天，温升=-⋅⋅⋅=-=∆⋅⋅-⋅-⋅-∆⋅⋅-∆⋅-⋅-)(24000.1260440)(5.015.05.0)11(5.0)1(max 1e e e eT T t k m tk m10.544C上表面边界温度0T ，散热温升为0，始终保持不变，0T = 18C第一层混凝土温度1,1T ，见计算图示中方框1，1,1T 的边界为0T 和0,2T ，在0,1T 的基础上考虑温升1T ∆，即C T T T T T 644.22475.02525.010,10,201,1=∆+⋅++⋅=第二层混凝土温度1,2T ，见计算图示中方框2，1,2T 的边界为0,1T 和0,3T ，在0,2T 的基础上考虑温升1T ∆，即C T T T T T 544.20475.02525.010,20,30,11,2=∆+⋅++⋅=m m m第三层混凝土温度1,3T ，见计算图示中方框3，1,3T 的边界为0,2T 和0'T ，在0,3T 的基础上考虑温升1T ∆，即2,003,13,010.5250.47522.6442T T T T T C'+=+⋅+∆=︒下表面边界温度0'T ，需要考虑散热温升2/1T ∆，所以需每一步都需进行修正。

大体积混凝土温度应力计算

大体积混凝土温度应力计算1.大体积混凝土温度计算1）最大绝热温升值（二式取其一）表3-1不同品种、强度等级水泥的水化热表3-2系数m根据公式（3-2），配合比取硅酸盐水泥360kg 计算:T h ⑶=33.21 T h （7）=51.02 T h （28）=57.992）混凝土中心计算温度（m e K * F ）* Qc * Pm e（1—mt（3-1）T h —混凝土最大绝热温升「C ）； M 混凝土中水泥用量（kg/m ）；F — 混凝土中活性掺合料用量（kg/m ）； c — 混凝土比热，取 0.97kJ/（kg • K ）； P -混凝土密度，取2400 （ kg/m 3）; e 为常数，取2.718 ; T — —混凝土龄期（d ）; m 系数，随浇筑温度而改变，查表 3-2h （t式中:T K t） = T j T h（ t）* （ t）（3-3）式中:T j ――混凝土浇筑温度「C ）;T i （t ）――t 龄期混凝土中心计算温度（C ）;E （t ）――t 龄期降温系数，查表3-3同时要考虑混凝土的养护、模板、外加剂、掺合料的影响；表3-3降温系数E根据公式（3-3）, T 取25（t ）取浇筑层厚1.5m 龄期3天6天27天计算,T i(3)=41.32 T i(7)=48.47 T i(28)=27.903）混凝土表层（表面下50~100mn 处）温度（1）保温材料厚度表3-4几种保温材料导热系数二 0.5hK(K -T b( T- Tmax2)式中:S ——-保温材料厚度（m ；入x — —所选保温材料导热系数 [W/(m • K)]； T2―― -混凝土表面温度（C ）；(3-4)T q ――施工期大气平均温度（C ）；入一一混凝土导热系数，取2.33W/（m • K ）; T m ax 计算的混凝土最高温度（C ）;计算时可取 T 2-T q =15~20C, T max -T 2=20~25C ；水1000 0.58 泡沫塑料20-50 0.035~0.047木模板500~700 0.23 膨胀珍珠岩40~300 0.019~0.065木屑0.17 油毡0.05草袋150 0.14 膨胀聚苯板「15~25 0.042 空气0.03 泡沫混凝土0.10表3-5传热系数修正值保温层种类K1 K21 :仅由容易透风的材料组成（如草袋、稻草板、锯末、沙子） 2.6 3.02 由易透风材料组成，但在混凝土面层上再铺一层不透风材料 2.0 2.33 在易透风保温材料上铺一层不透风材料 1.6 1.94 在易透风保温材料上下各铺一层不易透风的材料 1.3 1.55 仅由不易透风材料组成（如油布、帆布、棉麻毡、胶合板） 1.3 1.5i2根据公式(3-4 )h取1.5 ,入x取0.04 ,入取2.33 ,T2-Tq 取15C, Tmax-T2取25°C, Kb取2,计算8 =0.015m=15mm（2）混凝土表面模板及保温层的传热系数£(3-6)F~q式中：B ――混凝土表面模板及保护层等的传热系数［W/（m2• K）］;“一一各保护层材料厚度（m）;入i――各保温层材料导热系数［W/（m • K）］;B q――空气层的传热系数，取 23［W/（m2• K）］。

大体积混凝土温度应力和收缩应力计算书-secret

大体积混凝土温度应力和收缩应力计算书由于混凝土为C 30 S 8，厚度为1300mm ，为大体积混凝土，故选用水化热低的矿渣425#水泥,辅以外加剂和掺合料.根据以往施工资料,掺外加剂和掺合料的C 30 S 8大体混凝土每立方米用料,矿425#水泥390kg 水泥发热量335kj/kg,预计8月份施工大气温度最高为35℃以上，混凝土浇筑温度控制在26℃以内，进行计算分析。

(1)混凝土温度应力分析 1）混凝土最终绝热温升 ==ρC Q T t 0c )(m =57.6℃式中T (t)—混凝土最终绝热温升m c —每立方米混凝土水泥用量 Q o —每公斤水泥水化热量 C —混凝土比热 ρ—混凝土密度2）混凝土内部不同龄期温度 ①求不同龄期绝热温升混凝土块体的实际温升,受到混凝土块体厚度变化的影响,因此与绝热温升有一定的差异。

算得水化热温升与混凝土块体厚度有关的系数ξ值，如表7-10。

不同龄期水化热温升与混凝土厚度有关系数ξ值表7-10T t =T （t ）·ξ式中T t —混凝土不同龄期的绝热温升T(t)—混凝土最高绝热温升ξ—不同龄期水化热温升与混凝土厚度有关值经计算列于下表7-11不同龄期的绝热温升（℃）表7-11②不同龄期混凝土中心最高温度Ｔmax＝T j＋T t式中T max—不同龄期混凝土中心最高温度T j—混凝土浇筑温度T t—不同龄混凝土绝热温升计算结果列于表7-12不同龄期混凝土中心最高温度表7-123）混凝土温度应力本底板按外约束为二维时的温度应力(包括收缩)来考虑计算①各龄期混凝土的收缩变形值及收缩当量温差a.各龄期收缩变形&y(t)＝&0y(1-e-0.01t)×M1×M2x……xMn式中&y(t)—龄期t时混凝土的收缩变形值&0y—混凝土的最终收缩值,取3.24×10-4/℃M1．M2……Mn各种非标准条件下的修正系数本工程根据用料及施工方式修正系数取值如表7-13修正系数取值表7-13经计算得出收缩变形如表7-15各龄期混凝土收缩变形值表7-15b.各龄期收缩当量温差将混凝土的收缩变形换算成当量温差式中—各龄期混凝土收缩当量温差(℃)&y (t)—各龄期混凝土收缩变形—混凝土的线膨胀系数，取10×10-6/℃ 计算结果列于表7-16各龄期收缩当量温差表7-16②各龄期混凝土的最大综合温度差 ΔT(t)＝T j ＋T(t)＋T y (t)-T q 式中ΔT(t)—各龄期混凝土最大综合温差T j —混凝土浇筑温度,取26℃ T(t)—龄期t 时的绝热温升 T y (t)—龄期t 时的收缩当量温差T q —混凝土浇筑后达到稳定时的温度,取年平均气温25℃计算结果列表7-17各龄期混凝土最大综合温度差表7-17③各龄期混凝土弹性模量 E(t)＝E h (1-e -0.09t )式中E(t)—混凝土龄期t 时的弹性模量(MPa)E h —混凝土最终弹性模量(MPa) C 30混凝土取3.0×104(MPa) 计算结果列表7-18混凝土龄期t 时的强性模量表7-18④混凝土徐变松驰系数、外约束系数、泊桑比及线膨胀系数 a.松驰系数,根据有关资料取值列表7-19混凝土龄期t 时的松驰系数表7-19b.外约束系数(R) 按一般土地基，取R=0.5c.混凝土泊桑比(μ) 从取0.15d.混凝土线膨胀系数(α) α取10×10-6/℃⑤不同龄期混凝土的温度应力 σ(t)=-RS T E t h t t ⨯⨯-∆⨯⨯)()()(1μα式中σ(t)—龄期t 时混凝土温度(包括收缩)应力E (t)—龄期t 时混凝土弹性模量 α—混凝土线膨胀系数ΔT(t)—龄期t 时混凝土综合温差 μ—混凝土泊桑比S h(t)—龄期t 时混凝土松驰系数 R —外约束系数计算结果列表7-20不同龄期混凝土温度(包括收缩)应力表7-204)结论C 30混凝土 28d R L =1.43(MPa) 同龄期混凝土 R L (12d)=0.75R1=1.07(MPa) 所以:()07.196.173.043.112=>==k R d L σ由计算可知基础在露天养护期间混凝土有可能出现裂缝，在此期间混凝土表面应采取养护和保温措施，使养护温度加大，综合温度减小，则可控制裂缝出现。

超长结构温度应力计算探讨精

超长结构温度应力计算探讨一、温度作用的特点:温度作用是在规定时期内结构或结构构件由于温度场变化所引起的作用,具有以下特点:1温度作用是由结构材料“热胀冷缩”效应被结构内、外约束阻碍而在结构内产生的内力作用,属于间接作用;2温度作用随外界环境的变化而变化,有明显的时间性,属于可变作用;3建筑结构从开始建造到拆除都会受到所处温度场影响,因而温度作用伴随着结构的生命全周期过程;4引起结构温度变化因素很多,有气候季节变化、太阳暴晒辐射和其它人为因素(如火灾等,诱因多样性使温度作用有别于其它(荷载作用。

二、温度作用的规范规定:2.1什么时候需要进行温度作用计算根据温度作用的特点可知,结构中产生的温度作用大小主要与结构材料线膨胀系数和结构长度有关。

表1为常用材料线膨胀系数αT,可见结构钢和混凝土的线膨胀系数非常接近。

正因为如此,在计算钢筋混凝土结构的温度作用时才可以只按混凝土一种材料近似考虑。

材料确定的情况下,长度越长,温度作用越大。

在完全没有约束的情况下,总长为100m、截面为600x600的普通混凝土梁温度每升高或降低20℃,梁长度将增加或减少20mm;如果端部的变形完全受到约束,将在梁内部产生约2160KN(按强度等级为C30计算的轴向压力或拉力,该力约为混凝土轴向抗拉强度标准值的3倍。

表1: 常用材料的线膨胀系数αT材料线膨胀系数αT(×10-6/℃轻骨料混凝土7普通混凝土10砌体6~10钢,锻铁,铸铁12不锈钢16铝,铝合金24实际结构不可能没有约束,总会在结构中产生温度应力,当结构长度较小时,可忽略温度应力和温度变形对结构的影响。

现行规范根据不同的结构形式给出该长度(温度区段长度经验值,详见表2,当结构超出该长度时才有必要进行温度作用计算。

表2: 钢筋混凝土结构伸缩缝最大间距(m结构类型室内或土中露天排架结构装配式100 70框架结构装配式75 50 现浇式55 35剪力墙结构装配式65 40 现浇式45 30挡土墙、地下室墙壁等类结构装配式40 30 现浇式30 20建筑结构设计时,应首先采取有效构造措施来减少或消除温度作用效应,如设置结构的活动支座或节点、设置温度缝、采用隔热保温措施等。

教程2_2:温度应力计算的有限元分析如果所示AB为一装在两个刚性支承间的杆件。

杆长l为2m，横截面积A为0.01m2,材料的弹性模量E为200GPa，线胀系数α=12.5×10-6 1/°C,试求温度升高 ∆T=40°C时杆内的温度应力。

此习题文件名: temp。

(天津大学苏翼林编《材料力学》上册第45页习题3.4)图温度应力的计算分析模型此题理论解为σ＝α×E×∆T＝=12.5×10-6×200×109×40＝100×106Pa。

交互式的求解过程1进入ANSYS程序→ANSYS 8.0 →Configure ANSYS Products →file Management→input job name: temp→RunANSYS Utility Menu: PlotCtrls→Style→Hidden-Line Options→select full modelANSYS Utility Menu: Parameters→Angular Units→select Degree2选择单元类型ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete… →Add… →select Link 2D spar 1 →OK (back to Element Types window)→Close (the Element Type window)3定义实常数ANSYS Main Menu: Preprocessor→Real Constants→Add/Edit/Delete…→Add…→select Type 1→OK→input AREA:0.01→OK →Close4定义材料参数4.1 ANSYS Main Menu: Preprocessor →Material Props →Material Models…→Structural→Linear→Elastic→Isotropic→input EX:200e9→OK→选择Thermal Expansion→Coefficient→Isotropic→input ALPX:12.5e-6→OK→Close (the Material Props window)4.2 ANSYS Main Menu: Preprocessor→Loads→Define Loads→Settings →Reference Temp…→input Reference Temperature:70→OK4.3 ANSYS Main Menu: Preprocessor→Modeling→Create→Elements→Elem Attributes…→MAT select 1,REAL select 15生成有限元模型5.1 生成节点ANSYS Main Menu:Preprocessor →Modeling →Create →Nodes →In Active CS→input:1(0,0,0)→Apply→input:2(0.5,0,0)→Apply→input:3(1,0,0)→Apply→input:4(1.5,0,0)→Apply→input:5(2,0,0)→OK5.2 生成杆件ANSYS Main Menu: Preprocessor→Modeling→Create→Elements→Auto Numbered→Thru Nodes→select 1,2节点→Apply→select 2,3节点→Apply→select 3,4节点→Apply→select 4,5节点→OK6模型施加约束6.1 分别给1,5两个节点施加约束ANSYS Main Menu:Preprocessor→Loads→Define Loads→Apply→Structural →Displacement→On Notes→select 1,5两节点→OK→select Lab2:All DOF →OK6.2ANSYS Main Menu:Preprocessor→Loads→Define Loads→Apply→Structral→Temperature→Uniform Temp…→input Uniform Temperature: 1107 分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →Close8 结果显示8.1 ANSYS Main Menu: General Postproc →Element Table→Define Table…→Add…→input Nu:0,Lab:Force,在左侧表中select By sequence num,在右侧表中select SMICS,在右侧表下的文本框input 1 →Apply(back to Element Table Data window) →Add…→input Nu:0,Lab:Stress,在左侧表中select By sequence num,在右侧表中select LS,在右侧表下的文本框input 1→OK(back to Element Table Data window) →Close8.2 ANSYS Main Menu: General Postproc→Plot Results→Contour Plot→Line Elem Res…→select LabI: STRESS, LabJ: STRESS→OK9 退出系统ANSYS Utility Menu: File →Exit →Save Everything→OK。

大体积混凝土温度应力计算

计算结果分析
温度应力分布情况应力与应变关系裂缝产生原因及分布规律计算结果与实际监测数据的对比分析
结论与建议
结论：大体积混凝土温度应力计算案例分析表明，温度应力对混凝土结构的影响较大，需要采取有效的措施进行控制。
建议：在设计和施工过程中，应充分考虑温度应力的影响，采取适当的构造措施和施工方法，以减少温度应力对混凝土结构的影响。
求解温度场：通过有限元法或有限差分法等数值计算方法，求解大体积混凝土的温度场。
计算应力应变：根据温度场计算结果，结合弹性力学理论，计算大体积混凝土的应力应变。
建立数学模型
确定温度场和应力场的基本方程
建立温度应力和收缩应力的计算公式
添加标题
添加标题
确定边界条件和初始条件
添加标题
添加标题
考虑混凝土的弹塑性本构关系
Part Five
大体积混凝土温度应力计算案例分析
工程概况
工程名称：大体积混凝土温度应力计算案例分析建设地点：某市建设规模：建筑面积约为XX平方米建设单位：某建筑公司
计算模型建立
确定计算模型：根据实际情况选择合适的计算模型，如有限元法、有限差分法等。建立温度场：根据混凝土的物理性质和边界条件，建立温度场方程。确定初始条件和边界条件：根据实际情况确定初始温度和边界温度。求解温度场：采用合适的数值方法求解温度场方程，得到各点的温度分布。
确定材料参数
混凝土的弹性模量混凝土的热膨胀系数混凝土的导热系数混凝土的密度
求解方程
建立数学模型
求解温度场方程
确定边界条件和初始条件
计算温度应力
结果分析
计算结果：根据计算公式和参数，得出大体积混凝土温度应力计算结果结果分析：分析计算结果，确定大体积混凝土的温度应力分布和变化规律影响因素：分析各因素对大体积混凝土温度应力的影响程度和作用机制优化建议：根据计算结果和分析，提出优化大体积混凝土温度应力的建议和措施

水泥混凝土路面温度应力的计算与分析

水泥混凝土路面温度应力的计算与分析近年来，随着城市化进程的加速和交通运输的不断发展，水泥混凝土路面的应用范围越来越广泛。

在使用过程中，路面温度的变化不仅会影响路面的性能和寿命，还会导致路面产生应力，进而影响路面的稳定性和安全性。

因此，对水泥混凝土路面温度应力进行计算和分析具有重要意义。

一、水泥混凝土路面温度应力的影响因素水泥混凝土路面温度应力的大小受到多个因素的影响，主要包括以下几个方面：1.路面厚度：路面厚度是影响路面温度应力的重要因素，厚度越大，路面承受的应力就越小。

2.水泥混凝土的强度：水泥混凝土的强度直接影响路面的承载能力，强度越高，路面承受的应力就越大。

3.路面温度：路面温度是影响路面温度应力的主要因素，温度升高会导致路面产生膨胀应力，降温会导致路面产生收缩应力。

4.材料的热物性质：材料的热物性质是影响路面温度应力的重要因素，包括热导率、热容和热膨胀系数等。

二、水泥混凝土路面温度应力的计算方法水泥混凝土路面温度应力的计算方法主要包括两种：经验公式法和有限元法。

1.经验公式法经验公式法是通过经验公式计算出路面的热应变和温度应力，其计算公式为：ε = αΔTσ = Eε其中，ε为路面的热应变，α为路面的热膨胀系数，ΔT为路面的温度变化量；σ为路面的温度应力，E为路面的弹性模量。

2.有限元法有限元法是通过建立数学模型，采用数值计算方法对路面温度应力进行计算。

该方法可以考虑路面的复杂结构和材料特性，计算结果更为精确。

其计算过程主要包括以下几个步骤：（1）建立数学模型：根据路面的实际情况，建立数学模型，包括路面的几何形状和材料特性等。

（2）划分网格：将路面划分成有限个小单元，每个小单元称为单元网格。

（3）确定边界条件：确定路面的边界条件，包括路面的温度边界和约束边界等。

（4）求解方程：根据路面的初始温度和边界条件，求解热传导方程和力学方程，得到路面的温度分布和应力分布。

（5）分析结果：根据计算结果，分析路面的温度应力分布情况，评估路面的稳定性和安全性。

温度应力计算公式

温度应力计算公式
温度应力计算公式是一种用于计算热源变化过程中温度变化所引起的材料应力的公式。

它的基本原理是利用材料的热膨胀系数来计算材料温度变化引起的应力。

一般来讲，温度应力计算公式可以表示为：
σ=α*(ΔT)*E，其中，σ表示材料的应力，α表示热膨胀系数，ΔT表示温度变化量，E表示材料的弹性模量。

根据上述温度应力计算公式，当温度发生变化时，材料的应力将会发生变化。

若在此情况下材料的温度变化比较大，材料的应力也将会变化比较大，需要注意材料的热膨胀系数α和材料弹性模量E的选择和计算，以便更准确的计算出材料的应力。

温度应力计算

第四节温度应力计算一、温度对结构的影响1温度影响(1)年温差影响指气温随季节发生周期性变化时对结构物所引起的作用。

假定温度沿结构截面高度方向以均值变化。

则Ar = r2-r,该温差对结构的影响表现为：对无水平约束的结构，只引起结构纵向均匀伸缩；对有水平约束的结构，不仅引起结构纵向均匀伸缩，还将引起结构内温度次内力；(2)局部温差影响指日照温差或混凝土水化热等影响。

A：混凝土水化热主要在施工过程中发生的。

混凝土水化热处理不好，易导致混凝土早期裂缝。

在大体积混凝土施工时，混凝土水化热的问题很突出，必须采取措施控制过高的温度。

如埋入水管散热等。

B：日照温差是在结构运营期间发生的。

日照温差是通过各种不同的传热方式在结构内部形成瞬时的温度场。

桥梁结构为空间结构，所以温度场是三维方向和时间的函数，即：Ti=f(x9y9z9t)该类三维温度场问题较为复杂。

在桥梁分析计算中常采用简化近似方法解决。

假定桥梁沿长度方向的温度变化为一致，则简化为二维温度场，即：T i=f(x,z,t)进一步假定截面沿横向或竖向的温度变化也为一致，则可简化为一维温度场。

如只考虑竖向温度变化的一维温度场为：T严g)我国桥梁设计规范对结构沿梁高方向的温度场规定了有如下几种型式:2温度梯度f （z, t）（1）线性温度变化梁截面变形服从平截面假定。

对静定结构，只引起结构变形，不产生温度次内力；对超静定结构，不但引起结构变形，而且产生温度次内力;（2）非线性温度变化梁在挠曲变形时，截面上的纵向纤维因温差的伸缩受到约束，从而产生约束温度应力，称为温度自应力。

对静定结构，只产生截面的温度自应力；对超静定结构，不但产生截面的温度自应力，而且产生温度次应力；二、基本结构上温度自应力计算1计算简图2计算公式三、连续梁温度次内力及温度次应力计算采用结构力学中的力法求解。

四、我国公路桥梁设计规范中温度应力计算公式规定：T形截面连续梁由于日照引起桥面板与其它部分温度差，从而产生内力。

超长结构温度应力计算探讨精

超长结构温度应力计算探讨一、温度作用的特点:温度作用是在规定时期内结构或结构构件由于温度场变化所引起的作用,具有以下特点:1温度作用是由结构材料“热胀冷缩”效应被结构内、外约束阻碍而在结构内产生的内力作用,属于间接作用;2 温度作用随外界环境的变化而变化,有明显的时间性,属于可变作用;3 建筑结构从开始建造到拆除都会受到所处温度场影响,因而温度作用伴随着结构的生命全周期过程;4 引起结构温度变化因素很多,有气候季节变化、太阳暴晒辐射和其它人为因素（如火灾等,诱因多样性使温度作用有别于其它（荷载作用。

二、温度作用的规范规定:2.1什么时候需要进行温度作用计算根据温度作用的特点可知,结构中产生的温度作用大小主要与结构材料线膨胀系数和结构长度有关。

表1为常用材料线膨胀系数a T可见结构钢和混凝土的线膨胀系数非常接近。

正因为如此,在计算钢筋混凝土结构的温度作用时才可以只按混凝土一种材料近似考虑。

材料确定的情况下,长度越长,温度作用越大。

在完全没有约束的情况下，总长为100m、截面为600x600的普通混凝土梁温度每升高或降低20C,梁长度将增加或减少20mm;如果端部的变形完全受到约束，将在梁内部产生约2160KN（按强度等级为C30计算的轴向压力或拉力，该力约为混凝土轴向抗拉强度标准值的3 倍。

表1: 常用材料的线膨胀系数aT材料线膨胀系数a T（X16/ C轻骨料混凝土7普通混凝土10砌体6~10钢,锻铁,铸铁12不锈钢16铝,铝合金24实际结构不可能没有约束,总会在结构中产生温度应力,当结构长度较小时,可忽略温度应力和温度变形对结构的影响。

现行规范根据不同的结构形式给出该长度（温度区段长度经验值,详见表2,当结构超出该长度时才有必要进行温度作用计算。

表2: 钢筋混凝土结构伸缩缝最大间距（m结构类型室内或土中露天排架结构装配式100 70框架结构装配式75 50 现浇式55 35剪力墙结构装配式65 40 现浇式45 30挡土墙、地下室墙壁等类结构装配式40 30 现浇式30 20建筑结构设计时,应首先采取有效构造措施来减少或消除温度作用效应,如设置结构的活动支座或节点、设置温度缝、采用隔热保温措施等。

大体积混凝土温度和温度应力计算

大体积混凝土温度和温度应力计算在大体积混凝土施工前，必须进行温度和温度应力的计算，并预先采取相应的技术措施控制温度差值，控制裂缝的开展，做到心中有数，科学指导施工，确保大体积混凝土的施工质量。

（一）温度计算搅拌站提供的混凝土每立方米各项原材料用量及温度如下：水泥：367kg，11℃；砂子：730kg，13℃，含水率为3%；石子：1083kg，9℃，含水率为2%；水：195kg，9℃；粉煤灰：35kg，11℃；外加剂：27kg，11℃。

混凝土拌合物的温度：T0＝[0.9(mceTce＋msaTsa＋mgTg)+4.2Tw(mw－ωsamsa－ωgmg)＋c1(ωsamsa＋Tsa＋wgmgTg)－c2(wsamsa＋wgmg)]÷［4.2mw ＋0.9(mce＋msa＋mg)］式中T0——混凝土拌合物的温度(℃)；mw、mce、msa、mg——水、水泥、砂、石的用量(kg)；Tw、Tce、Tsa、Tg——水、水泥、砂、石的温度(℃)；wsa、wg——砂、石的含水率(%)；c1、c2——水的比热容(kJ/kg·K)及溶解热(kJ／kg)。

当骨料温度＞0℃时，C1=4.2，C2=0；≤0℃时，c1=2.1，c2=335。

为计算简便，粉煤灰和外加剂的重量均计算在水泥的重量内。

T0＝[0.9(429×11＋730×13＋1083×9)＋4.2×9(195－3%×730－2%×1083)＋4.2(3%×730×13＋2%×1083×9)－0]÷[4.2×195＋0.9(429＋730＋1083)]=10.3℃。

混凝土拌合物的出机温度：T1=T0－0.16(T0－Ti)式中T1——混凝土拌合物的出机温度(℃)；Ti——搅拌棚内温度(℃)。

T1=10.3－0.16(10.3－14)＝10.9℃3.混凝土拌合物浇筑完成对的温度T2＝T1－(att＋0.032n)(T1－Ta)式中T2——混凝土拌合物经运输至浇筑完成时的温度(℃)；a——温度损失系数(h-1)；tt——混凝土自运输至浇筑完成时的时间(h)；n——混凝土转运次数；Ta——运输时的环境气温(℃)。

水泥混凝土路面温度应力的计算与分析

水泥混凝土路面温度应力的计算与分析水泥混凝土路面的温度应力是路面施工和使用过程中需要考虑的一个重要问题，它对路面的稳定性和耐久性有着直接的影响。

在本篇文章中，我将详细介绍水泥混凝土路面温度应力的计算与分析方法，并分享我的观点和理解。

一、温度应力的原因与表现水泥混凝土路面温度应力主要由两个原因引起：温度变化和限制条件。

当路面受到温度变化的作用时，水泥混凝土路面会产生热胀冷缩效应，从而产生内部的温度应力。

路面的几何限制条件（如交通荷载、边界约束等）也会导致温度应力的产生。

这些温度应力在路面表面的表现形式是裂缝和变形。

由于水泥混凝土的有限的抗拉强度，温度引起的应力超过其抗拉强度时，路面就会产生裂缝。

由于温度应力的作用，路面可能会出现变形现象，如变形、凸起等。

二、温度应力的计算与分析方法下面我将介绍两种常用的水泥混凝土路面温度应力的计算与分析方法。

1. 数值模拟方法数值模拟方法是目前常用的一种计算水泥混凝土路面温度应力的方法。

它基于有限元原理，通过将路面划分为小的单元，对每个单元进行温度场和应力场的计算，最后通过求解大量单元的方程组得到整体的温度应力分布。

数值模拟方法的优点在于能够考虑复杂的边界条件和材料性能，并且计算结果准确可靠。

然而，该方法需要较为复杂的数值计算技术，对计算机硬件和软件要求较高，而且计算过程较为繁琐。

2. 经验公式方法经验公式方法是另一种计算水泥混凝土路面温度应力的方法。

该方法基于已有的实测数据和经验公式，通过简化计算过程，得到大致的温度应力估计值。

这种方法的优点是简单易行，不需要复杂的计算过程和专业的数值模拟技术。

然而，由于经验公式方法忽略了一些影响因素和细节，因此计算结果可能不够精确。

该方法更适用于一般性的工程设计和初步评估。

三、个人观点与理解在我看来，水泥混凝土路面温度应力的计算与分析是确保路面稳定性和耐久性的重要环节。

准确地计算和分析温度应力，不仅可以指导工程设计和施工过程，还可以为路面维护和养护提供依据。

超长结构温度应力计算

超长结构温度应力计算比如说，咱们夏天吃冰棒的时候，刚从冰箱里拿出来，冰棒是硬邦邦的。

可是过一会儿，在热空气里，冰棒就会慢慢化掉，还会滴答滴答地流水呢。

这是因为温度变高了，冰棒的状态就发生了变化。

超长结构也会这样哦。

想象一下有一个很长很长的铁轨，就像一条长长的大蛇躺在地上。

在寒冷的冬天，铁轨变得特别冷，就像我们冷得缩成一团的时候。

这时候铁轨会收缩，要是没有足够的空间让它收缩，它就会很难受，就像我们穿着小鞋挤脚一样。

到了炎热的夏天呢，铁轨被太阳晒得滚烫，就像我们在大太阳下跑了一圈浑身发热。

这时候铁轨就会膨胀，要是周围的东西限制它膨胀，它内部就会产生一种力量，这就是温度应力啦。

那怎么去计算这个温度应力呢？咱们可以把超长结构想象成是由很多小部分组成的。

就像搭积木一样，每一块积木就像是结构里的一小部分。

当温度变化的时候，这些小部分有的想变大，有的想变小。

如果它们不能自由地变化，就会互相挤压或者拉扯。

再举个例子，我们有一串长长的珠子项链。

如果把这串项链放在很冷的地方，珠子之间的距离可能会变小一点；要是放在很热的地方，珠子之间的距离可能就会变大一点。

如果我们把项链两端固定住，不让珠子自由地改变距离，那珠子之间就会有力量产生，这就有点像超长结构的温度应力啦。

在计算的时候呢，我们要考虑很多东西。

比如说温度到底变化了多少度，就像我们要知道冰棒从冰箱里拿出来后温度升高了多少度一样。

还有这个超长结构是什么材料做的，不同的材料就像不同的东西一样，有的东西很容易热胀冷缩，有的就没那么容易。

就像橡皮和木头，橡皮很容易被拉长或者压扁，木头就相对难一些。

混凝土温度应力计算

ቤተ መጻሕፍቲ ባይዱ
混凝土温度应力计算
土建工程大体积混凝土最高温升值可按式（4-49）计算。
式中，T′max 为混凝土内部的最高温升值（℃）；t0为混凝土浇筑温度（℃），计算时，在无气温和浇筑温度的关系值时，可采用计划浇筑日期的当地平均气温（℃）；Q为每立方米混凝土中水泥的用量（kg/m3），上述两式适用于强度等级为42.5级的矿渣硅酸盐水泥；F为每立方米混凝土中粉煤灰的用量（kg/m3）。
高层建筑施工
混凝土温度应力计算
1. 混凝土绝热最高温升值计算
大体积混凝土中心部分的最高温度，在绝热条件下是混凝土浇筑温度与水泥水热化之和。但实际的施工条件表明，混凝土内部的温度与外界环境之间必然存在着温差，加上结构物的四周又具备一定的散热条件，因此在新浇筑的混凝土与其周围环境之间必然会发生热能交换。故大体积混凝土内部的最高温度，是由浇筑温度、水泥水化后产生的水化热量全部转化为温升后的最后温度，称为绝热最高温升，一般用Tmax表示，可按式（4-48）计算。
混凝土温度应力计算
不同龄期几种常用水泥在常温下释放的水化热值如表4-14 所示。从表中可以看出，水泥水化热值与水泥品种、水泥强度等级和混凝土龄期等因素有关。
注：表中数值是按平均硬化温度为15 ℃时编制的，当平均温度为7～10 ℃时，表中数值按60%～70%采用；当采用粉煤灰硅酸盐水泥、火山灰硅酸盐水泥时，其水化热值可参考矿渣硅酸盐水泥的数值。
混凝土温度应力计算
2. 混凝土最高温升值计算
自1979年以来，对已施工的许多大体积混凝土结构的现场实测升温、降温数据资料，经过统计整理分析后得出：凡混凝土结构厚度在1.8 m以下的，在计算最高温升值时，可以忽略水灰比、单位用水量、浇筑工艺及浇筑速度等次要因素的影响，而只考虑单位体积水泥用量及混凝土浇筑温度这两个主要影响因素，以简便的经验公式进行计算。工程实践证明，其精确程度完全可以满足指导施工的要求，其计算值与实测值相比误差较小。

大体积混凝土温度和温度应力计算

大体积混凝土温度和温度应力计算在大体积混凝土施工前，必须进行温度和温度应力的计算，并预先采取相应的技术措施控制温度差值，控制裂缝的发展，做到心中有数，科学指导施工，确保大体积混凝土的施工质量。

4.1温度计算1、混凝土拌合物的温度混凝土拌合物的温度是各种原材料入机温度的中和。

温度计算：水泥：328 Kg 70℃砂子：742 Kg 35℃含水率为3%石子：1070Kg 35℃含水率为2%水：185 Kg 25℃粉煤灰：67 Kg 35℃外加剂：8 Kg 30℃TO=[0.9(MceTce+MsaTsa+MgTg)+4.2Tw(Mw-WsaMsa-WgMg)+C1(WsaMsaTsa+WgMgTg)-C2(WsaMsa+WgMg)]/[4.2Mw+0.9(Mce+Msa+Mg)]式中：TO ——混凝土拌合物的温度(℃)Mw、Mce、Msa、Mg ——水、水泥、砂、石每m3的用量(kg/m3) Tw、Tce、Tsa、Tg ——水、水泥、砂、石入机前温度Wsa、Wg ——砂、石的含水率(%)C 1、C2——水的比热溶(kJ/Kg K)及溶解热(kJ/Kg)C 1=4.2，C2=0(当骨料温度>0℃时)TO=[0.9(328×70+67×35+8×30+742×35+1070×35)+4.2×25(185-742×3%-1070×2%)+4.2(3%×742×35+2%×1070×35)-0]/[4.2×185+0.9(328+742+1070)]=37.49℃2、混凝土拌合物的出机温度T 1=T－0.16（T－Ti）式中： T1——混凝土拌合物的出机温度（℃）Ti——搅拌棚内温度，约30℃∴ T1=37.49－0.16（37.49－30）=36.3℃3、混凝土拌合物浇筑完成时的温度T2= T1－(αtt＋0.032n)(T1－Ta)℃式中：T2——混凝土拌合物经运输至浇筑完成时的温度（℃）α——温度损失系数取0.25tt——混凝土自运输至浇筑完成时的时间取0.7h n ——混凝土转运次数取3Ta——运输时的环境气温取35T2=36.3－(0.25×0.7＋0.032×3)(36.3－35)=35.95℃混凝土拌合物浇筑完成时温度计算中略去了模板和钢筋的吸热影响。

(整理)温度场和温度应力计算

附计算书3：温度场和温度应力计算一、温度场计算计算以本工程1.2m 厚底板为例，用差分法计算底板28d 水化热温升曲线。

计算中各参数的取值如下：W ——每m 3胶凝材料用量，440kg/ m 3；Q ——胶凝材料水化热总量（kJ/kg ）；，本例采用实测值260kJ/kg ；c ——混凝土的比热，取1.0kJ/ (kg ∙C )；ρ——混凝土的质量密度，取2400kg/ m 3；α——导温系数，取0.0035m 2/h ；m ，取0.5。

混凝土的入模温度取10C ，地基温度为18C ，大气温度为18C 。

温度场计算差分公式如下：1,1,,1,,222(21)2n k n kn k n kn k T T t t T aT a T x x -+++∆∆=∙--+∆∆∆ （B.4.2-1）⑴试算t ∆、x ∆，确定2x t∆∆α。

取t ∆ = 0.5天 = 12小时，x ∆ = 0.4m ，即分3层则412625.04.0120035.022≈=⨯=∆∆x t α，可行。

代入该值得出相应的差分法公式为k k n kn k n k n T T T T T ∆+⋅++⋅=+-+,,1,11,475.02525.0⑵画出相应的计算示意图，并进行计算。

底板厚1.2m ，分3层，每层0.4m ，相应的计算示意如下图。

从上至下各层混凝土的温度分别用1T 、2T 、3T 表示，相应k 时刻各层的温度即为k T ,1、k T ,2、k T ,3。

混凝土与大气接触的上表面边界温度用0T 表示，与地基接触的下表面边界温度用0'T 表示。

k = 0，即第05.00=⋅=∆⋅t k 天，上表面边界0T ，取大气温度，0T = 18C 各层混凝土温度取入模温度，即0,1T =0,2T = 0,3T = 10C下表面边界0'T ，取地基温度，0'T = 18C ；k = 1，即第5.05.01=⋅=∆⋅t k 天，温升=-⋅⋅⋅=-=∆⋅⋅-⋅-⋅-∆⋅⋅-∆⋅-⋅-)(24000.1260440)(5.015.05.0)11(5.0)1(max 1e e e eT T t k m tk m10.544C上表面边界温度0T ，散热温升为0，始终保持不变，0T = 18C第一层混凝土温度1,1T ，见计算图示中方框1，1,1T 的边界为0T 和0,2T ，在0,1T 的基础上考虑温升1T ∆，即C T T T T T 644.22475.02525.010,10,201,1=∆+⋅++⋅=第二层混凝土温度1,2T ，见计算图示中方框2，1,2T 的边界为0,1T 和0,3T ，在0,2T 的基础上考虑温升1T ∆，即C T T T T T 544.20475.02525.010,20,30,11,2=∆+⋅++⋅=m m m第三层混凝土温度1,3T ，见计算图示中方框3，1,3T 的边界为0,2T 和0'T ，在0,3T 的基础上考虑温升1T ∆，即2,003,13,010.5250.47522.6442T T T T T C'+=+⋅+∆=︒下表面边界温度0'T ，需要考虑散热温升2/1T ∆，所以需每一步都需进行修正。