第二章 平面机构的运动分析
第2章 平面机构的运动简图及其自由度

二. 绘制机构运动简图的目的: 机构运动简图与真实机构具有完全相同的运动
特性,主要用于简明地表达机构的组成情况和运动 情况,进行运动分析,作为运动设计的目标和构造 设计的依据。也可对机构进行力分析并作为专利性 质的判据。
三. 机构运动简图中运动副的表示方法 机构运动简图中运动副(转动副、移动副)的表示方法如
说明:当原动件数多于机构的自由度时,机构的运动难以确 定。
如图所示静定的桁架(图 a)和超静定的桁架(图 b) ,自由度分别为0和 -1 ,即各构件之间不可 能运动。
桁架在机构分析中作为一个构件(结构体)来对待。 综上所述可知,机构具有确定运动的条件是:机构的
自由度F>0且等于原动件数。
局部自由度
错误
F=3n-2PL-PH= 3*3-2*(2+1)-1=2
正确
F=3n-2PL-PH= 3*2-2*2-1=1
一般在高副接触处,若有滚子存在,则滚子绕自身轴线转动 的自由度属于局部自由度,采用滚子结构的目的在于将高副 间的滑动摩擦转换为滚动摩擦,以减轻摩擦和磨损。
3. 虚约束
对机构的运动不起独立限制作用的约束称为虚约束。如平行 四边形机构;如图a所示为机车车轮联动机构,图b为其机构 运动简图。
例2-1 绘制如图 (a)所示的颚式破碎机主体机构的运 动简图。
解: (1)分析机构的组成及运动情况 (2) 确定运动副的类型及数量 (3) 选定投影面和比例尺,定出各运动副的相对位置,
绘制出机构运动简图如图 (b)所示。
活塞泵
例:油泵机构 1圆盘 2柱塞 3 构件 4机架
B 1 A
运动副是使两构件直接接触并能产生一定相对运动的 联接。是由两构件组成的可动联接。运动副是约束运 动的,构件组成运动副后,其独立运动受到约束,自 由度便随之减少。如:轴与轴承、凸轮与从动件
平面机构的运动分析

❖绝对瞬心:运动构件和机架之间的瞬心。
绝对瞬心也就是运动构件上瞬时绝对速度等于零的点。
❖相对瞬心:两个运动构件之间的瞬心。
相对瞬心也就是两个运动构件的同速重合点。
2.机构中瞬心的数目
设机构由K个构件组成,该机构的瞬心的总数为:
N = K(k-1)/2
7
3.机构中瞬心位置的确定
(1)两构件组成运动副 根据瞬心的定义,通过观察直接确定两构件的瞬心位
联接两绝对加速度终点 的矢量代表相应两点间 的相对加速度
c'
P'
e'
30
b' c"
2.组成移动副两活动构件的重合点间的运动关系。
(重合点法) 图示机构中,已知各构件的长度、原动件1的位置1 及等角速度ω1,求机构在图示位置时构件3的速度、 加速度。
31
▪ 活动构件1、2组成移动副, ▪ 作平面复杂运动的构件2上的另一个基本运动副是
vP13 P12
P13
P23 ω3 P34
P14
注意:图解法的特点体现在从“机构位置图”中直
接量出两点之间的距离。
15
提问:
1)如何求构件2的角速度ω2? 2) ω3=0时,构件1的角位置1 ?
P24
P23
P12
P13
P34
16
P14
例2:如图所示为一曲柄滑块机构,已知l AB=30mm, l BC=65mm,原动件1的位置1=145° 及等角速度ω1 = 10rad/s,求机构在该位置时滑块3的速度。
C点
B点
构件2
影像原理
35
E点
2.速度分析
▪
VC = VB + VCB
第02章--平面机构及自由度计算PPT课件

F3 n2P LP H
10
2.3.2 计算平面机构自由度时应注意的事项
实际工作中,机构的组成比较复杂,运用公式 计算 F3n2PLPH 自由度时可能出现差错,这是由于机构中常常存在一些特 殊的结构形式,计算时需要特殊处理。
(1) 复合铰链 (2) 局部自由度 (3) 虚约束
图2-3 构件的自由度 4
1.1.3 课程任务
❖ 机构由若干个相互联接起来的构件组成。机构中两构件之间 直接接触并能作确定相对运动的可动联接称为运动副。如图 2-1(b)所示的内燃机的轴与轴承之间的联接,活塞与汽缸之 间的联接,凸轮与推杆之间的联接,两齿轮的齿和齿之间的 联接等。
❖ 两个构件构成运动副后,构件的某些独立运动受到限制,这 种运动副对构件的独立运动所加的限制称为约束。运动副每 引入一个约束,构件就失去一个自由度。
平面机构及自由度计算
所有构件均在同一平面或相互平行的平面内运动的机构 称为平面机构。工程中常用机构大多数都是平面机构。如图 2-1(a)所示的卡车自动卸料机构、如图2-1(b)所示的内燃机 中的机构都属于平面机构。
图2-1 平面机构 1
平面机构及自由度计算
2.1 平面机构的组成 2.2 平面机构运动简图 2.3 平面机构的自由度计算
11
2.3.3 平面机构具有确定运动的条件
机构相对机构是由构件和运动副组成的系统,机构要实 现预期的运动传递和变换,必须使其运动具有可能性和确 定性。
如图2-14(a)所示的机构,自由度F=0;如图2-14(b)所 示的机构,自由度F=-1,机构不能运动。
如图2-15所示的五杆机构,自由度F=2,若取构件1为 主动件,当只给定主动件1 的位置角1时,从动件2、3、 4的位置既可为实线位置,也可为虚线所处的位置,因此其 运动是不确定的。若取构件1、4为主动件,使构件1、4都 处于给定位置1、4时,才使从动件获得确定运动。
1.机构的运动分析

第二章机构的运动分析• 2.1 对机构进行运动分析的目的和方法• 2.2 用速度瞬心法进行速度分析• 2.3 相对运动图解法• 2.4 解析法•2.1 对机构进行运动分析的目的和方法一、平面机构运动分析的目的1. 求解机构中某些点的运动轨迹或位移,确定机构的运动空间2.求解机构某些构件的速度、加速度,了解机构的工作性能3.为力分析作前期工作构件的惯性力与其加速度成正比,惯性力矩与其角加速度成正比。
二、运动分析的方法复数法矩阵法矢量法速度瞬心法相对运动图解法(一)图解法(二)解析法(三)实验法2.2 用速度瞬心法进行速度分析2.2.1 瞬心的基本概念2.2.2 用瞬心法进行机构的速度分析2.2.1 瞬心的基本概念一、瞬心概念二、平面机构瞬心的数目三、瞬心位置的确定在任一瞬时,两个作平面相对运动的构件都可以看成是围绕一个瞬时重合点作相对转动。
瞬时重合点若你站在机架上看是等速重合点或同速点瞬时回转中心瞬心一、瞬心A 1(A 2)B 1(B 2)12A2A1V B2B1V P 12平面运动两构件肯定存在一个相对速度为零,绝对速度相同的点.如果你站在机架上看那就是同速点二、平面机构瞬心的数目2(1)2NN N K C -==假设机构中含有N 个构件,每两个构件之间有一个瞬心,则全部瞬心的数目三、瞬心位置的确定1.两个构件之间用运动副连接的瞬心位置2.两个构件之间没有用运动副连接的瞬心位置1.两个构件之间用运动副连接的瞬心位置(1)两个构件用转动副连接时的瞬心位置(2)两个构件用移动副连接时的瞬心位置(3)两构件用平面高副连接时的瞬心位置12 P12P12P121122(1)两个构件用转动副连接时的瞬心位置P 1212∞(2)两个构件用移动副连接时的瞬心位置半径无穷大的转动副(3)两个构件用平面高副连接时的瞬心位置纯滚动连滚带滑2.两构件之间没有用运动副连接时的瞬心位置(1)三心定理(2)瞬心多边形法的步骤(1)三心定理作平面运动的三个构件有三个瞬心,且位于同一直线上。
第2章-平面机构运动分析(解析法)

复数矢量法
复数矢量法是将机构看成一封闭矢量 多边形,并用复数形式表示该机构的封闭 矢量方程式,再将矢量方程式分别对所建 立的直角坐标系取投影。
Hale Waihona Puke 1、铰链四杆机构2、曲柄滑块机构
3、导杆机构
§2-4 用解析法求机构的 位置、速度和加速度
图解法的缺点:
1、分析结果精度低; 2、作图繁琐、费时,不适用于一个运动周期的分析。 3、不便于把机构分析与综合问题联系起来。 随着计算机应用的普及,解析法得到了广泛的应用。 方法:复数矢量法、矩阵法、杆组法等。 思路: 由机构的几何条件,建立机构的位置方程,然后就位置方程对 时间求一阶导数,得速度方程,求二阶导数得到机构的加速度方 程。
第2章平面机构的自由度和运动简图

作者: 潘存云教授
(2)参与组成一个转动副和一个移动副的构件的表示: 滑块上加转动副
(II)
中国地质大学专用
作者: 潘存云教授
(3)参与组成三个转动副的构件的表示: 用三角形表示,在三角形内加剖面线或在三个角上 涂以焊缝的标记以表示三角形是一个刚性整体
(III)
如果三个转动副中心在一条直线上,可用下图表示该构件:
中国地质大学专用
作者: 潘存云教授
例题1:绘制下图左示颚式破碎机的机构运动简图: 例题 :绘制下图左示颚式破碎机的机构运动简图:
2 B
A
1
3 D C 4
中国地质大学专用
作者: 潘存云教授
解:1构件为机架,2构件为偏心轴,3构件为动颚,4构件为肘板。 机架1和偏心轴2形成的转动副中心在A点(偏心轴绕A点转动), 偏心轴2和动颚3形成的转动副中心在B点, 动颚3和肘板4形成的转动副中心在C点, 肘板4和机架1形成的转动副中心在D点。 a. 选取一合适的机器工作位置 (使所绘制的机构运动简图清晰易读); b. 根据机器上各构件的实际尺寸按比例确定出 机器上各运动副的相对位置(最关键), 机器上各运动副的相对位置(最关键), 在这些位置上画出相应的运动副符号; c. 连接相关的运动副得到各构件; d. 在作为机架的构件上打上阴影线 (标出机架 在作为机架的构件上打上阴影线; 标出机架 标出机架) e. 标出原动件(在原动件构件上标出指示运动方向的箭头)。 标出原动件(在原动件构件上标出指示运动方向的箭头) 绘制的机构运动简图如上图右所示。
中国地质大学专用 作者: 潘存云教授
常见的移动副的表示如下图所示:
(IV-1)
(IV-2)
(IV-3)
两活动构件组成的移动副的表示
《机械原理》知识要点

1
A e
2 4
P24
P 13
B
C
3
第三章 平面连杆机构及其设计
重 点
平面四杆机构的基本类型 平面四杆机构的基本知识
第三章 平面连杆机构及其设计
一、平面四杆机构的主要类型
1、铰链四杆机构
2、曲柄滑块机构
3、导杆机构
第三章 平面连杆机构及其设计
二、铰链四杆机构的类型
速度瞬心法
图解法
◆两构件重合点间的运动关系
第二章 平面机构的运动分析
一、速度瞬心的概念
两个构件的瞬时等速重合点(同速点)
瞬心数
N K ( K 1) 2
构件数—K
二、瞬心位置的确定
1、直接观察法(两构件以运动副相联) 2、利用三心定理求(两构件间没有构成运动副)
三心定理:三个构件的三个瞬心必定在一条直线上
机构的组成原理——任何机构都是由若干个杆组依次联接到
原动件和机架上而构成的
第一章 平面机构的结构分析
3、机构的结构分析
机构的结构分析是指把机构分解为基本杆组、原动件和 机架,是机构组成的反过程,又称为拆杆组。
拆分原则
首先,从远离原动件的部分开始拆分; 试拆时,先试拆低级别杆组;
每拆完一个杆组,剩余的部分仍然是一个完整机构。
第六章 轮系及其设计
找基本周转轮系的一般方法
先找行星轮:
几何轴线绕另一个齿轮的几何轴线转动的齿轮
再找行星架
支持行星轮的构件
找中心轮
几何轴线与行星架的回转轴线重合 直接与行星轮相啮合的齿轮
一个基本周转轮系
行星轮、行星架、中心轮
第2章--平面机构运动简图和自由度

我受到了表扬 从小到大我受到过许多表扬,每次 受到表 扬我都 是喜滋 滋
的。但是有一次表扬却是苦涩的。
记得读三年级时,我期终考试失误了, 导
致数学成绩只得了89分。我看着那成 绩单上 的红红 的、刺 眼的89 这个数 ,不知 揉
了多少次眼睛。眼睛都被我揉红了。 我看着 这个令 我心酸 心痛的 数字, 不敢相 信
(2)选定视图平面。为将机构运动简图表达清楚,必须先选好投影 面,为此可以选择机械的多数构件的运动平面作为投影面。
上一页 下一页
§2.2 平面机构的运动简图
必要时也可就机械的不同部分选择两个或更多个投影面,然后扩展到 同一图面上,或者将主运动简图上难以表达清楚的部分另绘局部简图, 总之,以表达清楚、正确为原则。
式(2.2)可以判断、检验或确定机构原动件的个数;同时说明活动构件、 低副、高副个数如何分配,才能组成机构。
2.3.2计算平面机构自由度应注意的事项
在计算机构的自由度时,往往会遇到按公式计算出的自由度数目与
机构的实际自由度数目不相符的情况。这往往是因为在应用公式计算
机构的自由度时,还有某些应该注意的事项未能正确考虑的缘故。现
将应该注意的主要事项简述如下。
1.复合铰链
两个以上的构件同时在一处以转动副相连接,就构成了所谓的复合
铰链。
上一页 下一页
§2.3 平面机构的自由度
如图2-13所示,它是三个构件在一起以转动副相连接而构成的复合
铰链。由图2-13(b)可以看出,这三个构件共同构成的是两个转动
副。同理,若有m个构件以复合铰链相连接时,其构成的转动副数
千万只蚂蚁再爬似的。心底里暗暗地 说:“ 妈妈, 对不起 ,我骗 了你! ”
第
二天,我们全家去了福建玩。说真的 我玩得 十分不 爽,因 为我的 心老想 着成绩 单
第二章 平面机构的运动分析图解法及解析法3

l1 l 2 l 4 l 3
将上述矢量方程向 X,Y轴投影得:
x : l 1 cos1 l 2 cos2
l 4 l 3 cos3 ( 1 ) y : l 1 sin 1 l 2 sin 2 l 3 sin 3 (2)
x : l 1 cos1 l 2 cos2 l 4 l 3 cos3 y : l 1 sin 1 l 2 sin 2 l 3 sin 3
位移方程 速度方程 轨迹(角位移) 速度(角速度) 加速度(角加速度)
s s (t ) v s ds dt a v dv dt
加速度方程
方法:①瞬心法 ②图解法 ③解析法
求机构的速度和角速度 简易直观,精度低,有限个位置 过程规范,结果完整
2.2 用瞬心法进行机构的速度分析 (Instant center of velocity ) 一、速度瞬心的概念 定义:两个互作平面平行运动的刚体上绝对速度相等
A B B C
2
2
C
2
)
同理,对于2 也可求得:
D 2 l 1 l 2 sin 1 F l
2 1
“”代表机构中C点在AD之下。
D sin 2 E cos 2 F 0
E = 2 l 2 ( l 1 cos1 l 4 ) 2 l 1 l 4 cos1
l
2 2
② 确定瞬心数目和位置 N=3 P12在高副法线n-n上,
P13 P23 P12
3
P23
n
∞
2
③求构件2的速度
V2 VP12 1 P 13 P 12 L
(方向向上)
P13 P 12
w1
第2章--机构运动简图

C: 复合铰链 M 和 N 、 E 虚约束 和F: G: 局部自由度
小结:
1、运动副的定义和分类 运动副:由两构件直接接触形成的可动联接
分类:高副(点或线接触的运动副)和低副(面接触的运动副)
2、能绘制机构运动简图 3、重点掌握平面机构的自由度计算及注意事项,明确复合铰链 局部自由度、虚约束等
1)平面机构自由度的计算公式: F 3n 2PL PH
F 3n 2PL PH 34 24 2
2
n7 PL 10 PH 0
F 3n 2PL PH 3 7 210 0
1
n4 PL 4 PH 2
F 3n 2PL PH 34 24 2
2
n7 PL 10 PH 0
F 3n 2PL PH 3 7 210 0
1
n9
用图形符号表示高副时,一 般需把两构件在接触点处的 曲线轮廓画出(图a),但对于 齿轮机构,习惯上只画出两 齿轮的节圆(见表1-1)。
二、 构件的分类及其表示符号
1. 构件的分类
机 架 —机构中的固定构件; 支撑活动件,只有一个
原动件 主动件
—按给定已知运动规律独立运 动的构件;一般机构有一个
常在其上给出表示其运动形式 的箭头。
1)平行四边形结构
A
2)两构件之间构成多个转动轴线 重合的转动副;
3)两构件之间构成多个导路平行 的移动副;
虚约束常出现在下列场合:
1)平行四边形结构 2)两构件之间构成多个转动轴线重合的转动副; 3)两构件之间构成多个导路平行的移动副;
4)机构中对传递运动不起独立作用的对称部分
5)两构件多点接触形成平面高副,
5、给各构件和运动副编号,并在 原动件上用箭头表示其运动形式和 方向
机械设计 第02章 平面机构的运动学动力学分析

总结
机架 原动件 从动件
一、构件 + 运动副 运动链 机构
计算公式: F=3n - 2PL
-
PH
二、运动链成为机构的条件:F > 0, 原动件数 = 自由度 三、平面运动链自由度计算方法和注意事项 四、机构运动简图的定义及作用 1 2 3
S3
• 通过分析自由构件自由度、不同运动副引 入的约束,得出平面机构自由度计算公式 • 运动链成为机构的条件:原动件数=F • 根据运动简图计算机构的自由度 • 计算机构自由度的注意事项: • (1)复合铰链 • (2)局部自由度 • (3)虚约束:连接点的轨迹重合、导路平 行、法线重合、同轴转动副、天平、对运 动不起作用的对称部分
ω3 3
P23
VP23
P13 n
∴ω 3=ω 2·(P13P23/P12P23) ω 3方向与ω 2相反。
相对瞬心位于两绝对瞬心之间,两构件转向相反。
3.求传动比 定义:两构件角速度之比为传动比。 2 ω 3 /ω 2 = P12P23 / P13P23 P12 ω 2
推广到一般: 1 ω i /ω j =P1jPij / P1iPij 结论:
方向 //
沿BA 沿CB
CB
vC、 aC大小 、 方向 、 大小 、 方向
2 2
影像法:由构件上两点求第三点
• 与机构上的三角 形相似,字母转 向相同。
vE vB vEB vE vC vEC
• 加速度影像法:
aE aB an a EB EB aE aC an a EC EC
2
3 P34
P14 4
举例:求图示六杆机构的速度瞬心。 解:瞬心数为:N=n(n-1)/2=15 n=6 1.作瞬心多边形圆
机械原理习题与答案解析
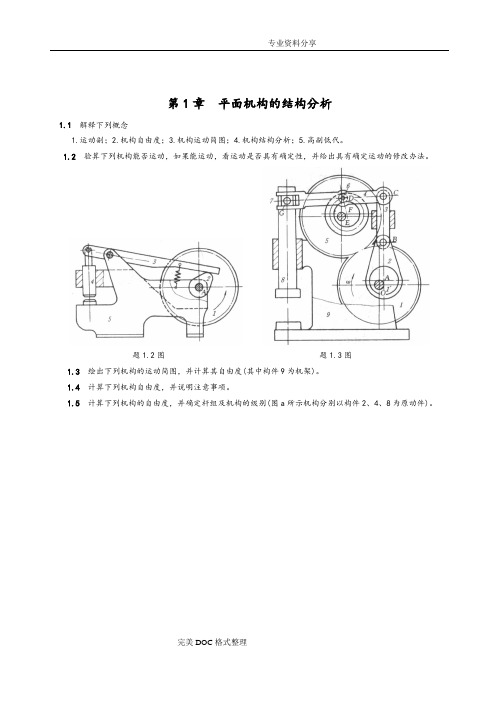
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE=120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
机械设计基础教案ppt课件

一、平面机构自由度的计算
移动副:约束了沿y轴方向的移动和在xOy平面内的 转动, 只保留沿x轴方向的移动;
转动副:约束了x、 y两个方向的移动, 只保留一个转动;
高副:只约束了沿接触处公法线n-n方向的移动。
单个自由构件的自由度为 3
低副引入两个约束!
高副引入一个约束!
活动构件数 构件总自由度 低副约束数
(1) 转动副连接两构件运动轨迹重合AB、CD、EF平行且相
等 (2)两构件组成多个转动副、且各转动副轴线重合 (3)两构件组成多个移动副、且各转动副导路平行 或者重合 (4)两构件组成多个平面高副、且各高副接触点处公法线重合 (5)对机构运动不起作用的对称部分如:行星轮
B2
E
1
5
A
F4
(a)
CB
学习难点
复合铰链、局部自由度和虚约束的识别和处理
• 作业: 2-6(a), (c), (d), (f)
•
2-8
• 思考:2-10
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
n
3×n
2 × PL
计算公式: F=3n-(2PL +Ph )
要求:记住上述公式,并能熟练应用。
高副约束数 1 × Ph
F3n2P LP H
n 式中, 为活动构件个数; PL 为低副个数; PH 为高副个数。
n = 3 Pl= 4 F = 3×3–2×4 = 1
n=4
Pl = 5
F = 3×4–2×5 = 2
F=3×4-2×4-2=2
例2-7 图示2-28组合机构中的轴线yy//xx;且齿轮2及凸 轮4固定在同一轴线上,计算其机构的自由度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
vA2 A1 w21l AP
vA
A B ●P
vA2A1 vB
B2(B1)
vB2B1
●P12
vB 2 B1 w21lBP
21 2 1
速度瞬心为互相作平面相对运动的两构件上,瞬时 相对速度为零的重合点;或者说,瞬时绝对速度相等的 重合点 ( 即等速重合点 ) 。若该点的绝对速度为零则为绝 对瞬心;若不等于零则为相对瞬心,即: VP1= V P2 或 VP1P2=0
AB
2
故
aB a A a
t BA
a
n BA
23
t a BA
B aB
aA
aB a A a
t BA
a
aBA
n BA
n a BA
A
aA
即:平面图形内任一点的加速度等于基点的加速度与 相对基点转动的切向加速度和法向加速度的矢量和。 这就是平面运动的加速度合成法或称为基点法。
图解法:取速度比例尺
v
实际速度值 m / s 图示长度 mm
27
(2)速度分析(解C点续)
C
vC vB vCB
方向:⊥CD ⊥AB 大小: ? lAB1 ⊥BC ?
B 1 A 4
2 2 2 E 3 3 3 D (a)
1 1
作出速度图p-bc,如图(b)所示则:
p-bce称为速度图; p ——速度极点; b、c、e分别称为构件2上相应点
18
哥氏加速度等于牵连角速度矢与点的相对速度矢的矢积的两倍。
ak 2e vr
ak的大小为:
ak 2evr sin q
其中 q 为 e 与 vr 两矢量间的最小夹 角。矢ak方向垂直于e和vr,指向按右 手螺旋法则确定。 工程中常见的平面机构中e和vr是垂直的,此时ak=2evr; 且vr按e转向转90°就是ak的方向。
P24 P15
(3) 三心定理求瞬心
1 6 2
P26
P36
P34
P25 P12 2 P45 P23
P35
3
P16
5 4
3 P13
P46
4
5 P56
6
P14
1
15
§2-3 用相对运动图解法求机构的速度和加速度
1.矢量方程图解法的基本原理和方法:用相对运动原理列出
构件上点与点之间的相对运动矢量方程,然后作图求解矢 量方程。 2.机构运动分析的两类问题: ◆ 同一构件两点间; ◆ 两构件重合点间。
22
用基点法求平面图形内各点的加速度 如图所示。由牵连运动为平动的加速度合成定理,有
aa ae ar
由于牵连运动为平动,所以ae=aA,于是有
t a BA
aB aA aBA
而 其中
B aB
aA
aBA
a BA a
a
n BA
t BA
a
n BA
a
A
n BA
aA
t aBA AB
t aa
n aa
t ae
n ae
t ar
n ar
ak
20
3 在同一构件上两点间的速度及加速度的求法(基点法)
(1)基点法的实质 如果在平面图形上任取一点O'定义为基点,假想在基 点上固结一随基点O'平移的动系O'x'y',那么刚体平面运动 可以看成是随基点O'的平移和绕基点O'的转动这两部分运 动的合成。 y y'
例:图示曲柄滑块机构,求V3。
V3 =V3
P13
∞ P34 P13 P12 1 4 2
P24 ∞ P34
=V1
P13 =
P14 P13 ×l
×1
平移法:组成移动副两构件 的瞬心线可以垂直于导路线
P14
1
3 P23
随意平移。
12
(3)滑动兼滚动的高副机构(齿轮、凸轮机构)
例:已知各构件的尺寸、凸轮的角速度1,求推杆速度V2 。 V2= V2P12=V1P12= P12 P13 ×l ×1
VK2 K 2 2 P12 1 ( K2,K3) 3 3 P13 VK3
设:K代表P23,假设K不在P12、 P13连线上,根据瞬心定义:
VK2=VK3(同速点) 由图可知: VK2VK3 假设不成立(连起码的方向都不 可能一致),因而K不是瞬心,只 有在连线上才能保证同方向。
9
例:求图中机构所有的速度瞬心 解:1.瞬心数 K = 4(4-1)/2 = 6 2.直观法可得P12、P23、P34、P41。 3.三心定理法 实际上可以根据瞬心下标进行瞬心确定——下标消去法。
6 I
7
H 6 5 8 F J
5
E F
高副低代
8 E J 1 K O 9
G
D
3
4
B 2 A 10
D
3
4 B 2
A
11
C
1 O1 O 9
5
C
拆分基本杆组:
G
6
8 J E I
7
H
7 I G 5 E
H 6 8 F J
5
F
D
3
4 B 2 A 11
D
3
4 B 2 A 11 1 O1 O 9
O1
C
1 O 9
C
vC v pc
vCB v bc
b
vEB
e
vCB
vB
vE
c p
vC
28
(b)
ቤተ መጻሕፍቲ ባይዱ
解E点:
2
C
vE vB vEB
方向: ? 大小: ? ⊥AB ⊥EB lAB1 lEB2
1 A 4
2 B 1 1
2 E
3 3 3 D
在图(b)的基础上,过点b作
(a)
be = vEB/v ,得e点,则 vE=vpe 。
vB vA vBA
两类问题:
同一构件两点间 (刚体运动) a a a n a B A BA BA 两构件重合点间 r k (点的运动) aB 2 aB1 aB 2 B1 aB 2 B1
16
vB 2 vB1 vB 2 B1
知识回顾:
相对运动· 牵连运动· 绝对运动 用点的合成运动理论分析点的运动时,必须选定两个参 考系,区分三种运动: (1)动点相对于定参考系的运动,称为绝对运动; (2)动点相对于动参考系的运动,称为相对运动; (3)动参考系相对于定参考系的运动,称为牵连运动; (4)动点相对于定参考系的速度、加速度,称为动点的绝 对速度va、绝对加速度aa; (5)动点相对于动参考系的速度、加速度,称为动点的相 对速度vr、相对加速度ar; (6)在动参考系上与动点相重合的那一点(牵连点)的速度和 加速度称为动点的牵连速度ve和牵连加速度ae。
19
当牵连运动为平动时, e=0,因此ak=0,此时有
aa ae ar
当牵连运动为平动时,动点在某瞬时的绝对加速度等于该瞬 时它的牵连加速度与相对加速度的矢量和。
注意:选择1个动点;确定2组坐标系;区分3种运动。
选择动点和动系的原则:动点不能在动系上;动点相对动系 的轨迹明显,方向或大小易确定;动参考系可以无限大。
17
点的速度合成定理:动点在某一瞬时的绝对速度等于它在该瞬 时的牵连速度与相对速度的矢量和。
va ve vr
点的加速度合成定理:动点在某瞬时的绝对加速度等于该瞬 时它的牵连加速度、相对加速度与哥氏加速度的矢量和。
aa ae ar ak
其中:a
k
2e vr
,为哥氏加速度
3
2.速度瞬心的性质
1)两构件上相对速度为零的重合点VP1P2=0,且是瞬时的。
2 )当 VP1=VP2=0,称为绝对瞬心,即其中一构件为机架;相对 机架的绝对瞬时转动。 3)当VP1=VP2≠0,称为相对瞬心,即两构件均为活动构件;具 有相同绝对速度的重合点。
4)两构件之间的相对运动可视为绕速度瞬心的转动。 5)相对速度VP1P2=0,但相对加速度aP1P2≠0。 3. 机构中速度瞬心的数目
2 B 1 A 4 (a)
26
2 E
3 3 3 D
1 1
解:(1)取合适的长度比例尺l,根据原动件1的给定位置及 机构尺寸,准确作出机构运动简图,如图(a)所示。
(2)速度分析
C 2 2 B 1 A 4 (a) 1 1 2 E 3 3 3 D
vC vB vCB
方向:⊥CD ⊥AB 大小: ? lAB1 ⊥BC ?
24
问题: 1、图示四杆机构, 已知杆1的角速度, 求此瞬时杆件2、3的 角速度。
C
2
B
3
ω1
1
A
4
D
2、同一构件上,已知一点的速度和加速度,如何 求另一点的速度和加速度? 3、不同的两构件,有重合点,已知其中一个构件 重合点的速度和加速度,如何求另一构件重合点 的速度和加速度?
25
(2)速度图和加速度图: 例1: 在图a所示的铰链四杆机构中,已知各构件长度及原动 件1的位置、角速度1和角加速度1,求构件2和构件3的角速 度2和3、角加速度2和3,以及构件2上E点的速度E和加 速度aE。 C 2
II级机构
6
4.机构中速度瞬心位置的确定
(1)直观法—通过运动副直接
连接的两个构件
P12
1
2
2 3 1
结论:组成转动副的两构件 其速度瞬心在转动副中心 ∞ P12 1 2
移动副连接的两个构件
转动副连接的两个构件
4
结论:组成移动副的两构件其速度 瞬心在垂直于导路线的无穷远处
