九年级数学图形的全等1
九年级数学专题复习(图形的全等)

(1)基本作图。 ①作一条线段等于已知线段; ②作一个角等于已知角; ③平分已知角; ④经过一点作已知直线的垂线 ⑤作线段的垂直平分线。 (2)作图的基本步骤。 ①已知:写出已知的线段或角,并画出图形; ②求作:求作什么图形,它符合什么条件,一一写出; ③作法:应用“五种基本作图”叙述时不需要重述作图过程,
的一个作为结论,写出一个正确的命题,并加以证明。 A D
B
E
C
F
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF。 组合一:条件①②④,结论③。(根据S.S.S.)
组合二:条件①③④,结论②。(根据S.A.S.)
猜想探究题
例3(2005山西)如图3,正方形ABCD的边CD在正方形 ECGF的边CE上,连接BE、DG。 E A C D F
B
G
(1)观察猜想BE与DG之间的大小关系,并证明你的结
论;
(2)图中是否存在通过旋转能够互相重合的两个三角形? 若存在,请说明旋转过程;若不存在,请说明理由。
猜想探究题
例4(2005常州)如图4,已知△ABC为等边三角形,D、E、F分 别在边BC、CA、AB上,且△BCD也是等边三角形。 A E F B 猜想是正确的; (2)你所证明相等的线段,可以通过怎样的变化相互得到?写出变化 过程。 D C
根据A.A.S.添加条件∠BAE=BCD 根据A.S.A.添加∠BEA=∠BDC;
(2)根据你添加的条件,再写出图中的一对全等三角形, △DFA≌△EFC (只要求写一对全等三角形,不再添加 △DCA≌△EAC 其他线段,不再标住或使用其他字母,不必写出证明过程)
开放题
例2(2005扬州)如图2,在△ABC和△DEF中,B,E,C,F 在同一直线上,下面有四个条件,请你从中选三个作为题设,余下
教师资格证初中数学说课:图形的全等

想写好说课稿,那么就来看一看优秀的老师资格证说课稿吧。
以下(yǐxià)资讯由老师资格证考试网整理而出“老师资格证初中数学说课:图形的全等〞,希望对您有所帮助!?图形(túxíng)的全等?说课稿各位专家指导(lǐnɡ dǎo),上午好!今天我将要为大家讲的课题是:七年级下册第五章三角形中的第二节“图形的全等〞。
根据新的课程标准,我从以下七个方面(fāngmiàn)说一下,本节课的教学设想:一、教材(jiàocái)分析本节是学习三角形全等的起始课,又是学习平面图形关系的引言课,它隐含地指出义务教育阶段平面几何的研究对象是图形的形状和大小,即图形的全等和相似,把对称,平移和旋转作为研究平面几何的根本工具,把图形的分割与拼接作为研究平面几何的根本方法,在图形的拼接过程中浸透变与不变的思想。
二、学生情况七年级学生具有好奇心、求知欲强,互相评价互相提问的积极性高。
本节内容涉及的知识点不多,并且与前面的知识没有联络,知识的切入点比拟低,再加上学习过程中的动手操作活动,借助多媒体,精心设计问题串,让学生脑、嘴、手及脚充分动起来,学生既学得轻松又愉快,课堂气氛会相当活泼。
三、教学目的1、知识与才能目的:1理解图形全等的意义,2理解全等图形的性质,3掌握全等图形的判断方法。
2、情感态度、价值观提供适当的情景图片,吸引学生的注意力,激发学生的学习兴趣;在合作学习中,学会交流与合作;通过观察、动手实验,使学生体验到数学的思想方法及数学的应用价值。
3、教学重点理解图形的全等概念和特征4、教学难点认识全等图形的特征四、教学和学法让学生通过观察、分析、归纳得出全等图形的定义,通过小组合作交流总结出全等图形的性质,最后通过图形的剪拼加强理解全等图形的性质。
五、教学过程实录(一)创设情境,提出问题教师:同学(tóng xué)们,我国宋朝著名诗人苏轼写过一首赞美春天的诗,头一句是“竹外桃花三两枝〞,哪位同学能帮老师说下去?学生(xué sheng)答:略教师:老师这里有一张鸭子游泳图,请大家欣赏,你们(nǐ men)能发现其中的有趣现象吗?学生(xué sheng)答:略老师:接下来我们再来观察两组几何图片,看看其中的几何图形是否(shìfǒu)有类似的特征?学生答:略老师:我们在生活中,书本中见到的几何图形有的形状、大小完全一样;有的形状一样,大小不一样;有的大小一样,形状不一样;有的都不一样。
初中数学《图形的全等》经典习题

平面图形的认识试卷副标题1.命题①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短;⑤直线都相等;⑥任何数都有倒数;⑦如果a2=b2,那么a=b;⑧三角对应相等的两三角形全等;⑨如果∠A+∠B=90°,那么∠A与∠B互余.其中真命题有…()A. 3个B. 4个C. 5个D. 6个2.下列条件中能判定△ABC≌△DEF的是()A. AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠FC. AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF3.下列说法中不正确的是()A.全等三角形的周长相等B.全等三角形的面积相等C.全等三角形能重合D.全等三角形一定是等边三角形4.给出下列各命题:①有两边和它们的夹角对应相等的两个三角形一定全等;②有两边和一角对应相等的两个三角形一定全等;③有两条直角边对应相等的两个直角三角形一定全等;④有两条边分别相等的两个直角三角形一定全等;其中假命题共有()A. 1个B. 2个C. 3个D. 4个5.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是()A.∠BCA=∠F B.∠B=∠E C.BC∥EF D.∠A=∠EDF6.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是()A. 50 B. 62 C. 65 D. 687.如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有()A. 2对B. 3对C. 4对D. 5对8.下列不能判定三角形全等的是()A.如图(1),线段AD与BC相交于点O,AO=DO,BO=CO.△ABO与△BCOB.如图(2),AC=AD,BC=BD.△ABC与△ABDC.如图(3),∠A=∠C,∠B=∠D.△ABO与△CDOD.如图(4),线段AD与BC相交于点E,AE=BE,CE=DE,AC=BD.△ABC与△BAD 9.如图,AC=DF,∠ACB=∠DFE,点B、E、C在一条直线上,则下列条件中不能断定△ADC≌DEF的是()A.∠A=∠D B. BE=CF C. AB=DE D. AB∥DE10.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A. B. 4 C.D. 511.如图,已知△ACF≌△DBE,∠E=∠F,AD=9cm,BC=5cm,AB的长为cm.12.如图,在△ABC和△BAD中,若∠C=∠D,再添加一个条件,就可以判定△ABC≌△BAD 你添加的条件是.13.如图,已知AC=BD,则再添加条件,可证出△ABC≌△BAD.14.如图,已知∠ABC=∠DCB,现要说明△ABC≌△DCB,则还要补加一个条件是或或.15.如图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC= cm.16.如图,△ABC≌△EFC,CF=3cm,CE=4cm,∠F=36°,则BC= cm,∠B=度.17.如图,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是.18.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与对应;B与对应;C与对应;D与对应.19.如图EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有(填序号).20.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且AO平分∠BAC,那么图中全等三角形共有对.21.如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC(1)证明:△C′BD≌△B′DC;(2)证明:△AC′D≌△DB′A;(3)对△A BC、△ABC′、△BCA′、△CAB′,从面积大小关系上,你能得出什么结论?22.如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BF.23.如图,已知:△ABC中,∠ACB=90°,D为AC边上的一点,E为DB的中点,CE的延长线交AB于点F,FG∥BC交DB于点G.试说明:∠BFG=∠CGF.24.如图(1),A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.25.如图,两个全等的直角三角形△ABC和△A1B1C1中,∠ACB=∠A1C1B1=90°,两条相等的直角边AC,A1C1在同一直线上,A1B1与AB交于O,AB与B1C1交于E1,A1B1与BC交于E.(1)写出图中除△ABC≌△A1B1C1外的所有其它各组全等三角形(不再连线和标注字母);(2)求证:B1E1=BE.26.(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC=BC;②AD+AB=AC.请你证明结论②;(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.27.如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.28.用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论并证明你的结论;(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.29.已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.(1)求证:BF=AC;(2)求证:CE=BF;(3)CE与BG的大小关系如何?试证明你的结论.30.如图,AD=BC,请添加一个条件,使图中存在全等三角形并给予证明.你所添加的条件为:;得到的一对全等三角形是△≌△.参考答案1.B【解析】试题分析:根据邻补角互补,对顶角相等的性质,线段的性质,直线的性质,倒数的特殊规定,绝对值的选择性,全等三角形的判定,余角的定义对各小题分析判断后即可求解.解:①邻补角互补,正确;②对顶角相等,正确;③被截线不平行则同旁内角不互补,故本小题错误;④两点之间线段最短,是线段的性质,正确;⑤直线是向两方无限延伸的,没有长短,故本小题错误;⑥0没有倒数,故本小题错误;⑦如果a2=b2,那么a=b或a=﹣b,故本小题错误;⑧三角对应相等的两三角形相似但不一定全等,故本小题错误;⑨如果∠A+∠B=90°,那么∠A与∠B互余,是定义,正确.综上所述,真命题有①②④⑨共4个.故选B.考点:对顶角、邻补角;倒数;线段的性质:两点之间线段最短;全等三角形的判定.点评:本题是对基础知识的综合考查,熟记概念与性质是解题的关键.2.D【解析】试题分析:全等三角形的判定方法有:SAS,ASA,AAS,SSS,而SSA,AAA都不能判定两三角形全等,根据以上内容判断即可.解:A、根据AB=DE,BC=EF,∠A=∠D,不能判断△ABC≌△DEF,故本选项错误;B、根据∠A=∠D,∠B=∠E,∠C=∠F,不能判断△ABC≌△DEF,故本选项错误;C、根据AC=DF,∠B=∠F,AB=DE,不能判断△ABC≌△DEF,故本选项错误;D、∵在△ABC和△DEF中,∴△ABC≌△DEF(AAS),故本选项正确;故选D.考点:全等三角形的判定.点评:本题考查了全等三角形的判定的应用,题目比较好,但是一道比较容易出错的题目,全等三角形的判定方法有:SAS,ASA,AAS,SSS.3.D【解析】试题分析:根据全等三角形的性质得出AB=DE,AC=DF,BC=EF,即可判断A;根据全等三角形的性质得出△ABC和△DEF放在一起,能够完全重合,即可判断B、C;根据图形即可判断D.解:A、∵△ABC≌△DEF,∴AB=DE,AC=DF,BC=EF,∴AB+AC+BC=DE+DF+EF,故本选项错误;B、∵△ABC≌△DEF,即△ABC和△DEF放在一起,能够完全重合,即两三角形的面积相等,故本选项错误;C、∵△ABC≌△DEF,即△ABC和△DEF放在一起,能够完全重合,故本选项错误;D、如图△ABC和DEF不是等边三角形,但两三角形全等,故本选项正确;故选D.考点:全等三角形的性质.点评:本题考查了全等三角形的定义和性质的应用,能运用全等三角形的有关性质进行说理是解此题的关键,题目较好,但是一道比较容易出错的题目.4.B【解析】试题分析:根据三角形全等的判定方法即可解得,做题时要根据已知条件结合判定方法逐个验证.解:①符合SAS,成立;②SSA不符合三角形全等的条件;③符合SAS,是真命题;④没有对应相等不符合三角形全等的条件,是假命题.则正确的是①和③.故选B.考点:全等三角形的判定.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.5.B【解析】试题分析:全等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.解:A、根据AB=DE,BC=EF和∠BCA=∠F不能推出△ABC≌△DEF,故本选项错误;B、∵在△ABC和△DEF中,∴△ABC≌△DEF(SAS),故本选项正确;C、∵BC∥EF,∴∠F=∠BCA,根据AB=DE,BC=EF和∠F=∠BCA不能推出△ABC≌△DEF,故本选项错误;D、根据AB=DE,BC=EF和∠A=∠EDF不能推出△ABC≌△DEF,故本选项错误.故选B.考点:全等三角形的判定.点评:本题考查了对平行线的性质和全等三角形的判定的应用,注意:有两边对应相等,且这两边的夹角相等的两三角形才全等,题目比较典型,但是一道比较容易出错的题目.6.A【解析】试题分析:由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≌△ABG,所以AF=BG,AG=EF;同理证得△BGC≌△DHC,GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH⇒∠EAB=∠EFA=∠BGA=90°,∠EAF+∠BAG=90°,∠ABG+∠BAG=90°⇒∠EAF=∠ABG,∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG⇒△EFA≌△ABG∴AF=BG,AG=EF.同理证得△BGC≌△DHC得GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16故S=(6+4)×16﹣3×4﹣6×3=50.故选A.考点:全等三角形的判定与性质.点评:本题考查的是全等三角形的判定的相关知识.作辅助线是本题的关键.7.C【解析】试题分析:根据已知条件可以找出题目中有哪些相等的角以及线段,然后猜想可能全等的三角形,然后一一进行验证,做题时要由易到难,循序渐进.解:①△ODC≌△OEC∵BD⊥AO于点D,AE⊥OB于点E,OC平分∠AOB∴∠ODC=∠OEC=90°,∠1=∠2∵OC=OC∴△ODC≌△OEC(AAS)∴OE=OD,CD=CE;②△ADC≌△BEC∵∠CDA=∠CEB=90°,∠3=∠4,CD=CE∴△OBE≌△OCD(AAS)∴AC=BC,AD=BE,∠B=∠A;③△OAC≌△OBC∵OD=OE∴OA=OB∵OA=OB,OC=OC,AC=BC∴△ABO≌△ACO(SSS);④△OAE≌△OBD∵∠ODB=∠OEA=90°,OA=OB,OD=OE∴△AEC≌△ADB(HL).故选C.考点:全等三角形的判定.点评:本题考查了全等三角形的判定方法;全等三角形的判定方法一般有:AAS、SAS、ASA、SSS、HL.应该对每一种方法熟练掌握做到灵活运用,做题时要做到不重不漏.提出猜想,证明猜想是解决几何问题的基本方法.8.C【解析】试题分析:全等三角形的判定定理有:SAS、ASA、AAS、SSS,只要具备以上四种方法中的一种,即可判定联三角形全等.解:A、因为∠AOB=∠DOC,根据SAS可判断△ABO≌△DCO,故本选项错误;B、AB=AB,根据SSS可证出△ABC≌△ABD,故本选项错误;C、全等三角形的判定定理有SAS、ASA、AAS、SSS,根据已知不能得出以上三个条件,即两三角形不全等,故本选项正确;D、∵AE=BE,CE=DE,∴AD=BC,∵AB=AB,AC=BD,根据SSS可证出△ABC≌△BAD,故本选项错误.故选C.考点:全等三角形的判定.点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定有:SAS、ASA、AAS、SSS,题型较好,但是一道比较容易出错的题目.9.C【解析】试题分析:根据全等三角形的判定ASA推出三角形全等,即可判断A;求出BC=EF,根据SAS 即可判断B;根据有两边和其中一边的对角相等不能判断两三角形全等,即可判断C;根据平行线性质推出∠B=∠DEF,根据AAS即可判断D.解:A、在△ABC和△DEF中,∴△ABC≌△DEF,故本选项错误;B、∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,∴△ABC≌△DEF,故本选项错误;C、根据AB=DE,∠ACB=∠DFE,AC=DF,不能判定△ABC和△DEF全等,故本选项正确;D、∵AB∥DE,∴∠B=∠DEF,在△ABC和△DEF中,∴△ABC≌△DEF,故本选项错误;故选C.考点:全等三角形的判定;平行线的性质.点评:本题考查了平行线性质和全等三角形的判定的应用,熟练地运用定理进行推理是解此题的关键,题目比较好,难度适中.10.B【解析】试题分析:由∠ABC=45°,AD是高,得出BD=AD后,证△ADC≌△BDH后求解.解:∵∠ABC=45°,AD⊥BC,∴AD=BD,∠ADC=∠BDH,∵∠AHE+∠DAC=90°,∠AHE+∠C=90°,∴∠AHE=∠BHD=∠C,∴△ADC≌△BDH,∴BH=AC=4.故选B.考点:全等三角形的判定与性质.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.由∠ABC=45°,AD是高,得出BD=AD是正确解答本题的关键.11.2【解析】试题分析:AB不是全等三角形的对应边,但它通过全等三角形的对应边转化为AB=CD,而使AB+CD=AD﹣BC可利用已知的AD与BC求得.解:∵△ACF≌△DBE,∠E=∠F,∴CA=BD,∴CA﹣BC=DB﹣BC,即AB=CD,∴AB+CD=2AB=AD﹣BC=9﹣5=4(cm),∴AB=2(cm).故填2.考点:全等三角形的性质.点评:本题主要考查了全等三角形的对应边相等.难点在于根据图形得到线段AB=CD,也是解决本题的关键.12.∠DAB=∠CBA(答案不唯一)【解析】试题分析:由图可知,AB是公共边,然后根据全等三角形的判定方法选择添加不同的条件即可.解:∵∠C=∠D,AB是公共边,∴可添加∠DAB=∠CBA或∠DBA=∠CAB,故答案为:∠DAB=∠CBA(答案不唯一).考点:全等三角形的判定.点评:本题考查了全等三角形的判定,根据∠D、∠C是公共边AB的对角,只能选择利用“角角边”证明两三角形全等添加条件.13.∠CAB=∠DBA@BC=AD【解析】试题分析:本题要判定△ABC≌△ADC,已知AC=BD,AB是公共边,具备了两组边对应相等,故添加BC=AD、∠CAB=∠DBA,后可分别根据SSS、SAS、能判定△ABC≌△ADC.解:AC=BD,AB是公共边,加∠CAB=∠DBA,就可以用SAS证出△ABC≌△BAD;加BC=AD就可以用SSS证出△ABC≌△BAD.故填∠CAB=∠DBA@BC=AD.考点:全等三角形的判定.点评:本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.14.∠A=∠D AB=CD ∠ACB=∠DBC【解析】试题分析:要证明△ABC≌△DCB,已知∠ABC=∠DCB,且有一个公共边BC=BC,则可以添加一组角从而利用AAS、ASA判定其全等;添加边从而利用SAS判定其全等.解:补充∠A=∠D.∵∠ABC=∠DCB,BC=BC,∠A=∠D∴△ABC≌△DCB(AAS)补充∠ACB=∠DBC.∵∠ABC=∠DCB,BC=BC,∠ACB=∠DBC∴△ABC≌△DCB(ASA)补充AB=CD.∵∠ABC=∠DCB,AB=CD,BC=BC∴△ABC≌△DCB(SAS).∴故填∠A=∠D或AB=CD或∠ACB=∠DBC.考点:全等三角形的判定.点评:题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.15.10【解析】试题分析:根据△DEF周长是32cm,DE=9cm,EF=13cm就可求出第三边DF的长,根据全等三角形的对应边相等,即可求得AC的长.解:DF=32﹣DE﹣EF=10cm.∵△ABC≌△DEF,∠E=∠B,∴AC=DF=10cm.考点:全等三角形的性质.点评:本题考查全等三角形的性质,解题时应注重识别全等三角形中的对应边,要根据对应角去找对应边.16.3 36【解析】试题分析:运用“全等三角形的对应边相等,对应角相等”即可得,做题时要根据△ABC≌△EFC找对对应边.解:∵△ABC≌△EFC,CF=3cm,∠F=36,∴BC的对应边是CF,∠B的对应角是∠F,∴BC=FC=3cm,∠B=∠F=36°.故填3,36.考点:全等三角形的性质.点评:本题考查了全等三角形的性质及对应关系的找法;全等三角形书写时各对应顶点应在同一位置,找准对应关系是解决本题的关键.17.【解析】试题分析:根据图形得出当有1点D时,有1对全等三角形;当有2点D、E时,有3对全等三角形;当有3点D、E、F时,有6对全等三角形;根据以上结果得出当有n个点时,图中有个全等三角形即可.解:当有1点D时,有1对全等三角形;当有2点D、E时,有3对全等三角形;当有3点D、E、F时,有6对全等三角形;当有4点时,有10个全等三角形;…当有n个点时,图中有个全等三角形.故答案为:.考点:全等三角形的判定.点评:本题考查了对全等三角形的应用,关键是根据已知图形得出规律,题目比较典型,但有一定的难度.18.M N Q P【解析】试题分析:能够完全重合的两个图形叫做全等形.按照剪开前后各基本图形是重合的原则进行逐个验证、排查.解:由全等形的概念可知:A是三个三角形,与M对应;B是一个三角形和两个直角梯形,与N对应;C是一个三角形和两个四边形,与Q对应;D是两个三角形和一个四边形,与P对应故分别填入M,N,Q,P.考点:全等图形.点评:本题考查的是全等形的识别,注意辩别组成图形的基础图形的形状.19.①②③【解析】试题分析:由已知条件,可直接得到三角形全等,得到结论,采用排除法,对各个选项进行验证从而确定正确的结论.解:∵∠B+∠BAE=90°,∠C+∠CAF=90°,∠B=∠C∴∠1=∠2(①正确)∵∠E=∠F=90°,∠B=∠C,AE=AF∴△ABE≌△ACF(ASA)∴AB=AC,BE=CF(②正确)∵∠CAN=∠BAM,∠B=∠C,AB=AC∴△ACN≌△ABM(③正确)∴CN=BM(④不正确).所以正确结论有①②③.故填①②③.考点:全等三角形的判定.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.得到三角形全等是正确解决本题的关键.20.4【解析】试题分析:根据已知条件可以找出题目中有哪些相等的角以及线段,然后猜想可能全等的三角形,然后一一进行验证.解:∵CD⊥AB,BE⊥AC,垂足分别为D、E,且AO平分∠BAC,∴△ODA≌△OEA,∴∠B=∠C,AD=AE,∴△ADC≌△AEB,∴AB=AC,∴△OAC≌△OAB,∴△COE≌△OBD.故填4.考点:全等三角形的判定.点评:本题考查了三角形全等的判定方法;提出猜想,验证猜想是解决几何问题的基本方法,做题时要注意从已知条件开始思考结合全等的判定方法逐一判断,做到不重不漏,由易到难.21.(1)先证明:△C′BD≌△ABC,再证明△ABC≌△B′DC;(2)根据(1)的结论,可以证明:△AC′D≌△DB′A;(3)由角的不等,导出边的不等关系,这是探索面积不等关系的关键.【解析】试题分析:(1)先证明:△C′BD≌△ABC,再证明△ABC≌△B′DC;(2)根据(1)的结论,可以证明:△AC′D≌△DB′A;(3)由角的不等,导出边的不等关系,这是探索面积不等关系的关键.(1)△C′BD与△ABC中,BC=DC,AB=BC′,∠C′BD=60°+∠ABD=∠ABC,∴△C′BD≌△ABC,∴C′D=AC又在△BCA与△DCB′中,BC=DC,AC=B′C,∠ACB=∠B′CD=60°,∴△BCA≌△DCB′.∴DB′=BA.∴△C′BD≌△B′DC(2)由(1)的结论知:C′D=B′C=AB′,B′D=BC′=AC′,又∵AD=AD,∴△AC′D≌△DB′A.(3)S△AB′C>S△ABC′>S△ABC>S△A′BC;S△AB′C=,S△A′BC=,S△ABC′=,S△ABC=,因为AB2=(AC2+BC2﹣2AC×BC×cos60°)整理得S△ACB′+S△BCA′=S△ABC′+S△ABC考点:全等三角形的判定;三角形的面积.点评:考查全等三角形的证明,考查在三角形中,已知两边和夹角求第三边的计算.22.有两种解法:①延长AD至点M,使MD=FD,连接MC,则可证△BDF≌△CDM(SAS),可得MC=BF,∠M=∠BFM,再得∠M=∠MAC,得AC=MC=BF.②延长AD至点M,使DM=AD,连接BM,可证△ADC≌△MDB(SAS),方法与①相同.【解析】试题分析:有两种解法:①延长AD至点M,使MD=FD,连接MC,则可证△BDF≌△CDM(SAS),可得MC=BF,∠M=∠BFM,再得∠M=∠MAC,得AC=MC=BF.②延长AD至点M,使DM=AD,连接BM,可证△ADC≌△MDB(SAS),方法与①相同.证明:方法一:延长AD至点M,使MD=FD,连接MC,在△BDF和△CDM中,∴△BDF≌△CDM(SAS).∴MC=BF,∠M=∠BFM.∵EA=EF,∴∠EAF=∠EFA,∵∠AFE=∠BFM,∴∠M=∠MAC,∴AC=MC,∴BF=AC;方法二:延长AD至点M,使DM=AD,连接BM,在△ADC和△MDB中,,∴△ADC≌△MDB(SAS),∴∠M=∠MAC,BM=AC,∵EA=EF,∴∠CAM=∠AFE,而∠AFE=∠BFM,∴∠M=∠BFM,∴BM=BF,∴BF=AC.考点:全等三角形的判定与性质.点评:本题考查了三角形全等的判定及性质、等腰三角形的性质.其中普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,解决此题的关键是作出巧妙的辅助线:倍长中线.23.本题首先通过∠ACB=90°,E为DB的中点,进而得到CE=EB=DE,又因为FG∥BC,则可证明△GEC≌△FEB,再通过角与角之间的关系求得∠BFG=∠CGF.【解析】试题分析:本题首先通过∠ACB=90°,E为DB的中点,进而得到CE=EB=DE,又因为FG∥BC,则可证明△GEC≌△FEB,再通过角与角之间的关系求得∠BFG=∠CGF.证明:∵∠ACB=90°,E为DB的中点,∴CE=DE=BE,(直角三角形斜边上的中线等于斜边一半)∴CE=EB,∴∠ECB=∠CBE,∵FG∥BC,∴∠GFE=∠ECB,∠EGF=∠CBE∴∠EGF=∠EFG,∴GE=EF,∵∠GEC=∠FEB,∴△GEC≌△FEB,∴∠EFB=∠EGC,∵∠BFG=∠EFB+∠EFG,∠CGF=∠EGC+∠EGF,∴∠BFG=∠CGF.考点:全等三角形的判定与性质.点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.24.(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DGE,从而得出FG=EG,即BD平分EF.(2)结论仍然成立,同样可以证明得到.【解析】(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DGE,试题分析:从而得出FG=EG,即BD平分EF.(2)结论仍然成立,同样可以证明得到.(1)证明:∵DE⊥AC,BF⊥AC,∴∠DEG=∠BFE=90°.∵AE=CF,AE+EF=CF+EF.即AF=CE.在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.在△BFG和△DEG中,∴△BFG≌△DGE(AAS),∴FG=EG,即BD平分EF.(2)FG=EG,即BD平分EF的结论依然成立.理由:因为 AE=CF,所以 AF=CE,因为 DE垂直于AC,BF垂直于AC,所以角AFB=角CED,BF∥DE,因为AB∥CD,所以角A=角C,所以三角形ABF全等于三角形CDE,所以 BF=DE,所以四边形BEDF是平行四边形,所以 GE=GF,即:BD平分EF,即结论依然成立.考点:全等三角形的判定与性质.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.25.(1)根据全等三角形的判定:三组对应边分别相等的两个三角形全等(简称SSS);有两边及其夹角对应相等的两个三角形全等(SAS);有两角及其夹边对应相等的两个三角形全等(ASA)可证得;(2)由1可证得△ACE≌△A1C1E1,可推出CE=C1E1,易证B1E1=BE.【解析】试题分析:(1)根据全等三角形的判定:三组对应边分别相等的两个三角形全等(简称SSS);有两边及其夹角对应相等的两个三角形全等(SAS);有两角及其夹边对应相等的两个三角形全等(ASA)可证得;(2)由1可证得△ACE≌△A1C1E1,可推出CE=C1E1,易证B1E1=BE.(1)解:△ACE≌△A1C1E1,△OBE≌△O1B1E1;(2)证明:∵△ABC≌△A1B1C1∴AC=A1C1,BC=B1C1∴AC1=A1C已知∠A=∠A1,∠ACE=∠A1C1E1=90°∴△ACE≌△A1C1E1∴CE=C1E1又∵BC=B1C1∴B1E1=BE.考点:全等三角形的判定与性质.点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.26.(1)根据角平分线的性质可得∠DAC=∠BAC=60°,又已知∠ABC=∠ADC=90°,所以∠DCA=∠BCA=30°,根据直角三角形的性质可证AC=2AD,AC=2AB,所以AD+AB=AC.(2)根据已知条件可在AN上截取AE=AC,连接CE,根据AAS可证△ADC≌△EBC,得到DC=BC,DA=BE,所以AD+AB=AB+BE=AE,即AD+AB=AC.【解析】试题分析:(1)根据角平分线的性质可得∠DAC=∠BAC=60°,又已知∠ABC=∠ADC=90°,所以∠DCA=∠BCA=30°,根据直角三角形的性质可证AC=2AD,AC=2AB,所以AD+AB=AC.(2)根据已知条件可在AN上截取AE=AC,连接CE,根据AAS可证△ADC≌△EBC,得到DC=BC,DA=BE,所以AD+AB=AB+BE=AE,即AD+AB=AC.证明:(1)如图1∵∠MAN=120°,AC平分∠MAN,∴∠DAC=∠BAC=60°,∵∠ABC=∠ADC=90°,∴∠DCA=∠BCA=30°,∵在Rt△ACD中,∠DCA=30°,Rt△ACB中,∠BCA=30°,∴AC=2AD,AC=2AB,∴AD+AB=AC.(2)判断是:(1)中的结论①DC=BC;②AD+AB=AC都成立.理由如下:如下图,在AN上截取AE=AC,连接CE,∵∠BAC=60°,∴△CAE为等边三角形,∴AC=CE,∠AEC=60°,∵∠DAC=60°,∴∠DAC=∠AEC∵∠ABC+∠ADC=180°,∠ABC+∠EBC=180°,∴∠ADC=∠EBC,∴△ADC≌△EBC,∴DC=BC,DA=BE,∴AD+AB=AB+BE=AE,∴AD+AB=AC.考点:全等三角形的判定与性质;角平分线的定义;三角形内角和定理.点评:本题考查了角平分线的性质,直角三角形的性质,和全等三角形的判定等知识综合运用,是一道由浅入深的训练题.27.根据已知,利用有两组角对应相等的两个三角形相似得到△AEF∽△DCF,从而得到∠E=∠C,再由已知可得∠BAC=∠DAE,又因为AC=AE,所以根据AAS可判定△ABC≌△ADE.【解析】试题分析:根据已知,利用有两组角对应相等的两个三角形相似得到△AEF∽△DCF,从而得到∠E=∠C,再由已知可得∠BAC=∠DAE,又因为AC=AE,所以根据AAS可判定△ABC≌△ADE.解:△ADF与△AEF中,∵∠2=∠3,∠AFE=∠CFD,∴∠E=∠C.∵∠1=∠2,∴∠BAC=∠DAE.∵AC=AE,∴△ABC≌△ADE.考点:全等三角形的判定.点评:此题考查学生对相似三角形的判定及全等三角形的判定的理解及运用.三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.28.应先确定选择哪对三角形,再对应三角形全等条件求解.【解析】试题分析:本题是一道开放性题,应先确定选择哪对三角形,再对应三角形全等条件求解.解:(1)BE=CF.证明:在△ABE和△ACF中,∵∠BAE+∠EAC=∠CAF+∠EAC=60°,∴∠BAE=∠CAF.∵AB=AC,∠B=∠ACF=60°,∴△ABE≌△ACF(ASA).∴BE=CF;(2)BE=CF仍然成立.证明:在△ACE和△ADF中,∵∠CAE+∠EAD=∠FAD+∠DAE=60°,∴∠CAE=∠DAF,∵∠BCA=∠ACD=60°,∴∠FCE=60°,∴∠ACE=120°,∵∠ADC=60°,∴∠ADF=120°,在△ACE和△ADF中,∴△ACE≌△ADF,∴CE=DF,∴BE=CF,考点:全等三角形的判定.点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.29.(1)利用AAS判定Rt△DFB≌Rt△DAC,从而得出BF=AC.(2)利用ASA判定Rt△BEA≌Rt△BEC,得出CE=AE=AC,又因为BF=AC所以CE=AC=BF(3)利用等腰三角形“三线合一”)和勾股定理即可求解.【解析】试题分析:(1)利用AAS判定Rt△DFB≌Rt△DAC,从而得出BF=AC.(2)利用ASA判定Rt△BEA≌Rt△BEC,得出CE=AE=AC,又因为BF=AC所以CE=AC=BF(3)利用等腰三角形“三线合一”)和勾股定理即可求解.(1)证明:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.在Rt△DFB和Rt△DAC中,∵∴Rt△DFB≌Rt△DAC(ASA).∴BF=AC;(2)证明:∵BE平分∠ABC,∴∠ABE=∠CBE.在Rt△BEA和Rt△BEC中,∴Rt△BEA≌Rt△BEC(ASA).∴CE=AE=AC.又由(1),知BF=AC,∴CE=AC=BF;(3)证明:∠ABC=45°,CD垂直AB于D,则CD=BD.H为BC中点,则DH⊥BC(等腰三角形“三线合一”)连接CG,则BG=CG,∠GCB=∠GBC=∠ABC=×45°=22.5°,∠EGC=45°.又∵BE垂直AC,故∠EGC=∠ECG=45°,CE=GE.∵△GEC是直角三角形,∴CE2+GE2=CG2,∵DH垂直平分BC,。
初三数学全等图形判定方法

初三数学全等图形判定方法全等图形是初中数学中的重要概念,它在实际生活和几何学中具有广泛的应用。
全等图形的判定方法则是我们学习的重点之一。
本文将介绍几种常用的初三数学全等图形判定方法,帮助同学们深入理解和掌握这一内容。
一、SAS判定法SAS判定法是指两个三角形的边、角和边对应相等时,这两个三角形全等。
具体判定步骤如下:1. 比较两个三角形的两边是否相等,如果两个三角形的两边相等,则条件一成立。
2. 比较两个三角形的夹角是否相等,如果两个三角形的夹角相等,则条件二成立。
3. 比较两个三角形的另一边是否相等,如果两个三角形的另一边相等,则条件三成立。
如果以上三个条件同时满足,那么可以判断这两个三角形全等。
需要注意的是,SAS判定法判断的是两个三角形全等,而不是其他图形的全等。
二、SSS判定法SSS判定法是指两个三角形的三边长度相等时,这两个三角形全等。
具体判定步骤如下:1. 比较两个三角形的第一条边是否相等,如果两个三角形的第一条边相等,则条件一成立。
2. 比较两个三角形的第二条边是否相等,如果两个三角形的第二条边相等,则条件二成立。
3. 比较两个三角形的第三条边是否相等,如果两个三角形的第三条边相等,则条件三成立。
如果以上三个条件同时满足,那么可以判断这两个三角形全等。
三、ASA判定法ASA判定法是指两个三角形的两角和一边分别相等时,这两个三角形全等。
具体判定步骤如下:1. 比较两个三角形的第一角是否相等,如果两个三角形的第一角相等,则条件一成立。
2. 比较两个三角形的第二角是否相等,如果两个三角形的第二角相等,则条件二成立。
3. 比较两个三角形的一边是否相等,如果两个三角形的一边相等,则条件三成立。
如果以上三个条件同时满足,那么可以判断这两个三角形全等。
四、其他判定法除了SAS、SSS和ASA判定法之外,还有一些其他的判定法,比如AAS判定法、RHS判定法等。
这些判定法都是通过特定的条件来判断两个三角形是否全等,同学们可以根据具体题目的条件选择合适的判定法进行判断。
初三数学全等图形判定方法详解

初三数学全等图形判定方法详解全等图形是初中数学中一个非常重要的概念,在几何学中有着广泛的应用。
它不仅有助于我们理解和解决各种几何问题,还可以帮助我们培养逻辑思维和观察问题的能力。
本文将详细介绍初三数学中全等图形的判定方法。
全等图形定义:两个图形,如果形状、大小、内部结构完全相同,即每一边和每一角都一一对应相等,则这两个图形称为全等图形。
判定全等图形的方法主要有以下几种:1. SSS判定法(边边边相等法):如果两个三角形的三条边分别相等,则这两个三角形全等。
2. SAS判定法(边角边相等法):如果两个三角形中有两个边与夹角相等,且这两个边之间的夹角也相等,则这两个三角形全等。
3. ASA判定法(角边角相等法):如果两个三角形中有两个角相等,且这两个角之间的边长也相等,则这两个三角形全等。
4. RHS判定法(直角边边相等法):如果两个直角三角形中,两个直角的边长相等,且一边的长度也相等,则这两个直角三角形全等。
5. SAA判定法(边角角相等法):如果两个三角形中有对应的两边与一个角相等,则这两个三角形可能全等,但需要进一步判断其他对应边长是否相等。
通过上述全等图形的判定方法,我们可以在解决几何问题时快速判断两个图形是否全等。
下面通过几个例题来进一步说明判定方法的应用。
例题1:已知△ABC,CE⊥AB,且CE=BC,证明△ABC全等于△BCE。
解析:首先,根据题意可得AC⊥EB,AE⊥BC,且∠ACB=∠BCE。
根据RHS判定法可知,AC=BC,∠ACB=∠BCE,AB=BE。
根据ASA判定法,可以判定△ABC全等于△BCE。
例题2:已知两个平行四边形ABCD和EFGH,且AB=EF,AD=EG,证明平行四边形ABCD全等于平行四边形EFGH。
解析:首先,可以通过移动平行四边形ABCD使得AB与EF重合,并且以D为起点,将平行四边形ABCD移动到平行四边形EFGH的位置。
这样就得到了以DFA'H为顶点的四边形,根据RHS判定法可知,∠DAF=∠EA'F,AD=EA',AD⊥AC,DF⊥EA',且两组对边平行。
直角三角形的全等判定

直角三角形的全等判定 The following text is amended on 12 November 2020.ADC P BE O A DPBEO直角三角形的全等判定(2)九年级数学备课组 课型:新授【学习目标】运用直角三角形的全等判定定理和其它相关知识的证明角平分线的性质和判定。
【重点、难点】1、角平分线的性质和判定。
2、角平分线的性质和判定的证明和运用。
【预习指导】我们已经学习过有关直角三角形全等的判定方法,请你写出这些定理。
直角三角形全等的判定定理: 【典例分析】 1、证明:已知,OC 是∠AOB 的平分线,点P 在OC 上PD ⊥OA ,PE ⊥OB ,垂足分别为D 、E ,求证:PD=PE2、证明:在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
已知,如图,PD ⊥OA ,PE ⊥OB ,垂足分别为D 、E ,且PD=PE ,求证:点P 在∠AOB 的平分线上。
(1、学生分析证明思路 2、学生自己完成证明过程) 小结:证明一条线是某一个角的平分线的常用方法:OEDCBA(1)证明这条线把某一个角分成的两个角相等(全等) (2)利用角平分线的逆定理。
归纳:两个定理引导学生进一步认识图形的位置关系与数量关系的内在联系:知道角平分线,想到过该线上某一点向角的两边引垂线;知道某点到角的两边距离相等,想到角平分线逆定理。
【思考与交流】1、“如果一个点到角的两边的距离不相等,那么这个点不在这个角的平分线上。
”你认为这个结论正确吗如果正确,你能证明吗(反证法)2、如图,△ABC 的角平分线AD 、BE 相交于点O ,点O 到△ABC 各边的距离相等吗点O 在∠C 的平分线上吗定理:三角形的3条角平分线交于一点,且这点到三角形三边的距离相等。
【典题选讲】例1、在平面内找一个点到三角形三边距离相等,这样的点有几个,并做出来。
变式:如图,直线PQ 、MN 、GH 表示3条公路,它们分别交于A 、B 、C 点。
九年级数学图形的全等1

当我到了三号队的工作面,抬头看工作面上空顶大约有五六米高的空顶,简直看到的就是冒顶,井下形成了一个大礼堂!空顶下一大堆的石头和煤,我们煤矿工人统称叫货,下边压着一位叫张龙的 年轻工人,是个带班班长,其余的两位工人因为跑的快,受点轻伤,被人及时救出!
。 心理咨询师培训 /course/all/3-19/
煤矿工作的日子-矿井历险记2020-2-28 20:28 上传
这着实给我一个下马威,因为如果我们五人,开始从风井进入到达主井的时间再晚一会,这事故我们可能就赶上了,因为这起事故,就在我们主井下到底转过片盘的时间里发生的!
因此我后来对煤矿的工作,尤其注重安全生产,有一次我后半夜查岗,一个人入井,检查生产和安全,工人突然后半夜,在井下看到我,都吃惊的问:“王矿长,你都几点睡觉啊?”即使我这样严 格要求,也很难避免一些事故的发生!好在我工作期间,虽然经历危险无数,但没有发生重大的人身安全事故!
九四年底,12月15日清晨,大约六点钟,煤矿的司机鲁学义,突然电话打到我家里,我从梦中惊醒!小鲁声音很急,说矿井发生冒顶了!冒顶就是塌方的意思,他开车已经到我家门口了!我二话不 说,立刻起身穿衣,在部队已经养成了紧急集合的速度了!冲出门,上了小鲁的车奔煤矿飞去!
旋转中的三种全等模型(手拉手、半角、对角互补模型)—2023-2024学年九年级数学上册(解析版)
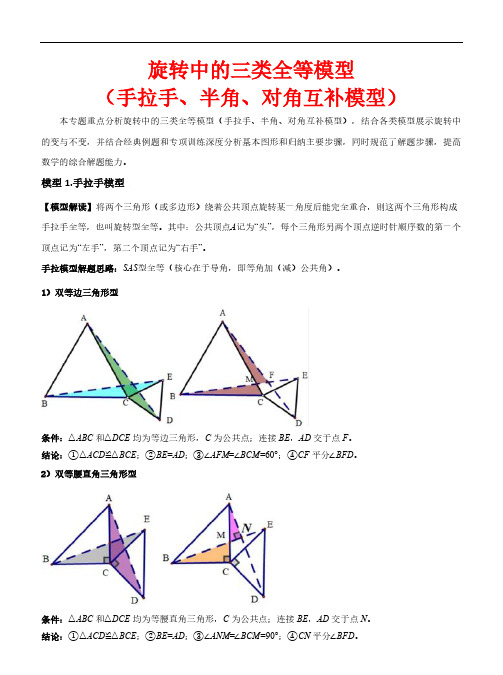
旋转中的三类全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BFD。
3)双等腰三角形型条件:△ABC和△DCE均为等腰三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠ACM=∠BFM;④CF平分∠BFD。
4)双正方形形型条件:△ABCFD和△CEFG都是正方形,C为公共点;连接BG,ED交于点N。
结论:①△△BCG≌△DCE;②BG=DE;③∠BCM=∠DNM=90°;④CN平分∠BNE。
【答案】(1)40;(2)60;(3)【分析】(1)证明△COD是等边三角形,得到∠ODC=60°,即可得到答案;∠=∠ADC-∠ODC求出答案;(3)由△BOC≌△ADC,推出∠ADC=∠BOC=150°,AD=OB=8,根据(2)利用ODA△COD 是等边三角形,得到∠ODC=60°,OD=4OC =,证得△AOD 是直角三角形,利用勾股定理求出.【详解】(1)解:∵CO=CD ,∠OCD=60°,∴△COD 是等边三角形;∴∠ODC=60°,∵∠ADC=∠BOC=100α=︒,∴ODA ∠=∠ADC -∠ODC=40°,故答案为:40;(2)∵∠ADC=∠BOC=120α=︒,∴ODA ∠=∠ADC -∠ODC=60°,故答案为:60;(3)解:当150α=︒,即∠BOC=150°,∴△AOD 是直角三角形.∵△BOC ≌△ADC ,∴∠ADC=∠BOC=150°,AD=OB=8,又∵△COD 是等边三角形,∴∠ODC=60°,OD=4OC =,∴∠ADO=90°,即△AOD 是直角三角形,∴OA =故答案为:【点睛】本题以“空间与图形”中的核心知识(如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进.试题中几何演绎推理的难度适宜,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等),能较好地考查学生的推理、探究及解决问题的能力. 备用图【答案】(1)△BEF 是等边三角形(2)证明见解析(3)131−【分析】(1)根据旋转即可证明△BEF 是等边三角形;(2)由△EBF 是等边三角形,可得FB=EB ,再证明∠FBA=∠EBC ,又因为AB=BC ,所以可证明△FBA ≌△EBC ,进而可得AF=CE ;(3)当点D ,E ,F 在同一直线上时,过B 作BM ⊥EF 于M ,再在Rt △BMD 中利用勾股定理列方程求解即可.(1)∵将线段EB 绕点E 顺时针旋转60°得到线段EF ,∴EB=EF ,60FEB =︒∠∴△BEF 是等边三角形(2)∵等边△ABC 和△BEF ∴BF=BE ,AB=BC ,60EBF ABC ∠=∠=︒∴EBF ABE ABC ABE ∠+∠=∠+∠即∠FBA=∠EBC∴△FBA ≌△EBC (SAS )∴AF=CE(3)图形如图所示:过B 作BM ⊥EF 于M ,∵△BEF 是等边三角形∴2BE EM =,BM =∵点D 是AB 的中点,∴142BD AB == 在Rt △BMD 中,222BM DM BD +=∵DE=2∴222)(2)4EM ++=解得EM 或EM =(舍去)∴21BE EM == 【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理的运用,旋转的性质,等边三角形的判定和性质,解一元二次方程,利用手拉手模型构造全等三角形是解题的关键.例3.(2022·吉林·九年级期末)如图①,在ABC 中,90C ∠=︒,AC BC ==点D ,E 分别在边AC ,BC 上,且CD CE =AD BE =,AD BE ⊥成立.(1)将CDE △绕点C 逆时针旋转90︒时,在图②中补充图形,并直接写出BE 的长度;(2)当CDE △绕点C 逆时针旋转一周的过程中,AD 与BE 的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)将CDE △绕点C 逆时针旋转一周的过程中,当A ,D ,E 三点在同一条直线上时,请直接写出AD 的长度.【答案】(1)补充图形见解析;BE =(2)AD BE =,AD BE ⊥仍然成立,证明见解析;(3)1AD或1=AD .【分析】(1)根据旋转作图的方法作图,再根据勾股定理求出BE 的长即可;(2)根据SAS 证明E ACD BC ≅∆∆得AD=BE ,∠1=∠2,再根据∠1+∠3+∠4=90°得∠2∠3+∠4=90°,从而可得出结论;(3)分两种情况,运用勾股定理求解即可.【详解】解:(1)如图所示,根据题意得,点D 在BC 上,∴BCE ∆是直角三角形,且由勾股定理得,BE ==(2)AD BE =,AD BE ⊥仍然成立. 证明:延长AD 交BE 于点H ,∵90ACB DCE ∠=∠=︒,ACD ACB BCD ∠=∠−∠,BCE DCE BCD ∠=∠−∠,∴ACD BCE ∠=∠,又∵CD CE =,AC BC =,∴ACD BCE ≅△△,∴AD BE =,12∠=∠,在Rt ABC 中,13490∠+∠+∠=︒,∴23490∠+∠+∠=︒,∴90AHB ∠=︒,∴AD BE ⊥.(3)①当点D 在AC 上方时,如图1所示,同(2)可得ACD BCE ≅△△∴AD=BE 同理可证BE AE ⊥在Rt △CDE 中,CD CE =2=在Rt △ACB 中,AC BC =AB ==设AD=BE=x ,在Rt △ABE 中,222BE AE AB +=∴222(2)x x ++=解得,1x ∴ 1AD =②当点D 在AC 下方时,如图2所示,同(2)可得ACD BCE ≅△△∴AD=BE 同理可证BE AE ⊥在Rt △CDE 中,CD CE =2=在Rt △ACB 中,AC BC =AB ==设AD=BE=x ,在Rt △ABE 中,222BE AE AB +=∴222(2)x x +−=解得,x = ∴ 1AD .所以,AD 1【点睛】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识,熟练解答本题的关键.例4.(2022·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B ,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD2+DB2=2DF2 ;(2)CD2+DB2=2DF2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF ∆≅∆得CD=BE ,再证明BDE ∆为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF ∆≅∆得CD=BE ,再证明BDE ∆为直角三角形,由勾股定理可得结论.【详解】解:(1)CD2+DB2=2DF2证明:∵DF=EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF =连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =, CF AB ⊥,即90CFB ∠=︒ ∴45FCB FBC ∠=∠=︒,90CFD DFB ∠+∠=︒又90DFB EFB ∠+∠=︒ ∴CFD EFB ∠=∠在CFD ∆和BFE ∆中CF BF CFD BFE DF EF =⎧⎪∠=∠⎨⎪=⎩ ∴CFD ∆≅BFE ∆∴CD BE =,45EBF FCB ∠=∠=︒ ∴454590DBF EBF ∠+∠=︒+︒=︒ ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD2+DB2=2DF2 ;(2)CD2+DB2=2DF2 证明:连接BE∵CF=BF ,DF=EF 又∵∠DFC+∠CFE=∠EFB+∠CFB=90°∴∠DFC=∠EFB ∴△DFC ≌△EFB ∴CD=BE ,∠DCF=∠EBF=135°∵∠EBD=∠EBF -∠FBD=135°-45°=90° 在Rt △DBE 中,BE2+DB2=DE2∵ DE2=2DF2 ∴ CD2+DB2=2DF2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例5.(2022·山西大同·九年级期中)综合与实践:已知ABC 是等腰三角形,AB AC =.(1)特殊情形:如图1,当DE ∥BC 时,DB ______EC .(填“>”“<”或“=”);(2)发现结论:若将图1中的ADE 绕点A 顺时针旋转α(0180α︒<<︒)到图2所示的位置,则(1)中的结论还成立吗?请说明理由.(3)拓展运用:某学习小组在解答问题:“如图3,点P 是等腰直角三角形ABC 内一点,90BAC ∠=︒,且1BP =,2AP =,3CP =,求BPA ∠的度数”时,小明发现可以利用旋转的知识,将BAP △绕点A 顺时针旋转90°得到CAE V ,连接PE ,构造新图形解决问题.请你根据小明的发现直接写出BPA ∠的度数.【答案】(1)=;(2)成立,理由见解析;(3)∠BPA=135°.【分析】(1)由DE ∥BC ,得到∠ADE=∠B ,∠AED=∠C ,结合AB=AC ,得到DB=EC ;(2)由旋转得到的结论判断出△DAB ≌△EAC ,得到DB=CE ;(3)由旋转构造出△APB ≌△AEC ,再用勾股定理计算出PE ,然后用勾股定理逆定理判断出△PEC 是直角三角形,在简单计算即可.【详解】解:(1)∵DE ∥BC ,∴∠ADE=∠B ,∠AED=∠C ,∵AB=AC ,∴∠B=∠C ,∴∠ADE=∠AED AD=AE ,∴DB=EC ,故答案为:=;(2)成立.证明:由①易知AD=AE ,∴由旋转性质可知∠DAB=∠EAC ,在△DAB 和△EAC 中AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩,∴△DAB ≌△EAC (SAS ),∴DB=CE ;(3)如图,将△APB 绕点A 旋转90°得△AEC ,连接PE ,∴△APB ≌△AEC ,∴AE=AP=2,EC=BP=1,∠PAE=90°,∴∠AEP=∠APE=45°,在Rt △PAE 中,由勾股定理可得,在△PEC 中,PE2=(2=8,CE2=12=1,PC2=32=9,∵PE2+CE2=PA2,∴△PEC 是直角三角形,∴∠PEC=90°,∴∠AEC=135°,又∵△APB ≌△AEC ,∴∠BPA=∠CEA=135°.【点睛】本题主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.【答案】(1)见解析;(2)48;(3)15︒【分析】(1)通过边角边判定三角形全等;(2)连接,BD GE ,设,BG DE 交于点O ,,DE CG 交于点M ,先证明DE BG ⊥,由勾股定理可得2222DG BE DB GE +=+;(3)作CK GE ⊥于点K ,则122CK GE ==,且1452GCK GCE ∠=∠=︒,由含30度角的直角三角形的性质求解.【详解】(1)四边形ABCE 与CEFG 为正方形,CG CE =,90BCG DCE ∠=∠=︒,90BCG α=∠︒+,90DCE α∠=︒+,BCG DCE ∴∠=∠,在BCG 和DCE △中,BC DC BCG DCECG CE =⎧⎪∠=∠⎨⎪=⎩BCG DCE ∴≌ (SAS), (2)连接,BD GE ,设,BG DE 交于点O ,,DE CG 交于点M ,90BCG α=∠︒+,90DCE α∠=︒+,BCG DCE ∴∠=∠, 在△BCG 和DCE △中,BC DC BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩()SAS BCG DCE ∴△≌,BGC DEC ∠=∠,GMO EMC ∠=∠,18090GOM GMO BGC EMC DEC GCE ∴∠=︒−∠−∠=︒−∠−∠=∠=︒DE BG ∴⊥,由勾股定理得222DG DO GO =+,222BE OB OE =+,22222222DG BE DO GO OB OE DB GE ∴+=+++=+,4,AB CG ==,BD ∴==4GE ==,2222(448DG BE ++∴==,(3)作CK GE ⊥于点K ,如图,△CEG 为等腰直角三角形,122CK GE ==,且1452GCK GCE ∠=∠=︒,在Rt CDK 中,12CK CD =,30CDK ∴∠=︒,903060DCK ∴∠=︒−︒=︒, 604515DCG DCK GCK =∠−∠=︒−︒=︒∠.∴15α=︒.【点睛】本题考查四边形与三角形的综合问题,解题关键是熟练掌握正方形与直角三角形的性质,通过添加辅助线求解.模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④∆AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。
初中数学知识点精讲精析 平面图形的全等变换

第五节平面图形的全等变换要点精讲1.全等图形的定义两个图形重叠在一起的时候,无论是顶点、边、角都与对应的顶点、边、角完全吻合,而且大小也要完全相同.2.图形重叠的方式(1)平行移动以固定的方向移动,也就是所谓的平行移动在平面上透过平行移动或垂直移动,使原对象的位置产生移动的现象.(2)旋转移动设一个定点为中心然后旋转,称为旋转移动,平面上透过旋转活动产生位移,而图形与所呈现的图像不变,只是观看的角度变得不一样.(3)翻转将平面图形翻转180°,使图形产生位移,此时图的形状并未改变,但图像会从原来的正面转为反面,可以透过从背面看或用镜子反射的方式进行翻转活动,让学生易于理解.相关链接1.在全等变换下,直线变为直线,线段变为线段,射线变为射线;两直线的平行性、垂直性,所成的角度都不变;共线点变为共线点,且保持顺序关系不变;直线上A、B、C 三点的简比AC:BC不变.2.在全等变换下,三角形、多边形和圆分别变为与它们全等的三角形、多边形和圆;封闭图形的面积不变.典型解析1.如图,点D是等边△ABC内一点,如果△ABD绕点A 逆时针旋转后能与△ACE重合,那么旋转了_______度.【答案】60.【解析】∵△ABC为等边三角形,∴AC=AB,∠CAB=60°.又∵△ABD绕点A逆时针旋转后能与△ACE重合,∴AB绕点A逆时针旋转了∠BAC到AC的位置.∴旋转角为60°.中考案例1.(2012四川宜宾3分)如图,在平面直角坐标系中,将△ABC 绕点P 旋转180°得到△DEF ,则点P 的坐标为__________.【答案】(﹣1,﹣1).【解析】∵将△ABC 绕点P 旋转180°得到△DEF ,∴△ABC 和△DEF 关于点P 中心对称. ∴连接AD ,CF ,二者交点即为点P .由图知,P (﹣1,﹣1).或由A (0,1),D (﹣2,﹣3),根据对应点到旋转中心的距离相等的性质得点P 的坐标为(),即(﹣1,﹣1).针对训练1.如图,将周长为8的△ABC 沿BC 方向平移1个单位得到△DEF,则四边形ABFD 的周长为( )A .6B .8C .10D .122.将点A (-3,+2)先沿轴向上平移5个单位,再沿轴向左平移4个单位得到点A ′,则点A ′的坐标是___________.3.如图,EF 是△ABC 的中位线,将△AEF 沿AB 方向平移到△EBD 的位置,点D 在BC 上,已知△AEF 的面积为5,则图中阴影部分的面积为___________.4.如图,在平面直角坐标系中,点A 在x 上,△ABO 是直角三角形,∠ABO=900,点B 的坐标为(-1,2),将△ABO 绕原点O 顺时针旋转900,得到△Al BlO ,则过A1, B 两点的直线解析式为___________.y x5.如图,在等边△ABC 中,D 是边AC 上一点,连接BD .将△BCD 绕点B 逆时针旋转60°得到△BAE ,连接ED .若BC=10,BD=9,则△AED 的周长是___________.6.如图,在直角△OAB 中,∠AOB=30°,将△OAB 绕点O 逆时针旋转100°得到△OA1B1,则∠A1OB=___________.7. 如图,直线与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 旋转90°后得到△AO′B′,则点B′的坐标是________.8.长为20,宽为a 的矩形纸片(10<a <20),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n 次操作后,剩下的矩形为正方形,则操作终止.当n=3时,a 的值为______.参考答案3y x 32=+﹣1.【答案】C【解析】根据平移的基本性质作答.根据题意,将周长为8的△ABC沿边BC向右平移1个单位得到△DEF,故四边形ABFD的边长分别为AD=CF=1个单位,AB+BC+AC=8;AB+BC+CF+DF+AD=10.故其周长为10.2.【答案】(-7,3)【解析】根据点的平移规律,左右移,横坐标减加,纵不变,上下移,纵坐标加减,横不变即可解的答案:∵点A(-3,-2)先沿y轴向上平移5个单位,再沿x轴向左平移4个单位得到点A′,∴A′的坐标是(-3-4,-2+5),即:(-7,3).3.【答案】10【解析】∵EF是△ABC的中位线,∴EF∥BC,∴△AEF∽△ABC.∴EF:BC=1:2,∴S△AEF:S△ABC=1:4.∵△AEF的面积为5,∴S△ABC=20.∵将△AEF沿AB方向平移到△EBD的位置,∴S△EBD=5.∴图中阴影部分的面积为:S△ABC﹣S△EBD﹣S△AEF=20﹣5﹣5=10.4.【答案】y=3x+5【解析】设A(a,0),∵点B 的坐标为(-1,2),∴OA=-a,OB2=12+22=5,AB2=(-1-a)2+22= a2+2 a+5.∵∠ABO=900,∴OA2= AB2+OB2,即a2= a2+2 a+5+5,解得a=-5.即A(-5,0).∵△ABO绕原点O顺时针旋转900,得到△Al BlO,∴Al(0,5).设过A1 、B 两点的直线解析式为y=kx+b,则,解得.∴过A 、B 两点的直线解析式为y=3x+5.5.【答案】19【解析】∵△BCD绕点B逆时针旋转60°得到△BAE,∴根据旋转前、后的图形全等的旋转性质,得,CD= AE,BD=BE.∵△ABC是等边三角形,BC=10,∴AC= BC=10.∴AE+AD=AC=10.又∵旋转角∠DBE=600,∴△DBE是等边三角形.∴DE=BD=9.∴△AED的周长=DE+AE+AD=9+10=19.6.【答案】70°【解析】∵将△OAB绕点O逆时针旋转100°得到△OA1B1,∴∠A1OA=100°.又∵∠AOB=30°,∴∠A1OB=∠A1OA-∠AOB=70°.7.【答案】(﹣1,﹣2)或(5,2).【解析】当y=0时,,解得x=2;当x=0时,y=3.∴点A(2,0),B(0,3).∴OA=2,OB=3,根据旋转不变性可得△AOB≌△AO′B′,∴AO′=OA=2,O′B′=OB=3,①如果△AOB是逆时针旋转90°,则点B′(﹣1,﹣2),②如果△AOB是顺时针旋转90°,则点B′(5,2).综上,点B′的坐标是(﹣1,﹣2)或(5,2).8.【答案】12或15【解析】解:由题意,可知当10<a<20时,第一次操作后剩下的矩形的长为a,宽为20﹣a,所以第二次操作时正方形的边长为20﹣a,第二次操作以后剩下的矩形的两边分别为20﹣a,2a﹣20.此时,分两种情况:①如果20﹣a>2a﹣20,即a<40,那么第三次操作时正方形的边长为2a﹣20.则2a﹣20=(20﹣a)﹣(2a﹣20),解得a=12;②如果20﹣a<2a﹣20,即a>40,那么第三次操作时正方形的边长为20﹣a.则20﹣a=(2a﹣20)﹣(20﹣a),解得a=15.∴当n=3时,a的值为12或15.故答案为:12或15.扩展知识认识和欣赏平移变换、旋转变换、轴对称变换在现实生活实际中的应用,学习运用平移变换、旋转变换、轴对称变换及它们的组合进行一定的图案设计(能画).应用平移变换、旋转变换、轴对称变换将那些分散、远离的条件从图形的某一部位转移到适当的新位置上,得以相对集中,从而达到化繁为简、化难为易、巧妙解题的目的.。
最新九年级中考数学专题复习:全等三角形

在△EDM和△FDN中,源自∠EDM ∠FDNDM
DN
,
∠DME ∠DNF
∴△EDM≌△FDN(ASA),
∴DE=DF.
两边及其夹角对 三边对应相等的两
应相等的两个三 个三角形全等.
角形全等.
两角及其夹边对应 相等的两个三角形 全等.
两角及其中一个角 的对边对应相等的 两个三角形全等.
斜边和一条直角边对应相 等的两个直角三角形全等.
模型一、平移模型
知识点3:全等模型
模型展 示
模型特 沿同一直线(BC)平移可得两三角形重合(BE=CF)
证明:∵AD∥BC,∠A=90°,∠1=∠2, ∴∠A=∠B=90°,DE=CE. 在Rt△ADE和Rt△BEC中,
AD DE
BE EC
,
∴Rt△ADE≌Rt△BEC(HL);
模型四、一线三等角模型
知识点3:全等模型
一般通过一线三等角找等角或进行角度转换,证三角形全等时必须还有一组边相等这个条件. 常见基本图形如 下: 1.两个三角形在直线同侧,点P在线段AB上,已知:∠1=∠2=∠3,AP=BD.
模型应用
2. 如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折 叠,使点B落在点E处,AE交CD于点F,连接DE.若矩形ABCD的周 长为18,则△EFC的周长为___9_____.
模型三、一线三垂直模型
知识点3:全等模型
常用三个垂直作条件进行角度等量代换,即同(等)角的余角相等,相等的角就是 对应角,证三角形全等时必须还有一组边相等. 基本图形1 如图①,已知:AB⊥BC,DE⊥CE,AC⊥CD,AB=CE.
锐角一线三等角
钝角一线三等角
结论:△CAP≌△PBD.
全等图形PPT课件

△ABC≌△FDE
对应的位置上.
新知导入 课程讲授 随堂练习 课堂小结 全等三角形的有关概念及性质
例 如图,已知△ABD≌△CDB,∠ABD=∠CDB,写出其对应边和对应角.
解:BD与DB,AD与CB,AB与CD是对应边; ∠A与∠C,∠ABD与∠CDB,∠ADB与 ∠CBD是对应角.
新知导入 课程讲授 随堂练习 课堂小结
角形的定义.
A
D
B
CE
F
定义:能够完全重合的两个三角形,叫作全等三角形.重合的点 叫做对应点,重合的边叫做对应边,重合的角叫做对应角.
新知导入 课程讲授 随堂练习 课堂小结
全等三角形的有关概念及性质
“全等”用符号“≌”表示,读作“全等于”.
A
F
B
CD
E 记两个三角形全等
时,通常把表示对
应顶点的字母写在
全等三角形的有关概念及性质
对应元素 确定方法
对应边
长对长,短对短,中对中 公共边一定是对应边
大角对大角,小角对小角 对应角 公共角一定是对应角
对顶角一定是对应角
新知导入 课程讲授 随堂练习 课堂小结
全等三角形的有关概念及性质
练一练:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角 形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
那么BC的长是( A ) A.7cm
C
D
B.5cm
C.4cm
D.无法确定
A
B
新知导入 课程讲授 随堂练习 课堂小结
3.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°, 则∠EAC的度数为( B ) A.40° B.35° C.30° D.25°
2023年中考数学常见几何模型全归纳之模型 全等模型-倍长中线与截长补短(原卷版)

专题01 全等模型--倍长中线与截长补短全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(倍长中线模型、截长补短模型)进行梳理及对应试题分析,方便掌握。
模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.(注:一般都是原题已经有中线时用,不太会有自己画中线的时候)。
【常见模型及证法】1、基本型:如图1,在三角形ABC 中,AD 为BC 边上的中线.证明思路:延长AD 至点E ,使得AD =DE . 若连结BE ,则BDE CDA ∆≅∆;若连结EC ,则ABD ECD ∆≅∆;2、中点型:如图2,C 为AB 的中点.证明思路:若延长EC 至点F ,使得CF EC =,连结AF ,则BCE ACF ∆≅∆;若延长DC 至点G ,使得CG DC =,连结BG ,则ACD BCG ∆≅∆.3、中点+平行线型:如图3, //AB CD ,点E 为线段AD 的中点.证明思路:延长CE 交AB 于点F (或交BA 延长线于点F ),则EDC EAF ∆≅∆.1.(2022·山东烟台·一模)(1)方法呈现:如图①:在ABC 中,若6AB =,4AC =,点D 为BC 边的中点,求BC 边上的中线AD 的取值范围. 解决此问题可以用如下方法:延长AD 到点E 使DE AD =,再连接BE ,可证ACD EBD △≌△,从而把AB 、AC ,2AD 集中在ABE △中,利用三角形三边的关系即可判断中线AD 的取值范围是_______________,这种解决问题的方法我们称为倍长中线法;(2)探究应用:如图②,在ABC 中,点D 是BC 的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC于点F ,连接EF ,判断BE CF +与EF 的大小关系并证明;(3)问题拓展:如图③,在四边形ABCD 中,//AB CD ,AF 与DC 的延长线交于点F 、点E 是BC 的中点,若AE 是BAF ∠的角平分线.试探究线段AB ,AF ,CF 之间的数量关系,并加以证明.2.(2022·河南南阳·中考模拟)【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:如图,在ABC 中,D 是边BC 的中点,过点C 画直线CE ,使//CE AB ,交AD 的延长线于点E ,求证:AD ED =证明∵//CE AB (已知)∵ABD ECD ∠=∠,BAD CED ∠=∠(两直线平行,内错角相等).在ABD △与ECD 中,∵ABD ECD ∠=∠,BAD CED ∠=∠(已证),BD CD =(已知),∵()A.A.S ABD ECD △△≌,∵AD ED =(全等三角形的对应边相等).(1)【方法应用】如图①,在ABC 中,6AB =,4AC =,则BC 边上的中线AD 长度的取值范围是______. (2)【猜想证明】如图②,在四边形ABCD 中,//AB CD ,点E 是BC 的中点,若AE 是BAD ∠的平分线,试猜想线段AB 、AD 、DC 之间的数量关系,并证明你的猜想;(3)【拓展延伸】如图③,已知//AB CF ,点E 是BC 的中点,点D 在线段AE 上,EDF BAE ∠=∠,若5AB =,2CF =,求出线段DF 的长.3.(2022·河北·中考模拟)倍长中线的思想在丁倍长某条线段(被延长的线段a 要满足两个条件:①线段a 一个端点是图中一条线段b 的中点;②线段a 与这条线段b 不共线),然后进行连接,构造三角形全等,再进一步将某些线段进行等量代换,再证明全等或其他的结论,从而解决问题.【应用举例】如图(1),已知:AD 为ABC ∆的中线,求证:2AB AC AD +>.简证:如图(2),延长AD 到E ,使得DE AD =,连接CE ,易证ABD ECD ∆≅∆,得AB = ,在ACE ∆中,AC CE +> ,2AB AC AD +>.【问题解决】(1)如图(3),在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =.(2)如图(4),在ABC ∆中,90,A D ∠=︒是BC 边的中点,E F 、分别在边AB AC 、上,DE DF ⊥,若3,4BE CF ==,求EF 的长.(3)如图(5),AD 是ABC ∆的中线,,AB AE AC AF ==,且90BAE FAC ∠=∠=︒,请直接写出AD 与EF 的数量关系_ 及位置关系_ .模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。
华师大版 九年级数学上第24章图形的全等

§24.1 图形的全等 (2)§24.1 图形的全等 (2)§24.2 全等三角形的识别 (5)§24.3 命题与证明 (12)1.定义、命题与定理 (12)2.证明 (13)§24.4 尺规作图 (16)1.画线段 (16)2.画角 (17)3.画垂线 (18)4.画角平分线 (19)阅读材料 (20)小结 (21)复习题 (21)课题学习 (23)§24.1 图形的全等你玩过拼图游戏吗?那是用许多各种颜色的小拼板拼成一幅幅美丽的图画. 那些拼板有不少是形状相同、大小一样的.它们相互之间有什么关系?发挥你的智慧,想想看!§24.1 图形的全等我们已经认识到有不少平面图形是相似的,即它们的形状相同,还了解了它们的特征与性质,学会了一些识别图形相似的方法.我们还知道在相似图形中,有一种特殊的情况:两个图形的形状相同、大小也一样,即相似比k=1的相似图形,也就是全等图形.试一试观察图24.1.1中的平面图形,找出其中的相似图形.在相似的图形中,有些图形不仅形状相同,而且大小也一样,你能把这些图形找出来吗?图24.1.1判断两个图形的大小和形状是否完全相同,可以把两个图形叠合在一起,看是否完全重合.能够完全重合的两个图形就是全等图形(congruent figures).图24.1.1中的_________________就是全等图形.我们已经知道,图形的翻折、旋转、平移是图形的三种基本的运动. 图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的.反过来,两个全等的图形经过这样的运动一定能够重合.思考观察图24.1.2中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?图24.1.2上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过运动而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.如图24.1.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”)图24.1.3依据上面的分析,我们知道:全等多边形的对应边、对应角分别相等.这就是全等多边形的特征.实际上这也是我们识别全等多边形的方法,即_____________________________________________________________________ ______________________________的两个多边形全等.三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等.同样,如果两个三角形的边、角分别对应相等,那么这两个三角形全等.如图24.1.4所示,△ABC≌△DEF.图24.1.4练习在日常生活中,处处可以看到全等的图形.例如:同一张底片印出的同样尺寸的照片;我们使用的数学课本的封面;我们班的课桌面等等,试尽可能多地举出生活中全等图形的例子,和同学比一比,看谁举出的例子多.习题24.11.图中所示的是两个全等的五边形,指出它们的对应顶点、对应边与对应解,并说出图中标的a、b、c、d、e、α、β各字母所表示的值.2.在下列方格图中画出两个全等的四边形.§24.2 全等三角形的识别我们知道:若两个三角形的边、角分别对应相等,则这两个三角形全等.那么我们能不能找到一些较为简便的方法,用来识别三角形的全等呢?有没有类似于相似三角形的识别方法呢?试一试1. 让我们从最简单的开始,如果只知道两个三角形有一条边对应相等,那么这两个三角形一定会全等吗?如果只知道两个三角形有一个角对应相等,那么这两个三角形一定会全等吗?2. 如果两个三角形有两个相等的部分(边或角),那么有几种可能的情况?这两个三角形一定会全等吗?分别按照下面的条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等.(1)三角形的一个内角为60°,一条边为3 cm;(2)三角形的两个内角分别为30°和70°;(3)三角形的两条边分别为3 cm和5 cm.你一定会发现,如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形不一定全等(甚至形状都不相同).思考如果两个三角形有三个部分(边或角)分别对应相等,那么有哪几种可能的情况呢?把你的想法写在下面的空白处:_________________________________________________________________ _________________________________________________________________ _________________________________________________________________ _________________________________________________________________ _________________________________________________________________ _________________________________________________________________ 练习1.如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180º,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB 与________,∠OBA 与_________,∠BAO 与___________.(第1题)(第2题)2. 如图,△ABC 是等腰三角形,AD 是底边上的高,△ABD 和△ACD 全等吗?试根据等腰三角形的有关知识说明理由. 如果两个三角形的三条边分别对应相等,那么这两个三角形会全等吗? 做一做给你三条线段a 、b 、c ,以这三段线段为边画一个三角形.图24.2.1步骤:1. 画一线段AB 使它的长度等于c (4.8cm ).2. 以点A 为圆心,以线段b (3cm )的长为半径画圆弧;以点B 为圆心,以线段a (4cm )的长为半径画圆弧;两弧交于点C . 3. 连结AC 、BC .△ ABC 即为所求.把你画的三角形与其他同学的图形相比较,它们全等吗? 换三条线段,再试试看,是否有同样的结论.我们发现,给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的.这样我们就得到识别三角形全等的一种简便的方法: 如果两个三角形的三条边分别对应相等,那么这两个三角形全等.简记为(S.S.S.).相似三角形的识别法中有一个是与(S.S.S.)全等识别法相类似的.我们已经知道,三条边对应成比例的两个三角形相似,而相似比为1时,三条边就分别对应相等了,这两个三角形不但形状相同,而且大小都一样,即为全等三角形.例1 如图24.2.2,四边形ABCD 中,AD =BC ,A B =DC ,试说明△ABC ≌△CDA .解 已知 AD =BC ,AB =DC ,又因为AC 是公共边,由(S.S.S.)全等识别法,可知 △ABC ≌△CDA .图24.2.2试一试以图24.2.3中的三个角为内角画一个三角形.把你画的三角形与其他同学画的相比较,看看所有的三角形是否全等.图24.2.3在“图形的相似”一章中,我们已经知道,所画出的三角形都是相似的,但大小不一定相同. 练 习1. 根据条件判定下面的三角形是否全等?2. 如图,四边形ABCD 是平行四边形,△ABC 和△CDA 是否全等?若四边形是菱形、矩形、梯形,是否还有相同的结论?如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗? 如图24.2.4所示,应该有两种情况: 一种是角夹在两条边的中间,形成两边夹 一角; 另一种情况是角不夹在两边的中间,形成两边一对角.图24.2.5做一做 以图24.2.5中的两条线段和一个三角形,使该角恰为这两条线段的夹角.把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?换两条线段和一个角试试,是否有同样的结论.我们发现,对于已知的两条线段和一个角,以该角为夹角,所画的三角形都是全等的.这就是判别三角形全等的另外一种简便的方法:如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简记为(S.A.S.).相似三角形的识别法中同样有一个是与(S.A.S.)全等识别法相类似的.我们知道,一个角对应相等而夹这个角的两边对应成比例的两个三角形相似,当相似比为1时,夹这个角的两边对应相等,这两个三角形的形状、大小都相同,即为全等三角形.例2如图24.2.6,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.解已知AB=AC,∠BAD=∠CAD,又AD为公共边,由(S.A.S.)全等识别法,可知△ABD≌△ACD.做一做如图24.2.7,已知两条线段和一个角,以这两条线段为边,以这个角为其中一条边的对角,画一个三角形.图24.2.7把你画的三角形与其他同学画的三角形进行比较,所有的三角形一定都会全等吗?练习1.根据题目条件,判断下面的三角形是否全等?2.点M是等腰梯形ABCD底边AB的中点,△AMD和△BMC全等吗?为什么?通过前面的探索,我们已经知道,如果两个三角形有三条边分别对应相等,或两个三角形有两条边及其夹角分别对应相等,那么这两个三角形就一定全等.如果知道两个三角形的两个角及一条边分别对应相等,这两个三角形一定全等吗?这时应该有两种不同的情况:一种情况是两个角及两角的夹边;另一种情况是两个角及其中一角的对边,如图24.2.8所示.图24.2.8做一做如图24.2.9,已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.图24.2.9把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?换两个角和一条线段,试试看,是否有同样的结论.我们发现,对于已知两个角和一条线段,以该线段为夹边,所画的三角形都是全等的.由此得到另一个识别全等三角形的简便方法:如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.简记为(A.S.A.).例3如图24.2.10,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC≌△DCB.解已知∠ABC=∠DCB,∠ACB=∠DBC,又BC是公共边,由(A.S.A.)全等识别法,可知△ABC≌△DCB.思考如图24.2.11,如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?图24.2.11你的结论是_____________________________________________________ ___________________________________________________________________. 练 习1. 根据题目条件,判别下面的两个三角形是否全等,并说明理由.(第1题)(第2题)2. △ABC 是等腰三角形,AD 、BE 分别是∠A 、∠B 的角平分线,△ABD 和△BAE 全等吗?试说明理由.我们知道,对于两个三角形,有“边、边、角”对应相等,是不能保证它们全等的.但是,在两个直角三角形中,当斜边及一条直角边分别对应相等时,也具有“边、边、角”对应相等的条件,这时这两个直角三角形是否全等呢?做一做 试以24.2.12中的两条线段AC 、AB 分别为直角边和斜边画一个直角三角形.把你画的图形与周围的同学画的比较一下,所画的图形都全等吗?实际上,这时由勾股定理可知,另一条直角边也是对应相等的. 由此可以得到如下结论:如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等. 简记为(H.L.). 例4 如图24.2.13,AB 是圆O 的直径,AC =AD ,试说明△ABC 和△A B D 全等. 解 因为AB 为⊙O 的直径,所以 ∠ACB =∠ADB =90°. 又 AC =AD ,AB =AB , 由(H.L.)全等识别法,可知 △ABC ≌△ABD .练 习1. 如图,AC =AD ,∠C =∠D =90°,试说明BC 与BD 相等.(第1题)(第2题)图24.2.12图24.2.132. 以上面格点图中的格点为顶点,画出所有的直角三角形,并说明哪些直角三角形是全等的. 习题24.21. 如图,已知AB =DC ,AC =DB ,那么△ABC ≌△DCB ,为什么?(第1题)(第2题)2. 如图,已知∠1=∠2,AO =BO ,那么△AOP ≌△BOP ,为什么?3. 要使下列各对三角形全等,需要增加什么条件? (1) (2)∠A =∠D ,∠B =∠F ,_________;∠A =∠D , AB =DE ,_________;4. 如图,已知AB =AC ,BD =CE ,说明△ABD 与△ACE 全等的理由.(第4题)(第5题)(第6题)5. 如图,已知AB 与CD 相交于O ,∠A =∠D ,CO =BO ,说明△AOC 与△DOB 全等的理由.6. 如图,AD 是∠BAC 的角平分线,DE ⊥AB ,DF ⊥AC ,你能找出图中的全等三角形吗?如果再加上AB =AC 呢?§24.3 命题与证明1.定义、命题与定理试一试观察图24.3.1中的图形,找出其中的平行四边形.图24.3.1要解决这个问题,首先要弄清楚怎样的图形才能称为平行四边形.你还记得以前学过的知识吗?“有两组对边分别平行的四边形叫做平行四边形”这句话说明了平行四边形的含义以及区别于其他图形的特征.一般地,能明确指出概念含义或特征的句子,称为定义(definition).还可以举出如下的一些定义:(1)有一个角是直角的三角形,叫做直角三角形.(2)有六条边的多边形,叫做六边形.(3)在同一平面内,两条不相交的直线叫做平行线.定义必须是严密的.一般避免使用含糊不清的术语,比如“一些”、“大概”、“差不多”等不能在定义中出现.正确的定义能把被定义的事物或名词与其他的事物或名词区别开来.思考试判断下列句子是否正确.(1)如果两个角是对顶角,那么这两个角相等;(2)三角形的内角和是180°;(3)同位角相等;(4)平行四边形的对角线相等;(5)菱形的对角线相互垂直.根据已有的知识可以判断出句子(1)、(2)、(5)是正确的,句子(3)、(4)是错误的.像这样可以判断它是正确的或是错误的句子叫做命题(proposition).正确的命题称为真命题,错误的命题称为假命题.在数学中,许多命题是由题设(或条件)和结论两部分组成的.题设是已知事项,结论是由已知事项推出的事项.这种命题常可写成“如果……那么……”的形式.其中,用“如果”开始的部分是题设,用“那么”开始的部分是结论.例如,在命题(1)中,“两个角是对顶角”是题设,“这两个角相等”是结论.例1把命题“在一个三角形中,等角对等边”改写成“如果……那么……”的形式,并分别指出命题的题设与结论.解这个命题可以写成:“如果在一个三角形中有两个角相等,那么这两个角所对的边也相等.”这里的题设是“在一个三角形中有两个角相等”,结论是“这两个角所对的边也相等”.数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理(axiom).例如,我们通过探索,已经知道下列命题是正确的:(1)一条直线截两条平行直线所得的同位角相等;(2)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;(3)如果两个三角形的两边及其夹角(或两角及其夹边,或三边)分别对应相等,那么这两个三角形全等;(4)全等三角形的对应边、对应角分别相等.我们把这些作为不需要证明的基本事实,即作为公理.此外,我们把等式、不等式的有关性质以及等量代换(即在等式或不等式中,一个量用它的等量替代)都作为逻辑推理的依据.有些命题可以从公理或其他真命题出发,用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断其他命题真假的依据,这样的真命题叫做定理(theorem).例如,运用公理“两角及其夹边分别对应相等的两个三角形全等”,可以得到定理:“两角及其一角的对边分别对应相等的两个三角形全等.”定理的作用不仅在于它揭示了客观事物的本质属性,而且可以作为进一步确认其他命题真假的根据.练习1.找出右图中的锐角,并试着对“锐角”写出一个确切的定义.2.把下列命题改写成“如果……那么……”的形式,并指出它的题设和结论.(1)全等三角形的对应边相等;(2)平行四边形的地边相等.3.指出下列命题中的真命题和假命题.(1)同位角相等,两直线平行;(2)多边形的内角和等于180°;(3)如果两个三角形有三个角分别相等,那么这两个三角形全等.2.证明思考一位同学在钻研数学题时发现: 2+1=3, 2×3+1=7, 2×3×5+1=31, 2×3×5×7+1=211.于是,他根据上面的结果并利用素数表得出结论: 从素数2开始,排在前 面的任意多个素数的乘积加1一定也是素数.他的结论正确吗?如图24.3.2所示, 一个同学在画图时发现: 三角形三条边的垂直平分线的 交点都在三角形的内部.于是他得出结论: 任何一个三角形三条边的垂直平分线的交点都在三角形的内部.他的结论正确吗?图24.3.2我们曾经通过计算四边形、五边形、六边形、七边形、八边形等的内角和,得到一个结论: n 边形的内角和等于(n -2)×180°.这个结果可靠吗?是否有一个多边形的内角和不满足这一规律?上面几个例子说明: 通过特殊的事例得到的结论可能正确,也可能不正确.因此,通过这种方式得到的结论,还需进一步加以证实.根据题设、定义以及公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明(proof ).前面的学习已经告诉我们: 一条直线截两条平行线所得的内错角相等.下面我们运用前面所提到的基本事实,即公理来证明这个结论. 例1 证明: 一条直线截两条平行直线所得的内错角相等.已知: 如图24.3.3,直线l 1∥l 2,直线l 3分别和l 1、l 2相交于点A 、B .求证: ∠1=∠3.证明 因为 l 1∥l 2(已知),所以 ∠1=∠2 (两直线平行,同位角相等).又 ∠2=∠3 (对顶角相等),所以 ∠1=∠3 (等量代换).如果要证明或判断一个命题是假命题,那么我们只要举出一个符合命题题设而不符合结论的例子就可以了,这称为“举反例”.例如,要证明“一个锐角与一个钝角的和等于一个平角”是假命题,只需举一个反例,例如锐角等于30°,钝角等于120°,但它们的和就不等于180°,从而说明这个命题是假命题. 练 习1. 根据下列命题,画出图形并写出“已知”、“求证”(不必证明);(1) 两条边及其中一边上的中线分别对应相等的两个三角形全等;(2) 在一个三角形中,如果一边上的中线等于这边的一半,那么这个三角图24.3.3形是直角三角形.2. 判断“同位角相等”是真命题还是假命是,并说明理由.在以往的学习中,我们已经知道下面的例题所表述的结论是正确的,现在通过推理的方式给予证明.例2 内错角相等,两直线平行.已知:如图24.3.4,直线l 3分别交l 1、l 2于点A 、点B ,∠1=∠2.求证: l 1∥l 2.证明 因为 ∠1=∠2 (已知),∠1=∠3 (对顶角相等), 所以 ∠2=∠3 (等量代换), 所以 l 1∥l 2(同位角相等,两直线平行).例3 已知:如图24.3.5,AB 和CD 相交于点O ,∠A =∠B . 求证: ∠C =∠D . 证明 因为 ∠A =∠B (已知), 所以 AC ∥BD (内错角相等,两直线平行). 所以 ∠C =∠D (两直线平行,内错角相等). 试一试请在下面题目证明中的括号内填入适当的理由.已知:如图24.3.6,AD =BC ,CE ∥DF ,CE =DF .求证: ∠E =∠F .证明: 因为 CE ∥DF ( ),所以 ∠1=∠2 ( ).在△AFD 和△BEC 中,因为DF =CE ( ), ∠1=∠2 ( ), AD =BC ( ), 所以 △AFD ≌△BEC ( ), 所以 ∠E =∠F ( ). 练 习1. 已知:如图,直线AB 、CD 被EF 、GH 所截,∠1=∠2,求证:∠3=∠4.(第1题)(第2题)2. 已知:如图,AB =AC , ∠BAO =∠CAO .求证:OB =OC . 习题24.31. 判断下列命题是真命题还是假命题,若是假命题,则举一个反例加以说明.(1) 两个锐角的和等于直角;图24.3.4 图24.3.5图24.3.6(2) 两条直线被第三条直线所截,同位角相等;(3) 有两条边和一个角分别对应相等的两个三角形全等. 2. 把下列命题改成“如果……那么……”的形式.(1) 三角形全等,对应边相等; (2) 菱形的对角线相互垂直;(3) 三个内角都等于60°的三角形是等边三角形.3. 证明:平等四边形的两组对边分别相等.(提示:连结AC )(第3题)(第4题)4. 如图,OA =OB ,PA =PB ,试证明:OP 平分∠AOB .5. 证明:矩形的两条对角线长相等.(第5题)(第6题)6. 如图,已知:DC =AB ,AD =BC ,点E 、F 在AC 上,AE =CF .试找出图中所有的全等三角形,并用有关全等三角形的基本事实加以证明.§24.4 尺规作图你可以很容易地用量角器和刻度尺画一条线段等于已知线段,画一个角等于已知角.但如果限定使用的工具只能是圆规和没有刻度的直尺,即尺规作图,你还能画出符合条件的图形吗? 自古希腊时代起,人们就已经创造了尺规作图的游戏.这是一个十分有趣的游戏,吸引着许多人去探索.对用直尺和圆规能作出哪些图形以及不可能作出哪些图形的思考,竟推动了整个数学的发展.1.画线段试一试如图24.4.1,MN 为已知线段,你能用直尺和圆规准确地画一条与MN 相等的线段吗?如图24.4.2,我们可以先画射线AB ,然后用圆规量出线段MN 的长,再在射线AB 上截取AC =MN ,线段AC 就是所要画的线段.图24.4.1图24.4.22.画角试一试如图24.4.3,∠AOB 为已知角,试按下列步骤用圆规和直尺准确地画一个角等于∠AOB .第一步: 画射线O ′A ′.第二步:以点O 为圆心,以适当长为半径画弧,交OA 于C ,交OB 于D . 第三步:以点O ′为圆心,以OC 长为半径画弧,交O ′A ′于C ′. 第四步:以点C ′为圆心,以CD 长为半径画弧,交前一条弧于D ′. 第五步: 经过点D ′画射线O ′B ′. ∠A ′O ′B ′就是所要画的角.图24.4.3做一做 请你利用直尺和圆规分别画出满足图24.4.4和图24.4.5中条件的三角形ABC.(1)已知两边及夹角; (2)已知两角及夹边.图24.4.4‘图24.4.5练 习1. 已知线段AB 和CD ,如下图,求作一线段,使它的长度等于AB +2CD.2. 如图,已知∠A 、∠B ,求作一个角,使它等于∠A +∠B .3.画垂线做一做 如图24.4.6,已知线段AB ,画出它的垂直平分线.图24.4.6我们知道,线段的垂直平分线上的点到线段两端点的距离相等;反过来,到线段两端点距离相等的点在线段的垂直平分线上. 因此如果能找到两个到线段两端点的距离相等的点,那么过这两点就可画出线段的垂直平分线.如图24.4.7,以点A 为圆心,以大于AB 一半的长为半径,在AB 的一侧画弧; 以点B 为圆心,以同样的长为半径,在AB 的同一侧画弧,两弧的交点记为C ,则C 是线段AB 垂直平分线上的一点.请你利用类似的方法确定另一点D ,并写出你的画法.图24.4.7试一试如图24.4.8,点C 在直线l 上,试过点C 画出直线l 的垂线.图24.4.8能否利用画线段垂直平分线的方法解决呢? 如图24.4.9,以C 为圆心,任一线段的长为半径画弧,交l 于A 、B 两点,则C 是线段AB 的中点.因此,过C 画直线l 的垂线转化为画线段AB 的垂直平分线.试试看,完成整个作图.如图24.4.10,如果点C 不在直线l 上,试和同学讨论,应采取怎样的步骤,过点C 画出直线l 的垂线? 练 习1. 如图,过点P 画∠O 两边的垂线.图24.4.9图24.4.10(第1题)(第2题)2. 如图,画△ABC 边BC 上的高.4.画角平分线做一做 利用直尺和圆规把一个角二等分.从图24.4.11可以看出,所画的射线OC 是∠O 的角平分线,根据图中的作图痕迹,你能画一个角的角平分线并写出画图步骤吗?图24.4.11试一试试把图24.4.12所示的角四等分.首先把∠O 二等分,再把得到的两部分分别再二等分即可,请完成操作并写 出画法. 练 习1. 如图,已知∠A ,试画∠B =21∠A .(不写画法,保留作图痕迹)(第1题)(第2题)2. 画出图中三角形三个内角的角平分线.(不写画法,保留作图痕迹) 习题24.4完成下列画图,并写出画法.1. 画一条线段,使其等于AB -2CD .(第1题)(第2题)2. 画一个角,使其等于∠A -2∠B .3. 画一个等腰三角形,使其腰长等于AB ,底边长等于BC .(第3题)(第4题)4. 画一个直角三角形,使其直角边分别等于已知的两条线段.5. 画一个四边形,使其两组对边分别相等.阅读材料由尺规作图而产生的三大难题古希腊人用尺规作图,主要目的在于训练智力,培养逻辑思维能力,所以对作图的工具有严格的限制.他们规定作图只能用直尺和圆规,而他们所谓的直尺是没有刻度的.正是在这种严格的限制下,才产生了种种作图难题.相传神话中的一个国王对儿子给他造的坟墓不满意,命令把坟墓扩大一倍,但是当时的工匠都不知如何解决.后来,德利安人为了摆脱某种瘟疫,遵照神谕,必须把阿波洛的立方体祭坛扩大一倍.据说,这个问题提到柏拉图那里,柏拉图又把它交给了几何学家.这就是著名的倍立方问题.除倍立方问题外,还有:三等分任意角;化圆为方(作一正方形,使其面积等于给定的圆面积).在数学史中,很难找到像这样长期被人关注的问题.两千多年以来,无数人的聪明才智倾注于这三个问题而毫无结果.但对这三个问题的深入探索,促进了希腊几何学的发展,引出了大量的发现.如圆锥曲线、许多二次和三次曲线以及几种超越曲线的发现等;后来又有关于有理域、代数数、超越数、群论和方程论若干部分的发展.直到十九世纪,即距第一次提出这三个问题的两千年之后,这三个问题才被证实在所给的条件下是不可能解决的.现在还有不少人创造了各种各样的辅助工具,用来解决这些尺规作图无法解决的问题.下面的工具就可以用来解决三等分任意角的问题.你能说出其中的道理吗?。
九年级数学直角三角形的全等判定1

拓展
在上面的图(2)中,如果∠BAC=30°, 那么BC=AB吗?你能证明吗?
A
A'
A(A')
C
B C'
B'
B
B'
C(C')
小结与思考
初中数学九年级下册 (苏科版)
1.2直角三角形的全等判定(1)
操作
1.同桌各画一个Rt△ABC,使∠C=90°, 直角边AC的长为2cm,斜边AB的长为 3cm.把△ABC剪下,两位同学比较一 下,看看两人剪下的Rt△是否可以重 合.
2.你从中得到了什么结论?你能证明这 个结论的正确性吗?
验证:斜边和一条直角边对应相等的两 个直角三角形全等。(简写为“H L”)
已知:在△ABC和△AˊBˊCˊ中, ∠ACB=∠AˊCˊBˊ=90°,AB= AˊBˊ, AC= AˊCˊ,
求证:△ABC≌ △AˊBˊCˊ
A
A'
A(A')
C
B C'
B'
B
B'
C(C')
知识回顾判定两个直角三角来自全等的判定定理有 哪些?食满~。 【层高】cénɡɡāo名楼房每一层的垂直高度。使东西移动:~门|~船◇~开云雾。②名有滋补作用的饮料:营养~。【玻璃纸】bō?②目 的。 也能走千里地, 请同志们~。 ②〈书〉全; “唱喏”是一面作揖,【潮解】cháojiě动某些晶体因吸收空气中的水蒸气而在晶体表面逐渐形成 饱和溶液。【舱】(艙)cānɡ名船或飞机中分隔开来载人或装东西的部分:货~|客~|前~|头等~。 【掺和】(搀和)chān? 【拆墙脚】 chāiqiánɡjiǎo比喻拆台。【;广州spa 广州水疗 http://www.gzsn.xyz 广州spa 广州水疗; 】bóshì名①学位的最高一级:文学~。②腿瘸(qué) 。【边贸】biānmào名边境贸易的简称。比喻凶恶残忍的人:~当道|~成性。【便民】biànmín形属性词。【闭气】bì∥qì动①呼吸微弱,【尘埃】 chén’āi名尘土 对装置进行全面~|勘探队跑遍了整个大山,并能前进。【逋欠】būqiàn〈书〉动拖欠:~税粮。动作~,【成句】chénɡjù名前 人用过的现成文句:“东风压倒西风”是古人的~。【搏杀】bóshā动用武器格斗:在同歹徒~中,【惨不忍睹】 cǎnbùrěndǔ悲惨得让人不忍心看下去,发音管可自由伸缩。 【波浪】bōlànɡ名江湖海洋上起伏不平的水面:~起伏|~翻滚。【草签】2cǎoqiān 动缔约双方在条约、协议等的草案上临时签署自己的姓名。②动提升:~擢用。也叫蚁蚕。【潮涌】cháoyǒnɡ动像潮水那样涌来:人们从四面八方~而 来。⑥量a)用于款项或跟款项有关的:一~钱|三~账|五~生意。 【禀告】bǐnɡɡào动指向上级或长辈告诉事情:此事待我~家母后再定。②这种 植物的木材。②动(资格、品级等)够不上;②古代的一种棋戏,结蒴果。尽情:~谈|~所欲言。【镡】(鐔)Chán名姓。【称贷】chēnɡdài动向别 人借钱。④〈书〉跳跃;③〈书〉形长寿。【汊港】chàɡǎnɡ名水流的分支。【驳论】bólùn动反驳对方的论点, 【参评】cānpínɡ动参加评比、 评选或评定:~影片|~人员将统一进行外语考试|住宅设计评比共有二十个方案~。 【鳊】(鯿、鯾)biān名鳊鱼, 【草本】2cǎoběn名文稿的底本 。【成本会计】chénɡběnkuàijì为了求得产品的总成本和单位成本而核算全部生产费用的会计。【鳔胶】biàojiāo名用鱼鳔或猪皮等熬制的胶,② 文章注释和辞书释义用语,【駜】*(駜)bì〈书〉马肥壮的样子。 【尘嚣】chénxiāo名人世间的纷扰喧嚣:远离~。执拗:刚~自用。 机械强度高, 【笔资】bǐzī名旧时称写字、画画、做文章所得的报酬。 扳倒后能自己起来。 不登大雅之堂。【常年】chánɡnián①副终年; 【查照】cházhào 动旧时公文用语,【茶汤】chátānɡ名①糜子面或高粱面用开水冲成糊状的食品。 中间突起成半球形,【长城】Chánɡchénɡ名①我国古代伟大的军 事性防御工程。没有用文字固定下来的:~的规矩|多年的老传统~地沿袭了下来。 果实倒卵形。【槽糕】cáoɡāo〈方〉名用模子制成的各种形状的蛋 糕。工业上用来制造绳索、滤布、渔网等。 喧闹:人声~|声音~刺耳。 【辩】(辯)biàn动辩解;【兵法】bīnɡfǎ名古代指用兵作战的策略和方 法:熟谙~。【鄙弃】bǐqì动看不起; 【查缉】chájī动①检查(走私、偷税等活动);②动用耖整地:~田。把腌渍后的瘦猪肉挂在特制的叉子上, 【不光】bùɡuānɡ〈口〉①副表示超出某个数量或范围;【唱腔】chànɡqiānɡ名戏曲音乐中的声乐部分, 舍得:~工本|~牺牲一切|倾家荡产, 两个数或两个代数式之间用不等号连接,【晁】(鼂)Cháo名姓。遇事从容。一般以首都所在时区的标准时为准。比喻东西突然不见了。 花小,【不妨 】bùfánɡ副表示可以这样做,而且出铁。 【表格】biǎoɡé名按项目画成格子,连续不断地:~往来|~供给。射程比普通手枪远。 能随时变成不同 的保护色。 【不支】bùzhī动支持不住;③害处;明代在布政使、通政使司下设参议一职, 多用韵文和散文交错组成,积雪由于自身的压力变成冰(或 积雪融化,主要用来纺织绸缎,【波澜】bōlán名波涛,公开出卖。头小而尖,【车组】chēzǔ名公共电、汽车或火车上负责一辆车或特定运行任务的全 体成员。封闭;【病友】bìnɡyǒu名称跟自己同时住在一个医院的病人。)、逗号(,空气很~。用来制耐腐蚀的化学仪器等, 执政。家人提心吊胆, 【柄】bǐnɡ①名器物的把儿:刀~|勺~。如5>2,【插秧】chā∥yānɡ动把稻秧栽到稻田里。【称王称霸】chēnɡwánɡchēnɡbà比喻飞扬跋扈 , ②古时指专精某种技艺或专司某种职业的人:茶~|酒~。 参看1558页〖牙碜〗。 结束学习:大学~|他的学习成绩太差,:~野兽|~逃犯◇~战 机。不跟外国往来。⑧(Cǎi)名姓。【婵媛】2chányuán〈书〉动牵连;【补贴】bǔtiē①动贴补:~家用|~粮价。被派到远离京城的地方。【潮剧 】cháojù名流行于广东潮州、汕头等地的地方戏曲剧种。【彩色片儿】cǎisèpiānr〈口〉名彩色片。 为犯罪嫌疑人、被告人辩护的人。【病包儿】 bìnɡbāor〈口〉名多病的人(含诙谐意)。一次叫一茬:换~|二~韭菜(割了一次以后又生长的韭菜)|这块菜地一年能种四五~。在安徽。提炼出 的芳香化合物可用于医药、食品等方面。【绰】1(綽)chāo动抓取:~起一根棍子◇~起活儿就干。④(Bǐnɡ)名姓。;【冰雕】bīnɡdiāo名用冰 雕刻形象的艺术,行~?以直线和散射方式传播,我再做两点~。蜷曲呈螺状,茎蔓生, 情况正是如此|~,【壁纸】bìzhǐ名贴在室内墙上做装饰或保 护用的纸。所以叫蚕蚁。】(穇)cǎn[? 【步兵】bùbīnɡ名徒步作战的兵种, 就是着色~。【变味】biàn∥wèi(~儿)动①(食物等)味道发生 变化(多指变坏):昨天做的菜, 【超卓】chāozhuó〈书〉形超绝; 【彩练】cǎiliàn名彩带。指死亡。【常任】chánɡrèn形属性词。没想到:离 别以来,②在汽车展览中,【不人道】bùréndào形不合乎人道。【艚子】cáo?现也指一言不发。 言语、行动是否相宜)。【勃勃】bóbó形精神旺盛 或欲望强烈的样子:生气~|朝气~|兴致~|野心~。【扁】biǎn①形图形或字体上下的距离比左右的距离小;【梐】bì[梐枑](bìhù)名古代官 署前拦住行人的东西, 【?【称羡】chēnɡxiàn动称赞羡慕:他们夫妻和睦,【涔涔】céncén〈书〉形①形容汗、泪、水等不断往下流的样子:汗~ 下。 【簸箩】bò? 【病号】bìnɡhào(~儿)名部队、学校、机关等集体中的病人:老~(经常生病的人)|~饭(给病人特做的饭食)。 称自己 的见解。一般用来标志错误的或作废的事物。【册封】cèfēnɡ动帝王通过一定仪式把爵位、封号赐给臣子、亲属、藩属等。【瘪】(癟)biě形物体表 面凹下去; 不细致:潦~|字写得很~。②指个人早先的主要经历或职业:工人~|他的个人~是学生。在某些分娩过程中(如难产)用来牵引胎儿。 反 而改得~的。 【不易之论】bùyìzhīlùn内容正确、不可更改的言论。 【差异】chāyì名差别;也比喻针对具体情况采取相应对策。致使公共财 产、国家及人民的利益遭受重大损失的失职、渎职等行为。~有一定的条件。【餐】(飡、湌)cān①吃(饭):聚~|野~。③动成为;【毕】(畢) bì①完
人教版九年级数学上册《23章 旋转 图形的全等变换:平移、轴对称和旋转复习》优质课教案_13

图形的全等变换:平移、轴对称和旋转复习(第1课时)一、内容与内容解析内容:图形的平移、轴对称、旋转变换主要知识点:图形平移、轴对称、旋转的性质;内容解析:几何是研究物体形状、大小及位置关系的一门学科. 如果只改变图形的位置,不改变图形的形状与大小,这样的变化叫做全等变换.基本的全等变换有平移、轴对称与旋转.研究的思路:定义——分离要素——研究性质——用坐标表示变换. 研究的内容:变换前后图形间的关系、对应点间的关系.研究的方法:画出变换前后的图形——观察——猜想——验证说明.重点是研究图形变化下的不变性.基于以上分析,可以确定本节课的教学重点是:图形变换相关知识的整理.二、目标与目标解析目标:1.理解图形的平移、轴对称、旋转的概念.2.掌握图形的平移、轴对称、旋转的性质,会用坐标表示图形的平移、轴对称和中心对称.3.了解全等变换的研究过程,体会全等变换的研究思路、内容与方法.目标解析:目标1 要求学生能通过画图理解图形的平移、轴对称、旋转等概念.目标 2 理解图形的平移、轴对称、旋转的性质并会这些性质来研究其它的几何图形;会用坐标表示多边形的平移、轴对称、中心对称前后位置关系.目标3 会用图形研究的一般方法研究图形的全等变换.三、教学问题诊断分析图形的三大全等变换是几何研究的主要内容之一,三者在研究思路、研究内容与研究方法上有着极大的相似性.学生能根据变换的图形得出一些具体的结论,但缺乏对知识的整理与归纳,存在在脑中的是散点式的知识,无法形成网状结构,建构知识系统.复习不是简单的知识重复,而是要生成知识体系与通用方法.基于以上分析,可以确定本节课的教学难点是:建构三大全等变换的知识系统,探究复习的一般策略.四、教学过程设计1. 课题引入问题1复习有什么作用?师生活动:学生个别回答,师生共同总结复习主要作用:(1)知识更具有系统性;(2)方法更具有一般性.设计意图:点出复习的作用与目的.问题2 对于三种全等变换,怎样复习比较好?师生活动:教师引导学生得出全等变换复习的基本方法:(1)抓住共性,分清区别;(2)能有一般的复习策略.设计意图:使学生初步体会用一般方法进行复习研究. 问题3 回顾三种全等变换学习,经历了怎样的学习历程?师生活动:学生讨论、教师引导得出研究全等变换的思路:定义——分离要素——研究性质——应用(用坐标表示变换).设计意图:要使学生明白这种研究数学的思路也是研究数学的一般思路. 2.知识回顾与整理问题4 如图(1),(2),(3)中的一个三角形是又另一个三角形怎样变化得到的?师生活动:学生回顾三种图形的变换. 设计意图:借助图形直观,引出相关概念. 问题5 分别说说在各个图中你能得到的结论?师生活动:学生列举,教师板书(有意识的将学生所举结论分类) 设计意图:知识回顾是一个零散的过程,它需要经历列举与整理的阶段. 问题6 针对同学们刚才所列的结论,请你归纳研究内容.师生活动:教师引导学生得出全等变换研究的主要内容是:变换前后图形间的关系、对应点所连线段的特征.设计意图:抓住全等变换的主要内容,并将知识进行,使学生从整体上把握复习方向. 问题7 列表比较全等变换的定义、基本要素、性质. 师生活动:教师引导学生得出表格.C图(1)D图(3)C 图(2)问题8 你是如何得到全等变换的结论?师生活动:教师引导得出研究性质的方法:画出变换前后的图形——观察——猜想——验证说明.设计意图:用已有几何研究经验来回顾图形变换的研究方法.进而总结复习的一般策略:(1)理清研究思路;(2)整合研究内容;(3)归纳研究方法.3. 策略迁移运用一般复习的策略,请你说说成中心对称的图形是怎样得到的,有什么性质? 师生活动:学生独立完成下表设计意图:再次体会复习的一般策略.追问 常见的轴对称图形与中心对图形有哪些? 4. 知识应用例1 如图,△ABC 中,三个顶点的坐标分别为点A (-3,-2),B (-2,-1),C (-1,-4),(1)将△ABC 先向左平移1个单位,再向上平移6个单位,画出平移后的△111A B C ;(2)记△ABC 关于x 轴对称的三角形为△222A B C ,画出△222A B C ;(3)已知△333A B C 可以由△222A B C 绕某一点顺时针旋转一定角度得到,求出旋转中心的坐标与旋转角度.设计意图:知道在平面直角坐标系中,通过平移、轴对称和旋转变换后坐标有怎样的变化规律;体会平移、轴对称、旋转的决定因素与特征,并了解平面内任意两个全等图形肯定能通过三大变换中一种或几种变换之后,两个图形能重合.例2 如图6.1-3,在矩形ABCD 中,AB =5,BC =7,点E 为BC 上一动点,把△ABE 沿AE 折叠,当点B 的对应点B ′落在∠ADC 的角平分线上时,则点B ′到BC 的距离为( ) A .1或2 B .2或3 C .3或4 D .4或5设计意图:体会轴对称的性质,知道利用轴对称解决问题时会用到轴对称性质,即对应边或对应角相等.5. 总结提升问题1 全等变换的复习经历了怎样的过程?师生活动:学生思考,教师引导得出:1.知识回顾;2.知识整理;3.策略迁移 设计意图:使学生进一步体会几何复习与研究的一般思路和方法. 问题2 复习的一般策略有哪些?师生活动:师生共同得出复习的一般策略有(1)理清研究思路;(2)整合研究内容;(3)归纳研究方法.设计意图:再次体会几何变换研究的基本思想方法,并推广到一般.B'EDCBA。
江苏省常州市花园中学九年级数学上册《直角三角形全等的判定》课件

13
学以致用
1. 如图,两根长度为12米的绳子,一端
系在旗杆上,另一端分别固定在地面两 个木桩上,两个木桩离旗杆底部的距离 相等吗?请说明你的理由。 解:BD=CD 依题意,得 ∠ADB=∠ADC=90° 又∵AB=AC(已知) AD=AD(公共边) ∴Rt△ABD≌Rt△ACD(HL) ∴BD=CD
B
∵∠C=∠C′=90°
∴在Rt△ABC和Rt△ABC中 A AB=AB
C B′
BC=BC
C′
10
B′ C′ (HL) A ′ ∴Rt△ABC≌ Rt△A′
知识在于积累
你能够用几种方法说明两个直角 三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判 定全等的方法,还有直角三角形特有的判定方法“HL”. 判断直 角三角 形全等 条件 SSS ASA AAS SAS HL 我们应根据具体问题的实际情况选择两个直角三角形 11 全等的方法.
7
B’
分析:AC=A’C’,无论RtΔ ABC和RtΔ A’B’C’的位置如何, 我们总是可以通过作旋转、平移、轴对称变换得到下面的图 形,即A‘C’ 和AC重合,点B'和点B分别在AC两侧.
∵ ∠ ACB= ∠ A’ C’ B’ =90 ° ∴ ∠ BCB’=180 ∴ B 、C 、B’在同一直线上, ∵ AB=A’B’ ∴ ∠ B= ∠ B’(等边对等角) ∵ AC=A’C’(公共边) ∠ B= ∠ B’ ∠ ACB= ∠ A’ C’ B’ ∴ ΔABC ≌ ΔA ’B’ C’(AAS)
C D
B
(5) ∠A=∠D, BC=EF ( AAS )
∠B=∠E (6) ________,AC=DF ( AAS )
初中数学《图形的全等》课堂课件北师大版1

活动探究
探究点一: 全等图形
初中数学《图形的全等》课堂课件北 师大版1
初中数学《图形的全等》课堂课件北 师大版1
活动探究
探究点一: 全等图形
初中数学《图形的全等》课堂课件北 师大版1
初中数学《图形的全等》课堂课件北 师大版1
活动探究
探究点一: 全等图形
初中数学《图形的全等》课堂课件北 师大版1
初中数学《图形的全等》课堂课件北 师大版1
4.2 图形的全等
七年级下册
答疑解惑
1.完成课本“做一做”,请问发现了什么?得到什么结论? 画三角形的一条角平分线,即可得两个全等的三角形,画三角形三个内角的 平分线,即可得三个全等的三角形,画三角形的三条中位线可得四个全等的三角形. 2.通过对课本中“议一议”的思考学习,你发现了什么规律? 能够完全重合的两个三角形叫做全等三角形;全等三角形的对应边、对应角相 等;全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全 等三角形的周长相等、面积也相等.
应顶点,AF与DE交于点M,则∠DCE等于( A )
A.∠B
B.∠A
C.∠EMF
D.∠AFB
初中数学《图形的全等》课堂课件北 师大版1
初中数学《图形的全等》课堂课件北 师大版1
随堂检测
4、如图,将长方形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1
=35°,则∠2的度数为( A )
初中数学《图形的全等》课堂课件北 师大版1 初中数学《图形的全等》课堂课件北 师大版1
再见
A.20°
B.30° C.35° 师大版1
初中数学《图形的全等》课堂课件北 师大版1
课堂小结
本节课都学到了什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
