2014清华大学自主招生数学真题答案

合集下载

清华大学历年自主招生试题汇总

清华大学历年自主招生试题汇总以下是2014年清华“领军计划”部分面试题：1、怎么看待单独二孩政策？2、谈谈对节假日安排的看法，有什么建议？3、怎么看待社会公平？以下是2014年清华“自强计划”部分面试题：结构性参考题目：提问：在你的同龄人中，当有些同学在为上学、吃饭、治病乃至整个家庭的生计发愁时，另外一些同学则在享受美味的食品、穿着流行的服装、接受各种优质的教育培训。

你如何看待这一现象?你是否认为这是一种社会不公?追问：你心目中的社会公平是怎样的?是否能够实现?若能实现，简要阐述实现的方法;若不能实现，请说说为什么?自由提问参考题目：请讲一个你的经历中体现你“自强”的故事。

你对自己的大学生活有何规划?将来想从事何种职业?你认为自己的家乡至今仍然贫困的原因是有哪些?应该如何解决?你曾经遇到过的最大困难是什么?你是如何面对和解决的?考察点：主要考察学生的个人理想与社会理想，是否能够独立思考并勇于创新，是否能够采取积极的方式克服困难与挫折;是否能够保持积极向上的心态等。

以下是清华大学2013年自主招生复试考题：1.近期上海、南京、杭州等地连续出现“H7N9禽流感”感染病例引起关注，公众非常想知道这方面的相关信息。

假如你是一位新闻发言人，你认为公众需要什么样的信息?追问:假如你发布信息后，社会出现恐慌，那该怎么办?2.“人类一思考，上帝就发笑”。

请就人类社会发展与大自然的关系发表评论。

追问:基于你的评价，你打算在当下和未来做些什么?3.请以“我和诺贝尔奖的距离”为题发表一段2分钟的演讲，可准备1分钟。

4.除了当选的10位人物外，举出你认为应该入围“2013‘感动中国’的一位人物”，并阐述理由。

2008年清华大学自主招生考试题目选语文（此文与原考试选用的文章稍有出入）（语文试题应该算是完整版了）：关于文学和它的寄主的故事朱大可关于文学死亡的话题，已经成为众人激烈争论的焦点。

这场遍及全球的争论，映射了文学所面临的生存危机。

近几年清华、北大自主招生数学试题

近年北大清华自主招生试题汇编———————————————————————————————— 2010北大自主招生（三校联招） 1．（仅文科做）02απ<<，求证：sin tan ααα<<．（25分）2．AB 为边长为1的正五边形边上的点．证明：AB ．（25分） 3．AB 为21y x =-上在y 轴两侧的点，求过AB 的切线与x 轴围成面积的最小值．（25分） 4．向量OA 与OB 已知夹角，1OA =，2OB =，(1)OP t OA =-，OQ tOB =，01t ≤≤．PQ在0t 时取得最小值，问当0105t <<时，夹角的取值范围．（25分）5．（仅理科做）存不存在02x π<<，使得sin ,cos ,tan ,cot x x x x 为等差数列．（25分）2009北大自主招生数学试题1 圆内接四边形ABCD ，AB=1，BC=2，CD=3，DA=4。

求圆半径。

2 已知一无穷等差数列中有3项：13，25，41。

求证：2009为数列中一项。

3 是否存在实数x 使tanx+（根3）与cotx+（根3）为有理数？4 已知对任意x 均有acosx+bcos2x>=-1恒成立，求a+b 的最大值5 某次考试共有333名学生做对了1000道题。

做对3道及以下为不及格，6道及以上为优秀。

问不及格和优秀的人数哪个多？3 已知123123122331122331123123123123min(,,)min(,,)max(,,)max(,,)a a ab b b a a a a a a b b b b b b a a a b b b a a a b b b ++=++++=++≤≤求证：4 排球单循坏赛南方球队比北方球队多9支南方球队总得分是北方球队的9倍求证冠军是一支南方球队（胜得1分败得0分）5（理科）O-XYZ 坐标系内 xoy 平面系内202y x ≤≤-绕y 轴旋转一周构成一个不透光立体在点(1,0,1)设置一光源 xoy 平面内有一以原点为圆心的圆C 被光照到的长度为2π 求C 上未被照到的长度2009年清华大学自主招生数学试题的整数部分为a ，小数部分为b ()1求,a b ；()2求222ab a b ++； ()3求()2lim n n b b b →∞++ 2．()1,x y 为实数，且1x y +=，求证：对于任意正整数n ，222112n nn x y -+≥()2,,a b c 为正实数，求证：3a b cx y z++≥，其中,,x y z 为,,a b c 的一种排列 3．请写出所有三个数均为质数，且公差为8的等差数列，并证明你的结论4．已知椭圆22221x y a b+=，过椭圆左顶点(),0A a -的直线L 与椭圆交于Q ，与y 轴交于R ，过原点与L 平行的直线与椭圆交于P 求证：AQ ，AR 成等比数列5．已知sin cos 1t t +=，设cos sin s t i t =+，求2()1nf s s s s =+++6．随机挑选一个三位数I()1求I 含有因子5的概率；()2求I 中恰有两个数码相等的概率7．四面体ABCD 中，AB CD =，AC BD =，AD BC =()1求证：四面体每个面的三角形为锐角三角形；()2设三个面与底面BCD 所成的角分别为,,αβγ，求证：cos cos cos 1αβγ++=8．证明当,p q 均为奇数时，曲线222y x px q =-+与x 轴的交点横坐标为无理数 9．设1221,,,n a a a + 均为整数，性质P 为：对1221,,,n a a a + 中任意2n 个数，存在一种分法可将其分为两组，每组n 个数，使得两组所有元素的和相等求证：1221,,,n a a a + 全部相等当且仅当1221,,,n a a a + 具有性质P2009年清华大学自主招生数学试题（文科） 1．已知数列{}n a ，且()1n S na n n =+-()1求证：{}n a 是等差数列； ()2求,nn S a n⎛⎫⎪⎝⎭所在的直线方程 2．12名职员（其中3名为男性）被平均分配到3个部门()1求此3名男性被分别分到不同部门的概率； ()2求此3名男性被分到同一部门的概率；()3若有一男性被分到指定部门，求其他2人被分到其他不同部门的概率3．一元三次函数()f x 的三次项数为3a，()90f x x +<的解集为()1,2 ()1若()70f x a +=，求()f x 的解析式； ()2若()f x 在上单调增，求a 的范围4．已知PM PN -=()2,0M -，()2,0N ，求点P 的轨迹W ；直线()2y k x =-与W 交于点A 、B ，求S OAB （O 为原点） 5．设()12nx x x a n n++=∈()()()()()()12231n n n S x a x a x a x a x a x a -=--+--++--()1求证：30S ≤()2求4S 的最值，并给出此时1x ，2x ，3x ，4x 满足的条件()3若50S <，求1x ，2x ，3x ，4x ，5x 不符合时的条件2008届清华大学自主招生试题1. 已知,,a b c数；2. （1）一个四面体，证明：至少存在一个顶点，从其出发的三条棱组成一个三角形；（2）四面体一个顶点处的三个角分别是,,arctan 223ππ，求3π的面和arctan 2的面所成的二面角；3. 求正整数区间[],()m n m n <中，不能被3整除的整数之和；4. 已知sin cos αα+=α的取值范围；5. 若2lim ()(0)1,(2)()x f x f f x f x x →==-=，求()f x ；6. 证明：以原点为中心的面积大于4的矩形中，至少还有两个格点。

近十年清华北大自主招生试题汇总

1.（2007清华）对于集合2M R ⊆（表示二维点集），称M 为开集，当且仅当0,0P M r ∀∈∃>，使得{}2P R PP r M ∈<⊆⎰。

判断集合{}(,)4250x y x y +->⎰与集合{}(,)0,0x y x y ≥>⎰是否为开集，并证明你的结论。

2，（2009北大）已知,cos cos 21x R a x b x ∀∈+≥-恒成立，求max ()a b +3，（2009清华）已知,,0x y z >，a 、b 、c 是x 、y 、z 的一个排列。

求证：3a b c x y z ++≥。

4，（2006清华）已知a ，b 为非负数，44M a b =+，a+b=1，求M 的最值。

5，（2008北大）实数(1,2,i i a i b i ==满足123a a a b b b ++=++，122313122313a a a a a a bb b b bb ++=++，123123min(,,)min(,,)a a a b b b ≤。

求证：12312m a x (,,)m a x (,,)a a a b b b ≤。

6，（2009清华）试求出一个整系数多项式110()n n n n f x a x a x a --=+++…，使得()0f x =有一根为7，（2009清华）x>0,y>0,x+y=1,n 为正整数，求证：222112n n n xy -+≥8，（2007北大）已知22()5319653196f x x x x x =-++-+，求f(1)+f(2)+…＋f(50)。

9，（2006清华）设正三角形1T 的边长为a ，1n T +是n T 的中点三角形，n A 为n T 除去1n T +后剩下三个三角形内切圆面积之和，求1lim n k n k A →∞=∑。

10，（2008北大）数列{}1n n a ∞=定义如下：1234561,2,3,a a a a a a ======……（1）给定自然数n ，求使l a n =的L 的范围；（2）令221m m l l b a ==∑，求3limm m b m →∞。

2014届全国自主招生模考北约数学2答案

北约数学答案2 一、选择题二、解答题 7、解：由均值不等式得2222)]2()2[()()4()(c b c a b a c b a b a +++++=++++………………………(3分)ab c bc ac ab bc ac ab ⋅⋅⋅⋅+⋅+⋅+=++≥222224244)2222()2(22ab c bc ac ab 16884+++=,………………………(6分)∴)(16884)()4()(22c b a abcabc bc ac ab c b a abc c b a b a ++⋅+++≥++⋅++++ 488111()8()22222a ab b a bc c c b a c b a =+++++=+++++++ 100)25()215(85422522=⋅⋅⋅≥c b a c b a ,………………………(6分)等号成立当且仅当02>==c b a , 故k 的最大值为100 .………………………(3分)8、解：结论成立. ………………………(4分)由a 是有理数，可知对一切正整数n ，n a 为0或正有理数，可设n nn q p a =（n p 是非负整数，n q 是正整数，且,n n p q 互质）………………………(2分)由111p pa q q ==，可得q p <≤10；………………………(2分)若0≠n p ，设n n q p αβ=+（n p <≤β0，βα,是非负整数）则nn n p p q βα+= ，而由n n n q p a =得n n n p q a =1 11n n n n nq a a p p β+===，故β=+1n p ，nn p q =+1，可得nn p p <≤+10………………………(3分)若=n p ，则1=+n p ，………………………(2分)若q a a a a ,,,,321⋅⋅⋅均不为0，则这q 正整数(1,2,3,,)n p n q =L 互不相同且都小于q ，但小于q 的正整数共有1-q 个，矛盾.………………………(3分)故q a a a a ,,,,321⋅⋅⋅中至少有一个为0，即存在)1(q m m ≤≤，使得0=m a . 从而数列{}n a 中m a 以及它之后的项均为0，所以对于大于q 的自然数n ，都有0=n a………………………(2分)9、解：设所求的两位数为x,则有自然数s 、t ，满足10210(1),10510(1)s n s t n t x x x x <<+<<+………………………(6分)两式相乘得+t22101010(1)s n s t x x +<<+………………………(2分)因为x 是两位数，224242321099,10,(1)1010103,10(1)10001,31s t n s t x x x n s t x x x x x ++++≤≤≤+≤<<=++<<+<<+=所以10所以这个两位数是31.……………………(10分)10、解：因为B m =（b m1，b m2，b m3，b m4）满足．由b m1，b m2，b m3，b m4关系的对称性，只需考虑（b m2，b m3，b m4）与（a 1，a 2，a 3）的关系数的情况．……………………(4分)当b m1=0时，有．……………………(3分)==．……………………(4分)即b m1=0，且，，时，a1b m2+a2b m3+a3b m4的最大值为m．当时，，……………………(4分)得a1b m2+a2b m3+a3b m4m所以C（A，B m m（m=1，2，3，…，n）．……………………(3分)。

2014年数学(理)参考答案

数学（理）（北京卷）参考答案第 1 页（共 6 页）绝密★考试结束前2014年普通高等学校招生全国统一考试数学（理）（北京卷）参考答案一、选择题（共8小题，每小题5分，共40分）（1）C （2）A （3）B （4）C （5）D（6）D（7）D（8）B二、填空题（共6小题，每小题5分，共30分）（ 9 ）1-（10（11）221312x y -= 2y x =± （12）8 （13）36（14）π三、解答题（共6小题，共80分）（15）（共13分）解：（Ⅰ）在ADC △中，因为1cos 7ADC ∠=，所以sin ADC ∠=所以sin sin()BAD ADC B ∠=∠-∠sin cos cos sin ADC B ADC B =∠-∠1127=-=．（Ⅱ）在ABD △中，由正弦定理得8sin 3sin AB BAD BD ADB⋅∠===∠．在ABC △中，由余弦定理得 2222cos AC AB BC AB BC B =+-⋅⋅22185285492=+-⨯⨯⨯=．所以7AC =．（16）（共13分）解：（Ⅰ）根据投篮统计数据，在10场比赛中，李明投篮命中率超过0.6的场次有5场，分别是主场2，主场3，主场5，客场2，客场4．所以在随机选择的一场比赛中，李明的投篮命中率超过0.6的概率是0.5.（Ⅱ）设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”，事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”，事件C为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6,一场不超过0.6”．则C AB AB=，,A B独立．根据投篮统计数据，3()5P A=，2()5P B=．()()()P C P AB P AB=+33225555=⨯+⨯1325=．所以，在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6,一场不超过0.6的概率为13 25．（Ⅲ）EX x=．数学（理）（北京卷）参考答案第 2 页（共6 页）数学（理）（北京卷）参考答案第 3 页（共 6 页）（17）（共14分）解：（Ⅰ）在正方形AMDE 中，因为B 是AM 的中点，所以//AB DE ．又因为AB ⊄平面PDE ，所以//AB 平面PDE ．因为AB ⊂平面ABF ，且平面ABF 平面PDE FG =，所以//AB FG ．（Ⅱ）因为PA ⊥底面ABCDE ，所以PA AB ⊥，PA AE ⊥．如图建立空间直角坐标系Axyz ，则(0,0,0)A ，(1,0,0)B ，(2,1,0)C ，(0,0,2)P ，(0,1,1)F ，(1,1,0)BC −−→=．设平面ABF 的法向量为(,,)n x y z =，则0,0,AB AF −−→−−→⎧⋅=⎪⎨⎪⋅=⎩n n 即0,0.x y z =⎧⎨+=⎩ 令1z =，则1y =-．所以(0,1,1)=-n ．设直线BC 与平面ABF 所成角为α，则 sin |cos ,|||||BCBC BC α−−→−−→−−→⋅=〈〉=n n n 12=．因此直线BC 与平面ABF 所成角的大小为π6．设点H 的坐标为(,,)u v w ．因为点H 在棱PC 上，所以可设PH PC λ−−→−−→= (01λ<<)，即(,,2)(2,1,2)u v w λ-=-．所以2u λ=，v λ=，22w λ=-．因为n 是平面ABF 的法向量，所以0AH −−→⋅=n ，即(0,1,1)(2,,22)0λλλ-⋅-=．解得23λ=，所以点H 的坐标为422(,,)333．所以2PH =．数学（理）（北京卷）参考答案第 4 页（共 6 页）（18）（共13分）解：（Ⅰ）由()cos sin f x x x x =-得()cos sin cos sin f x x x x x x x '=--=-．因为在区间π(0,)2上()sin 0f x x x '=-<，所以()f x 在区间π[0,]2上单调递减．从而()(0)0f x f =≤．（Ⅱ）当0x >时，“sin x a x >”等价于“sin 0x ax ->”；“s i n xb x<”等价于“sin 0x bx -<”．令()sin g x x cx =-，则()cos g x x c '=-．当0c ≤时，()0g x >对任意π(0,)2x ∈恒成立．当1c ≥时，因为对任意π(0,)2x ∈，()cos 0g x x c '=-<，所以()g x 在区间π[0,]2上单调递减．从而()(0)0g x g <=对任意π(0,)2x ∈恒成立．当01c <<时，存在唯一的0π(0,)2x ∈使得00()cos 0g x x c '=-=．()g x 与()g x '在区间π(0,)2上的情况如下：因为(g x 00．进一步，“()0g x >对任意π(0,)2x ∈恒成立”当且仅当ππ()1022g c =-≥，即20πc <≤．综上所述，当且仅当2πc ≤时，()0g x >对任意π(0,)2x ∈恒成立；当且仅当1c ≥时，()0g x <对任意π(0,)2x ∈恒成立．所以，若sin x a b x <<对任意π(0,)2x ∈恒成立，则a 的最大值为2π，b 的最小值为1．数学（理）（北京卷）参考答案第 5 页（共 6 页）（19）（共14分）解：（Ⅰ）由题意，椭圆C 的标准方程为22142x y +=．所以24a =，22b =，从而2222c a b =-=．因此2a =，c 故椭圆C的离心率c e a ==．（Ⅱ）直线AB 与圆222x y +=相切．证明如下：设点,A B 的坐标分别为00(,),(,2)x y t ，其中00x ≠．因为OA OB ⊥，所以0OA OB −−→−−→⋅=，即0020tx y +=，解得02y t x =-．当0x t =时，202t y =-，代入椭圆C的方程，得t =故直线AB的方程为x =O 到直线AB的距离d 此时直线AB 与圆222x y +=相切．当0x t ≠时，直线AB 的方程为0022()y y x t x t--=--，即0000(2)()20y x x t y x ty ---+-=．圆心O 到直线AB 的距离d =．又220024x y +=，02y t x =-，故d ===此时直线AB 与圆222x y +=相切．数学（理）（北京卷）参考答案第 6 页（共 6 页）（20）（共13分）解：（Ⅰ）1()257T P =+=，21()1max{(),24}1max{7,6}8T P T P =++=+=．（Ⅱ）2()max{,}T P a b d a c d =++++，2()max{,}T P c d b c a b '=++++．当m a =时，2()max{,}T P c d b c a b c d b '=++++=++．因为a b d c b d ++++≤，且a c d c b d ++++≤，所以22()()T P T P '≤．当m d =时，2()max{,}T P c d b c a b c a b '=++++=++．因为a b d c a b ++++≤，且a c d c a b ++++≤，所以22()()T P T P '≤．所以无论m a =还是m d =，22()()T P T P '≤都成立．（Ⅲ）数对序列:(4,6),(11,11),(16,11),(11,8),(5,2)P 的5()T P 值最小，12345()10,()26,()42,()50,()52T P T P T P T P T P =====．。

2014-2015重点高中自主招生数学试题及答案 (2)

2014-2015重点高中自主招生数学模拟试题一．选择题（每小题5分，共40分）1.一个空间几何体的三视图如图所示,则该几何体的体积为（ D ）A．2π+B ．83πC ．4πD．2π2.已知A （1x ，1y ），B （2x ，2y ）是反比例函数xy 1=在平面直角坐标系xOy 的第一象限上图象的两点，满足2721=+y y ，3512=-x x . 则=∆AOB S （ B ） A ．11102 B. 12112 C. 13122 D. 141323.有2 015个整数，任取其中2 014个相加，其和恰可取到1，2，…，2 014这2 014个不同的整数值. 则这2 015个整数之和为（）A ．1 004 B. 1 005 C. 1 006 D. 1 0083.设2 015个整数为1x ，2x ，…，2015x .记1x +2x +…+2015x =M.不妨设M-i x =i （i =1，2，…，2014），M-2015x =A.则2014M=1+2+…+2014+A.故A 除以2014的余数为1007.从而，A=1007，M=1008.当i x =1008-i （i =1，2，…，2014），2015x =1时取到.4.有编号分别为1，2，3，4，5的5个红球和5个黑球，从中取出4个，则取出的球的编号互不相同的概率为 ( D )A. 521.B. 27.C. 13D. 8214、解从10个球中取出4个，不同的取法有410C 210=种.如果要求取出的球的编号互不相同，可以先从5个编号中选取4个编号，有45C 种选法.对于每一个编号，再选择球，有两种颜色可供挑选，所以取出的球的编号互不相同的取法有445C 280⋅=种.因此，取出的球的编号互不相同的概率为80821021=. 故选（D ）.5. 使得381n+是完全平方数的正整数n 有（ B ）2 2 2侧（左）视222正（主）视俯视图.A. 0个B. 1个C. 2个D. 3个5、解当4n ≤时，易知381n +不是完全平方数.故设4n k =+，其中k 为正整数，则38181(31)n k +=+.因为381n +是完全平方数，而81是平方数，则一定存在正整数x ，使得231k x +=，即231(1)(1)k x x x =-=+-，故1,1x x +-都是3的方幂.又两个数1,1x x +-相差2，所以只可能是3和1，从而2,1x k ==.因此，存在唯一的正整数45n k =+=，使得381n +为完全平方数.故选（B ）.6.如图，已知AB 为⊙O 的直径，C 为⊙O 上一点，C D ⊥AB 于D ，AD=9，BD=4，以C 为圆心，CD 为半径的圆与⊙O 相交于P,Q 两点，弦PQ 交CD 于E ，则PE •EQ 的值是（ D ）A ．24 B. 9 C. 36 D. 277.已知实系数一元二次方程x 2+(1+a)x+a+b+1=0的两实根为x 1,x 2,且0 ＜x 1＜1，x 2＞1，则ab 的取值范围（） A -1＜a b 21-≤ B -1＜a b ＜21- C -2＜a b 21-≤ D -2＜a b ＜21-8. 图中正方形ABCD 边长为2，从各边往外作等边三角形ABE 、BCF 、CDG 、DAH ，则四边形AFGD 的周长为 ( )A.4+26+22B. 2+26+22C. 4+23 +42 D ．4+23+42 二．填空题（每小题6分，共36分） 9.设由1～8的自然数写成的数列为1a ，2a ，…，8a .则32 .由题意记S=21a a -+32a a -+43a a -+54a a -+65a a -+76a a -+87a a -+18a a -. 该式去掉绝对值符号，在这个和的任意加项中，得到一正、一负两个自然数，为了使和达到最大的可能值，只须由1～4取负，由5～8取正，于是，S=2[（8+7+6+5）-（4+3+2+1）]=32.如48-+74-+17-+51-+25-+62-+36-+83-=32.10.记[]x 表示不超过实数x 的最大整数，a k =⎥⎦⎤⎢⎣⎡k 2014(k=1,2,, 100,则在这100个整数中，不同的整数的个数为 6911.设非负实数x,y,z 满足x+y+z=1,则t=29x ++24y ++21z +12．如图所示，线段OA = OB = OC =1，∠AOB = 60º，∠B OC = 30º，以OA ，OB ，OC 为直径画3个圆，两两的交点为M ，N ，P ，则阴影部分的曲边三角形的面积是．解：如图，连接AC ，AN ，BN ，AM ，BM ， MP ，NP ，OM ，ON ，OP ，易知∠OP A =∠OPC =90º，∠ANO =∠BNO = 90º，∠BMO =∠CNO = 90º，所以A ，P ，C 共线；A ，N ，B 共线；B ，M ，C 共线．由OA =OB =OC =1，可知P ，M ，N 分别是AC ，BC ，AB 的中点，MPNB 为平行四边形，BN =MP ，BM =NP ，所以BN 与MP 长度相等，BM 与NP 长度相等，因此，曲边三角形MPN 的面积= S MPNB =12S △ABC ，而 S △ABC = S AOCB – S △AOC = S△AOB + S △BOC – S△AOC 1142-所以，曲边三角形MPN 的面积=12S △ABC 13. 将一个44⨯棋盘中的8个小方格染成黑色，使得每行、每列都恰有两个黑色方格，则有不同的染法.（用数字作答）解：第一行染2个黑格有24C 种染法.第一行染好后，有如下三种情况：（1）第二行染的黑格均与第一行的黑格同列，这时其余行都只有一种染法；（2）第二行染的黑格与第一行的黑格均不同列，这时第三行有24C 种染法，第四行的染法随之确定；（3）第二行染的黑格恰有一个与第一行的黑格同列，这样的染法有4种，而在第一、第二这两行染好后，第三行染的黑格必然有1个与上面的黑格均不同列，这时第三行的染法有2种，第四行的染法随之确定. 因此，共有染法为()9024616=⨯++⨯种.填90.14.圆O 的半径为1，P 为圆周上一点，现将如图放置的边长为1的正方形（实线所示，正方形的顶点A 与点P 重合）沿圆周顺时针滚动。

14-18年北清自招龅牙领军数学真题-函数的性质与图像

清华领军2015.4.设函数()f x 的定义域为（-1，1），且满足：①()0,(1,0)f x x >∈-；②()()1x y f x f y f xy ⎛⎫++= ⎪+⎝⎭，(1,1)x y ∈-、，且()f x 为（）A.奇函数B.偶函数C.减函数D.有界函数清华领军2015.5.如图，已知直线y kx n =+与曲线()y f x =相切于两点，则()()F x f x kx =-有（）A.2个极大值点B.3个极大值点C.2个极小值点D.3个极小值点同时分入了导数类清华领军2015.23.设函数2sin π()1xf x x x =-+，则（）A.4()3f x ≤B.|()|5||f x x ≤C.由线()y f x =存在对称轴D.曲线()y f x =存在对称中心清华领军2015.30.设曲线L 的方程为42242(22)(2)0y x y x x +++-=，则（） A.L 是轴对称图形 B.L 是中心对称图形 C.22{(,)|1}L x y x y ⊂+≤ D.11(,)|22L x y y ⎧⎫⊂-≤≤⎨⎬⎩⎭同时分入函数的极值类清华领军2017.15.已知2()f x x ax b =++在(1,1)x ∈-上有两个零点。

求22a b -的取值范围。

A.(0,)+∞B.(0,2)C.(,2)-∞D.(2,2)-清华领军2017.21.满足35(3)40x y x x y ++++=的(,)x y （） A.在一条直线上 B.在一条抛物线上 C.为有限个 D.为无限个分类存疑北大自招2016.1. 求()212log 2x x -++的单调增区间。

1.【解答】1,22⎛⎫ ⎪⎝⎭要求()212log 2x x -++的单调增区间，由12log x 是在()0,+∞上的减函数，故即解2201,2122x x x x ⎧-++>⎪⎛⎫⇒∈⎨ ⎪>⎝⎭⎪⎩北大自招2016.5. 设x ，y ，z 3R ∈，求方程381nnnx y z ++≤，当n →+∞时确定的几何体的体积为________。

清华大学自主招生试题数学 Word版含解析

一、选择题1.设复数z=cos 23π+isin 23π，则2111-1z z +-=（） (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列，p,q,k,l 为正整数，则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点，O 是坐标原点，若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1)，且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x yf xy++，x 、y ∈(-1,1)，则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)−kx 有（）(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c ．若c=2，∠C=3π，且sinC+sin(B −A)−2sin2A=0,则有（） (A)b=2a (B)△ABC 的周长为3 (C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-，则（）(A)()f x 有极小值，但无最小值 (B) ()f x 有极大值，但无最大值 (C)若方程()f x =b 恰有一个实根，则b>36e(D)若方程()f x =b 恰有三个不同实根，则0<b<36e 8.已知A={(x,y)∣222x y r +=}，B={(x,y)∣222()()x a y b r -+-=，已知A∩B={(11,x y ),(22,x y )}，则（）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ，12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3，则5x+4y+3z 的最小值为（） (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ，若对任意正整数n ，总存在正整数m ，使得n S =m a ，则（）（A ）{n a }可能为等差数列（B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ，总存在正整数m ，使得n a =m S11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（） (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中，AB=2，AD=A 1A =1，则A 到平面1A BD 的距离为（）(A)13 (B)23(C)22 (D)6313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ，其面积为S ，则（）(A)若S=4，则k 的值唯一 (B)若S=12，则k 的值有2个(C)若D 为三角形，则0<k ≤23(D)若D 为五边形，则k>4 14.△ABC 的三边长是2,3,4，其外心为O ，则OA AB OB BC OC CA ⋅+⋅+⋅=（） (A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立，且P(B)=0.5，P(A −B)=0.2，则（）(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分，则这两部分的面积之比的（） (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形，则不同的选法有（）(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ，使得圆周222x y r +=上恰好有n 个整点，则n 可以等于（） (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|，则（） (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数，a =(mcosα,msinα)，b =(ncosβ,nsinβ)，其中α,β∈[0,2π)α,β∈[0,2π)．定义向量12a =(2m α2m α),12b =(2n β2n β)，记θ=α−β，则（）(A)12a ·12a =a (B)1122a b ⋅=2mn θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足：1a =6，13n n n a a n++=，则（） (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中，下列方程表示的图形是椭圆的有（）（A ）ρ=1cos sin θθ+ （B ）ρ=12sin θ+ （C ）ρ=12cos θ- （D ）ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+，则（）（A ）()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ，若△ABC 为锐角三角形，则（） (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1)，若(0)f =(0)f '=1，则存在实数δ∈(0,1)，使得（） (A)()f x >0，x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1，x ∈(0,δ) (D)()f x >1，x ∈(−δ,0)26.在直角坐标系中，已知A(−1,0)，B(1,0)．若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n)，总存在两个不同的点i P ,j P ，使得|sin ∠A i P B −sin ∠A j P B|≤13，则n 的最小值为（）(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1，则22x y + ）(A)最小值为45 (B)最小值为25(C)最大值为1 (D)最大值为12328.对于50个黑球和49个白球的任意排列（从左到右排成一行），则（）(A)存在一个黑球，它右侧的白球和黑球一样多 (B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（） (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0，则（） (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()333(cossin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]663i ππ-+- 31sin )6623i i ππ+=1，选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ，与公差d 的符号有关，选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅2211221111(1)(1)x x x x ++2121111x x +++11122||||x x +⋅=2，正确；答案(B),|OA|+|OB|≥2||||OA OB ⋅22,正确；答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程，错误；答案(D)，原点到直线AB ：(111x x -)x-y+1=0的距离2111()1x x -+1，正确。

清华大学自主招生面试题

以下是小编为大家做了的2014年清华大学自主招生笔试题目!!!一、中英文综合(200分)(一)、语文部分(95分)1、甲文：白居易的粉丝(9分)(1)、请解释什么是“白居易现象”。

(2)、“文章已满行人耳，一度思卿一怆然。

”一句中的“文章”指的是什么?(3)、陈至呼为“白舍人行诗图”的根据是什么?(4)、作者写到“打开整部中国文学史上，与大众如此呼吸相通，生息相关，声气相连，心神相交的文人，还真是很少见有与他相匹敌者。

”作者似乎另有感慨，作者感慨的是什么哪2、乙文：4年前与奥巴马的邂逅(11分)(略)(1)、请具体说明文中“如同奥巴马所期待的那样”指的是什么?(2)、下文为奥巴马当选总统后的演讲，请说明文中“我”的作用和下文中安·尼克松·库伯的作用分别是什么?3、丙文：历史与记忆(13分)(略)(1)、文中“记忆能否擦拭掉历史的尘垢，恢复其本来面目?”显然有两种回答：能或不能。

请选择一种，并举例论证。

(2)、“在押往集中营的火车上，她设法递出了令人揪心的一封明信片。

她说，她不知道她的孩子在哭泣，在挨饿?他要死了吗?她希望有人去照料一下她的孩子啊!这份明信片现在就在博物馆里展出。

"作者举这个例子的目的是什么?(3)、如果《中国发展年鉴》要增加一个词条“城市记忆”，请你做一个解释。

(30字以内)4、丁文：传统油画过气了吗?(12分)(略)(1)、最后说这种诗意又是“东方式”的，怎么理解?(2).式微一词出自哪?它的意思是什么?(3)、文中与架上油画意思相同的词还有哪些?(请写出两个)(4)、传统油画仍是绘画艺术中魅力犹存的主流样式。

在作者看来，原因是什么5、甲--丁文：作文(1)、下面的词都是与原文相关的词汇，选择其中的5个，做简单的解释。

(5分)IT 粉丝过气涂鸦小众化(2)、上面四篇文章是选自某一期报纸的某一版面，请你为这个版面拟一个称谓，并说明你的构想(800字左右)(45分)(二)、英语部分(80分)1、10个词汇题，给出一句话，将其中一个词划线，从A、B、C、D中选出与划线词意思相近的词。

2014高中自主对外招生数学试卷和答案

高中自主招生考试数学(试卷满分：150分考试时间：120分钟)准考证号姓名座位号注意事项：1.全卷三大题，22小题，试卷共4页，另有答题卡；2.答案一律写在答题卡上，否则不能得分．一.选择题(本题有6个小题,每小题4分,共24分．每小题只有一个选项是正确的.) 1．如果1-=ab ,那么两个实数a ,b 一定是( )A ．互为倒数B ．-1和+1C ．互为相反数D ．互为负倒数 2．下列运算正确的是（） A ．()b a ab 33= B ．1-=+--ba ba C ．326a a a =÷ D ．222)(b a b a +=+3．已知一组数据：12，5，9，5，14，下列说法不正确的是（）A ．平均数是9B ．中位数是9C ．众数是5D ．极差是5 4．长方体的主视图、俯视图如右图所示，则其左视图面积为（）A ．3B ．4C ．12D ．16 5．在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、双曲线、圆，在看不见图形的情况下随机摸出1张，这张卡片上的图形既是中心对称图形又是轴对称图形的概率是（） A ．16 B ．13 C ．12 D ．236．如图，已知⊙O 的半径为r ，C 、D 是直径AB 的同侧圆周上的两点，100AOC ∠=，D 是BC 的中点，动点P 在线段AB 上，则PC ＋PD 的最小值为（） A ．r Br CDr CPDO BA（第6题）二．填空题(本题有8个小题，每小题5分．共40分) 7．实数b a ,满足0132=+-b a ，则ba 的值为．9．在同一坐标系中，图形a 是图形b 向上平移3个单位长度，再向左平移2个单位得到，如果图形a 中A 点的坐标为（4，－2），则图形b 中与A 点对应的A '点的坐标为___ ____. 10．如图，在四边形纸片ABCD 中，∠A =130°，∠C =40°，现将其右下角向内折出∆FGE ，折痕为EF ，恰使GF ∥AD ，GE ∥CD ，则∠B 的度数为．11．对于实数a 、b ，定义运算⊗如下：=⊗b a ⎪⎩⎪⎨⎧≠≤≠>-)0,()0,(a b a a a b a a b b，例如1612424==⊗-. 计算 [][]=⊗-⨯⊗2)3(23 .13．已知直线1y x =，213y x =+，633+-=x y 的图象如图所示，无论x 取何值，当y 总取1y 、2y 、3y 中的最小值时， y 的最大值为14．若关于t 的不等式组0214t a t -≥⎧⎨+≤⎩恰好有三个整数解，则关于x 的一次函数14y x a=- 的图像与反比例函数32a y x+=的图像的公共点的个数为 . （第12题）G FE DCBA（第10题）三、解答题(本题有8个小题，共86分，解答应写出文字说明,证明过程或推演步骤.) 15．（本题满分7分）计算01( 3.14)(sin30)4cos 45π︒-︒-++-16．（本题满分9分）已知2)2()]2()()[(22=-÷-++--y y x y y x y x ．求228242x x y x y---的值．17．（本题满分10分）如图，直线AB 交双曲线()y 0kx x=>于A ，B 两点，交x 轴于点C (4,0)a ， AB =2BC ，过点B 作BM ⊥x 轴于点M ，连结OA ，若OM =3MC ，S △OAC =8，则k 的值为多少？18. （本题满分10分）如图，在菱形ABCD 中，AB ＝23，∠A ＝60°，以点D 为圆心的⊙D 与AB 相切于点E ，与DC 相交于点F . （1）求证：⊙D 与BC 也相切；（2）求劣弧EF 的长(结果保留π)．19．（本小题满分12分）某商家计划从厂家采购A ，B 两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．（1）求A 产品的采购数量与采购单价的函数关系式；（2）该商家分别以1760元/件和1700元/件的销售单价出售A ，B 两种产品，且全部售完，在A 产品的采购数量不小于11且不大于15的条件下，求采购A 种产品多少件时总利润最大，并求最大利润．（第18题）（第17题）ABCCDDEE FFA20．（本小题满分12分）如图，在△ABC 中，∠CAB =90°，D 是斜边BC 上的中点，E 、F 分别是AB 、AC 边上的点，且DE ⊥DF .（1）若AB =AC ，BE +CF =4，求四边形AEDF 的面积。

2014年XXX数学试点班自主招生考试题解析

2014年XXX数学试点班自主招生考试题解析2014年XXX数学试点班自主招生考试题（A卷）总分：200分考试时间：2014-2-16 8:30-11:30一．填空题（每小题7分，共70分）1.若单位向量a，b满足|2a-3b|=10，则|3a+2b|=4.解析：由|2a-3b|=10平方得：13-12a·b=10，即a·b=1/4.则|3a+2b|=√(13+12a·b)=4.2.若非零复数z满足|z|+z·(1+i)-z=0，则复数z的实部为-2/5.解析：设z=x+yi(x,y∈R)，由|z|+z·(1+i)-z=0得：(x+y-y)+(x+2yi)=0，即2x+2yi=-(1+i)y。

则x=-2/5.3.无重复数字（不含4）且4与5不相邻的五位数共有个。

解析：用排除法。

不含5的无重复数字的五位数共A9=个，其中，4和5相邻的无重复数字的五位数共C7A4A2=1680个。

所以，无重复数字（不含4）且4与5不相邻的五位数共有-1680=个。

4.在三棱锥P-ABC中，底面为边长为3的正三角形，且PA=3，PB=4，PC=5，则三棱锥P-ABC的体积VP-ABC=11.解析：易知△PBC是直角三角形，取斜边PC的中点为O，因为AP=AB=AC，所以点A在平面PBC上的射影为直角△PBC的外心O，连接AO，即有AO⊥平面PBC。

在直角△AOP中，AO=√(AP^2-PO^2)=√(3^2-()^2)=√8，则VP-ABC=VA-PBC=1/3·S△PBC·AO=1/3·6·√8=11.5.在△ABC中，A为钝角，以下结论正确的是：①sinB<cosC；②sinA<XXX<2；④sinB+sinC<1.解析：A为钝角，则∠B+∠C<π/2.所以：①sinB<sin(π/2-∠C)=cosC；②sinA<sin(∠B+∠C)=XXX<sinB+sinC；③tanB+tanC=(sinB/cosB)+(sinC/cosC)<2；④sinB+sinC<1.故①②④正确。

清华大学自主招生试题含答案

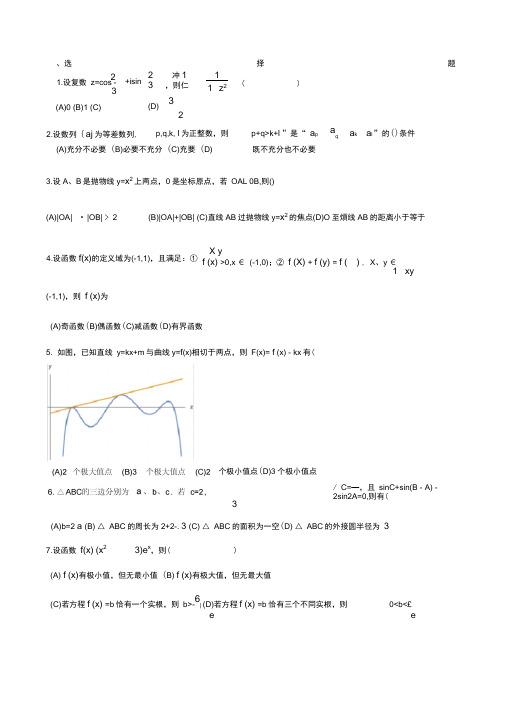
、选择题2( )(A)充分不必要(B)必要不充分(C)充要(D)3.设A、B是抛物线y=x2上两点，0是坐标原点，若OAL 0B,则()(A)|OA| •|OB| > 2 (B)|OA|+|OB| (C)直线AB过抛物线y=x2的焦点(D)O至煩线AB的距离小于等于X yf (x) >0,x € (-1,0)；② f (X) + f (y) = f ( ) , X、y €1 xy(-1,1)，则f (x)为(A)奇函数(B)偶函数(C)减函数(D)有界函数5. 如图，已知直线y=kx+m与曲线y=f(x)相切于两点，则F(x)= f (x) - kx有(/ C=—，且sinC+sin(B - A) -2sin2A=0,则有(3(A)b=2 a (B) △ ABC的周长为2+2-. 3 (C) △ ABC的面积为一空(D) △ ABC的外接圆半径为37.设函数f(x) (x23)e x，则( )(A) f (x)有极小值，但无最小值(B) f (x)有极大值，但无最大值(C)若方程f (x) =b恰有一个实根，则b>-6| (D)若方程f (x) =b恰有三个不同实根，则0<b<£e e1.设复数z=cos -3+isin (A)0 (B)1 (C) 2 冲13 ，则仁(D)3211 z22.设数列｛aj为等差数列, p,q,k, l为正整数，则p+q>k+l ”是“ a p aqa k a l ”的()条件既不充分也不必要4.设函数f(x)的定义域为(-1,1)，且满足：①个极小值点(D)3个极小值点8.已知 A={(x,y) 1 x 22 2y r },B={(x,y)1 (x2 2 2a) (y b) r ,已知 A n B={(x 1,yJ ,( X 2,y 2)},则()(A)0< a 2 b 2 <2r 2(B)aXX 2) b(y1 y 2) 0(C)X 1 X 2 = a , y 1y 2=b (D)2a b 2 = 2ax 1 2by 19.已知非负实数x,y,z满足4x 24y 22z +2z=3, 则5x+4y+3z 的最小值为()(A)1 (B)2 (C)3 (D)410.设数列｛ a n ｝的前n 项和为S n ，若对任意正整数n ,总存在正整数 m,使得S n =a m ，则( )(A )｛ a n ｝可能为等差数列(B )｛ a n ｝可能为等比数列(c )｛a n ｝的任意一项均可写成｛a n ｝的两项之差(D)对任意正整数n ，总存在正整数 m 使得a n = S m 11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测： 3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名•比赛后发现没有并列名次，且甲、乙、丙、丁中只有 1人猜对比赛结果，此人是( )(A)甲(B)乙(C)丙(D) 丁1(A)若S=4,则k 的值唯一(B) 若S=^，贝U k 的值有2个22(C)若D 为三角形，则0<k <(D)若D 为五边形，则312.长方体 ABCDAEGD 中,AB=2, AD=A A 1=1，贝U A 到平面 A BD 的距离为((A) - (B)3(D)13.设不等式组|x| |y| 2 y 2 k(x 1)所表示的区域为 D,其面积为S,U(k>414. △ ABC 勺三边长是 2,3,4，其外心为 0,则 uuu uuu OA AB uuu uuu uuur uuu OB BC 0C CA =((A)0 (B)-15 (C) -21(D)229 215. 设随机事件 A 与B 互相独立，且 P(B)=0.5(A)P(A)=0.4 (B)P(B -A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916. 过厶ABC 的重心作直线将厶 3(A)最小值为一(B)最小值为417. 从正15边形的顶点中选出,P(A- B)=0.2，则(ABC 分成两部分，则这两部分的面积之比的(4 4(C)最大值为一533个构成钝角三角形，5(D 最大值为一4则不同的选法有((A)105 种(B)225 种(C)315 种(D)420 种18. 已知存在实数r，使得圆周x2y2 r2上恰好有n个整点，则n可以等于(22.在极坐标系中，下列方程表示的图形是椭圆的有(4 2 1 V2(A)最小值为一(B)最小值为一 (C)最大值为1 (D)最大值为--------------------5 5 3(A)4 (B)6 (C)8 (D)1219. 设复数z 满足2|z| w |z-1|，则(1(A)|z|的最大值为1 (B)|z| 的最小值为—(C)z321的虚部的最大值为2(D)z 的实部的最大值为13320.设 m,n 是大于零的实数， a =(mcos a ,msin a ),b =(ncos 3 ,nsin 3 )，其中 a , B€ [0,2 n ) a , B€r 1, _[0,2 n ) •定义向量 a 2 =( 、、. m cos — ,、. m sin 一 ), b 2=(、. n 2cos — 2 ，、齐 sin —)，记 9 = a - 3,贝U2r [ r 1 r r 1 r 1 ___ (A) a 2 • a 2 = a (B) a 2 b 2=、.mn cos — (C) 2r] r] … |a 2 b 2|4、一 mn sin 2 —4r 1 r] 2 _ 2 (D) |a 2 b 2 |24, mncos 2 —421.设数列｛ a n ｝满足：a 1=6, an 1，则((A) ? n € N?, a n <(n 1)3 (B) ? n € N?, a n 丰 2015 (C) ? n € N?, a n 为完全平方数(D)? n € N?, a n 为完全立方数1 (A )p=cos sin23. 设函数 f(x)s in x，则( x x 14(A ) f(x) w (B)| f (x) | w 5|x| (C)曲线 y= f (x)存在对称轴324. △ ABC 的三边分别为a ,b,c ，若△ ABC 为锐角三角形，则((B )p=—1(C ) 2 sin1p= —2 cos(D )(D) 1 1 2si n曲线y= f (x)存在对称中心(A)si nA>cosB (B)ta nA>cotB (C) a 2 b 2 c 2 (D) a 3 b 3 c 325.设函数f (x)的定义域是(-1,1), 若f(0) = f (0) =1,则存在实数 s€ (0,1)，使得()(A) f (x) >0, x € (- S , S) (B)f (x)在(-S , S )上单调递增 (C) f (x) >1, x € (0, S) (D)f (x)>1 , x € (- S ,0)26.在直角坐标系中，已知A(-1,0),B(1,0) •若对于y 轴上的任意n 个不同的点 P k (k=1,2，…,n)，总存在两个不同的点R ,P j ,1使得 |sin / A P j B-sin / A P j B| w —,贝V n 的最小值为( 3(A)3 (B)4(C)5 (D)627.设非负实数x,y 满足2x+y=1，则 x+ x 2 y 2 的()128.对于50个黑球和49个白球的任意排列(从左到右排成一行)，则((A)存在一个黑球，它右侧的白球和黑球一样多(B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个 29.从1,2,3,4,5 中挑出三个不同数字组成五位数, 同的五位数有( (A)300 个(B)450其中有两个数字各用两次，例如 12231,则能得到的不 30.设曲线L 的方程为 (A)L 是轴对称图形 (C)L ? {(x,y) I ##A nswer##1.【解析】丄1-z) 个(C)900 y 4 (2x 2(B)L 个(D)1800 个 2 4 2 2)y (x 2x ) =0,则(是中心对称图形 1 (D)L ? {(x,y)zz 1 zz_______ 1 - 2. 21-cos i sin332 cos 3..2 i sin ___ 3 2 2i sin32sin 2 i 2sin cos —3 3 3 cos0 isinO 2sin — [cos( —) i sin(-)i sin(3、、3(cos —2-洽 2os(cos( i sin ) 27) i sin(67)]丄(cos — isi n —.3 6 6△ )=1,选 B22.【简解】 a p (a k Q )=[(p+q)-(k+l)]d ，与公差 d 的符号有关，选 3.【解析】设A( 2X 1,X 1 ),B( 2 uuu uuu X 2,X 2 ), OA OB =X 1X 2(1 X 1X 2) =0 X 2 X1 答案(A), |0A| l OBI ^x^(1 好)4(1 —1^) = j1 X2 1 2 X 11 > /2 2|X 1 | 丄=2,正确; |X 1 | 答案(B),|OA|+|OB| > 2..|OA 「|OB| > 2 .2,正确；答案(C),直线 AB 的斜率为 2 22^=X 2 x 2 x 1X1程为 y- xj =( x 1 1)(x-x 1),焦点(0, 1)不满足方程，错误；答案(D)，原点到直线AB ：(4X11)x-y+ 仁X 1的距离d=w 1,正确。

2016清华大学自主招生暨领军计划数学试题(精校word版,带解析)-历年自主招生考试数学试题大全

2016年清华大学自主招生暨领军计划试题1．已知函数x e a x x f )()(2+=有最小值，则函数a x x x g ++=2)(2的零点个数为（） A ．0 B ．1 C ．2 D ．取决于a 的值【答案】C【解析】注意)()(/x g e x f x=，答案C ．2．已知ABC ∆的三个内角C B A ,,所对的边为c b a ,,．下列条件中，能使得ABC ∆的形状唯一确定的有（）A ．Z c b a ∈==,2,1B ．B bC a C c A a A sin sin 2sin sin ,1500=+=C ．060,0sin cos )cos(cos sin cos ==++C C B C B C B A D ．060,1,3===A b a【答案】AD ．3．已知函数x x g x x f ln )(,1)(2=-=，下列说法中正确的有（） A ．)(),(x g x f 在点)0,1(处有公切线B ．存在)(x f 的某条切线与)(x g 的某条切线平行C ．)(),(x g x f 有且只有一个交点D ．)(),(x g x f 有且只有两个交点【答案】BD【解析】注意到1-=x y 为函数)(x g 在)0,1(处的切线，如图，因此答案BD ．4．过抛物线x y 42=的焦点F 作直线交抛物线于B A ,两点，M 为线段AB 的中点．下列说法中正确的有（）A ．以线段AB 为直径的圆与直线23-=x 一定相离 B ．||AB 的最小值为4 C ．||AB 的最小值为2D ．以线段BM 为直径的圆与y 轴一定相切【答案】AB【解析】对于选项A ，点M 到准线1-=x 的距离为||21|)||(|21AB BF AF =+，于是以线段AB 为直径的圆与直线1-=x 一定相切，进而与直线23-=x 一定相离；对于选项B ，C ，设)4,4(2a a A ，则)1,41(2a a B -，于是2414||22++=aa AB ，最小值为4．也可将||AB 转化为AB 中点到准线的距离的2倍去得到最小值；对于选项D ，显然BD 中点的横坐标与||21BM 不一定相等，因此命题错误．5．已知21,F F 是椭圆)0(1:2222>>=+b a by a x C 的左、右焦点，P 是椭圆C 上一点．下列说法中正确的有（） A ．b a 2=时，满足02190=∠PF F 的点P 有两个 B ．b a 2>时，满足02190=∠PF F 的点P 有四个C ．21F PF ∆的周长小于a 4D ．21F PF ∆的面积小于等于22a【答案】ABCD ．【解析】对于选项A ，B ，椭圆中使得21PF F ∠最大的点P 位于短轴的两个端点；对于选项C ，21PF F ∆的周长为ac a 422<+；选项D ，21PF F ∆的面积为22212121212||||21sin ||||21a PF PF PF F PF PF =⎪⎭⎫ ⎝⎛+≤∠⋅． 6．甲、乙、丙、丁四个人参加比赛，有两花获奖．比赛结果揭晓之前，四个人作了如下猜测：甲：两名获奖者在乙、丙、丁中；乙：我没有获奖，丙获奖了；丙：甲、丁中有且只有一个获奖；丁：乙说得对．已知四个人中有且只有两个人的猜测是正确的，那么两个获奖者是（） A ．甲B ．乙C ．丙D ．丁【答案】BD【解析】乙和丁同时正确或者同时错误，分类即可，答案：BD ．7．已知AB 为圆O 的一条弦（非直径），AB OC ⊥于C ，P 为圆O 上任意一点，直线PA 与直线OC 相交于点M ，直线PB 与直线OC 相交于点N ．以下说法正确的有（） A ．P B M O ,,,四点共圆 B ．N B M A ,,,四点共圆 C ．N P O A ,,,四点共圆D ．以上三个说法均不对【答案】AC【解析】对于选项A ，OPM OAM OBM ∠=∠=∠即得；对于选项B ，若命题成立，则MN 为直径，必然有MAN ∠为直角，不符合题意；对于选项C ，MAN MOP MBN ∠=∠=∠即得．答案：AC ． 8．C B A C B A cos cos cos sin sin sin ++>++是ABC ∆为锐角三角形的（） A ．充分非必要条件 B ．必要非充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】必要性：由于1cos sin )2sin(sin sin sin >+=-+>+B B B B C B π，类似地，有1sin sin ,1sin sin >+>+A B A C ，于是C B A C B A cos cos cos sin sin sin ++>++．不充分性：当4,2ππ===C B A 时，不等式成立，但ABC ∆不是锐角三角形．9．已知z y x ,,为正整数，且z y x ≤≤，那么方程21111=++z y x 的解的组数为（） A ．8B ．10C ．11D ．12【答案】B 【解析】由于xz y x 311121≤++=，故63≤≤x ．若3=x ，则36)6)(6(=--z y ，可得)12,12(),15,10(),18,9(),24,8(),42,7(),(=z y ；若4=x ，则16)4)(4(=--z y ，可得)8,8(),12,6(),20,5(),(=z y ；若5=x ，则6,5,320,211103=≤≤+=y y y z y ，进而解得)10,5,5(),,(=z y x ；若6=x ，则9)3)(3(=--z y ，可得))6,6(),(=z y ．答案：B ．10．集合},,,{21n a a a A =，任取A a a A a a A a a n k j i i k k j j i ∈+∈+∈+≤<<≤,,,1这三个式子中至少有一个成立，则n 的最大值为（） A ．6B ．7C ．8D ．9【答案】B11．已知000121,61,1===γβα，则下列各式中成立的有（） A ．3tan tan tan tan tan tan =++αγγββαB ．3tan tan tan tan tan tan -=++αγγββαC ．3tan tan tan tan tan tan =++γβαγβαD ．3tan tan tan tan tan tan -=++γβαγβα【答案】BD 【解析】令γβαtan ,tan ,tan ===z y x ，则3111=+-=+-=+-zxzx yz y z xy x y ，所以)1(3),1(3),1(3zx z x yz y z xy z y +=-+=-+=-，以上三式相加，即有3-=++zx yz xy ．类似地，有)11(311),11(311),11(311+=-+=-+=-zxx z yz z y xy y x ，以上三式相加，即有3111-=++=++xyzzy x zx yz xy ．答案BD ． 12．已知实数c b a ,,满足1=++c b a ，则141414+++++c b a 的最大值也最小值乘积属于区间（）A ．)12,11(B ．)13,12(C ．)14,13(D ．)15,14(【答案】B【解析】设函数14)(+=x x f ，则其导函数142)(/+=x x f ，作出)(x f 的图象，函数)(x f 的图象在31=x 处的切线321)31(7212+-=x y ，以及函数)(x f 的图象过点)0,41(-和)7,23(的割线7174+=x y ，如图，于是可得321)31(7212147174+-≤+≤+x x x ，左侧等号当41-=x 或23=x 时取得；右侧等号当31=x 时取得．因此原式的最大值为21，当31===c b a 时取得；最小值为7，当23,41=-==c b a 时取得，从而原式的最大值与最小值的乘积为)169,144(37∈．答案B ．13．已知1,1,,,222=++=++∈z y x z y x R z y x ，则下列结论正确的有（） A ．xyz 的最大值为0 B ．xyz 的最大值为274- C ．z 的最大值为32D ．z 的最小值为31-【答案】ABD14．数列}{n a 满足)(6,2,1*1221N n a a a a a n n n ∈-===++，对任意正整数n ，以下说法中正确的有（）A ．n n n a a a 221++-为定值 B ．)9(mod 1≡n a 或)9(mod 2≡n aC ．741-+n n a a 为完全平方数D ．781-+n n a a 为完全平方数【答案】ACD 【解析】因为2112221122213226)6(++++++++++++-=--=-n n n n n n n n n n n a a a a a a a a a a a nn n n n n n a a a a a a a 22121122)6(++++++-=+-=，选项A 正确；由于113=a ，故76)6(2121121221-=+-=--=-++++++n n n n n n n n n n n a a a a a a a a a a a ，又对任意正整数恒成立，所以211211)(78,)(74n n n n n n n n a a a a a a a a +=--=-++++，故选项C 、D 正确．计算前几个数可判断选项B 错误．说明：若数列}{n a 满足n n n a pa a -=++12，则n n n a a a 221++-为定值．15．若复数z 满足11=+zz ，则z 可以取到的值有（） A ．21B ．21-C ．215-D ．215+ 【答案】CD 【解析】因为11||1||=+≤-zz z z ，故215||215+≤≤-z ，等号分别当i z 215+=和i z 215-=时取得．答案CD ．16．从正2016边形的顶点中任取若干个，顺次相连构成多边形，若正多边形的个数为（） A ．6552 B ．4536 C ．3528 D ．2016 【答案】C【解析】从2016的约数中去掉1，2，其余的约数均可作为正多边形的边数．设从2016个顶点中选出k 个构成正多边形，这样的正多边形有k2016个，因此所求的正多边形的个数就是2016的所有约数之和减去2016和1008．考虑到732201625⨯⨯=，因此所求正多边形的个数为352810082016)71)(931)(32168421(=--++++++++．答案C ．17．已知椭圆)0(12222>>=+b a b y a x 与直线x y l x y l 21:,21:21-==，过椭圆上一点P 作21,l l 的平行线，分别交21,l l 于N M ,两点．若||MN 为定值，则=ba（） A ．2B ．3C ．2D ．5【答案】C【解析】设点),(00y x P ，可得)2141,21(),2141,21(00000000y x y x N y x y x M +--++，故意2020441||y x MN +=为定值，所以2,1641422===b a b a ，答案：C ．说明：（1）若将两条直线的方程改为kx y ±=，则kb a 1=；（2）两条相交直线上各取一点N M ,，使得||MN 为定值，则线段MN 中点Q 的轨迹为圆或椭圆．18．关于y x ,的不定方程y x 21652=+的正整数解的组数为（） A ．0B ．1C ．2D ．3【答案】B19．因为实数的乘法满足交换律与结合律，所以若干个实数相乘的时候，可以有不同的次序．例如，三个实数c b a ,,相乘的时候，可以有 ),(),(,)(,)(ca b ab c c ba c ab 等等不同的次序．记n 个实数相乘时不同的次序有n I 种，则（）A ．22=IB ．123=IC ．964=ID ．1205=I 【答案】B【解析】根据卡特兰数的定义，可得1121221)!1(!1------=⋅==n n n n nn n n C n n C nA C I ．答案：AB ．关于卡特兰数的相关知识见《卡特兰数——计数映射方法的伟大胜利》．20．甲乙丙丁4个人进行网球淘汰赛，规定首先甲乙一组、丙丁一组进行比赛，两组的胜者争夺冠军．4个人相互比赛的胜率如表所示：表中的每个数字表示其所在的选手击败其所在列的选手的概率，例如甲击败乙的概率是0.3，乙击败丁的概率是0.4．那么甲刻冠军的概率是．【答案】0.165【解析】根据概率的乘法公式，所示概率为165.0)8.05.03.05.0(3.0=⨯+⨯．21．在正三棱锥ABC P -中，ABC ∆的边长为1．设点P 到平面ABC 的距离为x ，异面直线CP AB ,的距离为y ．则=∞→y x lim ．【答案】23 【解析】当∞→x 时，CP 趋于与平面ABC 垂直，所求极限为ABC ∆中AB 边上的高，为23． 22．如图，正方体1111D C B A ABCD -的棱长为1，中心为A A E A BC BF O 1141,21,==，则四面体OEBF 的体积为．【答案】196【解析】如图，EBF G EBF O OEBF V V V --==21961161212111=⋅==--B BCC E GBF E V V ．23．=+-⎰-dx x x n n )sin 1()(22012ππ ．【答案】0【解析】根据题意，有0)sin 1()sin 1()(21222012=+=+-⎰⎰---dx x x dx x x n n n n ππππ．24．实数y x ,满足223224)(y x y x =+，则22y x +的最大值为．【答案】1【解析】根据题意，有22222322)(4)(y x y x y x +≤=+，于是122≤+y x ，等号当2122==y x 时取得，因此所求最大值为1．25．z y x ,,均为非负实数，满足427)23()1()21(222=+++++z t x ，则z y x ++的最大值与最小值分别为．【答案】2322- 【解析】由柯西不等式可知，当且仅当)0,21,1(),,(=z y x 时，z y x ++取到最大值23．根据题意，有41332222=+++++z y x z y x ，于是,)(3)(4132y z y x z y x +++++≤解得2322-≥++z y x ．于是z y x ++的最小值当)2322,0,0(),(-=yz x 时取得，为2322-． 26．若O 为ABC ∆内一点，满足2:3:4::=∆∆∆COA BOC AOB S S S ，设AC AB AO μλ+=，则=+μλ ．【答案】23【解析】根据奔驰定理，有329492=+=+μλ． 27．已知复数32sin32cos ππi z +=，则=+++2223z z z z ．【答案】1322i - 【解析】根据题意，有i i z z z z z z 232135sin 35cos 122223-=+=-=+=+++ππ． 28．已知z 为非零复数，zz 40,10的实部与虚部均为不小于1的正数，则在复平面中，z 所对应的向量OP 的端点P 运动所形成的图形的面积为 . 【答案】20010033003π+-【解析】设),(R y x yi x z ∈+=，由于2||4040z z z =，于是⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥,140,140,110,1102222y x y y x x y x 如图，弓形面积为1003100)6sin 6(20212-=-⋅⋅πππ，四边形ABCD 的面积为100310010)10310(212-=⋅-⋅. 于是所示求面积为30031003200)1003100()1003100(2-+=-+-ππ. 29．若334tan =x ，则=+++xx x x x x x x x x x cos sin cos 2cos sin 2cos 4cos 2sin 4cos 8cos 4sin ．【答案】3【解析】根据题意，有xx x x x x x x x x x cos sin cos 2cos sin 2cos 4cos 2sin 4cos 8cos 4sin +++ 38tan tan )tan 2(tan )2tan 4(tan )4tan 8(tan ==+-+-+-=x x x x x x x x ．30．将16个数：4个1，4个2，4个3，4个4填入一个44⨯的数表中，要求每行、每列都恰好有两个偶数，共有种填法．【答案】44100031．设A 是集合}14,,3,2,1{ 的子集，从A 中任取3个元素，由小到大排列之后都不能构成等差数列，则A 中元素个数的最大值为．【答案】8【解析】一方面，设},,,{21k a a a A =，其中141,*≤≤∈k N k ．不妨假设k a a a <<< 21．若9≥k ，由题意，7,33513≥-≥-a a a a ，且1335a a a a -≠-，故715≥-a a ．同理759≥-a a ．又因为1559a a a a -≠-，所以1519≥-a a ，矛盾！故8≤k ．另一方面，取}14,13,11,10,5,4,2,1{ A ，满足题意．综上所述，A 中元素个数的最大值为8．。

2014年自招【数学】笔试真题与北京清华园教育讲义比较

2014年自主招生数学真题与《北京清华园自招讲义》相同或相近部分对照比较第一部分：北约联盟第2题：10个人分成3组（3、3、4），共有____种分法。

A.1070B.2014C.2100D.4200.解：43106222100C CA=（种）。

（这里有平均分组问题）。

在今年寒假讲义ppt第十三讲337页重点讲了排列组合中的“平均分组”问题：A.解：设,,1a x b y a b =-=-∴+=，14ab ≤21117)224xy xy ≥+=+≥或直接取12x y ==-又13,.44x y =-=-2014寒假讲义第十讲 ppt 第257页：2013年暑假讲义ppt 第259页：第7题. 证明：0tan3是无理数所以0000tan6,tan12,tan 24,tan30,Q Q Q Q ∈∈∈∈矛盾。

2014寒假讲义第十讲 ppt 第257页：有理数的四则运算仍是有理数，任何一个有理数都可设成qp的形式。

第8题：已知实二次函数()f x 和()g x 满足，()()f x g x =和()3()0f x g x +=都只有一对重根，()0f x =有两个不相等的实根，证明：()0g x =无实根。

证明：设()()22,,f x ax bx c g x dx ex f =++=++由()()2()()()0,f x g x a d x b e x c f =⇒-+-+-=因为上述一元二次方程有相等实数根 2()4()(),b e a d c f ∴-=--①同理有：2(3)4(3)(3)b e a d c f +=++，②⨯①3+②得：223124b e ac fd +=+ 注意到()()22240,4440g x b ac e df b ac ->∆=-=--<所以()0g x =无实根。

2013年暑假讲义PPT 第46、47页：解：没有.解法一：因为2()(1)0f x x ax b x c -=+-+=无实数根，所以2(1)40b ac ∆=--<； (())0f f x x -=．222()()0a ax bx cb ax bxc c x ++++++-=22222()()0a ax bx c ax ax b ax bx c c x ++-+++++-=．2222()()(1)(1)(1)0a ax bx c x ax bx c x b ax b x c b ++-++++++-++=．3.（2008上海交大）已知函数2()f x ax bx c =++，(0)a ≠且()f x x = 没有实数根．那么(())f f x x =是否有实数根？并证明你的结论．222(1)(1)(1)(1)0a ax b x c ax b x c b ax b x c ⎡⎤⎡⎤⎡⎤+-+++++++-+=⎣⎦⎣⎦⎣⎦． 222(1)(1)10ax b x c a x a b x ac b ⎡⎤⎡⎤+-++++++=⎣⎦⎣⎦．于是有2(1)0ax b x c +-+=或22(1)10a x a b x ac b +++++=．21(1)40b ac ∆=--<； 2222(1)4(1)a b a ac b ∆=+-++222(1)4440a b ac a ⎡⎤=---<<⎣⎦。

清华自主招生数学创新试题汇编

清华自主招生数学创新试题汇编(共33页)-本页仅作为预览文档封面，使用时请删除本页-1、（Ⅰ）已知函数：1()2()(),([0,),)n n n f x x a x a x n N -*=+-+∈+∞∈求函数()f x 的最小值;（Ⅱ）证明:()(0,0,)22n n na b a b a b n N *++≥>>∈；（Ⅲ）定理:若123,,k a a a a 均为正数,则有123123()n n nnn k ka a a a a a a a kk++++++++≥ 成立(其中2,,)k k N k *≥∈为常数．请你构造一个函数()g x ，证明：当1231,,,,,k k a a a a a +均为正数时，12311231()11n n nn n k k a a a a a a a a k k ++++++++++≥++．解：（Ⅰ）令111'()2()0n n n f x nx n a x ---=-+=得11(2)()2n n x a x x a x x a --=+∴=+∴=…2分当0x a ≤≤时，2x x a <+ '()0f x ∴≤ 故()f x 在[0,]a 上递减．当,'()0x a f x >>故()f x 在(,)a +∞上递增．所以，当x a =时，()f x 的最小值为()0f a =.….4分（Ⅱ）由0b >，有()()0f b f a ≥= 即1()2()()0n n n n f b a b a b -=+-+≥故()(0,0,)22n n na b a b a b n N *++≥>>∈．………………………………………5分（Ⅲ）证明:要证：12311231()11n n nn n k k a a a a a a a a k k ++++++++++≥++只要证：112311231(1)()()n n n nnn k k k a a a a a a a a -+++++++≥++++设()g x =1123123(1)()()n n n nn n k a a a x a a a x -+++++-++++…………………7分则11112'()(1)()n n n k g x k nx n a a a x ---=+⋅-++++令'()0g x =得12ka a a x k+++= (8)分当0x ≤≤12ka a a k+++时，1112'()[(]()n n k g x n kx x n a a a x --=+-++++≤111212()()0n n k k n a a a x n a a a x --++++-++++=故12()[0,]ka a a g x k+++在上递减，类似地可证12()(,)ka a a g x k++++∞在递增所以12()ka a a x g x k+++=当时，的最小值为12()ka a a g k+++………………10分而11212121212()(1)[()]()n n n n n nk k k k k a a a a a a a a a g k a a a a a a k k k-+++++++++=+++++-++++ =1121212(1)[()()(1)()]n n n nnn n k k k nk k a a a a a a k a a a k -++++++++-++++=11212(1)[()()]n n n nn nkk nk k a a a k a a a k -++++-+++=1112121(1)[()()]n n n nn n k k n k k a a a a a a k---++++-+++由定理知: 11212()()0n n nnn k k k a a a a a a -+++-+++≥ 故12()0ka a a g k+++≥1211[0,)()()0kk k a a a a g a g k+++++∈+∞∴≥≥故112311231(1)()()n n n nnn k k k a a a a a a a a -+++++++≥++++即:12311231()11n n nn n k k a a a a a a a a k k ++++++++++≥++.…………………………..14分答案：5354321b b b b b b =••••3、10．定义一种运算“*”：对于自然数n 满足以下运算性质：（i ）1*1=1，（ii ）（n +1）*1=n *1+1，则n *1等于A ．nB ．n +1C ．n -1D ．2n 答案：D4、若)(n f 为*)(12N n n ∈+的各位数字之和，如：1971142=+，17791=++，则17)14(=f ;记=∈===+)8(*,)),(()(,)),(()(),()(20081121f N k n f f n f n f f n f n f n f k k 则 ____答案：55、下面的一组图形为某一四棱锥S-ABCD 的侧面与底面。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 1 1 1 1 易知当 p ( , ) 时, f ( p ) 0, p ( 2 2 4 2 30
所以当 p
1 1 ,1) 时, f ( p ) 0 , 4 30
1 1 1 时, f ( p ) 有唯一极大值,也是最大值. 2 4 30
三.【解析】易 f x
p 1
.
p 1
(2)由 | an 1 || np n qan || np n | | qan | n | p |n | an | ,所以 | an 1 | | an | n | p |n , 于是 | an | | an 1 | n 1) | p |n 1 ( n 2) 由累加法得 an an an 1 an 1 an 2 a2 a1 a1 ( n 2) 故 | an || p | 2 | p |2 ( n 1) | p |n 1
b2 b , yF , a cos sin
1 b3 b3 | xE | | xF | , 2 a | sin 2 | a
于是 S EOF
当且仅当 M (
2 2 a, b) 时,上述等号成立. 2 2
2
法二：设切点弦方程为： x0 x y0 y r ，则 E (
2014 年华约高水平大学自主选拔学业能力测试（数学）
参考答案
一.【解析】五个数任取四个应该可以得到 C54 5 个不同的和,现条件中只有 4 个不同的和,故必有两个和值相同.而这五个和值之和为 4( x1 x2 x3 x4 x5 ) ,是 4 的倍数,所以这个相同的和值只可能是 46,从而有： x1 x2 x3 x4 x5
设 f ( p ) 6 p 5 15 p 4 10 p 3 p , p
所以令 f ( p ) 0 时,即 p 2 p
1 30
1 1
0 ,得 p
4 30
2

1 1 1 ; 2 4 30
1 1 1 1 又因为 p ( ,1) ,所以取 p , 2 2 4 30
代入得 f ( x ) f (G ( F ( x ))), f ( f 1 ( F ( x ))) F ( x) f ( x ) , 所以 f ( x ) 为奇函数.
五.【解析】设 M ( a cos , b sin )( [0, 2 )) ,直线 PQ 为点 M 关于圆 x 2 y 2 b 2 的切点弦, 其方程为 (a cos ) x (b sin ) y b 2 , 从而 xE
所以 x0 y0
六.【解析】 (1)当 q 1 时, an 1 an np n ,则 an an 1 ( n 1) p n 1 ( n 2) 由累加法得 an an an 1 an 1 an 2 a2 a1 a1 ( n 2) , 即 an p 2 p 2 3 p 3 (n 1) p n 1 ( n 2) ……(1)
b2 b2 , 0) ， F (0, )， x0 2 y0 2
1 1 b4 S OE OF 2 2 ， 2 2 x0 y0
又因为
x0 2 y0 2 x0 2 y0 2 1 2 ， a2 b2 a 2b 2
x2 y2 ab 1 b 4 b3 ，所以 S 。 .（当且仅当 02 02 时） 2 a b 2 ab a 2
p(1 p n 1 ) (n 1) p n ( n 1) p n 1 np n p 1 p 所以 an ,当 n 1 时, a1 0 也适合; 1 p (1 p )2
n( n 1) 2 于是 an n 1 n ( n 1) p np p (1 p) 2
x x x x x2 x2 从而 n((1 Байду номын сангаас e n ) n n((1 ) (1 )) n n(1 2 ) n n(1 n 2 ) n x 2 ,即证. n n n n n
1 1 cos 2 x sin 2 x 2a sin x b sin 2 x 2a sin x b , 2 2
2
令 t sin x , 则问题等价于 g (t ) t 2at b
1 在 [1,1] 上的最大值和最小值分别为 1 和 4 . 2
44 45 46 46 47 57 , 4 故这五个数分别为 57-44=13,57-45=12,57-46=11,57-47=10,57-46=11, 即 10,11,11,12,13.
二.【解析】若共比赛了 3 局,则甲赢得比赛的概率为 p 3 ; 若共赛了 4 局,则最后一局甲胜,甲赢得比赛的概率为 C32 p 3 (1 p ) ; 若共比赛了 5 局,则最后一局甲胜,甲赢比赛的概率为 C42 p 3 (1 p ) 2 ,因此
1
当 p 1 时, a n
n( n 1) ; 当 n 1 时, a1 0 也适合; 2
2
当 p 1 时, pan p 2 2 p 3 (n 1) p n ……(2) 由(1)-(2)得 an pan p p 2 p 3 p n 1 ( n 1) p n ,
于是 an 有上界.
七.【证明】
x x 原不等式等价于 n x 2 n((1 ) e n ) n . n
当 x 2 n ,上述不等式左边非正,不等式成立;
当 x 2 n 时,由 e y 1 y ( y 0) 及贝努力不等式 (1 y ) n 1 ny ( n 1, y 1) ,
q p 3 C32 p 3 (1 p ) C42 p 3 (1 p ) 2 ,
所以 q p p 3 C32 p 3 (1 p ) C42 p 3 (1 p ) 2 p 6 p 5 15 p 4 10 p 3 p , p
1 ; 2
1 ,则 f ( p ) 30 p 4 60 p 3 30 p 2 1 , 2 1 即 f ( p ) 30 p 4 60 p 3 30 p 2 1 30[ p 2 ( p 2 2 p 1) ] , 30 1 1 1 所以 f ( p ) 30[ p 2 ( p 1) 2 ] 30( p 2 p )( p 2 p ), 30 30 30 1 1 又因为 p ( ,1) ,所以 p 2 p ,故 p 2 p 0, 2 30
消去 b 得 a 2 2a 4 0 ,解得 a 1 5 (0,1) ,舍去. 综上①②可知, a
5 , b 1 为所求. 4
四.【解析】 (1)证明:由反函数定义可知 y f ( g ( x)) 的反函数为 x f ( g ( y )) , 所以 f 1 ( x) f 1 ( f ( g ( y ))) g ( y ) , 从而 g 1 ( f 1 ( x )) g 1 ( g ( y )) y , 所以 y g 1 ( f 1 ( x)) 为 y f ( g ( x)) 的反函数. (2)由 G ( x) 的反函数是 F ( x) , 故 G ( F ( x)) G (G 1 ( x )) x , 则 f ( x ) f (G ( F ( x ))), 又因为 G ( x) f 1 ( x) , 所以 G ( F ( x)) f 1 ( F ( x )) ,
(n 1) | p |n 1 n | p |n | p | , (1 | p |) 2
而 (n 1) | p |n 1 n | p |n (n 1) | p |n n | p | | p |n 0 , 于是当 n 2 时,有 | an |
| p| ,显然 a1 0 也成立. (1 | p |) 2
①当对称轴 t a 1 ,即 a 1 时,则 g (t ) 在 [1,1] 上递减,则：
1 5 g ( 1) 2a b 1, a , 2 ,解得 4 g (1) 2a b 1 4 b 1 2 1 g ( a) a 2 b 1 2 ②当对称轴 1 a 0 ,即 0 a 1 时,则 , 1 g (1) 2a b 4 2