人教版七年级数学有理数复习专题讲义
第一章+有理数+第8课+有理数相关概念复习课件2024-2025学年人教版数学七年级上册

6
(4)+(+6)=__________;
12
(5)|-12|=_________;
(6)-|-12|=_________.
-12
9. 填空:
6和-6
(1)到原点的距离等于6的数有2个,分别是__________;
-7或7
(2)若|x|=7,则x=__________;
4或-4
(3)一个数的绝对值是4,则这个数是__________;
正方向
(2)数轴的三要素:①__________;②____________;③
原点
单位长度
____________.
注意:数轴的三要素缺一不可.
原点将数轴(原点除外)分成两部分,其中正方向一侧
的部分叫作数轴的正半轴,另一侧的部分叫作数轴的
负半轴。
知识点 4 相反数
符号
(1)相反数:只有________不同的两个数叫做互为相反数.
+0.04
-0.03
( 表示
圆形零件的直径,单位:mm),抽查了5个零件,超过
规定的记作正数,不足的记作负数,数据如下表(单位:
mm).
(1)哪些产品是符合要求的?
(2)在符合要求的产品中哪个质量最好?请用绝对值的
知识加以说明.
解:(1)1号,3号,4号产品是符合要求的;
(2)因为|+0.018|<|-0.021|<|+0.031|,
(4)若|a-4|+|b-3|=0,则a=_______,b=_______.
4
3
10. 比较大小,用“>”或“<”填空:
<
>
(1)15________0;
(2)-12________5;
<
>
七年级数学考点大串讲(人教版):有理数(17个考点梳理)(解析版)
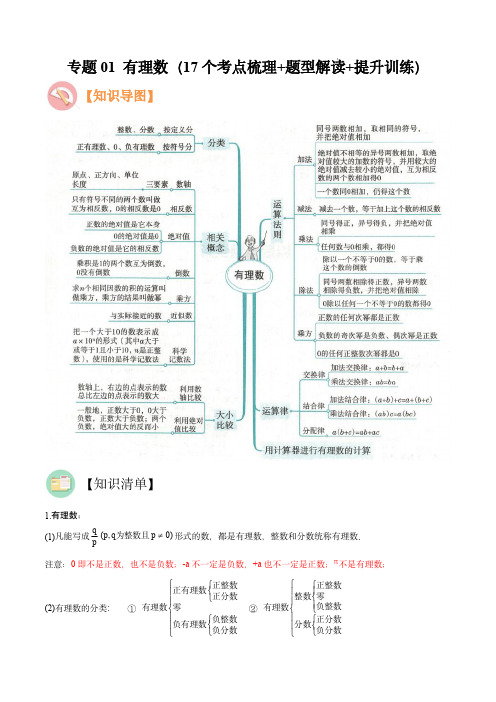
专题01有理数(17个考点梳理+题型解读+提升训练)【知识导图】【知识清单】1.有理数:(1)凡能写成)0p q ,p (pq为整数且形式的数,都是有理数,整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数; 不是有理数;(2)有理数的分类:①负分数负整数负有理数零正分数正整数正有理数有理数②负分数正分数分数负整数零正整数整数有理数(3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数 0和正整数;a >0 a 是正数;a <0 a 是负数;a≥0 a 是正数或0 a 是非负数;a≤0 a 是负数或0 a 是非正数.【例1】把下列各数填在相应的大括号里:2 ,-3.14,0,18%,435,2019,227,132 ,-1整数: ______...;正分数: ______...;非负有理数: ______....【答案】2 ,0,2019,-1;18%,435 ,227;0,18%,435,2019,227【分析】根据整数(包括正整数,0和负整数),正分数(大于0的分数)以及非负有理数(包括0和正有理数)的定义解答即可.【详解】解:22 ,443355,整数: 2,0,2019,1 ;正分数:42218%,3,57;非负有理数:4220,18%,3,2019,57.故答案为:2 ,0,2019,-1;18%,435 ,227;0,18%,435,2019,227.【点睛】本题考查的是有理数的分类,多重符号的化简,绝对值的含义,掌握有理数的分类是解题的关键,难点是非负有理数的理解.2.数轴:数轴是规定了原点、正方向、单位长度(数轴的三要素)的一条直线.【例2】.(2023•馆陶县校级模拟)如图,数轴上的两个点分别表示数a 和﹣2,则a 可以是()A .﹣3B .﹣1C .1D .2【分析】根据数轴上,右边的数总比左边的大得到a 的取值范围,进而得出答案.【解答】解:根据数轴得:a <﹣2,∴a 可以是﹣3.故选:A .【点评】本题考查了数轴,掌握数轴上,右边的数总比左边的大是解题的关键.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)注意:a-b+c 的相反数是-(a-b+c)=-a+b-c ;a-b 的相反数是b-a ;a+b 的相反数是-a-b ;(3)相反数的和为0 a+b=0 a 、b 互为相反数.(4)相反数的商为-1.(5)相反数的绝对值相等【例3】如果m 的相反数是最大的负整数,n 的相反数是它本身,则m n 的值为()A .1B .0C .2D .-1【答案】A【分析】先根据相反数的定义确定m 、n 的值,再代入m +n ,计算即可求出其值.【详解】∵m 的相反数是最大的负整数,n 的相反数是它本身,∴m =1,n =0,∴m +n =1+0=1,故A 选项是正确答案.4.绝对值:(1)正数的绝对值等于它本身,0的绝对值是0,负数的绝对值等于它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2)绝对值可表示为:)0a (a )0a (0)0a (a a 或)0()0(a a a a a ;(3)0a 1aa ;0a 1aa ;(4)|a|是重要的非负数,即|a|≥0,非负性;【例4】(2022秋•寻乌县期末)请根据图示的对话解答下列问题.(1)a =,b =.(2)已知|m ﹣a |+|b +n |=0,求mn的值.【解答】解:(1)∵a 与2互为相反数,而2的相反数是﹣2,∴a =﹣2,∵b 与﹣互为倒数,而﹣的倒数是﹣3,∴b =﹣3,故答案为:﹣2,﹣3;(2)∵|m ﹣a |+|b +n |=0,∴m ﹣a =0,b +n =0,又∵a =﹣2,b =﹣3,∴m =﹣2,n =3,∴mn =﹣2×3=﹣6,答:mn 的值为﹣6.【点评】本题考查的是非负数的性质,相反数以及互为倒数,掌握相反数、倒数的定义以及绝对值的非负性是正确解答的前提.5.有理数比大小:(1)正数永远比0大,负数永远比0小;(2)正数大于一切负数;(3)两个负数比较,绝对值大的反而小;(4)数轴上的两个数,右边的数总比左边的数大;(5)-1,-2,+1,+4,-0.5,以上数据表示与标准质量的差,绝对值越小,越接近标准。
第1章 有理数(单元复习课件)七年级数学上册(人教版2024)

7. 【2024宁波新视角操作探究题】数轴是一个非常重要的数学
工具,它使数和数轴上的点建立起对应关系,揭示了数与点
之间的内在联系,它是“数形结合”的基础.小锦在草稿纸上
画了一条数轴(如图) 进行操作探究.
操作一:
(1)折叠纸面,若使1表示的点与-1表示的点重合,则-3
表示的点与
3 表示的点重合;
易错点三 数轴上点的位置不确定而漏解
例 3.在数轴上与表示-3的点相距10个单位长度的点表示的数是
.
正解:
当与-3相距10个单位长度的点在-3的右侧时,
-3+10=7;
当与-3相距10个单位长度的点在-3的左侧时,
-3-10=-13.
故答案为7 或-13.
错解剖析:
在数轴上与-3相距10个单位长度的点有可能在-3的右侧也有可能在-3的左
的数为 -6
.
5. 【新视角结论开放题】已知数轴上点 A 表示的数是-1,点 B
在点 A 的左侧,则点 B 表示的数可能是 -4(答案不唯一)
.
6. 画出数轴,并在数轴上表示下列各数,再将这些数用
“<”连接起来.
-4,1 ,3,-(-0.5),-|-2|.
解: 如图所示.
由数轴得,-4<-|-2|<-(-0.5)<1 <3.
025,-1
;
(3)正有理数:
,+15%,101,3.14,0.618
(4)非正整数:
0,-2 025 ;
(5)非负数:
;
,0,+15%,101,3.14,0.618
第1章 有理数 人教版七年级数学上册单元复习课件(共38张PPT)

知识点四:有理数的混合运算 有理数的运算有加法、减法、乘法、除法和乘方.进行混合 运算时,运算顺序是: (1)先乘方,再乘除,最后加减; (2)同级运算,按从左到右的顺序进行; (3)如有括号,先做括号内的运算,按小括号、中括号、大 括号依次进行.
13.【例1】下面的说法正确的是( D ) A.有理数的绝对值一定比0大 B.有理数的相反数一定比0小 C.若两个数的绝对值相等,则这两个数相等 D.互为相反数的两个数的绝对值相等
20.【例8】(创新题)观察下列所给的式子,解答下列问题: 1+3=22; 1+3+5=32; 1+3+5+7=42; 1+3+5+7+9=52;…. (1)1+3+5+7+…+29= 225 ; (2)1+3+5+…+(2n-1)= n2 ;(n为正整数) (3)21+23+25+…+57+59= 800 .
16.【例4】(创新题)若x为有理数,式子2 023-|x+2|存在最
大值,则这个最大值是( B )
A.2 022
B.2 023
C.2 024
D.2 025
小结:直接利用绝对值的性质得出|x+2|的最小值为0.
小结:明确有理数混合运算的计算方法,并合理运用运算律.
18.【例6】(全国视野)(2022泸州改编)若(a-2)2+|b+3|=0, 求ab的值. 解:由题意得a-2=0,b+3=0, 可得a=2,b=-3, 所以ab=2×(-3)=-6.
(3)相反数:只有符号不同的两个数叫做互为相反数,0的相 反数是0. 互为相反数的两个数到原点的距离相等.
(4)绝对值:一个数在数轴上对应的点到原点的距离叫做这 个数的绝对值. 一个正数的绝对值是它本身;一个负数的绝对值是它的相反 数;0的绝对值是0. (5)倒数:乘积是1的两个数互为倒数.
七年级数学上册《有理数》复习课件 新人教版

-(-2/9),
1/2,-1/4 正整数有:12,|-8| 负分数有:-3.14,-2/5,-1/4 非负数有:12,0,-(-2/9),|-8|,1/2
5
例2,在数轴上表示绝对值不小于2而又不大于5.1的
所有整数;并求出绝对值少于4的所有整数的和与积
1、10盒火柴如果以每盒100根 为准,超过的根数记作正数,不 足的根数记作负数,每盒数据记 录如下: +3,+2,0,-1,-2,-3, -2,+3,-2,-2。 求这10盒火柴共有多少根.
15
创新:
2、如图,是用火柴棒摆成的一个大三角形,它是由九 个小三角形组成的,试将1、2、3、4、5、6、7、8、9分 别填入这9个小三角形哪(每个小三角形内只填一个数), 要求靠近大三角形每条边的每五个数相加的和相等,请 想一想,怎样填这些数才能使五个数的和尽可能大一些, 这五个数的和最大是多少?
有理数的概念
注意:零是自然数 概念:有理数、数轴、相反数、绝对值、倒数 分类(1):整数和分数(2):正有理数、负理有数和 零 法则:有理数的加、减、乘、除法法则 运算律:加法、乘法的交换律、结合律,分配律 方法:有理数大小的比较方法 体验:数形结合和数学知识来源于社会实践的原理
解(略) 例3,数X,Y在数轴上的对应点如下 图,化简|X-Y|-|Y+X|+|Y-X| X
6
0
Y
解:|X-Y|-|Y+X|+|Y-X|=Y-X-Y-X+Y-X=Y-3X
要点:
数轴的三要素:原点、正方向和单位长度 数a的相反数是-a,相反数是它本身的数是0,一个数乘以 -1就变为原数的相反数 互为相反数的两个数的绝对值相等,互为相反数的和为 0, 1除以一个数就变为这个数的倒数,互为倒数的积为1
七年级数学上册同步精品讲义(人教版):有理数(教师版)(人教版)

5
1 3
为负分数,不是负整数,故
D
选项不符合题意;
故选:A
【点睛】
此题考查了有理数的分类,掌握有理数的分类是解题的关键.
2.(2022·全国·七年级课时练习)下列说法正确的是( )
A.正有理数和负有理数组成全体有理数 B.零既不是正数,也不是负数 C.0.5 既不是整数,也不是分数,因而它不是有理数 D.在有理数中,零的意义表示没有 【答案】B 【解析】 【分析】 根据有理数的意义和分类逐项进行判断即可. 【详解】 解:A.有理数分为正有理数、0、负有理数,故此选项不符合题意; B.0 既不是正数,也不是负数,是最小的非负整数,故此选项符合题意; C.0.5 就是十分之五,是分数,是有理数,故此选项不符合题意; D.0 不仅可以表示没有,也可以表示实际的意义,如,在标准条件下,冰与水的混合物的冰与水的混合物 的温度为 0℃,故此项不符合题意. 故选:B. 【点睛】 本题考查有理数 0 的意义和性质,掌握 0 的意义和性质是正确判断的前提.
专题 1.2 有理数
目标导航
1.有理数的概念 ⑴正整数、0、负整数统称为整数(0 和正整数统称为自然数) ⑵正分数和负分数统称为分数 ⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。 理解:只有能化成分数的数才是有理数。①π是无限不循环小数,不能写成分数形式,不是有理数。②有限 小数和无限循环小数都可化成分数,都是有理数。3,整数也能化成分数,也是有理数 注意:引入负数以后,奇数和偶数的范围也扩大了,像-2,-4,-6,-8…也是偶数,-1,-3,-5…也是奇数。 2.有理数的分类 ⑴按有理数的意义分类
②a≤0,<═> |a|=-a (非正数的绝对值等于其相反数;绝对值等于其相反数的数是非正数。) 6.有理数大小的比较 ⑴利用数轴比较两个数的大小:数轴上的两个数相比较,左边的总比右边的小; ⑵利用绝对值比较两个负数的大小:两个负数比较大小,绝对值大的反而小;异号两数比较大小,正数大 于负数。
人教版七年级数学上册第一章《有理数》复习PPT课件

2/ 3 化简(1)-|-2/3|=___ ;
1/
由绝对值求数
3. 若|a|=3,则a=____ -1 ±3 ;|a+1|=0,则a=____ 若|a+1|=3,则a=____ 2,-4
1 4、已知a>0,ab<0,化简|a-b+4|-|b-a-3|=_____ 。
5、若
a a
> ,若 =1,则a____0
×
×
考点二:有理数的分类
一、按整数、分数分类:
整数
正整数 0 负整数 正分数 负分数
二、按正数、负数分类:
正有理数
正整数
正分数
有 理 数
有 理 数
0 负有理数
分数
负整数 负分数
1、0和正数 叫非负数 2、0和负数 叫非正数
3、0和负整数 叫非正整数
4、0和正整数叫非负整数 也叫自然数
分数 。 5、有限小数和无限循环小数属于_____
下列各式中用了哪条运算律?如何用字母表示? 1、(-4) × 8=8 ×(-4) ab=ba 乘法交换律: 2、[(-8)+5]+(-4)=(-8)+[5+(-4)] 加法结合律:( a+b)+c=a+(b+c) 2 1 2 1 3、 (6) [ ( )] (6) (6) ( ) 3 2 3 2 分配律: a(b+c)=ab+bc 4、[29×(-5/6)] ×(-12)=29×[(-5/6) ×(-12)] 乘法结合律:(ab)c=a(bc) 5、(-8)+(-9)=(-9)+(-8) 加法交换律: a+b=b+a
乘法三结合 1、积为整数结合 解 题 技 能
人教版数学七年级上 册第一章 有理数 (基本概念部分) 期末复习课件

课后作业:
1、已知a、b互为相反数,c、d互为倒数,m是绝 对值最小的数,求 (a m b) (m cd )2007的值.
2、已知:(a b)2 | b 4 | 0, 求a 2 b2的值 3、若(a -1) 2 与 | b - 2 | 互为相反数,求a 3 b3
4(:1)若(x-1)2+|y+4|=0,则3x+5y=____ (2)若|a-3|+ |3a-4b|=0,则-2a+8b=____
(3)|3-|+|4- |=____
(4)已知|x|=3,|y|=2,且x<y,则x+y=____
…} …}
负分数集{ -0.1, -3.14 正有理数集{ 1, 25,200%,6/7 负有理数集{ -0.1,-789, -20,-3.14
…} …} …}
自然数集{ 1, 25, 0, 200%
…}
有理数集 {1, -0.1, -789, 25, 0, -20, -3.14, 200%, 6/7…}
A整数 B负数 C非负数 D非正数
2、下列语句中正确的是( D)
A数轴上的点只能表示整数 B数轴上的点只能表示分数 C数轴上的点只能表示有理数 D所有有理数都可以用数轴上的点表示出来 3、若两个有理数在数轴上的对应点分别在原点的两侧, 则这两个数相除所得的商( B ) A.一定是正数 B.一定是负数 C.等于零 D、正、负数不确定
负数 < 0 < 正数
填空题
1.与原点的距离为三个单位的点有2__个,他们分别表
示的有理数是+_3_和_-3_。 2.与+3表示的点距离2000个单位的点有_2_个,他们 分别表示的有理数是_2_00_3_ 和_-1_9_9_7 。 3.+3表示的点与-2表示的点距离是_5_个单位。
2024年初中七年级数学下册同步讲义(人教版)专题1.5 有理数的乘方(学生版)(人教版)
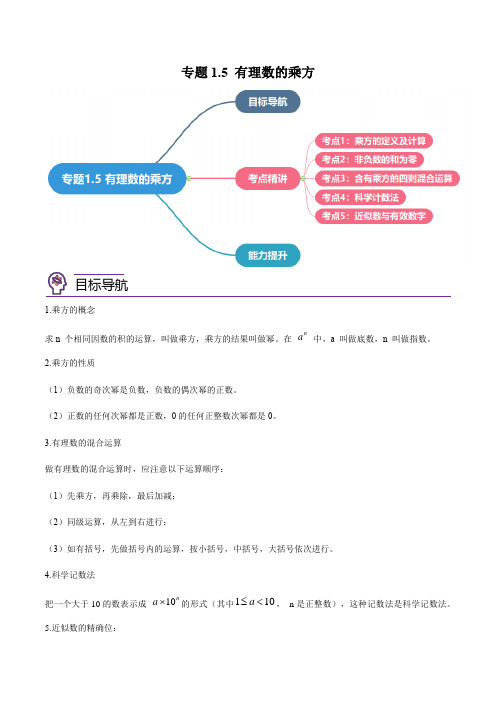
专题1.5 有理数的乘方1.乘方的概念求n 个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。
在 n a 中,a 叫做底数,n 叫做指数。
2.乘方的性质(1)负数的奇次幂是负数,负数的偶次幂的正数。
(2)正数的任何次幂都是正数,0的任何正整数次幂都是0。
3.有理数的混合运算做有理数的混合运算时,应注意以下运算顺序:(1)先乘方,再乘除,最后加减;(2)同级运算,从左到右进行;(3)如有括号,先做括号内的运算,按小括号,中括号,大括号依次进行。
4.科学记数法把一个大于10的数表示成 n a 10⨯的形式(其中101<≤a , n 是正整数),这种记数法是科学记数法。
5.近似数的精确位:目标导航一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位. 有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字 考点1:乘方的定义及计算典例:(1)(2022·全国·七年级)把式子(﹣2)×(﹣2)×(﹣2)×(﹣2)写成乘方的形式 __. (2)(2022·黑龙江·哈尔滨市第六十九中学校期中)下列各组数中,数值相等的是( ).A .23与32B .32-与()32-C .23-与()23-D .232⨯与()232⨯ 巩固练习1.(2022·黑龙江·哈尔滨德强学校期中)下列计算正确的是( )A .224-=-B .()224--=C .()236-=D .()311-= 2.(2022·黑龙江绥化·期末)22-的倒数等于( )A .4-B .4C .14D .14- 3.(2022·四川成都·二模)计算2(2)(5)-⨯-的结果等于( )A .10B .50-C .50D .204.(2022·河北邯郸·三模)计算:222333m n ++++⨯⨯⨯=个个( ) A .23m n + B .23+m n C .32m n + D .23n m +5.(2022·黑龙江·哈尔滨市萧红中学期中)有理数2(1)-,42-,312⎛⎫-+ ⎪⎝⎭,|3|--,0,(5)--,3(2)-中正数的个数有( )A .1个B .2个C .3个D .4个6.(2022·全国·七年级)a ,b 互为相反数,下列各数中,一定互为相反数的一组为( )考点精讲A .a 2与b 2B .a 3与b 5C .a 2n 与b 2n (n 为正整数)D .a 2n +1与b 2n +1(n 为正整数) 7.(2022·上海·位育中学期中)56-的底数是 ____________ .考点2:非负数的和为零典例:(2022·河北邢台·一模)若(a -1)2+|b -a +3|=0,则a =_____,b =_____.巩固练习1.(2022·湖南长沙·七年级期末)已知()22650x y -++=,则x y 的值为( ).A .15B .15-C .125-D .125 2.(2022·黑龙江·哈尔滨市第六十九中学校期中)若()230a b b ++-=,则b a =______.3.(2022·广西崇左·七年级期末)若2|1|(2)0x y -++=,则2022()x y +=________.4.(2022·上海市闵行区颛桥中学期中)已(m - 4)2 + 3n += 0 知,则nm 的值是_________________ 考点3:含有乘方的四则混合运算典例:(1)(2022·陕西渭南·七年级期末)计算:()()20222515153⎛⎫--+-÷-+- ⎪⎝⎭. (2)(2022·江西赣州·七年级期末)计算:20214(1)2(2)43-⨯--÷+- 巩固练习1.(2022·黑龙江·哈尔滨工业大学附属中学校期中)计算:(1)()()32412453⎡⎤---÷⨯--⎣⎦(2)251136412⎡⎤⎛⎫-+-+-÷ ⎪⎢⎥⎝⎭⎣⎦ 2.(2022·内蒙古· 七年级期末)计算: (1)211(1)323⎛⎫-÷--⨯- ⎪⎝⎭(2)2332025(2)41(1)3⎡⎤⎛⎫⨯--÷-++-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.(3)22112(6)(4)()4⎡⎤--⨯-+-÷-⎣⎦3.(2022·河南南阳·七年级期末)计算 (1)()()5753362964⎛⎫-+-⨯-+- ⎪⎝⎭(2)()()()()224313110.5153232---⨯⨯--+-⨯-÷ 4.(2022·全国·七年级)定义一种新运算“☆”,规则为:m ☆n =mn +mn ﹣n ,例如:2☆3=23+2×3﹣3=8+6﹣3=11,解答下列问题:(1)(﹣2)☆4;(2)(﹣1)☆[(﹣5)☆2].考点4:科学计数法典例:(1)(2022·河北沧州·七年级期末)2022年6月5日,神舟十四号载人飞船发射升空,三位航天员入驻距离地球约400000米的中国空间站,开启为期半年的太空任务.将400000用科学记数法表示应为( ) A .6410⨯B .40.410⨯C .5410⨯D .60.410⨯方法或规律点拨此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.(2)(2022·河北·石家庄市第四十一中学模拟预测)一个整数x 用科学记数法表示为281.38110⨯,则x 的位数为( )A .27B .28C .29D .30 巩固练习1.(2022·宁夏·银川市第三中学模拟预测)2021年5月11日,我国第七次人口普查结果发布.宁夏回族自治区总人口达到720万这个数字用科学记数法表示为( )A .7.2×106B .7.2×105C .0.72×107D .0.72×1062.(2022·浙江绍兴·二模)据人民日报报道,截至2022年4月5日,15省份38000多名医务人员驰援上海.其中38000用科学记数法表示为( )A .3.8×103B .3.8×104C .0.38×105D .0.38×1063.(2022·河南南阳·二模)华为最新款手机芯片“麒麟990”是一种微型处理器,每秒可进行100亿次运算,它工作2022秒可进行的运算次数用科学记数法表示为( )A .140.202210⨯B .1220.2210⨯C .132.02210⨯D .142.02210⨯4.(2022·北京·中考真题)截至2021年12月31日,长江干流六座梯级水电站全年累计发电量达2628.83亿千瓦时,相当于减排二氧化碳约2.2亿吨.将262 883 000 000用科学记数法表示应为( ) A .1026.288310⨯ B .112.6288310⨯ C .122.6288310⨯ D .120.26288310⨯5.(2022·全国·七年级)一个整数81550…0用科学记数法表示为108.15510⨯,则原数中“0”的个数为( ) A .4 B .6 C .7 D .106.(2022·全国·七年级课时练习)全面推进新农村建设是改善农村居住环境,提高农民生活水平的必经之路.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资81.02310⨯元资金.数据81.02310⨯可表示为( )A .0.1023亿B .1.023亿C .10.23亿D .102.3亿考点5:近似数与有效数字典例: (1)(2022·全国·七年级课时练习)近似数37.5的实际值表示大于或等于 ___而小于 ___的数.从2020年7月23日发射,到2021年2月10日,“天问一号”探测器飞行了7个月才进入环火星轨道总飞行里程约475490000千米,数据475490000精确到百万位并用科学记数法表示为 ___.(2)(2022·全国·七年级课时练习)数a 四舍五入后的近似值为1.30,则a 的取值范围是( ) A .1.295 1.305a <<B .1.295 1.305a ≤<C .1.295 1.305a <≤D .1.295 1.305a ≤≤巩固练习1.(2022·黑龙江·哈尔滨市第六十九中学校期中)数3.14159精确到百分位约为( ).A .3.14B .3.15C .3.141D .3.1422.(2021·云南·景谷傣族彝族自治县教育体育局教研室七年级期末)用四舍五入法对0.07011取近似值,其中错误的是( )A .0.1(精确到0.1)B .0.07(精确到千分位)C .0.07(精确到0.01)D .0.0701(精确到0.0001)3.(2022·全国·七年级)在近似数0.0270中,共有( )有效数字.A .5个B .4个C .3个D .2个4.(2022·江苏苏州·二模)截止2021年1月10日14:26,美国新冠疫情累计确诊人数为22 699 938,精确到万位,用科学记数法表示为( )A .22.699938×108B .22.7×1010C .2.27×108D .2.270×1075.(2022·河北·平泉市教育局教研室七年级期末)下列对圆周率π的取值说法错误..的是( ) A . 3.0π≈(精确到个位)B .31π≈.(精确到十分位)C .31π≈.(精确到0.1)D . 3.14π≈(精确到百分位)6.(2022·全国·七年级课时练习)近似数4.50所示的数a 的取值范围是( )A .4.495 4.505a ≤<B .4.040 4.60a ≤<C .4.495 4.505a ≤≤D .4.500 4.5056a ≤<7.(2022·上海市西南模范中学九年级阶段练习)长江的长度约为6211300米,用科学记数法并保留三个有效数字可表示为______米.8.(2022·黑龙江·哈尔滨市萧红中学期中)按四舍五入法取近似数:2.704≈_________(精确到0.01). 9.(2021·全国·课时练习)对非负有理数数x “四舍五入”到个位的值记为<x >.例如:<0>=<0.48>=0,<0.64>=<1.493>=1,<18.75>=<19.499>=19,….解决下列问题:(1)<π>= (π为圆周率);(2)若<x >=6,则x 的取值范围是 .一、单选题(每题3分)1.(2022·福建厦门·七年级期末)下列式子可以表示2的3次方的是( )A .222++B .32C .33+D .23 2.(2022·全国·七年级课时练习)据科学家估计,地球的年龄大约是4.6×109年,4.6×109是一个( ) A .7位数B .8位数C .9位数D .10位数3.(2022·天津南开·二模)今年4月16日,神舟十三号载人飞船返回舱在东风着陆场预定区域安全着陆,三位航天员顺利返回地面,神舟十三号载人飞行任务取得圆满成功.已知神舟十三号飞行过程中近地距离200000m ,远地距离356000m .将“356000”用科学记数法表示为( )A .435.610⨯B .53.5610⨯C .63.5610⨯D .60.35610⨯4.(2022·河南南阳·七年级期末)对于有理数a b ,,规定了一种运算:2a b a ab ⊗=-.如2121121⊗=-⨯=-,则计算()532⎡⎤-⊗⊗-⎣⎦的值是( )A .100-B .100C .1-D .905.(2022·福建·厦门双十中学七年级期末)观察下列三组数的运算:3(2)8-=-,328-=-;3(3)27-=-,3327-=-;3(4)64-=-,3446-=-.联系这些具体数的乘方,可以发现规律.下列用字母a 表示的式子:①当0a <时,33()a a =-;②当0a >时,33()a a -=-.其中表示的规律正确的是( )A .①B .②C .①、②都正确D .①、②都不正确6.(2022·江苏扬州·二模)任取一个正整数,若是奇数,就将该数乘3加1;若是偶数,就将该数除以2.反能力提升复进行上述运算,经过有限次的步骤,必然进入循环圈1421→→→.这就是数学史上著名的“冰雹猜想”(又称“角谷猜想”).如果对于正整数m ,经过n 步变换,第一次到达1,就称为n 步“雹程”.如取3m =,由上述运算法则得出:3105168421→→→→→→→,共需经过7个步骤变成1,得7n =.则下列命题错误的是( )A .当7m =时,16n =B .若5n =,则m 只能是5C .若2n =,则m 只能是4D .随着m 的增大,n 不一定也增大二、填空题(每题3分)7.(2022·福建·模拟预测)计算:3(1)|2|-+-=___________.8.(2022·江苏镇江·七年级期末)一个整数6250…0用科学记数法表示为96.2510⨯,则原数中“0”的个数为______.9.(2020·浙江·七年级期末)把a 精确到千分位得到的近似数是6.010,则a 的范围是________. 10.(2022·北京大兴·二模)某超市对某品牌袋装茶叶搞促销活动商家将该品牌袋装茶叶按以下五种类型出售:A 类有一袋茶叶,B 类有二袋茶叶,C 类有三袋茶叶,D 类有五袋茶叶,E 类有七袋茶叶,价格如下表:小云准备在该超市购买6袋上述品牌的茶叶,则购买茶叶的总费用最低为___________元.11.(2020·浙江杭州·七年级期中)已知a 和n 都是正整数,且16n a =,则a 可能取的值是_____. 12.(2022·广东梅州·一模)已知某快递公司的收费标准为:首重10元/千克,续重6元/千克,即:寄一件物品,不超过1千克,收费10元;超过1千克的部分,每千克加收6元.小明在该快递公司寄一件4千克的物品,需要付费________元.三、解答题(13题5分,14题6分,15题7分)13.(2020·江西景德镇·七年级期中)计算: (1)1251631236⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭(2)221224143⎡⎤⎛⎫-⨯-÷--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦. 14.(2022·河北·平泉市教育局教研室七年级期末)在学习了有理数的计算后,数学王老师给出这样三道题: ①()112334⎛⎫÷-+⨯- ⎪⎝⎭;②()()10623-÷⨯-;③()()2423+-⨯⨯-. 甲、乙、丙三名同学各计算一道题,过程如下:甲同学:解①:原式()()()()112232332431824634⎡⎤⎛⎫=÷-+÷⨯-=⨯-⨯-+⨯⨯-=-= ⎪⎢⎥⎝⎭⎣⎦. 乙同学:解②:原式()()()()102362353331596=÷⨯--÷⨯-=⨯--⨯-=-+=-.丙同学:解③:原式()()()()()2432238343241212=⨯-⨯-+⨯⨯-=-⨯-+⨯-=-=.(1)甲、乙、丙三名同学的计算是否正确?(2)如果不正确,请你写出正确的计算过程.15.(2022·全国·七年级期末)2020年的“新冠肺炎”疫情的蔓延,使得医用口罩需求量大幅增加,巴中市某口罩加工厂为满足市场需求计划每天生产5000个,由于各种原因,实际每天生产量与计划每天生产量相比有出入,下表是2月份某一周的生产情况(超出为正,不足为负,单位:个)、(1)根据记录可知前三天共生产口罩 个;产量最多的一天比产量最少的一天多生产口罩 个;(2)该口罩加工厂实行计件工资制,每生产一个口罩需支付工人0.4元的工资,每个口罩的材料成本为0.6元,该工厂以每个1.5元的批发价将前5天的口罩全部售出后,为响应国家“一方有难,八方支援”的号召,决定将剩下两天的口罩全部捐出,试通过计算说明该工厂本周是赚了还是亏了?。
人教版七年级数学上册第一章:有理数总复习课件

[基础练习] 1☆如图所示的图形为四位同学画的数轴,其中正确的是
()
2☆在数轴上画出表示下列各数的点,并按从大到小的顺 序排列,用“>”号连接起来。 4, -|-2|, -4.5, 1, 0。
3 ①比-3大的负整数是____-_2_,_-;1 ②已知m是整数且4<m<3,则m为_____-3_,_-_2,__-1_,_0_,__1,。2 ③有理数中, 最大的负整数是__,最-1 小的正整数是__。最1 大的非正
;-(-8)的相反数是
;
- [+(-6)]=________;0的相反数是 ; a的相反数 是 ; 1 的相反数的倒数是______________ ;
8
• 2☆若a和b是互为相反数,则a+b=( )
A. –2a B .2b C. 0 D. 任意有理数
• 3(1)如果a=-13,那么-a=______;
即a·a·a· ··· ·a=
n个 幂
指数
②正数的任何次幂都是底正数数;
负数的奇次幂是负数, 负数的偶次幂是正数.
-3的平方是(9 )
平方是9的数是(±3)
• (1)2×32和(2×3)2有什么区分?
各等于什么?
9
• (2)32和23有什么区分?±各等3于
什么?
(3)-34和(-3)4有什么区分?各 等于什么?
判断:
①带“-”号的数都是负数
②-a一定是负数
③不存在既不是正数,也不是负数的数
④0℃表示没有温度
增加-20%,实际的意思是
.
甲比乙大-3表示的意思是
.
2.有理数:整数和分数统称有理数。
有理数
整数 分数
正整数 零 负整数 正分数
人教版数学七年级上册(新)单元复习课件:第一章《有理数》

第一章 有理数 小结复习
正整数 0
负整数 正分数 负分数
用点表示有理数 (点与数的对
应) 。
整数
有理数 数轴
分数
有理数在数轴上的 位置关系得出绝对 值、相反数及比较 有理数的大小。
绝对值
相反数
大小比较
数轴的建立把形和数结合起来,利用数轴能直观地理解有理数 的有关概念,比较有理数的大小,理解绝对值、相反数和直观 地研究有理数的运算。
-4
4
-2 2
-4 -3 –2 –1 0 1 2 3 4
5、绝对值: ①数轴上看,一个数的绝对值就是表示这个数的点与原点的距离 叫做a的绝对值。 a的绝对值就是数a所表示点到原点的距离。表示成︱a︱。 (︱a︱≥0,一个数的绝对值是非负数)
a
a
a ( a 0)
-3 –2 –1 0
②绝对值的性质: | a |
正数的绝对值是它本身;
1 0
23
(a 0) a (a 0)
4
负数的绝对值是它的相反数;
0的绝对值是0. ③互为相反数的两个数的绝对值相等。
即︱a︱=︱-a︱且︱a-b︱=︱b-a︱ ④利用绝对值比较大小:两个负数,绝对值大的反而小。其步骤
如下:第一步分别求出两个负数的绝对值,第二步比较这两个绝 对值的大小,第三步根据性质比较。
有理数的意义具正有数相和反负意数义的量
有理数的分类按按性定质义分分类类((整正数数、、0分、数负的数关的系关) 系)
数轴
相反数
有理数有理数的概念倒绝对数值
近似数与有效数字
科学记数法
有理数大小的较
有理数的运算有基理本数运的算运及算法顺则序
人教版七年级数学上册 2.1 有理数的加法与减法(第二章 有理数的运算 自学、复习、上课课件)

感悟新知
知1-练
特别提醒:有理数加法的结果:可正,可负,可为 零,可能比两个加数都大,如3 +5 =8;可能比两个 加数都小,如(-3)+(-5)=-8;可能比一个加数大, 比另一个加数小,如(-3)+5 =2 .
感悟新知
知1-练
2-1.[期中·杭州拱墅区]已知x > 0,y < 0,且|x| < |y|,则
知2-练
感悟新知
例 4 计算:(+13)+(-12)+(+37)+(-78)
知2-练
解题秘方:先把正数、负数分别结合,再计算.
数的绝对值的和.
感悟新知
知1-讲
(2)绝对值不相等的异号两数相加,和取绝对值较大的加数 的符号,且和的绝对值等于加数的绝对值中较大者与较 小者的差. 互为相反数的两个数相加得0 . 同号两数相加: 绝对不相等的异号两数相加:
感悟新知
(3)一个数与0 相加,仍得这个数.
知1-讲
感悟新知
2. 有理数加法运算的各种情况如下表
加,而且适用于三个以上有理数相加.
2.利用有理数的加法交换律交换加数位置时,各加数
要连同其性质符号一起交换.
3.根据需要灵活利用加法运算律,可以达到简化计算
的目的.
感悟新知
知2-练
例 3 计算:(- 143)+( - 147)+ 143+(- 1137). 解题秘方:先找相反数,然后利用加法交换律和结
1. 有理数加法的运算律
运算律
文字叙述
加法交 两个数相加,交换加数
换律
的位置,和不变
加法结 合律
三个数相加,先把前两 个数相加,或者先把后
两个数相加,和不变
知2-讲
用字母表示 a+b=b+a (a+b)+c=a+
人教版七年级上册数学课件:第一章有理数复习(共98张PPT)

则a= ±5 ,b= -8 。
科学记数法、近似数
1. 把一个大于10的数记成a×10n的形式,其中a是整数 数位只有一位的数,这种记数法叫做科学记数法 .
2..与实际完全符合的数是准确数,接近实际但又与实际 数值有差别的数叫近似数。
3.精确度: 一个近似数四舍五入到哪一位,就称这个数
精确到哪一位.
2)0的相反数是0.
3)若a、b互为相反数,则a+b=0.
-4
4
-2 2
-4 -3 –2 –1 0 1 2 3 4
相反数
1、-5的相反数是 5 ; 2、-((-17))如的果相a反=数-是1-37,那;么-a=__1__3__;
(2)如果-x=-6,那么x=___6___; 3、 a+2的相反数是_-_(_a__+_2;)或-a-2
分数有:-3.14,- 2 , -(- 2 ), 1 ,- 1 5 924
正整数有:12,|-8|
非负整数集有
负分数有:-3.14,- 2 ,- 1 54
非负数有:12,0,-(- 2 ),|-8|, 1 92
数轴定义及性质
规定了原点、正方向和单位长度的直线.
-3 –2 –1 0 1 2 3 4
1) 在数轴上表示的两个数,右边的数总比左边的数大;
(2)原式=(-3)+(-18)=-21 (3)原式=0 +(+3)= 3 (4)原式= (-3) +(+18)= 15
加减法可以统一成加法
把下式写成省略加号的和的形式,并把它读出来 (-3)+(-8)-(-6)+(-7)
解:原式=-3-8+6-7 读作“-3,-8,+6,-7的和 或负3减8加6减7
人教版七年级数学上册第章有理数单元复习课件

四舍五入到某一位,就说这个数近似数精确到那一位. 2.由近似数判断精确度
考点一 正、负数的意义
例1 下列各数中,哪些是正数?哪些是负数?
+0.005,-100, 2 3
,-
5 4 ,0.333…,-4,
5,0.
导引:直接根据定义判断即可.
解:正数:+0.005, 2, 0.333, 5; 3
4.相反数 (1)只有符号不同的两个数叫做互为相反数 (2)互为相反数的两个数到原点的距离相等
5.绝对值 (1)一个数在数轴上对应的点到原点的距离 叫做这个数的绝对值 (2)一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数. 0的绝对值是0.
6.有理数大小的比较 (1)数轴上表示的两个数,右边的总比左边的大. (2)正数大于0,0大于负数,正数大于负数;
负数:-100, - 5,-4. 4
考点一 正、负数的意义
注意带单位
例2 如果-4米表示向东走4米,那么向西走2米记作+_2_米___. 【解析】根据题意,可知向东记为负,向西记为正, 故向西走2米记做+2米.
方法总结
根据相反意义合理使用正、负数对实际问题进行表示. 一般情况下,把向北(东)、上升、增加、收入等规定为正, 把它们的相反意义规定为负
⑤ 0℃表示没有温度
( ×)
【解析】①0不带“-”号,但0不是正数,故①错误;
②正数的相反数是负数,故②正确;③同①,故③错
误;④同③,故④错误;⑤0℃并不是表示没有温度,
它是介于正温度与负温度之间,故⑤错误.
方法总结
0既不是正数也不是负数,0的相反数是它本身. 0不仅能表示没有,而且表示正、负之间的分界值.
人教版七年级上册数学《有理数》说课教学复习课件

3.判 断:
(1)0是整数(√) (2)自然数一定是整数(√)
× (3)0一定是正整数( )×
4(.4填)空整:数一定是自然数( ) (1)有理数中,是整数而不是正数的是__负__整__数__和__0_;
⑤负分数一定是负有理数.
其中正确的有
A.1个 B.2个
C.3个
(C )
D.4个
例2:把下列各数填在相应的集合中:
3, 1 ,0,4,π,2.12, 0.65, 300%, 0.6 , 22
2
7
正数集合:{
};
负数集合:{
};
分数集合:{
};
整数集合:{
};
非负有理数集合:{
};
有理数集合:{
•
2.0.1,-0.5,5.32,-150.25, 等0.为3什么被列为分数?
它们都可以化为分数:
0.1= 1 10
0.5= 1 2
150.25=150 1 601
4
4
5.32=5 8 133 25 25
•
0. 3
1
3
这些能化为分数的 小数,都看作为分 数
概念归纳
正整数、零和负整数统称整数. 正分数和负分数统称分数.
思考什么是有理数? 1 , 2 , 3 , 0,- 1, -2 , - 3 ,1/2 , 2/3 , 15/7 , 0.1 , 5.32 ,
-0.5 , -5/2 , -2/3 , -1/7 , -150.25。
分析:分数都可以化为有限小数或无限循环小数的形式,同时 有限小数和无限循环小数又都可以化为分数。
第一章有理数复习(一)课件人教版数学七年级上册

… };
非负整数集合 {
… };
有理数集合 {
… }.
初中数学
二、例题精讲
例1 把下列各数填在相应的大括号内:
27,
1, 5
8.5,
14,
23,
•
0.5,
4
0, 3.14,
24
.
考查:有理数的有理数 分数
负整数 正分数 负分数
二、例题精讲
例1 把下列各数填在相应的大括号内:
例2
①
2
与
2; ②
2
与
1 2
;③
2
与
1;④ 2
2与
1; 2
以上各组数中,互为倒数的是 __③____④_____;
互为相反数的是__①________;
绝对值相同的是__________.
相反数:只有符号不同的两个数叫做互为相反数. 0的相反数是0. a的相反数为-a.
初中数学
二、例题精讲
例2
①
a a 0
a
a 0 a 0 a 0
二、例题精讲 例2 小结:
①一个数的倒数与原数同号; ②互为相反数的两个数绝对值一定相同; ③如果两个数的绝对值相同,
那么这两个数相等或互为相反数.
初中数学
二、例题精讲
例3 (1)比较大小(用“ > ”、“ < ”或“ = ”连接).
3 ___>____ 4
… };
负数集合
{
1
,
14,
2
3
,
•
0.5,
3.14
…
};
5
4
初中数学
二、例题精讲
例1 把下列各数填在相应的大括号内:
人教版2024新版七年级数学上册课件:第二章 有理数的运算 小结与复习

知识回顾
➢ 有理数减法法则: 减去一个数,等于加这个数的相反数.
➢ 有理数乘法法则: 1. 两数相乘,同号得正,异号得负,且积的绝对值等于乘 数的绝对值的积. 2. 任何数与0相乘,都得0.
知识回顾
➢ 有理数除法法则: 1. 除以一个不等于0的数,等于乘这个数的倒数. 2. 两数相除,同号得正,异号得负,且商的绝对值等于被 除数的绝对值除以除数的绝对值的商. 3. 0除以任何一个不等于0的数,都得0.
64 9
.
随堂练习
7.计算:
(3)
{1+[116
−(−
34)3]
×(-2)4
}
÷
(−
1 16
−
3 4
−
12);
解:(3)原式=[1+(116
+
2674)
×16]
÷
(−Βιβλιοθήκη 1 16−12 16
−
186)
= (1+1+ 247) ÷ (− 2116)
=
35 4
×
(
−
16 21
)
=
−
35 4
×
16 21
= − 230.
随堂练习
1.计算.
(1)150+250 =__4_0_0_; (2)-15+(-23) =_-__3_8_; (3)-5-65=_-__7_0_; (4)-26-(-15) =__-__1_1_; (5)(-6)×(-16) =___9_6__;
(6)(- 13)×27=__-__9___;(7)8÷(-16) =__-__12___;
知识回顾
➢ 有理数的混合运算顺序: 1.先乘方,再乘除,最后加减; 2.同级运算,从左到右进行; 3.如有括号,先做括号内的运算,按小括号、中括号、大括号 依次进行.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小结:绝对值具有非负性;0 的绝对值是 0。 五、有理数的运算法则 1、 (1)加法法则:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,绝对 值相等时和为 0,绝对值不相等时,取绝对值较大的数的符号,并用较大的绝对值减去较 小的绝对值;一个数同 0 相加,仍得这个数。 (2)加法运算律:①交换律:a + b = b + a;②结合律:(a + b)+ c = a + (b + c)。 2、 (1)减法法则:减去一个数等于加上这个数的相反数。 (2)字母表示:a - b = a +(-b)。 3、 (1)乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘仍 得 0。 (2)乘法法则的推广:几个不为 0 的有理数相乘,积的符号由负因数的个数决定,当 负因数有奇数个时,积为负,当负因数有偶数个时,积为正。 (3)倒数:乘积为 1 的两个有理数互为倒数;字母表示:a·b = 1。0 没有倒数。 (4)乘法运算律:①交换律:a·b = b·a;②结合律:(a·b)·c = a·(b·c) ;③分配率: a(b+c)= ab + ac。 4、 (1)除法法则一:两数相除,同号得正,异号得负,并把绝对值相除;0 除以任何不等 于 0 的数都是 0,0 不能做除数。 (2)除法法则二:除以一个数等于乘以这个数的倒数;字母表示:a÷b = a× 小结:加法、乘法有运算律,减法、除法没有运算律,只有运算性质。 5、 ( 1)乘方:一般地,求 n 个相同因数 a 的乘积的运算就叫做乘方,即 a×a×…×a = an, 其中乘方的结果叫做幂,a 叫做底数,n 叫做指数。 n个
七年级数学上册有理数及其运算专题复习
知识回顾: 一、有理数 1、概念:整数和分数统称为有理数。 2、有理数的分类: (1)按定义分: 整数 有理数 正整数 0 负整数 正分数 分数 负分数 (2)按性质分: 正整数 正有理数 有理数 0 负有理数 负整数 负分数 小结:“非负数”包括正有理数和 0,“非正数”包括负有理数和 0。0 不属于正有理数也不属 于负有理数。 二、数轴 1、概念:规定了原点、正方向、单位长度的直线,叫做数轴。 (数轴“三要素”) 2、数轴上的点与有理数的关系:所有的有理数都可以用数轴上的点表示,0 用原点表示, 正有理数用原点右边的点表示,负有理数用原点左边的点表示。 小结:数轴上,右边的数比左边的数大。 三、相反数 1、概念:如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这 两个数互为相反数,特别地,0 的相反数是 0。 2、几何意义:在数轴上,表示互为相反数的两个点,位于原点两侧,并且与原点的距离相 正分数
1 (a≠0) 。 思考:0a=0,则 a 的取值范围为 a>0. a
六、有理数的混合运算顺序:先算乘方,再算乘除,最后算加减;如果有括号就先算括号 里面的,同一级运算从左到右依次进行。 七、科学记数法 一般地,一个大于 10 的数可以表示成 a×10n 的形式,其中 1≤a<10,n 是正整数,这种记 数方法叫做科学记数法。 考点攻略: 考点一:用正数和负数表示具有相反意义的量 方法技巧:用正数和负数表示具有相反意义的量,关键是看规定哪种意义的量为正, 则与之相反意义的量为负。 考点二:有理数及其分类 方法技巧:理清楚有理数的两种分类方法,分类时必须按照同一标准进行,不能混 淆;0 属于有理数,但它既不是正数也不是负数,0 是正负数的分界点。 考点三:相反数和绝对值 易错点:0 的绝对值是 0,0 的相反数是 0。相反数是一对符号相反,绝对值相同的数。 绝对值相同的数可能是一对相反数,也可能相等。 方法技巧:要求一个数的绝对值,应先判断这个数是正数、负数还是 0,再根据绝对 值的定义确定去掉绝对值符号后的结果。判断一对数是不是相反数,看它们的和是否等于 0。 考点四:有理数的大小比较 方法技巧:正数大于 0,负数小于 0,正数大于负数;利用数轴来比较,数轴上右边的 数比左边的大;对于负数的大小比较,可以利用它们的绝对值来比较,绝对值大的负数反 而小。 考点五:数轴与有理数运算 方法技巧:从数轴上不但可以看出字母的符号,还可以看出相关字母的绝对值之间的
课堂练习: 一、选择题: 1.计算(-1)2+(-1)3=( ) A.-2 B.-1 C.0 D.2
2.计算-(-1)2012 的结果是( ) A.1 B.-1 C.2012 D.-2012
2.若(a-2)2+|b+3|=0,则(a+b)1024 的值是( ) A.0Байду номын сангаасC.-1 B.1 D.1024
1 。 b
(2)乘方运算的符号法则:正数的任何次幂都是正数,负数的奇次幂是负数,负数的 偶次幂是正数。 小结:底数不为 0 的数,零次幂都等于 1,用字母表示:a0 = 1(a≠0) ;指数为 1 的幂等于 它的底数,用字母表示: a1 = a;指数为 -1 的幂等于它的底数的倒数,用字母表示: a-1 =
大小关系。 考点六:有理数的混合运算 易错点:(1)-22 与(-2)2 不同,-22 的底数是 2, (-2)2 的底数是-2。 (2)在计算 12÷(
1 1 1 )时,要先计算括号内的,除法没有运算律。 2 3 4
( 3)有理数的混合运算一定要按照顺序进行,同时要注意每一步运算的符 号。 考点七:有理数运算的应用 方法技巧:在实际问题中,如果所求结果与方向无关,而至于距离有关时,通常通过 计算数的绝对值解决问题。 考点八:科学记数法 方法技巧:用科学记数法 a×10n 表示大数时,要注意两点: (1)a 的整数部分只有 一位,它大于或等于 1 但是小于 10;(2)n 是正整数,它的值等于原数的整数位数减 1.
等。 字母表示:如果 a、b 互为相反数,那么 a+b=0。 四、绝对值 1、概念:在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值。 2、绝对值的求法:正数的绝对值是它本身,负数的绝对值是它的相反数,0 的绝对值是 0。用字母表示: |a| = 0 -a a (a>0) (a=0) (a<0)
