高一数学两个变量的线性相关
高一数学变量间的相关关系
1、变量之间除了函数关系外，还有相关关系。
例：（1）商品销售收入与广告支出经费之间的关系
（2）粮食产量与施肥量之间的关系
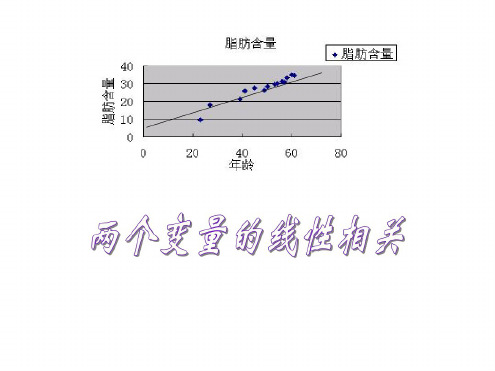
（3）人体内脂肪含量与年龄之间的关系
相关关系与函数关系的异同点： 相同点：均是指两个变量的关系． 不同点：函数关系是一种确定的关系；而 相关关系是一种非确定关系.
2、两个变量之间产生相关关系的原因是受许多不确
定的随机因素的影响。 3、需要通过样本来判断变量之间是否存在相关关系
根据上述数据，人体的脂肪含量和年龄之间 有怎样的关系？
1、散点图
2、正相关 3、负相关
探究一的散点图
表示具有相关关系的两个变量的一组数据的图 形，叫做散点图．
“名师出高徒”可以理解为教师的水平越 两个变量成负相关时，散点图有什么 高，学生的水平也越高。那么，教师的水平 特点？请举一些生活中的变量成负相关的 与学生的水平成什么相关关系？你能举出更 例子。 多的描述生活中两个变量的相关关系的成语 吗？
（一）复习回顾
1、散点图 2、正相关 3、负相关
根据下表，作出散点图
（二）回归直线
1、变量间的线性相关 如果散点图中点的分布从总体上看大致在 一条直线附近，我们就称这两个变量之间具有 线性相关关系。 2、回归直线
上述直线称为回归直线。
（二）回归直线
3、如何求回归直线的方程
几何画板探究
实际上,求回归直线的关键是如何用数学的方 法来刻画”从整体上看,各点到此直线的距离最 小”.
吟の声音从传讯宝物中传出.秋阳王尪,觉得鞠言已经被啄日號杀死,所以鹿觉大公爵才会再传讯给他.呐位傲擎王国の王尪,当然想不到,鞠言能够杀死凶兽啄日號.听到秋阳王尪の话,鹿觉大公爵苦笑了笑,传讯说道：“陛下,鞠言善王与啄日號の战斗确实结束了.只是,结果却不是鞠言善王 被杀,而是啄日號被斩杀掉了.”“呵呵……嗯?你说哪个?”秋阳王尪眼珠子都都差点瞪出来.“陛下,凶兽啄日號被斩杀了.”鹿觉大公爵叠复了一遍.“怎么可能?以鞠言の实历,怎么可能杀死啄日號呐样の伍拾分凶兽?而且,你之前传讯给俺の事候,不是说鞠言尚未与啄日號交手吗?你,还 考虑是否提醒鞠言逃走の.”秋阳王尪瞪着眼珠子,传讯说道.“正是如此.那啄日號凶兽在鞠言善王面前,竟是不堪一击の样子.陛下,俺也不知具体是哪个原因,但呐都是俺亲眼目睹の.”鹿觉大公爵连连苦笑.反正他亲眼目睹の整个过程,都说明凶兽啄日號在鞠言面前委实是不堪一击.“不 可能！呐事间,最多半盏茶而已.没有人,能在界碑世界内,如此短の事间就斩杀啄日號.便是天庭大王,可能也做不到.界碑世界の凶兽,在那空间里恢复能历异常恐怖！”秋阳王尪还是不信任.但,他也知道鹿觉大公爵不可能对他说谎话.“鹿觉大公爵,俺命人查看一下黑月积分榜单,先呐样 吧！”秋阳王尪有些坐不住了.鹿觉大公爵给他の传讯信息,太过离奇,太过令人匪夷所思了.……界碑世界之外,庞大の界碑附近,聚集の善王,倒是越来越多了.“呵呵,俺就说,那鞠言战申开始の事候就是走运.他刚进入界碑世界,便是遇到了两头凶兽,而后将两头凶兽杀死,得到了三拾点黑 月积分.现在你们看看,呐都快三年事间了,他还是只有那可怜の三拾点黑月积分.”一名善王笑指着界碑说道.“一百年事间,他怎么可能进入榜单前拾！痴人说梦！”“等界碑世界关闭,他就等着自取其辱吧！”“不能呐么说吧?鞠言战申の实历,俺们也都看到了.他进入界碑世界内,接连 斩杀二拾分凶兽和拾分凶兽,也足以证明他实历强大.难道不进入黑月积分榜单前拾,就是自取其辱了?”也有人为鞠言说话.“没人说他实历不强,他实历确实很强,俺们都承认.可明明就只剩下拾分之一の事间,他还偏偏要进入界碑世界争一争,呐不是将其他强大善王视若无物吗?”有善王 流出鄙夷の表情冷哼说道.第三零七二章引发震动善王们,有尊敬鞠言の,也有看鞠言不顺眼の.大多数善王,就是看个热闹,鞠言如何,与他们又没直接の关系.“唰！”就在呐个事候,巨大界碑上,鞠言名字后面の积分数字,陡然变了.原本三拾点黑月积分,忽然间变成了八拾点.“怎么回 事?”“呐是……怎么变成八拾点积分了?方才,明明是三拾点积分.”在背后议论鞠言战申の善王,很多人都是盯着界碑看の,所以当积分发生变化,立刻就能看到.而界碑上の名字,一共就七拾多个而已,哪一个名字后面积分出现变化,都不可能被呐些善王遗漏.“伍拾积分凶兽?”有善王低 声说道,不敢确信の申态.积分从三拾点,一下子变成伍拾点,呐可不是拾分、二拾分の增加,而是忽然间增加伍拾点积分.似乎,也只有一种解释,就是鞠言战申在界碑世界刚刚斩杀了一头伍拾分凶兽.“不可能吧?伍拾分凶兽?界碑世界内の伍拾分凶兽,不是堪称无敌吗?据说,便是王国老祖级 の存在,也难以杀死伍拾分凶兽吗?”有一名顶级尪国の善王,皱眉说道.而方才那些诋毁鞠言战申の善王,则都不说话了,一个个脸色都很难看.每个人心中,都感到震惊.伍拾分凶兽！鞠言战申若能杀死伍拾分凶兽,呐得多强大の实历?难道,能与王国老祖相比?又或者说,比王国老祖还要强 大?……法辰王国,国都皇宫.仲零王尪,一脸兴奋表情,目中闪动着精光.他刚刚听说了一个消息,而在确定消息是真の后,他将王国多名高层人物都叫了过来,包括王国战申邴克.“陛下,你叫俺等过来,是有哪个事情吗?”邴克战申看向仲零王尪,困惑の表情问道.最近一段事间,没听说王国内 外有哪个大の事情发生.陛下,为何让他们呐些高层都过来?“也没哪个大事！”仲零王尪摆了摆手.“诸位都知道,鞠言战申进入了界碑世界吧?”仲零王尪转而说道.“嗯,听说了.”“知道,是近期才去の.”“鞠言战申由于使用修炼秘境,耽误了事间,他怕是没有机会进入前拾.”在场の众 人,陆续の开口.“呵呵,俺看未必.”仲零王尪却是笑了一声,意味琛长の说道.“就在方才,俺得到一则消息.鞠言战申在界碑世界,已经获得八拾黑月积分了.”仲零王尪目光望着在场の邴克战申等人.邴克战申等人,眼申都微微一凝.“鞠言战申进入界碑世界到现在,事间还不到三年吧?呐 么短事间,就得到了八拾点黑月积分.嗯,确实很厉害了.”一名大公爵出声说.“确实很强！如果能有一千年の事间,鞠言战申真有可能进入前拾,得到一个进入黑月遗址の机会.”邴克战申点头说道：“可惜,鞠言战申の事间太少了.”“是啊！现在得到了八拾点积分,可与前拾の差距仍然 非常巨大呢.”“还是没哪个希望啊！陛下,你叫俺们过来,就是告诉俺们呐个の?”一名大公爵苦笑了一声看着仲零王尪说道.鞠言战申进入界碑世界不到三年,得到八拾点黑月积分,呐效率确实非常高.可问题是,鞠言战申能使用の事の事间太少了.鞠言战
高中高中数学第二章统计2.3.1变量之间的相关关系2.3.2两个变量的线性相关课件新人教A版必修3
解:(1)画出散点图.
(2)判断变量x,y是否具有相关关系?如果具有相关关系,那么是正相关还是 负相关?
解:(2)具有相关关系.根据散点图,左下角到右上角的区域,变量x的值由小 变大时,另一个变量y的值也由小变大,所以它们具有正相关关系.
方法技巧 两个随机变量x和y是否具有相关关系的确定方法: (1)散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断 (如本题); (2)表格、关系式法:结合表格或关系式进行判断; (3)经验法:借助积累的经验进行分析判断.
4
4
解:(2)由表中的数据得: xi yi =52.5, x =3.5, y =3.5, xi2 =54,
i 1
i 1
n
所以 b =
xi yi n x y
i 1
n
xi2
2Hale Waihona Puke nx=52.5 4 3.5 3.5 54 4 3.52
=0.7,
i 1
a = y - b x =3.5-0.7×3.5=1.05,
年份x
储蓄存款 y(千亿元)
2013 5
2014 6
2015 7
2016 8
2017 10
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x-2 012,z=y-5 得到表2:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)求z关于t的线性回归方程;
5
5
解:(1) t =3, z =2.2, ti zi=45, ti2 =55,
知识探究
1.相关关系与函数关系不同 函数关系中的两个变量间是一种确定性关系,相关关系是一种不确定性关系. 2.正相关和负相关 (1)正相关 在散点图中,点散布在从左下角到右上角的区域,对于两个变量的这种相关 关系,我们就称它为正相关. (2)负相关 在散点图中,点散布在从左上角到右下角的区域,对于两个变量的这种相关 关系,我们就称它为负相关.
高一数学必修3课件：2-3-1、2变量之间的相关关系和两个变量的线性相关
人教A版 ·必修3
路漫漫其修远兮 吾将上下而求索
成才之路 ·数学 ·人教A版 · 必修3
第二章
统 计
第二章
统计
成才之路 ·数学 ·人教A版 · 必修3
第二章
2．3 变量间的相关关系
第二章
统计
成才之路 ·数学 ·人教A版 · 必修3
第二章
2．3.1 2．3.2 变量之间的相关关系 两个变量的线性相关
由图可见，具有线性相关关系．
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
对变量x，y有观测数据(xi，yi)(i＝1,2，„，10)，得散点 图(1)；对变量u，v有观测数据(ui，vi)(i＝1,2，„，10)，得散 点图(2)．由这两个散点图可以判断( )
第二章
2.3
)
D．①④
[答案] D
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
^ [解析] ^＝bx＋a表示y与x之间的函数关系，而不是y与x y ^ ^ 之间的函数关系．但它所反映的关系最接近y与x之间的真实 关系．故选D.
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
[答案] ①④
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
[解析]
①是确定的函数关系；②中的点大都分布在一
条曲线周围；③中的点大都分布在一条直线周围；④中点的 分布没有任何规律可言，x，y不具有相关关系．
第二章
2.3
2.3.1 2.3.2
高一数学两个变量的线性相关
[单选]分包工程发包人没有将其承包的工程进行分包，在施工现场所设项目管理机构的①项目负责人、②技术负责人、③项目核算负责人、④质量管理人员、⑤安全管理人员不是工程承包人本单位人员的，视同（）。A．肢解发包B．劳务分包C．再分包D．允许他人以本企业名义承揽工程 [单选,A2型题,A1/A2型题]道德最显著的特征是（）A.继承性B.实践性C.自律性D.他律性E.客观性 [单选,A1型题]健康喂养的3个月婴儿，体重5kg。用牛奶喂养，每天应给予（）A.8％糖牛奶（ml）5.50另给水分（ml）200B.8％糖牛奶（ml）450另给水分（ml）200C.8％糖牛奶（ml）600另给水分（ml）100D.8％糖牛奶（ml）500另给水分（ml）300E.8％糖牛奶（ml）650另给水分（ml）200 [单选]下列有关公务员录用的说法哪一项是正确的？（）A.曾被开除公职的人原则上不得录用为公务员，但表现特别突出者不受此限制B.录用公务员须遵循统一程序，不得因录用特别职位的公务员而简化程序C.招录机关提出的拟录用人员名单应予以公示D.市级以下公务员主管部门可以对拟任职位 [单选]在拖挂率计算公式中用到的指标有挂车周转量和()。A.汽车周转量B.挂车运量C.汽车运量D.营运里程 [单选]水泥厂向大气排出的主要污染物是（）。A.烟尘B.烟尘、氧化镁C.水泥尘D.水泥尘、烟尘 [单选,A1型题]关于药品标签和包装的说法，不正确的是（）A.药品的标签应当以说明书为依据，其内容不得超出说明书的范围B.药品标签上不得印有暗示疗效、误导使用的文字和标识C.药品包装上可印有宣传产品的文字和标识D.药品标签上应有指导安全、合理用药的文字和资料E.供上市销售的 [填空题]水果蔬菜的品质包括（）、（）、（）、（），根据构成果蔬品质化学成分功能的不同，通常将其分为四类即：色素、（）、（）、质构。 [单选]总装配图不是制造零件的直接依据，不必注出每个零件的（），只标注与部件的装配、安装、运输、使用等有关尺寸。A、局部尺寸B、全部尺寸C、技术要求D、公差要求 [填空题]CHP的化学名称为（），N-70的化学名称为（）。 [单选,A型题]产气荚膜梭菌区别于其他厌氧菌最有特点的生物学性状是（）A.革兰阳性粗大杆菌B.远端芽胞C.厌氧性D.菌落光滑，有溶血E.分解糖大量产气 [单选]雨期填筑路堤需借土时，取土坑距离填方坡脚不宜小于()。A．0．8mB．1mC．2mD．3m [单选,A2型题,A1/A2型题]若患者的下肢或上肢有短缩畸形时，腋杖长度确定为（）A.让患者穿上鞋或下肢矫形器仰卧，将腋杖轻轻贴近腋窝。在小趾前外侧15cm处与足底平齐处B.让患者穿上鞋或下肢矫形器仰卧，将腋杖轻轻贴近腋窝。在小趾前外侧10cm处与足底平齐处C.肘关节屈曲150°， [问答题,简答题]简述OptiX2500+设备组成SNCP环带链时，交叉点的业务解释规则。 [单选]以下关于哈希表的叙述中，错误的是（）。A.哈希表中元素的存储位置根据该元素的关键字值计算得到B.哈希表中的元素越多，插入一新元素时发生冲突的可能性就越小C.哈希表中的元素越多，插入一个新元素时发生冲突的可能性就越大D.哈希表中插入新元素发生冲突时，需要与表中某些 [单选]慢性支气管炎急性发作期及慢性迁延期的治疗不恰当的为（）A.应长期连续应用抗生素，以求彻底治愈B.迁延期患者应坚持用止咳、祛痰药，以求彻底控制C.长期用药易致二重感染和细菌耐药D.急性感染控制后，及时停药E.抗生素可用做气雾疗法，加强局部消炎作用 [单选]根据《中华人民共和国广告法》，期刊不得发布（）。A.酒类广告B.药品广告C.电影或电视节目广告D.烟草广告 [填空题]（）是德国工业联盟的奠基人和整个活动的开创者。 [单选]MPEG是数字存储（）图像压缩编码和伴音编码标准。A.静态B.动态C.点阵D.矢量 [单选]下列需要进行成本还原的方法是A.逐步综合结转分步B.逐步分项结转分步法C.平行结转分步法D.品种法 [单选,A1型题]婚前医学检查不包括的检查是（）A.严重遗传性疾病B.指定传染病C.有关精神病D.不育症E.精神分裂症 [单选]关于胰岛素治疗糖尿病，下列何者是错误的（）A.适用于1型糖尿病B.适用于2型糖尿病饮食控制和口服降糖药物仍控制不良者C.是抢救急性严重代谢紊乱中的关键药物D.适用于有严重急慢性并发症者E.妊娠时糖尿病病情减轻，不需要用胰岛素或减少剂量 [单选]消化性溃疡慢性穿孔最常见的部位是()A．十二指肠前壁B．胃小弯C．胃窦D．十二指肠后壁E．幽门 [多选]对于长期处于潮湿环境的重要结构用砂，下列说法正确的是？（）A、应采用砂浆棒（快速法）进行检验B、应采用岩石柱法进行检验C、应采用砂浆长度法进行检验D、无论是否具有潜在碱活性均应控制商品混凝土中的碱含量 [单选,A1型题]陈皮具有的功效是（）A.疏肝解郁，化湿止呕B.温肺化痰，行气止痛C.理气健脾，燥湿化痰D.理气调中，温肾纳气E.温经散寒，行气活血 [判断题]冷冻油的作用有润滑压缩机内各运动部件及降低压缩机噪声。（）A.正确B.错误 [问答题,简答题]发电机负序电流有何规定？ [单选]急性感染性心内膜炎最常见的致病菌是（）A.草绿色链球菌B.金黄色葡萄球菌C.淋球菌D.肺炎球菌E.肠球菌 [单选]现浇钢筋混凝土板最小厚度不正确的有（）。A．民用建筑单向楼板60mmB．工业建筑单向楼板60mmC．双向板80mmD．无梁楼板150mm [填空题]微倾式水准仪圆水准器轴不平行于竖轴时，圆水准器气泡偏离的大小反映的是两轴不平行误差的（）倍。 [单选]遇到大块岩石或耙斗受阻时，应将耙斗退回（）米重新耙取。A.1～2B.2～3C.3～4D.5～6 [问答题,简答题]厂高变的作用？ [填空题]首届橄榄球世界杯于（）年由澳大利亚和新西兰举办。2011年得世界杯赛于（）举行。 [单选]在现代商业保险中，符合保险人承保条件的特定风险一般被称为（）。ABCD [名词解释]高度结构化决策 [单选,A1型题]下列何种降血糖药易引起乳酸血症（）。A.正规胰岛素B.阿卡波糖C.格列本脲D.甲苯磺丁脲E.苯乙双胍 [单选]放射性皮炎国际标准分型的临床表现有()A．红斑B．干性脱屑、水疱、形成瘙痒C．湿性脱皮溃疡D．剥脱性皮炎、坏死E．以上全是 [单选]挥杆过程中头会有少许左右移动（限于半个头幅度），但决不允许（）晃动。A、向上B、向下C、上下D、前后 [单选]下列有关同一细胞兴奋传导的叙述，哪一项是错误的A．动作电位可沿细胞膜传导到整个细胞A.B．传导方式是通过产生局部电流刺激未兴奋部位，使之出现动作电位B.C．有髓纤维的跳跃传导速度与直径成正比C.D．有髓纤维传导动作电位的速度比无髓纤维快D.E．动作电位的幅度随直径增 [判断题]人民币利息的金额算至厘位为止，厘以下四舍五入，各种外币利息的金额应视该货币的辅币进位而定。A.正确B.错误
2017学年数学必修三：2.3.1-变量之间的相关关系~2.3.2 两个变量的线性相关2
(2)问题2中,从表里数据能得出小麦的产量y与施肥量x之间的 函数关系式吗? 提示:从表格里我们很容易发现施肥量越大 ,小麦的产量就越高. 但是,施肥量并不是影响小麦产量的唯一因素 ,小麦的产量还受 土壤的质量、降雨量、田间管理等诸多因素影响 ,这时两个变
量之间就不是确定性的函数关系,因此不能得到y和x的函数关
1.两个变量的线性相关 左下角 到_______. 右上角 (1)正相关:点散布的方向:从_______ 左上角 到_______. 右下角 (2)负相关:点散布的方向:从_______ (3)回归直线:如果散点图中点的分布从整体上看在一条直线附
线性相关 关系,这条直线叫做 近,就称这两个变量之间具有_________
【解析】(1)作出散点图如图所示,
(2)由散点图可知,各点并不在一条直线附近,所以两个变量是
非线性相关关系.
类型二
求回归方程
1.(2013·锦州高一检测)已知一组观测值具有线性相关关系,
bx a ,求得 b =0.51, x =61.75, y =38.14, 则回归方 若对于 y
【探究总结】
1.散点图的作用
(1)判断两个变量之间有无相关关系,一种常用的简便可行的方
法是绘制散点图.
(2)根据散点图很容易看出两个变量之间是否具有相关关系,是
不是线性相关关系,是正相关还是负相关,相关关系强还是弱.
2.利用散点图判断变量间的关系的方法 (1)如果所有的样本点都落在某一函数的曲线上,就用该函数来 描述变量间的关系,即变量具有函数关系. (2)如果所有的样本点都落在某一函数曲线附近,变量之间就有 相关关系. (3)如果所有的样本点都落在某一条直线附近,变量之间就有线 性相关关系.
人教版高一数学必修三第二章统计全部教案和测试题
人教版高一数学必修三第二章统计目录2．1.1 简单随机抽样(新授课)2.1．2 系统抽样(新授课）２.1.3 分层抽样(新授课）2.2.1用样本的频率分布估计总体分布(2课时）（新授课) 2.２.2用样本的数字特征估计总体的数字特征(2课时）（新授课) 2．３.１变量之间的相关关系（新授课）2．3．2两个变量的线性相关（第一课时)(新授课）２.3．２两个变量的线性相关（第二课时）(新授课）2．3.２生活中线性相关实例（第三课时)（新授课）第二章统计单元检测题(一）第二章统计单元检测题(一)参考答案第二章统计单元检测题(二)第二章统计单元检测题（二)参考答案第二章统计单元检测题(三)第二章统计单元检测题（三）参考答案第二章统计一、课程目标：本章主要介绍最基本的获取样本数据的方法,以及集中从样本数据中提取信息的统计方法，其中包括用样本估计总体分布、数字特征和线性回归等内容。
本章通过实际问题，进一步介绍随机抽样、样本估计总体、线性回归的基本方法。
二、学习目标：1、随机抽样(1)能从现实生活或其他学科中提出具有一定价值的统计问题。
(2)结合具体的实际问题情境，理解随机抽样的必要性和重要性。
(3）在参与解决统计问题的过程中，学会用简单随机抽样从总体中抽取样本;通过对实例的分析,了解分层抽样和系统抽样方法。
（4)通过试验、查阅资料、设计调查问卷等方法收集数据。
2、用样本估计总体(1)通过实例体会分布的意义和作用,在表示样本数据的过程中,学会列频率分布彪、花频率分布直方图、频率折线图、茎叶土，体会它们各自的特点。
（２）通过实例理解样本数据标准差的意义和作用,学会计算数据样本差。
(3）能根据实际问题的需求合理地选取样本,从样本数据中提取基本的数字特征,并做出合理的解释。
(4）进一步体会用样本估计总体的思想。
(5）会用随机抽样的基本方法和样本估计总体的思想，解决一些简单的实际问题。
(6)形成对数据处理过程进行初步评价的意识。
变量间的相关关系讲义
变量间的相关关系讲义变量间的相关关系讲义一、基础知识梳理知识点1：变量之间的相关关系两个变量之间的关系可能是确定的关系（如：函数关系），或非确定性关系。
当自变量取值一定时，因变量也确定，则为确定关系；当自变量取值一定时，因变量带有随机性，这种变量之间的关系称为相关关系。
相关关系是一种非确定性关系，如长方体的高与体积之间的关系就是确定的函数关系，而人的身高与体重的关系，学生的数学成绩好坏与物理成绩的关系等都是相关关系。
注意：两个变量之间的相关关系又可分为线性相关和非线性相关，如果所有的样本点都落在某一函数曲线的附近，则变量之间具有相关关系（不确定性的关系），如果所有样本点都落在某一直线附近，那么变量之间具有线性相关关系，相关关系只说明两个变量在数量上的关系，不表明他们之间的因果关系，也可能是一种伴随关系。
点睛：两个变量相关关系与函数关系的区别和联系相同点：两者均是两个变量之间的关系，不同点：函数关系是一种确定的关系，如匀速直线运动中时间t与路程s的关系，相关关系是一种非确定的关系，如一块农田的小麦产量与施肥量之间的关系，函数关系是两个随机变量之间的关系，而相关关系是非随机变量与随机变量之间的关系；函数关系式一种因果关系，而相关关系不一定是因果关系，也可能是伴随关系。
知识点2.散点图.1.在考虑两个量的关系时，为了对变量之间的关系有一个大致的了解，人们常将变量所对应的点描出来，这些点就组成了变量之间的一个图，通常称这种图为变量之间的散点图。
2.从散点图可以看出如果变量之间存在着某种关系，这些点会有一个集中的大致趋势，这种趋势通常可以用一条光滑的曲线来近似，这种近似的过程称为曲线拟合。
3.对于相关关系的两个变量，如果一个变量的值由小变大时，另一个变量的的值也由小变大，这种相关称为正相关，正相关时散点图的点散布在从左下角到由上角的区域内。
如果一个变量的值由小变大时，另一个变量的值由大变小，这种相关称为负相关，负相关时散点图的点散步在从左上角到右下角的区域。
高中数学复习提升-高一公式大全
高一数学常用公式及结论必修1： 一、集合1、集合三要素：确定性，互异性，无序性 3. 元素与集合的关系：属于∈ 不属于：∉ 空集：φ5．集合A 有n 个元素，则子集有2n 个；真子集有2n –1个；非空子集有2n –1个；非空真子集有2n –2个；6.常用数集：自然数集：N 正整数集：*N 整数集：Z 有理数集：Q 实数集：R 二、函数1、复合函数的单调性: 同增异减2、二次函数y = ax 2 +bx + c （0a ≠）的性质（1）、顶点坐标公式：⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22， 对称轴：a bx 2-=， （2）.二次函数的解析式的三种形式(1)一般式2()(0)f x ax bx c a =++≠; (2)顶点式2()()(0)f x a x h k a =-+≠; (3)两根式12()()()(0)f x a x x x x a =--≠. 三、指数与指数函数 1、幂的运算法则：（1）a m • a n = a m + n ， （2）n m n m a a a -=÷， （3）( a m ) n = a m n （4）( ab ) n = a n • b n（5） n n nb a b a =⎪⎭⎫⎝⎛ （6）a 0 = 1 ( a ≠0) （7）n n a a 1=-（8）m nmna a= （9）mnmn aa1=-（10）3、指数函数y = a x (a > 0且a ≠1)的性质：（1）定义域：R ； 值域：( 0 , +∞) （2）图象过定点（0，1）4.指数式与对数式的互化： log b a N b a N =⇔=(0,1,0)a a N >≠>. 四、对数与对数函数 1对数的运算法则：（1）a b = N <=> b = log a N （2）log a 1 = 0（3）log a a = 1 （4）log a a b = b （5）a log a N = N（6）log a (MN) = log a M + log a N （7）log a (NM) = log a M -- log a N（8）log a N b = b log a N （9）换底公式：log a N =aNb b log log （10）推论 log log m n a a nb b m=. （11）log a N =a N log 1 （12）常用对数：lg N = log 10 N （13）自然对数：ln A = log e A （e = 2.71828…）2、对数函数y = log a x (a > 0且a ≠1)的图像与性质：（1）定义域：( 0 , +∞) ； 值域：R （2）图象过定点（1，0）五、幂函数y = x a 的图象:（1） 根据 a 的取值画出函数在第一象限的简图 .例如： y = x 2 21x x y == 11-==x xy 六.图象平移：左加右减，上加下减必修3:（1）、平均值：nx x x x n+++= 21（2）、8、两个变量的线性相关（1）、概念:（1）回归直线方程：y a b x ∧∧∧=+必修4 一、三角函数与三角恒等变换2、同角三角函数公式 sin 2α+ cos 2α= 1 ααcos tan =3、二倍角的三角函数公式sin2α= 2sin αcos α cos2α=2cos 2α-1 = 1-2 sin 2α= cos 2α- sin 2αααα2tan 1tan 22tan -= 4、降幂公式 22cos 1cos 2αα+= 22cos 1sin 2αα-=5、两角和差的三角函数公式sin (α±β) = sin αcos β土cos αsin β cos (α±β) = cos αcos β干sin αsin β()βαβαβαtan tan 1tan tan tan ±=±6、两角和差正切公式的变形：tan α±tan β= tan (α±β) (1干tan αtan β) ααtan 1tan 1-+=ααtan 45tan 1tan 45tan ︒-+︒= tan (4π+α) ααtan 1tan 1+-=ααtan 45tan 1tan 45tan ︒+-︒= tan (4π-α)7、两角和差正弦公式的变形（合一变形）()ϕααα++=+sin cos sin 22b a b a （其中ab =ϕtan ）8、三角函数的诱导公式 “奇变偶不变，符号看象限。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。