[例2-6] 试用长除法求 的z反变换。
第二章 反z变换

外处处解析,C为D
D
zn C3 z 3
Cn C2
z1 z2
C
1
C
留数法思路
1. 2. 由于积分围线c在X(z)的收敛域内,所以首先要确定收敛域, 如未给定要根据其极点确定。 考虑被积函数X(z)zn-1在c内或c外的极点的情况确定用(a)式或 (b)式来计算。原则是选择X(z)zn-1有有限个极点且极点阶次有 限的区域来求留数,而尽量避免求z=∞的留数。 如收敛域在一圆外,应计算n>0时的x(n),选择(a)式,因 为此时在c内有有限个阶次有限的极点,zn-1在z=0处解析; 如收敛域在一圆内,应计算n<0时的x(n),选择(b)式; 当收敛域在某一圆环内,应利用X(z)在c内的极点求得n>0的 x(n),而利用c外的极点求得n<0的x(n). n=0的情形要单独地与n>0的情况同样处理
2.7.3 Z反变换
即由Z变换式X(z)求相应的序列x(n), 常用 Z-1[x(z)]表示, 1 n 1 x ( n) X ( z ) z dz c ( Rx , Rx ) 2j c 逆z变换是一个对X(z)zn-1进行的围线积分,积 分路径C是一条在X(z)收敛环域(Rx-,Rx+) 以内反时针方向绕原点一周的单围线。
(3) 收敛域1/3 <∣z∣< 1:
此时收敛域在一个环内,
X0(z)的极点 z1=1在围线c之外,而 z2=1/3在围线c之 内, 于是有:
1 1 1 x3 (n) Re s[ X 1 ( z ), z ] ( ) n 3 2 3 • 当n≥1-m=0时,
• 当n<1-m=0时,
由Z变换X(z)求其相应的序列x(n),有下面的Z反变换关系式:
例试用长除法求的z反变换

—14 —14 - —116 Z-1
—116 Z-1 —116 Z-1- —614 Z-2
—614 Z -2 —614 Z-2 - —215—6 Z-3
—215—6 Z-3
...
得X (z) 1 ( z 5 z 4 z 3 z 2 4z 15 64 16 4
Z[h(n)], Rn
z
Rn
,
则有:Y (z) Z[ y(n)] 1 X ( z )H (v)v1dv
2j c v
1
2j
X (v)H ( z )v1dv;
c
v
Rx Rn
z Rx Rn
其中,C是在变量V平面上,X(z/v),H(v)公共收敛
域内环原点的一条逆时针单封闭围线。 (证明从略)
(
16z 4z
z
z
1
)
4Hale Waihona Puke 4Z+Z2 + —41 Z3+ 1—16 Z 4+ —614 Z5 + ...
) 4-Z 16 Z 16 Z - 4 Z2
4 Z2
4 Z2 - Z3
Z3
Z 3 - —14 Z 4
—14 —14
Z4 Z4
-
—116
Z
5
—116 Z 5
.. .
1+ —14 Z-1+11—6 Z-2 + 6—14 Z -3...
1 [e j0n e j0n ]u(n) 2
Z[anu(n)]
1 1 az1
,
z
a
Z反变换
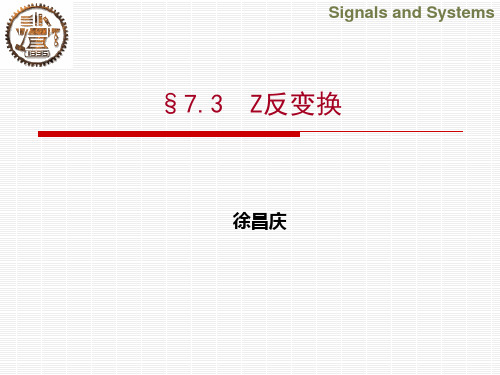
s j 1
Bj z z zi j
2020/6/23
Am的求取方法就是一阶极 点的求取方法
Bj
1 (s
d s j
j)!
dz
s
j
(z zi )s
X (z)
z
zzi
高阶极点时,X(z)还可以展开成
X (z)
A0
M m1
Am z
z zm
s j 1
Cj z z zi j
这时,Cs
( z
(1), z 3时,x(n)是右边序列
x(n)
2 3
(n)
0.5n
1 3
3n
u(n)
2 (n) 0.5n 3n1 u(n) 3
x(n) lim x(z) 0 z
2020/6/23
(2), z 0.5时,x(n)是左边序列
x(n)
2
(n)
1
n
u(n
1)
3n1u(n
1)
3
2
x(n) lim x(z) 0
n
u
(n
1)
1 3
3n
u(n
1)
x(n)
2 3
(n)
1 2
n
u(n
1)
1 3
3n
u(n
1)
(3),0.5 z 3时,双边序列
n 1时,围线内极点z 0.5
2020/6/23
x(n) Res X (z)zn1 z0.5
1 2
n
,
n
1
n 0时,围线内极点
z 0, z 0.5
15 z2 45 z3 30 z4
31z3 30z4 x(n) (2n 1)u(n)
同济大学数字信号处理课件第二章2z反变换

1 F ( z )在围线c内只有一阶极点z 4 x ( n ) Re s[ F ( z )] 1
z
j Im[ z ]
C
1 z n 1 ( z ) 1 4 (4 z )( z 1/ 4) z 4 n 4 15
4
1/ 4
0
4 Re[ z ]
当n 1时 1 F ( z )在围线c内有一阶极点z 和-(n 1)阶极点z 0 4 而围线c外只有一阶极点z=4,且F(z)的分母多项式
X ( z ) [a 1 z a 2 z 2 a 3 z 3 …] - an z n
n 1
x(n) a n u( n 1)
z 例:X ( z ) , 1/4< z 4,求z反变换 (4 z )( z 1/ 4)
2
解:X(z)的Roc为环状,故x(n)是双边序列 极点z=1/4对应右边序列,极点z=4对应左边序列 先把X(z)展成部分分式
z2 例1:X ( z ) , 1/4< z 4,求其z反变换 (4 z )( z 1/ 4) z2 n 1 解:x (n ) z dz c ( Rx , Rx ) 2 j c (4 z )( z 1/ 4) 2 n 1 z z n 1 其中:F ( z ) z (4 z )( z 1/ 4) (4 z )( z 1/ 4) 当n 1时 1
根据复变函数理论,若函数X(z)在环状区域 Rx z Rx , (Rx 0, Rx ) 内是解析的,则 在此区域内X(z)可展开成罗朗级数,即
X ( z)
而
Cn
n
n C z n
Z反变换方法

第27讲 Z反变换计算方法
z 反变换主要方法
幂级数展开法 部分分式展开法 留数法
幂级数展开法
F (z) f (n)zn
n0
f (0)z0 f (1)z1 f (2)z2 L
根据单边z变换的定义,因果序列的象函数是z-1的 幂级数,其各项的系数就是相应的序列值,再求出其 闭合表示式即为原序列 f (n) 。
Ki
F(z) z
(z
z i)
zzi
z0 0
( i = 0,1,2,N)
N
z反变换,原序列为 f (n) Ki(zi)n (n)
i 1
部分分式展开法
例3
已知F (z)
z2 z 1 z2 3z 2
求原序列 f (n)
解
F (z) z2 z 1 K1 K2 3K
z z(z 1)(z 2) z z 1 z 2
幂级数展开法有时不能得到解析表达式
部分分式展开法
z变换式的一般形式 F (z) N (z) bm zm bm1zm1 K b1z b0 D(z) an zn an1zn1 K a1z a0
式中m n 。若 m n 时,利用长除法得到一个z 的多项式和一个
真分式。部分分式展开法与拉氏反变换的部分分式法类似,所不
同的是,一般是对 F(z) 展开为部分分式,以保证每个分式中都具
z
有基本变换形式 z 。
z a
部分分式展开法
(n)
z z 1
➢
已知F(z)后,应先对F ( z ) 展开部分分式。 z
(1) F(z)仅有一阶单极点,则可展开为
an (n) z
z a
式中系数
F ( z ) N
逆z变换

极点时,可以展开成以下的部分分式的形式:
X (z)
A0
N k 1
Ak 1 zk z1
z max[ zk ]
N
则其逆Z变换为:x(n) A0 (n) Ak zknu(n)
k 1
说 明 : a.X(z) 较 简 单 时 可 按 算 术 展 开 求 各 系 数
Ak(k=0,1…,N) 。
b.X(z) 较 复 杂 时 可 按 留 数 定 理 求 各 系 数
k 1,, s
3.围线积分法(留数法)
x(n) 1 X (z)zn1dz
2j c
式中C为收敛域中的一条逆时针环绕原点的闭合曲线。
若被积函数 X (z)zn1是有理分式,一般采用留数定理来计 算围线积分 。根据留数定理, x(n) 等于围线C内全部极 点留数之和,即:
x(n) Re s[X (z)zn1, ak ]
直接用长除法进行逆变换
X z xnz n n
(是一个z 的幂级数)
x(2)z2 x(1)z1 x(0)z0 x(1)z1 x(2)z2
级数的系数就是序列 xn
注意:
在用长除法将X(Z)展开成幂级数 形式之前,应先根据给定的收敛域 是圆外域还是圆内域,确定x(n) 是右边序列还是左边序列。
5z 3 4z 4
例1:
因为 X (z) x(0)z0 x(1)z 1 x(2)z 2
所以 xn 0, 1, 2, 3, 4, 因为长除结果无常数项,则x0 0。
例2:
X z z z
z2 2z 1 1 2z z2
z 1
z 2z2 3z3 4z4
1 2z z2 z z 2z2 z3
X(z)
N(z) D(z)
例2-6试用长除法求的z反变换-精选
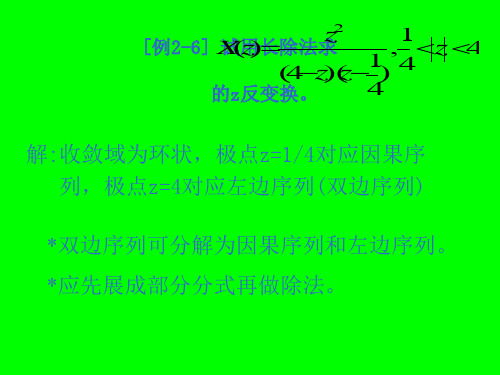
Z[u(n)] z , z 1 z 1
Z[u(n 3)] z3 z z2 , z 1 z 1 z 1
z
z2 z2 z 1
Z[x(n)]
z 1 z 1
z2
, z 1
3. Z域尺度变换(乘以指数序列)
如果 Z [x(n) ]X (z),R xzR x,则
Z [a nx (n ) ]X (z); a
证明:X ( z )
x(n) z n , 对其两端求导得
n
dX ( z ) d [ x (n) z n ] x (n) d ( z n )
dz
dz n
n
dz
nx (n ) z n 1 z 1
nx(n)z n
n
n
即, Z [nx (n)] z dX ( z ) dz
5. 共轭序列
如果 Z [x(n) ]X (z),R xzR x ,则
Z[x*(n)]X*(z*),Rx z Rx ; 其中, x*(n)为x(n)的共轭序列。
证明:Z[x*(n)] x*(n)zn [x(n)(z*)n]*
n
n
[ x(n)(z*)n]*X*(z*),Rxz Rx; n
证明:X(z) x(n)u(n)zn x(n)zn
n
n0
x(0)x(1)z1 x(2)z2
显然,limX(z) x(0) z
8. 终值定理
对于因果序 x(n)列 ,且 X(z) Z[x(n)]的极点 在单位圆内,且单 只位 允圆 许 z上 1处有一 阶极点,则有
limx(n)
n
lzi m1[(z1)X(z)]Res[X(z)]z1
6. 翻褶序列
如果 Z [x(n) ]X (z),R xzR x ,则
第3章 离散序列

2、收敛条件: X(z)收敛的充要条件是绝对可和。
n
x n Z n M
三、一些序列的收敛域
(1)、预备知识 阿贝尔定理: 如果级数 x n Z ,在 Z Z 0收敛,那么,满足
x
0
n
双边序列指n为任意值时,x(n)皆有值的序列,即左边 序列和右边序列之和。
X ( z)
n
x ( n) z n x ( n) z n
n0
n
1
x ( n) z n
第一项为右边序列(因果)其收敛域为: z Rx
第二项为左边序列,其收敛域为: 0 z Rx
序列相乘
x(n) y(n) {x(0) y(0), x(1) y(1), x(2) y(2), , x(n) y(n), }
序列权乘
a{x(n)} {ax(n)} {ax(0), ax(1), ax(2), ax(n), }
第二节 离散时间信号序列
序列延时:对序列进行一定的移位。可以表示为
第二节 离散时间信号序列
单位抽样序列
(n) 1 ,
0 , n0 n0
δ (n) 1
x(n) nu(n)
单位阶跃序列
1 , u(n) 0 , 斜变序列 n0 n0
u(n) 1
o
n
…
o
x(n)
1
2
3
4
5
n
x(n) nu(n)
… -3 -2 -1 0 1 2 3 n
数字信号处理——第2章 离散时间傅里叶变换与Z变换

• 总结:
①序列ZT的收敛域以极点为边界(包含0 和 ②收敛域内不含任何极点,可以包含0 ③相同的零极点可能对应不同的收敛域,即: 不同的序列可能有相同的ZT ④收敛域汇总:右外、左内、双环、有限长z平面
)
常见典型序列z变换
序列 Z变换 收敛域
z a
z b
注意:只有z变换和它的收敛域两者在一起才和序列相对应。 其它序列见P54: 表2-1 几种序列的z变换
2.3
z反变换
Z反变换: 从X(z)中还原出原序列x(n)
X ( z ) ZT [ x ( n)]
n
x (n) z n
实质:求X(z)幂级数展开式
Z反变换的求解方法: 留数定理法
部分分式法
长除法
1. 留数定理法
根据复变函数理论,可以推导出
x ( n)
1 2 j
X ( z ) z n 1dz
1 1 3z 1
n
z 2
2 n u ( n)
z 3
3
n
n
u (n 1)
x n 2 u n 3 u n 1
3. 幂级数法(长除法)
如果序列的ZT能表示成幂级数的形式,则序列x(n) 是幂 级数 说明: ①这种方法只对某些特殊的ZT有效。 ②如果ZT为有理函数,可用长除法将X(z)展开成幂级 数。 若为右边序列(特例:因果序列),将X(z)展开成负幂 级数; 若为左边序列(特例:反因果序列),将X(z)展开成正 幂级数; 中
z z 1 1 X z 1 z 2 z 3 1 2z 1 3 z 1
1 ZT [a u (n)] z a 1 1 az 1 n ZT [a u (n 1)] z a 1 1 az
[例2-6] 试用长除法求 的z反变换。
![[例2-6] 试用长除法求 的z反变换。](https://img.taocdn.com/s3/m/86169fc25fbfc77da269b1fb.png)
Z 证明:[x(n) ∗h(n)] = = = =
∞ ∞
n=−∞
[x(n) ∗h(n)]z−n ∑
∞
n=−∞ m=−∞ ∞
[ ∑x(m)h(n − m)]z−n ∑ x(m)[ ∑h(n − m)z−n ] ∑
n=−∞ ∞ ∞ ∞
m=−∞
m=−∞ ∞
x(m)[ ∑h(l)z−l ]z−m ∑
l =−∞
*即满足均匀性与叠加性; *收敛域为两者重叠部分。
[例2-7]已知 x(n) = cos(ω0n)u(n) ,求其z变换。
1 jω0n − jω0n ]u(n) 解: Qcos(ω0n)u(n) = [e + e 2 1 n Z[a u(n)] = ,z >a −1 1− az 1 jω0n jω0 ∴Z[e u(n)] = , z > e =1 jω0 −1 1−e z 1 − jω0n − jω0 , z > e =1 Z[e u(n)] = − jω0 −1 1−e z 1 1 1 因此 Z[cos(ω0n)ቤተ መጻሕፍቲ ባይዱ(n)] = [ , + ], z >1 − jω0 −1 jω0 −1 2 1−e z 1−e z
=
n=−∞
∑ − nx(n)z
∞
−n− 1
= −z
− 1
n=−∞
nx(n)z−n ∑
∞
dX (z) 即 Z[nx(n)] = −z , dz
5. 共轭序列 如果 Z[x(n)] = X(z), Rx− < z < Rx+ ,则
Z[x (n)] = X (z ) , x− < z < Rx+ ; R
对 因 序 x(n), X(z) = Z[x(n)] 极 于 果 列 且 的 点 在 位 内 且 允 单 圆 z =1 有 单 圆 , 只 许 位 上 处 一 阶 点 则 极 , 有 lim x(n) = lim[(z −1 X(z)] = R s[X(z)]z=1 ) e
§5-2 反z变换

x ( n ) = A0 δ ( n ) + ∑ Ai p in u ( n )
i =1 N
N
x ( n ) = A0 δ ( n ) − ∑ Ai p in u ( − n − 1)
i =1
M
x ( n ) = A0 δ ( n ) − ∑ Ai p u ( − n − 1) +
《Signals & Systems》
《信号与系统》
电子技术教研室
其中x2(n)是环外极点对应部分的反变换,x3(n)是环内极点对应部分 的反变换。 练习:试用幂级数展开法求 与0<|z|<1时的z反变换。
X ( z) = 1 z ( z − 1) 2
当收敛域分别是|z|>1
1.(n − 2)u (n − 2)
《信号与系统》
1 x(n) = 2πj
∫
C
X (z)z
n −1
dz
电子技术教研室
例题1:已知序列的z变换及其收敛域如下,试用留数法求其z反变
换。
z2 X ( z) = ( z − 1)( z − 0.5)
z >1
j Im{z}
解:由留数法
z n +1 x ( n ) = ∑ Re s[ ] z = zi ( z − 1)( z − 0 .5 ) i
作长除
2 z 2 + 6 z 3 + 14 z 4 0.5 − 1.5 z + z 2 z 2 z 2 − 3z 3 + 2 z 4 4 3z 3 3 − 2z 4 3z − 9 z + 6 z 5 5 7z4 − 6 z 7 z 4 − 21z 5 + 14 z 6
反Z变换

1− az−1 az−1 az−1 − a2 z−2 a2 z−2 X (z) =1+ az−1 + a2z−2 + a3z−3 +… a2 z−2 − a3z−3 ∞ a3z−3 = an z−n ⋮
∑
n=0
∴x(n) = anu(n)
11
1 例:用长除法求 X (z) = , < z < 4 z反变换 1 4 (4 − z)(z − ) 4
解:X(z)的Roc为环状,故x(n)是双边序列 X(z)的Roc为环状, x(n)是双边序列 为环状 极点z=1/4对应右边序列,极点z=4对应左边序列 极点z=1/4对应右边序列,极点z=4对应左边序列 z=1/4对应右边序列 z=4 先把X(z)展成部分分式 先把X(z)展成部分分式 X(z)
7
B(z) X (z) = = A(z)
M −N
bi z−i ∑ 1+ ∑ai z−i
i=1 i=0 N
M
r Ak Ck −n X (z) = ∑Bn z +∑ + −1 ∑ 1− zk z k=1 (1− zi z−1)k n=0 k =1
N−r
M≥N时,才存在Bn;Zk为X(z)的各单极点, X(z)的各单极点 的各单极点, 才存在Bn; Bn X(z)的一个 阶极点。而系数A 的一个r 分别为: Zi为X(z)的一个r阶极点。而系数Ak,Ck分别为:
14
内容小结
• 留数法、部分分式法、幂级数展开法(主要一阶) 留数法、部分分式法、幂级数展开法(主要一阶) matlab关注: matlab关注: 关注 多项式法:poly、residuez(留数法) 多项式法:poly、residuez(留数法) 留数法 长除法: 长除法:deconv
第2章z变换

解:
X(z)(12z1)11(0.5z1)
z2
(z2)(z0.5)
X(z)
zபைடு நூலகம்
A1 A2
z (z2)(z0.5) z2 z0.5
A1
[( z 2)
X
(z) z
]z2
4 3
A2
[( z
0.5)
X (z)
z
] z 0.5
1 3
X (z) 4 z 1 z 3 z 2 3 z 0.5
同样的,当|b|>|z|时,这是无穷递缩等比级数,收敛。
故其和为X
(z)
b1z 1 b1z
j Im[z]
z z b
收敛域: z b
Re[ z ] b
*收敛域在模最小的极(左边序列极点)点所在的圆内。
一个结论
• 由上面两个例子来看,Z变换表达式一样, 不代表序列相同,还得看他们的收敛域 是否一致。
• 这一点类似于差分方程不能唯一确定序 列,必须给出边界条件。
大家看一下书48页的例题2-4
§2-3 Z反变换
一.定义:
已知X(z)及其收敛域,反过来求序列x(n)
的变换称作Z反变换。
记作 x(n) : Z1[X(z)]
z变换公式:
正: X(z) x(n)zn, n
Rx z Rx
反: x(n) 1
n 1 n 2
2.部分分式法
有理式:数字和字符经有限次加、减、乘、除运算 所得的式子。
有理分式:含字符的式子做分母的有理式,或两个多项 式的商。分子的次数低于分母时称为真分式。
部分分式:把x的一个实系数的真分式分解成几个分式
a
axb
的和,使各分式具有 ( x A ) k 或 (x2 AxB)k
Z变换

8 z 19 X ( z) 2 z 5z 6
| z | 3
Z=sym('(8*z-19)/(z^2-5*z+6)'); x=iztrans(Z); simplify(x) ans= -19/6*charfcn[0](n)+5*3^(n-1)+3*2^(n-1) charfcn[0](n)是(n)函数在MATLAB符号工具箱中的表 示,反变换后的函数形式为:
三、实验原理
MATLAB实现
在MATLAB中系统函数的零极点就可通过函数roots得到, 也可借助DSP工具箱中的函数tf2zp得到,tf2zp的语句格 式为: [R,P,K]=tf2zp(B,A) 其中,B与A分别表示分子与分母多项式的系数向量。 它的作用是将H(z)的有理分式表示式转换为零极点增益 形式:
b=[0,0,1]; a=poly([1,1,2]); [r,p,k]=residuez(b,a);
得到 r= 1.0000 -0.0000 + 0.0000i -1.0000 + 0.0000i p=
2.0000 1.0000 + 0.0000i 1.0000 - 0.0000i []
%初始输入分子多项式的项数 %初始输入分子多项式的项数 %求三个系数[r,p,k]
X ( z)
0.36 0.24 0.4 1 0.5 z 1 1 0.3333z 1 (1 0.3333z 1 ) 2
x(n) [0.36 (0.5) n 0.24 (0.3333 ) n 0.4(n 1)(0.3333 ) n ]u(n)
三、实验原理n n x ( n ) Nhomakorabeaz
其中,符号表示取z变换,z是复变量。 相应地,单边z变换定义为:
z变换,反Z变换两部分补充PPT

Ak (1 z k z 1 ) X ( z )
Re s[
X ( z) , zk ] z
Z变换补充材料
15
逆Z变换
2、高阶极点 当上述有理分式中的M≥N且具有高阶极点时,若设除 单极点外,在zi 处还有一个s阶的极点,则其展开式 修
Bk z k
1
j Im[ z ]
n
n
a z
Z平面 收敛域
0
a
Re[ z ]
为保证收敛,则
X ( z) 1
z 1 或 | z || a | a
1 z z 1 ( a ) z a | z | | a |
Z变换补充材料
3
Z变换的定义
例3:求序列 x (n)= 解: ( z ) X (1/3)|n| 的Z变换。
零点:0,极点:3,1/3
Z变换补充材料 4
Z变换的收敛域
Z变换的收敛域 对于任意给定的序列 x(n) ,使其Z变换收敛的所有 z值的集合称为 X (z ) 的收敛域。 其收敛的充要条件是满足绝对可和条件,即:
n
x ( n) z n
1 1 1 收敛 不定 发散
根据级数收敛的阿贝尔定理
lim
n
an
n
对于不同的序列 x(n) ,可求得相应的收敛域。
5
Z变换补充材料
Z变换的收敛域
收敛域内不包含任何极点,在极点处,X(z)为无穷大, Z变换不收敛。 有限长序列的收敛域为整个Z平面, 可能除开z=0, z=。 右边有限长序列: X(z)=x(1)z-1+ x(2)z2+···· |z|>0 左边有限长序列: X(z)=x(-1)z1+x(2)z2+···· |z|< 如果是右边序列,并且|z|=位于收敛域内,那么, |z|>也位于收敛域内。
求z反变换——精选推荐

1、已知234()315X z z z z z --=+++- (0||z <<∞),求z 反变换。
解:[]()()(2)3(1)()(3)5(4)x n X z n n n n n δδδδδ==+++++---Z2、已知2()(2)(1/2)z X z z z =--,分别求出收敛域为||2z >、||1/2z <和1/2||2z <<时的z 反变换()x n 。
解:()(2)(1/2)X z zz z z =-- ()X z z为真分式,有两个极点12z =、21/2z =,其部分分式展开为: 12()21/2K K X z z z z =+-- 部分分式系数为:12()4(2)3z X z K z z==-=-21/2()1(1/2)3z X z K z z ==-= 则()4/31/321/2X z z z z =-+-- 41()3231/2z z X z z z =-⨯+⨯-- ① 当收敛域为||2z >时,-1()[()]x n X z =Z 为因果序列,则:-1-41()[()]22()33n n x n X z u n ⎡⎤==-⨯+⨯⎢⎥⎣⎦Z② 当收敛域为||1/2z <时,-1()[()]x n X z =Z 为逆因果序列,则:-14141()[()]22(1)22(2)3333n n n n x n X z u n u n --⎡⎤⎡⎤==⨯-⨯--=⨯---⎢⎥⎢⎥⎣⎦⎣⎦Z③ 当收敛域为1/2||2z <<时,-1()[()]x n X z =Z 为双边序列,因此X (z )收敛域圆环以内的极点属于因果子序列的z 变换,圆环以外的极点属于逆因果子序列的z 变换,即极点21/2z =的部分分式对应于因果序列,12z =的部分分式对应于逆因果序列,则:-1-41()[()]2(1)2()33n n x n X z u n u n ==⨯--+⨯Z3、知系统的差分方程5(1)()(1)()2y n y n y n x n --++=,该系统不限定为因果、稳定系统,试求出系统单位抽样响应()h n 的三种可选方案。
2.3z反变换

第二章 z变换(2.3)
主 讲:熊美英 E-mail:wax8301@ 九江学院电子工程学院
1
第二章 z变换
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8
引言 z变换的定义及收敛域 z反变换 z变换的基本性质和定理 z变换与拉普拉斯变换、傅立叶变换的关系 序列的傅里叶变换 傅里叶变换的一些对称性质 离散系统的系统函数及频率响应
6
二、求z反变换的方法: 1、围线积分法(留数法); 2、部分分式展开法; 3、长除法。
7
1、围线积分法(留数法) 根据复变函数理论,若函数X(z)在环状区域 内解析,则在此区域可展开 成罗朗级数的形式:
其中:
1 n 1dz, c ( R , R ) Cn X ( z ) z x x c 2j
如果能将X(z) 展开成几个简单的分式的和的 形式,而简单形式的z反变换可通过查表2-1直接 求得。
21
如果能将X(z) 展开成几个简单的分式的和的形式, 而简单形式的z反变换可通过查表2-1直接求得。 也就是:
x(n) z 1[ X ( z )] z 1[ X 1 ( z )] z 1[ X 2 ( z )] ... z 1[ X K ( z )] x1 (n) x2 (n) ... x K (n)
26
求系数A1、A2:
27
又|z|>2,收敛域在两个极点之外,是什么序列?
28
若用待定系数法求系数A1、A2:
则分子相等
应对所用z成立。
令z 0.5,可求A2 1 / 3 令z 2,可求A1 4 / 3
29
[例]:利用部分分式法,求 的z反变换。 解: 又|z|<0.5,收敛域在两个极点之内,是什么序列?
自动控制原理--z变换理论部分例题讲解

jn
j0
znE(z) 右
6.3 z变换理论
2. 实位移定理
② 超前定理
Ze(t
nT
)
zn
E(z)
n1
e(kT
)
z
k
k0
证:左 e(kT nT ) zk zn e(kT nT ) z(kn)
k0
k0
jkn
zn
e( jT ) z j
z
n
e( jT ) z j
n1
e(
E(z) 8 z 1 z 7 (z 0.8) 7 (z 0.1)
t
t
e(t ) (8 0.8T 0.1T ) / 7 e(nT ) (8 0.8n 0.1n ) / 7
e*(t ) (8 0.8n 0.1n ) / 7 (t n E(z)
e(0) e(1) z1 e(2) z2 e(3) z3
lim E(z) e(0)
z
例8
0.792 z2 E(z) (z 1)[z2 0.416z 0.208]
e(0) lim E(z) 0 z
6.3 z变换理论
5. 终值定理
lime(nT) lim (z 1) E(z)
e j nT e j nT
zn
1 (e jT z 1 )n (e jT z 1 )n 2 j n0
1 2j
1 1 e jT z 1
1
e
1
j T
z
1
1 2j
z z e jT
z z e jT
1
z(e jT e jT )
z sinT
2 j z 2 (e jT e jT )z 1 z2 2 cos T z 1
z变换性质.

k 1
7
例4:教材例3.15
F (z)
z (z 1)2 (z 2)
b1 (z 1)
b2 z (z 1)2
(z
c 2)
求得b2=b1=-1, c=2,代入 b1ak1 b2kak1 k 1
▼长除法; ▼部分分式法; ▼留数计算法
一.长除法
分母首一化,逐项相除; 给出各拍数值。
例1:求下式的Z反变换
Y
(z)
5z
2
12z 1.5z
0.5
z2
2.4z 0.3z 0.1
(演算)
3
MATLAB程序: v=[0 12 0 0 0 0 0 0] u=[5 -1.5 0.5] [q, r]=deconv(v, u) q=[0 2.4 0.72 –0.024 –0.0792 –0.0214]
傅里叶变换的性质拉普拉斯变换性质傅里叶变换性质z变换z变换的意义傅里叶变换基本性质二维傅里叶变换性质z变换的定义z变换表逆z变换
1
复习 1. Z变换的主要性质:
(1)平移定理(滞后定理)
Z[ y(kT nT )] znY (z)
(掌握)
(2)初值定理
y(0) lim y(kT ) limY (z)
i 1
注意:(1)一个重极点pj只有一个留数。 (2)若F(z)的分子中不含公因子z,则留数
计算法得出的f(kT)只适用于k>0情况,
k=0应通过初值定理求出。
(3)留数法可以求得Z反变换的解析式。
教材:例3.19(自学)
10
例:用留数法求Z的反变换
F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z X (z) = Z[x(n)] = , z > a; z −a z z − 1 H(z) = Z[h(n)] = − az z −b z −b z a z −a , z > b; = − = z −b z −b z −b z z −a z ∴ (z) = X (z)H(z) = Y = z − a z −b z −b X (z) 极 与 (z) 零 相 , (z) 的 点 H 的 点 消 Y 的 敛 扩 , z >b. 收 域 大 为 ∴y(n) = x(n) ∗h(n) = Z−1[Y(z)] = bnu(n)
Z变换的基本性质和定理 §4-4 Z变换的基本性质和定理
1.线性 1.线性 如果 Z[x(n)] = X(z), Rx− < z < Rx+ 则有:
Z[ y(n)] = Y(z), Ry− < z < Ry+
Z[ax(n) +by(n)] = aX(z) +bY(z), m Rx−, Ry− ) < z < m Rx+ , Ry+ ) ax( in(
∞
序列的线性加权(Z域求导数) (Z域求导数 4. 序列的线性加权(Z域求导数)
如果 Z[x(n)] = X(z), Rx− < z < Rx+ ,则
d Z[nx(n)] = −z X(z), Rx− < z < Rx+ dz 证明: (z) = ∑x(n)z , 对 两 求 得 X 其 端 导
∞ −n n=−∞ ∞ ∞ dX (z) d d −n = [ ∑ x(n)z ] = ∑x(n) (z−n ) dz dz n=−∞ dz n=−∞
如果 Z[x(n)] = X(z), Rx− < z < Rx+ ,则
1 1 1 Z[x(−n)] = X ( ) ; <z< z Rx− Rx+
证明: Z[x(−n)] =
∞ n=−∞
x(−n)z−n = ∑x(n)zn ∑
n=−∞ −1 −n
∞
∞
1 = ∑x(n)(z ) =X( ) , x− < z−1 < Rx+ , R z n=−∞ 1 1 即 <z< Rx+ Rx−
*即满足均匀性与叠加性; *收敛域为两者重叠部分。
[例2-7]已知 x(n) = cos(ω0n)u(n) ,求其z变换。
1 jω0n − jω0n ]u(n) 解: Qcos(ω0n)u(n) = [e + e 2 1 n Z[a u(n)] = ,z >a −1 1− az 1 jω0n jω0 ∴Z[e u(n)] = , z > e =1 jω0 −1 1−e z 1 − jω0n − jω0 , z > e =1 Z[e u(n)] = − jω0 −1 1−e z 1 1 1 因此 Z[cos(ω0n)u(n)] = [ , + ], z >1 − jω0 −1 jω0 −1 2 1−e z 1−e z
X (z) 4 16 A = [(4 − z) ]z=4 = = 1 1 z 15 4− 4 1 1 X (z) 4 = 1 A = [(z − ) ] 1 = 2 z= 1 4 z 15 4 4− 4
X(z) 16/15 1/15 = + z 4− z z − 1 4 16 z 1 z ∴X(z) = + 15 4 − z 15 z − 1 4 1 16z z = ( + ) 15 4 − z z − 1 4
n
= ∑[∑x(m)]z
n=0 m=0
∞
n
−nΒιβλιοθήκη 可 , , m的 值 围 别 n∈[0, ∞], 知 n 取 范 分 为 m∈[m = n, ∞] 交 求 次 , , 换 和 序 得
Z[∑x(m)] = ∑[∑x(m)]z−n =∑x(m)∑z−n
m=0 ∞ n=0 m=0 −1 m=0 n=m
n
∞
对 因 序 x(n), X(z) = Z[x(n)] 极 于 果 列 且 的 点 在 位 内 且 允 单 圆 z =1 有 单 圆 , 只 许 位 上 处 一 阶 点 则 极 , 有 lim x(n) = lim[(z −1 X(z)] = R s[X(z)]z=1 ) e
n→ ∞ z→ 1
证明: [x(n +1) − x(n)] = (z −1)X(z) = ∑[x(n +1) − x(n)]z−n Z
1 Z- — 4
)
Z
1 Z- — 4 1 — 4 1 1 —- — 4 16
Z
-1
1 — Z-1 16 1 — 16
Z -
-1
1 — 64
Z
-2
1 — Z -2 64 1 — 64
Z -
-2
-3 1 —— Z 256
1 -3 —— Z 256
...
z5 z 4 z3 1 得 (z) = (L + + + z2 + 4z X 15 64 16 4 z−1 z−2 z−3 +1+ + + +L ) 4 16 64 1 n+2 , n ≤ −1 15 (4) 进 得 x(n) = 而 : 1 (1)n , n ≥ 0 15 4
其中,C是在变量V平面上,X(z/v),H(v)公共收敛 域内环原点的一条逆时针单封闭围线。 (证明从略)
[例2-10]
已 x(n) = a u(n), h(n) = b u(n −1 知 ),
n
n−1
求 (z) = Z[x(n)h(n)]. Y
z , z > a; 解: QX (z) = Z[x(n)] = z −a 1 H(z) = Z[h(n)] = , z > b; z −b 1 1 v ∴ (z) = Z[x(n)h(n)] = Y ∫cv − a z dv π 2 j −b v 1 v = ∫c(v − a)(z −bv) dv, z > ab; 2 j π
≤∞
lim(z −1)X(z) = lim ∑[x(m+1) − x(m)1
z→ 1 n→∞ m=−1 n→∞ n→∞ z→ 1
n
−m
= lim{[ x(0) −0] +[x(1) − x(0)] +L+[x(n +1) − x(n)]} = lim[x(n +1)] = lim x(n)
n→∞
∴lim(z −1)X(z) = lim x(n)
n→∞
9. 有限项累加特性
对 因 序 x(n), X(z) = Z[x(n)], z > Rx−, 于 果 列 且 z 则 [∑x(m)] = Z X(z), z > m Rx−,1] ax[ z −1 m=0
证明:令 (n) = ∑x(m), Z[y(n)] = Z[∑x(m)] y
m=0 m=0 n n
4-Z) 16 Z
1 1 1 4Z+Z2 + —Z 3 + 16 4+ —Z5 + ... —Z 64 4
16 Z - 4 Z2 4 Z2 4 Z2 - Z3 Z3 1 Z3 - — Z 4 4 1 — Z4 4 1 1 4 —Z -—Z5 4 16 1 — Z5 16
.. .
1 -1 1 -2 — 1 1+ — Z +16 Z + 64 Z -3... — 4
7. 初值定理
对 因 序 x(n), x(0) = lim X (z)。 于 果 列 则
z→∞
证明:X(z) =
n=−∞
∑ x(n)u(n)z = ∑x(n)z
−n n=0 −1 −2
∞
∞
−n
= x(0) + x(1)z + x(2)z +L 显然 lim X(z) = x(0) ,
z→∞
8. 终值定理
域尺度变换(乘以指数序列) 3. Z域尺度变换(乘以指数序列)
如果 Z[x(n)] = X(z), Rx− < z < Rx+ ,则
z Z[a x(n)] = X ( ) ; a Rx− < z < a Rx+ a
n
证明:
Z[an x(n)] = ∑an x(n)z−n
n=−∞
∞
z −n z = ∑ x(n)( ) = X( ) ; a a n=−∞ z Rx− < < Rx+;即 a Rx− < z < a Rx+ a
=[ ∑x(m z−m]H(z) )
m=−∞
= X (z)H(z), m [ Rx− , Rh− ] < z < m [ Rx+ , R + ] ax in h
[例2-9] 已 x(n) = anu(n), h(n) = bnu(n) − abn−1u(n −1 知 ),
求 (n) = x(n) ∗h(n), b < a. y
如 y(n) = x(n) ∗h(n) = 果
m=−∞
∑x(m)h(n −m)
∞
而 X(z) = Z[x(n)] , Rx− < z < Rx+ , 且 H(z) = Z[h(n)] , Rn− < z < Rn+, 则 : (z) = Z[ y(n)] = X(z)H(z) 有 Y m Rx−, Rh− ] < z < m Rx+ , Rh+ ] ax[ in[
Z 证明:[x(n) ∗h(n)] = = = =
∞ ∞
n=−∞
