五年级上学期图形面积奥数题
五年级奥数题:图形与面积含详细答案

翔迪学校五年级专题强化:图形与面积年级 班 姓名 得分一、填空题3. 下图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是______平方厘米.4. 下图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是______平方厘米.5. 在ABC ∆中,DC BD 2=,BE AE =,已知ABC ∆的面积是18平方厘米,则四边形AEDC 的面积等于______平方厘米.6. 下图是边长为4厘米的正方形,AE =5厘米、OB 是______厘米.7. 如图正方形ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽DE 是______厘米.9. 如下图,正方形ABCD 的边长为12, P 是边AB 上的任意一点,M 、N 、I 、H 分别是边BC 、AD 上的三等分点,E 、F 、G 是边CD 上的四等分点,图中阴影部分的面积是______.10. 下图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD 的面积是______平方厘米.二、解答题11. 图中正六边形ABCDEF 的面积是54.PF AP 2=,BQ CQ 2=,求阴影四边形CEPQ 的面积.12. 如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13. 一个周长是56厘米的大长方形,按图35中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是: 2:1:=B A ,2:1:=C B .而在(2)中相应的比例是3:1:=''B A ,3:1:=''C B .又知,长方形D '的宽减去D 的宽所得到的差,与D '的长减去在D 的长所得到的差之比为1:3.求大长方7=,将图形分成两部分,左边部分面积是38,右边部分面积是65.那么三角形ADG 面积是______.五年级奥数题:图形与面积一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是 _________ 厘米.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是 _________ .3.(3分) 如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是 _________ 平方厘米.4.(3分)(2014?长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是 _________ 平方厘米.5.(3分)在△ABC 中,BD=2DC ,AE=BE ,已知△ABC 的面积是18平方厘米,则四边形AEDC 的面积等于 _________ 平方厘米.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB 是 _________ 厘米.7.(3分) 如图正方形ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽DE 是 _________ 厘米.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是_________.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是_________.10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是_________平方厘米.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.14.(2012?武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是_________.2010年五年级奥数题:图形与面积(B)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是170厘米.考点:巧算周长.分析:要求该图形的周长,先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,然后先算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.解答:解:400÷16=25(平方厘米),因为5×5=25(平方厘米),所以每个小正方形的边长为5厘米,周长为:(5×4+5×4+5×3+5×2+5×3+5)×2,=85×2,=170(厘米);答:它的周长是170厘米.点评:此类题解答的关键是先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,进而算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是25.考点:组合图形的面积.分析:此题需要进行图形分解:“7”分成一个长方形、一个等腰直角三角形、一个平行四边形;“2”分成一个梯形、一个平行四边形、一个长方形;“1”分成一个梯形和两个长方形.然后进行图形转换,依据题目条件即可求出结果.解答:解:“7”所占的面积和=+3+4=,“2”所占的面积和=3+4+3=10,“1”所占的面积和=+7=,那么7,2,1三个数字所占的面积之和=++10=25.故答案为:25.点评:此题关键是进行图形分解和转换.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是 6.5平方厘米.考点:组合图形的面积.分析:由图可以观察出:大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积.解答:解:大正方形的面积为4×4=16(平方厘米);粗线以外的图形面积为:整格有3个,左上,右上,右中,右下,左中,右中,共有3++5×=9.5(平方厘米);所以粗线围成的图形面积为16﹣9.5=6.5(平方厘米);答:粗线围成的图形面积是6.5平方厘米.故此题答案为:6.5.点评:此题关键是对图形进行合理地割补.4.(3分)(2014?长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是24平方厘米.考点:组合图形的面积.分析:两个正方形的面积减去两个空白三角形的面积.解答:解:4×4+8×8﹣×4×(4+8)﹣×8×8,=16+64﹣24﹣32,=24(cm2);答:阴影的面积是24cm2.故答案为:24.点评:求组合图形面积的化为求常用图形面积的和与差求解.5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于12平方厘米.考点:相似三角形的性质(份数、比例);三角形的周长和面积.分析:根据题意,连接AD,即可知道△ABD和△ADC的关系,△ADE和△BDE的关系,由此即可求出四边形AEDC的面积.解答:解:连接AD,因为BD=2DC,所以,S△ABD=2S△ADC,即,S△ABD=18×=12(平方厘米),又因为,AE=BE,所以,S△ADE=S△BDE,即,S△BDE=12×=6(平方厘米),所以AEDC的面积是:18﹣6=12(平方厘米);故答案为:12.点评:解答此题的关键是,根据题意,添加辅助线,帮助我们找到三角形之间的关系,由此即可解答.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是 3.2厘米.考点:组合图形的面积.分析:连接BE、AF可以看出,三角形ABE的面积是正方形面积的一半,再依据三角形面积公式就可以求出OB 的长度.解答:解:如图连接BE、AF,则BE与AF相交于D点S△ADE=S△BDF则S△ABE=S正方形=×(4×4)=8(平方厘米);OB=8×2÷5=3.2(厘米);答:OB是3.2厘米.故答案为:3.2.点评:此题主要考查三角形和正方形的面积公式,将数据代入公式即可.7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE 是 3.2厘米.考点:组合图形的面积.分析:连接AG,则可以依据题目条件求出三角形AGD的面积,因为DG已知,进而可以求三角形AGD的高,也就是长方形的宽,问题得解.解答:解:如图连接AGS△AGD=S正方形ABCD﹣S△CDG﹣S△ABG,=4×4﹣3×4÷2﹣1×4÷2=16﹣6﹣2=8(平方厘米);8×2÷5=3.2(厘米);答:长方形的宽是3.2厘米.故答案为:3.2.点评:依据题目条件做出合适的辅助线,问题得解.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是243.考点:组合图形的面积.分析:从图中可以看出每上、下两个小矩形的一个边是相邻的,也就是说长是相等的,那么根据矩形的面积公式知,如果长相同,面积之比也就是宽之比,反之宽之比也就是面积之比;由中间面积20和16的矩形,可以算出空着的小矩形面积,最后把所有小矩形面积加起来就是大矩形的面积.解答:解:由图和题意知,中间上、下小矩形的面积比是:20:16=5:4,所以宽之比是5:4,那么,A:36=5:4得A=45;25:B=5:4得B=20;30:C=5:4得C=24;D:12=5:4得D=15;所以大矩形的面积=45+36+25+20+20+16+30+24+15+12=243;故答案为:243.点评:此题考查了如果长方形的长相同,宽之比等于面积之比,还考查了比例的有关知识.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是60.考点:组合图形的面积.分析:根据题意:正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,可连接DP,然后再利用三角形的面积公式进行计算即可得到答案.解答:解:阴影部分的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2×(AP+BP)=36+2×12=36+24=60.答:这个图形阴影部分的面积是60.点评:此题主要考查的是三角形的面积公式.10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是4平方厘米.考点:重叠问题;三角形的周长和面积.分析:因为S△EFC+S△GHC=四边形EFGH面积÷2=12,S△AEF+S△AGH=四边形EFGH面积÷2=12,所以S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影部分的总面积是10平方厘米=2平方厘米.所以:四边形ABCD面积=S△ECH﹣(S△ABE+S△ADH)=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米.解答:解:由题意推出:S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影面积10平方厘米=2平方厘米.所以:四边形ABCD面积=S△ECH﹣(S△ABE+S△ADH)=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米.故答案为:4.点评:此题在重叠问题中考查了三角形的周长和面积公式,此题设计的非常精彩.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.考点:等积变形(位移、割补).分析:如图,将正六边形ABCDEF等分为54个小正三角形,根据平行四边形对角线平分平行四边形面积,采用数小三角形的办法来计算面积.解答:解:如图,S△PEF=3,S△CDE=9,S四边形ABQP=11.上述三块面积之和为3+9+11=23.因此,阴影四边形CEPQ面积为54﹣23=31.点评:此题主要利用面积分割,用数基本小三角形面积来解决问题.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.考点:等积变形(位移、割补).分析:由图及题意知,可把涂阴影部分小正六角星形等分成12个小三角形,且都与外围的6个空白小三角形面积相等,已知涂阴影部分的小正六角星形面积是16平方厘米,可求出大正六角星形中心正六边形的面积,而这个正六边形又可等分成6个小正三角形,且它们与外围六个大角的面积相等,进而可求出大正六角星形面积解答:解:如下图所示,涂阴影部分小正六角星形可等分成12个小三角形,且都与外围的6个空白小三角形面积相等,所以正六边形ABCDEF的面积:16÷12×(12+6)=24(平方厘米);又由于正六边形ABCDEF又可等分成6个小正三角形,且它们与外围六个大角的面积相等,所以大正六角星形面积:24×2=48(平方厘米);答:大正六角星形面积是48平方厘米.点评:此题要借助求正六边形的面积来解答,它既可看作是18个小正三角形,又可看作是6个大点的正三角形组成.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.考点:比的应用;图形划分.分析:要求大长方形的面积,需求出它的长和宽,由条件“在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3”可知:D的宽是大长方形宽的,D′的宽是大长方形宽的,D的长是×(28﹣大长方形的宽),D′的长是×(28﹣大长方形的宽),由此便可以列式计算.解答:解:设大长方形的宽为x,则长为28﹣x因为D的宽=x,D′的宽=x,所以,D′的宽﹣D的宽=.D长=×(28﹣x),D′长=×(28﹣x),D′长﹣D长=×(28﹣x),由题设可知:=即=,于是=,x=8.于是,大长方形的长=28﹣8=20,从而大长方形的面积为8×20=160平方厘米.答:大长方形的面积是160平方米.点评:此题比较复杂,主要考查比的关系,应利用比的意义,找清数量见的比,再利用题目条件,就可以进行计算求得结果.14.(2012?武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是40.考点:三角形的周长和面积.分析:可以把S△ADE看成是一个整体,根据各线段的关系和左右两部分面积的关系,可以列出一个方程,求出S△ADE的面积,然后再根据所求三角形与S△ADE的关系求出答案.解答:解:由题意知,S△AEG=3S△ADE,S△BFE=S△BEC,设S△ADE=X,则S△AEG=3X,S△BFE=(38﹣X),可列出方程:(38﹣X)+3X=65,解方程,得:x=10,所以S△ADG=10×(1+3)=40.故答案为:40.点评:此题考查了如何利用边的关系求三角形的面积.。
五年级奥数平面图形面积

For personal use only in study and research; not for commercial use平面图形的面积计算正方形:①四条边都相等。
②四个角都是直角。
③有四条对称轴。
S=a2长方形:①对边相等。
②四个角都是直角。
③有二条对称轴。
S=ab平行四边形:①两组对边平行且相等。
②对角相等,相邻的两个角之和为180°③平行四边形容易变形。
S=ah三角形:①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角,具有稳定性。
S=ah÷2梯形:①只有一组对边平行。
②中位线等于上下底和的一半。
S=(a+b)h÷2组合图形:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
精典例题例1:已知平行四边形的的面积是28平方厘米,求阴影图形的面积。
思路点拨先根据平行四边形的面积和高,就可以求出平行四边形的底,再减去5cm,求出阴影图形的底,根据三角形面积公式求出面积。
模仿练习如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)例2:已知大正方形的边长是5厘米,小正方形的边长是4厘米,求阴影部分的面积。
思路点拨连接AC,三角形GEA和三角形GEC同底等高。
模仿练习正方形的边长分别是10厘米、6厘米,阴影部分的面积是平方厘米。
例3:如图,ABCD是边长为4分米的正方形,长方形DEFG的长是5分米,求长方形DEFG的宽。
思路点拨连接AG ,三角形ADG 的面积等于长方形面积的一半,同时也等于正方形面积的一半。
模仿练习如图,ABCD 是正方形,EDGF 是长方形,CD=6厘米,DG=8厘米,求宽ED=? 例4:如图,已知四边形ABCD 被它的两条对角线分成四个三角形,其中甲的面积是1,乙的面积是2,丙的面积是3,求丁的面积。
五年级奥数题图形及面积含详细答案

五年级奥数题:图形与面积一、填空题〔共10小题,每题3分,总分值30分〕1.〔3分〕如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,则它的周长是_________ 厘米.2.〔3分〕第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.则7,2,1三个数字所占的面积之和是_________ .3.〔3分〕如图中每一小方格的面积都是1平方厘米,则用粗线围成的图形面积是_________ 平方厘米.4.〔3分〕〔2014•模拟〕如图的两个正方形,边长分别为8厘米和4厘米,则阴影局部的面积是_________ 平方厘米.5.〔3分〕在△ABC中,BD=2DC,AE=BE,△ABC的面积是18平方厘米,则四边形AEDC的面积等于_________ 平方厘米.6.〔3分〕如图是边长为4厘米的正方形,AE=5厘米、OB是_________ 厘米.7.〔3分〕如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,则它的宽DE 是_________ 厘米.8.〔3分〕如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如下图,则这个大矩形的面积是_________ .9.〔3分〕如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影局部的面积是_________ .10.〔3分〕图中的长方形的长和宽分别是6厘米和4厘米,阴影局部的总面积是10平方厘米,四边形ABCD 的面积是_________ 平方厘米.二、解答题〔共4小题,总分值0分〕11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.12.如图,涂阴影局部的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中〔1〕与〔2〕所示意那样,划分为四个小长方形.在〔1〕中小长方形面积的比是:A:B=1:2,B:C=1:2.而在〔2〕中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.14.〔2012•模拟〕如图,CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两局部,左边局部面积是38,右边局部面积是65,则三角形ADG的面积是_________ .2010年五年级奥数题:图形与面积〔B〕参考答案与试题解析一、填空题〔共10小题,每题3分,总分值30分〕1.〔3分〕如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,则它的周长是170 厘米.考点:巧算周长.分析:要求该图形的周长,先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,然后先算出该图形的外周的长,因为、外的长相等,再乘2即可得出结论.解答:解:400÷16=25〔平方厘米〕,因为5×5=25〔平方厘米〕,所以每个小正方形的边长为5厘米,周长为:〔5×4+5×4+5×3+5×2+5×3+5〕×2,=85×2,=170〔厘米〕;答:它的周长是170厘米.点评:此类题解答的关键是先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,进而算出该图形的外周的长,因为、外的长相等,再乘2即可得出结论.2.〔3分〕第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.则7,2,1三个数字所占的面积之和是25 .考点:组合图形的面积.分析:此题需要进展图形分解:"7〞分成一个长方形、一个等腰直角三角形、一个平行四边形;"2〞分成一个梯形、一个平行四边形、一个长方形;"1〞分成一个梯形和两个长方形.然后进展图形转换,依据题目条件即可求出结果.解答:解:"7〞所占的面积和=+3+4=,"2〞所占的面积和=3+4+3=10,"1〞所占的面积和=+7=,则7,2,1三个数字所占的面积之和=++10=25.故答案为:25.点评:此题关键是进展图形分解和转换.3.〔3分〕如图中每一小方格的面积都是1平方厘米,则用粗线围成的图形面积是 6.5 平方厘米.考点:组合图形的面积.分析:由图可以观察出:大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积.解答:解:大正方形的面积为4×4=16〔平方厘米〕;粗线以外的图形面积为:整格有3个,左上,右上,右中,右下,左中,右中,共有3++5×=9.5〔平方厘米〕;所以粗线围成的图形面积为16﹣9.5=6.5〔平方厘米〕;答:粗线围成的图形面积是6.5平方厘米.故此题答案为:6.5.点评:此题关键是对图形进展合理地割补.4.〔3分〕〔2014•模拟〕如图的两个正方形,边长分别为8厘米和4厘米,则阴影局部的面积是24 平方厘米.考点:组合图形的面积.分析:两个正方形的面积减去两个空白三角形的面积.解答:解:4×4+8×8﹣×4×〔4+8〕﹣×8×8,=16+64﹣24﹣32,=24〔cm2〕;答:阴影的面积是24cm2.故答案为:24.点评:求组合图形面积的化为求常用图形面积的和与差求解.5.〔3分〕在△ABC中,BD=2DC,AE=BE,△ABC的面积是18平方厘米,则四边形AEDC的面积等于12 平方厘米.考点:相似三角形的性质〔份数、比例〕;三角形的周长和面积.分析:根据题意,连接AD,即可知道△ABD和△ADC的关系,△ADE和△BDE的关系,由此即可求出四边形AEDC的面积.解答:解:连接AD,因为BD=2DC,所以,S△ABD=2S△ADC,即,S△ABD=18×=12〔平方厘米〕,又因为,AE=BE,所以,S△ADE=S△BDE,即,S△BDE=12×=6〔平方厘米〕,所以AEDC的面积是:18﹣6=12〔平方厘米〕;故答案为:12.点评:解答此题的关键是,根据题意,添加辅助线,帮助我们找到三角形之间的关系,由此即可解答.6.〔3分〕如图是边长为4厘米的正方形,AE=5厘米、OB是 3.2 厘米.考点:组合图形的面积.分析:连接BE、AF可以看出,三角形ABE的面积是正方形面积的一半,再依据三角形面积公式就可以求出OB 的长度.解答:解:如图连接BE、AF,则BE与AF相交于D点S△ADE=S△BDF则S△ABE=S正方形=×〔4×4〕=8〔平方厘米〕;OB=8×2÷5=3.2〔厘米〕;答:OB是3.2厘米.故答案为:3.2.点评:此题主要考察三角形和正方形的面积公式,将数据代入公式即可.7.〔3分〕如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,则它的宽DE 是 3.2 厘米.考点:组合图形的面积.分析:连接AG,则可以依据题目条件求出三角形AGD的面积,因为DG,进而可以求三角形AGD的高,也就是长方形的宽,问题得解.解答:解:如图连接AGS△AGD=S正方形ABCD﹣S△CDG﹣S△ABG,=4×4﹣3×4÷2﹣1×4÷2=16﹣6﹣2=8〔平方厘米〕;8×2÷5=3.2〔厘米〕;答:长方形的宽是3.2厘米.故答案为:3.2.点评:依据题目条件做出适宜的辅助线,问题得解.8.〔3分〕如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如下图,则这个大矩形的面积是243 .考点:组合图形的面积.分析:从图中可以看出每上、下两个小矩形的一个边是相邻的,也就是说长是相等的,则根据矩形的面积公式知,如果长一样,面积之比也就是宽之比,反之宽之比也就是面积之比;由中间面积20和16的矩形,可以算出空着的小矩形面积,最后把所有小矩形面积加起来就是大矩形的面积.解答:解:由图和题意知,中间上、下小矩形的面积比是:20:16=5:4,所以宽之比是5:4,则,A:36=5:4得A=45;25:B=5:4得B=20;30:C=5:4得C=24;D:12=5:4得D=15;所以大矩形的面积=45+36+25+20+20+16+30+24+15+12=243;故答案为:243.点评:此题考察了如果长方形的长一样,宽之比等于面积之比,还考察了比例的有关知识.9.〔3分〕如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影局部的面积是60 .考点:组合图形的面积.分析:根据题意:正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,可连接DP,然后再利用三角形的面积公式进展计算即可得到答案.解答:解:阴影局部的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2×〔AP+BP〕=36+2×12=36+24=60.答:这个图形阴影局部的面积是60.点评:此题主要考察的是三角形的面积公式.10.〔3分〕图中的长方形的长和宽分别是6厘米和4厘米,阴影局部的总面积是10平方厘米,四边形ABCD 的面积是 4 平方厘米.考点:重叠问题;三角形的周长和面积.分析:因为S△EFC+S△GHC=四边形EFGH面积÷2=12,S△AEF+S△AGH=四边形EFGH面积÷2=12,所以S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影局部的总面积是10平方厘米=2平方厘米.所以:四边形ABCD面积=S△ECH﹣〔S△ABE+S△ADH〕=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米.解答:解:由题意推出:S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影面积10平方厘米=2平方厘米.所以:四边形ABCD面积=S△ECH﹣〔S△ABE+S△ADH〕=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米.故答案为:4.点评:此题在重叠问题中考察了三角形的周长和面积公式,此题设计的非常精彩.二、解答题〔共4小题,总分值0分〕11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.考点:等积变形〔位移、割补〕.分析:如图,将正六边形ABCDEF等分为54个小正三角形,根据平行四边形对角线平分平行四边形面积,采用数小三角形的方法来计算面积.解答:解:如图,S△PEF=3,S△CDE=9,S四边形ABQP=11.上述三块面积之和为3+9+11=23.因此,阴影四边形CEPQ面积为54﹣23=31.点评:此题主要利用面积分割,用数根本小三角形面积来解决问题.12.如图,涂阴影局部的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.考点:等积变形〔位移、割补〕.分析:由图及题意知,可把涂阴影局部小正六角星形等分成12个小三角形,且都与外围的6个空白小三角形面积相等,涂阴影局部的小正六角星形面积是16平方厘米,可求出大正六角星形中心正六边形的面积,而这个正六边形又可等分成6个小正三角形,且它们与外围六个大角的面积相等,进而可求出大正六角星形面积解答:解:如下列图所示,涂阴影局部小正六角星形可等分成12个小三角形,且都与外围的6个空白小三角形面积相等,所以正六边形ABCDEF的面积:16÷12×〔12+6〕=24〔平方厘米〕;又由于正六边形ABCDEF又可等分成6个小正三角形,且它们与外围六个大角的面积相等,所以大正六角星形面积:24×2=48〔平方厘米〕;答:大正六角星形面积是48平方厘米.点评:此题要借助求正六边形的面积来解答,它既可看作是18个小正三角形,又可看作是6个大点的正三角形组成.13.一个周长是56厘米的大长方形,按图中〔1〕与〔2〕所示意那样,划分为四个小长方形.在〔1〕中小长方形面积的比是:A:B=1:2,B:C=1:2.而在〔2〕中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.考点:比的应用;图形划分.分析:要求大长方形的面积,需求出它的长和宽,由条件"在〔1〕中小长方形面积的比是:A:B=1:2,B:C=1:2.而在〔2〕中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3〞可知:D的宽是大长方形宽的,D′的宽是大长方形宽的,D的长是×〔28﹣大长方形的宽〕,D′的长是×〔28﹣大长方形的宽〕,由此便可以列式计算.解答:解:设大长方形的宽为*,则长为28﹣*因为D的宽=*,D′的宽=*,所以,D′的宽﹣D的宽=.D长=×〔28﹣*〕,D′长=×〔28﹣*〕,D′长﹣D长=×〔28﹣*〕,由题设可知:=即=,于是=,*=8.于是,大长方形的长=28﹣8=20,从而大长方形的面积为8×20=160平方厘米.答:大长方形的面积是160平方米.点评:此题比拟复杂,主要考察比的关系,应利用比的意义,找清数量见的比,再利用题目条件,就可以进展计算求得结果.14.〔2012•模拟〕如图,CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两局部,左边局部面积是38,右边局部面积是65,则三角形ADG的面积是40 .考点:三角形的周长和面积.分析:可以把S△ADE看成是一个整体,根据各线段的关系和左右两局部面积的关系,可以列出一个方程,求出S△ADE的面积,然后再根据所求三角形与S△ADE的关系求出答案.解答:解:由题意知,S=3S△ADE,S△BFE=S△BEC,△AEG设S△ADE=*,则S△AEG=3*,S△BFE=〔38﹣*〕,可列出方程:〔38﹣*〕+3*=65,解方程,得:*=10,所以S△ADG=10×〔1+3〕=40.故答案为:40.点评:此题考察了如何利用边的关系求三角形的面积.。
五年级奥数题图形与面积含详细标准答案

五年级奥数题:图形与面积一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是_________厘米.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是_________.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是_________平方厘米.4.(3分)(2014?长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_________平方厘米.5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC 的面积等于_________平方厘米.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是_________ 厘米.7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE是_________厘米.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是_________.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是_________.10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是_________平方厘米.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.2 / 1012.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.14.(2012?武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是_________.3 / 102010年五年级奥数题:图形与面积(B)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是170厘米.考点:巧算周长.分析:要求该图形的周长,先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,然后先算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.解答:解:400÷16=25(平方厘米),因为5×5=25(平方厘米),所以每个小正方形的边长为5厘米,周长为:(5×4+5×4+5×3+5×2+5×3+5)×2,=85×2,=170(厘米);答:它的周长是170厘米.点评:此类题解答的关键是先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,进而算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是25.考点:组合图形的面积.分析:此题需要进行图形分解:“7”分成一个长方形、一个等腰直角三角形、一个平行四边形;“2”分成一个梯形、一个平行四边形、一个长方形;“1”分成一个梯形和两个长方形.然后进行图形转换,依据题目条件即可求出结果.解答:解:“7”所占的面积和=+3+4=,“2”所占的面积和=3+4+3=10,“1”所占的面积和=+7=,++10=25.那么7,2,1三个数字所占的面积之和=故答案为:25.点评:此题关键是进行图形分解和转换.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是6.5平方厘米.4 / 10组合图形的面积考由图可以观察出:大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积分析(平方厘米解:大正方形的面积4=1解答=9.53++5×左中3个,左上,右上,右中,右下,,右中,共有粗线以外的图形面积为:整格有(平方厘米);(平方厘米);﹣所以粗线围成的图形面积为169.5=6.5 6.5平方厘米.答:粗线围成的图形面积是 6.5.故此题答案为:此题关键是对图形进行合理地割补.点评:平方厘米,那么阴影部分的面积是分)(2014?长沙模拟)如图的两个正方形,边长分别为8厘米和4244.(3厘米.考点:组合图形的面积.分析:两个正方形的面积减去两个空白三角形的面积.解答:8,)﹣4+8×8××解:4×4+88﹣×4×(,﹣24﹣32=16+642;cm)(=242.答:阴影的面积是24cm 24.故答案为:求组合图形面积的化为求常用图形面积的和与差求解.点评:12的面积等于的面积是△ABC18平方厘米,则四边形AEDCAE=BEABC35.(分)在△中,BD=2DC,,已知平方厘米.相似三角形的性质(份数、比例);三角形的周长和面积.考点:的关系,由此即可求出四边形BDE△的关系,ABD根据题意,连接分析:AD,即可知道△和△ADC△ADE和的面积.AEDC 解答:,,因为BD=2DC解:连接AD ABD=2S△ADC,△所以,S△即,SABD=18(平方厘米)=12,×又因为,AE=BE,5 / 10ADE=BD所以S=6(平方厘米),即,S△BDE=12×6=12(平方厘米);所以AEDC的面积是:18﹣故答案为:12.点评:解答此题的关键是,根据题意,添加辅助线,帮助我们找到三角形之间的关系,由此即可解答.厘米.厘米、OB是3.26.(3分)如图是边长为4厘米的正方形,AE=5组合图形的面积考O的面积是正方形面积的一半,再依据三角形面积公式就可以求A可以看出,三角AB连分析B的长度A相交解:如图连BA,B解答:BDF△S△ADE=S 则=8(平方厘米);(4×4)×S△ABE=S正方形= (厘米);OB=8×2÷5=3.2 3.2厘米.答:OB 是.故答案为:3.2 此题主要考查三角形和正方形的面积公式,将数据代入公式即可.点评:DE5厘米,那么它的宽厘米,长方形DEFG的长DG是34 .7(3分)如图正方形ABCD的边长是厘米,CG是厘米.是 3.2:组合图形的面积.考点的高,DG的面积,因为已知,进而可以求三角形AGDAGDAG 分析:连接,则可以依据题目条件求出三角形也就是长方形的宽,问题得解.AG解答:解:如图连接6 / 10S,=S﹣S﹣S ABGCDG△△△AGDABCD正方形2 4÷2﹣1××4﹣3×4÷=426﹣=16﹣(平方厘米);=8 (厘米);2÷5=3.28×3.2厘米.答:长方形的宽是3.2.故答案为:依据题目条件做出合适的辅助线,问题得解.点评:.24310个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是8.(3分)如图,一个矩形被分成组合图形的面积.考点:从图中可以看出每上、下两个小矩形的一个边是相邻的,也就是说长是相等的,那么根据矩形的面积公式分析:的矩形,可16知,如果长相同,面积之比也就是宽之比,反之宽之比也就是面积之比;由中间面积20和以算出空着的小矩形面积,最后把所有小矩形面积加起来就是大矩形的面积.解:由图和题意知,解答:,:4中间上、下小矩形的面积比是:20:16=5 ,:4所以宽之比是5 A=45;得:36=5:4那么,A B=20;B=5:4得25:C=24;C=5:4得30:D=15;:4得D:12=5 ;=45+36+25+20+20+16+30+24+15+12=243所以大矩形的面积.故答案为:243 此题考查了如果长方形的长相同,宽之比等于面积之比,还考查了比例的有关知识.点评:上的三等、AD、IH分别是边BC是边12,PAB上的任意一点,M、N、的边长为(9.3分)如图,正方形ABCD .上的四等分点,图中阴影部分的面积是60E分点,、F、G是边CD组合图形的面积.考点:上的三ADBC、HN上的任意一点,M、、I、分别是边ABP12ABCD 分析:根据题意:正方形的边长为,是边,然后再利用三角形的面积公式进行计算即可得到答DP上的四等分点,可连接是边、、等分点,EFGCD 案.7 / 10 解答BPMAPDADEAD解:阴影部分的面D×BP4×××3×12+=×4×AP+×3×12+=2AP+18+18+2BPAP+BP)=36+2×(12 =36+2×=36+24=60..答:这个图形阴影部分的面积是60 此题主要考查的是三角形的面积公式.点评:的厘米,阴影部分的总面积是10平方厘米,四边形ABCD分)10.(3 图中的长方形的长和宽分别是6厘米和4 4平方厘米.面积是:重叠问题;三角形的周长和面积.考点,2=12÷2=12,S△AEF+S△AGH=四边形EFGH 面积÷GHC=分析:因为S△EFC+S△四边形EFGH面积平方÷△DGC=四边形EFGH面积2﹣阴影部分的总面积是10平方厘米=2ADH=S所以S△ABE+S△△BFC+S 厘米.2=4平方厘米.﹣÷4﹣2=6=ECH所以:四边形ABCD面积=S△﹣(S△ABE+S△ADH)四边形ABCD面积平﹣阴影面积10平方厘米=2DGC=S解答:解:由题意推出:△ABE+S△ADH=S △BFC+S△四边形EFGH面积÷2 方厘米.﹣)=四边形ABCD面积÷42=6﹣2=4平方厘米.ADHS=S所以:四边形ABCD面积△ECH﹣(△ABE+S△故答案为:4.此题在重叠问题中考查了三角形的周长和面积公式,此题设计的非常精彩.点评:0分)二、解答题(共4小题,满分的面CQ=2BQ,求阴影四边形CEPQAP=2PFABCDEF11.图中正六边形的面积是54.,积..考点:等积变形(位移、割补)个小正三角形,根据平行四边形对角线平分平行四边形面积,采用分析:54ABCDEF等分为如图,将正六边形数小三角形的办法来计算面积.解答:解:如图,PEF=3S△,S,CDE=9S△四边形ABQP=11.8 / 1023=3.因此,阴影四边CEP面积5上述三块面积之和3+9+11=2此题主要利用面积分割,用数基本小三角形面积来解决问题点评平方厘米.问:大正六角星形面积是多少平方厘米..如图,涂阴影部分的小正六角星形面积是1612等积变形(位移、割补考个空白小三角形面个小三角形,且都与外围分析由图及题意知,可把涂阴影部分小正六角星形等分1平方厘米,可求出大正六角星形中心正六边形的面积,相等,已知涂阴影部分的小正六角星形面积1个小正三角形,且它们与外围六个大角的面积相等,进而可求出大正六角星这个正六边形又可等分面解:如下图所示解答:6个空白小三角形面积相等,涂阴影部分小正六角星形可等分成12个小三角形,且都与外围的(平方厘米);12+6)=24×所以正六边形ABCDEF的面积:16÷12(6个小正三角形,且它们与外围六个大角的面积相等,又由于正六边形ABCDEF又可等分成(平方厘米);24×2=48所以大正六角星形面积:48平方厘米.答:大正六角星形面积是个大点的正三角形组个小正三角形,又可看作是6 此题要借助求正六边形的面积来解答,它既可看作是18点评:成.)中小长方形1)与(2)所示意那样,划分为四个小长方形.在(13.一个周长是56厘米的大长方形,按图中(1D'.又知,长方形:33,B':C'=1)中相应的比例是:C=1:2.而在(2A':B'=1:B面积的比是:A:B=1:2,.求大长方形的面积.:3的长减去在D的长所得到的差之比为1的宽所得到的差,与的宽减去DD'比的应用;图形划分.考点:::C=12,B:“在(1)中小长方形面积的比是:A:B=1要求大长方形的面积,需求出它的长和宽,由条件分析:的宽所得到的差,D.又知,长方形D'的宽减去,3B':C'=1:3.而在(22)中相应的比例是A':B'=1:′,D的宽是大长方形宽的”可知:D的宽是大长方形宽的,1与D'的长减去在D的长所得到的差之比为:3′﹣大长方形的宽),由此便可以列式计算.(×﹣大长方形的宽)D的长是×(28,D的长是28 ,则长为x28﹣x 解答:解:设大长方形的宽为′′D.=DD的宽=x,所以,的宽﹣的宽,=D因为的宽x′28×长D=(﹣)﹣=长,)xD(×28x,9 / 10 2长D:=由题设可知,于是=,即x=8.= 8于是,大长方形的长=28﹣8=20,从而大长方形的面积为×20=160平方厘米.答:大长方形的面积是160平方米.此题比较复杂,主要考查比的关系,应利用比的意义,找清数量见的比,再利用题目条件,就可以进行计点评:算求得结果.,左边部分面积是38,FG=6直线AB将图形分成两部分,CD=514.(2012?武汉模拟)如图,已知,DE=7,EF=15,.的面积是4065右边部分面积是,那么三角形ADG考点:三角形的周长和面积.分析:看成是一个整体,根据各线段的关系和左右两部分面积的关系,可以列出一个方程,求出可以把S ADE△S的关系求出答案.S的面积,然后再根据所求三角形与ADE△△ADE解答:=3S解:由题意知,S,S=,S BEC△ADEBFE△△AEG△X),(S=3X=X设S,则S,=38﹣BFEADE△△△AEG)(可列出方程:38﹣X+3X=65,,解方程,得:x=10 =40.)(=10×所以S1+3ADG△故答案为:40.此题考查了如何利用边的关系求三角形的面积.点评:10 / 10。
五年级奥数题几何面积及答案

关注我关注我
五年级奥数题几何面积及答案
图中ABCD是梯形,三角形ADE面积是1.8,三角形ABF的面积是9,三角形BCF的面积是27.那么阴影部分面积是多少?【答案解析】设△ADF的面积为"上",△BCF的面积为"下",△ABF的面积为"左",△DCF的面积为"右".左=右=9;上×下=左×右=9×9=81,而下=27,所以上=81÷27=3.△ADE的面积为1.8,那么△AEF的面积为1.2,则EF:DF= : =1.2:3=0.4.△CEF与△CDF的面积比也为EF与DF的比,所以有 =0.4× =0.4×(3+9)=4.8.即阴影部分面积为4.8.
分类精心精选精品文档,欢迎下载,所有文档经过整理后分类挑选加工,下载后可重新编辑,正文所有带XX或是空格类下载后可自行代入字词。
1。
小学五年级奥数题——图形面积练习

小学五年级奥数题:图形面积
1、如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=1/3AB,已知四边形EDCA的面积是35,求三角形ABC的面积?
2、正方形ABFD的面积为100平方厘米,直角三
角形ABC的面积,比直角三角形(CDE的面积大30平
方厘米,求DE的长是多少?
小学五年级奥数题:图形面积(答案)
1、如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=1/3AB,已知四边形EDCA的面积是35,求三角形ABC的面积.
解答:根据定理:
所以四边形ACDE的面积就是6-1=5份,这样三角形35÷5×6 =42。
2、正方形ABFD的面积为100平方厘米,直角三角形ABC的面积,比直角三角形(CDE的面积大30平方厘米,求DE的长是
多少?
解:公共部分的运用,三角形ABC面积-三角形CDE的面积=3 0,
两部分都加上公共部分(四边形BCDF),正方形ABFD-三角形B FE=30,所以三角形BFE的面积为70,所以FE的长为70×2÷1 0=14,所以DE=4。
五年级数学奥数题面积题

五年级数学奥数题面积题
【原创版】
目录
1.题目概述
2.题目解析
3.解题思路
4.解答过程
5.题目答案
正文
1.题目概述
这是一道针对五年级学生的数学奥数题,主要考察学生对面积知识的理解和运用。
题目内容为一个长方形的长为 10 厘米,宽为 6 厘米,求这个长方形的面积。
2.题目解析
长方形的面积计算公式为:面积 = 长×宽。
根据题目所给的数据,长方形的长为 10 厘米,宽为 6 厘米,所以可以通过公式计算出它的面积。
3.解题思路
首先,要明确题目所求的是长方形的面积,根据公式,面积等于长乘以宽。
然后,将题目中给出的长和宽代入公式进行计算。
4.解答过程
根据公式,长方形的面积 = 长×宽,将题目中给出的长和宽代入公式,得到:
面积 = 10 厘米× 6 厘米 = 60 平方厘米
所以,这个长方形的面积是 60 平方厘米。
5.题目答案
这道题目的答案是 60 平方厘米。
奥数拓展第六讲:多边形的面积综合-数学五年级上册含参考答案

奥数拓展第六讲:多边形的面积综合-数学五年级上册一、选择题1.比较下面阴影部分的面积,()是错误的。
①②③④A.图①中阴影部分的面积等于图②中阴影部分的面积B.图②中阴影部分的面积等于图③中阴影部分的面积C.图③中阴影部分的面积不等于图④中阴影部分的面积的是()。
A.面积变大B.面积变小C.面积不变D.无法确定4.七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,把一幅七巧板按如图①所示进行1~7编号,1~7号分别对应着七巧板的七块。
图②所示的“天鹅”是由这幅七巧板拼成的,“天鹅”头颈由3号和6号块构成,其面积为3,则图①大正方形的边长为()。
A.8 B.6 C.4 D.25.将一个梯形割补成一个三角形(如图所示),面积和原来相比(),周长与原来相比()。
A.不变;变大B.不变;变小C.变小;变大D.无法确定6.如图中两个正方形的边长分别是6厘米和4厘米,阴影部分的面积是()平方厘米。
A.20 B.18 C.16 D.22二、填空题7.下图中ABCD是梯形,ABED是平行四边形,其中几个三角形面积如图所示(单位:平方厘米),阴影部分的面积是( )平方厘米。
8.图中ABCD为正方形,E为AB的中点,阴影部分的面积是21cm2,正方形ABCD的面积是( )cm2。
9.如图,在三角形ABC 中,D 是边AB 的中点,可知AD =BD ,则三角形BCD 与三角形ACD 的面积相等。
(1)如图①,在三角形ABC 中,D 、E 分别是AB 和AC 两边的中点。
已知三角形ADE 的面积是2cm 2,则三角形ABC 的面积是( )cm 2。
(2)如图②,在三角形ABC 中,把AB 边三等分、AC 边四等分。
已知三角形ADE 的面积是2cm 2,则三角形ABC 的面积是( )cm 2。
(3)如图③,在平行四边形ABCD 中,把AB 边五等分、AD 边六等分。
已知平行四边形ABCD 的面积是15cm 2,则三角形AEF 的面积是( )cm 2。
五年级奥数图形面积

图 形 面 积【基本原则】各种具有一定综合性的直线形面积问题,重点是需要利用同底或同高的两三角形的面积相除的商等于对应高或对应底相除的商这一性质的问题,其中包括四边形和梯形被两条对角线分割而成的4个小三角形之间的面积关系.【典型例题】1.图16-1中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍, EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?【分析与解】ABD ,ABC 等高,所以面积的比为底的比,有12ABD ABCS BD SBC ==,所以ABD S=1122ABCS ⨯=⨯180=90(平方厘米).同理有13ABE ABDAE SS AD=⨯=×90=30(平方厘米),34AFE ABEFE S S BE=⨯=×30=22.5(平方厘米).即三角形AEF 的面积是22.5平方厘米.2.如图16-2,把四边形ABCD 的各边都延长2倍,得到一个新四边形EFGH 如果ABCD 的面积是5平方厘米,则EFGH 的面积是多少平方厘米?【分析与解】 方法一:如下图,连接BD ,ED ,BG ,有EAD 、ADB 同高,所以面积比为底的比,有2EADABDABDEA SS SAB==.同理36EAHEADEADABD AHSS SSAD===.类似的,还可得6FCGBCDSS=,有()66EAHFCGABDBCDABCD SSSSS +=+==30平方厘米.连接AC ,AF ,HC ,还可得6EFBABCSS=,6DHGACDSS=,有()66EFBDHGABCACDABCD SSSSS +=+==30平方厘米.有四边形EFGH 的面积为EAH,FCG,EFB,DHG,ABCD 的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD ,有EAH 、△ABD 中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAHS=6ABDS.类似的,还可得FCGS =6BCDS,有EAHS+FCGS=6(ABDS+BCDS)=6ABCD S =30平方厘米.连接AC ,还可得EFB S =6ABC S,DHG S=6ACDS,有EFBS+DHG S=6(ABC S+ACDS)=6ABCD S=30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和,即为30+30+5=65平方厘米.评注:方法二用到了一个比较重要的性质,若两个三角形的某对夹角相等或互补(和为180°),那么构成这个角的两边乘积的比为面积比.这个原则,我们可以在中学数学中的三角部分学到,当然我们也可以简单的利用比例性质及图形变换来说明,有兴趣的同学可以自己试试.3.图16-3中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?【分析与解】 方法一:如下图所示,为了方便叙述,将某些点标上字母.因为△ADE 、△DEC 高相同,所以面积比为底的比,有ADE DECS S=AEEC,所以ADE S =AEEC×6.同理有ABE BCES S=AEEC,所以ABE S =AEEC×7.所以有△ADE 与△ABE 的面积比为6:7.又有它们的面积和为52-(6+7)=39(公顷.)所以ADE S=767+×39=18(公顷),ABE S =767+×39=21(公顷.)显然,最大的三角形的面积为21公顷.方法二:直接运用例2评注中的重要原则,在△ABE ,△CDE 中有∠AEB=∠CED ,所以△ABE ,△CDE 的面积比为(AE ×EB):(CE ×DE).同理有△ADE ,△BCE 的面积比为(AE ×DE):(BE ×EC). 所以有ABES×CDE S=ADES×BCES,也就是说在所有凸四边形中,连接顶点得到2条对角线,有图形分成上、下、左、右4个部分,有:上、下部分的面积之积等于左右部分的面积之积. 即ABE S×6=ADE S×7,所以有△ABE 与△ADE 的面积比为7:6,ABE S=767+×39=21公顷,ADE S=667+×39=18公顷. 显然,最大的三角形的面积为21公顷.评注:在方法二中,给出一个很重要的性质:在所有凸四边形中,连接顶点得到2条对角线,有图形分成上、下、左、右4个部分,有:上、下部分的面积之积等于左右部分的面积之积.希望大家牢牢记住,并学会在具体问题中加以运用.4. 如图16-4,已知.AE=15AC ,CD=14BC ,BF=16AB ,那么DEF ABC 三角形的面积三角形的面积等于多少?【分析与解】 如下图,连接AD ,BE ,CF.有△ABE ,△ABC 的高相等,面积比为底的比,则有ABE ABCSS=AEAC,所以ABE S =AEAC×ABC S =15ABCS同理有AEF S=AFABABE S ,即=AEF S=15×56ABC S =16ABC S . 类似的还可以得到CDE S =14×45ABC S =15ABC S ,BDF S =16×13ABC S =18ABC S .所以有DEF S =ABC S -(AEF S +CDE S +BDF S )=(1-16-15-18)ABC S =61120ABC S . 即DEF ABC 三角形的面积三角形的面积为61120.5.如图16-5,长方形ABCD 的面积是2平方厘米,EC=2DE ,F 是DG 的中点.阴影部分的面积是多少平方厘米?【分析与解】 如下图,连接FC ,△DBF 、△BFG 的面积相等,设为x 平方厘米;△FGC 、△DFC 的面积相等,设为y 平方厘米,那么△DEF 的面积为13y 平方厘米.BCD S=2x+2y=1,BDE S=x+13y=l ×13=13.所以有x+y=0.53x+y=1⎧⎨⎩①②.比较②、①式,②式左边比①式左边多2x ,②式右边比①式右边大0.5,有2x=0.5,即x=0.25,y=0.25.而阴影部分面积为y+23y=53×0.25=512平方厘米.评注:将这种先利用两块独立的图形来表达相关图形的面积,再根据已知条件列出一个二元一次方程组,最终求出解的方法称为“凌氏类蝶形法”.类蝶形问题必须找好两块独立的图形,还必须将边的比例关系转化为面积的比例关系.类似的还有一道题:△ABC 中,G 是AC 的中点,D 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已△ABM 的面积比四边形FCGN 的面积大1.2平方厘米,则△ABC 的面积是_______平方厘米? 有兴趣的同学可以自己试试.6.如图16-6,已知D 是BC 中点,E 是CD 的中点,F 是AC 的中点.三角形ABC 由①~⑥这6部分组成,其中②比⑤多6平方厘米.那么三角形ABC 的面积是多少平方厘米?【分析与解】 因为E 是DC 中点,F 为Ac 中点,有AD=2FE 且阳平行于AD ,则四边形ADEF 为梯形.在梯形ADEF 中有③=④,②×⑤=③×④,②:⑤=A 2D :F 2E =4.又已知②-⑤=6,所以⑤=6÷(4-1)=2,②=⑤×4:8,所以②×⑤=④×④:16,而③=④,所以③=④=4,梯形ADEF 的面积为②、③、④、⑤四块图形的面积和,为8+4+4+2=18.有△CEF 与△ADC 的面积比为CE 平方与CD 平方的比,即为1:4.所以△ADC 面积为梯形ADEF 面积的44-1=43,即为18×43=24.因为D 是BC 中点,所以△ABD 与△ADC 的面积相等,而△ABC 的面积为△ABD 、△ADC 的面积和,即为24+24=48平方厘米.三角形ABC 的面积为48平方厘米.评注:梯形中连接两条对角线.则分梯形为4部分,称之为:上、下、左、右.如下图:运用比例知识,知道:①上、下部分的面积比等于上、下边平方的比. ②左、右部分的面积相等.③上、下部分的面积之积等于左、右部分的面积之积.7.图16-7是一个各条边分别为5厘米、12厘米、13厘米的直角三角形.如图16-8,将它的短直角边对折到斜边上去与斜边相重合,那么图16—8中的阴影部分(即未被盖住的部分)的面积是多少平方厘米?【分析与解】 如下图,为了方便说明,将某些点标上字母.有∠ABC 为直角,而∠CED=∠ABC ,所以∠CED 也为直角.而CE=CB=5.△ADE 与△CED 同高,所以面积比为底的比,及ADE CEDS S=AE EC =13-55=85,设△ADE 的面积为“8”,则△CED 的面积为“5”.△CED 是由△CDB 折叠而成,所以有△CED 、△CDB 面积相等,△ABC 是由△ADE 、△CED 、△CDB 组成,所以ABC S=“8”+“5”+“5”=“18”对应为12×5×12=30,所以“1”份对应为53,那么△ADE的面积为8×53=1313平方厘米. 即阴影部分的面积为1313平方厘米.8.如图16-9,在一个梯形内有两个三角形的面积分别为10与12,已知梯形的上底长是下底长的23.那么余下阴影部分的面积是多少?【分析与解】 不妨设上底长2,那么下底长3,则上面部分的三角形的高为10÷2×2=10,下面部分的三角形的高为12÷3×2=8,则梯形的高为lO+8=18.所以梯形的面积为12×(2+3)×18=45,所以余下阴影部分的面积为45-10-12=23.评注:这道题中上下底、梯形的高都不确定,但是余下阴影部分的面积却是确定的值,所以面积值与上下底、高的确定值无关,所以可以大胆假设,当然也可以谨慎的将上底设为2x 下底为3x .9.图16-10中ABCD 是梯形,三角形ADE 面积是1.8,三角形ABF 的面积是9,三角形BCF 的面积是27.那么阴影部分面积是多少?【分析与解】 设△ADF 的面积为“上”,△BCF 的面积为“下”, △ABF 的面积为“左”,△DCF 的面积为“右”.左=右=9;上×下=左×右=9×9=81,而下=27,所以上=81÷27=3.△ADE 的面积为1.8,那么△AEF 的面积为1.2,则EF :DF=AEF S :AEDS=1.2:3=0.4.△CEF 与△CDF 的面积比也为EF 与DF 的比,所以有ACES=0.4×ACDS=0.4×(3+9)=4.8.即阴影部分面积为4.8.10.如图16-11,梯形ABCD 的上底AD 长为3厘米,下底BC 长为9厘米,而三角形ABO 的面积为12平方厘米.则梯形ABCD 的面积为多少平方厘米?【分析与解】 △ADD 与△BCO 的面积比为AD 平方与BC 平方的比,即为9:81=19.而△DCO 与△ABO 的面积相等为12,又BCOS ABOS×DCOS=ADOS×BCOS=12×12=144,因为144÷9=4×4,所以ADO S=4,则BCOS=4×9=36,而梯形ABCD 的面积为△ADO 、△BCO 、△ABO 、△CDO 的面积和,即为4+36+12+12=64平方厘米.即梯形ABCD 的面积为64平方厘米.11.如图16-12,BD ,CF 将长方形ABCD 分成4块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米.问:绿色四边形面积是多少平方厘米?【分析与解】 连接BF ,四边形BCDF 为梯形,则BFE 的面积与黄色CDE 的面积相等为 6.6636FEDBCEBFECDESSSS⨯=⨯=⨯=,所以3649BCES=÷=.9615BCDBECCDES S S=+=+=.又因为BD 是长方形ABCD 的对角线,15ABDBCDS S==所以FED15411ABDS SS =-=-=绿色四边形ABEF 红色.绿色四边形面积为11平方厘米.12.如图16-13,平行四边形ABCD 周长为75厘米.以BC 为底时高是14厘米;以CD 为底时高是16厘米.求平行四边形ABCD 的面积.【分析与解】 因为平行四边形面积等于底与对应高的积,所以有14×BC=16 ×CD ,即BC :CD=8:7,而2(BC+CD)=75,所以BC=20,以BC 为底,对应高为14,20×14=280,所以平行四边形ABCD 的面积为280平方厘米.13.如图16-14,一个正方形被分成4个小长方形,它们的面积分别是110平方米、15平方米、310平方米和25平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?【分析与解】为了方便叙述,将某些点标上字母,如下图:大正方形的面积为32111105510+++=,所以大正方形的边长应为1. 上面两个长方形的面积之比为32:105=3:4,所以IG=47.下面两个长方形的面积之比为11:510=2:l,所以IG=13.那么LI=4157321-=,那么阴影小正方形的面积为55252121441⨯=.14.图16-15中外侧的四边形是一边长为10厘米的正方形,求阴影部分的面积.【分析与解】如下图所示,所以阴影部分在图中为四边形EFGH.设阴影部分面积为“阴”平方厘米,正方形内的其他部分面积设为“空”平方厘米.DGH 、HMG 的面积相等,GCF 与GPF ;FBE 与 EOF ,HAE 与HNE 这3对三角形的面积也相等.阴一空=2×3=6,阴+空=lO ×10=100. 阴=(6+100)÷2=53.即阴影部分的面积为53平方厘米.15.如图16-16,长方形被其内的一些直线划分成了若干块,已知边上有3块面积分别是13,35,49.那么图中阴影部分的面积是多少?【分析与解】 如下图所示,为了方便叙述,将部分区域标上序号,设阴影部分面积为“阴”:(49+①+35)+(13+②)= 12矩形的面积, ①+阴+②=12矩形的面积. 比较上面两个式子可得阴影部分的面积为97.。
小学五年级奥数第13课《面积计算》试题附答案
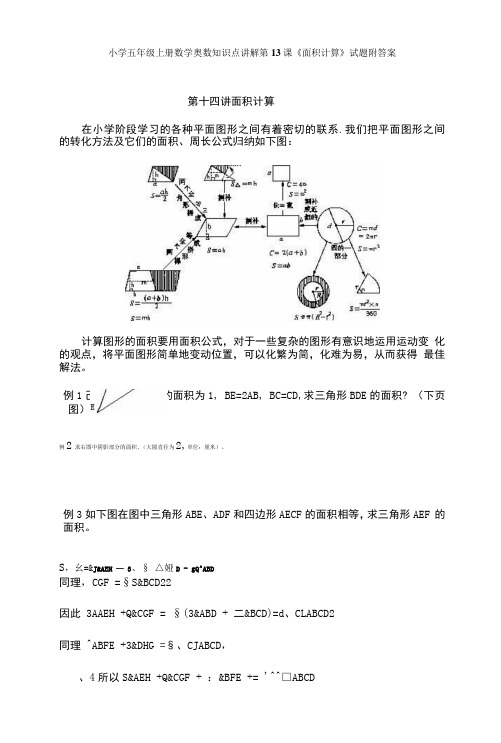
小学五年级上册数学奥数知识点讲解第13课《面积计算》试题附答案第十四讲面积计算在小学阶段学习的各种平面图形之间有着密切的联系.我们把平面图形之间的转化方法及它们的面积、周长公式归纳如下图:计算图形的面积要用面积公式,对于一些复杂的图形有意识地运用运动变化的观点,将平面图形简单地变动位置,可以化繁为简,化难为易,从而获得最佳解法。
例1己知三角形ABC的面积为1, BE=2AB, BC=CD,求三角形BDE的面积? (下页图)例2求右图中阴影部分的面积.(大圆直径为2,单位:厘米)。
例3如下图在图中三角形ABE、ADF和四边形AECF的面积相等,求三角形AEF 的面积。
S,幺=&J&AEH — 3、§ △娅D - gQ^ABD同理,CGF =§S&BCD22因此3AAEH +Q&CGF = §(3&ABD + 二&BCD)=d、CLABCD2同理^ABFE +3&DHG =§、CJABCD,、4所以S&AEH +Q&CGF + :&BFE += '^^□ABCD所以S[JEFGH = (1g) ScJABCD =□此CD即四边形EFGH的面积:四边形ABCD面积=5 :9。
例8如右图,己知三角形ABC的三条高必定交于一点,如记成P点, 请你讲明黑+北+福=1为什么成立?AJJ b 匕Cr分析与解答从右图中可以看出APBC和AABC是同底的两个三角形, 它们的面积之比等于它们对应高的比,所以2=黑•.同理可得:L 右图是一个圆心角为45°的扇形,其中直角三角形B0C 的直角边为6厘 米,求阴影部分面积。
2 .在右图中,阴影部分A 的面积比阴影部分B 的面积大10. 5平方厘米,求线 段BC 的长度?sQ&PCA=PE $&PAB二西=PF CF'所以 s s s“△PBC 十 2&PCA 十 2 APABQ AAB CJ AAB C° AAB CPD PE PF = + + ——。
五年级上册奥数面积计算(例题含答案)

第十四讲面积计算在小学阶段学习的各种平面图形之间有着密切的联系.我们把平面图形之间的转化方法及它们的面积、周长公式归纳如下图:计算图形的面积要用面积公式,对于一些复杂的图形有意识地运用运动变化的观点,将平面图形简单地变动位置,可以化繁为简,化难为易,从而获得最佳解法。
例1 已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?分析利用已给的线段间的比例关系、已给的三角形的面积以及三角形的面积公式,设法把三角形BDE划分成一些与三角形ABC的面积成相应比例的三角形.这样,三角形BDE的面积就能求得了。
解:见上图,连结CE.对于三角形ABC与三角形BEC,分别把AB和BE可知,S△BEC =2S△ABC=2.显然,三角形BEC和三角形CED是两个等底(BC=CD)、等高的三角形,因此S△CED =S△BEC=2。
这样,S△BDE =S△BEC+S△CED=4。
例2 求右图中阴影部分的面积.(大圆直径为2,单位:厘米)。
分析:解题时可以先将图形下半部分翻转拼接为下图.然后将图中的小圆移至中心从图中不难看出求原图中阴影部分的面积就是求一个圆环的面积。
解:大圆半径:2÷2=1(厘米)小圆半径:1÷2=0.5(厘米)阴影面积:3.14×(12-0.52)=2.355(平方厘米)答:阴影部分的面积是2.355平方厘米.例3 如下图.在图中三角形ABE、ADF和四边形AECF的面积相等,求三角形AEF的面积。
分析三角形AEF的面积等于四边形AECF的面积减去三角形ECF的面积.因为长方形ABCD的面积等于三角形ABE、ADF和四边形AECF的面积和,长方形ABCD的长、宽分别为9厘米和6厘米,因此很容易求出它的面积.所以解题关键在于求出三角形ECF的面积。
EC的长度.同理可以求出FC的长度.这样三角形ECF的面积可以求出,使问题得解。
解:长方形ABCD的面积:9×6=54(平方厘米);四边形AECF及三角形ABE、AFD的面积相等,是:EC的长度:9-18×2÷6=3(厘米);FC的长度:6-18×2÷9=2(厘米);三角形AEF的面积:18-3×2÷2=15(平方厘米)。
(完整word版)五年级上学期图形面积奥数题
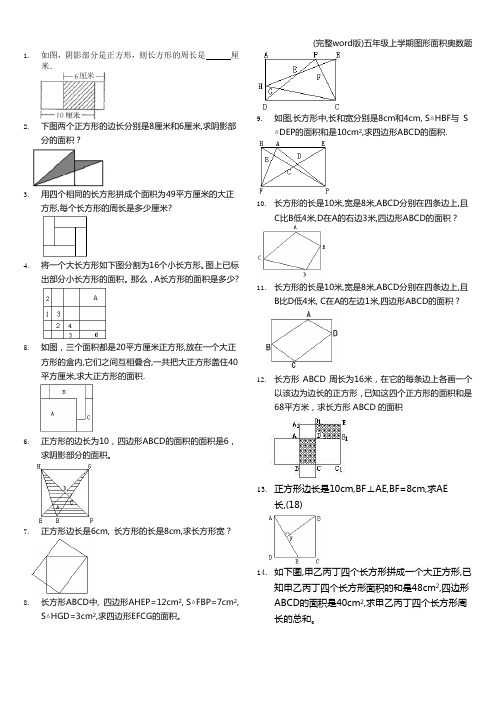
(完整word版)五年级上学期图形面积奥数题1.如图,阴影部分是正方形,则长方形的周长是厘米.2.下图两个正方形的边长分别是8厘米和6厘米,求阴影部分的面积?3.用四个相同的长方形拼成个面积为49平方厘米的大正方形,每个长方形的周长是多少厘米?4.将一个大长方形如下图分割为16个小长方形。
图上已标出部分小长方形的面积。
那么,A长方形的面积是多少?5.如图,三个面积都是20平方厘米正方形,放在一个大正方形的盒内,它们之间互相叠合,一共把大正方形盖住40平方厘米,求大正方形的面积.6.正方形的边长为10,四边形ABCD的面积的面积是6,求阴影部分的面积。
7.正方形边长是6cm, 长方形的长是8cm,求长方形宽?8.长方形ABCD中, 四边形AHEP=12cm2, S△FBP=7cm2,S△HGD=3cm 2,求四边形EFCG的面积。
9.如图,长方形中,长和宽分别是8cm和4cm, S△HBF与S△DEP的面积和是10cm 2,求四边形ABCD的面积.10.长方形的长是10米,宽是8米,ABCD分别在四条边上,且C比B低4米,D在A的右边3米,四边形ABCD的面积?11.长方形的长是10米,宽是8米,ABCD分别在四条边上,且B比D低4米, C在A的左边1米,四边形ABCD的面积?12.长方形ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方米,求长方形ABCD的面积13.正方形边长是10cm,BF⊥AE,BF=8cm,求AE长,(18)14.如下图,甲乙丙丁四个长方形拼成一个大正方形,已知甲乙丙丁四个长方形面积的和是48cm2,四边形ABCD的面积是40cm2,求甲乙丙丁四个长方形周长的总和。
(完整word版)五年级上学期图形面积奥数题列方程解应用题15.张明用272元买了一件上衣一顶帽子和一双鞋子,上衣比鞋贵60元,鞋比帽子贵70元。
求上衣、鞋子和帽子各多少钱?16.在一个除法算式里,被除数、除数、商与余数的和是289,已知商是10,余数是2,那么被除数是多少?17.全班同学站队排成若干行,若每行10人则多5人,若每行12人则少3人。
五年级奥数题:图形与面积含详细答案

.翔迪学校五年级专题强化:图形与面积年级班姓名得分一、填空题3. 下图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是______平方厘米.4. 下图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是______平方厘米.5. 在ABC∆的面积是18平方厘米,则四边形AEDC的面积=,BEBD2∆中,DCAE=,已知ABC等于______平方厘米.6. 下图是边长为4厘米的正方形,AE=5厘米、OB是______厘米.7. 如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE是______厘米.9. 如下图,正方形ABCD的边长为12, P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是______.10. 下图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD 的面积是______平方厘米.二、解答题11. 图中正六边形ABCDEF 的面积是54.PF AP 2=,BQ CQ 2=,求阴影四边形CEPQ 的面积.12. 如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13. 一个周长是56厘米的大长方形,按图35中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是: 2:1:=B A ,2:1:=C B .而在(2)中相应的比例是3:1:=''B A ,3:1:=''C B .又知,长方形D '的宽减去D 的宽所得到的差,与D '的长减去在D 的长所得到的差之比为1:3.求大长方形的面积.14. 如图,已知5=CD ,7=DE ,15=EF ,6=FG .直线AB 将图形分成两部分,左边部分面积是38,右边部分面积是65.那么三角形ADG 面积是______.五年级奥数题:图形与面积一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是_________厘米.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是_________.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是_________平方厘米.4.(3分)(2014•长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_________平方厘米.5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于_________平方厘米.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是_________厘米.7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE 是_________厘米.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是_________.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是_________.10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是_________平方厘米.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.14.(2012•武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是_________.2010年五年级奥数题:图形与面积(B)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是170厘米.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是25.+3+4=+7=,+3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是 6.5平方厘米.左上右上,右中右下,左中右中3+×4.(3分)(2014•长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是24平方厘米.××5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于12平方厘米.×=12×6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是 3.2厘米.ABE==7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE 是 3.2厘米.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是243.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是60.×AP+×AD+AD+AP+××12+10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是4平方厘米.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.,的宽是大长方形宽的的长是×的长是×=x=××:==,于是=,14.(2012•武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是40.S=(。
五年级上册数学奥数

必考奥数题型在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体(下图),求这个立体图形的表面积。
【答案】这个立体图形的表面积为214平方分米。
分析:我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面:5×5×2=50(平方分米)侧面:小正方体的四个侧面和大正方体的四个侧面5×5×4=100(平方分米)4×4×4=64(平方分米)这个立体图形的表面积为:50+100+64=214(平方分米)一项工程,由甲先做,再由甲乙两队合作,又做了16天完成。
已知甲乙两队的工效比是2:3,甲乙两队独立完成这项工程各需多少天?解:甲乙的工作效率和=(1-)÷16=÷16=甲的工作效率=÷(2+3)×2=乙的工作效率=-=那么甲单独完成需要1÷=50天乙单独完成需要1÷=天=33天一项工程甲独完成要10天,乙独做需15天,丙队要20天,3队一起干,甲队因事走了,结果共用了六天,甲队实际干了多少天?解:乙丙的工作效率和=乙丙都做6天,完成甲完成全部的那么甲实际干了天一项工程,甲队单独做20天完成,乙队单独做30天完成,现在乙队先做5天后,剩下的由甲、乙两队合作,还需要多少天完成?解:乙5天完成5×甲乙合作的工作效率=那么还需要(1-)÷=5天一批零件,甲乙两人合做5.5天可以超额完成这批零件的0.1,现在先由甲做2天,后由甲乙合作两天,最后再由乙接着做4天完成任务,这批零件如果由乙单独做几天可以完成?解:将全部零件看作单位1那么甲乙的工作效率和=(1+0.1)÷5.5=整个过程是甲工作2+2=4天乙工作2+4=6天相当于甲乙合作4天,完成×4=那么乙单独做6-4=2天完成1-=所以乙单独完成需要2÷=10天一个工程项目,乙单独完成工程的时间是甲队的2倍;甲乙两队合作完成工程需要20天;甲队每天工作费用为1000元,乙每天为550元,从以上信息,从节约资金角度,公司应选择哪个?应付工程队费用多少?解:甲乙的工作效率和=甲乙的工作时间比=1:2那么甲乙的工作效率比=2:1所以甲的工作效率=乙的工作效率=甲单独完成需要1÷=30天乙单独完成需要1÷=60天甲单独完成需要1000×30=30000元乙单独完成需要550×60=33000元甲乙合作完成需要(1000+550)×20=31000元很明显,甲单独完成需要的钱数最少选择甲,需要付30000元工程费。
五年级数学(上册)《组合图形的面积》试题及答案及五年级数学上册平面图形的面积归纳与练习

五年级数奥数:《组合图形的面积》1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积- 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= 3.5×2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,阴影部分是正方形,则长方形的周长是厘米.
2.下图两个正方形的边长分别是8厘米和6厘米,求阴影部分的
面积?
3.用四个相同的长方形拼成个面积为49平方厘米的大正方形,
每个长方形的周长是多少厘米
4.将一个大长方形如下图分割为16个小长方形。
图上已标出部
分小长方形的面积。
那么,A长方形的面积是多少
5.如图,三个面积都是20平方厘米正方形,放在一个大正方形
的盒内,它们之间互相叠合,一共把大正方形盖住40平方厘米,求大正方形的面积.
6.正方形的边长为10,四边形ABCD的面积的面积是6,求阴影
部分的面积。
7.正方形边长是6cm,长方形的长是8cm,求长方形宽?
8.长方形ABCD中,四边形AHEP=12cm2,S△FBP=7cm2,S△HGD=3cm2,
求四边形EFCG的面积。
9.如图,长方形中,长和宽分别是8cm和4cm,S△HBF与S△DEP
的面积和是10cm2,求四边形ABCD的面积.
10.长方形的长是10米,宽是8米,ABCD分别在四条边上,且C比
B低4米,D在A的右边3米,四边形ABCD的面积?
11.长方形的长是10米,宽是8米,ABCD分别在四条边上,且B比
D低4米,C在A的左边1米,四边形ABCD的面积?
12.长方形ABCD周长为16米,在它的每条边上各画一个以该边
为边长的正方形,已知这四个正方形的面积和是68平方米,求长方形ABCD的面积
13.正方形边长是10cm,BF⊥AE,BF=8cm,求AE长,(18)
14.如下图,甲乙丙丁四个长方形拼成一个大正方形,已知
甲乙丙丁四个长方形面积的和是48cm2,四边形ABCD的
面积是40cm2,求甲乙丙丁四个长方形周长的总和。
列方程解应用题
15.张明用272元买了一件上衣一顶帽子和一双鞋子,上衣
比鞋贵60元,鞋比帽子贵70元。
求上衣、鞋子和帽子各多少钱
16.在一个除法算式里,被除数、除数、商与余数的和是
289,已知商是10,余数是2,那么被除数是多少
17.全班同学站队排成若干行,若每行10人则多5人,若每
行12人则少3人。
排成了多少行有多少同学。
