环路定理
《环路定理》课件

欢迎来到《环路定理》的PPT课件!在这次的介绍中,我们将探讨环路定理 的定义、基本原理、应用场景、推导过程、计算方法以及与其他电路定律的 联系,同时还会分析一些实际案例。
环路定理的定义
什么是环路定理?
环路定理是一项用于分析电路的基本方法,它揭示了电流在闭合回路中的行为。
环路定理的重要性
在修复电子设备时,环 路定理可以帮助我们找 到故障元件并进行更精 确的维修。
环路定理的推导过程
1
建立回路方程
根据电路结构和电路元件之间的关系建立回路方程。
2
应用欧姆定律
根据欧姆定律计算回路中的电流,将其代入回路方程。
3
解方程求解
通过数学方法解方程,求得各个未知变量的数值。
环路定理的计算方法
计算步骤 选择回路方向
通过环路定理,我们可以更好地理解电路中各个元件之间的关系,从而解析电路中的电流和 电压。
环路定理的公式
环路定理可以用数学公式表示为:ΣV = 0,即沿着闭合回路的电压之和等于零。
环路定理的基本原理
电阻与电压关系
环路定理基于电阻与电压之间 的关系,根据欧姆定律计算回 路中的电流。
基尔霍夫定律
电流的交叉与合并
环路定理是基尔霍夫定律之一, 基尔霍夫定律是电路分析的基 础。
环路定理考虑了电流在回路中 的交叉和合并,帮助我们分析 复杂电路。
环路定理的应用场景
1 电路设计
2 故障排查
3 电子设备维修
环路定理可以帮助电路 设计师更好地分析电路, 优化电路结构和性能。
当电路出现故障时,使 用环路定理可以帮助我 们快速定位并解决问题。
建立方程 代入变量值 求解未知变量
计算方法 根据实际情况选择回路的方向Fra bibliotek可以简化计算。
安培环路定理

安培环路定理
安培环路定理,又称为安培定理或安培第二定理,是电磁学中的一条重要定理,描述了由电流所产生的磁场的性质。
它是由法国物理学家安德烈-玛丽·安培在19世纪初提出的。
安培环路定理是基于麦克斯韦方程组中的一个方程,可以用来计算磁场的强度。
根据该定理,通过电流所形成的磁场的磁感应强度H,沿着任意封闭曲线所围成的面积S的总磁通量Φ,与该封闭曲线所围成的电流之间的关系为:
∮H·dl = ∫∫S B·dS = Φ
其中,H是磁场的强度,dl是沿着闭合曲线的微元路径元素,B是磁感应强度,dS是平面面元素,Φ是通过该曲线所围成的面积的磁通量。
安培环路定理本质上是一个积分方程,可以通过对曲线的路径和曲面的选择来灵活地应用。
根据闭合曲线的选择不同,可以得到更方便的计算磁场的方法。
通常情况下,选择封闭曲线为简单的几何形状,例如圆形、矩形或直线,可以大大简化计算的过程。
安培环路定理的应用广泛,可以用于解决与电流所产生的磁场相关的问题。
例如,在电磁铁中,可以利用安培环路定理计算铁芯的磁场分布;在电感器中,可以通过该定理计算电感量。
此外,还可以利用安培环路定理推导出其他电磁学中的重要定理,如磁场的叠加定理和比奥-萨伐尔定律等。
综上所述,安培环路定理是电磁学中的一条基本定理,描述了电流所产生的磁场的性质。
通过应用安培环路定理,可以方便地计算出磁场的强度和分布,解决各种与电流和磁场相关的问题,为电磁学的研究和应用提供了重要的理论基础。
环路定理_精品文档

环路定理环路定理是电路理论中最基本的定律之一。
它是电工学和电子学的基础,能够帮助我们理解电路中电流和电压的分布。
环路定理是基于基尔霍夫定律的,其中基尔霍夫定律提供了电流的守恒原理。
在本文中,我们将学习环路定理的概念、应用和实例。
环路定理也被称为基尔霍夫环路定律。
它规定了在一个封闭的回路中,电流总和为零。
这是因为电流在一个电路中是连续不断地流动的,它必须回到初始点,这样才能满足电流的守恒。
环路定理可以通过以下公式来表示:∑(V_n) = 0其中,∑(V_n)表示在回路中所有电压源的总和,如果电压源是正极连接到负极,则视为正电压。
环路定理的主要思想是电势差的总和必须为零。
环路定理的应用非常广泛。
它可以用于解决各种电路中的问题,包括电流分布、电压分布和电阻的计算。
此外,环路定理也可以用于设计电路中的电流源和电压源。
环路定理的一个典型应用是计算电路中的未知电流。
通过在回路上画出合适的方向,利用环路定理可以得到多个方程,通过这些方程可以求解未知电流的值。
这对于分析电路中的电流分布和电压分布非常有用。
另一个重要的应用是计算电路中的电压降。
通过在回路上选择不同的路径,可以得到多个环路方程。
这些方程可以用来计算电路中各个电阻上的电压降。
通过运用环路定理,我们可以简化计算过程,提高计算效率。
环路定理在实际应用中非常有用。
例如,在电路板的设计和制造中,我们需要考虑电流分布和电压分布,以确保电路的正常工作。
通过使用环路定理,我们可以更好地理解电路中电流和电压的分布情况,并进行相关的改进。
除了电路设计外,环路定理还在电力系统中扮演着重要角色。
在电力传输过程中,我们经常需要估算输电线路中的电阻和电压降,以确保电力的正常传输。
通过应用环路定理,我们可以预测电力传输中的潜在问题,并采取相应的措施来解决这些问题。
在实际的环境中,环路定理可能会受到一些限制。
例如,当电路中存在非线性元件(如二极管和晶体管)时,环路定理可能不适用。
安培环路定理

(1)管内:取L矩形回路 abcda
边在轴上,两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证,无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
安培环路定理与留数定理

安培环路定理与留数定理安培环路定理和留数定理是两个在不同数学领域中使用的定理,它们分别属于电磁学和复变函数论。
安培环路定理(Ampere's Circuital Law)是电磁学中的一个基本定理,它描述了稳恒磁场中磁感应强度B与产生该磁场的电流之间的关系。
定理指出,在一个稳恒磁场中,磁感应强度B沿着任何闭合路径的线积分,等于这个闭合路径所包围的所有电流的代数和乘以磁导率。
这个定理可以由毕奥-萨伐尔定律推导出来,它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。
留数定理(Residue Theorem)则是复变函数论中的一个重要定理,它描述了函数在一个闭合曲线上的积分与该曲线内部函数的奇点之间的关系。
定理指出,如果函数f(z)在一个闭合曲线C所围的区域内除了有限个孤立奇点外是解析的,那么函数f(z)沿着曲线C的积分等于2πi乘以函数在C内部所有孤立奇点的留数之和。
这个定理在复变函数论中有着广泛的应用,特别是在计算复变函数的积分和求解微分方程时。
虽然安培环路定理和留数定理在数学形式上具有一定的相似性,即都是将一个曲线上的积分转化为该曲线内部某种量的代数和,但它们的物理意义和应用领域是不同的。
安培环路定理是描述稳恒磁场中磁感应强度和电流之间的关系,而留数定理则是描述复变函数在闭合曲线上的积分与该函数在曲线内部奇点的关系。
尽管如此,有一些学者和研究人员试图将留数定理用于电磁学中的一些问题,例如通过构造合适的复磁场来推导安培环路定理。
这种尝试在一定程度上揭示了电磁学与复变函数论之间的内在联系,也为解决一些复杂的电磁学问题提供了新的思路和方法。
总的来说,安培环路定理和留数定理虽然都是数学和物理学中的重要定理,但它们的应用领域和物理意义是不同的。
安培环路定理主要用于描述稳恒磁场中磁感应强度和电流之间的关系,而留数定理则主要用于复变函数论中的积分和微分方程求解等问题。
尽管它们在数学形式上具有一定的相似性,但它们的本质和应用是不同的。
《安培环路定理》课件

安培环路定理的应用实例
应用实例
在复杂电路中,可以利用安培环路定理来计算磁场分布和电流之间的关系,从而确定电流的大小和方向,为电路设计和分析提供重要的理论支持。
总结词
安培环路定理在电路分析中具有重要应用,能够简化复杂电路的分析过程。
详细描述
在电路分析中,安培环路定理可以用来计算磁场分布和电流之间的关系,从而确定电流的大小和方向,为电路设计和分析提供重要的理论支持。
《安培环路定理》PPT课件
目录
CONTENTS
安培环路定理的概述安培环路定理的公式及推导安培环路定理的应用实例安培环路定理的深入思考习题与思考
安培环路定理的概述
安培环路定理是描述磁场与电流之间关系的物理定理。
安培环路定理表述为在磁感应线圈中,磁场与电流之间的关系满足闭合回路的定律,即磁场沿闭合回路的积分等于穿过该回路的电流代数和。
安培环路定理是麦克斯韦方程组中的一个组成部分,它描述了磁场与电流之间的关系。
随着科学技术的发展,安培环路定理的应用范围越来越广泛,特别是在新能源、新材料等领域中有着广泛的应用前景。
发展趋势
未来对于安培环路定理的研究将更加深入,需要进一步探索其在复杂电磁场问题中的应用,以及与其他物理场的相互作用机制。同时,也需要加强与其他学科的交叉研究,推动安培环路定理在各个领域中的应用和发展。
总结词
总结词
安培环路定理公式中的物理量包括磁感应强度B、电流I、半径r等。
详细描述
磁感应强度B是描述磁场强弱的物理量,其单位是特斯拉(T)。电流I是指穿过导体的电流大小,其单位是安培(A)。半径r是指环绕导线的圆心到导线之间的距离,其单位是米(m)。这些物理量在安培环路定理公式中具有特定的数学关系,反映了磁场与电流之间的相互作用。
简述安培环路定理

简述安培环路定理
安培环路定理,又称电流定律,是电子技术中重要的基本定理。
它是1745年由安培发现的。
它指出,任何完整封闭环路中,由电源或电容器提供的电势差总称为电势差V。
电流I在环路中以电导率γ流通,所以电流I可以用以下公式来表示:V=I x。
安培环路定理是一组电路定理,主要涉及电流、电压、电阻以及电势。
它是建立在电流流向定律(也称作Kirchhoff定律)的基础上的。
它是基于物理和电路学的几个事实和原理,由电流定律(也称作Kirchhoff定律)定义的。
安培环路定理中假定所有元件都是线性元件。
安培环路定理以及电流定律可以用于确定任何给定环路中穿过
它的电流及电压,从而形成电路的基本模型。
它可以用来解决复杂的电路,如多节点电路、三极管电路、反馈电路、脉冲电路、放大器等,它是电子技术中最重要的基本定理之一。
安培环路定理的另外一个重要的应用就是确定电路的性能参数。
比如,可以用它来确定电路的电阻、电容、电感以及参数等。
如果把它们结合起来,可以很快地计算出电路的稳定性、增益以及频率响应特性。
安培环路定理可以应用于不同理论,以及不同技术领域,比如电子技术、电路技术、数学理论等。
安培环路定理是电子技术中一个重要的基础,几乎所有的电子设计都会用到它。
总之,安培环路定理是一个重要的电子理论,它可以用于设计现
代电子设备。
它可以用来解决复杂的电路,并且可以确定电路的性能参数。
它也被广泛用于不同的理论和技术领域,所以它在现代电子技术中起到了重要的作用。
静电场的环路定理的数学表示式为

静电场的环路定理的数学表示式为
静电场的环路定理是物理学中一个重要的定理,它描述了电场的流动规律。
它
的数学表示式为:
∮E·dl=0
其中,E表示电场,dl表示电场的矢量,∮表示积分。
静电场的环路定理指出,在一个闭合的环路上,电场的矢量积分为零。
这意味着,在一个闭合的环路上,电场的矢量总和为零,也就是说,电场的流动是不变的,不会有任何变化。
静电场的环路定理可以用来解释电场的流动规律,也可以用来计算电场的大小。
它可以用来解决电场的问题,也可以用来计算电场的分布情况。
静电场的环路定理是物理学中一个重要的定理,它描述了电场的流动规律,并
且可以用来解决电场的问题。
它的数学表示式为∮E·dl=0,其中,E表示电场,
dl表示电场的矢量,∮表示积分。
它指出,在一个闭合的环路上,电场的矢量积
分为零,也就是说,电场的流动是不变的,不会有任何变化。
它可以用来解释电场的流动规律,也可以用来计算电场的大小,从而解决电场的问题。
环路定理的公式

环路定理的公式
1. 静电场环路定理。
- 公式:∮_L→E· d→l = 0。
- 含义:
- 在静电场中,电场强度→E沿任意闭合路径L的线积分等于零。
这表明静电场是保守场,电场力做功与路径无关,只与始末位置有关。
2. 安培环路定理(真空中稳恒磁场)
- 公式:∮_L→B· d→l=μ_0∑_i = 1^nI_i。
- 含义:
- 对于稳恒磁场,磁感应强度→B沿任意闭合路径L的线积分等于真空磁导率μ_0乘以穿过以该闭合路径为边界的任意曲面的电流的代数和∑_i = 1^nI_i。
这里电流的正负由右手螺旋定则确定,当电流方向与闭合路径的绕行方向符合右手螺旋关系时,电流取正,反之取负。
一般形式下的安培环路定理

安培环路定理,也被称为“安培法则”或“安培第一定律”,是电磁学中的基本定律之一,描述了电流在闭合回路中所产生的磁场。
一般形式下的安培环路定理可以表述为:
在任意闭合回路上沿着路径积分的磁场矢量B的总和等于该回路所包围的电流I的总和乘以真空中的常数μ₀。
数学表达式为:
∮B ·dl = μ₀* ΣI,
其中,
∮表示沿闭合回路的路径积分,
B 是磁感应强度的矢量,
dl 是路径元素的矢量微元,
μ₀是真空中的磁导率(μ₀≈4π×10⁻⁷N/A²),
ΣI 是通过闭合回路的电流总和。
这个定理说明了磁场是由电流所产生的,并且通过闭合回路的电流之间存在着相互作用。
根据安培环路定理,我们可以计算磁场的大小和方向,从而对电路中的电流和磁场进行分析和计算。
需要注意的是,安培环路定理仅适用于恒定电流情况下的稳态条件,不适用于变化的电流或非稳态情况。
在这些情况下,我们需要使用麦克斯韦方程组来描述电磁场的行为。
安培环路定理的推导与应用

安培环路定理的推导与应用安培环路定理是电磁学中的重要定律之一,它描述了电流在闭合回路中所围成的磁通量与电路中的总电流的关系。
本文将对安培环路定理的推导进行讲解,并介绍一些其在实际应用中的例子。
一、安培环路定理的推导安培环路定理是由法国物理学家安培在19世纪初提出的。
它的数学表达形式是:∮B·dl = μ0·I其中,∮B·dl表示磁场B在闭合回路上的环路积分,μ0为真空中的磁导率,I为该回路中的总电流。
推导安培环路定理的基本思路是利用法拉第电磁感应定律和高斯定理。
我们知道,根据法拉第电磁感应定律,磁感应强度B的变化率与电场强度E的闭合回路积分之比等于贯穿该回路的总电流I:∮(B·dl)/(dt) = -∫E·ds = -dΦE/dt其中,ΦE表示电场的通量。
再根据高斯定理,可以将闭合回路上的磁场积分转化为磁通量的二重积分:∮B·dl = ∬(∇×B)·dS结合以上两个式子,可得到安培环路定理的数学表达式:∬(∇×B)·dS = -μ0·dΦE/dt = -μ0·d/dt(∬E·dS)经过进一步的推导和化简,可以得到安培环路定理的最终形式。
二、安培环路定理的应用安培环路定理可以应用于各种电磁场问题的求解中,下面将介绍几个实际应用的例子。
1. 电磁铁电磁铁是一种利用电流通过线圈时产生的磁场吸引铁磁物质的装置。
根据安培环路定理,可以计算电磁铁中磁场的分布情况,从而设计合适的线圈参数,使得电磁铁的吸引力能够满足实际需求。
2. 变压器变压器是一种利用电磁感应原理来改变电压的装置。
在变压器的设计和工作过程中,安培环路定理可以用来分析和计算铁芯中的磁场分布情况,从而确定绕组的布置和匝数比。
3. 电感电感是电路中常见的一种元件,它的基本单位是亨利(Henry)。
利用安培环路定理,可以计算电感器中的磁场分布情况,从而更好地理解和分析电感元件的特性。
环路定理

∫ B dl = ∑I
L 0 L内
i
∫ B dl = ∑I
L 0
内
几点说明: 几点说明:
1)B是L上dl处的磁感应强度,是由空间所 ) 是 上 处的磁感应强度 处的磁感应强度, 有电流共同产生叠加的结果. 有电流共同产生叠加的结果. 2)I内是被 所包围的电流,∑I内则是 所包 ) 是被L所包围的电流 所包围的电流, 则是L所包 围的电流代数和. 围的电流代数和. 3)定理揭示了真空中B的环流只跟被包围的 )定理揭示了真空中 的环流只跟被包围的 电流代数和有关,没有被L所包围的电流对 所包围的电流对B 电流代数和有关,没有被 所包围的电流对 的环流没有贡献. 的环流没有贡献. 4)∫LB d l ≠ o 说明为非保守场 也称涡旋场 . ) 说明为非保守场(也称涡旋场 也称涡旋场). 5)学习时注意与电场的高斯定理进行比较. )学习时注意与电场的高斯定理进行比较.
× × × × ×
×
×
×
R1 R2 解:分析磁场分布: 分析磁场分布: 已知:R1,R2匝数N 已知: 匝数 电流I 电流
作半径为r的安培环路 作半径为 的安培环路L 的安培环路
π 当 R R << r 取圆周的平均值代替 2 r 2 1
R +R 2 L =2 π 1 平 2 0NI N B= = 0nI n = L L 平 平
R r L
1)作半径为 r (R ≤ r < ∞) ) 的安培环路L 的安培环路L
r
R
也是以中心 轴线为对称 的分布. 的分布.
∫ B dl = ∑I = I ∫ B dl = ∫ Bcos0 dl = I B∫ dl =B2πr = I I
BC
10、环路定理N

r
r
I
在导线外是以中心轴为对称的磁场
在载流导体内: I
r
R
也是以中心轴线为 对称的分布。
作安培环路ABCDA
3、螺绕环(罗兰环)的磁场分布
R1
rR
2
解:分析磁场分布:
R1 R2 已知:R1、R2匝数N 电流I
作半径为r的安培环路L
R
O
R
P
B
假若磁场不 平行轴线。
O P
R
B
以OO’为轴 旋转180度;
O’ 即电流分布相同 R B 但磁场方向却不 同?
L
当 R2 R1 r 取圆周的平均值代替 2r
磁场的分布为:
例4:有一导体,由“无限多”根平行排列的细导 线组成,每根导线都“无限长”且均通以电流 I 。 设单位长度上的导线数目为n,求证:这无限长 的电流片各处的磁感应强度:B 1 0 nI
证明: 分析磁场分布:
一、何谓安培环路定理
二、无限长载流直导线周围磁场的环流
安培环路定理: 磁感应强度沿任一闭合路径L的线积分(B的环 流)பைடு நூலகம்于穿过这个环路所有电流强度的代数和 的 0 倍。
B d l I 0 i
环路定理_电势
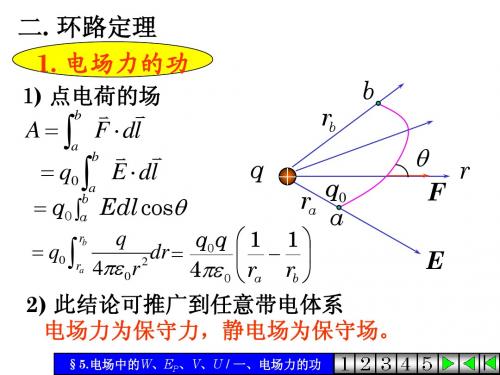
等势面、 与 的微分关系 §5.等势面、E与U的微分关系 / 二、等势面性质 等势面
3) 场强与电势的微分关系
v v U a − U b = −dU = E ⋅ d l v v −dU = E ⋅ dl = Ex dx + E y dy + Ez dz
∂U ∂U ∂U Ey = − Ez = − Ex = − ∂y ∂x ∂z U + dU v ∂U v ∂U v ∂U v E = −( i+ j+ k) U ∂x ∂y ∂z
a
电荷在点电荷场中的电势能( 电荷在点电荷场中的电势能(选无穷远 为零势能点) 为零势能点) q0 q 电势能是标量 标量, 电势能是标量 W= 电势能是属于系统的. 4πε 0 r 电势能是属于系统的
电场中的W、 §5.电场中的 、EP、V、U / 三、电势能 电场中的 、
4. 电势差和电势
电势差
电场中的W、 §5.电场中的 、EP、V、U / 一、电场力的功 电场中的 、
2. 环路定理
1) 定理表述 静电场中电场强度沿任意闭合路径的线 积分等于零。 积分等于零。
∫
L
v v E ⋅ dl = 0
高斯定理说明静电场是有源场 高斯定理说明静电场是有源场, 环路定理说 有源场 明静电场是保守力场 无旋场。 保守力场或 明静电场是保守力场或无旋场。
R2 r R2 r
R2
2
∞ R2
q1
− q2
o R1 III II I
=∫
r
∞
q1 − q2 +∫ dr 2 R2 4πε r 0
4πε 0r
q1
2
dr
R2
高斯面
1 q1 1 q2 = − 4πε 0 r 4πε 0 R2
磁场的安培环路定理及其应用

B
0 Ir
2R2
(r
R)
可作出B的值随r的变化曲线,如 右图所示。
2.长直载流螺线管的磁场
【例8-7】设无限长载流直螺线管的缠绕密度(即单位长度 上的线圈匝数)为n,通有电流I,求该螺线管内的磁场。
【解】由电流分布的对称性可知,螺线管内的磁感应线是平
行轴线的直线,方向沿电流的右手螺旋方向,而且在同一磁感应
L B dl B ab
穿过矩形回路abcda的线圈匝数为 nab,通过每匝线圈的电
流为I,所以穿过回路的电流总和为 nI ab,于是由安培环路定理 得
所以
Bab 0nI ab
B 0nI
从上式可以看出:磁感应线B的大小与环形回路ab边在管内 的位置无关,表明无限长载流直螺线管的磁场是均匀的磁场。
可得
L B dl B 2r 0I
B 0I (r R)
2r
当r<R时,根据安培环路定理有
L B dl B 2r 0 L内 Ii
由于在圆柱体内电流密度是均匀的,即电流密度为j=I/πR2 通过截面积πr2的电流为
于是有
L内
Ii
jr 2
Ir 2 R2
可得
B L
dl
B
2r
0
L内
Ii
0
Ir 2 R2
线上B的大小处处相等。管外的磁场很弱,可以忽略不计。
过管内任意场点作如右图所示 矩形回路abcda,在回路的cd段上 以及bc和da段的管外部分,均有B =0,在bc和da段的管内部分,B与 dl相互垂直,即B·dl=0,回路的ab 段上各点B的大小相等,方向与dl 一致,所以沿闭合路径abcda上B的 环流为
综上所述,我们知道应用安培环路定理可以计算某些对称 分布电流的磁感应强度,下表所示为几种常用的对称分布电流 的磁感应强度计算式。
安培环路定理右手螺旋法则

安培环路定理右手螺旋法则
安培环路定理右手螺旋法则也被称为安培定则,是表示电流和电流激发磁场的磁感线方向间关系的定则。
具体来说,有以下三种情形:
- 通电直导线中的安培定则(安培定则一):用右手握住通电直导线,让大拇指指向电流的方向,那么四指指向就是磁感线的环绕方向。
- 通电螺线管中的安培定则(安培定则二):用右手握住通电螺线管,让四指指向电流的方向,那么大拇指所指的那一端是通电螺线管的N极。
- 判断环形电流的磁场方向的安培定则:让右手弯曲的四指与环形电流的方向一致,伸直的拇指所指的方向就是环形导线轴线上磁感线的方向。
安培环路定理右手螺旋法则在电磁学中应用广泛,是理解电磁现象的基础。
环路定理

解:
a
r P
x
U=
q 4 0 x2 +a2 πε
x
dU qx E = Ex = − = 2 2 32 dx 4 0(x +a ) πε
U(x, y, z) =C
• 常用一组等势面描述静电场,并规定相邻两等势面之间的 常用一组等势面描述静电场, 电势差相等。 电势差相等。
点电荷的电场线与等势面
+
电偶极子的电场线与等势面
+ +
+ +
+
+
+
+场线的关系: 等势面与电场线的关系: (a) 等势面与电场线处处正交; 等势面与电场线处处正交; 电场线指向电势降低的方向; (b) 电场线指向电势降低的方向; (c) 等势面和电场线密集处场强量值大,稀疏处场强量值小。 等势面和电场线密集处场强量值大,稀疏处场强量值小。
q
r
a
r+dr r dl θ r q0 E
结论:在点电荷电场中, 结论:在点电荷电场中,电场力所作的功只与试验电荷始末 位置有关,而与试验电荷运动路径无关。 位置有关,而与试验电荷运动路径无关。
(2)在任意电荷系的电场中: 在任意电荷系的电场中:
r v E = ∑Ei
r r v r v r A= q0 ∫ E⋅ dl = q0 ∫ ∑E ⋅ dl = ∑ 0 ∫ E ⋅ dl = ∑A q i i i
例2、 均匀带电圆板,半径为 R ,电荷面密度为 σ 。求轴线上 均匀带电圆板, 电势。 任一点 P 的电势。 解: dU =
dq 4 0 x +r πε
2 2
dr r
R P
dq =σ2π rdr
安培环路定理

11.6.1 安培环路定理 11.6.2 安培环路定理的应用
一、安培环路定理
在真空中的稳恒电流磁场中,磁感应强度B 沿任意
闭合曲线的线积分(也称B 的环流),等于穿过该积分
回路的所有电流强度的代数和的 倍0 。
B dl 0I 与环路成右旋关系的电流取正
L
例:
I4
B dl μ0(I1 I2 2I3)
解 (1) 导体中的电流密度为
J I π (a2 b2)
a
B1
J
B2 b O M O
dJ
利用补偿法
半径为a的实心圆柱体在M点产生的磁感强度为B1,半 径为b的实心圆柱体在M点产生的磁感强度为B2,其上 通过的电流方向相反,电流密度相同。
磁感强度用安培环路定理计算
r
设M点到O点的距离为r,
B1 dl B1 2πr 0πr2J
3)计算
I i
4)由
B dl
L
0
I 求B i
1:“无限长”载流圆柱导体内外磁场的分布 已知:I 、R,电流沿轴向在截面上均匀分布
电流及其产生的磁场具有轴对称分布
I
作积分回路如图
R
r R
则B沿该闭合回路的环流为:
B dl Bdl 2πrB
l
l
根据安培环路定理:
B
dl
μ 0
I
l
则:B
B1
μ0 Jr 2
a
B1
J
B2 b O M O
dJ
B2 dl B2 2π(d r) 0π(d r)2 J
B2
μ0 J(d 2
r)
M点磁感强度为 B = B1+B2
静电场的环路定理数学表达式

环路定理,又称电路定理,是古典电学中和静电学中一种基本定理。
它指出,通过任何一个回路的电势差,等于那个回路上所有电压源之和,减去所有电阻电压降的结果。
环路定理的数学表达式为:
U = Σ
E − ΣV
其中,U表示回路中任意一点间的电势差,ΣE是表示电路中电源的电势和,而ΣV则表示电路中所有电阻电压降之和。
环路定理可以让我们更有效地了解和分析电路,因此被广泛应用于电子学中。
环路定理描述了电路中特定电势点处的电势,即该点处的总电势就是所有电势源的总和减去所有电阻的电压降的总和。
环路定理的数学表达式可以用来求解任意多个任意形状的电路中任意一点间的电势。
例如,在一个由十个恒定电阻组成的电路中,若电阻1至电阻8间的电势上升了4V,电阻2至电阻8间的电势降低了2V,则用环路定理可获得该环路的总电势U不变,270V不变。
环路定理的应用也广泛,几乎可以用来分析任何类型的电路,甚至包括以太网电路系统、静电绝缘体电场等。
总之,环路定理是一种基本的古典电学定理,它的数学表达式 U =
Σ
E − ΣV 能够帮助我们求解任意形状电路中任意一点间的电势差,其应用范围也极为广泛。
因此,环路定理以及它的数学表达式,对于我们正确理解和分析电路非常重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E U(gradU)
i j k x y z
矢量微分算符
直角坐标系表示
• E总是沿着指向电势减少的方向——E与Δn相反 • 在数学场论中把
U : 称作梯度
A: A:
称作散度 称作旋度
静电场的基本方程的微分形式
• 数学场论公式
A dS AdV 面积分 体积分
S
V
A dl ( A) dS 线积分 面积分
– 电场力做正功,电势能将减少 – 电场力做负功,电势能将增加
电势的定义
0 电场付出能量,能量减少
APQ WPQ
( 电 势 能 的 减 少,与 场 源 和q0均 有 关
0 电场吸收能量,能量增加
• 从中扣除q0,即引入电势
WPQ
q0
APQ q0
UPQ
Q
E dl
P
P、Q两点之间的电势差定义为
于静电场力沿任意闭合回路做功
恒等于零
Edl 0
在任意电场中取一闭合回路,将试探电荷沿路径
L从 p——Q——P,电场力所做的功为
Q
P
A q0
E dl q0
P(
E
L1 )
d
l
q0
E dl
Q( L2 )
L
Q
Q
q0
E
p(L1 )
dl
q0
E dl 0
p(L2 )
Edl 0
讨论
电场强度和电势
• 已知场强 • 已知电势
可求电势 可否求场强?
等势面
等势面与电力线处处正交 证明:设一试探电荷q0沿任意一个等势面作一任意元
位移dl电场力所做的元功
dA q0 E dl q0Edlcos 0 cos 0
E dl
2
– 等势面密集处场强大,稀疏处场强小
– 证明:设:电场中任意两个相邻等势面之间的电势差 为一定的值,按这一规定画出等势面图(见图),以 点电荷为例,其电势为
Q
Q
F cosdl Fdr
P
P
rQ Fdr qq0
rP '
4 0
rQ dr r rP' 2
APQ
qq0
4 0
rQ dr r rP ' 2
qq0
4 0
1 rp'
1 rQ
q0
rQ E(r)dr
rP '
静电场力做功只与起点终点有关,与路径无关
点电荷组产生的场
q1, q2 , , qn
E E1 E2 En
从P点到Q点移动单位正电荷时电场力所作的功
单位正电荷的电势能差
空间某点的电势值
• 为了确定某点的值,还需要选择零点
• 一般选择无穷远为势能零点,P点电势值为
U ( p) U P
AP q0
E dl
P
两点之间电势差可表为两点电势值之差
Q
Q
UPQ
Edl
P
Edl
P
E dl U (P) U (Q)
静电场的基本
若=0 2U=0 拉普拉斯方程
微分方程
例1.利用场强与电势梯度的关系, 计算均匀带电 细圆环轴线上一点的场强。
解:
u u(x) 1
q
40 R2 x2
u 1
q
Ex
x
x
(
4 0
) R2 x2
1
qx
4 0 (R2 x2 ) 32
Ey Ez 0
rr E Exi
1
4 0
U (r) 1 q
4 0 r
微分
dU (r)
1
4 0
q r2
dr
因为相邻等势面电势差为一定值,所以有
dr r , dU U
r 4 0 r 2 U
q
半径之差∝r2
定值
而
E
1 r2
r 越 大 r 2越 大,等 势面 间 距越 大,越 稀,E越 小
r 越 小 r 2越 小,等 势面 间 距越 小,越 密,E越 大
(
dq ) rP
1
4 0
dq rP
讨论
• 电势与场强一样是一个描述场本身性质的物理量, 与试探电荷无关,是标量。电势叠加是标量叠加。
• 电势UP:P与无穷处电势差 • 电势零点 选取
– 可以任意选取,两点间的电势差与电势零点选择无关。 – 对有限大小的带电体,一般选择无穷远为电势零点
• 问题
– 选无穷远为零点, 总是合适么?
qx r (R2 x2)32 i
例2.计算电偶极子电场中任一点的场强
解:
u
u(x,
y)
1
4 0
(x2
px y2)32
Ex
u x
x
(
1
4 0
(x2
px y2)32
)
Ey
u y
( y
1
4 0
(x2
px y2)32
)
B点(x=0) A点(y=0)
r E
p
4 0 y3
r i
r E
p
20 x3
B r r RB E • dl
q
dr q ( 1 1 )
A
RA 40r2
40 RA RB
2.如图已知+q 、-q、R
①求单位正电荷沿odc 移至c ,电场力所作的功
a Aoc
uo
uc
0
(q
4 0 3R
q )
4 0 R
d
b
c
q
q 0 q
6 0 R
RRR
② 将单位负电荷由
O电场力所作的功
AO u uo 0
Y
上的电势分布。 已知:R、q
解:方法一 微元法
dl
r
Z
R
OxP• Xd来自 dq4 0r
dl 4 0r
方法二 定义法 由电场强度的分布
qx
2R dl 2R
uP
du
0 4 0r 4 0r
E 4 0 ( x2 R2 )32
qxdx
q
u
Edx
xp
xp4 0 ( x 2
R2
3
)2
4 0 R2 x 2
r i
q
•
y
•B
r
O
l
l
•
q
A
•
x
§4 环路定理
静电场力做功与路径无关
• 电荷间的作用力是有心力 ——环路定理 • 讨论静电场的环流
流速场的环流
0 有旋
v dl 0 无旋
静电场:电力线不闭合
Edl 0
可以猜到静电场的环流为零
证明
• 单个点电荷产生的场
– 把试探电荷q0从P移到Q
APQ
Q
F dl
P
单位:1V(伏特)=1J/C
电势叠加原理
• 点电荷组有
Ui
1
4 0
qi ri
UP
Edl
P
P E1 dl
P E2 dl
P Ek dl
U P1 U P2 U Pk U pi
i
连续带电体有
UP P E dl dU
dU 1
40
P
drq2 dr
1
4 0
• 在证明Gauss定理中,说电力必须与r2成反比,那 么 在 环 路 定 理 的 证 明 中 是 否 也 必 须 要 求 与 r2 成 反 比?
• 答:不一定 如弹性力 f kr 也有类似性质
哪些力具有做功与路径无关这种性质?
引力 重力
引入引力势能 引入重力势能
势函数
弹性力 静电力
引入弹性势能 引入静电势能
每项均与路径无关,只与位置有关
任意有限大的带电体产生的电场
• 可以将带电体无限分割成微元,每一个 微元均为一点电荷 ——点电荷组
• 结论:在任何电场中移动试探电荷时, 电场力所做的功除了与电场本身有关外, 只与试探电荷的大小及其起点、终点有 关,与移动电荷所走过的路径无关
静电场的环路定理
• 静电场力做功与路径无关 等价
q2
u 4 q1 28.8102V
4 0 r
O
r
q4
q3
②将 q0 1.0109 c 从 0 电场力所作的功
A0 q0 (u u0 ) q0 (0 28.8102 ) 28.8107 J
③求该过程中电势能的改变
A0 W W0 28.8107 0 电势能
例2、求均匀带电圆环轴线
电势计算的两种方法:
根据已知的场强分布,按定义计算
r r
uP E • dl P
由点电荷电势公式,利用电势叠加原理计算
u
ui
qi
4 0 ri
u
du
dq
4 0r
例1 、求电偶极子电场中任一点P的电势
由叠加原理
Y
uP
u1
u2
q
4 0 r1
q
4 0 r2
q(r2 r1)
4 0 r1r2
• 在电场中把试探电荷从P移至Q电场力所做的功
Q
Q
APQ
P
F dl
q0
q0 Q P E1
E dl P Q dl
P
E2
dl
Q P
En
dl
q0
4
0
q1 rp1
q1 rQ1
q2 rp 2
q2 rQ 2
qn rpn
qn rQn
P到 q1 的距离
Q到q1的 距离
电势梯度
