解析几何知识点总结复习题
解析几何重点题型归纳

解析几何重点题型归纳1、设函数3()32f x x x =-++分别在12x x 、处取得极小值、极大值.xoy 平面上点A B 、的坐标分别为11()x f x (,)、22()x f x (,),该平面上动点P 满足•4PA PB =u u u r u u u r,点Q 是点P 关于直线2(4)y x =-的对称点.求 (I)求点A B 、的坐标; (II)求动点Q 的轨迹方程.2、在直角坐标系xOy 中,以O 为圆心的圆与直线43=-y x 相切. (Ⅰ)求圆O 的方程;(Ⅱ)圆O 与x 轴相交于A 、B 两点,圆内的动点P 使|PA |、|PO |、|PB | 成等比数列,求、的取值范围.3、已知,点在轴上,点在轴的正半轴,点在直线上,且满足,. (Ⅰ)当点在轴上移动时,求动点的轨迹方程;(Ⅱ)过的直线与轨迹交于、两点,又过、作轨迹的切线、,当,求直线的方程.4、已知抛物线C :22x py=()0p >的焦点为F ,A 、B 是抛物线C 上异于坐标原点O 的不同两点,抛物线C 在点A 、B 处的切线分别为1l 、2l ,且12l l ⊥,1l 与2l 相交于点D . (1) 求点D 的纵坐标; (2) 证明:A 、B 、F 三点共线;(3) 假设点D 的坐标为3,12⎛⎫- ⎪⎝⎭,问是否存在经过A 、B 两点且与1l 、2l 都相切的圆, 若存在,求出该圆的方程;若不存在,请说明理由.5、 已知椭圆2222:1(0)x y C a b a b +=>>,过右焦点F 的直线l 与C 相交于A 、B 两点,当l 的斜率为1时,坐标原点O 到l(I )求a ,b 的值;(II )C 上是否存在点P ,使得当l 绕F 转到某一位置时,有OP OA OB =+u u u r u u u r u u u r成立?若存在,求出所有的P 的坐标与l 的方程;若不存在,说明理由。
6、双曲线的中心为原点O ,焦点在x 轴上,两条渐近线分别为12l l ,,经过右焦点F 垂直于1l 的直线分别交12l l ,于A B ,两点.已知OA AB OB u u u r u u u r u u u r 、、成等差数列,且BF u u u r 与FA u u u r同向.(Ⅰ)求双曲线的离心率;(Ⅱ)设AB 被双曲线所截得的线段的长为4,求双曲线的方程.7、设椭圆中心在坐标原点,(20)(01)A B ,,,是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点.(Ⅰ)若6ED DF =u u u r u u u r,求k 的值; (Ⅱ)求四边形AEBF 面积的最大值.8、如图,已知抛物线2:E y x =与圆222:(4)(0)M x y r r -+=>相交于A 、B 、C 、D 四个点。
解析几何知识点总结复习

一、直线与方程基础:1、直线的倾斜角α: [0,)απ∈2、直线的斜率k : 2121tan y y k x x α-==-; 注意:倾斜角为90°的直线的斜率不存在。
3、直线方程的五种形式:①点斜式:00()y y k x x -=-;②斜截式:y kx b =+;③一般式:0Ax By C ++=;④截距式:1x y a b+=; ⑤两点式:121121y y y y x x x x --=-- 注意:各种形式的直线方程所能表示和不能表示的直线。
4、两直线平行与垂直的充要条件:1111:0l A x B y C ++=,2222:0l A x B y C ++=,1l ∥2l 12211221A B A B C B C B =⎧⇔⎨≠⎩;1212120l l A A B B ⊥⇔+= .5、相关公式:①两点距离公式:11(,)M x y ,22(,)N x y ,MN =②中点坐标公式:11(,)M x y ,22(,)N x y ,则线段MN 的中点1122(,)22x y x y P ++; ③点到直线距离公式: 00(,)P x y ,:0l Ax By C ++=,则点P 到直线l的距离d =;④两平行直线间的距离公式:11:0l Ax By C ++=,22:0l Ax By C ++=,则平行直线1l 与2l之间的距离d =⑤到角公式:(补充)直线1111:0l A x B y C ++=到直线2222:0l A x B y C ++=的角为θ,(0,)(,)22ππθπ∈,则2112tan 1k k k k θ-=+⋅ .(两倾斜角差的正切) 二、直线与圆,圆与圆基础:1、圆的标准方程:222()()x a y b r -+-=;确定圆的两个要素:圆心(,)C a b ,半径r ;2、圆的一般方程:220x y Dx Ey F ++++=,(2240D E F +->);3、点00(,)P x y 与圆222:()()C x a y b r -+-=的位置关系:点00(,)P x y 在圆内⇔ 22200()()x a y b r -+-<;点00(,)P x y 在圆上⇔ 22200()()x a y b r -+-=;点00(,)P x y 在圆外⇔ 22200()()x a y b r -+->;4、直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=的位置关系:从几何角度看:令圆心(,)C a b 到直线:0l Ax By C ++=的距离为d ,相离⇔d r >;相切⇔=d r ;相交⇔0d r ≤<;若直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=相交于两点M ,N ,则弦长MN =从代数角度看:联立:0l Ax By C ++=与圆222:()()C x a y b r -+-=,消去y (或x )得一元二次方程,24b ac ∆=-,相离⇔0∆<;相切⇔0∆=;相交⇔0∆>;相交时的弦长1212MN x x y y =-=- . 5、圆与圆的位置关系: 相离,外切,相交,内切,内含 .圆2221111:()()O x x y y r -+-=;圆2222222:()()O x x y y r -+-=, 根据这三个量之间的大小关系来确定:12r r -,12O O ,12rr +; 相离⇔1212O O r r >+;外切⇔1212O O r r =+;相交⇔121212r r O O r r -<<+;内切⇔1212O O r r =-;内含⇔12120O O r r ≤<-;6、两圆2221111:()()O x x y y r -+-=①;圆2222222:()()O x x y y r -+-=②若相交,则相交弦所在的直线方程的求法:交轨法: ①式-②式,整理化简即可得到相交弦所在直线方程 .三、椭圆:1、(第一)定义:12122PF PF a F F +=>;2、椭圆标准方程及离心率:焦点在x 轴上的椭圆标准方程为:22221(0)x y a b a b+=>>; :a 长半轴;b :短半轴;:c 半焦距 .椭圆中a ,b ,c 的关系:222a b c =+;椭圆的离心率(0,1)c e a=∈ . 3、弦长公式: 直线:l y kx b =+与椭圆2222:1()x y C m n m n+=≠交于两点11(,)M x y ,22(,)N x y ,则相交时的弦长1212MN x x y y =-=- . 弦长公式是由两点距离公式与两点斜率公式推导出来,故适用性比较广。
解析几何复习题-数学试题

解析几何复习题-数学试题(一)选择题1、从点P(m, 3)向圆(x + 2)2 + (y +2)2 = 1引切线, 则一条切线长的最小值为A.B.5 C.D.2、若曲线x2-y2 = a2与(x-1)2 + y2 = 1恰有三个不同的公共点, 则a的值为A.-1 B.0 C.1 D.不存在3、曲线有一条准线的方程是x = 9, 则a的值为A.B.C.D.4、参数方程所表示的曲线是A.椭圆的一部分B.双曲线的一部分C.抛物线的一部分, 且过点D.抛物线的一部分, 且过点5、过点(2, 3)作直线l, 使l与双曲线恰有一个公共点, 这样的直线l共有A.一条B.二条C.三条D.四条6、定义离心率为的椭圆为“优美椭圆”, 设(a > b > 0)为“优美椭圆”, F、A分别是它的左焦点和右顶点, B是它的短轴的一个端点, 则ÐABF为A.60° B.75° C.90° D.120°7、在圆x2 + y2 = 5x内, 过点有n条弦的长度成等差数列, 最小弦长为数列的首项a, 最大弦长为an, 若公差, 则n的取值集合为A.B.C.D.8、直线与圆x2 + y2 = 1在第一象限内有两个不同的交点, 则m的取值范围是A.1 < m < 2 B.C.D.9、极坐标方程表示的曲线是A.椭圆B.抛物线C.圆D.双曲线10、设a, b, c是ABC中ÐA, ÐB, ÐC所对边的边长, 则直线sinA·x + ay + c = 0与bx-sinB·y + sinC = 0的位置关系是A.平行B.重合C.垂直D.相交但不垂直(二)填空题11、有下列命题:(1)到两个定点的距离的和等于常数的点的轨迹是椭圆;(2)到两个定点的距离的和等于差的绝对值为常数的点的轨迹为双曲线;(3)到定直线和定点F(-c, 0)的距离之比为(c > a > 0)的点的轨迹为双曲线;(4)到定点。
解析几何知识点复习

1、直线的倾斜角是直线向上方向与x 轴正方向所成的角,当直线是x 轴或与x 轴平行时,直线的倾斜角是0°,直线倾斜角的范围是),0[π.当直线与x 轴不垂直时,倾斜角的正切值称为直线的斜率. [举例]已知直线1l 的斜率是33,直线2l 过坐标原点且倾斜角是1l 倾斜角的两倍,求直线2l 的方程.2、若直线的倾斜角为α,直线的斜率为k ,则α与k 的关系是:tan ,[0,)(,)222k ππααππα⎧∈⎪⎪=⎨⎪⎪⎩ 不存在,=; arctan ,0arctan ,0k k k k απ≥⎧⎨+<⎩=. [举例]已知直线l 的方程为)0(,0≠=++ab c by ax 且l 不经过第二象限,求直线l 的倾斜角的大小 (用含,a b 的反三角形式表示)*截距式1=+ba ,在x 轴y 轴上的截距分别为b a ,与坐标轴不平行且不过坐标原点.这种形式虽不是最主要的,但特别注意的是当直线过坐标原点(不是坐标轴)时,直线在两坐标轴上的截距也相等,直线在两坐标轴上的截距相等,则此直线的斜率为-1,或此直线过原点.[举例]与圆1)2()1(22=-+-y x 相切,且在两坐标轴上截距相等的直线有――( )A 、2条;B 、3条;C 、4条;D 、5条.4、求直线的方程时要特别注意直线的斜率是否存在的情况,不确定时要注意分类讨论,漏解肯定是斜率不存在的情况.要明确解析几何是“用代数方法解决几何问题”的道理,所以做解析几何问题不要“忘形”. [举例]过点)3,2(P 与坐标原点距离为2的直线方程是___________.5、两直线位置关系讨论的主要依据是两直线的斜率,要注意斜率不存在时的情况.掌握点到直线的距离公式、两平行直线之间的距离公式、两直线的夹角公式.由一般式方程判断两直线之间的关系:直线1l :11111,(,0B A C y B x A =++不全为0)、2l :0222=++C y B x A ,(22,B A 不全为0).则21//l l 的充要条件是01221=-B A B A 且1221C A C A -与-21C B 12C B 至少有一个不为零;21l l ⊥的充要条件是02121=+B B A A ;1l 与2l 相交的充要条件是01221≠-B A B A .[举例1]直线21,l l 斜率相等是21//l l 的――――――――――――――――――( ) A 、充分不必要条件;B 、必要不充分条件;C 、充要条件;D 、既不充分又不必要条件.[举例2]直线l 过点)3,2(P 与以)3,1(),2,3(--B A 为端点的线段AB 有公共点,则直线l 倾斜角的取值范围是_________.6、点A 、B 关于直线l 对称即l 是线段AB 的垂直平分线,垂直是斜率关系,平分说明AB 的中点在l 上.特别注意:当对称轴所在直线的斜率为1或-1时,对称点的坐标可用代入的方法求得.即点),(00y x 关于直线0=++c y x 的对称点是),(00c x c y ----;点),(00y x 关于直线0=+-c y x 的对称点是),(00c x c y +-.[举例1]将一张画有直角坐标系的图纸折叠使点)0,2(A 与点(0,6)B 重合,若点)0,3(C 与点D 重合,则点D 的坐标为_____;[举例2]抛物线C 1:x y 22=关于直线02=+-y x 对称的抛物线为C 2,则C 2的焦点坐标为______.7、直线与圆的位置关系的判断主要是利用点(圆心)到直线的距离来判断.设圆C 的半径是r ,圆心到直线L 的距离是d ,当r d >时,直线L 与圆C 相离;当r d =时,直线L 与圆C 相切;当r d <时,直线L 与圆C 相交.求直线被圆所截的弦长可用圆半径、弦心距、弦长一半组成直角三角形来求解. [举例1]已知点),(b a 是圆222r y x =+外的一点,则直线2r by ax =+与圆的位置关系是[举例2]若圆O :222r y x =+上有且只有两点到直线01543:=-+y x l 的距离为2,则圆的半径r 的取值范围是__________.8、确定圆的方程可以利用圆的标准方程222)()(r b y a x =-+-,即确定圆心坐标与半径;也可以利用圆的一般方程022=++++F Ey Dx y x ,即确定系数D 、E 、F.要注意的是方程022=++++F Ey Dx y x 表示圆的充要条件是0422>-+F E D .确定一个圆的方程需要三个互相独立的条件(因为标准方程与一般方程中都三个待定的系数).[举例1]二次方程022=+++++F Ey Dx Cy Bxy Ax 表示圆的充要条件是_____;[举例2]圆C 被y 轴截得的弦长是2,被x 轴分成的两段弧长之比为3:1,求圆心C 的轨迹方程.9、掌握圆的基本特征:圆上任意两点的垂直平分线是圆的直径所在的直线;直线平分圆的充要条件是此直线一定过该圆的圆心;与两定点连线所成角为直角的动点的轨迹是以定线段为直径的圆(或圆弧)等. [举例1]直线l 过定点)0,4(M 与圆422=+y x 交于A 、B 两点,则弦AB 中点N 的轨迹方程为_____________;[举例2]直线l 过定点)0,4(M 与圆422=+y x 交于A 、B 两点,O 是坐标原点,则△AOB 面积的 最大值为_______;[举例3]已知A 是圆064222=-+-+y ax y x 上任意一点,点A 关于直线012=++y x 的对称点也在圆上,那么实数a 的值为_____.10、两圆之间的位置关系的判断主要是利用两圆的半径的差或和与两圆的圆心距之间的大小关系.设圆A 的半径为1r ,圆B 的半径为2r (不妨设21r r >),则有:(1)21||r r AB +>,两圆外离;(2)21||r r AB +=,则两圆外切;(3)2121||r r AB r r +<<-,则两圆相交;(4)21||r r AB -=,则两圆内切;(5)21||r r AB -<,则两圆内含.关注:两圆的位置关系也可以由两圆的公切线的条数上来分.[举例1]已知动圆C 与定圆M :1)2(22=+-y x 相切,且与y 轴相切,求圆心C 的轨迹方程;[举例2]已知)3,0(M ,一动圆I 过点M 与圆N :16)3(22=++y x 内切. (1)求动圆圆心I 的轨迹C 的方程;(2)经过点(2,0)Q 作直线l 交曲线C 于A 、B 两点,设+=,当四边形OAPB 的面积 最大时,求直线l 的方程. 11、椭圆的定义中要注意隐含的条件:定值大于两定点之间的距离.掌握椭圆基本量之间的关系,分清长轴、短轴、焦距、半长轴、半短轴、半焦距.椭圆最基本的几何性质是定义的逆用:“椭圆上任意一点到两焦点的距离之和等于长轴的长”.[举例1]已知复数z 满足4|2||2|=++-i z i z ,则z 对应点的轨迹是_______;[举例2]设P 是以21,F F 为焦点的椭圆)0(12222>>=+b a by a x 上的一点,若点P 满足:121210,tan 2PF PF PF F ⋅=∠= ,则椭圆的焦距与长轴的比值为―――――――――( )A 、21;B 、32;C 、31;D 、35.12、椭圆中一些常见的结论要记住,这对解决选择填空等客观性问题时比较方便,如:椭圆的基本量c b a ,,蕴含在焦点、中心、短轴端点所构成的直角三角形中;椭圆的短轴的端点对两焦点的张角是椭圆上点与两焦点张角(与两焦点连线夹角)的最大值;短半轴、长半轴的几何意义是椭圆上点与中心距离的最小值与最大值;焦点到椭圆上点的距离的最大值与最小值分别是c a +与c a -;过椭圆焦点的弦长最大值是长轴长,最小值是垂直于长轴所在直线的弦(有时称为通径,其长为ab 22).[举例1]一直线l 过椭圆12422=+y x 的左焦点,被椭圆截得的弦长为2,则直线l 的方程为_____;[举例2]椭圆13422=+y x 上有2012个不同的点122012,,,P P P ,椭圆的右焦点为F ,数列{||}(1,2,3,,201n FP n = 是公差为d 的等差数列,则d 的取值范围是_____.13、椭圆)0(12222>>=+b a by a x 上任意一点P 与两焦点21,F F 构成的三角形可称为椭圆的焦点三角形.焦点三角形的周长为定值)22(c a +,利用解三角形的方法可以得出:当21PF F ∠=θ时,此三角形的面积为2tan2b θ(引起注意的是此结论的推导过程要掌握).[举例]已知点)0,2(),0,2(B A -,点C 在直线1=y 上满足BC AC ⊥,则以A 、B 为焦点过点C 的椭圆方程为____________.14、双曲线的定义中的隐含条件是“两焦点之间的距离大于定值(实轴长)”,双曲线基本量之间的关系要与椭圆基本量的关系区分开来,从定义上来说椭圆与双曲线的定义是一字之差,方程是一符号之差,但两者之间的几何性质完全不同.[举例]一双曲线C 以椭圆12422=+x x 的焦点为顶点,长轴顶点为焦点,则此双曲线的方程为____.15、渐近线是双曲线特有的几何性质,要特别注意双曲线的渐近线方程,理解“渐近”的意义.双曲线12222=-b y a x 的渐近线的方程为02222=-b y a x ,与双曲线12222=-b y a x 共渐近线的双曲线可以设成λ=-2222by a x (其中0≠λ是待定的系数),双曲线的焦点到双曲线的渐近线的距离是虚半轴长b . [举例1]一双曲线与1322=-y x 有共同渐近线且与椭圆1322=+y x 有共同焦点,则此双曲线的方程为________;[举例2]若关于x 的方程)2(12+=-x k x 有两个不等的实数根,则实数k 的取值范围是___.16、记住双曲线中常见的结论:(1)过双曲线焦点的直线被双曲线同支截得的弦长的最小值是通径(垂直于实轴的弦长),被两支截得的弦长的最小值是实轴的长;(2)双曲线焦点到同侧一支上的点的距离最小值是a c -,到异侧一支上点的距离最小值是a c +;(3)双曲线12222=-b y a x 的焦点为21,F F ,P 是双曲线上的一点,若θ=∠21PF F ,则△21PF F 的面积为22b cot θ(仿椭圆焦点三角形面积推导).[举例1]已知双曲线的方程为116922=-y x ,P 是双曲线上的一点,F 1、F 2分别是它的两个焦点,若7||1=PF ,则=||2PF ______;[举例2]椭圆12622=+y x 和双曲线221x y a -=的公共焦点为21,F F ,P 是它们的一个公共点,则=∠21cos PF F _____;[举例3]双曲线)1(122>=-n y nx 的两焦点为P F F ,,21是此双曲线上的一点,且满足||||21PF PF +=22+n ,则△21F PF 的面积为________.17、抛物线是高考命题中出现频率最高的圆锥曲线.仅从标准方程上,抛物线就有四种不同的形式,要注意开口方向与标准方程的关系.不要将抛物线的标准方程与二次函数的表达式相混淆. [举例]抛物线24x y =的焦点坐标是_____;准线方程是_____.18、记住抛物线的常见性质:(1)抛物线上任意一点到焦点距离等于它到准线的距离;(2)过抛物线的焦点与顶点的直线是抛物线的对称轴;(3)顶点、焦点、准线之间的关系;(4)过焦点与对称轴垂直的弦称为抛物线的通径,抛物线)0(22>=p px y 的通径长为p 2;(5)通径是过抛物线焦点的弦中长度最小的一条.[举例1]已知抛物线的焦点为)1,1(F ,对称轴为x y =,且过M (3,2),则此抛物线的准线方程为__;[举例2]直线l 过抛物线y x 42=的焦点与抛物线交于A 、B 两点,若A 、B 两点到x 轴的距离之和等于3,则这样的直线l 有―――――――――――――――――( )A 、1条;B 、2条;C 、3条;D 、不存在.19、过抛物线的焦点的直线被抛物线截得的弦称为抛物线的焦点弦.以抛物线)0(22>=p px y 为例,焦点弦有下列常用性质:设抛物线)0(22>=p px y 的焦点为F ,),(),,(2211y x B y x A 是抛物线上的两点.(1)A 、B 、F 三点共线的充分必要条件是)4(221221p x x p y y =-=;(2)p x x AB ++=21||;(3)若AB 过焦点,则以AB 为直径的圆与抛物线的准线相切;(4)AB 过焦点,则⋅为定值;(5)AB 过焦点,211=+[举例1]直线l 过抛物线的焦点与抛物线交于A 、B 两点,O 是抛物线的顶点,则△ABO 的形状是――――――――――――――――――――――――――――――――( )A 、 直角三角形;B 、锐角三角形;C 、钝角三角形;D 、不确定与抛物线的开口大小有关.[举例2]求证:过抛物线)0(22>=p px y 焦点的所有弦长的最小值是p 2.20、“点差法”是解决直线与圆锥曲线位置关系中与弦的中点有关问题的常用方法.“点”是指弦端点、弦中点;“差”是指将弦端点坐标代入曲线方程作差.由点差法可以利用弦中点的坐标表示出弦所在直线的斜率.[举例]已知点M 是椭圆12222=+by a x 的一条不垂直于对称轴的弦AB 的中点,O 是坐标原点,设OM 、AB 的斜率分别为21,k k ,则21k k ⋅=―――――――――――――( )A 、22b a ;B 、22a b ;C 、22a b -;D 、22ba -.21、当直线过x 轴上的定点)0,(a A 时,若直线不是x 轴,则此直线方程可以设成a my x +=.这样可以避免讨论直线斜率是否存在.[举例]设直线l 过椭圆1422=+y x 的右焦点,与椭圆相交于A 、B 两点,O 是坐标原点,当△OAB 的面积最大时,求直线l 的方程.22、求动点的轨迹方程要能充分地将“动”与“定”有机的联系起来,以“定”制“动”.也可以先由动点定轨迹后方程.常见动点的轨迹要熟记.[举例1]设点P 为双曲线1422=-y x 上的动点,F 是它的左焦点,M 是线段PF 的中点,则点M 的轨迹方程是_____;[举例2]已知椭圆的焦点是21,F F ,P 是椭圆上的一个动点.如果延长P F 1到Q ,使得||||2PF PQ =,那么动点Q 的轨迹是―――――――――――――――――――( )A 、圆;B 、椭圆;C 、双曲线的一支;D 、抛物线.23、直线与圆锥曲线之间的位置关系的讨论主要是转化为方程根的个数的讨论,联立直线与圆锥曲线方程得方程组,消去其中一个量得到关于另一个变量的一元二次方程,利用根的判别式进行讨论,但要注意二方面:一是直线的斜率是否存在,二是所得方程是否为一元二次方程.直线与非封闭曲线(双曲线、抛物[举例]已知直线l 过点)1,1(M ,双曲线C :1322=-y x .(1)若直线l 与双曲线有且仅有一个公共点,求直线l 的方程;(2)若直线与双曲线的右支有两个不同的交点,求直线l 斜率的取值范围;(3)是否存在直线l 使其与双曲线的有两个不同的交点A 、B ,且以AB 为直径的圆过坐标原点?若存在求出此直线的斜率,不存在说明理由.24、运用平面向量综合知识,探求动点轨迹方程,还可再进一步探求曲线的性质。
解析几何知识点总结(高考复习)

1. 直线与方程1、倾斜角与斜率:1212tan x x y y k −−==α2、直线方程:⑴点斜式:()00x x k y y −=− ⑵斜截式:b kx y +=⑶两点式:121121y y y y x x x x −−=−− ⑷截距式:1x y a b+= ⑸一般式:0=++C By Ax3、对于直线:222111:,:b x k y l b x k y l +=+=有: ⑴≠=⇔212121//b b k k l l ; ⑵1l 和2l 相交12k k ⇔≠; ⑶1l 和2l 重合==⇔2121b b k k ;⑷12121−=⇔⊥k k l l .4、对于直线::,0:22221111=++=++C y B x A l C y B x A l 有:⑴≠=⇔1221122121//C B C B B A B A l l ;⑵1l 和2l 相交1221B A B A ≠⇔;⑶1l 和2l 重合 ==⇔12211221C B C B B A B A ;⑷0212121=+⇔⊥B B A A l l .5、两点间距离公式:()()21221221y y x x P P −+−=6、点到直线距离公式:2200BA CBy Ax d +++=7、两平行线间的距离公式:1l :01=++C By Ax 与2l :02=++C By Ax 平行,则2221BA C C d +−=2. 圆与方程1、圆的方程:⑴标准方程:()()222r b y a x =−+−其中圆心为(,)a b ,半径为r .⑵一般方程:022=++++F Ey Dx y x . 其中圆心为(,)22DE−−,半径为r =2、直线与圆的位置关系直线0=++C By Ax 与圆222)()(r b y a x =−+−的位置关系有三种:0<∆⇔⇔>相离r d ;0=∆⇔⇔=相切r d ; 0>∆⇔⇔<相交r d .弦长公式:222d r l −==3、两圆位置关系:21O O d = ⑴外离:r R d +>; ⑵外切:r R d +=;⑶相交:r R d r R +<<−; ⑷内切:r R d −=; ⑸内含:r R d −<.3、空间中两点间距离公式:()()()21221221221z z y y x x P P −+−+−=3.椭圆4.双曲线5.抛物线图形若干公式1、 两点间距离:若)y ,x (B ),y ,x (A 2211,则212212)()(y y x x AB −+−=2、 平行线间距离:若0C By Ax :l ,0C By Ax :l 2211=++=++,则:2221BA C C d +−=3、 点到直线的距离: 22BA CBy Ax d +++=o o4、 直线与圆锥曲线相交的弦长公式:=+=0)y ,x (F bkx y 则:2122))(1(x x k AB −+=5、 若A ),(),,(2211y x B y x ,P (x ,y )。
解析几何综合复习题

综合复习题一、填空题1. __只有大小的量______________________________________ 叫做数量 ;2. __既有大小又有方向的量______________________________________ 叫做矢量 ;3. __模等于1的矢量___________________________________ 叫做单位矢量 ;4. 平行于同一直线的一组矢量叫做 _共线_______________ 矢量 ;5. 平行于同一平面的一组矢量叫做 __共面_______________ 矢量 ;6. 两矢量共线的充要条件是它们线性 ___相关________________ ;7. 三矢量不共面的充要条件是它们线性 ______无关___________ ;8. __________方向角的余弦__________________________ 叫做方向余弦 ;9. 两矢量a⊥b充要条件是 ____a_*b=0____________________ ;10. 三矢a,b,c量共面的充要条件是 ______(a×b)*c=0_______________ ;11. 两矢量a∥b的充要条件是 _a×b=0,或对应分量成比例 ;12. 矢量与坐标轴所成的角叫做 _方向角;13. 把平面上的一切单位矢量归结到共同的始点,则它们的终点构成____单位圆 ;14. 把空间中一切单位矢量归结到共同的始点,则它们的终点构成单位球面__ ;15. 方程叫做空间曲线的 ______________ 方程 ;16. 坐标平面yOz的方程是 _____________________________ ;17. 坐标平面xOz的方程是 ______________________________ ;18. 坐标平面xOy的方程是 _____________________________ ;19. 方程叫做曲面的 ______________________ 方程 ;20. 空间直线的标准方程为______________________________ ;21. 两平面A i x+B i y+C i z+D i=0 (i=1, 2)相互垂直的充要条件是___________________ ;22. 点M0(x0, y0, z0)到平面Ax+By+Cz+D=0的距离是 _______ ;23. 平面的一般方程是 _________________________ ;24. 直线的方向余弦cosα, cosβ, cosγ满足的关系式为_________ ;25. 给定直线l:==和平面π:Ax+By+Cz+D=0, 则l与π相交的充要条件是 ________________________ ;26. 直线l与平面π平行的充要条件是 _____________________ ;27. 直线l在平面π上的充要条件是_______________________;28. 给定l i:== (i=1, 2), 则l1与l2异面的充要条件是___________________________ ;29. 直线l1与l2相交的充要条件是 ________________________ ;30. 直线l1与l2平行的充要条件是 _________________________ ;31. 直线l1与l2重合的充要条件是 _________________________ ;32. 空间中通过同一直线的所有平面的集合叫做 ____________ ;33. 空间中平行于同一平面的所有平面的集合叫做 __________ ;34. 在空间, 由平行于定方向且与一条定曲线相交的一族平行直线所产生的曲面叫做____________________;35. 在空间, 过一定点且与定曲线相交的一族直线所产生的曲面叫做___________ ;36. 在空间, 一曲线绕定直线旋转一周所产生的曲面叫做 __________________ ;37. 在直角坐标系下, 椭球面的标准方程是 ________________________ ;38. 在直角坐标系下, 单叶双曲面的标准方程是 ____________________ ;39. 在直角坐标系下, 双叶双曲面的标准方程是 ____________________ ;40. 在直角坐标系下, 椭圆抛物面的标准方程是 ____________________ ;41. 在直角坐标系下, 双曲抛物面的标准方程是 ____________________ ;42. 柱面、锥面、椭球面、单叶(双叶)双曲面、椭圆(双曲)抛物面中是直纹曲面的有 ___________ _____________________;43. 单叶双曲面过一定点的直母线有 ___________ 条;44. 满足条件Φ (X, Y)≠0的方向叫做二次曲线的 ___________ ;45. 没有实渐近方向的二次曲线叫做 __________________ 型曲线;46. 有两个实渐近方向的二次曲线叫做 __________________ 型曲线;47. 只有一个实渐近方向的二次曲线叫做 __________________ 型曲线;48. 有唯一 __________________ 的二次曲线叫做中心二次曲线;49. 没有中心的二次曲线叫做 __________________ 二次曲线;50. 有一条中心直线的二次曲线叫做 __________________ 二次曲线;51. 二次曲线F (x, y)=0的奇点(x0, y0)满足的条件是 ________________ ;52. 二次曲线一族平行弦中点的轨迹叫做二次曲线的 _______________ ;53. ___________ 二次曲线的直径都过二次曲线的中心;54. 无心二次曲线的直径都 ___________ 二次曲线的渐近方向;55. 线心二次曲线的直径只有一条,即二次曲线的 ___________ ;56. 二次曲线垂直于其共轭弦的直径叫做二次曲线的 ______________ ;57. 二次曲线的特征根都是 ____________________________ ;58. 二次曲线特征根不能 ____________________________ ;59. 中心二次曲线至少有 ________________________ 条主直径;60. 非中心二次曲线中只有 ______________________ 条主直径;61. ___________ 二次曲线可分类为椭圆、虚椭圆、双曲线、点、二条相交直线;62. ____________________________ 二次曲线的图像是抛物线;63. ___________ 二次曲线可分类为两平行直线、两平行共轭虚直线、两重合直线;二、判断题(正确的打“√”,错误的打“×”)1. 若, 共线,, 共线,则, 也共线; ()2. 若, , 共面,, , 共面,则, , 共面;()3. , , 中,若, 共线, 则, , 共面; ()4.平行于同一方向的两矢量相等;()5. 位移、力、速度和加速度都是数量; ()6. 所有零矢量都相等; ()7. 自由矢量就是方向和模任意的矢量; ()8. 零矢量的方向一定; ()9.在自由矢量的意义下, 平行于同一平面的一组矢量不能在同一平面上;()10. 彼此平行且有共同始点的一组矢量一定在同一条直线上; ()11. 若≠,则表示与同方向的单位矢量; ()12. 若⊥,则 |+|=|-|; ()13. 若, 同向,则 |+|=||+||; ()14. 若, 反向,则 |-|=||+||; ()15. 若, 反向, 且||≥||,则 |+|=||-||; ()16. 若, 同向, 且||≥||,则 |-|=||-||; ()17. 第I卦限内点 (x, y, z) 的符号为 (+, ―, ―); ()18. 第II卦限内点 (x, y, z) 的符号为 (+, +, ―);()19. 第III卦限内点 (x, y, z) 的符号为 (-, +, ―); ()20. 第IV卦限内点 (x, y, z) 的符号为 (-, ― ,+); ()21. 射影矢量=(射影) ;()22. 射影=|| cos∠(, );()23. 射影(+)=射影+射影;()24. 射影(λ)=λ射影;()25. 在{O;,,,}下, =X+Y+Z, 则射影=Y; ()26. 两坐标面xOy与yOz所成二面角的平分面方程是x+y=0; ()27. 两坐标面xOy与yOz所成二面角的平分面方程是x-z=0; ()28. 两坐标同xOy与xOz所成二面角的平分面方程是x+z=0; ()29. 两坐标面xOy与xOz所成二面角的平分面方程是y-z=0; ( )30. 两坐标面xOz与yOz所成二面角的平分面方程是x-y=0; ( )31. (+)⋅=⋅+⋅; ()32. (λ)⋅=⋅(λ);()33. ⋅=2;()34. -(×)=×;()35. ×+×=(+)×;()36. 平面的矢量式参数方程为=+u+v;()37. 平面的坐标式参数方程为()38. 平面的一般方程为Ax+By+Cz+D=0;()39. 平面的法式方程为x cosα+y cosβ+zcosγ+p=0;()40. 平面的截距式方程为++=0;()41. 空间直线与平面的位置关系有相交和平行两种;()42. 空间两直线的位置关系有平行、重合、相交三种;()43. 两平面的位置关系有平行、相交、重合三种;()44. 点到平面的离差等于点到平面的距离;()45. 平面Ax+By+Cz+D=0通过原点的充要条件是D=0; ()46. 将椭圆绕x轴所得旋转曲面方程为:++=1;()47. 将椭圆绕y轴所得旋转曲面方程为:++=1; ()48. 将双曲线绕z轴所得旋转曲面方程为:+-=1;()49. 将双曲线绕y轴所得旋转曲面方程为:--=1;()50. 将抛物线绕z轴所得旋转曲面方程为:x2+y2=2pz;()51. 二次曲线的中心就是它的奇点;()52. 若M是二次曲线的奇点, 则该二次曲线过M的切线是唯一的; ()53. 二次曲线的一族平行弦中点的轨迹是一条直线;()54. 经过移轴变换可以消去二次曲线方程中的xy 项;()55. 在任意转轴变换下, 二次曲线新旧方程的一次项系数满足;()56. F(x, y)=xF1(x, y)+yF2(x, y) +F3(x, y);()57. F(x, y)=Φ(x, y)+2a13x+2a23y+a33;()58. 在直线方程Ax+By+C=0中, 若A, B, C与三个实数成比例,则该直线为虚直线;()59. 二次曲线的奇点满足F1 (x, y)=F2 (x, y)=F3 (x, y)=0;()60. Φ (x, y)=x (a11x+a12y)+y (a12x+a22y);()三、选择题(从四个备选答案中选出唯一正确的一个)1. 两个矢量是否相等,由它们的()决定.A. 始点;B. 模;C. 方向;D. 模和方向.2. 若, , 共面,, , 共面,则, , ()共面.A. 不一定;B. 一定; B. 一定不; D. 共线.3. 把平行于某一直线的一切矢量归结到共同的始点,则它们的终点构成()A. 一点;B. 线段;C. 直线;D. 射线.4. 下列等式中不成立的是()A.+=+;B. ⋅=⋅;C. ×=×;D. λ (μ)=μ (λ).5. 关于零矢量的描述不正确的是()A. 模不定;B.方向不定;C. 模为0;D.模定方向不定.6. 非零矢量与的下列关系中不正确的是()A. =;B. =;C. ||=;D. ||=1.7. 第VIII卦限的点 (x, y, z) 的符号是()A. (+, +, +);B. (―, ―, ―)C. (+, ―, ―)D. (-, +, +).8. 下列等式中错误的是()A. ⋅=||||cos∠(, );B. ⋅=||射影;C. ⋅=||射影;D. ⋅=||⋅||9. 下列等式错误的是()A. ⋅=||2;B. 2=||2;C. ||=;D. =.10. ×+×+×=()A. 0;B. 3;C. 1;D. .11. ⋅+⋅+⋅=()A. 0;B. 3;C. ;D. 1.12. 若, , 两两相互垂直,且模均为1,则++的模为()A.; B.3; C.0; D. 1.13. 下列运算不满足交换律的是()A. 矢性积;B. 数性积;C. 矢量加法;D. 数量乘法.14. 方程在空间表示()A. yOz面;B. xOy面;C. z轴;D. x轴.15. 在空间,y轴的方程不能写成()A. B. ; C. y=0; D. ==.16. 平面的矢量式参数方程是()A. ++=1;B. Ax+By+Cz+D=0;C. x cosα+y cosβ+z cosγ-p=0;D.=+u+v.17. 平面的法式方程是()A. ++=1;B. Ax+By+Cz+D=0;C. x cosα+y cosβ+z cosγ-p=0;D. =+u+v.18. 平面的截距式方程是()A. ++=1;B. Ax+By+Cz+D=0;C. x cosα+y cosβ+z cosγ-p=0;D. =+u+v.19. 平面的一般方程是()A. ++=1;B. Ax+By+Cz+D=0;C. x cosα+y cosβ+z cosγ-p=0;D. =+u+v.20. 平面的法式方程中的常数项必满足()A. ≤0;B. ≥0;C. <0;D.>0.21. 将平面方程Ax+By+Cz=0化为法式方程时,法式化因子的符号()A. 任选;B. 与B异号;C. 与A异号;D.与C异号.22. 点M0与平面π间的离差δ=-2, 则M0到π的距离d为()A. -2;B. 2;C.-1;D. 1.23. 直线的坐标式参数方程是()A. ==;B.C. D.==.24. 直线的标准方程是()A. ==;B.C. D.==.25. 直线的两点式方程是()A. ==;B.C. D.==.26. 直线的一般方程是()A. ==;B.C. ;D.==.27. 直线通过原点的条件是其一般方程中的常数项D1, D2满足()A. D1=D2=0;B. D1=0, D2≠0;C. D1≠0, D2=0;D. D1≠0, D2≠0.28. 直线的方向角α, β, γ不满足关系式()A. cos2α+cos2β+cos2γ=1;B. sin2α+sin2β+sin2γ=1;C. sin2α+sin2β+sin2γ=2;D. cos2(π-α)+cos2(π-β)+cos2(π-γ)=1.29. 两平面2x+3y+6z+1=0与4x+6y+12z+1=0之间的距离是()A. 0;B.C.D..30. 设直线与此同时三坐标面的夹角为λ, μ, v, 则下列式子中不成立的是()A. sin2λ+sin2μ+sin2ν=1;B. cos2λ+cos2μ+cos2ν=2;C. cos2λ+cos2μ+cos2ν=1;D. sin2(π-λ)+sin2(π-μ)+sin2(π-ν)=1.31. 关于x-x0, y-y0, z-z0的二次齐次方程表示()A. 柱面;B. 顶点在(x0, y0, z0)的锥面;C. 旋转曲面;D.平面.32. 将曲线Γ: 绕y轴旋转一周所得旋转曲面的方程为()A. F=0;B. F=0;C. F=0;D. F=0.33. 将曲线Γ:绕x轴旋转一周所得旋转曲面的方程为()A. F;B. F=0;C. F=0;D. F=0.34. 将曲线Γ:绕z轴旋转一周所得旋转曲面的方程为()A. F;B. F=0;C. F=0;D. F=0.35. 将曲线Γ:绕z轴旋转一周所得旋转曲面的方程为()A. x2+y2=2z;B. x2+z2=2y;C. y2+z2=2x;D. y2=.36. 下列方程中表示单叶双曲面的是()A. ++=1;B. +-=1;C. +-=-1;D. --=1.37. 椭球面++=1与xOy坐标面的交线方程为()A. +=1;B.;C. z=0;D. .38. 下列方程中表示双叶双曲面的是()A. --=-1;B. -+=1;C. --+=1;D. +-=1.39. 下列方程中表示双曲抛物面的是()A. x2+y2=2z;B. 3x2-2y2=z;C. x2-y2=z2;D. x2+y2=z2.40. 二次曲线方程通过移轴变换后不变的是()A. 二次项系数;B. 一次项系数;C. 常数项;D. 都不变.41. 二次曲线方程通过转轴变换后不变的是()A. 二次项系数;B. 一次项系数;C. 常数项;D. 都不变.42. 下列曲面中是直纹曲面的是()A. 椭球面;B. 柱面;C. 球面;D. 双叶双曲面.43.已知二次曲线方程中Φ(x,y)=x2+2x y+y2,则I2=()A. 1;B. 0;C. -1;D. 2.44.已知二次曲线方程中Φ(x,y)=x2+2x y+y2,则I1=()A. 1;B. 0;C. -1;D. 2.45. 中心二次曲线至少有()条主直径.A. 1;B. 2;C. 3;D. 4.46. 二次曲线的奇点()是它的中心.A. 不一定;B. 一定不;C. 一定;D. 以上都不对.47. 有奇点的二次曲线一定是()A. 中心曲线;B. 无心曲线;C. 线心曲线;D.圆.48. 二次曲线的特征根()A不全为0; B. 全不为0; C.全为0; D. ≥0.49. 二次曲线的特征根()A. 都是虚数;B. 都是实数;C. 一实一虚;D. 全为0.50. 椭圆+=1的一对共轭直径的斜率k与k'满足()A. kk'=;B. kk'=-;C. kk'=-;D. kk'=.51. 二次曲线在直角坐标变换下的半不变量为()A. I1;B. I2;C. I3;D. K1.52. 简化方程为I1 y2+=0的二次曲线是()A. 中心曲线;B. 无心曲线;C. 线心曲线;D. 圆.53. 二次曲线表示两条直线(实的或虚的,不同的或重合的)的充要条件是()A. I1=0;B. I2=0;C.I3=0;D. K1=0.四、计算题1. 求通过点P (1, 1, 1)且与直线l1:==, l2: ==都相交的直线方程.2. 求异面直线l1:==与l2: ==的公垂线方程.3. 求通过直线且与平面x-4y-8z+12=0垂直的平面方程.4. 求通过点A (-3, 0, 1)和B (2, -5, 1)的直线方程.5. 求平行于平面3x+2y+z=0且在x轴上截距等于-2的平面.6. 已知一平面过M0(x0, y0, z0) (z0≠0), 且在x轴、y轴上的截距分别为a, b(ab≠0), 求其方程.7. 求二次曲线x2-2xy+y2-1=0 的渐近方向,并指出其类型.8. 求二次曲线2x2+xy-y2-x+y-1=0的渐近线.9. 如图,求直角△ABC的斜边AC绕直角边AB旋转所得圆锥面的方程(∠BAC=α).10. 求二次曲线F (x, y) ≡x2-2xy+y2-4x=0 的主方向与主直径.11. 求椭圆+=1 的主方向与主直径.12. 求双曲线-=1的主方向与主直径.13. 在双曲抛物面-=z上求平行于平面3x+2y-4z=0的直母线.14. 求二次曲面F(x, y, z)≡2xy+2xz+2yz+9=0 的主方向与主径面.15. 求二次曲面F(x, y, z)≡5x2+2y2+2z2-2xy+2xz-4yz-4y-4z+4=0的奇向.16. 求以直线==为轴, 半径为r的圆柱面方程.17. 求二次曲面-+=1 与三坐标面的交线方程,并指出其名称.18. 已知各锥面的顶点在原点,准线为,求锥面的方程.19. 求二次曲线x2-xy-y2-x-y=0 与x2+2xy+y2-x+y=0的公共直径.五、证明题1. ⊥的充要条件是⋅=0.2. //的充要条件是×=.3. (⋅)2+(×)2=22.4. 若×+×+×=, 则, , 共面.5. 若二次曲线的I1=0, 则I2<0.6. 二次曲线的特征根不全为0.7. 二次曲线的特征根全是实数.8. 由二次曲线的特征根λ≠0确定的主方向X:Y是二次曲线的非渐近方向.9. 由二次曲线的特征根λ=0确定的主方向X:Y是二次曲线的渐近方向.10. 在任意转轴变换下, 二次曲线新旧方程的一次项系数满足.11. 二次曲线x2+2xy+ay2+x+by-4=0有一条中心直线的充要条件是a=b=1.12. 两条二次曲线x2-xy+y2+2x-4y=0与 5x2+4xy+2y2-24x-12y+18=0 的中心在直线x+2y-4=0上.13. 两条二次曲线x2-2xy+y2+4x-4y-3=0 与x2-xy+y2+2x-4y=0的公共直径为x-y+2=0.14. 中心二次曲线ax2+2hxy+ay2=d 的两条主直径为x2-y2=0.15. 二次曲线两不同特征根确定的主方向相互垂直.16. 已知直线l:与π:4x-3y+7z-7=0, 试证直线l在平面π上.17. 试证两直线==与==为异面直线.六、化简二次曲线方程,并作出图形.1. x2-3xy+y2+10x-10y+21=0.2. 2xy-4x-2y+3=0.3. x2-xy+y2+2x-4y=0.4. x2+6xy+y2+6x+2y-1=0.5. 5x2+8xy+5y2-18x-18y+9=0.6. x2-2xy+y2+2x-2y-3=0.7.x2+2xy+y2+2x+y=0.综合复习题答案一、1. 只有大小的量;2. 既有大小、又有方向的量;3. 模等于1的矢量;4. 共线矢量;5. 共面矢量;6. 相关;7. 无关;8. 方向角的余弦;9. =0;10. ()=0, 或线性相关;11. ×=,或对应分量成比例;12. 方向角;13. 单位圆;14. 单位球面;15. 一般;16. x=0;17. y=0;18. z=0;19. 参数;20. ==;21. A1A2+B1B2+C1C2=0;22. d=;23.Ax+By+Cz+D=0 (A, B, C不全为0);24. cos2α+cos2β+cos2γ=1;25.AX+BY+CZ≠0;26. AX+BY+CZ=0, Ax0+By0+Cz0+D≠0;27. AX+BY+C=0, Ax0+By0+Cz0+D=0;28. ∆=≠0;29. ∆=0, X1:Y1:Z1≠X2:Y2:Z2;30. ∆=0, X1:Y1:Z1=X2:Y2:Z2 ≠ (x2-x1):(y2-y1):(z2-z1);31. ∆=0, X1:Y1:Z1 = X2:Y2:Z2=(x2-x1):(y2-y1):(z2-z1);32. 有轴平面束;33.平行平面束;34. 柱面;35. 锥面;36. 旋转曲面;37. ++=1 (a≥b≥c>0);38. +-=1 (a>0, b>0, c>0);39. +-=-1 (a>0, b>0, c>0);40. +=2z (a>0, b>0);41. -=2z (a>0, b>0);42. 柱面,锥面,单叶双曲面,双曲抛物面;43. 两条;44. 非渐近方向;45. 椭圆;46. 双曲;47. 抛物;48. 中心;49. 无心;50. 线心;51. F1 (x0, y0)=F2 (x0, y0)=F3 (x0, y0)=0;52. 直径;53. 中心;54. 平行于;55. 中心直线;56. 主直径;57. 实数;58. 全为零;59. 两;60. 一;61. 中心;62. 无心;63. 线心;二、1. √;2. ×;3. √;4. ×;5. ×;6. √;7. ×;8. ×;9. ×; 10. √;11. √; 12. √; 13. √; 14. √; 15. √; 16. √; 17. ×; 18. ×; 19. ×; 20. ×;21. √; 22. √; 23. √; 24. √; 25. √; 26. ×; 27. √; 28. ×; 29. √; 30. √;31. √; 32. √; 33. √; 34. √; 35. √; 36. √; 37. √; 38. √; 39. ×; 40. ×;41. ×; 42. ×; 43. √; 44. ×; 45. √; 46. √; 47. √; 48. √; 49. √; 50. √;51. ×; 52. ×; 53. √; 54. ×; 55. √; 56. √; 57. √; 58. ×; 59. √; 60. √.三、1. D;2. A;3. C;4. C;5. A;6. B;7. C;8. D;9. D; 10. D; 11.B; 12. A; 13. A; 14. C; 15. C; 16. D; 17. C; 18. A; 19. B; 20. A;21. A; 22. B; 23. B; 24. A; 25. D; 26. C; 27. A; 28. B; 29. D; 30. C;31. B; 32. D; 33.A; 34. B; 35.A; 36.B; 37.D; 38. C; 39. B; 40. A;41. C; 42. B; 43. B; 44. D; 45. B; 46. C; 47. C; 48. A; 49. B; 50. C;51. D; 52. C; 53. C.四、1. ==;2.(z轴);3. 4x+5y-2z+12=0;4. ==;5. 3x+2y+z+6=0;6.设所求平面在z轴上的截距为c≠0,则所求平面方程为++=1, 因平面过M0 (x0, y0, z0),于是++=1, = (1--), 故所求平面为++ (1--)=1;7. (-1):1, 抛物型;8. 3x+3y-2=0, 6x-3y-1=0;9. 提示:取A为原点,AB为z轴, ABC所在平面为yOz面建立坐标系, 设B的坐标为(0, 0,a), 则AC的方程为, 从而得锥面方程为ctg2α (x2+y2)-z2=0 (0≤z≤a);10. (-1):1(非渐近主方向), 1:1(渐近主方向), x-y-1=0;11. 1:0, 0:1, x=0, y=0;12. 1:0, 0:1, x=0, y=0;13. 与;14. 1:1:1及与平面x+y+z=0平行的一切方向;x+y+z=0及过中心(0, 0, 0)且垂直于x+y+z =0 的一切平面;15. 0:1:1;16. (ny-mz)2+(lz-nx)2+(mx-ly)2=r2 (l2+m2+n2);17. (双曲线); (椭圆); (双曲线);18. --=0;19. 5x+5y+2=0;20. 2x+3y+z+4=0.五、略.六、1. 由坐标变换公式得:-=1(双曲线).2. 由坐标变换公式得:x'2-y'2=1 (双曲线).3. 由坐标变换公式得:+=1 (椭圆).4. 由坐标变换公式得:-=1 (双曲线).5. 由坐标变换公式得:x'2+=1 (椭圆).6. 由坐标变换公式得:y'2=2 (一对平行直线).7. 由坐标变换公式得:y'2=-x (抛物线).。
高中 平面解析几何 两条直线的位置关系 知识点+例题

辅导讲义――两条直线的位置关系[巩固]已知两条直线l1:ax-by+4=0和l2:(a-1)x+y+b=0,求满足下列条件的a,b的值.(1)l1⊥l2,且l1过点(-3,-1);(2)l1∥l2,且坐标原点到这两条直线的距离相等.题型二:两直线相交[例]求经过直线l1:3x+2y-1=0和l2:5x+2y+1=0的交点,且垂直于直线l3:3x-5y+6=0的直线l的方程.[巩固]如图,设一直线过点(-1,1),它被两平行直线l1:x+2y-1=0,l2:x+2y-3=0所截的线段的中点在直线l3:x-y-1=0上,求其方程.的交点坐标为(0,2),又点(2,3)关于y 轴的对称点为(-2,3),所以反射光线过点(-2,3)与(0,2),由两点式知A 正确. 3.若A (-3,-4),B (6,3)两点到直线l :ax +y +1=0的距离相等,则a =_____________.解析 依题意,|-3a -4+1|a 2+1=|6a +3+1|a 2+1, 解得a =-79或a =-13.4.已知直线3x +4y -3=0与直线6x +my +14=0平行,则它们之间的距离是_________.解析 ∵63=m 4≠-143,∴m =8,直线6x +my +14=0.可化为3x +4y +7=0,两平行线之间的距离d =|-3-7|32+42=2.5.如图,已知A (4,0)、B (0,4),从点P (2,0)射出的光线经直线AB 反射后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是_____________.解析 由题意知点P 关于直线AB 的对称点为D (4,2),关于y 轴的对称点为C (-2,0),则光线所经过的路程PMN 的长为|CD |=210.6.与直线l 1:3x +2y -6=0和直线l 2:6x +4y -3=0等距离的直线方程是______________.答案 12x +8y -15=0解析 l 2:6x +4y -3=0化为3x +2y -32=0,所以l 1与l 2平行,设与l 1,l 2等距离的直线l 的方程为3x +2y +c =0,则:|c +6|=|c +32|,解得c =-154,所以l 的方程为12x +8y -15=0.7.已知点A (-1,1),B (2,-2),若直线l :x +my +m =0与线段AB 相交(包含端点的情况),则实数m 的取值范围 是______________. 答案 ⎝⎛⎦⎤-∞,12∪[2,+∞) 所以直线恒过定点P (0,-1).∵点A (-1,1),B (2,-2),∴k P A =-2,k PB =-12,∵直线l :x +my +m =0与线段AB 相交(包含端点的情况), ∴-1m ≤-2或-1m ≥-12,∴m ≤12或m ≥2(经验证m =0也符合题意).∴实数m 的取值范围是⎝⎛⎦⎤-∞,12∪[2,+∞). 8.将一张坐标纸折叠一次,使得点(0,2)与点(4,0)重合,点(7,3)与点(m ,n )重合,则m +n =________.答案 345解析 由题意可知纸的折痕应是点(0,2)与点(4,0)连线的中垂线,即直线y =2x -3,它也是点(7,3)与点(m ,n )连线的中垂线,于是⎩⎪⎨⎪⎧3+n 2=2×7+m2-3,n -3m -7=-12,解析 圆心为O (1,0),由于P (2,2)在圆(x -1)2+y 2=5上,∴P 为切点,OP 与P 点处的切线垂直.∴k OP =2-02-1=2, 又点P 处的切线与直线ax -y +1=0垂直.∴a =k OP =2,选C.12.如图,已知直线l 1∥l 2,点A 是l 1,l 2之间的定点,点A 到l 1,l 2之间的距离分别为3和2,点B是l 2上的一动点,作AC ⊥AB ,且AC 与l 1交于点C ,则△ABC 的面积的最小值为________.答案 6解析 以A 为坐标原点,平行于l 1的直线为x 轴,建立如图所示的直角坐标系,设B (a ,-2),C (b,3).∵AC ⊥AB ,∴ab -6=0,ab =6,b =6a. Rt △ABC 的面积S =12a 2+4·b 2+9 =12a 2+4·36a 2+9=12 72+9a 2+144a 2 ≥1272+72=6.13.点P (2,1)到直线l :mx -y -3=0(m ∈R )的最大距离是________.答案 2 5解析 直线l 经过定点Q (0,-3),如图所示.由图知,当PQ ⊥l 时,点P (2,1)到直线l 的距离取得最大值|PQ |=(2-0)2+(1+3)2=25,所以点P (2,1)到直线l 的最大距离为2 5.14.(2013·四川)在平面直角坐标系内,到点A (1,2),B (1,5),C (3,6),D (7,-1)的距离之和最小的点的坐标是________.答案 (2,4)解析 设平面上任一点M ,因为|MA |+|MC |≥|AC |,当且仅当A ,M ,C 共线时取等号,同理|MB |+|MD |≥|BD |,当且仅当B ,M ,D 共线时取等号,连接AC ,BD 交于一点M ,若|MA |+|MC |+|MB |+|MD |最小,则点M 为所求.又k AC =6-23-1=2, ∴直线AC 的方程为y -2=2(x -1),即2x -y =0.①又k BD =5-(-1)1-7=-1, ∴直线BD 的方程为y -5=-(x -1),即x +y -6=0.②由①②得⎩⎪⎨⎪⎧ 2x -y =0,x +y -6=0,∴⎩⎪⎨⎪⎧x =2,y =4,∴M (2,。
解析几何例题和知识点总结

解析几何例题和知识点总结解析几何是数学中的一个重要分支,它通过坐标和方程来研究几何图形的性质和关系。
在学习解析几何的过程中,掌握典型的例题和重要的知识点是非常关键的。
接下来,让我们一起深入探讨一些常见的解析几何例题,并对相关知识点进行总结。
一、直线的方程直线是解析几何中最基本的图形之一。
直线的方程有多种形式,如点斜式、斜截式、两点式、一般式等。
例如:已知直线经过点$(1,2)$,斜率为$3$,求直线方程。
我们可以使用点斜式:$y y_1 = k(x x_1)$,其中$(x_1, y_1)$是已知点的坐标,$k$是斜率。
代入可得:$y 2 = 3(x 1)$,化简得到:$y = 3x 1$直线方程的一般式为$Ax + By + C = 0$,其中$A$、$B$不同时为$0$。
知识点总结:1、掌握直线斜率的计算方法,若两点坐标为$(x_1, y_1)$,$(x_2, y_2)$,则斜率$k =\frac{y_2 y_1}{x_2 x_1}$。
2、熟练运用各种直线方程的形式,根据已知条件选择合适的形式来求解直线方程。
二、圆的方程圆的标准方程为$(x a)^2 +(y b)^2 = r^2$,其中$(a, b)$是圆心坐标,$r$是半径。
例题:求以点$(2, -1)$为圆心,半径为$3$的圆的方程。
答案为:$(x 2)^2 +(y + 1)^2 = 9$圆的一般方程为$x^2 + y^2 + Dx + Ey + F = 0$,通过配方可以转化为标准方程。
知识点总结:1、理解圆的标准方程和一般方程的形式及特点。
2、能根据已知条件求出圆的方程,包括圆心和半径的确定。
三、椭圆椭圆的标准方程有两种形式:$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$(焦点在$x$轴上)和$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$(焦点在$y$轴上),其中$a$和$b$分别表示长半轴和短半轴的长度。
「空间解析几何复习资料含答案」

空间解析几何练习题1. 求点),,(c b a M 分别关于(1)xz 坐标面(2)x 轴(3)原点 对称点的坐标.2. 设 )2,,3(x A -与)4,2,1(-B 两点间的距离为29,试求x .3. 证明 )3,2,1(A )5,1,3(B )3,4,2(C 是一个直角三角形的三个顶点.4. 设ABC ∆的三边a BC =,b CA =,c AB =,三边的中点依次为D ,E,F ,试用向量c b a表示 AD ,BE ,CF ,并证明:0=++CF BE AD .5. 已知:k j i a 2+-=,k j i b -+=3求b a 32+,b a 32-.6. 已知:向量a 与x 轴,y 轴间的夹角分别为060=α,0120=β求该向量a 与z 轴间的夹角γ.7. 设向量a 的模是5,它与x 轴的夹角为4π,求向量a 在x 轴上的投影. 8. 已知:空间中的三点)2,1,0(-A ,)5,3,1(-B ,)2,1,3(--C 计算:AC AB 32-,AC AB 4+.9. 设{}1,0,2-=a ,{}2,2,1--=b 试求b a -,b a 52+,b a +3. 10. 设:{}1,2,2-=a ,试求与a 同方向的单位向量.11. 设:k j i a 253++=,k j i b 742--=,k j i c 45-+=,c b a u -+=34试求(1)u 在y 轴上的投影;(2)u 在x 轴和z 轴上的分向量;. 12. 证明:22)()(b a b a b a -=-⋅+. 13. 设:{}1,0,3-=a ,{}3,1,2--=b 求b a ⋅,∧⋅)(b a .14. 设→→→→-+=k j x i a 2,→→→→+-=k j i b 23且→→⊥b a 求x 15. 设{}2,1,0-=a ,{}1,1,2-=b 求与a 和b 都垂直的单位向量.16. 已知:空间中的三点)0,1,1(A ,)3,1,2(-B ,)2,1,2(-C 求ABC ∆的面积.17. (1)设a ∥b 求b a ⋅ (2)1==求b a ⋅18. 3=5=,试确定常数k 使b k a +,b k a -相互垂直.19. 设向量a 与b 互相垂直,∧⋅)(c a 3π=,∧⋅)(c b 6π=1=2=3=b ++.20. 设:k j i a 53+-=,k j i b 32+--=求b a ⋅21. 设:k j i a --=63,k j i b 54-+=求(1)a a ⋅;(2))3()23(b a b a -⋅+;(3)a 与b 的夹角.22. 设:∧⋅)(b a 6π=1=3=,.23. 设:{}2,1,1-=a ,{}1,2,1--=b ,试求:(1)b a ⋅;(2)b a ⨯;(3)∧⋅)cos(b a .24. 3=26=72=,求b a ⋅.25. 设a 与b 相互垂直,3=4=,试求(1))()(b a b a -⨯+;(2))2()3(b a b a -⨯-. 26. 设:0=++c b a 证明:a c c b b a ⨯=⨯=⨯27. 已知:k j i a -+=23,k j i b 2+-=,求(1)b a ⨯;(2))32()2(b a b a -⨯+;(3)i b a ⨯+)((4)b i a +⨯. 28. 求与{}1,2,2=a {}6,10,8---=b 都垂直的单位向量.29. 已知:{}1,6,3--=a ,{}5,4,1-=b ,{}12,4,3-=c 求c b a b c a )()(⋅+⋅在向量c 上的投影. 30. 设:d c b a ⨯=⨯,d b c a ⨯=⨯且c b ≠,d a ≠证明d a -与c b -必共线. 31. 设:b a 3+与b a 57-垂直,b a 4-与b a 27-垂直,求非零向量a 与b 的夹角.32. 设:{}6,3,2-=a {}2,2,1--=b 向量c 在向量a 与b 423=,求向量c 的坐标.33. 4=3=,∧⋅)(b a 6π=求以b a 2+和b a 3-为边的平行四边形面积.34. 求过点)1,2,7(0-P ,且以{}3,4,2-=n 为法向量的平面方程.ﻩ35. 过点)1,0,1(0-P 且平行于平面53=--z y x 的平面方程. ﻩ36. 过点)2,3,1(-M 且垂直于过点)1,2,2(-A 与)1,2,3(B 的平面方程. 37. 过点)2,1,3(-A ,)1,1,4(--B ,)2,0,2(C 的平面方程.38. 过点)1,1,2(0P 且平行于向量{}1,1,2=a 和{}3,2,3-=b 的平面方程.39. 过点M o (1,1-,1)且垂直于平面01201=+++=+--z y x z y x 及的平面方程. 40. 将平面方程 01832=+-+z y x 化为截距式方程,并指出在各坐标轴上的截距.41. 建立下列平面方程(1)过点(3-,1,2-)及z 轴;(2)过点A(3-,1,2-)和B(3,0,5)且平行于x 轴; (3)平行于x y 面,且过点A(3,1,5-);(4)过点P 1(1,5-,1)和P 2(3,2,2-)且垂直于x z 面. 42. 求下列各对平面间的夹角(1),62=+-z y x 32=++z y x ;(2)09543=--+z y x ,07662=-++z y x . 43. 求下列直线方程(1)过点(2,1-,3-)且平行于向量{}123,,--=s ; (2)过点M o (3,4,2-)且平行z 轴; (3)过点M 1(1,2,3)和M 2(1,0,4); (4)过原点,且与平面0623=-+-z y x 垂直. 44. 将下列直线方程化为标准方程(1)⎩⎨⎧=--+=-+-084230432z y x z y x ; (2)⎩⎨⎧-=+=422z y y x ; (3)⎩⎨⎧=+=-+00123z y z x45. 将下列直线方程化成参数式方程(1)⎩⎨⎧-==-+-250125z y z y x ; (2)⎪⎩⎪⎨⎧=-+=-025126y z x .46. 求过点(1,1,1)且同时平行于平面012=+-+z y x 及012=+-+z y x 的直线方程.47. 求过点(3,1,2-)且通过直线12354zy x =+=-的平面方程. 48. 求通过两直线211111-=-+=-z y x 与 112111-=+=--z y x 的平面方程. 64.求下列各对直线的夹角 (1)74211+=-=-z y x ,131256--=-=+z y x ; (2)⎩⎨⎧=-+-=-+-012309335z y x z y x ,⎩⎨⎧=-++=+-+0188302322z y x z y x .49. 证明直线31141+=-=-z y x 与 ⎩⎨⎧=--+=++0207z y x z y x 相互平行. 50. 设直线 l的方程为:nz y x 42311+=--=- 求n为何值时,直线l 与平面052=+--z y x 平行?51. 作一平面,使它通过z 轴,且与平面0752=--+z y x 的夹角为3π.52. 设直线l在平面01:=+++z y x π 内,通过直线⎩⎨⎧=+=++0201:1z x z y l与平面π的交点,且与直线l1垂直、求直线l 的方程. 53. 求过点(1,2,1)而且与直线⎩⎨⎧=-+-=+-+01012z y x z y x 与 ⎩⎨⎧=+-=+-02z y x z y x 平行的平面方程. 54. 一动点到坐标原点的距离等于它到平面04=-z 的距离,求它的轨迹方程.55. 直线⎩⎨⎧=-+=-+023012:z x y x l 与平面012:=--+z y x π 是否平行?若不平行,求直线l与平面π的交点,若平行,求直线l 与平面π的距离.56. 设直线l经过两直线35811:1--==--z y x l ,⎪⎩⎪⎨⎧--=+=+=tz t y tx l 101152143:2 的交点,而且与直线l 1与l 2都垂直,求直线l 的方程. 57. 已知直线:⎩⎨⎧=-+-=+-+04201:1z y x z y x l 及点 )213(,,-p 过点p作直线l与直线l 1垂直相交,求直线l的方程.58. 方程:019224222=-+--++z y x z y x 是否为球面方程,若是球面方程,求其球心坐标及半径. 59. 判断方程:11462222=-+-++z y x z y x 是否为球面方程,若是球面方程,求其球心坐标及半径.60. 将曲线:⎩⎨⎧==052y xz 绕x 轴旋转一周,求所成的旋转曲面方程.61. 将曲线:⎩⎨⎧==+0369422z y x 绕y 轴旋转一周,求所成的旋转曲面方程.62. 说明下列旋转曲面是怎样形成的(1)10343222=++z y x ; (2)24222=+-z y x ; (3)1222=--z y x ; (4)222)(y x a z +=-. 63. 指出下列方程在空间中表示什么样的几何图形(1)14322=+y x ; (2)13222=-y x ; (3)x z 42=; (4)13422=+z y .自测题 (A )(一) 选择题1.点M)5,1,4(-到 x y 坐标面的距离为( )A.5 B.4 C.1 D.422.点A )3,1,2(-关于y z 坐标面的对称点坐标 ( ) A.)3,1,2(-- B .)3,1,2(-- C.)3,1,2(- D .)3,1,2(-- 3.已知向量{}{}{}3,1,4,2,2,2,1,5,3--==-=c b a ,则=+-c b a 432( )A .{}16,0,20B .{}20,4,5-C .{}20,0,16- D.{}16,0,20- 4.设向量k j i a 424--=,k j i b 236+-=,则)3)(23(b a b a +-=( ) A.20 B .16- C.32 D.32-5.已知:→→-AB prj D C B A CD,则)2,3,3(),1,1,1(),7,1,5(),3,2,1(= ( )A.4 B .1 C.21D.2 6.设=-⨯+-+=+-=)()(22b a b a k j i b k j i a ,则, ( ) A .k j i 53++- B.k j i 1062++- C.k j i 1062-- D .k j i 543++ 7.设平面方程为0=-y x ,则其位置( )A .平行于x 轴 B.平行于y 轴 C.平行于z 轴 D.过z 轴. 8.平面0372=++-z y x 与平面0153=-++z y x 的位置关系( ) A.平行 B.垂直 C.相交 D.重合 9.直线37423zy x =-+=-+与平面03224=---z y x 的位置关系( ) A.平行 B .垂直 C.斜交 D .直线在平面内 10.设点)0,1,0(-A 到直线⎩⎨⎧=-+=+-07201z x y 的距离为( )A.5 B .61 C.51 D.81 (二) 填空题1.设=--x B x A ,则,两点间的距离为,,与29)421()2,,3(_________.2.设c b a u 23-+-=,c b a v +-=2,则=-v u 32_______________. 3.当m=_____________时,k j i 532+-与k j m i 23-+互相垂直.4.设kj i a ++=2,kj i b 22+-=,kj i c 243+-=,则)(b a prj c += .4. 设k j i a +-=2,k j i b 32-+=,则)2()2(b a b a -⨯+=_________. 5. 与)0,3,4()1,2,3(--B A 和等距离的点的轨迹方程为_______________. 6. 过点),,(715,),,(204-且平行于z 轴的平面方程_______________. 7. 设平面:03222,01=--+=+-+z y x z y x 与 平行,则它们之间的距离_________.8. 过点),,(382-且垂直平面0232=--+z y x 直线方程为______________. 10.曲面方程为:44222=++z y x ,它是由曲线________绕_____________旋转而成的.(三) 解答题1.求平行于{}的单位向量2,3,6-=a .2.已知作用于一点的三个力{}{}{}5,4,3,3,2,1,4,3,2321-==--=F F F 求合力的大小与方向.3. 如果{}1,1,2-=a ,{}1,2,1-=b 求a 在b 上的投影.4. 用向量方法,求顶点在)4,4,3(),5,3,1(),1,1,2(-----的三角形的三个内角. 5. 设k i a 2+-=,k j i b -+=2,k j i c 22++=,试将下列各式用k j i ,,表示. (1) c b a ⨯⨯)(; (2))()(c a b a ⨯⨯⨯.6. 求经过点(1,2,0)且通过z 轴的平面方程.7. 在平面02=--z y x 上找一点p,使它与点),5,1,2()1,3,4(-)3,1,2(--及之间的距离相等. 8. 求过 )1,0,0(),0,1,0(),0,0,1( 的圆的方程,并求该圆在坐标平面xoy 上的投影曲线方程. 9.求过点(1,2,1)且同时平行0132=-++z y x 和053=+-+z y x 两平面的直线方程. 10.方程:12222=++z y x 表示什么图形?自测题(B)(一) 选择题1.设{}{}{}0,2,1,3,1,1,1,3,2-=-=-=c b a ,则=⨯⨯c b a )(( ) A .8 B .10 C.{}1,1,0-- D.{}21,1,22.设{}{}2,2,2,2,1,1-=-=b a ,则同时垂直于a 和b 的单位向量( ) A.}0,21,21{± B.}0,21,21{± C.}0,2,2{± D.}0,2,2{±3.若==-+=b a b k j i a ,则,14//236( ) A.)4612(k j i -+± B.)612(j i +± C.)412(k i -± D.)46(k j -± 4.若ϕ的夹角与,则3121321)2,1,2(),1,2,2(),1,1,1(M M M M M M M ( ) A .6π B .2π C.3π D.4π5.过)320()231(),412(321,,和,,,,M M M ---,的平面方程( ) A.015914=--+z y x B.06872=--+z y x C .015914=-+-z y x D.015914=-++z y x 6.求平面062=-+-z y x 与平面052=-++z y x 的夹角( ) A.2π B .6π C.3π D .4π 7.直线⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A 各系数满足( )条件,使它与y 轴相交.A.021==A A B.2121D D B B =C.021==C CD.021==D D 8.设点⎩⎨⎧=-+-=+-+-04201)2,1,3(z y x z y x l M o ,直线,则M O 到l 的距离为( )A .223 B .553 C.453 D.229.直线夹角为与平面62241312=++-=-=-z y x z y x ( ) A.30o B .60o C .90o D .65arcsin10.过点)5,2,1(---且和三个坐标平面都相切的球面方程( )A .22225)1()1()1(=+++++z y x B.22225)5()5()5(=+++++z y x C.22225)2()2()2(=+++++z y x D.22225)5()5()5(=-+-+-z y x (二) 填空题1.设k j i a 32+-=,j i b +=2,k j i c ++-=,则c b a 与+是否平行__________. 2.设}8,5,3{=a ,}7,4,2{--=b ,}4,1,5{-=c ,则c b a -+34在x 轴上的投影_________________.3.化简:=⨯--⨯+++⨯++a c b b c b a c c b a )()()(__________________.4.直线 ⎩⎨⎧=---=-+-01205235:z y x z y x l 和平面 07734:=-+-z y x π的___________位置关系.5.过直线⎩⎨⎧=+-+=-+-025014z y x z y x 且与x 轴平行的平面方程___________________.6.原点==+-k kz y x ,则,的距离为到平面262)0,0,0(_________________. 7.与平面0522=+++z y x ,且与三个坐标面所构成的四面体体积为1的平面方程_____________________.8.动点到点(0,0,5)的距离等于它到x 轴的距离的曲面方程为________________. 9.曲面方程:259916222=--z y x 则曲面名称为________________.10.曲线⎪⎩⎪⎨⎧-+-=--=2222)1()1(2y x z yx z 在y z 面上的投影方程______________. (三) 解答题1.设}0,1,1{},1,1,0{},1,1,1{===c b a 并令c z b y a x d ++=(x ,y ,z 为数量) 求 (1)d ; (2)当z y x d ,,}3,2,1{时,=. 2.求平行于}2,3,6{-=a 的单位向量.3.确定k值,使三个平面:328,1423,23=--=++=+-z y x z y x z y kx 通过同一条直线.4.已知两个不平行的向量a 与b ,2=⋅b a 1=4=,设)(3)(2Xa b b a c -⨯=,求(1))(c b a +⋅; (; (3)的夹角余与c b 弦. 5.求以向量i k k j j i +++,,为棱的平行六面体的体积. 6.垂直平分连接)3,5,2(),1,3,4(B A -的线段的平面方程.7.求与平面4362=+-z y x 平行平面,使点)8,2,3(为这两个平面公垂线中点.8.在平面02=--z y x 上找一点p 使它与点)3,1,2()1,3,4(),5,1,2(---及之间的距离相等. 9.方程:0448422=-+-+y x y x 表示什么曲面?9. 方程组⎩⎨⎧=-++=--++0122046222z y x y x z y x 图形是什么?若是一个圆,求出它的中心与半径.参考答案 参考答案练习题1.(1)),,(c b a -; (2)),,(c b a --; (3)),,(c b a ---.2.51-==x x 或. 3.算出距离后,证明满足勾股定理 4.略5.k j i b a ++=+1132; k j i b a 75732+--=-.6.13545或=γ. 7.225. 8.}13,4,11{4},18,8,11{32-=+-=-AC AB AC AB .9.}5,2,7{3},12,10,9{52},1,2,1{--=+--=+=-b a b a b a . 10.单位向量为}31,32,32{-.11.(1)7; (2)u 在x 轴的分向量i 13,u 在z 轴的分向量k 9-; (3)299=u.12.利用数量积运算法则. 13.9-=⋅b a ; 70359arccos)(-=∧πb a . 14.x =4. 15.单位向量:)24(211k j i ++±. 16.1723=∆ABC S .17.(1)若a 与b 同向,则b a b a ⋅=⋅,若a 与b反向,则b a b a ⋅-=⋅;(2))cos(b a ∧.18.53±=k . 19.3617+=++c b a . 20.16=⋅b a .21.(1)46; (2)2-; (3)4838arccos)(-=∧πb a . 22.23. 23.(1)3; (2)k j i 333--; (3)21.24.30±。
2025年高考数学解析几何知识点总结

2025年高考数学解析几何知识点总结解析几何是高中数学的重要组成部分,在高考中占有较大的比重。
它将代数与几何巧妙地结合在一起,通过建立坐标系,用代数方法研究几何图形的性质。
下面为大家详细总结 2025 年高考数学中解析几何的相关知识点。
一、直线方程1、直线的倾斜角与斜率倾斜角:直线与 x 轴正方向所成的角,范围是0, π)。
斜率:当倾斜角不是 90°时,斜率 k =tanα(α 为倾斜角)。
过两点 P1(x1, y1),P2(x2, y2)(x1 ≠ x2)的直线的斜率 k =(y2 y1) /(x2 x1)。
2、直线方程的几种形式点斜式:y y1 = k(x x1) (直线过点(x1, y1),斜率为 k)斜截式:y = kx + b (k 为斜率,b 为直线在 y 轴上的截距)两点式:(y y1) /(y2 y1) =(x x1) /(x2 x1) (直线过两点(x1, y1),(x2, y2))截距式:x / a + y / b = 1 (a 为直线在 x 轴上的截距,b 为直线在 y 轴上的截距)一般式:Ax + By + C = 0 (A、B 不同时为 0)二、两条直线的位置关系1、平行两条直线斜率都不存在时,平行。
两条直线斜率都存在时,斜率相等,纵截距不相等,则平行。
2、垂直两条直线斜率都存在时,斜率之积为-1,则垂直。
一条直线斜率为 0,另一条直线斜率不存在,则垂直。
3、交点联立两条直线的方程,求解即可得到交点坐标。
三、圆的方程1、圆的标准方程(x a)²+(y b)²= r²(圆心为(a, b),半径为 r)2、圆的一般方程x²+ y²+ Dx + Ey + F = 0 (D²+ E² 4F > 0 时,表示圆,圆心为(D/2, E/2),半径为√(D²+ E² 4F) / 2)四、直线与圆的位置关系1、几何法比较圆心到直线的距离 d 与半径 r 的大小关系。
数学解析几何2024高考知识点清单总结与题型练习

数学解析几何2024高考知识点清单总结与题型练习一、直线的方程与性质直线的一般式方程为Ax+By+C=0,其中A、B、C为常数且A与B不同时为0。
直线的斜截式方程为y=kx+b,其中k为直线的斜率,b为直线与y轴的交点坐标。
直线的截距式方程为x/a+y/b=1,其中a、b为直线与坐标轴的截距。
二、直线与平面的位置关系直线与平面的关系可分为以下几种情况:1. 直线与平面相交:直线与平面交于一点,方程组有唯一解。
2. 直线与平面平行:直线与平面无交点,方程组无解。
3. 直线包含于平面:直线上的每一点都在平面上,方程组有无数解。
三、平面的方程与性质平面的一般式方程为Ax+By+Cz+D=0,其中A、B、C、D为常数且A、B、C不同时为0。
平面的点法式方程为Ax+By+Cz+D=0,其中A、B、C为法向量的分量。
平面的截距式方程为x/a+y/b+z/c=1,其中a、b、c为平面与坐标轴的截距。
四、直线与直线的位置关系直线与直线的位置关系可分为以下情况:1. 相交于一点:两条直线交于一点,方程组有唯一解。
2. 平行:两条直线的斜率相等但截距不相等,方程组无解。
3. 重合:两条直线完全重合,方程组有无数解。
五、直线与平面的位置关系直线与平面的位置关系可分为以下情况:1. 相交于一点:直线与平面交于一点,方程组有唯一解。
2. 平行:直线与平面无交点,方程组无解。
3. 直线包含于平面:直线上的每一点都在平面上,方程组有无数解。
六、空间几何体的体积与表面积计算常见空间几何体的体积与表面积计算公式如下:1. 立方体体积公式:V=a^3,其中a为边长。
2. 球体体积公式:V=(4/3)πr^3,其中r为半径。
3. 圆柱体体积公式:V=πr^2h,其中r为底面半径,h为高度。
4. 圆锥体体积公式:V=(1/3)πr^2h,其中r为底面半径,h为高度。
七、题型练习1. 已知直线L1:2x+y-1=0与直线L2:x-y+2=0,求直线L1与L2的交点坐标。
几何证明与解析几何例题和知识点总结

几何证明与解析几何例题和知识点总结在数学的广袤领域中,几何证明与解析几何犹如两颗璀璨的明珠,闪耀着智慧的光芒。
它们既是数学学习中的重点,也是难点。
接下来,让我们一同深入探索这两个重要的数学分支,通过例题来加深对知识点的理解和掌握。
一、几何证明几何证明是通过逻辑推理和几何定理来证明几何图形的性质和关系。
(一)基本定理和公理1、两点确定一条直线。
2、两点之间线段最短。
3、过直线外一点有且仅有一条直线与已知直线平行。
(二)三角形的相关定理1、三角形内角和为 180 度。
2、三角形的任意两边之和大于第三边。
(三)全等三角形的判定1、 SSS(边边边):三边对应相等的两个三角形全等。
例:在三角形 ABC 和三角形 DEF 中,AB = DE,BC = EF,AC = DF,所以三角形 ABC 全等于三角形 DEF。
2、 SAS(边角边):两边及其夹角对应相等的两个三角形全等。
例如:已知三角形 ABC 和三角形 DEF,AB = DE,∠A =∠D,AC = DF,可证明两个三角形全等。
3、 ASA(角边角):两角及其夹边对应相等的两个三角形全等。
4、 AAS(角角边):两角及其一角的对边对应相等的两个三角形全等。
5、 RHS(直角、斜边、边):在直角三角形中,斜边和一条直角边对应相等的两个直角三角形全等。
(四)相似三角形的判定1、平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
2、三边对应成比例的两个三角形相似。
3、两边对应成比例且夹角相等的两个三角形相似。
4、两角对应相等的两个三角形相似。
(五)例题分析例 1:已知在三角形 ABC 中,AB = AC,∠A = 36°,BD 是角平分线。
求证:AD²= CD × AC证明:因为 AB = AC,∠A = 36°,所以∠ABC =∠C = 72°。
因为 BD 是角平分线,所以∠ABD =∠DBC = 36°。
(完整版)解析几何题库

解析几何题库一、选择题1.已知圆C 与直线x -y =0 及x -y -4=0都相切,圆心在直线x +y =0上,则圆C 的方程为 A.22(1)(1)2x y ++-= B. 22(1)(1)2x y -++= C.22(1)(1)2x y -+-= D. 22(1)(1)2x y +++=【解析】圆心在x +y =0上,排除C 、D,再结合图象,或者验证A 、B 中圆心到两直线的距离等于半径2即可. 【答案】B 2.直线1y x =+与圆221x y +=的位置关系为( )A .相切B .相交但直线不过圆心C .直线过圆心D .相离【解析】圆心(0,0)为到直线1y x =+,即10x y -+=的距离2d ==,而012<<,选B 。
【答案】B 3.圆心在y 轴上,半径为1,且过点(1,2)的圆的方程为( )A .22(2)1xy +-=B .22(2)1xy ++=C .22(1)(3)1x y -+-=D .22(3)1xy +-=解法1(直接法):设圆心坐标为(0,)b1=,解得2b =,故圆的方程为22(2)1x y +-=。
解法2(数形结合法):由作图根据点(1,2)到圆心的距离为1易知圆心为(0,2),故圆的方程为22(2)1x y +-=解法3(验证法):将点(1,2)代入四个选择支,排除B ,D ,又由于圆心在y 轴上,排除C 。
【答案】A4.点P (4,-2)与圆224x y +=上任一点连续的中点轨迹方程是( )A.22(2)(1)1x y -++= B.22(2)(1)4x y -++=C.22(4)(2)4x y ++-=D.22(2)(1)1x y ++-=【解析】设圆上任一点为Q (s ,t ),PQ 的中点为A (x ,y ),解得:⎩⎨⎧+=-=2242y t x s ,代入圆方程,得(2x -4)2+(2y+2)2=4,整理,得:22(2)(1)1x y -++=【答案】A 5.已知直线12:(3)(4)10,:2(3)230,l kx k y l k x y -+-+=--+=与平行,则k 得值是( )A. 1或3B.1或5C.3或5D.1或2【解析】当k =3时,两直线平行,当k ≠3k -3,解得:k =5,故选C 。
解析几何知识点管综

解析几何知识点管综一、直线。
1. 直线的倾斜角与斜率。
- 倾斜角α:直线l向上的方向与x轴正方向所成的最小正角,α∈[0,π)。
- 斜率k = tanα(α≠(π)/(2)),经过两点P_1(x_1,y_1),P_2(x_2,y_2)(x_1≠x_2)的直线的斜率k=(y_2 - y_1)/(x_2 - x_1)。
2. 直线方程的几种形式。
- 点斜式:y - y_0=k(x - x_0)(直线过点(x_0,y_0),斜率为k)。
- 斜截式:y = kx + b(k为斜率,b为直线在y轴上的截距)。
- 两点式:(y - y_1)/(y_2 - y_1)=(x - x_1)/(x_2 - x_1)(x_1≠ x_2,y_1≠ y_2,直线过两点(x_1,y_1),(x_2,y_2))。
- 截距式:(x)/(a)+(y)/(b)=1(a≠0,b≠0,a为x轴上的截距,b为y轴上的截距)。
- 一般式:Ax + By+C = 0(A、B不同时为0)。
3. 两直线的位置关系。
- 平行:l_1:y = k_1x + b_1,l_2:y = k_2x + b_2,则l_1∥ l_2Leftrightarrow k_1 = k_2且b_1≠ b_2;对于l_1:A_1x + B_1y + C_1 = 0,l_2:A_2x + B_2y + C_2 = 0,l_1∥ l_2Leftrightarrow(A_1)/(A_2)=(B_1)/(B_2)≠(C_1)/(C_2)。
- 垂直:l_1:y = k_1x + b_1,l_2:y = k_2x + b_2,则l_1⊥ l_2Leftrightarrowk_1k_2=- 1;对于l_1:A_1x + B_1y + C_1 = 0,l_2:A_2x + B_2y + C_2 = 0,l_1⊥l_2Leftrightarrow A_1A_2 + B_1B_2 = 0。
- 相交:联立两直线方程求解交点坐标。
解析几何基础100题

解析几何基础100题一、选择题:1. 若双曲线22221x y a b -=-的离心率为54,则两条渐近线的方程为A0916X Y ±= B 0169X Y ±= C 034X Y ±= D 043X Y±= 解 答:C易错原因:审题不认真,混淆双曲线标准方程中的a 和题目中方程的a 的意义.2. 椭圆的短轴长为2,长轴是短轴的2倍,则椭圆的中心到其准线的距离是解 答:D易错原因:短轴长误认为是b3.过定点(1,2)作两直线与圆2222150x y kx y k ++++-=相切,则k 的取值范围是A k>2B —3〈k<2C k<—3或k>2D 以上皆不对 解 答:D易错原因:忽略题中方程必须是圆的方程,有些学生不考虑2240D E F +->4.设双曲线22221(0)x y a b a b-=>>的半焦距为C ,直线L 过(,0),(0,)a b 两点,已知原点到直线L 的距离为4,则双曲线的离心率为A 2B 2或233C 2D 233解 答:D易错原因:忽略条件0a b >>对离心率范围的限制.5.已知二面角βα--l 的平面角为θ,PA α⊥,PB β⊥,A ,B 为垂足,且PA=4,PB=5,设A 、B 到二面角的棱l 的距离为别为y x ,,当θ变化时,点),(y x 的轨迹是下列图形中的A B C D 解 答: D易错原因:只注意寻找,x y 的关系式,而未考虑实际问题中,x y 的范围。
6.若曲线24y x =-(2)y k x =-+3有两个不同的公共点,则实数 k 的取值范围是A 01k ≤≤B 304k ≤≤ C 314k -<≤ D 10k -<≤ 解 答:C易错原因:将曲线24y x =-转化为224x y -=时不考虑纵坐标的范围;另外没有看清过点(2,—3)且与渐近线y x =平行的直线与双曲线的位置关系。
专题-解析几何知识点汇总(全)
直线的方程1、直线的方程:类型直线方程方向向量d法向量n斜率k截距x轴/y轴/两点式x x1y y1x2x1y2y1(x2x1,y2y1)(y2y1,x1x2)y2y1x2x1点方向式点法向式点斜式截距式斜截式x xy yu va(x x) b(y y) 0(u,v)(v, u)vuab//(b, a)(1,k)( m,n)(1,k)(B, A)(a,b)(k, 1)(n,m)(k, 1)(A,B)//y yk(x x)x y1m ny kx bAx By C 0knm//m/nbCBkAB一般式C A注意:(1)点法向式方程和一般式方程可以表示所有的直线;(2)两点式方程和点方向式方程不能表示垂直于x轴或垂直于y轴的直线;(3)点斜式方程和斜截式方程不能表示垂直于x轴的直线;(4)截距式方程不能表示经过原点的直线.2、直线的倾斜角和斜率:(1)直线的倾斜角为平面直角坐标系中直线与x轴正半轴的夹角.取值范围: [0, );(2)直线的斜率:tan , [0,) (, )22k不存在,2;k 0 0k 2 0 0k tan 在[0, )和 k 不存在 = 2(2, )上单调递增.2k 0 2 y 2 y 1(3)若直线过点(x x ,x 1 x 21,y 1),(x 2,y 2),则该直线的斜率k 2 x 1,k R .不存在,x 1 x 23、两条直线的位置关系:已知l 1:a 1x b 1y c 1 0,l 2:a 2x b 2y c 2 0,则(1)系数法:①l 1 l 2 a 1a 2 b 1b 2 0;特别地,若l 1的斜率为k 1,l 2的斜率为k 2,l 1 l 2 k 1 k 2 1;②l 1与l 2相交 a 1b 2 a 2b 1;③l 1与l 2重合 a 1:b 1:c 1 a 2:b 2:c 2;④l 与l a 1:b 1 a 2:b 212平行 a .1:c 1 a 2:c 2或b 1:c 1 b 2:c 2(2)向量法:已知l 的法向量为 n11 (a 1,b 1),l 2的法向量为n 2 (a 2,b 2),则①l l12 n 1 n 20 a 1a 2 b 1b 2 0;特别地,若l 1的斜率为k 1,l 2的斜率为k 2,则l 1 l 2 k 1 k 2 1;②l l1与2相交 n 1与n 2不平行 a 1b 2 a 2b 1;③l 1与l 2平行或重合 n 1与n 2平行 a 1b 2 a 2b 1.(3)行列式法:已知Da 1b 1a ,Db 1xc 12b 2c 2b ,D y a 1c 12a 2c ,则21l 1与l2相交 D 0;②l1与l2重合 D D x D y 0;则③1与2平行 l l D 0.D x、D y 不全为零4、两条相交直线l 1:a 1x b 1y c 1 0和l 2:a 2x b 2y c 2 0的夹角 :(1)若l 1、l 2的法向量分别为n 1 (a 1,b 2)、n 2 (a 2,b 2),且l 1、l 2的方向向量分别为d 1、d 2,则n n 2cos 1n 1 n 2a 1a 2b 1b 2a 12 b 12 a 22 b 22d 1 d 2 或cos, [0,];2d 1 d 2(2)若l 1、l 2的斜率分别为k 1、k 2,且l 1到l 2的角为 1,l 2到l 1的角为 2,则tank k 1k k 2k 1 k 2, [0,);tan 1 2,tan 2 1.1 k 1k 21 k 1k 21 k 1k 225、点到直线的距离公式:(1)点P (x 0,y 0)到直线l :Ax By C 0的距离为dAx 0 By 0 CA B22;(2)直线l 1:Ax By C 1 0与直线l 2:Ax By C 2 0的距离为dC 1 C 2A B22.6、直线l :Ax By C 0同侧/异侧:(1)Ax 0 By 0 C 0(A 0) P (x 0,y 0)在直线l :Ax By C 0(A 0)的右侧;Ax 0 By 0 C 0(A 0) P (x 0,y 0)在直线l :Ax By C 0(A 0)的左侧.(2)点M (x 1,y 1)、N (x 2,y 2)在直线l 同侧 (Ax 1 By 1 C )(Ax 2 By 2 C ) 0;点M (x 1,y 1)、N (x 2,y 2)在直线l 异侧 (Ax 1 By 1 C )(Ax 2 By 2 C ) 0.7、点关于直线的对称问题:点直线P (x 0,y 0)x 轴P (x 0, y 0)y 轴P ( x 0,y 0)y xP (y 0,x 0)y xP ( y 0, x 0)x mP (2m x 0,y 0)y n P (x 0,2n y 0)对称点补充:①点P(x0,y)关于直线y x b的对称的点为P (yb,xb);②点P(x0,y)关于直线y x b的对称的点为P (b y,b x);A(n y) B(m x)③点P(x0,y)关于直线Ax By C 0的对称点P (m,n)满足 m x.n yA B C 022或者P (m,n),其中 8、三线共点问题:三条互不平行的直线l1:a1x b1y c10,直线l2:a2x b2y c20,直线l3:a3x b3y c30共m x0 2AD Ax By C,D 022.A Bn y0 2BDa1点的充要条件是a2b1b2b3c1c20.c3a39、直线系方程:具有某一个共同性质的一簇直线称为直线系.(1)平行直线系:①斜率为k0(常数)的直线系:,例:y 2x b;y kx b(b为参数)②平行于直线A0x By 0的直线系:Ax By C 0(C为参数).(2)过已知点的直线系:①以斜率k作为参数的直线系:y y0 k(x x),直线过定点(x,y);②以斜率k作为参数的直线系:y kx b0,直线过定点(0,b).③过两条直线l1:A1x B1y C10,l2:A2x B2y C20的交点的直线系:A 1x B1y C1(A2x B2y C2) 0( 为参数).注意:对于①②,过定点且平行于y轴或与y轴重合的直线不在直线系内;对于③,其中直线l2不在直线系内.10、定直线上动点与两定点距离和差问题:(1)定直线上动点与两定点距离和:问题已知定直线l上动点P,两个定点A、B,求PA PB的取值范围.取值范围A、B在l的解答步骤同侧 A B,AB, ①作点A关于l的对称点A ;②联结A B,交l于M;③点M为最小值状态点.①联结AB交l于M;②点M为最小值状态点.异侧(2)定直线上动点与两定点距离差:已知定直线l上动点P,两个定点A、B,点A、B到l的距离分别为d1、d2,问题直线AB与直线l的夹角为 ,求PA PB的取值范围.A、B在l的d1与d2的大小关系d1d2取值范围解答步骤①联结AB并延长交l于M;②点M为最大值状态点./①联结BA并延长交l于M;②点M为最小值状态点.①作点A关于l的对称点A ;②联结A B并延长交l于M;③点M为最大值状态点./①作点A关于l的对称点A ;②联结BA 并延长交l于M;2AB cos ,ABAB,ABAB,AB cos同侧d1 d2d 1 d2d 1 d2A B cos ,A BA B,A BA B,AB cos异侧d1d2d1d2点M为最小值状态点.曲线的方程(一)曲线的方程概论1、轴对称的两个曲线:曲线对称轴曲线F(x,y) 0x轴F(x, y) 0y轴y x y x x m y n F( x,y) 0F(y,x) 0F( y, x) 0F(2m x,y) 0F(x,2n y) 0补充:①曲线F (x ,y ) 0关于y x b 对称的曲线方程为F (y b ,x b ) 0;②曲线F (x ,y ) 0关于y x b 对称的曲线方程为F (b y ,b x ) 0.2、中心对称的两个曲线:曲线对称中心曲线F (x ,y ) 03、轴对称的曲线:曲线对称轴条件(m ,n )F (2m x ,2n y ) 0F (x ,y ) 0y x F (y ,x ) F (x ,y )补充:y x F ( y , x ) F (x ,y )x mF (2m x ,y ) F (x ,y )y nF (x ,2n y ) F (x ,y )a b对称。
高中数学解析几何基础复习 题集附答案

高中数学解析几何基础复习题集附答案高中数学解析几何基础复习题集附答案在高中数学中,解析几何是一个非常重要的内容。
解析几何是指在直角坐标系中,通过代数的方法来研究几何问题。
掌握解析几何的基础知识对于学习高中数学以及应用数学都非常有帮助。
为了帮助大家进行复习,下面将提供一些高中数学解析几何基础题目,并附上详细的答案解析。
1. 已知直线L1:2x + 3y = 5和L2: y = 4x - 1,求两直线的交点坐标。
解析:首先将直线L1和L2的方程组合,得到2x + 3(4x - 1) = 5,化简得到14x - 3 = 5,继续化简得到14x = 8,x = 8/14 = 4/7。
代入L2的方程求y的值,得到y = 4(4/7) - 1 = 16/7 - 7/7 = 9/7。
所以两直线的交点坐标为(4/7, 9/7)。
2. 已知直线L:x + y = 4和曲线C:x^2 + y^2 = 5,求直线与曲线的交点坐标。
解析:将直线L的方程代入曲线C的方程中,得到(x + y)^2 + y^2 = 5,展开得到x^2 + y^2 + 2xy + y^2 = 5,化简得到x^2 + 2xy + 2y^2 = 5。
由于直线L与曲线C有交点,所以存在某个x和y满足这个方程。
观察方程的左边,可以发现它可以写成(x + y)^2 + y^2 = 5,也就是(x +y)^2 = 5 - y^2。
由于(x + y)^2必须大于等于0,所以5 - y^2必须大于等于0,解这个不等式得到-√5 ≤ y ≤ √5。
将y的取值范围代入方程(x +y)^2 = 5 - y^2,解得x = 4 - y。
因此,两直线的交点坐标为(x, y) = (4 - y, y),其中-√5 ≤ y ≤ √5。
3. 已知平面内三点A(1, 2),B(3, -4),C(-2, 3),判断是否共线。
解析:判断三点是否共线可以利用向量的共线条件。
设有两个向量AB和AC,若这两个向量共线,则存在一个实数k,使得AB = kAC。
!平面解析几何知识点汇总含答案

平面解析几何1.直线方程、倾斜角与斜率。
2.直线之间的位置关系。
3.圆的方程、半径及圆心坐标。
4.直线与圆的位置关系。
5.椭圆、双曲线及抛物线的标准方程。
6.椭圆、双曲线与抛物线的焦点坐标,焦半径,长轴、短轴、渐近线、准线方程,第二定义,通径长和焦准距。
7.直线与圆锥曲线的位置关系。
例1.已知两点A(-3,4)、B(3,2),过点P(2,-1)的直线l 与线段AB 有公共点.求直线l 的斜率的取值范围.解:如图,为使直线l 与线段AB 有公共点,则直线l 的倾斜角应介于直线PB 的倾斜角与直线PA 的倾斜角之间,所以,当l 的倾斜角小于90°时,有k ≥k PB ;当l 的倾斜角大于90°时,则有k ≤k PA .∵ k PA =4-(-1)-3-2=-1,k PB =2-(-1)3-2=3.∴ k ≤-1或k ≥3.例2. 已知直线kx +y -k =0与射线3x -4y +5=0(x ≥-1)有交点,求实数k 的取值范围.解:kx +y -k =0k(x -1)+y =0,直线系过定点(1,0)斜率k′=-k ,可画图看出k ′∈⎝⎛⎭⎫34,+∞∪⎝⎛⎦⎤-∞,-14,∴ k ∈(-∞,-34)∪⎣⎡⎭⎫14,+∞.(或者由两直线方程联立,消去y 得x =4k -53+4k ≥-1,即4k -14k +3≥0k ≥14或k<-34)例3.已知直线l :5ax -5y -a +3=0.(1) 求证:不论a 为何值,直线l 总经过第一象限; (2) 为使直线l 不经过第二象限,求a 的取值范围.(1) 证明:将直线l 的方程整理为y -35=a(x -15),∴ 直线l 的斜率为a ,且过定点A(15,35),而点A ⎝⎛⎭⎫15,35在第一象限,∴ 直线l 恒过第一象限.(2) 解:要使直线l 不经过第二象限,则直线l 所在的区域介于AO 和AB 之间,如图,包含直线AO ,但不包含直线AB.∴ a ≥3.例4. 两条平行直线分别过点P(-2,-2)、Q(1,3),它们之间的距离为d ,如果这两条直线各自绕着P 、Q 旋转并且保持互相平行.(1) 求d 的变化范围;(2) 用d 表示这两条直线的斜率;(3) 当d 取最大值时,求两条直线的方程.解:(1) (解法1)设过点P(-2,-2)的直线l 1方程为Ax +By +C 1=0,过点Q(1,3)的直线l 2方程为Ax +By +C 2=0,由于点P 、Q 在直线上,得-2A -2B +C 1=0,A +3B +C 2=0, 两式相减得C 1-C 2=3A +5B ,两直线间的距离d =|C 1-C 2|A 2+B 2=|3A +5B|A 2+B 2,即(d 2-9)A 2-30AB +(d 2-25)B 2=0.(*) ① 当B ≠0时,两直线斜率存在,有(d 2-9)⎝⎛⎭⎫A B 2-30⎝⎛⎭⎫A B +d 2-25=0.由d>0及Δ≥0,得(-30)2-4(d 2-9)(d 2-25)≥0, 从而0<d ≤34;② 当B =0时,两直线分别为x =-2与x =1,它们间的距离为3,满足上述结论. 综上所述,d 的取值范围是(0,34]. (解法2)两平行直线在旋转过程中,0<d ≤PQ ,而PQ =34,故d 的取值范围是(0,34],(2) 当B ≠0时,两直线的斜率存在,从方程(*)中解得A B =15±d 34-d 2d 2-9,直线的斜率k=-AB =-15±d 34-d 2d 2-9.(3) 当d =34时,k =-A B =-35,对应两条直线分别为l 1:3x +5y +16=0,l 2:3x +5y-18=0.例5. 已知以点C ⎝⎛⎭⎫t ,2t (t ∈R ,t ≠0)为圆心的圆与x 轴交于O 、A 两点,与y 轴交于O 、B 两点,其中O 为原点.(1) 求证:△OAB 的面积为定值;(2) 设直线y =-2x +4与圆C 交于点M 、N ,若OM =ON ,求圆C 的方程.(1) 证明:∵圆C 过原点O ,∴OC 2=t 2+4t 2.设圆C 的方程是(x -t)2+⎝⎛⎭⎫y -2t 2=t 2+4t2 .令x =0,得y 1=0,y 2=4t ;令y =0,得x 1=0,x 2=2t ,∴S △OAB =12OA ×OB =12×⎪⎪⎪⎪4t ×|2t|=4,即△OAB 的面积为定值.(2) 解:∵OM =ON ,CM =CN ,∴OC 垂直平分线段是MN.∵k MN =-2,∴k oc =12,∴直线OC 的方程是y =12x .∴2t =12t ,解得t =2或t =-2.当t =2时,圆心C 的坐标为(2,1),OC =5,此时C 到直线y =-2x +4的距离d =15<5,圆C 与直线y =-2x +4相交于两点.当t =-2时,圆心C 的坐标为(-2,-1),OC =5,此时C 到直线y =-2x +4的距离d =95>5,圆C与直线y =-2x +4不相交,∴t =-2不符合题意故舍去.∴圆C 的方程为 (x -2)2+(y -1)2=5 .例6. 在平面直角坐标系xOy 中,已知圆C :x 2+y 2=r 2和直线l :x =a(其中r 和a 均为常数,且0 < r < a),M 为l 上一动点,A 1,A 2为圆C 与x 轴的两个交点,直线MA 1,MA 2与圆C 的另一个交点分别为P 、Q.(1) 若r =2,M 点的坐标为(4,2),求直线PQ 方程; (2) 求证:直线PQ 过定点,并求定点的坐标. (1) 解:当r =2,M(4,2), 则A 1(-2,0),A 2(2,0).直线MA 1的方程:x -3y +2=0,解⎩⎪⎨⎪⎧x 2+y 2=4,x -3y +2=0得P ⎝⎛⎭⎫85,65. 直线MA 2的方程:x -y -2=0, 解⎩⎪⎨⎪⎧x 2+y 2=4,x -y -2=0得Q(0,-2). 由两点式,得直线PQ 方程为2x -y -2=0.(2) 证明:(证法1)由题设得A 1(-r ,0),A 2(r ,0). 设M(a ,t),直线MA 1的方程是y =t a +r (x +r),直线MA 2的方程是y =ta -r(x -r).解⎩⎪⎨⎪⎧x 2+y 2=r 2,y =ta +r(x +r ), 得P ⎝ ⎛⎭⎪⎫r (a +r )2-rt 2(a +r )2+t 2,2tr (a +r )(a +r )2+t 2. 解⎩⎪⎨⎪⎧x 2+y 2=r 2,y =ta -r(x -r ), 得Q ⎝ ⎛⎭⎪⎫rt 2-r (a -r )2(a -r )2+t2,-2tr (a -r )(a -r )2+t 2. 于是直线PQ 的斜率k PQ =2ata 2-t 2-r 2,直线PQ 的方程为y -2tr (a +r )(a +r )2+t 2=2ata 2-t 2-r 2(x -r (a +r )2-rt 2(a +r )2+t 2).上式中令y =0,得x =r 2a,是一个与t 无关的常数.故直线PQ 过定点⎝⎛⎭⎫r 2a ,0.(证法2)由题设得A 1(-r ,0),A 2(r ,0). 设M(a ,t),直线MA 1的方程是y =ta +r (x +r),与圆C 的交点P 设为P(x 1,y 1).直线MA 2的方程是:y =ta -r(x -r),与圆C 的交点Q 设为Q(x 2,y 2).则点P(x 1,y 1),Q(x 2,y 2)在曲线[(a +r)y -t(x +r)][(a -r)y -t(x -r)]=0上, 化简得(a 2-r 2)y 2-2ty(ax -r 2)+t 2(x 2-r 2)=0,①又有P(x 1,y 1),Q(x 2,y 2)在圆C 上,圆C :x 2+y 2-r 2=0. ②①-t 2×②得(a 2-r 2)y 2-2ty(ax -r 2)-t 2(x 2-r 2)-t 2(x 2+y 2-r 2)=0, 化简得(a 2-r 2)y -2t(ax -r 2)-t 2y =0.所以直线PQ 的方程为(a 2-r 2)y -2t(ax -r 2)-t 2y =0.③在③中令y =0得x =r 2a,故直线PQ 过定点⎝⎛⎭⎫r 2a ,0 例7. 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个焦点是F(1,0),且离心率为12.(1) 求椭圆C 的方程;(2) 设经过点F 的直线交椭圆C 于M 、N 两点,线段MN 的垂直平分线交y 轴于点P(0,y 0),求y 0的取值范围.解:(1) 设椭圆C 的半焦距是c. 依题意,得c =1.因为椭圆C 的离心率为12,所以a =2c =2,b 2=a 2-c 2=3.故椭圆C 的方程为x 24+y 23=1.(2) 当MN ⊥x 轴时,显然y 0=0.当MN 与x 轴不垂直时,可设直线MN 的方程为y =k(x -1)(k ≠0).由⎩⎪⎨⎪⎧y =k (x -1),x 24+y 23=1,消去y 并整理得(3+4k 2)x 2-8k 2x +4(k 2-3)=0. 设M(x 1,y 1),N(x 2,y 2),线段MN 的中点为Q(x 3,y 3),则x 1+x 2=8k 23+4k 2.所以x 3=x 1+x 22=4k 23+4k 2,y 3=k(x 3-1)=-3k 3+4k 2. 线段MN 的垂直平分线的方程为y +3k 3+4k 2=-1k ⎝⎛⎭⎫x -4k 23+4k 2.在上述方程中,令x =0,得y 0=k 3+4k 2=13k+4k . 当k <0时,3k +4k ≤-43;当k >0时,3k +4k ≥4 3.所以-312≤y 0<0或0<y 0≤312.综上,y 0的取值范围是⎣⎡⎦⎤-312,312.例8.如图,椭圆C :x 216+y24=1的右顶点是A ,上、下两个顶点分别为B 、D ,四边形OAMB是矩形(O 为坐标原点),点E 、P 分别是线段OA 、AM 的中点.(1) 求证:直线DE 与直线BP 的交点在椭圆C 上;(2) 过点B 的直线l 1、l 2与椭圆C 分别交于点R 、S(不同于B),且它们的斜率k 1、k 2满足k 1k 2=-14,求证:直线RS 过定点,并求出此定点的坐标.证明:(1) 由题意,得A(4,0),B(0,2),D(0,-2),E(2,0),P(4,1).所以直线DE的方程为y =x -2,直线BP 的方程为y =-14x +2.解方程组⎩⎪⎨⎪⎧y =x -2,y =-14x +2,得⎩⎨⎧x =165,y =65,所以直线DE 与直线BP 的交点坐标为⎝⎛⎭⎫165,65.因为⎝⎛⎭⎫165216+⎝⎛⎭⎫6524=1,所以点⎝⎛⎭⎫165,65在椭圆x 216+y 24=1上.即直线DE 与直线BP 的交点在椭圆C 上.(2) 直线BR 的方程为y =k 1x +2.解方程组⎩⎪⎨⎪⎧y =k 1x +2,x 216+y 24=1,得⎩⎪⎨⎪⎧x =0,y =2或⎩⎪⎨⎪⎧x =-16k 11+4k 21,y =2-8k 211+4k 21, 所以点R 的坐标为⎝ ⎛⎭⎪⎫-16k 11+4k 21,2-8k 211+4k 21.因为k 1k 2=-14,所以直线BS 的斜率k 2=-14k 1.直线BS 的方程为y =-14k 1x +2.解方程组⎩⎨⎧y =-14k 1x +2,x 216+y 24=1,得⎩⎪⎨⎪⎧x =0,y =2或⎩⎪⎨⎪⎧x =16k 11+4k 21,y =8k 21-21+4k 21.所以点S 的坐标为⎝ ⎛⎭⎪⎫16k 11+4k 21,8k 21-21+4k 21.所以R 、S 关于坐标原点O 对称,故R 、O 、S 三点共线,即直线RS 过定点O ,O 点坐标为(0,0).例9.设A 、B 分别为双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右顶点,双曲线的实轴长为43,焦点到渐近线的距离为 3.(1) 求双曲线的方程;(2) 已知直线y =33x -2与双曲线的右支交于M 、N 两点,且在双曲线的右支上存在点D ,使OM →+ON →=tOD →,求t 的值及点D 的坐标.解:(1) 由题意知a =23,故一条渐近线为y =b 23x ,即bx -23y =0,则|bc|b 2+12=3,得b 2=3,故双曲线的方程为x 212-y 23=1.(2) 设M(x 1,y 1),N(x 2,y 2),D(x 0,y 0),则x 1+x 2=tx 0,y 1+y 2=ty 0, 将直线方程代入双曲线方程得x 2-163x +84=0, 则x 1+x 2=163,y 1+y 2=12,则⎩⎨⎧x 0y 0=433,x 2012-y 203=1,得⎩⎨⎧x 0=43,y 0=3, 故t =4,点D 的坐标为(43,3).例10. 已知抛物线C :y =ax 2(a 为非零常数)的焦点为F ,点P 为抛物线C 上一个动点,过点P 且与抛物线C 相切的直线记为l.(1) 求F 的坐标;(2) 当点P 在何处时,点F 到直线l 的距离最小?解:(1) 抛物线方程为x 2=1ay ,故焦点F 的坐标为⎝⎛⎭⎫0,14a . (2) 设P(x 0,y 0) 则 y 0=ax 20 .∵y ′0=2ax 0, ∴在P 点处抛物线(二次函数)的切线的斜率 k =2ax 0,∴切线l 的方程是y-y 0=k(x -x 0),即y -ax 20=2ax 0·(x -x 0),即2ax 0x -y -ax 20=0.∴焦点F 到切线l 的距离d =⎪⎪⎪⎪0-14a -ax 20(2ax 0)2+(-1)2=14|a|4a 2x 20+1≥14|a|,当且仅当 x 0=0时上式取“=”,此时P 的坐标是(0,0),∴当P 在(0,0)处时,焦点F 到切线l 的距离最小.例11.如图,在直角坐标系xOy 中,已知椭圆C :x 24+y 23=1上一点P ⎝⎛⎭⎫1,32,过点P 的直线l 1、l 2与椭圆C 分别交于A 、B(不同于P),且它们的斜率k 1、k 2满足k 1k 2=-34.(1) 求证:直线AB 过定点; (2) 求△PAB 面积的最大值.(1) 证明:(证法1)设直线l 1的方程为y =k 1(x -1)+32,联立⎩⎨⎧y =k 1(x -1)+32,x 24+y23=1,得(3+4k 21)x 2+(12k 1-8k 21)x +4k 21-12k 1-3=0,解得x =1或x =4k 21-12k 1-33+4k 21,即点A 的坐标为⎝ ⎛⎭⎪⎫4k 21-12k 1-33+4k 21,-12k 21-12k 1+92(3+4k 21).同理点B 的坐标为⎝ ⎛⎭⎪⎫4k 22-12k 2-33+4k 22,-12k 22-12k 2+92(3+4k 22).因为k 1k 2=-34,即k 2=-34k 1,所以4k 22-12k 2-33+4k 22=4⎝⎛⎭⎫-34k 12-12⎝⎛⎭⎫-34k 1-33+4⎝⎛⎭⎫-34k 12=-4k 21+12k 1+33+4k 21,同理可得-12k 22-12k 2+92(3+4k 22)=12k 21+12k 1-92(3+4k 21).所以A 、B 关于原点O 对称,即直线AB 过定点O.(证法2)设A(x 0,y 0),则由x 204+y 203=1得y 20=3-34x 20.设点A 关于原点O 的对称点为A ′(-x 0,-y 0),直线PA′的斜率为k 3,则k 1k 3=32-y 01-x 0·32+y 01+x 0=94-y 201-x 20=94-⎝⎛⎭⎫3-34x 201-x 20=34x 20-341-x 20=-34.又k 1k 2=-34,所以k 2=k 3,从而P 、B 、A′三点共线.因为B 、A′都在椭圆C 上,所以B 与A′重合.所以A 、B 关于原点O 对称,即直线AB 过定点O.(2) 解:由(1)可设A(x 0,y 0),B(-x 0,-y 0),x 0≠±1,则直线AB 的方程为y 0x -x 0y=0,所以AB =2x 20+y 20,点P 到直线AB 的距离为d =⎪⎪⎪⎪y 0-32x 0x 20+y 20,所以S △PAB =12·AB ·d =12·2x 20+y 20·⎪⎪⎪⎪y 0-32x 0x 20+y 20=⎪⎪⎪⎪y 0-32x 0. (解法1)令t =y 0-32x 0,则y 0=32x 0+t ,代入x 204+y 203=1得x 20+tx 0+t 23-1=0.令Δ=t 2-4⎝⎛⎭⎫t23-1≥0,解得|t|≤23,当且仅当⎩⎪⎨⎪⎧x 0=3,y 0=-32或⎩⎪⎨⎪⎧x 0=-3,y 0=32时,|t|有最大值23,即△PAB 面积的最大值为2 3.(解法2)⎪⎪⎪⎪y 0-32x 02=94x 20-3x 0y 0+y 20.因为-3x 0y 0=32(-x 0)(2y 0)≤32·(-x 0)2+(2y 0)22=3x 20+12y 204,所以⎪⎪⎪⎪y 0-32x 02≤94x 20+3x 20+12y 204+y 20=3x 20+4y 20=12,从而⎪⎪⎪⎪y 0-32x 0≤23,当且仅当-x 0=2y 0,即⎩⎪⎨⎪⎧x 0=3,y 0=-32或⎩⎪⎨⎪⎧x 0=-3,y 0=32时,△PAB 面积的最大值为2 3. 例12. 如图,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,以椭圆C 的左顶点T 为圆心作圆T :(x +2)2+y 2=r 2(r >0),设圆T 与椭圆C 交于点M 与点N.(1) 求椭圆C 的方程;(2) 求TM →·TN →的最小值,并求此时圆T 的方程;(3) 设点P 是椭圆C 上异于M 、N 的任意一点,且直线MP 、NP 分别与x 轴交于点R 、S ,O 为坐标原点,求证:OR·OS 为定值.(1) 解:依题意,得a =2,e =c a =32,∴ c =3,b =a 2-c 2=1.故椭圆C 的方程为x24+y 2=1.(2) 解:易知点M 与点N 关于x 轴对称,设M(x 1,y 1),N(x 1,-y 1),不妨设y 1>0.由于点M 在椭圆C 上,∴ y 21=1-x 214.(*)由已知T(-2,0),则TM →=(x 1+2,y 1),TN →=(x 1+2,-y 1),∴ TM →·TN →=(x 1+2,y 1)·(x 1+2,-y 1)=(x 1+2)2-y 21=(x 1+2)2-⎝⎛⎭⎫1-x 214=54x 21+4x 1+3=54⎝⎛⎭⎫x 1+852-15. 由于-2<x 1<2,故当x 1=-85时,TM →·TN →取得最小值-15.把x 1=-85代入(*)式,得y 1=35,故M ⎝⎛⎭⎫-85,35. 又点M 在圆T 上,代入圆的方程得r 2=1325.故圆T 的方程为(x +2)2+y 2=1325.(3) 证明:设P(x 0,y 0),则直线MP 的方程为y -y 0=y 0-y 1x 0-x 1(x -x 0),令y =0,得x R =x 1y 0-x 0y 1y 0-y 1,同理:x S =x 1y 0+x 0y 1y 0+y 1,故x R ·x S =x 21y 20-x 20y 21y 20-y 21.(**)又点M 与点P 在椭圆上,故x 20=4(1-y 20),x 21=4(1-y 21), 代入(**)式,得x R ·x S =4(1-y 21)(y 20-4)(1-y 20)y 21y 20-y 21=4⎝ ⎛⎭⎪⎫y 20-y 21y 20-y 21=4. 所以OR·OS =|x R |·|x S |=|x R ·x S |=4为定值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
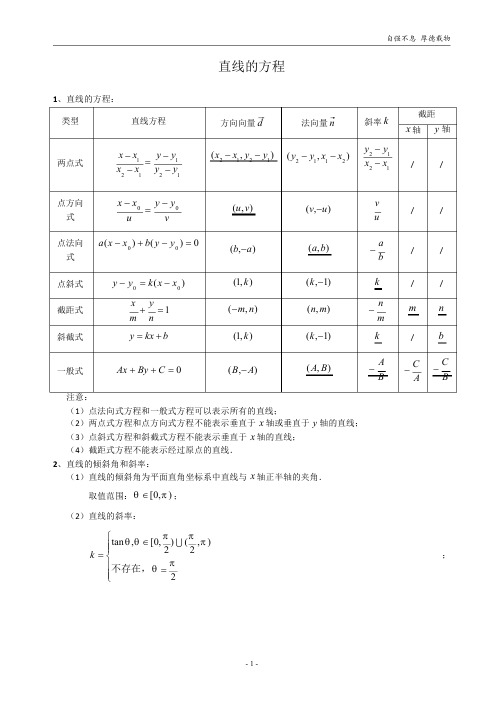
一、直线与方程基础:1、直线的倾斜角α: [0,)απ∈)2、直线的斜率k :2121tan y y k x x α-==-;注意:倾斜角为90°的直线的斜率不存在。
3、直线方程的五种形式: ①点斜式:00()y y k x x -=-; ②斜截式:y kx b =+; ③一般式:0Ax By C ++=;、④截距式:1x ya b+=;⑤两点式:121121y y y y x x x x --=--注意:各种形式的直线方程所能表示和不能表示的直线。
4、两直线平行与垂直的充要条件:1111:0l A x B y C ++=,2222:0l A x B y C ++=,1l ∥2l 12211221A B A B C B C B =⎧⇔⎨≠⎩;1212120l l A A B B ⊥⇔+= .¥5、相关公式:①两点距离公式:11(,)M x y ,22(,)N x y ,MN =②中点坐标公式:11(,)M x y ,22(,)N x y , 则线段MN 的中点1122(,)22x y x y P ++; ③点到直线距离公式: 00(,)P x y ,:0l Ax By C ++=,@则点P 到直线l的距离d =;④两平行直线间的距离公式:11:0l Ax By C ++=,22:0l Ax By C ++=, 则平行直线1l 与2l之间的距离d =⑤到角公式:(补充)直线1111:0l A x B y C ++=到直线2222:0l A x B y C ++=的角为θ,(0,)(,)22ππθπ∈,则2112tan 1k k k k θ-=+⋅ .(两倾斜角差的正切)二、直线与圆,圆与圆基础:1、圆的标准方程:222()()x a y b r -+-=; 确定圆的两个要素:圆心(,)C a b ,半径r ;;2、圆的一般方程:220x y Dx Ey F ++++=,(2240D E F +->);3、点00(,)P x y 与圆222:()()C x a y b r -+-=的位置关系: 点00(,)P x y 在圆内⇔ 22200()()x a y b r -+-<; 点00(,)P x y 在圆上⇔ 22200()()x a y b r -+-=;点00(,)P x y 在圆外⇔ 22200()()x a y b r -+->;4、直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=的位置关系: 从几何角度看:、令圆心(,)C a b 到直线:0l Ax By C ++=的距离为d , 相离⇔d r >; 相切⇔=d r ; 相交⇔0d r ≤<;若直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=相交于两点M ,N ,则弦长MN =从代数角度看:,联立:0l Ax By C ++=与圆222:()()C x a y b r -+-=, 消去y (或x )得一元二次方程,24b ac ∆=-, 相离⇔0∆<; 相切⇔0∆=; 相交⇔0∆>;相交时的弦长1212MN x x y y =-=- .5、圆与圆的位置关系: 相离,外切,相交,内切,内含 .,圆2221111:()()O x x y y r -+-=;圆2222222:()()O x x y y r -+-=, 根据这三个量之间的大小关系来确定:12r r -,12O O ,12r r +; 相离⇔1212O O r r >+; 外切⇔1212O O r r =+; 相交⇔121212r r O O r r -<<+;内切⇔1212O O r r =-; 内含⇔12120O O r r ≤<-;~6、两圆2221111:()()O x x y y r -+-=①;圆2222222:()()O x x y y r -+-=②若相交,则相交弦所在的直线方程的求法:交轨法: ①式-②式,整理化简即可得到相交弦所在直线方程 .三、椭圆:1、(第一)定义:12122PF PF a F F +=>;2、椭圆标准方程及离心率:焦点在x 轴上的椭圆标准方程为:22221(0)x y a b a b+=>>;::a 长半轴;b :短半轴;:c 半焦距 .椭圆中a ,b ,c 的关系:222a b c =+; 椭圆的离心率(0,1)ce a=∈ . 3、弦长公式:直线:l y kx b =+与椭圆2222:1()x y C m n m n+=≠交于两点11(,)M x y ,22(,)N x y ,则相交时的弦长1212MN x x y y =-=- . 弦长公式是由两点距离公式与两点斜率公式推导出来,故适用性比较广。
-4、中点弦结论(点差法):椭圆2222:1()x y C m n m n+=≠上的两点11(,)M x y ,22(,)N x y ,弦MN 的中点1212(,)22x x y y P ++,则22MN OP n k k m⋅=- .5、焦点三角形面积:—椭圆2222:1(0)x y C a b a b+=>>的两个焦点分别为1F 、2F ,点P 是椭圆C 上除左、右端点外的一点,令12F PF θ∠=,则: 122tan2PF F S b θ∆=⋅ .该公式是由三角形面积公式、椭圆第一定义、余弦定理结合三角恒等变换推导出来。
6、直线与椭圆位置关系:联立:0l Ax By C ++=与椭圆2222:1()x y C m n m n+=≠,消去y (或x )得一元二次方程,24b ac ∆=-, 相离⇔0∆<;|相切⇔0∆=; 相交⇔0∆>;7、与点坐标相关的面积公式:(0,0)O ,11(,)A x y ,22(,)B x y ,点O ,A ,B 不在一条直线上,则:122112OAB S x y x y ∆=-. 该公式是由三角形面积公式、余弦定理结合三角恒等式推导出。
四、双曲线:(类比椭圆来学习双曲线)`1、定义:12122PF PF a F F -=<;2、双曲线标准方程及离心率、渐近线方程:焦点在x 轴上的双曲线标准方程为:22221(0,0)x y a b a b-=>>;:a 实半轴;b :虚半轴;:c 半焦距 .双曲线中a ,b ,c 的关系:222c a b =+;双曲线的离心率(1,)ce a=∈+∞ ; 焦点在x 轴上的双曲线的渐近线方程为by x a=±; )焦点到渐近线的距离d b = .焦点在y 轴上的双曲线相关性质可以类比。
3、弦长公式:直线:l y kx b =+与双曲线2222:1(0,0)x y C a b a b-=>>交于两点11(,)M x y ,22(,)N x y ,则相交时的弦长1212MN x x y y =-=- . 4、中点弦结论(点差法):双曲线2222:1(0,0)x y C a b a b-=>>上的两点11(,)M x y ,22(,)N x y ,~弦MN 的中点1212(,)22x x y y P ++,则22MN OPb k k a⋅= . 5、焦点三角形面积:双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点分别为1F 、2F ,点P 是双曲线C 上除左、右端点外的一点,令12F PF θ∠=,则:122tan2PF F b S θ∆=.6、直线与双曲线位置关系:①当直线l 与双曲线C 的其中一条渐近线重合时,显然直线l 与双曲线C 无交点;/②当直线l 与双曲线C 的其中一条渐近线平行时,有且仅有一个交点,此时联立直线方程与双曲线方程,会得到一个一次方程(二次项系数为0); ③当直线l 与双曲线C 的渐近线既不平行也不重合时,此时联立直线方程与双曲线方程,消去y (或x )得一元二次方程,24b ac ∆=-, 相离⇔0∆<; 相切⇔0∆=; 相交⇔0∆>;!五、抛物线:1、定义:P l PF d -= (到定点的距离等于到定直线的距离的这样的点的轨迹即为抛物线).、2、标准方程:22(0)y px p =>(开口朝右的抛物线,开口朝其它方向的抛物线方程及其它性质可以类比。
) 焦点(,0)2p F ,准线:2pl x =-,离心率1e =. 3、常见性质: ① 普通的弦长公式:直线y kx b =+与抛物线22(0)y px p =>相交于两点11(,)M x y ,22(,)N x y ,12y y - .②过焦点(,0)2F 的特殊弦长公式及12x x 与12y y : (i )若弦MN 过焦点(,0)2p F ,则弦长1222sin pMN x x p α=++=(α为倾斜角); (ii )2124p x x =,212y y p =- .③过抛物线2:2(0)C y px p =>的顶点(0,0)O 作两条互相垂直的射线OM 、ON 分别与抛物线C 交于两点M ,N ,弦MN 与x 轴交于点P ,则(2,0)P p ,即:4OP OF =.反之亦然,即:若4OP OF =,则90MON ∠=︒.4、抛物线中过焦点弦的其它性质(补充,作为了解,切记不能死记硬背。
如死记硬背,如下知识点不如不用掌握。
可以尝试证明。
)%设MN 是过抛物线22(0)y px p =>焦点F 的弦,11(,)M x y ,22(,)N x y , 如图(抛物线图2), 则:①22sin MON p S α∆=; ②112MF NF p+=; ③以MN 为直径的圆与准线相切;④90PFQ ∠=︒;⑤以MF 或NF 为直径的圆与y 轴相切 .]5、直线与抛物线的位置关系:①若直线与抛物线的对称轴平行或重合,则有一个交点;②若直线与抛物线的对称轴不平行,也不垂直,则根据判别式∆的符号来确定交点个数;③若直线与抛物线的对称轴垂直,画图数形结合很容易判断交点个数。
~圆锥曲线大题常见题型(归纳总结):题型一、求点的轨迹问题: 常见方法:①直接法:(设出所求点(,)P x y ,根据题意列出等式,建立起y 与x 的关系。
) 如椭圆的标准方程的求出,本身就是利用这种方法。
②几何定义法:根据题意画出图形,通过已知条件及所学知识(如三角形中位线、圆与圆内切与外切,直线与圆相切的等价条件)得出所求点(,)P x y 满足圆的几何定义或椭圆、双曲线、抛物线的定义,从而求出点的轨迹方程;③伴随动点转化法: 该类题型的特征往往是: 其中一个动点如点00(,)Q x y 的轨迹方程是已知的,另有一个定点A 或多个定点,所求动点(,)P x y 与定点A 和动点00(,)Q x y 有着一定关系。
