3–1动讲义能质点动能定理
质点系的动能定理

质点系的动能定理
质点系的动能定理是一种重要的物理定理,它描述了质点系的动能变化,可以用来描述物理现象中发生的物理过程。
它可以说是物理学的基本定理,是研究力学运动的基础。
质点系的动能定理定义了质点系的动能E,它定义了质点系的总能量。
它的公式可以用E=mv^2/2来表示,其中m为质量,v为速度。
它表明,质点系的动能大小与其质量和速度的平方有关,即质点系的动能与其运动速度的平方成正比。
质点系的动能定理还可以推导出牛顿第二定律,即物体受到力的作用时,动能变化的速度等于这个力大小的积分。
换言之,可以用Fdt=mdv来表示,其中F表示物体受到的外力大小,dt表示时间段,m表示质量,dv表示速度变化量。
质点系的动能定理也可以用来推导牛顿第三定律,即作用力的大小等于反作用力的大小。
用F=ma表示,其中F表示作用力的大小,m 表示质量,a表示加速度。
质点系的动能定理通过分析物体受到外力时动能变化的特征,可以解释物体动力学运动的基本原理,提供了研究动力学的有力工具,为探究物理规律提供了理论指导。
- 1 -。
04 3-1 质点和质点系的动量定理

t2
F1+F2 dt (m1v1 m2v2 ) (m1v10 m2v20 )
t1
作用在两质点组成的系统的合外力的冲量等于系统内两质 点动量之和的增量,即系统动量的增量。
2、多个质点的情况
t2 t2 n n n Fi外 dt+ Fi内 dt m i v i m i v i 0 i 1 i 1 t1 i 1 t1 i 1 n
3-4 动能定理
一、功与功率
1、功
•恒力的功 力对质点所作的功等于该力在位移 方向上的分量与位移大小的乘积
F m
F
S
m
说明 •功是标量,没有方向,只有大小,但有正负 p/2,功W为正值,力对物体作正功; p /2,功W=0, 力对物体不作功; p /2,功W为负值,力对物体作负功,或 物体克服该力作功。 •单位:焦耳(J) 1J=1N· m
i i i
ex ex 若质点系所受的合外力为零 F Fi 0
则系统的总动量守恒,即
讨论
ex dp ex i F , F 0, P C dt
p pi
保持不变 .
i
1)系统的动量守恒是指系统的总动量不变,系 统内任一物体的动量是可变的, 各物体的动量必相 对于同一惯性参考系 .
W=F S dW=F dS
•变力的功 分成许多微小的位移元,在每一个 位移元内,力所作的功为
Z
dr
b
F
dW F dr F cos dr
总功
a O
Y
W
•合力的功
B
A
B X F dr F cosdr
质点和质点系的动能定理.ppt

△Ek随惯性系的不同而不同
关
系:
Ek p /(2m)
2
4 – 3
质点和质点系的动能定理
例: 一质量为1.0kg 的小球系在长为1.0m 细绳下端 , 绳 的上端固定在天花板上 . 起初把绳子放在与竖直线成 30 角处, 然后放手使小球沿圆弧下落 . 试求绳与竖直线成 10 角时小球的速率 . 解:
(2)由于力和质点间的相对距离不因参照系的改变而改变,
故一对内力做功之和与参考系的选择无关。即成对力的总功具 有与参考系选择无关的不变性质。 为方便起见,计算时可认为其中一个质点静止,将参照 系固定在该质点上:并以该质点所在位置为原点,再计算另 一质点受力所做的功。
4 – 3
(3 )
质点和质点系的动能定理
—— 有限的过程的动能定理.
即,合外力对质点所做的功等于质点动能的增量。
Note:
若质点速度接近光速,则动能定理的叙述 不变,但动能表达式改变!
4 – 3
质点和质点系的动能定理
一 质点的动能定理
dv Ft m A F dr Ft dr Ft ds dt v2 v2 dv 1 1 2 2 A m ds mvdv mv2 mv1 v1 v1 dt 2 2
a m
b x
由动能定理有: ( v0= 0 )
a 1 2 mv mgb k ( x a )dx b 2 1 k (b a ) 2 mgb
2 1 k 2 2 v (b a) 2 gb m
4 – 3
质点和质点系的动能定理
例:m=1kg的物体,在坐标原点处从静止出 发沿x 轴运动,合力 F (3 2 x)i (SI), 则在x=0~3m内,合力作功A = ; x=3m处,物体速率v = . 解:
质点系动能定理

质点系动能定理质点系动能定理一、引言在物理学中,动能是描述物体运动状态的一种重要物理量,它与物体的质量和速度有关。
当一个质点或多个质点组成的系统发生运动时,其总动能可以表示为各个质点的动能之和。
本文将介绍质点系动能定理,即描述多个质点组成的系统总动能与各个质点的动能之间的关系。
二、定义1. 质点:没有大小和形状,只有位置和速度等运动状态特征的物体。
2. 动能:一个物体由于运动而具有的能量。
3. 质点系:由多个质点组成的系统。
三、公式推导假设一个由n个质点组成的系统,其各自的速度分别为v1,v2,...,vn,则每一个质点所具有的动能可表示为:Ek1 = 1/2 * m1 * v1^2Ek2 = 1/2 * m2 * v2^2...Ekn = 1/2 * mn * vn^2其中m1,m2,...,mn分别为各自对应的质量。
整个系统所具有的总动能可表示为:Et = Ek1 + Ek2 + ... + Ekn= 1/2 * m1 * v1^2 + 1/2 * m2 * v2^2 + ... + 1/2 * mn * vn^2将质点的速度分解为各个方向上的分量,即v1 = vx1 + vy1 + vz1,同理可得v2 = vx2 + vy2 + vz2,...,vn = vxn + vyn + vzn。
则系统所具有的总动能可表示为:Et = 1/2 * m1 * (vx1^2+vy1^2+vz1^2)+ 1/2 * m2 * (vx2^2+vy2^2+vz2^2)+ ...+ 1/2 * mn * (vxn^2+vyn^2+vzn^3)将各个质点的速度平方项展开并相加,得到:Et = 1/2 * (m1*vx1^2+m2*vx22+...+mn*vxn^3)+ 1/2 * (m1*vy12+m22*vy22+...+mn*vyn^3)+ 1/4 * (m12*vz12+m22*vz22+...+mn*vzn^3)由此可知,一个质点系的总动能与各个质点的动能之和相等。
大学物理第二章动能定理
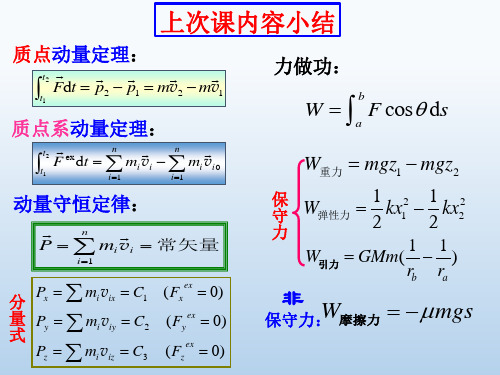
例题3. 如图,一轻绳跨过一定滑轮,两边分别拴有质量
为m及M的物体,M离地面的高度为h: (1)若滑轮质量及
摩擦力不计,m与桌面的摩擦也不计,开始时两物体均静
止,求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为,结果又如何?
解:
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理:
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得:
t2 t1
M外dt
L2
L1
注意:只有外力矩对质点系的角动量变化有贡献,
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
简述质点系的动能定理

简述质点系的动能定理质点系的动能定理是物理学中一个重要的定理,描述了质点系动能的变化与力的做功的关系。
它为我们理解物体运动和能量转化提供了重要的指导。
下面我将用中文生成一篇生动、全面、有指导意义的文章,来简述质点系的动能定理。
动能是物体运动所具有的能量,是物体的运动状态和速度的量值函数,它与质点的质量和速度平方成正比。
动能定理是指在作用力的作用下,质点系的动能的变化等于作用力所做的功。
这个定理为我们提供了量化物体运动能量变化的方法。
首先,动能定理表达了质点系动能的改变量与力的做功之间的关系。
当一个力作用在一个质点上时,这个力可以改变质点的动能。
如果力的大小不变,质点所受到的力与速度的方向一致,那么该力将加速质点运动,而其动能也将增加。
根据动能定理,质点的动能的改变量等于力所做的功。
这个功可以通过力的大小、质点的位移和力与位移之间的夹角来计算,这就是功的一般表达式。
其次,动能定理也告诉我们,质点系动能的改变量等于系统所受到的外力做的功,减去系统内部力做的功。
系统内部力在物体运动中不会做功,因为它们之间的力均衡,能量转化只发生在系统与外部环境之间。
因此,动能定理还可以看作是能量守恒定律的一个特例。
能量守恒是物理学中最基本的定理之一,它描述了能量在物体间的转化和传递过程。
最后,动能定理也可以推广到多个质点组成的质点系中。
对于多个质点组成的质点系,它们的总动能的改变量等于外力所做的功,减去内部力所做的功。
内部力是质点系内部各个质点之间相互作用的力。
这个定理在研究多体物理系统和复杂机械装置中有着广泛的应用。
总之,质点系的动能定理告诉我们了质点系动能变化与力的做功之间的关系,提供了量化物体运动能量变化的方法。
它是能量守恒的特例,也可以推广到多个质点组成的质点系中。
了解并应用动能定理,可以帮助我们更好地理解物体运动和能量转化的过程,为物理学研究和工程实践提供了重要的指导。
质点的动能定理

解得
0 1 mv2 f Gs 2
s v2 l (sin f cos ) 2 fg f
显然,若测得水平滑行距离s,则可求得车厢运动的阻力因数为
f l sin h s l cos s s1
式中,h 为坡道高度;s1 为坡道的水平投影长度。这就给出了车厢运动阻力因数的
实验测定方法。
理论力学
1 2
mv22
1 2
mv12
W12
v1 0
W12 mgR(1 cos )
图11-13
代入动能定理得
1 2mv22mgR(1 cos )(1)
物体离开圆柱表面时的速度v2可用其他方程求出。
(4)求速度v2。物体M在离开圆柱表面处的动力学方程沿法线方向的投影形 式为
man mg cos FN
二、质点的动能定理
设质量为m的质点M在力F(合力)的作用下沿曲线运动,如图11-12所示。
由质点动力学基本方程
ma F
考虑到 a dv/dt ,代入上式得 等式两边均点乘dr,则有
m dv F dt
m dv dr F dr dt
或写为
mv dv F dr
v dv 1 d(v v) 1 d(v)2
考虑到an v22 /R,且离开时 FN 0,于是有
m v22 mg cos
R 由式(1)和(2)两式联立可解得
cos 2 , 48.19
3
(2)
例11-2
如图 11-14 所示,车厢沿倾角为 的轨道自溜运行。坡道长为 l ,车厢运行时所受
的阻力与轨道的法向约束力成正比,即 F f FN , f 为车厢运动阻力因数。试求车 厢自 A 处由静止溜到 B 处的速度及停止在 C 处时沿水平轨道所滑行的距离 s。
3质点系的动能定理

对 m1 、m2 应用质点 动能定理,
W 1 外 W 1内 E k 1 E k 10 W 2 外 W 2 内 E k 2 E k 20
v 10 v 1
m1 f12 f 21 m2
F1
1
1'
r1 r2
由于 m1 、m2 为一个 系统,将上两式相 加:
2'
2
v 20 v 2
Hale Waihona Puke F2§3.质点系的动能定理 / 一、质点系的动能定理
i 1
W i 外 W i 内 E ki E ki 0
i 1 i 1 i 1 n
n
n
n
n
令
E k E ki
i 1 n n
为质点系的动能,
i 1
W i外 W i内 E k E k 0 E k
第三节
质点系的动 能定理
一、质点系的动能定理
两个或两个以上的质点组成的系统。 上一节研究了一个质点的动能定理, 如果研究的对象为质点系,动能定理又如 何表示?以最简单的两个质点组成的质点 系为研究对象。
两个质点质量为 m1、 m2 ,受外力F1、 F2,内力为f12、f21,初速度为v10、v20, 末速度为v1、v2,位移为 r1 , r2
i 1
质点系的动能定理 合外力与合内力作功代数和,等于质 点系动能的增量。
§3.质点系的动能定理 / 一、质点系的动能定理
设计制作
干耀国
山东科技大学济南校区
§3.质点系的动能定理
质点的动能定理

mgl(cos cos 0 )
P
18
例题
l 1.0 m o θ 10 W mgl(cos cos 0 ) 1 2 1 2 由动能定理 W mv mv0 2 2
得 v
m 1.0 kg o 0 30
0
d
2 gl (cos cos 0 )
xi 0 xi 0 x1
3
功
质点沿曲线运动时变力的功 B * 元功 dW F cos dr i Fi ds dr dr dW F cos ds F dr1 F1 * dW F dr A B B W F dr F cos ds
1
FT v ds
l
1.53 m s
P
19
一对力 概念 分别作用在两个物体上的大小相等、方 向相反的力, 我们称之为“一对力”。 注意 一对力通常是作用力与反作用力,但也可
以不是。一对力中的两个力也并不要求必须
在同一直线上。
F2
2
1
F1 F2
一对力的功
dW对 F1 dr1 F2 dr2 F2 d (r2 r1 ) F2 dr21
dr21 是m2相对于m1的元位移。
一对力所做的功,
等于其中一个质点受的
B1
dr1 m F1
1
B2
dr F2 2 m2
力和该质点相对另一质
2 0
bt 2 m
t
x
11
质点的动能
W F dr
而
Ft dr Ft ds dv Ft m dt
大学物理之质点系的动能定理.ppt
注意
内力可以改变质点系的动能
第三章 动量守恒定律和能量守恒定律
3 – 5 保守力与非保守力 势能
物理学教程 (第二版)
二 质点系的功能原理
质点系动能定理 W ex W in Ek Ek0
W in Wiin Wcin Wnicn
i
非保守 力的功
Wcin ( Epi Epi0 ) Ep Ep0
物理学教程 (第二版)
的相互碰作撞用两. 物体互F相ex接触 时F 间in 极短而互p作i 用C力 较大
i
完全弹性碰撞 两物体碰撞之后, 它们的动能之
和不变 .
Ek Ek1 Ek2 C
非弹性碰撞 由于非保守力的作用 ,两物体碰撞
后,使机械能转换为热能、声能,化学能等其他形式
的能量 .
完全非弹性碰撞 两物体碰撞后,以同一速度运动 .
向相同. 若碰撞是完全弹性的, 求碰撞后的速度 v1和v2.
解 取速度方向为正向,由动
量守恒定律得
m1v10 m2v20 m1v1 m2v2
m1(v10 v1) m2 (v2 v20 )
由机械能守恒定律得
1 2
m1v120
1 2
m2 v220
1 2
m1v12
1 2
m2 v22
碰前
m1
v10
质点系的动量定理:系统所受合外力的冲量等
于系统动量的t增2 F量e
。
xdt
t1
n i 1
mi vi
n mi vi0
i 1
第三章 动量守恒定律和能量守恒定律
3 – 5 保守力与非保守力 势能
物理学教程 (第二版)
二. 质点系动量守恒定律
质点系所受合外力为零,系统总动量守恒。即
动能定理质点动能与力的关系

动能定理质点动能与力的关系动能定理是力学中的基本定律之一,它描述了质点的动能与所受外力之间的关系。
根据动能定理,质点的动能的变化等于作用在质点上的合外力所做的功。
这一定理为我们理解物体的运动提供了深入的观察。
1. 动能与力的定义首先,我们先来了解一下动能和力的定义。
动能是物体由于运动而具有的能量,通常用符号K来表示。
根据经典力学,质点的动能可以用以下公式表示:K = 1/2mv^2,其中m为质点的质量,v为质点的速度。
而力是物体之间相互作用的效果,是引起物体运动状态发生改变的原因。
力的大小通常用符号F表示。
2. 动能定理的表达形式动能定理可以用数学的形式来表示,即∆K = W,其中∆K表示动能的变化,W表示外力所做的功。
动能的变化可以用K₂- K₁来表示,即∆K = K₂ - K₁,其中K₂表示物体在某一时刻的动能,K₁则表示物体在另一时刻的动能。
功则是力在质点运动方向上的分量乘以质点在该方向上的位移,即W = F·d。
3. 动能定理的推导为了推导动能定理,我们先考虑单位时间内对质点做功的关系。
单位时间内力对质点做的功可以用∆W来表示,而质点在单位时间内速度的变化可以用∆v表示。
根据牛顿第二定律F = ma,可以将∆W表达为∆W = F∆r,其中a为质点的加速度,∆r为质点在单位时间内的位移。
将质点的速度记为v,则∆v可以表示为∆v = v₂ - v₁。
将力表示为F = ma,并将F和∆r进行合并得到∆W = m(v₂ - v₁)∆r。
将质点的质量m乘到括号里面得到∆W = mv₂∆r - mv₁∆r。
由于质点在各个时刻的位置与时间无关,因此∆r可以用∆t来表示。
代入恒定时间的定义,∆W = mv₂∆r - mv₁∆r可以简化为∆W = mv₂∆r - mv₁∆t。
将∆W表示为单位时间的功率P,即P = ∆W/∆t,则P = mv₂∆r/∆t - mv₁∆r/∆t。
因为v₂∆r/∆t等于v₂,v₁∆r/∆t等于v₁,所以P = mv₂ - mv₁。
质点动能定理的内容及公式

质点动能定理的内容及公式在物理学的奇妙世界里,质点动能定理可是个相当重要的角色!咱们一起来瞧瞧它到底是咋回事。
质点动能定理说的呀,就是合外力对质点所做的功等于质点动能的增量。
这听起来可能有点抽象,别急,咱慢慢解释。
想象一下,有个小球在光滑的水平面上被一个力推着往前跑。
这个力一直在做功,小球跑得越来越快,它的动能也就越来越大。
这个过程中,力做的功就等于小球动能增加的量。
公式呢,就是 W 合= ΔEk 。
其中,W 合表示合外力做的功,ΔEk 表示动能的增量。
那动能又是什么呢?动能就是物体由于运动而具有的能量。
对于一个质点,它的动能 Ek = 1/2 mv²,这里的 m 是质点的质量,v 是质点的速度。
我记得有一次给学生们讲这个知识点的时候,有个调皮的小家伙就问我:“老师,这动能定理有啥用啊,能让我考试多得分吗?”我笑着回答他:“这可不光是为了考试得分,它在生活中也有大用处呢!”就比如说,汽车加速的时候,发动机提供的力做功,让汽车的动能增加,速度也就上去了。
还有火箭发射,燃料燃烧产生的推力做功,让火箭的动能不断增大,从而飞向太空。
咱们再回到公式上来,合外力做的功可以是一个力做的功,也可以是多个力做功的总和。
如果多个力同时作用在质点上,那就要分别计算每个力做的功,然后加起来,看看是不是等于动能的增量。
给大家举个例子吧。
假设一个质量为 2kg 的物体,在水平方向受到一个大小为 5N 的恒力作用,运动了 4m ,初速度为 2m/s 。
那我们先来算合外力做的功,合外力 F 合 = 5N ,位移 s = 4m ,所以 W 合 = F合 s = 5×4 = 20J 。
再算物体的初动能 Ek1 = 1/2×2×2² = 4J ,末动能 Ek2 = 1/2×2×v²,这里的 v 可以通过运动学公式 v² - v0² = 2as 来算,其中 a = F 合 / m =5/2 = 2.5m/s²,所以 v² - 2² = 2×2.5×4 ,解得 v = 6m/s ,那么末动能 Ek2 = 1/2×2×6² = 36J 。
质点系的动能定理
T1 0
T21Biblioteka 2(m1R12 )12
1 2
m2 2 2
1 2
势力场:场力作功只决定于力作用点的始末位置,而与 路径无关的力场。如:重力场、万有引力场、弹性力场
保守力:势力场内对应的场力。如:重力、万有引力、 弹性力等
二、势能
势能:势力场中,质点从位置 M 0 运动到位置 M1,有
势力所作功称为位置
M
相对位置
1
M 0的势能。
V
M1 F dr
Wi
We i
Wi i
对于刚体:
Wi i
0
对于可变形体:
Wi i
0
§13-3 功率、功率方程
一、功率
功率:单位时间内力所做的功,即
P w
dt
P
w
dt
F dr dt
F v
F v
对于作用于刚体上的力(力偶)功率:
P w
dt
M z d
dt
§13-1 力的功
一、力的功
力的功是力在一段路程内对物体作用的积累效应 的度量。力做功的结果是使物体的机械能发生变化
1、常力功的计算 常力在直线位移下所作的功
W F cosθ s F s
F
力的功是代数量
A1
s
A2
2、变力功的计算
(1)自然表达式 则力在微段路径上 所作元功为:
z
F
B:在某瞬时,在速度瞬心不明显时候,也可将平面 运功刚体的运动视为绕质心的定轴转动和随质心的平动 两部分运动的合成。
大学物理-第三章-动量守恒定律和能量守恒定律

20
★一对作用力与反作用力的功只与相对位移有关
f ji
ri
f ij
rij
rj
0
dW
jidWij
f
ji
dri
fij drj
f ji fij
fji f ji
(dd(rriidrrjj))
f ji
drij
S
S u
动量的相 对性和动量定 理的不变性
F(t)
t1 m
v1
光滑
v 2
m t2
参考系 t1 时刻 t2 时刻
动量定理
S系
S’系
mv1
mv2
m(v1 u) m(v2 u)
t2 t1
F (t )dt
mv2
mv1
5
例3-1: 作用在质量为1kg 的物体上的力 F=6t+3,如果物体在这
0=m1(v1+v2)+m2v2
v2
m1v1 m1 m2
x
t 0
v2dt
m1 m1 m2
t 0
v1dt
L
t
0 v1dt
x m1L 0.8m m1 m2
负号表示船移动的方向与人前进的方向相反。
17
3-4 动能定理
一、功的概念(work) 功率(power) 1、恒力的功
2、动能定理
2
1
或
F
dr
F
dr
1 2
mv22
由质点系动能定理课件

BIG DATA EMPOWERS TO CREATE A NEW ERA
04
质点系动能定理的扩展与深化
动能定理与动量定理的关系
动能定理描述了质点系动能的变化与外力所做的功之间的关系,而动量定理描述了质点系动 量的变化与外力之间的关系。两者都揭示了力对物体运动状态的影响,但关注的物理量不同 。
动能定理和动量定理在形式上可以相互推导,它们都是牛顿第二定律在不同情况下的表现形 式。
速度分解法
将速度分解为垂直和平行于作用力的 方向,利用平行方向不受力,垂直方 向受力影响速度大小,简化计算。
复杂问题的求解思路
01
02
03
04
受力分析
首先对质点进行受力分析,确 定各力的方向和大小。
运动分析
分析质点的运动状态,确定初 速度和末速度,以及运动轨迹
。
选择合适的参考系
选择合适的参考系可以使问题 简化,通常选择惯性参考系。
THANKS
感谢观看
列方程求解
根据受力分析和运动分析的结 果,列出质点动能定理的方程
,解方程得出结果。
动能定理与其他物理定律的综合应用
动能定理与牛顿第二定律的综合应用
当已知外力时,利用牛顿第二定律求出加速度,再结合运动学公式求出速度和位移,最 后利用动能定理验证结果。
动能定理与机械能守恒定律的综合应用
当只有重力和弹力做功时,可以利用机械能守恒定律求出速度和位移,再利用动能定理 验证结果。
,但动能定理仍然适用。
在分析问题时,可以根据需要选择使用 机械能守恒定律或动能定理。如果需要 考虑外力做功的影响,则使用动能定理
更为方便。
动能定理在相对论中的表现形式
在相对论中,动能的形式与经典 力学有所不同。相对论中的动能 包括了物体的质量以及其速度的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
n
n
W Wi Fi ri
i1
i1
n B
W lim Firi
ri 0i1
Fdr
A
这就是计算功最一般的公式。
首页
上页
下页
B
末页
退出
3-1 动能 质点动能定理
结论 (1)功是力沿质点运动轨迹进行线积分计算的,
因此功是力对空间的累积效应(为什么?)。一般地 说,功的值既与质点运动的始末位置有关,也与运动 的路径有关。
在本章中我们将介绍能量和动量的基本概念, 讨论在力学中物体能量和动量变化的原因和所遵 从的基本规律,从而从另一个侧面进一步揭示物 质运动规律。
首页
上页
下页
末页
退出
导言
3-1 动能 质点动能定理
牛顿定律是瞬时规律。
但是实际问题中我们有时往往研究的是 一个过程的积累效果。
有些过程的细节非常复杂,
如:碰撞问题(宏观) 散射问题(微观)
解:根据动能定理,平均阻力所做的功应等于子 弹动能的增量,即
fs01mv2 2
(6)功随时间的变化率 Fx
叫功率(Power),用P表示,
按此定义有
PdWF drF v O xA
dx
x xB
dt dt
单位:瓦特(Watt) 1W=1J/s,1kW=103W
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
【例题3-2】图3-4是一机器人手臂,它用于控 制自动监视系统中的一台摄像机的位置,其动力来源于 一台电动机,电动机给机器人手臂的作用力可表示为
Wx2 x1
Fdx00.0 .015F 00016xx202dx
F0
x
x3 18x02
0.0 5 0 0.0 1 0
0.36J
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
力为【F 例 题(y 2 3 -x 32 】)i 一 3 质x 点 j,在y 运xy动平轨面迹上方运程动为,y所受x2力。 求的
(4)在直角坐标系中
F F x i F yj F zk
d r d x i d y j d z k
W F x d x F y d y F zd z
WW xW yW z
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
(5)当质点只受x方向的变力作用时,功也常用 图示法来计算,如图所示,曲线表示 F x 随x坐标变化 的函数关系,曲线下的面积就等于变力 F x 所做功的代 数值。
退出
3-1 动能 质点动能定理
二、质点动能定理
质点从A运动到B,在任
一点力所作的元功:
d W F d r F co |d r |s
dr
θ
F
又 Fcosmtamddvt
vA
ALeabharlann W B F d r v B m d v |d r |v B m v d v
A
v A d t
v A
B vB
W12mvB 2 12mv2A
F(x) F016xx202
其中 F0 2.0N, x0 0.007m 0,
x是机器人手臂的位置。如果机
器人手臂的位置由 x10.01m 0 变到 x20.05m 0的位置,试计
算电动机作了多少功?
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
解:这是一个变力做功的问题,并且力的大小只与 x有关,由变力做功的计算公式得电动机做功为
为m 。求力所做的功。
解:由恒力做功的计算公式
W F r ( 3 i 4 j ) ( 2 i 2 j ) 2 . 0 J
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
2.变力做功
元功:
r
θ
W i F i r i |F i|| r i|cios Fi
A到B力所作的总功:
我们对过程的细节不感兴趣,只关心始末两个状态的 情况,于是从牛顿定律发展出新的研究课题。
首页
上页
下页
末页
退出
一、功
3-1 动能 质点动能定理
1.恒力做功
W |F || r |c os
W F r
F
θ
r
了 r 【 例2i题 32 - j1】位一移质,点式在中力F的F 单 位3i为N4,j位作移用的下单发位生
(2)与牛顿第二定律一样,动能定理也只适用于 惯性系。此外,在不同的惯性系中,质点的位移和速 度是不同的,因此,功和动能都依赖于惯性系的选取。
(3)动能的单位和量纲与功的单位和量纲是相同 的。
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
【例题3-4】一个质量为30g的子弹以500 m/s的速 率沿水平方向射入沙袋内,并到达深度为20cm处,求 沙袋对子弹的平均阻力。
3–1动能质点动能定理
精品
3-1 动能 质点动能定理
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
能量是度量物质运动的一种物理量。相应于 不同形式的运动,能量分为机械能、分子内能、 电能、化学能、原子能等。亦简称能。度量物体 状态改变过程中能量变化是功。动量也是量度物 质运动的一个物理量,动量的改变由物体受到的 冲量来量度。
动能:
Ek
1 mv2 2
作用于质点的合力所做的功,等于质点动能的增
量 。 这 个 结 论 称 为 动 能 定 理 ( theorem of kinetic
energy)。
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
说明 (1)功和动能之间的联系和区别。只有合外
力对质点做功,才能使质点的动能发生变化,功是能 量变化的量度。功是与在外力作用下质点的位置移动 过程相联系的,故功是一个过程量。而动能是质点在 运动中具有的能量,由质点的质量与速度决定,是表 征质点运动状态的一个物理量。质点的运动状态确定 时,速率就是确定的,动能也就是确定了,这可以说 动能是质点运动状态的单值函数。
质点从点A(0,0)运动到点B(2,4)过程中力 F所
做的功。
解:由 y x2 求微分可得
dy2xdx
W BF dr B [y (2x2)i3x j]y(dxidy j)
A
A
B [y (2x2)dx3xdy] A
2
W2(7x4x2)dx7x51x3 63J2
0
5
3 15 首页
上0页
下页
末页
(2)功是标量,且有正负,其正负取决于力和位 移间的夹角。
090 , dW 0
90 1 8 , 0 d W 0 9 F 0 d rd W 0
首页
上页
下页
末页
退出
3-1 动能 质点动能定理
(3)合力的功 = 分力的功的代数和 B
W A A BF (1dF ri )dA B rF 2dr W 1W 2
