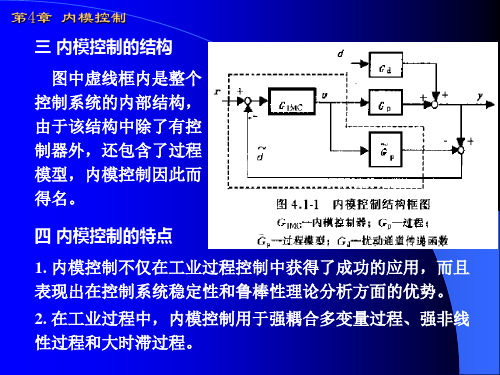
内模控制与预测控制

若无模型误差时仿真结果如下：
若实际对象模型为
Pm (s)
=
10s + s2 + 5s
20 + 10
e −0.9 s
，兼顾输出的平稳性和调节时间，反馈
滤波取α = 0.7 比较合适，仿真结果如下：
1.2 有限拍法设计控制器 Q 标称模型 Pm 的极点为 λ1 = 1.5262 + 0.6235i 和 λ2 = 1.5262 − 0.6235i
du=d*(Yr-P); % compute control increment
u=u+du;
% compute control output u(k)
sys=u;
% output u(k)
for n=6:-1:2
Du(n)=Du(n-1);
end
Du(1)=du;
R7 = 1+ 2.123λ + 3.0162λ 2 + 3.6062λ3 + 3.9401λ 4 + 4.098λ5 + 4.1525λ 6 S7 = 4.1556 − 4.6833λ +1.5277λ 2
G7 = R7B = 1.4680 + 2.1377λ + 2.3496λ 2 + 2.3413λ3 + 2.2539λ 4 + 2.1589λ5 + 2.0843λ6 − 4.0649λ7 模型预测方程 yp (k + 7) = S7 y(k ) + G7Δu(k +1) 令 p7 (k) = S7 y(k) + (G7 − g1 − g2λ)Δu(k +1) 模型预测方程 yp (k + 6) = p7 (k) + g1Δu(k +1) + g2Δu(k)
% initialize other parameters:
Yr=ones(2,1);
% reference input(unit step)
Y0=zeros(3,1);
% predictive initial values
Du=zeros(6,1);
% control increment values
设预测型号Yp = ⎡⎣ yp (k + 6) yp (k + 7)⎤⎦T ，控制量为 ΔU = [Δu(k) Δu(k +1)]T
令
P(k
)
=
⎡ ⎢ ⎣
p6 p7
(k (k
)⎤ )⎥⎦
，
G
=
⎡ ⎢ ⎣
g1 g2
0⎤
g1
⎥ ⎦
模型预测方程为：Yp = P + GΔU
2.2 滚动优化
参考信号Yr = [ yr (k + 6) yr (k + 7)]T
+
u3λLeabharlann 2+u4λ 3 )
+
usλ
4
= 0.5517 + 0.1791λ + 0.0003λ 2 − 0.4858λ3 + 0.2554λ 4
反馈滤波 F (λ) = 1−α 1 − αλ
Matlab 仿真中参考信号取幅值为 1 的阶跃信号，在 t=10 时刻加入干扰，干
扰是幅值为-0.5 的阶跃信号，Simulink 仿真图如下：
sizes.NumInputs
= 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0=[];
str = [];
ts=[0.2 0]; % sample time
S6=[4.1525 -4.6601 1.5076];
u=0;
G=[1.4680,0;2.1377 1.4680]; dd=inv(G'*G+W)*G';
d=dd(1,:)
function sys=mdlOutputs(t,x,y) global Yr Y0 Du S6 S7 G6 G7 d u for n=3:-1:2 Y0(n)=Y0(n-1); end Y0(1)=y; P6=S6*Y0+G6*Du; P7=S7*Y0+G7*Du; P=[P6;P7];
，
B
=
us
⎡⎢⎣λλ1244
(λ1 (λ2
− 1) ⎤ −1)⎥⎦
最优解U = W −1AT ( AW −1AT )−1 B ,求得
u0 = 0.5517 ， u1 = 0.7308 ， u3 = 0.7311 ， u4 = 0.2453 最优控制器
Q
=
u(λ) r(λ)
=
(1 −
λ )(u0
+
u1λ
内模控制与预测控制
姓名：张慧勇 学号：S082121
1 内模控制
已知对象的标称模型为
Pm (s)
=
10s + s2 + 5s
20 + 10
e−s
若采样周期Ts = 0.2 ，相应的离散模型为
Pm (z)
=
1.468z − 0.9789 z2 −1.123z + 0.3679
z −5
对象的纯时滞为 5，取 λ = z−1 ，则离散模型为
取拍数
k
=
3 时，控制器输出
u(λ)
=
u0
+
u1λ
+
u3λ
2
+
u4λ 3
+
usλ 4 1− λ
稳态值 us = Pm−1(1) = 0.5007
性能指标 J = U TWU ，其中加权矩阵 W 为单位阵；
约束条件 AU = B ，其中
A
=
⎡1 ⎢⎣1
λ1 λ2
λ12 λ22
λ13 λ23
⎤ ⎥ ⎦
若无模型误差时仿真结果如下：
若实际对象模型为
Pm (s)
=
10s + s2 + 5s
20 + 10
e −0.9 s
，，兼顾输出的平稳性和调节时间，反
馈滤波取α = 0.8 比较合适，仿真结果如下：
2 广义预测控制
对象模型
P(s)
=
10s + s2 + 5s
20 + 10
e−s
若采样周期Ts = 0.2 ，对象的纯时滞为 5，相应的离散模型为
switch flag, case 0, [sys,x0,str,ts] = mdlInitializeSizes; case 3, sys = mdlOutputs(t,x,y); case {1,2,4,9} sys = []; % do nothing otherwise error(['Unhandled flag=',num2str(flag)]);
预测型号Yp = ⎡⎣ yp (k + 6) yp (k + 7)⎤⎦T 跟踪误差 E = Yr − Yp
控制量为 ΔU = [Δu(k) Δu(k +1)]T
性能指标 J = ETW1E + ΔU TW2ΔU
其中W1
=
⎡1 ⎢⎣0
0⎤ 1⎥⎦
，
W2
=
⎡ρ
⎢ ⎣
0
0⎤
ρ
⎥ ⎦
求得最优解为 ΔU = (GTW1G + W2 )−1GTW1(Yr − P)
则控制器 Q
=
P −1 m+
f
= 1−1.123λ + 0.3679λ 2 1.468 − 0.9789λ
⋅ 0.5 1 − 0.5λ
反馈滤波
F
(λ
)
=
1−α 1 − αλ
Matlab 仿真中参考信号取幅值为 1 的阶跃信号，在 t=10 时刻加入干扰，干扰是
幅值为-0.5 的阶跃信号，Simulink 仿真图如下：
实际控制中只实行一步： Δu(k) = [1 0]ΔU
2.3 Matlab 仿真
仿真中参考信号取幅值为 1 的阶跃信号，在 t=5 时刻加入干扰，干扰是幅值 为-0.5 的阶跃信号，Simulink 仿真图如下：
2.3.1 控制量权重 ρ = 0 时，仿真结果如下：
2.3.2 控制量权重 ρ = 1 时，仿真结果如下：
取 A(λ) = (1− λ) A1(λ) = 1− 2.123λ +1.4909λ 2 − 0.3679λ3 ，对象的差分方程变为： A(λ) y(k + 6) = B(λ)Δu(k)
其中 Δu(k ) = u(k ) − u(k −1) 取预测时域长度 p = 7 ，控制时域长度 M = 2 通过求解 Diophantine 方程 ARj + λ jS j = 1, j = 6, 7 来获取模型预测方程 2.1.1 当 j=6 设 R6 = 1+ r61λ + r62λ 2 + r63λ 3 + r64λ 4 + r65λ 5 ， S6 = s60 + s61λ + s62λ 2 求解 Diophantine 方程 AR6 + λ 6S6 = 1 得：
R6 = 1+ 2.123λ + 3.0162λ 2 + 3.6062λ3 + 3.9401λ 4 + 4.098λ5 S6 = 4.1525 − 4.6601λ +1.5076λ 2
G6 = R6B = 1.4680 + 2.1377λ + 2.3496λ 2 + 2.3413λ3 + 2.2539λ 4 + 2.1589λ5 − 4.0115λ 6 模型预测方程 yp (k + 6) = S6 y(k) + G6Δu(k) 令 p6 (k) = S6 y(k) + (G6 − g1)Δu(k) 模型预测方程 yp (k + 6) = p6 (k) + g1Δu(k) 2.1.2 当 j=7 求解 Diophantine 方程 AR7 + λ 7S7 = 1，得